A Comprehensive Experimental Study on the Dynamic Identification of Historical Three-Arch Masonry Bridges Using Operational Modal Analysis

Abstract

This article presents an extensive experimental investigation of the dynamic characteristics of three-arch historical masonry bridges, using Operational Modal Analysis (OMA). The research thoroughly characterizes the dynamic behavior of four representative masonry bridges from the Apulia Region in Southern Italy through detailed experimental campaigns. These campaigns employed calibrated and optimally implemented accelerometric monitoring systems to acquire high-quality dynamic data under controlled excitation and environmental conditions. The selected bridges include the Santa Teresa Bridge in Bitonto, the Roman Bridge in Bovino, the Roman Bridge in Ascoli Satriano and a moderner road bridge on the Provincial Road SP123 in Troia; they span almost two millennia of construction history. The experimental framework incorporated several non-invasive excitation methods, including controlled vehicle passes, instrumented hammer impacts and ambient vibration tests, strategically chosen for optimal signal quality and heritage preservation. This investigation demonstrates the feasibility of capturing the dynamic behavior of these complex and specific historic structures through customized sensor configurations and various excitation methods. The resulting natural frequencies and mode shapes are accurate, robust, and reliable considering the extended data set used, and have allowed a rigorous seismic assessment. Eventually, this comprehensive data set establishes a fundamental basis for understanding and predicting the seismic response of several three-span masonry bridges to accurately identify their long-term resilience and effective conservation planning of these valuable and vulnerable heritage structures. In conclusion, the data comparison enabled the formulation of a predictive equation for the identification of the first natural frequency of bridges from geometric characteristics.

1. Introduction

Historical masonry bridges are considered significant cultural heritage and an integral component of the complex European infrastructural network. These bridges are a testament to centuries of engineering expertise, architectural design, and cultural significance. Within this expansive context, Italy, in particular, distinguishes itself with an extraordinary and unparalleled legacy, boasting an impressive approximate total of 10,000 masonry arch bridges integrated into its extensive railway system alone, as reported by [1]. These historic structures, many of which have exceeded their original lifespan, continue to play vital roles in transportation networks. They facilitate essential connectivity for both urban and rural communities and support significant economic activities. The deep and multifaceted historical, cultural, and engineering significance inherently attributed to these sites necessitates diligent, continuous, and scientifically informed preservation efforts [2]. This preservation challenge is especially complex in seismically active regions, such as Southern Italy, where the inherent vulnerability of aged masonry structures is substantially amplified by the dynamic forces induced by recurrent earthquake events. In geologically vulnerable regions, conducting a precise and meticulously evaluated assessment of structural vulnerability is not merely beneficial but is absolutely fundamental to guaranteeing public safety [3], ensuring the continuous functionality and resilience of critical infrastructure networks, and safeguarding the long-term structural integrity of these irreplaceable cultural monuments [4,5]. The urgency for a robust assessment is further underscored by the increasing awareness of compounding environmental stressors, including climate change impacts, which can exacerbate existing vulnerabilities through phenomena such as increased scouring, increased frequency of extreme temperature fluctuations, and enhanced material degradation [1,6,7,8].

Conventional assessment methodologies for masonry bridges have historically placed considerable reliance on qualitative visual inspections, frequently entailing subjective condition ratings based on observed cracking, material spalling, or visible deformation [9,10]. These approaches are often empirical, or rule-of-thumb methods rooted in centuries of engineering practice and past experience. While these traditional methods provide initial insights and are undeniably useful for preliminary screenings or identifying obvious signs of distress, they have proven to be inherently inadequate and often insufficient in providing comprehensive, quantitatively detailed, and sufficiently precise information concerning the actual structural performance and remaining load-bearing capacity of these complex bridges [11]. This inadequacy is particularly pronounced when structures are subjected to complex and dynamic loads such as those induced by seismic events, heavy vehicular traffic, or extreme environmental conditions, which can lead to non-linear structural responses. The inherent complexities involved in rigorously analyzing these structures stem from a confluence of several interconnected and challenging factors. These factors include:

• the intricate and often non-linear interactions occurring between the various interdependent structural elements (e.g., the arch barrel, spandrel walls, fill material, piers, and abutments all interact as a system) [12].
• the intrinsically heterogeneous, anisotropic, and non-linear behavior exhibited by masonry materials under various stress states (e.g., tension, compression, shear, and their combinations) [13,14,15].
• the cumulative and often damaging impact of aging processes, material degradation (e.g., mortar washout, stone erosion, freeze–thaw damage) [16,17,18].
• various environmental factors (e.g., differential settlements of foundations, creep of materials, scour around foundations) over extended periods of service [6,19].

Furthermore, a significant challenge for heritage structures is the frequent lack of comprehensive original design documentation and accurate as-built drawings or representations of alterations made over time. The utilization of indirect methodologies is imperative to comprehend their internal construction and structural behavior [20]. The dearth of historical data introduces an additional layer of uncertainty and complexity to the structural analysis and assessment.

In response to these pervasive analytical and diagnostic challenges, Operational Modal Analysis (OMA), has emerged as a highly efficient and robust non-destructive testing methodology [21]. The OMA has been meticulously engineered and optimized for the precise characterization of the dynamic features and inherent structural properties of a diverse array of civil engineering structures [22,23]. These structures encompass a wide range, including bridges, tall buildings, specialized industrial components, and historical monuments [3,12,23,24,25,26,27,28,29,30,31,32,33]. A significant and distinguishing advantage of OMA –in stark contrast to destructive testing methods that invariably affect, or even destroy the integrity of the monitored structure– is its principled reliance on either ambient environmental excitation (e.g., wind loading, microtremors from geological activity, distant traffic-induced vibrations, thermal gradients causing expansion/contraction) or controlled very low-level dynamic loading (e.g., pedestrian traffic, light vehicle passages at controlled speeds) to accurately determine critical modal properties [34]. These properties include the structure’s intrinsic natural frequencies (defined as the resonant frequencies at which the structure naturally exhibits a preference for vibration), the corresponding mode shapes (the spatial distribution of vibration amplitude across the structure at each natural frequency, representing the structure deformation during vibration), and the damping ratios (which quantify the rate of energy dissipation within the structure during vibration, indicating its ability to attenuate oscillations) [35]. This particular methodology is exceptionally well-suited and highly advantageous for application to heritage structures, specifically in scenarios where invasive testing methods are either strictly prohibited by rigorous conservation guidelines, deemed logistically impractical due to access limitations, or simply unfeasible due to paramount preservation concerns [23,36,37,38,39]. Recent and ongoing scientific research consistently highlights the growing value and widespread adoption of OMA for historic structures, demonstrating its effectiveness in various contexts, from individual elements like masonry vaults [13,26] to entire bridge systems [21,25,40,41,42,43,44,45]. However, the effectiveness of OMA strongly depends on the setup strategy of the monitoring system, especially the type, number, and placement of accelerometers [46].

The Apulia Region, situated in the southeastern area of Italy, presents a wealth of architectural heritage, including historic masonry bridges that span from classical Roman antiquity to the 19th century. Within this region, three-arch masonry bridges are particularly conspicuous and merit further study. Furthermore, the northernmost area of the region is located not far from areas of high seismic activity, as evidenced by the various earthquakes felt in this area, such as the San Giuliano di Puglia earthquake (2002), the Durazzo earthquake (2019), and the Gargano Coast earthquake (March 2025). Therefore, the masonry bridges of this region not only represent important cultural and identity landmarks, but often, being located along critical transportation corridors, are also vital to regional connectivity and economic activity.

The present study undertakes a systematic and comprehensive examination of four representative bridges specifically selected from this region for their historical significance, distinct structural typology, varying materials, and accessibility for experimental work. In particular, it concerns the bridges of Santa Teresa Bridge in Bitonto (19th century); the Roman Bridge in Bovino (1st century BC); the Roman Bridge in Ascoli Satriano (1st century AD); the bridge situated on SP123 Provincial Road between Troia and Orsara di Puglia (the beginning of 20th century). The inclusion of bridges from different historical periods facilitates an investigation into the evolution of structural behavior, the effects of long-term aging, material degradation, and cumulative damage on dynamic properties. This comparison is essential for the development of robust and generalizable assessment methodologies and setups applicable to three-arch masonry bridges of any historical period. Indeed, the overarching objective of this research is to establish a comprehensive, adaptable, and scientifically validated experimental framework for the robust dynamic characterization of three-arch masonry bridges. This aim is primarily accomplished through a meticulous and comparative analysis of various monitoring setups, sensor configurations, and excitation techniques. In fact, sensor arrangement critically affects the ability to capture both global and local modes of vibration of the structure. Strategic sensor placement, high-sensitivity instrumentation, and model-guided layout optimization jointly enhance the fidelity of dynamic identification [47]. The investigation systematically explores the performance, efficacy, and inherent limitations of multiple excitation techniques (ambient, controlled vehicle-induced, instrumented hammer impact) and various sensor configurations in accurately and reliably characterizing the modal properties of these complex and historically significant structures.

The geometry of masonry bridges, typically characterized by arches, spandrels, and fill material, poses unique challenges for dynamic testing. The response is often dominated by low-frequency global modes, but local modes associated with spandrel walls, arch barrels, or parapets can also be critical indicators of damage or instability [48]. Several studies have shown that an inadequate sensor layout can obscure the detection of such modes, leading to incomplete or biased modal identification. For example, refs. [49,50] highlighted that the limited accessibility of bridge intrados surfaces requires careful sensor distribution to ensure sensitivity to both vertical and lateral modes. More recent work [21] demonstrated that multi-setup campaigns, involving repositioning a reduced number of accelerometers across successive tests, provided richer modal information while maintaining a practical instrumentation effort. Another key issue concerns the density and configuration of accelerometer networks. While dense arrays may offer detailed mode shape resolution, practical and economic constraints often necessitate reduced setups. In such cases, optimal sensor placement (OSP) strategies can maximize information extraction from a limited number of accelerometers. Studies on masonry arch bridges [51,52] have emphasized that even small variations in sensor positioning significantly affect the identifiability of critical modes, particularly under low-amplitude ambient excitations. Moreover, triaxial accelerometers positioned at arch crowns, quarter spans, and supports have proven effective in capturing both symmetric and antisymmetric modes.

The present study aims to provide invaluable and actionable insights into the development of optimal, non-invasive, and cost-effective monitoring protocols specifically tailored for long-term assessment, effective structural health monitoring, and judicious preservation of these invaluable heritage bridges. This nondestructive approach is expected to ensure the continued serviceability of the site, enhance its safety (being consistent with general heritage conservation principles), and contribute to its cultural legacy for future generations. The comparative analysis was conducted with scientific precision and in accordance with international standards for OMA [23].

In contrast to preceding studies on the topic of OMA, this article presents a comparison of four distinct case studies pertaining to a single category of historical three-arch masonry bridge, whose monitoring was conducted utilizing different test setups. In this study, OMA is employed exclusively as a signal processing technique for both ambient acquisitions and operational ones with a specific forcing, with the objective of evaluating the dynamic characterization of the four case studies. This approach is well-established in extant literature [52,53]. The most significant aspect to emphasize is the comparison, both in terms of the different setups utilized for each bridge and the frequency results obtained, which enabled us to identify common characteristics; in particular, the frequencies of the first four natural modes of vibration and their corresponding mode shapes. The result of this comparison is therefore innovative because it was performed on results obtained from different test setups for the same niche construction typology, which is nevertheless widespread in the Mediterranean basin. This facilitated the identification of shared characteristics for a particular category of historic masonry structure. Consequently, this enabled the development and validation of a predictive formula to analytically obtain the first natural frequency with a low error value.

Furthermore, the data recorded in this comparative campaign will provide useful numerical dataset for the work of future researchers and freelance engineers [5,21,43] who will have to monitor typologically similar structures.

2. Historical and Morphological Background of the Case Studies

A comprehensive comparative study was conducted on four distinct three-arch masonry bridges. Each bridge was selected through a deliberate and systematic process due to its unique and representative characteristics. These characteristics span a wide range of factors, including the bridge’s age, its distinct geometric design, the diverse construction methodologies employed during its original construction, and its prevailing current operational conditions (e.g., traffic load, maintenance history). The objective of this selection strategy was to provide a thorough and representative sample of the masonry bridge typology commonly found in the Apulia Region, thereby enabling a robust comparative assessment in their dynamic identification. The bridges in this collection provide a comprehensive historical overview, spanning nearly two millennia of advancements in masonry bridge construction. This extensive temporal range provides a profoundly complete and insightful perspective for analytical comparison of their structural behavior, allowing for the systematic observation and understanding of masonry bridge material and design adaptations, as well as the long-term effects of environmental exposure, cumulative loading, and various degradation mechanisms over significant historical periods. A dataset of such heterogeneity is imperative for deriving generalizable conclusions regarding the dynamic behavior of masonry heritage infrastructures.

2.1. Historical and Architectural Context

The Santa Teresa Bridge (Figure 1a), located in Bitonto, is a notable and well-preserved example of a 19th-century masonry arch bridge. This distinctive structure, characteristic of the post-Napoleonic infrastructural expansion of Southern Italy, was constructed by the architect Castellucci following the 1846 flood. It is located on a well-maintained road with good access, at the entrance to the town. The bridge has benefited significantly from the implementation of regular maintenance programs, which serve to underscore its enduring importance within the local transportation network. The construction of the bridge primarily utilized local limestone stone and traditional mortar, reflecting the engineering principles that were prevalent during that historical period. The design incorporates semicircular arches with flood openings resting on massive walls equipped with breakwaters and on foundations connected by a strong basement, a structural element that enhances the bridge’s stability and resilience. The bridge is currently subject to active road traffic, supporting the vehicle loads typical of a provincial road. This condition is really important for investigating the bridge’s dynamic response under realistic operating conditions. The bridge’s noteworthy state of preservation, its well-documented historical and technological construction knowledge, as well as its maintenance interventions, and the service loads to which it is subjected, but also the moderate heritage protection status of this particular structure, make it an excellent case study for a comprehensive experimental investigation of this type of structure under operating conditions [42]. Moreover, its location in a semi-peripheral area of the city facilitates the execution of extensive and diversified experimental campaigns [28,54], following consolidated structural approaches, which also include loads with known forces. The corresponding structural dynamic identifications can be validated with Finite Element (FE) numerical models based on consolidated structural methodologies [13,14,15,55,56].

The Roman bridges at Bovino (Figure 1b) and Ascoli Satriano (Figure 1c) provide unequivocal evidence of the enduring legacy and unparalleled expertise of classical Roman engineering. The integrity and functionality of these structures stand as a testament to their architectural and engineering knowledge, despite the execution of maintenance and partial reconstruction interventions on both bridges, most recently on the bridge at Ascoli Satriano in 2023. It is evident that each bridge exhibits unique distinguishing features. However, they also share the fundamental construction principles characteristic of Roman bridge construction. These principles include the use of robust, often semicircular or segmental arches, massive and stable abutments, and resilient local stonework, typically ashlar [56,57,58]. The distinctions reflect site-specific adaptations to local topography and geology (e.g., spanning different riverbed conditions), variations in available building materials (e.g., specific types of local stone), and potentially evolving construction practices inherent to their respective construction periods within the broader Roman era. The bridge at Bovino (Figure 1b), erected in the 1st century BC, exemplifies a noteworthy and archetypal illustration of traditional Roman construction methodologies. The architectural style is distinguished by its imposing ashlar masonry, composed of large stone blocks meticulously cut and fitted, and by robust foundation systems designed for durability. Despite undergoing restoration over time, the structure has maintained its structural integrity to a considerable extent, particularly given its age. It continues to function effectively in the context of modern vehicular traffic, albeit a type of traffic for which it was not originally designed, for this reason is an interesting case study [25].

The Ascoli Satriano bridge (Figure 1c), built approximately a century and a half later, in the 1st century AD, is fundamentally similar to its Bovino counterpart in terms of Roman engineering principles. However, it is evident that the structure exhibits distinct geometric proportions, variations in arch-to-span ratios, and specific structural details. These include probably the type of internal infill material above the arches (which cannot be investigated being protected by the Superintendency of cultural heritage) and typological variations in the construction of the enclosure wall. Furthermore, these features potentially reflect territorial changes in the construction methods employed during that specific period. Compared to the Bovino bridge, this bridge is subject to a greater volume of vehicular traffic, including heavy vehicles such as tractors and agricultural vehicles. A thorough comparison of these two Roman structures, therefore, offers valuable insights into the adaptability, resilience, and subtle evolution of Roman engineering principles in bridge construction.

The SP123 Bridge in Troia (Figure 1d) was constructed in the 20th century, specifically in the mid-20th century, consistent with post-war infrastructure development in Italy. It provides a valuable opportunity for contemporary comparison within the established three-arch masonry bridge typology. Despite its relatively recent construction, this structure exemplifies the continuity of the arch bridge form, incorporating modern construction techniques and materials (e.g., modern cement-based mortar mixes for durability, and potentially more modern waterproofing solutions) while concurrently upholding the fundamental principles and aesthetics of traditional masonry bridge design. Its inclusion in the study offers distinct advantages for a comprehensive experimental methodology comparison due to several factors. Firstly, its excellent accessibility characteristics, it is located on a well-maintained provincial road. Secondly, its construction was relatively uniform and well-documented, often with available design drawings. Finally, its current operational conditions, which readily accommodate a multitude of testing approaches under highly controlled and comparative conditions. This contemporary bridge serves as a crucial benchmark, enabling researchers to distinguish between the dynamic characteristics inherent to all three-arch masonry bridges, regardless of age, and those specifically attributable to aging processes, historical construction practices, or long-term material degradation observed in the older structures. The juxtaposition of these four bridges, which span a vast historical timeline and represent distinct construction epochs, provides an exceptional and comprehensive dataset. This dataset provides understanding of how dynamic behavior and structural performance in masonry arch bridges evolve. A comparative approach is essential for assessing existing masonry bridge infrastructure in Europe and beyond.

2.2. Geometric and Structural Characteristics

The uniform three-arch configuration observed across all four invested bridges provided a robust and uniformly comparable structural framework for a detailed comparative analysis of their dynamic responses. The uniformity that is characteristic of the overall architectural typology permitted a precise examination of the influence of variations in span ratios, the geometric profiles of individual arches, and intricate construction details on the dynamic behavior of each structure [43]. This approach enables the isolation of variables related to design specifics and material properties, rather than the shape, thereby facilitating a more profound understanding of how subtle architectural and construction choices impact structural dynamics. The bridges exhibited a range of critical and variable aspects, encompassing foundation design, the specific construction techniques employed for abutments, and the fundamental arch-to-pier connections. The observed variations are indicative of a multifaceted interplay among historical construction practices, prevalent technologies, and the properties of local materials during the respective building periods. The aforementioned factors, when considered in conjunction with the unique characteristics of the bridge sites, contribute to the observed variations, which exhibit a high degree of diversity.

To ensure precise and comprehensive characterization of the geometries and structural configurations of these diverse structures, photogrammetric surveys and detailed geometric documentation techniques were employed extensively and rigorously [55]. Photogrammetry is a non-contact measurement technique involving the capture of multiple overlapping photographs and subsequent processing to generate precise three-dimensional models. It has proven to be a particularly valuable technique for the documentation of heritage structures. In fact, this method enabled the precise realization of detailed geometric models without necessitating physical contact or the potential damage to ancient masonry that would result from destructive measurements. In conclusion, this technique proved instrumental in accurately mapping arch geometry, identifying effective span-to-rise ratios ranging from 3:1 (flat arch) to 5:1 (round arch), and highlighting aesthetic choices across different periods.

The masonry construction for each bridge utilized stone materials sourced from the local region, thereby demonstrating varying degrees of regularity in the stonework. This ranged from the highly regular, meticulously cut, and precisely fitted ashlar masonry characteristic of the robust Roman bridges to the more diverse, irregular, and less uniform stone sizes and bonding patterns commonly found in later bridges. The latter often utilized rubble masonry or masonry with larger, unshaped stones set in abundant mortar. The type and quality of masonry significantly influence the overall rigidity, strength and durability of the structure. This, in turn, allows for the hypothesis of load distribution mechanisms.

The comprehensive geometric and material characterization establishes the fundamental foundation for subsequent steps, particularly the precise FE modeling. This model can then be meticulously calibrated and validated against experimental dynamic results to ensure its accuracy and reliability. Therefore, an understanding of these differences in construction and material properties is critical for the formulation of accurate numerical models, the prediction of the seismic behavior of these structures, and the devising of appropriate conservation and strengthening interventions, but also for the choice of the set-up and for a conscious and optimized arrangement during the experimental acquisitions.

3. Experimental Configurations: Methodological Design and Advanced Sensor Displacement Strategies

The meticulous design and precise implementation of the experimental configurations for each of the four bridges were carefully tailored, taking into paramount consideration their individual structural characteristics, the stringent and often unique requirements for heritage protection, and existing logistical and accessibility constraints [59]. Consequently, each specific setup represents a carefully considered and optimally balanced approach that sought to achieve a comprehensive dynamic characterization [28]. This approach adhered to practical implementation considerations and, crucially, maintained the paramount need for the preservation of these invaluable historical assets without causing any damage or irreversible alterations [54]. The adaptability of the setup proved to be a crucial factor in the successful execution of the experimental campaign.

For all monitoring campaigns, the sensors uniformly employed were high sensitivity “PCB 393B31” National Instruments (NI) accelerometers. These professional-grade, piezoelectric sensors are characterized by a nominal sensitivity of 1000 mV/g, ensuring the detection of even minute vibrations and low-amplitude ambient responses, which are often characteristic of very stiff or lightly excited structures. They possess a remarkably low broadband resolution of 0.000001 g rms, allowing for very fine and precise measurements, and a robust measurement range of ±0.5 g pk, making them suitable for a wide variety of dynamic events, including potential responses to controlled excitations, without saturation or clipping. Critically, their reliable frequency response spans a broad range of 0.1 ÷ 200 Hz (within a tight ±5% tolerance), making them ideally suited for capturing both low-frequency global modes (e.g., fundamental bending and torsional modes of the entire bridge) and higher-frequency localized vibrations (e.g., local modes of individual arches or spandrel walls) typical of complex bridge structures, as well as providing enough bandwidth for typical traffic-induced vibrations. The data acquisition system utilizes multiple synchronized cDAQ (CompactDAQ) modules from NI, chosen for their modularity, high channel count capabilities, and precise synchronization capabilities, which are essential for accurately resolving mode shapes from multiple sensor locations. These modules were configured with optimized channel settings, enabling real-time monitoring of signal quality, which was crucial for identifying any sensor malfunctions, cable issues, or excessive environmental noise during data collection, allowing for immediate corrective actions. They also facilitated the implementation of advanced triggering strategies, which were instrumental for effectively capturing transient responses during controlled excitations (e.g., vehicle impacts or instrumented hammer blows) with precise timing and consistency.

Ambient vibrations were consistently measured at a high sampling frequency of 1024 Hz, ensuring sufficient resolution for accurately capturing even higher modes without aliasing effects and providing a rich dataset for post-processing. Data collection periods for ambient vibrations varied from 10 to 15 min, systematically adjusted according to the inherent stiffness properties, expected modal frequencies, and ambient excitation levels of each bridge, ensuring adequate data length for robust modal identification using stochastic methods that rely on long time histories and statistical averaging.

For the controlled forced excitation tests –all with a duration of 3 min–, two distinct methodologies were employed depending on the bridge’s operational context, structural characteristics, and heritage preservation requirements. For the bridges in Bitonto (Santa Teresa) and Bovino (Roman Bridge), where vehicular access was feasible and controlled excitation by heavy vehicles was permissible, a 3.5-ton truck was utilized as the primary dynamic excitation source. This method allows for a distributed, quasi-static load that dynamically interacts with the bridge. To ensure repeatable and consistent loading conditions and generate clear impulsive forces that effectively excite the bridge’s natural frequencies, portable speed bumps (measuring 0.15 m in height and 0.5 m in width), were strategically positioned on the bridge deck at pre-determined locations (e.g., mid-span, quarter-span). The truck traversed these bumps at controlled, low speeds, generating repeatable impulsive forces that efficiently excited the structural modes without causing undue stress or damage to the historical structures. Indeed, for the forced tests conducted on the bridges in Ascoli Satriano (Roman Bridge) and Troia (SP123 Bridge), where vehicular traffic control was either more demanding, the structures were more sensitive to heavy loads, and the objective was to provide a controlled localized impulse, an instrumented hammer was chosen. Specifically, a “PCB-086D50” type impact hammer of NI with an Integrated Circuit Piezoelectric (ICB) sensor for force measurement was utilized. This allowed for precise control over the applied impulse force (magnitude and duration) and direct measurement of the input force, which is crucial for frequency response function-based modal analysis requiring both input and output measurements.

It is important to underline that each type of recorded test (ambiental or forced excitation tests) was repeated three times for each bridge.

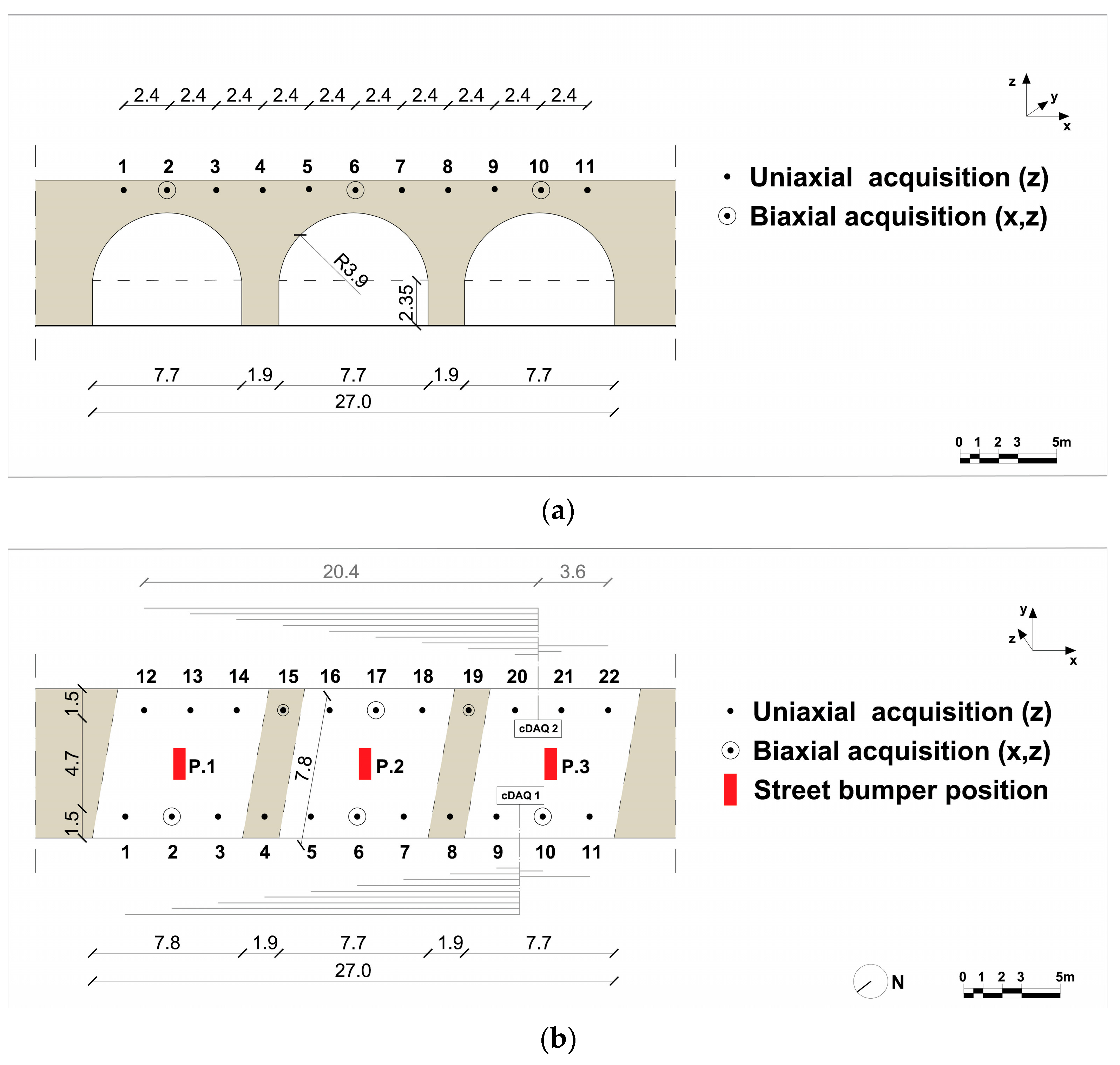
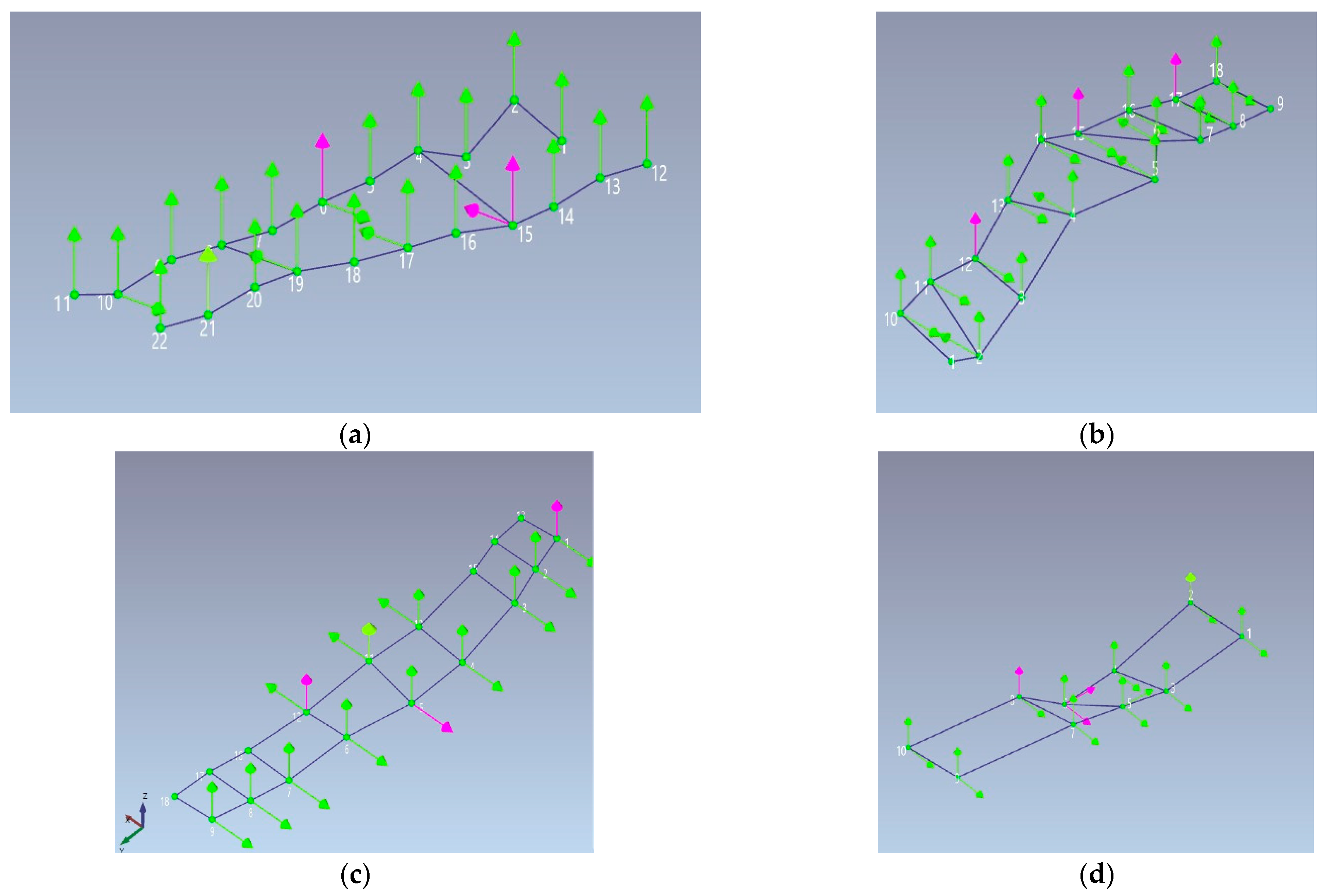
The Santa Teresa Bridge, owing to its relatively favorable accessibility conditions and its moderate heritage protection status, was subjected to the most extensive and densely instrumented monitoring arrangement among the four structures. A total of 28 high-sensitivity piezoelectric accelerometers were strategically installed across twenty-two distinct measurement positions as shown by Figure 2, ensuring comprehensive spatial coverage of the bridge deck, arches, and piers [25,42,55]. The sensor configuration included 22 monoaxial accelerometers primarily oriented vertically, specifically prioritizing the capture of fundamental vertical bending and global translational structural responses, which are often dominant and critical for bridge behavior under gravity and seismic loads. Six additional accelerometers were placed and oriented in a strategic manner to effectively characterize horizontal (transverse and longitudinal) responses. This provided crucial insights into lateral and torsional modes, which are particularly relevant for seismic assessment and understanding of the full three-dimensional dynamic behavior. Specifically, the bidirectional positions are observed at measuring points 6 and 17, corresponding to the keystone of the central arch; at points 2 and 10, corresponding to the keystones of the lateral arches; and at points 15 and 19, corresponding to two piers. The highly symmetric distribution of sensors across the bridge deck, with 11 measurement positions meticulously positioned on each side of the longitudinal axis, was designed to effectively capture both the global structural behavior and the localized dynamics of the individual arches, spandrel walls, and piers, facilitating the accurate identification of both global and local modes.

Data acquisition for the Santa Teresa Bridge was performed using multiple 4-channel cDAQ synchronized systems (see Figure 2), which were interconnected via Ethernet to a central processing unit for coordinated data logging, real-time visualization of sensor signals, and preliminary quality checks. The data was initially sampled at a high-rate of 1024 Hz, ensuring maximum fidelity and capturing all relevant frequency content up to the Nyquist frequency, and subsequently down sampled to 256 Hz for the analytical phase. This down-sampling optimized computational efficiency without significant loss of modal information for the frequency range of interest (typically below 50 Hz for large civil structures). The comprehensive testing protocol for this bridge encompassed four distinct ambient vibration tests, each ranging from 11 to 15 min in duration, allowing for sufficient data length for robust stochastic modal identification. These were further supplemented by six controlled vehicle excitation tests, which involved the precisely controlled passage of a 3.5-ton truck over the strategically positioned speed bumps (the red rectangle shown in Figure 2), generating repeatable dynamic inputs at controlled frequencies and increasing the energy input to excite higher modes more clearly.

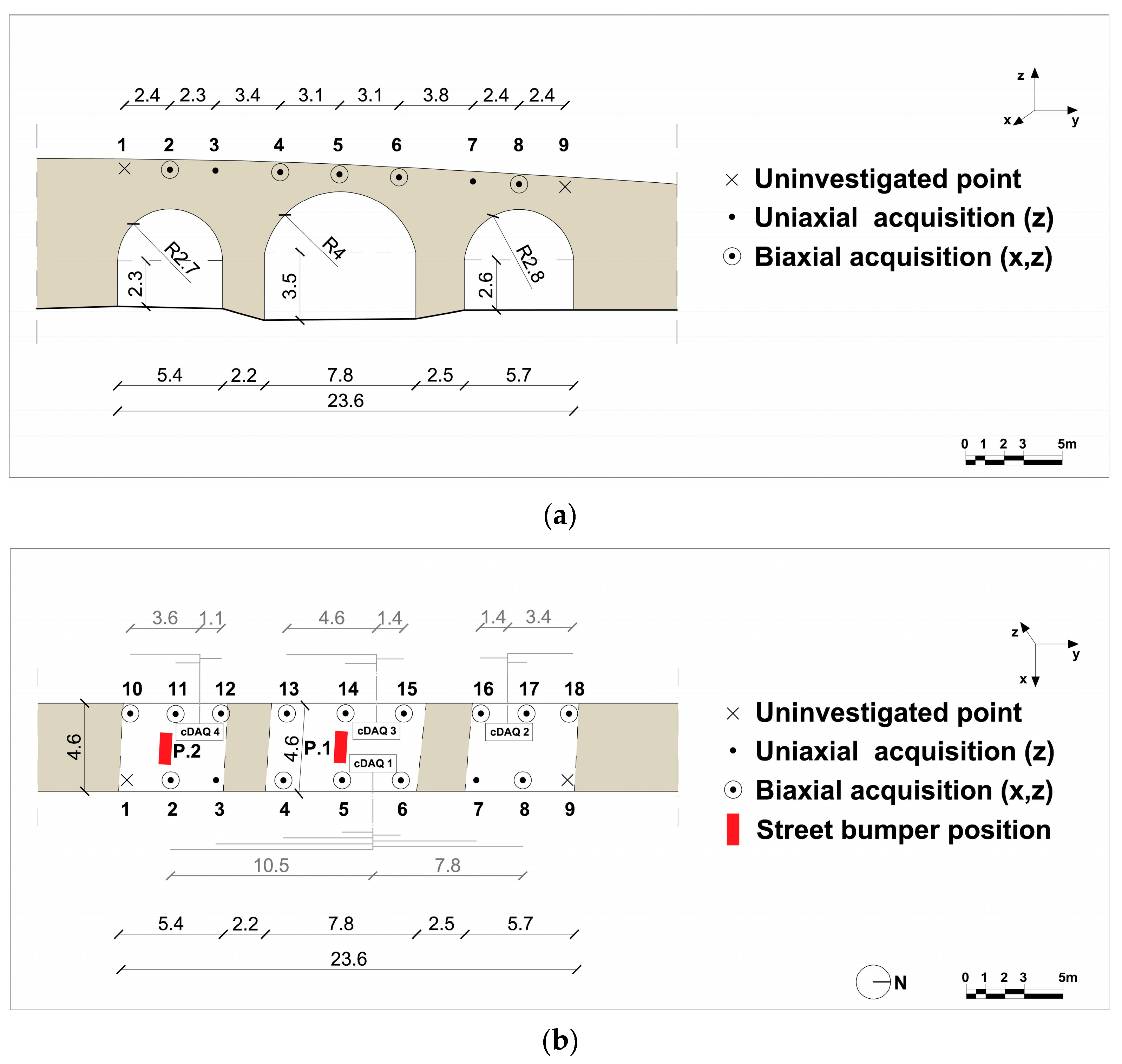
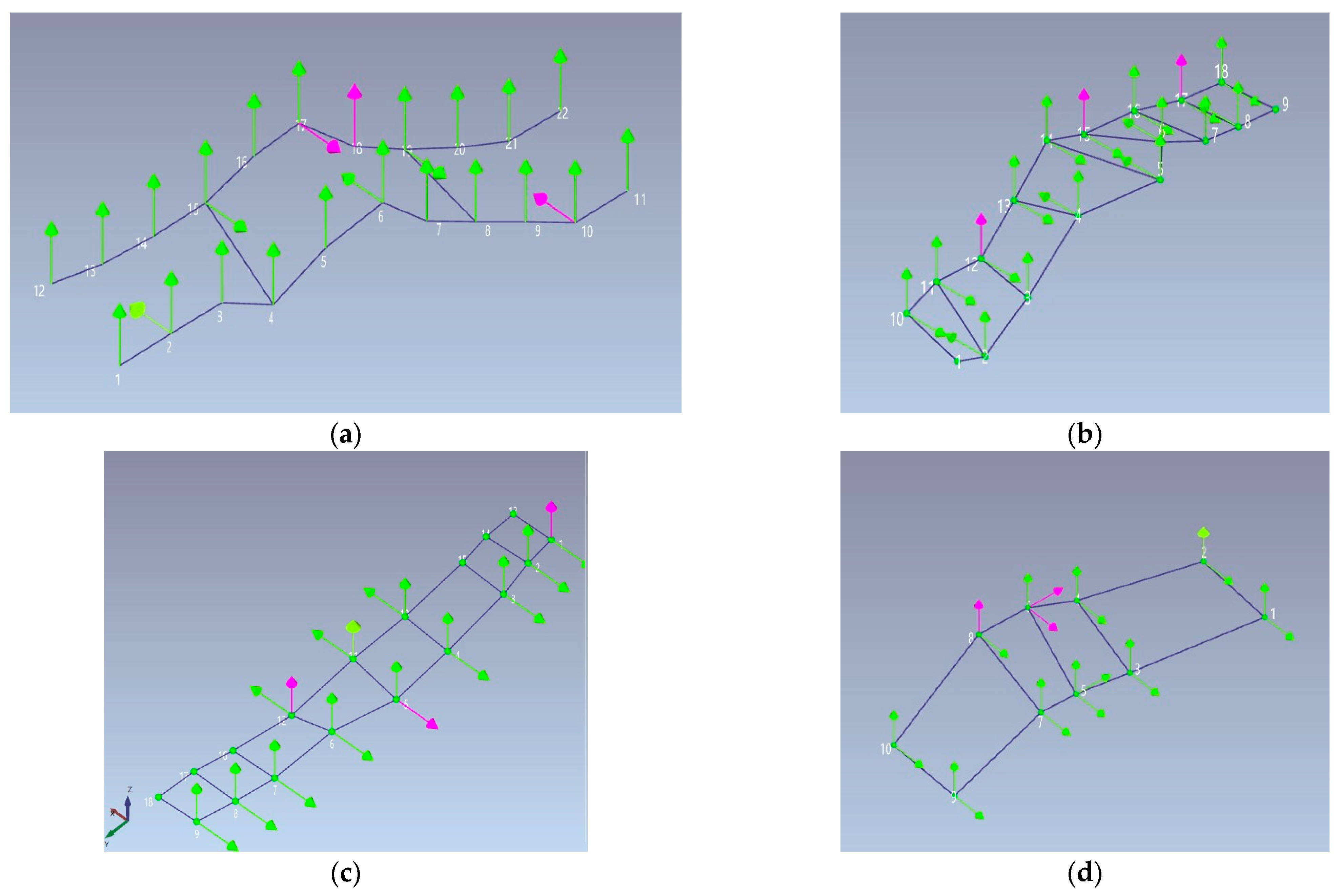
The Roman Bridge in Bovino, being an ancient and highly protected structure, necessitated a monitoring configuration that carefully balanced the imperative for comprehensive dynamic characterization with the inherent and stringent constraints imposed by its ancient construction, and its highly protected heritage status. The monitoring setup involved the deployment of 28 accelerometers across 16 measurement positions. Due to the geometry of the Roman arches –the irregular pier spacing, limited space on the abutment walls, and specific accessibility constraints–, as well as the number of available accelerometers by the research unit, the sensors were distributed asymmetrically along the structure. Nine measurement points were located on the west side and seven on the east side (omitting points 1 and 9, which are positioned at the haunches of the lateral arches on one side of the bridge deck), in order to capture the structure’s complex modal shapes as optimally as possible. In fact, the area of the lateral arches closest to the bridge abutments moves less, and accelerometers were placed in the symmetrical area of the deck at measurement points 10 and 18.

The accelerometers were placed in the vertical direction at all sixteen identified measurement points, while in the direction perpendicular to the deck axis, they were placed at only fourteen of the sixteen points (as shown in Figure 3b, they are missing at points 3 and 7). This final configuration allowed us to capture the complex three-dimensional response characteristics, which are particularly useful for understanding the bridge’s behavior under lateral loads and for distinguishing coupled mode shapes.

The sensor placement strategy for the Bovino Bridge critically required continuous archeological oversight and strict adherence to conservation protocols established by the local heritage authorities [60]. To avoid alterations or permanent damage to the ancient wall structure, only a temporary and completely reversible mounting system was used to fix the accelerometers, namely an adhesive that leaves no residue after removal. There is an absolute ban on drilling or other invasive actions to preserve historical integrity. The testing protocol for this bridge was extended to include ten ambient vibration tests, each of 10 min duration, ensuring a robust dataset for baseline characterization. Furthermore, 20 controlled vehicle excitation tests were conducted, meticulously distributed across two strategic positions on the bridge deck (red rectangle in Figure 3b) to ensure adequate and comprehensive excitation of all anticipated structural modes, despite the asymmetric geometry of the bridge. This dual-position vehicle testing approach was specifically developed for the Bovino Bridge to effectively account for its unequal arch-spans and varying stiffness along its length, maximizing the probability of exciting all significant modes and providing diverse excitation patterns.

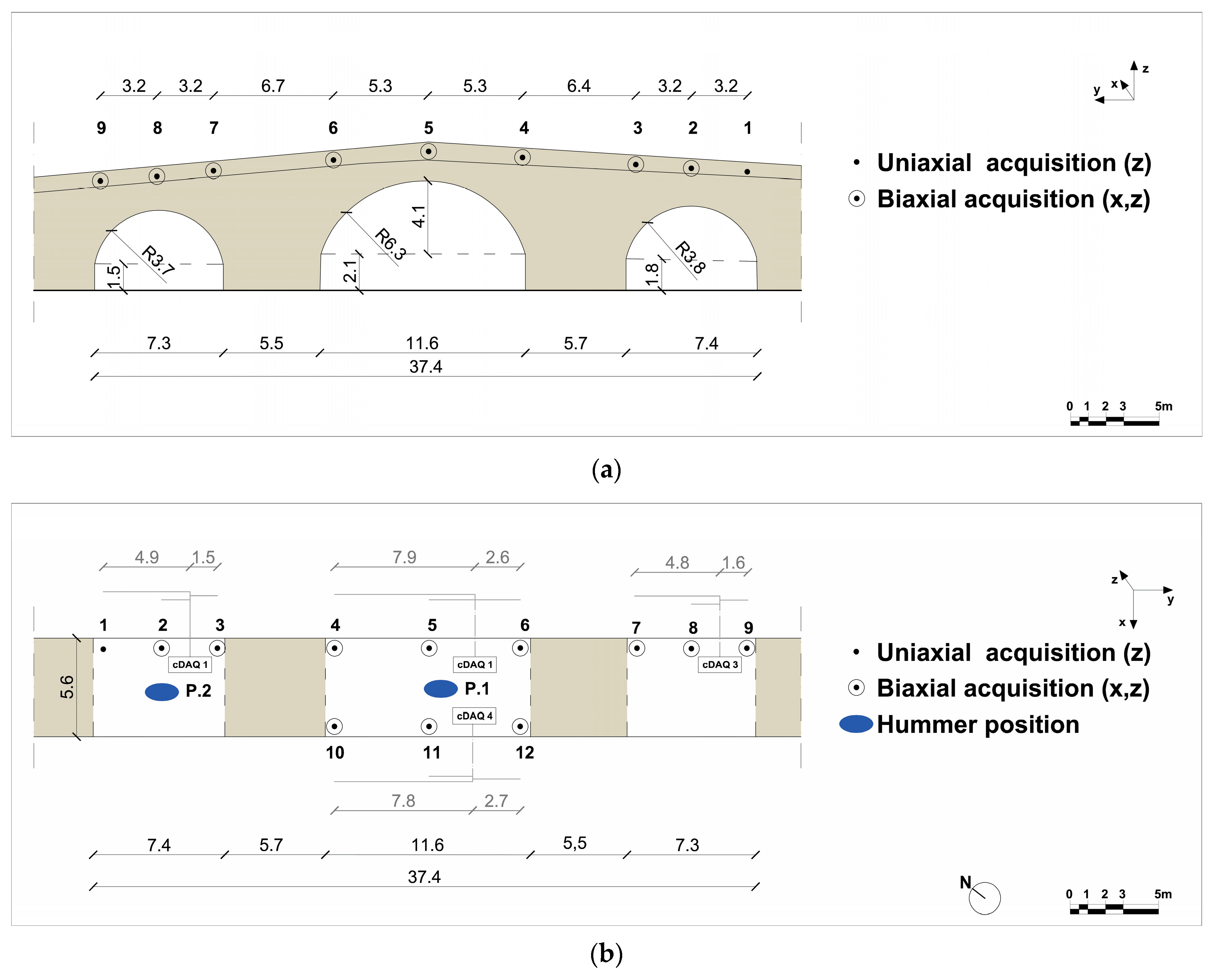
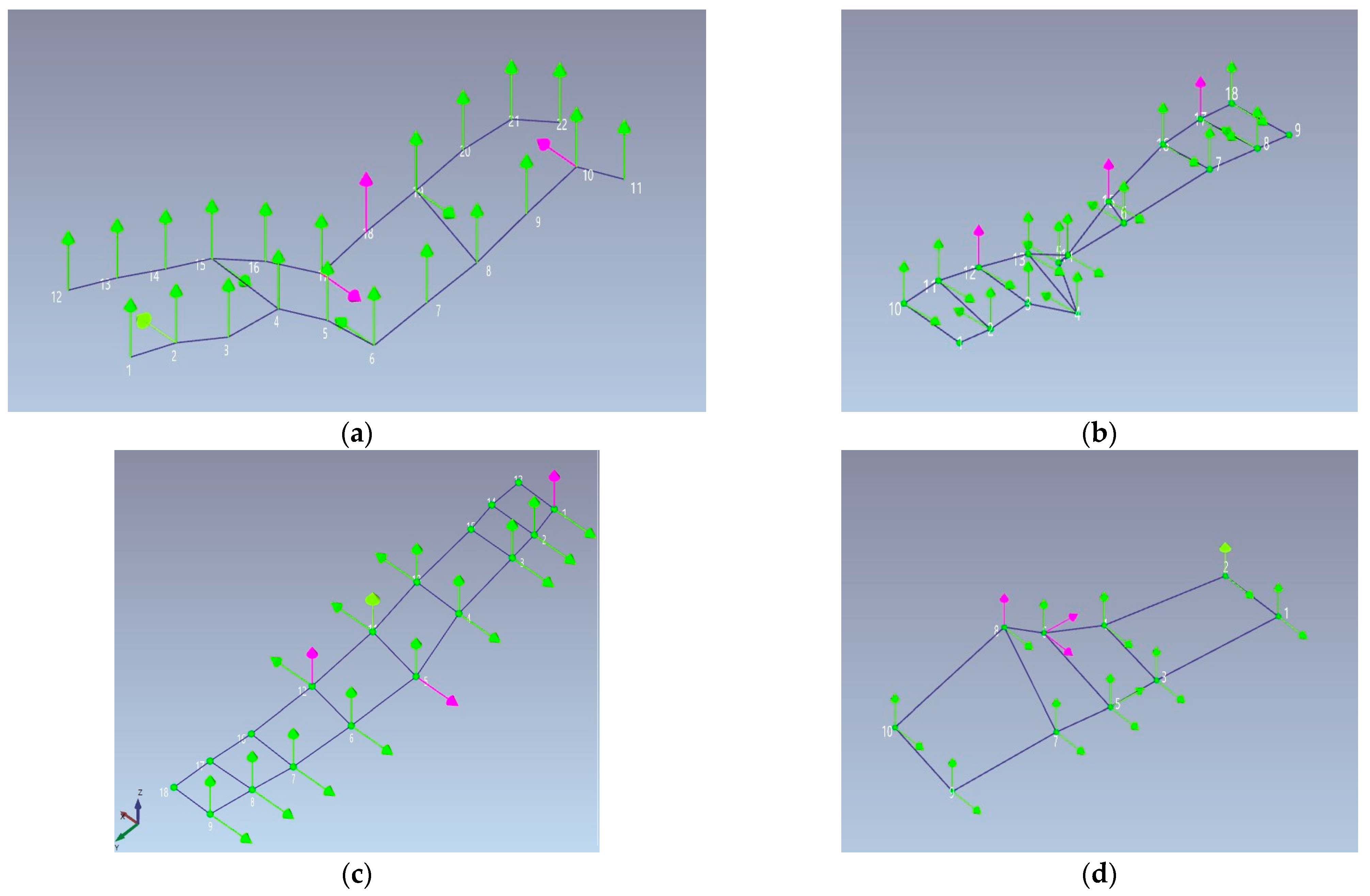
In the case of the Roman Bridge in Ascoli Satriano—a site with even more restrictive heritage constraints and with difficult access due to its location—, the monitoring configuration was carefully streamlined to N. 12 measurement points, equipped with a total of 23 accelerometers (see Figure 4). This configuration represented the minimum instrumentation density deemed capable of reliably capturing the fundamental and dominant modes while simultaneously minimizing intervention and environmental impact. It should be noted that minimum instrumentation density refers to the distribution of accelerometers rather than the number used; as can be seen in Figure 4b, only one side of the bridge deck was instrumented on the two lateral arches (accelerometers were therefore placed only at measurement points 1, 2, 3, 7, 8 and 9). With the notable exception of measurement point 1, which was monoaxial (Z-axis direction), all other equipped positions featured biaxial monitoring in both the vertical (X-axis) and transversal (Z-axis) directions. This maximized data captures per sensor location, providing more comprehensive information with fewer physical installations. So, the monitoring devices were strategically placed in specific locations, such as the keystones of the vaults and the haunches of the arches. Areas of historical interest, decorative elements, and visibly fragile sections of ancient masonry were deliberately avoided, thus prioritizing conservation above all else.

The reduced spatial resolution and the necessary compromise for the preservation of the historical heritage of the Ascoli Satriano Bridge were effectively compensated through several methodological adjustments, including extending the measurement duration for the environmental vibration tests (up to 15 min per test) and increasing the sensitivity of the equipment, ensuring that even low-amplitude responses arising from minimal environmental excitations were adequately captured and distinguishable from background noise. Excitation for this bridge was strictly limited to instrumented hammer tests, as vehicular traffic was unsuitable or not permitted for controlled testing due to its location and minimal deck geometry. This involved two sets of controlled impact tests using the aforementioned calibrated instrumented hammer, applying impulses at multiple positions along the bridge deck indicated by blue ovals in Figure 4b. The impact locations were meticulously selected to ensure optimal modal excitation while strictly adhering to heritage preservation constraints, avoiding direct impacts on ancient stone surfaces where possible, and using softer hammer tips (rubber) to minimize localized damage. The testing protocol included six ambient vibration tests, each lasting 15 min. This represented the longest duration among all bridges investigated. This extensive duration was specifically adopted to compensate for the minimal controlled excitation and to ensure the capture of low-amplitude ambient responses with sufficient signal quality for robust and reliable modal identification using stochastic methods.

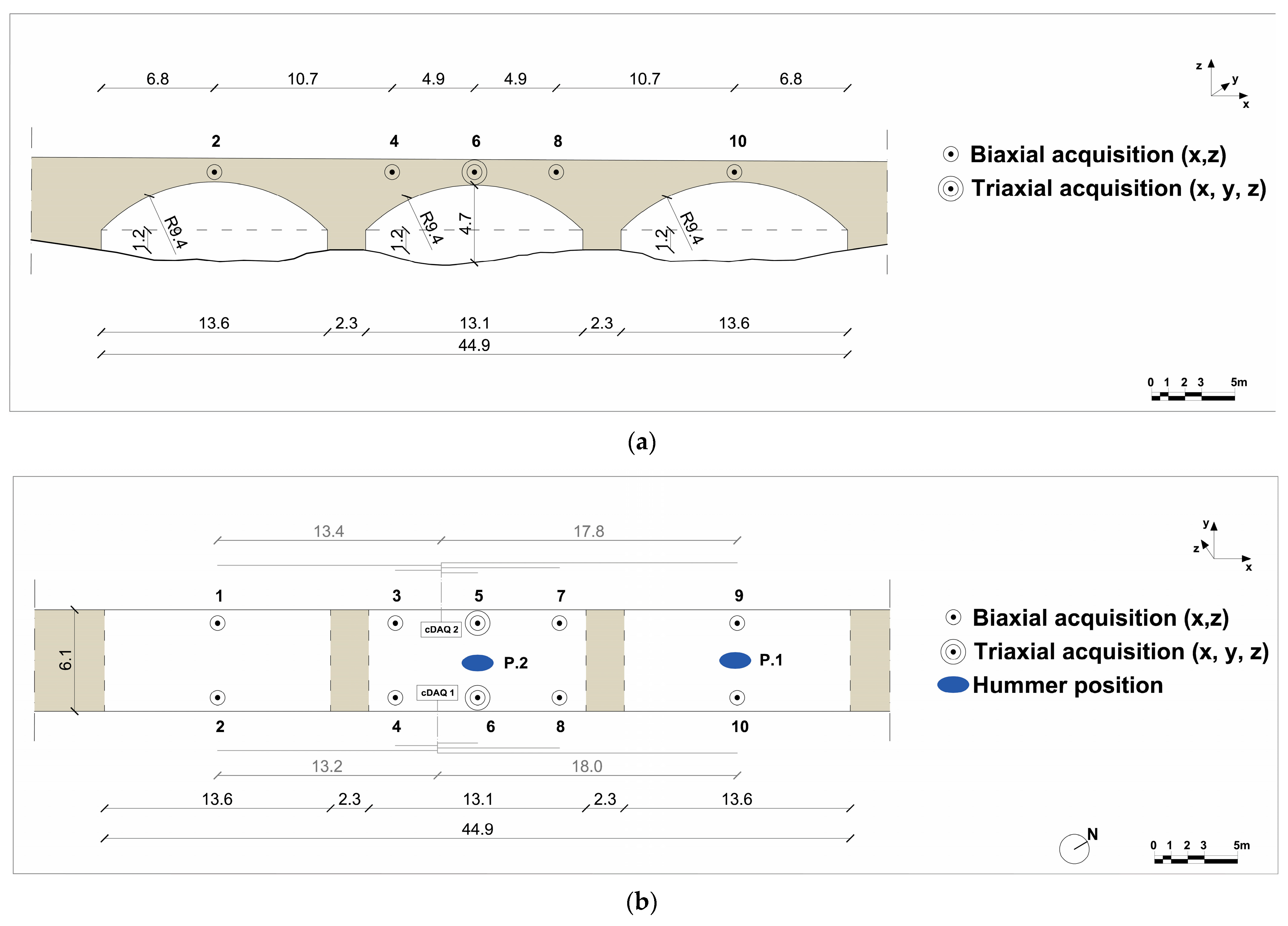
The SP123 Bridge in Troia is a relatively modern structure, built in the 20th century with contemporary materials and construction techniques. It presented a valuable opportunity to conduct a comprehensive methodology comparison under highly controlled and less restrictive conditions. This allowed for a broader exploration of excitation and sensor placement options and served as a crucial benchmark for understanding the dynamic behavior of a contemporary masonry infrastructure built with similar typological geometry.

The monitoring setup for the bridge consisted of N. 22 accelerometers (see Figure 5), which were positioned at 10 measurement points that were selected based on strategic considerations. The strategic placement of the accelerometers was informed by the insights gained from prior monitoring, with a particular emphasis on the central arch and the keystones of the bridge. In accordance with these two indications, the keystones of the central arch on both sides of the deck (points 5 and 6) were subjected to triaxial monitoring (X, Y, and Z axis directions), while the keystones of the lateral arches (points 1, 2, 9, and 10) were subjected to biaxial monitoring (X and Z axis directions). Similarly, the points 3, 4, 7, and 8, corresponding to the haunches of a central arch were also subjected to biaxial monitoring. Therefore, this configuration facilitates the comprehension of three-dimensional dynamic response, furnishes the most detailed modal information, and enables the differentiation of complex coupled modes. The deployment of the sensor distribution was meticulously optimized to suit the precise geometry of the bridge, which has a total length of 50.65 m, and its complex span arrangement. This necessitated careful consideration of both local and global modes identification requirements to avoid aliasing or missing critical modes due to insufficient spatial resolution.

The execution of experimental campaigns across all bridges required careful and extensive consideration of cable management and the critical maintenance of signal transmission quality. This was particularly significant given the substantial distances frequently present between sensor locations and the centralized data acquisition systems on these substantial bridge structures. To address this, three distinct categories of cable configurations were systematically employed across all bridges, using a standardized nomenclature to ensure consistency and comparability across the different sites: direct coaxial connections for sensors positioned in close proximity to acquisition modules (typically within 3 m); 20 m cable extensions for intermediate distances; and 20 m cable extensions for reaching the most distant sensor positions or for connecting multiple remote sensor clusters to a central DAQ unit. The precise characteristics of each monitoring system, including the total number of sensors deployed, the number of distinct measurement positions instrumented, and the distribution of various cable types, are summarized in

Table 1. Summary table of the different monitoring systems for the four bridges.

Bridge	Total Sensors	Measurement Points	Direct Connections	20 m Cable Extensions	60 m Cable Extensions	Test Methods	Sampling [Hz]
Bitonto	28	22	16	8	4	Ambient + Vehicle	1024
Bovino	28	16	25	2	1	Ambient + Vehicle	1024
Ascoli Satriano	23	12	15	4	4	Ambient + Hammer	1024
Troia	22	10	18	2	2	Ambient + Vehicle + Hammer	1024

. This table illustrates the adaptability of the setups to specific bridge geometries and access limitations.

The length of the cables (shown for the four bridges in Figure 2b, Figure 3b, Figure 4b and Figure 5b) had a significant impact on signal quality due to inherent electrical resistance, capacitance, and increased susceptibility to electromagnetic interference (EMI). These factors necessitated compensatory measures, such as enhanced electromagnetic shielding and precise impedance matching for more extended runs, to prevent signal attenuation, phase distortion, and external noise interference that could compromise the integrity of low-amplitude vibration signals [28]. It is essential to note that 60-m extensions, while indispensable for achieving comprehensive spatial coverage of larger structures and minimizing the number of distributed DAQ units, could have introduced substantial signal attenuation, increased noise pickup from ambient electromagnetic fields, and potential synchronization issues over very long runs if not carefully managed. These potential issues were effectively mitigated through the use of high-quality, low-noise coaxial cables specifically designed for accelerometer signals, rigorous attention to proper cable routing to minimize proximity to power lines or other noise sources, and the implementation of robust grounding techniques to prevent ground loops and common-mode noise. This standardized and meticulously documented approach to sensor installation and cable management facilitated consistent signal quality assessment for all investigated bridges and established reproducible and reliable installation strategies for future historic bridge monitoring campaigns. As a result, there was a significant improvement in scientific rigor, data quality, and the replicability of research outcomes. This could be an important factor for future long-term monitoring.

Finally, it is concluded that the selection of monitoring scenarios was based on the morphological and usage characteristics of each bridge. The implementation of these scenarios involved the use of specific setups, each comprising a particular number of accelerometers. These were generally positioned in accordance with the arch keystones or the arch haunches, as deemed appropriate. It is evident that, even though all four bridges belonged to the same structural typology of masonry three-arch bridges, each of them exhibited distinct geometric characteristics. On the Santa Teresa bridge, 28 sensors were utilized, which were positioned at 22 measurement points on the two sides of the deck (keystones and the haunches). Furthermore, on the Bovino bridge, 28 sensors were utilized, positioned at 16 measurement locations, exhibiting a less symmetrical distribution to align with the geometric characteristics of the bridge. The arrangement of sensors was conducted meticulously, with a total of nine sensors positioned on the western side of the deck, in conjunction with seven sensors on the eastern side. A total of 23 sensors were installed on the Roman bridge of Ascoli Satriano in 12 measurement points, with a higher density on the north-eastern face of the bridge deck. This choice was determined by the necessity to adhere to the bridge’s conservation constraints. At the end, a total of 22 sensors were installed on the SP123 bridge in Troia in 10 measurement points. This configuration was meticulously designed to preserve symmetry between the two faces of the bridge, while concurrently reducing the number of sensors on the lateral arches, particularly in the area corresponding to the arch haunches. As was the case with the Santa Teresa bridge, the elevated symmetry and geometric uniformity of the bridge in all directions guaranteed a more efficient arrangement of the measuring instruments. The Troia bridge is distinguished by its notably extensive central span length of 13 m, a measurement that surpasses the lengths observed in other bridges under consideration. A notable attribute of the Troia bridge is the uniformity of its three vaults, a condition that is only observed in the Santa Teresa bridge, where the central span length measures 7.72 m.

4. Experimental Results and Discussion

The comprehensive experimental campaigns conducted on the four different three-arch masonry bridges successfully identified their fundamental and higher-order dynamic characteristics with notable precision and confidence, thereby demonstrating the efficacy and adaptability of applying different setup approaches tailored to specific structural and heritage contexts. Furthermore, the detailed analysis of the results revealed significant and discernible relationships between a bridge’s intrinsic structural properties and some of its modal parameters (natural frequencies and characteristic mode shapes). These relationships are essential for understanding the dynamic behavior, the health and performance of historical structures. The identification of these critical modal parameters was achieved through the rigorous application of both frequency-domain and time-domain techniques, ensuring cross-validation and robustness of results, a standard practice in advanced modal analysis. Specifically, the well-established Curve Fitting in Frequency Domain (CFDD) method, which analyzes spectral densities and power spectral densities to identify peaks corresponding to modes, and the advanced Stochastic Subspace Identification with eXtended Un-weighted Principal Component (SSI-UPCX) algorithm, a powerful and robust time-domain technique particularly suitable for output-only modal analysis from ambient vibrations, were rigorously employed for the comprehensive processing and analysis of the acquired dynamic data. The identification process itself comprised two integral and interdependent components: an automated stabilization diagram analysis, and a meticulous manual verification process, involving also assessment of Modal Assurance Criterion (MAC) values, to ensure the utmost reliability, accuracy, and physical plausibility of the extracted modal parameters.

Table 2. Summary comparison tables for the natural frequencies identified for each “Three-Arch Masonry” bridge.

Bridge	Mode	Min. Frequency Mode [Hz]	Max. Frequency Mode [Hz]	Average Frequency Mode [Hz]	Standard Deviation σ	Principal Mode Shape	Interested Arches
Santa Teresa Bridge in Bitonto	1	9.00	9.50	9.20	0.26	Translational	All
	2	11.90	13.50	12.64	0.63	Vertical	All
	3	14.20	14.90	14.60	0.32	Vertical	Central
	4	15.70	17.70	16.50	0.53	Vertical	All
Roman Bridge of Bovino	1	11.04	11.40	11.24.	0.12	Translational	All
	2	12.22	12.78	12.46	0.17	Translational	Central
	3	13.29	14.20	13.71	0.39	Vertical-Translational	All
	4	14.15	14.75	14.36	0.34	Translational	Central
Roman Bridge of Ascoli Satriano	1	4.15	4.69	4.39	0.18	Translational	All
	2	5.28	5.41	5.35	0.07	Vertical	All
	3	6.19	6.37	6.29	0.07	Vertical	All
	4	6.73	7.11	6.89	0.12	Vertical	All
SP123 Bridge in Troia	1	8.19	8.45	8.34	0.11	Translational	All
	2	8.40	8.79	8.64	0.15	Vertical	All
	3	9.30	9.50	9.40	0.14	Vertical	Central
	4	9.53	9.53	9.53	0.00	Vertical	All

and Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 report all the average results obtained for each mode in the various experimental campaigns carried out for the four bridges.

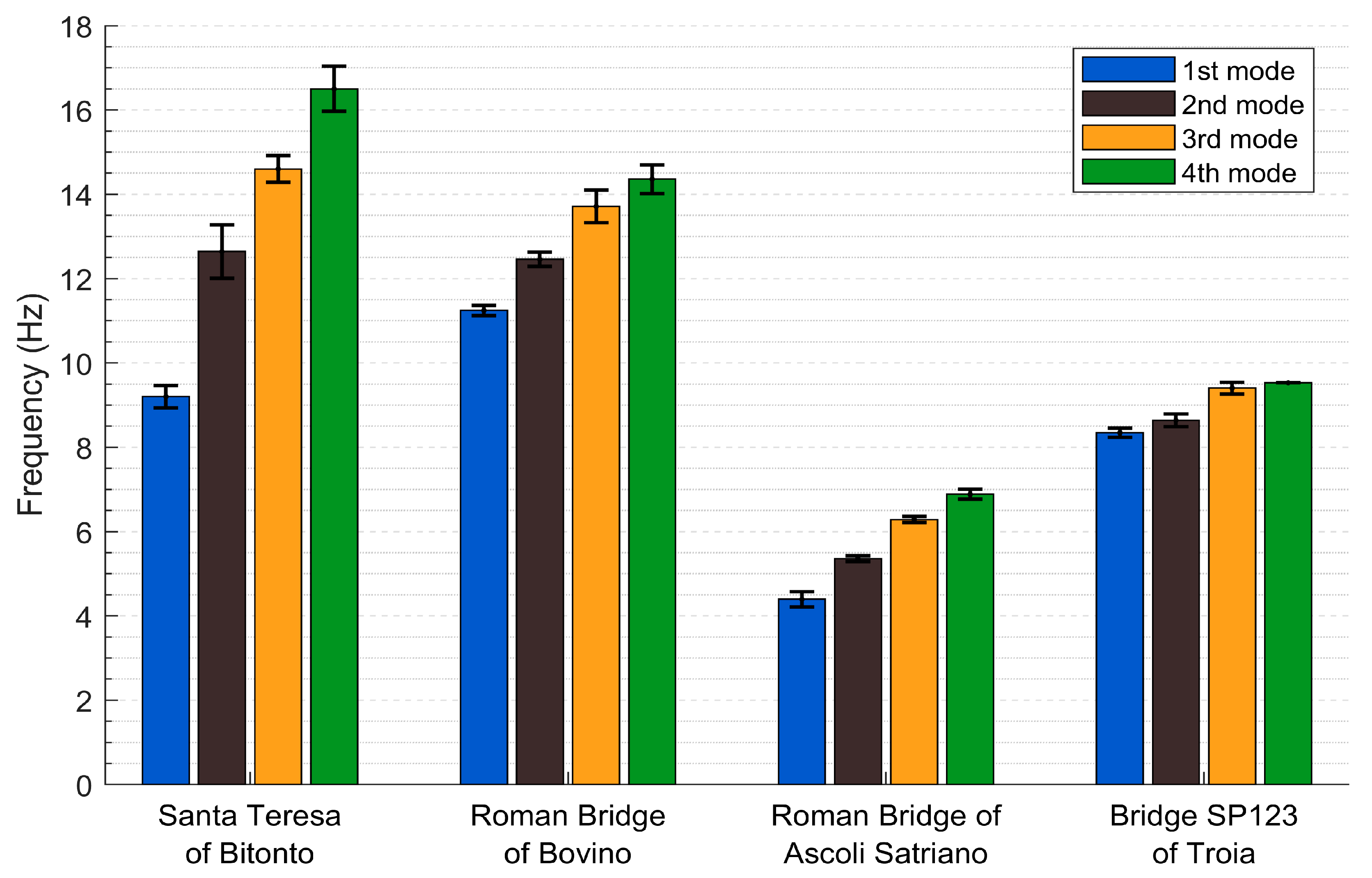
The Santa Teresa Bridge, a 19th-century construction with robust maintenance and relatively uniform materials, exhibited the broadest frequency range among the structures investigated. This broader range, indicative of a stiffer and more responsive structure capable of vibrating at higher frequencies, led to the identification of a total of five distinct and well-defined modes within the frequency range of 9.0 Hz to 19.7 Hz. The presence of both global and local modes, especially at higher frequencies, underscores the complex vibrational behavior of multi-span arch bridges and the importance of dense sensor arrays to capture these nuances, which are critical for accurate structural assessment.

The Roman Bridge in Bovino is an ancient and structurally complex structure with inherent geometric irregularities due to its unequal arch spans, the different orientation of piers, and construction age. It displayed intermediate dynamic characteristics compared to the Santa Teresa and Ascoli Satriano bridges. Five distinct modes were successfully identified within the 11.0 Hz to 17.5 Hz range (but the first four have a more stable average), suggesting a relatively stiff structure, indicative of squat Roman construction. The observed modal behavior for this bridge included a primary global translational response at 11.2 Hz, similar to the Santa Teresa Bridge’s fundamental mode but at a higher frequency, which is attributed to its more massive construction and smaller overall dimensions relative to its stiffness. Subsequent identified modes included central arch vertical modes at 12.5 Hz and 14.4 Hz, indicative of localized arch vibrations primarily affecting the main span. Additionally, a mixed vertical-translational behavior was evident at 13.7 Hz, highlighting the coupled nature of its dynamic response due to asymmetric geometry of piers in respect of the structure and potentially different stiffness contributions from its varied arch spans, a common characteristic in older, less symmetrically designed structures.

In contrast, the Roman Bridge in Ascoli Satriano presented the lowest natural frequencies among all the bridges studied, with four primary modes identified between 4.2 Hz and 7.1 Hz. These significantly lower frequencies are highly characteristic of a more flexible structure, resulting from geometry with humpback bridge (see Figure 4a), and differing foundational conditions (softer soil). The identified modes for this structure included a distinct global translational mode at 4.4 Hz, representing its fundamental lateral motion and indicating a notable flexibility in this direction, which is particularly concerning for seismic vulnerability. This was followed by successive vertical bending behaviors observed at 5.4 Hz, 6.3 Hz, and 6.9 Hz, suggesting multiple orders of vertical arch vibration and potentially localized damage. Thus, the significantly lower frequencies observed for this bridge, relative to Bovino, could be attributed to its geometry, its potentially longer spans, less robust construction in certain sections, and material deterioration over its extended service life.

The Troia Bridge, the youngest of the four bridges, exhibits the first five natural frequencies in a range between 8.3 Hz and 10.2 Hz. These frequencies are within the average range, and the first frequency is comparable to the first ones identified for the Bitonto Bridge, which is 100 years older and also squatter. These lower values indicate a more flexible structure and are likely due to a slight differential settlement of the piers caused by detected foundation problems. The modes identified for this structure include a distinct global translational mode at 8.3 Hz, which represents its principal displacement in the direction orthogonal to the deck axis and indicates its notable flexibility along this direction. This was followed by subsequent global sussultory behavior at 8.6 Hz and 9.5 Hz (on all arches), and local ones at 9.4 Hz, which identify a localized damage in progress supported by a visual inspection. It revealed the loss of linearity of the brick courses and the mortar layers at the intrados, longitudinal cracks of a few millimeters across half the arch span, pulverization of the masonry in some places with a depth greater than 3 cm, efflorescence in a limited area, restoration and subsequent interventions in the central band of the intrados and finally a portion of masonry missing on the lateral edge.

As illustrated in Figure 6, the mean natural frequency values for the first four vibration modes of the monitored bridges’ structures are presented. The standard deviations for each measurement series are also reported. As evidenced by the data, the variability of the acquired and processed data is consistently minimal, with a maximum range of 1 Hz observed for the Santa Teresa bridge in Bitonto. This corroborates the validity of the acquired data and the frequencies obtained, which exhibit variability that can be considered negligible.

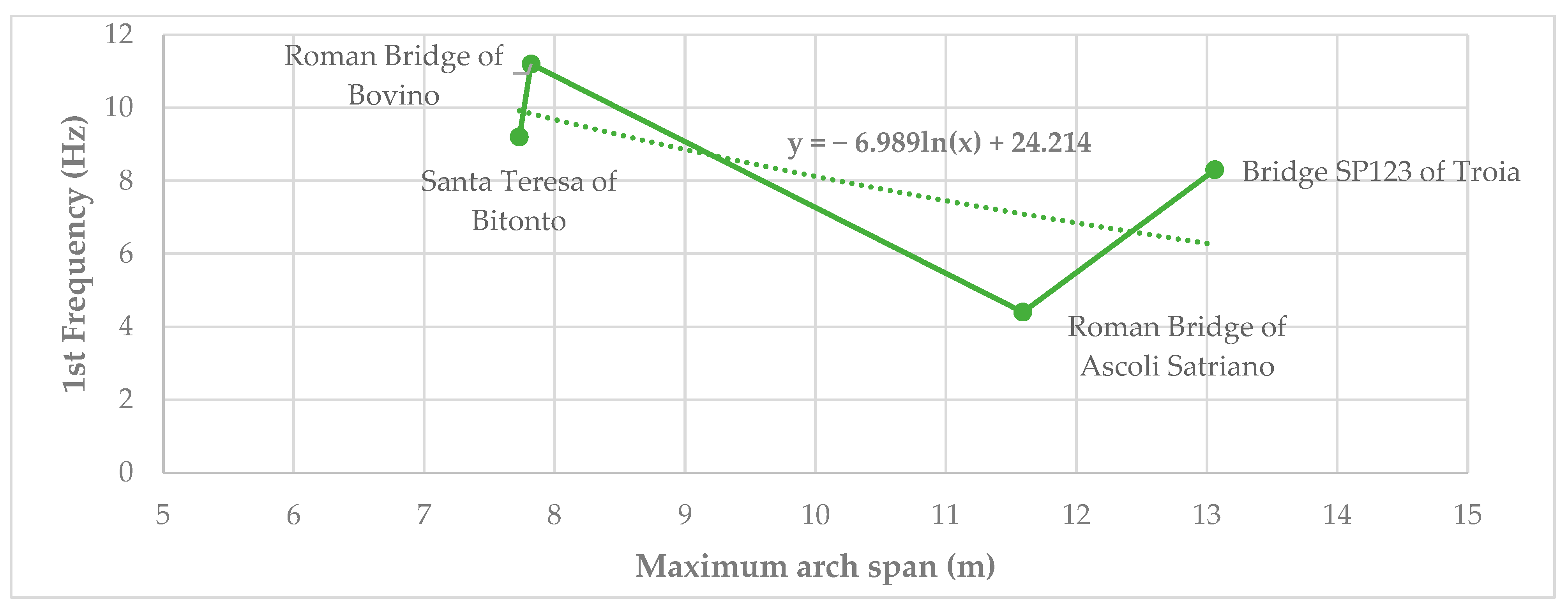
Figure 11 shows the variations in the first natural frequencies of the only three-arch bridges monitored in this study. In particular, the figure graphically correlates the first modes of the four three-arch bridges as a function of their maximum span size. Utilizing statistical regression analysis, a logarithmic relationship (1) was established between the first frequency and the maximum span for the four three-arch bridges investigated.

y = −6.989 ln(x) + 24.214

(1)

where x denotes the maximum span of the arches (m) and y represents the first natural frequency (Hz). The relationship presented in Formula (1) was derived from the experimentally determined natural frequencies of the four distinct three-span masonry bridges with varying lengths.

The validity of the proposed Formula (1) was subsequently confirmed by comparing its predictions with experimental measurements of the stone bridges reported in [48] having a maximum span between 5 and 15.50 m.

Specifically, the predicted values were compared to the experimental data for several historical bridges:

• For the 19th-century Pehlivanlı Bridge (Turkey), with a maximum span of 15.17 m, the experimental first frequency is 5.28 Hz, while the calculated value from Formula (1) is 5.21 Hz.
• For the Şahruh Bridge (Turkey) built in 1437, with a maximum span of 15.00 m, the experimental first frequency is 4.73 Hz, and the calculated value is 5.29 Hz.
• For the 19th-century Osmanbaba Bridge (Turkey), with a maximum span of 10 m, the experimental first frequency is equal to 8.85 Hz, and the calculated value of 8.12 Hz.
• For the Torul Bridge (Turkey) built in 1890, with a maximum span of 12.00 m, the experimental first frequency of 6.97 Hz, and the calculated value equal to 6.85 Hz.

The close agreement between the frequencies obtained from Formula (1) and those from reference [48], presenting a Percent Relative Error (PRE) equal to 2.58%, confirms the reliability of the proposed formula for bridges with a maximum span ranging from 5.00 to 15.50 m. It should be noted that, for geometric and construction reasons, this range is not too restrictive for the category of historic three-arch masonry bridges. Indeed, the preponderance of extant cases is congruent with these dimensions; also, the range of all the case studies (7.60 ÷ 13.10 m) and the validation cases (10.00 ÷ 15.17 m) coincide with this interval. The range was also validated on two bridges with larger spans (19.49 ÷ 25.20 m), but in those cases the PRE varied in the range of 40 ÷ 55%, specifically the frequency value decreased. It is reasonable to conclude that the PRE remains negligible and within the prescribed limits. This demonstrated that the logarithmic relationship between the first frequency and the maximum arch span can be a valuable tool for validating analytical results, even when the number of spans varies, as supported by comparisons with the experimental cases cited in [48].

The following final considerations are reported below:

• The consistency and reliability of the modal identification process were rigorously validated across a range of excitation methods employed for each bridge, providing high confidence in the results regardless of the excitation source. The controlled excitation of vehicles consistently provided superior signal-to-noise ratios (SNR) across all investigated frequency ranges. This results in clearer stabilization diagrams and more confident modal identification of both fundamental and higher-order modes. This phenomenon is principally attributable to the higher energy input and the controlled, repeatable nature of the excitation, which generates distinct peaks in the frequency response functions.
• Ambient vibration tests, which rely on naturally occurring excitations, have been demonstrated to be a reliable method for identifying fundamental and lower-order modes across all bridges, even in the absence of controlled inputs. This finding underscores the broad applicability, cost-effectiveness, and non-invasiveness of ambient vibration test for preliminary characterization and long-term monitoring of heritage structures. However, the system demonstrated inherent limitations in consistently identifying modes above approximately 15 Hz. These limitations are likely attributable to lower ambient energy content at higher frequencies and increased influence of environmental and sensor noise in that range, resulting in less distinct higher-frequency modes.
• Hammer testing is an effective and practical method for identifying primary modes, particularly in structures with restricted access or stringent heritage constraints. However, its ability to consistently identify higher-order modes across the entire structure is limited due to the transient nature of the excitation and the difficulty in exciting all modes comprehensively with a limited number of impact locations. This characteristic of the test typology renders it more appropriate for localized analysis or the identification of specific, well-defined modes.
• It has been demonstrated through experimental means that the placement of the accelerometers on the central span of the bridge provides more reliable results with regard to the mode shapes than the placement of said accelerometers on the lateral spans.
• The MAC values, a widely accepted measure of consistency between different OMA test setups, consistently exceeded 0.85 across all repeated tests for the identified modes, with a substantial majority of values surpassing 0.90. This exceptionally high consistency unequivocally confirms the excellent reliability, repeatability, and physical validity of the identification process. The identified modes are distinct, well-separated, and consistently observed, reinforcing confidence in the derived modal parameters.

The evaluation of the setup performance, particularly concerning sensor density and placement, revealed that strategic sensor placement, often informed by engineering judgment based on expected mode shapes and areas of maximum deformation, comparable results in terms of mode identification completeness and accuracy to more conventional uniform distribution approaches. This underscores the importance of intelligent experimental design by merely increasing the number of sensors without strategic placement, particularly when dealing with complex or irregularly shaped structures. It is imperative to note that all experimental approaches were meticulously conducted in full compliance with established heritage standards and strict conservation guidelines. This ensured that no damage, irreversible alteration, or adverse visual impact was inflicted on the structures. Concurrently, all predefined research objectives regarding comprehensive dynamic characterization were successfully achieved. This outcome provides substantial evidence for the feasibility, scientific validity, and ethical soundness of conducting comprehensive dynamic assessments on structures that are protected for their significant cultural and historical value. It demonstrates the capacity for modern engineering techniques, such as Structural Health Monitoring (SHM), to be integrated harmoniously and effectively with rigorous conservation ethics.

5. Conclusions

This study has established a scientifically validated and adaptable framework for the dynamic assessment of heritage masonry bridges, demonstrated through the experimental investigation of four three-arch bridges in the Apulia Region, Italy. The results confirm that OMA can reliably deliver precise structural characterization across varying levels of heritage protection, construction eras, and structural complexities—provided that experimental setups are carefully optimized to site-specific constraints, accessibility, and preservation requirements. The identification of fundamental and higher-order modal frequencies spanning a broad range, from a minimum of 4.2 Hz (for the flexible Roman Bridge in Ascoli Satriano) to a maximum of 16.5 Hz (for the stiffer Santa Teresa Bridge), has been shown to be an effective and versatile non-destructive testing technique for evaluating the structural integrity and dynamic behavior of structures. This method has been employed to assess structures that collectively represent over two millennia of continuous construction evolution and engineering history. The OMA enabled the identification of the natural frequency characteristics of the main modes of the four bridges. The comparison of the results highlighted the strict linkage between the recorded frequency values and the morphological and physical properties of the monitored structure.

The Santa Teresa Bridge exhibited the highest frequency values, as it is a relatively recent 19th-century construction that has undergone regular maintenance over the years. The continuous monitoring of material degradation has led to the extension of its lifespan, thereby enhancing its robustness and stiffness.

The Roman bridge of Bovino exhibited values that were near those of the first bridge, with a marginal decline observed in the third and fourth modes of vibration. This reduction can be attributed to the fact that the Bovino bridge is ancient and possesses a more complex and squat structure, as well as more irregular and asymmetrical characteristics in comparison to the Santa Teresa bridge. Furthermore, the modal response demonstrated the coupled nature of its dynamic response with a coupled vertical-translational behavior, despite the mass of the structure.

The Ascoli Satriano bridge shows the lowest frequency range among the four bridges. The reasons for this reduction are twofold. Firstly, the structure is more flexible and has a humpback shape compared to the others. In addition to these factors, it is imperative to consider the soil composition of the bridge’s foundation, which is characterized by its relative softness. The probable deterioration of the structural materials over time, in combination with the presence of longer and more slender spans, contributes to the high flexibility and reduced stiffness of this bridge.

The SP123 bridge in Troia exhibited natural frequencies that were higher than those of the Ascoli Satriano bridge but lower than those of the Bovino bridge. Indeed, the Troia bridge is the most recent structure, and it is characterized by a less massive morphology. Therefore, it is more flexible than the Bovino bridge. It should be noted that, during its useful life, some settlements in the foundation of piers may have occurred. Furthermore, there is some local damage, including cracks, detachments and deterioration of the external bricks and material on the central arch.

The research has shown the effectiveness of ambient vibration test as a universally applicable, minimally invasive, and cost-efficient method for preliminary characterization, baseline establishment, and long-term monitoring. Controlled vehicle-excitation tests, where feasible, offer superior signal quality and clearer modal identification, while hammer testing remains a valid alternative for highly protected structures despite its limitations for higher-order modes. Strategic sensor placement, informed by preliminary modeling and engineering judgment, proved as effective as uniform distribution, highlighting the importance of intelligent experimental design over sheer sensor quantity. The MAC values found are always greater than 0.85, with the majority exceeding 0.9. This result is of particular significance, as it demonstrates the degree of accuracy of the values obtained. The strong correlation between the mode shapes of each test provides substantial validation of the overall robustness of the results.

A notable outcome of this study is the establishment of a specialized preliminary experimental database of modal parameters for three-arch masonry bridges, particularly in seismically active regions. This provides essential baseline data for typological assessments, seismic vulnerability evaluations, and the development of quantitative, data-driven condition assessment protocols linking structural condition, construction era, and dynamic behavior. Furthermore, a logarithmic relationship between the first mode and the bridge’s maximum span was demonstrated, enabling the development of a formula validated on other case studies for the analytical identification of the first mode with an error of approximately 2.6%.

The proposed framework supports systematic preservation strategies and evidence-based decision-making, balancing public safety requirements with the conservation of cultural heritage. The standardization of such protocols can reinforce both national and international regulations aimed at safeguarding historic infrastructure. The findings of this study will serve as a significant component in the construction of a database containing data pertaining to the monitoring of historical masonry bridges. It is hoped that the contribution of this article, in conjunction with numerous others on bridges of the same structural typology, will serve as the basis for the enrichment of the data collected within potential online and open-source applications available to all. In this regard, the Geographic Information System (GIS) supported by its Mergin Maps tool could be considered an excellent open-source platform, with the potential to contain a vast collection of georeferenced archive data. This “Atlas” facilitates the collection and understanding of historical, geometrical, construction material and structural characteristics, as well as the results and setups of previous monitoring for each bridge loaded using a simple laptop or smartphone.

In summary, the efficacy of applying OMA to masonry bridges is intrinsically linked to the strategic design of the experimental setup. The proper selection, orientation, and distribution of accelerometers are not trivial technical considerations but rather decisive factors in the acquisition of precise modal parameters. These parameters, in turn, serve as the basis for critical applications such as finite element model updating, long-term monitoring, and damage detection, underscoring that careful planning of monitoring setups is a prerequisite for both scientific rigor and the preservation of historical masonry bridges.

Future works should extend the methodology to a broader range of bridge typologies, develop automated setup-optimization tools incorporating heritage constraints, advance heritage-tailored long-term monitoring strategies, and integrate complementary non-destructive evaluation methods to form comprehensive structural health assessment systems.