A Multidisciplinary Robust Collaborative Optimization Method Under Parameter Uncertainty Based on the Double-Layer EI–Kriging Model
Abstract
1. Introduction
2. Collaborative Optimization Method Based on Weight Distribution Difference Information
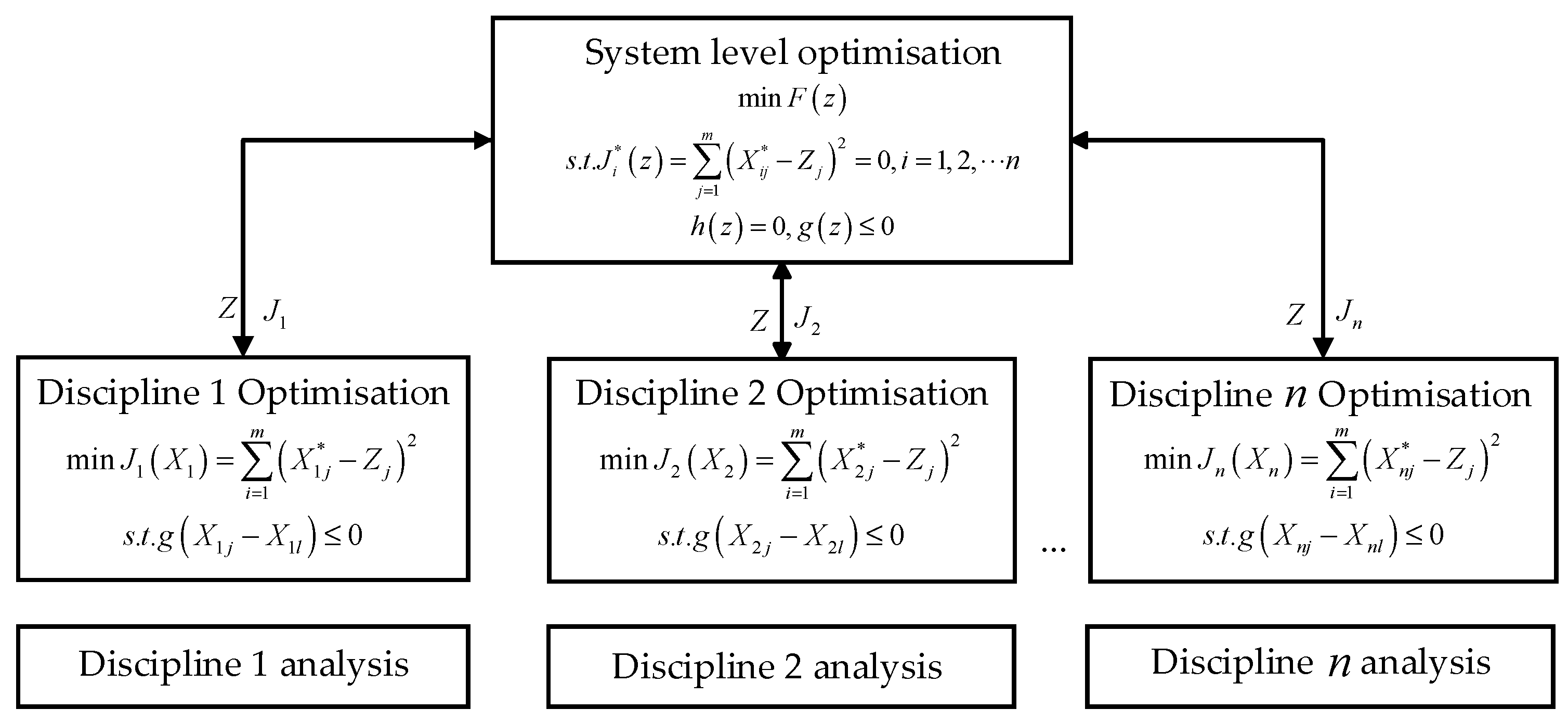
2.1. Traditional Collaborative Optimization (CO)
2.2. Collaborative Optimization Method Based on Weight Distribution Difference Information (CO-WDDI)
2.2.1. Disciplinary Differences
2.2.2. Discrepancy Between the System-Level Design Point and the Mean of Discipline-Level Design Points
2.2.3. Weighting Coefficients
2.2.4. Reformulation of the Relaxation Factor
2.2.5. Procedure of the CO-WDDI Method
3. Double-Layer Nested EI–Kriging Robust Optimization Model
3.1. EI–Kriging Model
3.1.1. Kriging Model
3.1.2. Expected Improvement Criterion (EI)
3.1.3. Model Construction Procedure
3.2. Double-Layered Nested EI–Kriging Robust Optimization Model (DL-EI–Kriging)
4. Multidisciplinary Robust Collaborative Optimization Method Under Parameter Uncertainty
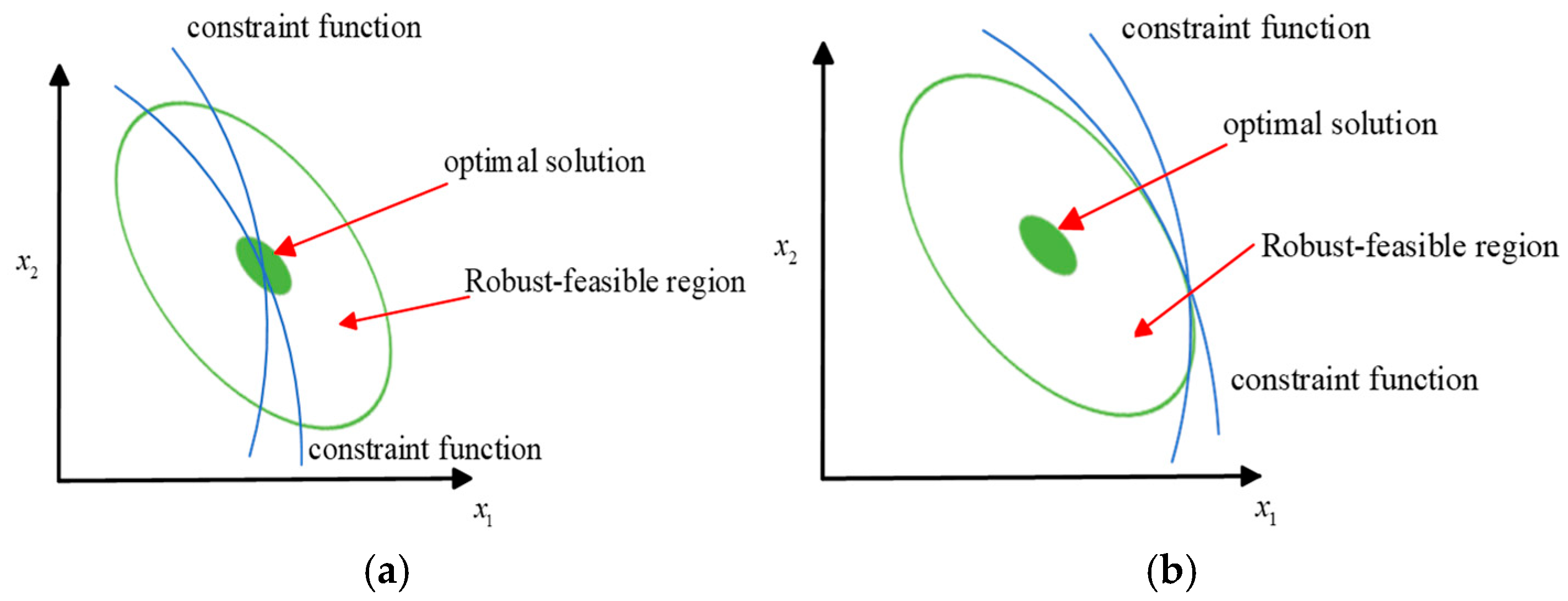
4.1. Robustness Analysis
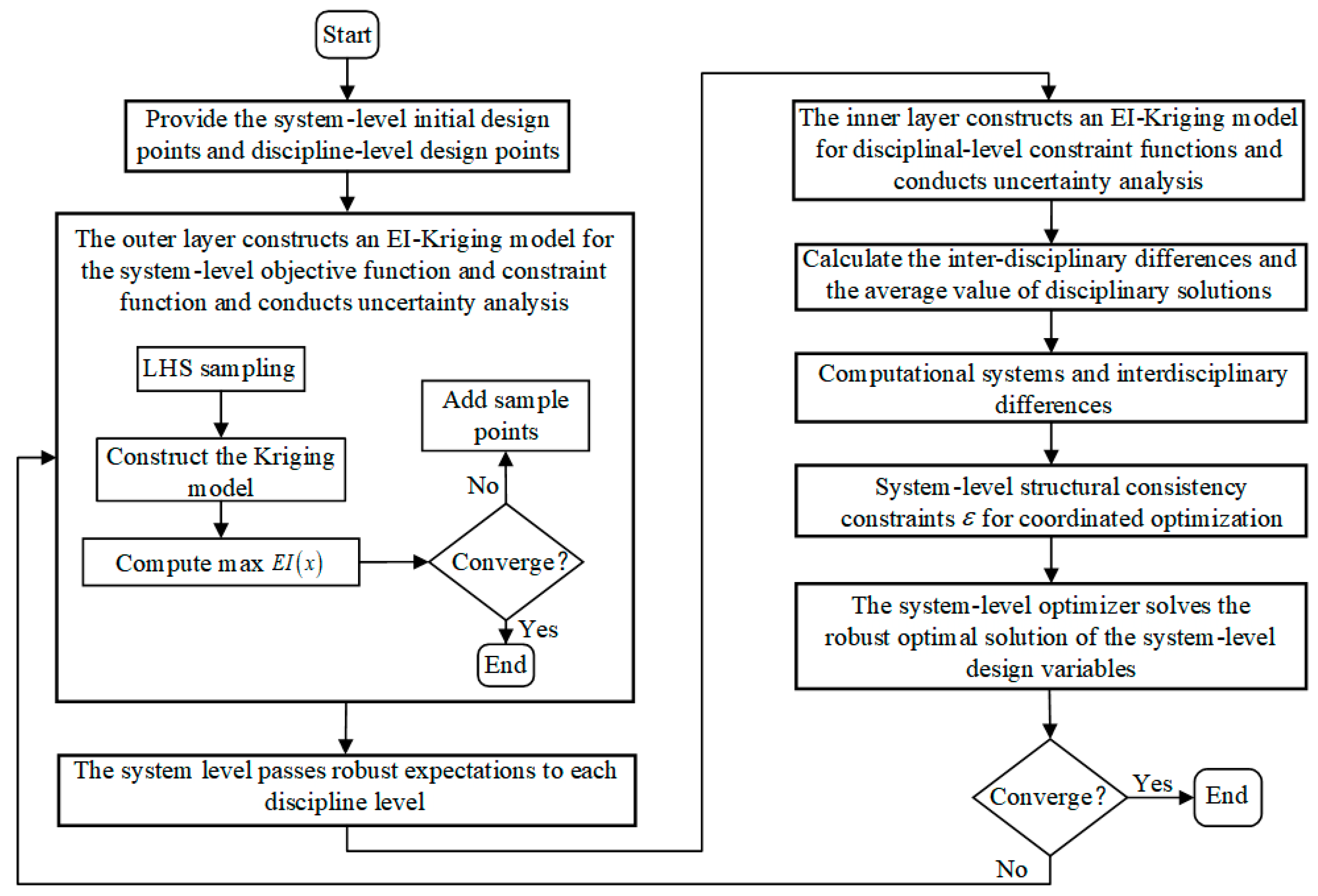
4.2. Procedure of the MRCO-PU Method
5. Experimental Validation
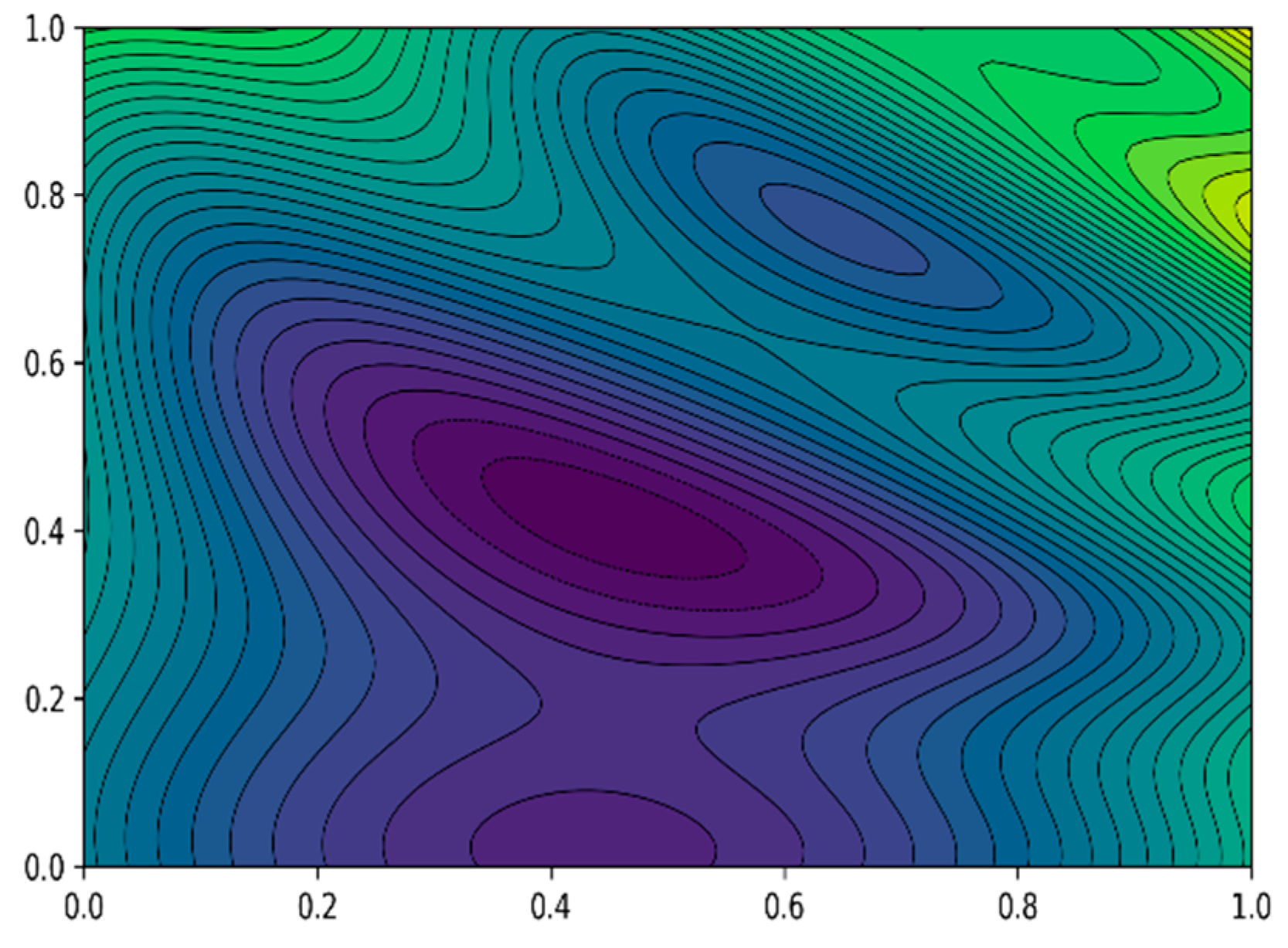
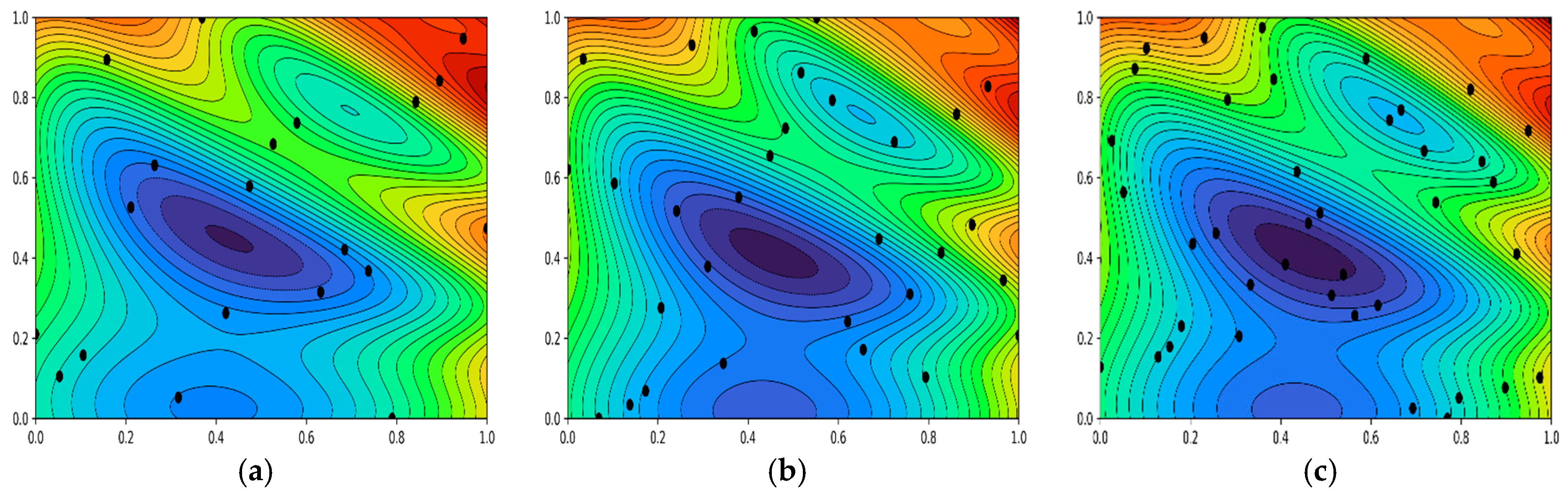
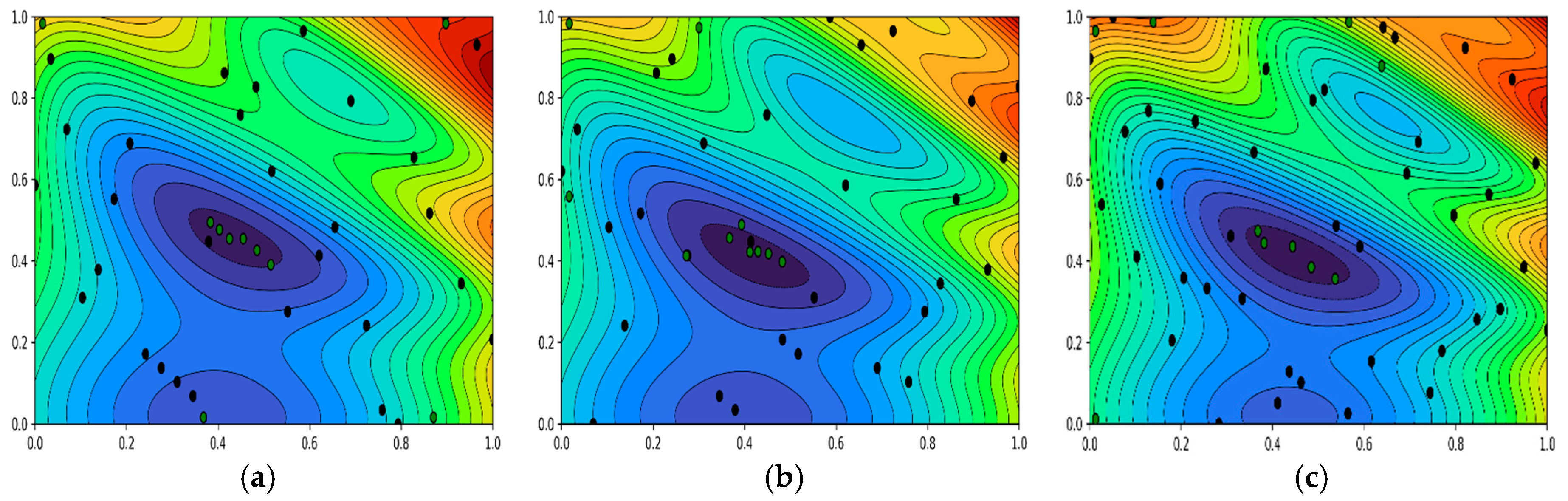
5.1. EI–Kriging Model Verification
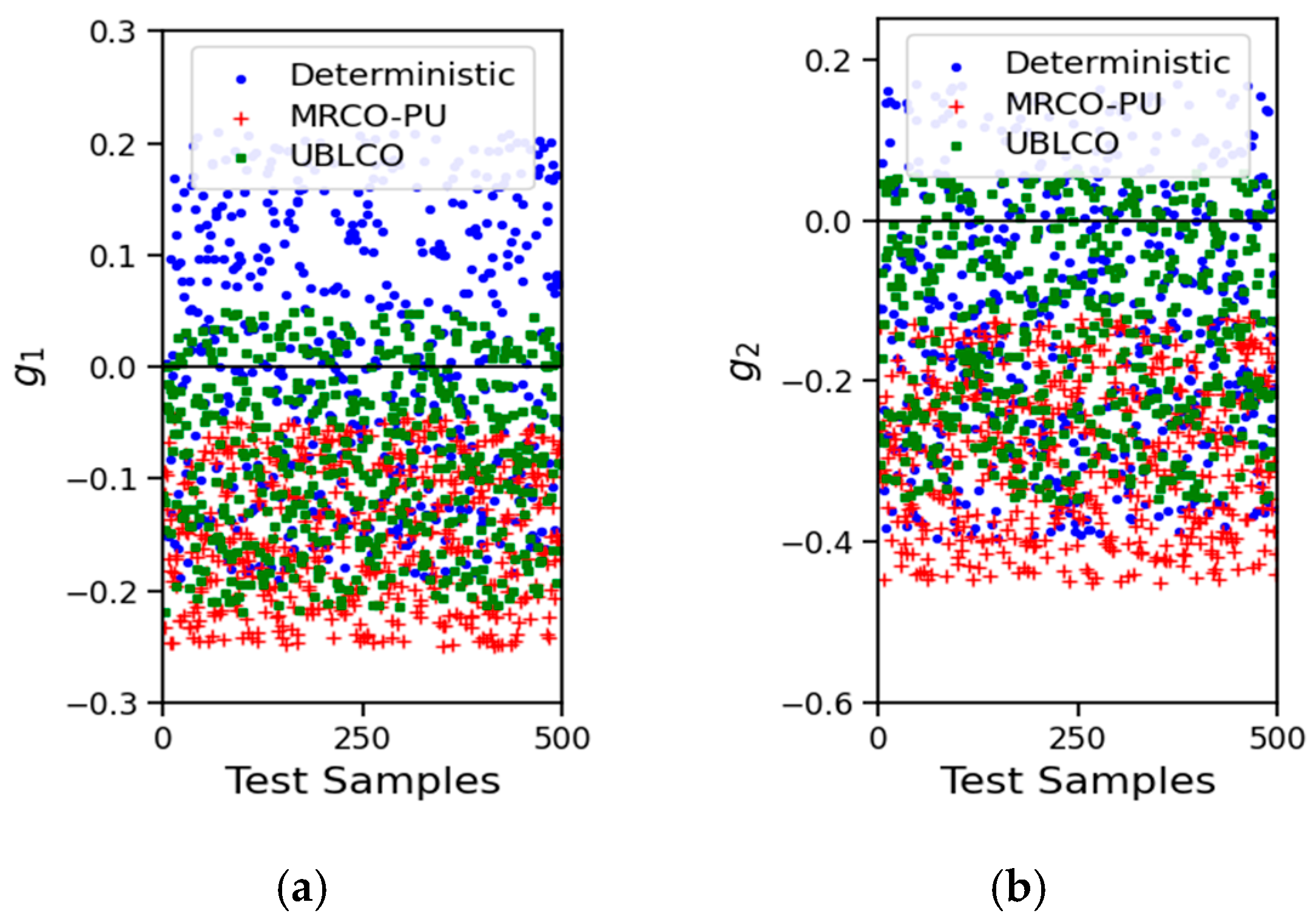
5.2. Mathematical Case Validation
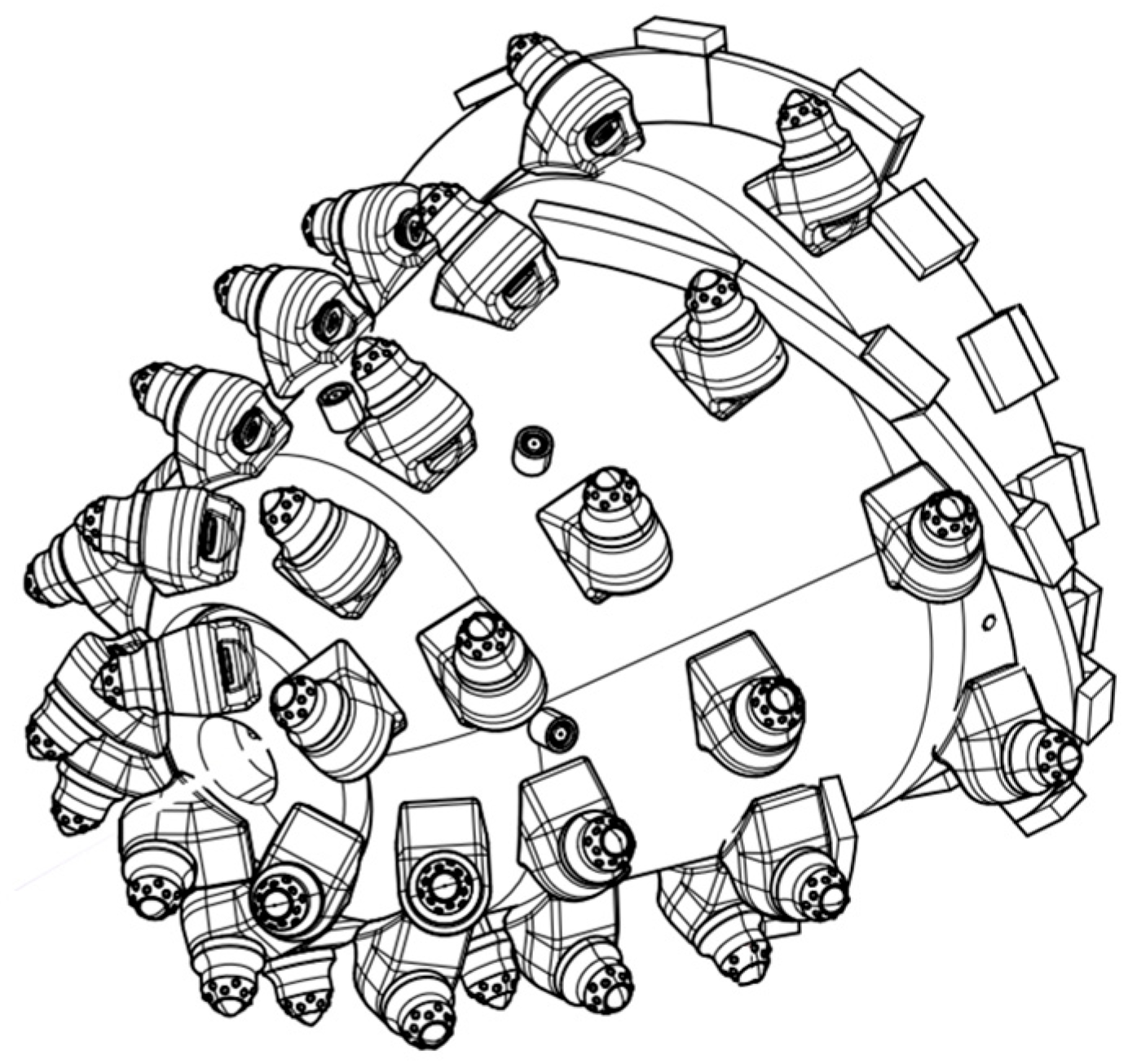
5.3. Engineering Case Validation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Luo, C.; Chen, J.; Liu, Y.; Xiang, H. Enhancing aerodynamic and aeroelastic performance of axial compressor through multi-degree-of-freedom parameterization and data-driven multidisciplinary optimization. Struct. Multidiscip. Optim. 2025, 68, 56. [Google Scholar] [CrossRef]
- Yildirim, A.; Jacobson, K.E.; Anibal, J.L.; Stanford, B.K.; Gray, J.S.; Mader, C.A.; Martins, J.R.R.A.; Kennedy, G.J. MPhys: A modular multiphysics library for coupled simulation and adjoint derivative computation. Struct. Multidiscip. Optim. 2025, 68, 15. [Google Scholar] [CrossRef]
- Song, Z.; Zheng, X.; Wang, B.; Zhou, K.; Adjei, R.A. Aerodynamic and structural multidisciplinary optimization design method of fan rotors based on blade curvature constraints. Aerosp. Sci. Technol. 2023, 136, 108187. [Google Scholar] [CrossRef]
- Sobieszczanski-Sobieski, J. Optimization by Decomposition: A Step from Hierarchic to Non-Hierarchic Systems; Air Force Symposium on Recent Advances in Multidisciplinary Analysis and Optimization; AIAA Paper-94-4325-CP; NASA Technical Reports Server: Washington, DC, USA, 1988. [Google Scholar]
- Meng, D.; Zhang, X.; Yang, Y.-J.; Xu, H.; Huang, H.-Z. Interaction balance optimization in multidisciplinary design optimization problems. Concurr. Eng. 2015, 24, 48–57. [Google Scholar] [CrossRef]
- Chen, Y.-J.; Huang, H. A novel conceptual design approach for autonomous underwater helicopter based on multidisciplinary collaborative optimization. Eng. Appl. Comput. Fluid Mech. 2024, 18, 2325494. [Google Scholar] [CrossRef]
- Zhang, J.; Tian, Y.; Liu, S.; Zhang, W. A novel multidisciplinary hierarchical collaborative optimization of the high-speed pantograph considering the uncertainty of joint clearances. Eng. Optim. 2024, 1–30. [Google Scholar] [CrossRef]
- Bao, Y.; Li, H.; Zhao, Y.; Li, L.; Zhang, Z.; Tang, Z. Global–local collaborative optimization method based on parametric sensitivity analysis and application to optimization of compressor blade. Struct. Multidiscip. Optim. 2025, 68, 19. [Google Scholar] [CrossRef]
- Mcharek, M.; Azib, T.; Hammadi, M.; Larouci, C.; Choley, J.Y. Multidisciplinary design optimization using knowledge management applied to an electronic throttle. COMPEL-Int. J. Comput. Math. Electr. Electron. Eng. 2020, 39, 353–362. [Google Scholar] [CrossRef]
- Sahay, S.; Upputuri, R.; Kumar, N. Optimal power flow-based approach for grid dispatch problems through Rao algorithms. J. Eng. Res. 2023, 11, 100032. [Google Scholar] [CrossRef]
- Li, W.; Niu, Y.; He, Y.; Garg, A.; Huang, H.; Gao, L. Multidisciplinary robust design optimization under combined parameter and surrogate model uncertainties: A new computational framework for sparse samples and extreme scenarios. Eng. Comput. 2025, 146, 1–21. [Google Scholar] [CrossRef]
- Wu, H.; Du, X. Time- and Space-Dependent Reliability-Based Design With Envelope Method. J. Mech. Des. 2023, 145, 031708. [Google Scholar] [CrossRef]
- Thompson, T.; McMullen, R.; Nemani, V.; Hu, Z.; Hu, C. A comparative study of acquisition functions for active learning kriging in reliability-based design optimization. Struct. Multidiscip. Optim. 2025, 68, 51. [Google Scholar] [CrossRef]
- Xu, H.W.; Li, W.; Li, M.F.; Hu, C.; Zhang, S.C.; Wang, X. Multidisciplinary robust design optimization based on time-varying sensitivity analysis. J. Mech. Sci. Technol. 2018, 32, 1195–1207. [Google Scholar] [CrossRef]
- Taguchi, G. Performance analysis design. Int. J. Prod. Res. 1978, 16, 521–530. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, X.; Li, D.; Lin, S.; Zhao, X. Robust-Oriented Optimization Design of Dual Three-Phase Slotted Permanent Magnet Hybrid Excitation Generator Considering Manufacturing Tolerances. IEEE Trans. Transp. Electrification 2024, 11, 4561–4573. [Google Scholar] [CrossRef]
- Najlaoui, B.; Alghafis, A.; Nejlaoui, M. Robust design of a low cost flat plate collector under uncertain design parameters. Energy Rep. 2023, 10, 2950–2961. [Google Scholar] [CrossRef]
- Lin, Q.; Zhou, Q.; Hu, J.; Cheng, Y.; Hu, Z. A Sequential Sampling Approach for Multi-Fidelity Surrogate Modeling-Based Robust Design Optimization. J. Mech. Des. 2022, 144, 111703. [Google Scholar] [CrossRef]
- Ma, Y.Z.; Li, C.X.; Wang, Y.Y.; Zhang, Z.Y.; Li, H.S.; Ding, A.N.; Rui, X.T. Robust design optimization of a multi-body system with aleatory and epistemic uncertainty. Reliab. Eng. Syst. Saf. 2024, 245, 110029. [Google Scholar] [CrossRef]
- Liu, F.; Yang, S.; Wang, H.; Zhang, W. Multidisciplinary design optimization of an autonomous underwater vehicles based on random uncertainty. Ocean Eng. 2024, 312, 119298. [Google Scholar] [CrossRef]
- Zhou, X.; Zhao, W.; Wang, C.; Wang, Y.; Chu, Y. Multidisciplinary Optimization Design of Electric Vehicle X-by-Wire Chassis Integrating Parameter Coupling and Uncertainties. IEEE Trans. Transp. Electrif. 2024, 11, 4765–4777. [Google Scholar] [CrossRef]
- Jin, Z.; Sun, X.; Cai, Y.; Tian, X. Robust Collaborative Optimization Design of Plug-In Hybrid Electric Bus Based on 6 Sigma Theory. IEEE Trans. Transp. Electrif. 2024, 10, 10253–10261. [Google Scholar] [CrossRef]
- Han, J.; Han, K.; Han, T.; Wang, Y.; Han, Y.; Lin, J. Data-driven distributionally robust optimization of low-carbon data center energy systems considering multi-task response and renewable energy uncertainty. J. Build. Eng. 2025, 102, 111937. [Google Scholar] [CrossRef]
- Cheng, J.; Peng, D.; Hu, W.; Liu, Z.; Tan, J. Collaborative robust topology optimization of FGMs considering hybrid bounded uncertainties based on the distance to ideal solution. Compos. Struct. 2024, 341, 118205. [Google Scholar] [CrossRef]
- Xiao, S.; Oladyshkin, S.; Nowak, W. Reliability analysis with stratified importance sampling based on adaptive Kriging. Reliab. Eng. Syst. Saf. 2020, 197, 106852. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, L.; Li, H.; Liu, X.; Chen, R. An adaptive dual-Kriging method based on parameter sensitivity analysis and application to vibration reduction optimization of helicopter rotor test-bed. Struct. Multidiscip. Optim. 2023, 66, 232. [Google Scholar] [CrossRef]
- Xiao, M.; Gao, L.; Shao, X.; Qiu, H.; Jiang, P. A generalized collaborative optimization method and its combination with kriging metamodels for engineering design. J. Eng. Des. 2012, 23, 379–399. [Google Scholar] [CrossRef]
- Kroo, I.; Altus, S.; Braun, R.; Gage, P.; Sobieski, I. Multidisciplinary Optimization Methods for Aircraft Preliminary Design; AIAA Paper-94-4325-CP; NASA Technical Reports Server: Washington, DC, USA, 1994. [Google Scholar]
- Cao, Z.M.; Zhao, J.; Wang, A. A multidisciplinary Collaborative Optimization Algorithm for Assigning Differential Information According to Weight. Comput. Simul. 2025, 42, 376–426. [Google Scholar]
- Yang, C.; Xia, Y. Interval uncertainty-oriented optimal control method for spacecraft attitude control. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 5460–5471. [Google Scholar] [CrossRef]
- Song, R.; Zhou, C.; Rui, J.; Li, H.; Li, J. A volume-ratio index for sensitivity analysis of time-dependent models with interval uncertainty inputs. Aerosp. Sci. Technol. 2025, 160, 110077. [Google Scholar] [CrossRef]
- Wang, X.; Wang, R.; Chen, X.; Wang, L.; Geng, X.; Fan, W. Interval prediction of responses for uncertain multidisciplinary system. Struct. Multidiscip. Optim. 2016, 55, 1945–1964. [Google Scholar] [CrossRef]
- Wang, L.; Chen, Z.; Yang, G.; Sun, Q.; Ge, J. An interval uncertain optimization method using back-propagation neural network differentiation. Comput. Methods Appl. Mech. Eng. 2020, 366, 113065. [Google Scholar] [CrossRef]
- Li, W.; Xiao, M.; Yi, Y.; Gao, L. Maximum variation analysis based analytical target cascading for multidisciplinary robust design optimization under interval uncertainty. Adv. Eng. Inform. 2019, 40, 81–92. [Google Scholar] [CrossRef]
- Kim, H.; Michelena, N.; Papalambros, P.; Jiang, T. Target cascading in optimal system design. J. Mech. Des. 2003, 125, 474–480. [Google Scholar] [CrossRef]
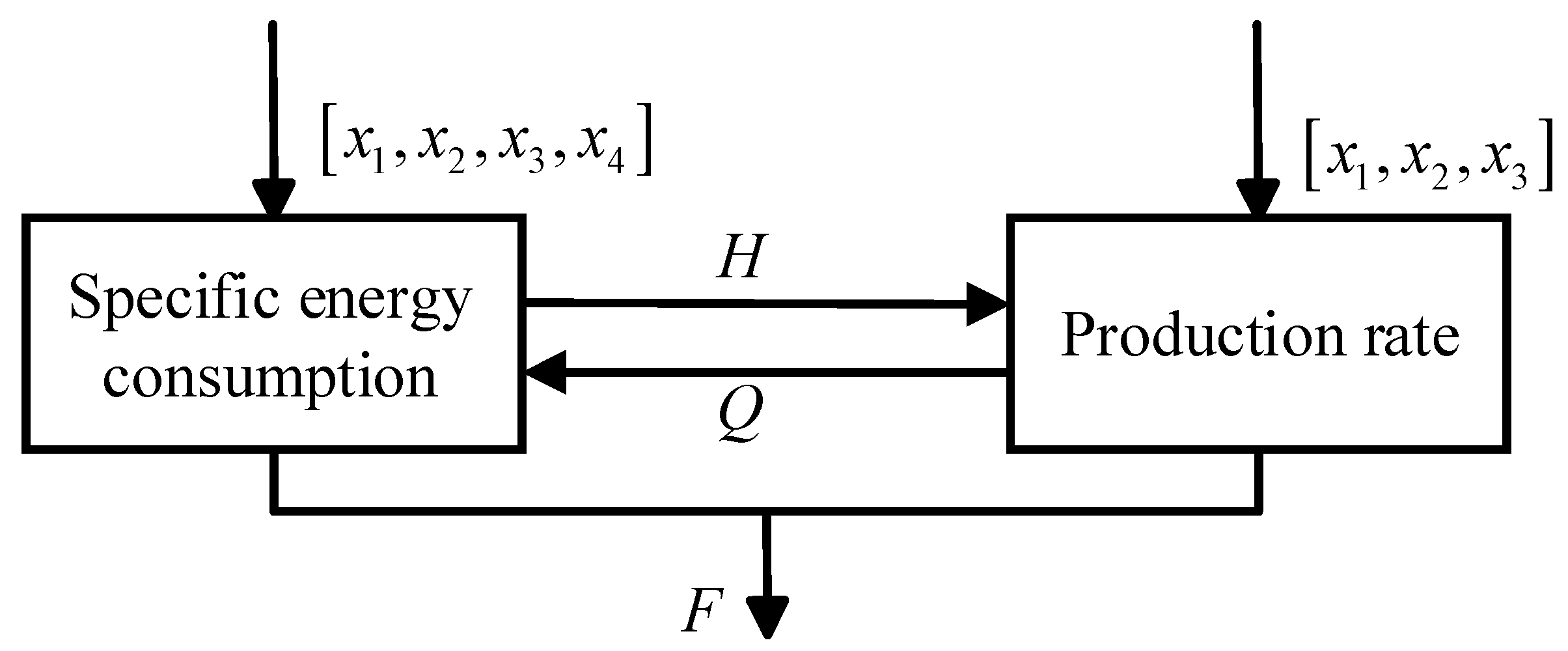
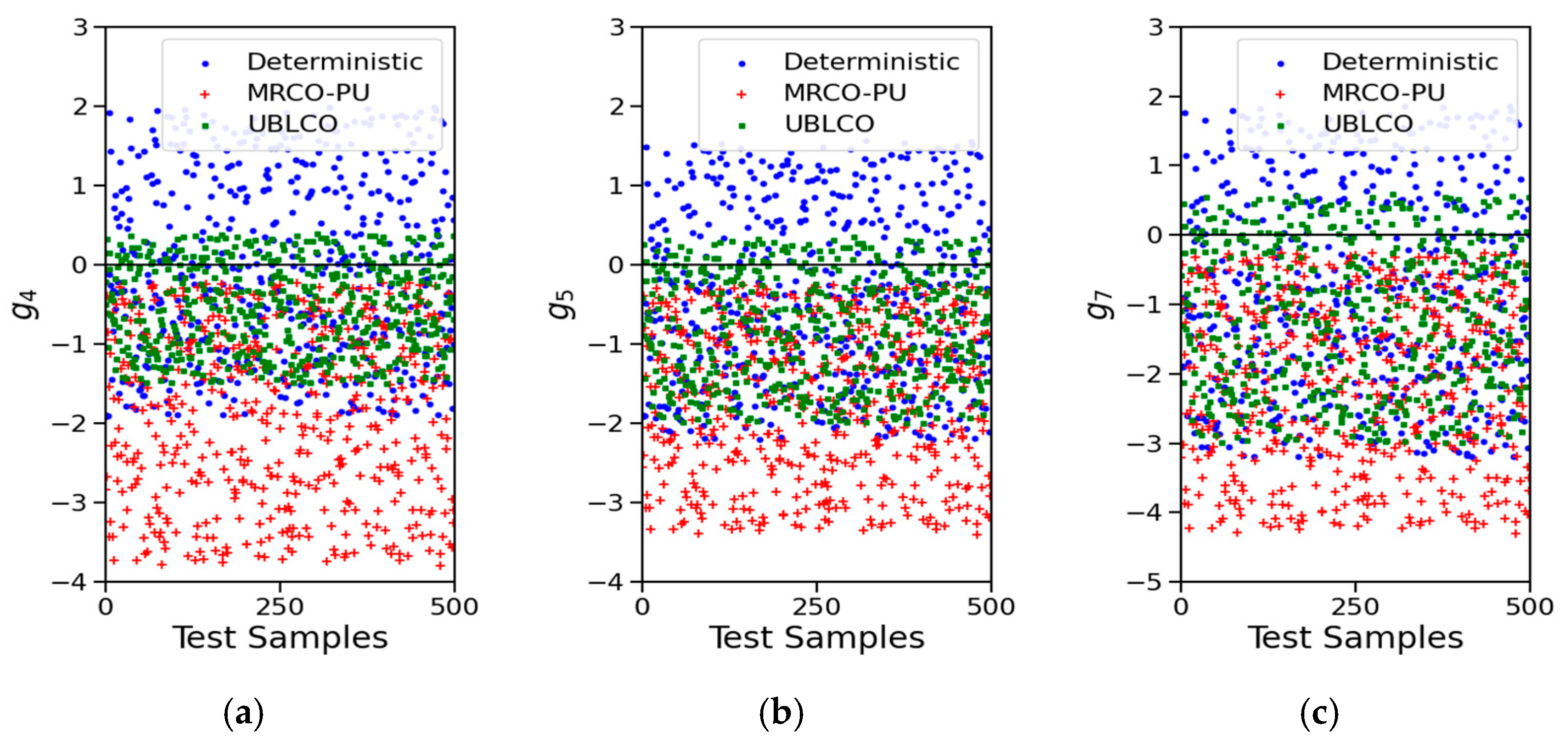
| Initial Points | Optimization Results | Objective Function Value | Number of Iterations | Computation Time | |
|---|---|---|---|---|---|
| ATC | (1, 0, 5, 4.38, 8.09) | (3.06, 0, 0.06, 7.02, 9.52) | 7.36 | 35 | 12s |
| (1, 1, 0, 5, 3) | (3.29, 0.11, −0.12, 6.65, 8.64) | 8.68 | 102 | 25s | |
| (−5, 0, 2.5, 26.96, 2.69) | (−3.99, 0, 0.17, 9.57, 3.78) | 6.32 | 57 | 14s | |
| Traditional CO | (1, 0, 5, 4.38, 8.09) | (3.14, 0, −0.28, 7.81, 10) | 7.52 | 24 | 4s |
| (1, 1, 0, 5, 3) | (3.17, 0, −0.25, 7.70, 9.14) | 7.46 | 89 | 11s | |
| (−5, 0, 2.5, 26.96, 2.69) | (−3.75, 0, 0, 8.96, 5.86) | 8.96 | 40 | 8s | |
| CO-WDDI | (1, 0, 5, 4.38, 8.09) | (3.23, 0, 0, 8, 6.72) | 8.00 | 16 | 4s |
| (1, 1, 0, 5, 3) | (3.73, 0, 0, 8, 7.27) | 8.00 | 20 | 3s | |
| (−5, 0, 2.5, 26.96, 2.69) | (−3.92, 0, 0, 8, 6.68) | 8.00 | 34 | 5s |
| Deterministic Optimization | 0.4856 | 0.4989 |
| Robust Optimization (UBLCO) | 0.9211 | 0.9038 |
| Robust Optimization (MRCO-PU) | 1.0 | 1.0 |
| Symbols | Deterministic Optimization | Robust Optimization (UBLCO) | Robust Optimization (MRCO-PU) | |
|---|---|---|---|---|
| Design Variables | 3.23 | 3.14 | 3.09 | |
| 0 | 0.48 | 0.66 | ||
| 0 | 0.36 | 0.30 | ||
| 8 | 7.87 | 7.34 | ||
| 6.72 | 6.84 | 7.03 | ||
| Objective Function Value | 8.00 | 8.17 | 8.08 |
| Design Variables | Variable Names | Unit | Initial Value | Range |
|---|---|---|---|---|
| Cutting head length L | mm | 900 | ||
| Cutting arm swing speed v | m/min | 0.92 | ||
| Average diameter of cutting head D | mm | 835 | ||
| Rotational speed of cutting head n | r/min | 46 |
| Initial Points | Optimization Results | Objective Function Value | Number of Iterations | Computation Time | |
|---|---|---|---|---|---|
| ATC | (900, 0.92, 835, 46) | (901, 0.98, 833, 47) | 90.55 | 46 | 15s |
| Traditional CO | (900, 0.92, 835, 46) | (902, 0.96, 832, 45) | 88.05 | 34 | 14s |
| CO-WDDI | (900, 0.92, 835, 46) | (899.96, 1.07, 830.8, 6.72) | 87.02 | 16 | 4s |
| Deterministic Optimization | 0.5891 | 0.6456 | 0.5739 |
| Robust Optimization (UBLCO) | 0.8893 | 0.9489 | 0.9148 |
| Robust Optimization (MRCO-PU) | 1.0 | 1.0 | 1.0 |
| Symbols | Deterministic Optimization | Robust Optimization (UBLCO) | Robust Optimization (MRCO-PU) | |
|---|---|---|---|---|
| Design Variables | 899.96 | 901.13 | 898.64 | |
| 1.07 | 1.01 | 1.02 | ||
| 830.8 | 829.8 | 830.5 | ||
| 36 | 36 | 38 | ||
| Specific energy consumption | 15.02 | 14.21 | 14.07 | |
| Productivity | 72.00 | 71.56 | 71.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, Z.; Wei, Z.; Chen, M.; Zhang, K.; Lang, L.; Luan, X.; Cheng, W. A Multidisciplinary Robust Collaborative Optimization Method Under Parameter Uncertainty Based on the Double-Layer EI–Kriging Model. Appl. Sci. 2025, 15, 10549. https://doi.org/10.3390/app151910549
Qiu Z, Wei Z, Chen M, Zhang K, Lang L, Luan X, Cheng W. A Multidisciplinary Robust Collaborative Optimization Method Under Parameter Uncertainty Based on the Double-Layer EI–Kriging Model. Applied Sciences. 2025; 15(19):10549. https://doi.org/10.3390/app151910549
Chicago/Turabian StyleQiu, Zhenglin, Zhe Wei, Mo Chen, Kai Zhang, Lang Lang, Xilin Luan, and Wenying Cheng. 2025. "A Multidisciplinary Robust Collaborative Optimization Method Under Parameter Uncertainty Based on the Double-Layer EI–Kriging Model" Applied Sciences 15, no. 19: 10549. https://doi.org/10.3390/app151910549
APA StyleQiu, Z., Wei, Z., Chen, M., Zhang, K., Lang, L., Luan, X., & Cheng, W. (2025). A Multidisciplinary Robust Collaborative Optimization Method Under Parameter Uncertainty Based on the Double-Layer EI–Kriging Model. Applied Sciences, 15(19), 10549. https://doi.org/10.3390/app151910549






