True Triaxial Investigation of the Effects of Principal Stresses and Injection Pressure on Induced Seismicity Behavior in Geothermal Reservoirs
Abstract
1. Introduction
2. Materials and Methods
2.1. Apparatus and Specimen
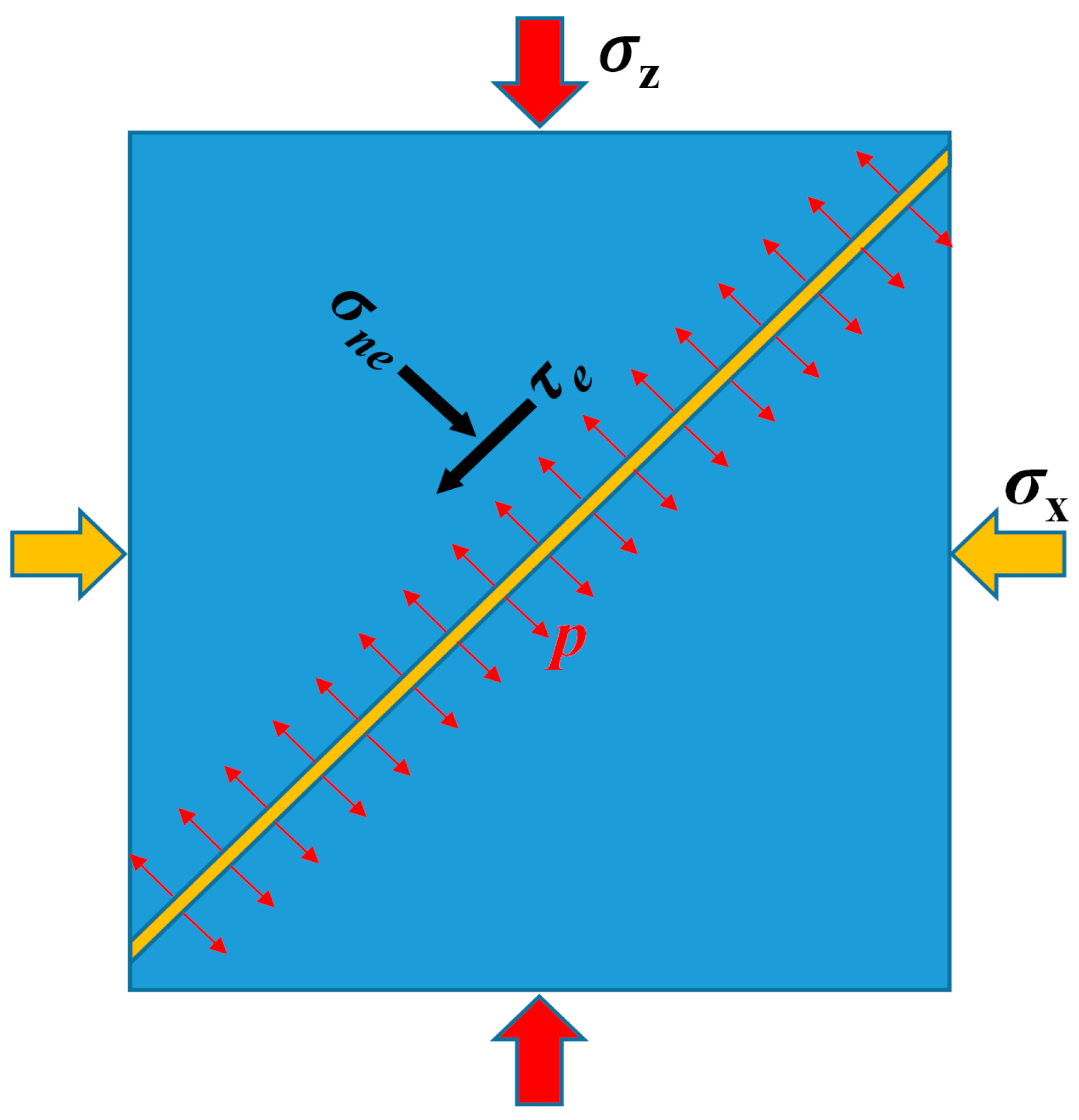
2.2. Stress Loading Setups
2.3. Data Processing and Analytical Framework
3. Results and Analysis
3.1. Influence of Intermediate Principal Stress on Fault Slip Behavior
3.1.1. Fault Slip Initiation Stress Under Different Intermediate Principal Stresses
3.1.2. Fault Slip Velocity Under Different Intermediate Principal Stresses
3.2. Influence of Minimum Principal Stress on Fault Slip Behavior
3.2.1. Fault Slip Initiation Stress Under Different Minimum Principal Stresses
3.2.2. Fault Slip Velocity Under Different Minimum Principal Stresses
3.3. Influence of Injection Pressure on Fault Slip Behavior
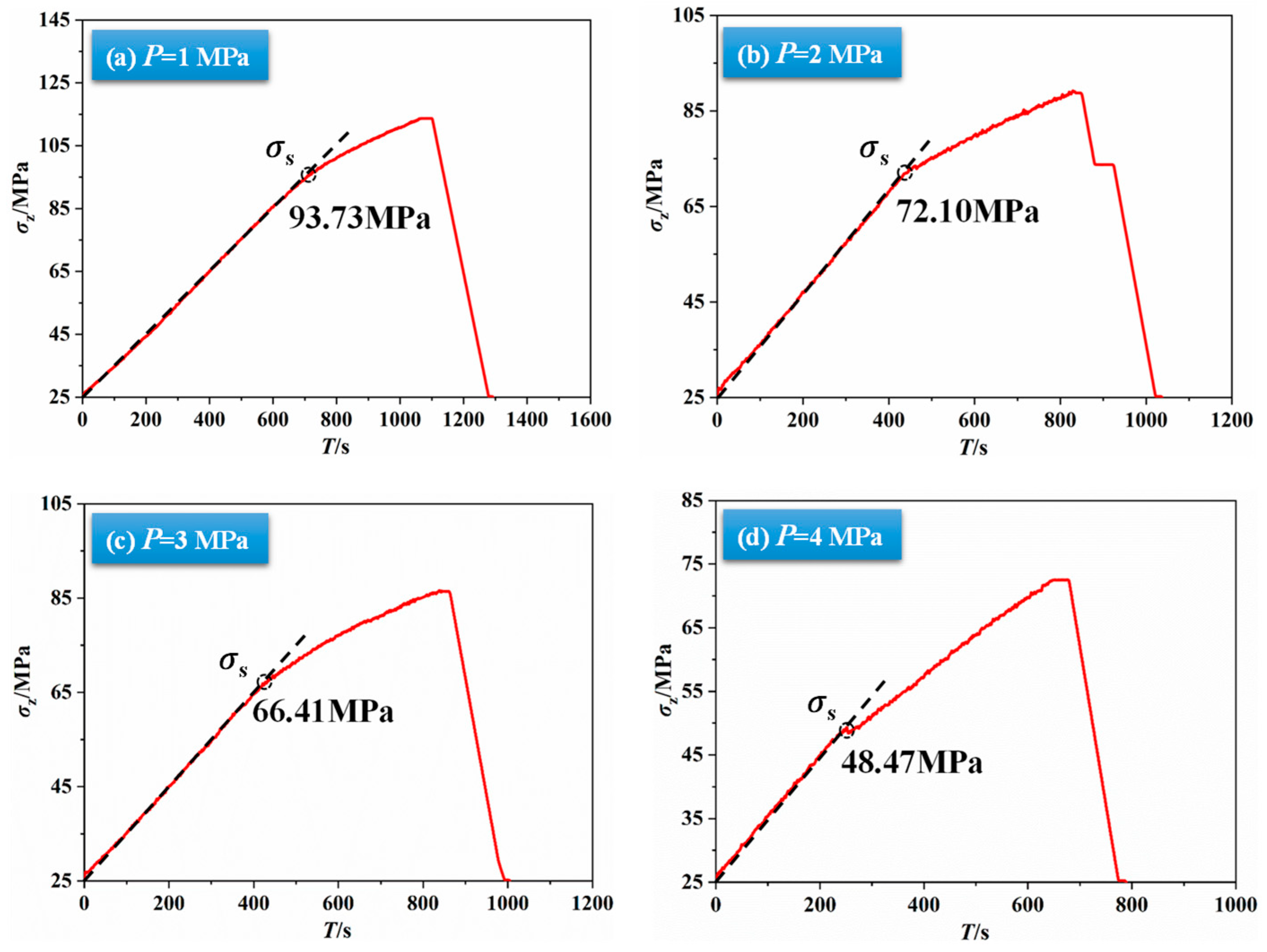
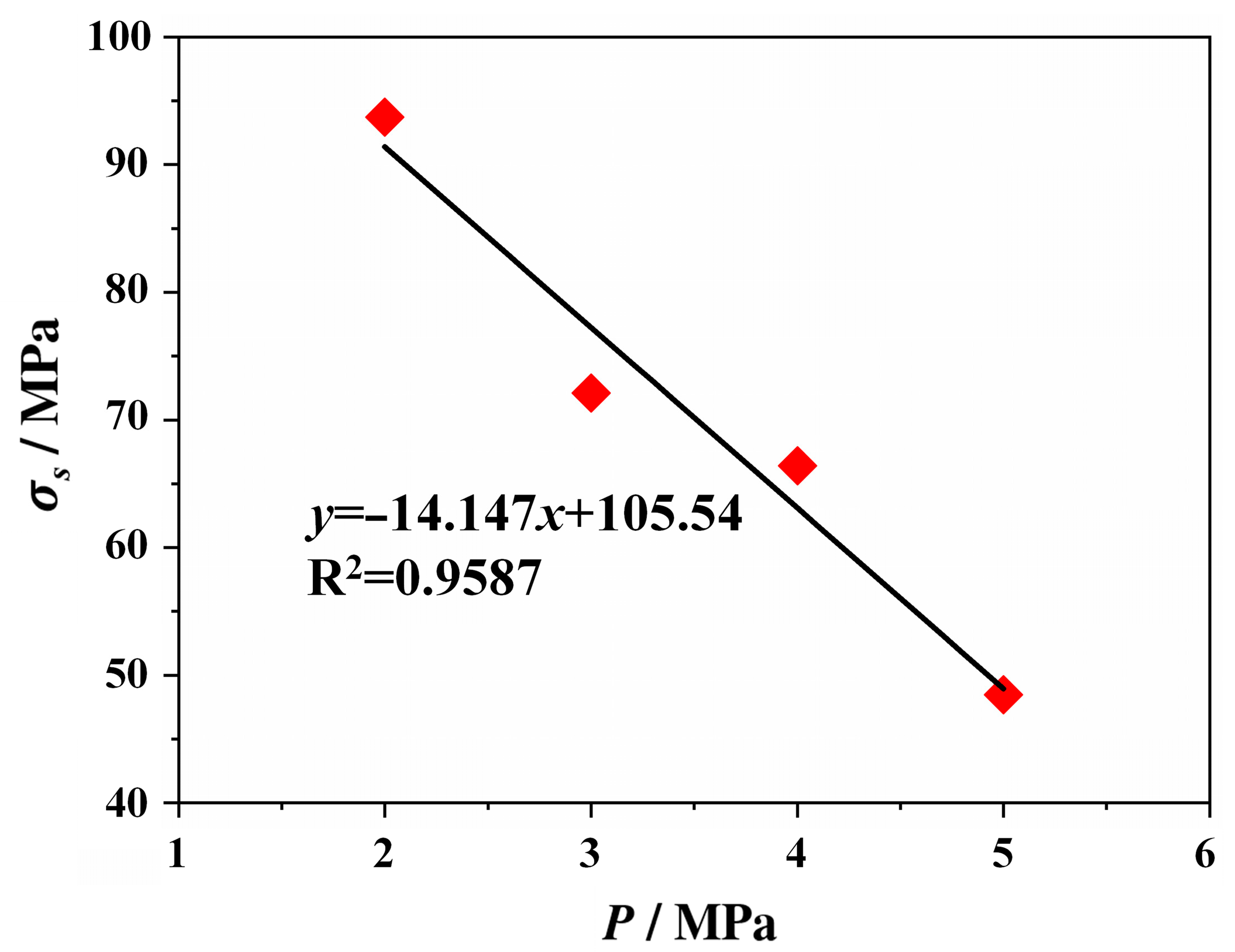
3.3.1. Fault Slip Initiation Stress Under Different Injection Pressures
3.3.2. Fault Slip Velocity Under Different Injection Pressures
4. Discussion
4.1. Engineering Implications for Geothermal Energy Development
4.2. Influence of 3-D Stress and Injection Pressure on Fault Slip Behavior
4.3. Pore Pressure Diffusion and Delayed Triggering Mechanisms Under Scale Effects
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shi, H.L.; Wang, G.L.; Lu, C.; Wang, W.L.; Liu, L.; Wei, Y.J. Enhancing geothermal energy recovery in Yangbajing: The role of natural and artificial fracture connectivity in EGS performance. Geothermics 2025, 132, 103438. [Google Scholar] [CrossRef]
- Wu, Z.Q.; Zhang, D.M.; Liang, Y.J.; He, S.F.; Xie, H.P.; Li, M.H. Mechanical and microstructural properties of Gonghe granite for enhanced geothermal systems: Thermal effects and energy evolution. J. Rock Mech. Geotech. Eng. 2025. [Google Scholar] [CrossRef]
- Zheng, J.X.; Sun, L.C.; Xu, X.; Long, X.T.; Gao, T.Y.; Xia, E.T.; Li, B.; Li, S.H.; Wang, J.; Mao, Z.Y.; et al. Feasibility of shallow geothermal energy for industrial heating using high-temperature heat pumps in Sichuan Province, China. Energy Sustain. Dev. 2025, 88, 101785. [Google Scholar] [CrossRef]
- Kalsariya, M.; Shah, A.; Patel, S.; Mandlik, S.; Raulji, R.; Shah, D.; Prajapati, M.; Shah, M. A Systematic Study on geothermal energy integrated water desalination: Challenges and opportunities. Unconv. Resour. 2025, 8, 100226. [Google Scholar] [CrossRef]
- Memon, A.R.; Makauskas, P.; Kaminskaitė-Baranauskienė, I.; Pal, M. Repurposing depleted hydrocarbon reservoirs for geothermal energy: A case study of the Vilkyčiai Cambrian sandstone in Lithuania. Energy Rep. 2025, 14, 243–253. [Google Scholar] [CrossRef]
- Slimene, M.B.; Khlifi, M.A.; Soliman, N.F.; Osman, H.; Amari, A.; Sabirov, S.; Mavlonov, A.; Safarova, L. Transient modeling and data-driven optimization of a hybrid geothermal–solar energy system for eco-friendly multigeneration: A case study approach to sustainable urban development. Process Saf. Environ. Prot. 2025, 202, 107717. [Google Scholar] [CrossRef]
- Feng, K.H.; Zhang, S.M. Integration of Electrolyser with Hybrid Renewable Energy System (Hydropower, Geothermal and Biomass) for Green Hydrogen in China. Energy 2025, 8, 137881. [Google Scholar] [CrossRef]
- Azzola, J.; Bremer, J. Applied geophysics in schools to raise knowledge and awareness about geothermal energy and seismology. Soc. Impacts 2025, 5, 100116. [Google Scholar] [CrossRef]
- Hu, Z.W.; Wang, H.Y. Feasibility study of geothermal assisted energy storage using hydraulic fracturing. Geoenergy Sci. Eng. 2024, 242, 213220. [Google Scholar] [CrossRef]
- Akdas, S.B.; Onur, M. Analytical solutions for predicting and optimizing geothermal energy extraction from an enhanced geothermal system with a multiple hydraulically fractured horizontal-well doublet. Renew. Energy 2022, 181, 567–580. [Google Scholar] [CrossRef]
- Aydın, H.; Camcı, U.; Akın, S. An experimental investigation of hydraulic fracturing mechanisms in menderes metamorphic rocks: Prospects for enhanced geothermal systems. Geothermics 2025, 130, 103328. [Google Scholar] [CrossRef]
- Li, M.Y.; Li, M.L.; Zhang, F.S.; Wu, Z.J.; Zhou, Y.; Zhang, X.F. Assessing the contribution of mineral composition to meso-macro progressive failure in granite under thermo-hydro-mechanical (THM) conditions: Inspiration for hydraulic fracturing in Enhanced Geothermal Systems (EGS). Int. J. Rock Mech. Min. Sci. 2025, 194, 106238. [Google Scholar] [CrossRef]
- Dai, H.; Yin, T.B.; Wu, Y.; Ma, J.X.; Guo, W.X.; Li, X.B. Characterization of fracture extension and damage evolution in hot dry rock by cycle hydraulic fracturing (CHF): Application of CHF in enhanced geothermal systems. Energy 2025, 330, 137007. [Google Scholar] [CrossRef]
- Zhang, Y.Y.; Li, Y.Y.; Zheng, H.; Fan, B.H. A novel fully coupled thermo-hydro-mechanical-damage model for hydraulic fracture propagation in fractured geothermal reservoirs. Comput. Geotech. 2025, 185, 107364. [Google Scholar] [CrossRef]
- An, M.K.; Huang, R.; Elsworth, D.; Zhang, F.S.; Dontsov, E. Thermoporoelastic stress perturbations from hydraulic fracturing and thermal depletion in enhanced geothermal systems (EGS) and implications for fault reactivation and seismicity. J. Rock Mech. Geotech. Eng. 2025, 17, 2893–2903. [Google Scholar] [CrossRef]
- Cao, W.Z.; Durucan, S.; Shi, J.Q.; Korre, A.; Ratouis, T.; Hjörleifsdóttir, V. Geothermal fluid extraction and injection-related fracture slip susceptibility and seismicity in naturally fractured rocks. Int. J. Rock Mech. Min. Sci. 2024, 183, 105939. [Google Scholar] [CrossRef]
- Park, S.; Kim, K.; Yoo, H.; Yim, J.H.; Min, K.B. Comprehensive in-situ stress estimation in a fractured geothermal reservoir in Pohang, South Korea using drilling data, hydraulic stimulations, and induced seismicity. Int. J. Rock Mech. Min. Sci. 2025, 186, 105978. [Google Scholar] [CrossRef]
- Xu, C.; Li, J.; Yang, R.Z.; Chen, J.R.; Tan, H. An Improved Fracture Seismic Method for identifying the drilling targets of medium-deep geothermal resources: A case study on heishan geothermal area. Geothermics 2024, 120, 103019. [Google Scholar] [CrossRef]
- Cao, R.; Cai, Y.Q.; Dor, J.; Liu, Q.J.; Poliakova, M.; Chen, D.; Wan, S.S.; Yan, Y.Y. Distribution and genesis of geothermal waters in the Xianshuihe fault zone, Western Sichuan plateau, China: Constraints on fracture system and regional seismic activities. Geothermics 2025, 125, 103150. [Google Scholar] [CrossRef]
- Kivi, I.R.; Vilarrasa, V.; Kim, K.; Yoo, H.J.; Min, K.B. On the role of poroelastic stressing and pore pressure diffusion in discrete fracture and fault system in triggering post-injection seismicity in enhanced geothermal systems. Int. J. Rock Mech. Min. Sci. 2024, 175, 105673. [Google Scholar] [CrossRef]
- Zhou, W.; Lanza, F.; Grigoratos, I.; Schultz, R.; Cousse, J.; Trutnevyte, E.; Muntendam-Bos, A.; Wiemer, S. Managing Induced Seismicity Risks From Enhanced Geothermal Systems: A Good Practice Guideline. Rev. Geophys. 2024, 62, e2024RG000849. [Google Scholar] [CrossRef]
- Lee, K.K.; Ellsworth, W.L.; Giardini, D.; Townend, J.; Ge, S.; Shimamoto, T.; Yeo, I.W.; Kang, T.S.; Rhie, J.; Sheen, D.H.; et al. Managing injection-induced seismic risks. Science 2019, 364, 730–732. [Google Scholar] [CrossRef]
- Ryu, H.S.; Kim, H.; Lee, J.Y.; Kaown, D.; Lee, K.K. Abnormal groundwater levels and microbial communities in the Pohang Enhanced Geothermal System site wells pre- and post-Mw 5.5 earthquake in Korea. Sci. Total Environ. 2022, 810, 152305. [Google Scholar] [CrossRef]
- Hong, T.K.; Lee, J.; Park, S.; Kim, W. Major influencing factors for the nucleation of the 15 November 2017 Mw 5.5 Pohang earthquake. Phys. Earth Planet. Inter. 2022, 323, 106833. [Google Scholar] [CrossRef]
- Choi, D.H.; Kwon, T.H.; Ko, K.W. Centrifuge Modeling of Soil Liquefaction Triggering: 2017 Pohang Earthquake. KSCE J. Civ. Eng. 2024, 28, 3176–3191. [Google Scholar] [CrossRef]
- Lv, Y.X.; Yuan, C.; Zhu, X.H.; Gan, Q.; Li, H.B. THMD analysis of fluid injection-induced fault reactivation and slip in EGS. Geothermics 2022, 99, 102303. [Google Scholar] [CrossRef]
- Yang, J.J.; Wang, J.G.; Li, P.; Leung, C. A study on pore-scale fracture deformation induced by the CO2-H2O-minerals reactions in CO2-based Enhanced Geothermal Systems. Geoenergy Sci. Eng. 2025, 250, 213840. [Google Scholar] [CrossRef]
- Ree, J.H.; Kim, K.H.; Lim, H.B.; Seo, W.; Kim, S.S.; An, X.Y.; Kim, Y.H. Fault reactivation and propagation during the 2017 Pohang earthquake sequence. Geothermics 2021, 92, 102048. [Google Scholar] [CrossRef]
- Zhou, L.; Ren, X.Y.; Zhou, J.P.; Li, H.L.; Gan, Q. Numerical study on the induced seismicity through hydraulic fracturing in the deep heat mining project in Basel, Switzerland using a pseudo dynamic model and considering fully hydro-mechanical coupling. Geothermics 2022, 105, 102538. [Google Scholar] [CrossRef]
- Okoroafor, E.R.; Co, C.; Horne, R.N. Numerical investigation of the impact of fracture aperture anisotropy on EGS thermal performance. Geothermics 2022, 100, 102354. [Google Scholar] [CrossRef]
- Liao, J.X.; Hu, K.; Mehmood, F.; Xu, B.; Teng, Y.H.; Wang, H.; Hou, Z.M.; Xie, Y.C. Embedded discrete fracture network method for numerical estimation of long-term performance of CO2-EGS under THM coupled framework. Energy 2024, 285, 128734. [Google Scholar] [CrossRef]
- Sabah, M.; Ameri, M.J.; Hofmann, H.; Ebrahimi, M. Numerical modeling of injection-induced earthquakes based on fully coupled thermo-poroelastic boundary element method. Geothermics 2022, 105, 102481. [Google Scholar] [CrossRef]
- Yang, Y.; Hu, D.W.; Wang, H.Z.; Wang, Y.T.; Guo, D.B.; Zhou, H. Experimental study on Sc-CO2 fracturing of granite under real-time high temperature and true triaxial stress. Int. J. Rock Mech. Min. Sci. 2024, 183, 105889. [Google Scholar] [CrossRef]
- Tan, P.; Pang, H.; Jin, Y.; Zhou, Z. Experiments and analysis of hydraulic fracturing in hot dry rock geothermal reservoirs using an improved large-size high-temperature true triaxial apparatus. Nat. Gas Ind. B 2024, 11, 83–94. [Google Scholar] [CrossRef]
- Huang, J.; Qin, C.Z.; Niu, Y.; Li, R.; Song, Z.L.; Wang, X.D. A method for monitoring acoustic emissions in geological media under coupled 3-D stress and fluid flow. J. Pet. Sci. Eng. 2022, 211, 110227. [Google Scholar] [CrossRef]
- Li, M.H.; Yin, G.Z.; Xu, J.; Li, W.P.; Song, Z.L.; Jiang, C.B. A Novel True Triaxial Apparatus to Study the Geomechanical and Fluid Flow Aspects of Energy Exploitations in Geological Formations. Rock Mech. Rock Eng. 2016, 49, 4647–4659. [Google Scholar] [CrossRef]
- He, Y.T.; Guo, Y.T.; Bi, Z.H.; Guo, W.H.; Chang, X. Study of field-scale carbon dioxide fracturing in hot dry rock reservoir based on a new 3D-THM coupled discrete block model. Geoenergy Sci. Eng. 2025, 247, 213675. [Google Scholar] [CrossRef]
- Reutz, E.H.; Galland, O. The effect of weak Mohr-Coulomb layers on the onset of caldera collapse-A limit analysis modelling approach. J. Volcanol. Geotherm. Res. 2023, 433, 107727. [Google Scholar] [CrossRef]
- Fagereng, Å.; Remitti, F.; Sibson, R.H. Incrementally developed slickenfibers—Geological record of repeating low stress-drop seismic events? Tectonophysics 2011, 510, 381–386. [Google Scholar] [CrossRef]
- Caporali, A.; Bruyninx, C.; Fernandes, R.; Ganas, A.; Kenyeres, A.; Lidberg, M.; Stangl, G.; Steffen, H.; Zurutuza, J. Stress drop at the Kephalonia Transform Zone estimated from the 2014 seismic sequence. Tectonophysics 2016, 666, 164–172. [Google Scholar] [CrossRef]
- Song, Z.L.; Yin, G.Z.; Ranjith, P.G.; Li, M.H.; Huang, J.; Liu, C. Influence of the intermediate principal stress on sandstone failure. Rock Mech. Rock Eng. 2019, 52, 3033–3046. [Google Scholar] [CrossRef]
- Wu, Z.R.; Zheng, Y.L.; Deng, B.Z.; Deng, S.X. Influence of intermediate principal stress on rock strength: Insights from closed crack evolution under true triaxial compression. Theor. Appl. Fract. Mech. 2025, 136, 104786. [Google Scholar] [CrossRef]
- Zhang, J.J.; Guo, L.L.; Li, S.Z.; Tao, W.; Ji, W.T.; Guo, Y.S.; Zhao, S.J.; Zhang, J.X.; Wang, G.Z. Deformation mechanisms of compressional overlapping area in strike-slip fault zone: Insights from experimental simulation. J. Struct. Geol. 2025, 199, 105503. [Google Scholar] [CrossRef]
- Zhang, J.C.; Zheng, H.R.; Wang, G.L.; Liu, Z.Q.; Qi, Y.C.; Huang, Z.W.; Fan, X. In-situ stresses, abnormal pore pressures and their impacts on the Triassic Xujiahe reservoirs in tectonically active western Sichuan basin. Mar. Pet. Geol. 2020, 122, 104708. [Google Scholar] [CrossRef]
- Rucker, C.; Erickson, B.A. Physics-informed deep learning of rate-and-state fault friction. Comput. Methods Appl. Mech. Eng. 2024, 430, 117211. [Google Scholar] [CrossRef]
- An, M.K.; Yin, Z.Y.; Zhang, F.S.; Huang, R.; Elsworth, D. Rate-and-state friction of epidote gouge under hydrothermal conditions and implications for the stability of subducting faults under greenschist metamorphic conditions. Tectonophysics 2024, 890, 230497. [Google Scholar] [CrossRef]
- Rutter, E.; Hackston, A. On the effective stress law for rock-on-rock frictional sliding, and fault slip triggered by means of fluid injection. Philos. Trans. R. Soc. A 2017, 375, 20160001. [Google Scholar] [CrossRef]
- Rattez, H.; Disidoro, F.; Sulem, J.; Veveakis, M. Influence of dissolution on long-term frictional properties of carbonate fault gouge. Geomech. Energy Environ. 2021, 26, 100234. [Google Scholar] [CrossRef]
- Keranen, K.M.; Weingarten, M.; Abers, G.A.; Bekins, A.; Ge, S. Induced earthquakes. Sharp increase in central Oklahoma seismicity since 2008 induced by massive wastewater injection. Science 2014, 345, 448–451. [Google Scholar] [CrossRef]
- Weingarten, M.; Ge, S.; Godt, J.W.; Bekins, B.A.; Rubinstein, J.L. High-rate injection is associated with the increase in U.S. mid-continent seismicity. Science 2015, 348, 1336–1340. [Google Scholar] [CrossRef] [PubMed]
- Ellsworth, W.L. Injection-Induced Earthquakes. Science 2013, 341, 1225942. [Google Scholar] [CrossRef] [PubMed]
- Jiang, G.Y.; Barbour, A.J.; Skoumal, R.J.; Materna, K.; Taron, J.; Crandall-Bear, A. Relatively stable pressure effects and time-increasing thermal contraction control Heber geothermal field deformation. Nat. Commun. 2024, 15, 5159. [Google Scholar] [CrossRef] [PubMed]
- Koirala, R.; Kwiatek, G.; Shirzaei, M.; Brodsky, E.; Cladouhos, T.; Swyer, M.; Goebel, T. Induced seismicity and surface deformation associated with long-term and abrupt geothermal operations in Blue Mountain, Nevada. Earth Planet. Sci. Lett. 2024, 643, 118883. [Google Scholar] [CrossRef]
- Yeo, I.W.; Brown, M.R.M.; Ge, S.; Lee, K.K. Causal mechanism of injection-induced earthquakes through the Mw 5.5 Pohang earthquake case study. Nat. Commun. 2020, 11, 2614. [Google Scholar] [CrossRef]


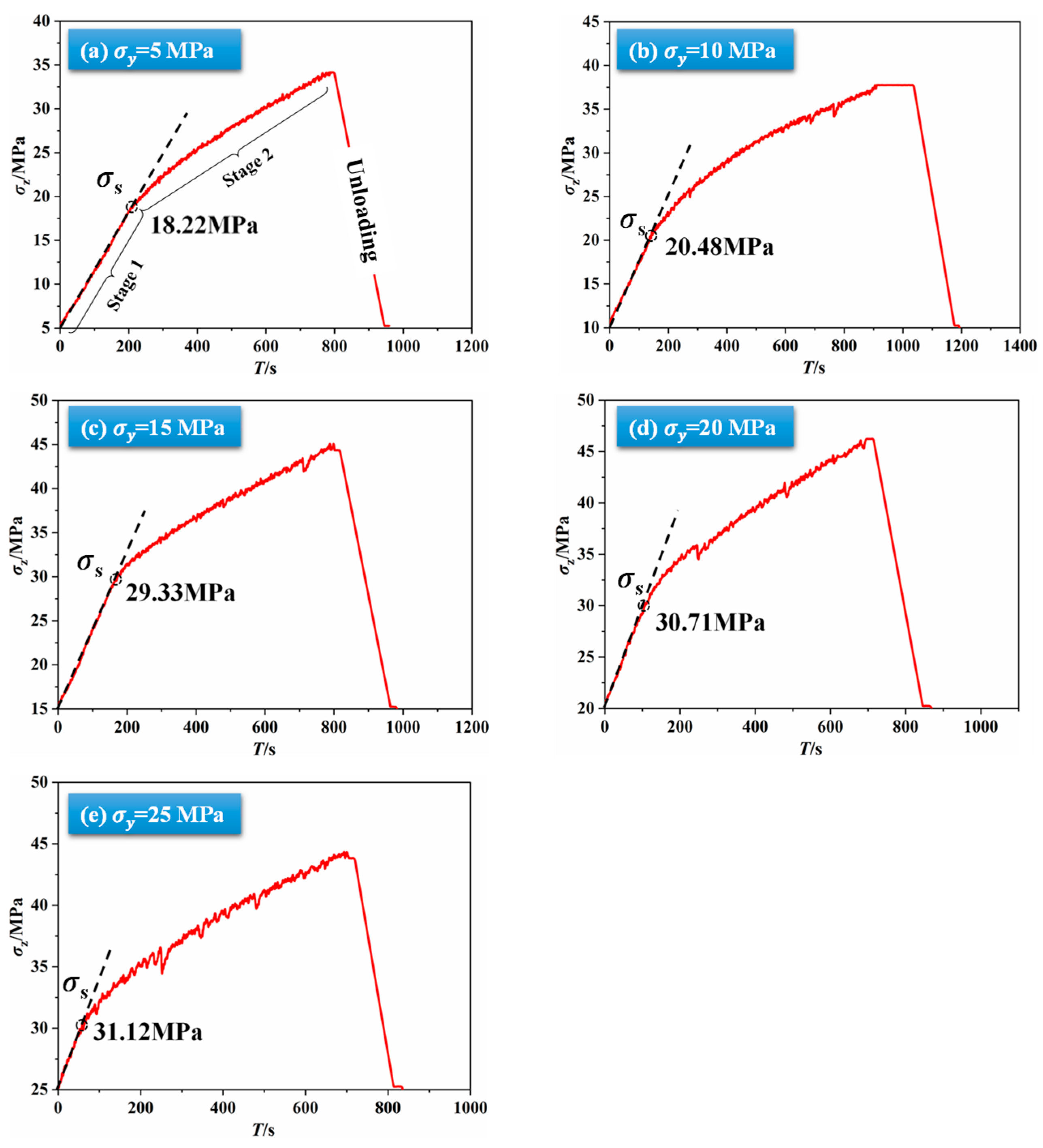
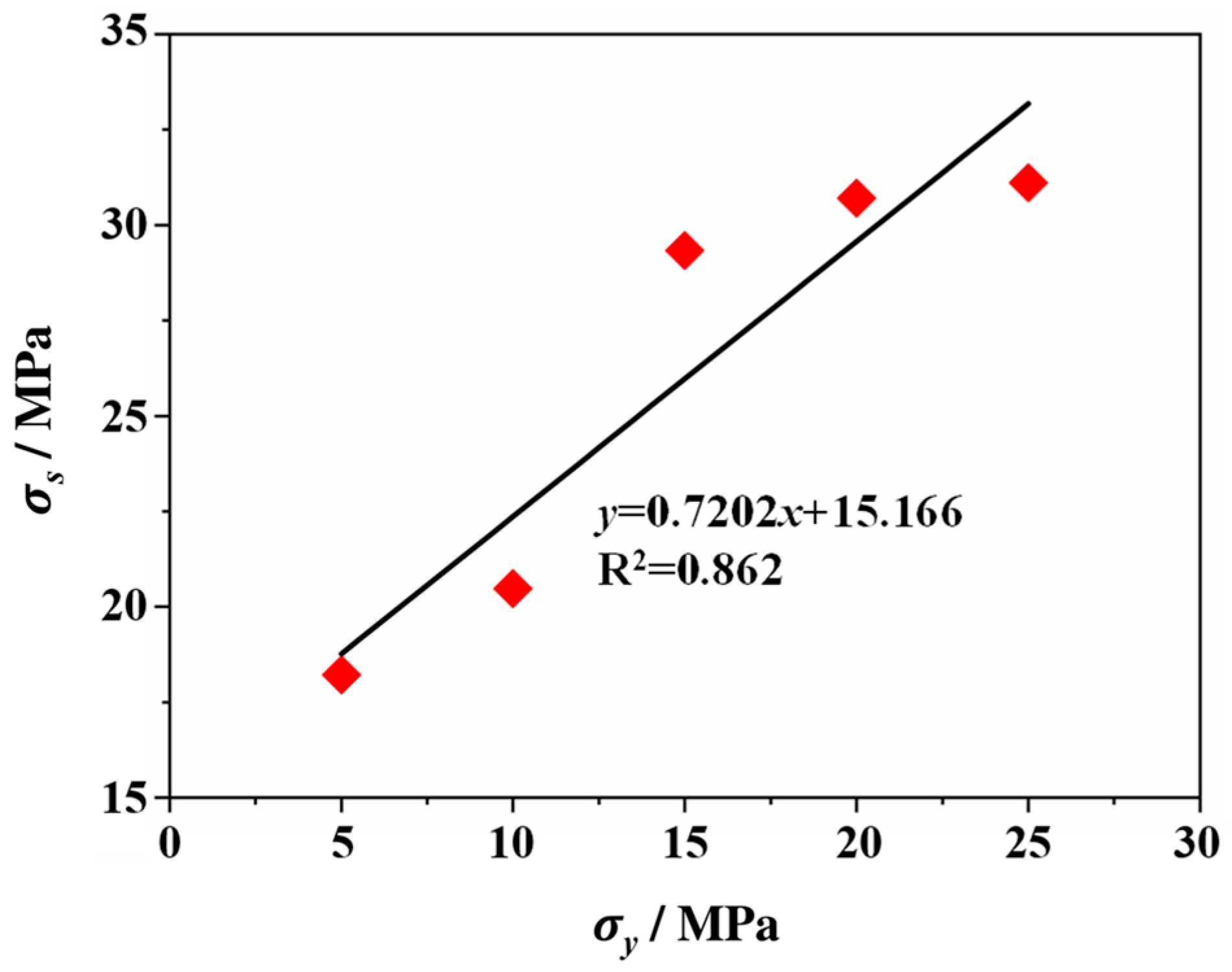
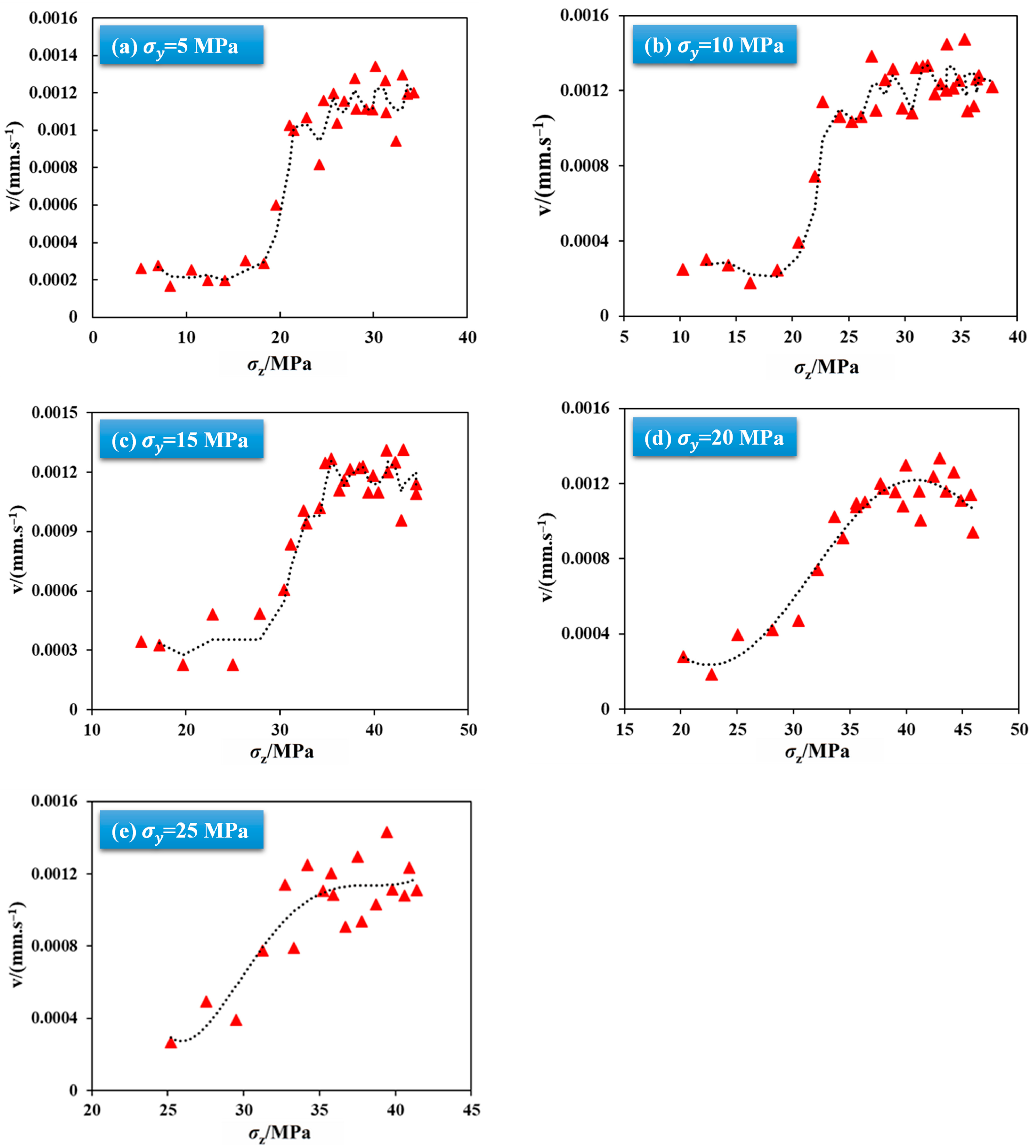

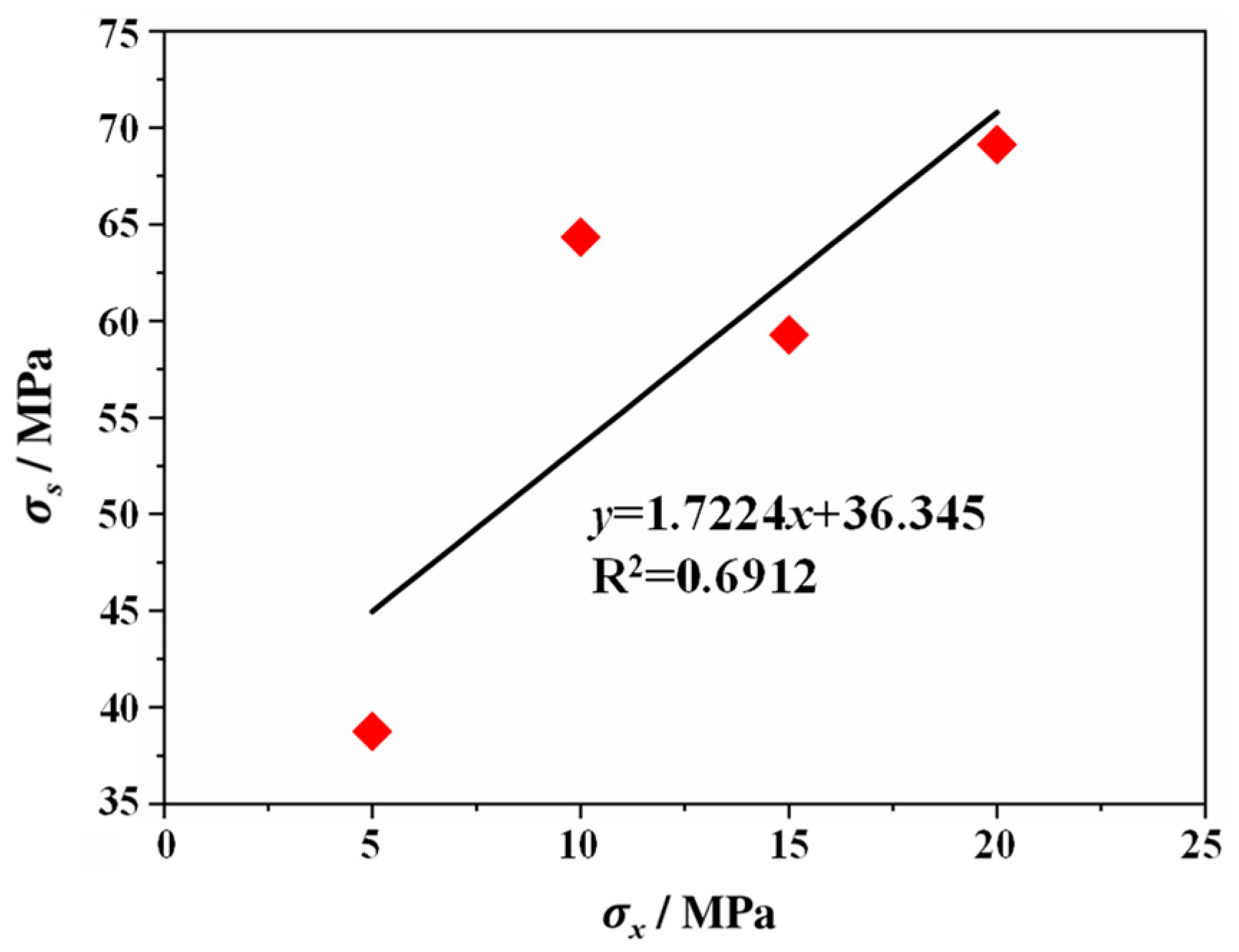


| Group | No. | σx (MPa) | σy (MPa) | P (MPa) | σz_r (mm/s) |
|---|---|---|---|---|---|
| I | 1 | 5 | 5 | 3 | 0.001 |
| 2 | 5 | 10 | |||
| 3 | 5 | 15 | |||
| 4 | 5 | 20 | |||
| 5 | 5 | 25 | |||
| II | 1 | 5 | 30 | 3 | 0.001 |
| 2 | 10 | 30 | |||
| 3 | 15 | 30 | |||
| 4 | 20 | 30 | |||
| III | 1 | 20 | 25 | 1 | 0.001 |
| 2 | 20 | 25 | 2 | ||
| 3 | 20 | 25 | 3 | ||
| 4 | 20 | 25 | 4 |
| σx (MPa) | σy (MPa) | P (MPa) | σz_r (mm/s) | σs (MPa) |
|---|---|---|---|---|
| 5 | 5 | 3 | 0.001 | 18.22 |
| 5 | 10 | 20.48 | ||
| 5 | 15 | 29.33 | ||
| 5 | 20 | 30.71 | ||
| 5 | 25 | 31.12 | ||
| 5 | 30 | 3 | 0.001 | 38.74 |
| 10 | 30 | 64.34 | ||
| 15 | 30 | 59.29 | ||
| 20 | 30 | 69.13 | ||
| 20 | 25 | 1 | 0.001 | 93.73 |
| 20 | 25 | 2 | 72.10 | |
| 20 | 25 | 3 | 66.41 | |
| 20 | 25 | 4 | 48.47 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, J.; Song, Z.; Zhao, H.; Liang, Q.; Huang, C. True Triaxial Investigation of the Effects of Principal Stresses and Injection Pressure on Induced Seismicity Behavior in Geothermal Reservoirs. Appl. Sci. 2025, 15, 10545. https://doi.org/10.3390/app151910545
Huang J, Song Z, Zhao H, Liang Q, Huang C. True Triaxial Investigation of the Effects of Principal Stresses and Injection Pressure on Induced Seismicity Behavior in Geothermal Reservoirs. Applied Sciences. 2025; 15(19):10545. https://doi.org/10.3390/app151910545
Chicago/Turabian StyleHuang, Jie, Zhenlong Song, Honggang Zhao, Qinming Liang, and Cheng Huang. 2025. "True Triaxial Investigation of the Effects of Principal Stresses and Injection Pressure on Induced Seismicity Behavior in Geothermal Reservoirs" Applied Sciences 15, no. 19: 10545. https://doi.org/10.3390/app151910545
APA StyleHuang, J., Song, Z., Zhao, H., Liang, Q., & Huang, C. (2025). True Triaxial Investigation of the Effects of Principal Stresses and Injection Pressure on Induced Seismicity Behavior in Geothermal Reservoirs. Applied Sciences, 15(19), 10545. https://doi.org/10.3390/app151910545





