Recursively Updated Probabilistic Model for Renewable Generation

Abstract

The Gaussian Mixture Model (GMM) is commonly used to formulate the probabilistic model for quantifying uncertainties in renewable generation. However, traditional static probabilistic models may not efficiently adapt and learn from newly forecasted and measured data. In this paper, we propose a recursively updated probabilistic model that leverages a recursive estimation method to update the parameters of the GMM based on continuously arriving data of renewable generation. This recursive modeling approach effectively incorporates new observations while discarding outdated samples, enabling the tracking of time-varying uncertainties in renewable generation in an incremental manner. Furthermore, we introduce an extra calibration stage to enhance the long-term accuracy of the probabilistic model after a large number of incremental updates. The main contribution is to address the potential degradation of performance caused by suboptimal incremental updates accumulated over time. Numerical tests demonstrate that the proposed model achieves 5–10% higher log likelihood in characterizing renewable generation uncertainties compared to purely recursive models, while reducing computational time by three to four orders of magnitude (1000 to 10,000 times) relative to conventional EM. These results highlight the proposed model’s suitability for real-time probabilistic modeling of renewable generation, with potential applications in system operation.

1. Introduction

The accelerating development of renewable generation has brought new challenges to the secure and economical operation of power systems [1,2], because its power output depends on fluctuating meteorological conditions such as wind speed and solar radiation [2,3,4].

In order to capture the uncertainties of renewable generation, it is crucial to establish the probabilistic model of actual power output beyond deterministic forecast values [5]. As a powerful probability density estimator, the Gaussian Mixture Model (GMM) is characterized by its outstanding flexibility to fit arbitrary multidimensional correlated random variables precisely [6]. Thus, GMM has been successfully applied to modeling spatial-temporal probabilistic characteristics of uncertain renewable generation [7,8].

Due to its favorable properties for chance-constrained programming, the GMM-based probabilistic model of renewable generation is also widely employed in the uncertainty-aware operation of power systems [9,10]. It serves as a robust tool for decision-making under uncertainty across a range of applications. For example, in unit commitment, the GMM helps optimize the day-ahead scheduling of generating units by probabilistically characterizing wind and solar power output [11]. Similarly, it is instrumental in economic dispatch [12,13,14,15], where it enables a more precise trade-off between operational costs and risks. Specifically, some studies use it to capture forecast errors [12] or embed it within a chance-constrained framework to enhance security [13], while others apply GMM to multi-area problems to efficiently handle uncertainty across interconnected grids [14,15]. Beyond this, the GMM proves crucial for the aggregation of distributed energy resources [16,17], as it provides a compact and accurate probabilistic representation of the collective output from numerous small generators, which is essential for effective grid management. The model also provides a powerful tool for the allocation of flexible ramping capacity [18,19] by quantifying the required ramping capability based on the probabilistic fluctuations of high-penetration renewable generation. By accurately modeling these needs, this approach helps optimize flexible resources like fast-ramping generators or energy storage systems to maintain grid balance and stability.

As a parametric probabilistic model, estimating parameters of GMM based on empirical data is essential to characterize spatial-temporal uncertainties of renewable generation precisely [20,21]. The well-known Expectation Maximization (EM) algorithm is the most acknowledged approach to estimate parameters of GMM from historical samples [22,23]. In the context of probabilistic modeling of renewable generation, the typical EM algorithm requires an offline training set composed of historical forecast and corresponding actual generation to tune parameters of GMM, and then the tuned GMM with static parameters is deployed online to predict uncertainties of renewable generation in the future [24].

In real-world power systems, numerous renewable energy sources continuously generate a large volume of data from forecast and measurement [25]. Probabilistic characteristics of renewable generation represented by these emerging samples are obviously time-varying due to meteorological fluctuations [26,27,28]. Static GMM trained on offline data cannot capture the non-stationary uncertainties of renewable generation in practice. Meanwhile, because the EM algorithm needs to traverse the entire dataset per iteration, re-estimating the parameters of GMM is a time-consuming and computationally intensive task considering the size of historical samples [29,30]. Thus, it is a critical issue to adjust parameters of GMM efficiently in response to continuously emerging data if we aim to track the time-varying uncertainties of renewable generation [31]. The ability to rapidly integrate new data streams into existing probabilistic models opens avenues for more responsive and adaptive decision-making in managing renewable energy resources.

In the field of machine learning and data mining, incremental or recursive estimation of Gaussian Mixture Model (GMM) parameters has garnered remarkable attention [32,33,34,35]. This approach is particularly advantageous as it addresses the significant computational burden associated with updating a probabilistic model dynamically [36,37]. Instead of relying on the entire dataset, the incremental update strategy modifies GMM parameters recursively using only information from new data samples. This recursive process allows for the efficient, on-the-fly adjustment of the model’s parameters as new data stream in, which is crucial for applications that require continuous model adaptation. This principle has been successfully extended to various domains, including the probabilistic modeling of renewable energy. For instance, the authors in [38] proposed a distributed variant of the incremental GMM update algorithm and applied it to the probabilistic modeling of wind power forecast errors. This demonstrates the practical utility of incremental GMM in handling large-scale dynamic data typical of modern power systems.

In this paper, we propose a comprehensive framework for updating the parameters of the GMM using continuously arriving samples. We focus on exploring the application of this framework as a recursively updated probabilistic model for renewable generation. This recursive update method addresses two main issues, which are often overlooked in existing research on incremental GMM.

Firstly, we introduce the calibration of GMM parameters to enhance the long-term performance of the probabilistic model after a large number of incremental updates. While previously proposed recursive update algorithms are computationally efficient, they do not guarantee the optimality of parameters. The inaccuracies accumulated after recursive updates may compromise the precision of the probabilistic model in characterizing the uncertainties of renewable generation. To mitigate this, we combine an efficient recursive update step with an auxiliary calibration step, periodically invoked to compensate for suboptimality introduced by the former and to prevent degradation of precision over time.

Secondly, our recursively updated probabilistic model allows for a bidirectional update of the training dataset by incorporating new observations of renewable generation while concurrently discarding outdated samples. This stands in contrast to previous research where the total size of the training dataset monotonically increases due to the continuous integration of new samples. As the archive of historical renewable generation grows, the decreasing ratio of upcoming new samples against existing samples weakens the influence of incremental updates. In contrast, our bidirectional update strategy mitigates the inflation of the training dataset by gradually replacing the oldest samples with new ones in an incremental manner. This ensures that the most recent samples are always emphasized, enabling the model to capture the latest trend of uncertainties more effectively.

The remainder of this paper is organized as follows: The probabilistic model of renewable generation with GMM and the conventional parameter estimation algorithm are introduced in Section 2 and Section 3 as prelude. The incremental update framework for GMM using streaming samples of renewable generation is proposed in Section 4. Section 5 presents the results of case study. Conclusions are drawn in Section 6.

2. Probabilistic Model of Renewable Generation with Gaussian Mixture Model

Suppose we have already obtained deterministic forecast curves of $N_R$ RESs with $T$ lookahead points. These forecasts can be denoted as a $N_R\times T$-dimensional vector (1) where $\mathrm{vec}$ represents the operator that reshapes the matrix as a vector. The corresponding actual power generated by $N_R$ RESs revealed after the forecast is denoted as ${\mathbf{P}}^a$ (2) with the same size of ${\mathbf{P}}^f$. The forecast error $\Delta P$ is defined as the difference between ${\mathbf{P}}^a$ and ${\mathbf{P}}^f$.

$${\mathbf{P}}^f=\mathrm{vec}\left(\left[\begin{array}{ccc}{P}_{1,1}^f& \dots & P_{1,T}^f\\ ⋮& \ddots & ⋮\\ P_{N_R,1}^f& \dots & P_{N_R,T}^f\end{array}\right]\right)$$

(1)

$${\mathbf{P}}^a=\mathrm{vec}\left(\left[\begin{array}{ccc}{P}_{1,1}^a& \dots & P_{1,T}^a\\ ⋮& \ddots & ⋮\\ P_{N_R,1}^a& \dots & P_{N_R,T}^a\end{array}\right]\right)$$

(2)

$$\Delta P={\mathbf{P}}^a-{\mathbf{P}}^f$$

(3)

If ${\mathbf{P}}^f$ and ${\mathbf{P}}^a$ are concatenated into a new $2\times N_R\times T$-dimensional vector ${\mathbf{P}}^{ob}$ to include the observed pairs between the forecast and the actual generation, the joint probability distribution of ${\mathbf{P}}^{ob}$ can be described by the Gaussian Mixture Model (GMM). ${\omega }_k,{\mathsf{\mu }}^k,{\mathbf{\Sigma }}^k$ denote the weight, expectation, and covariance matrix of each Gaussian component in GMM, respectively.

$${\mathbf{P}}^{ob}=\left[\begin{array}{c}{\mathbf{P}}^f\\ {\mathbf{P}}^a\end{array}\right]$$

(4)

$$PD{F}_{{\mathbf{P}}^{ob}}\left(x\right)={\displaystyle \sum _{k=1}^K{\omega }_{k}N\left(\mathbf{x}|{\mathsf{\mu }}^k,{\mathbf{\Sigma }}^k\right)}$$

(5)

$$N\left(x|\mathsf{\mu },\mathbf{\Sigma }\right)=\frac{\exp \left(-\frac{1}{2}{\left(\mathbf{x}-\mathsf{\mu }\right)}^T{\mathbf{\Sigma }}^{-1}\left(\mathbf{x}-\mathsf{\mu }\right)\right)}{\sqrt{{\left(2\pi \right)}^{\dim \left(\mathbf{x}\right)}\det \left(\mathbf{\Sigma }\right)}}$$

(6)

$${\displaystyle \sum _{k=1}^K{\omega }_k}=1,{\omega }_k>0$$

(7)

The mean vector and covariance matrix can be separated by different parts of ${\mathbf{P}}^{ob}$.

$${\mathsf{\mu }}^k=\left[\begin{array}{c}{\mathsf{\mu }}_f^k\\ {\mathsf{\mu }}_a^k\end{array}\right]$$

(8)

$${\mathbf{\Sigma }}^k=\left[\begin{array}{cc}{\mathbf{\Sigma }}_{ff}^k& {\mathbf{\Sigma }}_{fa}^k\\ {\mathbf{\Sigma }}_{af}^k& {\mathbf{\Sigma }}_{aa}^k\end{array}\right]$$

(9)

Once the joint probability model of ${\mathbf{P}}^{ob}$ is revealed, we are more interested in the conditional distribution of the actual generation ${\mathbf{P}}^a$ with respect to the deterministic forecast value known as ${\mathbf{P}}^{fcst}$ in advance. As pointed out by [2], the conditional distribution of ${\mathbf{P}}^a$ is still an $N_R\times T$-dimensional GMM whose parameters can be inferred from the joint probability model of ${\mathbf{P}}^{ob}$ analytically.

$$PD{F}_{{\mathbf{P}}^a}\left(x\left|{\mathbf{P}}^f={\mathbf{P}}^{fcst}\right.\right)={\displaystyle \sum _{k=1}^K{\overline{\omega }}_{k}N\left(\mathbf{x}|{\overline{\mu }}^k,{\overline{\Sigma }}^k\right)}$$

(10)

$${\overline{\omega }}_k=\frac{{\omega }_{k}N\left({\mathbf{p}}^{fcst}\left|{\mathsf{\mu }}_f^k,{\mathbf{\Sigma }}_f^k\right.\right)}{{\displaystyle \sum _{k=1}^K{\omega }_{k}N\left({\mathbf{p}}^{fcst}\left|{\mathsf{\mu }}_f^k,{\Sigma }_f^k\right.\right)}}$$

(11)

$${\overline{\mathsf{\mu }}}_k={\mathsf{\mu }}_a^k+{\mathbf{\Sigma }}_{af}^k{\left({\mathbf{\Sigma }}_{ff}^k\right)}^{-1}\left({\mathbf{p}}^{fcst}-{\mathsf{\mu }}_f^k\right)$$

(12)

$${\overline{\Sigma }}^k={\mathbf{\Sigma }}_{aa}^k-{\mathbf{\Sigma }}_{af}^k{\left({\mathbf{\Sigma }}_{ff}^k\right)}^{-1}{\mathbf{\Sigma }}_{fa}^k$$

(13)

The conditional distribution of forecast error $\Delta P$ is described as a GMM as well.

$$\begin{array}{ccc}PD{F}_{\Delta P}\left(\mathbf{x}\left|{\mathbf{P}}^f={\mathbf{p}}^{fcst}\right.\right)& =& PD{F}_{{\mathbf{P}}^a}\left(\mathbf{x}+{\mathbf{p}}^{fcst}\left|{\mathbf{P}}^f={\mathbf{p}}^{fcst}\right.\right)\\ & =& {\displaystyle \sum _{k=1}^K{\overline{\omega }}_{k}N\left(\mathbf{x}+{\mathbf{p}}^{fcst}|{\overline{\mathsf{\mu }}}^k,{\overline{\Sigma }}^k\right)}\end{array}$$

(14)

3. Parameter Estimation Algorithm for Probabilistic Model of Renewable Generation

As mentioned in Section 2, the key to an accurate model of renewable generation is the joint probability distribution of ${\mathbf{P}}^{ob}$ (5). The parameters of GMM $\mathsf{\Theta }$ (including weight, expectation, and covariance matrix of each Gaussian component) in (5) can be efficiently estimated by the Expectation Maximization (EM) algorithm. We will introduce the outline of the EM algorithm as the prerequisite of its incremental variation.

$$\mathsf{\Theta }=\left\{{\omega }_k,{\mathsf{\mu }}^k,{\mathbf{\Sigma }}^k\left|k=1,2,\dots K\right.\right\}$$

(15)

Step 1: $N$ samples of ${\mathbf{P}}^{ob}$ composed of historical forecast and actual generation data, $\left[{\mathbf{X}}_1,{\mathbf{X}}_2,\dots {\mathbf{X}}_N\right]$, are collected to formulate the training set.

Step 2: With the given number of components in GMM $K$, the parameters of GMM $\mathsf{\Theta }$ are initialized to bootstrap the EM algorithm. A commonly used approach is to execute k-means algorithm with $K$ clusters on the training set, then the parameters of the kth component is calculated based on training samples in the kth cluster ${\Omega }_k$. $N_k$ denotes the number of training samples belonging to ${\Omega }_k$.

$$w_k=\frac{N_k}{N}$$

(16)

$${\mathsf{\mu }}^k=\frac{1}{N_k}{\displaystyle \sum _{i\in {\Omega }_k}{\mathbf{X}}_i}$$

(17)

$${\mathbf{\Sigma }}^k=\frac{1}{N_k}{\displaystyle \sum _{i\in {\Omega }_k}\left({\mathbf{X}}_i-{\mathsf{\mu }}^k\right){\left({\mathbf{X}}_i-{\mathsf{\mu }}^k\right)}^T}$$

(18)

Step 3 (Expectation step, E-step): The responsibility of each training sample to each Gaussian component based on current parameters of GMM.

$$r_i^k=\frac{{\omega }_{k}N\left({\mathbf{X}}_i|{\mathsf{\mu }}^k,{\mathbf{\Sigma }}^k\right)}{{\displaystyle \sum _{k=1}^K{\omega }_{k}N\left({\mathbf{X}}_i|{\mathsf{\mu }}^k,{\mathbf{\Sigma }}^k\right)}}\left(i=1,2,\dots ,N\right)$$

(19)

Step 4 (Maximization step, M-step): The parameters of GMM are adjusted to maximize the total likelihood of training samples.

$$w_k=\frac{1}{N}{\displaystyle \sum _{i=1}^N{r}_i^k}$$

(20)

$${\mathsf{\mu }}^k=\frac{1}{{\displaystyle \sum _{i=1}^N{r}_i^k}}{\displaystyle \sum _{i=1}^N{r}_i^k{\mathbf{X}}_i}$$

(21)

$${\mathbf{\Sigma }}^k=\frac{1}{{\displaystyle \sum _{i=1}^N{r}_i^k}}{\displaystyle \sum _{i=1}^N{r}_i^k\left({\mathbf{X}}_i-{\mathsf{\mu }}^k\right){\left({\mathbf{X}}_i-{\mathsf{\mu }}^k\right)}^T}$$

(22)

Step 5: The log likelihood of training samples is calculated and compared with the result from the previous iteration. If their difference is smaller than the tolerable criteria, the EM algorithm has converged; otherwise, steps three and four are iteratively repeated to further improve the parameters of GMM.

$$\begin{array}{ccc}\mathcal{l}& =& \log {\displaystyle \prod _{i=1}^N\left[{\displaystyle \sum _{k=1}^K{\omega }_{k}N\left({\mathbf{X}}_i|{\mathsf{\mu }}^k,{\mathbf{\Sigma }}^k\right)}\right]}\\ & =& {\displaystyle \sum _{i=1}^N\log \left[{\displaystyle \sum _{k=1}^K{\omega }_{k}N\left({\mathbf{X}}_i|{\mathsf{\mu }}^k,{\mathbf{\Sigma }}^k\right)}\right]}\end{array}$$

(23)

Following these steps from one to five, we can effectively estimate the parameters of GMM with the goal of maximizing log likelihood of the whole training set under GMM.

4. Recursive Parameter Update for Streaming Samples of Renewable Generation

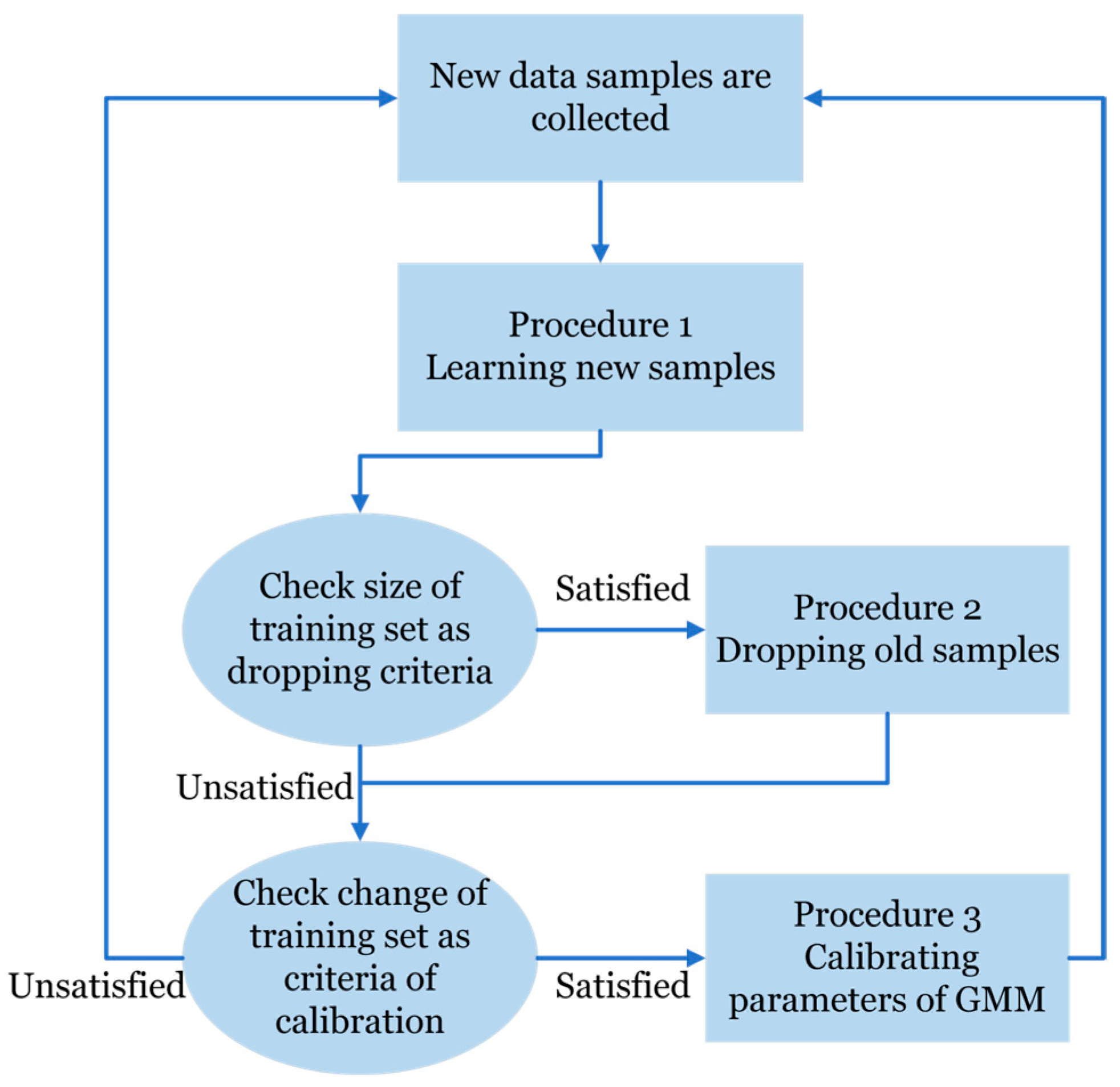
After estimating parameters in the joint probability distribution of ${\mathbf{P}}^{ob}$ (5), it can be employed to infer the conditional distribution of actual renewable generation based on the latest forecast values. During the operation of power systems, the forecasts of renewable generation and their corresponding actual values are continuously updated and cumulated in a streaming fashion. It is important to consolidate the recent observations of renewable generation with the pre-trained probabilistic model to improve its accuracy. Although we can abandon the existing model completely and estimate the parameters of GMM from scratch on the extended training set including new samples, this naïve approach is not scalable and highly inefficient for online application. Thus, we use the following three procedures to recursively update the parameters of joint probability distribution of ${\mathbf{P}}^{ob}$ by keeping track of the newly collected data samples with moderate computational overhead: First, learning new samples ensures that the probabilistic model incorporates the most recent forecast and measurement data of renewable generation, thereby capturing the latest time-varying uncertainty patterns. Second, removing old samples prevents outdated information from dominating the training set and ensures that the model emphasizes current conditions instead of being diluted by obsolete data. Third, calibration of parameters is introduced to correct suboptimality accumulated after multiple incremental updates.

4.1. Procedure 1 (Learning New Samples)

When $M$ new samples of ${\mathbf{P}}^{ob}$ are collected, the E-step and M-step in the original EM algorithm are adapted to update the parameters without traversing existing training samples.

In the E-step, we calculate responsibilities of new samples with existing parameters of GMM:

$$r_i^k=\frac{{\omega }_{k}N\left({\mathbf{X}}_i|{\mathsf{\mu }}^k,{\mathbf{\Sigma }}^k\right)}{{\displaystyle \sum _{k=1}^K{\omega }_{k}N\left({\mathbf{X}}_i|{\mathsf{\mu }}^k,{\mathbf{\Sigma }}^k\right)}}\left(i=N+1,\dots ,N+M\right)$$

(24)

In the M-step, the parameters should be updated using the extended training set with $N+M$ samples.

$$w_k^{new}=\frac{1}{N+M}{\displaystyle \sum _{i=1}^{N+M}{r}_i^k}$$

(25)

$${\mathsf{\mu }}^{k,new}=\frac{1}{{\displaystyle \sum _{i=1}^{N+M}{r}_i^k}}{\displaystyle \sum _{i=1}^{N+M}{r}_i^k{\mathbf{X}}_i}$$

(26)

$${\mathbf{\Sigma }}^{k,new}=\frac{1}{{\displaystyle \sum _{i=1}^{N+M}{r}_i^k}}{\displaystyle \sum _{i=1}^{N+M}{r}_i^k\left({\mathbf{X}}_i-{\mathsf{\mu }}^{k,new}\right){\left({\mathbf{X}}_i-{\mathsf{\mu }}^{k,new}\right)}^T}$$

(27)

By observing the difference between (25)–(27) and (20)–(22), the parameter update formulas above can be rewritten in the following equivalent recursive forms, (28)–(30), to avoid duplicate computation on the old training samples. The update formula of covariance matrix (30) depends on the equality (31).

$$w_k^{new}=\frac{1}{N+M}\left(N{w}_k+{\displaystyle \sum _{i=N+1}^{N+M}{r}_i^k}\right)$$

(28)

$$\begin{array}{ccc}{\mathsf{\mu }}^{k,new}& =& \frac{1}{{\displaystyle \sum _{i=1}^{N+M}{r}_i^k}}\left({\mathsf{\mu }}^k{\displaystyle \sum _{i=1}^N{r}_i^k}+{\displaystyle \sum _{i=N+1}^{N+M}{r}_i^k{\mathbf{X}}_i}\right)\\ & =& {\mathsf{\mu }}^k+\frac{1}{{\displaystyle \sum _{i=1}^{N+M}{r}_i^k}}{\displaystyle \sum _{i=N+1}^{N+M}{r}_i^k\left({\mathbf{X}}_i-{\mathsf{\mu }}^k\right)}\\ & =& {\mathsf{\mu }}^k+\frac{1}{\left(N+M\right)w_k^{new}}{\displaystyle \sum _{i=N+1}^{N+M}{r}_i^k\left({\mathbf{X}}_i-{\mathsf{\mu }}^k\right)}\end{array}$$

(29)

$$\begin{array}{cc}{\mathbf{\Sigma }}^{k,new}& =\frac{1}{{\displaystyle \sum _{i=1}^{N+M}{r}_i^k}}\left(\begin{array}{l}{\displaystyle \sum _{i=1}^N{r}_i^k\left({\mathbf{X}}_i-{\mathsf{\mu }}^{k,new}\right){\left({\mathbf{X}}_i-{\mathsf{\mu }}^{k,new}\right)}^T}+\\ {\displaystyle \sum _{i=N+1}^{N+M}{r}_i^k\left({\mathbf{X}}_i-{\mathsf{\mu }}^{k,new}\right){\left({\mathbf{X}}_i-{\mathsf{\mu }}^{k,new}\right)}^T}\end{array}\right)\\ & =\frac{N{w}_k}{\left(N+M\right)w_k^{new}}{\mathbf{\Sigma }}^k+\hfill \\ & \frac{N{w}_k}{\left(N+M\right)w_k^{new}}\left({\mathsf{\mu }}^k-{\mathsf{\mu }}^{k,new}\right){\left({\mathsf{\mu }}^k-{\mathsf{\mu }}^{k,new}\right)}^T+\hfill \\ & \frac{1}{\left(N+M\right)w_k^{new}}{\displaystyle \sum _{i=N+1}^{N+M}{r}_i^k\left({\mathbf{X}}_i-{\mathsf{\mu }}^{k,new}\right){\left({\mathbf{X}}_i-{\mathsf{\mu }}^{k,new}\right)}^T}\hfill \end{array}$$

(30)

$$\begin{array}{l}{\displaystyle \sum _{i=1}^N{r}_i^k\left({\mathbf{X}}_i-{\mathsf{\mu }}^{k,new}\right){\left({\mathbf{X}}_i-{\mathsf{\mu }}^{k,new}\right)}^T}\\ ={\displaystyle \sum _{i=1}^N{r}_i^k\left[\left({\mathbf{X}}_i-{\mathsf{\mu }}^k\right)+\left({\mathsf{\mu }}^k-{\mathsf{\mu }}^{k,new}\right)\right]{\left[\left({\mathbf{X}}_i-{\mathsf{\mu }}^k\right)+\left({\mathsf{\mu }}^k-{\mathsf{\mu }}^{k,new}\right)\right]}^T}\\ ={\displaystyle \sum _{i=1}^N{r}_i^k\left[\left({\mathbf{X}}_i-{\mathsf{\mu }}^k\right){\left({\mathbf{X}}_i-{\mathsf{\mu }}^k\right)}^T+\left({\mathsf{\mu }}^k-{\mathsf{\mu }}^{k,new}\right){\left({\mathsf{\mu }}^k-{\mathsf{\mu }}^{k,new}\right)}^T\right]}+\\ 2\left[{\displaystyle \sum _{i=1}^N{r}_i^k\left({\mathbf{X}}_i-{\mathsf{\mu }}^k\right)}\right]{\left({\mathsf{\mu }}^k-{\mathsf{\mu }}^{k,new}\right)}^T\\ ={\displaystyle \sum _{i=1}^N{r}_i^k}\left[{\mathbf{\Sigma }}^k+\left({\mathsf{\mu }}^k-{\mathsf{\mu }}^{k,new}\right){\left({\mathsf{\mu }}^k-{\mathsf{\mu }}^{k,new}\right)}^T\right]\end{array}$$

(31)

Because PDF formula of GMM contains the inverse of covariance matrix, Cholesky decomposition of each covariance matrix (32) where Cholesky factor $L$ is a lower triangular matrix is calculated and stored to avoid computing its inverse explicitly. ${\mathbf{\Sigma }}^{-1}\left(\mathbf{x}-\mathsf{\mu }\right)$ can be obtained by solving the linear systems $Ly=x-\mathsf{\mu }$ and ${\mathbf{L}}^{T}z=y$.

$$\mathbf{\Sigma }=L{\mathbf{L}}^T$$

(32)

Calculating the determinant of the covariance matrix is also straightforward with Cholesky decomposition.

$$\det \left(\mathbf{\Sigma }\right)={\left({\displaystyle \prod _{i=1}^{\dim \left(\mathbf{X}\right)}{L}_{ii}}\right)}^2$$

(33)

The computational complexity of calculating Cholesky decomposition of an $n\times n$ matrix is $O\left(n^3\right)$. However, Cholesky decomposition can be recursively updated with only $O\left(n^2\right)$ computations for basic operations:

1.

Scaling operation: If matrix $\Sigma$ is multiplied by a constant coefficient $c$, its Cholesky factor is multiplied by $\sqrt{c}$.

$$\tilde{\Sigma }=c\mathbf{\Sigma }=\tilde{L}{\tilde{L}}^T$$

(34)

$$\tilde{L}=\left(\sqrt{c}\right)L$$

(35)

2.

Rank-1 update operation: If matrix $\Sigma$ is updated by a rank-1 matrix (36) where $v$ is a vector, its Cholesky decomposition can be updated with $O\left(n^2\right)$ complexity. The detailed algorithm can be found in Section 6.5.4 of [39] and omitted here. There have been several implementations in well-known numerical software, such as cholupdate in MATLAB (R2024a) and lowrankupdate in Julia (1.10.2).

$$\tilde{\Sigma }=\mathbf{\Sigma }+v{\mathbf{v}}^T$$

(36)

The recursive update formula of covariance (30) is composed of one scaling operation and $M+1$ rank-1 update operations. Thus, Cholesky decomposition of the covariance matrix can also be updated recursively to reuse existing Cholesky factors.

4.2. Procedure Two (Removing Old Samples)

In parallel to learning new samples, we also want to remove some old samples from the training set to restrict its size and accommodate more recently updated samples. Here, we assume the $M$ oldest samples of ${\mathbf{P}}^{ob}$ (from No. 1 to No. $M$) are selected to be removed. The adapted versions of E-step and M-step for removing old samples are presented as follows:

In the E-step, responsibilities of old samples $r_i^k\left(i=1,\dots ,M\right)$ are retrieved from historical computational traces directly.

In the M-step, the parameters should be updated using the reduced training set with $N-M$ samples.

$$w_k^{new}=\frac{1}{N-M}{\displaystyle \sum _{i=M+1}^N{r}_i^k}$$

(37)

$${\mathsf{\mu }}^{k,new}=\frac{1}{{\displaystyle \sum _{i=M+1}^N{r}_i^k}}{\displaystyle \sum _{i=M+1}^N{r}_i^k{\mathbf{X}}_i}$$

(38)

$${\mathbf{\Sigma }}^{k,new}=\frac{1}{{\displaystyle \sum _{i=M+1}^N{r}_i^k}}{\displaystyle \sum _{i=M+1}^N{r}_i^k\left({\mathbf{X}}_i-{\mathsf{\mu }}^{k,new}\right){\left({\mathbf{X}}_i-{\mathsf{\mu }}^{k,new}\right)}^T}$$

(39)

Like learning new samples, the parameter update formulas can be rewritten in equivalent recursive forms to avoid computation on unaffected training samples.

$$w_k^{new}=\frac{1}{N-M}\left(N{w}_k-{\displaystyle \sum _{i=1}^M{r}_i^k}\right)$$

(40)

$$\begin{array}{ccc}{\mathsf{\mu }}^{k,new}& =& \frac{1}{{\displaystyle \sum _{i=M+1}^N{r}_i^k}}\left({\mathsf{\mu }}^k{\displaystyle \sum _{i=1}^N{r}_i^k}-{\displaystyle \sum _{i=1}^M{r}_i^k{\mathbf{X}}_i}\right)\\ & =& {\mathsf{\mu }}^k-\frac{1}{{\displaystyle \sum _{i=M+1}^N{r}_i^k}}{\displaystyle \sum _{i=1}^M{r}_i^k\left({\mathbf{X}}_i-{\mathsf{\mu }}^k\right)}\\ & =& {\mathsf{\mu }}^k-\frac{1}{\left(N-M\right)w_k^{new}}{\displaystyle \sum _{i=1}^M{r}_i^k\left({\mathbf{X}}_i-{\mathsf{\mu }}^k\right)}\end{array}$$

(41)

$$\begin{array}{cc}{\mathbf{\Sigma }}^{k,new}& =\frac{1}{{\displaystyle \sum _{i=M+1}^N{r}_i^k}}\left(\begin{array}{l}{\displaystyle \sum _{i=1}^N{r}_i^k\left({\mathbf{X}}_i-{\mathsf{\mu }}^{k,new}\right){\left({\mathbf{X}}_i-{\mathsf{\mu }}^{k,new}\right)}^T}-\\ {\displaystyle \sum _{i=1}^M{r}_i^k\left({\mathbf{X}}_i-{\mathsf{\mu }}^{k,new}\right){\left({\mathbf{X}}_i-{\mathsf{\mu }}^{k,new}\right)}^T}\end{array}\right)\hfill \\ & =\frac{N{w}_k}{\left(N-M\right)w_k^{new}}{\mathbf{\Sigma }}^k+\hfill \\ & \frac{N{w}_k}{\left(N-M\right)w_k^{new}}\left({\mathsf{\mu }}^k-{\mathsf{\mu }}^{k,new}\right){\left({\mathsf{\mu }}^k-{\mathsf{\mu }}^{k,new}\right)}^T-\hfill \\ & \frac{1}{\left(N-M\right)w_k^{new}}{\displaystyle \sum _{i=1}^M{r}_i^k\left({\mathbf{X}}_i-{\mathsf{\mu }}^{k,new}\right){\left({\mathbf{X}}_i-{\mathsf{\mu }}^{k,new}\right)}^T}\hfill \end{array}$$

(42)

4.3. Procedure Three (Calibration of GMM)

Learning new samples and removing old samples can be regarded as one adaptive E-step and M-step to update the parameters of GMM for renewable generation, where the convergence of parameter estimation is not achieved to ensure its optimality. Consequently, suboptimality might be accumulated after executing these incremental update procedures multiple times and undermining the performance and accuracy of GMM as a probabilistic model of renewable generation.

Thus, full-scale E-step and M-step should be executed on the whole training set (including both updated samples and initial samples not removed) for several iterations to calibrate parameters of the GMM. The algorithm has been described Section 2.

4.4. General Framework for Recursive Probabilistic Model

As illustrated in the flow chart in Figure 1, we propose the following framework to maintain a recursive probabilistic model of renewable generation based on continuously updated samples by composing three kinds of procedures discussed above.

• When new observations of renewable generation including forecast and actual generation are collected, procedure one is invoked to extend the training and update the parameters of probabilistic model.
• The size of the training set is used as the criterion to determine whether some old samples should be removed to keep its compactness. If the size is beyond the determined threshold, some old samples are disposed from the training set and procedure two is invoked to update the parameters of the probabilistic model accordingly.
• When the probabilistic model of forecast errors experiences multiple rounds of recursive updates, including learning new samples and removing old samples, its parameters should be calibrated by procedure three periodically. The change in training set is regarded as the triggering criteria of calibration. For example, we can invoke the calibration procedure if 5% of samples in the training set are replaced by new samples since the last calibration.

Remark (Analysis of computational complexity): For procedure one (learning new samples) and two (removing old samples), the computational complexity of their update formulas for parameters (28)–(30) and (40)–(42) is $O\left(MK{D}^2\right)$ where $D$ is the dimension of data samples ($D=2N_{R}T$ in our case). The performance of recursive update procedures is only related to the size of the alternated data samples and not affected by the size of the whole training set. Thus, they can be invoked frequently to deal with streaming samples without much computational effort.

Comparatively, a full-scale update of parameters (20)–(22) requires $O\left(NK{D}^2\right)$ operations. Because the alternated samples represent only a small fraction of the overall training set $M\ll N$, calibrating the model parameters is a more computationally expensive operation and should therefore be performed at a lower frequency.

5. Numerical Tests

The techno-economic WIND toolkit [40] from NREL serves as the data source for renewable generation in this section. The whole dataset contains aligned forecast and actual generation data for wind power for seven years at 120,000 sites in the US. The forecast data are available at a 1 h resolution for 1 h, 4 h, 6 h, and 24 h forecast horizons, and the actual generation is available at a 5 min resolution estimated from meteorological data. The 6 h ahead forecast and actual wind power generation of 40 sites (No. 205–244) are chosen as examples to establish the complete sample set of ${\mathbf{P}}^{ob}$ ($N_R=40,T=6$) with 1 h resolution for 7 years, where the actual generation is down sampled to align with forecast data. The dimension of ${\mathbf{P}}^{ob}$ is $2\times N_R\times T=480$. All numerical tests are implemented in Julia and executed on a laptop with Intel i7-1360P CPU and 32GB RAM.

The numerical tests are separated into two parts with different emphasis on precision and computational efficiency of the proposed recursively updated probabilistic model.

5.1. Comparing Precision to Characterize Uncertainties of Renewable Generation

We designed the following steps to emulate the continuous process of collecting new samples of ${\mathbf{P}}^{ob}$, updating the probabilistic model, and predicting the probability distribution of actual generation on the fly.

Step 1: The first 8760 samples of ${\mathbf{P}}^{ob}$ (for one entire year) are selected as the initial training set and the EM algorithm is employed to obtain the parameters of GMM for ${\mathbf{P}}^{ob}$.

Step 2: The next $N_{test}$ observations of ${\mathbf{P}}^{ob}$ are used to evaluate the performance of the probabilistic model of ${\mathbf{P}}^{ob}$. For each observation of forecast generation, with ${\mathbf{P}}^f$ denoted as ${\mathbf{p}}^{fcst}$, we can obtain the conditional distribution of actual generation ${\mathbf{P}}^a$ based on the GMM of ${\mathbf{P}}^{ob}$ according to (10). The log likelihood of corresponding actual generation ${\mathbf{p}}^{actl}$ under the conditional distribution is calculated as the performance index because higher likelihood means that the GMM of ${\mathbf{P}}^{ob}$ provides more precise characterization for randomness of wind power to predict actual generation based on the forecast value.

$$\begin{array}{c}L=\log \left[PD{F}_{{\mathbf{P}}^a}\left({\mathbf{p}}^{actl}\left|{\mathbf{P}}^f={\mathbf{p}}^{fcst}\right.\right)\right]\\ =\log \left[{\displaystyle \sum _{k=1}^K{\overline{\omega }}_{k}N\left({\mathbf{p}}^{actl}|{\overline{\mu }}^k,{\overline{\Sigma }}^k\right)}\right]\end{array}$$

(43)

Step 3: The $N_{test}$ observations of ${\mathbf{P}}^{ob}$ in step two are absorbed into the training set. If the total number of training samples $N$ exceeds the predetermined upper bound $N_{\max }$, the oldest $N-N_{app}$ samples are discarded to reduce the size of training set to an appropriate level $N_{app}$.

Step 4: The parameters of the GMM are updated according to the change in training samples in step three, and then we go back to step two and evaluate the performance of the probabilistic model of ${\mathbf{P}}^{ob}$ on new observations.

Steps two to four above are executed for $N_{iter}$ iterations, and all the parameters in our numerical tests are set as follows:

$$N_{iter}=3000,N_{test}=3,N_{\max }=20000,N_{app}=16000$$

(44)

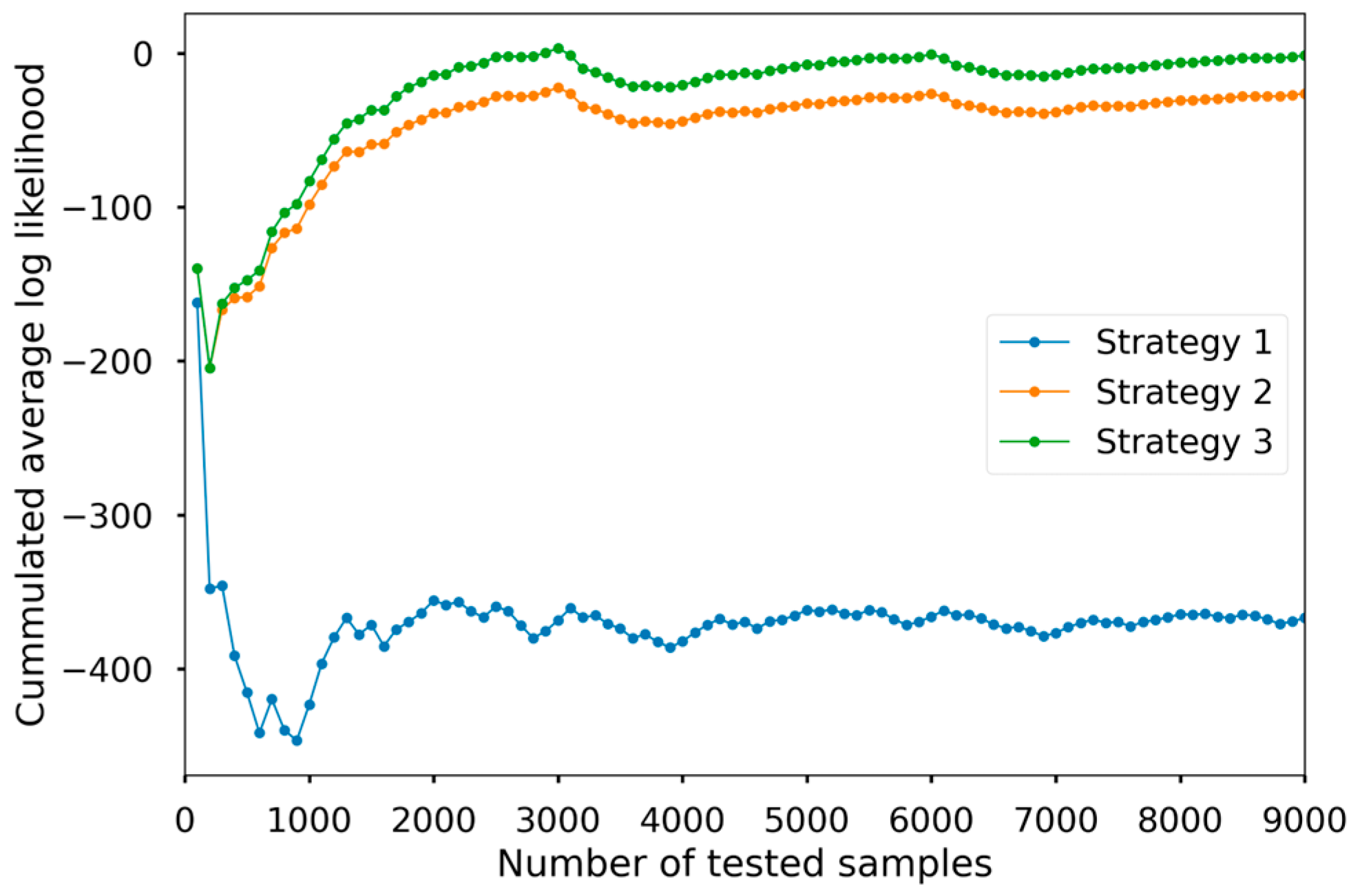
The following three strategies are used to update the parameters of GMM in step four and compare their influence on the performance of the probabilistic model of ${\mathbf{P}}^{ob}$:

Strategy 1 (Initial parameter): This strategy does not update the parameters of GMM and always uses the initial parameters of GMM obtained in step one.

Strategy 2 (Recursive update without calibration): This strategy updates the parameters of GMM with the proposed procedure 1 to learn new samples and procedure 2 to remove old samples but never invokes the calibration procedure.

Strategy 3 (Recursive update): Compared with the previous strategy, this strategy invokes the proposed procedure three automatically to calibrate the parameters of GMM if step two and three have been executed 50 times since the previous calibration.

We compare the accuracy of the probabilistic model via the log likelihood of actual generation under the GMM of ${\mathbf{P}}^{ob}$ calculated in step two. Each strategy has collected $N_{iter}\times N_{test}=9000$ results of log likelihood. We calculate the cumulated average log likelihood for comparison. The results of the three strategies are shown in Figure 2.

$$L_{cumavg}\left(n\right)=\frac{1}{n}{\displaystyle \sum _{i=1}^n{L}_i}$$

(45)

As shown in Figure 2, the proposed strategy three exhibits the highest cumulated average log likelihood among all probabilistic models. It proves that the combination of recursive updates and calibration steps can effectively update the probabilistic model of renewable generation to capture its time-varying characteristics. The performance of strategy two is approximately equal to strategy three in the initial stages due to the effectiveness of the recursive update, but the gap between strategy two and three grows and then stabilizes when more and more new observations of renewable generation are collected. The performance degradation of strategy two can be explained by its lack of a calibration step, which is essential to compensate for suboptimality accumulated in recursive update steps. To serve as a control group, strategy one demonstrated substantially lower performance versus the remaining strategies that severely degrade as more samples of renewable generation are observed, which highlights the necessity of updating the probabilistic model based on new data samples.

Based on comparisons on the precision of predictions, the proposed recursive probabilistic model has the following advantages compared to the other two approaches.

• Compared with the static probabilistic model with fixed parameters, the recursive probabilistic model can adapt to new observations of renewable generation and update internal parameters of GMM dynamically. Thus, the predicted probability distribution of actual generation is more accurate and does not degrade due to outdated historical samples.
• Compared with the recursive probabilistic model without calibration in previous studies, our model demonstrates higher long-term accuracy in the prediction of renewable generation. The improvement is mainly attributed to periodic calibration procedures to overcome the suboptimality of parameters accumulated during recursive updates.

5.2. Comparing Computational Time to Acquire Parameters of Probabilistic Model of Renewable Generation

In this section, we conduct two experiments to demonstrate computational efficiency to accommodate new observations of renewable generation provided by the recursive probabilistic model compared with GMM tuned by a conventional full-scale EM algorithm.

In general, we assume that there are $N$ historical samples of renewable generation ${\mathbf{P}}^{ob}$ and the probabilistic model in the form of GMM has been tuned via EM algorithm. The task is to update the parameters of the probabilistic model with knowledge of $N_{extra}$ new observations of ${\mathbf{P}}^{ob}$. The conventional full-scale EM algorithm reconstructs the parameters of the GMM on the whole training set including $N+N_{extra}$ observations by executing E-step and M-step in Section 3 iteratively. Meanwhile, the proposed recursive probabilistic model updates the parameters of GMM by traversing $N_{extra}$ new observation once without iteration.

The first experiment fixes $N_{extra}$ as 10 and enlarges $N$ from 8760 (12 months of samples) to 20,440 (28 months of samples) in interval of 4 months. The performance of the two approaches is shown in

Table 1. Comparison of computational time to update parameters of GMM in Experiment 1.

$\mathit{N}$		8760	11,680	14,600	17,520	20,400
Recursive update		0.129 s	0.063 s	0.129 s	0.113 s	0.053 s
EM	Total time	124 s	176 s	229 s	589 s	649 s
	Iterations	31	19	22	39	41
	Time per iteration	4.0 s	9.3 s	10.4 s	15.1 s	15.8 s

. The recursive probabilistic model demonstrates minor fluctuations in computational time, maintaining performance below 0.13 s constantly. Notably, this efficiency persists regardless of the increasing number of existing samples $N$.

In contrast to the recursive probabilistic model, the full-scale EM algorithm exhibits a rapid escalation in total computational time as the sample size increases. This increase is influenced by two main factors: the number of iterations the EM algorithm undergoes, and the duration of each iteration. The number of iterations is particularly sensitive to the initial parameters, which are often derived from clustering methods like k-means and the criteria set for convergence. Meanwhile, the time spent on each iteration is approximately proportional to the total size of the training samples. This is because each iteration of the EM algorithm requires processing all the samples, making the process more time-consuming as the sample size grows.

Empirical evidence from Table 1 supports these observations. It shows that the average time spent per iteration increases about fourfold, from 4.0 s to 15.8 s, as the sample size expands from 8760 to 20,440. When the sample size reaches 20,440, the total computational time for the full EM algorithm soars to 649 s. This duration is nearly 12,000 times longer than that of the recursive probabilistic model, underscoring the significant difference in scalability and efficiency between the two methodologies.

The second experiment was conducted with a fixed parameter, $N=11680$, while varying the number of new samples $N_{extra}$ between 10 and 90. This setup was designed to elucidate the relationship between the number of new samples and the computational efficiency of the two methods. The result of the experiment is presented in

Table 2. Comparison of computational time to update parameters of GMM in Experiment 2.

${\mathit{N}}_{\mathit{e}\mathit{x}\mathit{t}\mathit{r}\mathit{a}}$		10	30	50	70	90
Recursive update		0.051 s	0.113 s	0.205 s	0.238 s	0.340 s
EM	Total time	191 s	192 s	345 s	374 s	417 s
	Iterations	19	20	31	39	32
	Time per iteration	10.1 s	9.6 s	11.1 s	9.6 s	13.0 s

.

The time consumed by the recursive update process is positively related to the quantity of processed new samples $N_{extra}$ and grows at an approximately linear rate. This empirical finding is in harmony with our prior theoretical analysis regarding computational complexity, underscoring the predictability of the recursive update’s performance. In contrast, the iteration time for the full EM algorithm displayed a tendency to oscillate around the 10 s mark. This pattern can be attributed to the algorithm’s computational complexity being more acutely affected by minor variations in the total number of samples $N+N_{extra}$ (ranging from 11,690 to 11,770), rather than the number of new samples.

The recursive update procedure adeptly integrates up to 90 new observations in a mere 0.34 s, demonstrating remarkable computational efficiency. This performance is especially noteworthy when juxtaposed with the full-scale EM algorithm, where the recursive update method requires less than 0.1% of the time needed by its counterpart (417 s).

The experiments conducted in this section demonstrate a significant reduction in computational time when employing the proposed recursive update algorithm, as opposed to the traditional full-scale EM algorithm. A key observation is that the degree of acceleration is influenced by the ratio of existing samples to the newly added samples, which leads to a remarkable 1000- to 10,000-fold decrease in computational time as evidenced in our experiments.

In scenarios where the number of renewable energy sources expands, the computational demands of the full EM algorithm for updating a new batch of observations could become impractically burdensome, potentially extending to several hours. In contrast, the recursive probabilistic model demonstrated the capability to accomplish similar tasks within a matter of seconds. The efficiency and agility of the recursive update algorithm highlight its potential for online probabilistic modeling, particularly in processing real-time streaming data. This aspect is especially pertinent in practical applications involving renewable energy generation, where timely and efficient data processing is paramount.

5.3. Discussion

To highlight the relative merits of different GMM updating strategies, as detailed in

Table 3. Comparison of GMM updating methods.

Method	Updating Mechanism	Treatment of Old Samples	Calibration	Computational Efficiency	Accuracy
Proposed method	Recursive incremental update with calibration	Discarded	Yes	Very high, 1000 to 10,000 times faster than full EM	High long-term accuracy
Recursive GMM with forgetting factor [34]	Recursive update with fixed forgetting factor λ	Down-weighted	No	High, optimized matrix inversion, determinant updates	Good accuracy, but depends on λ
Online GMM with forgetting [38]	Recursive Bayesian EM update	Down-weighted	No	High, incremental updates only	Good short-term accuracy, but bias accumulates
Traditional EM	Batch EM re-estimation	Retained	No	Low	Accurate for static data

, we compare the proposed recursive GMM with sample elimination and calibration against two representative approaches from recent studies, as well as the conventional EM-based static GMM. The comparison focuses on the updating mechanism, treatment of historical data, calibration strategy, computational efficiency, and accuracy performance.

The conventional EM algorithm achieves high accuracy in static settings but lacks adaptability to non-stationary environments, and its computational burden increases significantly with data size. The recursive GMM with a forgetting factor [34] effectively emphasizes recent data and enables efficient online updating. However, it relies heavily on the proper selection of the forgetting parameter and does not address the long-term accuracy degradation problem. Similarly, the online GMM with a forgetting factor [38] provides rapid adaptation for renewable energy forecasting, but the absence of a calibration mechanism may lead to accumulated bias over time.

In contrast, the proposed method integrates recursive incremental updating, sample elimination, and periodic calibration, thereby maintaining computational efficiency while ensuring long-term stability. By discarding outdated samples, the model captures the most recent stochastic behavior, and the calibration step prevents cumulative errors in recursive updates. Numerical experiments confirm that this approach achieves a favorable balance between real-time adaptability and long-term accuracy, making it particularly suitable for renewable energy scenarios with significant variability.

6. Conclusions

We propose a recursively updated probabilistic model based on the GMM for renewable generation, aimed at continuously tracking time-varying uncertainties using emerging forecasted and measured data. Our approach leverages an efficient incremental learning algorithm, allowing the parameters of the probabilistic model to be autonomously adjusted by learning from new observations and discarding old ones simultaneously, with slight computational burden. Furthermore, a periodic calibration step is introduced to maintain the long-term performance of the probabilistic model after a large number of recursive updates.

In our numerical experiments conducted on empirical data of wind power, our recursive model demonstrates higher precision in prediction compared to existing recursive update strategies, which improves the average log likelihood of predictions by approximately 5–10% over long-term updates. It also shows a significant reduction in computational time when compared to conventional full-scale EM algorithms. For instance, updating parameters with 20,000 training samples and 10 new observations required only 0.13 s, whereas the conventional EM algorithm took 649 s, nearly 5000 times slower.

In practice, the significance of this study lies in its ability to cope with the inherently time-varying characteristics of renewable generation. Unlike static offline models that quickly become outdated, the proposed recursive method provides a computationally efficient and accurate tool to dynamically update probabilistic models in real time, thereby offering strong potential for application in power system operation.

The proposed method has one limitation. Each step of the incremental update is computationally efficient but cannot guarantee parameter optimality; while the periodic full calibration ensures accuracy through multiple iterations, it is computationally expensive. How to coordinate these two procedures to achieve a better trade-off between efficiency and accuracy remains an open question for future research.