Dynamic Modeling and Experimental Validation of the Photovoltaic/Thermal System
Abstract
1. Introduction
- comprehensive modelling of the entire PV/T system, including both the PV/T module and the TES,
- accurate consideration of optical losses in the PV/T module,
- long-term experimental validation over the full course of a year,
- validation using high-resolution five-minute data,
- performance assessment under different climatic conditions (sunny, cloudy, and overcast days),
- use of six quantitative error indicators, ensuring robust confirmation of model accuracy.
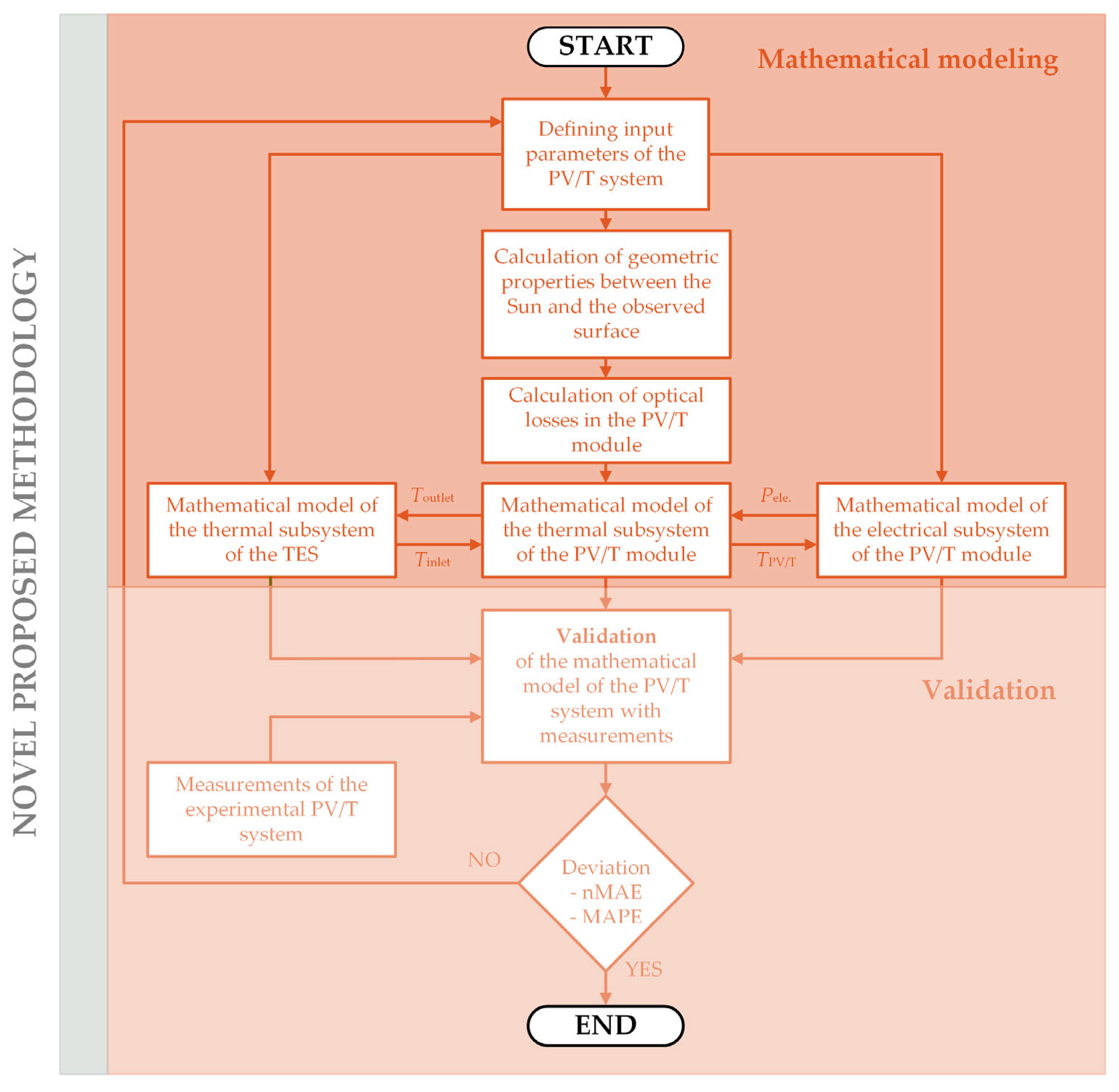
2. Materials and Methods
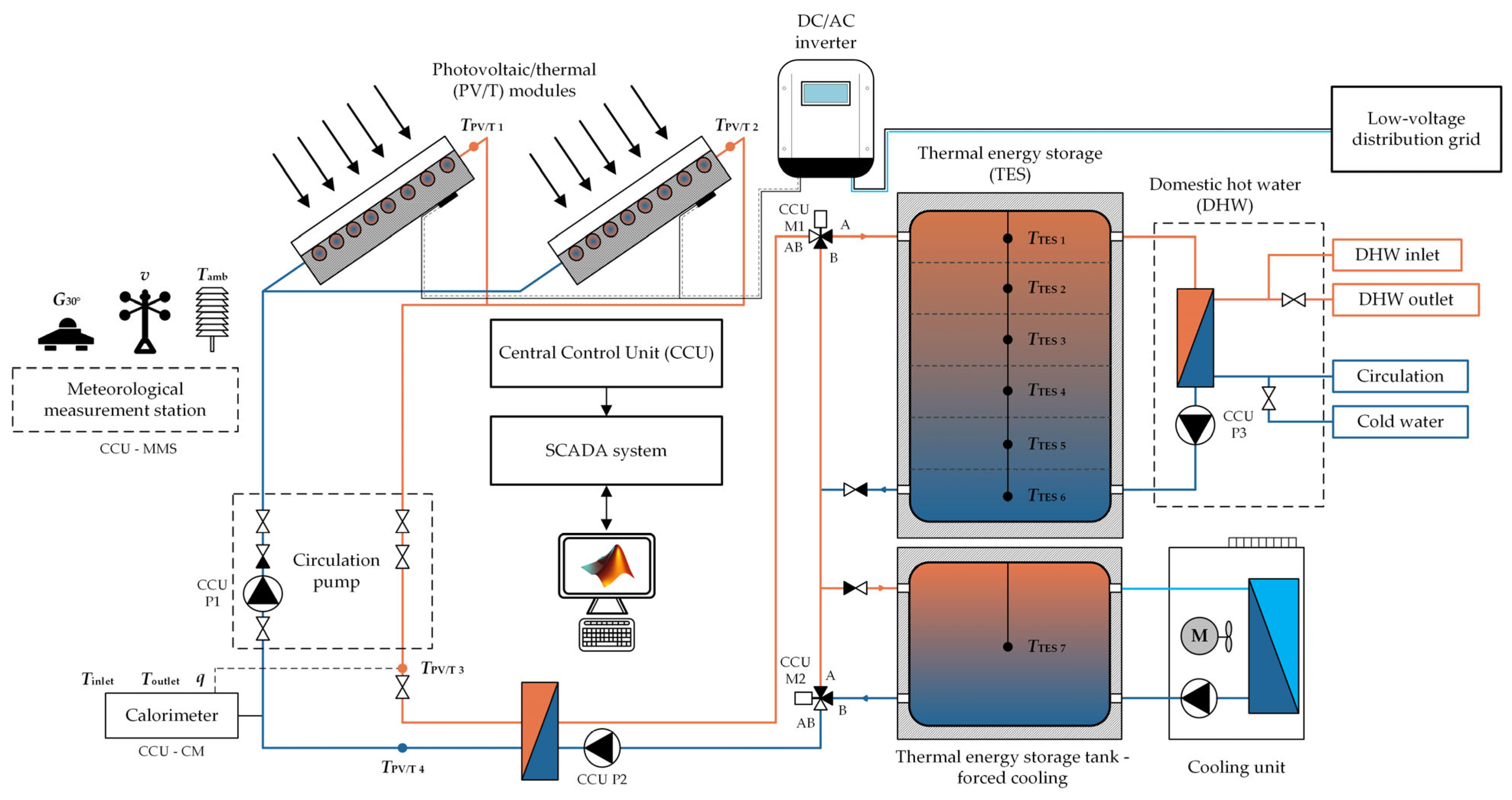
2.1. Data Collection
2.2. Mathematical Modeling of the Photovoltaic/Thermal Module
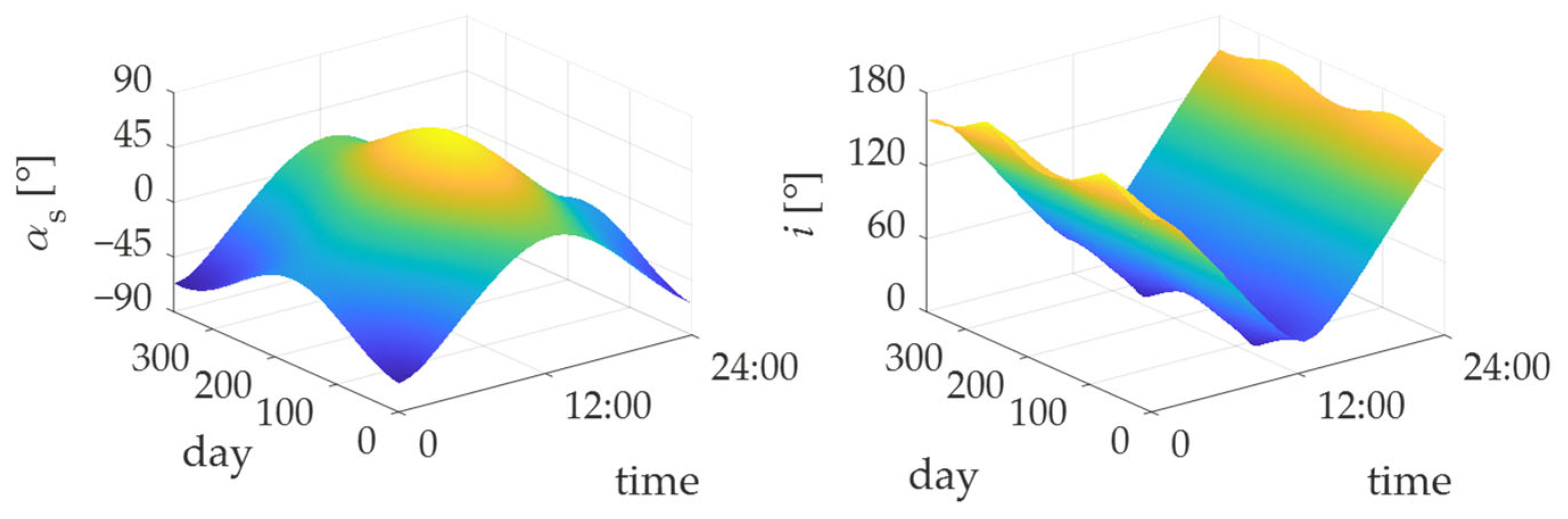
2.2.1. Electrical Subsystem of the Photovoltaic/Thermal Module
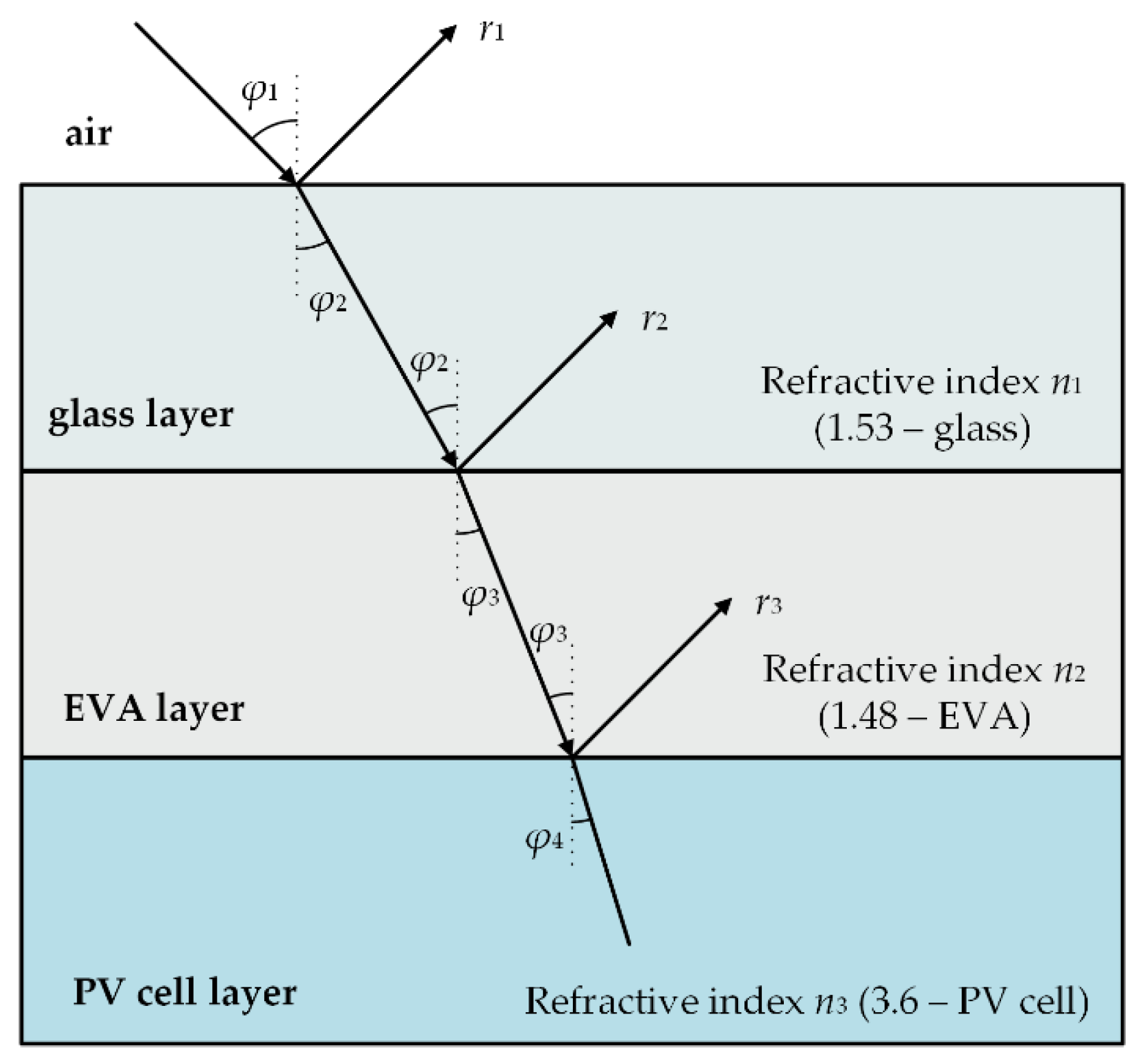
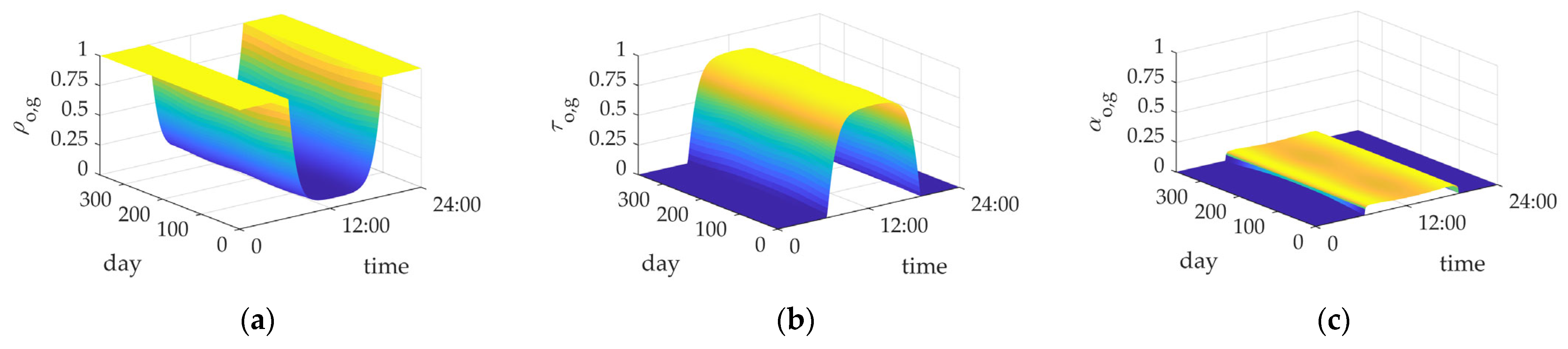
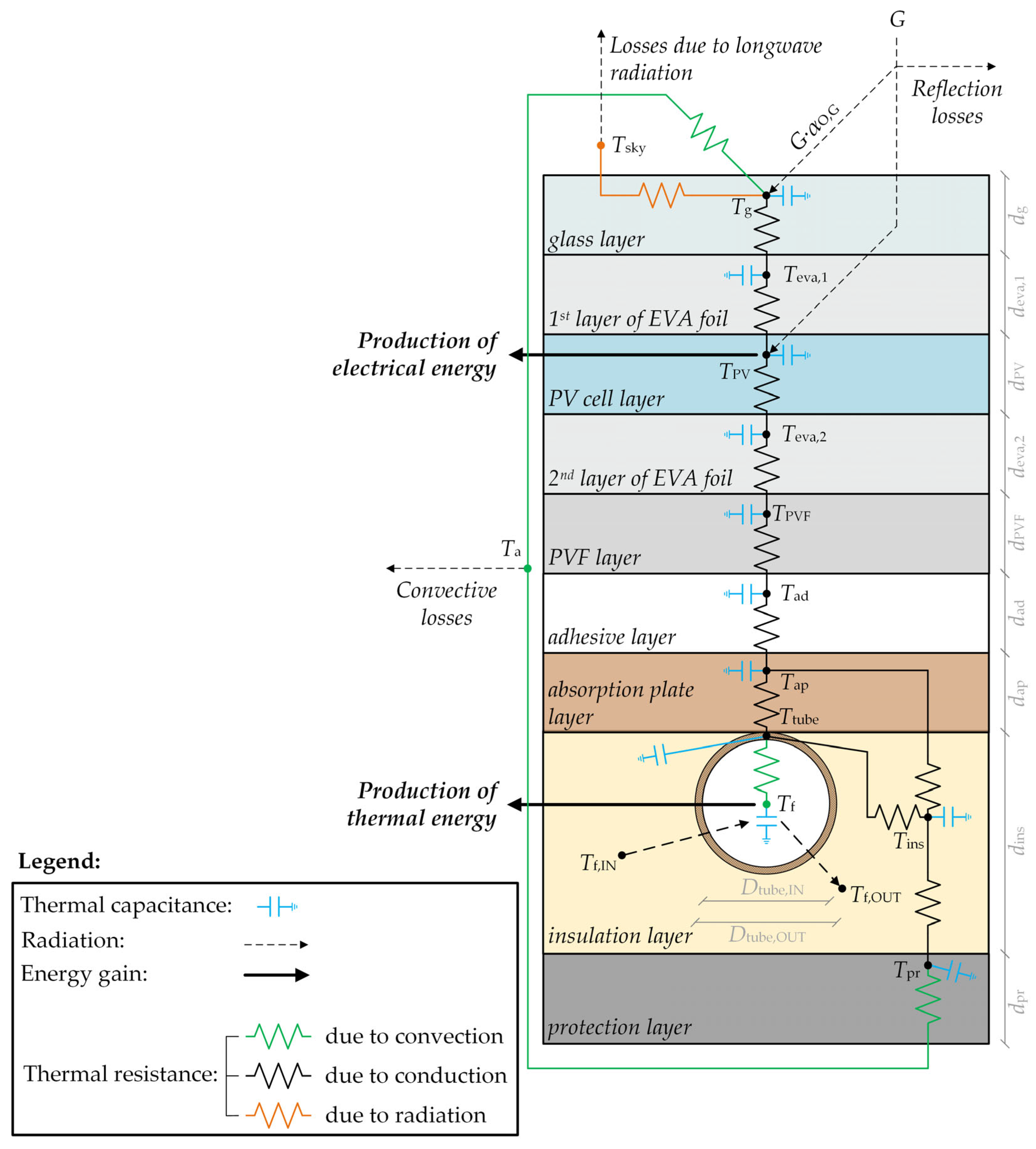
2.2.2. Thermal Subsystem of the Photovoltaic/Thermal Module
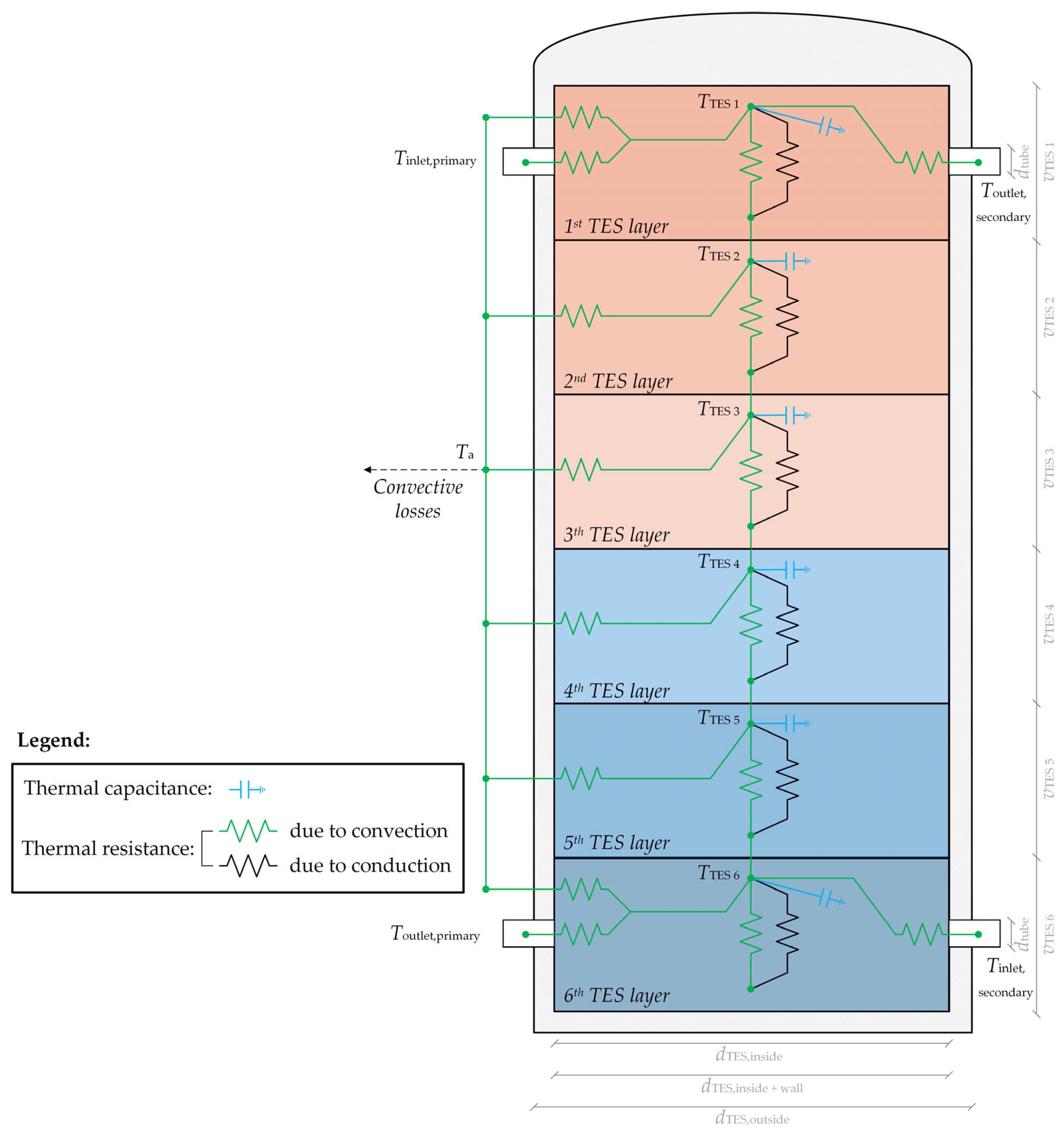
2.3. Mathematical Model of the Thermal Energy Storage Tank
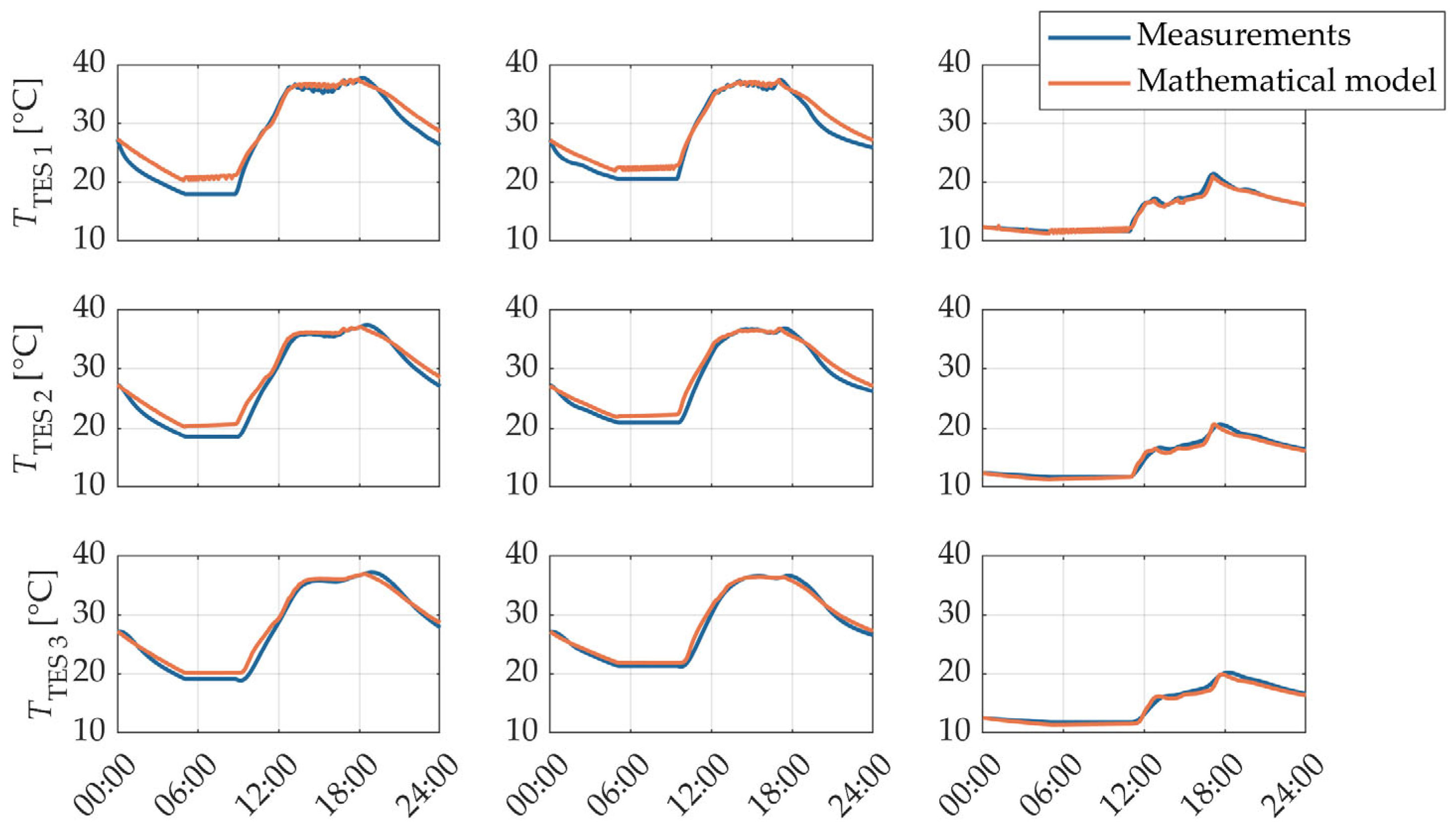
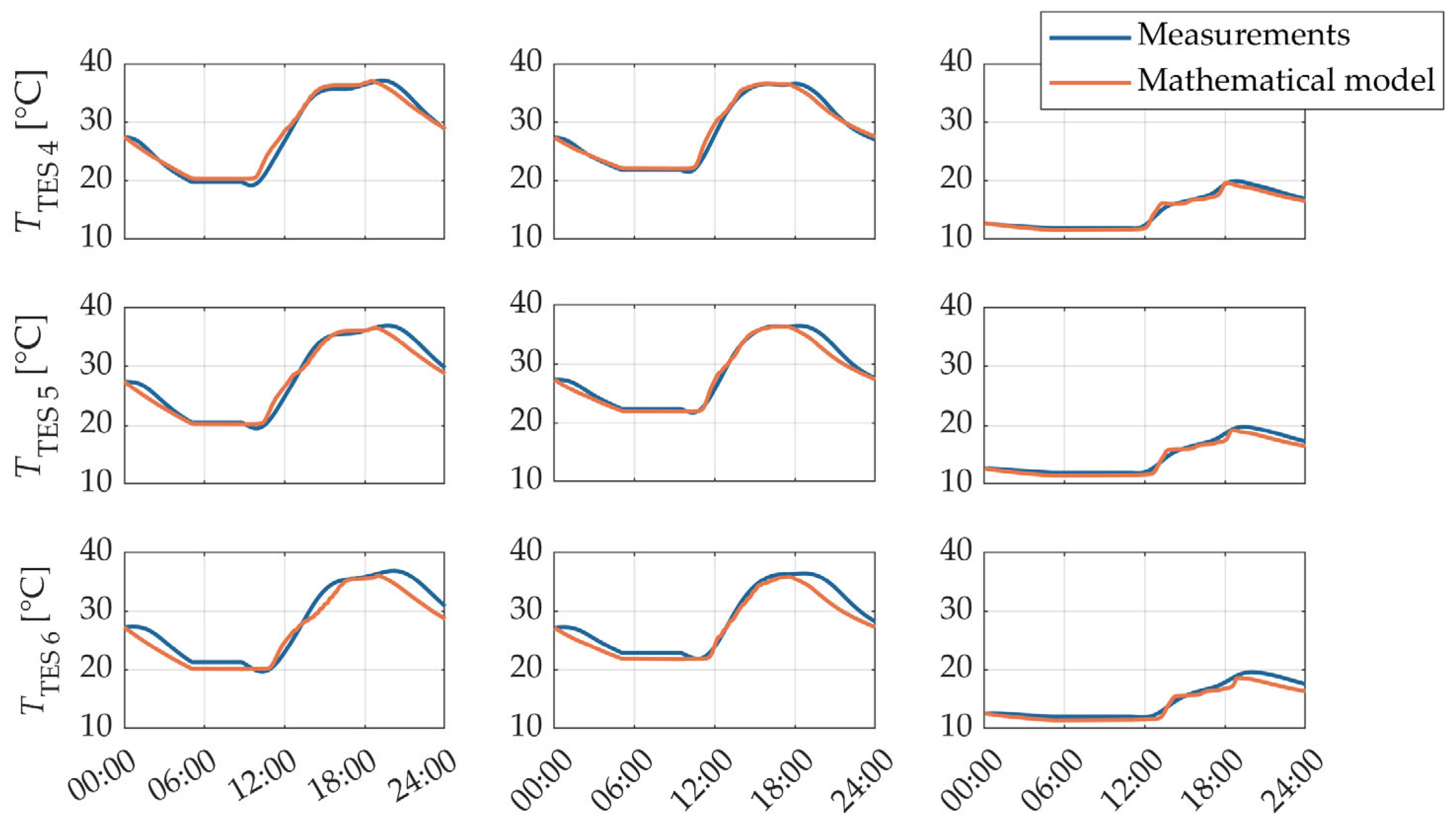
2.4. Experimental Validation of the Mathematical Model of the Photovoltaic/Thermal System
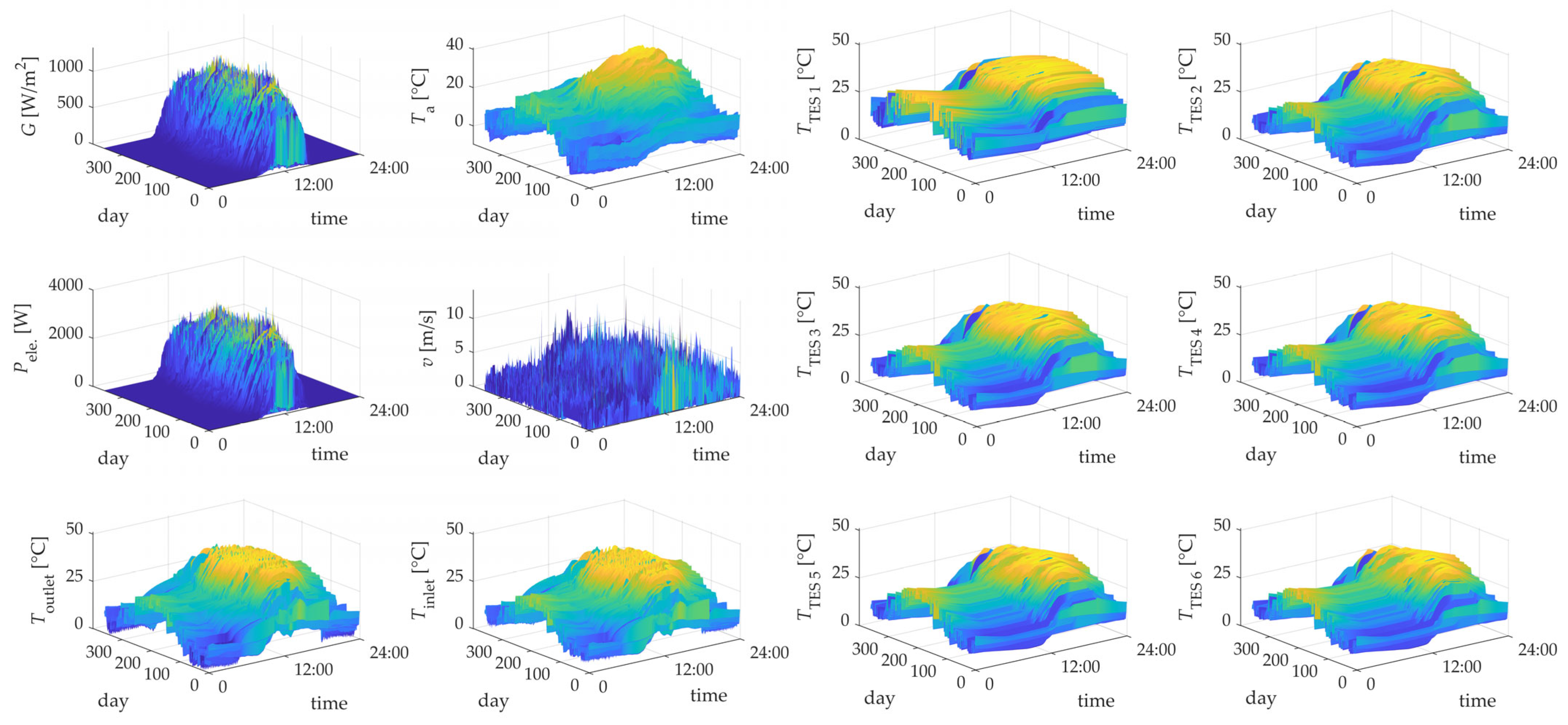
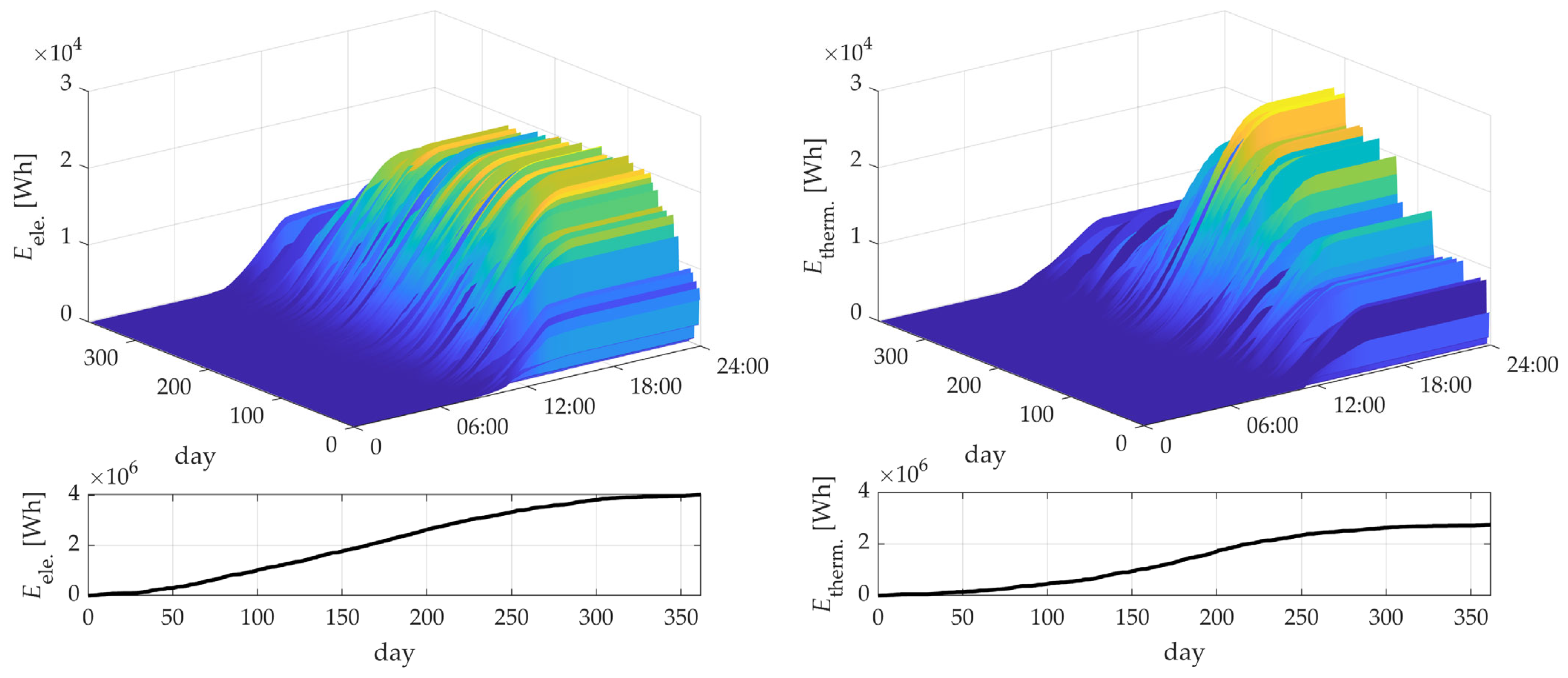
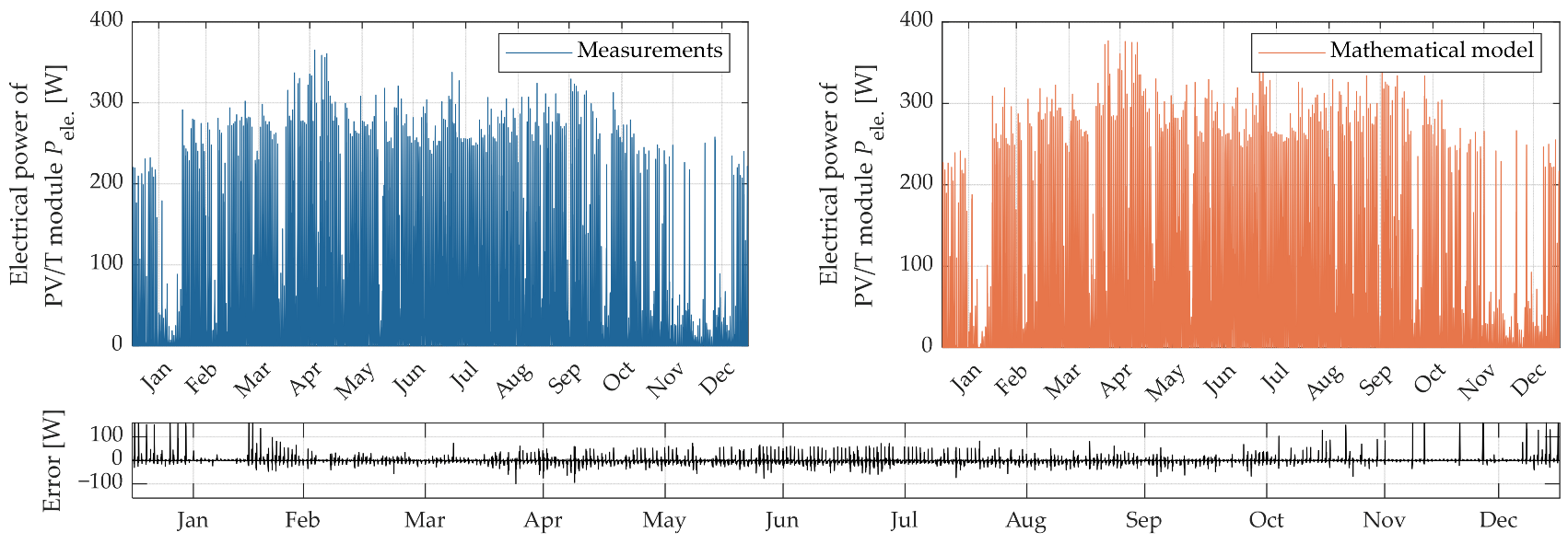
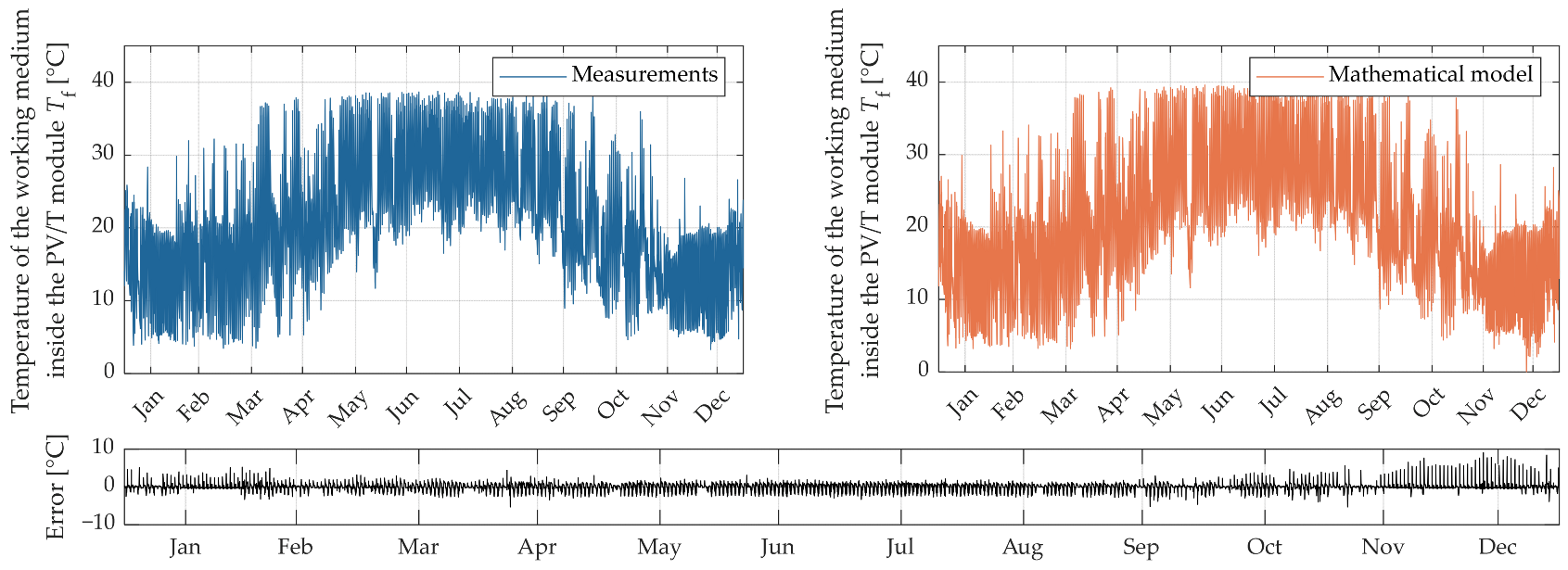
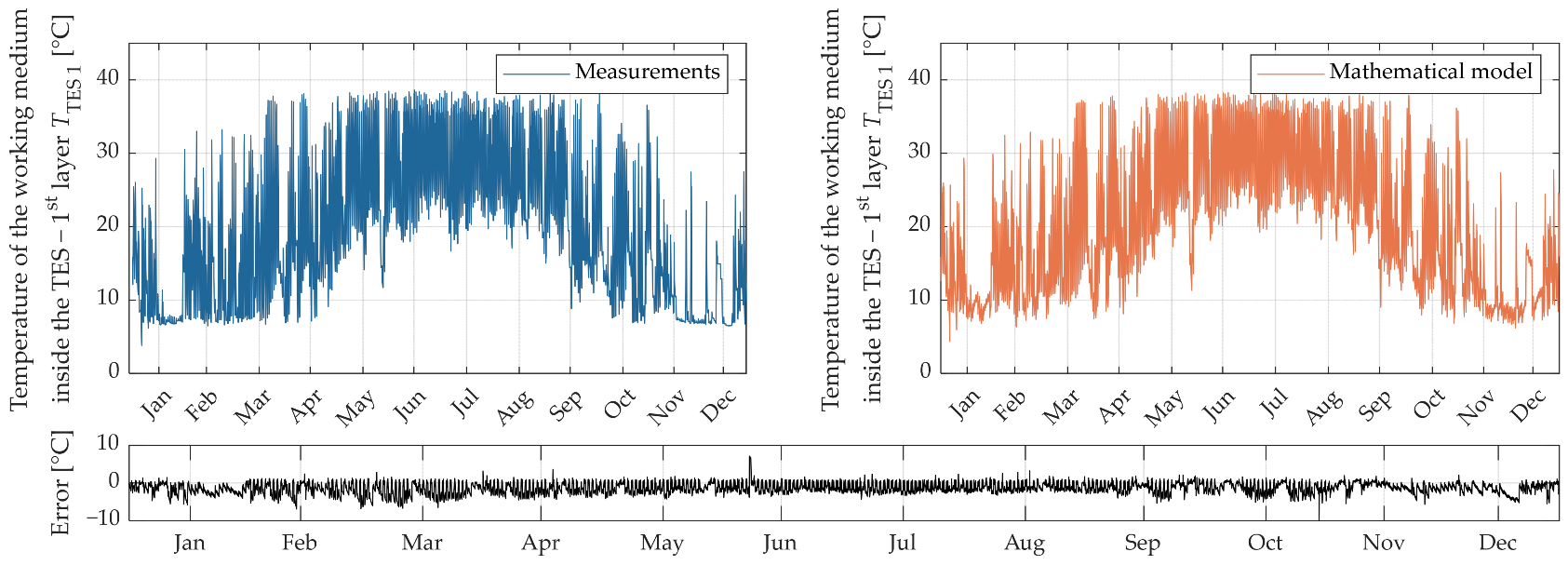
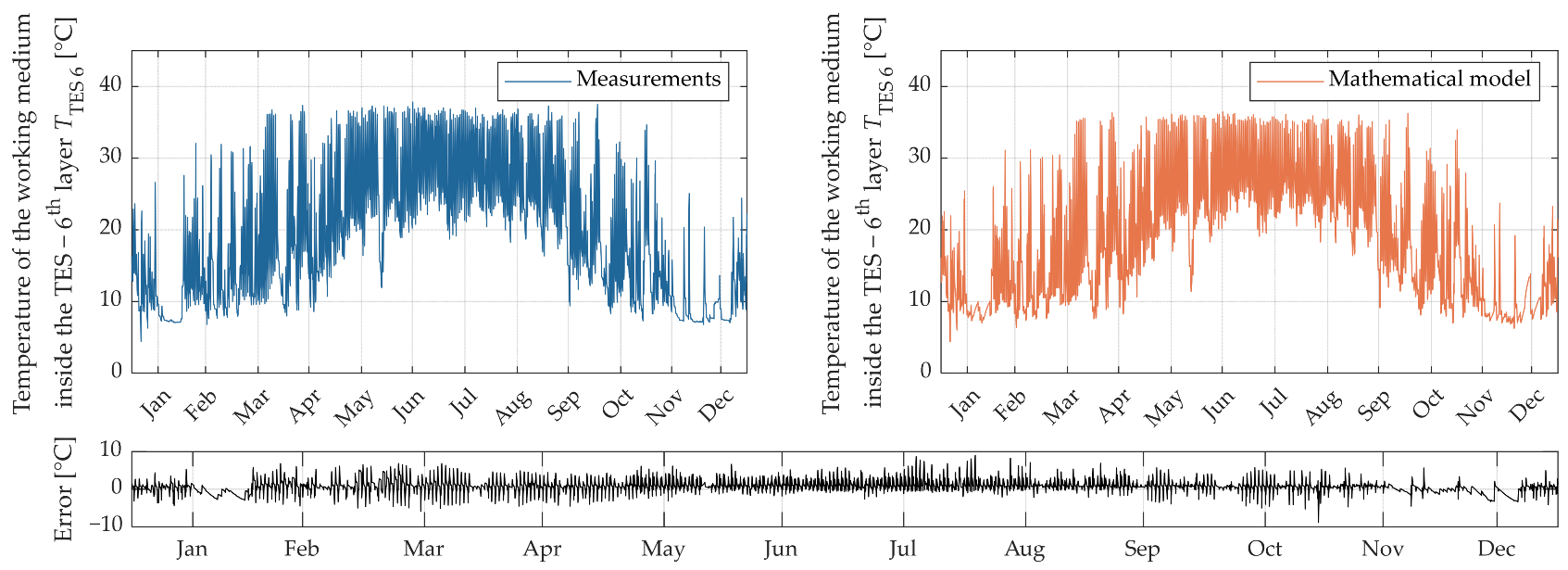
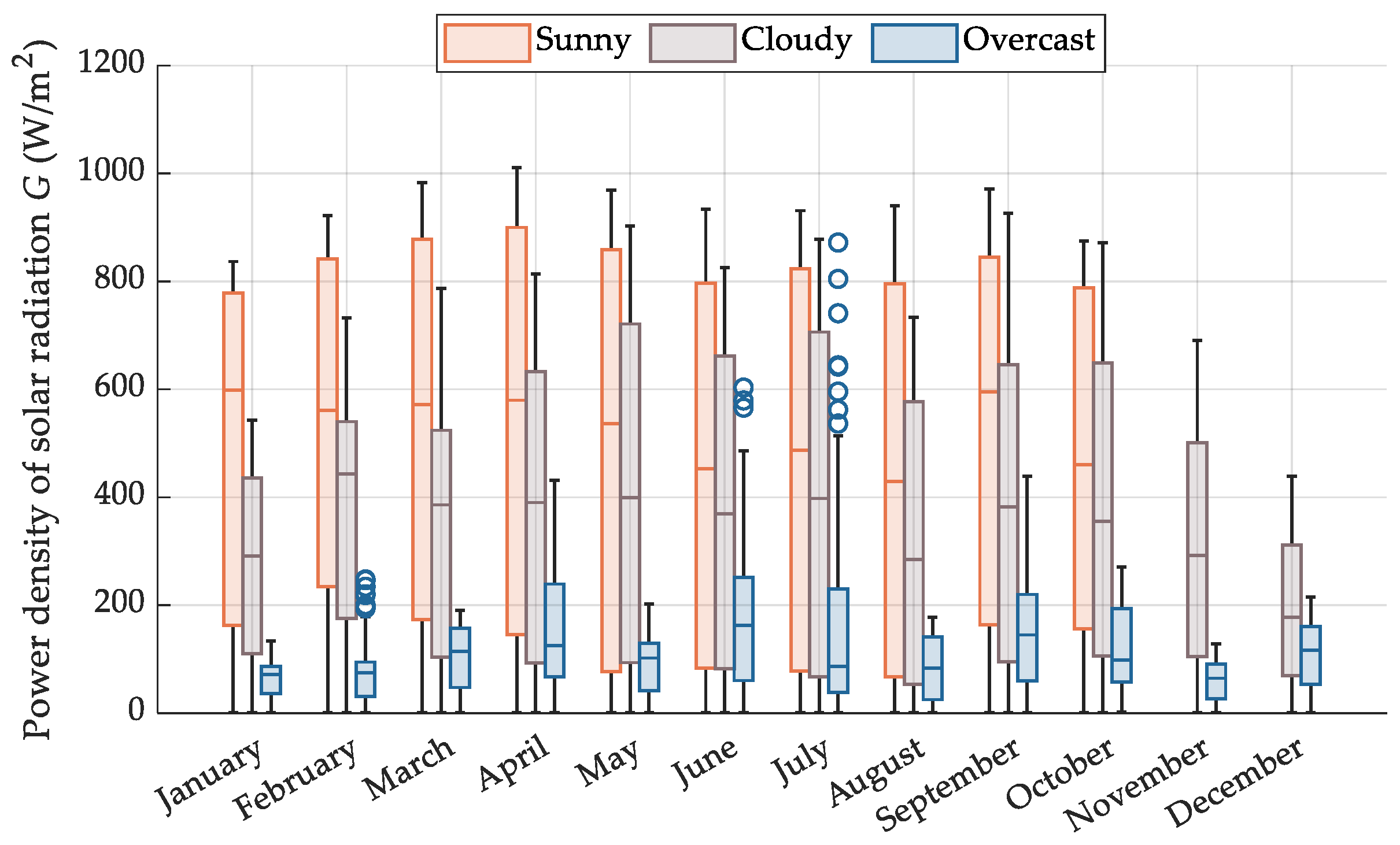
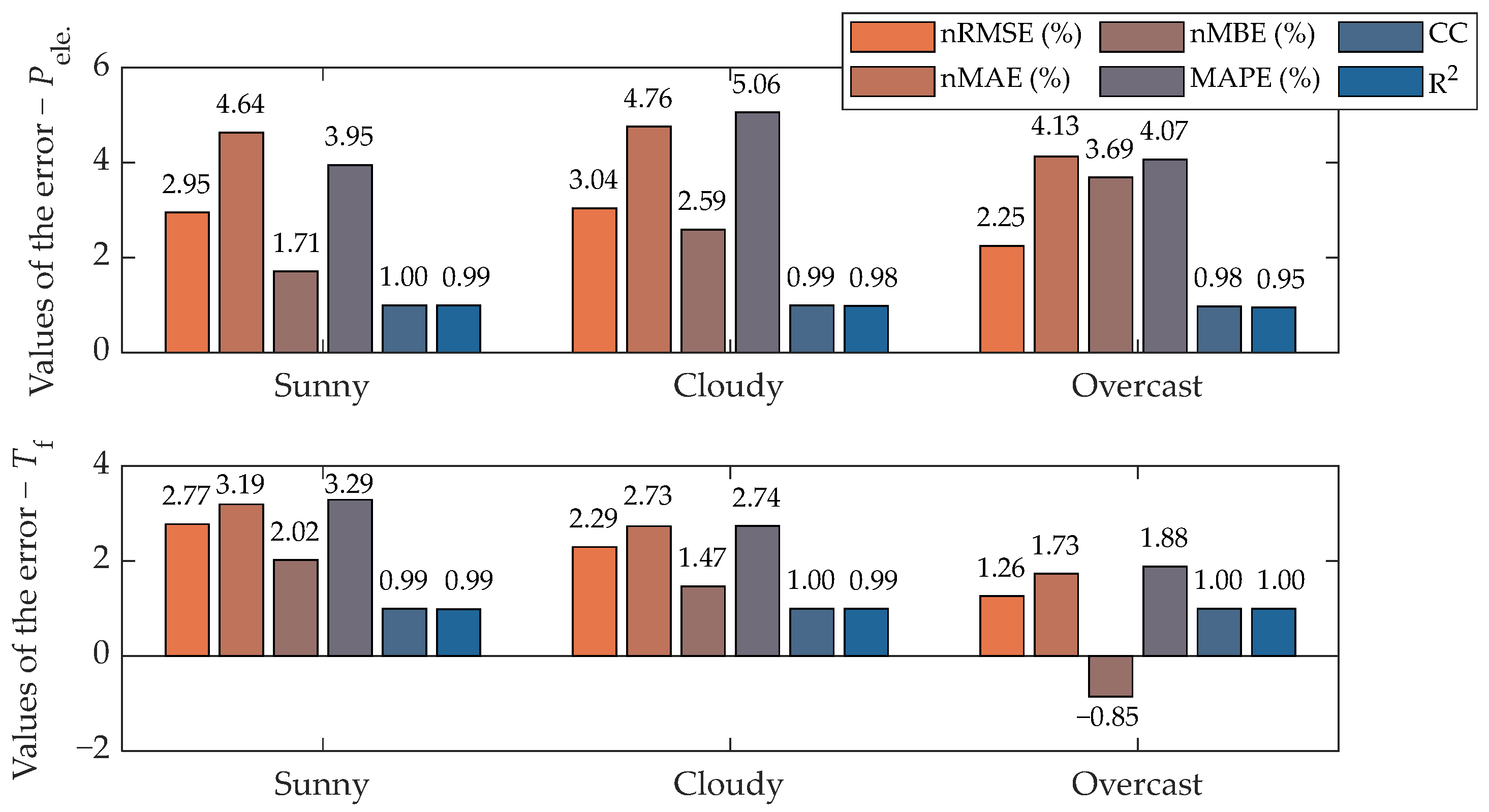
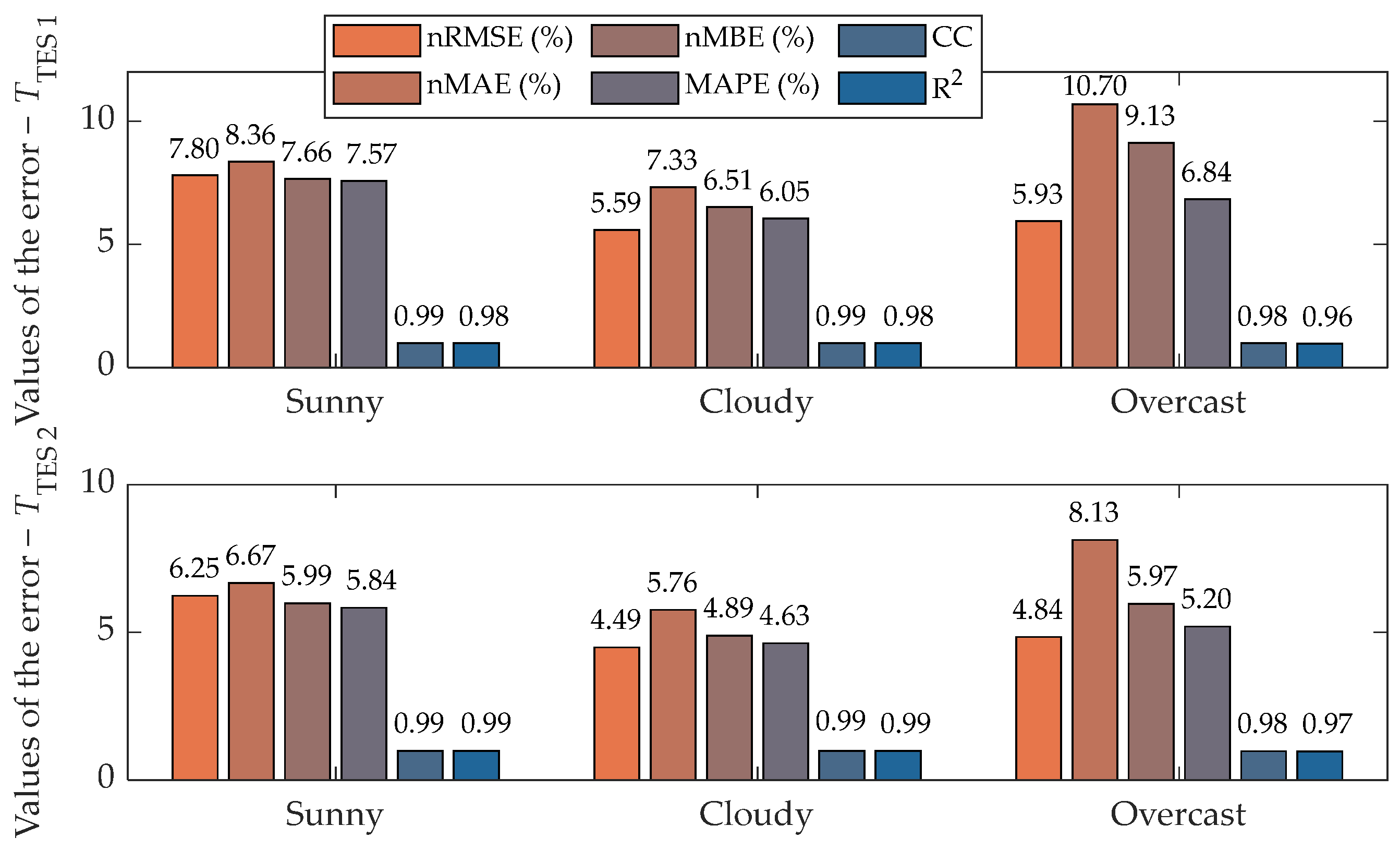
3. Results
4. Discussion
5. Conclusions
- (i)
- Comprehensive modeling of the entire PV/T system (novel methodology).
- (ii)
- Accurate consideration of optical losses in the PV/T module.
- (iii)
- Validation of the mathematical model using measurements from a highly accurate experimental PV/T system (applied approach).
- (iv)
- Long-term validation covering the entire year under different weather conditions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AC | Alternating Current |
| CC | Correction Coefficient |
| CCU | Central Control Unit |
| CFD | Computational Fluid Dynamics |
| DC | Direct Current |
| DHW | Domestic Hot Water |
| EVA | Ethylene-Vinyl Acetate |
| LST | Local Solar Time |
| LSTM | Local Standard Time Meridians |
| LT | Local Time |
| MAPE | Mean Absolute Percentage Error |
| MMS | Meteorological Measurement Station |
| nMAE | normalized Mean Absolute Error |
| nMBE | normalized Mean Bias Error |
| nRMSE | normalized Root Mean Square Error |
| PFV | Polyvinyl Fluoride |
| PV | Photovoltaic |
| PV/T | Photovoltaic/thermal |
| R2 | Determination coefficient |
| SCADA | Supervisory Control And Data Acquisition |
| TES | Thermal Energy Storage |
| UTC | Universal Coordinated Time |
| MPPT | Maximum Power Point Tracking |
References
- Mesquita, I.; Andrade, L.; Mendes, A. Temperature Impact on Perovskite Solar Cells Under Operation. Chemsuschem 2019, 12, 2186–2194. [Google Scholar] [CrossRef]
- Jordan, D.; Kurtz, S. Photovoltaic Degradation Rates—An Analytical Review. Prog. Photovolt. 2013, 21, 12–29. [Google Scholar] [CrossRef]
- Radziemska, E. The effect of temperature on the power drop in crystalline silicon solar cells. Renew. Energy 2003, 28, 1–12. [Google Scholar] [CrossRef]
- Wu, S.; Zhang, Q.; Xiao, L.; Guo, F. A heat pipe photovoltaic/thermal (PV/T) hybrid system and its performance evaluation. Energy Build. 2011, 43, 3558–3567. [Google Scholar] [CrossRef]
- Kamel, M.; Elbanhawy, A.; El-Nasr, M. A novel methodology to compare between side-by-side photovoltaics and thermal collectors against hybrid photovoltaic thermal collectors. Energy Conv. Manag. 2019, 202, 12196. [Google Scholar] [CrossRef]
- Hu, H.; Wang, R.; Fang, G. Dynamic Characteristics Modeling of a Hybrid Photovoltaic-Thermal Heat Pump System. Int. J. Green Energy 2010, 7, 537–551. [Google Scholar] [CrossRef]
- Salameh, T.; Tawalbeh, M.; Juaidi, A.; Abdallah, R.; Hamid, A. A novel three-dimensional numerical model for PV/T water system in hot climate region. Renew. Energy 2021, 164, 1320–1333. [Google Scholar] [CrossRef]
- Sakellariou, E.; Axaopoulos, P. Simulation and experimental performance analysis of a modified PV panel to a PVT collector. Sol. Energy 2017, 155, 715–726. [Google Scholar] [CrossRef]
- Shahsavar, A.; Ameri, M. Experimental investigation and modeling of a direct-coupled PV/T air collector. Sol. Energy 2010, 84, 1938–1958. [Google Scholar] [CrossRef]
- Dubey, S.; Tiwari, G.N. Analysis of PV/T flat plate water collectors connected in series. Sol. Energy 2009, 83, 1485–1498. [Google Scholar] [CrossRef]
- Tonui, J.K.; Tripanagnostopoulos, Y. Performance improvement of PV/T solar collectors with natural air flow operation. Sol. Energy 2008, 82, 1–12. [Google Scholar] [CrossRef]
- Tonui, J.K.; Tripanagnostopoulos, Y. Air-cooled PV/T solar collectors with low cost performance improvements. Sol. Energy 2007, 81, 498–511. [Google Scholar] [CrossRef]
- Misha, S.; Abdullah, A.L.; Tamaldin, N.; Rosli, M.A.M.; Sachit, F.A. Simulation CFD and experimental investigation of PVT water system under natural Malaysian weather conditions. Energy Rep. 2020, 6, 28–44. [Google Scholar] [CrossRef]
- Shan, F.; Tang, F.; Cao, L.; Fang, G. Comparative simulation analyses on dynamic performances of photovoltaic-thermal solar collectors with different configurations. Energy Conv. Manag. 2014, 87, 778–786. [Google Scholar] [CrossRef]
- Touafek, K.; Haddadi, M.; Malek, A. Modeling and Experimental Validation of a New Hybrid Photovoltaic Thermal Collector. Ieee Trans. Energy Convers. 2011, 26, 176–183. [Google Scholar] [CrossRef]
- Aste, N.; Del Pero, C.; Leonforte, F.; Manfren, M. Performance monitoring and modeling of an uncovered photovoltaic-thermal (PVT) water collector. Sol. Energy 2016, 135, 551–568. [Google Scholar] [CrossRef]
- Aste, N.; Leonforte, F.; Del Pero, C. Design, modeling and performance monitoring of a photovoltaic-thermal (PVT) water collector. Sol. Energy 2015, 112, 85–99. [Google Scholar] [CrossRef]
- Amrizal, N.; Chemisana, D.; Rosell, J.I. Hybrid photovoltaic-thermal solar collectors dynamic modeling. Appl. Energy 2013, 101, 797–807. [Google Scholar] [CrossRef]
- Amrizal, N.; Chemisana, D.; Rosell, J.I.; Barrau, J. A dynamic model based on the piston flow concept for the thermal characterization of solar collectors. Appl. Energy 2012, 94, 244–250. [Google Scholar] [CrossRef]
- Jarimi, H.; Abu Bakar, M.N.; Othman, M.; Din, M.H. Bi-fluid photovoltaic/thermal (PV/T) solar collector: Experimental validation of a 2-D theoretical model. Renew. Energy 2016, 85, 1052–1067. [Google Scholar] [CrossRef]
- Zhou, J.; Ma, X.; Zhao, X.; Yuan, Y.; Yu, M.; Li, J. Numerical simulation and experimental validation of a micro-channel PV/T modules based direct-expansion solar heat pump system. Renew. Energy 2020, 145, 1992–2004. [Google Scholar] [CrossRef]
- Zhang, H.; Liang, K.; Chen, H.; Gao, D.; Guo, X. Thermal and electrical performance of low-concentrating PV/T and flat-plate PV/T systems: A comparative study. Energy 2019, 177, 66–76. [Google Scholar] [CrossRef]
- Zhang, P.; Rong, X.; Yang, X.; Zhang, D. Design and performance simulation of a novel hybrid PV/T-air dual source heat pump system based on a three-fluid heat exchanger. Sol. Energy 2019, 191, 505–517. [Google Scholar] [CrossRef]
- Su, D.; Jia, Y.; Huang, X.; Alva, G.; Tang, Y.; Fang, G. Dynamic performance analysis of photovoltaic-thermal solar collector with dual channels for different fluids. Energy Conv. Manag. 2016, 120, 13–24. [Google Scholar] [CrossRef]
- Kuo, C.-F.J.; Lee, Y.-W.; Umar, M.L.; Yang, P.-C. Dynamic modeling, practical verification and energy benefit analysis of a photovoltaic and thermal composite module system. Energy Conv. Manag. 2017, 154, 470–481. [Google Scholar]
- Cai, J.; Ji, J.; Wang, Y.; Zhou, F.; Yu, B. A novel PV/T-air dual source heat pump water heater system: Dynamic simulation and performance characterization. Energy Conv. Manag. 2017, 148, 635–645. [Google Scholar] [CrossRef]
- Simonetti, R.; Molinaroli, L.; Manzolini, G. Development and validation of a comprehensive dynamic mathematical model for hybrid PV/T solar collectors. Appl. Therm. Eng. 2018, 133, 543–554. [Google Scholar] [CrossRef]
- Yu, Q.; Hu, M.; Li, J.; Wang, Y.; Pei, G. Development of a 2D temperature-irradiance coupling model for performance characterizations of the flat-plate photovoltaic/thermal (PV/T) collector. Renew. Energy 2020, 153, 404–419. [Google Scholar] [CrossRef]
- Guarracino, I.; Freeman, J.; Ramos, A.; Kalogirou, S.A.; Ekins-Daukes, N.J.; Markides, C.N. Systematic testing of hybrid PV-thermal (PVT) solar collectors in steady-state and dynamic outdoor conditions. Appl. Energy 2019, 240, 1014–1030. [Google Scholar] [CrossRef]
- Guarracino, I.; Mellor, A.; Ekins-Daukes, N.J.; Markides, C.N. Dynamic coupled thermal-and-electrical modelling of sheet-and-tube hybrid photovoltaic/thermal (PVT) collectors. Appl. Therm. Eng. 2016, 101, 778–795. [Google Scholar] [CrossRef]
- Pierrick, H.; Christophe, M.; Leon, G.; Patrick, D. Dynamic numerical model of a high efficiency PV-T collector integrated into a domestic hot water system. Sol. Energy 2015, 111, 68–81. [Google Scholar] [CrossRef]
- Das, D.; Kalita, P.; Dewan, A.; Tanweer, S. Development of a novel thermal model for a PV/T collector and its experimental analysis. Sol. Energy 2019, 188, 631–643. [Google Scholar] [CrossRef]
- da Silva, R.M.; Fernandes, J.L.M. Hybrid photovoltaic/thermal (PV/T) solar systems simulation with Simulink/Matlab. Sol. Energy 2010, 84, 1985–1996. [Google Scholar] [CrossRef]
- Ji, J.; He, H.; Chow, T.; Pei, G.; He, W.; Liu, K. Distributed dynamic modeling and experimental study of PV evaporator in a PV/T solar-assisted heat pump. Int. J. Heat Mass Transf. 2009, 52, 1365–1373. [Google Scholar] [CrossRef]
- Fan, W.; Kokogiannakis, G.; Ma, Z.; Cooper, P. Development of a dynamic model for a hybrid photovoltaic thermal collector—Solar air heater with fins. Renew. Energy 2017, 101, 816–834. [Google Scholar] [CrossRef]
- Hussain, M.I.; Kim, J.-T. Performance Optimization of Unglazed Nanofluid Photovoltaic/Thermal System: Energy and Exergy Analyses. Int. J. Photoenergy 2018, 2018, 95013. [Google Scholar] [CrossRef]
- Sakellariou, E.; Axaopoulos, P. An experimentally validated, transient model for sheet and tube PVT collector. Sol. Energy 2018, 174, 709–718. [Google Scholar] [CrossRef]
- Chaibi, Y.; El Rhafiki, T.; Simón-Allué, R.; Guedea, I.; Luaces, C.; Gajate, O.; Kousksou, T.; Zeraouli, Y. Physical models for the design of photovoltaic/thermal collector systems. Sol. Energy 2021, 226, 134–146. [Google Scholar] [CrossRef]
- Chow, T. Performance analysis of photovoltaic-thermal collector by explicit dynamic model. Sol. Energy 2003, 75, 143–152. [Google Scholar] [CrossRef]
- Dubey, S.; Tiwari, G. Thermal modeling of a combined system of photovoltaic thermal (PV/T) solar water heater. Sol. Energy 2008, 82, 602–612. [Google Scholar] [CrossRef]
- El Fouas, C.; Hajji, B.; Gagliano, A.; Tina, G.; Aneli, S. Numerical model and experimental validation of the electrical and thermal performances of photovoltaic/thermal plant. Energy Conv. Manag. 2020, 220, 12939. [Google Scholar] [CrossRef]
- Jidhesh, P.; Arjunan, T.; Gunasekar, N. Thermal modeling and experimental validation of semitransparent photovoltaic- thermal hybrid collector using CuO nanofluid. J. Clean. Prod. 2021, 316, 28360. [Google Scholar] [CrossRef]
- Ben Youssef, W.; Maatallah, T.; Menezo, C.; Ben Nasrallah, S. Modeling and optimization of a solar system based on concentrating photovoltaic/thermal collector. Sol. Energy 2018, 170, 301–313. [Google Scholar] [CrossRef]
- Khelifa, A.; Touafek, K.; Ben Moussa, H. Approach for the modelling of hybrid photovoltaic-thermal solar collector. IET Renew. Power Gener. 2015, 9, 207–217. [Google Scholar] [CrossRef]
- Li, S.; Karava, P.; Currie, S.; Lin, W.; Savory, E. Energy modeling of photovoltaic thermal systems with corrugated unglazed transpired solar collectors—Part 1: Model development and validation. Sol. Energy 2014, 102, 282–296. [Google Scholar] [CrossRef]
- Mustapha, M.; Fudholi, A.; Nazri, N.; Zaini, M.; Rosli, N.; Sulong, W.; Sopian, K. Mathematical modeling and experimental validation of bifacial photovoltaic-thermal system with mirror reflector. Case Stud. Therm. Eng. 2023, 43, 2800. [Google Scholar] [CrossRef]
- Rejeb, O.; Sardarabadi, M.; Ménézo, C.; Passandideh-Fard, M.; Dhaou, M.; Jemni, A. Numerical and model validation of uncovered nanofluid sheet and tube type photovoltaic thermal solar system. Energy Conv. Manag. 2016, 110, 367–377. [Google Scholar] [CrossRef]
- Sarhaddi, F.; Farahat, S.; Ajam, H.; Behzadmehr, A.; Adeli, M. An improved thermal and electrical model for a solar photovoltaic thermal (PV/T) air collector. Appl. Energy 2010, 87, 2328–2339. [Google Scholar] [CrossRef]
- Shan, F.; Cao, L.; Fang, G. Dynamic performances modeling of a photovoltaic-thermal collector with water heating in buildings. Energy Build. 2013, 66, 485–494. [Google Scholar] [CrossRef]
- Singh, G.; Dwivedi, V.; Yadav, J.; Tiwari, G. Experimental validation of thermal model of hybrid photovoltaic thermal (HPVT) double slope active solar still. Desalination Water Treat. 2012, 45, 182–190. [Google Scholar] [CrossRef]
- Sredensek, K.; Seme, S.; Stumberger, B.; Hadziselimovic, M.; Chowdhury, A.; Praunseis, Z. Experimental Validation of a Dynamic Photovoltaic/Thermal Collector Model in Combination with a Thermal Energy Storage Tank. Energies 2021, 14, 8162. [Google Scholar] [CrossRef]
- Veynandt, F.; Klanatsky, P.; Plank, H.; Heschl, C. Hybrid photovoltaic-thermal solar collector modelling with parameter identification using operation data. Energy Build. 2023, 295, 13277. [Google Scholar] [CrossRef]
- Moradi, K.; Jafari, F.; Moghaddam, F.; Shafiee, Q. Dynamic modeling of photovoltaic-thermal systems using polynomial regression. Renew. Energy 2025, 250, 23242. [Google Scholar] [CrossRef]
- Alayi, R.; Kasaeian, A.; Atabi, F. Optical modeling and optimization of parabolic trough concentration photovoltaic/thermal system. Environ. Prog. Sustain. Energy 2020, 39, 13303. [Google Scholar] [CrossRef]
- Nash, A.L.; Badithela, A.; Jain, N. Dynamic modeling of a sensible thermal energy storage tank with an immersed coil heat exchanger under three operation modes. Appl. Energy 2017, 195, 877–889. [Google Scholar] [CrossRef]
- Maveety, J.; Razani, A. A two-dimensional numerical investigation of the optimal removal time and entropy production rate for a sensible thermal storage system. Energy 1996, 21, 1265–1276. [Google Scholar] [CrossRef]
- Nelson, J.; Balakrishnan, A.; Murthy, S. Parametric studies on thermally stratified chilled water storage systems. Appl. Therm. Eng. 1999, 19, 89–115. [Google Scholar] [CrossRef]
- Abdulla, A.; Reddy, K.S. Effect of operating parameters on thermal performance of molten salt packed-bed thermocline thermal energy storage system for concentrating solar power plants. Int. J. Therm. Sci. 2017, 121, 30–44. [Google Scholar] [CrossRef]
- Raccanello, J.; Rech, S.; Lazzaretto, A. Simplified dynamic modeling of single-tank thermal energy storage systems. Energy 2019, 182, 1154–1172. [Google Scholar] [CrossRef]
- Rahman, A.; Smith, A.D.; Fumo, N. Performance modeling and parametric study of a stratified water thermal storage tank. Appl. Therm. Eng. 2016, 100, 668–679. [Google Scholar] [CrossRef]
- Berkenkamp, F.; Gwerder, M. Hybrid model predictive control of stratified thermal storages in buildings. Energy Build. 2014, 84, 233–240. [Google Scholar] [CrossRef]
- Bird, T.J.; Jain, N. Dynamic modeling and validation of a micro-combined heat and power system with integrated thermal energy storage. Appl. Energy 2020, 271, 14955. [Google Scholar] [CrossRef]
- De la Cruz-Loredo, I.; Zinsmeister, D.; Licklederer, T.; Ugalde-Loo, C.E.; Morales, D.A.; Bastida, H.; Peric, V.S.; Saleem, A. Experimental validation of a hybrid 1-D multi-node model of a hot water thermal energy storage tank. Appl. Energy 2023, 332, 20556. [Google Scholar] [CrossRef]
- Kreuzinger, T.; Bitzer, M.; Marquardt, W. State estimation of a stratified storage tank. Control Eng. Pract. 2008, 16, 308–320. [Google Scholar] [CrossRef]
- Lago, J.; De Ridder, F.; Mazairac, W.; De Schutter, B. A 1-dimensional continuous and smooth model for thermally stratified storage tanks including mixing and buoyancy. Appl. Energy 2019, 248, 640–655. [Google Scholar] [CrossRef]
- Nelson, J.; Balakrishnan, A.; Murthy, S. Transient analysis of energy storage in a thermally stratified water tank. Int. J. Energy Res. 1998, 22, 867–883. [Google Scholar] [CrossRef]
- Riebel, A.; Wolde, I.; Escobar, R.; Barraza, R.; Cardemil, J.M. Transient modeling of stratified thermal storage tanks: Comparison of 1D models and the Advanced Flowrate Distribution method. Case Stud. Therm. Eng. 2024, 61, 5084. [Google Scholar] [CrossRef]
- Saloux, E.; Candanedo, J.A. Modelling stratified thermal energy storage tanks using an advanced flowrate distribution of the received flow. Appl. Energy 2019, 241, 34–45. [Google Scholar] [CrossRef]
- Soares, A.; Camargo, J.; Al-Koussa, J.; Diriken, J.; Van Bael, J.; Lago, J. Efficient temperature estimation for thermally stratified storage tanks with buoyancy and mixing effects. J. Energy Storage 2022, 50, 4488. [Google Scholar] [CrossRef]
- Yin, H.; Ding, J.; Jiang, R.; Yang, X. Thermocline characteristics of molten-salt thermal energy storage in porous packed-bed tank. Appl. Therm. Eng. 2017, 110, 855–863. [Google Scholar] [CrossRef]
- Karim, A.; Burnett, A.; Fawzia, S. Investigation of Stratified Thermal Storage Tank Performance for Heating and Cooling Applications. Energies 2018, 11, 1049. [Google Scholar] [CrossRef]
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Processes; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Yamada, T.; Nakamura, H.; Sugiura, T.; Sakuta, K.; Kurokawa, K. Reflection loss analysis by optical modeling of PV module. Sol. Energy Mater. Sol. Cells 2001, 67, 405–413. [Google Scholar] [CrossRef]
- Li, C.; Spataru, S.; Zhang, K.; Yang, Y.; Wei, H. A Multi-State Dynamic Thermal Model for Accurate Photovoltaic Cell Temperature Estimation. IEEE J. Photovolt. 2020, 10, 1465–1473. [Google Scholar] [CrossRef]



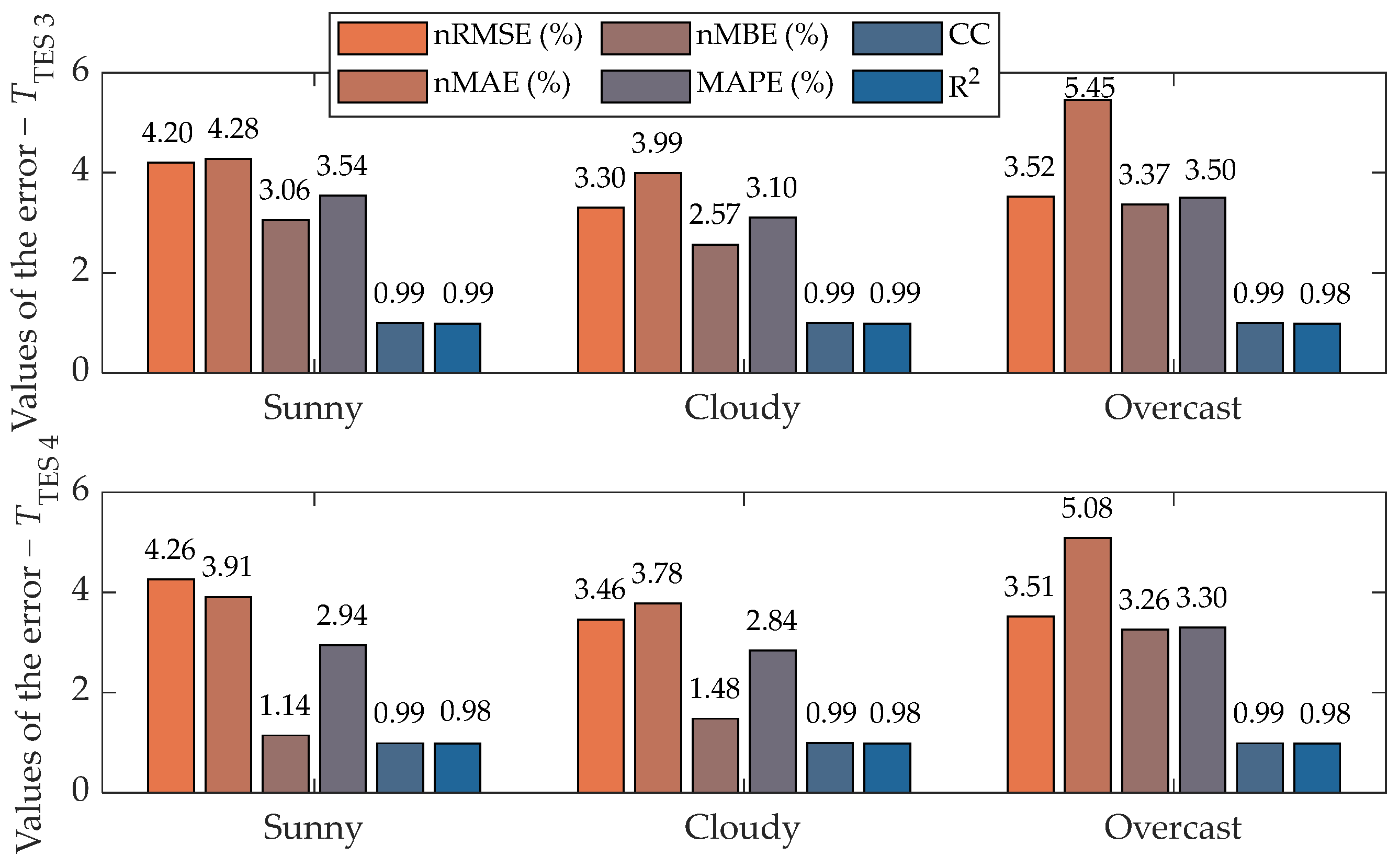

| Component | Manufacturer | Type | Description |
|---|---|---|---|
| PV/T modules (a) | Solimpeks (Konya, Turkey) | Volther | Pele. = 330 W; Ptherm. = 855 W |
| Inverter (b) | SMA (Niestetal, Germany) | Sunny Boy 3.6 | PDC = 5500 W; PAC = 3680 W |
| Central control unit (c) | Siemens (Munich, Germany) | S7-300 PLC | Cycle time ≥ 0.1 µs/bit operation |
| Pyranometer (d) | Kipp & Zonen (Delft, The Netherlands) | SMP3-A | 300 to 2800 nm; |
| Atmospheric temperature sensor (e) | Ames (Brezovica pri Ljubljani, Slovenia) | TPR 159 | −40 to +60 °C; +/−0.15 °C; 0.1 °C |
| Anemometer (f) | Ames (Brezovica pri Ljubljani, Slovenia) | VMT 107 A | 0 m/s–50 m/s; +/−0.5 m/s; 0.1 m/s |
| TES (g) | Wolf (Mainburg, Germany) | SE-2-500 | Volume: 500 L |
| Heat exchanger (h) | Danfoss (Nordborg, Denmark) | XB 37H-1 40 | Plates: 40; 25 bar; −10 °C to +180 °C |
| TES—forced cooling unit (i) | Aermec (Bevilacqua, Italy) | ANL 041A | Pcool. = 9.6 kW; Pheat. = 10.6 kW |
| Circulation pump P1 in P2 (j,k) | Grundfos (Bjerringbro, Denmark) | Alpha 2 | 3.8 m3/h; +2 °C to +110 °C; 1.0 MPa |
| Circulation pump P3 (l) | Wilo SE (Dortmund, Germany) | Maxo | 11.8 m3/h; −20 °C to +110 °C; 1.0 MPa |
| Calorimeter (m) | Landis+Gyr (Zug, Switzerland) | T330 | 1.2–5.0 m3/h; 5–105 °C |
| Spring | Summer | Autumn | Winter | Annual Average | |
|---|---|---|---|---|---|
| Pele. (W) | 0.426 | 0.251 | 0.302 | 0.534 | 3.261 |
| Tf (°C) | 3.212 | 0.861 | 1.060 | 1.344 | 1.534 |
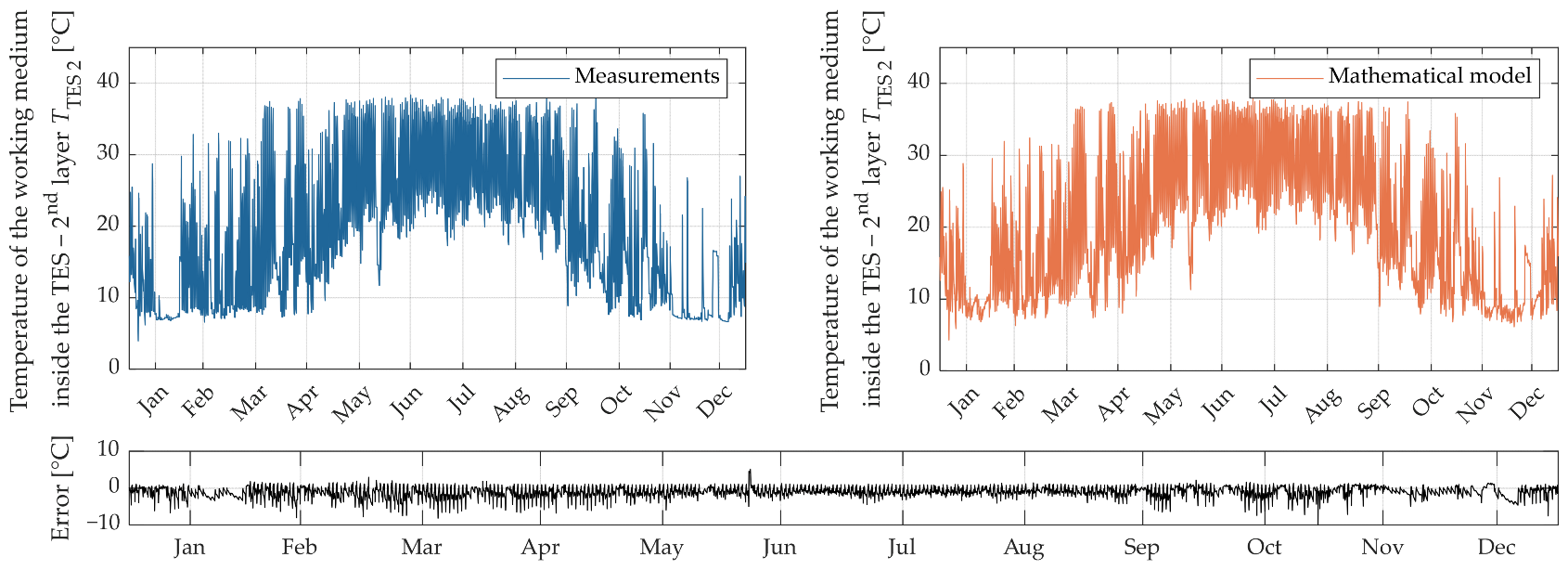
| TTES 1 (°C) | 1.189 | 0.215 | 1.281 | 1.579 | 1.574 |
| TTES 2 (°C) | 0.873 | 0.255 | 0.905 | 1.243 | 1.233 |
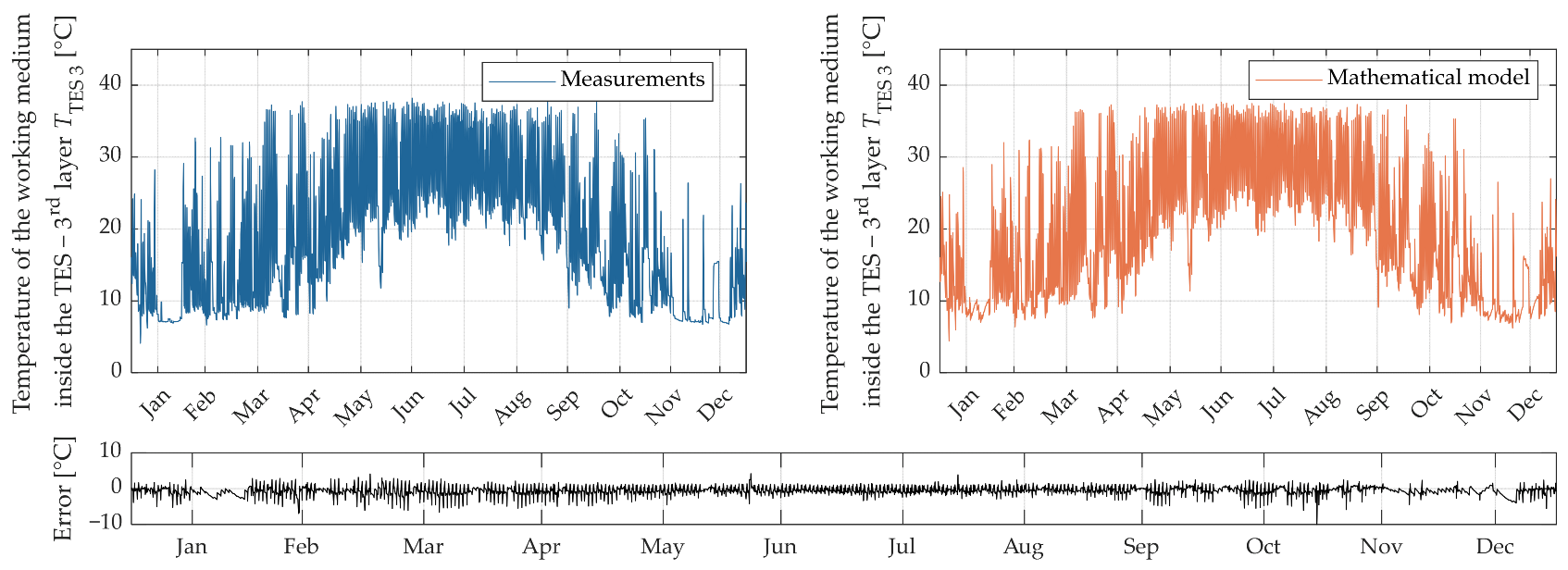
| TTES 3 (°C) | 0.579 | 0.240 | 0.552 | 0.846 | 0.842 |
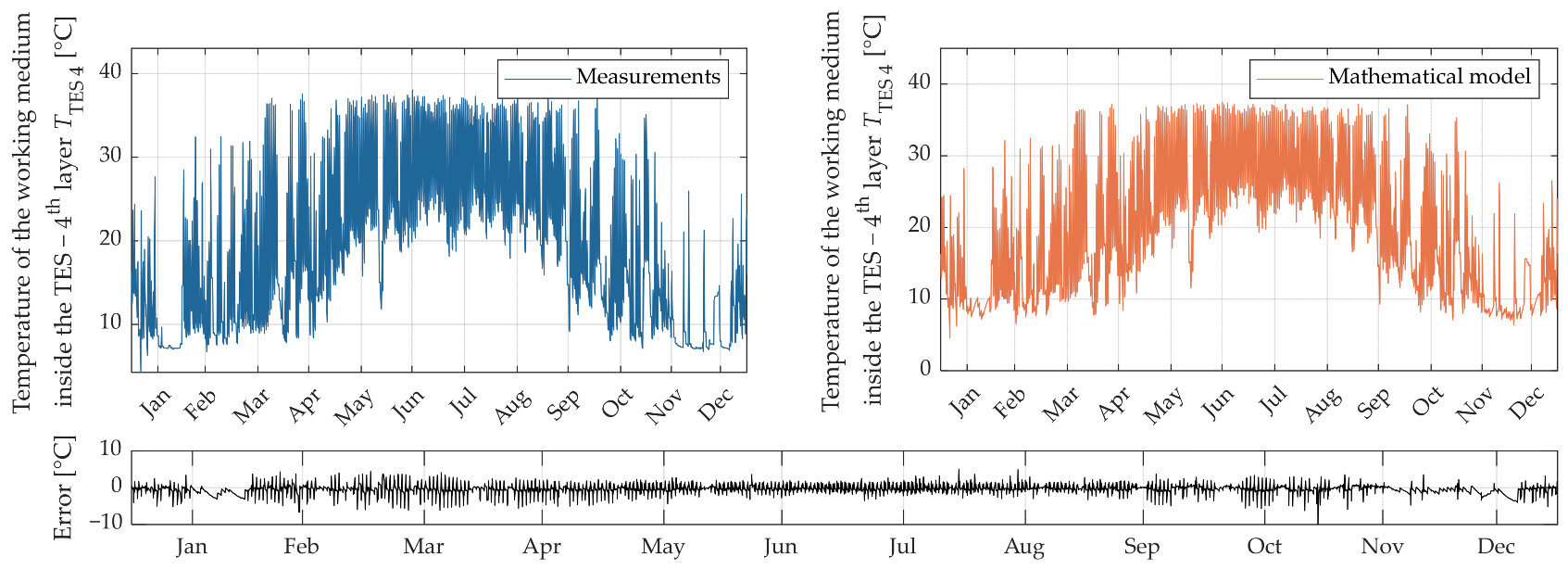
| TTES 4 (°C) | 0.589 | 0.178 | 0.508 | 0.801 | 0.791 |
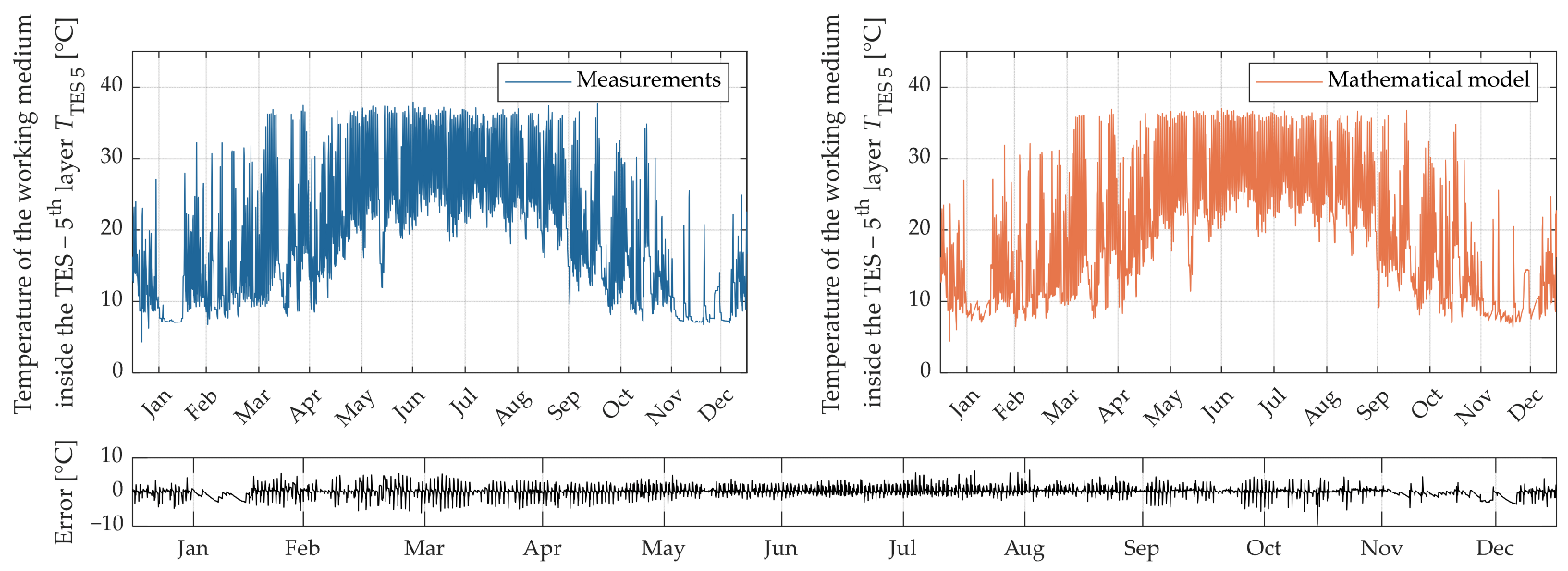
| TTES 5 (°C) | 0.586 | 0.469 | 0.498 | 0.873 | 0.873 |
| TTES 6 (°C) | 0.908 | 0.696 | 0.885 | 1.299 | 1.290 |
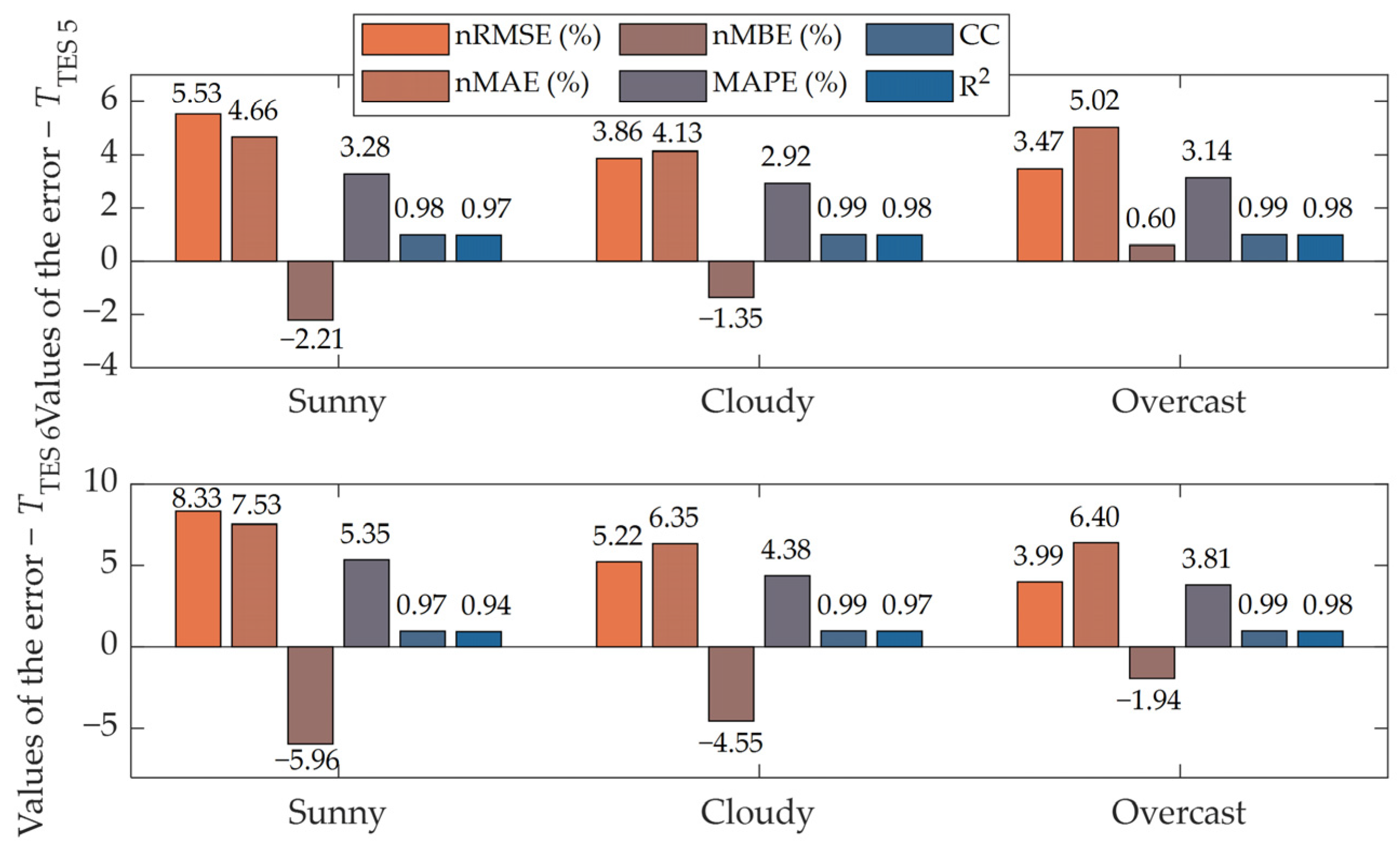
| nRMSE | nMAE | nMBE | MAPE | CC | R2 | |
|---|---|---|---|---|---|---|
| Error value—TTES 1 | 6.44% | 8.79% | 7.76% | 5.62% | 0.987 | 0.973 |
| Error value—TTES 2 | 5.19% | 5.33% | 5.62% | 5.22% | 0.983 | 0.983 |
| Error value—TTES 3 | 3.72% | 4.57% | 3.00% | 3.38% | 0.990 | 0.986 |
| Error value—TTES 4 | 3.74% | 4.26% | 1.96% | 3.03% | 0.990 | 0.980 |
| Error value—TTES 5 | 4.29% | 4.60% | 1.39% | 3.11% | 0.986 | 0.976 |
| Error value—TTES 6 | 5.85% | 6.76% | 4.15% | 4.51% | 0.983 | 0.963 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sredenšek, K.; Simonič, E.; Deželak, K.; Bizjak, M.; Lukač, N.; Seme, S. Dynamic Modeling and Experimental Validation of the Photovoltaic/Thermal System. Appl. Sci. 2025, 15, 10505. https://doi.org/10.3390/app151910505
Sredenšek K, Simonič E, Deželak K, Bizjak M, Lukač N, Seme S. Dynamic Modeling and Experimental Validation of the Photovoltaic/Thermal System. Applied Sciences. 2025; 15(19):10505. https://doi.org/10.3390/app151910505
Chicago/Turabian StyleSredenšek, Klemen, Eva Simonič, Klemen Deželak, Marko Bizjak, Niko Lukač, and Sebastijan Seme. 2025. "Dynamic Modeling and Experimental Validation of the Photovoltaic/Thermal System" Applied Sciences 15, no. 19: 10505. https://doi.org/10.3390/app151910505
APA StyleSredenšek, K., Simonič, E., Deželak, K., Bizjak, M., Lukač, N., & Seme, S. (2025). Dynamic Modeling and Experimental Validation of the Photovoltaic/Thermal System. Applied Sciences, 15(19), 10505. https://doi.org/10.3390/app151910505









