Node Classification of Imbalanced Data Using Ensemble Graph Neural Networks
Abstract
1. Introduction
- (1)
- First, we propose an ensemble graph-neural approach tailored to class-imbalanced node classification. By randomly undersampling majority-class samples, multiple balanced training subsets are created. Several GCN base classifiers are trained in parallel, and their predictions are aggregated through a majority voting scheme.
- (2)
- We build an online comment relational graph and perform fake-review detection using graph convolutional networks. The framework explicitly tackles the challenge of imbalanced class distributions within graph data, reducing the tendency of traditional GCNs to favor majority classes.
- (3)
- We conduct the framework’s effectiveness across two different types of tasks (node classification and fake review detection) and three real-world datasets, consistently demonstrating performance improvements.
2. Related Work
2.1. Imbalanced Data
2.2. Imbalanced Node Classification Methods Based on GNN
3. Methodology
3.1. Problem Definition
3.2. Base Classifier Model Based on GCN
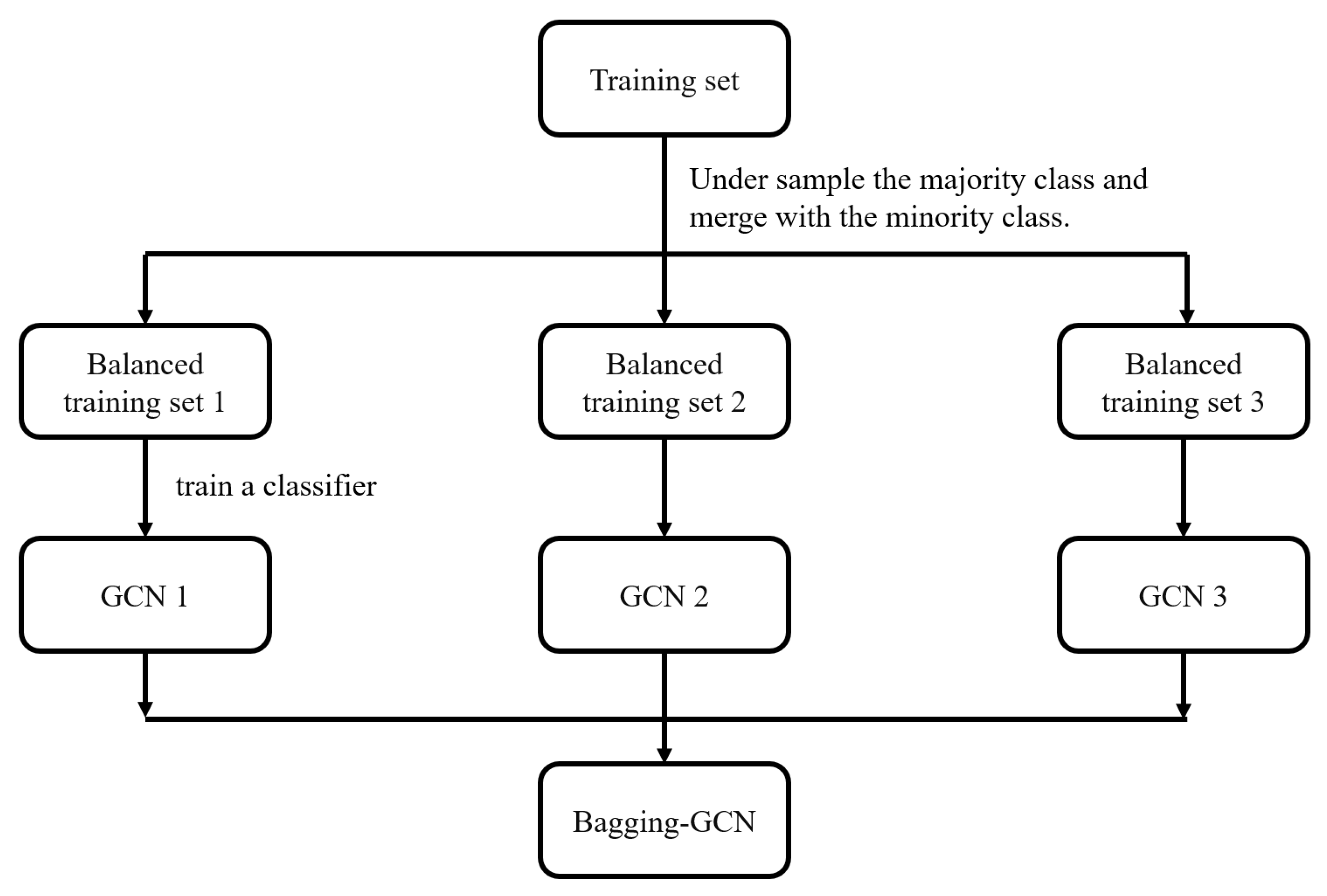
3.3. Bagging-GCN Model
- (1)
- Divide the dataset into training, validation, and test subsets following the experimental protocol.
- (2)
- On the training split, randomly undersample the majority class and merge it with all minority samples to obtain a balanced training subset; repeat this procedure M times to generate M distinct balanced training sets.
- (3)
- Train a GCN base classifier using each of the balanced training sets, resulting in M different GCN base classifiers.
- (4)
- Compose the M different GCN base classifiers into the Bagging-GCN ensemble classifier.
- (5)
- During prediction, input the samples from the test set into the GCN ensemble classifier. Based on the voting outcomes of the individual GCN base classifiers, the final predicted class of each sample is determined.
| Algorithm 1: Bagging-GCN algorithm. |
 |
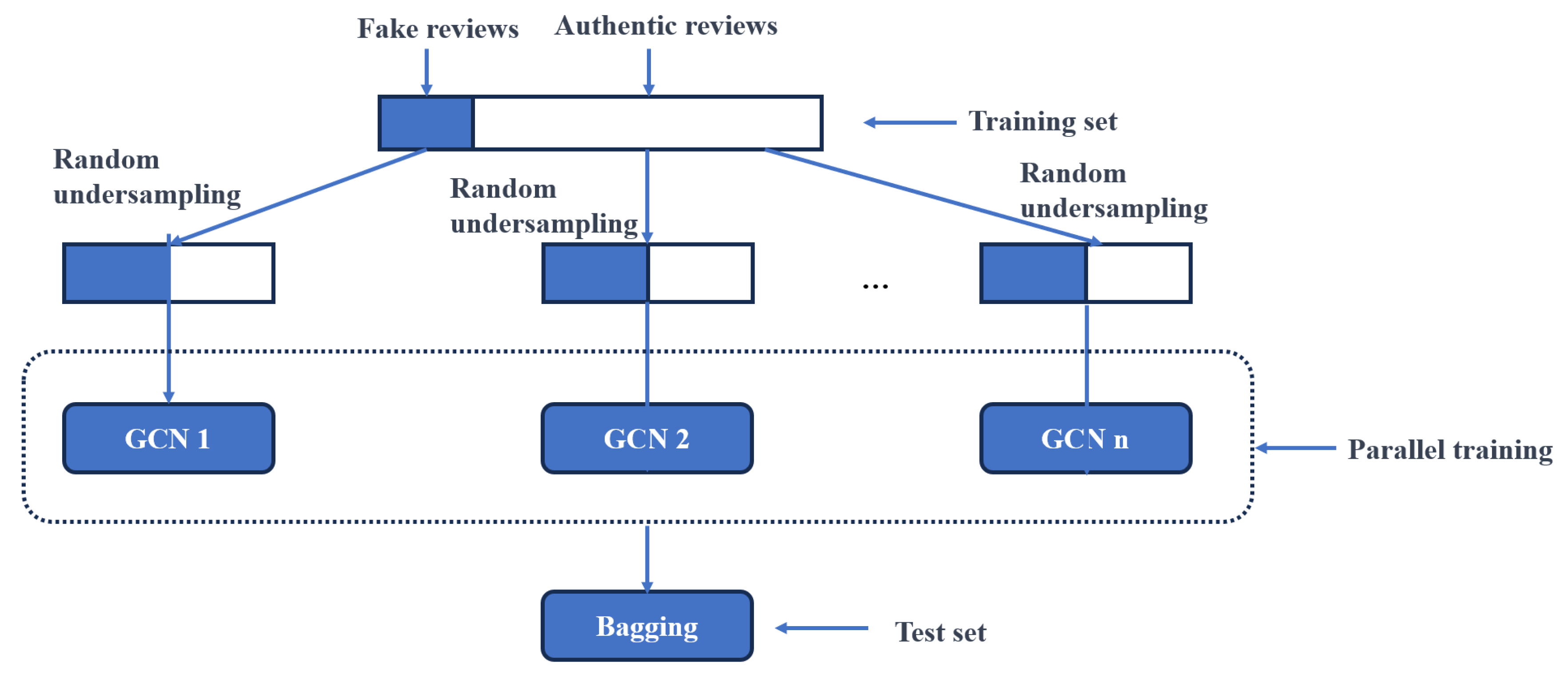
3.4. Detecting Fake Reviews Using Bagging-GCN
- (1)
- Preprocess the original online review dataset, standardizing all features to improve classification performance in subsequent classifiers.
- (2)
- Represent each review as a node and combine three relation-specific subgraphs derived from the dataset: R–U–R, R–S–R, and R–T–R.
- (3)
- Perform a stratified split of the processed data into training, validation, and test sets with a distribution for each class.
- (4)
- Due to class imbalance, the resulting training set is skewed. Apply random undersampling to the genuine review samples and combine them with fake review samples to form a balanced training set, improving the training of models and their classification performance.
- (5)
- Train the training set using GCN-based base classifiers. Optimize the base classification model using gradient descent and backpropagation.
- (6)
- Repeat step 4 to obtain multiple distinct training sets. Train GCN-based base classifiers in parallel on these sets to independently extract and learn data features.
- (7)
- Integrate multiple base classifiers into a strong classifier. Aggregate the predictions from various base classifiers using majority voting to obtain the final prediction.
- (8)
- Evaluate the proposed Bagging-GCN based on the final prediction results.
4. Experimental Evaluation
4.1. Datasets
4.1.1. Node Classification Datasets
4.1.2. Fake Review Detection Dataset
4.2. Evaluation Metrics
- (1)
- Confusion Matrix
- (2)
- Accuracy (Acc)
- (3)
- F1 Score
- (4)
- AUC
4.3. Experiments on Imbalanced Node Classification
4.3.1. Experimental Setup
4.3.2. Experimental Results and Analysis
- (1)
- Comparison Between Bagging-GCN and Baseline Methods
- (2)
- Impact of the Number of Base Classifiers
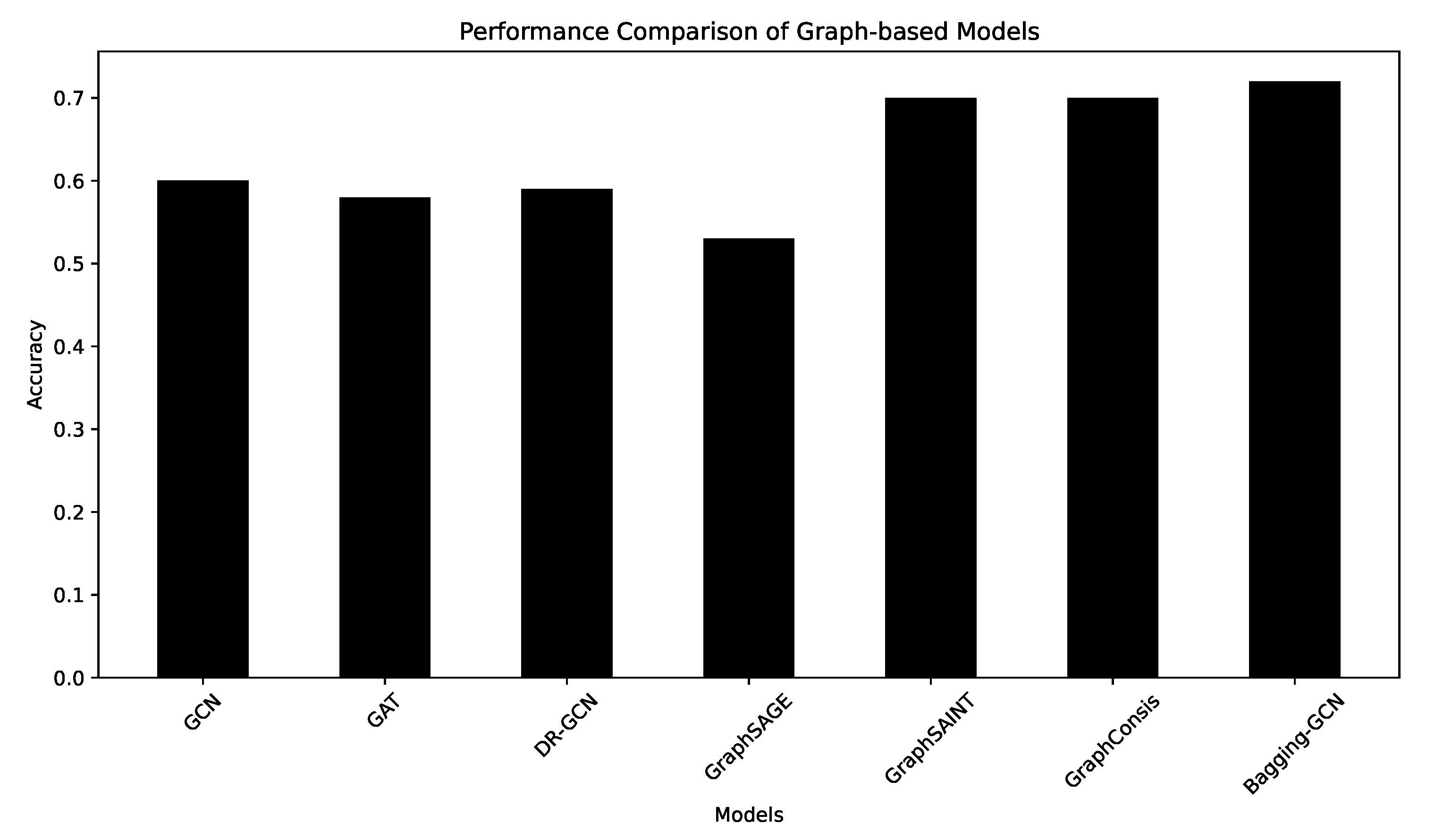
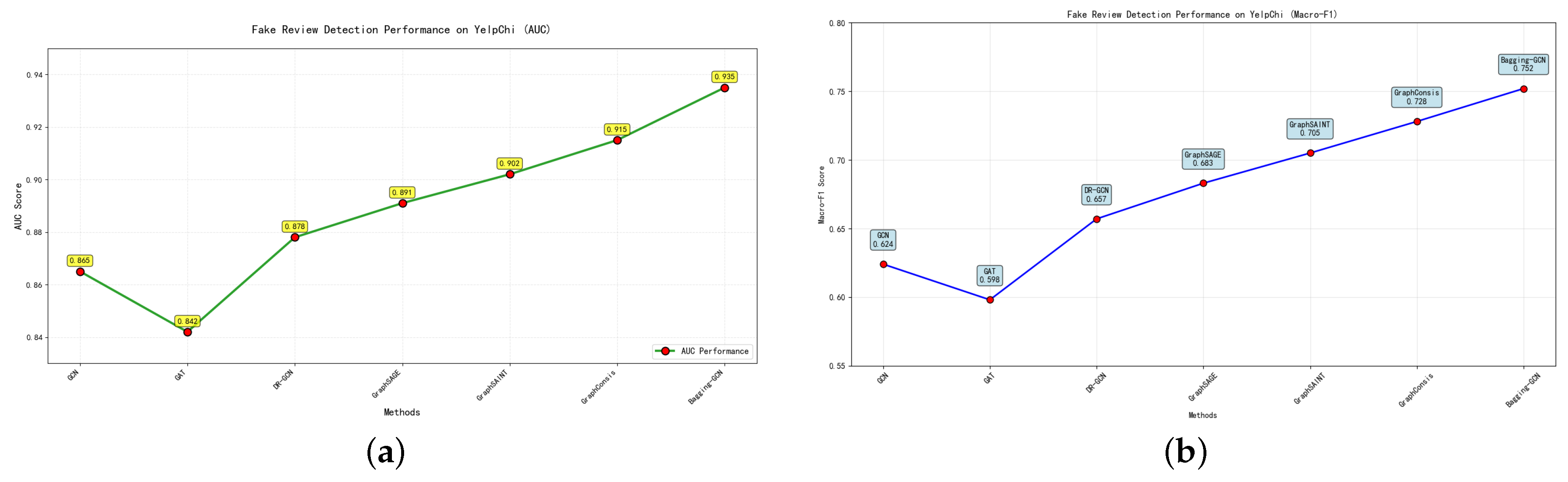
4.4. Result on Fake Review Detection Dataset
Experimental Results and Analysis
4.5. Parameter Values Used in Our Experiments
4.6. Rationale for Synthetic Imbalance and Generalizability
5. Conclusions and Future Work
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, S.; Yin, H.; Chen, T.; Nguyen, Q.V.H.; Huang, Z.; Cui, L. GCN-Based User Representation Learning for Unifying Robust Recommendation and Fraudster Detection. In Proceedings of the 43rd international ACM SIGIR Conference on Research and Development in Information Retrieval, Virtual Event, China, 25–30 July 2020; pp. 689–698. [Google Scholar]
- Hafez, I.Y.; Hafez, A.Y.; Saleh, A.; El-Mageed, A.A.A.; Abohany, A.A. A systematic review of AI-enhanced techniques in credit card fraud detection. J. Big Data 2025, 12, 6. [Google Scholar] [CrossRef]
- Zhong, Q.; Liu, Y.; Ao, X.; Hu, B.; Feng, J.; Tang, J.; He, Q. Financial Defaulter Detection on Online Credit Payment via Multi-view Attributed Heterogeneous Information Network. In Proceedings of the Web Conference 2020, Taipei, Taiwan, 20–24 April 2020; pp. 785–795. [Google Scholar]
- Yang, Y.; Sun, Y.; Li, F.; Guan, B.; Liu, J.; Shang, J. MGCNRF: Prediction of Disease-Related miRNAs Based on Multiple Graph Convolutional Networks and Random Forest. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 15701–15709. [Google Scholar] [CrossRef] [PubMed]
- Xie, B.; Ma, X.; Xue, S.; Beheshti, A.; Yang, J.; Fan, H.; Wu, J. Multiknowledge and LLM-Inspired Heterogeneous Graph Neural Network for Fake News Detection. IEEE Trans. Comput. Soc. Syst. 2025, 12, 682–694. [Google Scholar] [CrossRef]
- Chen, R.; Li, G.; Dai, C. DRGCN: Dual Residual Graph Convolutional Network for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Zhao, T.; Zhang, X.; Wang, S. GraphSMOTE: Imbalanced Node Classification on Graphs with Graph Neural Networks. In Proceedings of the 14th ACM International Conference on Web Search and Data Mining, Virtual Event, Israel, 8–12 March 2021; pp. 833–841. [Google Scholar]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic Minority Over-sampling Technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Xu, L. Machine Learning Solutions for Classification and Regions of Interest Analysis on Imbalanced Datasets. Ph.D. Thesis, University of Tampere, Tampere, Finland, 2024. [Google Scholar]
- Shah, K.A.; Halim, Z.; Anwar, S.; Hsu, C.; Rida, I. Multi-sensor data fusion for smart healthcare: Optimizing specialty-based classification of imbalanced EMRs. Inf. Fusion 2026, 125, 103503. [Google Scholar] [CrossRef]
- Luo, J.; Liu, L.; He, Y.; Tan, K. An efficient boundary prediction method based on multi-fidelity Gaussian classification process for class-imbalance. Eng. Appl. Artif. Intell. 2025, 149, 110549. [Google Scholar] [CrossRef]
- Mildenberger, D.; Hager, P.; Rueckert, D.; Menten, M.J. A Tale of Two Classes: Adapting Supervised Contrastive Learning to Binary Imbalanced Datasets. In Proceedings of the Computer Vision and Pattern Recognition Conference, Nashville, Tennessee, 10–17 June 2025; pp. 10305–10314. [Google Scholar]
- Chen, W.; Yang, K.; Yu, Z.; Shi, Y.; Chen, C.L.P. A survey on imbalanced learning: Latest research, applications and future directions. Artif. Intell. Rev. 2024, 57, 137. [Google Scholar] [CrossRef]
- Sun, H.; Li, J.; Zhu, X. A Novel Expandable Borderline Smote Over-Sampling Method for Class Imbalance Problem. IEEE Trans. Knowl. Data Eng. 2025, 37, 2183–2199. [Google Scholar] [CrossRef]
- Kachan, O.; Savchenko, A.V.; Gusev, G. Simplicial SMOTE: Oversampling Solution to the Imbalanced Learning Problem. In Proceedings of the KDD, Toronto, ON, Canada, 3–7 August 2025; pp. 625–635. [Google Scholar]
- Chang, A.; Fontaine, M.C.; Booth, S.; Mataric, M.J.; Nikolaidis, S. Quality-Diversity Generative Sampling for Learning with Synthetic Data. In Proceedings of the AAAI Conference on Artificial Intelligence, Philadelphia, PA, USA, 25 February–4 March 2025; pp. 19805–19812. [Google Scholar]
- Kumar, N.S.; Rao, K.N.; Govardhan, A.; Reddy, K.S.; Mahmood, A.M. Undersampled K-means approach for handling imbalanced distributed data. Prog. Artif. Intell. 2014, 3, 29–38. [Google Scholar] [CrossRef]
- Cui, Y.; Jia, M.; Lin, T.; Song, Y.; Belongie, S.J. Class-Balanced Loss Based on Effective Number of Samples. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 9268–9277. [Google Scholar]
- Lin, T.; Goyal, P.; Girshick, R.B.; He, K.; Dollár, P. Focal Loss for Dense Object Detection. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2999–3007. [Google Scholar]
- Li, B.; Liu, Y.; Wang, X. Gradient Harmonized Single-Stage Detector. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 29–31 January 2019; pp. 8577–8584. [Google Scholar]
- Klikowski, J.; Wozniak, M. Deterministic Sampling Classifier with weighted Bagging for drifted imbalanced data stream classification. Appl. Soft Comput. 2022, 122, 108855. [Google Scholar] [CrossRef]
- Jafarzadeh, H.; MahdianPari, M.; Gill, E.; Mohammadimanesh, F.; Homayouni, S. Bagging and Boosting Ensemble Classifiers for Classification of Multispectral, Hyperspectral and PolSAR Data: A Comparative Evaluation. Remote. Sens. 2021, 13, 4405. [Google Scholar] [CrossRef]
- Li, J.; Zhu, X.; Wang, J. AdaBoost.C2: Boosting Classifiers Chains for Multi-Label Classification. In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; pp. 8580–8587. [Google Scholar]
- Parthasarathy, S.; Lakshminarayanan, A.R. BS-SC Model: A Novel Method for Predicting Child Abuse Using Borderline-SMOTE Enabled Stacking Classifier. Comput. Syst. Sci. Eng. 2023, 46, 1311–1336. [Google Scholar]
- Sharma, N.; Joshi, D. DRGCN-BiLSTM: An Electrocardiogram Heartbeat Classification Using Dynamic Spatial-Temporal Graph Convolutional and Bidirectional Long-Short Term Memory Technique. IEEE Trans. Consum. Electron. 2025, 71, 579–593. [Google Scholar] [CrossRef]
- Zhang, L.; Yan, X.; He, J.; Li, R.; Chu, W. DRGCN: Dynamic Evolving Initial Residual for Deep Graph Convolutional Networks. In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; pp. 11254–11261. [Google Scholar]
- Liu, Z.; Li, Y.; Chen, N.; Wang, Q.; Hooi, B.; He, B. A Survey of Imbalanced Learning on Graphs: Problems, Techniques, and Future Directions. IEEE Trans. Knowl. Data Eng. 2025, 37, 3132–3152. [Google Scholar] [CrossRef]
- Ju, W.; Mao, Z.; Yi, S.; Qin, Y.; Gu, Y.; Xiao, Z.; Shen, J.; Qiao, Z.; Zhang, M. Cluster-guided Contrastive Class-imbalanced Graph Classification. In Proceedings of the AAAI Conference on Artificial Intelligence, Philadelphia, PA, USA, 25 February 25–4 March 2025; pp. 11924–11932. [Google Scholar]
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C.; Yu, P.S. A Comprehensive Survey on Graph Neural Networks. IEEE Trans. Neural Networks Learn. Syst. 2021, 32, 4–24. [Google Scholar]
- Li, S.; Li, Y.; Wu, X.; Otaibi, S.A.; Tian, Z. Imbalanced Malware Family Classification Using Multimodal Fusion and Weight Self-Learning. IEEE Trans. Intell. Transp. Syst. 2023, 24, 7642–7652. [Google Scholar]
- Zeng, L.; Li, L.; Gao, Z.; Zhao, P.; Li, J. ImGCL: Revisiting Graph Contrastive Learning on Imbalanced Node Classification. In Proceedings of the AAAI conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; pp. 11138–11146. [Google Scholar]
- Zhou, M.; Gong, Z. GraphSR: A Data Augmentation Algorithm for Imbalanced Node Classification. In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; pp. 4954–4962. [Google Scholar]
- Pang, Y.; Peng, L.; Zhang, H.; Chen, Z.; Yang, B. Imbalanced ensemble learning leveraging a novel data-level diversity metric. Pattern Recognit. 2025, 157, 110886. [Google Scholar]
- Han, M.; Guo, H.; Wang, W. A new data complexity measure for multi-class imbalanced classification tasks. Pattern Recognit. 2025, 157, 110881. [Google Scholar]
- Xia, F.; Wang, L.; Tang, T.; Chen, X.; Kong, X.; Oatley, G.; King, I. CenGCN: Centralized Convolutional Networks with Vertex Imbalance for Scale-Free Graphs. IEEE Trans. Knowl. Data Eng. 2023, 35, 4555–4569. [Google Scholar] [CrossRef]
- Chen, Y.; Lu, C. RankMix: Data Augmentation for Weakly Supervised Learning of Classifying Whole Slide Images with Diverse Sizes and Imbalanced Categories. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 23936–23945. [Google Scholar]
- Qu, L.; Zhu, H.; Zheng, R.; Shi, Y.; Yin, H. ImGAGN: Imbalanced Network Embedding via Generative Adversarial Graph Networks. In Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, Singapore, 14–18 August 2021; pp. 1390–1398. [Google Scholar]
- Liu, Y.; Ao, X.; Qin, Z.; Chi, J.; Feng, J.; Yang, H.; He, Q. Pick and Choose: A GNN-based Imbalanced Learning Approach for Fraud Detection. In Proceedings of the Web Conference 2021, Ljubljana, Slovenia, 19–23 April 2021; pp. 3168–3177. [Google Scholar]
- Wu, L.; Lin, H.; Gao, Z.; Tan, C.; Li, S.Z. GraphMixup: Improving Class-Imbalanced Node Classification on Graphs by Self-supervised Context Prediction. In Joint European Conference on Machine Learning and Knowledge Discovery in Databases; Springer Nature: Cham, Switzerland, 2022. [Google Scholar]
- Li, X.; Jiang, Y.; Liu, Y.; Zhang, J.; Yin, S.; Luo, H. RAGCN: Region Aggregation Graph Convolutional Network for Bone Age Assessment From X-Ray Images. IEEE Trans. Instrum. Meas. 2022, 71, 1–12. [Google Scholar] [CrossRef]
- Sun, K.; Zhu, Z.; Lin, Z. AdaGCN: Adaboosting Graph Convolutional Networks into Deep Models. In Proceedings of the ICLR, Virtual Event, Austria, 3–7 May 2021. [Google Scholar]
- Hamilton, W.L.; Ying, Z.; Leskovec, J. Inductive Representation Learning on Large Graphs. In Proceedings of the NIPS, Long Beach, CA, USA, 4–9 December 2017; pp. 1024–1034. [Google Scholar]
- Zeng, H.; Zhou, H.; Srivastava, A.; Kannan, R.; Prasanna, V.K. GraphSAINT: Graph Sampling Based Inductive Learning Method. arXiv 2020, arXiv:1907.04931. [Google Scholar] [CrossRef]
- Liu, Z.; Dou, Y.; Yu, P.S.; Deng, Y.; Peng, H. Alleviating the Inconsistency Problem of Applying Graph Neural Network to Fraud Detection. In Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval, Virtual Event, China, 25–30 July 2020; pp. 1569–1572. [Google Scholar]
- Park, J.; Song, J.; Yang, E. GraphENS: Neighbor-Aware Ego Network Synthesis for Class-Imbalanced Node Classification. 2022. Available online: https://openreview.net/forum?id=MXEl7i-iru (accessed on 28 January 2022).
- Makansi, O.; Ilg, E.; Çiçek, Ö.; Brox, T. Overcoming Limitations of Mixture Density Networks: A Sampling and Fitting Framework for Multimodal Future Prediction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–17 June 2019; pp. 7144–7153. [Google Scholar]
- Wang, Z.; Ye, X.; Wang, C.; Cui, J.; Yu, P.S. Network Embedding with Completely-Imbalanced Labels. IEEE Trans. Knowl. Data Eng. 2021, 33, 3634–3647. [Google Scholar] [CrossRef]
- Oh, J.; Cho, K.; Bruna, J. Advancing GraphSAGE with A Data-Driven Node Sampling. arXiv 2019, arXiv:1904.12935. [Google Scholar]
- Barakat, A.; Bianchi, P. Convergence Rates of a Momentum Algorithm with Bounded Adaptive Step Size for Nonconvex Optimization. In Proceedings of the Asian Conference on Machine Learning, Bangkok, Thailand, 18–20 November 2020; Volume 129, pp. 225–240. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-Supervised Classification with Graph Convolutional Networks. In Proceedings of the ICLR, Toulon, France, 24–26 April 2017. [Google Scholar]
- Velickovic, P.; Cucurull, G.; Casanova, A.; Romero, A.; Liò, P.; Bengio, Y. Graph Attention Networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
| Dataset | Node | Edge | IR | Relations | #Relations |
|---|---|---|---|---|---|
| Yelpchi | 45,954 | 3,846,979 | 5.9 | R-U-R | 49,315 |
| R-S-R | 3,402,743 | ||||
| R-T-R | 573,616 |
| Methods | Cora | BlogCatalog | ||||
|---|---|---|---|---|---|---|
| Acc | AUC | Macro-F1 | Acc | AUC | Macro-F1 | |
| GraphENS | 0.681 ± 0.003 | 0.914 ± 0.002 | 0.684 ± 0.003 | 0.210 ± 0.004 | 0.586 ± 0.002 | 0.074 ± 0.002 |
| Over-sampling | 0.692 ± 0.009 | 0.918 ± 0.005 | 0.666 ± 0.008 | 0.203 ± 0.004 | 0.599 ± 0.003 | 0.077 ± 0.001 |
| Re-weight | 0.697 ± 0.008 | 0.928 ± 0.005 | 0.684 ± 0.004 | 0.206 ± 0.005 | 0.587 ± 0.003 | 0.075 ± 0.003 |
| SMOTE | 0.696 ± 0.001 | 0.920± 0.008 | 0.673 ± 0.003 | 0.205 ± 0.004 | 0.595 ± 0.003 | 0.077 ± 0.001 |
| Embed-SMOTE | 0.683 ± 0.007 | 0.913 ± 0.002 | 0.673 ± 0.002 | 0.205 ± 0.003 | 0.588 ± 0.002 | 0.076 ± 0.001 |
| RECT | 0.685 ± 0.0013 | 0.921 ± 0.007 | 0.689 ± 0.006 | 0.202 ± 0.007 | 0.593 ± 0.004 | 0.073 ± 0.003 |
| DRGCN | 0.694 ± 0.0011 | 0.932 ± 0.006 | 0.691 ± 0.007 | 0.208 ± 0.006 | 0.603 ± 0.005 | 0.078 ± 0.004 |
| GraphSMOTE | 0.736 ± 0.001 | 0.934 ± 0.002 | 0.727 ± 0.001 | 0.215 ± 0.01 | 0.591 ± 0.01 | 0.080 ± 0.005 |
| Bagging-GCN | 0.770 ± 0.001 | 0.932 ± 0.009 | 0.750 ± 0.009 | 0.240 ± 0.005 | 0.609 ± 0.002 | 0.085 ± 0.002 |
| Base Classifiers | Acc | AUC | Macro-F1 |
|---|---|---|---|
| 3 | 0.752 ± 0.001 | 0.912 ± 0.005 | 0.719 ± 0.004 |
| 5 | 0.768 ± 0.001 | 0.928 ± 0.002 | 0.732 ± 0.009 |
| 7 | 0.770 ± 0.001 | 0.932 ± 0.009 | 0.750 ± 0.009 |
| 9 | 0.737 ± 0.002 | 0.923 ± 0.006 | 0.704 ± 0.008 |
| 11 | 0.737 ± 0.005 | 0.921 ± 0.008 | 0.701 ± 0.002 |
| Parameter | Value(s) Used |
|---|---|
| Number of Base Classifiers (M) | 7 (optimal after ablation) |
| Learning Rate | 0.01 |
| Weight Decay | |
| Hidden Units | 16 |
| Dropout Rate | 0.5 |
| Training Epochs | Up to 5000 (until convergence) |
| Imbalance Ratio (IR) | 0.5 (for Cora); natural imbalance (others) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, Y. Node Classification of Imbalanced Data Using Ensemble Graph Neural Networks. Appl. Sci. 2025, 15, 10440. https://doi.org/10.3390/app151910440
Liang Y. Node Classification of Imbalanced Data Using Ensemble Graph Neural Networks. Applied Sciences. 2025; 15(19):10440. https://doi.org/10.3390/app151910440
Chicago/Turabian StyleLiang, Yuan. 2025. "Node Classification of Imbalanced Data Using Ensemble Graph Neural Networks" Applied Sciences 15, no. 19: 10440. https://doi.org/10.3390/app151910440
APA StyleLiang, Y. (2025). Node Classification of Imbalanced Data Using Ensemble Graph Neural Networks. Applied Sciences, 15(19), 10440. https://doi.org/10.3390/app151910440






