Portfolio Management Strategies Based on Deep Temporal Clustering

Abstract

Portfolio management (PM) facilitates optimal investing decisions and enables organizations to control risks and achieve stable financial growth. Advances in machine learning, mostly through supervised learning, are drastically changing the way in which PM is conducted. More recently, unsupervised learning is also emerging as a paradigm that can support the creation of diversified and profitable portfolios through stock clustering. In the corresponding literature, there is significant evidence that cluster-informed methods can outperform both traditional and supervised approaches to PM. However, these works are few and have not considered state-of-the-art deep learning approaches for clustering, while stock allocation is often limited to equally weighted portfolios or mean-variance optimization (MVO). To address these issues, we propose a cluster-informed PM method based on deep temporal clustering (DTC) along with our recommended parameters for training convergence, combined with the conditional drawdown at risk (CDaR) portfolio allocation method. Unlike MVO, CDaR considers tail risk and can minimize extreme price drawdowns. Cluster validity metrics reveal that DTC outperforms previously proposed stock clustering methods. Furthermore, DTC enhanced by CDaR achieves a higher expected Sortino ratio (1.1) compared to previous works in clustering-based PM. Additional Brinson attribution and maximum drawdown analyses further confirm the robustness of our method.

1. Introduction

Stock markets form a cornerstone of modern economy, as they enable companies to raise capital through equity financing and facilitate the trading of company shares [1]. In portfolio management (PM), stocks and their derivatives are key financial instruments for investors [2]. The central problem of PM is to determine optimal portfolio weights (i.e., the relative amounts invested) for each stock, with near-zero weights interpreted as stocks that should be excluded from the portfolio. The simplest strategy is the equally weighted portfolio (EWP), in which portfolio weights are equally distributed across the considered stocks [3]. In 1952, Markowitz introduced mean-variance optimization (MVO), which to this day is considered an important method for portfolio optimization [4]. This method uses quadratic optimization to estimate an efficient frontier of portfolios, which includes portfolios that have maximum return (minimum risk) for a given level of risk (return) [5].

According to Kim et al. [6], portfolio optimization can be further deconstructed into two phases, known as stock selection and stock allocation. Stock selection determines the set of stocks that will be considered in the next phase, while stock allocation determines the portfolio weights for the selected stocks. Whereas MVO can implicitly bypass the first phase by removing stocks with weights that are near-zero, there is significant evidence that a preliminary phase of stock selection can improve the overall performance of the portfolio [6,7].

Machine learning (ML) is the leading paradigm for tackling highly complex and data-intensive problems [8]. The vast majority of ML-based investing strategies employ some form of supervised, reinforcement, or unsupervised learning (e.g., [6,9,10]). Based on a comparison of search results from four academic search engines (SemanticScholar, ScienceDirect, RefSeek, and GoogleScholar) in the context of investing strategies, it is evident that supervised and reinforcement learning have received several times more attention compared to unsupervised learning.

Nevertheless, recent works highlight unsupervised learning as an emerging paradigm for PM based on stock clustering [6,11,12]. In this regard, unsupervised learning can be more adaptive to changing market conditions, presenting several benefits compared to the previous paradigms. Cluster-informed PM strategies resolve the labeling bias inherent in supervised approaches [13]. Stocks that belong to different clusters are more likely to be uncorrelated; as such, the information extracted from clustering is valuable for constructing highly diversified portfolios [7].

However, there are still only a few works on cluster-based PM, a field in which we also identified several research gaps based on our literature review (Section 2). First, most works involve static vector clustering, which does not take into account the temporal nature of financial data. Second, a detailed comparison of traditional time series clustering methods such as dynamic time warping (DTW) [14] with modern deep learning (DL) methods for clustering is lacking in the stock selection literature. Third, there are several renowned financial engineering and portfolio allocation methods that have not yet been considered as preprocessing and postprocessing steps surrounding the stock clustering process. Finally, any proposed solution should be evaluated on an extended number of consecutive years in order to prove its efficacy.

In this paper, we propose portfolio management—deep temporal clustering (PM-DTC), a DL-based portfolio management system for stock investing trained on Standard & Poor’s 500 (S&P 500), Dow Jones Industrial Average (DJIA) and NASDAQ stocks. To the best of our knowledge, this is the first application of deep temporal clustering (DTC) [15] to the stock selection problem. Our proposed solution has three phases, and provides the following contributions to the field of unsupervised PM strategies:

• Stock pre-filtering: We include filters based on locally weighted scatterplot smoothing (LOWESS), kurtosis, and betas. Although these are fundamental tools in the financial literature [16], they have not been considered in previous stock clustering approaches.
• Stock clustering and selection: We propose a DTC model that is able to outperform previous approaches in stock clustering. After the clustering process, we use a sampling method based on entropy minimization and the Jenks–Fisher algorithm [17] to derive the final stocks in the portfolio.
• Stock allocation: We show that integration with a recent tail risk model, namely, conditional drawdown at risk (CDaR) [18] combined with Ledoit–Wolf shrinkage for covariance matrix estimation [19], is able to outperform previous PM methods.

In addition, the aforementioned steps are compared with well-established alternatives for clustering and portfolio optimization, including self-organizing map (SOM) and hierarchical risk parity (HRP) [20,21]. The final evaluation of profit and loss (PnL) reveals the outstanding Sharpe ratio of the proposed solution, which surpasses the performance of several benchmark indices and previous works.

Furthermore, the portfolio evaluation process is more comprehensive than in previous studies. By applying a Brinson performance attribution analysis within the Global Industry Classification Standard (GICS) framework, we demonstrate the model’s effectiveness in simultaneously allocating across sectors and selecting individual stocks. In addition, a wealth drawdown analysis highlights the robustness of the proposed strategy during the 2022 market downturn.

The remainder of the paper is organized as follows: Section 2 investigates several related works that have employed unsupervised learning in the field of PM; Section 3 presents the data, methodology, and assumptions of our experiments; Section 4 reveals and compares the experimental results, also analyzing the performance of each subsystem; finally, Section 5 concludes the paper.

2. Related Work

Recent works in empirical finance and machine learning, such as Gu et al. [22] and Zhou et al. [23], have shown that neural network models trained via supervised learning outperform traditional linear econometric approaches in stock price forecasting. While this finding is well-established in the supervised learning literature, there is considerably less research comparing traditional and neural-based clustering methods. As will be shown in the following paragraphs, most prior studies have not incorporated neural-based clustering in their experiments. Therefore, a major focus of this paper is to provide additional evidence on the relative merits of neural clustering methods by benchmarking them against traditional clustering techniques in a financial context.

Interestingly, the performance gains we observe in our unsupervised learning experiments parallel those reported in the supervised learning literature, suggesting a consistent advantage of deep learning across both paradigms. We further show that deep learning can discover profitable long positions with low downside risk, which is in alignment with the work of Avramov et al. [24]. The following paragraphs briefly summarize the PM literature related to unsupervised learning and clustering.

Zhang et al. [12] applied differential evolution (DE) to cluster Financial Times Stock Exchange (FTSE) and DJIA stocks. A nested two-level PM approach was used to combine both intra-cluster asset weights and cluster weights. Three portfolio management methods were investigated: EWP, MVO, and Tobin tangency allocation. Instead of relying on cluster validity metrics, the Sharpe ratio was used to guide the clustering process. The nested approach achieved improved the Sharpe ratio and weight stability. In [11], Nanda et al. performed clustering to log returns and valuation ratios of Bombay Stock Exchange data. They compared three algorithms (K-means, fuzzy C-means and SOM), and evaluated the results based on internal validity metrics. The results revealed that bisecting K-means was the best performing method. Although it improved computation time of MVO, their proposed method was not able to outperform the benchmark index (Sensex).

Using data from two Chinese stock markets for the period ranging from 2000 to 2014, Ren et al. [25] proposed a minimum spanning tree (MST) method on stock correlation graphs in order to classify portfolios as central or peripheral, also considering different market conditions. Their results showed that EWP on clustered stocks could consistently outperform the random allocation strategy. Yogas et al. [7] applied PM to KOMPAS-100 stocks using weekly log returns. They used parameters estimated through a P-spline interpolation of time series data as features for stock clustering. For each cluster, a non-dominated set of stocks based on profit-to-risk ratio was selected. Following this, cluster-informed versions of MVO and EWP outperformed the corresponding baselines.

In addition to the immediate grouping of stocks, clustering has more applications in PM. Kim et al. [6] combined agglomerative clustering with a sequential forward feature selector on S&P 500 stocks. They used a graph-based ranking algorithm for stock allocation and a hybrid of supervised learning models for stock allocation. The integrated system achieved a 58.2% compounded annual growth rate with 0.1% transaction fees, outperforming several previous approaches.

More recently, [26] demonstrated that transformer models can support profitable PM strategies. Experimenting with data from three stock markets, they showed that their proposed Adaptive Long-Short Pattern Transformer (ALSP-TF) could yield higher profits compared to RNNs. Nevertheless, their supervised learning approach did not involve stock clustering, instead considering a learning-to-rank task. After extensive research, we did not detect any recent works applying unsupervised learning with transformers for stock clustering and PM.

In summary, there is significant evidence for the usefulness of clustering in PM. However, we observe that many works overlook the importance of transaction fees, and only few consider experiments on extended time periods. More importantly, there is a lack of unsupervised DL approaches. This paper addresses these issues by proposing a PM method based on DTC, which is further evaluated with realistic transaction fees over a long time period.

3. Data and Methodology

This section presents the dataset, features, and preprocessing rules used in the experiments. Following this, it introduces the stock clustering and selection methods. Moreover, it also explains the PM methods used for portfolio allocation. Finally, it includes evaluation methods and a description of the integrated system.

3.1. Stock Dataset and Technical Indicators

Because no real consensus has been reached among the investing community regarding an optimal technical indicator (TI) strategy, we opt for a strategy comprised of various indicators. These indicators are broadly accepted within the community while at the same time encompassing a wide range of TI categories [27].

Therefore, we construct several TIs for our experiments, with more details concerning them presented in

Table 1. Technical indicator strategy description.

Category	Technical Indicator	Length (Days)	Fast Period	Slow Period	Signal Line
Trend	Exponential Moving Average (EMA)	50	-	-	-
	Exponential Moving Average (EMA)	200	-	-	-
	Average Directional Index (ADX)	50	-	-	30
	Aroon Oscillator (AROON)	14	-	-	-
Momentum	Rate of Change (ROC)	14	-	-	-
	Stochastic Oscillator (STOCH)	-	14	3	-
	Relative Strength Index (RSI)	14	-	-	-
	Moving Average Convergence/Divergence (MACD)	-	12	26	9
	Williams %R	20	-	-	-
Volume	Accumulation/Distribution Oscillator (ADOSC)	-	12	26	-
Momentum Oscillator	Commodity Channel Index (CCI)	20	-	-	-
Volatility	Standard Deviation (STDEV)	30	-	-	-

. The vast majority of TIs require OHLCV (Open, High, Low, Close, Volume) price data. The AlphaVantage and Yahoo Finance application programming interfaces (APIs) were used to retrieve historical OHLCV data of publicly traded stocks; specifically, we used the adjusted variants of prices, which are generally preferred over unadjusted as they offer a more accurate representation of the stock’s underlying value by accounting for dividends, stock splits, and new stock offerings. As in the majority of previous works in PM, we use a daily sampling frequency of market data. Concentrating solely on US markets, we retrieved data for a total of approximately 6000 stocks currently trading on US exchanges. This study focuses exclusively on stocks listed on the NYSE and NASDAQ, which are generally regarded as investable within the financial industry. In addition, the proposed strategies are restricted to long positions, thereby avoiding the risks associated with extreme short positions.

3.2. Pre-Filtering Methods

Pre-filtering steps are standard econometric methods that aim to remove stocks with excessive market risk. In the first step, the beta coefficient, denoted as $\beta$, is estimated for each stock. This coefficient measures the sensitivity of a stock’s returns to changes in the overall market returns. Absolute values of beta higher than one indicate higher sensitivity to market movements, ignoring the direction of sensitivity. Whereas PM can alleviate idiosyncratic risk through diversification, systematic risk cannot be completely diversified through PM, as it is related to macroeconomic and geopolitical conditions. Thus, to reduce the systematic risk of our portfolio, stocks with $\left|\beta \right|>1$ were removed, as they experience larger fluctuations than the market.

Following this, the statistical measure of kurtosis, denoted as k, was used to determine which stocks have leptokurtic return distributions, defined as $k>3$. The return distributions of these stocks possess relatively higher probability density on their tails, which indicates that extreme price volatility is more likely for these stocks. Therefore, these stocks were removed in order to reduce the overall portfolio risk. The third criterion for stock pre-filtering was the standard deviation of log returns, denoted as $\sigma$. Specifically, stocks for which $\sigma$ fell outside the interquartile range (IQR) were removed.

After smoothing the log return data with LOWESS regression, a number of statistical distributions were evaluated based on goodness-of-fit criteria. The best-performing in terms of the sum of squares error (SSE) and Bayesian information criterion (BIC) was a generalized hyperbolic distribution. Stocks that fell outside of the symmetrical 95% confidence interval of this distribution were removed from the dataset.

3.3. Stock Clustering and Selection

We compare five different methods for stock clustering based on technical indicator data. The first is K-means, a baseline clustering approach that requires the specification of a distance function, most commonly the Euclidean distance. In this paper, we instead use the DTW distance, which has the advantage of considering the temporal nature of time series data. The second method is agglomerative hierarchical clustering (HC) [28] based on the DTW distance. For this method, it is also necessary to define a cluster-to-cluster distance function; we experimented with options including single linkage, average linkage, complete linkage, and the Ward method [28]. The third method is K-shape [29], an iterative method specifically designed to handle input in the form of time series. To achieve this, it uses normalized cross-correlation to capture temporal patterns in the data.

For the neural network approaches, the first is a SOM that uses DTW distance; in this case, the DTW distance uses competition and adaptation to determine which stocks will be assigned to the closest neural units. The second approach is DTC, a modern encoder–decoder type neural architecture that aims to optimize two losses. The first loss is the mean squared error (MSE) time series reconstruction loss, the minimization of which forces the encoder to learn a dense vector representation of the time series. The second is the Kullback–Leibler (KL) divergence [30], which leads to well-separated clusters. We rely on two cluster validity indices in order to evaluate the results of the aforementioned clustering methods. Specifically, we intend to minimize the Davies–Bouldin (DB) index and maximize the Calinski–Harabasz (CH) index [31].

The results of clustering are used to facilitate the selection of stocks. For this purpose, we designed two methods: two-step Sharpe ratio and entropy-based selection. The Sharpe ratio is a widely used metric for measuring the profit-to-risk potential of a stock or portfolio. Assuming an expected return r, volatility $\sigma$, and risk-free rate $r_f$, it is computed as in Equation (1). For our experiments, we set the risk-free rate to $r_f=3\%$, which is slightly above the recent 2020–2024 average (2.5%). Using a higher value adds a margin of safety, ensuring that performance metrics reflect genuine outperformance beyond a conservative baseline. The factor $\sqrt{252}$ refers to the number of trading days in a year.

$$\mathrm{Sharpe}\mathrm{ratio}=\sqrt{252}{\displaystyle \frac{r-r_f}{\sigma }}$$

(1)

For the first method, it is possible to assign a Sharpe ratio score to every cluster in order to rank them by averaging the Sharpe ratios of their constituent stocks. At this point, the method requires two parameters, $n_c$ and $n_s$. The first is the number of highest-ranking clusters such that only stocks for the top-$n_c$ clusters will be considered; afterwards, only the $n_s$ stocks that are closest to the cluster centroid are included in the portfolio.

In the second method, every stock is assigned to one of three classes (poor, average, or good) based on its performance during the observation period. The Jenks optimization method was used to find the best break points separating the three classes. Subsequently, a cluster entropy score is computed with reference to the above classes. Based on this, only clusters that are relatively homogeneous (i.e., with most stocks in the cluster having the same label) and are mostly composed of stocks with good performance are selected for portfolio optimization.

3.4. Portfolio Optimization Methods

We considered four methods to determine portfolio weights: MVO, HRP, Monte Carlo optimization (MCO), and CDaR. MVO uses quadratic programming to optimize the tradeoff between low volatility and high expected returns. The generic formula is shown in Equation (2), in which r and $\Sigma$ are the expected returns and covariance, respectively, while $\lambda$ controls the tradeoff between risk and return. Specifically, this generates a number of non-dominated portfolios called the efficient frontier; then, four types of portfolios can be computed that are on the efficient frontier: (a) the minimum volatility portfolio, (b) the tangency portfolio (i.e, the maximum Sharpe ratio portfolio), (c) the portfolio with the highest return subject to a volatility target, and (d) the portfolio with the lowest volatility subject to an expected return target.

$$\begin{array}{cc}\hfill \underset{w}{max}& w^{T}r-\lambda w^T\Sigma w\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& -1\le w_i\le 1\hfill \end{array}$$

(2)

The main inputs required for MVO are the expected returns and the returns covariance matrix; however, as the standard expectation formula on log returns provides noisy results, we instead use the capital asset pricing model [5] returns, which are more stable. Additionally, the Ledoit–Wolf shrinkage estimator is used during the covariance matrix computation in order to reduce the detection of false correlations. Regarding the MVO process itself, short-selling is made possible by allowing negative weights and L2 regularization is used to penalize near-zero weights, which increases the number of stocks in the portfolio. The regularization parameter $\gamma$ can be tuned to match the desired regularization level; however, for relatively small portfolios such as in our case, setting this parameter to 1 eliminates most negligible weights.

For MCO, we used 5000 Monte Carlo trials to generate random portfolio weights. The optimization step selects the random portfolio that achieves the highest Sharpe ratio. HRP uses a hierarchical clustering dendrogram scheme; starting from the leaves and pairs of stocks, portfolios of adjacent stocks are recursively optimized and merged following the tree hierarchy until the optimal portfolio is formed in the root node. As this algorithm is based on hierarchical clustering, there are several cluster linkage options: single, complete, average, weighted, centroid, median, and Ward’s method.

The last method is CDaR, which combines the ideas of price drawdowns (a drawdown is defined as the percentage decrease between a peak and a trough in the stock price signal) and conditional value at risk (CVaR). Unlike MVO, which uses covariance to express risk, CDaR considers the tail risk score by averaging the worst $p\times 100$ percent price drawdowns, and additionally employs quadratic optimization to minimize this score. Regarding the optimization, we examined three alternatives: (a) CDaR minimization, (b) CDaR minimization for a target return, and (c) return maximization given a target CDaR. Finally, for p, we considered the recommended value of 5%, which means that CDaR represents the mean losses of all drawdowns that are so extreme that they happen only 5% of the time.

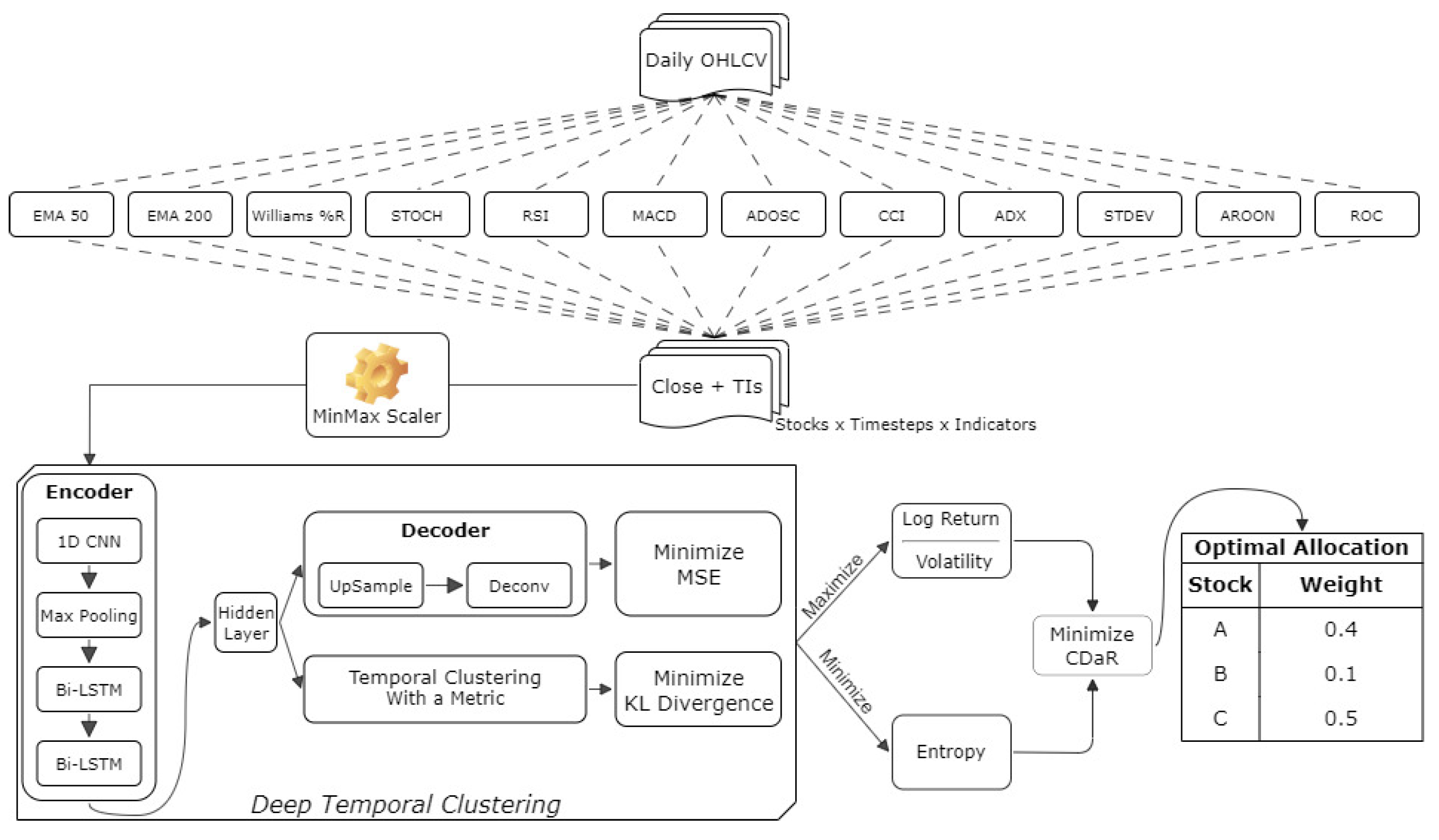
3.5. The Integrated Stock Investing System (PM-DTC)

The computational modules described in Section 3.1, Section 3.2, Section 3.3 and Section 3.4 have been integrated in a completely automated stock investing system, which we call PM-DTC. Specifically, PM-DTC combines the best-performing methods of each step; therefore, the final architecture is based on DTC with entropy-based stock selection and CDaR minimization for stock allocation. A graphical illustration of the complete PM-DTC architecture is provided in Figure 1. The same illustration also depicts the DL architecture of DTC.

DTC was originally proposed with a default set of parameters in order to avoid dataset-specific tuning to the greatest extent possible [15]. However, our preliminary experiments indicated significant instability in reducing the combined loss function. To mitigate this issue and to ensure numerical stability during training, key network parameters were adjusted accordingly. Most notably, the number of convolutional neural network (CNN) [32] layers was increased from 50 to 100, their kernel size was increased from 10 to 25, and the number of bidirectional long short-term memory (Bi-LSTM) [32] units was augmented from 50 to 250 (first Bi-LSTM) and from 1 to 5 (second Bi-LSTM). Moreover, the constant learning rate of the optimizer was interchanged with a polynomial decay learning rate scheduler, where the decay power was set to 0.5. Finally, an early stopping criterion was imposed after the changes in cluster assignments fell below the threshold of 0.5% (0.1% originally) for three consecutive training epochs (patience factor). More details regarding the optimal configuration of each clustering method are provided in the next section.

4. Experimental Results

This section presents the hyperparameters chosen for each clustering method. Afterwards, it reveals the clustering performance results on nine years of previously unseen data. Finally, it provides the financial evaluation results for the corresponding PM strategies.

4.1. Hyperparameter Tuning

For our experiments, the clustering methods were tuned through hyperparameter grid search using the period 2001–2019. The DTW K-means hyperparameters were the number of clusters, maximum iterations, number of random initializations, and number of iterations for computing each cluster’s barycenter. The former two hyperparameters were also used by K-shape, along with the tolerance for convergence. For DTW HC, the hyperparameters were the observation linkage method and convergence criterion. The best configuration for each method is shown in

Table 2. Optimal hyperparameters for each clustering method.

Method	Clusters	Parameters
DTW K-means	25	max_iter: 100, n_init: 3, metric: dtw, max_iter_barycenter: 50
K-shape	dynamic	max_iter: 25, n_init: 5, tolerance: ${10}^{-6}$
DTW HC	25	distance: dtw, linkage: complete, criterion: maxclust
DTW SOM	dynamic	som_shape: (5, 5), feature_weights: equal, sigma: 1.0, learning_rate: 0.5, neighborhood_function: gaussian, num_iterations: 10000
DTC	dynamic	cnn_units: 100, cnn_kernel_size: 25, bilstm_layers: [250, 5], lr_scheduler: polynomial, lr_decay_power: 0.5, patience: 3, min_perc_allocations_change: 0.005

.

For DTW SOM, we considered the neural grid shape, learning rate, neighborhood sigma/function, and iterations. DTC requires the specification of the CNN architecture shape, CNN kernel size, BiLSTM architecture shape, learning rate scheduler, and decay power. To enable early stopping, it also requires the minimum percentage change of clustering allocations and the corresponding patience.

In Section 3.3, we mentioned two stock selection approaches which follow the stock clustering process. As these also require the specification of some parameters, they were tuned using the same period (2001–2019). For the cluster-level Sharpe approach, the optimal parameters were $n_c=10$ (number of clusters) and $n_s=5$ (number of stocks nearest to each centroid), while for the minimum entropy approach the optimal number of clusters was 5.

Subsequently, we employed a rolling validation scheme on previously unseen data, with five trials in the years 2020–2024. For each validation year, the previous year was considered the observation period. In each trial, the observation period was used for stock clustering and the estimation of portfolio weights, whereas the investing strategy was conducted and evaluated during the validation period. For the investing simulation, we considered a reasonable transaction fee of 1% per trade. The upcoming sections present and compare the performance of the stock clustering and portfolio optimization methods, revealing the best-performing approach.

4.2. Results of Stock Clustering

Table 3. Year-over-year comparison of internal clustering validation measures.

		Observation Year
Clustering Method	Metric	2020	2021	2022	2023	2024	Mean
DTW K-means	CH	29.83	26.47	22.89	31.42	27.95	27.71
	DB	3.19	3.41	3.67	3.28	3.52	3.41
DTW SOM	CH	10.24	8.93	11.28	14.67	12.41	11.51
	DB	4.89	4.76	5.21	4.95	5.08	4.98
DTC	CH	199.32	187.45	195.73	203.88	191.67	195.61
	DB	0.73	0.89	0.76	0.82	0.95	0.83
DTW HC	CH	16.57	17.84	16.92	19.73	18.56	17.92
	DB	3.95	3.71	4.02	3.84	3.93	3.89
K-shape	CH	8.74	9.12	12.65	10.89	11.43	10.57
	DB	4.58	4.28	5.06	4.67	4.91	4.70

Note: Bold values indicate the best performance for each measure across all columns (years and mean).

presents the performance results for the five clustering approaches measured using two cluster validity metrics for the years 2020–2024. Regarding the CH metric, DTC significantly outperforms the other methods in every year, while the second-best method is the baseline approach (DTW K-means). Averaged across all years, DTC offers a considerable improvement compared to DTW K-means (195.61 vs. 27.71), which corresponds to an approximately +600% improvement in average CH. DTW SOM, K-shape, and DTW HC are clearly dominated by the baseline in every year.

The DB results are highly in agreement with the aforementioned results, with DTC achieving the lowest DB scores for all years. The average DB scores for DTC and DTW K-means are 0.83 and 3.41 respectively, corresponding to a 75.7% reduction in average DB. Again, no other method is able to consistently outperform the baseline approach.

In summary, both cluster validity metrics indicate the superiority of DTC on the stock clustering task. DTW K-means has the second-best performance, with scores that fall far behind those of DTC. DTW SOM, K-shape, and DTW HC are clearly dominated by better alternatives.

4.3. Results of Investing Strategy

The previous section established DTC as the best stock clustering method. Furthermore, preliminary experiments in the 2001–2019 period led to the selection of the entropy sampling method, which when combined with DTC completes our stock selection pipeline. Following this, the different PM approaches were evaluated from 2020–2024 in terms of the annual log return, volatility, and Sharpe ratio. The corresponding results are provided in

Table 4. Comparison of portfolio optimization methods over the simulation years.

		Simulation Year
Optimization	Metric	2020	2021	2022	2023	2024	Mean
MVO (Min Volatility)	Log returns	8.91%	18.43%	−2.67%	24.67%	6.72%	11.21%
	Volatility	30.14%	11.87%	17.89%	20.95%	11.84%	18.54%
	Sharpe ratio	0.176	1.368	−0.371	1.145	0.249	0.514
MVO (Max Sharpe)	Log returns	11.76%	−1.23%	31.89%	7.79%	15.11%	13.06%
	Volatility	33.82%	13.56%	18.72%	23.33%	12.91%	20.47%
	Sharpe ratio	0.251	1.536	−0.279	1.439	0.329	0.655
MVO (10% return)	Log returns	9.37%	11.92%	18.84%	8.25%	16.03%	12.88%
	Volatility	31.67%	12.43%	16.56%	21.72%	12.28%	18.93%
	Sharpe ratio	0.196	1.161	−0.298	0.770	0.392	0.445
HRP (complete linkage)	Log returns	10.24%	29.83%	1.89%	26.45%	9.84%	9.64%
	Volatility	29.09%	12.87%	16.43%	22.36%	11.62%	18.47%
	Sharpe ratio	0.321	2.390	−0.127	1.175	0.546	0.863
MCO	Log returns	7.89%	15.34%	1.89%	21.73%	6.91%	10.75%
	Volatility	32.45%	13.09%	17.47%	22.04%	12.92%	19.60%
	Sharpe ratio	0.170	0.961	−0.336	0.992	0.244	0.406
Min CDaR	Log returns	13.82%	37.55%	30.20%	40.21%	20.97%	18.73%
	Volatility	33.62%	12.24%	12.59%	22.39%	11.43%	18.45%
	Sharpe ratio	0.322	2.265	-0.074	2.032	0.481	1.005

Note: Bold values denote the best mean performance for each measure.

. Concretely, the experimental evaluation of this investing strategy delineates that CDaR is able to generate the highest returns in every year.

Because it considers both return and volatility, the Sharpe ratio is the profit-to-risk measure that should ultimately determine the best PM method. The results reveal that the CDaR portfolio generates the best Sharpe ratios across the evaluation period. Even in years for which the CDaR portfolio is more volatile than another portfolio (e.g., 2023), the Sharpe ratio indicates that this is justified by excessively higher returns compared to the less volatile portfolio.

Across all years, CDaR achieves the highest average Sharpe ratio at 1.005. The ranking for the other methods is as follows: HRP (0.863), MVO Max Sharpe (0.655), MVO Min Volatility (0.514), MVO 10% (0.445), MCO (0.406).

4.4. Portfolio Performance Attribution

This section focuses on the evaluation and performance attribution of the best-performing portfolio, PM-DTC. The evaluation steps include a sector-level Brinson performance attribution analysis, an investigation of profitability in comparison with standard benchmark indices, and reporting of the Sortino ratio (SR) and maximum drawdown (MDD) measures. Specifically, we apply the widely used Brinson–Hood–Beebower (BHB) framework for performance attribution [33], using the S&P 500 the as benchmark. The BHB model decomposes the portfolio active return into three components: (a) the allocation effect (AE), (b) the selection Effect (SE), and (c) the interaction effect (IE).

The AE captures the impact of overweighting or underweighting benchmark sectors relative to their benchmark returns, i.e., whether the strategy allocated more capital to sectors where the benchmark performed well. The SE reflects the contribution of stock selection within each sector, conditional on the benchmark sector weights, i.e., whether the strategy outperformed the benchmark within those sectors. Finally, the IE represents the joint effect of allocation and selection decisions, measuring whether the strategy both overweighted sectors and simultaneously achieved superior returns within them. Therefore, the interaction effect measures the combined skill in sector allocation and stock selection decisions [34].

We consider the standard Global Industry Classification Standard (GICS) sectors for this analysis: Basic Materials, Communication Services, Consumer Cyclical, Consumer Defensive, Energy, Financial Services, Healthcare, Industrials, Real Estate, Technology, and Utilities. The results of the Brinson attribution analysis across 2020–2024 are provided in

Table 5. Brinson attribution effects for PM-DTC in the period 2020–2024.

	2020	2021	2022	2023	2024	Average	Cumulative
AE	−10.39%	1.88%	13.30%	−14.07%	−1.54%	−2.16%	−14.37%
SE	−11.43%	−5.96%	9.66%	−7.34%	−11.62%	−5.34%	−29.19%
IE	6.27%	2.25%	−4.58%	46.52%	1.06%	10.30%	69.35%

Note: Average refers to the mean annual contribution of each effect across years. Cumulative refers to the compounded contribution over the full sample period (2020–2024).

.

The average attribution effects for allocation (AE = –2.16%), selection (SE = –5.34%), and interaction (IE = 10.30%) provide insight into the sources of outperformance for the PM-DTC strategy. The negative AE indicates that the strategy did not systematically overweight sectors in which the benchmark performed well, while the negative SE suggests weaker stock selection relative to the benchmark within given sector weights. However, because the strategy does not explicitly optimize for independent sector or stock selection, these results are not surprising. Importantly, the positive IE demonstrates that the model generates alpha primarily through interaction effects by overweighting sectors in which its stock selection tends to outperform.

This emphasis on interaction by PM-DTC aligns with the literature on performance attribution. According to Laker [35], the interaction term plays a valuable role in explaining a portfolio’s active performance, and is sometimes more explanatory than the other attributes.

The cumulative IE effect amounts to 69.35% over the validation period (2020–2024), underscoring its dominant role in explaining relative returns. Following decomposition by Brinson and Fachler [36], the additive stock-selection skill is provided by SE + IE, which in this case equals 40.16% (–29.19% + 69.35%). Thus, although pure stock selection (SE) is negative, the interaction component (IE) more than compensates, highlighting that the strategy’s stock selection ability becomes evident only when considered jointly with sector allocation.

Figure 2 displays the wealth trajectories during the validation period for the proposed strategy and three benchmark indices (S&P 500, NASDAQ, and DJIA). The results indicate that the proposed strategy achieved higher overall returns relative to the benchmarks. Notably, it delivered a modest positive return during the 2022 market downturn, when all benchmark indices (particularly NASDAQ) experienced significant losses. In 2023 and 2024, the strategy continued to grow at a faster pace than the benchmarks.

The biggest drawdown (MDD) for PM-DTC was 35.7% and occurred at the start of 2020. The corresponding drawdowns for the S&P 500, NASDAQ and DJIA were 36.1%, 39.41%, and 39.73%. The drawdowns for S&P 500 and DJIA took place in 2020 and were similar to that of PM-DTC, whereas for NASDAQ it occurred during the 2022 stock market decline. Figure 3 illustrates the two MDD periods for PM-DTC and NASDAQ.

Finally, the Sortino ratio for PM-DTC was 1.10, compared to 0.66 for S&P 500, 0.74 for NASDAQ, and 0.43 for DJIA. Given that the Sortino ratio is widely regarded as a more representative measure of risk-adjusted returns focused on downside risk, these results provide further evidence that the proposed strategy delivered substantially superior performance relative to passive benchmarks.

5. Conclusions

Stock clustering is a proven approach that can improve the profit-to-risk ratio of portfolio optimization strategies. Our literature review revealed several research opportunities in this field. Specifically, few works have considered modern DL approaches for clustering and PM methods that go beyond the traditional MVO paradigm. In addition, important econometric methods that can be used for stock pre-filtering have been overlooked. Based on these research gaps, the following paragraphs outline the contributions of this work.

In this paper we propose PM-DTC, a fully automated investing strategy that combines two modules for stock clustering and stock allocation. The former module uses the DTC clustering method with entropy-based stock sampling, while the latter uses a CDaR implementation. Both modules were able to outperform previously proposed solutions in their corresponding tasks, including popular methods such as DTW clustering and MVO. Our experiments demonstrated the superiority of PM-DTC for a period of five years. The proposed system was able to achieve an average annualized Sortino ratio of 1.1, while its robustness was further confirmed through Brinson attribution and maximum drawdown analyses.

Another contribution is our comparison of a large array of stock clustering and portfolio optimization methods, including DTW K-means, DTW HC, K-shape, SOM, DTC, MVO, MCO, HRP, and CDaR. Multiple configurations of the aforementioned methods were evaluated, using cluster validity metrics for the clustering methods and investment performance metrics for the PM methods.

To conclude, we mention a few directions for future work. First, fundamental and macroeconomic data such as company balance sheets, income statements, and cash flows could be included in the clustering process. Second, supervised learning could be considered as a method for integrating return forecasts in the stock selection process. Third, it would be possible to experiment with more aggressive portfolios that include stocks spanning a wider range of beta values and/or that fall outside the IQR, with the aim of potentially enhancing excess returns.