Efficient Sparse Quasi-Newton Algorithm for Multi-Physics Coupled Acid Fracturing Model in Carbonate Reservoirs

Abstract

Acid stimulation is a widely used technique for enhancing hydrocarbon recovery from carbonate reservoir formations. In this study, a mathematical model is developed to describe acidizing-induced pressure behavior in carbonate rocks, based on fluid dynamics and acid transport equations. The model is discretized using the finite volume method, resulting in a numerical framework suitable for simulating acidizing processes in carbonate reservoirs. Due to the model’s inherent characteristics—strong nonlinearity and the presence of high-dimensional sparse systems of equations—a sparse quasi-Newton method is proposed to efficiently solve the resulting system. Numerical experiments confirm the practicality and effectiveness of the proposed approach.

1. Introduction

Carbonate rock reservoirs are influenced by a combination of original rock properties, tectonics, and karstification, resulting in complex spatial pore structures and strong heterogeneity [1]. High-resolution grids (millions to billions of cells) are required to accurately capture their complex structures, which traditional models struggle to represent properly. The complex flow physics in carbonate rocks (multiphase flow, compositional changes, phase transitions, and complex relative permeability and capillary pressure curves) lead to discrete equations with strong nonlinearity and tight coupling. Acidizing is a primary method for geological modification of fracture-cavity carbonate reservoirs [2]. Research on numerical modeling methods for acidizing pressure in carbonate reservoirs can reveal how fractures and cavities influence the acidizing process, thereby providing theoretical guidance for optimizing acidizing treatments and improving stimulation effectiveness [3].

The carbonate rock acidizing pressure model incorporates multiple physical processes such as fracture flow, acid transport and reaction kinetics, and rock matrix deformation. Acidizing pressure numerical simulation is an effective method for reconstructing the multi-physics processes during acidizing stimulation, including formation fracturing induced by fluid pressure, acid mass transfer and chemical reactions, and the evolution of acid-etched fracture conductivity under confining pressure conditions [4]. Current carbonate rock acidizing pressure numerical models primarily focus on multi-scale fracture characterization, coupled multi-physics field solutions, and the integration of high-performance computational methods.

Compared with the finite difference method, the finite volume method combines the geometric flexibility of finite elements with rigorous conservation properties at both local and global scales. Forsyth applied the finite volume method for numerical simulation of multiphase flow in porous media [5]. After discretization using the finite volume method, the carbonate rock acidizing pressure model generates a strongly coupled, nonlinear, high-dimensional, sparse system of equations.

A known sparse quasi-Newton update was presented independently by Schubert [6], Toint [7,8,9], and Broyden [10] and analyzed by Marwil [11]. Unlike Broyden’s and Schubert’s methods, A new quasi-Newton update is proposed based on the least relative change in the updated matrix by Bogle [12]. In [10,11,12], they pay attention to Broyden’s rank-one update. These methods have proved quite successful for nonlinear equations but have the drawback for optimization problems that the matrix B* is nonsymmetric.

This paper develops a sparse quasi-Newton algorithm for solving multi-physics coupled models of carbonate rock acidizing pressure. By exploiting the inherent sparsity of the model, only the non-zero elements in the quasi-Newton matrix are updated. This approach overcomes computational challenges in large-scale high-resolution simulations, enhances computational efficiency and feasibility, improves the capability to solve complex nonlinear systems, and reduces computational costs. Numerical experiments demonstrate that the method provides superior convergence characteristics, proving its significance for the efficient development of carbonate reservoirs with complex heterogeneity.

The paper is organized as follows: Section 2 presents the mathematical model of carbonate rock acidizing pressure and the nonlinear system of equations obtained after the finite volume method discretization. Section 3 introduces the proposed sparse quasi-Newton method. Section 4 conducts numerical experiments to validate the method’s efficiency. The final section provides concluding remarks.

2. Mathematical Model and Discretization

2.1. Hydrodynamic Model of Carbonate Acid Fracturing

The Navier–Stokes–Darcy equations are used to simulate the fluid flow behavior in carbonate rocks, and a mathematical model describing the acid dissolution process in carbonate rock reservoirs is established [13].

2.1.1. Mass Conservation Equation

The mass conservation principle for a compressible fluid is expressed by the continuity equation:

$${\displaystyle \frac{𝜕({\rho }_f{\varphi }_f)}{𝜕t}}+\nabla \cdot ({\rho }_f{\varphi }_f{U}_f)=0,$$

(1)

where ${\rho }_f$ is the acid fluid density (which varies with concentration as ${\rho }_f={\rho }_0(1+\gamma c)$, ${\varphi }_f$ is the dynamic porosity (updated by the chemical reaction ${\displaystyle \frac{𝜕{\varphi }_f}{𝜕t}}=k_{r}c(1-{\varphi }_f)$, and $U_f$ is the velocity vector.

2.1.2. Momentum Conservation Equation

During acid fracturing, fluid flows through the pore–fracture system. The modified Navier–Stokes equations account for Darcy drag, Forchheimer inertial effects at high flow rates, and time-dependent porosity and permeability changes due to chemical reactions. The momentum conservation equation takes the following form:

$${\displaystyle \frac{𝜕({\rho }_f{\varphi }_f{U}_f)}{𝜕t}}+\nabla \cdot ({\rho }_f{\varphi }_f{U}_f{U}_f)=-{\varphi }_f\nabla p+\nabla \cdot ({\varphi }_f\mu {\tau }_f)+{\varphi }_f{\rho }_{f}g-\left({\displaystyle \frac{\mu {\varphi }_f}{K}}+\beta {\rho }_f{\varphi }_f|U_f|\right)U_f,$$

(2)

where ${\tau }_f=\nabla U_f+{(\nabla U_f)}^T-{\displaystyle \frac{2}{3}}(\nabla \cdot U_f)I$ is the viscous stress tensor for Newtonian fluids, $\mu$ is the dynamic viscosity of the fluid, which characterizes the internal friction property of the fluid that resists shear deformation, $K=K_0{\displaystyle \frac{{\varphi }_f^3}{{(1-{\varphi }_f)}^2}}$ is the porosity-dependent permeability (Kozeny–Carman relationship), and $\beta$ is the Forchheimer coefficient.

2.1.3. Acid Transport Equation

The transport of acid species in the porous medium is governed by the following advection–dispersion–reaction equation:

$${\displaystyle \frac{𝜕({\varphi }_f{\rho }_f{C}_f)}{𝜕t}}+\nabla \cdot ({\rho }_f{U}_f{C}_f)-\nabla \cdot ({\varphi }_f{\rho }_f{\mathit{D}}_{\mathit{eff}}\nabla C_f)=-{\alpha }_{s}R(C_s),$$

(3)

where $C_f$ is the average acid concentration in the fluid phase (%), and $R(C_s)$ is the rate of acid consumption per unit volume and time due to the chemical reaction with minerals, which depends on the surface acid concentration $C_s$. $D_{eff}$ is the effective diffusion coefficient, a macroscopic parameter describing the combined effects of molecular diffusion and pore structure on acid transport in porous media. It depends on the acid’s molecular diffusivity ($D_m$), the medium’s porosity ($\varphi$) and tortuosity ($\tau$), and hydrodynamic conditions. A common relation is $D_{eff}={\displaystyle \frac{\varphi }{\tau }}{D}_m$, showing proportionality to porosity and inverse proportionality to tortuosity. ${\alpha }_s$ represents the specific reactive surface area, which refers to the effective mineral surface area per unit volume of porous media that participates in acid-rock chemical reactions.

2.2. Finite Volume Method Discretization

2.2.1. Discretization of the Mass Conservation Equation

Integrating the mass conservation Equation (1) over the control volume $P$ and applying Gauss’s divergence theorem, we derive the following:

$${\displaystyle {\int }_{V_P}\frac{𝜕({\rho }_f{\varphi }_f)}{𝜕t}}dV+{\displaystyle {\int }_{V_P}\nabla }\cdot ({\rho }_f{\varphi }_f{U}_f)dV=0.$$

(4)

After discretization, we obtain the following:

$$V_P{\displaystyle \frac{{({\rho }_f{\varphi }_f)}_P^{n+1}-{({\rho }_f{\varphi }_f)}_P^n}{\Delta t}}+{\displaystyle \sum _f{({\rho }_f{\varphi }_f)}_f^{n+1}}{U}_{ff}^{n+1}\cdot A_f=0,$$

(5)

where $f$ represents the faces of control volume $P$, and $A_f$ is the area vector of face $f$ (outward normal).

2.2.2. Discretization of the Momentum Conservation Equation

Integrate the momentum conservation Equation (2) over the control volume $P$, we obtain the following:

$$\begin{array}{c}{\int }_{V_P}{\displaystyle \frac{𝜕\left({\rho }_f{\varphi }_f{\mathit{U}}_{\mathit{f}}\right)}{𝜕t}}dV+{\int }_{V_P}\nabla \cdot ({\rho }_f{\varphi }_f{\mathbf{U}}_{\mathbf{f}}{\mathbf{U}}_{\mathbf{f}})dV=\\ -{\int }_{V_P}{\varphi }_f\nabla pdV+{\int }_{V_P}\nabla \cdot ({\varphi }_f\mu {\tau }_f)dV+{\int }_{V_P}{\varphi }_f{\rho }_{f}gdV\\ -{\int }_{V_P}\left({\displaystyle \frac{\mu {\varphi }_f}{K}}+\beta {\rho }_f{\varphi }_f|{\mathbf{U}}_{\mathbf{f}}|\right){\mathbf{U}}_{\mathbf{f}}dV.\end{array}$$

(6)

From discrete nonlinear equations, we obtain the following:

$$\begin{array}{c}\hfill V_P{\displaystyle \frac{({\rho }_f{\varphi }_f{\mathbf{U}}_{\mathbf{f}}{)}_P^{n+1}-({\rho }_f{\varphi }_f{\mathbf{U}}_{\mathbf{f}}{)}_P^n}{\Delta t}}+\sum _f({\rho }_f{\varphi }_f{)}_f^{n+1}{\mathbf{U}}_{{\mathbf{f}}_{\mathrm{f}}}^{\mathrm{n}+1}({\mathbf{U}}_{{\mathbf{f}}_{\mathrm{f}}}^{\mathrm{n}+1}{A}_f)=\hfill \\ \hfill -{\varphi }_{fp}^{n+1}\sum _f{p}_f^{n+1}{A}_f+\sum _f({\varphi }_f\mu {)}_f^{n+1}({\tau }_f{)}_f^{n+1}{A}_f+{\varphi }_{fp}^{n+1}({\rho }_f{)}_p^{n+1}g{V}_P\hfill \\ \hfill -V_P\left({\left({\displaystyle \frac{\mu {\varphi }_f}{K}}\right)}_P^{n+1}+\beta ({\rho }_f{\varphi }_f{)}_P^{n+1}|{\mathbf{U}}_{\mathbf{f}\mathrm{p}}^{\mathrm{n}+1}|\right){\mathbf{U}}_{\mathbf{f}}.\hfill \end{array}$$

(7)

Similarly, the acid transport Equation (3) can be discretized using the finite volume method. The nonlinear equation system obtained from the discretization is a five-diagonal or block five-diagonal for two-dimensional cases and a seven-diagonal or block seven-diagonal for three-dimensional cases.

3. Sparse Quasi-Newton Methods

After spatial discretization of the acid fracturing model in carbonate reservoirs, the result is a large and sparse nonlinear system, which can be written as follows:

$$F\left(x\right)=0, x\in R^n,$$

(8)

where $F:R^n\to R^n$ is a continuously differentiable function. We denote $J\left(x\right)$ as the Jacobian matrix of $F\left(x\right)$ at $x$. Specifically, we have the following:

$$F\left(x\right)=\left(F_1\right(x),F_2(x),\dots ,F_n(x){)}^{\top },$$

(9)

and

$$J\left(x\right)=(\nabla F_1(x),\nabla F_2(x),\dots ,\nabla F_n(x){)}^{\top }.$$

(10)

By linearization, the nonlinear Equation (8) at an iterative point $x_k$, we obtain the Newton–Raphson method:

$$x_{k+1}=x_k-J\left(x_k{)}^{-1}F\right(x_k).$$

(11)

Newton’s method needs to compute the exact Jacobian matrix. To avoid computing the Jacobian matrix, quasi-Newton methods have been proposed, where $J\left(x_k\right)$ is approximated by a quasi-Newton matrix $B_k\in R^{n\times n}$.

The quasi-Newton methods generate an iteration as follows:

$$x_{k+1}=x_k+{\alpha }_k{d}_k,$$

(12)

where the step length ${\alpha }_k>0$ is determined by some line search strategies, and $d_k$ is the quasi-Newton direction obtained by solving the subproblem

$$F\left(x_k\right)+B_k{d}_k=0.$$

(13)

Usually, the quasi-Newton matrix $B_k$ satisfies the secant condition.

$$s^k=x_{k+1}-x_k={\alpha }_k{d}_k,$$

(14)

$$y^k=F\left(x_{k+1}\right)-F\left(x_k\right).$$

(15)

The quasi-Newton matrix $B_k$ can be updated by various quasi-Newton update formulae, such as the Broyden family of update formulae.

Theorem 1

[14]. Suppose $F:R^n\to R^n$ satisfies:

(1)

$F$ is continuously differentiable in an open convex set $D$,

(2)

There exists an $x*\in D$ such that $F(x*)=0$ and $J(x*)$ is nonsingular.

• There exists a constant, $L>0$ such that

$${‖J\left(x\right)-J\left(y\right)‖}_F\le L{‖x-y‖}_2 forallx,y\in D.$$

(16)

Then, there exists $\epsilon$, $\delta >0$ such that, if $x_0\in D$ satisfies ${‖x_0-x*‖}_2<\epsilon$ and ${‖B_0-J(x*)‖}_F<\delta$ for nonsingular $B_0$:

1. Broyden’s method generates $\left(B_k\right)$ with $B_k$ nonsingular,

2. $\left(x_k\right)$ converges to $x*$,

3. The convergence is superlinear:

$$\underset{k\to \infty }{lim}{\displaystyle \frac{{‖x_{k+1}-x*‖}_2}{{‖x_k-x*‖}_2}}=0.$$

(17)

3.1. Sparse Quasi-Newton Update Methods

The difficulty with large problems is that the quasi-Newton update formulae require $n^2/2$ memory locations, which often becomes impractical as $n$ increases. If the Jacobian matrix of $F\left(x\right)$ has a sparsity pattern, and an approximation to the Jacobian matrix is stored with only the non-zero elements approximated, the problem may become computationally tractable.

We know that even if $B_k$ has the sparsity pattern, $B_{k+1}$ defined by Broyden update formulae will not. In order to modify $B_{k+1}$ so that it has the desired sparsity, similar to reference [15], we give a kind of sparse quasi-Newton update method. We first denote by $K$ the set of ordered pairs of integers $(i,j)$ such that:

$$\left(J\right(x){)}_{ij}=0, (i,j)\in K,$$

(18)

where $K\subseteq \{1,\dots ,n\}\times \{1,\dots ,n\}$. Then, it is natural to ask that for all $k$, $(B_k{)}_{ij}=0$, $(i,j)\in K$. We consider the system of linear equations:

$$Q^k\lambda =y^k-B_k{s}^k,$$

(19)

where

$$\begin{gathered} s(i{)}_j^k=\left\{\begin{array}{ll}{s}_j^k& (i,j)\notin I,\\ 0& (i,j)\in I,\end{array}\right. \\ {Q}_{ij}^k=s(i{)}_j^{k}s(j{)}_i^k+{\delta }_{ij}{‖s(i{)}^k‖}^2, \end{gathered}$$

(20)

and where $s(i{)}^k$ is the vector whose components are $\left\{s\right(i{)}_j^k;j=1,2,\dots ,n\}$.

The sparse quasi-Newton update formula is as follows:

$$B_{ij}^{k+1}=B_{ij}^k+s(i{)}_j^k{\lambda }_i+{\lambda }_{j}s(j{)}_i^k.$$

(21)

Clearly, $B_{k+1}$ is symmetric and possesses the desired sparseness.

3.2. Computation of the Step Length

We define the merit function:

$$f(x)={\displaystyle \frac{1}{2}}F(x{)}^{T}F(x).$$

(22)

The search step length ${\alpha }_k$ is required to satisfy the Wolfe conditions:

$$f(x_k+{\alpha }_k{d}_k)\le f\left(x_k\right)+c_1{\alpha }_k{g}_k^T{d}_k,$$

(23)

$$\nabla f(x_k+{\alpha }_k{d}_k{)}^T{d}_k\ge c_2{g}_k^T{d}_k,$$

(24)

The parameters $c_1$ and $c_2$ are used in the line search procedure, corresponding to the constants in the Wolfe conditions. They are chosen such that $0<c_1<c_2<1$, where $c_1$ controls the sufficient decrease condition and $c_2$ ensures a reasonable step size, where $g_k=B\left(x{)}^{T}F\right(x)$. In practical computation, the directional derivative in (24) is approximated as follows:

$$\nabla f(x_k+{\alpha }_k{d}_k{)}^T{d}_k={\displaystyle \frac{f(x_k+({\alpha }_k+h\left)d_k\right)-f(x_k+({\alpha }_k-h\left)d_k\right)}{2h}}.$$

(25)

The parameter $h$ in Equation (25) is chosen to balance the truncation error ($O(h^2)$) and the round-off error ($O({\displaystyle \frac{\epsilon }{h}})$), where $\epsilon$ is the machine epsilon. The theoretically optimal value is ${\epsilon }^{\frac{1}{3}}$, which corresponds to $h\approx {10}^{-5}$ to ${10}^{-6}$ in double-precision arithmetic. This choice ensures that the approximation maintains the global convergence properties while having minimal impact on the local convergence rate in practical applications.

3.3. Sparse Quasi-Newton Algorithm

The following is the sparse quasi-Newton algorithm for solving nonlinear equation systems.

• Step 1: Given an initial point $x_0$, a symmetric positive definite initial matrix $B_0$, line search parameters $0<c_1<c_2<1$, a convergence tolerance $ϵ>0$, and set the iteration counter $k=0$.
• Step 2: Compute $g_k=B_k^{T}F\left(x_k\right)$. If $\parallel g_k\parallel <ϵ$, stop; else, go to Step 3.
• Step 3: Compute search direction $d_k$ via (13).
• Step 4: Compute step size ${\alpha }_k$ via (23)–(25).
• Step 5: Update $x_{k+1}$ using (12).
• Step 6: Update $B_{k+1}$ via (21), increment $k\leftarrow k+1$, return to Step 2.

3.4. Parallel Computation of Quasi-Newton Matrix and GPU Acceleration Techniques

We note that the BFGS update (Broyden [16], Fletcher [17], Goldfarb [18], and Shanno [19]) can be decomposed into the sum of its rows. Dropping the subscript $k$, and replacing the subscript $k$ + 1 with the superscript *, the BFGS update is defined by the following:

$$\begin{array}{r}B*=B-{\displaystyle \frac{Bs{s}^{T}B}{s^{T}Bs}}+{\displaystyle \frac{y{y}^T}{y^{T}s}},\end{array}$$

(26)

then, the BFGS update can be written as follows:

$$B*=B-\sum _{i=1}^n{e}_i{e}_i^T{\displaystyle \frac{Bs{s}^{T}B}{s^{T}Bs}}+\sum _{i=1}^n{e}_i{e}_i^T{\displaystyle \frac{y{y}^T}{y^{T}s}}=B-\sum _{i=1}^n{e}_i\left(e_i^T{\displaystyle \frac{Bs{s}^{T}B}{s^{T}Bs}}-{\displaystyle \frac{e_i^{T}y{y}^T}{y^{T}s}}\right).$$

(27)

The efficient parallel computation of (27) can be achieved using multiple processors. GPU acceleration [20,21,22,23,24] is implemented as follows: during initialization, GPU parallel scanning computes the initial Jacobian and establishes the index set $K$; each component of the nonlinear system is mapped to GPU threads; $B_k$ is stored in row-major format; $f(x_k+{\alpha }_k{d}_k)$ is evaluated in parallel for multiple candidate step lengths.

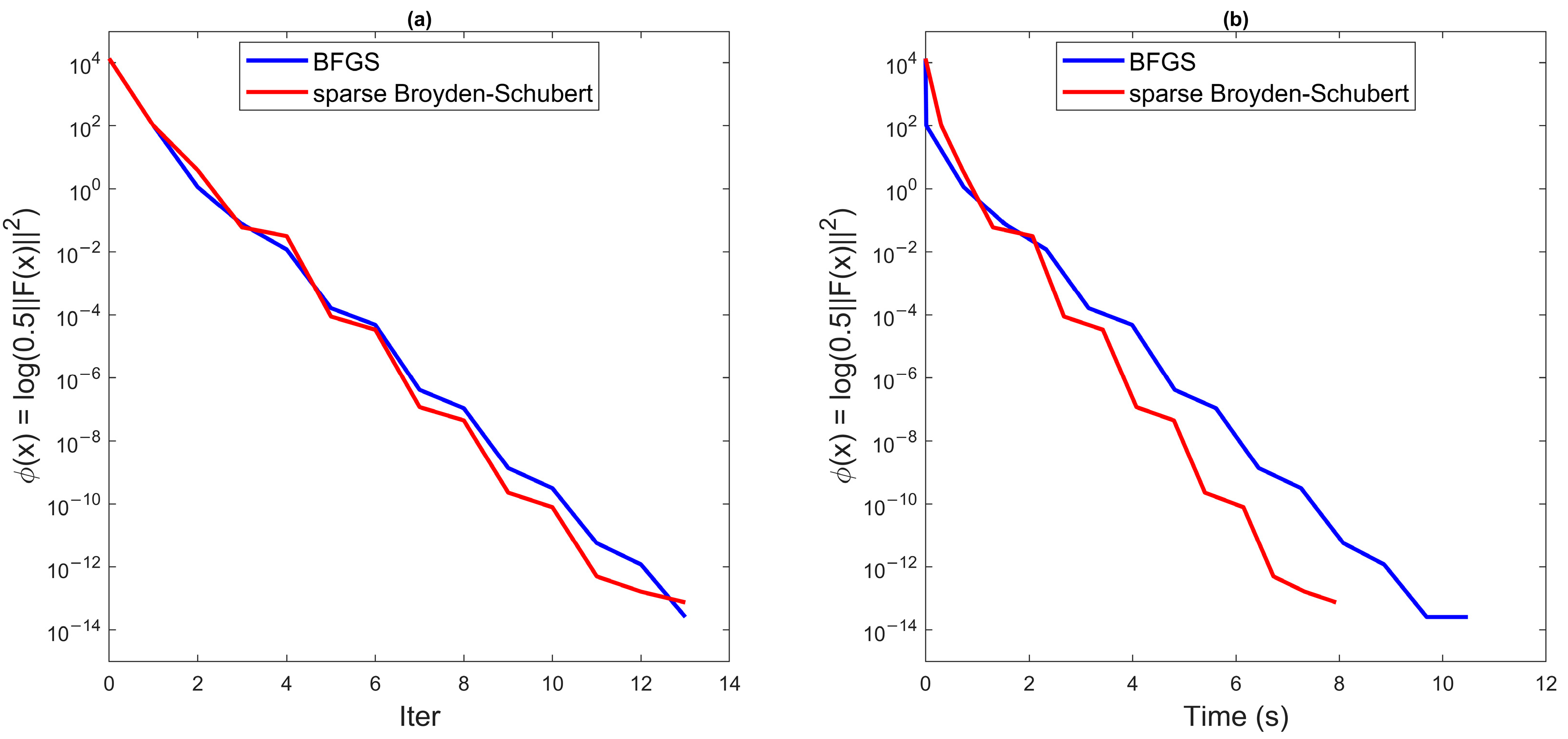
4. Numerical Experiments

4.1. Acid Fracturing Coupling Model

To evaluate the performance of sparse quasi-Newton algorithms in solving carbonate rock acid pressure multi-field coupling models, this section designs a comparative experiment between the sparse Broyden–Schubert method and the BFGS method. The testing environment is a Windows 10 operating system equipped with 16.00 GB of memory.

The test function selected for the experiment is a simplified carbonate rock acid pressure multi-field coupling model, whose Jacobian matrix has a tridiagonal structure, consistent with the high-dimensional sparse characteristics of the actual acid pressure numerical model after discretization.

$$\begin{array}{c}{F}_1=2x_1+exp\left(x_1\right)+x_2-5=0,\hfill \\ F_i=x_{i-1}+3x_i+exp\left(x_{i+1}\right)+x_{i+2}-sin\left(x_{i+1}\right)-4=0, i=2,\dots ,n-1,\hfill \\ F_n=x_{n-1}+2x_n+exp\left(x_n\right)-cos\left(x_n\right)-3=0,\hfill \\ x_0=(1,1,\dots ,1{)}^T.\hfill \end{array}$$

(28)

The algorithm parameters are set as follows: the convergence tolerance is $\epsilon ={10}^{-6}$, i.e., the algorithm is considered to have converged when the current gradient norm $\parallel g_k\parallel$ is less than $\epsilon$; Standard Wolfe line search is used, with line search parameters set to $c_1={10}^{-4}$ and $c_2=0.9$; the initial matrix is set to $B_0=J\left(x_0\right)$, where $J\left(x_0\right)$ is the value of the Jacobian matrix of the test function at the initial point $x_0$. This strategy provides a high-quality initial guess that captures the problem’s inherent structure, significantly accelerating early convergence. To ensure robustness, we apply minimal regularization: $B_0=J\left(x_0\right)+\epsilon$, where $\epsilon ={10}^{-6}$. Although this requires one Jacobian evaluation, it reduces total iterations and overall computation time substantially.

To evaluate the performance of the algorithm, multiple quantitative metrics are used. The dimension of the problem is represented by Dim. Iteration represents the total number of iterations performed to satisfy the convergence condition. $R$ represents the average convergence rate of the Broyden–Schubert method, which is used to quantify the average convergence speed of the algorithm throughout the iteration process. Its calculation formula is as follows:

$$R={\displaystyle \frac{1}{m}}ln\left({\displaystyle \frac{N_1}{N_m}}\right),$$

(29)

where $N_1=\parallel F\left(x_0\right)\parallel$ is the Euclidean norm of the initial residual, $N_m=\parallel F\left(x_k\right)\parallel$ is the residual norm at the final iteration point, and $m=Nfun/n$ is the total number of function component evaluations normalized by the problem dimension $n$, with Nfun being the total number of function component evaluations. This metric quantifies the computational efficiency in terms of function evaluations. A higher $R$ value indicates better convergence efficiency per function evaluation cost.

Tcpu denotes the total computation time consumed by the algorithm, measured in seconds. The comparison results between the sparse Broyden–Schubert method and the BFGS method for different problem dimensions are shown in

Table 1. Optimization performance comparison.

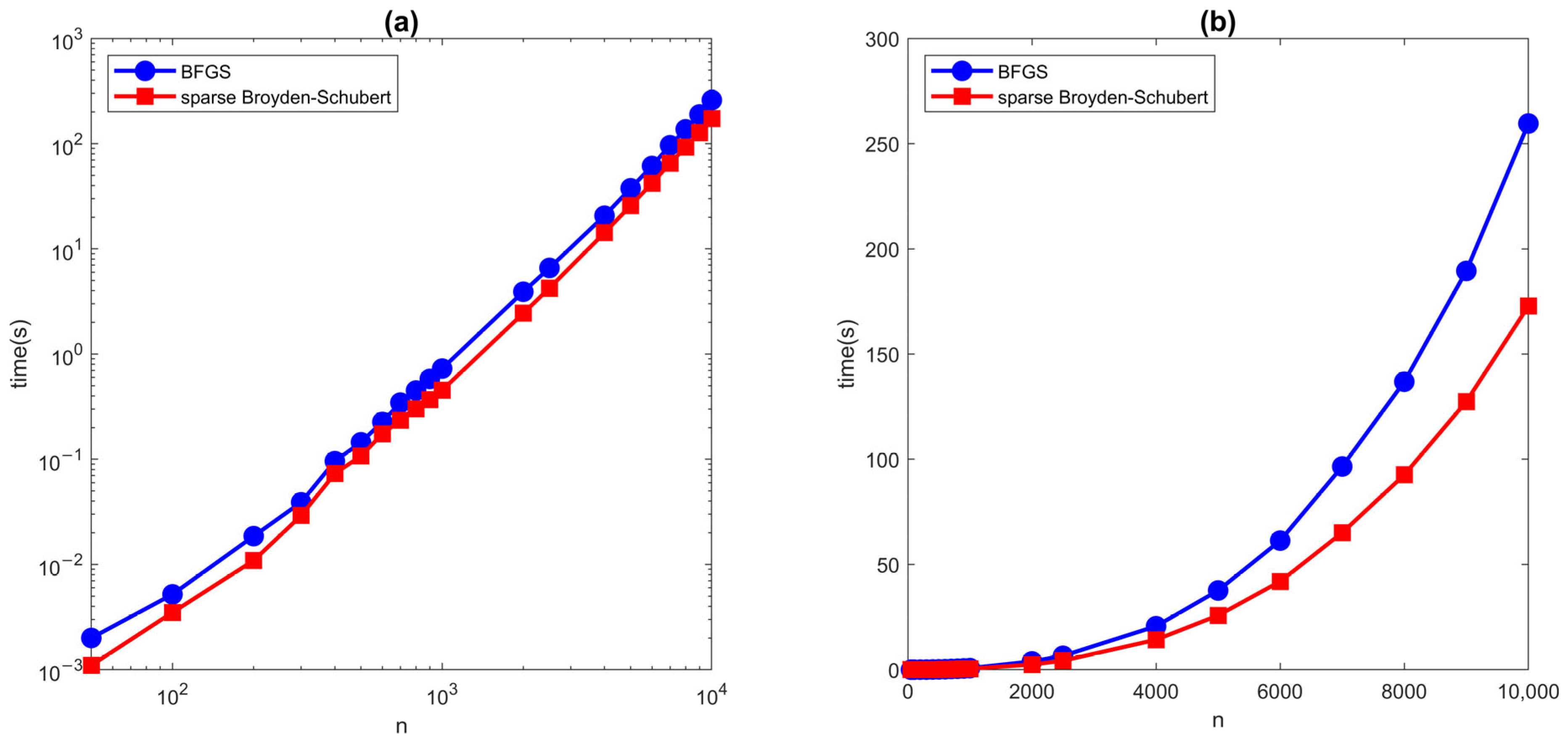
Dim	BFGS		Sparse Broyden Schubert
	Iteration	Tcpu (s)	Iteration	Tcpu (s)
50	14	0.0020	13	0.0011
100	15	0.0052	13	0.0035
200	15	0.0186	13	0.0109
300	15	0.0390	13	0.0292
400	15	0.0960	13	0.0731
500	15	0.1450	13	0.1074
600	15	0.2264	13	0.1743
700	15	0.3456	13	0.2345
800	15	0.4504	13	0.3022
900	15	0.5803	13	0.3694
1000	15	0.7275	13	0.4533
2000	15	3.9113	13	2.4461
2500	15	6.5859	13	4.2408
4000	14	20.6561	13	14.2332
5000	14	37.6264	13	25.7713
6000	14	61.3392	13	41.9309
7000	14	96.5590	13	65.1102
8000	14	136.8498	13	92.5859
9000	14	189.5147	13	127.4359
10,000	14	259.5736	13	172.7991

and

Table 2. Comparative optimization results.

$\mathit{n}$	Method	${\mathit{N}}_1$	${\mathit{N}}_{\mathit{m}}$	$\mathit{m}$	$\mathit{R}$
50	BFGS	21.3780	2.0820 × 10−7	27	0.6830
	Broyden–Schubert	21.3780	4.1610 × 10−8	27	0.7430
100	BFGS	30.1160	1.5070 × 10−7	29	0.6590
	Broyden–Schubert	30.1160	3.9490 × 10−8	27	0.7570
200	BFGS	42.5090	1.6970 × 10−7	29	0.6670
	Broyden–Schubert	42.5090	3.7350 × 10−8	27	0.7720
300	BFGS	52.0290	1.7890 × 10−7	29	0.6720
	Broyden–Schubert	52.0290	3.6850 × 10−8	27	0.7800
400	BFGS	60.0580	1.8650 × 10−7	29	0.6760
	Broyden–Schubert	60.0580	3.7110 × 10−8	27	0.7850
500	BFGS	67.1340	1.9120 × 10−7	29	0.6790
	Broyden–Schubert	67.1340	3.7730 × 10−8	27	0.7890
600	BFGS	73.5320	1.9330 × 10−7	29	0.6810
	Broyden–Schubert	73.5320	3.8510 × 10−8	27	0.7910
700	BFGS	79.4170	1.9340 × 10−7	29	0.6840
	Broyden–Schubert	79.4170	3.9340 × 10−8	27	0.7940
800	BFGS	84.8940	1.9220 × 10−7	29	0.6860
	Broyden–Schubert	84.8940	4.0170 × 10−8	27	0.7950
900	BFGS	90.0390	1.9010 × 10−7	29	0.6890
	Broyden–Schubert	90.0390	4.0960 × 10−8	27	0.7970
1000	BFGS	94.9050	1.8740 × 10−7	29	0.6910
	Broyden–Schubert	94.9050	4.1700 × 10−8	27	0.7980
2000	BFGS	134.1900	1.4810 × 10−7	29	0.7110
	Broyden–Schubert	134.1900	4.6820 × 10−8	27	0.8070
2500	BFGS	150.0230	1.2660 × 10−7	29	0.7200
	Broyden–Schubert	150.0230	4.8330 × 10−8	27	0.8090
4000	BFGS	189.7550	1.5590 × 10−7	27	0.7750
	Broyden–Schubert	189.7550	5.1050 × 10−8	27	0.8160
5000	BFGS	212.1490	1.1350 × 10−7	27	0.7910
	Broyden–Schubert	212.1490	5.2090 × 10−8	27	0.8200
6000	BFGS	232.3940	9.3630 × 10−8	27	0.8010
	Broyden–Schubert	232.3940	5.2830 × 10−8	27	0.8220
7000	BFGS	251.0120	8.4680 × 10−8	27	0.8080
	Broyden–Schubert	251.0120	5.3380 × 10−8	27	0.8250
8000	BFGS	268.3410	8.0460 × 10−8	27	0.8120
	Broyden–Schubert	268.3410	5.3810 × 10−8	27	0.8270
9000	BFGS	284.6170	7.8430 × 10−8	27	0.8150
	Broyden–Schubert	284.6170	5.4140 × 10−8	27	0.8290
10,000	BFGS	300.0120	7.7540 × 10−8	27	0.8180
	Broyden–Schubert	300.0120	5.4420 × 10−8	27	0.8310

.

From the experimental results, it can be seen that under all problem dimensions, the number of iterations and equivalent iterations ($m$) of the sparse Broyden–Schubert method is both fewer than those of the BFGS method, indicating higher convergence efficiency and lower total computational cost in function evaluation. The average convergence rate ($R$) of the sparse Broyden–Schubert method is consistently higher than that of the BFGS method. A higher $R$ value indicates faster residual decay per unit computational cost, suggesting that this method achieves faster convergence by exploiting the tridiagonal sparsity pattern of the Jacobian matrix.

As the number of problem dimensions increases, the time advantage of the sparse Broyden–Schubert method becomes increasingly evident. At low dimensions ($\mathrm{n}=100$), the time difference is within 5%; however, at higher dimensions ($\mathrm{n}=4000$), the sparse Broyden–Schubert method saves approximately 31% in computation time compared to the BFGS method. This characteristic makes it more advantageous for handling large-scale numerical computation problems, particularly suitable for solving high-dimensional sparse equation systems such as carbonate rock acid pressure models.

To clearly compare the efficiency of the BFGS and the sparse Broyden–Schubert method in solving this problem, we selected a problem dimension of $n=3000$ and plotted the objective function value ${\displaystyle \frac{1}{2}}\parallel F(x){\parallel }^2$ as a function of the number of iterations and computation time.

The sparse Broyden–Schubert method demonstrates significant computational efficiency advantages when solving large-scale linear systems of equations. As shown in Figure 1, subfigure (a) (the relationship between $log\left({\displaystyle \frac{1}{2}}\parallel F(x){\parallel }^2\right)$ and the number of iterations) demonstrates that The sparse Broyden–Schubert method exhibits excellent convergence from the early stages of iteration, with the objective function value decreasing by several orders of magnitude after only four iterations, rapidly approaching the neighborhood of the optimal solution; subfigure (b) (relationship with computation time) further validates its time efficiency—when the objective function reaches a practical accuracy of 10⁻⁶, The sparse Broyden–Schubert method requires fewer iterations and reduces the computation time by 25–30% compared to the BFGS method.

The core of this advantage lies in a balance between update frequency and computational cost achieved by the sparse Broyden–Schubert method. Additionally, the sparsity-preserving technique adopted by the sparse Broyden–Schubert method results in lower memory usage, and this memory efficiency is highly valuable in practical engineering applications for large-scale problems.

Analysis of the time complexity using Figure 2a,b show that the sparse Broyden–Schubert (the sparse Broyden–Schubert) method demonstrates a significant scalability advantage when handling problems of varying sizes. Specifically, in subplot (a), which uses a double-logarithmic coordinate system, the time complexity curves of both the BFGS and the sparse Broyden–Schubert method exhibit a stable, approximately linear upward trend. This linear trend indicates that both methods have polynomial time complexity of the same order. However, the relative positions of the curves show that the sparse Broyden–Schubert method’s curve consistently remains below the BFGS method’s curve. This consistent offset indicates that, even for the same order of complexity, the actual computational cost of the sparse Broyden–Schubert method is significantly lower than that of the BFGS method, confirming its superior computational efficiency.

Subplot (b), which uses a linear coordinate system, more clearly illustrates the scaling behavior of the two methods. When the problem dimension $n$ is less than 2000, the distance between the two curves is small, indicating that the computational time of both methods is similar and the advantage of the sparse Broyden–Schubert method is not yet pronounced. However, when the problem size exceeds the critical value of $n=2000$, the performance gap between the methods widens sharply: the BFGS method exhibits a sharp increase in computational time, and its curve’s slope increases significantly.

In contrast, the sparse Broyden–Schubert method’s time consumption curve maintains a relatively gentle growth slope, and even as the problem size continues to increase, its computational time increases at a much slower rate. This clear divergence demonstrates that the sparse Broyden–Schubert method exhibits superior scalability in large-scale problem-solving scenarios and can better adapt to increasing problem sizes.

Overall, the sparse Broyden–Schubert method demonstrates significant advantages in three key aspects: computational efficiency (Tcpu), computational cost ($m$), and convergence performance ($R$). These advantages become more pronounced as the problem dimension increases ($n\ge 1000$), validating its practicality and efficiency in solving carbonate rock acid pressure multi-field coupling models.

4.2. Nonlinear Heat Conduction Multi-Physics Coupling Model

To validate the efficacy of the sparse quasi-Newton algorithm across a broader spectrum of application problems, this section introduces a new test model: a simplified nonlinear multi-field coupled heat transfer model. This model describes a steady-state temperature field problem incorporating radiation and convective heat dissipation. Its governing equations, after discretization via the finite difference method, yield a high-dimensional nonlinear system characterized by a tridiagonal Jacobian matrix structure. Both in physical background and mathematical formulation, this model differs significantly from the acid fracturing model presented in Section 4.1 (28), thereby serving to evaluate the algorithm’s universal performance across diverse application scenarios.

The discrete form of the simplified heat conduction model is as follows:

$$\begin{array}{c}{F}_1=k\left(T_2-2T_1+T_{left}\right)-\sigma \left(T_4^4-T_{\theta }^4\right)-h(T_1-T_{\theta })=0,\hfill \\ F_i=k\left(T_{i+1}-2T_i+T_{i-1}\right)-\sigma \left(T_i^4-T_{\theta }^4\right)-h(T_i-T_{\theta })=0, i=2,\dots ,n-1,\hfill \\ F_n=k\left(T_{right}-2T_n+T_{n-1}\right)-\sigma \left(T_n^4-T_{\theta }^4\right)-h(T_n-T_{\theta })=0,\hfill \\ T_0=(1,1,\dots ,1{)}^T.\hfill \end{array}$$

Here, $T_i$ denotes the temperature at the i-th node (the variable to be solved), $k$ is the thermal conductivity, $\sigma$ is the radiation coefficient, $h$ is the convective heat transfer coefficient, $T_{\theta }$ is the ambient temperature, and $T_{left}$ and $T_{right}$ are the fixed temperatures at the left and right boundaries, respectively. All physical quantities have been nondimensionalized to improve numerical stability. The Jacobian matrix of this model is not only sparse (tridiagonal) but also exhibits stronger nonlinearity due to the nonlinear radiation term $T_i^4$, making it a more challenging case for testing algorithms.

To ensure a fair comparison, we maintain exactly the same algorithm parameter settings (convergence tolerance $\epsilon ={10}^{-6}$, Wolfe line search condition, initial matrix $B_0=J\left(x_0\right)+\epsilon$, and performance evaluation metrics as in Section 4.1 (the original test). In the model, the scaling parameter is selected as: $k=0.1;\sigma =0.01;h=0.05;T_{\theta }=0.5;T_{left}=1.0;T_{right}=0.8.$

Table 3. Performance comparison on the heat conduction model.

Dim	BFGS		Sparse Broyden Schubert
	Iteration	Tcpu (s)	Iteration	Tcpu (s)
500	6	0.0124	3	0.0076
1000	6	0.0544	3	0.0349
2000	6	0.2532	4	0.2096
2500	6	0.4003	4	0.3378
4000	6	1.2043	4	1.0850
5000	7	2.4818	4	1.8392
6000	7	3.7230	4	2.8919
7500	7	5.4478	4	4.3431
8000	7	7.6342	4	6.1400
9000	7	10.0049	4	8.1452
10,000	7	13.4487	4	10.7674
20,000	7	81.1970	4	69.0125
30,000	7	275.0223	4	221.1731

and

Table 4. Comparative results with additional heat conduction model.

$\mathit{n}$	Method	${\mathit{N}}_1$	${\mathit{N}}_{\mathit{m}}$	$\mathit{m}$	$\mathit{R}$
500	BFGS	0.2630	6.279 × 10−6	11	0.968
	Broyden–Schubert	0.2630	1.163 × 10−5	7	1.433
1000	BFGS	0.3720	8.932 × 10−6	11	0.967
	Broyden–Schubert	0.3720	1.568 × 10−5	7	1.439
2000	BFGS	0.5270	1.267 × 10−5	11	0.967
	Broyden–Schubert	0.5270	5.633 × 10−7	9	1.528
2500	BFGS	0.5890	1.417 × 10−5	11	0.967
	Broyden–Schubert	0.5890	5.657 × 10−7	9	1.540
4000	BFGS	0.7450	1.794 × 10−5	11	0.967
	Broyden–Schubert	0.7450	5.726 × 10−7	9	1.564
5000	BFGS	0.8330	1.8740 × 10−7	13	0.971
	Broyden–Schubert	0.8330	5.771 × 10−7	9	1.576
6000	BFGS	0.9120	3.008 × 10−6	13	0.971
	Broyden–Schubert	0.9120	5.814 × 10−7	9	1.585
7000	BFGS	0.9850	3.250 × 10−6	13	0.971
	Broyden–Schubert	0.9850	5.858 × 10−7	9	1.593
8000	BFGS	1.0530	3.474 × 10−6	13	0.971
	Broyden–Schubert	1.0530	5.901 × 10−7	9	1.599
9000	BFGS	1.1170	3.686 × 10−6	13	0.971
	Broyden–Schubert	1.1170	5.943 × 10−7	9	1.605
10,000	BFGS	1.1780	3.885 × 10−6	13	0.971
	Broyden–Schubert	1.1780	5.986 × 10−7	9	1.610
20,000	BFGS	1.6650	5.496 × 10−6	13	0.971
	Broyden–Schubert	1.6650	6.391 × 10−7	9	1.641
30,000	BFGS	2.0400	6.732 × 10−6	13	0.971
	Broyden–Schubert	2.0400	6.772 × 10−7	9	1.658

present a performance comparison between the sparse Broyden–Schubert method and the BFGS method for solving the nonlinear coupled thermos-hydro-mechanical-chemical (THMC) heat conduction model. The results demonstrate that the sparse Broyden–Schubert method exhibits significant advantages across multiple metrics.

In terms of iterative efficiency, this method achieves fewer iterations across all tested dimensions. In the 2000-dimensional problem, it converges in only four iterations, showing a notable improvement compared to the six iterations required by the BFGS method. This advantage primarily stems from the algorithm’s use of a precisely constructed initial Jacobian matrix. This initial matrix accurately captures the tridiagonal dominant structure resulting from the discretization of the heat conduction term, providing a high-quality structured initial guess for the iterative process and thereby significantly enhancing the accuracy of the search direction.

In terms of function evaluation efficiency, the sparse Broyden–Schubert method requires a significantly lower total number of component function evaluations than the BFGS method, reflecting a substantial computational advantage. This indicates that each function evaluation contributes more effectively to error reduction, resulting in a faster convergence rate. The underlying reason lies in the sparse update mechanism, which strictly preserves the sparsity pattern of the Jacobian matrix and aligns closely with the inherent mathematical structure of the problem.

Regarding computational time, the advantage of the sparse Broyden–Schubert method becomes more pronounced as the problem size increases. In the 2000-dimensional case, it reduces computation time by approximately 17% compared to the BFGS method. This performance gap further widens in higher-dimensional problems, such as the 10,000-dimensional case 24%. For large-scale problems, the use of sparse matrix operations effectively reduces memory access overhead and cache miss rates, thereby enhancing practical computational efficiency.

Particularly noteworthy is that this experiment validates the generality and robustness of the sparse Broyden–Schubert method when applied to problems with diverse physical backgrounds and mathematical properties. Although the heat conduction model differs significantly from the previously studied acid fracturing model in both physical mechanisms and sources of nonlinearity, the method still demonstrates superior performance. This indicates that its advantages do not stem from adaptation to a specific problem but rather from a universal utilization of the sparse structure of the Jacobian matrix. Even when confronted with numerical perturbations caused by the strongly nonlinear radiation term $T_i^4$, the algorithm maintains strong stability, owing to its high-quality initialization strategy and moderate regularization mechanism, which together ensure a reasonable starting point for iterations and robustness throughout the numerical process.

In summary, as a quasi-Newton algorithm that fully exploits the sparse nature of the Jacobian matrix, the sparse Broyden–Schubert method provides an efficient, stable, and general numerical framework for solving nonlinear systems with sparse structures. It demonstrates broad application prospects in addressing multi-physics coupling problems.

5. Discussion

This study addresses the computational challenges in simulating the multi-physics coupling of permeability, acid concentration, pressure, and velocity fields during carbonate rock acid fracturing. A mathematical model is established and discretized using the finite volume method, resulting in a large-scale system of nonlinear equations. This system exhibits a clear structured sparsity, and to improve solution efficiency, the sparse Broyden–Schubert method—a quasi-Newton algorithm designed for sparse structures—is adopted. Results show that this method significantly outperforms the classical BFGS algorithm in terms of computational speed and numerical stability, enabling more efficient solutions for such high-dimensional nonlinear problems.

From a theoretical perspective, although the superlinear convergence of quasi-Newton methods (Theorem 1) is an asymptotic property independent of dimension $n$, the practical impact of $n$ lies in how long it takes to reach this regime. For classical BFGS, which updates a dense $n\times n$ matrix, superlinear convergence typically emerges after $O\left(n\right)$ iterations, once sufficient directional information has been gathered to form a high-quality Hessian approximation. The sparse Broyden–Schubert method used here exploits the known sparsity pattern of the Jacobian, drastically reducing the number of free parameters that need to be estimated. As a result, it accumulates the necessary curvature information much faster than dense methods, often entering the superlinear phase in far fewer than $O\left(n\right)$ iterations. This explains the improved convergence rates in Table 1 and Table 2 and highlights a broader advantage: sparsity not only reduces per-iteration cost but also accelerates the overall convergence process by shortening the initial learning phase.

The key advantage of the method lies in its effective utilization of the Jacobian matrix structure. Under the finite volume discretization, variables interact locally, leading to a regular tridiagonal sparse pattern in the Jacobian. The sparse Broyden–Schubert method takes full advantage of this feature by restricting updates to non-zero entries only, avoiding the expensive full-matrix operations required in BFGS. This not only reduces the computational cost per iteration but also significantly lowers memory usage, thereby accelerating convergence. Specifically, it requires fewer iterations, fewer function evaluations, and achieves a faster average convergence rate. Since nonlinear solvers typically dominate the overall simulation time, this improvement is of practical significance.

The performance trend in Figure 2 demonstrates that the sparse quasi-Newton method exhibits superior scalability. While both algorithms perform comparably on small-scale instances (e.g., $n=100$), their behaviors diverge significantly as the system size increases—particularly beyond $n=2000$. The sharp rise in BFGS computation time reflects its inherent limitation: full-rank updates lead to cubic complexity in matrix operations, which becomes prohibitive at scale. In contrast, the sparse Broyden–Schubert method maintains a nearly linear growth in computational cost, thanks to its restricted update pattern that aligns with the underlying tridiagonal structure. This structural compatibility not only reduces arithmetic operations per iteration but also minimizes memory bandwidth pressure, resulting in a 31% CPU time saving at $n=4000$. Such scalability is essential for practical deployment in large-scale reservoir simulations, where model fidelity often demands high spatial resolution.

Similarly, the convergence profile in Figure 1 reveals more than just speed—it reflects algorithmic robustness. The rapid drop in residual by several orders of magnitude within the initial iterations suggests that the sparse method captures the dominant curvature directions of the nonlinear system more effectively. This qualitative behavior aligns with the aforementioned theoretical analysis: due to entering the superlinear convergence phase earlier, the rate of residual decline improves at fewer iterations. When translated into wall-clock time, this translates to a 25–30% reduction in time-to-solution to reach 10⁻⁶ accuracy. This real-time advantage directly impacts workflows in reservoir engineering, enabling faster turnaround for iterative tasks such as history matching, sensitivity studies, and parametric design optimization.

To further validate the method’s general applicability beyond acid fracturing contexts, we conducted additional tests using a nonlinear multi-field coupled heat transfer model, which also yields a tridiagonal Jacobian structure. The sparse Broyden–Schubert method again demonstrated consistent superiority, reducing iteration counts by 39% and computation time by 28% on average compared to BFGS at dimensions ranging from 500 to 30,000. This confirms that the algorithm’s efficiency is not problem-specific but rather stems from its ability to exploit structured sparsity common in many discretized PDE systems.

The main contribution of this work is the successful application of a sparse quasi-Newton method—less used in engineering simulations previously—to the complex, multi-physics problem of acid fracturing in carbonate rocks, along with a systematic evaluation of its performance. We observe that the sparse structure generated by the finite volume discretization aligns well with the algorithm’s update mechanism, forming a smooth workflow from “modeling” to “discretization” to “numerical solution.” This highlights an important insight: in numerical simulation, selecting a solver that matches the inherent structure of the problem can be more effective than simply pursuing algorithmic complexity.

In summary, the sparse Broyden–Schubert method demonstrates strong computational efficiency, stable convergence, and excellent scalability when solving multi-physics coupled nonlinear systems in acid-fracturing simulations. This study not only validates its practical value in engineering applications but also theoretically elucidates the source of its efficiency advantages: sparsity simultaneously reduces per-iteration cost and accelerates the overall convergence process. It provides a feasible and efficient numerical solution for large-scale acid fracturing modeling. Future work will explore its extension to more complex scenarios, including intricate fracture geometries, unstructured grids, and parallel computing environments.

6. Conclusions

Based on the evolutionary characteristics of carbonate rock acid fracturing, a mathematical model was established that considers the multi-physics coupling among permeability, acid concentration, pressure, and velocity fields. The model was discretized using the finite volume method, resulting in a large-scale nonlinear system of equations. To solve this system, we used the sparse Broyden–Schubert method and performed corresponding numerical experiments.

Numerical results from both the acid fracturing model and the additional thermal conduction coupling model demonstrate the significant advantages of the proposed algorithm over the conventional BFGS method. For the acid fracturing model, the sparse Broyden–Schubert method achieves a reduction in the number of iterations across all dimensions and shortens the average computation time by 30% compared to the BFGS method. Similarly, in the thermal conduction model, the proposed method maintains a 30% improvement in iteration efficiency, reduces computation time by 20–35%, and consistently exhibits superior average convergence rates across all tested dimensions.

While the proposed sparse quasi-Newton method demonstrates significant computational advantages for acid-fracturing simulations, its applicability is subject to certain limitations. The model currently omits thermal and geomechanical couplings, which may restrict its use in environments where these effects are pronounced. Additionally, the dependency on an initial Jacobian evaluation and limited validation under realistic field conditions warrants further research. Future work will focus on extending the model to incorporate additional physics, developing adaptive Jacobian initialization strategies, and validating the method with field–data integration.

The results demonstrate that the adopted sparse quasi-Newton method is both computationally efficient and practically effective for acid-fracturing simulations in carbonate formations, while also exhibiting strong potential for extension to other multi-physics coupling problems in reservoir engineering.