A Hybrid Semi-Supervised Tri-Training Framework Integrating Traditional Classifiers and Lightweight CNN for High-Resolution Remote Sensing Image Classification

Abstract

High-resolution remote sensing imagery offers detailed spatial and semantic insights into the Earth’s surface, yet its classification remains hindered by the limited availability of labeled data, primarily due to the substantial expense and time required for manual annotation. To overcome this challenge, we propose a hybrid semi-supervised tri-training framework that integrates traditional classification methods with a lightweight convolutional neural network. By combining heterogeneous learners with complementary strengths, the framework iteratively assigns pseudo-labels to unlabeled samples and collaboratively refines model performance in a co-training manner. Additionally, a landscape-metric-guided relearning module is introduced to incorporate spatial configuration and land cover composition, further enhancing the framework’s representational capacity and classification robustness. Experiments were conducted on four high-resolution multispectral datasets (QuickBird (QB), WorldView-2 (WV-2), GeoEye-1 (GE-1), and ZY-3) covering diverse land-cover types and spatial resolutions. The results demonstrate that the proposed method surpasses state-of-the-art baselines by 1.5–10% while generating more spatially coherent classification maps.

1. Introduction

With the rapid advancement of spaceborne imaging technologies, high-spatial resolution remote sensing (HRRS) imagery has become an indispensable resource for Earth surface monitoring, owing to its capability to capture fine-grained spatial, spectral, and structural information [1,2]. Accurate classification of such imagery is critical for numerous applications, including land use mapping, environmental change detection, and urban planning [3]. Beyond these technical uses, it also directly informs evidence-based land use policy decisions, enabling governments to optimize resource allocation, promote sustainable urban development, and implement targeted conservation strategies [4].

Despite the increasing availability of HRRS imagery, the performance of machine learning (ML) and deep learning (DL) methods is often constrained by the scarcity of labeled data. State-of-the-art DL models typically require large-scale, high-quality annotations to generalize effectively [5,6]. In remote sensing, each high-resolution image contains millions of pixels, and generating pixel- or object-level labels is labor-intensive and costly, often requiring domain expertise. Furthermore, datasets frequently exhibit class imbalance, with some land-cover types or rare features underrepresented, while ground-truth coverage is sparse due to environmental limitations [7]. These constraints can lead to overfitting, reduced robustness, and substantial drops in model accuracy, with empirical studies showing significant performance gaps when labeled data are insufficient. Furthermore, DL models are computationally intensive and parameter-heavy, posing additional challenges in resource-limited environments. Collectively, these issues highlight the need for approaches that use abundant unlabeled data to improve generalization under limited supervision [8,9].

Recent advancements in DL have significantly enriched the methodological framework for HRRS image classification. Modern neural network architectures, including convolutional neural networks (CNNs) and Transformer-based models, have demonstrated remarkable capabilities in extracting intricate spectral–spatial features, effectively addressing complex intra-class variability and high inter-class similarity in HRRS imagery. For instance, Fayaz et al. Fayaz, Nam, Dang, Song and Moon [1] explored transfer learning with Inception-v3 and DenseNet121 for land-cover classification, showing that pre-trained models on large datasets substantially improve generalization and accuracy under limited labeled data. Liu et al. proposed STConvNeXt, a lightweight CNN incorporating split-based mobile convolutions and hierarchical tree structures, achieving both computational efficiency and enhanced classification performance [10]. Additionally, graph neural networks and attention-based transformers have been applied to capture long-range dependencies and fine-grained contextual information, further improving land-cover discrimination [11,12]. These innovations reflect the growing trend towards using more complex and efficient models to address the challenges of HRRS classification.

In parallel with these advances, self-supervised learning (SSL) has emerged as a powerful paradigm, enabling feature extractors to leverage large volumes of unlabeled data and mitigate the problem of scarce annotations. Nezhad et al. demonstrated an SSL framework with pretext tasks such as colorization and patch prediction, enhanced by attention mechanisms and transformer architectures, highlighting SSL’s ability to extract discriminative and generalizable features [13]. Attention mechanisms, exemplified by RISENet with its multi-layer dynamic spatial channel fusion, have proven effective for capturing long-range dependencies and preserving fine spatial details in complex remote sensing scenes [14,15]. These SSL frameworks significantly reduce the reliance on labeled data, making them ideal for scenarios with limited annotations.

Hybrid approaches that integrate deep learning models with traditional classifiers, graph-based models, or spatial regularization techniques have proven highly effective in balancing representational capacity and robustness under limited supervision [16,17]. Recent studies have demonstrated several successful strategies leveraging these hybrid methodologies [18]. For example, attention-enhanced CNNs and Transformer-based frameworks have been applied to HRRS semantic segmentation, significantly improving feature extraction and spatial coherence [17,19]. Additionally, SSL combined with region-level descriptors has shown improved generalization by capturing structural and semantic relationships in HRRS imagery [20]. Furthermore, hybrid semi-supervised models that combine CNNs with graph-based or ensemble learning techniques have demonstrated superior performance in addressing challenges such as class imbalance and label scarcity [21,22,23]. Semi-supervised scene classification methods, such as the Semi-Supervised Prototype-based Consistency (SSPC) and self-learning semantic segmentation approaches, have effectively expanded training datasets through pseudo-labeling, significantly improving classification accuracy with minimal labeled data [24]. These developments highlight the growing trend of combining multiple learning strategies to overcome the challenges of label scarcity and computational efficiency in HRRS classification.

Tri-training, a popular SSL technique, has been shown to be effective in integrating heterogeneous classifiers to iteratively assign pseudo-labels through majority voting, thus improving model generalization [25,26]. However, standard tri-training faces challenges, including the propagation of erroneous pseudo-labels during early iterations and pixel-level inconsistencies that result in salt-and-pepper noise [27,28]. To address these issues, prior studies have introduced spatial–contextual relearning strategies, incorporating spatial descriptors such as the gray-level co-occurrence matrix (GLCM) [29], wavelet transforms [30], and morphological profiles [31] to improve spatial coherence and smooth classification results. Object-based approaches, such as multiscale segmentation, have also been proposed to improve classification accuracy by focusing on region-level features and reducing the impact of scale-sensitive parameters [32,33].

To overcome these challenges, we propose a hybrid semi-supervised tri-training framework that combines traditional machine learning classifiers with a lightweight convolutional neural network. The framework is further enhanced by a spatial-contextual relearning module, which is guided by landscape metrics. The key contributions of this work are as follows:

• Hybrid Tri-Training with Heterogeneous Classifiers: We construct a tri-training ensemble that integrates traditional classifiers with a lightweight CNN to exploit their complementary strengths. While traditional models are more robust under limited supervision, CNNs excel at capturing high-level semantic and spatial features. This heterogeneous design enhances decision diversity compared to homogeneous ensembles and improves robustness in label-scarce scenarios by jointly assigning pseudo-labels and iteratively refining predictions.
• Landscape Metric-Guided Relearning: To mitigate pseudo-label noise and enhance spatial consistency, we introduce a relearning module based on landscape metrics. These metrics quantify spatial composition and configuration at the regional level, enabling more effective capture of structural semantics and improved delineation of land cover boundaries.
• Uncertainty-Aware Pseudo-Label Selection (UPS): To further improve classification around class boundaries, we incorporate an uncertainty-aware strategy for pseudo-label refinement. By selectively including low-confidence samples near decision edges, the model achieves more accurate boundary recognition and greater overall robustness.

We validate the proposed framework using four benchmark high-resolution multispectral datasets. Experimental results show that our method achieves higher accuracy under limited supervision while producing more spatially coherent classification maps.

The rest of this paper is organized as follows: Section 2 introduces the proposed methodology in detail. Section 3 describes the datasets and experimental settings. Section 4 presents the results and performance analysis. Finally, Section 5 concludes the study.

2. Methodology

2.1. Overview of the Proposed Framework

To address the challenges associated with limited labeled samples, high intra-class variability, and spatial fragmentation in high-resolution remote sensing image classification, we propose a hybrid semi-supervised tri-training framework. This framework integrates traditional machine learning classifiers and a lightweight CNN within a mutually reinforcing iterative loop. The goal is to enhance model robustness and spatial coherence under weak supervision.

As illustrated in Figure 1, the framework consists of three tightly coupled modules, each designed to address a specific limitation of conventional tri-training methods and collaboratively improve classification performance:

• Iterative Landscape Metric Relearning (ILMR) (Section 2.2): This module enhances spatial structural awareness by extracting landscape-level metrics—such as compactness and shape complexity—from intermediate classification maps. These metrics are then used to guide the generation and refinement of pseudo-labels, particularly in ambiguous or spatially fragmented regions.
• Uncertainty-aware Pseudo-label Selection (UPS) (Section 2.3): To mitigate confirmation bias and error accumulation, a dual-threshold mechanism is employed. This strategy filters pseudo-labeled samples based on inter-classifier consensus and predictive uncertainty, allowing only reliable samples to be incorporated into the labeled dataset.
• Tri-training with hybrid base learners (Section 2.4): The above modules are integrated into an iterative tri-training scheme, where traditional classifiers and lightweight CNN models cooperatively refine predictions and expand supervision, achieving complementary learning from spatial structural perspectives.

The proposed method leverages the decision diversity of heterogeneous learners and the spatial regularization introduced by ILMR to progressively adapt the model to unlabeled data with minimal risk of error propagation.

2.2. Iterative Landscape Metric Relearning (ILMR)

Relearning-based strategies via spatial regularities have proven effective in improving land cover classification [28,33]. Building on this, the ILMR method introduces a closed-loop technique that progressively refines model predictions by integrating structural information into the learning process.

Step 1: Landscape Metric Extraction. After each training iteration, the current pseudo-labeled map is segmented into contiguous patches via connected component analysis. For each $p$ assigned to class $i$, a set of landscape metrics ${\mathcal{l}}_m$ is computed to characterize its spatial configuration. The following metrics are computed:

• Mean patch size (MPS): Reflects average patch area;
• Largest patch index (LPI): Quantifies the dominance of the largest patch;
• Edge density (ED): Indicates fragmented or boundary regions;
• Mean shape index (MSI): Measures the geometric complexity of patches;
• (See Appendix A for definitions and computations of all eight metrics.)

Together, these metrics encode both spatial composition and configuration at the landscape level. They are integrated into the tri-training framework to iteratively refine pseudo-labels, enhancing the model’s ability to generate spatially coherent and structurally consistent classification maps.

Given a pixel p, we define a square moving window centered at p over the current classified map. The set of pixels within the window that are assigned to class i is denoted as $W_i(p)$. Then, the landscape feature associated with metric m for class i at location p is denoted as

$$f_m^i(p)={\mathcal{l}}_m(W_i(p))$$

(1)

where $f_m^i(p)$ represents the landscape feature value within the window, and as mentioned above, ${\mathcal{l}}_m(.)$ is the computation function for metric m (e.g., patch density, edge density, shape index) over the window. The full landscape feature vector for class i at location p, encompassing all m selected metrics, is given by

$$f^i(p)=\left[f_1^i(p),f_2^i(p),\dots ,f_m^i(p)\right]$$

(2)

Subsequently, landscape features for all land cover classes $F(p)$ are written as

$$F(p)=\left[f^1(p),f^2,\dots ,f^K(p)\right]$$

(3)

where K is the number of land cover classes. This formulation allows us to derive class-wise spatial descriptors for each pixel, which are then fed back into the iterative learning process as auxiliary features to enhance structural consistency.

These features serve as auxiliary input channels to the classifiers. The enriched input at position p denoted $\tilde{X}(p)$ is obtained by concatenating original image features $X(p)$ with landscape features:

$$\tilde{X}(p)=\left[\tilde{X}(p)\oplus F(p)\right]$$

(4)

where $\oplus$ indicates channel-wise feature concatenation.

Step 2: Relearning Process. The enriched inputs $\tilde{X}(p)$ are used to retrain all base classifiers. New pseudo-labels are generated, landscape metrics are recomputed, and the cycle continues. This closed-loop feedback enforces local spatial coherence, regularizing predictions without additional annotations. The classifiers continue this cycle until convergence (e.g., stable validation accuracy or max iterations). By enforcing local spatial regularities, ILMR significantly improves classification consistency, particularly in fragmented or ambiguous regions. It synergizes ensemble learning with structural regularization to produce more reliable and interpretable land cover maps.

Note: “Landscape” refers to local patch configuration in the classification map, not ecological landscape units.

2.3. Uncertainty-Aware Pseudo-Label Selection (UPS)

To ensure reliable pseudo-label propagation, we introduce an Uncertainty-aware Pseudo-label Selection (UPS) strategy. This approach aims to filter out low-confidence or potentially noisy predictions, which frequently arise near class boundaries and can adversely affect model performance if left unchecked. To further stabilize training, a dual-threshold mechanism is applied: samples with low target confidence are excluded unless peer classifiers provide both label agreement and high-certainty predictions. This design suppresses error reinforcement, leverages reliable supervision, and improves robustness against confirmation bias and error accumulation.

For each unlabeled sample $x\in U$, three classifiers ($C_1,C_2,C_3$) independently generate a predicted label $y\in Y$ along with an associated certainty score ($C(x)\in \left[0,1\right]$). A majority voting scheme is employed to determine label consensus; that is, only those samples for which at least two classifiers agree on the predicted label are considered suitable for pseudo-labeling [34].

$$C(x)={\displaystyle \sum _{k=1}^{K-1}\left({\tilde{p}}_k(x)-{\tilde{p}}_{k+1}(x)\right)\times \frac{1}{k}}$$

(5)

where ${\tilde{p}}_1(x),\dots ,{\tilde{p}}_k(x),\dots ,{\tilde{p}}_K(x)$ represent the multi-class probabilistic outputs in descending order, and K is the number of information classes. A larger value of $C(x)$ foreshadows a more reliable classification of pixel x. This step produces both the pseudo-label map and the associated certainty maps for all three classifiers.

To further refine the pseudo-label selection, we compute the certainty extremum across classifiers for each unlabeled sample:

$$C_{\max }(x)=\max \left\{C_1(x),C_2(x),C_3(x)\right\} C_{\min }(x)=\min \left\{C_1(x),C_2(x),C_3(x)\right\}$$

(6)

We then compute classifier-wise certainty bounds and apply a dual-threshold criterion: Accept a sample for classifier $C_j$ if

• The other two classifiers agree on a label;
• ${C_j}^{\prime }s$ certainty ${\alpha }_j<T_{\min }$, but at least one classifier’s certainty $>T_{\max }$.

Such samples are then added to the training pool of the uncertain classifier, benefiting from its peers’ reliable predictions.

This dual-threshold criterion ensures the selective incorporation of pseudo-labels based on two essential conditions: (1) the target classifier demonstrates low confidence in its current prediction, signaling a potential area for improvement, and (2) at least one peer classifier provides a high-confidence prediction, offering a reliable supervisory signal. By combining these conditions, the mechanism incorporates only reliable pseudo-labels from peer agreement while filtering out uncertain predictions from the target classifier, effectively mitigating confirmation bias, preventing error accumulation, and stabilizing the semi-supervised training process [21].

2.4. Tri-Training with Hybrid Base Learners

Integrating the above modules into a unified learning framework, we design an iterative training algorithm that alternates between UPS-based pseudo-labeling and ILMR-based structural refinement, which is summarized in Algorithm 1.

The proposed algorithm follows an iterative semi-supervised tri-training manner that progressively expands the labeled training set by pseudo-labeling high-confidence samples and refining uncertain predictions through spatial feedback. At each iteration, multiple base classifiers are trained on the current labeled and pseudo-labeled data. For the unlabeled samples, a confidence-aware voting strategy is applied to identify high-consistency, high-confidence predictions, which are directly incorporated as pseudo-labels. Meanwhile, samples in ambiguous regions (characterized by low inter-classifier confidence agreement) are passed to the ILMR module. This module extracts landscape-level spatial descriptors (e.g., compactness, fragmentation) from intermediate classification results and uses them to guide structural pseudo-label generation. By jointly leveraging reliable predictions and spatial regularization, the algorithm enhances the semantic consistency and boundary accuracy of land cover classification in a progressive, data-efficient manner. This joint optimization strategy capitalizes on the complementarity of traditional classifiers and CNN models, combining discriminative power, interpretability, and structural sensitivity.

In particular, the integration of traditional classifiers with a lightweight CNN is intended to exploit model complementarity within the tri-training framework. Traditional classifiers exhibit strong stability and robustness in small-sample conditions, whereas CNNs are suited at learning hierarchical semantic and spatial-contextual representations. Their heterogeneous design enriches decision diversity and mitigates the limitations of homogeneous ensembles, thereby enhancing generalization across heterogeneous landscapes and improving the stability of semi-supervised optimization.

Algorithm 1: Semi-supervised Land Cover Classification via Tri-training with hybrid base learners

Input: Labeled dataset: $\mathcal{L}=\{(x_i ,y_i )\}$ Unlabeled dataset: $U=\{x_j \}$ Ensemble of base classifiers: $M={\{f_k \}}_{k=1}^K$ High/low confidence thresholds: $T_{\max }$ and $T_{\min }$ Max iterations: T

Procedure: 1. Initialize pseudo-label set $P\leftarrow \varnothing$ 2. For iteration $t=1$ to T do 2.1. Train/update base classifiers $\mathcal{M}$ on $\mathcal{L}\cup P$ 2.2. Initialize temporary sets $P_{high} \leftarrow \varnothing$, $Q_{ILMR} \leftarrow \varnothing$ 2.3. for each $x\in U$do (a) Obtain predictions $\{f_k (x)\}$, labels $\left\{{\widehat{y}}_k\right\}$ and probabilities (b) Compute agreement score $A(x)$ and confidence bounds $C_{\max }(x)$, $C_{min} (x)$ (c) if $A(x)\ge {\tau }_a$ and $C_{\max }(x)>T_{\max }$ then Add $(x,{\widehat{y}}_{\mathrm{maj}})$ to ${\mathcal{P}}_{\mathrm{high}}$ (d) else if $A(x)\ge {\tau }_a$ and $C_{min} (x)<T_{\min }$ Add $(x,{\widehat{y}}_{\mathrm{maj}})$ to $Q_{ILMR}$ 2.4. Generate coarse land cover map using $P_{high}$ 2.5. Extract landscape metrics $F_i$ from patches in the coarse map 2.6. Augment $Q_{ILMR}$ samples with corresponding metrics $F_i$ 2.7. Generate structural pseudo-labels for $Q_{ILMR}$ via ILMR module 2.8. Update pseudo-label set: $P\leftarrow P\cup P_{high} \cup Q_{ILMR}$ labels 2.9. Optionally update thresholds $T_{\max }$ and $T_{\min }$ adaptively 3. End For

Output: Trained hybrid classifier ensemble and final pseudo-label map.

Note: At each iteration, samples satisfying the dual-threshold UPS criterion are selectively incorporated as pseudo-labels, while low-confidence or ambiguous samples are refined through the ILMR module. The pseudo-label set is updated iteratively, and confidence thresholds can be adaptively adjusted, progressively enhancing classification accuracy, spatial coherence, and stability in the semi-supervised learning process.

3. Experimental Parameters and Datasets

3.1. Parameter Settings

The experiments were conducted on a workstation running Windows 10, equipped with an Intel Core i7-6700 CPU @ 3.40 GHz (Intel, Santa Clara, CA, USA), 16 GB DDR4 1600 MHz RAM, and an NVIDIA GeForce RTX 3060 GPU with 12 GB memory (NVIDIA, Santa Clara, CA, USA). The software environment included Python 3.9, TensorFlow 2.8, and PyTorch 1.12, with CUDA 11.3 and cuDNN 8.2 support. The parameter settings used in the proposed framework are closely aligned with the methodology described in Section 2. To ensure reproducibility and facilitate understanding, the experimental configurations are detailed below. The sensitivity analysis of key parameters is discussed in Section 4.

1.

To ensure model diversity and complementary strengths, three different classifiers were integrated: a lightweight Convolutional Neural Network (CNN), Random Forest (RF), and Logistic Regression via Splitting and Augmented Lagrangian (LORSAL). The CNN was employed to capture hierarchical semantic and spatial–contextual representations, trained with a learning rate of 0.001, the Adam optimizer, a batch size of 32, and a maximum of 100 epochs. The detailed CNN architecture is provided in Section 3.2. RF was adopted for its robustness under small-sample conditions, with 200 trees constructed to balance computational efficiency and classification accuracy [35]. LORSAL was included for its stability and interpretability in high-dimensional feature spaces. Its regularization parameter was set to λ = 0.001, and the maximum number of iterations was fixed at 1000, consistent with standard practices reported in previous study [36]. By combining these classifiers within the tri-training framework, the system capitalizes on their complementary advantages, enriching decision diversity and enhancing generalization across heterogeneous landscapes.

2.

ILMR: In order to simultaneously capture the details and characterize the neighborhood extent (e.g., the spatial pattern and arrangement of the land-cover classes), a window size of 9 × 9 pixels was used.

3.

Training: For each class, 50 samples were randomly selected from the reference map to train the classification model, while the remaining reference samples were reserved for accuracy assessment.

4.

Accuracy assessment: Overall accuracy (OA) was computed from the confusion matrix for the quantitative assessment.

3.2. CNN Architecture

To enhance the discriminative capacity of the proposed ensemble framework, we integrate a lightweight convolutional neural network (CNN) as one of the base classifiers. Compared with traditional machine learning methods, CNNs exhibit superior capability in capturing local spatial-spectral correlations and hierarchical features. The detailed architecture is illustrated in Figure 2 and comprises the following layers:

Input Layer: $9\times 9\times d$ image patches (d denotes the concatenated dimension of the spectral bands and landscape features). This composite input enables the CNN to simultaneously learn spectral–spatial patterns and contextual land-cover information.

Convolution layer1 (Convol1): A convolutional layer with 32 filters of size 3 × 3 and ReLU activation, designed to extract basic spatial-spectral patterns.

Convolution layer2 (Convol2): A second convolutional layer with 64 filters of size 3 × 3, also followed by ReLU activation, which learns more abstract and discriminative feature representations.

Max-Pooling: A max-pooling layer with a kernel size of 2 × 2 to down-sample the feature maps and reduce spatial dimensionality while retaining dominant activations.

Flatten: The pooled feature maps are flattened into a one-dimensional vector to facilitate dense-layer computation.

Fully Connected (FC) Layer: A fully connected layer with 128 units and ReLU activation serves to further integrate learned features across all channels.

Dropout: To alleviate overfitting, a dropout layer with a rate of 0.5 is applied during training.

Output Layer: A final dense layer with C units (C equal to the number of land-cover classes), using soft-max activation to output the class probabilities.

3.3. Datasets

To validate the effectiveness of the proposed method, experiments were conducted on four multispectral remote sensing datasets (HRRS) datasets: GeoEye-1 Wuhan (GE-1), QuickBird Wuhan (QB), WorldView-2 Hainan (WV-2), and ZY-3 Wuhan (ZY-3). The corresponding reference maps were manually delineated based on extensive field investigations and prior knowledge of the study areas, ensuring the accuracy and reliability of the ground truth. The number of reference samples is shown in

Table 1. Number of reference samples (in pixels) for the four high-resolution datasets.

Class	QB	WV-2	GE-1	ZY-3
Buildings	18,296	11,578	20,074	15,818
Roads	5103	5356	3187	13,564
Trees	17,415	14,086	5370	6154
Grass	9179	7417	4098	3065
Water	16,614	11,209	-	3928
Soil	3709	22,189	18,249	4659
Shadow	4378	1427	1330	4722

. The main characteristics of the four datasets are summarized as follows:

• QB dataset: Acquired by the QuickBird satellite, this dataset contains 1123 × 748 pixels, covering four spectral bands with a spatial resolution of 2.4 m (Figure 3a);
• WV-2 dataset: Captured by the WorldView-2 high-spatial-resolution (HSR) sensor, this dataset comprises eight multispectral bands at a 2-m spatial resolution, with an image size of 600 × 520 pixels (Figure 3b);
• GE-1 dataset: Provided by the GeoEye-1 satellite, the images consist of 908 × 607 pixels, offering four spectral bands at a 2-m spatial resolution (Figure 3c);
• ZY-3 dataset: Acquired by ZY-3, China’s first civilian high-resolution mapping satellite, this dataset contains 651 × 499 pixels with four spectral bands and a spatial resolution of 5.8 m (Figure 3d).

4. Results and Discussion

In this section, we comprehensively evaluate the effectiveness of the proposed CNN-based framework that integrates both spectral and landscape features. Experiments were conducted on four HRRS datasets: GE-1, QB, WV-2, and ZY-3. The evaluation includes quantitative and qualitative comparisons, ablation studies, parameter sensitivity analysis, and robustness assessment experiments.

• Comparison of Classification Performance.

  Table 2. Classification performance (Overall Accuracy %, mean ± standard deviation).

  Method	QB	WV-2	GE-1	ZY-3
  RF	86.21 ± 0.45	88.12 ± 0.39	84.75 ± 0.53	82.30 ± 0.61
  LORSAL	87.40 ± 0.47	89.01 ± 0.42	86.20 ± 0.48	83.95 ± 0.57
  CNN	89.75 ± 0.36	91.28 ± 0.31	88.32 ± 0.45	88.77 ± 0.40
  Ours	91.62 ± 0.29	92.96 ± 0.27	91.91 ± 0.34	92.25 ± 0.35

  presents the overall accuracy (OA) values, reported as mean ± standard deviation, for different classification methods evaluated on four datasets (QB, WV-2, GE-1, and ZY-3) over five independent runs. The results clearly indicate that the proposed method outperforms the baseline approaches (RF, LORSAL, and CNN) across all datasets. Notably, the proposed tri-training framework consistently achieves the highest OA, demonstrating its superior classification capability.

This performance gain is primarily attributed to the synergistic integration of the ILMR and UPS modules within the framework, which jointly enhance class separability while effectively preserving edge details. After five iterations, the proposed method achieves OA values of 91.6%, 92.9%, 91.9%, and 92.3% on the QB, WV-2, GE-1, and ZY-3 datasets, respectively. Compared to RF and LORSAL, our approach shows significant improvements of approximately 5.4–10% in OA, indicating its superiority in capturing complex spectral–spatial relationships. While the CNN baseline already yields strong performance, our method achieves further accuracy gains of 1.5–3.6%, suggesting that the proposed enhancements (e.g., advanced spatial feature integration or attention mechanisms) offer substantial benefits even over deep learning approaches. The improvement is particularly pronounced on GE-1 and ZY-3, where CNN struggles with class fragmentation and boundary confusion, but our framework achieves improvements of more than 3%, underscoring its robustness to challenging data distributions and sensor characteristics.

Importantly, these gains can be directly attributed to the specific contributions of each module. The ILMR module increases category independence and enforces spatial regularity through landscape metrics, which effectively suppresses salt-and-pepper noise and alleviates pixel-level inconsistencies, but may also lead to blurred object boundaries due to over-smoothing. The UPS module, based on a dual-threshold sample selection strategy, filters out unreliable predictions and prevents error reinforcement, thereby reducing excessive smoothing and maintaining edge sharpness, though residual inconsistencies may still occur in highly complex regions. To overcome these limitations, the hybrid tri-training integrates classifiers with complementary strengths, ensuring more reliable pseudo-label propagation and significantly improving stability across iterations.

To rigorously assess the significance of these improvements, paired t-tests were conducted between the proposed method and each baseline. As summarized in

Table 3. Paired t-test p-values between the proposed method and baselines (all p-values are below 0.05, indicating statistically significant improvements).

Comparison	QB	WV-2	GE-1	ZY-3
Ours vs. RF	2.4 × 10−4	1.8 × 10−4	3.2 × 10−4	4.7 × 10−4
Ours vs. LORSAL	3.1 × 10−3	2.7 × 10−3	2.9 × 10−3	3.4 × 10−3
Ours vs. CNN	1.9 × 10−2	2.2 × 10−2	2.5 × 10−2	1.8 × 10−2

, all p-values are below the 0.05 significance level, confirming that the observed improvements are statistically significant across all datasets. Additionally, the relatively small standard deviations across multiple runs further indicate the stability and robustness of the proposed framework. Taken together, these findings verify that the hybrid tri-training method, through the complementary contributions of ILMR and UPS, not only reduces noise and pixel-level inconsistencies but also preserves fine-grained object structures. This synergistic effect ultimately leads to significant and consistent performance improvements across diverse datasets.

2.

Visual Inspection of Classification Maps. Figure 4 presents the classification maps produced by the proposed method across the four datasets. Compared with the raw output (Figure 4a), where evident misclassifications occur among spectrally similar classes (e.g., roads, buildings, and soil) and salt-and-pepper noise is prominent due to the inclusion of unreliable pseudo-labels, the proposed method achieves significantly cleaner and more coherent results. While the relearning-landscape method (Figure 4b) effectively reduces salt-and-pepper noise by extracting spatial regularities, it suffers from over-smoothing, leading to blurred object boundaries.

In contrast, the proposed framework (Figure 4c) produces visually consistent maps with sharp object edges and well-preserved structural integrity. These improvements can be attributed to the complementary modules within our design: the UPS module avoids excessive smoothing by filtering out unreliable pseudo-labels, the ILMR module enhances spatial coherence while reducing pixel-level inconsistencies, and the hybrid tri-training mechanism stabilizes the pseudo-labeling process by integrating diverse classifiers. The combined effect is a clear reduction in salt-and-pepper noise and improved preservation of object boundaries, fully consistent with the quantitative accuracy gains reported in Table 2 and Table 3.

3.

Ablation Study. To assess the individual contributions of the proposed modules—ILMR, UPS, and hybrid tri-training, we conducted a comprehensive ablation study by using QB dataset. The QB dataset was selected due to its complex urban landscape, where salt-and-pepper noise and pixel-level inconsistencies are more pronounced. The following model variants were compared:

• Model1-baseline: A traditional tri-training framework with homogeneous classifiers, without ILMR or UPS, which suffers from unrefined pseudo-labeling and is prone to noise;
• Model2-ILMR only: Incorporating ILMR for spatial regularization, but without UPS, to assess its effect on improving spatial coherence;
• Model3-UPS only: Incorporating UPS for pseudo-label filtering, but without ILMR, to assess its effect on reducing label noise;
• Model4-Full model (Ours): The complete framework integrating both ILMR and UPS, to verify the synergistic effect between the two modules.

In the ablation study, we systematically evaluated the individual and combined effects of the proposed ILMR and UPS modules by constructing four model variants (as shown in

Table 4. The OA and Kappa coefficient achieved by each variant.

Variant	OA (%)	Kappa	Highlights
Model1	82.6	0.76	Easily trapped by boundary noise and fragmented predictions
Model2	85.2	0.81	Improved spatial coherence and patch integrity
Model3	84.3	0.79	Reduced label noise, but residual fragmentation remains
Model4	91.6	0.91	Synergy between spatial and uncertainty modules

). The results demonstrate that the ILMR module significantly enhances spatial consistency by incorporating patch-level descriptors such as compactness and shape index, effectively reducing over-segmentation, particularly in fragmented or ambiguous regions (e.g., small vegetation patches). In contrast, the UPS module improves the reliability of pseudo-labels through uncertainty-aware selection, mitigating label noise propagation, especially near class boundaries. However, it does not fully resolve issues of spatial incoherence. When both modules are integrated into the full framework, the model benefits from the complementary strengths of structural regularization and reliable supervision signals. This synergy leads to more stable convergence, improved boundary delineation, and superior generalization to unlabeled regions. As shown in Figure 4, compared to noisy and fragmented outputs from raw pseudo-labels or single-module configurations, the full model yields cleaner, more coherent, and semantically accurate classification maps.

4.

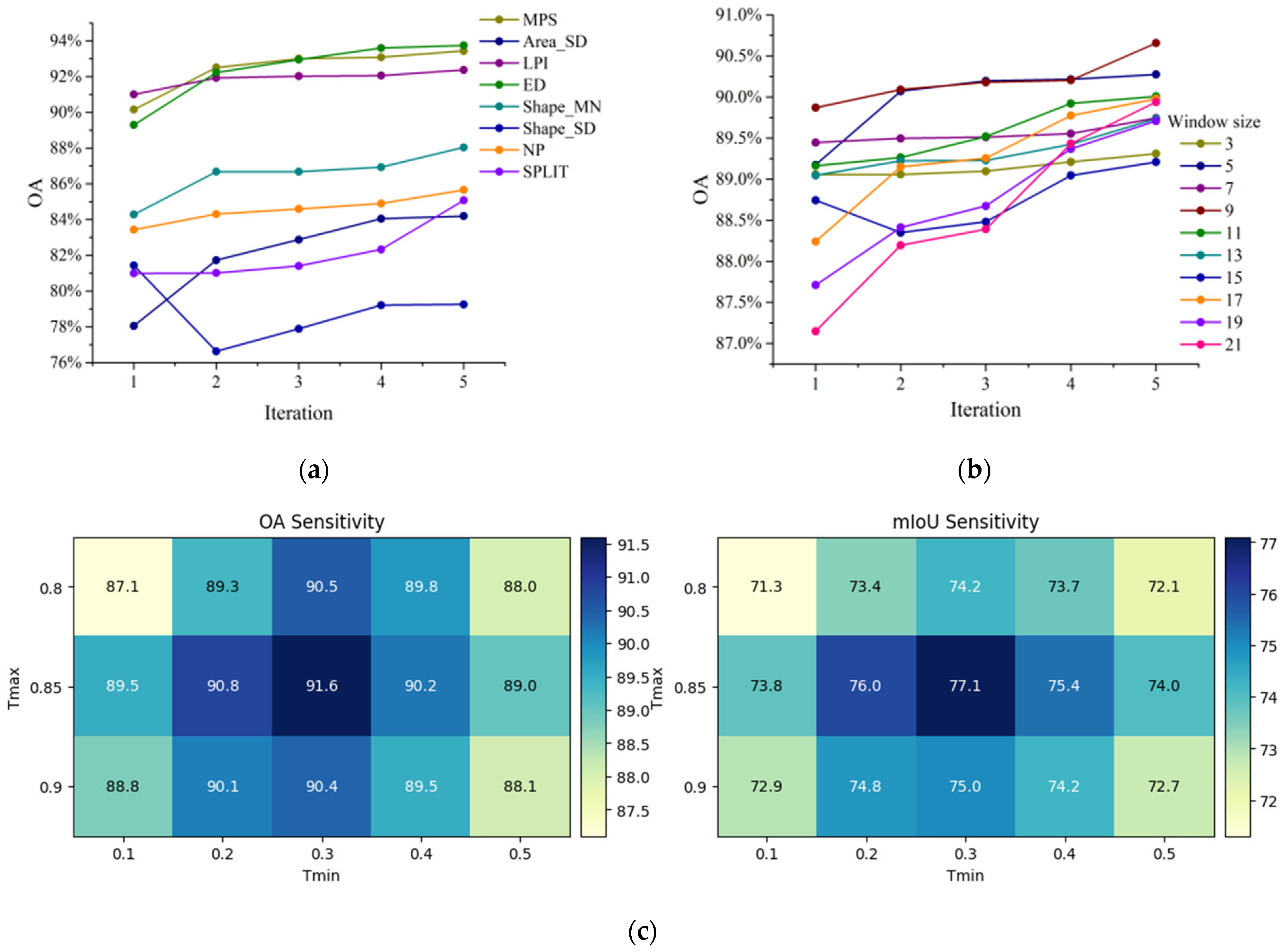
Parameter Sensitivity Analysis. To further assess the robustness and adaptability of the proposed framework, a comprehensive sensitivity analysis was performed on key parameters. As illustrated in Figure 5, this analysis provides deeper insights into the model’s behavior under varying configurations and assists in identifying optimal parameter settings for practical applications. Specifically, eight widely used landscape metrics (as listed in

Table A1. Landscape pattern metrics used for the relearning (for more details, refer to [28]).

Metrics	Formula	Main Content
Mean patch size (MPS)	$\mathrm{MPS}={\displaystyle \frac{{\sum }_{i=1}^n{a}_i}{n}}$	$a_i$ is the area $\left({\mathrm{m}}^2\right)$ of patch i n is the number of patches for class i
Standard deviation of area (AREA_SD)	$\mathrm{AREA}\_\mathrm{SD}=\mathrm{Std}\left({\displaystyle \bigcup _{i=1}^n}{a}_i\right)$	$a_i$ is the area $\left({\mathrm{m}}^2\right)$ of patch i
Largest patch index	$\mathrm{LPI}={\displaystyle \frac{{max}_{i=1}^n\left(a_i\right)}{A}}$	$a_i$ is the area $\left({\mathrm{m}}^2\right)$ of patch i A is the total landscape area (m2)
Edge density (ED)	${\displaystyle \frac{E}{A}}$	E is the total length of edges in the landscape, and A is the total landscape area (m2)
Mean shape index (SHAPE_MN)	${\displaystyle \frac{{\sum }_{i=1}^n\frac{p_i}{2\sqrt{\pi a_i}}}{n}}$	$p_i$ is the perimeter of land-cover patch i, $a_i$ is the area of the land-cover patch, and n is the number of patches within the landscape
Standard deviation of shape index (SHAPE_SD)	$\mathrm{Std}\left({\displaystyle \bigcup _{i=1}^n}{\displaystyle \frac{p_i}{2\sqrt{\pi a_i}}}\right)$	$p_i$ is the perimeter of land-cover patch i, $a_i$ is the area of the land-cover patch, and n is the number of patches within the landscape
Number of patches (NP)	$\mathrm{NP}=n_i$	$n_i$ is the number of patches for class i
Splitting index (SPLIT)	$\mathrm{SPLIT}={\displaystyle \frac{A^2}{{\sum }_{i=1}^n{a_i}^2}}$	$a_i$ is the area $\left({\mathrm{m}}^2\right)$ of patch i A is the total landscape area (m2)

in Appendix A) were evaluated during the relearning-landscape process using the GE-1 dataset, which features representative urban landscape characteristics. Figure 5a presents the classification results obtained by individually incorporating each landscape metric during the relearning stage. The model achieves convergence within 3–4 iterations, indicating efficient adaptation. Among the tested metrics, Edge Density (ED), Largest Patch Index (LPI), and Mean Patch Size (MPS) yielded the highest classification accuracies, highlighting their effectiveness in capturing spatial structural information.

As shown in Figure 5b, the effect of window size on landscape feature computation was evaluated. A window that is too small may fail to capture adequate contextual information, whereas an excessively large window may obscure important local details. Using three representative metrics (MPS, LPI, and ED), the results indicate that a window size of 9 × 9 pixels can provide a favorable balance, enabling accurate and consistent landscape characterization.

Figure 5c shows that the model achieves its best performance when using a moderate combination of $T_{\min }=0.3$ and $T_{\max }=0.85$, reaching an overall accuracy (OA) of 91.6% and a mean Intersection over Union (mIoU) of 77.1%. Specifically, mIoU—a widely used metric in semantic segmentation—quantifies the average overlap between predicted and ground-truth regions across all classes, providing a more comprehensive evaluation of segmentation consistency than OA alone. When $T_{\min }$ is too low (e.g., 0.1), excessive noisy pseudo-labels are introduced; conversely, overly high values (e.g., 0.5) result in limited supervision by excluding informative samples. The model remains relatively robust to $T_{\max }$ variation around 0.85; however, excessively conservative thresholds (e.g., 0.95) may filter out valuable pseudo-labeled data, thereby limiting performance gains.

5.

Computational Efficiency and Practical Implications. We conducted a comprehensive comparative analysis against several state-of-the-art deep learning models, including DeepLabV3+ [37], HRNet [38], and SegFormer [39]. The quantitative results (

Table 5. Comparison of classification accuracy and computational efficiency on the QB dataset (over 5 runs).

Method	OA (%)	Parameters (M)	Training Time (min)	Inference Time (s)
DeepLabV3+	89.21 ± 0.41	39.8	125	18.5
HRNet	90.35 ± 0.35	28.5	138	22.1
SegFormer	91.57 ± 0.30	13.1	115	9.8
Proposed Tri-training	91.62 ± 0.29	1.4	95	3.2

) reveal several notable advantages of our method in terms of computational efficiency.

The proposed framework exhibits exceptional parameter efficiency, with a total complexity of approximately 1.4 million parameters, nearly an order of magnitude lower than standard deep learning models. This lightweight architecture stems from the strategic integration of heterogeneous base learners: the CNN component contributes 0.42 M parameters, the Random Forest ensemble (200 trees) corresponds to approximately 1.0 M parameters, and the LORSAL classifier adds negligible complexity (<0.01 M).

Notably, despite the iterative nature of the tri-training process, our framework demonstrates superior training efficiency, completing in 95 min, which is faster than all compared deep learning baselines. This efficiency arises from the rapid update cycles of the traditional classifiers (RF and LORSAL) combined with the compact CNN architecture. More importantly, for practical deployment, the inference time of 3.2 s represents a substantial improvement, being approximately three times faster than SegFormer and nearly six times faster than HRNet.

These computational advantages are achieved without compromising classification accuracy. Our method maintains competitive performance (91.62% OA) compared to the best pure deep learning model (SegFormer at 91.57% OA), demonstrating an excellent balance between performance and efficiency. This favorable trade-off positions our framework as particularly suitable for large-scale applications or scenarios requiring rapid analysis, especially under constrained computational resources.

5. Conclusions

This study presents a hybrid semi-supervised tri-training framework that integrates traditional classifiers with a lightweight CNN for the classification of HRRS imagery under limited supervision. By introducing two key components (ILMR and UPS) into a tri-training architecture, the proposed method effectively addresses the dual challenges of spatial fragmentation and label noise propagation commonly encountered in HRRS classification tasks.

ILMR enhances spatial coherence by iteratively incorporating landscape-level structural descriptors into the learning process, while UPS ensures the reliability of pseudo-labels by filtering uncertain predictions based on inter-classifier agreement and confidence thresholds. The integration of these modules within a tri-training framework that leverages heterogeneous learners (CNN, RF, and LORSAL) enables complementary feature learning from both spectral and spatial domains.

Extensive experiments conducted on four benchmark datasets (QB, WV-2, GE-1, and ZY-3) demonstrate that the proposed method consistently outperforms state-of-the-art baselines in terms of accuracy, robustness, and spatial consistency. Nevertheless, challenges remain, particularly in relation to the quality of initial samples and the computational burden of the framework. Future efforts should focus on enhancing efficiency and reducing dependency on sample selection to ensure broader applicability. Overall, this framework bridges deep learning and spatial–structural modeling, providing a direction for semi-supervised remote sensing research.