Abstract
This study evaluates the performance of the Precise Point Positioning with Ambiguity Resolution (PPP-AR) method under varying durations and software platforms in determining the optimal placement of Ground Control Points (GCPs) for use in photogrammetric products generated by Unmanned Aerial Vehicles (UAVs) over valley-type rugged terrain. In the field experiment, six GCPs and twenty checkpoints were established, and GNSS measurements with 5-s intervals were collected for 2 h at the GCPs. The collected GNSS data were segmented into 3-min and 10-min intervals, and PPP-AR-based solutions were generated for the complete datasets as well as for the 3- and 10-min subsets. The software tools used for PPP-AR processing included CSRS-PPP, Pride PPP-AR, PPP Arisen, and raPPPid. Eleven photogrammetric models were constructed using the coordinates obtained, and their accuracies were assessed using the checkpoints. The results indicate that, in terms of horizontal accuracy, the best performance was achieved using CSRS-PPP and Pride PPP-AR with 10-min observation durations. The static GNSS method yielded the most precise results for vertical accuracy, while among PPP-AR solutions the 10-min CSRS-PPP application demonstrated superior performance. Additionally, models were generated using only three GCPs placed according to different strategies, revealing that satisfactory levels of accuracy can be achieved when GCPs are strategically positioned. This study demonstrates that the PPP-AR method can be reliably utilized for high-accuracy GCP acquisition within short durations, even in challenging terrain conditions.
1. Introduction
Advancements in Global Navigation Satellite System (GNSS) technologies have significantly improved geodetic surveying techniques and enhanced positional accuracy. Among the widely used GNSS-based positioning techniques, Real-Time Kinematic (RTK) and Continuously Operating Reference Stations (CORS) represent relative positioning methods, whereas Precise Point Positioning (PPP) and Precise Point Positioning with Ambiguity Resolution (PPP-AR) are classified as absolute positioning methods. Each technique presents unique advantages and disadvantages depending on the terrain type. While RTK provides centimeter-level accuracy, its performance is influenced by the distance to the base station, making it more efficient in open areas [1,2,3]. CORS offers similar accuracy across wider areas, but its reliance on infrastructure limits its usability in regions lacking internet access [4]. PPP allows for highly accurate positioning globally without the need for a local base station; however, it requires long convergence times and access to precise satellite orbit data, which limits its effectiveness in real-time applications [5,6]. PPP-AR enhances the PPP method by resolving carrier-phase ambiguities, leading to faster and more reliable positioning [7,8]. This advantage makes PPP-AR particularly suitable in terrains such as valleys, where signal obstructions often degrade the performance of reference station-based methods like RTK and CORS. By relying on global correction services, PPP-AR reduces dependency on local infrastructure and yields more stable results in geographically challenging areas.
Nowadays, UAV-based photogrammetry is widely integrated into geodetic measurement techniques for high-accuracy mapping and modeling [9,10,11]. The positional accuracy of UAV-derived photogrammetric products is directly linked to the GNSS technique used and the accuracy of Ground Control Point (GCP) measurements. GCPs minimize georeferencing errors in aerial imagery and enhance the overall accuracy of photogrammetric processes [12]. Techniques such as RTK, CORS, PPP, and PPP-AR can be employed in GCP measurements to achieve various levels of accuracy. RTK and CORS provide centimeter-level accuracy through local reference stations, whereas PPP and PPP-AR operate with global corrections, reducing reliance on infrastructure but differing processing time [13]. The distribution and measurement methods of GCPs vary based on the terrain. A few well-distributed GCPs may suffice in open and flat areas, while rugged or forested regions may require more GCPs and strategic placement [14]. In regions such as valleys or narrow canyons where GNSS signals weaken, PPP-AR can reduce infrastructure dependency and enhance positioning accuracy.
The primary challenge addressed in this study is achieving high-accuracy positioning in rugged and narrow terrains such as valleys. In such environments, GNSS signals frequently experience interruption or degradation due to topographical constraints, negatively impacting the performance of conventional methods. While RTK and CORS perform well in open terrain, their effectiveness declines in valley-type areas. Research has shown that GNSS signal outages in valleys and narrow passes limit the accuracy of traditional methods [15,16]. In contrast, PPP-AR offers a promising alternative. By utilizing global corrections and resolving carrier-phase ambiguities, PPP-AR ensures high positional accuracy and fast convergence times even in areas with limited signal availability, making it a more suitable choice for constrained environments.
Recent studies have emphasized the potential of the PPP method for accurate positioning in challenging terrains, including valleys and urban canyons. For example, Li et al. [17] integrated LiDAR-based SLAM with PPP to overcome GNSS signal degradation in urban canyon environments, achieving improved positioning accuracy. Similarly, Li et al. [18] highlighted the superiority of PPP-RTK over conventional GNSS methods in signal-obstructed environments. İlçi and Peker [19] demonstrated that real-time kinematic PPP significantly enhances stability and accuracy by minimizing reliance on local infrastructure. Kim et al. [20] found RTK GNSS outperforming standalone GNSS and conventional PPP in obstructed mine sites. Geng et al. [21] also showed that multi-GNSS PPP effectively reduces multipath errors in overlapping signal frequencies, increasing GNSS reliability. Zhang et al. [22] proposed an enhanced vision-aided GNSS positioning method to improve signal accuracy in deep canyons. By utilizing a sky-pointing camera, the method classifies NLOS, LOS, and multipath signals simultaneously and employs an adaptive C/N0 model to further distinguish between them. Kinematic and static experiments demonstrate that the proposed approach significantly outperforms traditional GNSS and vision-aided GNSS methods in 3D positioning accuracy. These findings affirm the suitability of PPP and PPP-AR in mitigating GNSS signal degradation under challenging terrains. Moreover, PPP-AR offers faster convergence and more reliable results in valley environments.
Although various studies above have applied PPP-AR in forested environments, urban canyons, or mining sites, the unique challenges of valley-type terrains, such as abrupt slope transitions, narrow GNSS signal visibility windows, and multipath effects intensified by concave landforms, remain underexplored. Unlike urban canyons where signal loss is more predictable due to building geometry, valleys present non-uniform topographical obstructions that lead to rapidly changing satellite geometry. This study is one of the first to evaluate how short-duration PPP-AR sessions perform under these highly variable signal conditions. By focusing on GCP acquisition with 3- and 10-min observation windows, it introduces an efficiency-oriented approach tailored to constrained environments like valleys—where prolonged measurement durations are often impractical.
This study explores the potential benefits of the PPP-AR method for generating photogrammetric products with high horizontal and vertical accuracy. The goal is to contribute to producing precise geospatial data for applications in planning, engineering, and disaster management, especially in narrow and signal-degraded areas. Understanding the potential of PPP-AR to overcome these challenges is a critical step toward advancing geodetic surveying and mapping. To this end, GCPs and checkpoints were established in a valley terrain, and simultaneous GNSS observations were conducted for two hours at the GCPs. The checkpoints were measured using Network RTK (CORS-TR). A UAV flight was conducted over the region using a DJI Phantom 4, and eleven different photogrammetric models were generated. During block adjustment, coordinates from static GNSS (using complete 2-h data) and PPP-AR techniques (using three- and ten-minute subsets) were used. With four different PPP-AR software platforms employed, a comparative analysis was conducted to identify the optimal measurement duration and software combination for valley-type terrain.
2. Materials and Methods
A valley terrain was selected as the study area, and GCPs along with check points were established throughout the region. Various geodetic surveying methods were employed to determine the coordinates of these points with high accuracy. Subsequently, a UAV flight was conducted over the study area using a DJI Phantom 4 drone, and photogrammetric models were generated based on the coordinates obtained through geodetic processing.
2.1. Study Area Description
The approximate center of the selected study area is located at [38.0117, 32.4979] in decimal degrees, which corresponds to four decimal places and provides sufficient precision for UAV-based mapping. The selected valley area is situated at elevations ranging from approximately 1145 to 1165 m. It features a dry streambed approximately 10 m wide, with the steepest slopes located along the southwest-facing side. The valley’s cross-sections exhibit slopes with a maximum gradient of 35% and an average gradient of 8% (refer to Figure 1). Geographically, the valley is positioned between the road leading to the Ardıçlı Neighborhood and a residential housing complex, situated about 1750 m from the Konya Technical University Campus and 1950 m (as the crow flies) from the Faculty of Engineering and Natural Sciences in Konya, Turkiye.
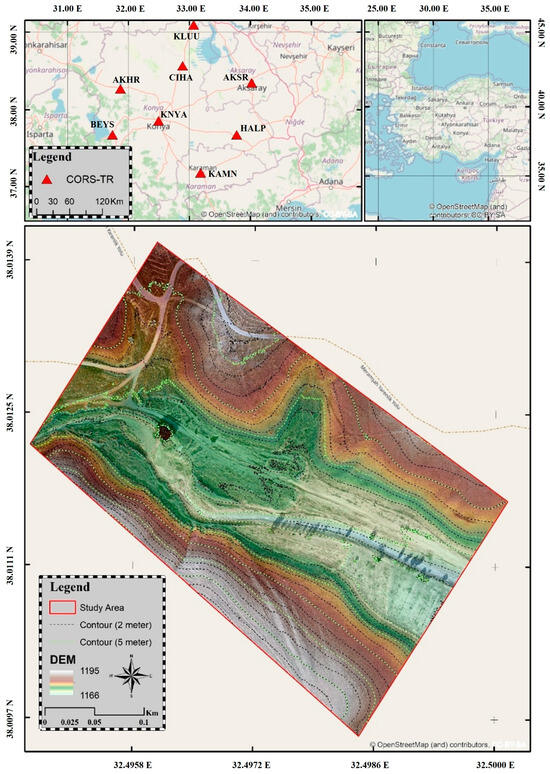
Figure 1.
The IGS stations used in the study.
2.2. Photogrammetric Processes
Photogrammetric imaging acquisitions were conducted using the DJI Phantom 4 Pro UAV with an integrated RGB (Red, Green, Blue) camera. Flight plans were created at a fixed altitude with 80% forward and 70% side overlap. These overlap ratios are critical for producing high-accuracy point clouds and ensuring the geometric integrity of the model. Three separate flight plans were executed, maintaining a ground sampling distance (GSD) of approximately 2 cm. Only nadir images were acquired during the flights, and no oblique imagery was used.
The valley chosen as the study area has a highly variable slope. The study design aimed to prevent potential GNSS receiver signal reception issues in these sloped areas, so an optimized flight plan was created for this region. Due to the topographic features, flight plans were designed to reduce line-of-sight (LOS) constraints along the valley. Flight altitude, image orientation, and overlap ratios were carefully planned to minimize LOS issues. In this context, forward and side overlaps of 80% and 70% were used, and nadir imaging was selected to ensure geometric accuracy. Special care was taken to ensure that the GSD (due to the fixed-altitude flight plan) did not vary significantly. As a result, the flight plan was designed to keep the GSD in the resulting images within a 10% variation. These parameters were chosen after testing different configurations, balancing between image redundancy and coverage efficiency.
Camera calibration parameters were assumed based on factory settings, and the internal orientation parameters were calculated using the self-calibration approach within the photogrammetric block structure. Image processing was carried out using Agisoft Metashape Professional software (v2.1), which included the steps of image alignment, sparse point cloud generation, GCP integration with block adjustment, dense point cloud generation, mesh modeling, and orthomosaic production.
During the photogrammetric block adjustment phase, eleven models were generated using the GCP coordinates determined by different GNSS positioning techniques. Generating eleven models allowed for analyzing how positional accuracy is affected by the GNSS technique and observation duration. The accuracy of each model was evaluated by comparing it to checkpoints measurement obtained through GNSS-based field surveys, and RMSE error analysis was performed.
2.3. Geodetic GNSS Measurements
GNSS data used in this study were collected using high-precision dual-frequency GNSS receivers: Javad Triumph-1 and Topcon Hiper Pro. The technical parameters of Javad Triumph-1 and Topcon Hiper Pro was given in Table 1. Static observation sessions of 2 h were conducted at the ground control points (GCPs), using a 5-s recording interval and a 10° satellite elevation mask. For the checkpoints, 5-epoch measurements were taken using the Network-RTK method. GCP coordinates were determined using both long-term static measurements and the PPP-AR technique through four different software solutions.

Table 1.
The technical parameters of GNSS receivers.
2.3.1. Static GNSS Positioning
The static GNSS technique is a method that provides high positional accuracy through long-term observations. It is based on simultaneous data collection by at least two GNSS receivers placed at fixed locations for a specific period. This enables the calculation of baseline vectors between stations with high precision. For engineering applications, 1–2 h sessions are generally sufficient, while 10–24 h sessions are recommended for regional or global geophysical studies [23]. During the observations, the receivers were fixed and operated continuously.
The static method improves positional accuracy by applying differential GNSS techniques, which help mitigate atmospheric, orbital, and clock errors. In this study, CORS-TR stations in the surrounding area were used as reference points for determining the GCP coordinates, and a geodetic network adjustment was performed based on these reference stations. The baseline distances to reference points were varying between 1.2 km and 263 km. The reference stations were shown in Figure 1, and the GCPs were shown in Figure 2.
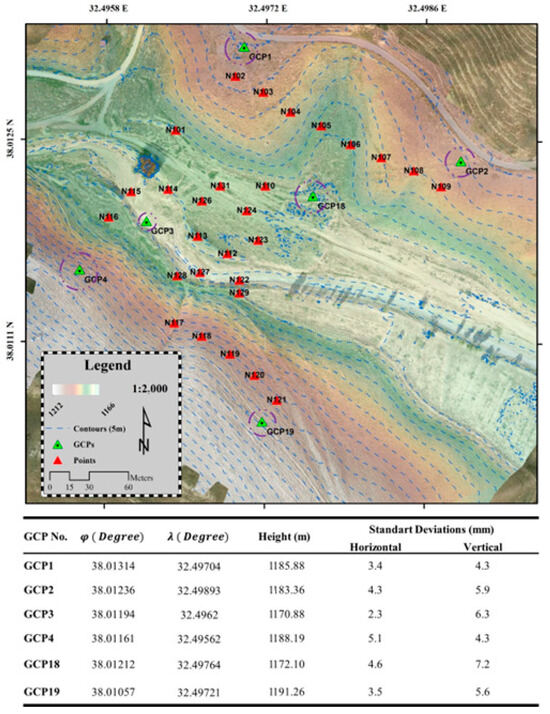
Figure 2.
Distribution of GCPs across the study area with horizontal and vertical errors determined based on the static surveying technique.
2.3.2. PPP-AR Method
The PPP-AR method achieves centimeter-level positioning accuracy by estimating the integer ambiguity of carrier-phase observations [24]. In applying this method, various error sources such as satellite and receiver clock errors, orbital inaccuracies, and ionospheric and tropospheric delays are either modeled with high precision or corrected using external data sources [25]. According to the mathematical model of the method, the ionosphere-free GPS pseudorange and carrier-phase observations can be expressed as follows [26,27,28].
where
and
and are the ionosphere-free pseudorange observation and carrier-phase observation, respectively. Correspondingly, and are the ionosphere-free pseudorange bias at the receiver and the satellite, and are the ionosphere-free combination phase bias at the receiver and the satellite, respectively.
Meanwhile, we have the Melbourne–Wübbena (MW) combination observable as follows:
where and are the wide-lane (WL) wavelength and narrow-lane (NL) wavelength; is the WL ambiguity. The MW combination eliminates ionospheric delay, the geometric distance from the satellite to the receiver, the satellite clock and the receiver clock. It is only affected by multipath, measurement noise, and hardware delays. Since the WL wavelength can reach up to 86 cm, determining the integer ambiguity becomes easier. In other words, the WL ambiguity is resolved using the MW combination . The corresponding receiver-phase bias and satellite-phase bias:
After resolving the WL ambiguity with the MW combination, the equation can be transformed into the ionosphere-free combination equation as follows:
where represents the resolved WL ambiguity; denotes the narrow-lane (NL) ambiguity; and represents the ionosphere-free combined carrier phase observation after resolving the WL ambiguity.
According to the mathematical model defined in Equations (1)–(14), the precise orbit and clock products provided by Wuhan University were used during the data processing phase. Ionospheric delays were mitigated using the double-differencing method in the static assessment and the ionosphere-free approach in the PPP-AR method [29]. For ambiguity resolution, statistical filtering methods correcting phase biases and the Melbourne–Wübbena (MW) combination were employed. Given their widespread use in GNSS data processing, the following software tools were used: CSRS-PPP (v.4), PPP Arisen (v.1), Pride PPP-AR (v.3.1.4), and raPPPid (v.2.3). In Pride PPP-AR, 10-min GNSS sessions were processed, whereas in CSRS-PPP, PPP Arisen, and raPPPid, both 3- and 10-min observation intervals were evaluated, resulting in seven distinct coordinate solutions for the GCPs.
2.3.3. Software Implementations of PPP-AR
In this study, software platforms that offer GNSS data processing capabilities of open-source software such as CSRS-PPP or Pride PPP-AR, as well as robust error modeling and global service integration, were selected. All selected platforms in this study are used for PPP post solution. The general features of the selected platforms are given below.
CSRS-PPP is an online GNSS data processing service developed by the Canadian Geodetic Survey (NRCan). Users can obtain precise positioning information simply by uploading GPS or GNSS observation files. CSRS-PPP performs absolute positioning using IGS and CODE precise orbit and clock data, while also modeling ionospheric and tropospheric delays. Operating in both static and kinematic modes, it is widely used due to its user-friendly interface. Since an update on October 20, 2020, CSRS-PPP supports integer ambiguity resolution [30,31].
PPP Arisen is an advanced GNSS processing software that integrates traditional PPP with ambiguity resolution. By correcting for atmospheric and orbital errors, it enables faster convergence and centimeter-level accuracy using the PPP-AR approach [32]. PPP Arisen is optimized for dynamic applications and supports real-time positioning. It also accommodates multiple GNSS constellations (GPS, GLONASS, Galileo, BeiDou), enabling global high-accuracy positioning.
Pride PPP-AR is a high-accuracy positioning software that utilizes the PPP-AR method with integer ambiguity resolution. By incorporating precise satellite clock and orbit data, it offers faster convergence and more stable positioning than traditional PPP solutions [33]. It is especially effective for long-baseline or remote-area applications and is widely used in academic research and engineering projects.
raPPPid, developed by the Vienna University of Technology (TU Wien), is an open-source software package designed for PPP based on GNSS signals. It processes both single- and multi-frequency GNSS observations and delivers high-precision positioning results. Thanks to its flexible architecture and user-friendly interface, it supports both high-end geodetic receivers and lower-quality data sources such as smartphones. By applying techniques like PPP-AR and ionospheric pseudo-observations, raPPPid aims to shorten convergence times [34]. It is a powerful tool for precise GNSS data processing and improving positioning accuracy. Final IGS sp3 and clock files were used all solutions in this study except for CSRS-PPP. CSRS-PPP benefits from precise satellite orbit and clock corrections provided by International GNSS Service (IGS), Center for orbit Determination in Europe (CODE) and includes robust tropospheric delay modeling, which likely contributed to its superior vertical accuracy.
2.4. Accuracy Assessment and General Workflow
In this study, the differences between the terrain coordinates derived from CORS-TR at the checkpoints and those obtained from the various photogrammetric models were calculated.
In Equation (15), , , denote the coordinates obtained from the photogrammetrically generated 3D model or orthomosaics. , , denote the Network-RTK-based terrarin coordinates. Accuracy analysis was performed to determine the spatial accuracy (horizontal and vertical) of the generated outputs. Root Mean Square Error (RMSE) analysis, which is the most commonly used statistical method in accuracy determination, was preferred:
Then, the horizontal RMSE was calculated using the RMSE values along the y and x axes:
In the study, the question “What was the sequence of the entire process?” can be answered in five steps as shown in Figure 3:
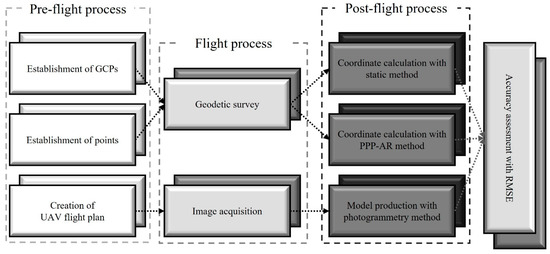
Figure 3.
General workflow diagram of the study.
- GCP and checkpoints establishment,
- GNSS measurement observation,
- Image acquisition with UAV,
- GNSS data processing (PPP-AR and static methods) and
- Photogrammetric model generation and accuracy analysis.
3. Findings and Discussion
In this study, a valley-type terrain was selected, and six GCPs and twenty checkpoints were established to reflect the characteristic features of the terrain. Two-hour static GNSS observations were conducted on the GCPs, and the data were processed using the PPP-AR method as described in Equations (1)–(14) with different software tools, dividing the data into 10-min and 3-min intervals. In standard PPP applications, 10-min session duration was preferred because it is sufficient to obtain a convergent solution [35,36]. In the first stage of the study, block adjustments were made using the coordinates of the six GCPs obtained from eight different scenarios, resulting in eight output products. The coordinates of the checkpoints obtained from these products were read, and the errors were calculated using Equation (15). The method with the best geodetic accuracy was found to be the static measurement method. Therefore, in all the graphs created (Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9) to evaluate the errors calculated using Equation (15), errors from the Static 120 m method are included for reference.
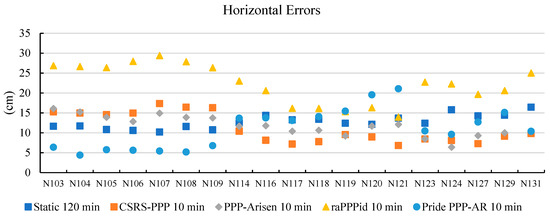
Figure 4.
Horizontal errors for static method and 10-min PPP-AR.
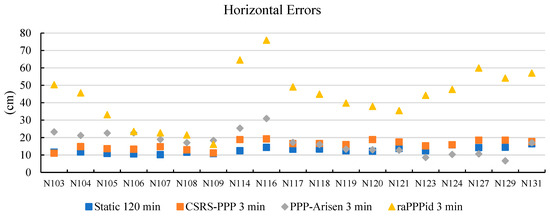
Figure 5.
Horizontal errors for static method and 3-min PPP-AR.
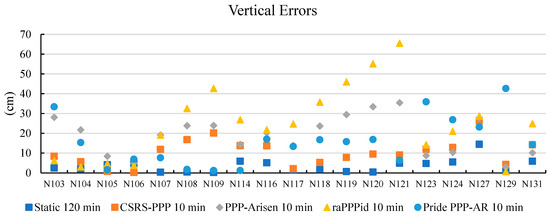
Figure 6.
Vertical errors for static method and 10-min PPP-AR.
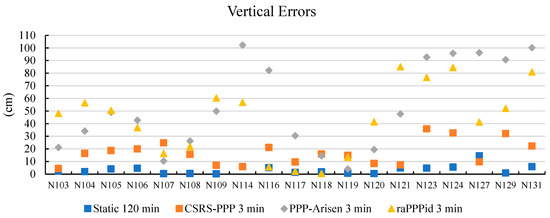
Figure 7.
Vertical errors for static method and 3-min PPP-AR.
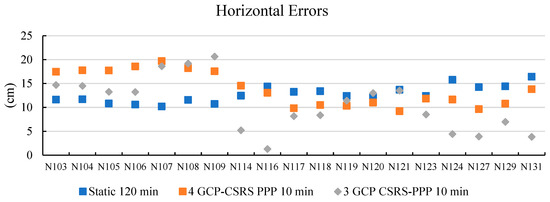
Figure 8.
Horizontal errors of models adjusted with static methof, 4 GCP, and 3 GCP coordinates.
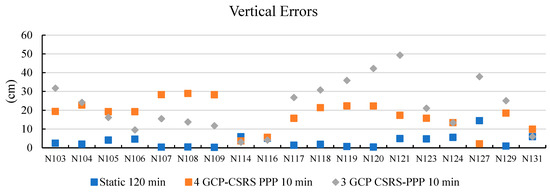
Figure 9.
Vertical errors of models adjusted with static method, 4 GCP, and 3 GCP coordinates.
Figure 4 shows the horizontal positioning errors at the checkpoints. The horizontal positions of points N103, N1404, N105, N106, N107, N108, and N109 could be read with errors ranging from 4.4 to 6.8 cm using the model adjusted with GCPs based on Pride PPP-AR 10-min data. For the same points, the errors were as follows: Static 120 min ranged from 10.2 to 11.6 cm, CSRS-PPP 10 min ranged from 14.6 to 17.3 cm, PPP-Arisen 10 min ranged from 12.8 to 16.1 cm, and raPPPid 10 min ranged from 26.4 to 29.4 cm. For the remaining points, CSRS-PPP 10 min showed the best horizontal positioning accuracy with errors ranging from 7.2 to 10.4 cm. This was followed by PPP-Arisen 10 min with errors between 6.4 and 11.8 cm, Static 120 min with errors from 12.5 to 16.4 cm, Pride PPP-AR 10 min with errors from 9.6 to 21.1 cm, and raPPPid 10 min with errors from 13.9 to 25.0 cm. Some of the results from raPPPid 10 min showed jumps, which are believed to be due to the solution algorithm used by raPPPid. The findings obtained with the 10-min PPP-AR solutions are presented in Figure 3. Bilgen [37] mentioned that the PPP-AR method could converge to a solution in 2.5 min. In UAV operations, minimizing the time spent on terrestrial measurements is desired. Therefore, GCP coordinates were determined using the PPP-AR method with 3-min measurement intervals, and photogrammetric models were generated. The horizontal positioning errors calculated from the coordinates read from these models are given in Figure 5.
According to Figure 5, it can be stated that CSRS-PPP 3 min resulted in errors between 11.0 and 19.2 cm, while Static 120 min resulted in errors between 10.2 and 16.4 cm. The model adjusted with the CSRS-PPP 3 min coordinates provides the accuracy closest to the static measurement method. CSRS-PPP 3 min is followed by PPP-Arisen 3 min with errors ranging from 6.7 to 30.9 cm and raPPPid 3 min with errors ranging from 16.1 to 75.9 cm. Figure 5 shows that the raPPPid-based model mostly gave errors above 30 cm, while other software solutions resulted in errors of 20 cm or below. The findings suggest that using CSRS-PPP or PPP-Arisen software would be more suitable for a 3-min observation duration.
According to Figure 6, the vertical error for Static 120 min ranges from 0.2 to 14.5 cm. The point heights obtained from the CSRS-PPP 10 min-based model showed vertical errors between 0.2 and 26.2 cm, PPP-Arisen 10 min between 2.9 and 35.5 cm, Pride PPP-AR 10 min between 1.2 and 42.6 cm, and raPPPid 10 min between 0.6 and 65.5 cm. Except for the Static method and CSRS-PPP, the other software solutions generally caused errors above 20 cm. Regarding vertical errors, CSRS-PPP is the best software for the PPP-AR method with a 10-min observation duration.
In UAV operations, the time spent on terrestrial measurements is desired to be as short as possible, so vertical errors were analyzed using 3-min measurements. Figure 7 shows that CSRS-PPP 3 min provided the closest accuracy to the Static method. The vertical errors for CSRS-PPP 3 min ranged from 4.4 to 35.9 cm. In comparison, PPP-Arisen 3 min and raPPPid 3 min typically showed errors above 30 cm. Vertical errors approaching nearly 1 m were observed in PPP-Arisen and raPPPid software. After these analyses, a second phase of the study was conducted to investigate the impact of the number of GCPs and whether GCPs were located at critical topographic points (such as valleys and ridges) on the model. Makineci et al. [26] suggested that four GCPs at the model’s corners provided ideal accuracy. In this study, it was determined that CSRS-PPP 10 min yielded the best results in terms of both horizontal and vertical errors. Therefore, in the second phase, two additional topographic models were generated with GCPs selected at four corners and three GCPs selected at two corners and one inside valley section. The coordinates of the GCPs were determined using CSRS-PPP software with 10-min measurements and were used in the block adjustment process.
Figure 8 shows the horizontal errors of the two models mentioned and the Static method. The horizontal errors of the 4 GCP-CSRS PPP 10 min model ranged from 9.2 to 19.7 cm, while the horizontal errors of the 3 GCP-CSRS PPP 10 min model ranged from 1.3 to 20.7 cm. In the model generated with three GCPs, horizontal errors were found to be less than 8.5 cm at points N114, N116, N117, N118, N123, N124, N127, N129, and N131, which are close to the GCPs used in the adjustment.
The results obtained from the 120-min static observations indicate a precision level of approximately 10–20 cm. This level of accuracy is not sufficient for high-precision engineering or cadastral surveying, which generally require centimeter or sub-centimeter positioning. However, it can be effectively applied in several geoscientific and environmental domains. For instance, decimeter-level accuracy is adequate for topographic mapping at medium scales (1/5000–1/10,000), monitoring of land subsidence and landslides, hydrological modeling, and geomorphological studies where relative rather than absolute precision is the primary requirement. Furthermore, such accuracy is also acceptable for various environmental monitoring tasks and thematic mapping applications that do not demand fine-scale detail.
Figure 9 shows the vertical errors of models adjusted with 4 GCPs, 3 GCPs, and the Static method. The vertical errors of the 4 GCP-CSRS PPP 10 min model range from 2.2 to 28.9 cm, while the vertical errors of the 3 GCP-CSRS PPP 10 min model range from 3.0 to 49.3 cm. The vertical errors closest to the Static method were observed at points N114 and N116. At N114, the vertical error from the 4 GCP model was 3.7 cm, and from the 3 GCP model, it was 3.0 cm. At N116, these values were 5.6 cm and 4.1 cm, respectively. Since these two points are very close to the GCPs used in the model adjustment, their vertical errors are also minimal.
Figure 10 presents box plot diagrams to provide insights into the distribution of horizontal errors obtained by comparing the coordinates read from models generated in different scenarios with the field coordinates. According to Figure 10, the narrowest range of horizontal errors is associated with Static 120 min, and the widest range is attributed to raPPPid 3 min. No outliers were found in any of the scenarios. The average errors of PPP-AR-based models are as follows: 3 GCP CSRS-PPP 10 min, Pride PPP-AR 10 min, CSRS-PPP 10 min, PPP-Arisen 10 min, Static 120 min, 4 GCP CSRS-PPP 10 min, CSRS-PPP 3 min, PPP-Arisen 3 min, raPPPid 10 min, and raPPPid 3 min, with average errors of 10.7, 11.0, 11.1, 11.7, 12.8, 13.9, 15.8, 17.2, 22.3, and 43.3 cm, respectively. The median errors of these models are 11.4, 10.5, 9.6, 11.7, 12.4, 13.1, 16.0, 17.1, 22.7, and 44.9 cm, respectively. Additionally, the horizontal errors in the models appear to follow a normal distribution. When the numerical values of the errors’ means are ordered from smallest to largest, the models based on 3 GCP CSRS-PPP 10 min, Pride PPP-AR 10 min, and CSRS-PPP 10 min occupy in the first quartile. Based on this, it can be concluded that for photogrammetric generation, if GCP coordinates are determined using the PPP-AR method, using a 10-min observation period with either CSRS-PPP or Pride PPP-AR software will provide the ideal horizontal accuracy.
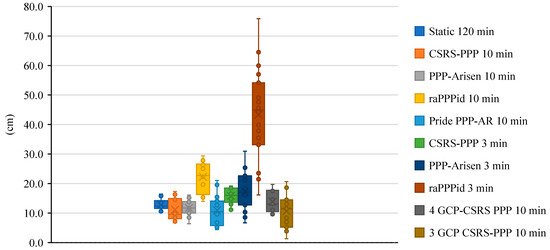
Figure 10.
Box plot diagrams of horizontal errors.
Figure 11 presents the box plot diagrams showing the distribution of vertical errors. According to Figure 11, the narrowest range of vertical errors is associated with Static 120 min, and the widest range is attributed to PPP-Arisen 3 min. In the Static 120 min scenario, one outlier is observed. This may be due to the sudden slope change in the land topography (Figure 2). The average vertical errors for PPP-AR-based models are as follows: Static 120 min, CSRS-PPP 10 min, Pride PPP-AR 10 min, CSRS-PPP 3 min, 4 GCP CSRS-PPP 10 min, PPP-Arisen 10 min, 3 GCP CSRS-PPP 10 min, raPPPid 10 min, raPPPid 3 min, and PPP-Arisen 3 min, with average errors of 3.5, 10.2, 15.7, 17.0, 17.6, 19.0, 22.0, 25.1, 43.7, and 53.1 cm, respectively. The median errors for these models are 2.4, 9.5, 15.3, 15.9, 19.2, 20.3, 21.0, 24.7, 48.1, and 47.7 cm, respectively. The closeness between the average and median values of the errors suggests that vertical errors follow a normal distribution. When the average errors are ordered from smallest to largest, the models based on Static 120 min, CSRS-PPP 10 min, and Pride PPP-AR 10 min occupy in the first quartile. Based on this, it can be concluded that for photogrammetric production, if GCP coordinates are determined using the PPP-AR method, using a 10-min observation period with either CSRS-PPP or Pride PPP-AR software will provide the best vertical accuracy.
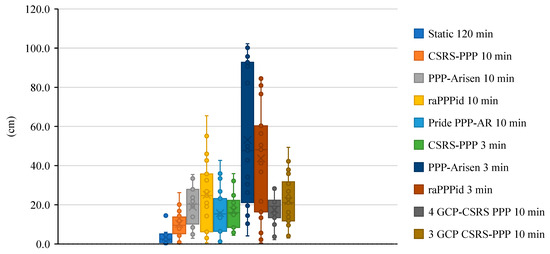
Figure 11.
Box plot diagrams of vertical errors.
As illustrated in Figure 10 and Figure 11, noticeable differences in precision were observed among the evaluated PPP software solutions. These variations can primarily be attributed to the different ambiguity resolution strategies and atmospheric error modeling adopted by each service. For example, CSRS-PPP implements a robust integer ambiguity resolution method combined with high-quality precise orbit and clock corrections, which leads to more stable results in both horizontal and vertical components. In contrast, raPPPid and PPP-Arisen employ distinct algorithms and rely on slightly different datasets for satellite clock and orbit corrections, which may cause larger variations in precision. Moreover, differences in tropospheric modeling and the convergence strategies of each software also contribute to the observed discrepancies. This highlights that the choice of PPP service has a direct impact on the final positioning accuracy, particularly in challenging environments such as narrow valleys.
In the third and final phase of the study, a photogrammetric model was generated without using any GCPs. RMSE values were calculated for all models using Equations (15)–(17), and the results are presented in Table 2 and Table 3. According to Table 2, the horizontal accuracies of the models are as follows: CSRS-PPP 10 min, Pride PPP-AR 10 min, PPP-Arisen 10 min, 3 GCP CSRS-PPP 10 min, Static 120 min, 4 GCP-CSRS PPP 10 min, CSRS-PPP 3 min, PPP-Arisen 3 min, raPPPid 10 min, raPPPid 3 min, and No GCP, with horizontal accuracies of 11.7, 12.0, 12.0, 12.0, 12.9, 14.3, 16.0, 18.2, 22.8, 46.0, and 408.1 cm, respectively.

Table 2.
Comparative horizontal accuracy analysis of photogrammetric models with geodetic measurements.

Table 3.
Comparative vertical accuracy analysis of photogrammetric models with geodetic measurements.
According to Table 3, The vertical accuracies are as follows: Static 120 min, CSRS-PPP 10 min, 4 GCP-CSRS PPP 10 min, CSRS-PPP 3 min, Pride PPP-AR 10 min, PPP-Arisen 10 min, 3 GCP CSRS-PPP 10 min, raPPPid 10 min, raPPPid 3 min, PPP-Arisen 3 min, and No GCP, with vertical accuracies of 4.8, 12.1, 19.2, 19.3, 19.7, 21.2, 25.6, 30.7, 51.4, 63.0, and 449.7 cm, respectively. The model created using CSRS-PPP 10 min for block adjustment (Model 2) provides the best horizontal accuracy (11.7 cm), while the model adjusted using Static 120 min provides the best vertical accuracy. Model 11, created without using any GCPs, has the worst accuracy for both horizontal and vertical directions. Proposing a new approach for GNSS positioning in canyons, Zhang et al. [22] achieved less than 10 m RMSE in all three directions in the kinematic experiment and achieved horizontal and vertical accuracy improvements of 41.20% and 40.28%, respectively. In the static experiment, 3D positioning RMSEs were reduced by 4.81 m and 2.36 m, respectively. In Table 2 and Table 3, mostly better results were obtained compared to Zhang et al. [22].
As shown in Table 2, the vertical accuracy achieved in this study is at the decimeter level. This accuracy is not sufficient for engineering surveying, cadastral mapping, or large-scale construction projects, where centimeter-level precision is mandatory. However, it is still valuable for a wide range of applications. Decimeter-level vertical accuracy is acceptable for generating digital elevation models (DEMs) at medium mapping scales (1/5000–1/10,000), hydrological and watershed analysis, geomorphological studies, and environmental monitoring projects such as flood risk assessment and landform evolution analysis. In such cases, the achieved precision provides reliable and cost-effective results without the need for more resource-intensive high-precision GNSS techniques.
4. Conclusions
The observed variability in model accuracy across different PPP-AR software tools highlights the influence of algorithmic architecture, error modeling capacity, and external data integration strategies. For instance, CSRS-PPP benefits from precise satellite orbit and clock corrections provided by International GNSS Service (IGS), Center for orbit Determination in Europe (CODE) and includes robust tropospheric delay modeling, which likely contributed to its superior vertical accuracy. On the other hand, raPPPid’s open-source nature, while offering flexibility, may be limited by its current default ambiguity resolution filters and atmospheric correction models. The differences between closed-box and open-source tools (e.g., raPPPid) further suggest that not only the PPP-AR methodology but also software-specific implementations significantly affect performance. Therefore, this study does not merely compare outcomes but provides practitioner-level guidance on the suitability of each tool for short-duration positioning in obstructed terrains.
This study evaluates the impact of various PPP-AR-based software solutions and observation durations on determining GCP coordinates during the photogrammetric model generation process over valley-type terrain. To this end, GCPs and checkpoints were established within the study area. Synchronous GNSS observations were conducted at the GCPs for two hours and were adjusted using data from eight nearby CORS-TR stations. The checkpoints were measured using the Network RTK method, based on the CORS-TR network. Following a medium-altitude UAV flight using a DJI Phantom 4, photogrammetric products were generated under eleven scenarios. In the block adjustment phase, GCP coordinates were derived from static GNSS observations (2-h duration) and PPP-AR techniques using short observation periods ranging between 3 and 10 min. The following results were obtained:
- Horizontal Accuracy: The most successful results were achieved using CSRS-PPP and Pride PPP-AR with 10-min observation durations. Additionally, in the model generated using only three GCPs (3 GCPs—CSRS-PPP, 10 min), comparable accuracy levels could be achieved when GCPs were strategically positioned.
- Vertical Accuracy: The 120-min static GNSS method achieved the lowest error values. Among PPP-AR methods, CSRS-PPP delivered the best vertical accuracy with a 10-min observation period, while the Pride PPP-AR 10-min model also yielded noteworthy results.
- Short Observation Periods: Although CSRS-PPP and PPP-Arisen produced lower horizontal errors than raPPPid in the 3-min sessions, the vertical accuracy values for this duration generally exceeded acceptable limits. Short observation periods were associated with higher error rates.
- Three-GCP Models: The strategic selection of GCPs at characteristic terrain features (e.g., valley bottoms and ridgelines) significantly influenced model accuracy. Models created with only three GCPs delivered satisfactory horizontal and vertical accuracy, especially at checkpoints located near the GCPs.
- Independence from Local Infrastructure: Since PPP-AR operates using corrections from global networks, it eliminates the need for local reference stations and provides consistent results even in geospatially constrained areas such as valleys.
In conclusion, for projects involving UAV-based mapping over valley-type terrain using PPP-AR for GCP coordinate determination:
- The CSRS-PPP, Pride PPP-AR, and 3 GCP-CSRS-PPP models with 10-min observation durations are recommended for horizontal accuracy.
- For vertical accuracy, the static 120-min method provides the highest precision, while among PPP-AR solutions, the 10-min CSRS-PPP model emerges as the most suitable alternative.
- Although the model without any GCPs produced highly inaccurate results (e.g., horizontal RMSE above 4 m), its inclusion serves to underscore the critical role of ground control in UAV-based photogrammetry. By contrasting this baseline scenario with all GCP-supported models, the study quantitatively demonstrates the minimum threshold of control point integration necessary for usable outputs. Thus, this scenario reinforces the necessity of strategic GCP placement even when using advanced GNSS positioning techniques like PPP-AR.
- While horizontal RMSE values around 10–20 cm may appear acceptable in some cases, their applicability varies based on the scale and precision requirements of the intended cartographic product. For instance, orthophoto generation and topographic maps at scales of 1/5000 or finer typically require horizontal positional accuracies below 10 cm. In contrast, large-scale planning or environmental monitoring applications may tolerate errors up to 20–30 cm. Therefore, the PPP-AR methods evaluated in this study, particularly the 10-min CSRS-PPP and Pride PPP-AR models, appear suitable for medium-precision applications, but may require supplemental correction techniques if intended for high-precision cadastral mapping.
- In contrast to existing literature focusing on PPP-AR in relatively uniform obstructed areas, this study contributes a new dimension by modeling short-term positioning performance in topographically volatile valley environments, where slope, terrain concavity, and satellite geometry interactions create unique GNSS challenges.
Accordingly, optimizing the number of GCPs and the duration of GNSS observations enhances efficiency in field operations by saving time and resources. It ensures the production of photogrammetric models without compromising accuracy. Using decimal degree coordinates and error circles for all GCPs, as in this study, will increase data reproducibility in future work. Such an approach will make UAV mission planning and repeated surveys more straightforward, particularly for long-term monitoring studies. Moreover, adopting fair data principles will improve accessibility and reuse of the datasets by both researchers and practitioners.
Author Contributions
Conceptualization, B.B., H.B.M. and S.B.; methodology, B.B., H.B.M. and S.B.; software, B.B., H.B.M. and S.B.; validation, B.B., H.B.M. and S.B.; formal analysis, B.B., H.B.M. and S.B.; investigation, B.B., H.B.M. and S.B.; resources, B.B., H.B.M. and S.B.; data curation, B.B., H.B.M. and S.B.; writing—original draft preparation, B.B., H.B.M. and S.B.; writing—review and editing, B.B., H.B.M. and S.B.; visualization, B.B., H.B.M. and S.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article; further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CORS | Continuously Operating Reference Stations |
| CSRS-PPP | Canadian Spatial Reference System Precise Point Positioning |
| GCP | Ground control point |
| GNSS | Global navigation satellite system |
| GPS | Global Positioning System |
| IGS | International GNSS Service |
| LiDAR | Light Detection and Ranging |
| MW | Melbourne–Wübbena |
| NL | Narrow-lane |
| NRCan | Natural Resources Canada |
| PPP | Precise point positioning |
| PPP-AR | Precise point positioning with ambiguity resolution |
| PPP-RTK | Precise point positioning-real time kinematic |
| RMSE | Root mean square error |
| RGB | Red, Green, Blue |
| RTK | Real-time kinematic |
| UAV | Unmanned aerial vehicle |
| WL | Wide-lane |
References
- Misra, P.; Enge, P. Global Positioning System: Signals, Measurements, and Performance, 2nd ed.; Ganga-Jamuna Press: Lincoln, NE, USA, 2011. [Google Scholar]
- Boquet, G.; Vilajosana, X.; Martinez, B. Feasibility of Providing High-Precision GNSS Correction Data through Non-Terrestrial Networks. IEEE Trans. Instrum. Meas. 2024, 73, 5503915. [Google Scholar] [CrossRef]
- Liu, R.; Liu, H.; Meng, X.; Li, T.; Hancock, C.M. Detecting GNSS spoofing and Re-localization on UAV based on imagery matching. Meas. Sci. Technol. 2025, 36, 016320. [Google Scholar] [CrossRef]
- Rizos, C.; Janssen, V.; Roberts, C.; Grinter, T. Precise Point Positioning: Is the era of differential GNSS positioning drawing to an end? In Proceedings of the FIG Working Week 2012, Rome, Italy, 6–10 May 2012. [Google Scholar]
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise Point Positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. Solid Earth 1997, 102, 5005–5017. [Google Scholar] [CrossRef]
- Yu, D.; Ji, B.; Liu, Y.; Wu, S.; Li, H.; Bian, S. Performance assessment of RTPPP positioning with SSR corrections and PPP-AR positioning with FCB for multi-GNSS from MADOCA products. Adv. Space Res. 2023, 71, 2924–2937. [Google Scholar] [CrossRef]
- Laurichesse, D.; Mercier, F.; Berthias, J.-P.; Broca, P.; Cerri, L. Integer ambiguity resolution on undifferenced GPS phase measurements and its application to PPP and satellite precise orbit determination. Navigation 2009, 56, 73–149. [Google Scholar] [CrossRef]
- Chi, C.; Zhang, X.; Liu, J.; Sun, Y.; Zhang, Z.; Zhan, X. GICI-LIB: A GNSS/INS/Camera Integrated Navigation Library. IEEE Robot. Autom. Lett. 2023, 8, 7970–7977. [Google Scholar] [CrossRef]
- Li, N.; Qiu, H.; Zhai, H.; Chen, Y.; Wang, J. Monitoring and Analysis of Slope Geological Hazards Based on UAV Images. Appl. Sci. 2025, 15, 5482. [Google Scholar] [CrossRef]
- Wang, L.; Wang, X.; Su, X.; Wen, S.; Wang, X.; Meng, Q.; Jiang, L. High-Resolution Mapping and Biomass Estimation of Suaeda salsa in Coastal Wetlands Using UAV Visible-Light Imagery and Hue Angle Inversion. Appl. Sci. 2025, 15, 7423. [Google Scholar] [CrossRef]
- Christofi, D.; Mettas, C.; Evagorou, E.; Stylianou, N.; Eliades, M.; Theocharidis, C.; Chatzipavlis, A.; Hasiotis, T.; Hadjimitsis, D. A Review of Open Remote Sensing Data with GIS, AI, and UAV Support for Shoreline Detection and Coastal Erosion Monitoring. Appl. Sci. 2025, 15, 4771. [Google Scholar] [CrossRef]
- Stott, E.; Williams, R.D.; Hoey, T.B. Ground Control Point Distribution for Accurate Kilometre-Scale Topographic Mapping Using an RTK-GNSS Unmanned Aerial Vehicle and SfM Photogrammetry. Drones 2020, 4, 55. [Google Scholar] [CrossRef]
- Yeh, M.L.; Chou, Y.T.; Yang, L.S. The Evaluation of GPS techniques for UAV-based Photogrammetry in Urban Area. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 1079–1084. [Google Scholar] [CrossRef]
- Zhong, H.; Duan, Y.; Tao, P.; Zhang, Z. Influence of ground control point reliability and distribution on UAV photogrammetric 3D mapping accuracy. Geo-Spat. Inf. Sci. 2025, 1–21. [Google Scholar] [CrossRef]
- Konakoglu, B.; Yilmaz, V. Evaluating the Performance of the Static PPP-AR in a Forest Environment. J. Surv. Eng. 2023, 150, 05023006. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, Y.; Shan, S.; Wang, Q.; Li, M.; Han, F.; Duan, X. An enhanced GNSS/INS navigation compensation method using LSTM-FPN for bridging GNSS outages. Meas. Sci. Technol. 2025, 36, 016339. [Google Scholar] [CrossRef]
- Li, T.; Pei, L.; Xiang, Y.; Wu, Q.; Xia, S.; Tao, L. P3-LOAM: PPP/LiDAR loosely coupled SLAM with accurate covariance estimation and robust RAIM in urban canyon environment. IEEE Sens. J. 2021, 21, 6660–6671. [Google Scholar] [CrossRef]
- Li, X.; Li, X.; Huang, J.; Shen, Z.; Wang, B.; Yuan, Y.; Zhang, K. Improving PPP–RTK in urban environment by tightly coupled integration of GNSS and INS. J. Geod. 2021, 95, 132. [Google Scholar] [CrossRef]
- İlçi, V.; Peker, A.U. The kinematic performance of real-time PPP services in challenging environment. Measurement 2022, 189, 110434. [Google Scholar] [CrossRef]
- Kim, H.; Hyun, C.-U.; Park, H.-D.; Cha, J. Image Mapping Accuracy Evaluation Using UAV with Standalone, Differential (RTK), and PPP GNSS Positioning Techniques in an Abandoned Mine Site. Sensors 2023, 23, 5858. [Google Scholar] [CrossRef]
- Geng, J.; Zhang, H.; Li, G.; Aoki, Y. Multipath mitigation for GPS/Galileo/BDS-3 precise point positioning with overlap-frequency signals. Satell. Navig. 2024, 5, 22. [Google Scholar] [CrossRef]
- Zhang, Z.; Yu, Y.; Li, X.; He, X. Reliable GNSS positioning and navigation with simultaneous multipath and NLOS mitigation by using camera and C/N0 at deep canyons. Meas. Sci. Technol. 2025, 36, 046308. [Google Scholar] [CrossRef]
- Bilgen, B.; Inal, C.; Bulbul, S. The Effect of Session Duration in Determination of Point Movements with GNSS. In Proceedings of the FIG Congress 2018, Istanbul, Türkiye, 6–11 May 2018. [Google Scholar]
- Liu, Y.; Hugentobler, U.; Duan, B. Improving Performance of Uncombined PPP-AR Model with Ambiguity Constraints. Remote Sens. 2024, 16, 4537. [Google Scholar] [CrossRef]
- Li, F.; Pan, C.; Li, Q.; Yang, J.; Gao, J.; Psimoulis, P.; Niu, L.; Kou, X.; Meng, X. An ambiguity subset selection algorithm based on the variation of check factors for BDS-3/BDS-2/GPS precise point positioning. GPS Solut. 2025, 29, 41. [Google Scholar] [CrossRef]
- Makineci, H.B.; Bilgen, B.; Bulbul, S. A New Precise Point Positioning with Ambiguity Resolution (PPP-AR) Approach for Ground Control Point Positioning for Photogrammetric Generation with Unmanned Aerial Vehicles. Drones 2024, 8, 456. [Google Scholar] [CrossRef]
- Geng, J.; Chen, X.; Pan, Y.; Zhao, Q. A modified phase clock/bias model to improve PPP ambiguity resolution at Wuhan University. J. Geod. 2019, 93, 2053–2067. [Google Scholar] [CrossRef]
- Loyer, S.; Perosanz, F.; Mercier, F.; Capdeville, H.; Marty, J.-C. Zero-difference GPS ambiguity resolution at CNES–CLS IGS Analysis Center. J. Geod. 2012, 86, 991–1003. [Google Scholar] [CrossRef]
- Naciri, N.; Bisnath, S.; Wübbena, G.; Wübbena, J.; Schmitz, M.; Vaclavovic, P.; Capua, R. GNSS PPP-AR utilizing local SSR corrections. GPS Solut. 2024, 28, 211. [Google Scholar] [CrossRef]
- Bilgen, B.; Bulbul, S.; Inal, C. Statistical Comparison on Accuracies of Web-Based Online PPP Services. J. Surv. Eng. 2022, 148, 04022009. [Google Scholar] [CrossRef]
- Bulbul, S.; Inal, C.; Bilgen, B. The Effect of Seasonal Changes on Precise Point Positioning. Konya J. Eng. Sci. 2022, 10, 274–286. [Google Scholar] [CrossRef]
- Zhang, C.; Guo, A.; Ni, S.; Xiao, G.; Xu, H. PPP-ARISEN: An open-source precise point positioning software with ambiguity resolution for interdisciplinary research of seismology, geodesy and geodynamics. GPS Solut. 2023, 27, 45. [Google Scholar] [CrossRef]
- Geng, J.; Chen, X.; Pan, Y.; Mao, S.; Li, C.; Zhou, J.; Zhang, K. PRIDE PPP-AR: An open-source software for GPS PPP ambiguity resolution. GPS Solut. 2019, 23, 91. [Google Scholar] [CrossRef]
- Glaner, M.F.; Weber, R. An open-source software package for Precise Point Positioning: raPPPid. GPS Solut. 2023, 27, 174. [Google Scholar] [CrossRef]
- Bulbul, S.; Bilgen, B.; Inal, C. The performance assessment of Precise Point Positioning (PPP) under various observation conditions. Measurement 2021, 171, 108780. [Google Scholar] [CrossRef]
- Bilgen, B.; Bulbul, S.; Makineci, H.B.M. Ground Control Points Positioning with PPP-AR Method for UAV-Based Block Adjustment; IntechOpen: London, UK, 2025. [Google Scholar] [CrossRef]
- Bilgen, B. Optimizing PPP-AR with BDS-3 and GPS: Positioning Performance Across Diverse Geographical Regions Under Mostly Quiet Space Weather Conditions. Atmosphere 2025, 16, 288. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

