Interval Type-II Fuzzy Broad Model Predictive Control Based on the Static and Dynamic Hybrid Event-Triggering Mechanism and Adaptive Compensation for Furnace Temperature in the MSWI Process
Abstract
1. Introduction
- (1)
- The FT prediction model based on IT2FBLS is proposed to obtain the IT2FB-MPC method, and an online learning algorithm is used to adapt it to the actual operating condition fluctuations.
- (2)
- SW technology was used to obtain historical error information (HEI) in real time, constructing the HEI-DETM method, which is combined with SETM to form the SDHETM method to prevent the system from false or non-triggering.
- (3)
- The adaptive compensation optimization control (ACOC) algorithm based on adaptive compensation control law (ACL) and rolling optimization control law (ROL) can compensate for the influence of ETM and disturbance on the control effect, and improve the control performance.
- (4)
- The convergence and stability of IT2FBLS and SDHETM-IT2FB-ACMPC were theoretically analyzed, and experimental verification based on actual operation data was also conducted.
2. Problem Formulation
2.1. Overview and Characteristic Analysis of the MSWI Process in Terms of FT Control
2.2. Model Predictive Control
3. Methods
3.1. Method Strategy
- (1)
- IT2FBLS prediction model. The input of this module is the manipulated variable (SV), disturbance variable (PV, FS, DS, AI) and controlled variable (FT) in a past period of time, and the output is the predicted value of the controlled variable in a future period of time (determined by the prediction horizon). This module consists of three parts. Firstly, the IT2FBLS model itself, which is also the core part of the module, is used to calculate the predicted output at future moments based on the obtained historical information. Secondly, the online learning algorithm, which calculates the difference between the predicted output and the expected output and uses the gradient descent method to update the model parameters in real time, thereby avoiding model mismatch. Finally, the prediction error correction, which is specifically proposed for model predictive control, is used to compensate for the prediction sequence with the error of the first item of the prediction sequence, thereby avoiding excessive errors from affecting the actual control effect.
- (2)
- ACOC algorithm. The input of this module is the error sequence between the compensated prediction sequence and the setpoint value, and the output is the optimal value of the manipulated variable for a future period of time (determined by the control horizon). This module consists of two parts, ROL and ACL. Specifically, the function of ROL is to minimize the objective function based on the existing prediction information, thereby iteratively optimizing the manipulated variable. The function of ACL is to adaptively adjust its size according to the actual control error, thereby compensating for ROL and avoiding the control system being affected by external disturbances.
- (3)
- SDHETM algorithm. This module uses the design of four triggering events to control the update of manipulated variables. If the system meets a certain triggering event at a certain moment, the optimal value of the manipulated variable is solved through the ACOC algorithm. This process can effectively avoid unnecessary updates of the manipulated variable and ensure that the controlled variable always remains close to the setpoint value.
3.2. Method Implementation
3.2.1. Interval Type-2 Fuzzy Broad Learning System (IT2FBLS) Predictive Model
Pre-Training Based on Historical Data
Online Learning Based on Real-Time Data
Predictive Error Compensation
3.2.2. Adaptive Compensation Optimization Control (ACOC)
Rolling Optimization Control Law (ROL)
Adaptive Compensation Control Law (ACL)
3.2.3. Static and Dynamic Hybrid Event-Triggering Mechanism (SDHETM)
SETM (ETM-1)
HEI-DETM (ETM-2)
3.2.4. Convergence and Stability Analysis
IT2FBLS Convergence
SDHETM-IT2FB-ACMPC Stability
- (1)
- The control error of SDHETM-IT2FB-ACMPC is bounded at any time, and it satisfies Equation (33).
- (2)
- The range of values available for the prediction horizon is sufficiently large, and the weighting factors of the objective function Equation (28) are time-invariant parameters.
- (3)
- The set threshold of the second trigger condition, Equation (39), is a positive real number with reasonable values.
4. Results and Discussion
4.1. Evaluation Indicators
4.2. Dataset Description
4.3. Prediction Model Experimental Results
- (1)
- BPNN: single output model, the number of inputs is 5, the number of hidden layers is 1, the number of hidden layer neurons is 8, the maximum number of convergences is 3000, the convergence error is 0.001, and the parameter learning rate is 0.005.
- (2)
- FNN: single output model, the number of inputs is 5, the number of fuzzy rules is 20, the parameter learning rate is 0.03, and the updated parameters include: membership function center, membership function width, and consequent connection weights;
- (3)
- IT2FNN: single output model, the number of inputs is 5, the number of fuzzy rules is 20, the upper and lower bound weighting factor is 0.3, the parameter learning rate is 0.01, and the updated parameters include: the upper and lower bounds of the membership function center, the width of the membership function, and the posterior connection weights.
- (4)
- FBLS: single output model, the number of inputs is 5, the number of FNN subsystems is 9, the number of subsystem fuzzy rules is 2, the number of enhancement nodes is 17, and the regularization coefficient is 2 × 10−30.
- (5)
- IT2FBLS: single output model, the number of inputs is 5, the number of FNN subsystems is 20, the number of subsystem fuzzy rules is 2, the number of enhancement nodes is 18, and the regularization coefficient is 2 × 10−30.
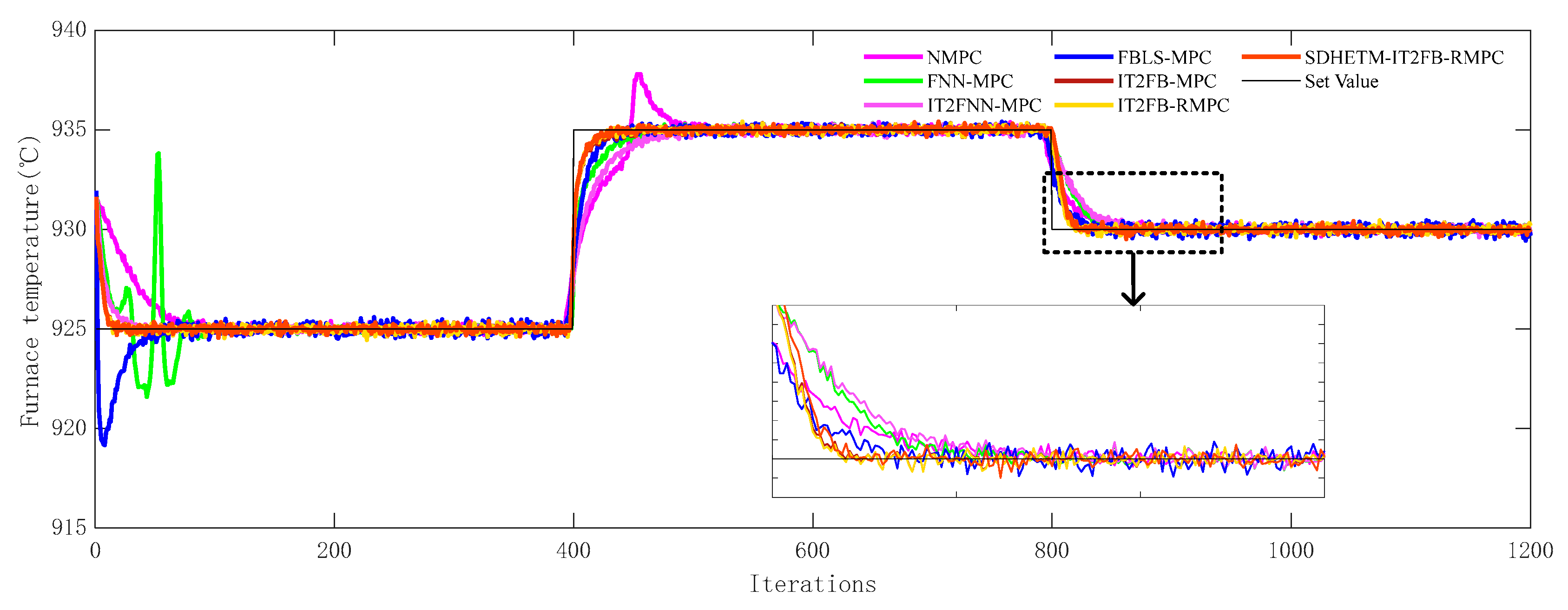
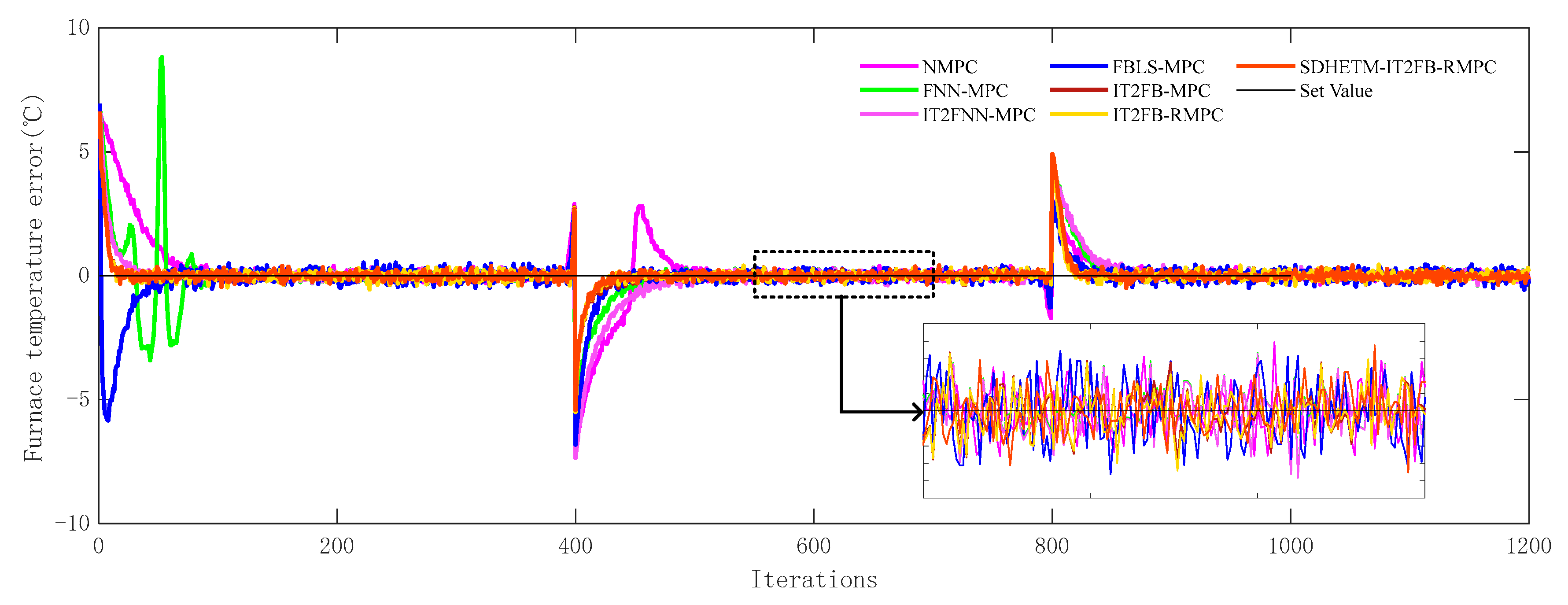
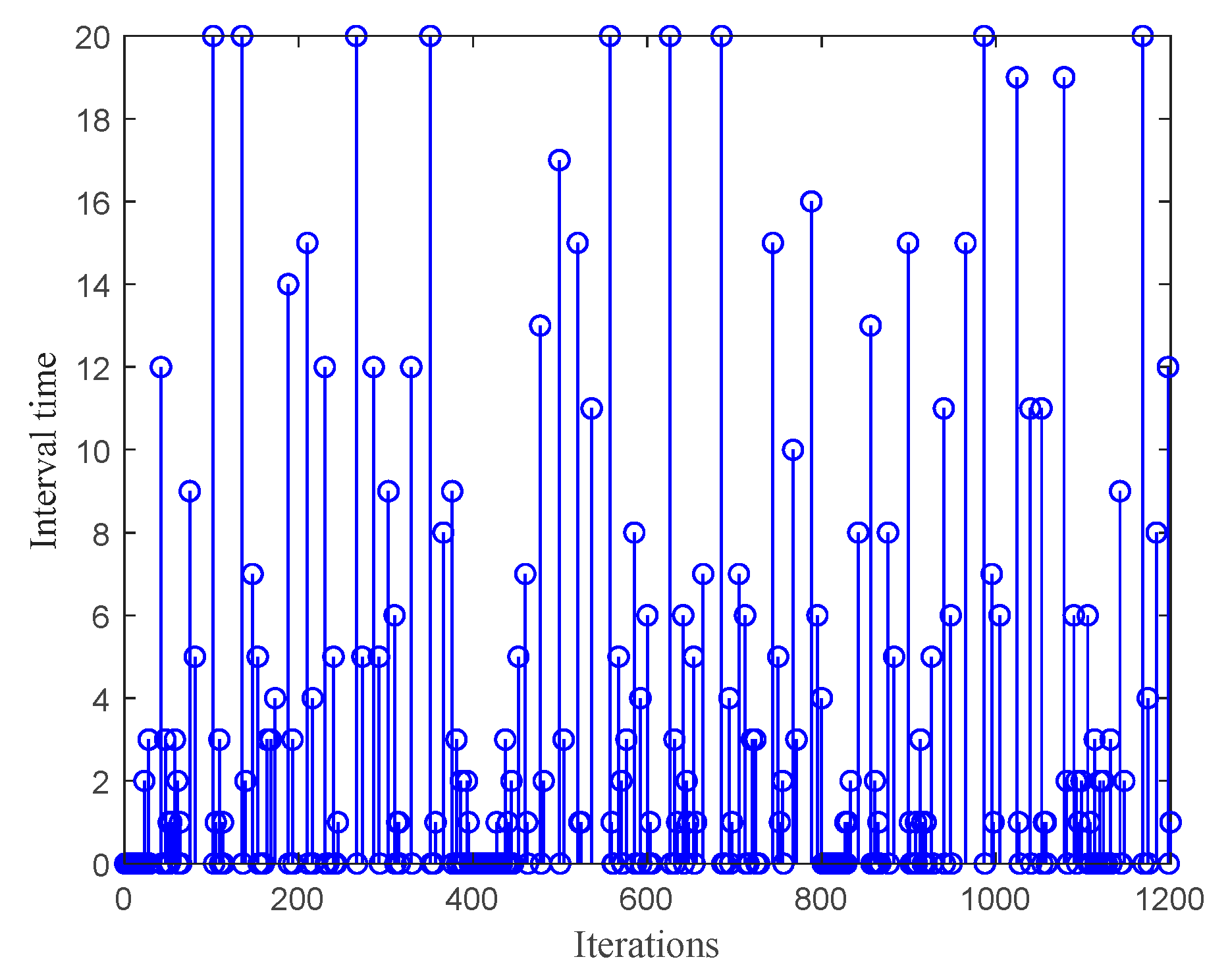
4.4. Tracking Control Experiment Results
- (1)
- SDHETM-IT2FB-ACMPC: The prediction horizon is 3, the control horizon is 1, the window size is 8, the static threshold of Event-1 is 0.25, the static threshold of Event-2 is 20, the upper and lower bounds of the dynamic threshold of Event-3 are [0.002, 0.5], the tight set of BNM is (−10, 10), the rolling optimization learning rate is 0.7, the dynamic threshold of event-3 is 0. The learning rates of the connection weights between the IT2FNN layer, the data input layer, and the prediction output layer are 1 × 10−4, 1 × 10−4 and 1 × 10−7, respectively, and the learning rate of the bias term of the enhancement layer is 1 × 10−7.
- (2)
- SDHETM-IT2FB-MPC: Same as SDHETM-IT2FB-ACMPC without ACOC-related parameters;
- (3)
- IT2FB-ACMPC: Same as SDHETM-IT2FB-ACMPC without SDHETM related parameters;
- (4)
- IT2FB-MPC: Same as SDHETM-IT2FB-ACMPC without ACOC and SDHETM related parameters;
- (5)
- I2T2FB-MPC: the prediction horizon is 3, the control horizon is 1, and the rolling optimization learning rate is 0.7.
- (6)
- LSTM-MPC: the prediction horizon is 6, the control horizon is 1, and the rolling optimization learning rate is 0.3.
- (7)
- FBLS-MPC: the prediction horizon is 6, the control horizon is 1, and the rolling optimization learning rate is 0.3.
- (8)
- IT2FNN-MPC: the prediction horizon is 6, the control horizon is 1, the rolling optimization learning rate is 0.1, the number of fuzzy rules is 20, the upper and lower bound ratio coefficient is 0.3, and the parameter update learning rate is 0.00001.
- (9)
- FNN-MPC: the prediction horizon is 2, the control horizon is 1, the learning rate of rolling optimization is 0.15, the number of fuzzy rules is 20, and the learning rate of parameter update is 0.1.
- (10)
- NMPC: the prediction horizon is 8, the control horizon is 1, and the rolling optimization learning rate is 0.00047.
- (1)
- IT2FBLS-ACN-PID, as one of the advanced FT control methods, has good control performance. However, compared with the method proposed in this article, all the indicators are worse, and it has the highest Devmax, indicating that its ability to handle frequent disturbances (i.e., robustness) still needs to be improved.
- (2)
- Compared with other MPC methods combined with fuzzy logic, the traditional NMPC method has a poor control effect. Only the Devmax values of FNN-MPC and IT2FNN-MPC are slightly higher than those of NMPC. This shows the excellent ability of fuzzy logic to deal with the strong uncertainty of CIP.
- (3)
- LSTM-MPC, as a type of MPC method based on deep neural networks, demonstrates superior control performance and has lower performance indicators. However, compared with MPC methods based on BLS, its performance indicators are worse, and the control performance still needs to be improved.
- (4)
- Compared with other MPC methods, the ISE and IAE of the proposed IT2FB-MPC and its improved method are significantly decreased. It indicates that this kind of controller has stronger robustness and adaptive ability, and can ensure that the FT control is more accurate and effective.
- (5)
- For the IT2FB-MPC and its improved method proposed in this article, Devmax is the same value. The reason may be that when the initial value of each variable and the prediction model are the same, the initial value of the actual FT value is also the same, resulting in the same Devmax value.
- (6)
- I2T2FB-MPC, as one of the advanced methods in the field of IT2FB-MPC, possesses excellent control performance. However, ISE and IAE are still lower than those of IT2FB-ACMPC, indicating that the ACOC algorithm effectively compensates for the impact of frequent disturbances on the controller, successfully enhancing its robustness and control accuracy.
- (7)
- IT2FB-ACMPC has the smallest ISE and IAE values, and Devmax remains unchanged, which indicates that the proposed ACOC algorithm can still eliminate some large error points and improve the overall control effect when ETM is not used to drive the control variable update.
- (8)
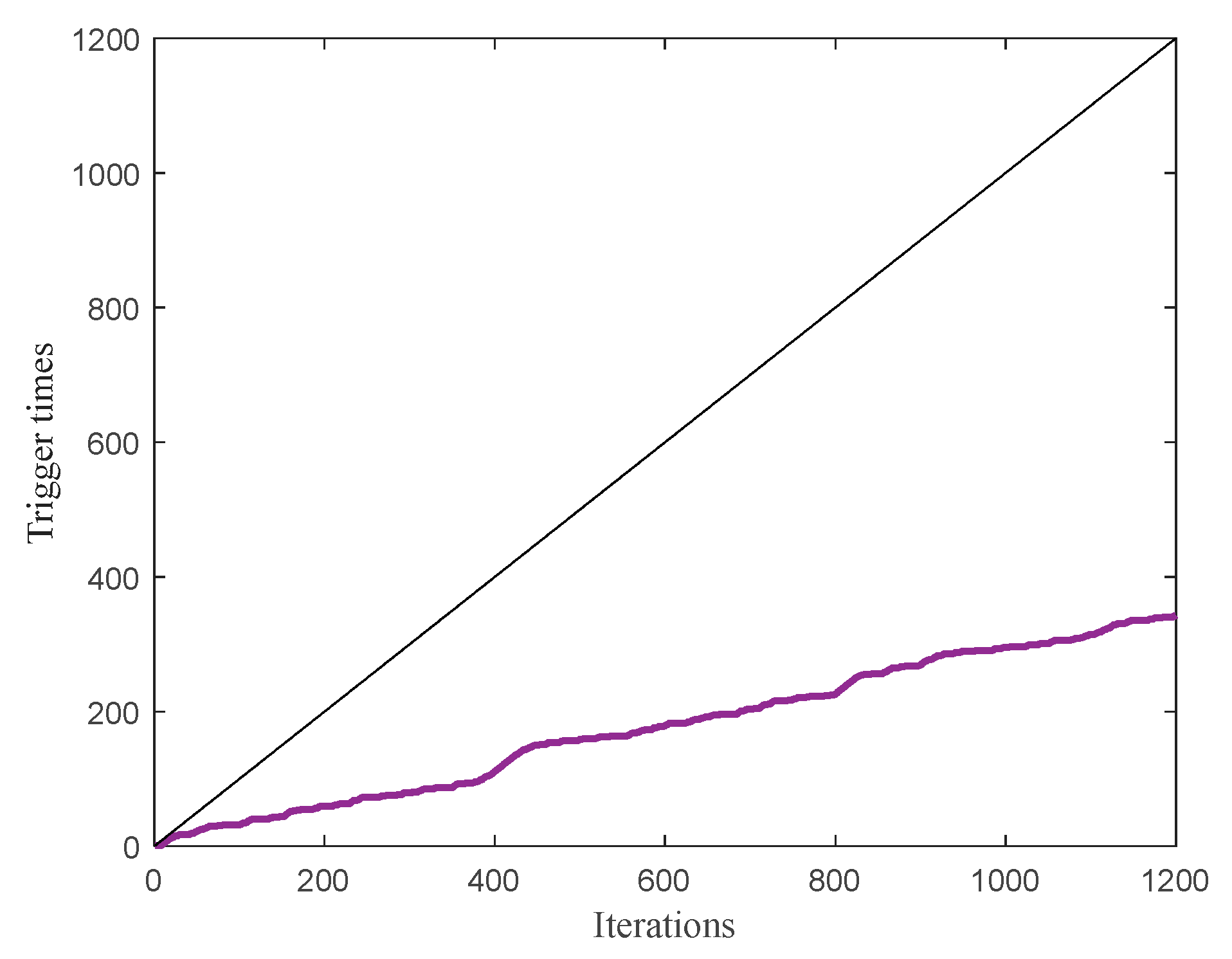
- Compared with IT2FB-MPC, the ISE and IAE of SDHETM-IT2FB-MPC are only increased by about 10.2% and 5%, respectively, Devmax remains unchanged, and the number of triggers is reduced by about 69.2%. This indicates that the proposed SDHETM can not only sacrifice a small part of control performance, but also reduce the trigger times. The proposed method greatly reduces the number of control variable updates and improves the service life of the equipment.
- (9)
- For SDHETM-IT2FB-ACMPC, compared with SDHETM-IT2FB-MPC, the number of triggers is reduced by 27 times, about 7.3%; ISE and IAE are reduced by about 2.8% and 3.7%, respectively, while Devmax remains unchanged. It shows that when ETM is used to drive the control update, the ACL can effectively improve the control effect of IT2FB-MPC, while ensuring that the number of control updates is at a low level.
4.5. Ablation Experiment for SDHETM
- (1)
- For SETM, although performance indicators can be guaranteed not to rise greatly, there is still room for further decline in trigger times. It indicates that the method appropriately increases the update times of control quantities in order to maintain the original control performance. However, this cannot guarantee the maximum extension of the equipment life in the actual control process.
- (2)
- For DETM, although the trigger times are significantly reduced, the corresponding performance indicators are significantly increased. It indicates that these methods sacrifice more control performance to reduce the number of control variable updates. This may affect the stability of the actual control process and cause economic losses.
- (3)
- Compared with other DETMs, the corresponding performance indicators of the HEI-DETM proposed in this article are significantly decreased. Thus, although the number of triggers is slightly increased, the improvement of control performance is more obvious.
- (4)
- Compared with Baseline and other methods, the ISE and IAE values of SDHETM proposed in this article only increase by 9.3% and 2%, respectively, while Devmax remains unchanged. Although the trigger times are the highest value, it is still reduced by 71.4% compared with Baseline, with only 343 trigger times.
| Controller | ISE | IAE | Devmax | Triggering Times |
|---|---|---|---|---|
| IT2FB-ACMPC (Baseline) | 0.2821 | 0.1930 | 6.6269 | 1200 |
| SETM-IT2FB-ACMPC [43] | 0.3178 (↑12.7%) | 0.1980 (↑2.6%) | 6.6269 (---) | 373 (↓68.9%) |
| DETM-IT2FB-ACMPC [30] | 0.3318 (↑17.6%) | 0.2286 (↑18.5%) | 6.6269 (---) | 330 (↓72.5%) |
| HEI-DETM-IT2FB-ACMPC | 0.3093 (↑9.6%) | 0.2049 (↑6.2%) | 6.6269 (---) | 363 (↓69.8%) |
| SDHETM-IT2FB-ACMPC | 0.3084 (↑9.3%) | 0.1969 (↑2%) | 6.6269 (---) | 343 (↓71.4%) |
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Number | Abbreviations | Meanings |
| 1 | MSW | Municipal Solid Waste |
| 2 | MSWI | Municipal Solid Waste Incineration |
| 3 | FT | Furnace Temperature |
| 4 | DDMPC | Data-driven Model Predictive Control |
| 5 | CIP | Complex Industrial Process |
| 6 | ANN | Artificial Neural Network |
| 7 | IT2FNN | Interval Type-II Fuzzy Neural Network |
| 8 | DNN | Deep Neural Network |
| 9 | BLS | Broad Learning System |
| 10 | IT2FBLS | Interval Type-II Fuzzy Broad Learning System |
| 11 | ETM | Event-triggering Mechanism |
| 12 | SETM | Static Event-triggering Mechanism |
| 13 | DETM | Dynamic Event-triggering Mechanism |
| 14 | SW | Sliding Window |
| 15 | SDHETM | Static and Dynamic Hybrid Event-triggering Mechanism |
| 16 | HEI | Historical Error Information |
| 17 | ACL | Adaptive Compensation Control Law |
| 18 | ROL | Rolling Optimization Control Law |
| 19 | ACOC | Adaptive Compensation Optimization Control |
| 20 | PCC | Pearson Correlation Coefficient |
| 21 | PV | Primary Air Volume |
| 22 | SV | Secondary Air Volume |
| 23 | FS | Feeder Even Speed |
| 24 | DS | Drying Grate Even Speed |
| 25 | AI | Ammonia Injection |
| 26 | NARX | Nonlinear Autoregressive Exogenous |
| 27 | BNM | Bounded Nonlinear Mapping |
| 28 | FE | Filtering Error |
| 29 | EFR | Error Fluctuation Ratio |
| 30 | MSE | Mean Square Error |
| 31 | RMSE | Root Mean Square Error |
| 32 | MAE | Mean Absolute Error |
| 33 | R2 | R-squared |
| 34 | ISE | Integral of Squared Error |
| 35 | IAE | Integral of Absolute Error |
| 36 | Devmax | Maximal Deviation from Setpoint |
References
- Gómez-Sanabria, A.; Kiesewetter, G.; Klimont, Z.; Schoepp, W.; Haberl, H. Potential for future reductions of global GHG and air pollutants from circular waste management systems. Nat. Commun. 2022, 13, 106. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.; Zhao, J.; Liu, J.-W.; Zhou, J.; Cheng, L.; Zhao, J.; Shao, Z.; Iris, Ç.; Pan, B.; Li, X.; et al. A review of China’s municipal solid waste (MSW) and comparison with international regions: Management and technologies in treatment and resource utilization. J. Clean. Prod. 2021, 293, 126144. [Google Scholar] [CrossRef]
- Qiao, J.F.; Guo, Z.H.; Tang, J. Dioxin emission concentration measurement approaches for municipal solid wastes incineration process: A survey. Acta Anat. Sin. 2020, 46, 1063–1089. [Google Scholar] [CrossRef]
- Tang, J.; Xia, H.; Yu, W.; Qiao, J.F. Research status and prospects of intelligent optimization control for municipal solid waste incineration process. Acta Anat. Sin. 2023, 49, 2019–2059. [Google Scholar] [CrossRef]
- Yang, D.K.; Kow, K.; Wang, W.L.; Meredith, W.; Zhang, G.L.; Mao, Y.P.; Xu, M.X. Co-treatment of municipal solid waste incineration fly ash and alumina-/silica-containing waste: A critical review. J. Hazard. Mater. 2024, 479, 135677. [Google Scholar] [CrossRef]
- Chuai, X.; Yang, Q.H.; Zhang, T.T.; Zhao, Y.C.; Wang, J.; Zhao, G.D.; Cui, X.Z.; Zhang, Y.L.; Zhang, T.L.; Xiong, Z.; et al. Speciation and leaching characteristics of heavy metals from municipal solid waste incineration fly ash. Fuel 2022, 328, 125338. [Google Scholar] [CrossRef]
- Ding, H.X.; Qiao, J.F.; Huang, W.M.; Yu, T. Event-triggered online learning fuzzy-neural robust control for furnace temperature in municipal solid waste incineration process. IEEE Trans. Autom. Sci. Eng. 2024, 21, 1201–1213. [Google Scholar] [CrossRef]
- Wang, T.Z.; Tang, J.; Xia, H.; Yang, C.L.; Yu, W.; Qiao, J.F. Data-driven multi-objective intelligent optimal control of municipal solid waste incineration process. Eng. Appl. Artif. Intell. 2024, 137A, 109157. [Google Scholar] [CrossRef]
- Shen, K.; Lu, J.D.; Li, Z.H.; Liu, G. An adaptive fuzzy approach for the incineration temperature control process. Fuel 2005, 84, 1144–1150. [Google Scholar] [CrossRef]
- Tian, H.; Tang, J.; Xia, H.; Yu, W.; Qiao, J.F. Bayesian optimization-based interval type-2 fuzzy neural network for furnace temperature control. IEEE Trans. Ind. Inf. 2025, 21, 505–514. [Google Scholar] [CrossRef]
- Wang, B.K.; Tang, J.; Xia, H.; Tian, H.; Wang, T.Z.; Wu, Z.W. Furnace Temperature Control for MSWI Process Based on Neural Network Predictive Controller. In Proceedings of the 2024 36th Chinese Control and Decision Conference (CCDC), Xi’an, China, 25–27 May 2024; pp. 1731–1736. [Google Scholar] [CrossRef]
- Hu, K.C.; Yan, A.J.; Wang, D.H. Nonlinear model predictive control of furnace temperature for a municipal solid waste incineration process. Control Theory Appl. 2024, 41, 2023–2032. [Google Scholar] [CrossRef]
- Liu, M.; Sun, Z.Q.; Hu, R.; Xia, Y.Q. Safety enhancement for nonlinear systems via learning-based model predictive control with Gaussian process regression. Neurocomputing 2024, 591, 127706. [Google Scholar] [CrossRef]
- Smarra, F.; Jain, A.; Rubeis, T.; Ambrosini, D.; D’Innocenzo, A.; Mangharam, R. Data-driven model predictive control using random forests for building energy optimization and climate control. Appl. Energy 2018, 226, 1252–1272. [Google Scholar] [CrossRef]
- Han, H.G.; Qiao, J.F.; Chen, Q.L. Model predictive control of dissolved oxygen concentration based on a self-organizing RBF neural network. Control Eng. Pract. 2012, 20, 465–476. [Google Scholar] [CrossRef]
- Fei, J.T.; Liu, L.H.J. Real-time nonlinear model predictive control of active power filter using self-feedback recurrent fuzzy neural network estimator. IEEE Trans. Ind. Electron. 2022, 69, 8366–8376. [Google Scholar] [CrossRef]
- Xie, S.W.; Xie, Y.F.; Huang, T.W.; Gui, W.H.; Yang, C.H. Generalized predictive control for industrial processes based on neuron adaptive splitting and merging RBF neural network. IEEE Trans. Ind. Electron. 2019, 66, 1192–1202. [Google Scholar] [CrossRef]
- Liu, X.; Zhao, T.Y.; Cao, J.T.; Li, P. Design of an interval type-2 fuzzy neural network sliding mode robust controller for higher stability of magnetic spacecraft attitude control. ISA Trans. 2023, 137, 144–159. [Google Scholar] [CrossRef]
- Tafti, B.; Teshnehlab, M.; Ahmadieh, M.K. Recurrent interval type-2 fuzzy wavelet neural network with stable learning algorithm: Application to model-based predictive control. Int. J. Fuzzy Syst. 2020, 22, 351–367. [Google Scholar] [CrossRef]
- Wang, M.X.; Wang, Y.F.; Chen, G. Interval type-2 fuzzy neural network based constrained GPC for NH3 flow in SCR de-NOx process. Neural. Comput. Appl. 2021, 33, 16057–16078. [Google Scholar] [CrossRef]
- Huang, K.K.; Wei, K.; Li, F.B.; Yang, C.H.; Gui, W.H. LSTM-MPC: A Deep Learning Based Predictive Control Method for Multimode Process Control. IEEE Trans. Ind. Electron. 2023, 70, 11544–11554. [Google Scholar] [CrossRef]
- Wang, G.M.; Jia, Q.S.; Qiao, J.F.; Bi, J.; Zhou, M.C. Deep Learning-Based Model Predictive Control for Continuous Stirred-Tank Reactor System. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 3643–3652. [Google Scholar] [CrossRef]
- Chen, C.L.P.; Liu, Z.L. Broad Learning System: An Effective and Efficient Incremental Learning System Without the Need for Deep Architecture. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 10–24. [Google Scholar] [CrossRef] [PubMed]
- Han, H.G.; Liu, Z.; Liu, H.X.; Qiao, J.F.; Chen, C.L.P. Type-2 Fuzzy Broad Learning System. IEEE Trans. Cybern. 2022, 52, 10352–10363. [Google Scholar] [CrossRef]
- Ding, H.X.; Qiao, J.F.; Huang, W.M.; Yu, T. Cooperative event-triggered fuzzy-neural multivariable control with multitask learning for municipal solid waste incineration process. IEEE Trans. Ind. Inf. 2024, 20, 765–774. [Google Scholar] [CrossRef]
- Boruah, N.; Roy, B.K. Event triggered nonlinear model predictive control for a wastewater treatment plant. J. Water Process Eng. 2019, 32, 100887. [Google Scholar] [CrossRef]
- Girard, A. Dynamic triggering mechanisms for event-triggered control. IEEE Trans. Autom. Control 2015, 60, 1992–1997. [Google Scholar] [CrossRef]
- Shi, T.; Shi, P.; Wu, Z.G. Dynamic Event-Triggered Asynchronous MPC of Markovian Jump Systems with Disturbances. IEEE Trans. Cybern. 2022, 52, 11639–11648. [Google Scholar] [CrossRef]
- Wang, C.C.; Geng, Q.; Liu, F.C.; Fu, L.N. Observer-based MPC for fuzzy cyber–physical system with hybrid attacks via a dynamic event-triggered mechanism. J. Frankl. Inst. 2024, 361, 106772. [Google Scholar] [CrossRef]
- Gu, Z.; Yue, D.; Park, J.H.; Xie, X.P. Memory-event-triggered fault detection of networked IT2 T-S fuzzy systems. IEEE Trans. Cybern. 2023, 53, 743–752. [Google Scholar] [CrossRef]
- Gu, Z.; Yue, D.; Ahn, C.K.; Yan, S.; Xie, X.P. Segment-weighted information-based event-triggered mechanism for networked control systems. IEEE Trans. Cybern. 2023, 53, 5336–5345. [Google Scholar] [CrossRef] [PubMed]
- Rong, N.N.; Wang, B.H.; Zhang, X.W.; Ji, Y. Dynamic event-based model predictive control of IT2 T-S fuzzy system. IEEE Trans. Circuits Syst. II-Exp. Briefs 2024, 71, 692–696. [Google Scholar] [CrossRef]
- Wang, Y.J.; Huang, J.Q.; Zhou, W.X.; Lu, F.; Xu, W.H. Neural network-based model predictive control with fuzzy-SQP optimization for direct thrust control of turbofan engine. Chin. J. Aeronaut. 2022, 35, 59–71. [Google Scholar] [CrossRef]
- Han, H.G.; Wang, C.Y.; Sun, H.Y.; Qiao, J.F. Data-based robust model predictive control for wastewater treatment process. J. Process Control 2022, 118, 115–125. [Google Scholar] [CrossRef]
- Tian, H.; Tang, J.; Aljerf, L.; Wang, T.Z.; Qiao, J.F. Furnace temperature control based on interval type-2 fuzzy broad learning system for municipal solid waste incineration process. Expert Syst. Appl. 2025, 280, 127530. [Google Scholar] [CrossRef]
- Noriega, J.R.; Wang, H. A direct adaptive neural-network control for unknown nonlinear systems and its application. IEEE Trans. Neural Netw. 1998, 9, 27–34. [Google Scholar] [CrossRef]
- Han, H.G.; Yang, F.F.; Sun, H.Y.; Qiao, J.F. Robust type-2 fuzzy neural control for wastewater treatment process with external disturbances. IEEE Trans. Autom. Sci. Eng. 2024, 21, 7230–7241. [Google Scholar] [CrossRef]
- Xiao, H.Z.; Chen, C.L.P. Incremental updating multirobot formation using nonlinear model predictive control method with general projection neural network. IEEE Trans. Ind. Electron. 2019, 66, 4502–4512. [Google Scholar] [CrossRef]
- Han, H.G.; Liu, Z.; Liu, H.X.; Qiao, J.F. Knowledge-Data-Driven Model Predictive Control for a Class of Nonlinear Systems. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 4492–4504. [Google Scholar] [CrossRef]
- Zhao, J.K.; Dai, H.L.; Wang, Z.Y.; Chen, C.; Cai, X.W.; Song, M.Y.; Guo, Z.C.; Zhang, S.; Wang, X.G.; Geng, H.Y. Self-organizing modeling and control of activated sludge process based on fuzzy neural network. J. Water Process Eng. 2023, 53, 103641. [Google Scholar] [CrossRef]
- Han, H.G.; Liu, Z.; Qiao, J.F. Fuzzy Neural Network-Based Model Predictive Control for Dissolved Oxygen Concentration of WWTPs. Int. J. Fuzzy Syst. 2019, 21, 1497–1510. [Google Scholar] [CrossRef]
- Tian, H.; Tang, J.; Xia, H.; Wang, T.Z.; Yu, W.; Qiao, J.F. Furnace Temperature Control Using IT2FBLS-based Reinforcement Learning PID for MSWI Process. Acta Automat. Sin. 2025, 51, 1626–1641. [Google Scholar] [CrossRef]
- Qiao, J.F.; Sun, J.; Meng, X. Event-triggered adaptive model predictive control of oxygen content for municipal solid waste incineration process. IEEE Trans. Autom. Sci. Eng. 2024, 21, 463–474. [Google Scholar] [CrossRef]
- Wang, B.K.; Tang, J.; Tian, H.; Yu, W.; Qiao, J.F. Improved Interval Type-II Fuzzy Broad MPC Method for Furnace Temperature of Municipal Solid Waste Incineration Process. IEEE Trans. Fuzzy Syst. 2025; to be published. [Google Scholar] [CrossRef]
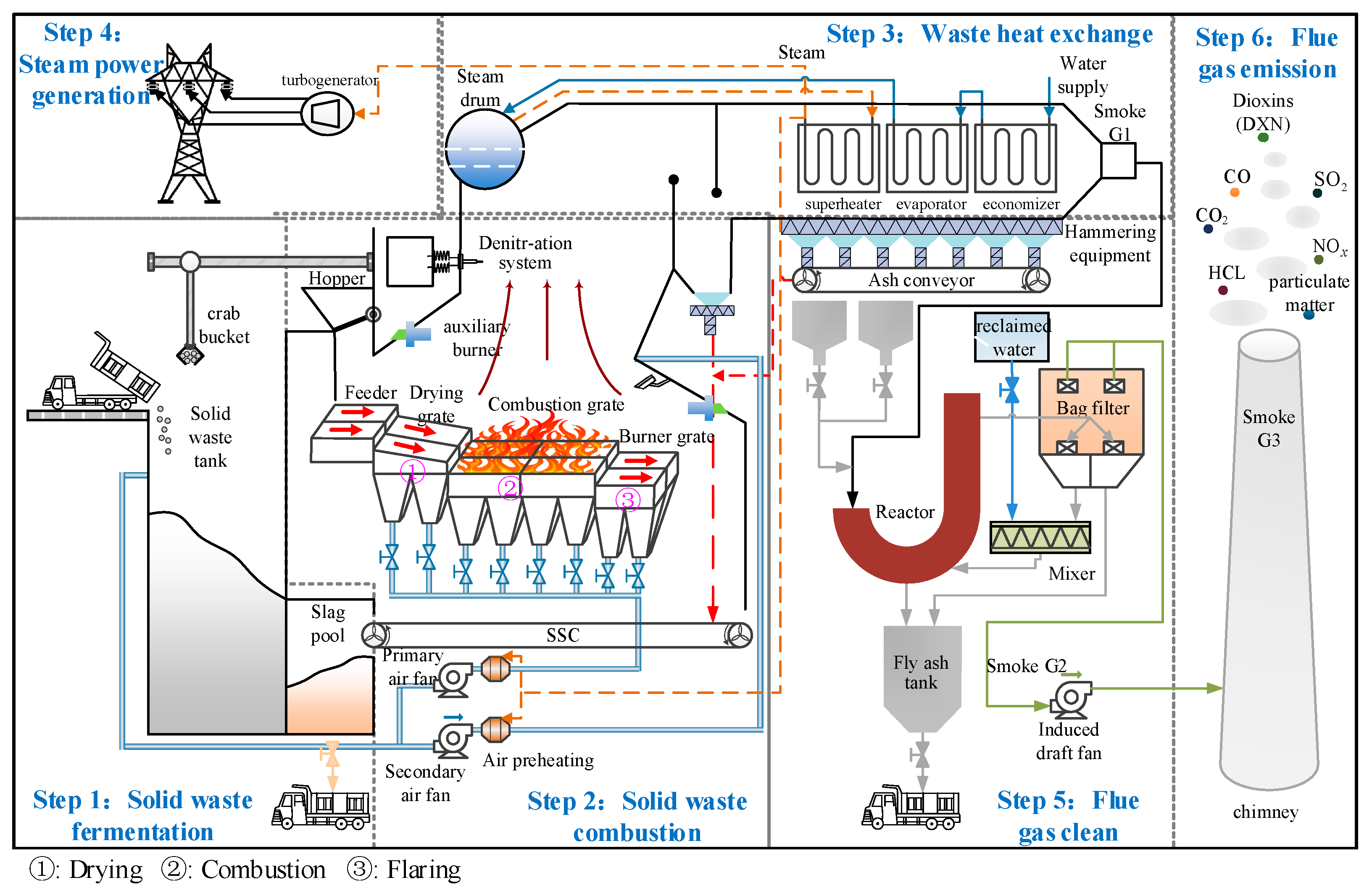
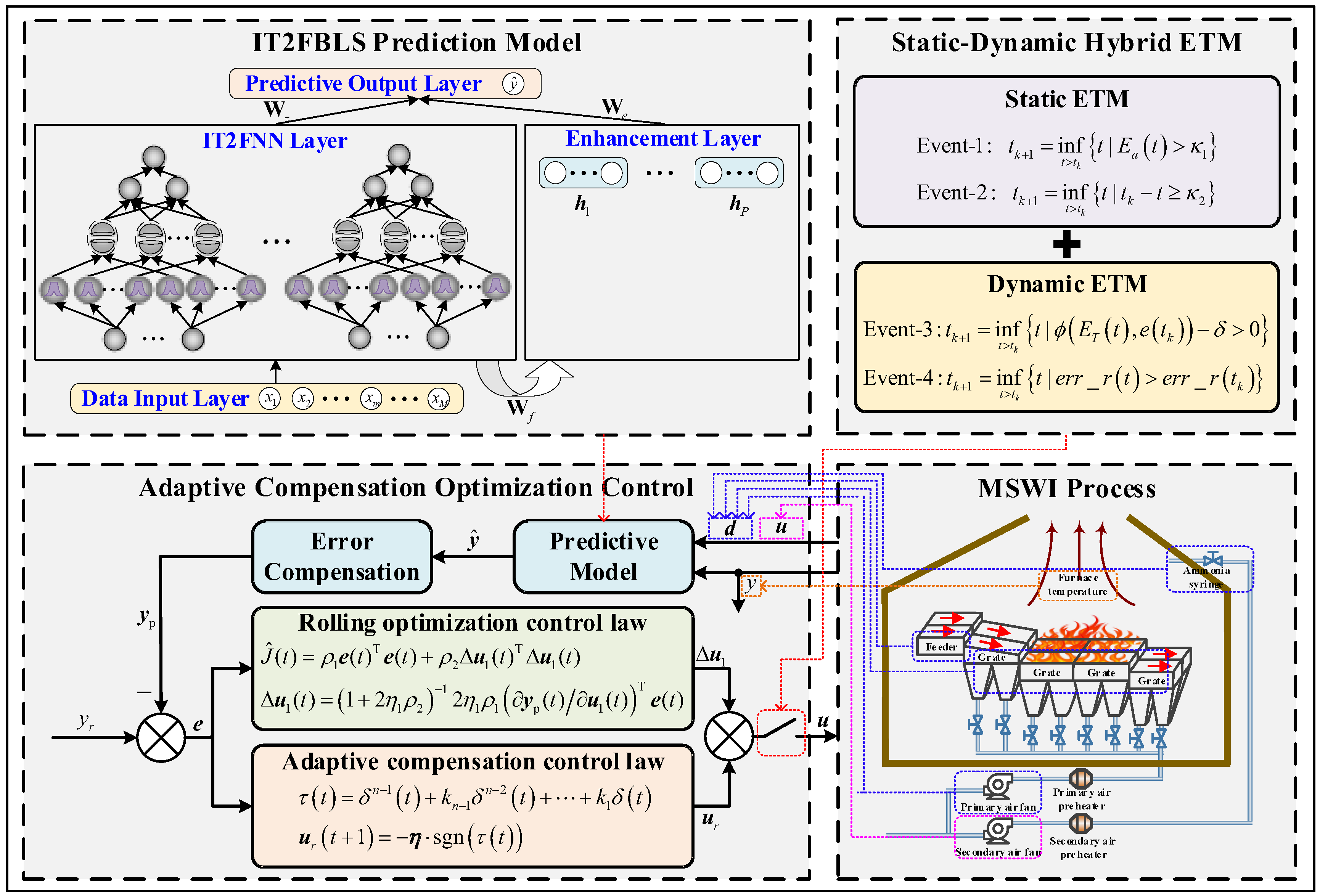
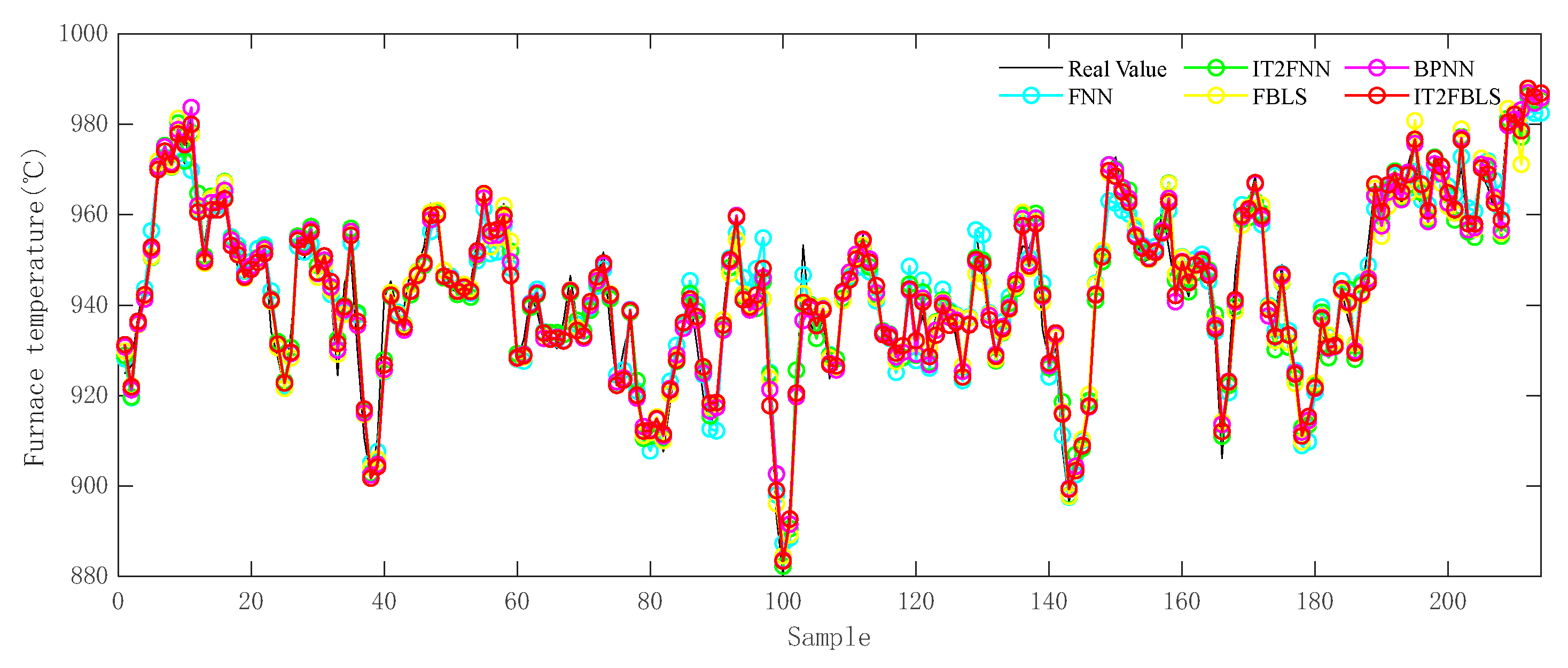
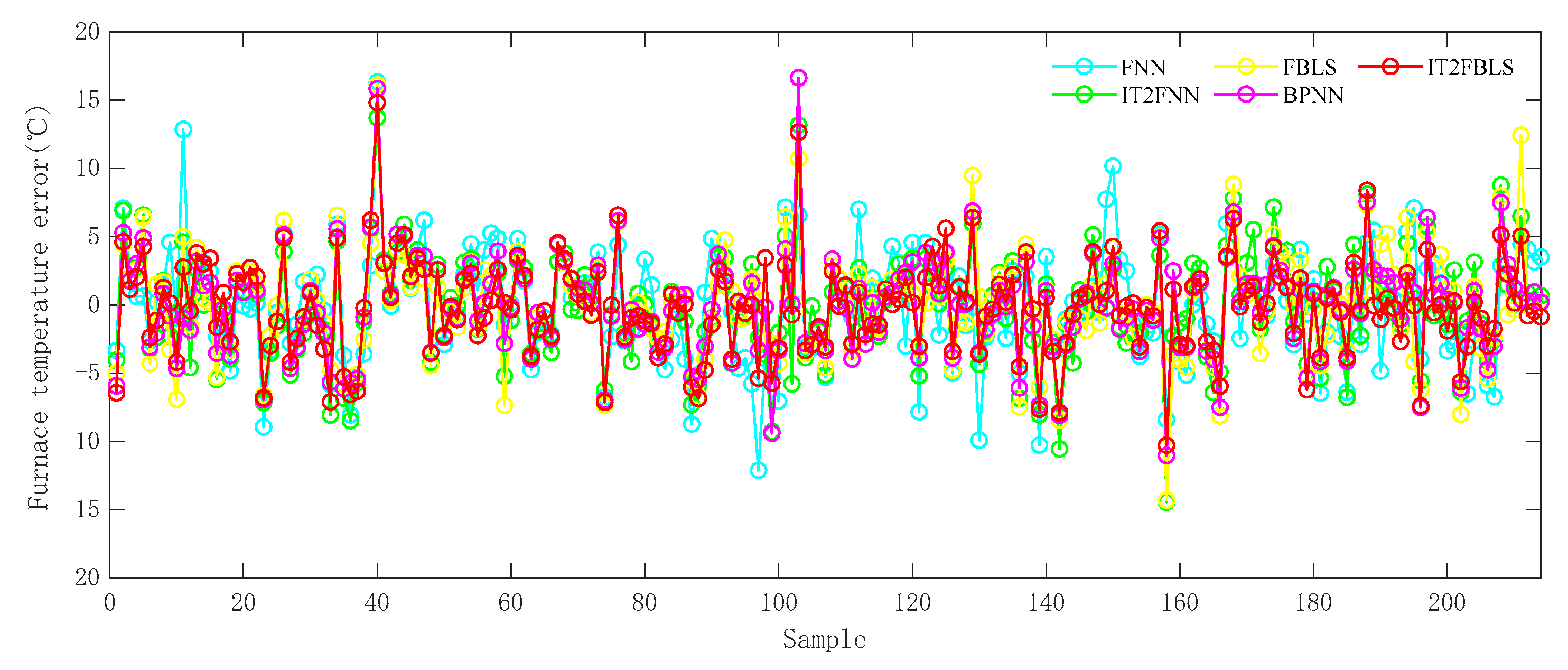

| Number | Variable | PCC Value |
|---|---|---|
| 1 | PV | 0.0553 |
| 2 | SV | 0.2045 |
| 3 | FS | 0.0621 |
| 4 | DS | 0.0589 |
| 5 | AI | −0.2947 |
| Variable | Unit | Variation Range |
|---|---|---|
| PV | m3/h | [53.78, 76.71] |
| SV | m3/h | [0, 20.88] |
| FS | % | [20, 53.75] |
| DS | % | [20, 60] |
| AI | L/h | [16.75, 84.42] |
| FT | °C | [922, 1066] |
| Model | MSE | RMSE | MAE | R2 |
|---|---|---|---|---|
| IT2FBLS | 1.1940 × 101 | 3.4554 × 100 | 2.5692 × 100 | 9.6730 × 10−1 |
| FBLS | 1.3331 × 101 | 3.6512 × 100 | 2.7148 × 100 | 9.6349 × 10−1 |
| IT2FNN [20] | 1.4990 × 101 | 3.8717 × 100 | 2.8950 × 100 | 9.5895 × 10−1 |
| FNN [41] | 1.5532 × 101 | 3.9411 × 100 | 3.0292 × 100 | 9.5747 × 10−1 |
| BPNN [11] | 1.9008 × 101 | 4.1079 × 100 | 3.2008 × 100 | 9.5379 × 10−1 |
| Controller | Performance Indicator | Triggering Times | ||
|---|---|---|---|---|
| ISE | IAE | DEVmax | ||
| IT2FBLS-ACN-PID [42] | 0.4626 | 0.3616 | 9.8708 | 1200 |
| NMPC [11] | 1.3456 | 0.4759 | 7.2667 | 1200 |
| FNN-MPC [41] | 1.0581 | 0.3953 | 8.8160 | 1200 |
| IT2FNN-MPC [20] | 0.7909 | 0.3338 | 7.3463 | 1200 |
| LSTM-MPC [43] | 0.6885 | 0.3485 | 6.9486 | 1200 |
| FBLS-MPC | 0.6695 | 0.3431 | 6.7202 | 1200 |
| IT2FB-MPC | 0.2880 | 0.1947 | 6.6269 | 1200 |
| I2T2FB-MPC [44] | 0.2872 | 0.1948 | 6.6269 | 1200 |
| IT2FB-ACMPC | 0.2821 | 0.1930 | 6.6269 | 1200 |
| SDHETM-IT2FB-MPC | 0.3174 | 0.2045 | 6.6269 | 370 |
| SDHETM-IT2FB-ACMPC | 0.3084 | 0.1969 | 6.6269 | 343 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Tang, J.; Wang, W.; Rong, J. Interval Type-II Fuzzy Broad Model Predictive Control Based on the Static and Dynamic Hybrid Event-Triggering Mechanism and Adaptive Compensation for Furnace Temperature in the MSWI Process. Appl. Sci. 2025, 15, 10329. https://doi.org/10.3390/app151910329
Wang B, Tang J, Wang W, Rong J. Interval Type-II Fuzzy Broad Model Predictive Control Based on the Static and Dynamic Hybrid Event-Triggering Mechanism and Adaptive Compensation for Furnace Temperature in the MSWI Process. Applied Sciences. 2025; 15(19):10329. https://doi.org/10.3390/app151910329
Chicago/Turabian StyleWang, Bokang, Jian Tang, Wei Wang, and Jian Rong. 2025. "Interval Type-II Fuzzy Broad Model Predictive Control Based on the Static and Dynamic Hybrid Event-Triggering Mechanism and Adaptive Compensation for Furnace Temperature in the MSWI Process" Applied Sciences 15, no. 19: 10329. https://doi.org/10.3390/app151910329
APA StyleWang, B., Tang, J., Wang, W., & Rong, J. (2025). Interval Type-II Fuzzy Broad Model Predictive Control Based on the Static and Dynamic Hybrid Event-Triggering Mechanism and Adaptive Compensation for Furnace Temperature in the MSWI Process. Applied Sciences, 15(19), 10329. https://doi.org/10.3390/app151910329






