Modeling and Experimental Analysis of Tofu-Drying Kinetics

Featured Application

This research supports the optimization of drying processes and enhances predictive modeling in food cooking applications.

Abstract

Drying critically shapes tofu’s texture, structure, and final appearance, whether it occurs during cooking or is applied intentionally in reprocessing. This study aimed to characterize the drying kinetics of tofu through experimental analysis and through modeling. Tofu samples were dried at temperatures ranging from 40 °C to 90 °C using a convective drying tunnel and an oven. Shrinkage and color changes were analyzed. Empirical models, a shrinking-core model and a newly developed oven-cooking model were tested against experimental data. The drying kinetics exhibited a constant and a decreasing rate phase, which were separated by a water content threshold of 2.56 ${\mathrm{kg}}_{\mathrm{W}}/{\mathrm{kg}}_{\mathrm{DS}}$. Tofu undergoes non-enzymatic browning and exhibited total shrinkage of 0.38. These physical changes were more significant at lower drying temperatures when the product was dried below a water content of 1.39 ${\mathrm{kg}}_{\mathrm{W}}/{\mathrm{kg}}_{\mathrm{DS}}$. The logarithmic model provided the best fit (${\mathrm{R}}^2\ge 0.9920$) to the experimental data. However, the cooking model shows good results as well (${\mathrm{R}}^2=0.9678$) and offers physical validity. This study provides evidence that the drying mechanisms of tofu are not temperature-dependent within the studied range. It also emphasizes the importance of drying time over drying temperature in the physical changes of the product. The successful fit of the cooking model highlights the link between drying and cooking processes, suggesting potential applications in both areas.

1. Introduction

Tofu is a traditional Chinese food product made from curdled soy milk. Its consumption has become widespread due to its nutritional value, health benefits, and suitability as an alternative to animal protein [1,2,3,4]. Tofu exists in a wide variety of forms, differentiated by water content. Silken tofu, also known as soft tofu, has a water content of about 87–90%, while firm tofu is pressed to reduce its moisture content, resulting in a more compact matrix with a water content of about 67–81% [5]. Finally, leisure-dried tofu is a reprocessed form of tofu that is dried before marinating to enhance its flavor [6]. Its production usually involves an extended drying phase of three hours at an elevated temperature of around 85 °C [7].

Drying is, therefore, a possible transformation process in the production and consumption of tofu. It occurs both in domestic cooking processes, like oven cooking, where it is one of the key processes [8], and in industrial settings like the production of leisure-dried tofu [7]. In particular, leisure-dried tofu has become increasingly popular on the market due to its taste, ready-to-eat attributes, and nutritious advantages [6,7,9]. Drying tofu changes its flavor and texture, creating a product that is crispy yet tender, and extends storage time by reducing the risk of spoilage [10]. Therefore, studying the drying kinetics of tofu has direct industrial applications.

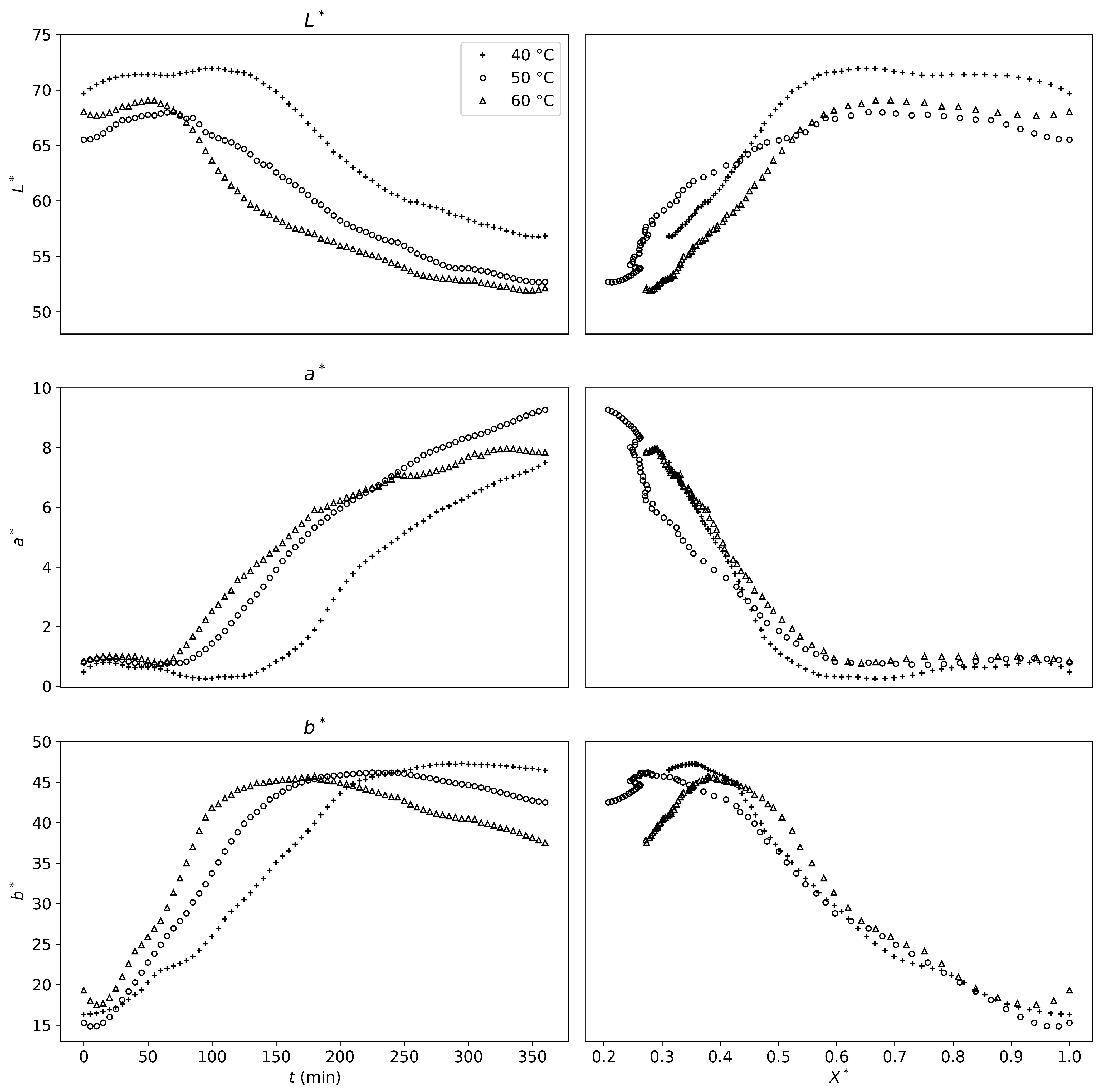
While water content is a key factor in tofu texture, it also influences other physical properties, such as color and shape [11]. Significant water loss inevitably leads to shrinkage and impacts the product’s coloration [12,13]. Since color and shape influence consumer acceptance [12], further examination of their relationship to the drying process is necessary.

Baik and Mittal [14] investigated the thermal properties of tofu as a function of water content, but the drying process itself has not been studied. The drying kinetics of soybean grains [15] and okara (a byproduct of soy milk and tofu production) [16,17,18] have been studied and characterized. Several empirical models, such as Page, Henderson, and Thompson, have been tested for soybean drying and have produced satisfactory results [15]. For okara, both empirical models [16] and physical models (heat and mass transfer [18]) have been successfully tested. While the drying kinetics of other soy-related products have been studied, this has not been the case for tofu itself.

In this study, the experimental results were compared to three types of models: simple empirical models [19], a shrinking-core model (SK) [20], and a newly developed phenomenological model for oven-cooking processes (the cooking model). Mathematical modeling of tofu drying kinetics serves multiple purposes. First, it helps us understand and predict the physical mechanisms involved in the drying process. Second, the two physics-based models examined here provide meaningful parameters that can inform process design [20,21]. Finally, this study evaluates a newly developed model for oven cooking. By linking drying dynamics to cooking processes through mathematical modeling, this study sheds light on the key mechanisms that influence cooking performance [22].

Therefore, the objective of this work is to characterize the drying kinetics of tofu at different temperatures using experimental analysis and modeling. Changes in shape and color during the drying process were also examined.

2. Materials and Methods

2.1. Experimental Methods

2.1.1. Tofu Samples

The tofu used in this study was plain, firm tofu, packaged in 250 g portions. It was purchased from a local supermarket (brand: Carrefour Bio, Brussels, Belgium). The outermost compressed layer formed during processing was removed from each fresh tofu block before it was cut into 8 cm³ cubes (2 cm edges). The nutrition facts for 100 g of the selected tofu are as follows: 8.1 g of fat, 2.0 g of carbohydrates, <0.5 g of dietary fiber, 12.0 g of protein, and <0.01 g of salt.

2.1.2. Drying Process

Drying experiments were conducted using two types of convective drying systems: a drying oven and a drying tunnel.

The thermal degradation of bioactive compounds in food occurs under different drying conditions, depending on the compound being studied [23,24]. Therefore, the experiments covered a wide range of temperatures, starting at 40 °C (higher than the usual ambient temperature), and ending at 90 °C (below the boiling point of water). Drying-oven experiments were performed using a Memmert UBF 400 unit (Memmert GmbH + Co. KG, Büchenbach, Germany), at 40, 50, 60, 70, 80, and 90 °C. The samples were weighed using a Sartorius Entris BCE2201I-1S balance (Sartorius AG, Göttingen, Germany) at the following time points: 0, 10, 20, 30, 40, 50, 70, 90, 120, 150, 180, 210, 240, and 270 min. All tests were conducted in triplicate.

Additional drying experiments were performed in a drying tunnel at temperatures of 40, 50, and 60 °C. The maximal achievable temperature for this setup was 60 °C. This apparatus allows for continuous weight monitoring (using a Sartorius Entris BCE2201I-1S) without interrupting the drying process and provides well-controlled drying conditions. Additionally, a Nikon D3100 camera (Nikon Corporation, Tokyo, Japan) ($4608\times 3072$ px) was positioned above the sample to acquire images and monitor physical changes during drying. This setup was described by Spreutels et al. [25] and is illustrated in Figure 1. The experiments were conducted with an airflow of 20 Nm³/h, and the mass and images were recorded every five minutes.

After each drying test, the dry mass of the sample m_DS was determined by placing it in a drying oven at 102 °C for three days until it reached a stable weight.

The average moisture content in dry basis, X_i (ith measure), was determined from the measured mass values m_i of the samples:

$$X_i={\displaystyle \frac{m_i-m_{DS}}{m_{DS}}}$$

(1)

The drying rate j was determined as follows:

$$j=-{\displaystyle \frac{dX}{dt}}$$

(2)

For a better comparison between the experiments, the values of X and j were normalized, respectively, by the initial moisture content, X₀, and the maximum evaporation rate, j_max:

$$X^{*}={\displaystyle \frac{X}{X_0}}$$

(3)

$$j^{*}={\displaystyle \frac{j}{j_{max}}}$$

(4)

2.1.3. Color and Size Variations

Images acquired in the drying tunnel were analyzed for color and size variation. The mean color was extracted from a fixed region (approximately $650\times 650$ px), and color changes $\mathsf{\Delta }{E}_i$ were calculated in the CIELAB color space (L* for lightness, a* for redness, and b* for yellowness [26]):

$$\mathsf{\Delta }{E}_i=\sqrt{{(L_0^{*}-L_i^{*})}^2+{(a_0^{*}-a_i^{*})}^2+{(b_0^{*}-b_i^{*})}^2}$$

(5)

To track the size of the sample, a grayscale threshold was applied to separate the sample from the background. Then, the projected area was estimated based on the pixel count and the image scale [27]. Extrapolating these results under the assumption of isotropic shrinkage yields a deduced volume and a total shrinkage S, which is the ratio of the final to the initial volume [13]:

$$S={\displaystyle \frac{V_{final}}{V_0}}$$

(6)

The size variations were compared to a shrinkage model developed by Bukamba Tshanga et al. [28]. This model describes how the relative volume of the product changes with water content and a fraction, $\alpha$, representing the lost liquid volume that is replaced by gas:

$${\displaystyle \frac{V_i}{V_0}}=1-{ϵ}_0(1-\alpha )(1-X_i^{*})$$

(7)

where ${ϵ}_0$ represents the initial porosity of the product, which was estimated as the ratio of the initial water volume present in the product (obtained from the experimental dry mass) to the initial volume of the product. The only parameter adjusted to the experimental data during the fitting process was $\alpha$. Since the model considers $\alpha$ to be constant, it is linear.

2.1.4. Data Processing

The drying rate j and color data $\mathsf{\Delta }E$ were smoothed using a Savitsky–Golay filter with a third-order polynomial and a window size of 13 points.

2.2. Mathematical Models

Six mathematical models of varying complexity were evaluated against experimental data: (i) four empirical models frequently used in drying kinetics [19,29], (ii) a physical model based on one-dimensional mass transport equations (the shrinking-core model (SK)) [20], and (iii) a newly developed heat and mass transfer model that simulates oven-based cooking processes (the cooking model, or the HMT model for abbreviation).

To evaluate the suitability of the models, two criteria were used: R² and root-mean-square error (RMSE):

$${\mathrm{R}}^2=1-{\displaystyle \frac{{\Sigma }_{i=1}^N{(y_{i,exp}-y_{i,pred})}^2}{{\Sigma }_{i=1}^N{(y_{i,exp}-{\overline{y}}_{exp})}^2}}$$

(8)

$$\mathrm{RMSE}={\displaystyle \frac{\sqrt{{\Sigma }_{i=1}^N{(y_{i,exp}-y_{i,pred})}^2}}{N}}$$

(9)

For all models, the fitted parameters were computed using the least squares method.

2.2.1. The Empirical Models

The selected empirical models are widely used in the literature to model food-drying kinetics [19,29]. The four chosen models are presented in

Table 1. Selected empirical mathematical models.

Model Name	Model	Fitted Parameters
Newton	$X^{*}=exp(-kt)$	k
Page	$X^{*}=exp(-k{t}^n)$	$k,n$
Henderson–Pabis	$X^{*}=aexp(-k{t}^n)$	$a,k,n$
Logarithmic	$X^{*}=aexp\left(kt\right)+c$	$a,k,c$

. The parameters for these models were fitted to the relative moisture content, X*, obtained experimentally (one fitting per experimental condition).

2.2.2. The Shrinking-Core Model

This model was initially developed to describe the process of air-drying yeast in a fluidized bed [20]. The parameters and geometry were adapted to the oven-drying process. The balance equations remain unchanged:

$${\displaystyle \frac{dX}{dt}}=-j$$

(10)

$$V_{oven}{\rho }_A{\displaystyle \frac{dY}{dt}}=Q(Y_{in}-Y)+m_{DS}j$$

(11)

$$Q(Y_{in}-Y)L_{vap}+Q{C}_{p_A}(T_{in}-T)=m_{DS}(C_{p_{DS}}+C_{p_W}X){\displaystyle \frac{dT}{dt}}+m_{DS}{C}_{p_W}(T-T_{in}){\displaystyle \frac{dX}{dt}}$$

(12)

Equation (10) is the balance equation for the water content in the solid (X) and is governed by the drying rate j. Equation (11) is the balance equation for the water content in the air of the convective drying oven (Y). It is governed by the volumetric flow rate of air entering the oven (Q) and the water evaporating from the product. Finally, Equation (12) is the balance equation for the global enthalpy of the system. On the left-hand side, the first term represents the energy carried by vapor due to phase change (with L_vap being the latent heat of vaporization). The second term represents the sensible heat carried by the oven air. The right-hand side of the equation is composed of two terms: the first term represents the heat required to change the temperature of the solid and its moisture, and the second term represents the energy associated with moisture variation.

These balance equations are coupled with a model that expresses j, allowing the drying process to be described as two distinct consecutive periods. These periods are separated by a critical water content X_crit, which is determined experimentally. The constant drying-rate period (phase I, when $X>X_{crit}$) is followed by a falling-rate period (phase II, when $X<X_{crit}$). For phase I, the drying rate j_I is expressed as follows:

$$j_I=k_{SK}a\left[C_{sat}\left(T\right)-{\displaystyle \frac{P}{R_{g}T}}{\displaystyle \frac{Y}{\frac{1}{M_A}+\frac{Y}{M_W}}}\right]$$

(13)

a is the solid’s specific surface area, and k_SK is the external mass transfer coefficient. The driving force is the difference between the saturation concentration (C_sat) and the actual vapor concentration. C_sat(T) follows the Clapeyron law [20].

For phase II, the drying rate j_II is expressed as follows:

$$j_{II}={\displaystyle \frac{a}{\frac{1}{k_{SK}}+\frac{1}{k_{intern}}}}\left[C_{sat}\left(T\right)-{\displaystyle \frac{P}{R_{g}T}}{\displaystyle \frac{Y}{\frac{1}{M_A}+\frac{Y}{M_W}}}\right]$$

(14)

During phase II, an internal resistance to mass transfer becomes a governing factor [20]. k_intern represents the internal mass transfer coefficient:

$$k_{intern}={\displaystyle \frac{D_{eff}}{L-L_{int}}}={\displaystyle \frac{D_{eff}}{L(1-\frac{X-X_{res}}{X_{crit}-X_{res}})}}$$

(15)

with L as the specific length of the sample and X_res as the residual water content. D_eff is the effective diffusion coefficient:

$$D_{eff}={\displaystyle \frac{{ϵ}_{SK}}{{\tau }_{SK}}}D=\xi D$$

(16)

In this model, porosity (${ϵ}_{SK}$) and tortuosity (${\tau }_{SK}$) are considered constant. The ratio between porosity and tortuosity is represented by the variable $\xi$.

The fitting method for this model involved adjusting k_SK and $\xi$ to the entire dataset, thereby including all experimental conditions within a single fitting procedure. Fitting was performed on the experimental drying rate j obtained from X, as stated in Equation (2). The main parameter values are presented in Section 3.3. The complete set of parameter values is available in Appendix A.

2.2.3. The Cooking Model

Cooking is the deliberate alteration of food products through the transfer of heat, which changes the products’ water content, mainly through evaporation. Therefore, drying is a key mechanism in controlling cooking, making it interesting to compare experimental data obtained for the drying process with a heat and mass transfer model developed for oven cooking. This one-dimensional model evaluates the local temperature and water content of the product during the process of oven cooking. The modeled system is represented in Figure 2.

Mass transfer is driven by diffusion:

$${\displaystyle \frac{\partial X}{\partial t}}=D_{eff}\left(X\right){\displaystyle \frac{{\partial }^{2}X}{\partial x^2}}$$

(17)

The effective diffusion coefficient D_eff considers both the molecular (D) and the capillary (D_cap) diffusion of water in the food matrix. D_cap is expressed as an empirical correlation depending on water content [30]. The developed expression of D_eff is as follows:

$$D_{eff}=D+D_{cap}=D+(1+B)Zexp(A+BX)$$

(18)

The heat transfer balance equation is as follows:

$${\displaystyle \frac{\partial T}{\partial t}}=\lambda {\displaystyle \frac{V}{m_{DS}(C_{p_{DS}}+C_{p_W}X)}}{\displaystyle \frac{{\partial }^{2}T}{\partial x^2}}+D_{eff}\left(X\right){\displaystyle \frac{C_{p_W}}{C_{p_{DS}}+C_{p_W}X}}{\displaystyle \frac{\partial X}{\partial x}}{\displaystyle \frac{\partial T}{\partial x}}$$

(19)

The first term on the right-hand side corresponds to the conductive term. The second term of the equation represents the energy convected by water transport in the product and depends on the gradients of both the water content and the temperature.

$\lambda$ is the thermal conductivity of the product in W/m/K and is a weighted sum of the thermal conductivities of water and of the dry product:

$$\lambda =\left({\displaystyle \frac{X}{1+X}}\right){\lambda }_W+\left(1-{\displaystyle \frac{X}{1+X}}\right){\lambda }_{DS},$$

(20)

The boundary condition for mass transfer is

$${\left.{\displaystyle \frac{\partial X}{\partial t}}\right|}_{x=0\mathrm{or}x=L}=-{\displaystyle \frac{\mathsf{\Omega }}{V}}{D}_{eff}\left(X\right){\displaystyle \frac{\partial X}{\partial x}}-j_{HMT}$$

(21)

including diffusion (the first term on the right-hand side) and evaporation (the second term on the right-hand side). j_HMT is the evaporation rate, which is specific to the cooking model:

$$j_{HMT}=k_{HMT}{\displaystyle \frac{\mathsf{\Omega }}{m_{DS}}}(C_{int}-C_A)$$

(22)

k_HMT is the mass transfer coefficient in m/s. Evaporation is driven by the difference in vapor concentration at the interface (C_int) and in the air (C_A). C_int is expressed as follows:

$$C_{int}={\displaystyle \frac{A_W\left(X\right)P_{sat}\left(T\right)M_W}{R_{g}T}}$$

(23)

To estimate C_int, the water activity A_W is calculated from the water content using the BET model, which describes desorption isotherms and relates X to A_W [31]:

$$X={\displaystyle \frac{A_W{K}_{BET}}{(1-A_W)(1+(K_{BET}-1)A_W)}}{X}_{BET}$$

(24)

K_BET is the BET constant, and X_BET is the monolayer moisture content.

It is assumed that the humidity at the interface corresponds to saturation at the temperature of the system, which is calculated using Clausius–Clapeyron’s law [32].

For heat transfer, the boundary condition is given by the following equation:

$$\lambda {\left.{\displaystyle \frac{\partial T}{\partial x}}\right|}_{x=0\mathrm{or}x=L}=C_{p_W}{\displaystyle \frac{m_{DS}}{V}}{D}_{eff}\left(X\right){\displaystyle \frac{\partial X}{\partial x}}(T-T_W)-h(T-T_{in})-L_{vap}{\displaystyle \frac{m_{DS}}{\mathsf{\Omega }}}{j}_{HMT}$$

(25)

The first term on the right-hand side represents the convective heat carried by moisture diffusion. The second term represents the convective heat loss to the ambient air. The last term represents the latent heat loss due to evaporation.

The model was fitted by adjusting six parameters to the entire dataset, encompassing all experimental conditions in a single fitting procedure. The fitted parameters were the empirical parameters A, B, and Z from Equation (18); the two parameters from the BET model (K_BET and X_BET); and the thermal conductivity of the dry product, ${\lambda }_{DS}$. Similar to the shrinking-core model, fitting was performed on the experimental drying rate j (Equation (2)). The main parameter values are presented in Section 3.3. The complete set of parameter values is provided in Appendix A.

3. Results

3.1. Drying Kinetics

3.1.1. Oven Dryer

The mean initial tofu water content ${\overline{X}}_0$ was $3.44\pm 0.26$   ${\mathrm{kg}}_{\mathrm{W}}/{\mathrm{kg}}_{\mathrm{DS}}$. Figure 3a shows how the relative moisture content X* changes over time during experiments conducted at different temperatures in the drying oven. Figures for oven-drying experiments are presented as the mean values obtained from triplicates. The individual values can be found in Appendix B and demonstrate the reproducibility of the results.

As expected, the drying rate increases with temperature. Figure 3b shows the relative drying rate j* as a function of the relative moisture content X*. After normalization, all the curves exhibit the same trend, suggesting that the drying mechanisms are not temperature-dependent within the studied temperature range.

Figure 3b also shows that the drying process can be divided into three sequential periods: an initial warming-up period (phase 0), followed by a constant drying-rate period (phase I), and a falling-rate period (phase II) [13]. The falling-rate period begins at $X=X_{crit}$, which was evaluated at 2.56 ${\mathrm{kg}}_{\mathrm{W}}/{\mathrm{kg}}_{\mathrm{DS}}$ (corresponding to $X^{*}=0.74$). To determine the value of X_crit, phase II was defined as beginning when the moisture content deviated by more than 10% from the mean value observed during phase I.

These three identified periods are characteristic stages of convective drying [13]. During the constant-rate period, drying is governed by external transport mechanisms, with evaporation of unbound water occurring at the product surface. Once X_crit is reached, internal transport mechanisms become rate-limiting [28], leading to a progressive reduction in the drying rate. These internal mechanisms are predominantly diffusion-controlled, involving both molecular diffusion and capillary transport [33].

3.1.2. Tunnel Dryer

Appendix C shows a comparison of the drying curves from the tunnel and oven-drying experiments conducted at the same temperatures. The results confirm the conclusion of Bukamba Tshanga et al. [28] that both drying methods result in very similar drying kinetics. Therefore, the tunnel dryer was used to obtain images for analyzing physical variations during drying.

3.2. Physical Variations During Drying

Physical variations in size and color were studied during the tunnel-drying process of tofu.

3.2.1. Size Variations During Drying

As can be seen in Figure 4 and Figure 5, the drying process substantially reduces the size of the product. After six hours of drying, the total shrinkage S was equal to 0.38 (Equation (6)).

In Figure 5b, a near-linear relationship is observed between normalized surface area, ${\mathsf{\Omega }}^{*}$, and relative water content, up to the threshold value of $X=1.39$   ${\mathrm{kg}}_{\mathrm{W}}/{\mathrm{kg}}_{\mathrm{DS}}$ (corresponding to $X^{*}=0.44$), indicating that shrinkage is strongly governed by water loss during drying. These observations suggest that water removal directly dictates structural deformation in tofu during drying. This means that shrinkage occurs as a continuous, moisture-driven process, likely due to the collapse of the porous matrix. In the literature, linear shrinkage models are usually applied to products where porosity development during drying is considered negligible [12].

The experiments were fitted to the shrinkage model presented in Equation (7) (see Appendix D for fitting figures). The fitting was satisfactory (${\mathrm{R}}^2>0.9677$) for the linear part of the drying process, above the threshold value for X. Across nearly all the experiments, the fitted values of $\alpha$ (the fraction of volume replaced by gas following liquid loss) were below ${10}^{-12}$ and can, therefore, be considered null. This suggests that during the first stage of the drying process, the porous matrix completely collapses, and no void space is preserved where water once resided.

As mentioned previously, the linear relationship between shape and water content only lasts until X reaches 1.39 ${\mathrm{kg}}_{\mathrm{W}}/{\mathrm{kg}}_{\mathrm{DS}}$. After this threshold, shrinkage becomes temperature-dependent and more significant at lower drying temperatures. This demonstrates that long exposure to drying conditions has a greater impact on product shape than temperature does overall in the drying process.

3.2.2. Color Variations During Drying

Progressive color changes in tofu samples during drying can be observed in Figure 4. The image analysis enabled us to quantify the evolution of the individual CIELAB components L*, a*, and b*. The graphical results for these components can be found in Appendix E. The observed trends, which are consistent with the visual inspection of the samples, confirm that drying induces a darkening of the surface, accompanied by enhanced red and yellow tones. These changes are characteristic of non-enzymatic browning reactions like Maillard reactions [34]. The evolution of the three color components L*, a*, and b* is consistent with trends already identified in the literature for tofu [34].

Figure 6a shows the total color difference $\mathsf{\Delta }E$ (Equation (5)) as a function of time. During the early stages of drying, samples exposed to higher temperatures exhibited more pronounced color changes. As drying progressed, $\mathsf{\Delta }E$ increased with time, eventually reaching a plateau. Interestingly, Figure 6b shows that, although color change mechanisms appear similar across temperatures at higher moisture contents, more intense discoloration is observed in samples dried at lower temperatures below a certain threshold (of around $X=1.38$   ${\mathrm{kg}}_{\mathrm{W}}/{\mathrm{kg}}_{\mathrm{DS}}$, corresponding to $X^{*}=0.42$). This suggests that longer drying times impact color more than drying temperature.

The thresholds at which color change and size variation become drying-temperature-dependent are quite close (respectively, $X=1.38$ ${\mathrm{kg}}_{\mathrm{W}}/{\mathrm{kg}}_{\mathrm{DS}}$ and $X=1.39$ ${\mathrm{kg}}_{\mathrm{W}}/{\mathrm{kg}}_{\mathrm{DS}}$). This means that if the targeted water content is below these thresholds, higher drying temperatures will alter the product less, in terms of both color and shape.

3.3. Mathematical Modeling

The models presented in Section 2.2 were adjusted to the experimental data from the oven-drying experiments. As discussed in Section 3.1, the kinetics are very similar for the two drying methods. Since the oven allows for a wider temperature range, the models were adjusted to the oven experiments instead of the tunnel-drying experiments.

3.3.1. The Empirical Models

The parameter values obtained from the fittings, along with the corresponding plots for the four empirical models, are presented in Appendix F. The logarithmic model produced the best fitting results (Figure 7), followed by the Henderson–Pabis model, the Page model, and finally, the Newton model. Despite the relatively high R² values obtained, the Newton model does not accurately represent the nonlinear trend of the experimental data. Thus, the Newton model appears to be too simple to describe the more complex drying kinetics of tofu. The other three models provided satisfactory results.

3.3.2. The Shrinking-Core Model

For the shrinking-core model, the values and correlations of the parameters are presented in

Table 2. Parameters used in the shrinking-core model for tofu drying.

Parameter	Value or Correlation	Unit	Method or Source
$k_{SK}$	$4.150\times {10}^{-3}$	m/s	fitted
$\xi$	$1.734\times {10}^{-1}$	−	fitted
$V_{oven}$	$5.3\times {10}^{-2}$	m3	known
$X_{crit}$	$2.56$	${\mathrm{kg}}_{\mathrm{W}}/{\mathrm{kg}}_{\mathrm{DS}}$	experimental
D	$1.87\times {10}^{-10}\times {\displaystyle \frac{T_{in}^{2.072}}{P}}$	${\mathrm{m}}^2/\mathrm{s}$	[35]
$C_{p_{DS}}$	$349.5\times \left(1-{\displaystyle \frac{X_0}{1+X_0}}\right)$	$\mathrm{J}/{\mathrm{kg}}_{\mathrm{DS}}/\mathrm{K}$	[12]
Q	$2\times {10}^{-4}$	${\mathrm{kg}}_{\mathrm{A}}/\mathrm{s}$	estimated
$X_{res}$	$0.00$	${\mathrm{kg}}_{\mathrm{W}}/{\mathrm{kg}}_{\mathrm{DS}}$	estimated
$Y_{in}$	$1\times {10}^{-3}$	${\mathrm{kg}}_{\mathrm{W}}/{\mathrm{kg}}_{\mathrm{A}}$	estimated

. The parameters k_SK and $\xi$ were optimized to fit the drying rate j obtained from the experimental data. The fitting criteria obtained are as follows: ${\mathrm{R}}^2=0.8782$ and $\mathrm{RMSE}=7.795\times {10}^{-6}$. D_eff can also be calculated for each drying temperature from the fitting results, ranging from $4.809\times {10}^{-6}$ to $6.537\times {10}^{-6}$ ${\mathrm{m}}^2/\mathrm{s}$. Figure 8 shows that overall, this model is capable of capturing the general drying trends. However, the fit does not perfectly align with the experimental data for all drying temperatures.

3.3.3. The Cooking Model

For the cooking model, a total of six parameters were fitted to the experimental drying rate j. These parameters were optimized to fit all the drying curves simultaneously. The values and correlations of the different parameters are presented in

Table 3. Parameters used in the cooking model for tofu drying.

Parameter	Value or Correlation	Unit	Method or Source
A	$-2.494$	−	fitted
B	$3.945$	${\mathrm{kg}}_{\mathrm{DS}}/{\mathrm{kg}}_{\mathrm{W}}$	fitted
Z	$8.261\times {10}^{-8}$	${\mathrm{m}}^2/\mathrm{s}$	fitted
${\lambda }_{DS}$	$1.513\times {10}^{-1}$	W/m/K	fitted
$K_{BET}$	$26.76$	−	fitted
$X_{BET}$	$0.632$	${\mathrm{kg}}_{\mathrm{W}}/{\mathrm{kg}}_{\mathrm{DS}}$	fitted
$C_{p_{DS}}$	$349.5\times \left(1-{\displaystyle \frac{X_0}{1+X_0}}\right)$	$\mathrm{J}/{\mathrm{kg}}_{\mathrm{DS}}/\mathrm{K}$	[12]
D	$1.87\times {10}^{-10}\times {\displaystyle \frac{T_{in}^{2.072}}{P}}$	${\mathrm{m}}^2/\mathrm{s}$	[35]
h	$Nu={\displaystyle \frac{hL}{k}}=0.094R{e}^{0.675}P{r}^{1/3}$	$\mathrm{W}/{\mathrm{m}}^2/\mathrm{K}$	[35]
$k_{HMT}$	$Sh={\displaystyle \frac{kL}{D}}=0.094R{e}^{0.675}S{c}^{1/3}$	m/s	[35]
$C_A$	$1.440\times {10}^{-3}$	${\mathrm{kg}}_{\mathrm{W}}/{\mathrm{m}}_{\mathrm{A}}^3$	estimated

. The best-fitting solution is shown in Figure 8, which demonstrates that this model accurately captures the drying kinetics and is smoother than the shrinking-core model. The obtained criteria were ${\mathrm{R}}^2=0.9678$ and $\mathrm{RMSE}=4.009\times {10}^{-6}$. In this model, D_eff is time-dependent (Equation (18)). Appendix G presents a figure showing the evolution of D_eff as a function of time, and the initial and final values for each experimental condition. These values correspond to the boundary positions and provide an accurate estimate of the order of magnitude because the D_eff gradient in the product is small. At 40 °C, the initial D_eff is equal to $8.957\times {10}^{-2}$ and reaches a final value of $3.425\times {10}^{-5}$   ${\mathrm{m}}^2/\mathrm{s}$. Similar orders of magnitude are obtained for the other experimental conditions. This shows that, at the beginning of the drying process, the capillary term (Equation (18)) is very high and gradually decreases until D_eff falls within the expected range for diffusion-driven transport [36].

To further test the cooking model, the same adjustment steps were applied to all the experimental data sets, with one temperature condition excluded each time (leave-one-out fitting). The fittings remained accurate (${\mathrm{R}}^2>0.9488$). The results are shown in Appendix H.

3.3.4. Model Comparison

To compare the performance of the six models, the best-fitting parameters were used to simulate drying under all experimental conditions. The resulting model predictions were then evaluated against the experimental moisture content data X, temperature by temperature. Therefore, the R² and RMSE presented in

Table 4. R² and RMSE values recalculated for the moisture content X at every experimental drying temperature using the parameters obtained from the fitting of six models (Newton, Page, Henderson–Pabis (H-P), logarithmic (log), shrinking core (SK), and cooking (HMT)) to the drying rate obtained from experimental data.

R2
T (°C)	Newton	Page	H-P	Log	SK	HMT
40	0.9792	0.9923	0.9933	0.9987	0.8552	0.9491
50	0.9314	0.9818	0.9905	0.9993	0.9312	0.9762
60	0.8911	0.9870	0.9884	0.9984	0.9624	0.9844
70	0.8249	0.9868	0.9878	0.9964	0.8257	0.9814
80	0.8108	0.9874	0.9883	0.9953	0.7290	0.9654
60	0.7426	0.9881	0.9887	0.9920	0.4408	0.8328
RMSE
T (°C)	Newton	Page	H-P	Log	SK	HMT
40	$3.443\times {10}^{-2}$	$2.100\times {10}^{-2}$	$1.949\times {10}^{-2}$	$8.725\times {10}^{-3}$	$9.091\times {10}^{-2}$	$5.390\times {10}^{-2}$
50	$5.631\times {10}^{-2}$	$2.237\times {10}^{-2}$	$2.096\times {10}^{-2}$	$5.665\times {10}^{-3}$	$5.640\times {10}^{-2}$	$3.318\times {10}^{-2}$
60	$7.741\times {10}^{-2}$	$2.672\times {10}^{-2}$	$2.524\times {10}^{-2}$	$9.479\times {10}^{-3}$	$4.546\times {10}^{-2}$	$2.927\times {10}^{-2}$
70	$8.606\times {10}^{-2}$	$2.365\times {10}^{-2}$	$2.271\times {10}^{-2}$	$1.233\times {10}^{-2}$	$8.586\times {10}^{-2}$	$2.808\times {10}^{-2}$
80	$9.624\times {10}^{-2}$	$2.483\times {10}^{-2}$	$2.393\times {10}^{-2}$	$1.517\times {10}^{-2}$	$1.152\times {10}^{-1}$	$4.117\times {10}^{-2}$
90	$1.112\times {10}^{-1}$	$2.394\times {10}^{-2}$	$2.325\times {10}^{-2}$	$1.957\times {10}^{-2}$	$1.638\times {10}^{-1}$	$8.959\times {10}^{-2}$

were calculated between the experimental and the predicted moisture content at each temperature.

The best-fitting model is the logarithmic model, followed by the Henderson–Pabis and the Page models. The cooking model has similar R² and RMSE values as the Page model, especially at intermediate temperatures (60 and 70 °C), for which the R² and RMSE values are the best. This is logical, as the parameters for the cooking model were fitted to all experimental curves simultaneously, while the parameters for the empirical models were fitted individually to each experimental condition.

The shrinking-core model has similar R² and RMSE values to the Newton model. However, unlike the Newton model, the shrinking-core model captures the allure of the experimental data (see Appendix F and Figure 8). The best-fitting results for the shrinking-core model are obtained at the three lower temperatures (40–60 °C). This can be explained by the allure of the fitted curves (see Figure 8): once a certain temperature is reached, the model compensates for the deviation from the experimental data by prematurely halting evaporation (the drying rate j drops to 0).

4. Discussion

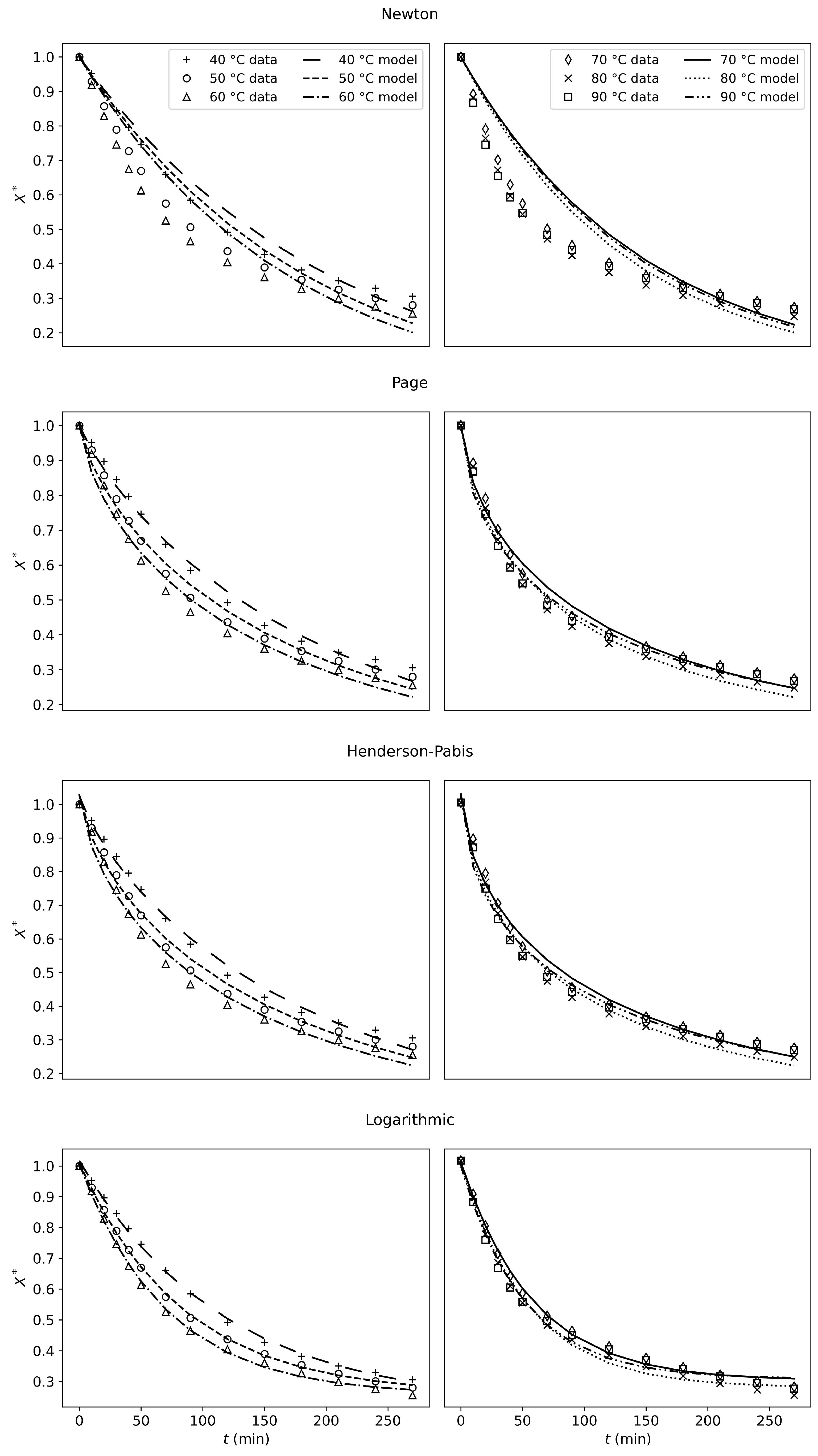
The modeling results show that the Newton model can only capture one linear drying mechanism, which is insufficient for describing the drying kinetics of tofu. This model lacks physical validity and should not be used to describe tofu-drying kinetics.

The Page, Henderson–Pabis, and Logarithmic models show good results and fit the experimental data well.

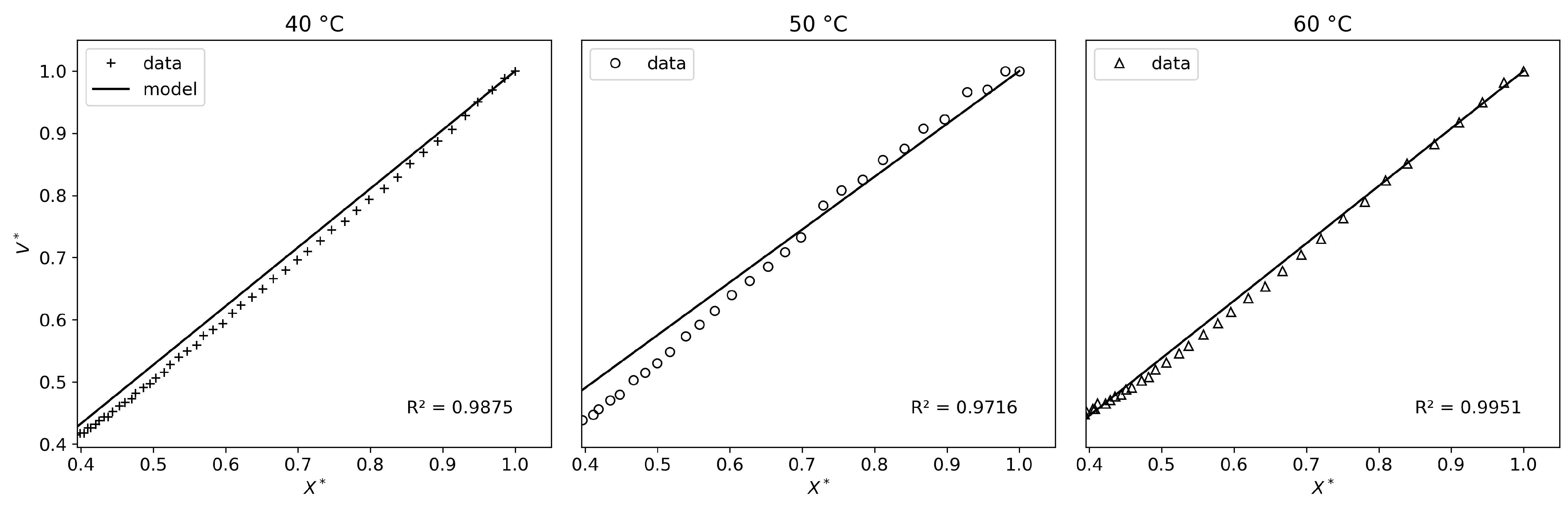
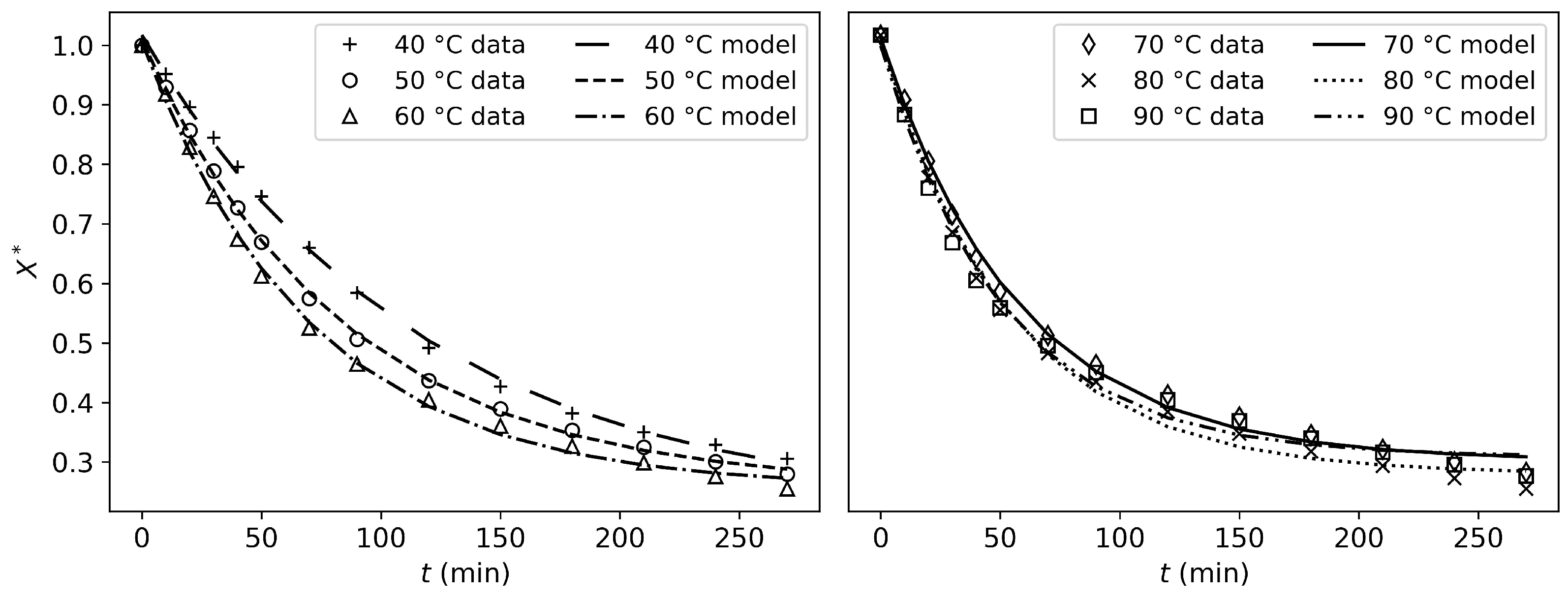
As shown in Figure 8, the shrinking-core model presents good results. Although the mean criteria values (R² and RMSE) are no better than those of the Newton model, the drying mechanisms are captured much more accurately. This makes sense, as the model is capable of predicting two distinct drying periods (constant-rate and falling-rate). However, while both distinct periods are captured, the fitting accuracy is not satisfactory for all experimental conditions. Specifically, from 70 °C to 90 °C, the model poorly describes the falling-rate period, compensating by prematurely halting evaporation (i.e., the drying rate j suddenly drops to zero, which has no physical validity). Therefore, this model could be used for control and optimization if the parameters were adapted to each experimental condition. However, it has no predictive or explanatory power, as fitting the parameters to all experimental conditions simultaneously does not produce satisfactory results for each condition, despite an overall satisfactory R².

The obtained value for k_SK is of the same order of magnitude as the value obtained for k_HMT using literature correlations (see Table 2 and Table 3). In this model, porosity and tortuosity are considered constant, meaning that shrinkage is not taken into account. Porosity was calculated for the initial volume of 2 cm³ and was found to be $0.86\pm 0.05$, which is quite high but still within the range observed for other porous food products in the literature [37]. High porosity was also observed through visual examination of the sample, which means that tofu is a product with low structure. This explains why the product collapses significantly. From the calculated porosity and the fitted $\xi$, tortuosity could be deduced, which was equal to $4.95\pm 0.31$. This value is quite high, but it is within the range of tortuosity determined for bread [38]. Finally, the effective diffusivity D_eff calculated from the fitting results for the shrinking-core model ranged from $4.809\times {10}^{-6}$ to $6.537\times {10}^{-6}$. This is near the expected range for food [36]. Overall, the fitted parameters obtained for the shrinking core model are consistent with literature data.

The cooking model results in the best fit to the experimental data j. This is confirmed by the good results of the R² and RMSE values and by Figure 8, where it can be seen that the drying kinetics are captured very well. Compared to the shrinking-core model, this model’s particularity is that it can predict a complex, multi-phasic drying process without breaking the model down into two periods.

Although the model is physics-based, some expressions remain empirical. The fitted parameters A, B, and Z have no physical meaning. However, these parameters allow us to calculate the effective diffusivity D_eff. The calculated values of D_eff fall outside the expected range for food products at the beginning of the drying process, but progressively approach the expected range as the process continues (see Appendix G) [36]. This is due to the capillary term that is taken into account in the expression of D_eff (Equation (18)). Initially, water transport is heavily influenced by capillary transport, which progressively diminishes throughout the process. Next, K_BET and X_BET have physical interpretations. K_BET reflects the strength of the interaction between the adsorbate and the surface. The fitted value for this constant is within the expected range for food, with a value of 26.76 [31]. X_BET is the monolayer capacity. The fitted value ($X_{BET}=0.632$) is about an order of magnitude higher than values reported in the literature for other food products [31]. Therefore, the suitability of the BET model to estimate the water content in the cooking model could be discussed, and other models could be used to replace this relationship. For example, the GAB model [31] could be used instead. Finally, the value obtained for the thermal conductivity of the dry product (${\lambda }_{DS}=1.513\times {10}^{-1}$ W/m/K) allows for the calculation of the thermal conductivity of the product before drying ($\lambda$ at $X=X_0$); the obtained value is $\lambda =4.987\times {10}^{-1}\pm 5.109\times {10}^{-3}$, which is consistent with values reported in the literature for other food products [39].

These fitting results demonstrate that the empirical, the shrinking-core, and the cooking models each have their own strengths and weaknesses.

Except for the Newton model, the empirical models fit the experimental data well. However, they lack physical meaning, and they have no predictive or explanatory power. Unlike the physical models, these models cannot fit the drying rate j.

Although the shrinking-core model shows weaker fitting results, it has only two fitted parameters. This is a significant advantage compared to the cooking model, which has six fitted parameters.

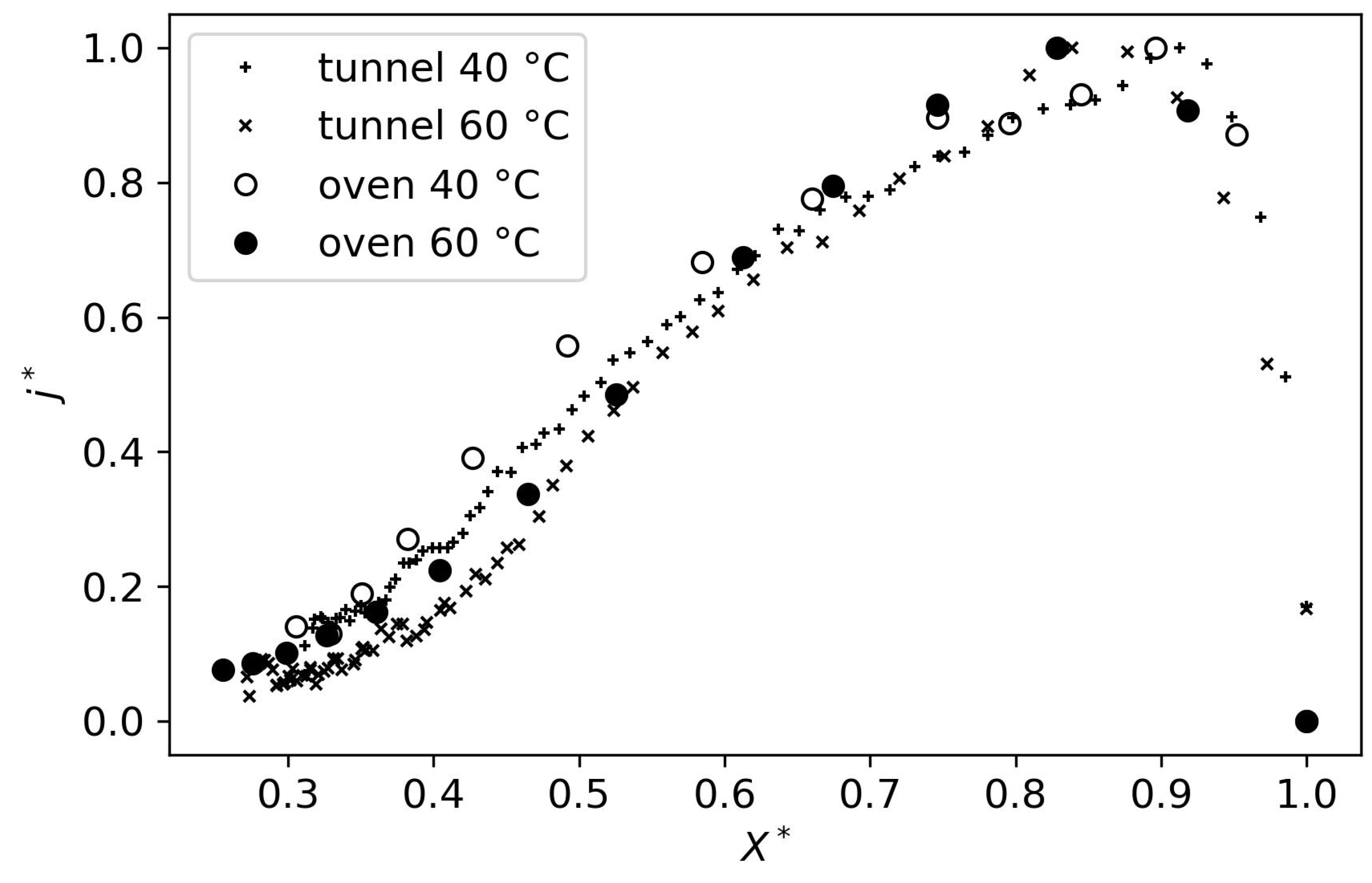
It is important to note that both physical models underwent a stringent fitting procedure. Only one set of parameters was adjusted to fit all experimental conditions. Moreover, the experimental data used for the fitting procedure consisted of the drying rate values j, to ensure that all the drying mechanisms were well captured. Even though fitting on X would have yielded better results, some physical phenomena, such as the distinct drying periods, are less pronounced in this data. This is why it was chosen to fit on j. Even with this strict fitting procedure, the physical models can compete with the results of the empirical models (Table 4).

Shrinkage is not taken into account in either of the models. Regarding experimental results, it would be a considerable improvement to take it into account for simulations.

5. Conclusions

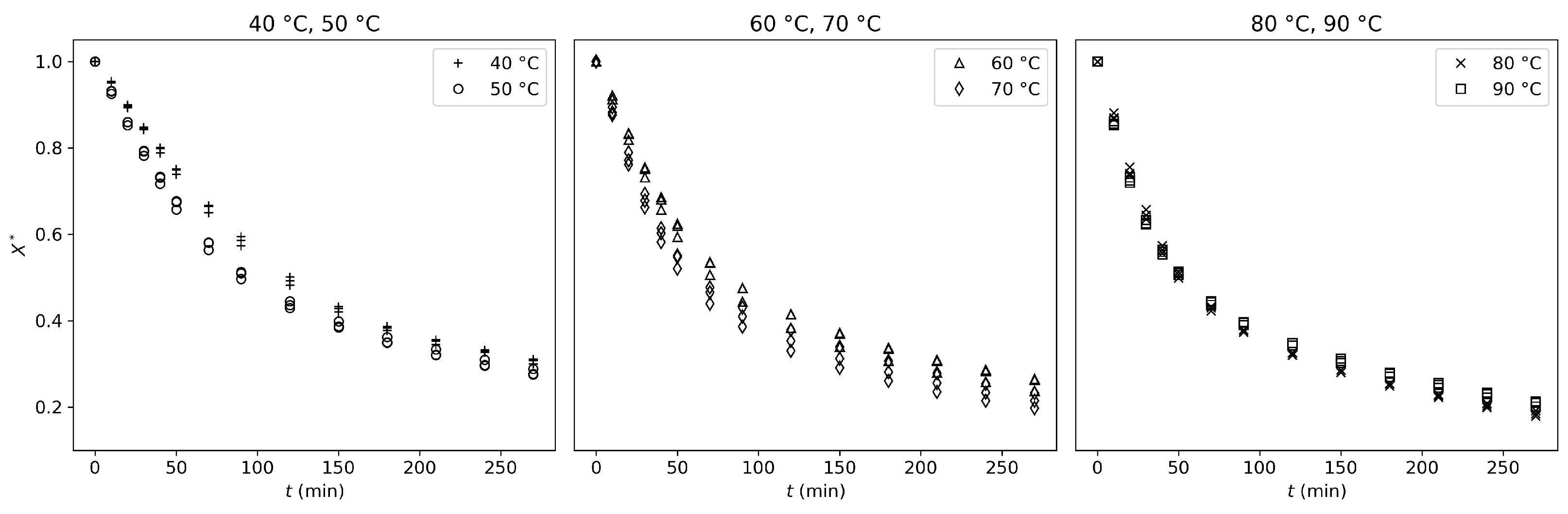
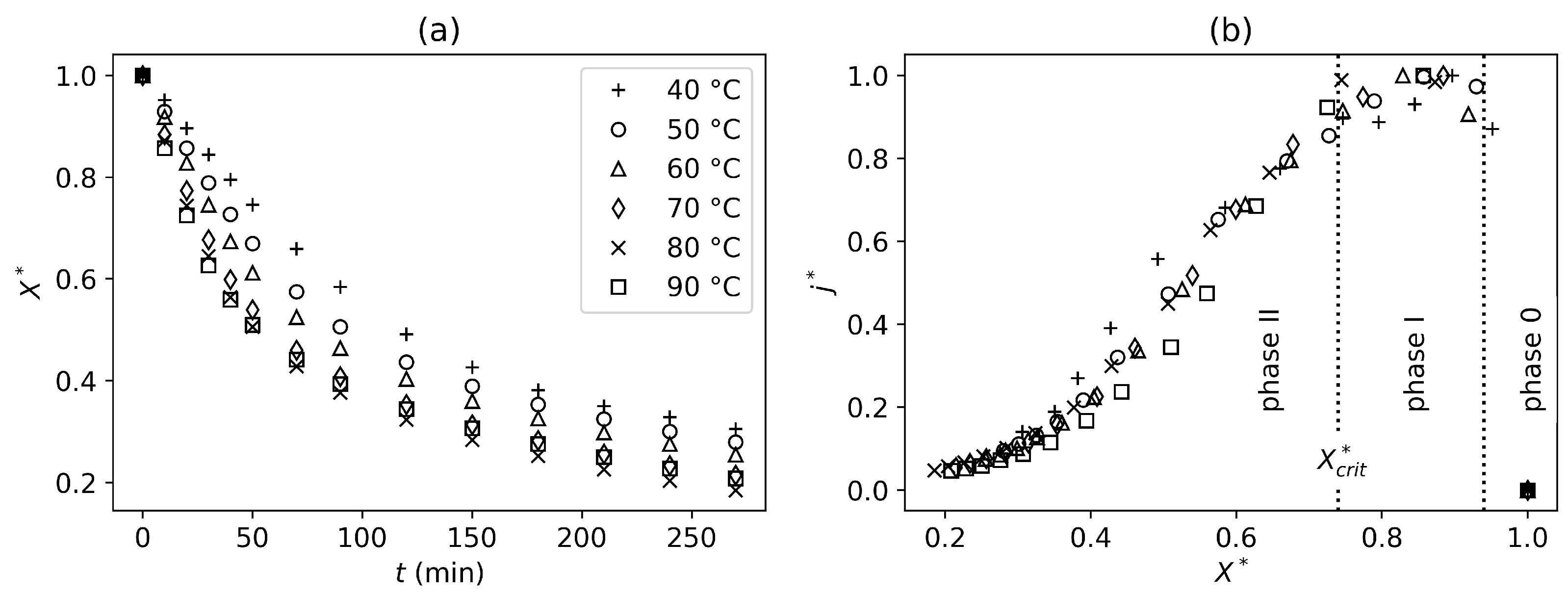
In this study, the convective drying behavior of tofu samples was investigated across a range of drying temperatures (40–90 °C), using both an oven and a tunnel dryer. Experimental analysis of the tofu-drying process showed that it can be described as a sequence of different mechanisms (drying phases I and II separated by $X_{crit}=2.56$   ${\mathrm{kg}}_{\mathrm{W}}/{\mathrm{kg}}_{\mathrm{DS}}$). These mechanisms are consistent across all studied temperatures, with higher temperatures resulting in faster drying.

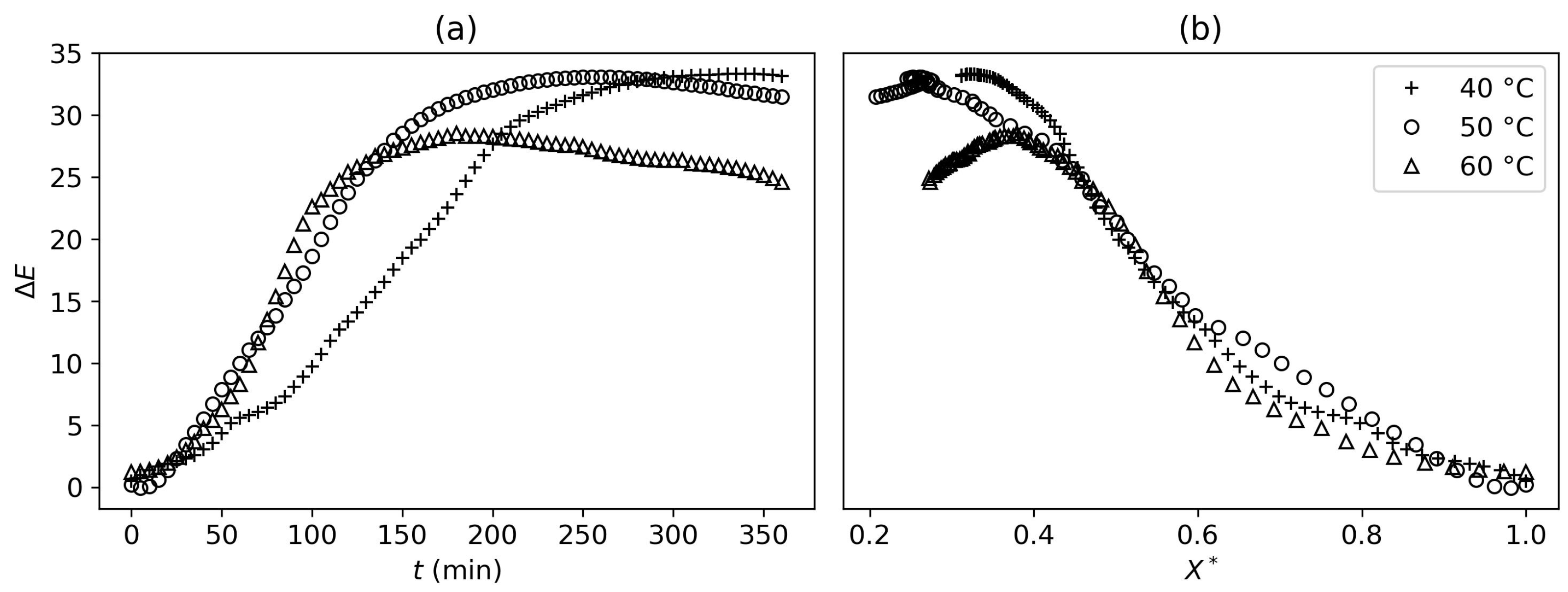
Drying further, a second threshold could be defined at $X=1.39$   ${\mathrm{kg}}_{\mathrm{W}}/{\mathrm{kg}}_{\mathrm{DS}}$, based on product shrinkage. Until that point, the shrinkage mechanisms were not temperature-dependent. However, once this threshold was reached, shrinkage became temperature-dependent and was more significant for lower drying temperatures (Figure 5). Similar observations were made for non-enzymatic browning at a very similar threshold (Figure 6).

It can be concluded that a faster drying process will reduce physical alterations of the product if the desired final water content is below $X=1.39$   ${\mathrm{kg}}_{\mathrm{W}}/{\mathrm{kg}}_{\mathrm{DS}}$. Therefore, higher drying temperatures should be prioritized to avoid these alterations.

Six models were assessed against the experimental data. The Newton model failed to adequately represent the drying behavior of tofu. The Logarithmic, Henderson–Pabis, and Page models showed good fitting results but lack physical validity. In contrast, both the shrinking core and the cooking models showed good capacity to predict the drying rate, while capturing the physical mechanisms occurring during the drying process. While the shrinking-core model requires separate fits for each experimental condition to properly capture the drying processes, it remains useful due to its simplicity, as it relies on only two fitting parameters. The newly developed cooking model delivered more accurate predictions (${\mathrm{R}}^2=0.9678$). It successfully captured the various drying periods without segmenting the process into distinct rate expressions. This offers a more comprehensive and adaptable approach despite its reliance on six adjustable parameters.

Future research should evaluate the accuracy of the cooking model for larger-scale drying processes. Additionally, since the model was accurate for oven-drying processes, it should be tested at higher temperatures to replicate cooking conditions. Taking physical variations, especially shrinkage, into account would also be a considerable improvement. Further study of the nutritional and structural changes in tofu during drying is also required.