Influence of Tiered Cyclic Shear Stress on Shear Friction and Instability Behavior of Marble Specimens with the Fractures
Abstract
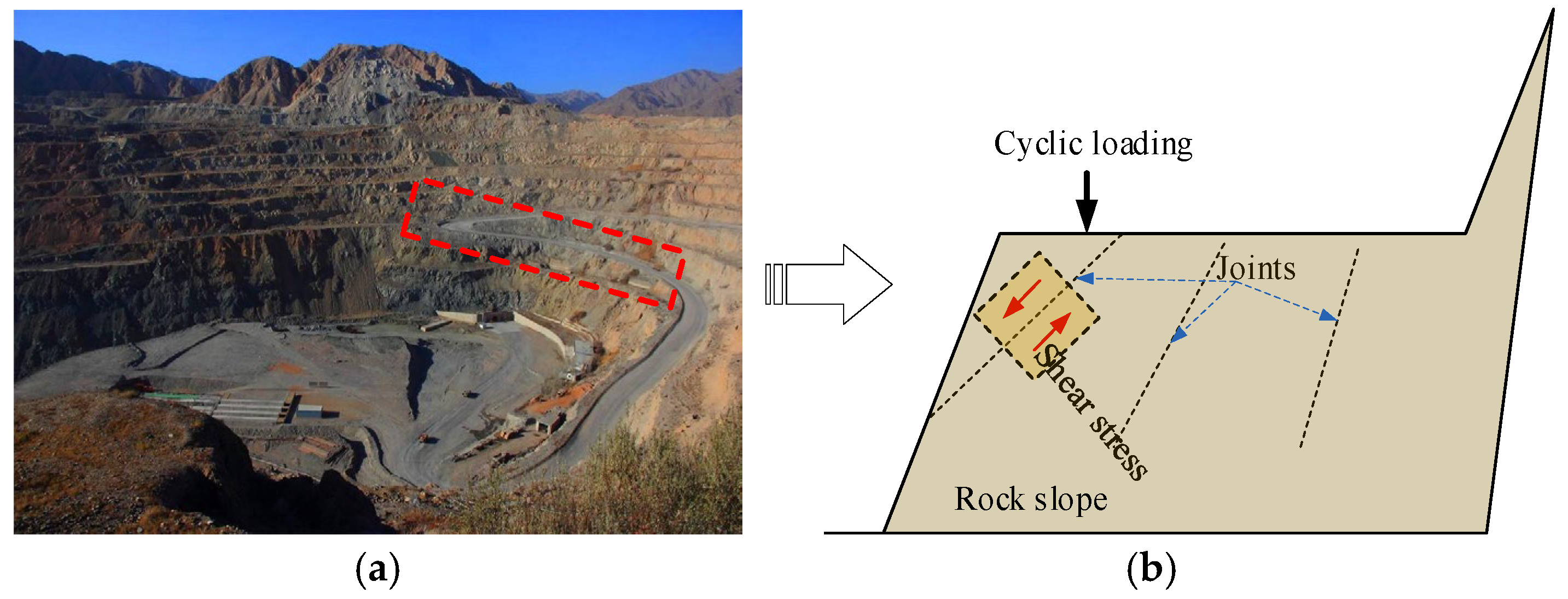
1. Introduction
2. Sample Preparation, Equipment and Test Procedure
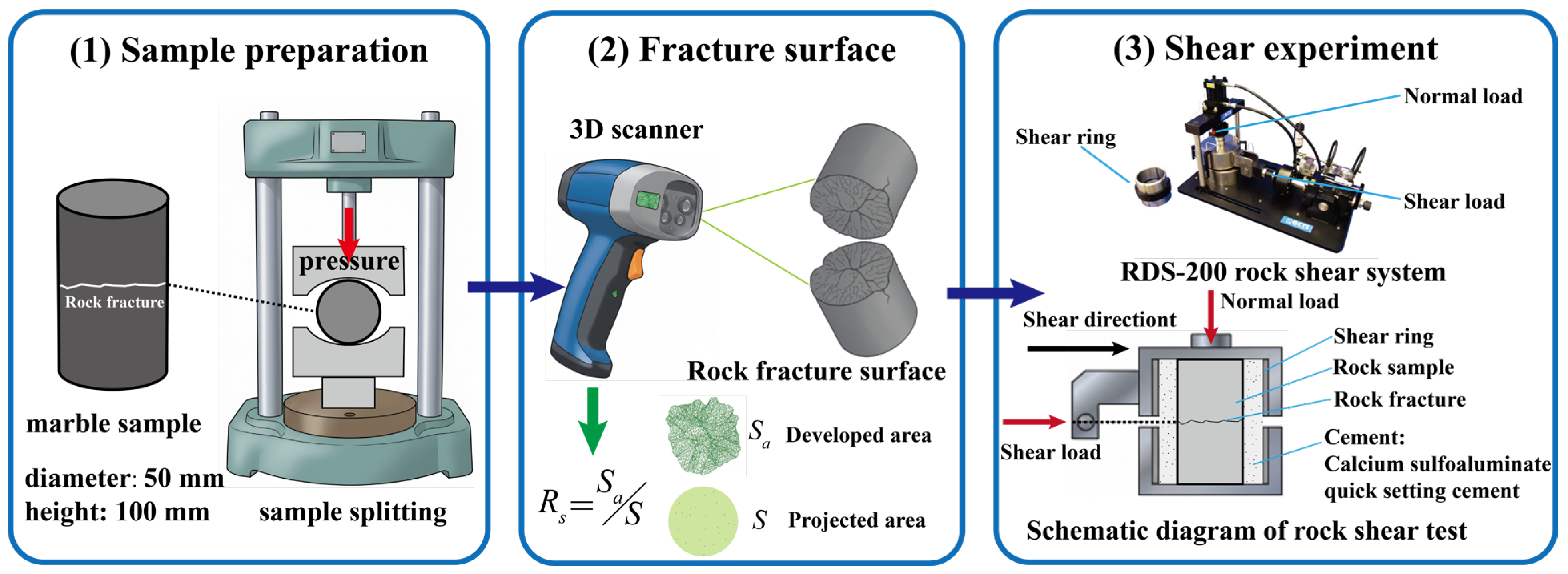
2.1. Marble Materials and Fracture Preparation
2.2. Experimental Equipment
2.3. Test Procedure
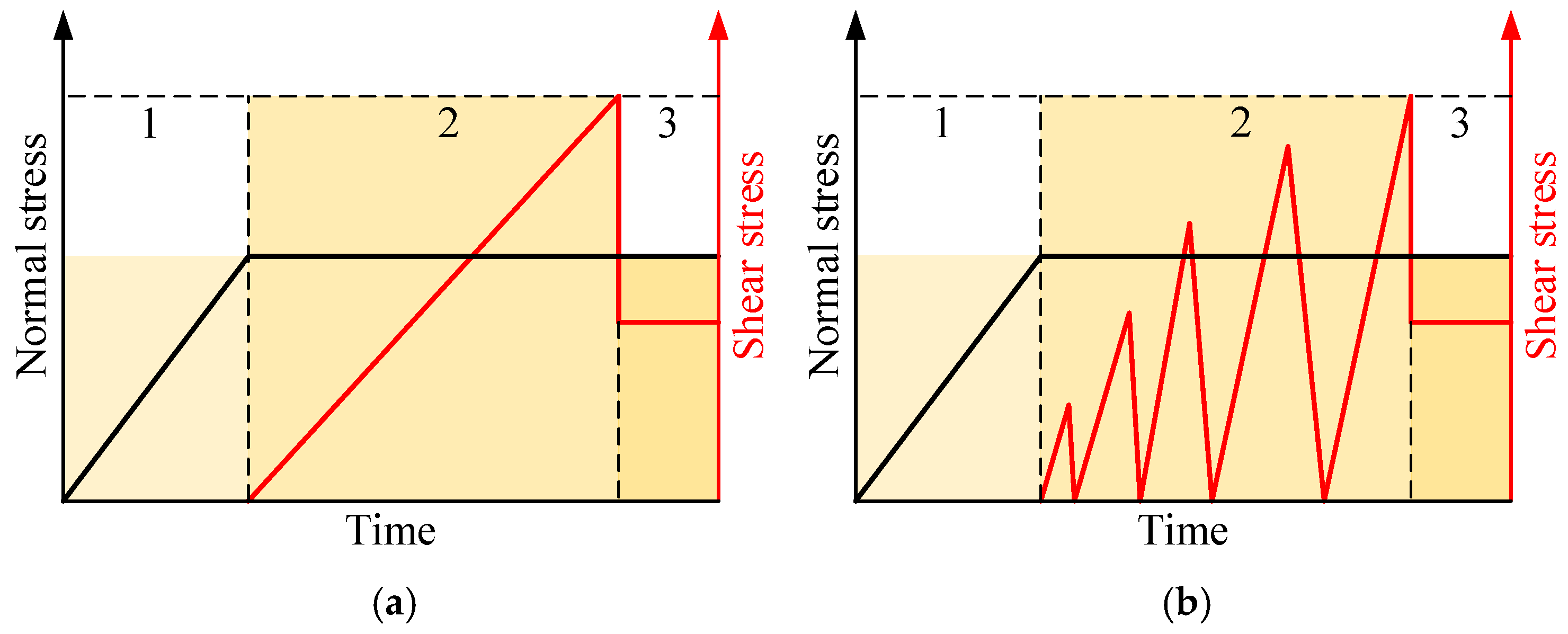
2.3.1. Direct Shear Test
2.3.2. Tiered Cyclic Shear Tests
3. Experimental Results and Analysis
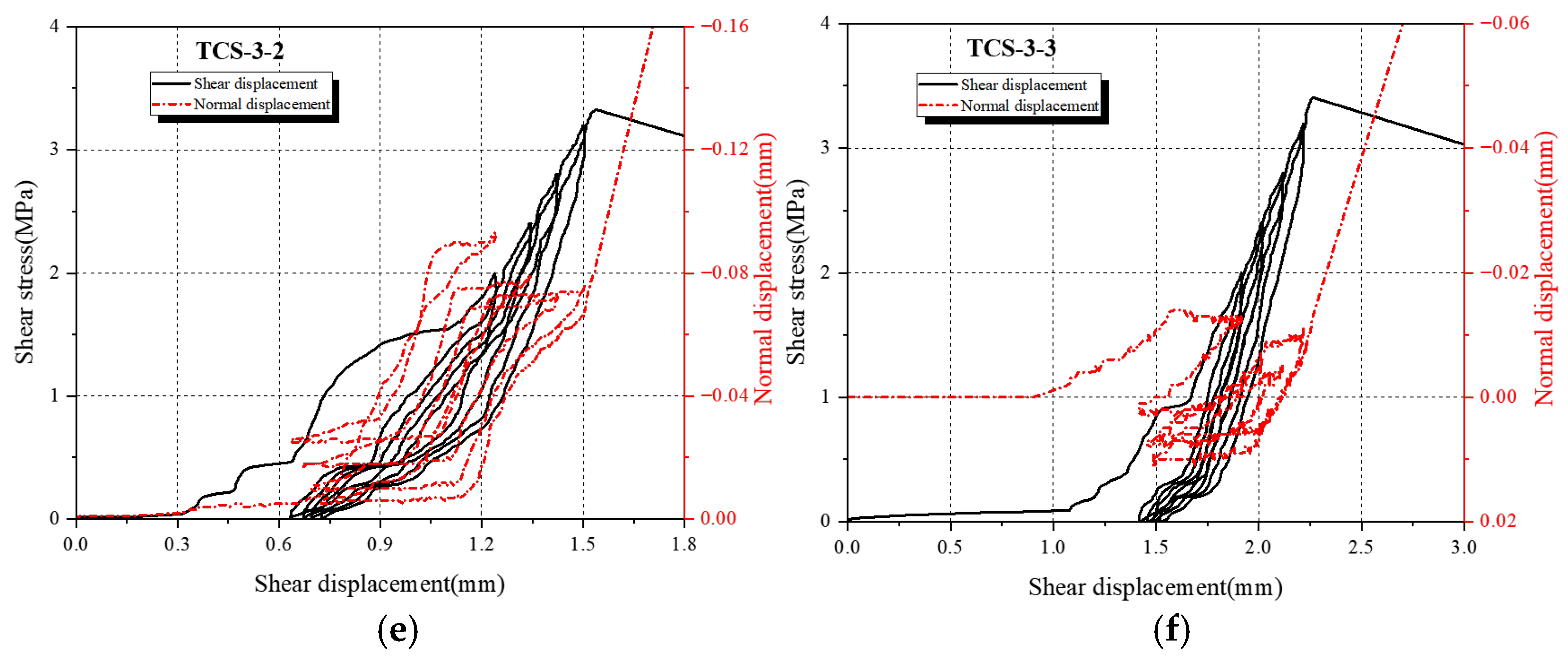
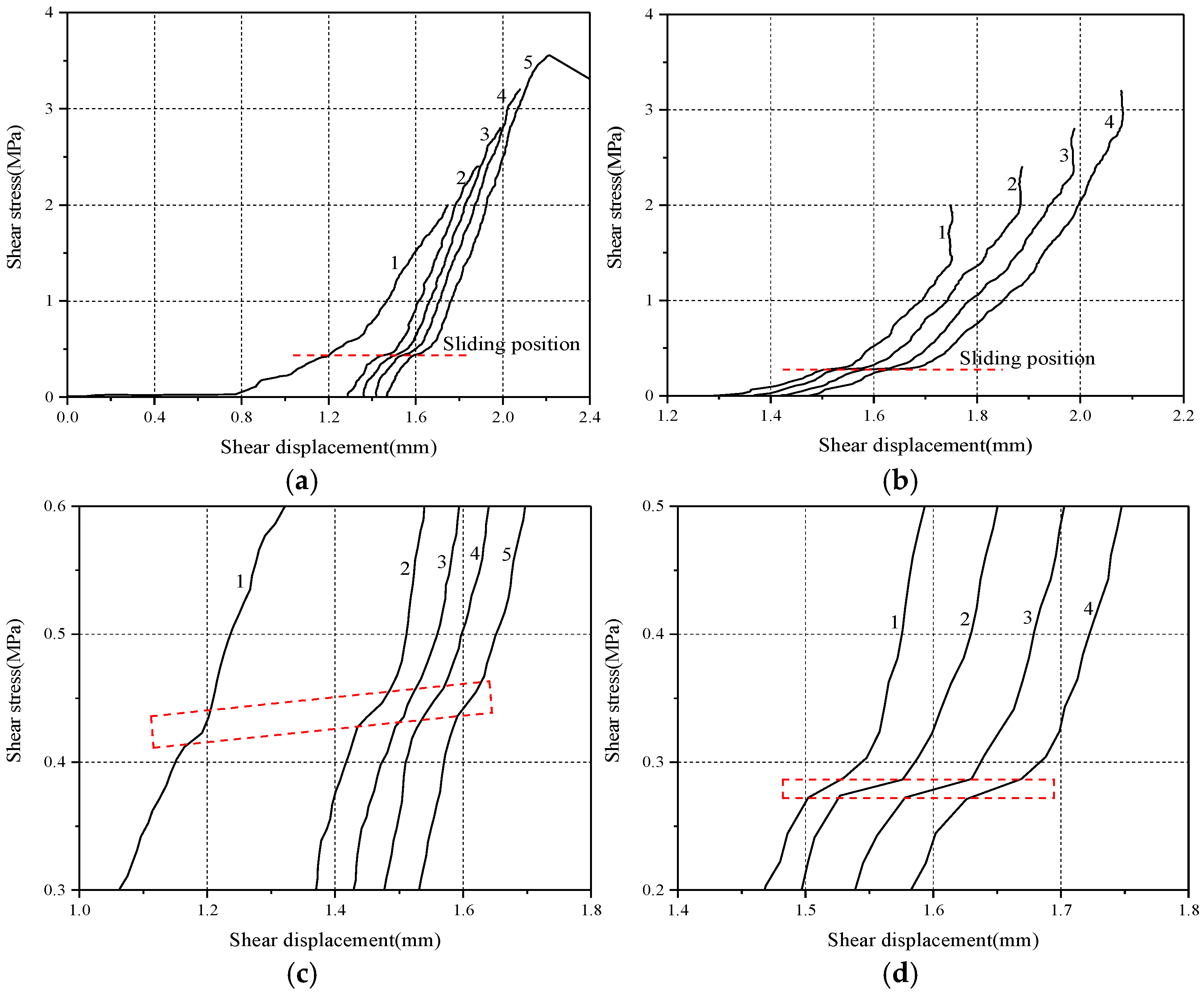
3.1. Shear Stress-Shear Displacement Curves
3.1.1. Changes of Shear Displacement
3.1.2. Residual Shear Displacement
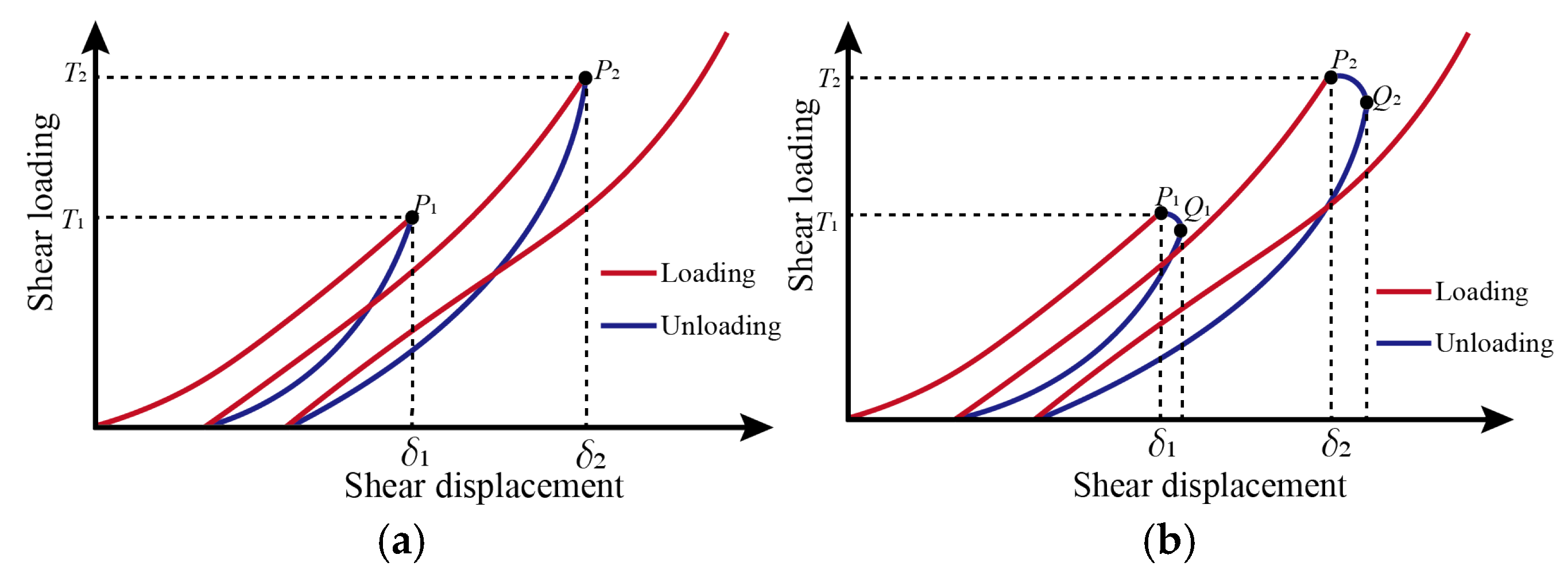
3.1.3. Shear Slip During Loading and Unloading
3.1.4. Shear Displacement Hysteresis
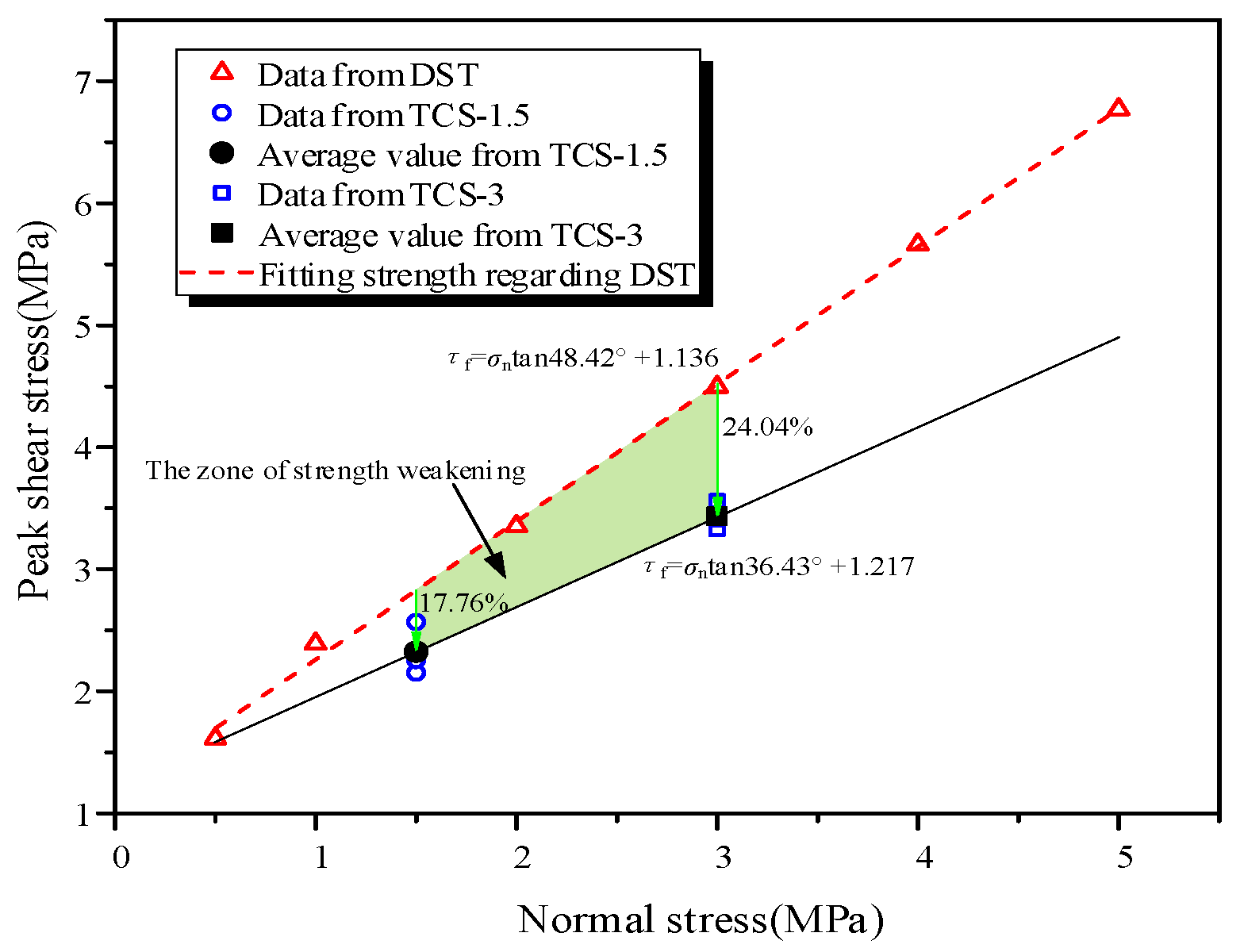
3.2. Peak Shear Stress
3.3. Failure Morphology
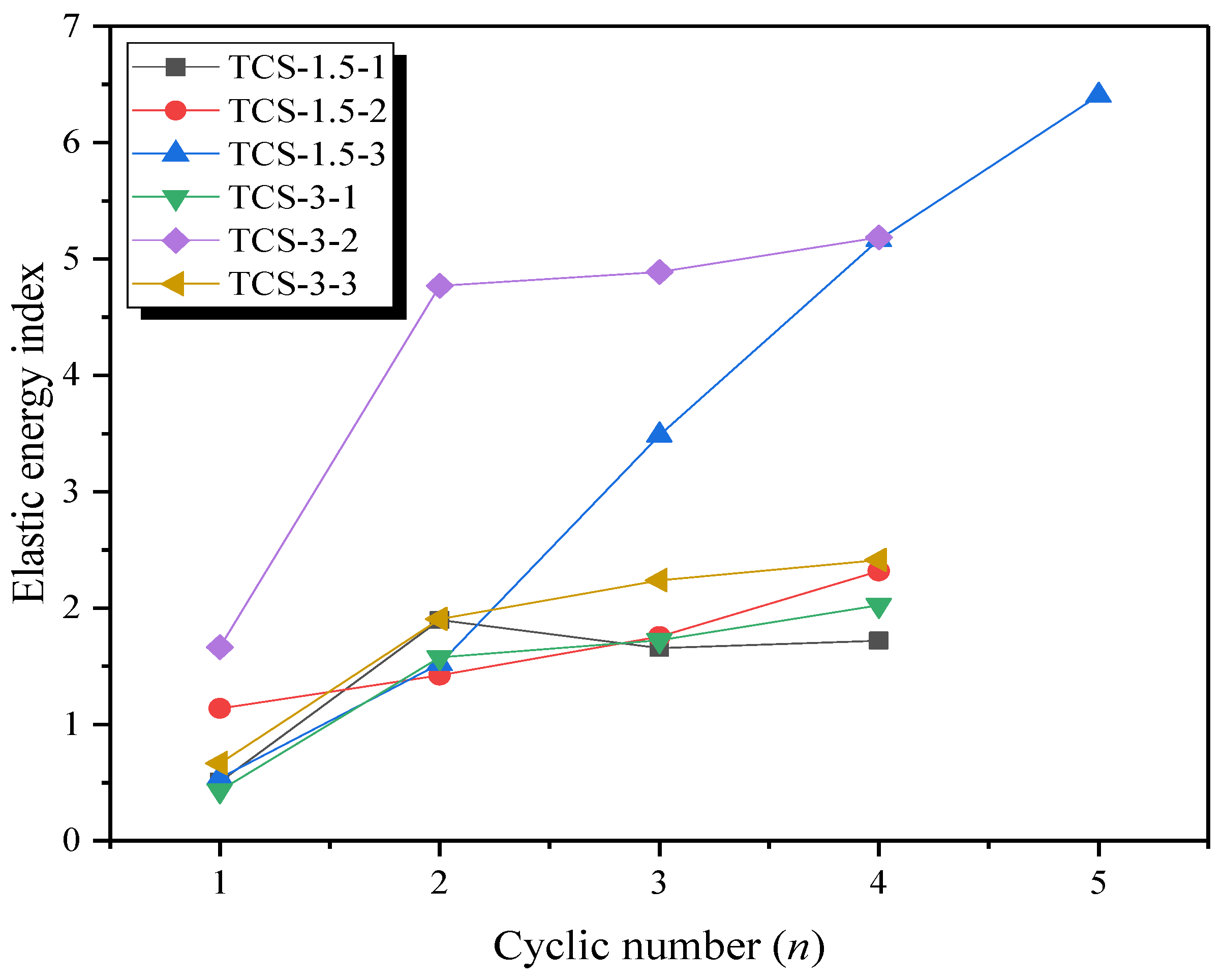
3.4. Energy Evolution
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ISRM | International Society for Rock Mechanics |
| TCS | Tiered Cyclic Shear |
| DST | Direct Shear Test |
| RSD | Residual Shear Displacement |
| σ | Normal Load |
| vl | Loading Rate |
| vu | Unloading Rate |
| Rs | Contour Area Ratio |
| U | Total Energy |
| Ue | Elastic Energy |
| Ud | Dissipated Energy |
| Sa | The Developed Area Of The Fracture Contour Surface |
| S | The Projected Area Of The Fracture Contour Surface |
| tf | Peak Shear Strength |
References
- Guo, N.; Li, C.; Liu, H.; Wang, Y. Dynamic Fracture and Energy Evolution Characterization of Naturally Fractured Granite Subjected to Multilevel Cyclic Loads. Geofluids 2021, 2021, 6685123. [Google Scholar] [CrossRef]
- Tang, Z.C.; Li, L.; Wang, X.C.; Zou, J.P. Influence of Cyclic Freezing-Thawing Treatment on Shear Behaviors of Granite Fracture under Dried and Saturated Conditions. Cold Reg. Sci. Technol. 2021, 181, 103192. [Google Scholar] [CrossRef]
- Tang, Z.C.; Zhang, Q.Z.; Peng, J.; Jiao, Y.Y. Experimental Study on the Water-Weakening Shear Behaviors of Sandstone Joints Collected from the Middle Region of Yunnan Province, P.R. China. Eng. Geol. 2019, 258, 105161. [Google Scholar] [CrossRef]
- Meng, F.; Wong, L.N.Y.; Zhou, H.; Wang, Z. Comparative Study on Dynamic Shear Behavior and Failure Mechanism of Two Types of Granite Joint. Eng. Geol. 2018, 245, 356–369. [Google Scholar] [CrossRef]
- Day, J.J.; Diederichs, M.S.; Hutchinson, D.J. New Direct Shear Testing Protocols and Analyses for Fractures and Healed Intrablock Rockmass Discontinuities. Eng. Geol. 2017, 229, 53–72. [Google Scholar] [CrossRef]
- Ge, Y.; Xie, Z.; Tang, H.; Chen, H.; Lin, Z.; Du, B. Determination of Shear Failure Regions of Rock Joints Based on Point Clouds and Image Segmentation. Eng. Geol. 2019, 260, 105250. [Google Scholar] [CrossRef]
- Fathi, A.; Moradian, Z.; Rivard, P.; Ballivy, G. Shear Mechanism of Rock Joints under Pre-Peak Cyclic Loading Condition. Int. J. Rock Mech. Min. Sci. 2016, 83, 197–210. [Google Scholar] [CrossRef]
- Kou, M.; Liu, X.; Tang, S.; Wang, Y. Experimental Study of the Prepeak Cyclic Shear Mechanical Behaviors of Artificial Rock Joints with Multiscale Asperities. Soil Dyn. Earthq. Eng. 2019, 120, 58–74. [Google Scholar] [CrossRef]
- Liu, X.; Kou, M.; Lu, Y.; Liu, Y. An Experimental Investigation on the Shear Mechanism of Fatigue Damage in Rock Joints under Pre-Peak Cyclic Loading Condition. Int. J. Fatigue 2018, 106, 175–184. [Google Scholar] [CrossRef]
- Liu, X.; Deng, Z.; Liu, Y.; Liu, S.; Lu, Y.; Han, Y. An experimental study on the cumulative damage and shear properties of rock joints under pre-peak cyclic shear loading. Chin. J. Rock Mech. Eng. 2018, 37, 2664–2675. [Google Scholar] [CrossRef]
- Yang, X.; Zhou, J.; Song, Y.; Han, X. Evolution characteristics of sliding displacement of rock interface under cyclic loading. J. China Coal Soc. 2019, 44, 3041–3048. [Google Scholar] [CrossRef]
- Ge, Y.; Tang, H.; Wang, L.; Xiong, C.; Zhang, S.; Wang, D. Strain energy evolution of penetrative rock joints under shear loading. Chin. J. Rock Mech. Eng. 2016, 35, 1111–1121. [Google Scholar] [CrossRef]
- Zhai, M.; Guo, B.; Li, B.; Jiao, F. Energy and deformation characteristics of rock joints under multi-stage shear loading-creep-unloading conditions. Rock Soil Mech. 2018, 39, 2865–2872, 2885. [Google Scholar] [CrossRef]
- Hashiguchi, K. Foundations of Elastoplasticity: Subloading Surface Model; Springer: Berlin/Heidelberg, Germany, 2017; ISBN 3-319-48821-X. [Google Scholar]
- Fathi, A.; Moradian, Z.; Rivard, P.; Ballivy, G.; Boyd, A.J. Geometric Effect of Asperities on Shear Mechanism of Rock Joints. Rock Mech. Rock Eng. 2016, 49, 801–820. [Google Scholar] [CrossRef]
- Guo, B.; Dong, H. Shear Failure Modes and AE Characteristics of Sandstone and Marble Fractures. Open Geosci. 2019, 11, 249–262. [Google Scholar] [CrossRef]
- Song, Y.; Deng, L.; Lyu, X.; Xu, H.; Zhao, Z. Study of acoustic emission characteristics and deformation evolution during rock frictional sliding. Rock Soil Mech. 2019, 40, 2899–2906, 2913. [Google Scholar] [CrossRef]
- Zhai, M.; Bai, H.; Wu, L. Shear Slip Instability Behavior of Rock Fractures under Prepeak Tiered Cyclic Shear Loading. Adv. Civ. Eng. 2020, 2020, 8851890. [Google Scholar] [CrossRef]
- Gao, Y.; Feng, X.-T. Study on Damage Evolution of Intact and Jointed Marble Subjected to Cyclic True Triaxial Loading. Eng. Fract. Mech. 2019, 215, 224–234. [Google Scholar] [CrossRef]
- Liu, X.S.; Ning, J.G.; Tan, Y.L.; Gu, Q.H. Damage Constitutive Model Based on Energy Dissipation for Intact Rock Subjected to Cyclic Loading. Int. J. Rock Mech. Min. Sci. 2016, 85, 27–32. [Google Scholar] [CrossRef]
- Peng, R.-D.; Ju, Y.; Gao, F.; Xie, H.-P.; Wang, P. Energy Analysis on Damage of Coal under Cyclical Triaxial Loading and Unloading Conditions. J. China Coal Soc. 2014, 39, 245–252. [Google Scholar]
- Song, D.; Wang, E.; Liu, J. Relationship between EMR and Dissipated Energy of Coal Rock Mass during Cyclic Loading Process. Saf. Sci. 2012, 50, 751–760. [Google Scholar] [CrossRef]
- Tang, L.; Zhao, Y.; Liao, J.; Liu, Q. Creep Experimental Study of Rocks Containing Weak Interlayer under Multilevel Loading and Unloading Cycles. Front. Earth Sci. 2020, 8, 519461. [Google Scholar] [CrossRef]
- Tang, Z.C.; Jiao, Y.Y.; Wong, L.N.Y.; Wang, X.C. Choosing Appropriate Parameters for Developing Empirical Shear Strength Criterion of Rock Joint: Review and New Insights. Rock Mech. Rock Eng. 2016, 49, 4479–4490. [Google Scholar] [CrossRef]
- Wang, X.; Lian, B.; Wang, J.; Feng, W.; Gu, T.-F. Creep Damage Properties of Sandstone under Dry-Wet Cycles. J. Mt. Sci. 2020, 17, 3112–3122. [Google Scholar] [CrossRef]
- Zuo, J.; Xie, H.; Meng, B.; Liu, J. Experimental Research on Loading-Unloading Behavior of Coal-Rock Combination Bodies at Different Stress Levels. Rock Soil Mech. 2011, 32, 1287–1296. [Google Scholar] [CrossRef]
- Li, Y.; Wu, W.; Tang, C.; Liu, B. Predicting the Shear Characteristics of Rock Joints with Asperity Degradation and Debris Backfilling under Cyclic Loading Conditions. Int. J. Rock Mech. Min. Sci. 2019, 120, 108–118. [Google Scholar] [CrossRef]
- Dong, H.; Guo, B.; Li, Y.; Si, K.; Wang, L. Empirical Formula of Shear Strength of Rock Fractures Based on 3D Morphology Parameters. Geotech. Geol. Eng. 2017, 35, 1169–1183. [Google Scholar] [CrossRef]
- Chen, Y.; Zuo, J.; Li, Z.; Dou, R. Experimental Investigation on the Crack Propagation Behaviors of Sandstone under Different Loading and Unloading Conditions. Int. J. Rock Mech. Min. Sci. 2020, 130, 104310. [Google Scholar] [CrossRef]
- Jiang, C.; Duan, M.; Yin, G.; Wang, J.; Lu, T.; Xu, J.; Zhang, D.; Huang, G. Experimental Study on Seepage Properties, AE Characteristics and Energy Dissipation of Coal under Tiered Cyclic Loading. Eng. Geol. 2017, 221, 114–123. [Google Scholar] [CrossRef]
- Peng, K.; Wang, Y.; Zou, Q.; Liu, Z.; Mou, J. Effect of Crack Angles on Energy Characteristics of Sandstones under a Complex Stress Path. Eng. Fract. Mech. 2019, 218, 106577. [Google Scholar] [CrossRef]
- Sheng, M.; Li, P.; Zhuang, X.; Wang, J. Influence of Cyclic Normal Stress on Shear Friction of EGS Granite Fractures. Eng. Fract. Mech. 2020, 238, 107268. [Google Scholar] [CrossRef]
- Song, Z.; Frühwirt, T.; Konietzky, H. Characteristics of Dissipated Energy of Concrete Subjected to Cyclic Loading. Constr. Build. Mater. 2018, 168, 47–60. [Google Scholar] [CrossRef]
- Song, Z.; Konietzky, H.; Frühwirt, T. Hysteresis Energy-Based Failure Indicators for Concrete and Brittle Rocks under the Condition of Fatigue Loading. Int. J. Fatigue 2018, 114, 298–310. [Google Scholar] [CrossRef]
- Wang, Y.; Li, C.; Liu, H.; Han, J. Fracture Failure Analysis of Freeze–Thawed Granite Containing Natural Fracture under Uniaxial Multi-Level Cyclic Loads. Theor. Appl. Fract. Mech. 2020, 110, 102782. [Google Scholar]
- Zhu, T.; Huang, D. Experimental Investigation of the Shear Mechanical Behavior of Sandstone under Unloading Normal Stress. Int. J. Rock Mech. Min. Sci. 2019, 114, 186–194. [Google Scholar]
- Li, D.; Sun, Z.; Xie, T.; Li, X.; Ranjith, P. Energy Evolution Characteristics of Hard Rock during Triaxial Failure with Different Loading and Unloading Paths. Eng. Geol. 2017, 228, 270–281. [Google Scholar] [CrossRef]
- Li, T.; Pei, X.; Wang, D.; Huang, R.; Tang, H. Nonlinear Behavior and Damage Model for Fractured Rock under Cyclic Loading Based on Energy Dissipation Principle. Eng. Fract. Mech. 2019, 206, 330–341. [Google Scholar] [CrossRef]
- Meng, Y.; Jing, H.; Yin, Q.; Gu, X. Investigation on mechanical and AE characteristics of yellow sandstone undergoing wetting-drying cycles. KSCE J. Civ. Eng. 2020, 24, 3267–3278. [Google Scholar] [CrossRef]
- Xie, H.; Li, L.; Peng, R.; Ju, Y. Energy Analysis and Criteria for Structural Failure of Rocks. J. Rock Mech. Geotech. Eng. 2009, 1, 11–20. [Google Scholar] [CrossRef]
- Zhu, X.-Y.; Chen, X.-D.; Dai, F. Mechanical Properties and Acoustic Emission Characteristics of the Bedrock of a Hydropower Station under Cyclic Triaxial Loading. Rock Mech. Rock Eng. 2020, 53, 5203–5221. [Google Scholar] [CrossRef]
- Xie, H.; Ju, Y.; Li, L. Criteria for strength and structural failure of rocks based on energy dissipation and energy release principles. Chin. J. Rock Mech. Eng. 2005, 24, 3003–3010. [Google Scholar]
- Jin, F.; Jiang, M.; Gao, X. Defining damage variable based on energy dissipation. Chin. J. Rock Mech. Eng. 2004, 23, 1976–1980. [Google Scholar]
- Gong, F.; Yan, J.; Li, X.; Luo, S. A Peak-Strength Strain Energy Storage Index for Rock Burst Proneness of Rock Materials. Int. J. Rock Mech. Min. Sci. 2019, 117, 76–89. [Google Scholar] [CrossRef]
- De Maio, U.; Gaetano, D.; Greco, F.; Lonetti, P.; Pranno, A. An Adaptive Cohesive Interface Model for Fracture Propagation Analysis in Heterogeneous Media. Eng. Fract. Mech. 2025, 325, 111330. [Google Scholar] [CrossRef]
- Tomporowski, D.; Nitka, M.; Tejchman, J. Application of the 3D DEM in the Modelling of Fractures in Pre-Flawed Marble Specimens during Uniaxial Compression. Eng. Fract. Mech. 2023, 277, 108978. [Google Scholar] [CrossRef]




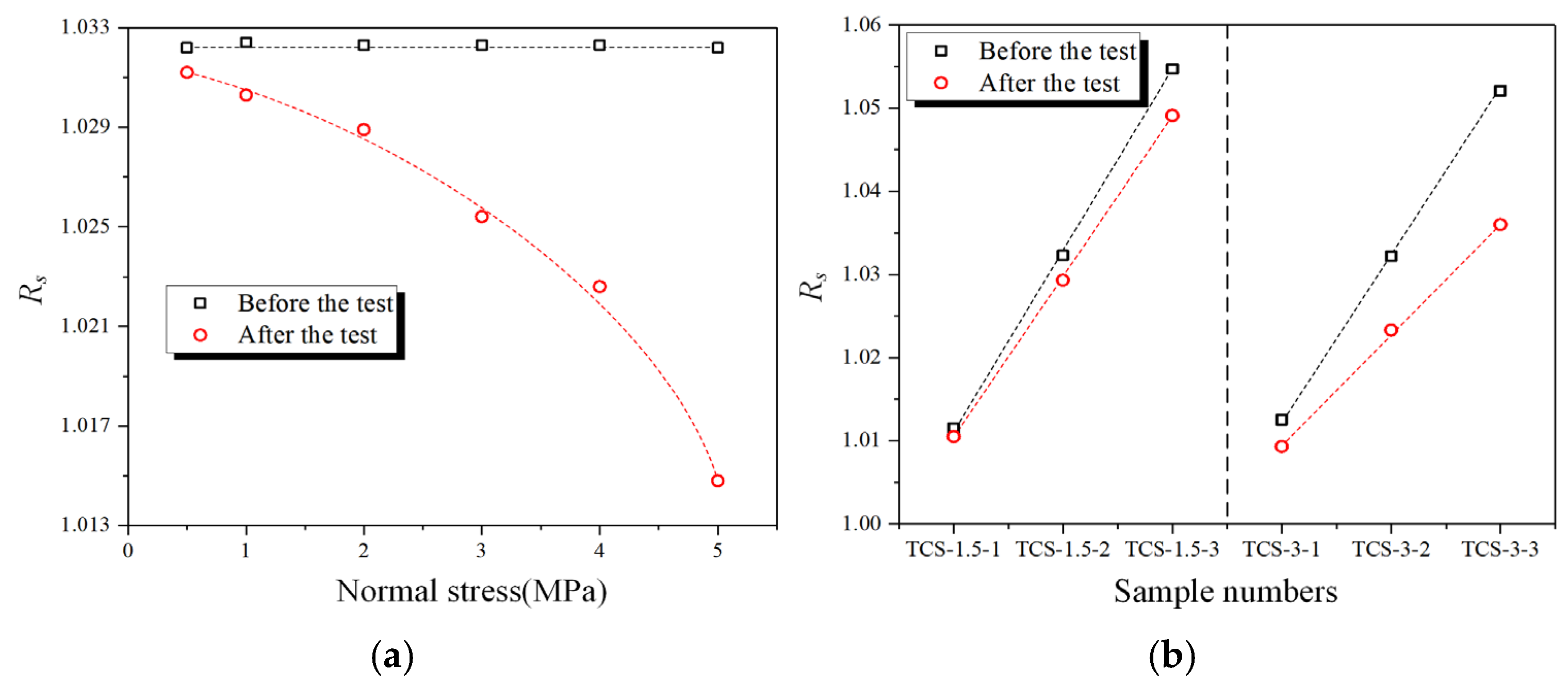

| Specimen | Rs | σ (MPa) | vl (KPa/s) | vu (KPa/s) |
|---|---|---|---|---|
| DST-0.5 | 1.03218 | 0.5 | 20 | 0 |
| DST-1 | 1.03241 | 1 | 20 | 0 |
| DST-2 | 1.03232 | 2 | 20 | 0 |
| DST-3 | 1.03225 | 3 | 20 | 0 |
| DST-4 | 1.03229 | 4 | 20 | 0 |
| DST-5 | 1.03219 | 5 | 20 | 0 |
| TCS-1.5-1 | 1.01146 | 1.5 | 20 | 10 |
| TCS-1.5-2 | 1.03227 | 1.5 | 20 | 10 |
| TCS-1.5-3 | 1.05466 | 1.5 | 20 | 10 |
| TCS-3-1 | 1.01248 | 3 | 20 | 10 |
| TCS-3-2 | 1.03218 | 3 | 20 | 10 |
| TCS-3-3 | 1.05212 | 3 | 20 | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Xia, Z.; Shan, C.; Xu, Q.; Yao, Q.; Li, H. Influence of Tiered Cyclic Shear Stress on Shear Friction and Instability Behavior of Marble Specimens with the Fractures. Appl. Sci. 2025, 15, 10308. https://doi.org/10.3390/app151910308
Li Y, Xia Z, Shan C, Xu Q, Yao Q, Li H. Influence of Tiered Cyclic Shear Stress on Shear Friction and Instability Behavior of Marble Specimens with the Fractures. Applied Sciences. 2025; 15(19):10308. https://doi.org/10.3390/app151910308
Chicago/Turabian StyleLi, Yinghu, Ze Xia, Changhao Shan, Qiang Xu, Qiangling Yao, and Haitao Li. 2025. "Influence of Tiered Cyclic Shear Stress on Shear Friction and Instability Behavior of Marble Specimens with the Fractures" Applied Sciences 15, no. 19: 10308. https://doi.org/10.3390/app151910308
APA StyleLi, Y., Xia, Z., Shan, C., Xu, Q., Yao, Q., & Li, H. (2025). Influence of Tiered Cyclic Shear Stress on Shear Friction and Instability Behavior of Marble Specimens with the Fractures. Applied Sciences, 15(19), 10308. https://doi.org/10.3390/app151910308






