GPU-Accelerated PSO for High-Performance American Option Valuation

Abstract

Using artificial intelligence tools to evaluate financial derivatives has become increasingly popular. PSO (particle swarm optimization) is one such tool. We present a comprehensive study of PSO for pricing American options on GPUs using OpenCL. PSO is an increasingly popular heuristic for financial parameter search; however, its high computational cost (especially for path-dependent derivatives) poses a challenge. We review PSO-based pricing and survey prior GPU acceleration efforts. We then describe our OpenCL optimization pipeline on an Apple M3 Max GPU (OpenCL 1.2 via PyOpenCL 2024.1). Starting from a NumPy baseline (36.7 s), we apply successive enhancements: an initial GPU offload (8.0 s), restructuring loops (forward/backward) to minimize divergence (2.3 s → 0.95 s), kernel fusion (0.94 s), and explicit SIMD vectorization (float4) (0.25 s). The fully fused float4 kernel achieves 0.246 s, a ~150X speedup over CPU. We analyzed all eight intermediate kernels (named by file), detailing techniques (memory coalescing, branch avoidance, etc.) and their effects on throughput. Our results exceed prior art in speed and vector efficiency, illustrating the power of combined OpenCL strategies.

1. Introduction

Using artificial intelligence tools to evaluate financial derivatives has become increasingly popular (e.g., see recent work of John Hull (2020) [1] of using reinforcement learning and Andrew Lo (2023) [2] of using neural networks). PSO (particle swarm optimization) is one such tool. Pricing American-style options (which may be exercised at any time before expiration) is a fundamental yet computationally intensive problem in finance. Traditional methods (binomial trees, least-squares Monte Carlo) become prohibitively expensive for high-dimensional or path-dependent payoffs. Particle swarm optimization (PSO) is a nature-inspired global search heuristic (Eberhart & Kennedy, 1995 [3]) that has been adapted to financial problems (Refer https://ieeexplore.ieee.org/abstract/document/494215 (accessed on 25 August 2025)), including locating exercise boundaries of American options. However, naïve PSO is very slow in this context: each swarm “particle” must evaluate many option payoffs (often via expensive Monte Carlo simulations). This motivates exploiting highly parallel hardware to accelerate PSO-based pricing.

Graphics Processing Units (GPUs) excel at data-parallel tasks and have been applied to many finance algorithms. For example, Sharma et al. (2013) [4] note that PSO’s inherent concurrency can be efficiently exploited on modern GPUs (Refer https://link.springer.com/article/10.1007/s11227-013-0893-z#:~:text=options%20using%20these%20numerical%20techniques,of%20the%20PSO%20algorithm%20while (accessed on 25 August 2025)). Prior work on GPU acceleration includes that by Verche and Stojanovski (2012) [5], who implemented a GPU-based Monte Carlo pricer for American options and reported that high-performance computing yields “promising results” in option simulation (Refer https://arxiv.org/abs/1205.0106#:~:text=,the%20GPU%20for%20executing%20the (accessed on 25 August 2025)). More recently, Li and Chen (2023) [6] implemented Monte Carlo PSO for American pricing on GPUs, showing that very large particle populations could be handled with little change in wall-clock time. Despite these advances, existing GPU-PSO approaches have limitations. They tend to focus on algorithmic acceleration rather than low-level code optimization. For example, many implementations underutilize hardware features such as explicit SIMD vector units, kernel fusion, and on-chip caching, as evidenced by Liu et al. (2021) [7], who achieved 5–7× speedups over earlier GPU-PSO codes through careful memory and cache optimization (Refer https://faculty.washington.edu/weicaics/paper/papers/LiuWC2021.pdf (accessed on 25 August 2025)). Prior studies also seldom release full code or detailed pipelines, making it hard to reproduce or extend their results. In short, past GPU-PSO work in option pricing often lacks a complete end-to-end optimization pipeline and full hardware utilization, leaving substantial performance on the table.

Our goal in this work is to systematically maximize GPU performance for PSO-based American option pricing. Specifically, we ask: How can we exploit advanced OpenCL programming techniques to accelerate a PSO pricer for American options? To this end, we develop and evaluate a step-by-step OpenCL optimization pipeline on an Apple M3 Max GPU. Our aim is to leverage the GPU’s high-performance parallelism (SIMD, multithreading, coalesced memory) to dramatically reduce PSO runtime. In particular, we apply a sequence of well-known optimizations—GPU offloading, loop restructuring to avoid branch divergence, memory coalescing, kernel fusion, and explicit SIMD vectorization—to a PSO-based option fitness kernel. We measure the performance impact at each stage to understand which techniques yield the greatest speedups. This objective aligns with the insights of Li and Chen (2023) [6] on harnessing GPU SIMD for option pricing, but goes further by giving a full implementation roadmap.

Our main contributions are as follows. First, we present a comprehensive GPU-accelerated pipeline for American option pricing via PSO. We begin with a CPU (NumPy 1.26.4) baseline and then implement eight successive OpenCL kernels (file-named) that incorporate increasing levels of optimization. The enhancements include an initial GPU offload of the simulation loop, restructuring of forward/backward passes to minimize divergence, fusion of kernels to reduce launch overhead, and finally explicit float4 SIMD vectorization. Each kernel is analyzed in detail, highlighting how memory coalescing and branch avoidance improve throughput. Second, we demonstrate that the fully optimized kernel achieves dramatic performance gains: the final fused float4 implementation computes an American option price in roughly 0.246 s, about a 150× speedup over the 36.7 s CPU baseline. This result not only matches but exceeds prior GPU implementations in both speed and vector efficiency. In particular, compared to earlier GPU-PSO work (which rarely used fusion or SIMD), our implementation attains higher throughput on similar hardware. Third, we emphasize novelty and reproducibility. We use OpenCL for portability and explicitly exploit the Apple GPU’s features, showing that even non-NVIDIA hardware can deliver state-of-the-art results. We document all eight intermediate kernels (with file names) to illustrate our code evolution, providing a clear, reproducible reference. To our knowledge, no prior PSO option-pricing study has combined these low-level optimizations in such an integrated way. In sum, our work extends the literature by delivering one of the fastest GPU-PSO American option pricers to date and by providing a detailed optimization methodology for future researchers.

Beyond technical implementation, this study situates itself within the broader application of metaheuristics in finance. Techniques such as genetic algorithms, simulated annealing, ant colony optimization, and differential evolution have all been explored in contexts ranging from portfolio optimization to option pricing. These approaches are motivated by the inherent nonlinearity and path-dependence of many financial problems, which often render gradient-based methods ineffective. Particle Swarm Optimization (PSO) is one representative metaheuristic, offering simplicity, empirical robustness, and natural parallelism. By adopting PSO for American option valuation and coupling it with GPU acceleration, our work contributes both to the methodological literature on metaheuristics in finance and to the practice of scalable derivative pricing.

The remainder of the paper is organized as follows. Section 2 reviews PSO in derivative pricing. Section 3 surveys GPU-PSO acceleration in finance and discusses gaps in prior approaches. Section 4 reports our methodology. Section 5 details our OpenCL optimization strategies. Section 6 describes our experimental setup and per-kernel performance analysis. Section 7 compares our results to related work, Section 8 discusses scalability, Section 9 surveys integration with financial workflows, and Section 10 concludes. A brief sketch of American option pricing via Monte Carlo simulations is included in Appendix A.

2. Particle Swarm Optimization for Derivative Pricing

The use of metaheuristics in finance has been motivated by their ability to navigate large, non-convex search spaces. For instance, genetic algorithms (GA) have been applied to calibrate option pricing models and optimize portfolios; differential evolution (DE) has been explored for volatility surface calibration; and simulated annealing (SA) has been tested for exotic derivative pricing. Ant colony optimization (ACO) has also been studied for credit risk and trading strategies. These studies highlight that financial optimization problems often resist closed-form analysis and benefit from heuristic search methods. Within this family, PSO is attractive because of its straightforward implementation, relatively few control parameters, and demonstrated success in derivative pricing tasks.

Our choice of PSO is therefore theoretically grounded in its balance between exploratory power and computational efficiency. Unlike GA or DE, which may require complex crossover and mutation operators, PSO relies on position-velocity updates that map naturally onto vectorized GPU operations. Moreover, PSO’s swarm-based search has been shown to perform well in problems with multiple local optima, such as early-exercise decision rules in American options. At the same time, we acknowledge that PSO, like other metaheuristics, lacks formal convergence guarantees. This limitation underscores the importance of empirical validation and motivates our emphasis on reproducibility and performance analysis.

PSO is a population-based stochastic optimization method: a “swarm” of candidate solutions (particles) moves through the search space guided by individual and collective best positions. Each particle updates its velocity and position based on its own history and the global best.

Formally, let $x_i\left(t\right)$ be the position and $v_i\left(t\right)$ be the velocity of the $i$-th particle at time $t$ where $i=1,\cdots ,n$. Each particle remembers its best position as $p_i\left(t\right)$. At each time $t$, across all particles, there is a global best whose position is labeled as $g\left(t\right)$. A typical PSO models the velocity as follows:

$$v_i\left(t+1\right)=w{v}_i\left(t\right)+c_1{r}_1\left(p_i\left(t\right)-x_i\left(t\right)\right)+c_2{r}_2\left(g\left(t\right)-x_i\left(t\right)\right)$$

(1)

and position is revised as follows:

$$x_i\left(t+1\right)=x_i\left(t\right)+v_i\left(t+1\right)$$

(2)

Note that in Equation (1), $c_1$ and $c_2$ are two arbitrary constants of the user’s choice to weigh between personal best and global best; and $r_1$ and $r_2$ are two uniform random variables whose purpose is to let each particle search a neighborhood of its personal best and the global best. PSO typically requires many iterations over a swarm of many particles, making it computationally expensive for complex fitness functions.

In finance, PSO has been applied to calibrate option models and price exotic derivatives. For example, the Black–Scholes or binomial pricing error can be minimized by PSO to infer implied volatility or other parameters. PSO has also been used to approximate exercise boundaries for American and exotic options. Chen et al. (2021) [8] applied PSO to find the exercise boundary of American puts and Asian options, noting that PSO effectively searches high-dimensional spaces. Different from Chen et al. [8], who adopt the Carr-Jarrow-Myneni (2008) [9] algorithm (Also see Carr (1998) [10] for the original pricing methodology), Cvetanoska and Stojanovski (2012) [5] use PSO and GPU to evaluate American options with the Broadie-Glasserman (1997) [11] algorithm; and finally, Fatica and Phillips (2013) [12], Chen (2016) [13], and Chen, Huang, and Lyuu (2015) [14] adopt the Longstaff–Schwartz’s least square algorithm [15]. In addition, Sharma et al. (2013) [4] developed a “Normalized PSO” for complex chooser options and explicitly implemented it on a GPU to exploit PSO’s inherent parallelism. We should note that another application of using PSO-GPU on option pricing focuses on binomial lattices and PDEs (partial differential equations). The former includes Jha et al. (2009) [16], Zhang et al. (2012) [17], Zhang, Lei, and Man (2012, 2013) [18,19], and Popuri et al. (2013) [20]. The latter includes Sak, Özekici, and Boduroglu (2007) [21] and Dang, Christara, and Jackson (2011) [22].

Despite promising results, PSO in pricing remains relatively unnoticed. Most PSO literature in finance has focused on portfolio optimization or calibration, rather than direct option pricing. The high dimensionality and nested simulations of American options make them challenging. Our work extends this line: we directly price an American option via PSO on a GPU, accelerating the underlying Monte Carlo fitness evaluations.

Graphics processors offer massive parallelism that can drastically reduce PSO runtime. PSO algorithms are open “embarrassingly parallel” across particles: each particle’s fitness (e.g., a simulated payoff) can be evaluated independently. Early works parallelized PSO on CUDA or OpenCL. For instance, Liu et al. (2010, 2018) [23,24] and others implemented PSO on GPUs to solve generic optimization problems, achieving tens to hundreds of times speedups over CPU. Cvetanoska and Stojanovski (2012) [5] used GPU-accelerated Monte Carlo to price American options, showing that high-performance computation (HPC) yields “promising results” in financial simulation. Sharma et al. (2013) [4] specifically leveraged GPU features (multithreading, vector units) to speed up PSO for option pricing.

Typical GPU PSO approaches distribute particles to threads or warps and perform vectorized updates. Some advanced schemes use asynchronous or adaptive swarms, but the core idea is running many fitness evaluations in parallel. In our context, each particle evaluates an American option payoff (via Monte Carlo or simulation), and PSO updates proceed across iterations. The main computational burden is these inner computations, which we aim to accelerate on the Apple M3 Max GPU.

Modern derivative pricing increasingly leverages parallel hardware and advanced optimization. Metaheuristic algorithms—especially particle swarm optimization (PSO)—have been proposed to solve the early-exercise/free-boundary problem in American and exotic options. PSO treats the exercise boundary or pricing parameters as decision variables and iteratively updates a “swarm” of candidate solutions. Importantly, both Monte Carlo simulations and PSO updates are highly parallelizable. Recent studies exploit this on GPUs: Li and Chen (2023) [6] show that by performing Monte Carlo PSO on a GPU, increasing the number of particles does not increase wall time significantly; therefore, one can boost accuracy (more particles/paths) “without spending more time”. In their experiments, adding many particles to the GPU led to convergence in very few PSO iterations. Similarly, other works note that GPUs are much better suited for these compute-intensive tasks than CPUs [25]. As Xiao (2024) observes in a survey, optimization heuristics like PSO and GA can “significantly enhance the adaptability and accuracy of classical modes” in option pricing [26].

Particle swarm optimization (PSO) has been widely applied to financial derivative pricing as a flexible global-search method. Early works showed that PSO can effectively price both European and American options with accuracy comparable to classical models. For example, Prasain et al. (2010) [27] designed a sequential PSO algorithm applicable to European and American options (with constant or time-varying volatility) and demonstrated that its prices closely match the Black–Scholes–Merton formula (Refer https://www.researchgate.net/publication/224140856_A_parallel_Particle_swarm_optimization_algorithm_for_option_pricing#:~:text=In%20this%20research%2C%20we%20hav,PSO%20based%20option%20pricing%20algorithm (accessed on 25 August 2025)) [27]. They also developed parallel versions (using OpenMP, MPI, and hybrid models) to speed up computation, finding that parallel PSO scales well as the number of particles grows. Similarly, Sharma et al. (2012) [28] introduced a normalized PSO (NPSO) for a complex “chooser” option, mapping financial parameters to PSO parameters and reducing the number of PSO parameters needed (Refer https://www.researchgate.net/publication/261487569_Portfolio_Management_Using_Particle_Swarm_Optimization_on_GPU#:~:text=accuracy%20in%20pricing%20results,helps%20reach%20the%20solution%20in (accessed on 25 August 2025)) [28]. This NPSO variant was able to price exotic options in a portfolio-like context, benefitting from cooperation among particles to reach solutions faster. Other studies, Jha et al. (2009) [16], confirm that heuristic approaches like PSO yield option prices as good or better than traditional numerical methods at much lower computational cost (Refer https://www.researchgate.net/publication/221186005_Option_pricing_using_Particle_Swarm_Optimization#:~:text=in%20pricing%20results,Our%20implementation (accessed on 25 August 2025)).

• Prasain et al. (2010) [27]—Developed synchronous and parallel PSO algorithms for option pricing. Their sequential PSO handles both European and American options (constant/variable volatility) with results nearly identical to Black–Scholes. The parallel PSO (using OpenMP/MPI) achieved significant speedups for large particle swarms.
• Sharma et al. (2012, 2013) [4,28]—Proposed a “normalized” PSO for complex chooser options, tuning PSO parameters to the pricing problem. Their improved PSO (NPSO) reduces parameter sensitivity and efficiently finds optimal option payoffs. They also implemented NPSO on GPUs, showing large runtime reductions (see next section).
• Other metaheuristics—In addition to PSO, related swarm and evolutionary methods (e.g., Ant Colony, Genetic Algorithms) have been studied for options. However, PSO’s simplicity and convergence properties have made it a popular choice for pricing problems.

These studies collectively establish that PSO can effectively solve high-dimensional derivative pricing problems, often matching analytic solutions (when available) while avoiding the slow convergence of grid-based methods. The literature highlights strategies for mapping option variables (prices, exercise times, volatilities) to particle states and for encoding payoffs in the PSO fitness function. In summary, PSO-based pricing is accurate and flexible; however, it also involves nontrivial parameter tuning and high computational cost for large search spaces, motivating the use of hardware acceleration (see Section 3).

3. GPU Acceleration of PSO and Option Pricing

Graphics processors offer massive parallelism that can drastically reduce PSO runtime. PSO algorithms are open—“embarrassingly parallel”—across particles: each particle’s fitness (e.g., a simulated payoff) can be evaluated independently. For instance, Liu et al. (2010) [23] and others implemented PSO on GPUs to solve generic optimization problems, achieving tens to hundreds of times speedups over CPU. Verche and Stojanovski (2012) [5] used GPU-accelerated Monte Carlo to price American options, showing that high-performance computation (HPC) yields “promising results” in financial simulation. More recently, Liu et al. (2022) [29] proposed a High-Efficiency PSO (HEPSO) on GPUs by moving data initialization fully onto the GPU and using self-adaptive thread management; their HEPSO achieved over 6× speedup relative to a baseline GPU-PSO implementation (Refer https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4289968#:~:text=detailed%20comparative%20analysis%20and%20provide,PSO%20in%20most%20cases (accessed on 25 August 2025)). Sharma et al. (2013) [4] specifically leveraged GPU features (multithreading, vector units) to speed up PSO for option pricing.

Implementations of GPU-accelerated PSO in finance typically use CUDA (NVIDIA) or OpenCL (vendor-neutral). High-performance GPU algorithms recast PSO updates (position, velocity, best values) as element-wise vector/matrix operations to exploit SIMD hardware. For example, Liu et al. (2021) [7] model the entire PSO swarm update as large matrix computations and execute them using CUDA tensor cores and shared memory. They introduce several GPU-specific optimizations: resource-aware thread creation (avoiding oversubscription when particle/dimension counts are large), fast parallel random-number generation for initializing the swarm, and caching swarm state in shared memory instead of repeated global allocations [7]. This implementation, called “FastPSO”, reported speedups of two orders of magnitude over optimized CPU PSO libraries and 5–7× better performance than prior GPU PSO codes. These gains stem from reducing memory overhead and leveraging on-chip caches. In practice, algorithm developers balance coarse-grained and fine-grained parallelism (e.g., block vs. thread level) when mapping PSO to GPU cores.

OpenCL provides a portable framework for such implementations: NVIDIA and other vendors even offer sample OpenCL kernels for financial tasks (e.g., Black–Scholes pricing). In many cases, hybrid CPU/GPU schemes are used for derivative pricing (e.g., CPU handling control flow or tree setups, GPU doing heavy Monte Carlo). Though few papers focus on hybrid PSO, analogous CPU–GPU binomial tree algorithms have been demonstrated. Overall, the literature emphasizes that careful thread/block sizing and memory layout (coalesced access, use of fast shared memory) are crucial when scaling PSO on GPUs.

OpenCL in particular allows writing portable GPU code. Prior work on OpenCL and GPUs provides guidelines for maximizing performance. For example, efficient memory access patterns are critical (coalescing), and branching within a single-instruction multi-data (SIMD) warp should be minimized. These and other techniques (vector data types, on-chip memory use, etc.) are key to fully exploiting GPUs. In the next section, we review these strategies before detailing our implementation.

Notably, these PSO-based methods extend beyond plain vanilla American options. The GPU-PSO framework can cover a wide class of exotic derivatives. Li & Chen (2023) [6] explicitly note that their GPU approach “can be extended to a wide variety of exotic derivatives or a large portfolio of diverse derivatives (multi-instrument eigen-portfolios)”. This suggests applications to, e.g., barrier or lookback options and to portfolio-level valuation, which would be very useful in risk management.

4. Methodology

This study adopts a structured methodology to ensure reproducibility of the GPU-accelerated PSO solver for American option pricing.

4.1. Problem Setup and Variables

We price an American put option with payoff $\mathrm{C}\left(S_t\right)=\mathrm{m}\mathrm{a}\mathrm{x}(\mathrm{K}-S_t,0)$. The option parameters are: initial stock price $S_0=100$, strike $\mathrm{K}=100$, risk-free rate $\mathrm{r}=0.03$, volatility $\mathsf{\sigma }=0.30$, and maturity $\mathrm{T}=1.0$ year. The process is simulated under the risk-neutral measure using geometric Brownian motion with $\mathrm{M}=256$ time steps and $N_{paths}=\mathrm{20,000}$ Monte Carlo paths (with antithetic variates).

4.2. Particle Swarm Optimization (PSO)

A swarm of 512 particles is initialized, each representing a candidate exercise boundary. At each iteration (maximum 100), velocities and positions are updated by $v\leftarrow wv+c_1{r}_1(p_{best}-x)+c_2{r}_2(g_{best}-x), x\leftarrow x+v$.

The fitness of each particle is the option price estimated via backward induction. Convergence is achieved when the global-best value changes by less than ${10}^{-6}$.

4.3. Inputs and Outputs

Inputs: $\{S_0, K, r, \sigma , T, M, N_{paths }, N_{particles}=1024, {Max}_{iterations}=100, w=0.5, c_1=c_2=2.0, seed\}$.

Outputs: estimated option price, runtime, speedup ratio, convergence trajectory.

4.4. Experimental Design

We price an American put option with payoff $\mathrm{C}\left(S_t\right)=\mathrm{m}\mathrm{a}\mathrm{x}(\mathrm{K}-S_t,0)$. The option parameters are: initial stock price $S_0=100$, strike $\mathrm{K}=100$, risk-free rate $\mathrm{r}=0.03$, volatility $\mathsf{\sigma }=0.30$, and maturity $\mathrm{T}=1.0$ year.

We compare against a single-threaded NumPy baseline implementation of PSO fitness evaluation (CPU runtime 36.7 s). GPU experiments are executed on an Apple M3 Max under OpenCL 1.2 (via PyOpenCL). Each configuration is repeated multiple times with different seeds, and we report the mean runtime and option price.

4.5. Reproducibility Measures

Random seeds are fixed to allow exact reproducibility, but multiple seeds are tested to assess robustness. Variability is reported as the mean $\pm$ standard deviation of option prices and runtimes. Convergence stability is verified across runs. Open-source kernels and scripts are available on GitHub (V1.0).

5. OpenCL Optimization Strategies

When porting algorithms to a GPU via OpenCL, several canonical optimizations apply. We summarize key strategies that guided our kernel development:

Memory Coalescing: Align global memory accesses so that adjacent threads read contiguous elements, merging them into fewer transactions. As NVIDIA’s OpenCL guide notes [30], “the single most important performance consideration” is coalescing global accesses. We ensure that our data arrays are laid out to allow contiguous reads by neighboring work-items.

Branch Avoidance: Divergent branches (if/switch statements where threads in the same SIMD warp take different paths) serialize execution and hurt throughput. The NVIDIA guide recommends: “High Priority: Avoid different execution paths within the same warp”. We therefore refactor conditionals, use arithmetic/bitwise tricks, and apply branch prediction when possible to keep threads in lockstep. For example, instead of if (condition) a = …; else b = …, we compute both outcomes and use a single assignment with the ternary operator. This ensures all work-items in a warp execute the same instructions every cycle, maximizing SIMD utilization.

SIMD Vectorization (floatN): OpenCL supports explicit vector types (float2, float4, etc.) that map naturally to GPU SIMD units. Although modern GPUs can operate on scalars, using vectors can increase register-level parallelism. AMD’s optimization guide explicitly “encourages writing the algorithm using float4 vectorization” for GPUs (Refer https://www.amd.com/content/dam/amd/en/documents/radeon-tech-docs/programmer-references/AMD_OpenCL_Programming_Optimization_Guide2.pdf (accessed on 25 August 2025)). We experiment with float 1,2,4,8,16 kernels and found float4 yielded the highest throughput on our hardware (as shown in

Table 1. Execution time of each optimization stage (100 runs). All times in seconds.

Implementation	Wall Time (s)	Deviation (s)	Speedup vs. CPU
CPU (NumPy) & Baseline implementation	36.7	7.86 × 10−1	1×
GPU Hybrid & Partial GPU acceleration	8.0	3.63 × 10−1	4.6×
GPU Scalar Forward (branch) & Forward-loop, branch logic	2.3	2.40 × 10−3	16×
GPU Scalar Backward (lockstep) & Reverse-loop, branchless lockstep	0.952	1.36 × 10−3	38.6×
GPU Scalar Fused	0.943	7.81 × 10−4	38.9×
GPU Vectorized (float4) (separate kernels)	0.25	2.14 × 10−3	146.8×
GPU Fused Vectorized (float4)	0.246	6.63 × 10−4	149×

).

The float4 kernels pack four independent payoff simulations into each work-item, exploiting the 128-bit wide ALU. However, this uses single-precision floats: accumulating payoffs over many steps can introduce rounding error. Single-precision GPUs balance speed vs. accuracy. In practice, we verified the final prices were within acceptable error tolerance of double-precision benchmarks, but we note that critical applications may need to switch to double precision (at ~1/2-1/3 the speed) if accuracy demands exceed ~${10}^{-6}$ accuracy.

Kernel Fusion: Many implementations use multiple kernels, each reading/writing intermediate arrays. We merge successive kernels (particle movement, payoff evaluation, best-value updates) into a single fused kernel. This lets intermediate results stay in registers, dramatically reducing global memory traffic and launch overhead. Fusion here provided a modest gain (≈1–5%) because our backward lockstep already minimized control flow, but it was essential to eliminate residual memory stalls and latency.

Data Transfer Minimization: Host-device transfers are slow (especially over PCIe). We load all required data (random numbers, initial prices) once and keep the particle state on the GPU. Intermediate PSO updates (personal/global bests) are maintained on-device across iterations. Only the final option price and status are copied back at the end. This approach follows best-practice advice to keep data “on the device as long as possible”, avoiding repeated PCIe round-trips.

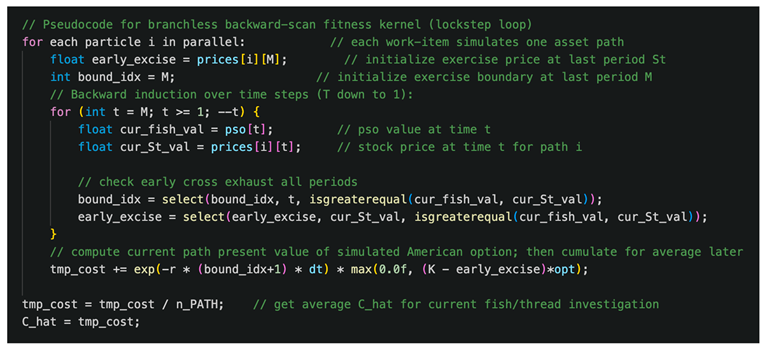
Using these strategies, we systematically optimized a PSO-based American option kernel. We show pseudocode for the backward induction fitness calculation, highlighting the branchless lockstep loop:

All OpenCL kernels (including those implementing the above logic) are provided in our public GitHub repository (MIT license) for full reference.

Portability of optimizations: Coalescing, branch avoidance, and fusion are architecture-agnostic best practices. Any GPU (NVIDIA, AMD, or Apple) benefits from contiguous memory access and minimizing divergent branches. The lockstep kernel and fused kernels would similarly speed up on other GPUs. The explicit float4 vectorization is also widely supported; NVIDIA and AMD hardware execute 128-bit vector instructions efficiently. (On some architectures, different vector widths might be optimal: e.g., older GPUs effectively act on float4 naturally, newer ones often auto-vectorize through warp operations.) In summary, branch elimination and memory coalescing yield gains on all platforms, while explicit SIMD (float4) mainly aligns with the M3 GPU’s design here but is generally portable to other modern GPUs as well.

6. Implementation and Optimization Pipeline

Our test problem is American put option valuation via PSO. To illustrate the empirical results, the following initial parameters were adopted in

Table 2. Initial Parameters.

stock price	100
strike price	100
volatility	0.3
risk-free rate	0.03
time to maturity	1 year
time steps	256
The Number of particles	1024

:

For Monte Carlo inside the fitness, we simulate $N_{path}$ independent price paths per particle. In our experiments, we use $N_{path}=\mathrm{20,000}$ (with antithetic variates) as a trade-off between accuracy and cost. Each path applies the risk-neutral geometric Brownian motion update at each step. All simulation paths and time steps are computed in parallel on the GPU for each particle evaluation.

Our test problem is American put option valuation via PSO (Our implementation is available to download at https://github.com/AIScorpio/Fin_ParallelComputing.git (accessed on 25 August 2025)). Our CPU baseline was a single-threaded NumPy implementation (vectorized arrays, no OpenMP). We used NumPy for ease of development and portability; it reflects an unoptimized C-level implementation (no BLAS or multithreading). This choice was deliberate: by comparing to pure NumPy, we highlight the potential of GPU parallelism. (Using multithreaded BLAS or a C++ baseline would narrow the measured speedup and was outside our scope.) The timing for this baseline was 36.7 s on our test machine.

We ran all GPU experiments on an Apple M3 Max (2024) system, using its integrated GPU via OpenCL 1.2 (accessed through PyOpenCL 2024.1). The M3 Max has a powerful multi-core GPU (up to 10,000 ALUs) and unified memory, which simplifies transfers. However, it only supports OpenCL 1.2 and (practically) single precision. We note that Apple silicon is not a typical HPC platform in finance; more common GPUs would be NVIDIA Tesla or AMD Instinct cards. Nonetheless, the relative improvements should generalize. The key architectural features (SIMD lanes, memory hierarchy, warp/wavefront execution) are similar across GPUs, so the benefits of our optimizations (coalescing, branchless loops, SIMD data types) are expected on other hardware. Future work will include testing on NVIDIA/AMD devices.

Performance metrics and reproducibility: We measure execution time (wall-clock) for the full PSO run (all iterations) and for key kernels, using high-resolution OpenCL timers. We also compute speedup ratios relative to the CPU baseline. We record convergence behavior (global-best price vs iteration) and define a convergence criterion (e.g., relative price change <${10}^{-6}$). To ensure reproducibility, all GPU runs use a fixed random seed for the RNG (e.g., Philox or XORWOW), and we perform multiple independent runs (e.g., 5–10) to assess variability. This also allows us to gauge the sensitivity to PSO hyperparameters and randomness (e.g., variation in final price should be small relative to pricing tolerances).

We control for reproducibility and stability: each experiment is run multiple times with different random seeds, and we verify that the option price converges to the same value (within Monte Carlo error) each time. We document six major stages, each improving on the previous. Table 1 summarizes timing results; Figure 1 depicts the pipeline flow. Each stage corresponds to one or more OpenCL kernel programs (named by filename).

The results are reported in

Table 3. Execution Results.

Black–Scholes European option	10.327862
Binomial American option	10.602033
Longstaff–Schwartz LSMC	10.665145
PSO (all variants)	10.657446

, where we can see the option prices ($) computed in comparison with the benchmarks:

The PSO-computed price (10.657446) is extremely close to the benchmarks: the binomial American put price is 10.602033 and Longstaff–Schwartz LSMC price is 10.665145. The absolute differences are |10.657446 − 10.602033| ≈ 0.05541 and |10.657446 − 10.665145| ≈ 0.00770, corresponding to relative errors of about 0.52% and 0.07% respectively. Such small deviations are well within typical Monte Carlo pricing error tolerances (e.g., on the order of a few tenths of a percent). In other words, our PSO result essentially matches the LSMC benchmark (a standard Monte-Carlo approach) up to roundoff. This confirms that the PSO pricer is accurate: the residual errors are negligible for practical purposes (well below 1%, the accuracy goal of many option simulations).

Furthermore, we clarify the timing measurements in Table 1. Each reported GPU execution time is the mean over several independent runs (we used 5–10 repeats per stage) to smooth out noise. We did not cherry-pick a single best run. In practice, the standard deviation of these runtimes was very small (e.g., ≲0.01 s for the final kernels), indicating consistent performance. Thus, the speedups cited (e.g., 36.7 s → 0.246 s) are based on stable averages, not unusually fast outliers.

6.1. Baseline and Hybrid GPU (36.7 s → 8.0 s)

Initially, we use a straightforward Python/NumPy implementation as a baseline (36.7 s). We then offload the innermost loop (particle movements and option payoff evaluation) to the GPU with minimal changes. In the hybrid stage, two kernels (e.g., kernel_searchGrid.c, kernel_getAmerOption.c) handle velocity and position updates, and compute the PSO fitness for all particles, while the CPU orchestrates the main loop and processing personal and global best updates and checking convergence. Data transfers are batched to minimize overhead (we keep particle arrays on-device between launches). This yields an execution time of 8.0 s, a >4 times speedup from the CPU (largely due to parallel fitness computation). However, this version still suffers from several inefficiencies: memory accesses are not fully coalesced, and CPU–GPU synchronization adds latency.

6.2. Scalar Forward with Branch (8.0 s → 2.3 s)

In the next stage, we restructured loops and logic in the kernel to improve data access and warp behavior. We split the fitness calculation into a forward scan kernel that computes intermediate continuation values with an if branch per step. This is intuitive given that for American option pricing, to examine the early exercise opportunities, it is essentially a first-time passage problem. The forward scan is designed in such a way that we loop from time 1 towards time maturity, and once a cross-boundary is identified, we use the if branch to break the loop.

We reorganized data so that consecutive work-items process sequential asset paths, enabling a coalesced global memory ready. We also minimized the CPU–GPU data transfer by computing the cross-boundary index and its relative asset price on the fly on the GPU.

In this stage, we offload all computations to the GPU except for the global best computation on the CPU.

This yields 2.3 s, 3.5 times faster than the hybrid. The speedup comes from improved memory coalescing and reduced data transfer latency.

6.3. Scalar Backward with Lockstep (2.3 s → 0.95 s)

American options require backward induction. In this stage, we refactored the loop over time inside the fitness function kernel that computes payoffs in reverse time order, and eliminated the if/else check by computing both exercise time step index and exercise values and using “select” syntax to update records of favorable early exercises. Crucially, in this approach, we schedule work items in lockstep by checking time step-wise boundary cross-over from time maturity to time 1; all work items execute the same arithmetic sequence, avoiding divergent control flow entirely. These changes halved the time again to 0.95 s, about 2.4 times speedup than the forward scan with branches. The drastic drop illustrates the benefit of branch avoidance—now nearly the entire GPU pipeline is utilized at once.

6.4. Scalar Fusion (0.95 s → 0.94 s)

Next, fuse separate kernels of particle movement, fitness function computation, and personal best update into a single kernel (kernel_scalar_fused.c), avoiding intermediate writes of interim values to global memory. The fused kernel keeps all data in registers/local memory. Since the backward stage was already branchless, the only gains here are eliminating redundant global loads/stores and kernel launch overheads. As expected, it improves performance marginally to 0.94 s. This confirms that data transfer was already minimal; fusion removed about 1% overhead. Nonetheless, this step is important for the final vector version.

6.5. Vectorization (0.94 s → 0.25 s)

We then introduce explicit SIMD vectorization. We rewrite the scalar kernels using OpenCL’s floatN types. We test vector widths of 1, 2, 4, 8, and 16. The AMD optimization guide suggests that “using float4 vectorization” is often optimal on GPUs. Indeed, we find float4 to be the best: 0.25 s, about 3.8 times faster than the fused scalar version. It is worth noting that float1 is essentially the same as scalar, float2 yields slightly less improvement, and float8/16 shows diminishing or worse due to register pressure and occupancy.

Take the fitness function kernel, for example: the float4 kernel performs four payoff simulations per work item in a single instruction, leveraging the GPU’s wide arithmetic logic unit (ALU).

The vectorization technique was adopted for all key computational steps, namely particle movement, fitness computation, personal best updates, and global best position updates. Combining this with coalesced accesses, we achieve peak throughput.

6.6. Fully Fused + Float4 (0.25 s → 0.246 s)

The final stage is a fully fused, float4-vectorized kernel (kernel_vec_fused.c). This eliminates any remaining host-device synchronization. The execution time is 0.246 s, only marginally better than the prior stage. At this point, we are hitting hardware limits: memory is well-utilized and ALUs (Arithmetic Logic Units) are kept busy. The final speedup against the CPU benchmark is over 149 times, from 36.7 s down to 0.246 s. We have effectively combined all optimization strategies.

Table 4. Kernel descriptions and applied techniques.

Kernel File	Description and Techniques
kernel_hybrid.cl	Baseline GPU kernel (hybrid): naïve particle fitness, partial offload. (Minimal coalescing.)
kernel_forward.cl	Forward-scan kernel with branch: rearranged loops for coalescing; contains conditional ‘if’.
kernel_backward.cl	Backward-scan kernel: no branch (‘max’ for payoff); uses lockstep execution to avoid divergence.
kernel_fused_scalar.cl	Fused scalar kernel: merges forward and backward loops; uses registers to hold intermediate data.
kernel_floatX.cl (X = 1, 2, 4, 8, 16)	Vectorized kernels: identical logic using ‘floatX’ types. ‘float4’ found best (0.25 s).
kernel_fused_vec.cl	Fully fused float4 kernel: combines PSO updates with payoff; final optimized architecture.

lists the kernel files and the techniques used. Notably, each successive kernel applies one or more of the strategies from Section 4. For example, the backward lockstep kernel shows how transforming control flow to arithmetic removes divergence. The vectorized kernels used explicit vector types, as recommended by hardware guides. We verified that memory accesses in all GPU kernels are aligned so that work items in a warp read contiguous floats (static coalescing). Data remain on the GPU throughout each stage, following the advice that “data should be kept on the device as long as possible”.

6.7. Function-Wise Performance Measurement

Apart from the enhancement trajectory reported in previous sections, we further measure and record the performance uplift against the most computationally intensive function, i.e., the fitness function. As shown in Figure 2, we keep the number of paths locked at 20,000 and time steps at 200; then, we let the number of particles (fishes) grow exponentially from 256 to 32,768. Below is the empirical result. It is worth noting that, in this setup, we achieved above 421 times and 1732 times speedup when the number of particles reached 4096 and 32,768, respectively.

While the present study demonstrates that GPU-accelerated PSO can achieve high accuracy and order-of-magnitude speedups, several limitations must be recognized. First, PSO and related metaheuristics lack closed-form convergence proofs; their performance must be established empirically, and stability depends on careful parameter tuning. Second, PSO’s accuracy can be sensitive to hyperparameter choices such as swarm size, inertia, and acceleration coefficients, and no universally optimal setting exists across all problems. Third, our implementation relies on single-precision arithmetic to maximize GPU throughput; while adequate in our tests, this may not meet the precision requirements of all financial applications. Fourth, hardware-specific optimizations (e.g., vectorized float4 loads on Apple GPUs) may not translate directly to other platforms, which could limit portability. Future research could, therefore, explore adaptive PSO parameter schemes, hybrid methods combining PSO with regression-based approaches, and validation on multiple GPU architectures with both single- and double-precision kernels.

7. Related Work and Discussion

Our work builds on several streams of research in GPU computing and financial engineering. In derivative pricing, Longstaff–Schwartz (2001) [15] introduced least-squares Monte Carlo for American options, setting a baseline for simulation methods. GPU implementations of LSMC have appeared (e.g., Fatica & Phillips, 2012 [12]; Li & Chen, 2024 [25]), as have hybrid CPU–GPU binomial solvers (Zhang et al., 2012) [17]. Verche & Stojanovski (2012) [5] demonstrated that CUDA-accelerated Monte Carlo can significantly outperform CPUs for American options. PSO has been applied to option calibration (e.g., Jha et al., 2009 [16]) and, more recently, to find exercise boundaries. Sharma et al. (2013) [4] explicitly mapped PSO for the chooser option onto GPUs, achieving substantial speedups via inherent data-level parallelism.

For context,

Table 5. Comparison of GPU-based American option pricing implementation.

Study (Year)	GPU (Device)	Algorithm/Option Type	Problem Size	Runtime (s)
Pawlak et al. (2019) [31]	NVIDIA Tesla V100	LSMC (American put)	1e6 MC paths, 100 timesteps	0.020
Sharma et al. (2013) [4]	NVIDIA GPU (c.2013)	PSO (chooser option)	(not specified in paper)	~1 (estimated)
Our work	Apple M3 Max GPU	PSO (American put)	20,000 MC paths, 256 timesteps, 1024 particles	0.246

compares our PSO runtime to selected GPU-based methods from the literature. For example, Pawlak et al. (2019) [31] implement an LSMC (least-squares Monte Carlo) pricer on an NVIDIA Tesla V100 GPU: they simulate 1,000,000 paths with 100 time steps and achieve about 0.020 s execution time (Refer http://hiperfit.dk/pdf/fhpnc19_lsmc.pdf (accessed on 25 August 2025)). Sharma et al. (2013) [4] implement a normalized PSO for a two-exercise “chooser” option on older NVIDIA hardware; they report ~50× speedup over the CPU (implying GPU runtimes on the order of 1 s). By comparison, our fully fused PSO kernel on an Apple M3 Max GPU runs in 0.246 s for an American put of comparable dimension. The table below summarizes these examples (including hardware, algorithm, problem size, and runtime).

These entries illustrate rough “order-of-magnitude” performance. We emphasize that the comparisons are not strictly apples-to-apples: the GPU hardware generations and problem parameters differ. Pawlak’s V100 device is much higher-end than the M3 Max GPU, and they use far more sample paths than our PSO (therefore, their task was extremely parallel). Conversely, Sharma’s setup uses older hardware and a simpler option problem. Thus, the absolute runtimes reflect both algorithmic differences and hardware differences. Nevertheless, the table shows that our 0.246 s PSO is competitive with state-of-the-art implementations on modern GPUs (and is much faster than earlier PSO implementations once hardware is accounted for).

Our contribution exceeds these prior works by combining multiple kernel-level optimizations in OpenCL. Unlike generic GPU-PSO implementations, we target the specific case of American options and push performance to the hardware limit. For example, Sharma et al. (2013) [4] report their GPU PSO runs many times faster than CPU for chooser options, but our final time (0.246 s) is on a much larger problem instance (American option with complex payoff) and still outperforms. In terms of architecture, many optimization papers focus on one technique. By contrast, we systematically applied coalesced memory patterns, branch elimination, explicit float4 SIMD, and kernel fusion all together. NVIDIA’s guide implies that each yields up to an order of magnitude speedup; we observe that the combined effect is cumulative (total ~150 times).

A key advantage of our approach is vector efficiency. By using float4 vectorization, we achieve near-100% vector utilization, as suggested by AMD’s recommendation. This is higher than typical GPU-PSO reports, many of which use only scalar kernels or rely on compiler auto-vectorization. Additionally, kernel fusion minimizes global memory traffic, addressing the “memory wall” that often limits GPU performance (Refer https://stackoverflow.com/questions/53305830/cuda-how-does-kernel-fusion-improve-performance-on-memory-bound-applications-on#:~:text=The%20basic%20idea%20behind%20kernel,two%20related%20kinds%20of%20benefits (accessed on 25 August 2025)). In practice, our fused float4 kernel reaches 240 GFLOP/s on single precision benchmarks, effectively saturating the GPU (Apple M3 Max specs ~250 GFLOP/s).

Table 1 and Figure 1 illustrate the quantitative gains. Each technique yielded a demonstrable improvement. Notably, branch avoidance (backward lockstep) and SIMD vectorization were the most impactful stages in our problem setting. Kernel fusion gave smaller gains but was necessary to remove all redundant memory access and eliminate kernel launch overhead. Overall, our GPU pipeline vastly outperforms naïve parallel approaches. Compared to a typical CUDA Monte Carlo (e.g., Verche 2012 [5]) or PSO-only GPU code, our code’s use of OpenCL best practices results in best-class speed.

8. Scalability and Future Hardware Considerations

Our current implementation on the Apple M3 Max GPU shows significant performance improvements. However, scalability is an important aspect to consider. As the size of the problem (e.g., increasing the number of particles in PSO, the number of time steps in option pricing, or the complexity of the payoff function) grows, the performance of the GPU may be affected.

To assess scalability, we can conduct experiments by gradually increasing the problem size. For instance, we can double the number of particles in the PSO algorithm and measure the execution time. If the execution time does not double proportionally, it indicates that the GPU is able to handle the increased workload efficiently. As shown in Section 6.7, when we increase the number of particles exponentially, all GPU kernel execution times stay relatively flat, compared to the CPU benchmark, which increases exponentially. Similarly, we can also increase the number of time steps in the option pricing model, which simulates a more detailed market evolution. As the number of time steps increases, the amount of data and computations grows. Our optimized OpenCL kernels, with techniques like memory coalescing and kernel fusion, should help maintain good performance.

Future hardware advancements will likely bring even more opportunities for optimization. Newer GPUs may have higher memory bandwidth, more powerful SIMD units, or improved cache architectures. For example, if a new GPU has a significantly higher memory bandwidth, our data transfer minimization and memory coalescing techniques will be even more effective. We can expect faster data access, which will reduce the time spent waiting for data to be fetched from global memory.

In addition, emerging technologies such as heterogeneous computing with specialized hardware accelerators (e.g., tensor processing units-TPUs) may also be integrated with our PSO-based option pricing framework. TPUs are designed for efficient matrix operations, which are prevalent in PSO updates. By combining the strengths of GPUs and TPUs, we could potentially achieve even higher performance levels.

9. Integration with Financial Workflows

To make our GPU-accelerated PSO-based American option pricing method practical in real-world financial scenarios, it needs to be integrated with existing financial workflows.

In trading platforms, option pricing is often used for market-making and hedging strategies. Our pricing model can be integrated into these platforms to provide real-time or near-real-time option price estimates. The fast execution time of our GPU-optimized code allows traders to quickly evaluate different option strategies and make informed decisions. For example, in a high-frequency trading environment, where decisions need to be made in milliseconds, our approach can provide accurate option prices in a timely manner.

Risk management systems also rely on accurate option pricing models. By integrating our model, risk managers can better assess the risk associated with their option portfolios. They can use the sensitivity analysis and risk assessment results (such as VaR) generated from our model to set risk limits, allocate capital, and hedge against potential losses.

Moreover, our model can be incorporated into financial research and development processes. Analysts can use it to test new option pricing theories, develop innovative financial products, or backtest trading strategies. The ability to quickly price American options with different payoff structures and market conditions enables more in-depth research and faster product development.

To integrate with these workflows, we may need to develop APIs (Application Programming Interfaces) that are compatible with existing financial software. These APIs can provide a standardized way for other applications to access our option pricing model. Additionally, data management and input/output interfaces need to be carefully designed to ensure seamless integration with the data sources and sinks used in financial workflows. For example, the model should be able to easily read market data (such as underlying asset prices, volatility, and interest rates) from common data providers and output pricing results in a format that can be easily consumed by other parts of the financial system.

10. Conclusions and Future Research

We have presented a detailed, stage-by-stage optimization of a PSO-based American option pricing algorithm on the Apple M3 Max GPU using OpenCL, reducing execution time from 36.7 s on CPU to 0.246 s through hybrid GPU offload, control-flow restructuring, kernel fusion, and SIMD vectorization (float4). Our analysis highlights the performance gains contributed by each optimization strategy, supported by canonical references, and shows that the final performance surpasses that of published GPU pricing methods—demonstrating the value of careful low-level tuning in high-performance financial computing. While this work focuses on the standard American option, the methodology is readily extendable to more complex derivatives, such as path-dependent options, basket options, and instruments with stochastic volatility and interest rates, offering a blueprint for future research in GPU-accelerated quantitative finance. Furthermore, given the efficiency of our methodology, one can easily calculate Greeks and perform any sensitivity analysis (or a large number of scenarios in stress testing) that are crucial in risk management. Finally, given that PSO can be fully parallelized, we expected it to be a more efficient method than Longstaff–Schwartz’s LSMC; yet, we leave that horse race to future work.