Feasibility of Implementing Motion-Compensated Magnetic Resonance Imaging Reconstruction on Graphics Processing Units Using Compute Unified Device Architecture
Abstract
1. Introduction
2. Theory
2.1. Joint Reconstruction of an Image and a Motion Model
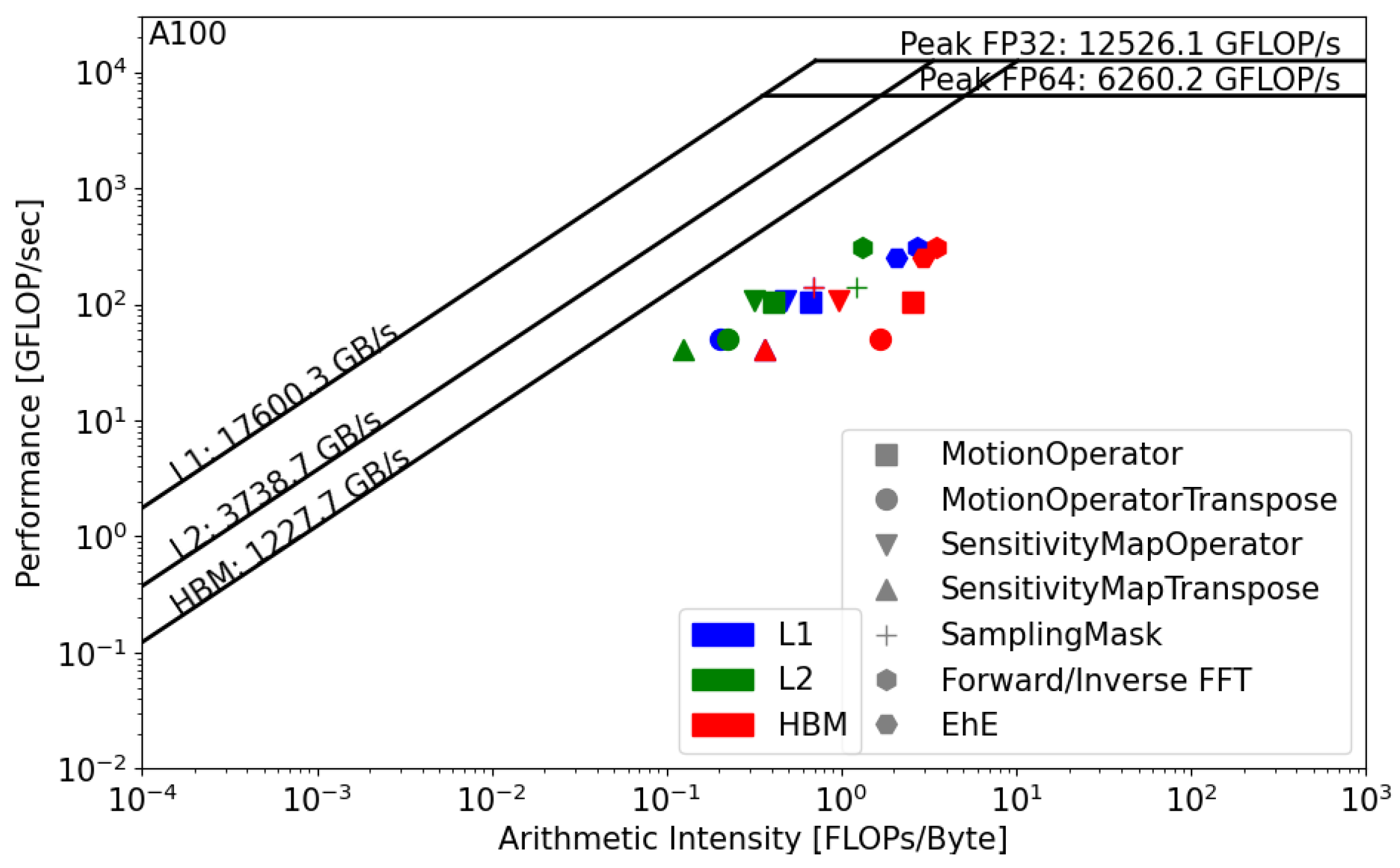
2.2. The Roofline Model
3. Methods
3.1. Data Acquisition
3.2. The Reconstruction Kernel
3.3. Cuda Implementation
3.4. The Test Machines
3.5. Performance Profiling
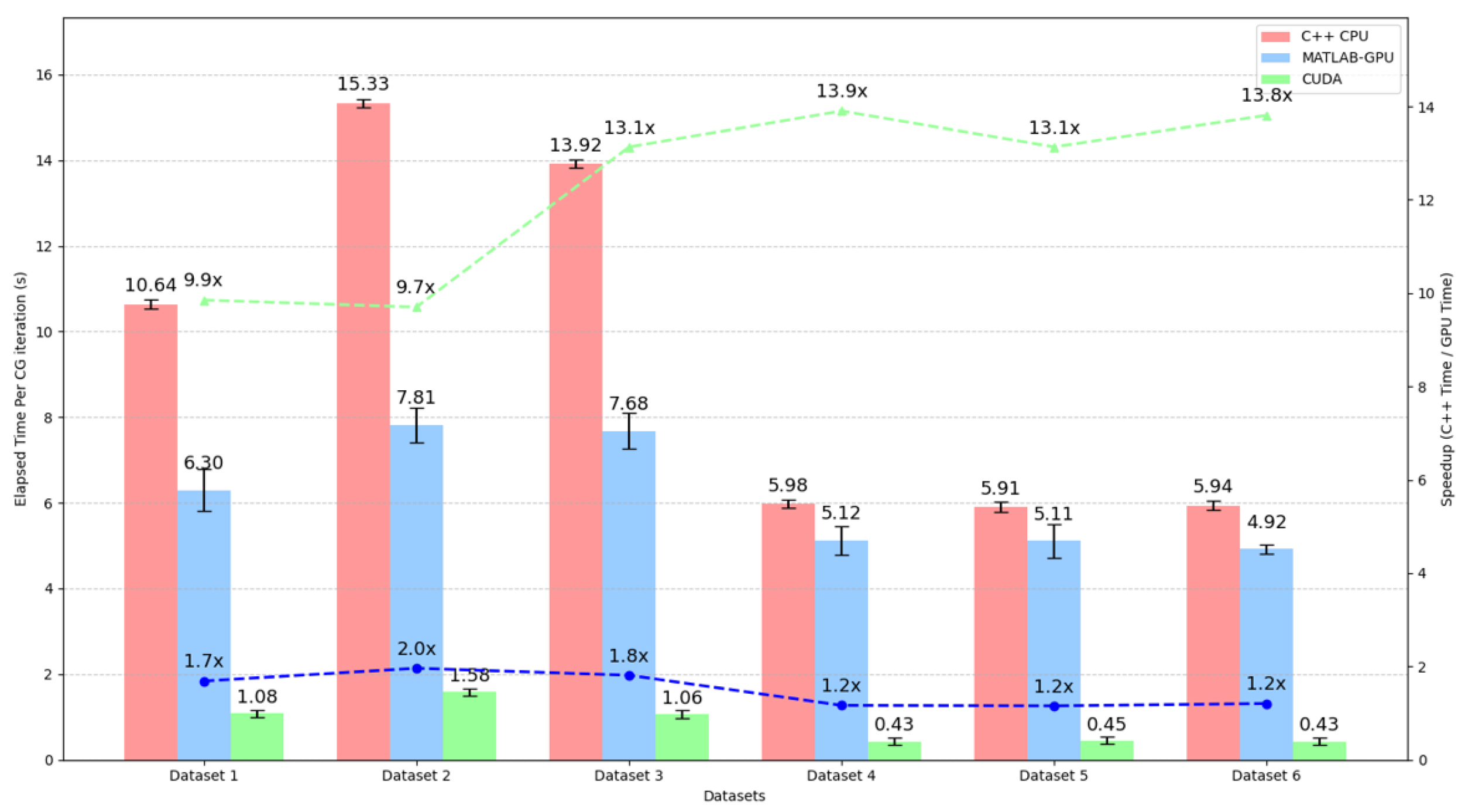
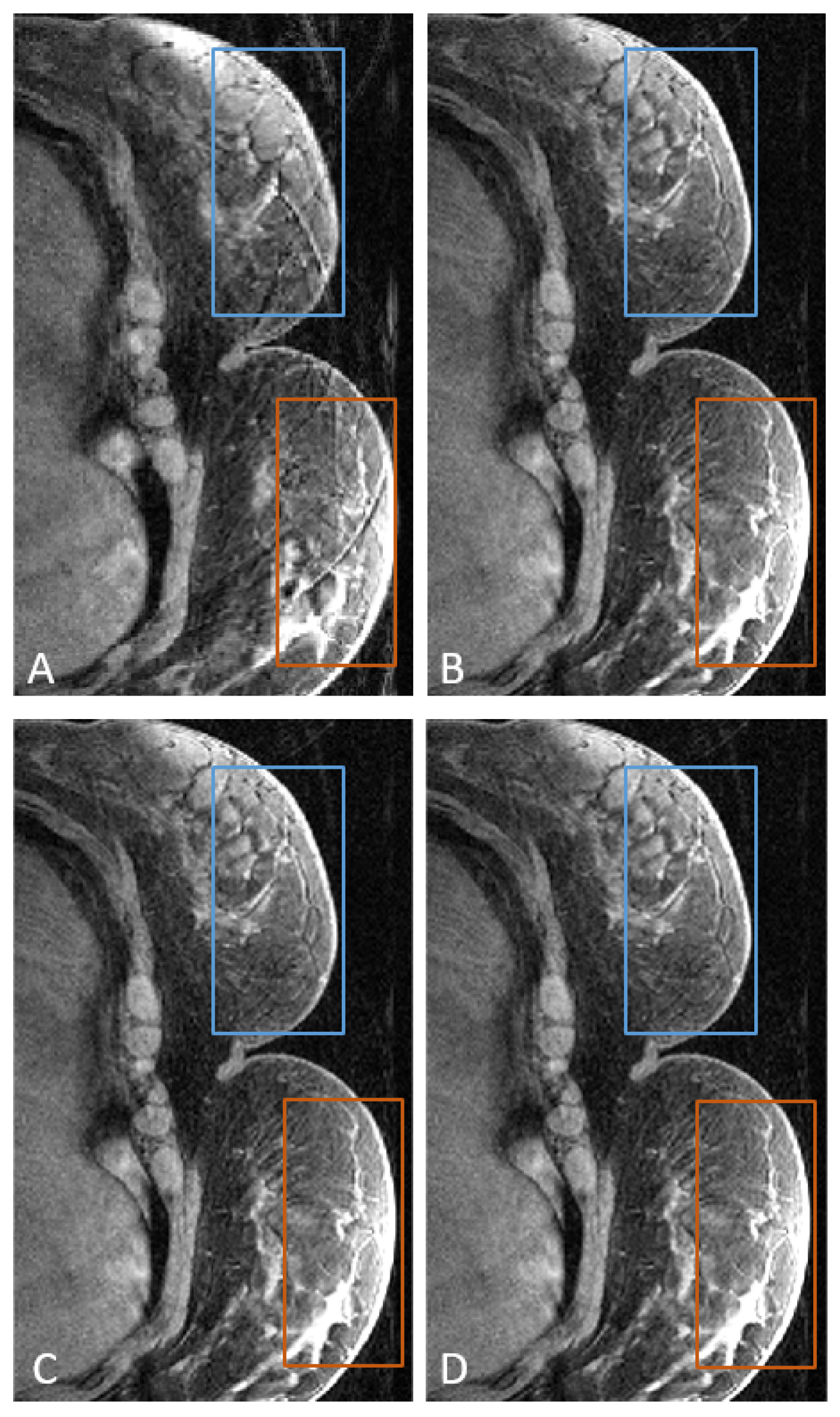
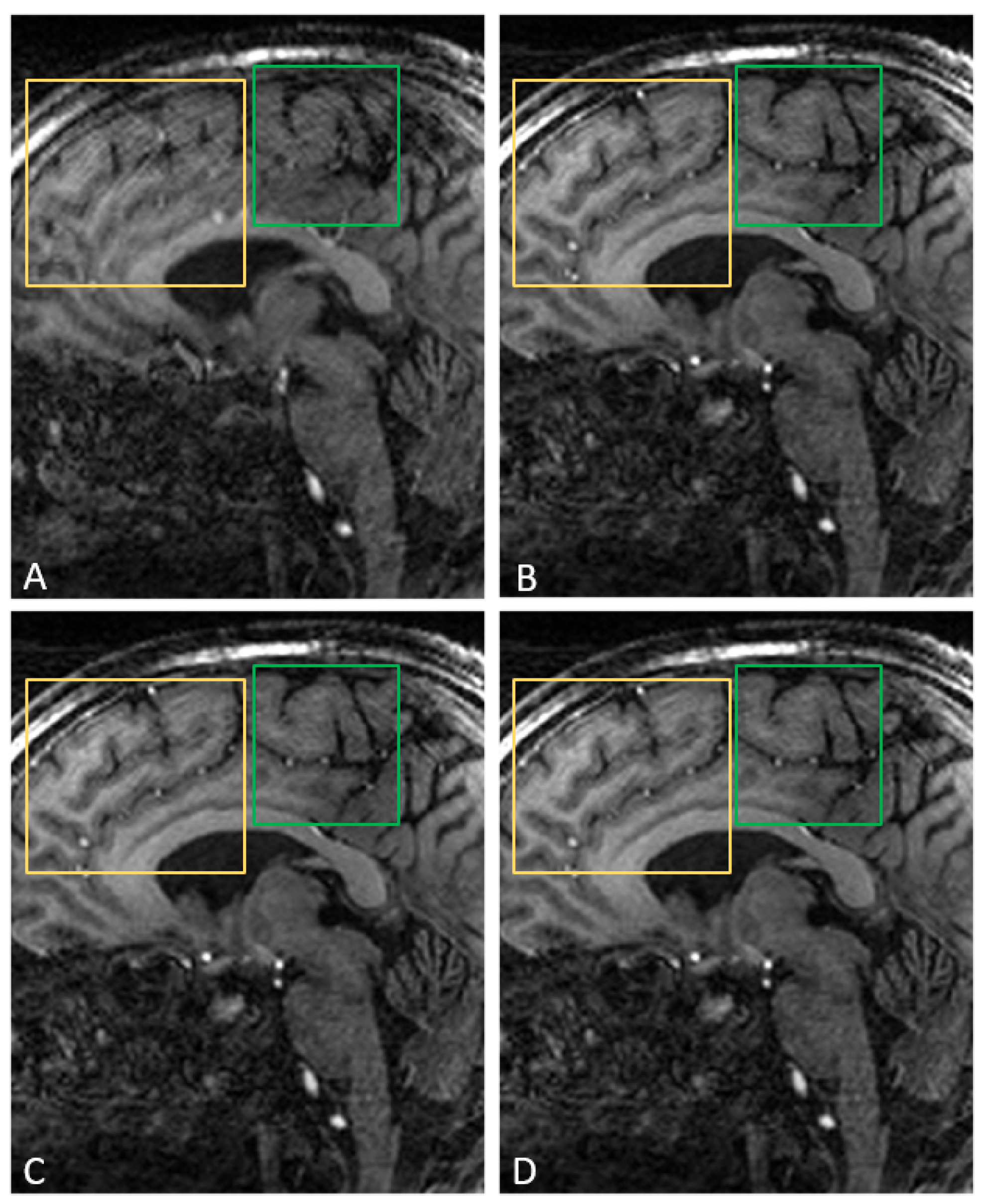
4. Results
5. Discussion
- Data storage in half precision: Reducing the memory footprint by using FP16 could significantly enhance memory bandwidth utilization. An initial test was conducted with this constraint, and the reconstructed image quality was not compromised.
- Improvement of cache usage: Achieved by optimizing memory access patterns to benefit from the large L2 cache on the A100 GPU.
- The Utilization of tensor cores could be also investigated to accelerate matrix-based kernels.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MRI | Magnetic Resonance Imaging |
| FP | Floating Point |
| GRICS | The Generalized Reconstruction by Inversion of Coupled Systems |
| GPU | Graphics Processing Unit |
| HPC | High-Performance Computing |
| CUDA | Compute Unified Device Architecture |
| MPRAGE | Magnetization-Prepared Rapid Gradient Echo |
| OpenMP | Open Multi-Processing |
| MPI | Message Passing Interface |
References
- Schaetz, S.; Voit, D.; Frahm, J.; Uecker, M. Accelerated Computing in Magnetic Resonance Imaging: Real-Time Imaging Using Nonlinear Inverse Reconstruction. Comput. Math. Methods Med. 2017, 2017, 3527269. [Google Scholar] [CrossRef]
- Fessler, J.A. Model-Based Image Reconstruction for MRI. IEEE Signal Process. Mag. 2010, 27, 81–89. [Google Scholar] [CrossRef] [PubMed]
- Gordon, Y.; Partovi, S.; Müller-Eschner, M.; Amarteifio, E.; Bäuerle, T.; Weber, M.A.; Kauczor, H.U.; Rengier, F. Dynamic Contrast-Enhanced Magnetic Resonance Imaging: Fundamentals and Application to the Evaluation of the Peripheral Perfusion. Cardiovasc. Diagn. Ther. 2014, 4, 147–164. [Google Scholar] [PubMed]
- Murphy, M.; Alley, M.; Demmel, J.; Keutzer, K.; Vasanawala, S.; Lustig, M. Fast ℓ1-SPIRiT Compressed Sensing Parallel Imaging MRI: Scalable Parallel Implementation and Clinically Feasible Runtime. IEEE Trans. Med. Imaging 2012, 31, 1250–1262. [Google Scholar] [CrossRef] [PubMed]
- Pruessmann, K.P.; Weiger, M.; Scheidegger, M.B.; Boesiger, P. SENSE: Sensitivity Encoding for Fast MRI. Magn. Reson. Med. 1999, 42, 952–962. [Google Scholar]
- Odille, F. Chapter 13—Motion-Corrected Reconstruction. In Advances in Magnetic Resonance Technology and Applications; Akçakaya, M., Doneva, M., Prieto, C., Eds.; Magnetic Resonance Image Reconstruction; Academic Press: Cambridge, MA, USA, 2022; Volume 7, pp. 355–389. [Google Scholar] [CrossRef]
- Wang, H.; Peng, H.; Chang, Y.; Liang, D. A survey of GPU-based acceleration techniques in MRI reconstructions. Quant. Imaging Med. Surg. 2018, 8, 196–208. [Google Scholar] [CrossRef] [PubMed]
- Stone, S.S.; Haldar, J.P.; Tsao, S.C.; Hwu, W.-m.W.; Sutton, B.P.; Liang, Z.P. Accelerating Advanced MRI Reconstructions on GPUs. J. Parallel Distrib. Comput. 2008, 68, 1307–1318. [Google Scholar] [CrossRef]
- Després, P.; Jia, X. A Review of GPU-Based Medical Image Reconstruction. Phys. Med. 2017, 42, 76–92. [Google Scholar] [CrossRef] [PubMed]
- Buck, I.; Hanrahan, P. Data Parallel Computation on Graphics Hardware; Technical Report; Stanford University: Stanford, CA, USA, 2003. [Google Scholar]
- Laganà, F.; Bibbò, L.; Calcagno, S.; Carlo, D.D.; Pullano, S.A.; Pratticò, D.; Angiulli, G. Smart Electronic Device-Based Monitoring of SAR and Temperature Variations in Indoor Human Tissue Interaction. Appl. Sci. 2025, 15, 2439. [Google Scholar] [CrossRef]
- Cook, S. CUDA Programming: A Developer’s Guide to Parallel Computing with GPUs, 1st ed.; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 2012. [Google Scholar]
- Zeroual, M.A.; Isaieva, K.; Vuissoz, P.A.; Odille, F. Performance Study of an MRI Motion-Compensated Reconstruction Program on Intel CPUs. Appl. Sci. 2024, 14, 9663. [Google Scholar] [CrossRef]
- Odille, F.; Vuissoz, P.A.; Marie, P.Y.; Felblinger, J. Generalized Reconstruction by Inversion of Coupled Systems (GRICS) Applied to Free-Breathing MRI. Magn. Reson. Med. 2008, 60, 355–389. [Google Scholar] [CrossRef] [PubMed]
- Williams, S.; Waterman, A.; Patterson, D. Roofline: An Insightful Visual Performance Model for Multicore Architectures. Commun. ACM 2009, 52, 65–76. [Google Scholar] [CrossRef]
- Isaieva, K.; Meullenet, C.; Vuissoz, P.A.; Fauvel, M.; Nohava, L.; Laistler, E.; Zeroual, M.A.; Henrot, P.; Felblinger, J.; Odille, F. Feasibility of Online Non-Rigid Motion Correction for High-Resolution Supine Breast MRI. Magn. Reson. Med. 2023, 90, 2130–2143. [Google Scholar] [CrossRef] [PubMed]
- Luong, M.; Ferr, G.; Chazel, E.; Gapais, P.F.; Gras, V.; Boulant, N.; Amadon, A. A Compact 16Tx-32Rx Geometrically Decoupled Phased Array for 11.7 T MRI. In Proceedings of the the 31st Annual Meeting of the ISMRM, London, UK, 7–12 May 2023; Volume 707. [Google Scholar]
- Mugler, J.P., III; Brookeman, J.R. Three-dimensional magnetization-prepared rapid gradient-echo imaging (3D MP RAGE). Magn. Reson. Med. 1990, 15, 152–157. [Google Scholar] [CrossRef] [PubMed]
- Cordero-Grande, L.; Ferrazzi, G.; Teixeira, R.P.A.G.; O’Muircheartaigh, J.; Price, A.N.; Hajnal, J.V. Motion-corrected MRI with DISORDER: Distributed and incoherent sample orders for reconstruction deblurring using encoding redundancy. Magn. Reson. Med. 2020, 84, 713–726. [Google Scholar] [CrossRef] [PubMed]
- NVIDIA Corporation. cuFFT Library User Guide; NVIDIA Corporation: Santa Clara, CA, USA, 2023. [Google Scholar]
- NVIDIA Corporation. cuBLAS Library User Guide; NVIDIA Corporation: Santa Clara, CA, USA, 2023. [Google Scholar]
- GitHub-Ebugger. Empirical Roofline Toolkit. Available online: https://github.com/ebugger/Empirical-Roofline-Toolkit (accessed on 4 March 2025).
- Nsight Compute. Available online: https://docs.nvidia.com/nsight-compute/NsightCompute/ (accessed on 7 March 2025).
- GitHub-Ebugger. Example Scripts for Plotting Roofline. Available online: https://github.com/cyanguwa/nersc-roofline (accessed on 18 March 2025).
- Hong, J.; Cho, S.; Park, G.; Yang, W.; Gong, Y.H.; Kim, G. Bandwidth-Effective DRAM Cache for GPUs with Storage-Class Memory. In Proceedings of the IEEE International Symposium on High-Performance Computer Architecture (HPCA), Edinburgh, UK, 2–6 March 2024; pp. 139–155. [Google Scholar]
- Kenyon, C.; Volkema, G.; Khanna, G. Overcoming Limitations of GPGPU-Computing in Scientific Applications. In Proceedings of the IEEE High Performance Extreme Computing Conference (HPEC), Waltham, MA, USA, 24–26 September 2019; pp. 1–9. [Google Scholar] [CrossRef]

| Dataset | ||||||
|---|---|---|---|---|---|---|
| 320 | 320 | 320 | 256 | 256 | 256 | |
| 470 | 470 | 550 | 208 | 208 | 208 | |
| 112 | 112 | 112 | 160 | 160 | 160 | |
| 20 | 30 | 26 | 32 | 32 | 32 | |
| 12 | 12 | 12 | 12 | 12 | 12 | |
| Magnetic Field | 3T | 3T | 3T | 7T | 7T | 7T |
| Device | AMD EPYC | NVIDIA A100 |
|---|---|---|
| Main Memory bandwidth (GB/s) | 221.1 | 1227.7 |
| L2 Bandwidth (GB/s) | 3242.2 | 3738.7 |
| Main Memory Size (GB) | 4000 | 40 |
| Main Memory Type | DDR4 | HBM2e |
| Nb Cores/SMs | 36 | 108 |
| Peak FP32 (GFLOP/s) | 1348 | 12,526.1 |
| Release year | 2021 | 2020 |
| Data | Metric |
|---|---|
| FP 64 | sm__sass_thread_inst_executed_op_fp64_pred_on.sum |
| FP 32 | sm__sass_thread_inst_executed_op_fp32_pred_on.sum |
| FP 16 | sm__sass_thread_inst_executed_op_fp16_pred_on.sum |
| Tensor Core | sm__inst_executed_pipe_tensor.sum |
| L1 cache | l1tex__t_bytes.sum |
| L2 cache | lts__t_bytes.sum |
| HBM | dram__bytes.sum |
| Dataset | NRMSE (CPU_Image, CUDA_Image) |
|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeroual, M.A.; Dudysheva, N.; Gras, V.; Mauconduit, F.; Isaieva, K.; Vuissoz, P.-A.; Odille, F. Feasibility of Implementing Motion-Compensated Magnetic Resonance Imaging Reconstruction on Graphics Processing Units Using Compute Unified Device Architecture. Appl. Sci. 2025, 15, 5840. https://doi.org/10.3390/app15115840
Zeroual MA, Dudysheva N, Gras V, Mauconduit F, Isaieva K, Vuissoz P-A, Odille F. Feasibility of Implementing Motion-Compensated Magnetic Resonance Imaging Reconstruction on Graphics Processing Units Using Compute Unified Device Architecture. Applied Sciences. 2025; 15(11):5840. https://doi.org/10.3390/app15115840
Chicago/Turabian StyleZeroual, Mohamed Aziz, Natalia Dudysheva, Vincent Gras, Franck Mauconduit, Karyna Isaieva, Pierre-André Vuissoz, and Freddy Odille. 2025. "Feasibility of Implementing Motion-Compensated Magnetic Resonance Imaging Reconstruction on Graphics Processing Units Using Compute Unified Device Architecture" Applied Sciences 15, no. 11: 5840. https://doi.org/10.3390/app15115840
APA StyleZeroual, M. A., Dudysheva, N., Gras, V., Mauconduit, F., Isaieva, K., Vuissoz, P.-A., & Odille, F. (2025). Feasibility of Implementing Motion-Compensated Magnetic Resonance Imaging Reconstruction on Graphics Processing Units Using Compute Unified Device Architecture. Applied Sciences, 15(11), 5840. https://doi.org/10.3390/app15115840








