Enhanced Expert Assessment of Asphalt-Layer Parameters Using the CIBRO Method: Implications for Pavement Quality and Monetary Deductions

Abstract

Each layer of the constructed asphalt pavement is evaluated by measuring its quality indicators, as specified in the construction regulations ĮT ASFALTAS 08, and comparing the obtained values with the corresponding design or threshold values. Due to inherent variability in material properties and systematic or random errors during the production, transport, and installation of the asphalt mixture, the quality indicators of the asphalt layers often deviate from their optimal values. When deviations exceed permissible deviations (PD) or limit values (LV), monetary deductions (MDs) are applied. This study presents normalised values and variation dynamics for 10 quality indicators of the asphalt layer subject to MDs in Lithuania. Using the expertise of 71 road construction professionals and multi-criteria decision-making (MCDM) methods, the influence of these deviations on road quality was assessed. The experts ranked all indicators using percentage weights and the Analytic Hierarchy Process (AHP) method. Expert consensus was verified using concordance coefficients and consistency ratios. After eight statistical outliers were excluded, adjusted weights were calculated based on responses from 63 experts. The proposed method, termed CIBRO (Criteria Importance But Rejected Outliers), enables the objective prioritisation of asphalt quality indicators. The CIBRO method enhances expert concordance and results reliability by aligning criterion ranks with the normal distribution, complementing the Kendall rank correlation approach. The findings highlight that insufficient compaction, inadequate layer thickness, and binder content deviations are the most influential factors that affect layer quality. In contrast, deviations in pavement width, friction coefficient, and surface evenness (measured with a 3 m straight edge) were found to have a lesser impact. The CIBRO method offers a robust approach to assessing the importance of the quality of the asphalt layer, supporting improvements in construction standards and pavement assessment systems.

1. Introduction

The fundamental purpose of any transport system is to improve the quality of life of its users. The achievement of this critically depends on the development of a high-quality transport infrastructure, which also contributes to a reduction in accidents and environmental pollution [1]. The benefits derived from the new road infrastructure are distributed among various stakeholders, including road users, construction contractors, and investors [2]. Research indicates that road users receive the most significant benefit (relative weight 0.3485), followed by road construction contractors (relative weight 0.3325), and road investors benefit the least (relative weight 0.3190) [3]. To realise these benefits, the asphalt paving industry constantly strives to improve the productivity of its labour, equipment, and material resources [4]. However, the construction process is inherently complex and causes substantial environmental impacts, with energy consumption and emissions influenced by numerous factors such as aggregate type, fuel, and production temperature [5]. The final quality of asphalt pavement is a function of many variables throughout the production chain, including the mixing time and temperature, which affect material homogeneity and binder viscosity, as well as the transport distance and cooling time of hot-mix asphalt (HMA) before it can be opened to traffic [6,7,8].

Given this complexity, quality control (QC) and quality assurance (QA) programmes are critical, as a decrease in product quality leads to increasing financial penalties for contractors [9]. Although statistical process control (SPC) can minimise cost overruns [10,11], the need for daily testing makes QA programmes expensive [12]. A key challenge is determining how to assess the final product, as producers prefer payment based on the quality of the material at the plant, while the QA samples are taken behind the paver, introducing variability [13]. The acceptance of the mixture and the determination of the pay factors are often based on aggregate gradation in various sieve sizes and the bituminous binder content [14].

The performance of an asphalt mixture is fundamentally governed by its composition and structure [15,16]. Mineral aggregates are the main primary component, and their properties—including gradation, particle shape, and size—significantly affect the resistance of the pavement to permanent deformation and fatigue [17,18,19,20,21]. The achievement of optimum bituminous binder content (OBBC) is crucial, as the binder coats and bonds aggregate particles, creating a durable, rut-resistant material [22]. The interaction and bond strength between the binder and the aggregate are essential for performance, especially when resisting moisture damage, which can cause a loss of strength and durability through adhesive or cohesive failure [23,24,25,26].

Aggregates in the construction of transport infrastructure exhibit variation due to inevitable segregation during production, loading, transport, laying, and compaction [27,28,29]. Increased aggregate heterogeneity requires more samples for representativeness [30]. The presence of filler reduces the optimum bituminous binder content, and higher filler concentrations result in stronger pavement due to better binder cohesivity and internal stability from good packing [31,32]. The air void content and structure within compacted asphalt are critically important, influencing resistance to rutting, fatigue cracking, and ageing [33,34,35,36]. The distribution of air void, affected by compaction, clearly influences the susceptibility to moisture and the rate of oxidation of bitumen [37]. Closely related is the thickness of the bitumen film (BFT), a calculated parameter important for durability [32,35,38,39,40]. Although thicker films improve ageing resistance, they can contribute to instability and rutting, whereas overly thin films are susceptible to moisture-induced stripping [41,42,43,44].

Real-world observations confirm pavement distress; for instance, statistical studies of 18 Lithuanian highways revealed greater depths of ruts in the first traffic lane, primarily used with heavy vehicles [45]. This underscores the direct relationship between traffic loading, material performance, and the need for robust quality control to minimise long-term pavement degradation.

Based on the critical need for quality control and assurance in asphalt paving, research has extensively explored how deviations in construction parameters directly affect the final performance of the asphalt mixture. For example, studies have simulated the impact of a 3% decrease in the degree of compaction or a 0.5% reduction in binder content, highlighting the sensitivity of pavement quality to even minor variances [28]. In parallel with understanding these parameter sensitivities, significant efforts have been made to investigate various methods for assessing pavement properties in the field. This includes innovative approaches such as using microwaves to determine optimal compaction, as well as employing ground-penetrating radar and dynamic cone penetrometers to accurately estimate layer thickness [29,46,47]. Furthermore, to enhance the reliability of existing quality assurance (QA) and quality control (QC) tools, studies have focused on developing advanced frameworks and new calibration methods, particularly to improve the performance of non-nuclear density gauges [48].

Highway engineers face complex problems influenced by these various conditions, and identifying effective solutions requires considerable expertise [49]. To address this, expert systems and multi-criteria decision-making (MCDM) methods such as the Analytic Hierarchy Process (AHP) are increasingly being used to help decision-makers identify and rank factors affecting pavement performance [50,51].

The aim of this work is to evaluate the significance of asphalt-layer indicators (criteria) to road pavement quality, specifically those for which monetary deductions are calculated due to non-compliance with limit values and exceeding permissible deviations. This evaluation will be achieved by applying multiple-criteria decision-making (MCDM) methods and utilising the knowledge and qualifications of road construction engineering specialists (experts).

2. Permissible Deviations and Limit Values of Asphalt-Layer Quality Indicators

The quality requirements for asphalt layers installed in the construction of Lithuanian roads are presented in the normative document ĮT ASFALTAS 08 (2008) [52]. Upon the acceptance of the installed asphalt pavement, the asphalt mixture used in it and the structural and geometric indicators of the layer constructed from it are tested. The parameters affecting the quality and durability of the new asphalt pavement can be categorised into two groups (Figure 1).

To manage potential defects, permissible deviations (PDs) and limit values (LVs) are provided for ten quality indicators, for the non-compliance of which monetary deductions (MDs) are calculated (

Table 1. Asphalt-layer quality indicators: deductions, deviations, and limits [52].

Symbol	Quality Criterion for the Monetary Deduction	Permissible Deviations (PDs) and Limit Values (LVs), Their Dates of Change
A	Insufficient layer thickness	(a) The deviation of an individual value of the thickness of the installed layer from the design thickness for an individual value cannot be greater than 10%, 15% or 25%. The deviations of the thickness average are smaller. (b) The limit value of the deviation of the thickness of the layer from the design thickness cannot be greater than 0.5 cm for an individual value and 0.4 cm for the arithmetic mean (from 28 April 2017). MDs are not calculated.
B	Lower binder content	(a) The binder content of a sample taken from the installed layer cannot deviate from the design value by more than the permissible deviations of 0.6% or 0.5%. As the sample size increases, the average deviation decreases. (b) The permissible value for a lower content is up to 0.3%, deduction from 0.31% to 0.59%, and limit—0.6% and more (from 10 July 2018).
C	Lower or higher fraction content > 2 mm (coarse aggregates) or 0.063–2 mm (fine aggregate)	(a) The granulometric composition of a sample taken from the installed layer cannot deviate from the design value by more than the permissible deviations of ±9%, ±8% or ±2.5%. As the sample size increases, the average deviation decreases. (b) The limit values for the deviation of the content of particles passing through a 2 mm sieve are ±5.1% or ±6.1% (from 10 July 2018, but MDs are not calculated).
D	Lower or higher content of fraction < 0.063 mm (mineral filler)	(a) The granulometric composition of a sample taken from the installed layer cannot deviate from the design value by more than the permissible deviations of +7% and −3%, ±3%, ±4.5% or ±2%. As the sample size increases, the average deviation decreases. (b) The limit values for the content of particles passing through a 0.063 mm sieve are ±2.6%, ±3.1% or ±3.6% (from 10 July 2018, but MDs are not calculated).
E	Lower degree of compaction	(a) The degree of compaction must meet these limit values: 97% or 96% for asphalt base courses, lower course, upper course of asphalt concrete and not less than 97% for stone mastic asphalt, porous asphalt, and the base-wearing course of asphalt. (b) Unchanged since 2008.
F	Exceeding the limit values for unevenness measured according to IRI requirements	(a) Unevenness measured according to IRI requirements must not exceed these limit values: 1.5 m/km (for highways), 2.5 m/km (for national roads), and 3.5 m/km (for regional roads made of asphalt base-wearing courses). (b) Motorways and expressways 1.0 m/km, other highways 1.5 m/km, national roads 2.0 m/km, and regional roads 3.0 m/km (from 10 July 2018).
G	Exceeding the limit values for unevenness measured with a 3 m straight edge	(a) The maximum clearance measured under a 3 m long straight edge cannot be greater than the limit value of 6 mm, 4 mm, or 3 mm for asphalt surface courses and not greater than 10 mm or 6 mm for the asphalt base, asphalt base-wearing course, and lower course. (b) Unchanged since 2008.
H	Exceeding the permissible deviation for the cross slope of the pavement	(a) The deviation in the pavement cross slope from the required (design) value must not be greater than the permissible value ±0.5%. In transition sections of carriageways intended for high-speed traffic with a smaller longitudinal (0.5%) and cross (1.5%) slope, it must not be greater than 0.3% in the decreasing direction. (b) Unchanged since 2008.
I	Exceeding the permissible deviation for the pavement width	(a) The deviation of the installed layer width from the design width must not be greater than the permissible −5 cm and +10 cm. (b) The deviations of the installed layer from the width specified in the project (contract) must not be greater than −5 cm and +5 cm (from 10 July 2018).
J	Lower coefficient of tyre-road friction	(a) The coefficient of tyre-road friction must not be less than the limit value of 0.40 (for highways) and 0.35 (for national and regional roads). (b) The values of the surface skid resistance indicator must not be less than the limit values of 0.55 for motorways and expressways, 0.50 for other highways, and 0.45 for national and regional roads (from 10 July 2018).

Note: MDs—monetary deductions.

). PDs are not calculated for the adhesion between layers, but they are determined.

The monetary deductions aim to ensure the quality of the asphalt layer, which depends on the quality of the materials, the quality of the design of the asphalt mix, and the parameters of the technological operations performed by the contractor. By minimising the actual deviations in the quality indicators and meeting their established limit values, the MDs are reduced, resulting in economic benefits for the contractor and better technical and operational characteristics of the road for the users. To achieve technical progress aimed at improving road transport infrastructure, over a 10-year period (2008–2018), the PDs and LVs of some quality indicators for asphalt layers in ĮT ASFALTAS 08 were changed by increasing requirements (Table 1).

The varying impact of asphalt-layer quality-indicator non-compliance on overall road quality suggests the utility of multi-criteria decision-making (MCDM) methods for defect significance assessment. The numerical assessments of the importance of the criteria by road construction specialists (experts) allow the calculation of the relative weights of asphalt-layer defects on road quality. The high qualifications, deep knowledge, and skills of experts in the construction of roads with asphalt pavement have a significant impact on the correct assessment of defects.

3. Research Methods

3.1. Defects Assessed in Asphalt Layer

The present study examined the importance of asphalt-pavement-layer quality indicators for road quality. These indicators, detailed in Table 1, are the basis for calculating the monetary deductions when the permissible deviations are exceeded or the limit values are not met. Figure 2 shows the flow chart for evaluating the effectiveness of criteria with the CIBRO method.

3.2. The Team of Experts

The authors of the study compiled a preliminary list of potential experts (road engineers) with knowledge and experience in the design, construction, maintenance, and operation of asphalt pavements. Each expert was personally spoken to about the purpose of the study and asked for their consent to provide a numerical assessment of the significance of the defects (criteria) in a prepared questionnaire (Appendix A,

Table A1. Expert survey questionnaire.

Quality-Indicator Symbol	Quality Criterion for the Monetary Deduction [52]	Rank (Place)	Percentage Weight in 100%
A	Insufficient layer thickness
B	Lower binder content
C	Lower or higher content of fraction > 2 mm (coarse aggregates) or 0.063–2 mm (sand)
D	Lower or higher content of fraction < 0.063 mm (mineral filler)
E	Lower degree of compaction
F	Exceeding the limit values for unevenness measured according to IRI requirements (IRI)
G	Exceeding the limit values for unevenness measured with a 3 m straight edge
H	Exceeding the permissible deviation for the cross slope of the pavement
I	Exceeding the permissible deviation for the pavement width
J	Lower coefficient of tyre–road friction
		Sum 55	100.0%

). Experts who agreed to participate in the study received a printed questionnaire that included instructions for its completion. The expert team consisted of 71 specialists.

3.3. The Questionnaire and Its Completion Procedure

In the questionnaire, the experts provided their name and surname, position, and work experience. This personal data is not disclosed, as experts were coded from E1 to E71. The experts assigned ranks (positions by importance) and percentage weights to defects (criteria), which were used to determine the significance assessments of the criteria for the entire expert team by calculating their normalised relative weights using the ARTIW-L (Average Rank Transformation into Weight-Linear), ARTIW-N (Average Rank Transformation into Weight-Nonlinear), and DPW (Direct Percentage Weight) methods. Each expert was able to assign ranks and percentage weights to the criteria independently. At the end of the questionnaire, the significance of the criteria was determined using the rather complex AHP (Analytic Hierarchy Process) method (Appendix A,

Table A2. AHP criteria pairwise comparison matrix.

Rank	Quality Indicator (Criterion)		Quality Indicator (Criterion) j = 1, 2, …, m										$\mathbf{Eigenvector} \left(\mathbf{Weight}\right) {\mathbf{\omega }}^{\mathbf{A}\mathbf{H}\mathbf{P}}$
			A	B	C	D	E	F	G	H	I	J
	Quality Indicator (Criterion) j = 1, 2, …, m	A	1
		B		1
		C			1
		D				1
		E					1
		F						1
		G							1
		H								1
		I									1
		J										1
												C.R.=

Sequence: from the most important criterion to the least important criterion.

). Not all experts did, at first, correctly fill in the pairwise comparison matrix. For some matrices, the consistency ratio, C.R. > 0.1, needed slight corrections to fully satisfy the transitivity condition. The best result was obtained when the AHP matrix filling process was supervised by one of the authors of this study, who is well versed in this method and, if necessary, advised the expert on how to avoid errors.

Before applying MCDM methods to process the initial data, all questionnaires filled out by experts were checked, and if necessary (when the sum of ranks was not equal to 55, and the sum of percentage weights was not equal to 100%), some of them were corrected. The correctness of the AHP method matrices was checked by calculating the C.R. If it did not meet the threshold value of 0.1, the matrix was checked and slightly corrected, and the C.R. was calculated again. If the correction did not yield a C.R. < 0.1, the matrix was rejected. To increase the reliability of the assessment results, it is recommended to apply several methods simultaneously: the coincidence of all or most of the results reduces the possibility of making a wrong decision [53].

3.4. Evaluation of the Consistency of the Opinions of the Expert Team

Initially, it was checked whether the assessments of the significance of 10 defects (criteria) for road quality by the team of 71 experts were non-contradictory, i.e., they did not differ significantly. Only with sufficient consistency of the expert team’s opinions can the arithmetic means of the numerical significance of the evaluated criteria be taken as a reliable result for solving the problem. The consistency in the opinions of the expert team is determined by calculating the Kendall coefficient of concordance W according to the following formula [54]:

$$W={\displaystyle \frac{12S}{n^2\left(m^3-m\right)}},$$

(1)

where n is the number of experts (j = 1, 2, …, n), m is the number of defects (criteria) being evaluated (i = 1, 2, …, m), and S is the sum of squared deviations of the sum of criteria ranks ${\displaystyle {\sum }_{j=1}^n{R}_{ij}}$ from the overall mean rank $\overline{R}={\displaystyle \frac{n\left(m+1\right)}{2}}$, calculated using Formula (2):

$$S={{\displaystyle {\sum }_{i=1}^m\left[{\displaystyle {\sum }_{j=1}^n{R}_{ij}-\frac{n\left(m+1\right)}{2}}\right]}}^2.$$

(2)

Only criteria ranks are suitable for calculating the Kendall coefficient of concordance.

Whether the expert team’s opinions are consistent was determined in the classical way by comparing the empirical value of the Chi-square Pearson’s statistic χ² with its critical value, ${\chi }_{v,\alpha }^2$, which depends on the degrees of freedom, v = m − 1, and the chosen significance level, α (taken as α = 0.05 or α = 0.01). The empirical χ² value is calculated from Formula (3):

$${\chi }^2={\displaystyle \frac{12S}{nm\left(m+1\right)}}.$$

(3)

When χ² is greater than ${\chi }_{v,\alpha }^2$, it is reasonably considered that the expert team’s opinions are non-contradictory, even though the criteria significance assessments in ranks by all experts are not identical, and there may be outliers in the assessment.

It was proposed [55] to compare the concordance coefficient W with its minimum (threshold) value W_min, which is calculated from Formula (4):

$$W_{\min }={\displaystyle \frac{{\chi }_{\alpha ,v}^2}{n\left(m-1\right)}}.$$

(4)

It was proposed [56] to calculate the ratio of the concordance coefficient, W, to its minimum value, W_min, from Formula (5) and to call it the compatibility coefficient:

$$k_c={\displaystyle \frac{W}{W_{\min }}}={\displaystyle \frac{{\chi }^2}{{\chi }_{v,\alpha }^2}}.$$

(5)

When k_c is greater than 1, the opinions of the expert team in assessing the significance of the criteria not only by rank but also by percentage weights or relative weights of the AHP method are sufficiently consistent. This allows the arithmetic mean of the significance estimates (ranks or relative weights) of each criterion to be taken as the solution to the problem.

3.5. Evaluation of Rank Variation, Normality, and Outliers

The ranks assigned to the criteria by the experts usually differ and have a certain variation, the magnitude of which is indicated by the standard deviation ${\sigma }_{iR}$:

$${\sigma }_{iR}=\sqrt{{\displaystyle \frac{{\displaystyle {\sum }_{j=1}^n{\left(R_{ij}-{\overline{R}}_i\right)}^2}}{n-1}}},$$

(6)

where ${\overline{R}}_i$ is the arithmetic mean of the ranks R_ij for the i-th criterion.

$${\overline{R}}_i={\displaystyle \frac{{\displaystyle {\sum }_{j=1}^n{R}_{ij}}}{n}}.$$

(7)

The average variation (variance, ${\sigma }_R^2$) of the significance estimates for the entire object under study (ten quality indicators of the asphalt layer of the road pavement), evaluated by m criteria of the same size n, can be calculated from Formula (8):

$${\sigma }_R^2={\displaystyle \frac{{\displaystyle {\sum }_{i=1}^m{\sigma }_{Ri}^2}}{m}},$$

(8)

where ${\sigma }_{Ri}$ is the standard deviation of the ranks R_ij for the i-th criterion; m is the number of criteria.

This Formula (8) can be used to calculate the average standard deviation of ranks ${\sigma }_R$ only if the rank variances ${\sigma }_{Ri}^2$ of the i-th criteria are statistically equal [57]. The rank variances calculated from samples of the same size n can be compared using Cochran’s test. The statistic ${\widehat{G}}_{\max }$ is calculated, which is the ratio of the maximum variance to the sum of all variances:

$${\widehat{G}}_{\max }={\displaystyle \frac{\underset{i}{\max }{\sigma }_{Ri}^2}{{\displaystyle {\sum }_{i=1}^m{\sigma }_{Ri}^2}}}$$

(9)

where $\underset{i}{\max }{\sigma }_{Ri}^2$ is the maximum variance of the ranks for the i-th criterion.

It can be assumed that the rank variances of the criteria are equal if the empirical value of the Cochran’s test statistic ${\widehat{G}}_{\max }$ is less than its critical value G_C(α, m, v), which depends on the significance level alpha, the number of variances compared (number of criteria) m, and the degrees of freedom v = n − 1 (where n is the number of experts). The value of G_C(α, m, v) is found in Table 152 [57].

When using Cochran’s test to determine the homogeneity of rank variances, it is necessary to ensure that the rank distribution follows a normal law. The normality of the criteria ranks can be assessed by the values of the skewness and kurtosis coefficients. The moduli of empirical skewness $\left|Sk\right|$ and kurtosis $\left|Ku\right|$ must be less than 3 standard deviations of skewness S_Sk (Formula (10)) and less than 5 standard deviations of kurtosis S_Ku (Formula (11)), respectively. The standard deviations of skewness and kurtosis, which depend only on the sample size (number of experts), n, are calculated from the following formulas:

$$S_{Sk}=\sqrt{{\displaystyle \frac{6n\left(n-1\right)}{\left(n-2\right)\left(n+1\right)\left(n+3\right)}}}$$

(10)

and

$$S_{Ku}=\sqrt{{\displaystyle \frac{24n{\left(n-1\right)}^2}{\left(n-3\right)\left(n-2\right)\left(n+3\right)\left(n+5\right)}}}$$

(11)

If the empirical concordance coefficient, W, is greater than its critical value, W_min (when k_c > 1), then the opinions of the expert team in assessing the significance of the object’s criteria are consistent (non-contradictory). The reason for the non-conformity of the ranks of the object’s criterion to the normal distribution, determined by the skewness and kurtosis values, is usually the presence of outliers in the criterion’s ranks. Significantly different rank values (outliers) from expert studies can be justifiably removed from the research data. Usually, values of the variation series that do not fall within the ${\overline{R}}_i\pm 3{\sigma }_{Ri}$ interval are considered outliers [58]. The upper threshold rank value, R_ijU, is calculated from Formula (12):

$$R_{ijU}={\overline{R}}_i+3{\sigma }_{Ri}$$

(12)

and

$$R_{ijL}={\overline{R}}_i-3{\sigma }_{Ri}$$

(13)

where ${\overline{R}}_i$ is the mean of the ranks of the i-th criterion (with outliers); ${\sigma }_{Ri}$ is the standard deviation of the ranks of the i-th criterion.

It is likely that, after the rank outliers are removed, the standard deviation of the ranks ${\sigma }_{Ri}$ will significantly decrease, and the empirical values of $\left|Sk\right|$ and $\left|Ku\right|$ will also decrease. The rank means ${\overline{R}}_i$ will change slightly: they will increase when the outliers are small rank values and decrease when the outliers are large rank values. If the significance assessment of all criteria by the j-th expert contains at least one rank that is an outlier, then the assessments of all criteria by this expert are removed from the study.

3.6. Calculation of Relative Weights of the Using MCDM Methods

In multiple-criteria evaluation, criteria weights are of great importance. In practice, subjective criteria weights determined by specialists/experts are commonly used. The types of elements in a decision matrix also play an important role in the evaluation of alternatives [59]. It is customary to evaluate the significance of the criteria by comparing their normalised relative weights, which range from 0 to 1. The more significant the indicator (criterion) describing the object under study, the greater its relative weight. Therefore, the significance of the criteria, determined by ranks, percentage weights, scores on a five-point scale, or scores on a ten-point scale, must be calculated as normalised relative weights, the sum of which is equal to 1.0000. This allows for a comparison of the weights of each criterion determined by different MCDM methods.

It is convenient to calculate the relative weights of these criteria ${\omega }_i^{ARTIW-L}$, from the mean ranks of the criteria ${\overline{R}}_i$, using the Average Rank Transformation into Weight-Linear (ARTIW-L) method, presented in 2011 [55]:

$${\omega }_i^{ARTIW-L}={\displaystyle \frac{m-{\overline{R}}_i+1}{{\displaystyle {\sum }_{i=1}^m{\overline{R}}_i}}}$$

(14)

From the mean ranks of the criteria ${\overline{R}}_i$, it is also possible to calculate the relative weights of these criteria ${\omega }_i^{ARTIW-N}$, using the Average Rank Transformation into Weight-Non-Linear (ARTIW-N) method, which shows a non-linear relationship between these variables [60]:

$${\omega }_i^{ARTIW-N}={\displaystyle \frac{\underset{i}{\min }{\overline{R}}_i}{{\overline{R}}_i\cdot {\displaystyle {\sum }_{i=1}^m\frac{\underset{i}{\min }{\overline{R}}_i}{{\overline{R}}_i}}}}$$

(15)

When evaluating the significance of the criteria of the object under study not by ranks but by percentage weights P_ij, the Direct Percentage Weight (DPW) method can be applied, which allows the calculation of the relative weights of these criteria [56]:

$${\overline{\omega }}_i^{DPW}={\displaystyle \frac{{\displaystyle {\sum }_{j=1}^n{P}_{ij}}}{100n}}$$

(16)

To determine the significance of the criteria, the popular but rather complex method of filling their pairwise comparison matrix, the Analytic Hierarchy Process (AHP), presented by T.L. Saaty [61], is suitable (Appendix A,

Table A3. The Fundamental (Saaty) Scale of Relative Importance Intensities in the AHP Method.

Importance Level	Definition
1	Factors are equally important
2	One factor is slightly more important than another
5	One factor is much more important than another
7	One factor is very much more important than another
9	One factor is incomparably more important than another
2, 4, 6, 8	Intermediate values

). The AHP is a reliable, rigorous, and robust method for eliciting and quantifying subjective judgements in multicriteria decision-making (MCDM). Despite the many benefits, the complications of the pairwise comparison process and the limitations of consistency in AHP are challenges that have been the subject of extensive research [62].

The AHP approach has been widely used in MCDM. It is very difficult to meet the consistency requirement of a comparison matrix (CM) in AHP. The authors [63] analyse the reasons for inconsistent CM in AHP and propose an improved AHP (IAHP) to improve the consistency of CM using a classification and ranking methodology.

From the matrix filled by the j-th expert, the eigenvector ${\omega }_{ij}^{AHP}$ is calculated for each i-th criterion, which is taken as the normalised relative weight of the criterion:

$${\omega }_{ij}^{AHP}={\displaystyle \frac{\sqrt[m]{{\displaystyle {\prod }_{j=1}^n{a}_{ij}}}}{{\displaystyle {\sum }_{i=1}^m\sqrt[m]{{\displaystyle {\prod }_{j=1}^n{a}_{ij}}}}}}$$

(17)

where $a_{ij}$ is the intensity of pairwise comparison assigned by the j-th expert to the i-th criterion (i, j = 1, 2, …, m) on a nine-point scale.

When filling the matrix of the AHP method, $\mathbf{A}={[a_{ij}]}_{m\times m}$, the criteria on the left side of the matrix are compared with the criteria at the top. By convention, the strength of comparison is always that an activity appearing in the column on the left against an activity appearing in the row on top [61].

The relative weight, ${\overline{\omega }}_i^{AHP}$, assigned to the i-th criterion by the expert team is calculated from Formula (18):

$${\overline{\omega }}_i^{AHP}={\displaystyle \frac{{\displaystyle {\sum }_{j=1}^n{\omega }_{ij}^{AHP}}}{n}}$$

(18)

where ${\omega }_{ij}^{AHP}$ is the weight assigned to the i-th criterion by the j-th expert using the AHP method.

The consistency of each pairwise comparison matrix filled by an expert is checked by calculating the consistency ratio, C.R. It is calculated by dividing the consistency index, C.I., by the random index, R.I. The consistency index, C.I., is calculated from Formula (19):

$$C.I.={\displaystyle \frac{{\lambda }_{\max }-m}{m-1}}$$

(19)

where m is the number of criteria that are evaluated (i = 1, 2, …, m); λ_max is the largest eigenvalue of the pairwise comparison matrix, which is calculated from Formula (20) [64,65,66].

$${\lambda }_{\max }={\displaystyle \frac{1}{m}}{\displaystyle {\sum }_{i=1}^m\frac{{\displaystyle {\sum }_{j=1}^m{a}_{ij}{\omega }_{ij}^{AHP}}}{{\omega }_{ij}^{AHP}}}$$

(20)

The random index, R.I., is taken from a table [61], or when the number of criteria, m > 10, it is calculated from Formula (21) [67]:

$$R.I.=1.98{\displaystyle \frac{m-2}{m}}$$

(21)

A consistency ratio of 0.10 or less is considered acceptable [61]. The resulting vector is accepted if C.R. is about 0.10 or less (0.20 may be tolerated, but not more) [68].

3.7. Results and Their Analysis

The significance of the parameters of the asphalt layers of road pavement structures, for which monetary deductions (MDs) are calculated for exceeding the permissible deviations (PDs) or not complying with the limit values (LVs) according to the requirements of ĮT ASFALTAS 08, determined by a team of 71 experts of rank, is presented in

Table 2. Significance of Asphalt Layer Indicators for Road Quality and Monetary Deductions (ARTIW-L, ARTIW-N; Expert Team n = 71).

Formula and Method	Quality Indicator (Criterion) i = 1, 2, …, m										Sum
	A	B	C	D	E	F	G	H	I	J
${\displaystyle {\sum }_{j=1}^n{R}_{ij}}$	163	168	328	349	147	467	517	518	674	574	3905
${\overline{R}}_i={\displaystyle {\sum }_{j=1}^n{R}_{ij}/n}$	2.296	2.366	4.620	4.916	2.070	6.577	7.282	7.296	9.493	8.084	55.000
${\displaystyle {\sum }_{j=1}^n{R}_{ij}-\frac{n\left(m+1\right)}{2}}$	−227.5	−222.5	−62.5	−41.5	−243.5	76.5	126.5	127.5	283.5	183.5	0.0
${\left[{\displaystyle {\sum }_{j=1}^n{R}_{ij}-\frac{n\left(m+1\right)}{2}}\right]}^2$	51,756	49,506	3906	1723	59,292	5852	16,002	16,257	80,372	33,672	318,338
${\sigma }_{Ri}=\sqrt{{\displaystyle \frac{{\displaystyle {\sum }_{j=1}^n{\left(R_{ij}-{\overline{R}}_i\right)}^2}}{n-1}}}$	1.792	0.898	1.467	1.619	1.073	1.518	1.136	1.281	1.453	1.528	–
Skewness	2.544	1.145	1.809	1.117	0.712	−0.807	−0.160	−0.873	−3.567	−1.505	–
Kurtosis	8.336	3.384	5.474	2.378	−0.158	4.352	0.327	1.334	12.786	1.673	–
ARTIW-L method:
${\omega }_i^{ARTIW-L}={\displaystyle \frac{m+1-{\overline{R}}_i}{{\displaystyle {\sum }_{i=1}^m{\overline{R}}_i}}}$	0.1583	0.1570	0.1160	0.1106	0.1624	0.0804	0.0676	0.0673	0.0274	0.0530	1.0000
Priority	2	3	4	5	1	6	7	8	10	9	55
ARTIW-N method:
$u_i={\displaystyle \frac{\underset{i}{\min }{\overline{R}}_i}{{\overline{R}}_i}}$	0.9016	0.8749	0.4481	0.4211	1	0.3147	0.2843	0.2837	0.2181	0.2561	5.0026
${\omega }_i^{ARTIW-N}={\displaystyle \frac{u_i}{{\displaystyle {\sum }_{i=1}^m{u}_i}}}$	0.1802	0.1749	0.0896	0.0842	0.1999	0.0629	0.0568	0.0567	0.0436	0.0512	1.0000
Priority	2	3	4	5	1	6	7	8	10	9	55

.

With the number of criteria, m = 10, and the number of experts, n = 71, the overall mean rank is $\overline{R}$ = 390.5. In this table, the calculated S = 318,338, according to Formula (2); therefore, from Formula (1), the Kendall coefficient of concordance is W = 0.765. The empirical Pearson’s chi-square statistic, χ² = 489.12, is 28.9 times greater than the minimum critical value when the significance level is α = 0.05, ${\chi }_{0.05;9}^2$ = 16.92. The minimum value of the concordance coefficient, calculated according to Formula (4), is W_min = 0.0265. The compatibility coefficient of the opinions of the expert team, calculated from Formula (5), is k_c = 28.9. Therefore, it can be reasonably stated that the opinions of the 71-expert team regarding the significance of the criteria are consistent.

Skewness and kurtosis, which indicate the nature of the rank variation and its conformity to the normal distribution, are compared with their standard deviations calculated from Formulas (10) and (11). The rank distribution of the criteria is normal when the modulus of the empirical skewness $\left|Sk\right|$ is less than 3S_Sk = 3 × 0.285 = 0.855 and when the modulus of kurtosis $\left|Ku\right|$ is less than 5S_Ku = 5 × 0.562 = 2.813. According to the empirical skewness, the ranks of criteria E, F, and G follow a normal distribution, while, according to kurtosis, the ranks of criteria D, E, G, H, and J follow a normal distribution (Table 2).

Assuming that the ranks of all criteria follow a normal distribution and are calculated from independent populations, the Cochran test can be used to compare the rank variances, ${\sigma }_{Ri}^2$, of all criteria. The standard deviations of the criteria ranks are presented in Table 2 and the variances in

Table 3. Indicators of rank variation (dispersion) for criteria, calculated from the assessments of the 71-expert team.

Statistic	Quality Indicator (Criterion) i = 1, 2, …, m										Sum
	A	B	C	D	E	F	G	H	I	J
${\sigma }_{Ri}$	1.792	0.898	1.467	1.619	1.073	1.518	1.136	1.281	1.453	1.528	–
${\sigma }_{Ri}^2$	3.211	0.806	2.152	2.621	1.151	2.305	1.291	1.641	2.111	2.335	19.624
Ri	78.05	37.95	31.75	32.93	51.84	23.08	15.60	17.56	15.30	18.90

.

Cochran’s test statistic, calculated from Formula (9):

$${\widehat{G}}_{\max }={\displaystyle \frac{\underset{i}{\max }{\sigma }_{Ri}^2}{{\displaystyle {\sum }_{i=1}^m{\sigma }_{Ri}^2}}}={\displaystyle \frac{3.211}{19.624}}=0.1636.$$

The critical tabular value of Cochran’s test statistic, G_C (0.05; 10; 70) = $0.1546$ [57], is less than the empirical statistic value of 0.1636; therefore, it cannot be stated that the criteria rank variances ${\sigma }_{Ri}^2$ are statistically equal with a probability of p = 0.05, i.e., with a 5% significance level.

From different (unequal) criteria rank variances, ${\overline{\sigma }}_{Ri}^2$, the overall average variance ${\sigma }_{Ri}^2$ for the entire object under study (asphalt layer) cannot be calculated using Formula (8). The degree of homogeneity of variances can likely be increased by removing outliers from the study. The threshold values for outliers of each criterion’s ranks, calculated from Formulas (12) and (13), and the serial numbers of the experts and their outlier (rejected) ranks assigned to the criteria are presented in

Table 4. Outliers in the ranking assessment of indicator significance.

Outlier Threshold Formula	Indicator (Criterion) i = 1, 2, …, m
	A	B	C	D	E	F	G	H	I	J
${\overline{R}}_i-3\cdot {\sigma }_{Ri}$	−3.08	−0.33	0.22	0.06	−1.15	2.02	3.87	3.45	5.13	3.50
${\overline{R}}_i+3\cdot {\sigma }_{Ri}$	7.67	5.06	9.02	9.77	5.29	11.13	10.69	11.14	13.85	12.67
Expert (rank)	E54 (10) E55 (10)	E19 (6)	E39 (10) E43 (10)	E21 (10)	–	E17 (1) E22 (1)	–	E39 (3)	E21 (4) E54 (3) E55 (3)	E19 (3)

Note: The number in parentheses is the rank of criterion R_ij that was removed as an outlier.

. The rankings submitted by experts E10, E17, E19, E21, E22, E39, E54, and E55 were classified as outliers, resulting in a total count of n₀ = 8.

The rank means ${\overline{R}}_i$ calculated with outliers were used to determine the significance of the criteria using the ARTIW-L and ARTIW-N methods (Table 2). The relative weights of the criteria, ${\omega }_i^{ARTIW-L}$ and ${\omega }_i^{ARTIW-N}$, were calculated from Formulas (14) and (15), and priorities were assigned to the criteria. The values of the relative weights of the criteria calculated from Formula (16) using the DPW method are presented in

Table 5. Significance of asphalt-layer indicators for monetary deductions, determined by 71 experts (DPW Method).

Formula and Method	Quality Indicator (Criterion) i = 1, 2, …, m										Sum
	A	B	C	D	E	F	G	H	I	J
${\displaystyle {\sum }_{j=1}^n{P}_{ij}}$	1262.4	1156.6	768	700.3	1217.3	521.5	432.4	442	229.9	369.6	7100
${\overline{P}}_i={\displaystyle {\sum }_{j=1}^n{P}_{ij}/n}$	17.78	16.29	10.82	9.86	17.14	7.35	6.09	6.22	3.24	5.21	100
${\sigma }_{Pi}=\sqrt{{\displaystyle \frac{{\displaystyle {\sum }_{j=1}^n{\left(P_{ij}-{\overline{P}}_i\right)}^2}}{n-1}}}$	5.833	3.044	3.123	2.922	3.796	2.900	2.009	2.346	2.423	2.691	–
Skewness (Sk)	0.389	0.045	−0.317	−0.293	0.779	2.912	0.215	1.284	2.377	1.210	–
Kurtosis (Ku)	0.270	0.633	2.660	1.425	1.335	12.703	0.146	2.715	6.768	1.558	–
DPW method:
${\overline{\omega }}_i^{DPW}={\displaystyle \frac{{\displaystyle {\sum }_{j=1}^n{P}_{ij}}}{100n}}$	0.1778	0.1629	0.1082	0.0986	0.1715	0.0734	0.0609	0.0622	0.0324	0.0521	1.0000
Priority	1	3	4	5	2	6	8	7	10	9	55

. The results indicate that the ranking of the two primary criteria, E and A, as well as G and H, was reversed when calculated using the ARTIW and DPW methods. Some experts did not maintain consistency in their evaluation of the criteria, assigning a higher rank to one criterion while attributing a higher percentage weight to another. In these cases, the expert’s assessment remains unchanged unless the evaluation is determined to be an outlier.

The relative weights, ${\omega }_{ij}^{AHP}$, of all criteria for each of the 71 experts were calculated using the AHP method from Formula (17). The average relative weights of the criteria ${\overline{\omega }}_i^{AHP}$, calculated from Formula (18), are presented in

Table 6. Significance of asphalt-layer indicators for monetary deductions, determined by 71 experts using AHP.

Formula and Method	Quality Indicator (Criterion) i = 1, 2, …, m										Sum
	A	B	C	D	E	F	G	H	I	J
${\omega }_{ij}^{AHP}={\displaystyle \frac{\sqrt[m]{{\displaystyle {\prod }_{j=1}^n{a}_{ij}}}}{{\displaystyle {\sum }_{i=1}^m\sqrt[m]{{\displaystyle {\prod }_{j=1}^n{a}_{ij}}}}}}$	$\mathrm{The} \mathrm{weight} \mathrm{of} \mathrm{the} \mathrm{criterion} {\omega }_{ij}^{AHP}$ is calculated from the elements aij of the pairwise comparison matrix filled out by each j-th expert. All matrices must be consistent (C.R. < 0.1)
${\displaystyle {\sum }_{j=1}^n{\omega }_{ij}^{AHP}}$	14.835	13.589	7.226	6.737	14.883	3.956	2.88	2.949	1.56	2.385	71.000
${\overline{\omega }}_i^{AHP}={\displaystyle \frac{{\displaystyle {\sum }_{j=1}^n{\omega }_{ij}^{AHP}}}{n}}$	0.2089	0.1914	0.1018	0.0949	0.2096	0.0557	0.0406	0.0415	0.022	0.0336	1.0000
${\sigma }_{{\omega }_i}^{AHP}$ $=\sqrt{{\displaystyle \frac{{\displaystyle {\sum }_{j=1}^n{\left({\omega }_{ij}^{AHP}-{\overline{\omega }}_i^{AHP}\right)}^2}}{n-1}}}$	0.072	0.043	0.039	0.044	0.058	0.042	0.018	0.024	0.026	0.025	–
Skewness (Sk)	−0.722	−0.299	1.341	1.443	−0.347	4.428	2.121	2.654	4.48	2.734	–
Kurtosis (Ku)	0.002	0.435	6.856	5.702	−0.884	22.432	8.384	9.092	19.586	8.65	–
Priority	2	3	4	5	1	6	8	7	10	9	55

. This table also presents the standard deviations, ${\sigma }_{{\omega }_i}^{AHP}$, skewness (Sk), and kurtosis (Ku) empirical values, which show that only the weight distributions of the most important criteria E, A, and B conform to the normal law, and the variances, ${\overline{\sigma }}_{{\omega }_i}^{AHP2}$, of all criteria differ significantly when their homogeneity is checked through Cochran’s test.

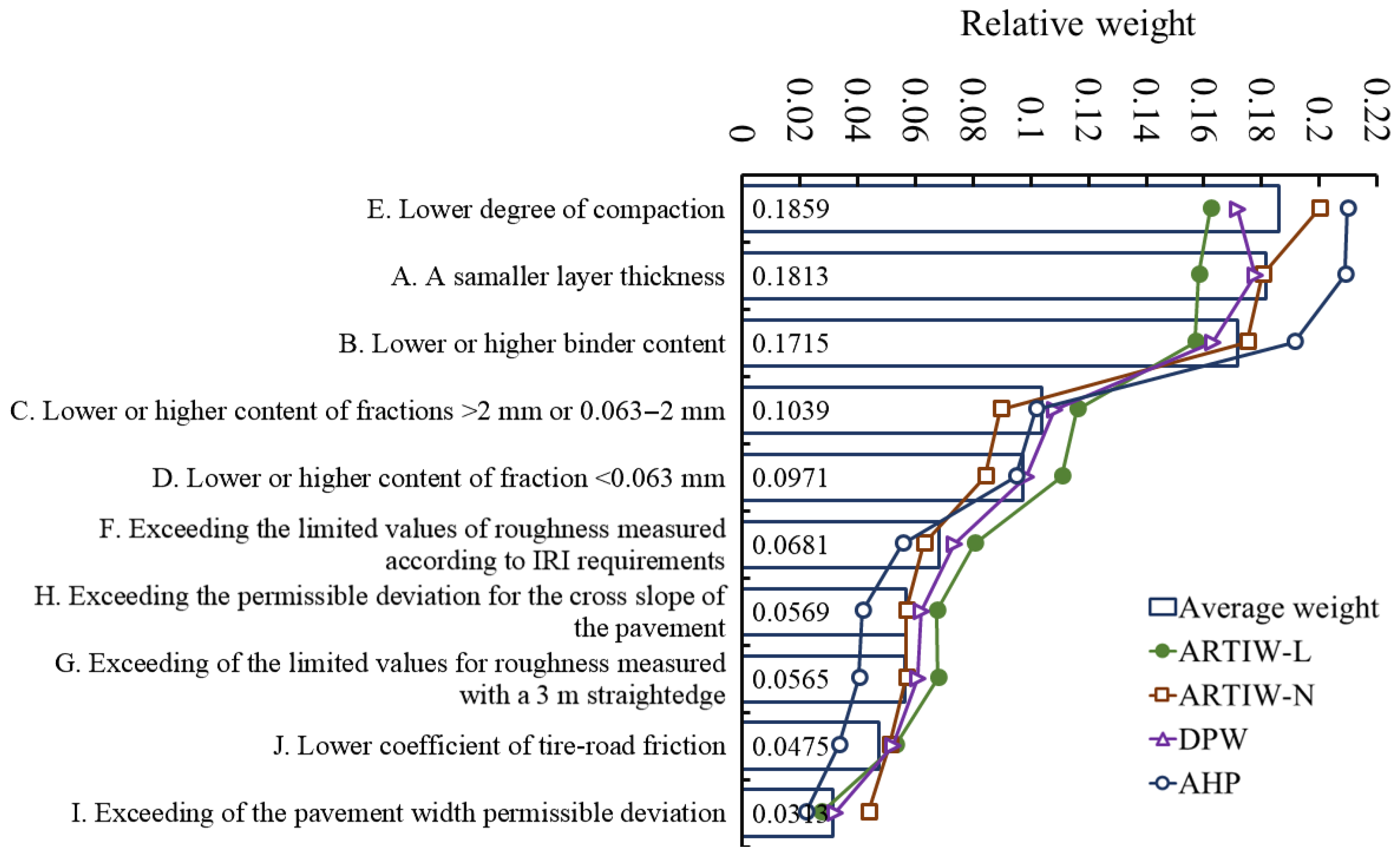
The averages of the relative weights of the criteria, evaluated by a team of 71 experts using four MCDM methods, show that the significance of the 10 indicators of the asphalt layer for the quality of the pavement on the road differs. Without rejecting outliers, the following sequence of significance criteria was obtained (Figure 3): $\mathrm{E}\succ \mathrm{A}\succ \mathrm{B}\succ \mathrm{C}\succ \mathrm{D}\succ \mathrm{F}\succ \mathrm{H}\succ \mathrm{G}\succ \mathrm{J}\succ \mathrm{I}$.

After eight outliers of the study criteria ranks were rejected (Table 4), the adjusted relative weights of the criteria were calculated from the remaining 63 expert assessments, which allowed for an evaluation of the influence of outliers on the relative significance of the criteria and the consistency of opinions. The overall mean rank, $\overline{R}=346.5$, the sum of squared deviations of the sum of criteria ranks ${\displaystyle {\sum }_{j=1}^n{R}_{ij}}$ from $\overline{R}$, is S = 283,884 (

Table 7. Significance of asphalt-layer indicators for road quality and monetary deductions (ARTIW-L, ARTIW-N; 63 Experts).

Formula and Method	Quality Indicator (Criterion) i = 1, 2, …, m										Sum
	A	B	C	D	E	F	G	H	I	J
${\displaystyle {\sum }_{j=1}^n{R}_{ij}}$	134	143	271	290	129	422	464	465	621	526	3465
${\overline{R}}_i={\displaystyle {\sum }_{j=1}^n{R}_{ij}/n}$	2.127	2.270	4.302	4.603	2.048	6.698	7.365	7.381	9.857	8.349	55.000
${\displaystyle {\sum }_{j=1}^n{R}_{ij}-\frac{n\left(m+1\right)}{2}}$	−212.5	−203.5	−75.5	−56.5	−217.5	75.5	117.5	118.5	274.5	179.5	0.0
${\left[{\displaystyle {\sum }_{j=1}^n{R}_{ij}-\frac{n\left(m+1\right)}{2}}\right]}^2$	45,156	41,412	5700	3192	47,306	5700	13,806	14,042	75,350	32,220	283,884
${\sigma }_{Ri}=\sqrt{{\displaystyle \frac{{\displaystyle {\sum }_{j=1}^n{\left(R_{ij}-{\overline{R}}_i\right)}^2}}{n-1}}}$	1.263	0.787	0.927	1.238	1.054	1.087	1.067	1.192	0.435	1.220	–
Skewness (Sk)	1.141	0.510	0.106	0.598	0.757	1.025	0.200	−0.670	−3.204	−1.590	–
Kurtosis (Ku)	1.173	1.203	5.497	3.934	0.104	1.758	−0.190	0.625	10.046	2.313	–
ARTIW-L method:
${\overline{\omega }}_i^{ARTIW-L}={\displaystyle \frac{m+1-{\overline{R}}_i}{{\displaystyle {\sum }_{i=1}^m{\overline{R}}_i}}}$	0.1613	0.1587	0.1218	0.1163	0.1628	0.0782	0.0661	0.0658	0.0208	0.0482	1.0000
Priority	2	3	4	5	1	6	7	8	10	9	55
ARTIW-N method:
$u_i={\displaystyle \frac{\underset{i}{\min }{\overline{R}}_i}{{\overline{R}}_i}}$	0.9629	0.9022	0.4761	0.4449	1	0.3058	0.2781	0.2775	0.2078	0.2453	5.1006
${\omega }_i^{ARTIW-N}={\displaystyle \frac{u_i}{{\displaystyle {\sum }_{i=1}^m{u}_i}}}$	0.1888	0.1769	0.0933	0.0872	0.1962	0.0599	0.0545	0.0544	0.0407	0.0481	1.0000
Priority	2	3	4	5	1	6	7	8	10	9	55

). The Kendall coefficient of concordance, W = 0.867, is approximately 10% higher than the W calculated for the ranks of the 71-expert team, which shows that after rejecting the outliers, the consistency of the experts’ opinions increased.

The statistic χ² = 491.57 is 29.1 times greater than its threshold value, ${\chi }_{0.05;9}^2=16.92$, and similarly, W = 0.867 is greater than W_min = 0.0298 by the same factor.

Using the ARTIW-L and ARTIW-N methods, the calculated relative weights and priorities of the criteria allowed for the creation of a sequence of criteria significance for road pavement quality: $\mathrm{E}\succ \mathrm{A}\succ \mathrm{B}\succ \mathrm{C}\succ \mathrm{D}\succ \mathrm{F}\succ \mathrm{G}\succ \mathrm{H}\succ \mathrm{J}\succ \mathrm{I}$ (Table 7). The sequence of criteria is the same as for the criteria with outliers (Figure 3).

Using the DPW and AHP methods without outliers, the calculated relative weights and priorities of the criteria are presented in

Table 8. DPW evaluation: expert assessment of asphalt-layer indicator impact on road quality and monetary deductions (n = 63).

Formula and Method	Quality Indicator (Criterion) i = 1, 2, …, m										Sum
	A	B	C	D	E	F	G	H	I	J
${\displaystyle {\sum }_{j=1}^n{P}_{ij}}$	1144	1042.5	716.1	649.6	1086.1	437.7	372.9	378.7	172.3	300.1	6300
${\overline{P}}_i={\displaystyle {\sum }_{j=1}^n{P}_{ij}/n}$	18.16	16.55	11.37	10.31	17.24	6.95	5.92	6.01	2.73	4.76	100.00
${\sigma }_{Pi}=\sqrt{{\displaystyle \frac{{\displaystyle {\sum }_{j=1}^n{\left(P_{ij}-{\overline{P}}_i\right)}^2}}{n-1}}}$	5.655	3.046	2.444	2.493	3.884	1.559	1.877	2.174	1.339	2.201	–
Skewness (Sk)	0.757	0.033	0.777	0.251	0.818	0.282	−0.055	1.012	0.742	1.024	–
Kurtosis (Ku)	−0.254	0.502	2.121	2.131	1.219	0.634	−0.108	1.516	0.522	1.297	–
DPW method:
${\overline{\omega }}_i^{DPW}={\displaystyle \frac{{\displaystyle {\sum }_{j=1}^n{P}_{ij}}}{100n}}$	0.1816	0.1655	0.1137	0.1031	0.1724	0.0695	0.0592	0.0601	0.0273	0.0476	1.0000
Priority	1	3	4	5	2	6	8	7	10	9	55

and

Table 9. AHP-determined significance of asphalt-layer indicators for road quality and monetary deductions (n = 63 Experts).

Formula and Method	Quality Indicator (Criterion) i = 1, 2, …, m										Sum
	A	B	C	D	E	F	G	H	I	J
${\omega }_{ij}^{AHP}={\displaystyle \frac{\sqrt[m]{{\displaystyle {\prod }_{j=1}^n{a}_{ij}}}}{{\displaystyle {\sum }_{i=1}^m\sqrt[m]{{\displaystyle {\prod }_{j=1}^n{a}_{ij}}}}}}$	$\mathrm{The} \mathrm{eigenvector} \left(\mathrm{weight}\right) {\omega }_{ij}^{AHP}$ of the i-th criterion is calculated from the elements $a_{ij}$ of the pairwise comparison matrix filled by each j-th expert. Each matrix must be consistent (C.R. < 0.1)
${\displaystyle {\sum }_{j=1}^n{\omega }_{ij}^{AHP}}$	13.426	12.31	6.796	6.361	13.23	3.102	2.450	2.506	0.993	1.827	–
${\overline{\omega }}_i^{AHP}={\displaystyle \frac{{\displaystyle {\sum }_{j=1}^n{\omega }_{ij}^{AHP}}}{n}}$	0.2131	0.1954	0.1079	0.1010	0.2100	0.0492	0.0389	0.0398	0.0158	0.0289	1.0000
${\sigma }_{{\omega }_i}^{AHP}$ $=\sqrt{{\displaystyle \frac{{\displaystyle {\sum }_{j=1}^n{\left({\omega }_{ij}^{AHP}-{\overline{\omega }}_i^{AHP}\right)}^2}}{n-1}}}$	0.067	0.040	0.035	0.041	0.057	0.016	0.014	0.021	0.003	0.017	–
Skewness (Sk)	−0.421	0.002	2.383	2.013	−0.335	0.420	0.602	2.166	2.831	2.691	–
Kurtosis (Ku)	−0.817	−0.065	10.49	7.729	−0.814	1.816	−0.187	6.122	11.293	9.044	–
Priority	1	3	4	5	2	6	8	7	10	9	55

. The sequence of criteria differs slightly: $\mathrm{A}\succ \mathrm{E}\succ \mathrm{B}\succ \mathrm{C}\succ \mathrm{D}\succ \mathrm{F}\succ \mathrm{H}\succ \mathrm{G}\succ \mathrm{J}\succ \mathrm{I}$.

The arithmetic means of the significances of the road pavement layer quality-indicator defects, expressed as relative weights and calculated using four MCDM methods, are presented in the bar chart (Figure 4). The sixty-three-expert team provided the following sequence of criteria significance: $\mathrm{A}\succ \mathrm{E}\succ \mathrm{B}\succ \mathrm{C}\succ \mathrm{D}\succ \mathrm{F}\succ \mathrm{H}\succ \mathrm{G}\succ \mathrm{J}\succ \mathrm{I}$.

After the number of experts was reduced from 71 to 63, the average weights of the criteria (defects) changed slightly (

Table 10. Change (difference) in the percentage of the global relative weights of quality indicators, calculated from the assessments of the 71 and 63 expert teams.

Formula	Quality Indicator (Criterion) i = 1, 2, …, m										Average Modulus
	A	B	C	D	E	F	G	H	I	J
$\Delta {\overline{\omega }}_i={\displaystyle \frac{{\overline{\omega }}_i^{n=63}-{\overline{\omega }}_i^{n=71}}{{\overline{\omega }}_i^{n=71}}}100$	2.7	−0.3	1.5	5.1	4.9	−5.7	−3.3	−3.2	−9.0	−16.6	5.2

). For the most important criteria, A, E, B, C, and D, they increased by up to 5%, while for the least important criteria, F, H, G, J, and I, they decreased by up to 16%.

The assumption that the criteria rank means are calculated from independent populations of the same size and that the ranks of all 10 criteria follow a normal distribution allows for the comparison of rank variances ${\sigma }_{Ri}^2$ using Cochran’s test (

Table 11. Variation indicators of criteria ranks, calculated from the evaluations of the 63 expert team.

Statistic	Quality Indicator (Criterion) i = 1, 2, …, m										Sum
	A	B	C	D	E	F	G	H	I	J
${\sigma }_{Ri}$	1.264	0.787	0.927	1.238	1.054	1.087	1.067	1.197	0.435	1.220	–
${\sigma }_{Ri}^2$	1.598	0.619	0.859	1.533	1.111	1.182	1.138	1.433	0.189	1.488	11.15

) by calculating the statistic according to Formula (9):

The critical value of Cochran’s test G_C (α, m, v) found from the table (Sachs, 1972) [57], when α = 0.05, m = 10, and v = 62, is equal to 0.1571. The calculated value, 0.1433, is less than the critical value, 0.1571, which indicates that the criteria rank variances, ${\sigma }_{Ri}^2$, presented in Table 11 are equal; i.e., there is no basis to reject the null hypothesis.

From the equal (homogeneous) variances, ${\sigma }_{Ri}^2$, of the asphalt-layer quality-indicator ranks, their average, ${\sigma }_R^2$, is calculated, which shows the average variation of all quality indicators of the road pavement:

$${\sigma }_R^2={\displaystyle \frac{{\displaystyle {\sum }_{i=1}^m{\sigma }_{Ri}^2}}{m}}={\displaystyle \frac{11.15}{10}}=1.115.$$

The overall standard deviation of the criteria ranks is ${\sigma }_R=1.056$.

The precision, ${\Delta }_R$, which indicates how much the criteria rank mean determined by the 63-expert team can differ from the population mean with 95% probability (t = 1.96) when the average standard deviation of ranks is ${\sigma }_R=1.056$, is calculated from the sample size formula [66,69,70]:

$${\Delta }_R=\sqrt{{\displaystyle \frac{t^2\times {\sigma }_R^2}{n}}}=\sqrt{{\displaystyle \frac{{1.96}^2\times {1.056}^2}{63}}}=0.26.$$

The precision, ${\Delta }_R=0.26$, calculated from the expert study reasonably allows for the statement that the average rank of the population for each quality indicator of the asphalt layer is within the interval ${\overline{R}}_i\pm 0.26$. Whether the calculated precision is sufficient is determined by the decision-maker. If the required precision is ${\Delta }_R=0.25$, then it is necessary to survey 69 experts, and if ${\Delta }_R=0.5$, then the number of experts, n, must be 18.

4. Conclusions

1. The quality of an installed asphalt layer is assessed by measuring the actual values of key road performance parameters, for which monetary deductions are applied when permissible deviations or limit values, as defined in the installation standard ĮT ASFALTAS 08, are exceeded. Such exceedances are classified as defects. This study evaluated the impact of these parameters on road pavement quality using various multi-criteria decision-making (MCDM) methods. A panel of 71 experienced road engineers assessed the significance of parameters through relative ranking, percentage weighting, and Analytic Hierarchy Process (AHP) comparisons. The application of four different MCDM methods improved the robustness and reliability of the evaluation results.

2. Experts consistently identified lower compaction, reduced layer thickness, and deviations in binder content—whether excessive or insufficient—as the most critical factors that affect road pavement quality. In contrast, pavement width deviations, a slightly lower tyre-road friction coefficient, and exceeding roughness limits (as measured by a 3 m straight edge) were found to have a relatively lower impact. Moderate importance parameters included deviations in the content of coarse aggregates (>2 mm) or sand (0.063–2 mm), variations in the mineral filler content (<0.063 mm), roughness exceeding the IRI requirements, and excessive deviation of the pavement cross slope.

3. The consistency of the expert evaluations is sufficiently high, as indicated by the Kendall coefficient of concordance W = 0.765, which exceeds the minimum threshold W_min = 0.0265 by a factor of 28.9. Additionally, all pairwise comparison matrices completed using the Analytic Hierarchy Process (AHP) method met the consistency requirement, with consistency ratios C.R. < 0.1 indicating non-contradictory judgements. These results justify the use of the arithmetic mean of the relative weight assessments of experts as a reliable and valid solution to evaluate the importance of quality criteria of the asphalt layer.

It was proposed to determine the outliers of the criteria ranks and, after removing them, to calculate the averages of the remaining assessments and the “improved” indicators of the consistency of the experts’ opinions. This new MCDM method, named CIBRO (Criteria Importance But Rejected Outliers) by the authors, showed that the significance of the most important criteria, expressed in relative weights, increased by up to 5%, while the significance of the least important criteria decreased by up to 16%. The CIBRO complements Kendall’s rank correlation method by enhancing the robustness of expert evaluations.

4. Assuming that the ranks of independent criteria are normally distributed and that their variances (excluding outliers) are the same (homogeneous), this assumption was tested using Cochran’s test. The result, ${\widehat{G}}_{\max }$= 0.1433, was lower than the critical value, G_C (0.05; 10; 62) = 0.1571, confirming variance homogeneity.

This statistical homogeneity enabled the calculation of the overall average variance of the significance of the criteria, ${\sigma }_R^2=1.115$. The overall high precision of the rank means, ${\Delta }_R=0.26$, was derived using the sample size formula for a team of 63 experts at a 95% confidence level.