Inter-Arm State-of-Charge Balancing Control Based on Arm Valley Voltage Adjustment in MMDTC-BESS
Abstract
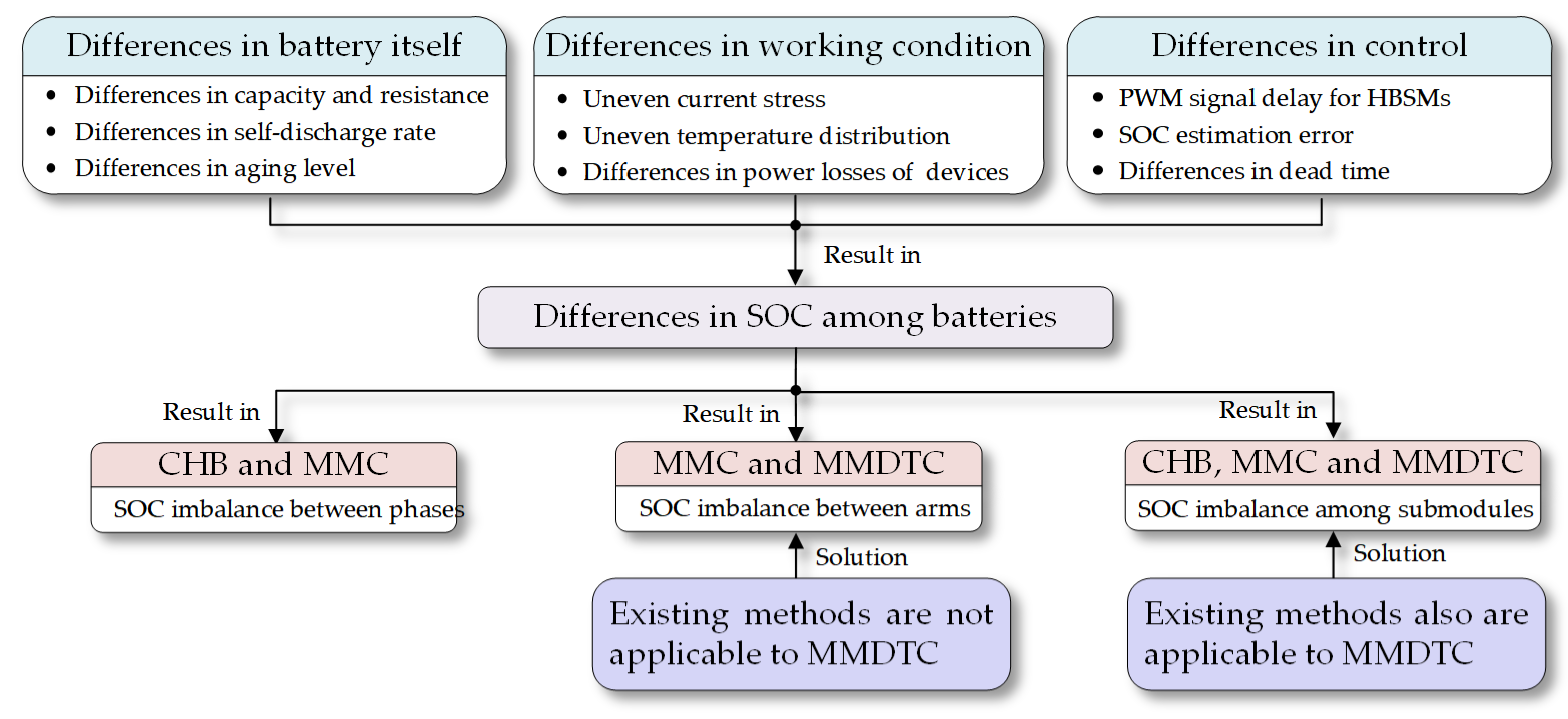
1. Introduction
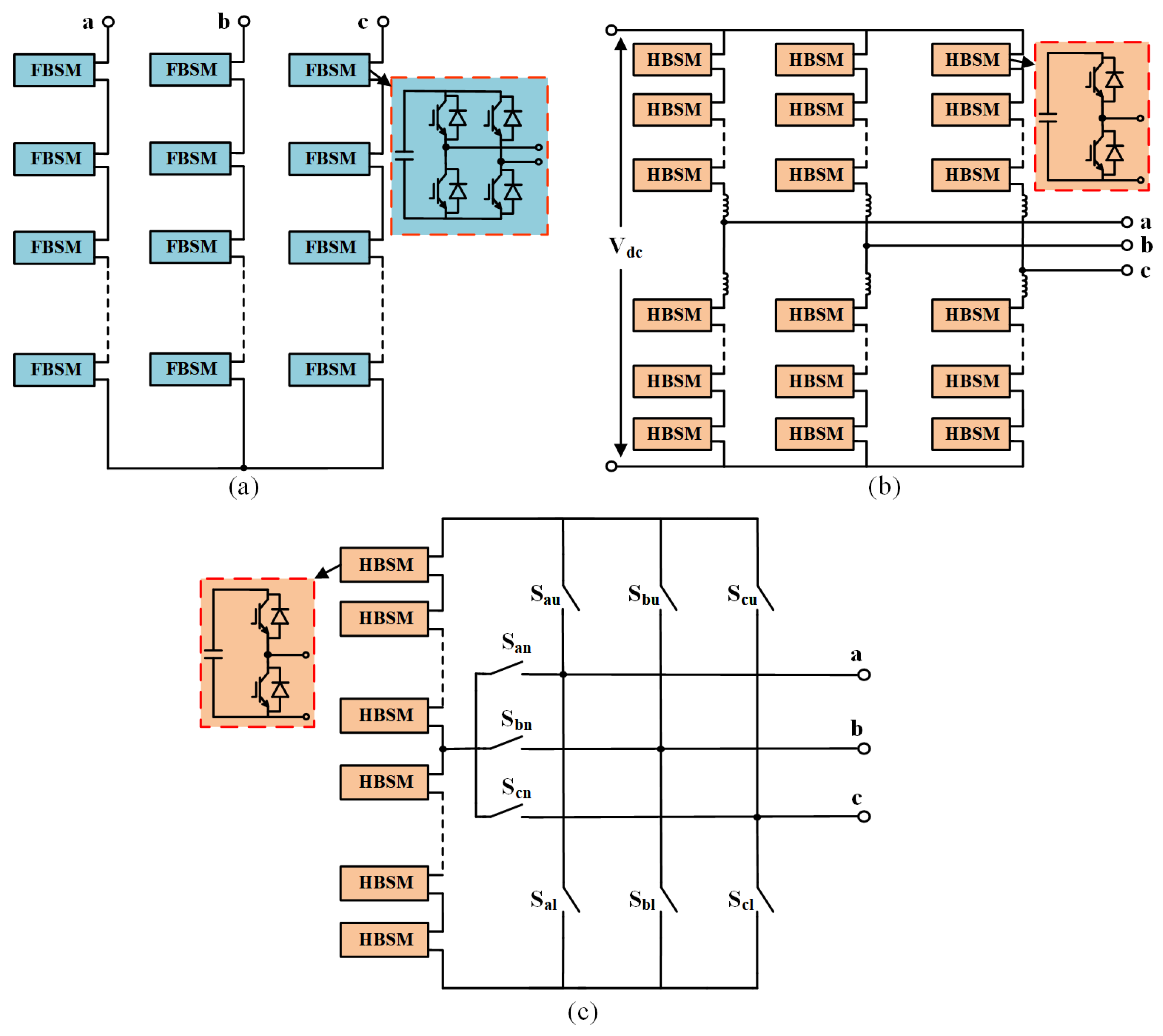
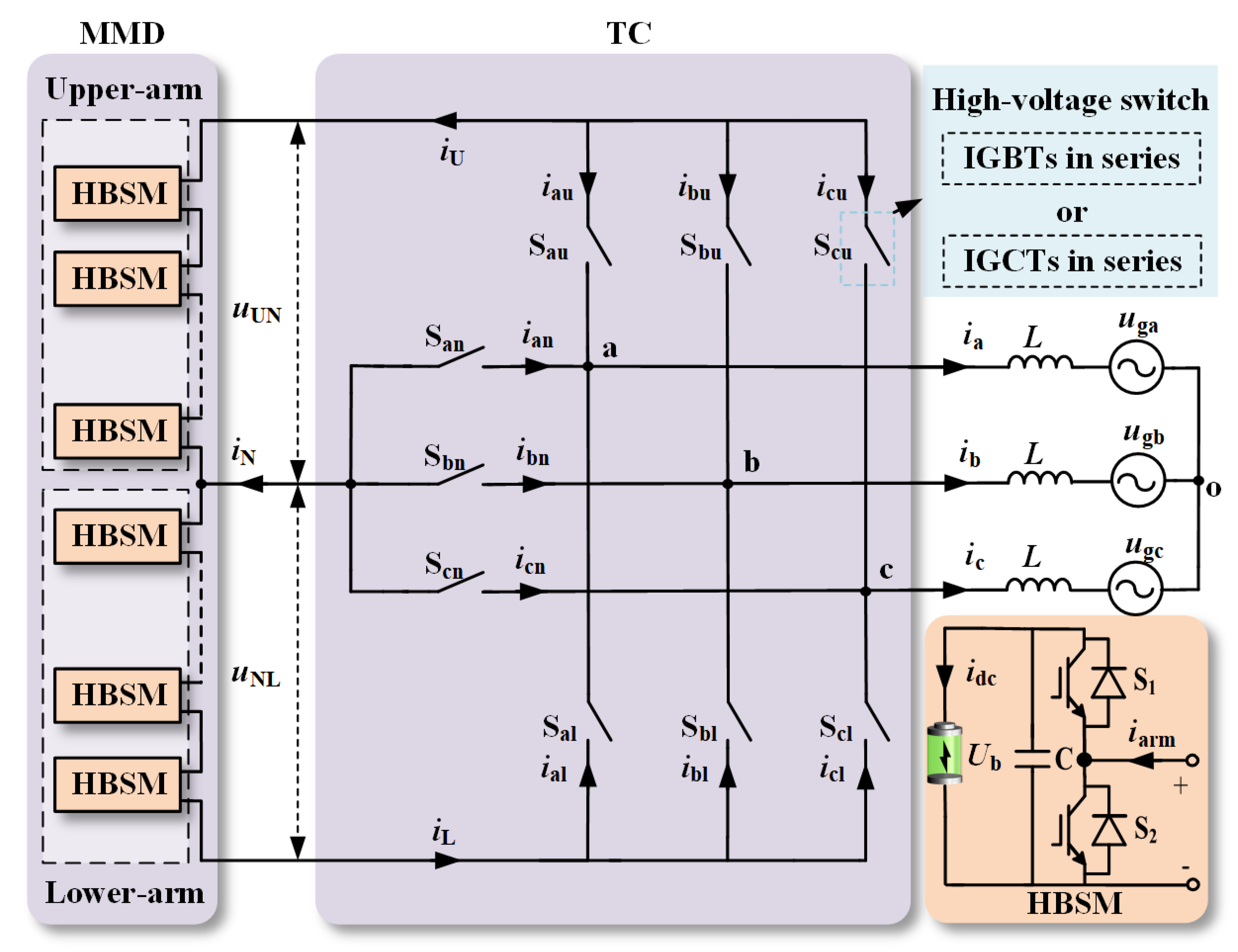
2. MMDTC-BESS Topology and Operating Principles
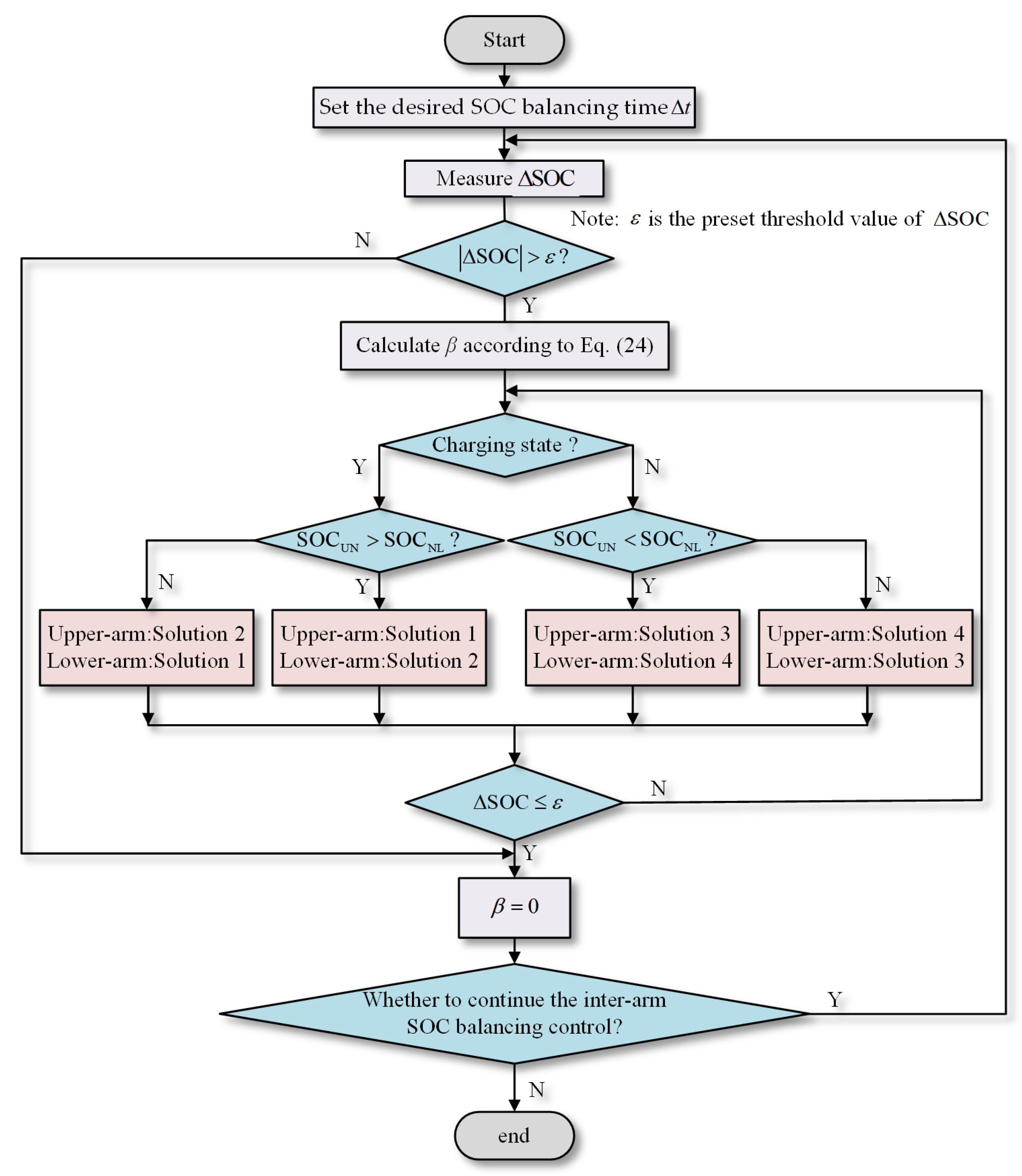
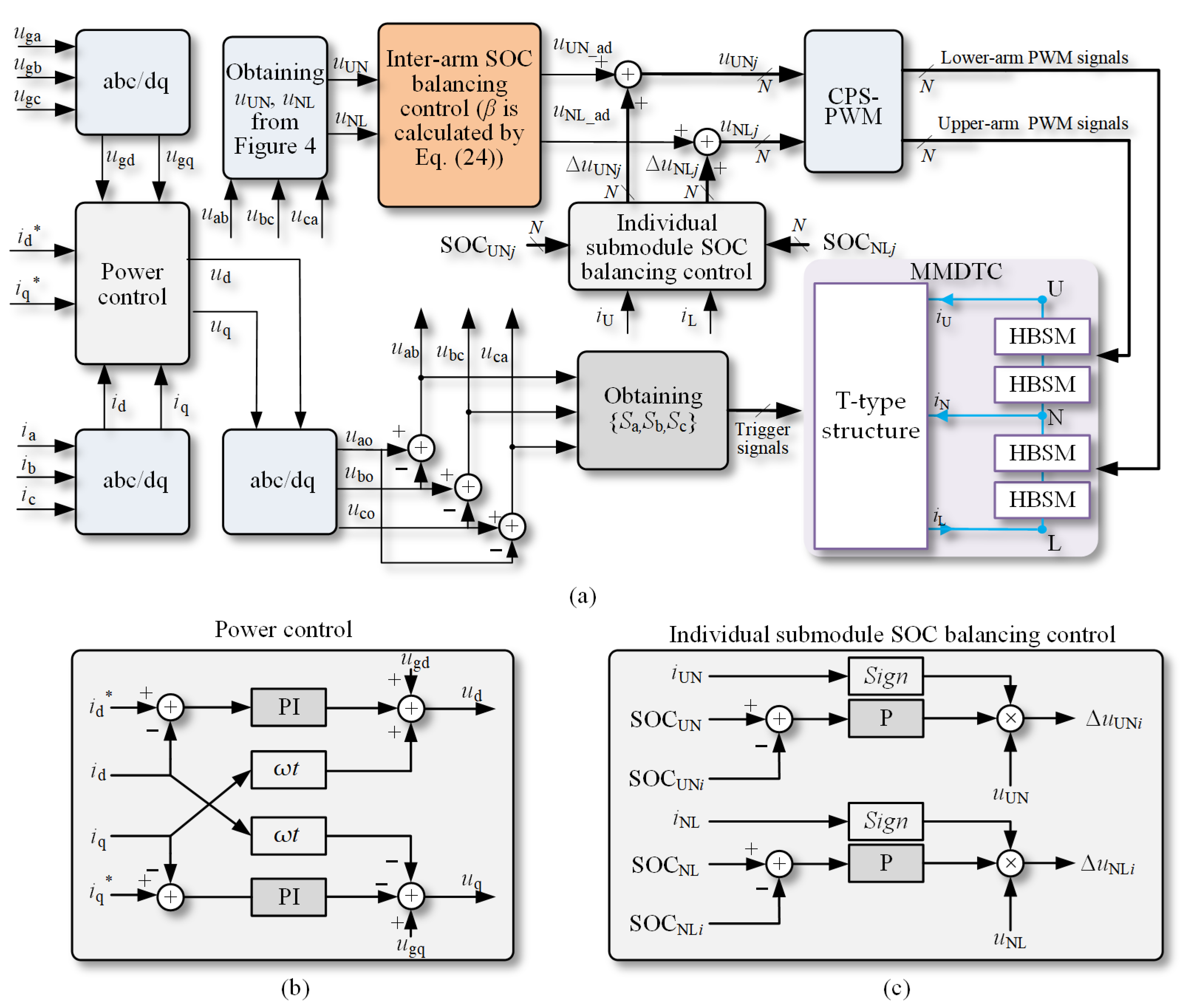
3. Proposed Inter-Arm SOC Balance Control Strategy
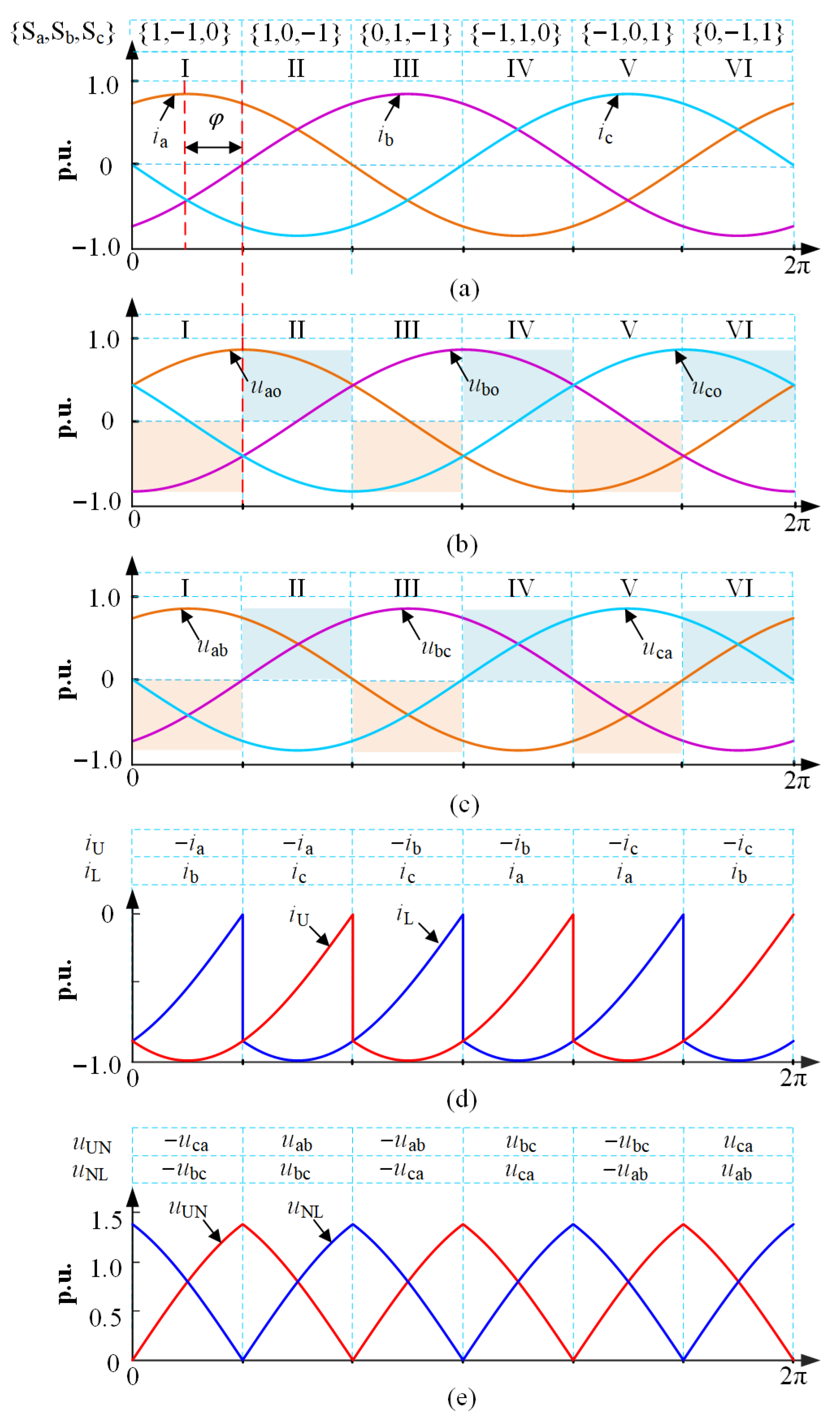
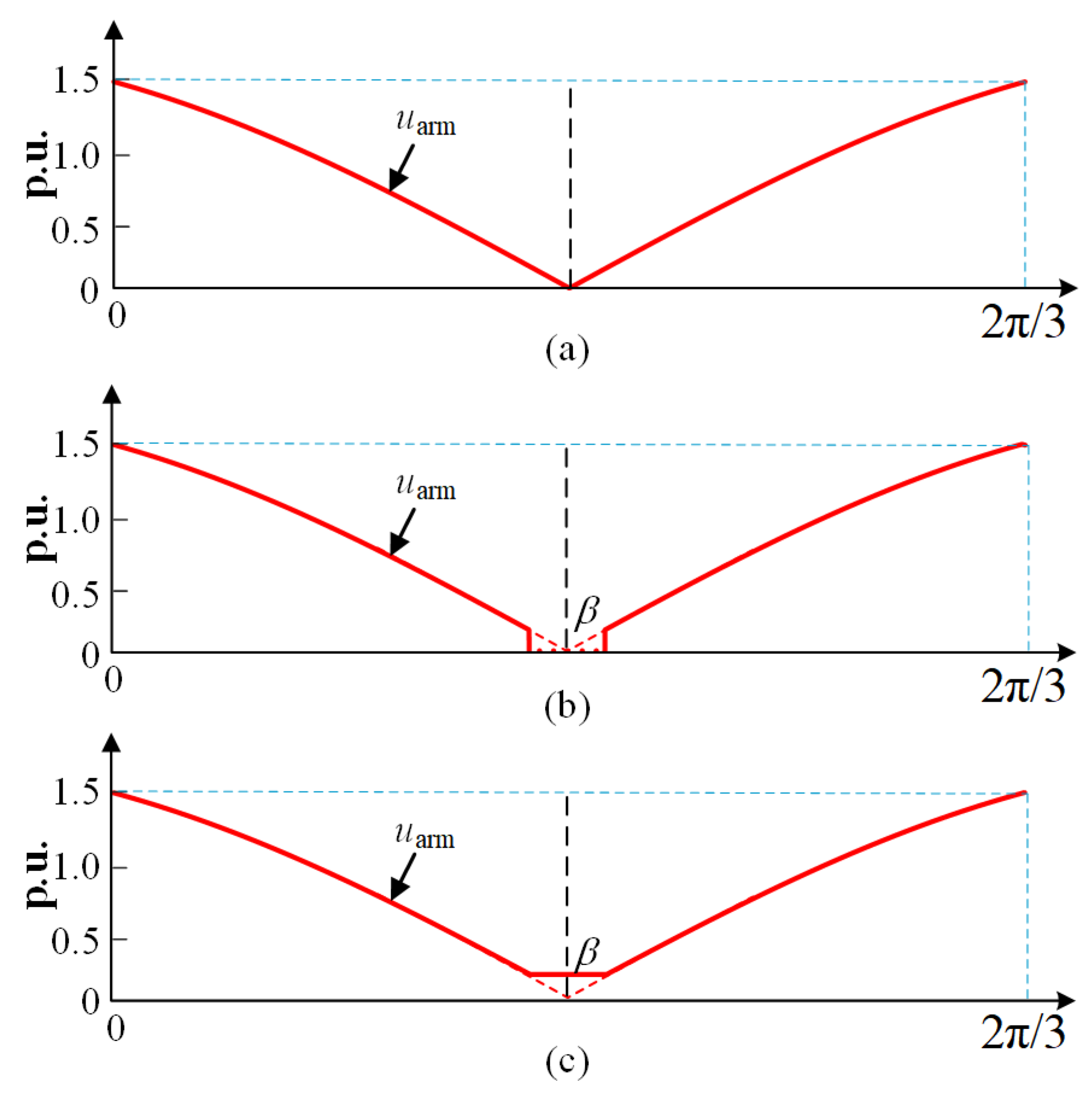
3.1. The Adjustment of Arm Valley Voltage
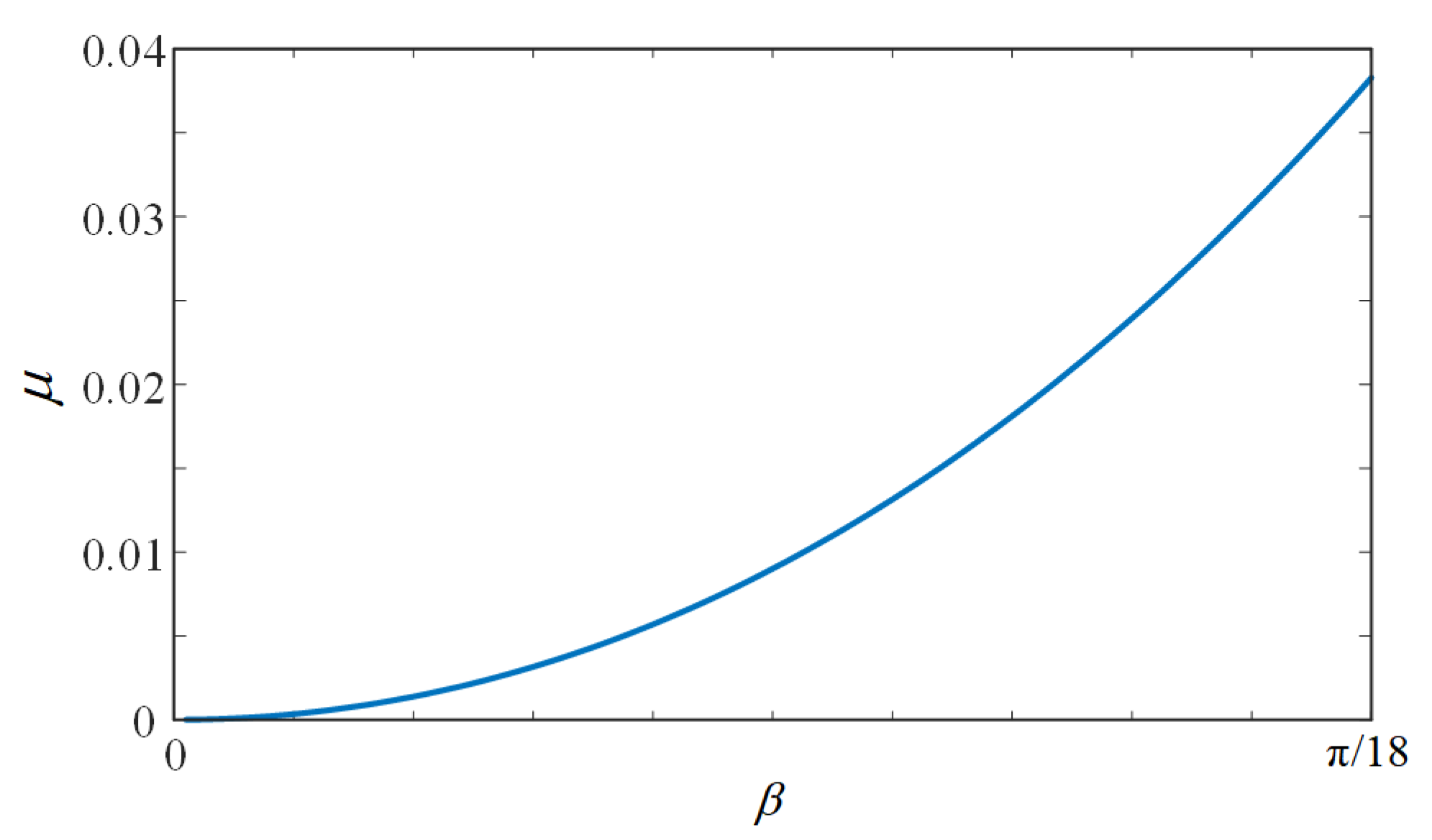
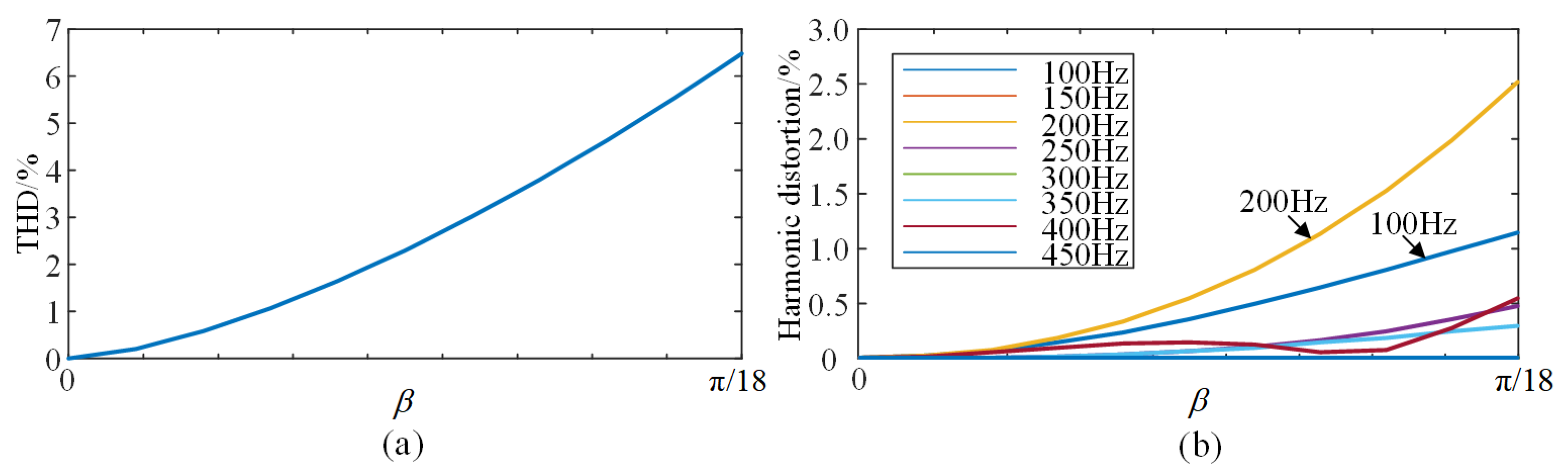
3.2. The Impact of Arm Voltage Valley Adjustment on Output Waveform Quality
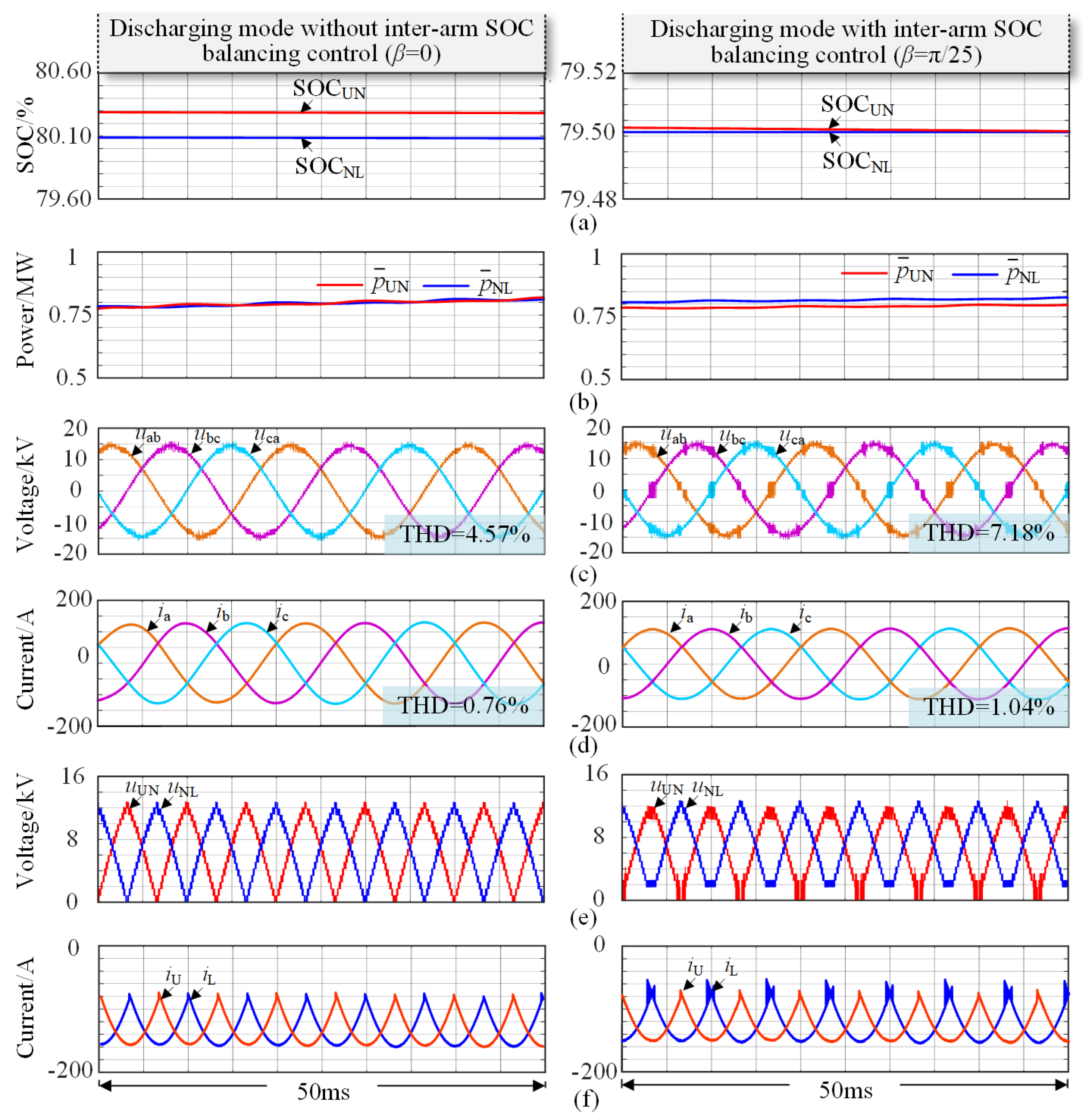
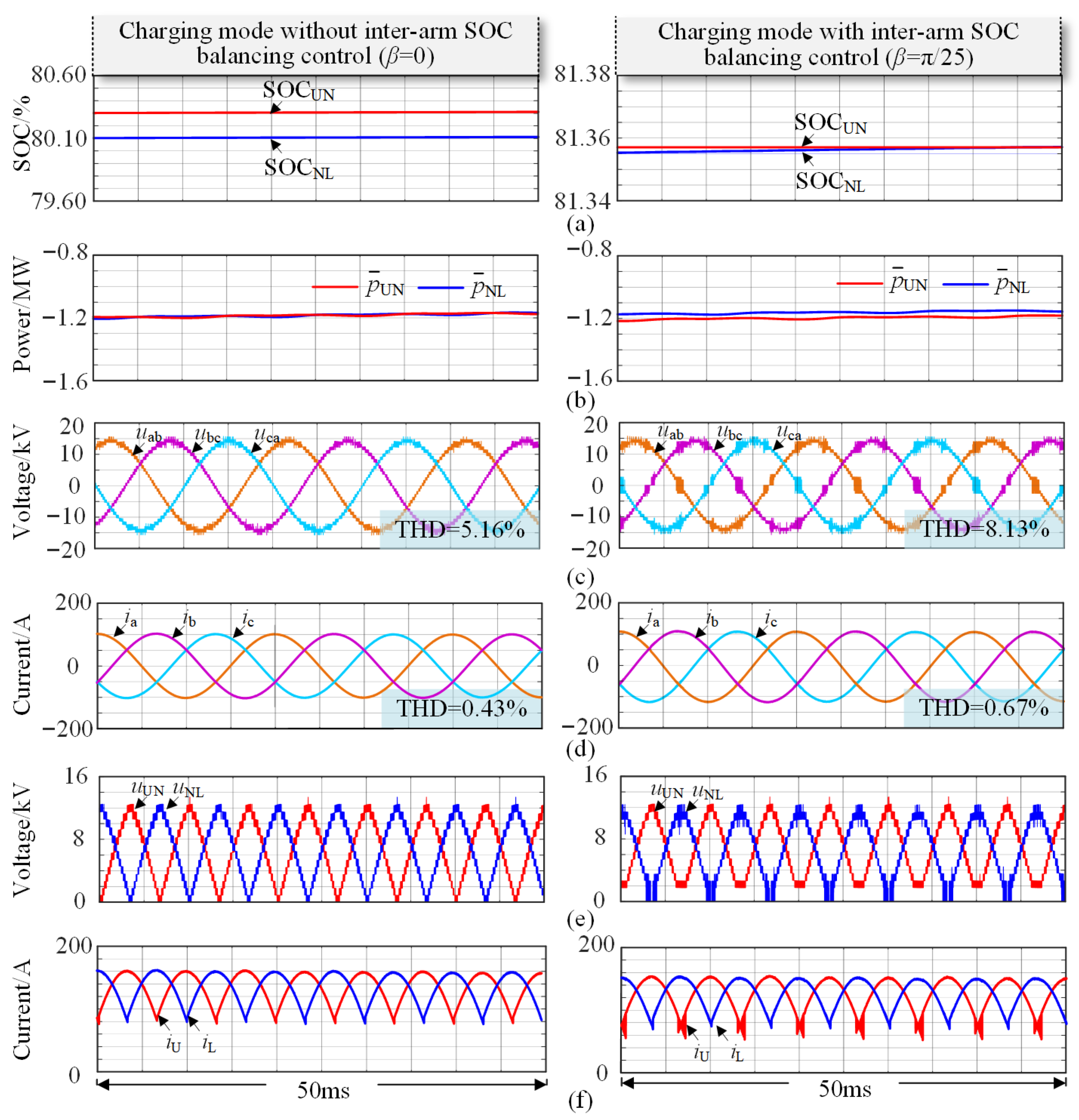
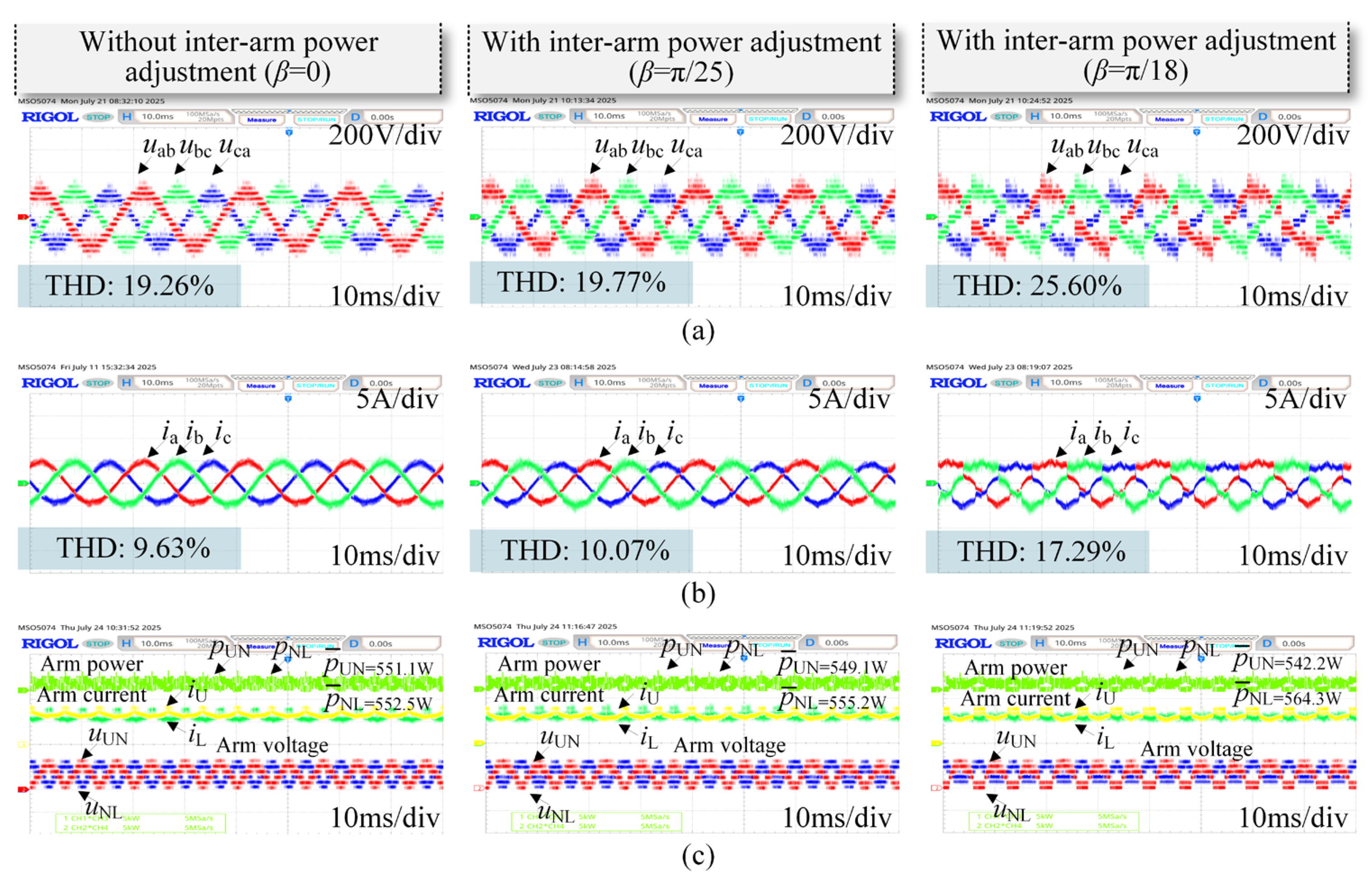
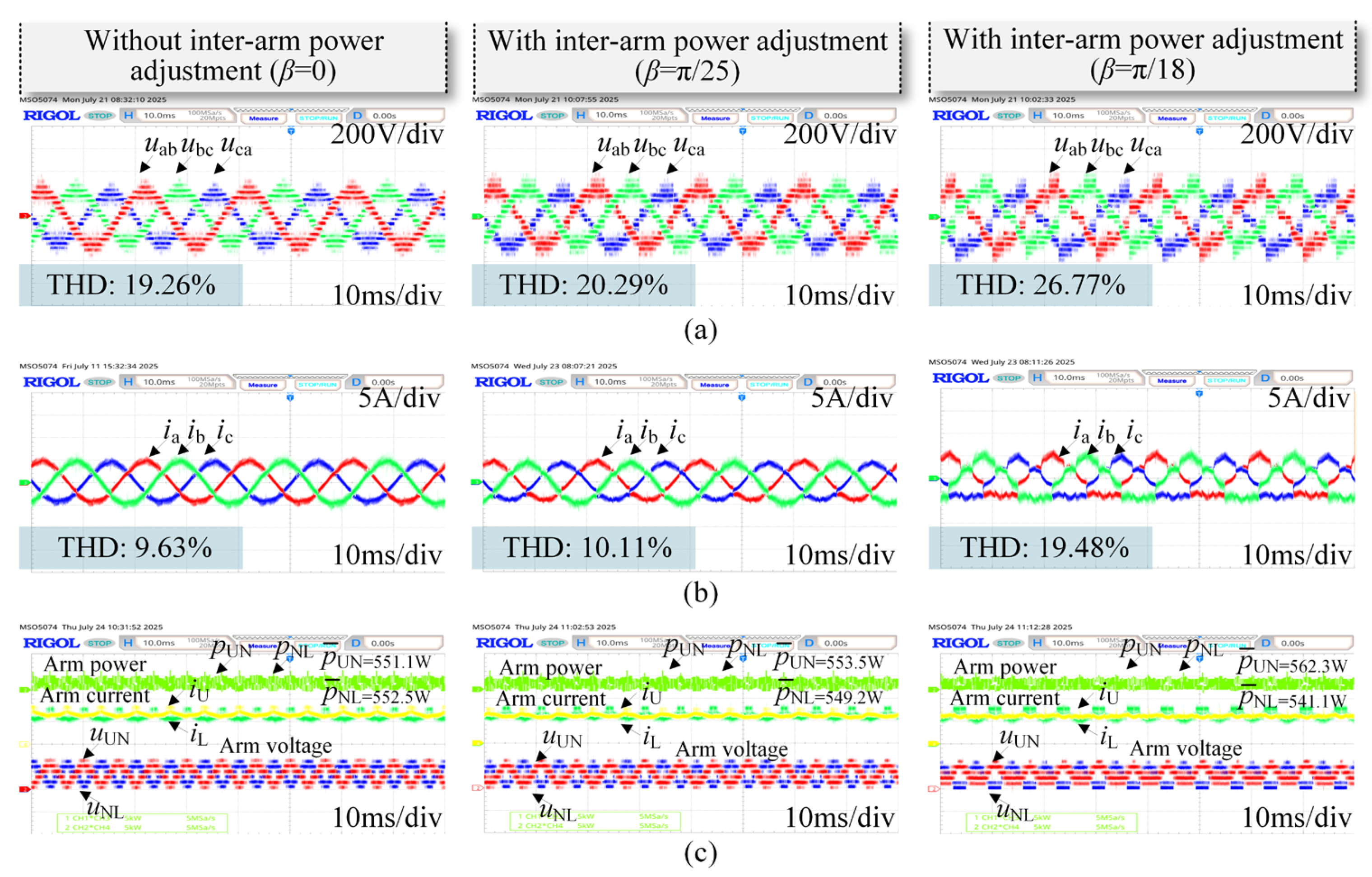
4. Simulation and Experimental Verification
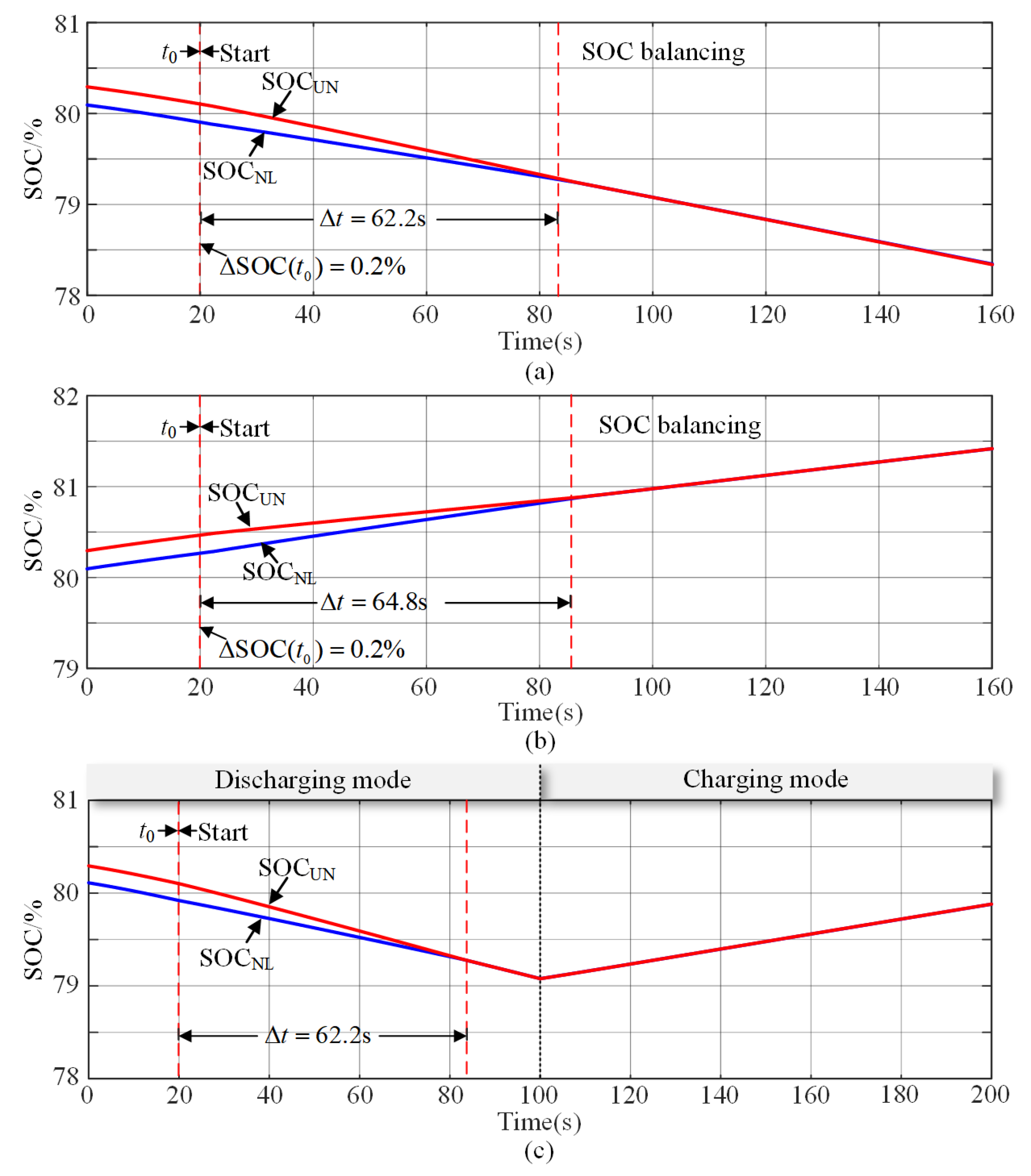
4.1. Simulation Verification
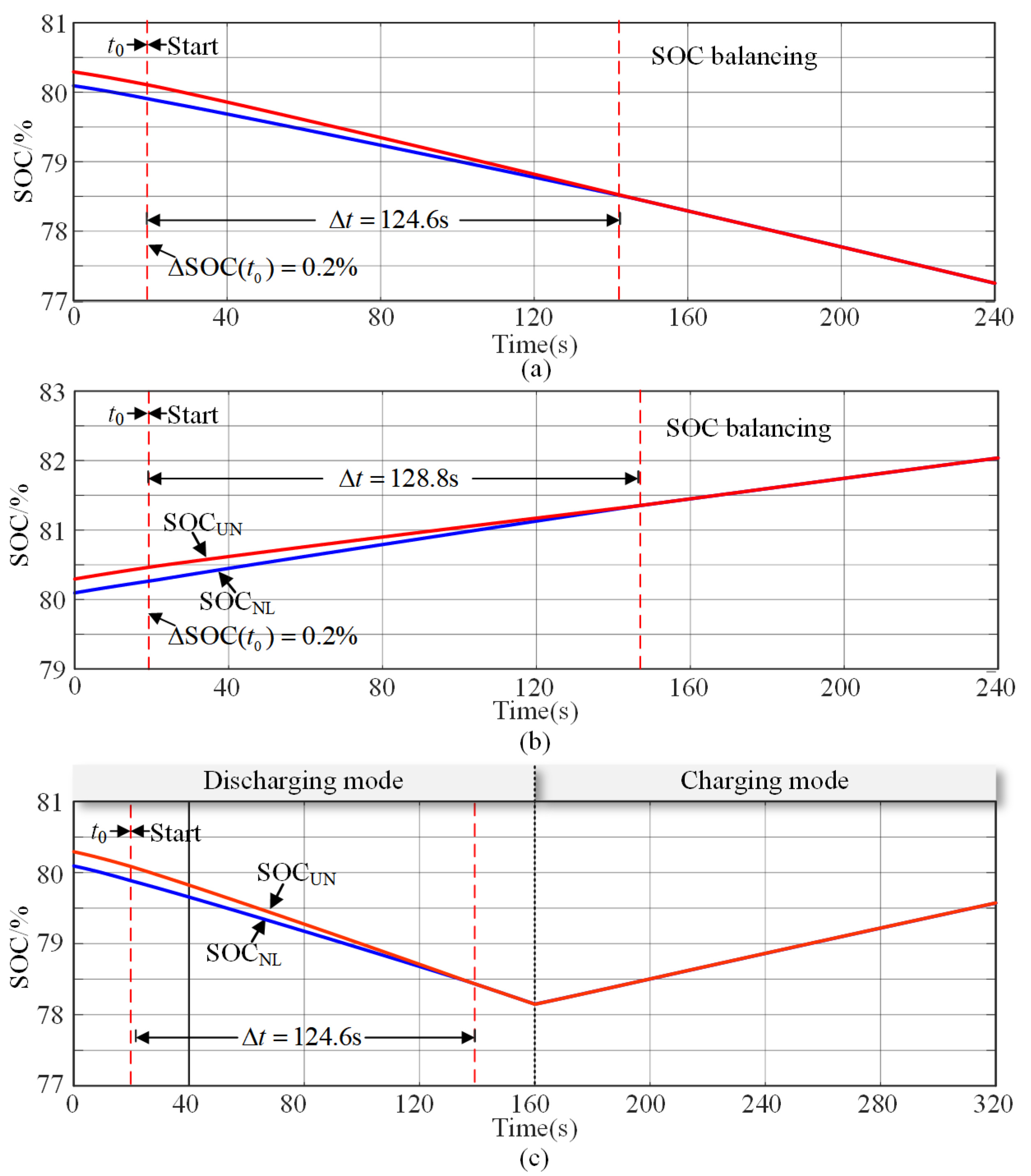
4.2. Experimental Verification
- Case 1: Assuming a discharging condition with low SOC in the upper arm.
- Case 2: Assuming a discharging condition with high SOC in the upper arm.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, J.; Fang, Z.; Wang, Q.; Zhang, M.; Li, Y.; Zhang, W. Optimal operation with dynamic partitioning strategy for centralized shared energy storage station with integration of large-scale renewable energy. J. Mod. Power Syst. Clean Energy 2024, 12, 359–370. [Google Scholar] [CrossRef]
- Byrne, R.H.; Nguyen, T.A.; Copp, D.A.; Chalamala, B.R.; Gyuk, I. Energy management and optimization methods for grid energy storage systems. IEEE Access 2018, 6, 13231–13260. [Google Scholar] [CrossRef]
- Mei, J. Control strategies for DC microgrid energy storage systems under SOC balancing objectives. In Proceedings of the 2022 9th International Forum on Electrical Engineering and Automation (IFEEA), Zhuhai, China; 2022; pp. 386–392. [Google Scholar]
- Nunna, H.S.V.S.K.; Sesetti, A.; Rathore, A.K.; Doolla, S. Multiagent-based energy trading platform for energy storage systems in distribution systems with interconnected microgrids. IEEE Trans. Ind. Appl. 2020, 56, 3207–3217. [Google Scholar] [CrossRef]
- Cui, Y.; Dai, Q.; Du, Y.; Zhu, T.; Zhang, S. Research on new energy storage grid-connected operation system for multi-scenarios. In Proceedings of the 2024 IEEE PES 16th Asia-Pacific Power and Energy Engineering Conference (APPEEC), Nanjing, China, 25–27 October 2024; pp. 1–5. [Google Scholar]
- Lin, X.; Zamora, R.; Baguley, C.A. A fullyfilter-based decentralized control with state of charge balancing strategy for battery energy storage systems in autonomous DC microgrid applications. IEEE Access 2021, 9, 15028–15040. [Google Scholar] [CrossRef]
- Xu, X.; Bishop, M.; Oikarinen, D.G.; Hao, C. Application and modeling of battery energy storage in power systems. CSEE J. Power Energy Syst. 2016, 2, 82–90. [Google Scholar] [CrossRef]
- Sun, Y.; Zhong, J.; Li, Z.; Tian, W.; Shahidehpour, M. Stochastic scheduling of battery-based energy storage transportation system with the penetration of wind power. IEEE Trans. Sustain. Energy 2017, 8, 135–144. [Google Scholar] [CrossRef]
- Yao, L.; Yang, B.; Cui, H.; Zhuang, J.; Ye, J.; Xue, J. Challenges and progresses of energy storage technology and its application. J. Mod. Power Syst. Clean Energy 2016, 4, 519–528. [Google Scholar] [CrossRef]
- Elrais, M.T.; Batarseh, I. Theoretical, simulation, and experimental comparison of GaN-based two-level and multilevel converters. In Proceedings of the 2022 IEEE 7th Southern Power Electronics Conference (SPEC), Denarau Island, Fiji, 5–8 December 2022; pp. 1–6. [Google Scholar]
- Harbi, I.; Rodriguez, J.; Poorfakhraei, A.; Vahedi, H.; Guse, M.; Trabelsi, M.; Abdelrahem, M.; Ahmed, M.; Fahad, M.; Lin, C.-H.; et al. Common DC-link multilevel converters: Topologies, control and industrial applications. IEEE Open J. Power Electron. 2023, 4, 512–538. [Google Scholar] [CrossRef]
- Katayama, M.; Ohno, T.; Obara, H.; Kawamura, A. Application of multi-level converter for fast current control in small-scale DC power network. IEEE Trans. Ind. Appl. 2019, 55, 2902–2909. [Google Scholar] [CrossRef]
- Ding, L.; Lian, Y.; Li, Y.W. Multilevel current source converters for high power medium voltage applications. CES Trans. Electr. Mach. Syst. 2017, 1, 306–314. [Google Scholar] [CrossRef]
- Bernet, D.; Hiller, M. A cascaded H-bridge-based multilevel converter with low energy pulsation for high-power grid applications. IEEE Trans. Power Electron. 2024, 39, 2305–2321. [Google Scholar] [CrossRef]
- Niu, D.; Gao, F.; Xu, T.; Ma, Z. Thyristor-based T-type converter with modular multilevel DC-link. IEEE Trans. Power Electron. 2022, 37, 6792–6806. [Google Scholar] [CrossRef]
- Niu, D.; Gao, F.; Xu, T.; Ma, Z. Low-Capacitance operation and its hierarchical control for STATCOM based on T-type converter with MMDTC. IEEE Trans. Power Electron. 2025, 40, 1153–1167. [Google Scholar]
- Lim, W.C.; Teo, B.C.T.; Lim, X.Y.; Siek, L.; Tan, E.L. Comparative analysis of passive, active, and hybrid cell balancing for optimal battery performance. In Proceedings of the 2024 International Conference on Electronics, Information, and Communication (ICEIC), Taipei, Taiwan, 9–11 July 2024; pp. 1–4. [Google Scholar]
- Buchinskiy, N.; Saitoh, H. SOC balancing mechanism to improve active power sharing among multiple ESS units in low-inertia power systems. In Proceedings of the 2023 IEEE PES Innovative Smart Grid Technologies—Asia (ISGT Asia), Auckland, New Zealand; 2023; pp. 1–5. [Google Scholar]
- Xiaofeng, Y.; Yao, X.; Bowei, C. Enhanced modular multilevel converter based battery energy storage system. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 1–5 October 2017; pp. 4914–4919. [Google Scholar]
- Wang, X.; Zhang, Y.; Dong, P.; Jia, N.; Zhu, X. Power allocation strategy for battery energy storage power station considering SOC equalization. In Proceedings of the 2023 26th International Conference on Electrical Machines and Systems (ICEMS), Zhuhai, China, 5–8 November 2023; pp. 4105–4109. [Google Scholar]
- Barresi, M.; De Simone, D.; Piegari, L. Direct State-of-Charge balancing control for modular multilevel converter integrating batteries. IEEE J. Emerg. Sel. Topics Power Electron. 2025, 13, 733–746. [Google Scholar] [CrossRef]
- Xu, J.; Wang, J.; Wang, F.; Wang, J.; Li, G. SOC balancing control based on predictive power model amongst supercapacitor packs in MMC with embedded energy storage system. IEEE Trans. Power Deliv. 2023, 38, 2641–2649. [Google Scholar] [CrossRef]
- Liang, G.; Rodriguez, E.; Farivar, G.G.; Yadav, G.N.B.; Beniwal, N.; Pou, J.; Konstantinou, G. A comparison of PI-based and sorting-based state of charge balancing methods in cascaded H-bridge converters. In Proceedings of the 2022 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 9–13 October 2022; pp. 1–7. [Google Scholar]
- Bian, K.; Wu, X.; Li, H.; Huang, C.; Cai, X. A power decoupling control strategy for CHB-BESS based on NLM. In Proceedings of the 2024 9th Asia Conference on Power and Electrical Engineering (ACPEE), Shanghai, China, 11–13 April 2024; pp. 2664–2668. [Google Scholar]
- Lee, T.L.; Chen, Y.H.; Zheng, W.T.; Lin, C.H. Power control of repurposing-battery modular multilevel converter. In Proceedings of the 2022 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 9–13 October 2022; pp. 1–7. [Google Scholar]
- Wang, Q. State of charge equalization control strategy of modular multilevel converter with battery energy storage system. In Proceedings of the 2020 5th International Conference on Power and Renewable Energy (ICPRE), Shanghai, China, 12–14 September 2020; pp. 316–320. [Google Scholar]
- Yu, X.; Wang, C.; Wang, Y.; Han, C. Arm average model and operational characteristics analysis of MMC with integrated battery energy storage system. In Proceedings of the 2023 IEEE 2nd International Power Electronics and Application Symposium (PEAS), Guangzhou, China, 10–13 November 2023; pp. 1426–1431. [Google Scholar]
- Pirooz, A.; Firouz, Y.; Van Mierlo, J.; Berecibar, M. Voltage vector redundancy exploitation for battery balancing in three-phase CHB-based modular energy storage systems. IEEE Trans. Ind. Electron. 2022, 69, 9364–9375. [Google Scholar] [CrossRef]
- Bharadwaj, V.; Panda, S.; Kundu, S.; Banerjee, S. Seven level CHB multilevel inverter based STATCOM using decoupled control and DC voltage balancing. In Proceedings of the IECON 2023-49th Annual Conference of the IEEE Industrial Electronics Society, Kolkata, India, 16–19 October 2023; pp. 1–6. [Google Scholar]
- Gomez, P.J.; Galvan, L.; Galvan, E.; Carrasco, J.M. Energy storage systems current ripple reduction for DC-link balancing method in hybrid CHB topology. In Proceedings of the IECON 2020 The 46th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 18–21 October 2020; pp. 1808–1813. [Google Scholar]
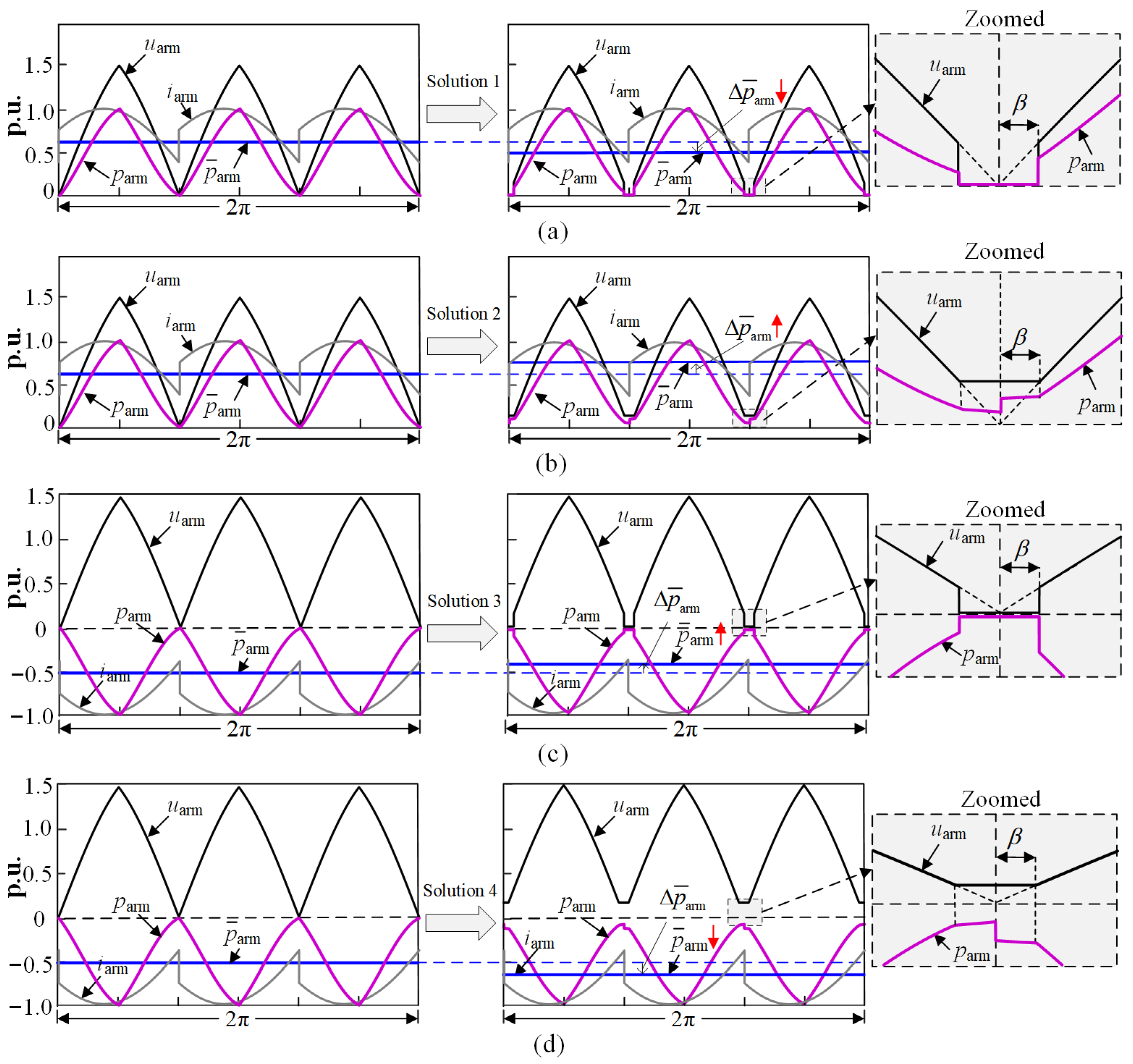


| Charging State | Discharging State | |||
|---|---|---|---|---|
| Upper-arm | Solution 1 | Solution 2 | Solution 3 | Solution 4 |
| Lower-arm | Solution 2 | Solution 1 | Solution 4 | Solution 3 |
| Variable | Symbol | Value |
|---|---|---|
| Rated grid line voltage | 10 kV | |
| Rated active power | P | 2 MW |
| Rated reactive power | Q | 0 |
| Grid-side filtering inductance | L | 5 mH |
| Number of submodules per arm | N | 20 |
| Battery pack voltage | 800 V | |
| Rated capacity of Battery | 200 Ah | |
| Submodule capacitance | 0.47 mF | |
| Switching frequency | fs | 1.5 kHz |
| Variable | Symbol | Value |
|---|---|---|
| Grid voltage | 110 V | |
| Rated amplitude of phase current | 5 A | |
| Grid-side filtering inductance | L | 4 mH |
| Number of submodules per arm | N | 5 |
| DC voltage of submodule | 50 V | |
| Submodule capacitance | 0.2 mF | |
| Switching frequency | fs | 5 kHz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, Q.; Niu, D.; Cui, X.; Wang, D.; Yu, D.; Zhang, L. Inter-Arm State-of-Charge Balancing Control Based on Arm Valley Voltage Adjustment in MMDTC-BESS. Appl. Sci. 2025, 15, 10196. https://doi.org/10.3390/app151810196
Yan Q, Niu D, Cui X, Wang D, Yu D, Zhang L. Inter-Arm State-of-Charge Balancing Control Based on Arm Valley Voltage Adjustment in MMDTC-BESS. Applied Sciences. 2025; 15(18):10196. https://doi.org/10.3390/app151810196
Chicago/Turabian StyleYan, Qizhong, Decun Niu, Xiangzheng Cui, Dong Wang, Dachuan Yu, and Lei Zhang. 2025. "Inter-Arm State-of-Charge Balancing Control Based on Arm Valley Voltage Adjustment in MMDTC-BESS" Applied Sciences 15, no. 18: 10196. https://doi.org/10.3390/app151810196
APA StyleYan, Q., Niu, D., Cui, X., Wang, D., Yu, D., & Zhang, L. (2025). Inter-Arm State-of-Charge Balancing Control Based on Arm Valley Voltage Adjustment in MMDTC-BESS. Applied Sciences, 15(18), 10196. https://doi.org/10.3390/app151810196









