Abstract
Deep neural network-based fault diagnosis is gaining significant attention within the Industry 4.0 framework, yet practical deployment is still hindered by domain shift, partial label mismatch, and class imbalance. In this regard, this paper proposes a Multi-Target Adversarial Learning for Partial Fault Diagnosis (MTAL-PFD), an extension of adversarial and discrepancy-based domain adaptation tailored to single-source, multi-target (1SmT) partial fault diagnosis in electric motor-driven systems. The framework transfers knowledge from a labeled source to multiple unlabeled target domains by combining dual 1D-CNN feature extractors with adversarial domain discriminators, an inconsistency-based regularizer to stabilize learning, and class-aware weighting to mitigate partial label shift by down-weighting outlier source classes. Thus, the proposed scheme combines a multi-objective approach with partial domain adaptation applied to the diagnosis of electric motor-driven systems. The proposed model is evaluated across 24 cross-domain tasks and varying operating conditions on two motor test benches, showing consistent improvements over representative baselines.
1. Introduction
The smart manufacturing environments have given way to the new paradigm of Industry 4.0, where the convergence between information technology and operational technology is characterized by the rise of cyber–physical systems and the integration of artificial intelligence, to address higher requirements in sustainability and production efficiency [1]. In this regard, industrial systems are expected to take advantage of such technological revolution increasing their related key performance indicators. Specifically, this is achieved by the application of novel Condition-Based Maintenance (CBM) schemes over related electrical rotatory machinery, since they still represent a critical component subjected to degradation and faults appearance.
The field of Machine Health Monitoring (MHM) has emerged as a prominent research area, attracting increasing attention from both academia and industry due to the rapid advancement of industrial technologies in recent years [2,3]. To ensure safe and efficient production environments, various fault diagnosis strategies have been developed within the framework of CBM. In this context, machine learning algorithms—particularly deep learning (DL) methods—have demonstrated remarkable capabilities in pattern recognition across diverse application domains. Consequently, the integration of these algorithms into MHM systems has shown significant potential to enhance diagnostic accuracy and reliability [4,5].
Although DL methods have achieved substantial progress in intelligent fault diagnosis, several critical challenges persist in machine health monitoring applications. First, there is the issue of distributional shift between the training (source domain) and testing (target domain) datasets. For example, in electric motor-driven systems, many diagnostic models assume identical operating conditions—such as speed and torque—between domains. However, in real manufacturing environments, this assumption rarely holds, as machinery often operates under multiple and variable conditions, and component wear occurs irregularly. Consequently, models trained under fixed conditions are prone to degraded performance when confronted with data drawn from different distributions. Second, there is often a limited availability of labeled data in the target domain. Industrial applications rarely provide sufficient fault samples, resulting in significant class imbalance between healthy and faulty states.
To mitigate distributional discrepancies, transfer learning techniques—particularly domain adaptation—have been proposed [6]. These methods aim to learn domain-invariant and discriminative features from a labeled source domain and transfer this knowledge to an unlabeled target domain. Deep neural networks have proven especially effective in this context due to their capacity for feature extraction and pattern recognition [7,8].
Despite promising results, existing domain adaptation methods generally assume a shared label space between source and target domains—a condition that is not always satisfied in real-world applications. In practice, the label space of the target domain is often a subset of that of the source domain. This leads to a third major issue: label space imbalance. To address this, the concept of partial fault diagnosis, also known as partial domain adaptation, has been introduced, where only a subset of fault categories is shared across domains. While classical domain adaptation techniques perform well in label-consistent settings, their performance degrades significantly under partial scenarios, as illustrated in Figure 1.
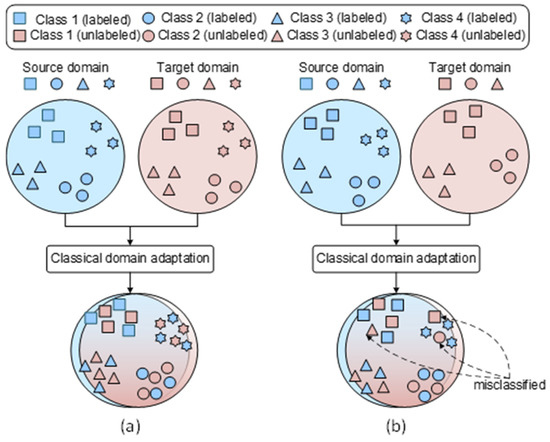
Figure 1.
Illustration of transfer fault diagnosis scenarios addressed by classical domain adaptation methods: (a) label-consistent fault diagnosis scenario; (b) partial fault diagnosis scenario.
Although some studies have addressed one or more of these issues [9,10,11,12], most existing approaches assume a single-source, single-target (1S1T) configuration. This severely limits their applicability in complex industrial settings, where multiple target domains—arising from diverse operating conditions—must be simultaneously considered. Hence, there is a pressing need for a holistic solution that addresses all three challenges while extending to multiple target domains to achieve more robust, generalizable, and reliable MHM systems.
To this end, the present work proposes a novel methodology for intelligent fault diagnosis that, for the first time in this field, combines adversarial learning for extracting domain-invariant features with an inconsistency-based domain adaptation model, specifically designed for the single-source, multi-target (1SmT) scenario under partial domain adaptation constraints.
The proposed framework is characterized by two core components. First, it reduces distributional divergence between the source and multiple target domains while simultaneously learning both domain-invariant and class-discriminative features. Second, it incorporates a fault-category weighting mechanism to identify and adapt only those categories shared between source and target domains, thereby excluding outlier classes that are not represented in the target domain.
Furthermore, the framework integrates modified one-dimensional convolutional neural networks (1D-CNNs) within several of its core modules. Specifically, it comprises two feature extractors, two domain discriminators, and two classifiers. An adversarial training strategy is adopted in which domain discriminators learn to distinguish between the source and each target domain based on extracted features, while classifiers aim to identify fault categories. This dual-module structure enables the incorporation of the inconsistency-based domain adaptation mechanism, which minimizes inter-domain divergence and effectively handles shared and non-shared label spaces.
Importantly, this approach accommodates machinery operating under varying conditions—such as differing speeds and torques—each associated with distinct fault categories. In other words, it enables accurate fault diagnosis across multiple domains, irrespective of the specific operational condition or label space associated with each domain.
The main contributions of this study can be summarized as follows:
- As an extension of adversarial and discrepancy-based domain adaptation tailored to single-source, multi-target (1SmT) partial fault diagnosis, an intelligent fault diagnosis framework, termed MTAL-PFD (Multi-Target Adversarial Learning for Partial Fault Diagnosis), is proposed to provide a comprehensive solution to prevailing diagnostic challenges. These include: (i) the presence of varying operating conditions in the monitored system, (ii) class imbalance between healthy and faulty conditions, and (iii) discrepancies in the number of fault categories between source and target domains, as addressed through partial fault diagnosis.
- The proposed method integrates the strengths of adversarial learning—used to transfer knowledge from a single labeled source domain to multiple unlabeled target domains—with the capabilities of an inconsistency-based domain adaptation model. This combined approach enables effective reduction in distributional divergence across domains in a single-source, multi-target (1SmT) configuration, implemented with balanced multi-target mini-batches and an averaged domain-adversarial loss across targets, while incorporating a class-aware weighting mechanism estimated jointly over targets to down-weight outlier source classes under partial domain adaptation scenarios, and a dual-branch inconsistency regularizer adapted to the multi-target setting to stabilize training.
- The framework is extensively evaluated under varying fault category distributions and multiple working conditions, using two distinct test benches, across 24 cross-domain tasks, to assess the performance and generalization capability of the proposed approach. Furthermore, a comparative analysis against state-of-the-art domain adaptation techniques is presented to demonstrate its effectiveness.
The results obtained demonstrate that the proposed intelligent fault diagnosis framework effectively addresses the partial fault diagnosis problem, exhibiting strong generalization capabilities across multiple target domains simultaneously. Comparative evaluations against state-of-the-art diagnostic methods confirm that the proposed approach substantially outperforms existing techniques, overcoming their principal limitations.
The remainder of this paper is structured as follows: Section 2 presents a review of the related work. Section 3 details the proposed methodology and its theoretical foundations. Section 4 discusses the experimental setup, results, and comparative analysis. Finally, Section 5 provides concluding remarks and outlines directions for future research.
2. Related Works
Most of the existing literature on intelligent fault diagnosis assumes scenarios in which the data distribution and label space are identical between training and testing datasets. These limitations have been progressively addressed in the CBM domain through the application of DL algorithms. Various neural network architectures have been employed, including autoencoders [13], deep belief networks (DBNs) [14], and convolutional neural networks (CNNs) [15]. A representative example is the study conducted by Shao et al. [16], where a deep autoencoder model was proposed for feature learning in fault diagnosis of rotating machinery. Similarly, Wen et al. [17] implemented a deep CNN architecture for data-driven fault diagnosis in electric motors and pumps. Along the same line, Shao et al. [18] developed a convolutional deep belief network for fault identification in electric locomotive bearings.
Transfer learning has garnered significant attention in recent years due to its ability to reuse knowledge learned by a model on one task—such as pattern recognition from a source to a target domain—to enhance performance on a related task involving different but related domains. In this context, domain adaptation methods have emerged as effective strategies for addressing changes in operating conditions, commonly referred to as domain shift, by reducing distributional discrepancies between source and target domains [19].
Recently, three primary approaches to domain adaptation have been proposed in the literature: (i) discrepancy-based domain adaptation, (ii) reconstruction-based domain adaptation, and (iii) adversarial-based domain adaptation.
Discrepancy-based methods aim to minimize the distribution gap between domains using distance metrics such as Kullback–Leibler divergence, Correlation Alignment (CORAL), Wasserstein distance, and Maximum Mean Discrepancy (MMD). These approaches emphasize aligning feature representations while enhancing the model’s learning ability. For example, Li et al. [20] proposed a deep generative neural network using artificial fault data and MMD to achieve cross-domain fault diagnosis in bearings. Similarly, Wang et al. [21] introduced a hierarchical deep domain adaptation method for fault diagnosis in power plants, where CORAL was used to quantify and reduce feature-space divergence.
Another class of domain adaptation methods is inspired by reconstruction techniques [22], which aim to replicate input data at the output in order to learn the underlying structure of the data. In this context, Lu et al. [23] proposed a weakly supervised domain-adaptive convolutional autoencoder that integrates reconstruction loss with MMD to capture shared features across healthy and faulty states in different domains.
Among these approaches, adversarial-based domain adaptation has gained considerable traction in the fault diagnosis community because it can learn domain-invariant features without target labels and mitigate covariate shift via a discriminator–extractor game (commonly realized with a gradient-reversal layer, GRL). Stable training typically benefits from scheduling the adversarial signal, balancing batch composition across domains (and per target when multiple targets are used), and lightly regularizing the discriminator; nevertheless, sensitivity to hyperparameters and the risk of negative transfer under partial label mismatch remain practical challenges. Within this line, GAN-based formulations have been widely explored to address variable operating conditions, noisy datasets, and limited fault samples [24]. For instance, Zou et al. [25] handled these issues with a GAN-based model; Chen et al. [26] proposed an adversarial domain transfer network for fault diagnosis between mismatched domains; Guo et al. [27] generated synthetic fault data to augment the training dataset under diverse operating conditions; and Han et al. [28] developed an adversarial framework specifically designed to address data imbalance in scenarios with few labeled samples.
Despite the progress made, only a limited number of adversarial domain adaptation studies address the partial fault diagnosis problem. Most of the available literature remains in its early stages and is primarily focused on image processing. For instance, Zhang et al. [29] introduced a weighted adversarial network for unsupervised partial domain adaptation, capable of identifying and suppressing outlier classes to reduce shifts in shared category distributions. Similarly, Li et al. [30] proposed class-weighted adversarial networks that prioritize transferring shared classes while ignoring source-specific outliers. Jiao et al. [31] also tackled the partial domain adaptation challenge by training a classifier inconsistency-based model to extract both discriminative and domain-invariant features.
To date, partial fault diagnosis has not been extensively explored in the context of machine health monitoring, and most existing works are restricted to single-source, single-target (1S1T) configurations. In this regard, the present work constitutes a meaningful advancement over the current state of the art by proposing an adversarial domain adaptation methodology specifically tailored for MHM applications. The proposed framework combines adversarial learning with an inconsistency-based model, enhancing generalization capability and enabling effective fault diagnosis across multiple target domains under partial label space conditions.
In this regard, the proposed approach in this paper builds on importance-weighted adversarial partial DA [29] and classifier-inconsistency-based adaptation [31]. Unlike these single-target formulations, MTAL-PFD optimizes a joint objective across multiple target domains by averaging domain losses and employing balanced multi-target batching. In addition, we integrate class-aware weighting in the multi-target setting to address partial label shift, and adapt the dual-branch inconsistency as a stability regularizer under 1SmT. This yields a single deployable model that generalizes across operating conditions, rather than training a separate model per target.
In the context of related work, it is worth noting a related line of research on disturbance-rejection and fault-tolerant control. Active Disturbance Rejection Control (ADRC) estimates and compensates unknown dynamics/disturbances online via an observer–feedback structure, and recent variants such as state-filtered disturbance rejection control and multilayer neurocontrol with ADRC enhance robustness for high-order uncertain nonlinear systems [32]. These approaches target closed-loop control objectives (tracking and stability under disturbances), whereas the present work addresses unsupervised domain adaptation for diagnostic classification under distribution shift and partial label mismatch. The two lines are complementary rather than competing; that is, the health indicators produced by MTAL-PFD can supervise or trigger fault-tolerant control actions.
3. Proposed Method
3.1. Problem Definition
Transfer learning in machine learning refers to the reuse of knowledge acquired while solving a task in a source domain to improve learning performance on a different but related task in a target domain. Let Xs ∈ ℝ(d × ns) represent the data from the source domain with its associated probability distribution Ps(Xs). Similarly, let Xt ∈ ℝ(d × nt) and Pt(Xt) denote the data and distribution in the target domain. Here, d is the dimensionality of each sample, while ns and nt denote the number of instances in the source and target domains, respectively. For quick reader reference, a table with the detailed nomenclature is provided in the corresponding section.
It is assumed that the data distributions differ between domains, i.e., Ps(Xs) ≠ Pt(Xt), which in the considered context reflects changes in working conditions. The proposed methodology operates in an unsupervised domain adaptation setting. Accordingly, the source domain provides labeled samples Ds = {(xis, yis)} for i = 1 to ns, where xis ∈ ℝd, while the target domain consists of unlabeled samples Dt = {xit} for i = 1 to nt.
Importantly, the label space of the source domain (Ys) is assumed to be different from that of the target domain (Yt) under a partial domain adaptation setting, where Yt is a subset of Ys (i.e., Yt ⊆ Ys). Consequently, it is essential to design an indicator extractor capable of learning both discriminative and domain-invariant features, while considering the label space discrepancy between domains.
At the same time, a fault classification model is developed to minimize the probability of incorrect predictions in the target domain, expressed as P(x,ᵧ) ∼ Pt [F(x) ≠ y], where F(x) denotes the predictive model applied to sample x. The goal is to achieve accurate fault classification despite the absence of labeled target data and the presence of a label space mismatch.
3.2. Preprocessing
The proposed methodology could be applied to different physical quantities in the electromechanical system under analysis, such as stator current, acoustic, or even thermal signals, by adjusting windowing, sampling rate, and normalization (e.g., using FFT/STFT magnitudes as input). However, throughout this study we consistently use vibration as the representative source of information for developing the fault-diagnosis tasks. Therefore, the vibration signal is first segmented into time windows of equal length, leading to an array of segments such as:
where L refers to the duration of the segmentation time window, and i represents the sampling index [6]. Subsequently, each segmented raw vibration signal is converted into its corresponding frequency-domain representation using the Fast Fourier Transform. The resulting frequency components are then normalized and serve as inputs to the adversarial learning framework. Due to the variability in the frequency spectrum, lower-amplitude harmonics may contribute minimally to the adjustment of network parameters when compared to dominant peak harmonics. To mitigate this effect, the frequency data are scaled according to standard normalization techniques, as described in [33].
In the scenarios considered, common failure mechanisms exhibit characteristic spectral signatures: (i) rolling-element bearings typically produce peaks and sideband groups around the characteristic defect frequencies and their harmonics due to amplitude/frequency modulation by shaft rotation [34]; (ii) gearbox faults often concentrate energy around the gear-mesh frequency and its harmonics, with sidebands at multiples of the shaft frequency indicative of tooth-mesh modulation [35]; and (iii) electromagnetic faults (e.g., partial demagnetization) may induce low-order harmonic content and modulation of rotational components via torque ripple, which manifests in the vibration spectrum as broadened low-frequency groups and changes around shaft-related harmonics [36]. These patterns motivate operating in the frequency domain and guide the architecture to attend to peaks, harmonic groups, and sidebands that are robust to moderate shifts in operating conditions. In general terms, because the input to the feature extractors is the magnitude spectrum of each window, early 1D convolutional kernels can be viewed as narrow-band detectors (local peaks/notches and short-range co-occurrences), whereas subsequent layers tend to aggregate across neighboring bins to capture harmonic bundles and sideband structures. In this regard, pooling layers provide limited tolerance to small frequency shifts (e.g., due to speed variations), and the dense layers integrate evidence across broader bands to yield class-discriminative representations [37]. Overall, the network emphasizes characteristic groups rather than isolated lines, which supports robustness under domain shift and partial label mismatch.
3.3. Domain Adaptation by Adversarial Learning
Generally, a transfer learning framework utilizing adversarial learning consists of three main components: a feature extractor G, a classifier C, and a domain discriminator D, with their respective parameters symbolized as , and . Adversarial learning involves the concurrent training of the three components through two distinct processes. First, the feature extractor G and the classifier C are employed for fault diagnosis (i.e., with the objective of distinguishing among health-fault categories) using labeled data from the source domain. Second, the features extracted by G are used to differentiate the source domain with respect to the target domain through the domain discriminator D (i.e., with the aim of confusing the discriminator).
Thus, on the one hand, the feature extractor module G and the classifier module C are trained on labeled data from the source domain to perform fault diagnosis, while, on the other hand, the feature extractor module G, together with the discriminator module D, aims to maximize the loss of discrimination capabilities, i.e., learning domain-invariant features for both source and target domains. Formally, the objective of such deep domain adaptation following an adversarial learning process is defined as [30]:
where and represent the classification loss and the domain discriminator loss, respectively, with the cross-entropy loss function being used for this objective; denotes the domain label; and symbolizes the penalty coefficient. Thus, Equations (3) and (4) describe the adversarial learning procedure aims to optimize the parameters , and , where , and are their optimal values, respectively.
Considering that the problem addressed involves partial fault diagnosis, where the target domain constitutes a subset of the source domain in terms of category space, i.e., , it is considered that the direct application of a conventional adversarial learning-based model for domain adaptation could lead to performance degradation, primarily due to the presence of atypical classes within the source domain, as shown in the previous Figure 1. Therefore, in the context of partial fault diagnosis, the challenge arises from the need to disregard the outlier classes in the source domain while facilitating domain adaptation for the shared classes between the source and target domains, for the latter of which the data are unlabelled.
3.4. Weighted Adversarial Learning
In order to properly address the partial fault diagnosis problem, it is proposed to perform domain adaptation by weighting the categories (i.e., health-fault conditions) that are common to both the source and target domains. In this context, an extension of adversarial and inconsistency-based adaptation tailored to single-source, multi-target partial fault diagnosis, MTAL-PFD, is proposed, as depicted in Figure 2. Thus, a conventional domain adversarial network is modified in this proposal such that a dual model of two 1-D CNNs is constructed, resulting in two feature extractor modules G1 and G2, two domain discriminator modules D1 and D2, and two classifier modules C1 and C2. The initial step involves training a fault identification model using only source domain data, which is achieved through the utilization of two feature extraction modules and two fault classifier modules. The output of each fault classifier is defined by , which establishes the probability distribution of each sample. The optimization objective is defined by the classification loss as follows:
where depicts the cross-entropy loss function, which is described as follows:
where stands the value 1 when , differently the value is 0.
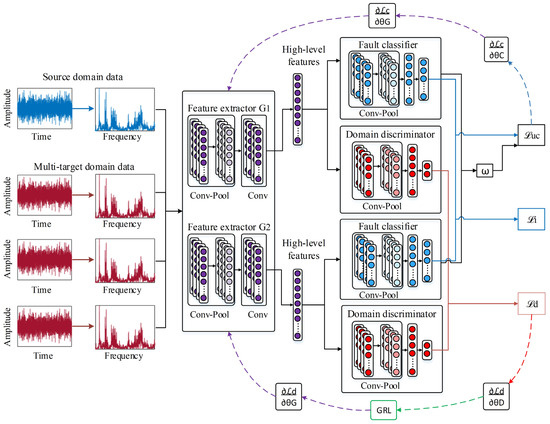
Figure 2.
Overview of the proposed domain adaptation strategy, MTAL-PFD, structured into three main components: feature extractors, classifiers, and discriminators.
Despite both networks being trained on the same source domain data, the parameters of each network will differ, since the parameter initialization is random and differentiated. The second stage consists of including the domain discriminator modules in the training, whose input is the feature mapping obtained from the two feature extractor modules. After the modules are integrated, the classification loss function is modified to account for both the inconsistency loss () and the domain discrimination loss (). The network parameters (i.e., , , ) are iteratively trained and updated using data from the source domain, along with data from various target domains. The class weighting is introduced with the objective of guiding the CNN model to predict the similarity of all target samples to the categories of the source domain, while seeking to penalize the outlier samples of the source domain; that is, the samples that are not related to the fault categories of the target domains. This can be achieved using the outputs of the two feature extractor modules, as these provide a measurement of the class probability distribution for each sample. Thus, the class distribution weight is determined by employing the two 1-dimensional CNNs, as outlined below:
where corresponds to a vector of -dimensional, as claimed by the definition, corresponds to the count of target samples, and represents the result of the modules from FC1 and FC2 for the i-th target sample; and stands the distinct output probabilities. Thus, in the single-source, multi-target (1SmT) setting with N unlabelled targets, target evidence across all targets is aggregated, , and the terms and in (6) pool samples from every unlabelled target. This yields a single set of class weights w used for all targets. Consequently, the class distribution of the training target data is captured by the weights, and based on these weights, the loss function of the classification is updated () as presented in Equation (8), in which represents the element of .
where represents the k-th element of .
Furthermore, to find a common feature space between the different domains, an inconsistency domain adaptation strategy is considered, where the so-called inconsistency loss term is adopted following [31]; mathematically expressed as follows:
where depicts the result of the output layer (i.e., softmax) of each of the fault classifier modules.
In addition, to improve feature learning and assist in reducing the difference between different domains (i.e., domain shift), domain discriminator blocks are introduced, following the adversarial learning theory. The difference between the true domain label and the predicted label is captured by the loss function, which quantifies the domain classification error. Thus, the final objective function of the proposed domain adaptation method is presented as:
where the value of is given by how the samples belonging to the same classes are grouped. On one hand, when instances of outlier classes are presented, it is expected that they will have little overlap between the domains, which implies that a small value of will result. On the other hand, a large value will be obtained for samples belonging to the same class when clustered closely. Mathematically, the loss function is defined as follows:
where and represents the cross-entropy loss computed for the source and target domains, correspondingly. depicts the result of the respective domain discriminator. and represents the penalty coefficients. and depicts the source-domain and the target-domain label, respectively. In the multi-target case, the target-side discriminator loss is instantiated as an average over targets; analogously, is computed on the source mini-batch. Mini-batches are constructed by balanced sampling from each unlabelled target to avoid bias toward larger targets. Thus, depicts a mechanism for guiding the network to focus on adapting shared classes between the source domain and the different target domains, while atypical classes should be ignored, and is estimated as follows:
where the weights for each source classes; represents the samples for the source class; is the count of samples in and represents the count of source classes.
Regarding the objective function of the model (10), it should be noted that is approached differently than the other loss functions (i.e., and ). and are optimized using the gradient descent optimization method. However, due to the dual objective of the adversarial learning process (i.e., maximizing the prediction loss and confusing the domain discriminator), a reverse optimization process needs to be implemented to address . In this regard, the Gradient Reversal Layer (GRL) is adopted for this objective. In particular, GRL employs identity mapping during the forward pass and in backpropagation, where it is used to reverse the sign of the gradients coming from the preceding layer. In summary, the complete training process of the proposed MTAL-PFD method is presented in Algorithm 1.
Finally, it is worth mentioning that to mitigate overfitting and promote stable training, non-overlapping train/validation/test partitions are employed, together with balanced sampling across target domains within each mini-batch, and an optimizer with a brief warm-up followed by cosine learning rate decay. We also apply early stopping based on a tolerance–patience criterion evaluated on a smoothed training objective. In addition, the dual-branch inconsistency term serves as an explicit stability regularizer. These measures are applied consistently across all experiments.
| Algorithm 1: Training of MTAL-PFD method. The and represents the number of epochs in different steps; is the batch size. |
| Input; Multiple target domains: is the different target domains; modules:, . Hyper-parameters: optimizer Adam with initial learning rate η0; learning rate schedule with linear warm-up Tw followed by cosine decay; early- stopping tolerance ε, patience P (checked per epoch), and moving-average window M for smoothing the total loss. 1: do 2: Randomly mini-batch of ; 3: Train using cross entropy algorithm. 4: end 5: Initialize optimizer and schedules (Adam at η0; set Tw, ε, P, M). 6: do 7: Update learning rate η ← schedule (i) (linear warm-up then cosine decay). 8: Randomly sample balanced mini-batches from and from each to (with equal quota m/N from each target). 9: Retrain; train using GRL (with Ld = Jds + 1N∑j = 1NJdt(j)). 10: weights for the categories by aggregating target-side evidence across all (j). 11: Perform the parameter optimization follow by Equation (10) (update G1, G2, FC1, FC2, DD1, DD2 with Adam using the current η). 12: Update the smoothed total loss (moving average over the last M ) < ε, increase a patience counter; stop when patience ≥ P. 13: end |
3.5. Network Architecture
The complete network architecture in regard to the proposed strategy is depicted in Figure 2. From a general perspective, six modules are adopted, i.e., two identical feature extractors, two identical fault classifiers, and two identical domain discriminators. Each feature extractor initially utilizes three convolutional layers with filter sizes of 3 and filter counts of 128, 64, and 32, respectively. Then, a flattening layer and a fully connected layer with 128 neurons are added, and the extracted high-level features are subsequently applied to domain and fault condition classification tasks. The fault classifier module utilizes two convolutional layers, with 32 and 16 filters of size 3, respectively. A dense layer with 64 neurons follows, and then neurons along with a softmax classifier are employed for fault diagnosis. To prevent overfitting, dropout is applied throughout the network, while leaky rectified linear units (ReLU) are used as activation functions in most layers. The network parameters are adjusted by means of backpropagation, and the Adam optimizer is employed for optimization. The architecture of the domain discriminator mirrors that of the fault classification model, beginning with a pair of convolutional layers comprising 256 and 128 filters, each utilizing a kernel size of 3. These are followed by two fully connected layers containing 512 and 128 units, respectively. To enable domain label identification, two output neurons are incorporated, and a softmax activation function is employed to facilitate the domain classification task.
4. Experiments
This section evaluates the proposed MTAL-PFD method. Since an electromechanical system is composed of different components and rolling bearings are vital elements, the experiments are performed on a system with multiple faults and on a set of bearing fault data, respectively. Both benchmarks are lab-controlled test benches; results should therefore be interpreted as bench-to-bench transfers across operating conditions rather than a direct in situ field validation. Additionally, five state-of-the-art approaches are benchmarked against the proposed method. The PyTorch 1.9.0 platform is used for experimental validation, and a tenfold cross-validation scheme is employed for each experiment in order to reduce singularities and statistically validate them.
4.1. Experimental Setups
- Multi-Fault Experimental Dataset: As shown in Figure 3, an electromechanical test system is used as the first experimental dataset. The test bench contains two identical ABB (Zurich, Switzerland) permanent magnet synchronous motors (PMSMs), one to drive the movement and another that acts as a load, a Khemo (Barcelona, Spain) gearbox to transmit the movement connected at one end to the driving motor and at the other end runs a screw that contains a moving part. Both PMSMs have 3 pairs of poles, and torque and speed are rated at 3.6 Nm and 6000 rpm, respectively. An ABB (Zurich, Switzerland) power converter ACSM1 model works to drive the motors. Four condition categories on the test bench have been considered, including (1) healthy condition, (2) demagnetization fault, (3) bearing fault, and (4) gearbox fault; details are described in Table 1. The experiments are conducted under four operating conditions, i.e., 30 Hz and 60 Hz of power frequency supply, in combination with 40% and 70% of the nominal load. Thus, there are four different domains: (30 Hz, 40%), (30 Hz, 70%), (60 Hz, 40%) and (60 Hz, 70%). Signal acquisition is performed using an Endevco (Depew, NY, USA) Isotron KS943B.100 vibration sensor mounted on the motor surface, operating at a sampling frequency of 10 kHz. For each working condition, 800 samples are collected, each containing 1024 data points. For reproducibility, raw signals may be shared upon reasonable request for academic, non-commercial use. Since this paper addresses the problem of partial fault diagnosis and the multiple-target issue, all operating conditions are used in the source domain; however, only a few samples of some operating conditions are selected for the target domains. To comprehensively evaluate the performance of the proposed method, 12 cross-domain experiments are performed. Comprehensive details of the conducted experiments are provided in Table 2, which are arbitrarily selected to address different partial transfer fault diagnosis scenarios. The experiments consist of using a working condition as the source domain, i.e., and the rest, i.e., , and , as multiple-target domains, where “#” denotes the number of condition categories utilized across the multiple target domains for training the feature extractors, classifier, and discriminator. Each of these transfer tasks is shown individually for clearer representation.
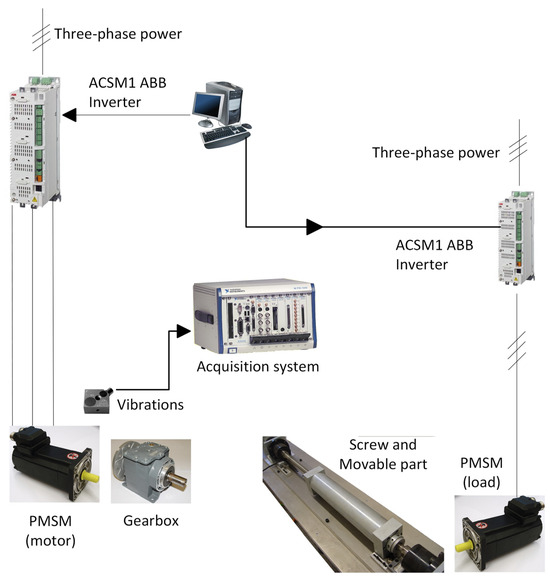 Figure 3. Scheme of the electromechanical test system from which the multi-fault experimental dataset is extracted.
Figure 3. Scheme of the electromechanical test system from which the multi-fault experimental dataset is extracted. Table 1. Different operation conditions of the multi-fault dataset.
Table 1. Different operation conditions of the multi-fault dataset. Table 2. Information of the partial transfer learning tasks under study.
Table 2. Information of the partial transfer learning tasks under study. - Rolling Bearing CWRU Dataset: Experiments are extended with a second dataset, in this case, a public bearing-based dataset from Case Western Reserve University [38]. The experimental test bench includes an electric motor, a torque transducer, a dynamometer, and an electric controller. Vibration signals are extracted from this test bench under four working conditions, i.e., 1797 rpm, 1772 rpm, 1750 rpm, and 1730 rpm, which implies four different domains , , and , respectively. Regarding condition categories, a healthy condition is considered, besides three types of fault, with each fault condition having three distinct severity degrees: 7, 14, and 21 mils (1 mil = 0.001 inches). Therefore, there are a total of ten health categories, which include: (1) healthy, (2) ball fault 7, (3) ball fault 14, (4) ball fault 21, (5) inner fault 7, (6) inner fault 14, (7) inner fault 21, (8) outer fault 7, (9) outer fault 14, and (10) outer fault 21. The vibration signals used for the experiments are extracted from the motor housing at the drive end, acquired at a sampling frequency of 12 kHz. For each category, there are 1000 samples, and each sample contains 1024 data points. Similar to the previous dataset experiments, 12 different partial transfer fault diagnosis scenarios are selected, described in Table 2. It should be noted that the selected scenarios correspond to representative experimental cases, which include non-partial, soft partial, and major partial tasks.
4.2. Comparative Methods and Parameter Configuration
For a more comprehensive evaluation of the proposed methodology, five popular domain adaptation-based methods have been considered for comparison purposes, including three shallow-based strategies and two deep-domain adaptation (DDA)-based strategies. Shallow-based strategies include Correlation Alignment (CORAL), Transfer Component Analysis (TCA), and Transfer AdaBoost (TrAdaBoost). DDA strategies include Deep Correlation Alignment (DeepCORAL) and Discriminative Adversarial Neural Network (DANN). To broaden deep adaptation coverage, an MMD-based deep baseline is also included under the same protocol, the MMD-DNN (Maximum Mean Discrepancy-Deep-Neural-Net). Regarding evaluation, typical evaluation methodologies were used, and all available data (i.e., source data and target data) were included for training the models. For fairness and direct comparability across baselines, all methods are trained and evaluated under the same 2:1 ratio between healthy and failure conditions across both datasets. For each task, results are obtained from independent runs with different random seeds.
The hyperparameters of each method were selected with reference to the relevant literature and through several trial-and-error configurations to obtain competitive results. Prior work commonly adopts a batch size of 32 to balance generalization and stability, which is adopted here. Implementation details are as follows: for Correlation Alignment (CORAL), a regularization parameter of 1 × 10−5 is used; Transfer AdaBoost employs a ridge-regression base classifier with 10 estimators and a learning rate of 1 × 10−1; DeepCORAL uses SGD with a learning rate of 1 × 10−3; the autoencoder comprises two hidden layers (10 neurons each) with ReLU activations and mean squared error (MSE) as the training loss; and DANN comprises three hidden layers (512, 512 and 256) with a two-layer domain discriminator (1024, 2), trained with Adam (learning rate 1 × 10−4) for 100 iterations. For MTAL-PFD, Adam with a brief warm-up followed by cosine learning rate decay is adopted, together with a batch size of 32 and the loss-term trade-offs described in Section 3. Similar to the DANN method, for MMD-DNN three hidden layers (512, 512 and 256) without a domain discriminator, trained with Adam (learning rate 1 × 10−4) for 100 iterations is applied.
To facilitate reproducibility on new datasets, recommended ranges and a concise tuning procedure are included. In line with adversarial/partial DA practice (e.g., [6,30,31]), batch sizes of 32–128 are recommended for 1D spectral inputs (larger values are feasible when memory permits, whereas very small batches may destabilize adversarial updates). With Adam, learning rates in the 10−4 range are typical (e.g., 1 × 10−4 in [6], 5 × 10−4 in [31]); for SGD-based baselines, learning rates between 10−2 and 10−1 are common. For the loss weights in MTAL-PFD, the classification term is used as the anchor (α0 = 1.0), with α1 = 0.05–0.20 (inconsistency/stability) and α2 = 0.5–1.5 (adversarial alignment) as starting ranges—α2 can be increased when the domain gap is large and decreased if training becomes unstable. A coarse-to-fine tuning protocol is applied: (i) select batch size and optimizer learning rate on source validation; (ii) fix those values and perform a small grid over α1 and α2 within the ranges above; (iii) choose the configuration that yields stable training curves (smoothed objective) and repeatable results across seeds, with early stopping to prevent overfitting. This procedure does not rely on target labels and provides a reproducible protocol.
4.3. Results of Multi-Fault Dataset
With regard to the performance of the proposed MTAL-PFD method, the following insights are extracted from the results in Table 3. Disaggregating the results, it is observed that in the cases of non-partial target classes (i.e., tasks T1, T4, T7, and T10), an average classification performance of 99.89% is achieved. In the cases of partial target classes (i.e., the remaining tasks), the average is 95.21%. Both observations demonstrate a performance similar to the global average across all considered tasks, i.e., 96.77%, indicating a stable performance in both partial and non-partial scenarios.

Table 3.
Evaluation of MTAL-PFD on the Multi-Fault Dataset in Comparison with State-of-the-Art Methods Based on Domain Adaptation.
Regarding the comparison with representative state-of-the-art methods, their performances in the non-partial target classes and partial target classes scenarios are clearly inferior, being between 70% and 84%, and between 65% and 81%, respectively. It is important to highlight that all cases exhibit an imbalance between the data from the considered conditions, specifically, a ratio of 2/1 for the healthy and failure conditions, respectively. In general terms, the proposed MTAL-PFD method improves between 14% and 28% over the reference methods. A homogeneous improvement across all tasks considered indicates consistent performance in scenarios which require domain adaptation, partial domain, and data imbalance management. However, despite the improvement, moderately high-performance values (i.e., around 80%) suggest that the selected scenarios represent highly complex cases that are not easily solvable.
From the application perspective (i.e., electric motors), it can be observed that cases where speed varies as part of the operational condition show a slightly lower performance percentage, i.e., less than 5%, compared to cases where speed is constant. This is consistent with the underlying physical effects in the system, as a variation in the main frequency alters the frequency axis profile of the characteristic harmonics for each condition with respect to the considered vibration signal. However, a variation in torque affects the amplitude proportion of these harmonics which has no significant effect in the expected frequency profile, only slightly simplifying the task of pattern characterization and recognition, which leads to concluding that the proposed method successfully adapts the patterns considered in the target classes.
It is worth noting task T6, which corresponds to the case with the highest standard deviation across the entire analysis, which represents a scenario where both the healthy category and the demagnetization fault are treated as partial target classes. Specifically, representative samples of the demagnetization fault under low torque, , are interpreted as being similar to the healthy condition under identical speed and torque settings. This behavior is consistent with the limited impact of demagnetization faults on the physical magnitude in low-torque scenarios and is further justified by the fact that the source domain corresponds to a higher torque reference, . Finally, high accuracies are observed in a subset of tasks, this fact is consistent with the experimental context considering that source and target share the same test bench and fault families, and the frequency-domain representation retains distinctive spectral markers (e.g., BPFI/BPFO/BSF groups for bearings; gear-mesh with shaft-frequency sidebands). Under these conditions, class boundaries remain comparatively stable across moderate changes in operating conditions. In addition, the behavior observed for MTAL-PFD aligns with the design choices, i.e., dual-branch with inconsistency regularization and class-aware weighting, which reduce variance and mitigate negative transfer in partial settings.
From a computational-cost perspective, all methods were trained on a standard workstation (Dell Precision 3630; Intel i7-8700; 32 GB DDR4; NVIDIA Quadro P2000) using identical train/validation/test splits for three representative transfers (T1–T3). Under this setup, MTAL-PFD completed one training run in 1 min 52 s on average (five trials). For reference, DANN and DCA required 8 min 28 s and 7 min 39 s, respectively, whereas CORAL and TrAdaBoost completed in 38 s and 42 s, TCA in 2 min 24 s, an, MMD-DNN reached 4 min 39 s. DANN, DCA and MMD-DNN typically reached the early-stopping criterion later, consistent with the additional adversarial optimization dynamics (training of the domain discriminators and stabilization of the min–max game), which increases the number of effective updates before convergence. By contrast, MTAL-PFD employs lightweight 1D-CNN branches together with balanced multi-target sampling and stability regularization (inconsistency term and learning rate schedule), which shortened the time-to-convergence under the same criterion.
From a qualitative perspective, the representation of the classes using t-SNE, as shown in Figure 4, demonstrates the superior ability of the proposed method to organize the classes and differentiate them, as evidenced by a reduced overlap among classes, decreased dispersion, and improved clustering across different working conditions. In accordance with standard practice for t-SNE visualizations, axis labels are omitted, since the embedding is defined up to rotation and scale and the axes do not carry domain-specific meaning; the plots are intended as qualitative diagnostics of feature-space structure, whereas Table 3 and Table 4 report the quantitative performance. As illustrated in Figure 4, the t-SNE projection of the learned features suggests a coherent structure: samples cluster by fault family, and within-class substructures often align with operating conditions. This qualitative topology is consistent with expected spectral patterns, namely peaks, harmonic groups, and sidebands around characteristic fault frequencies, and with the comparative performance trends observed across tasks. In general terms, the model appears to aggregate evidence across neighboring frequency bins, which may help explain its robustness to operating-condition shifts.
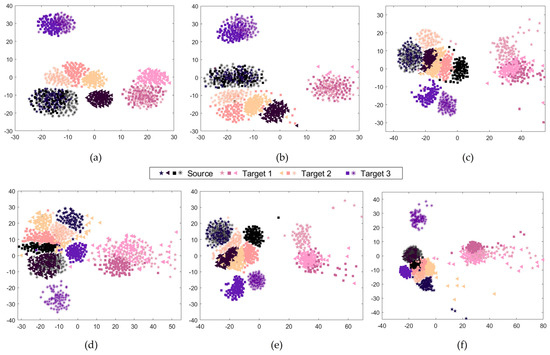
Figure 4.
Feature exploration via t-SNE. The representation corresponds to the features learned by the different methods through Tasks T1, T2 and T3. (a) MTAL-PFD. (b) DANN. (c) DCA. (d) TCA. (e) TrAdaBoost. (f) CORAL.

Table 4.
Evaluation of a single-extractor approach on the Multi-Fault Dataset.
Finally, to assess the contribution of the dual-branch design and the inconsistency term, a single-extractor variant was trained under the same protocol, removing the second branch and omitting the inconsistency penalty while preserving the class-weighting mechanism. On the Multi-Fault dataset, the single-extractor variant achieves an overall average accuracy of 76.8%, with 98.6% on non-partial transfers and 66.0% on partial transfers; by contrast, MTAL-PFD attains 96.77% under identical conditions. These results indicate that the dual-branch architecture, together with the inconsistency component, is critical for robustness under partial label mismatch. Results are provided in Table 4.
In the proposed MTAL-PFD, the dual feature extractors furnish two independently initialized views of the input, reducing variance from random initialization and enabling an explicit disagreement signal. The inconsistency term penalizes divergent predictions between branches on shared classes, acting as a stability regularizer that promotes class-consistent features under domain shift. The class-weighting mechanism down-weights out-of-scope source classes, mitigating negative transfer in partial label-mismatch scenarios. Together with balanced multi-target sampling and adversarial alignment, these elements support a single model that generalizes across targets. Consistent with this design, removing the second branch and the inconsistency regularizer primarily degrades performance on partial transfers.
4.4. Results of Rolling-Bearing CWRU Fault Dataset
Similar to the previous case, and with regard to the performance of the proposed MTAL-PFD method, the following insights are extracted from the results in Table 5. Disaggregating the results, it is observed that in the cases of non-partial target classes (i.e., tasks C1, C4, C7, and C10), an average classification performance of 85.32% is achieved. In the cases of partial target classes (i.e., the remaining tasks), the average is 96.57%. In this case study, the resulting performance in partial domain cases is slightly superior to that in non-partial cases. This could be attributed to the high number of classes considered (i.e., 10) and their proximity in the feature space, as many of the classes represent variations in degradation intensity but share the same fault and, therefore, a similar characteristic pattern in the vibration signal under consideration. Therefore, as more classes are considered, samples which correspond to the same type of fault but with different severity degrees will be prone to overlapping.

Table 5.
Evaluation of MTAL-PFD on the CWRU dataset in comparison with state-of-the-art methods based on domain adaptation.
Following the same analytical framework, it is necessary to mention that all cases consider an imbalance ratio of 2:1 for the healthy and failure conditions, respectively.
From the application perspective (i.e., electric motors), it is important to mention that the domain variations are primarily in speed, which adds an additional layer of complexity, as changes in rotational frequency affect the entire frequency spectrum of the vibration signal under consideration. For this reason, the performance achieved by the proposed method and the reference methods used is generally lower than that obtained in the previous case study. Nevertheless, the proposed method, MTAL-PFD, improves between 18% and 35% over the reference methods, reaching an average performance of 92.82%. These improvements are also homogeneous throughout all tasks, verifying that the combination of domain adaptation, partial domain, and data imbalance represents a highly complex scenario, and the proposed method successfully manages to address them.
5. Conclusions
This study presents an innovative intelligent fault diagnosis framework, denoted as MTAL-PFD (Multi-Target Adversarial Learning for Partial Fault Diagnosis), specifically designed to address three critical limitations inherent in current industrial condition monitoring approaches: (1) domain shifts arising from varying operational conditions, (2) class imbalance between healthy and faulty states, and (3) discrepancies in label spaces between source and target domains, characteristic of partial domain adaptation scenarios. To overcome these challenges, MTAL-PFD integrates adversarial learning with an inconsistency-based domain adaptation mechanism, facilitating effective knowledge transfer from a single labeled source domain to multiple unlabeled target domains (1SmT configuration). The proposed architecture employs a dual-branch one-dimensional convolutional neural network (1D-CNN), which enables category weighting to enhance the adaptation of shared classes while attenuating the influence of outlier categories.
The proposed methodology was validated using two benchmark datasets: a custom-built electromechanical multi-fault test bench and the publicly available CWRU bearing dataset, across 24 distinct partial transfer learning tasks. Experimental results demonstrate that MTAL-PFD achieves superior performance compared to five state-of-the-art domain adaptation methods, with average classification accuracies of 96.77% and 92.82%, respectively. Furthermore, the framework exhibits strong generalization capabilities under both partial and non-partial settings and demonstrates robustness to variations in torque, speed, and class distribution.
It is worth noting that, although the proposed MTAL-PFD is developed for the joint multi-target (simultaneous) setting, new unlabeled operating conditions may emerge sequentially. In such cases, MTAL-PFD could be applied by warm-starting from the current model, forming mini-batches that mix source samples with the current unlabeled target only, and re-estimating the class-aware weights online from target evidence. Early stopping, and optionally a lightweight output-consistency regularizer with respect to the previous model, would help maintain previously acquired performance. This procedure would retain a single deployed model and would not require target labels, and would constitute part of our future work in deployment settings.
Overall, the MTAL-PFD framework contributes to the advancement of scalable and adaptive fault diagnosis systems tailored for real-world industrial applications. Future work will explore integrating online learning strategies for real-time condition monitoring, broadening the assessment under stronger class imbalance, conducting a systematic interpretability study for spectral inputs, and performing external validation on in situ industrial recordings with environmental noise and installation variability.
Author Contributions
Conceptualization, F.A.E., M.D.-P. and J.J.S.-D.; Methodology, F.A.E., M.D.-P. and J.J.S.-D.; Software, F.A.E. and J.V.P.; Validation, M.D.-P. and J.J.S.-D.; Formal analysis, F.A.E., M.D.-P. and J.V.P.; Investigation, F.A.E., M.D.-P. and J.J.S.-D.; Resources, M.D.-P.; Data curation, F.A.E. and J.V.P.; Writing–original draft, F.A.E. and J.V.P.; Writing–review & editing, M.D.-P. and J.J.S.-D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Catalan Agency for Management of University and Research Grants under the grant Motion Control and Industrial Applications Research Group, MCIA.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Acknowledgments
The authors would like to express their deepest gratitude and remembrance to Roque A. Osornio-Rios for his invaluable scientific guidance, and for the inspiring example he set through both his professional excellence and personal integrity.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| Classifier | |
| Dimensionality of each sample | |
| Source-domain label | |
| Target-domain label | |
| Domain discriminator | |
| Labeled samples from the source domain | |
| Unlabeled samples from the target domain | |
| Samples of each of the source classes | |
| Result of the domain discriminator | |
| Number of epochs in each step | |
| Feature extractor | |
| Cross-entropy loss function | |
| Cross-entropy loss computed for the source domain | |
| Cross-entropy loss computed for the target domain | |
| L | Duration of the segmentation time window |
| Batch size | |
| Number of instances in the source domain | |
| Number of instances in the target domain | |
| Count of samples in the source class | |
| Count of the source classes | |
| Probability distribution associated with the data from the source domain | |
| Probability distribution associated with the data from the target domain | |
| Data from the source domain | |
| Data from the target domain | |
| Segmentation array of the vibration signal | |
| Output of the fault classifier modules | |
| Label space of the source domain | |
| Label space of the target domain | |
| Penalty coefficient | |
| Output of each classifier | |
| Loss objective function | |
| Classification loss | |
| Domain discrimination loss | |
| Inconsistency loss | |
| Updated classification loss | |
| Parameters of the classifier | |
| Parameters of the domain discriminator | |
| Parameters of the feature extractor | |
| Parameters of neural network model for domain discriminator | |
| Parameters of neural network model for classification | |
| Parameters of neural network for feature extraction | |
| Optimal value of the parameters of the classifier | |
| Optimal value of the parameters of the domain discriminator | |
| Optimal value of the parameters of the feature extractor | |
| Result of the output layer of each of the fault classifier modules | |
| Output probabilities from each of the classifier modules | |
| Class distribution weight | |
| Weights for the source classes |
References
- Duan, L.; Da Xu, L. Data Analytics in Industry 4.0: A Survey. Inf. Syst. Front. 2024, 26, 2287–2303. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, Y.; Xia, M.; Williams, D.; de Silva, C.W. A New Multisensor Partial Domain Adaptation Method for Machinery Fault Diagnosis Under Different Working Conditions. IEEE Trans. Instrum. Meas. 2023, 72, 3531410. [Google Scholar] [CrossRef]
- Jeong, H.; Kim, S.; Seo, D.; Kwon, J. Source-Free Domain Adaptation Framework for Rotary Machine Fault Diagnosis. Sensors 2025, 25, 4383. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Yan, F.; Yu, L.; Shen, C.; Hu, X.; Chen, J. A federated transfer learning method with low-quality knowledge filtering and dynamic model aggregation for rolling bearing fault diagnosis. Mech. Syst. Signal Process. 2023, 198, 110413. [Google Scholar] [CrossRef]
- Li, H.; Wang, G.; Shi, N.; Li, Y.; Hao, W.; Pang, C. A Lightweight Multi-Angle Feature Fusion CNN for Bearing Fault Diagnosis. Electronics 2025, 14, 2774. [Google Scholar] [CrossRef]
- Ragab, M.; Chen, Z.; Wu, M.; Li, H.; Kwoh, C.K.; Yan, R. Adversarial Multiple-Target Domain Adaptation for Fault Classification. IEEE Trans. Instrum. Meas. 2021, 70, 3500211. [Google Scholar] [CrossRef]
- Siddika, A.; Begum, M.; Al Farid, F.; Uddin, J.; Karim, H.A. Enhancing Software Defect Prediction Using Ensemble Techniques and Diverse Machine Learning Paradigms. Eng 2025, 6, 161. [Google Scholar] [CrossRef]
- Li, T.; Zhao, Z.; Sun, C.; Yan, R.; Chen, X. Domain Adversarial Graph Convolutional Network for Fault Diagnosis Under Variable Working Conditions. IEEE Trans. Instrum. Meas. 2021, 70, 3515010. [Google Scholar] [CrossRef]
- Zhang, G.; Li, Y.; Jiang, W.; Shu, L. A fault diagnosis method for wind turbines with limited labeled data based on balanced joint adaptive network. Neurocomputing 2022, 481, 133–153. [Google Scholar] [CrossRef]
- Yu, X.; Zhao, Z.; Zhang, X.; Zhang, Q.; Liu, Y.; Sun, C. Deep-Learning-Based Open Set Fault Diagnosis by Extreme Value Theory. IEEE Trans. Industr. Inform. 2022, 18, 185–196. [Google Scholar] [CrossRef]
- Chen, J.; Wang, J.; Zhu, J.; Lee, T.H.; de Silva, C.W. Unsupervised Cross-Domain Fault Diagnosis Using Feature Representation Alignment Networks for Rotating Machinery. IEEE ASME Trans. Mechatron. 2021, 26, 2770–2781. [Google Scholar] [CrossRef]
- Pikramenos, G.; Spyrou, E.; Perantonis, S.J. Extending Partial Domain Adaptation Algorithms to the Open-Set Setting. Appl. Sci. 2022, 12, 10052. [Google Scholar] [CrossRef]
- Li, Z.; Sun, Y.; Yang, L.; Zhao, Z.; Chen, X. Unsupervised Machine Anomaly Detection Using Autoencoder and Temporal Convolutional Network. IEEE Trans. Instrum. Meas. 2022, 71, 1–13. [Google Scholar] [CrossRef]
- Zhao, F.; Jiang, Y.; Cheng, C.; Wang, S. An improved fault diagnosis method for rolling bearings based on wavelet packet decomposition and network parameter optimization. Meas. Sci. Technol. 2024, 35, 25004. [Google Scholar] [CrossRef]
- Tran, M.Q.; Liu, M.K.; Tran, Q.V.; Nguyen, T.K. Effective Fault Diagnosis Based on Wavelet and Convolutional Attention Neural Network for Induction Motors. IEEE Trans. Instrum. Meas. 2022, 71, 3501613. [Google Scholar] [CrossRef]
- Shao, H.; Jiang, H.; Zhao, H.; Wang, F. A novel deep autoencoder feature learning method for rotating machinery fault diagnosis. Mech. Syst. Signal Process. 2017, 95, 187–204. [Google Scholar] [CrossRef]
- Wen, L.; Li, X.; Gao, L.; Zhang, Y. A New Convolutional Neural Network-Based Data-Driven Fault Diagnosis Method. IEEE Trans. Ind. Electron. 2018, 65, 5990–5998. [Google Scholar] [CrossRef]
- Shao, H.; Jiang, H.; Zhang, H.; Liang, T. Electric Locomotive Bearing Fault Diagnosis Using a Novel Convolutional Deep Belief Network. IEEE Trans. Ind. Electron. 2018, 65, 2727–2736. [Google Scholar] [CrossRef]
- Chen, P.; Zhao, R.; He, T.; Wei, K.; Yuan, J. A novel bearing fault diagnosis method based joint attention adversarial domain adaptation. Reliab. Eng. Syst. Saf. 2023, 237, 109345. [Google Scholar] [CrossRef]
- Li, X.; Zhang, W.; Ding, Q. Cross-Domain Fault Diagnosis of Rolling Element Bearings Using Deep Generative Neural Networks. IEEE Trans. Ind. Electron. 2019, 66, 5525–5534. [Google Scholar] [CrossRef]
- Wang, X.; He, H.; Li, L. A Hierarchical Deep Domain Adaptation Approach for Fault Diagnosis of Power Plant Thermal System. IEEE Trans. Ind. Inform. 2019, 15, 5139–5148. [Google Scholar] [CrossRef]
- Guo, L.; Yu, Y.; Liu, Y.; Gao, H.; Chen, T. Reconstruction Domain Adaptation Transfer Network for Partial Transfer Learning of Machinery Fault Diagnostics. IEEE Trans. Instrum. Meas. 2022, 71, 2502710. [Google Scholar] [CrossRef]
- Lu, N.; Yin, T. Transferable common feature space mining for fault diagnosis with imbalanced data. Mech. Syst. Signal Process. 2021, 156, 107654. [Google Scholar] [CrossRef]
- He, J.; Ouyang, M.; Chen, Z.; Chen, D.; Liu, S. A Deep Transfer Learning Fault Diagnosis Method Based on WGAN and Minimum Singular Value for Non-Homologous Bearing. IEEE Trans. Instrum. Meas. 2022, 71, 3509109. [Google Scholar] [CrossRef]
- Zou, L.; Li, Y.; Xu, F. An adversarial denoising convolutional neural network for fault diagnosis of rotating machinery under noisy environment and limited sample size case. Neurocomputing 2020, 407, 105–120. [Google Scholar] [CrossRef]
- Chen, Z.; He, G.; Li, J.; Liao, Y.; Gryllias, K.; Li, W. Domain Adversarial Transfer Network for Cross-Domain Fault Diagnosis of Rotary Machinery. IEEE Trans. Instrum. Meas. 2020, 69, 8702–8712. [Google Scholar] [CrossRef]
- Guo, Q.; Li, Y.; Song, Y.; Wang, D.; Chen, W. Intelligent fault diagnosis method based on full 1-D convolutional generative adversarial network. IEEE Trans. Ind. Inform. 2019, 16, 2044–2053. [Google Scholar] [CrossRef]
- Han, T.; Liu, C.; Yang, W.; Jiang, D. A novel adversarial learning framework in deep convolutional neural network for intelligent diagnosis of mechanical faults. Knowl. Based Syst. 2019, 165, 474–487. [Google Scholar] [CrossRef]
- Zhang, J.; Ding, Z.; Li, W.; Ogunbona, P. Importance weighted adversarial nets for partial domain adaptation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Li, X.; Zhang, W.; Ma, H.; Luo, Z.; Li, X. Partial transfer learning in machinery cross-domain fault diagnostics using class-weighted adversarial networks. Neural Netw. 2020, 129, 313–322. [Google Scholar] [CrossRef]
- Jiao, J.; Zhao, M.; Lin, J.; Ding, C. Classifier Inconsistency-Based Domain Adaptation Network for Partial Transfer Intelligent Diagnosis. IEEE Trans. Ind. Inform. 2020, 16, 5965–5974. [Google Scholar] [CrossRef]
- Carreño-Zagarra, J.J.; Moreno, J.C.; Guzmán, J.L. Optimal Active Disturbance Rejection Control for Second Order Systems. IEEE Access 2024, 12, 76244–76256. [Google Scholar] [CrossRef]
- Lu, W.; Liang, B.; Cheng, Y.; Meng, D.; Yang, J.; Zhang, T. Deep Model Based Domain Adaptation for Fault Diagnosis. IEEE Trans. Ind. Electron. 2017, 64, 2296–2305. [Google Scholar] [CrossRef]
- Yingying, G.; Xuezhi, Z.; Wen-Bin, S.; Weiguang, L.; Hui, L.; Chunliang, Z. Fault characteristic frequency analysis of elliptically shaped bearing. Measurement 2020, 155, 107544. [Google Scholar] [CrossRef]
- Ishikawa, T.; Igarashi, N. Failure Diagnosis of Demagnetization in Interior Permanent Magnet Synchronous Motors Using Vibration Characteristics. Appl. Sci. 2019, 9, 3111. [Google Scholar] [CrossRef]
- Zhi, S.; Shen, H.; Wang, T. Gearbox localized fault detection based on meshing frequency modulation analysis. Appl. Acoust. 2024, 219, 109943. [Google Scholar] [CrossRef]
- Ribeiro Junior, R.F.; dos Santos Areias, I.A.; Mendes Campos, M.; Teixeira, C.E.; Borges da Silva, L.E.; Ferreira Gomes, G. Fault detection and diagnosis in electric motors using 1d convolutional neural networks with multi-channel vibration signals. Measurement 2022, 190, 110759. [Google Scholar] [CrossRef]
- Smith, W.; Randall, R. Rolling element bearing diagnostics using the Case Western Reserve University data: A benchmark study. Mech. Syst. Signal Process. 2015, 64, 100–131. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).