Quantitative Hazard Assessment of Mining-Induced Seismicity Using Spatiotemporal b-Value Dynamics from Microseismic Monitoring
Abstract
1. Introduction
2. Materials and Methods
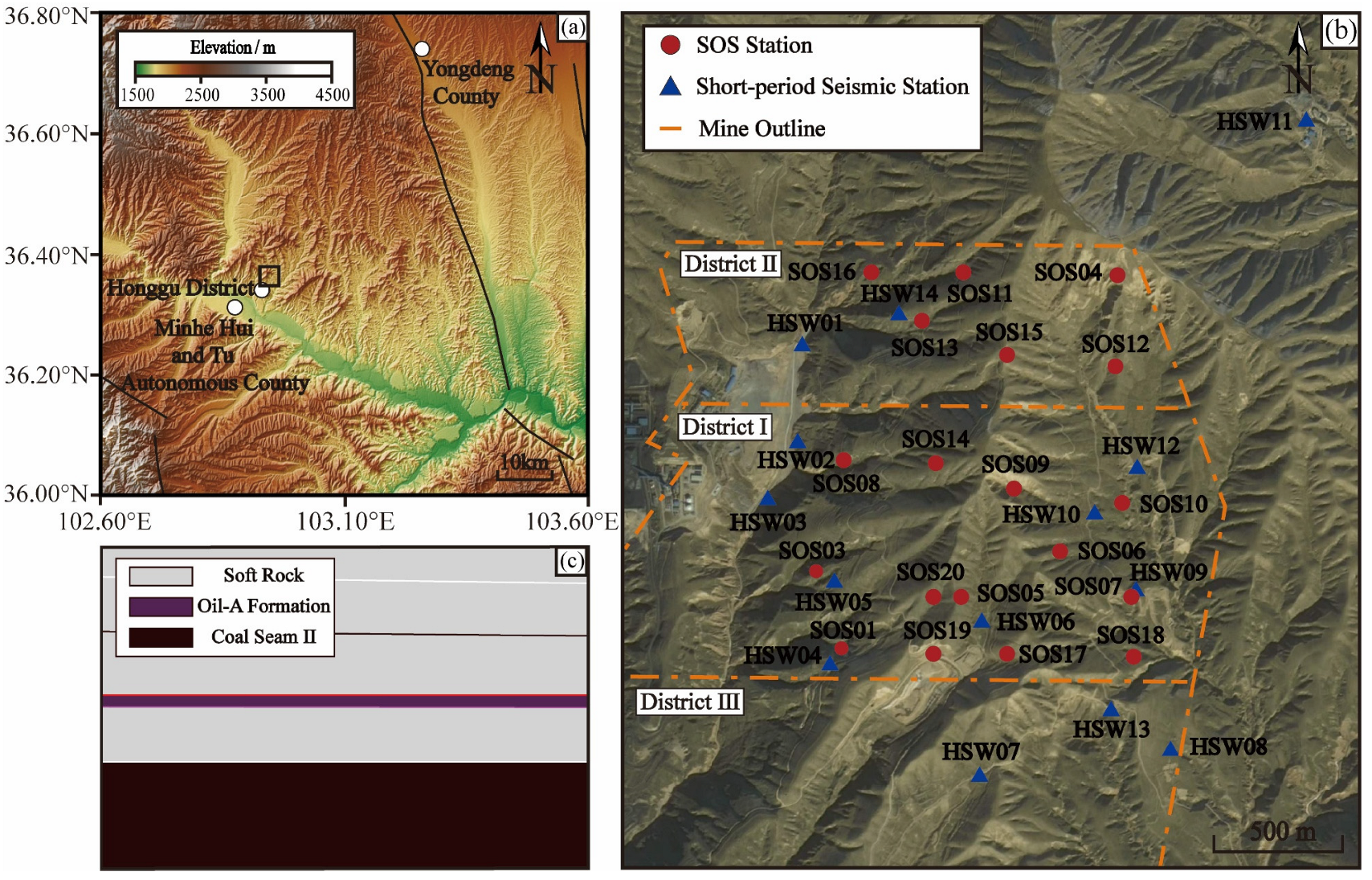
2.1. Seismic Catalog Data
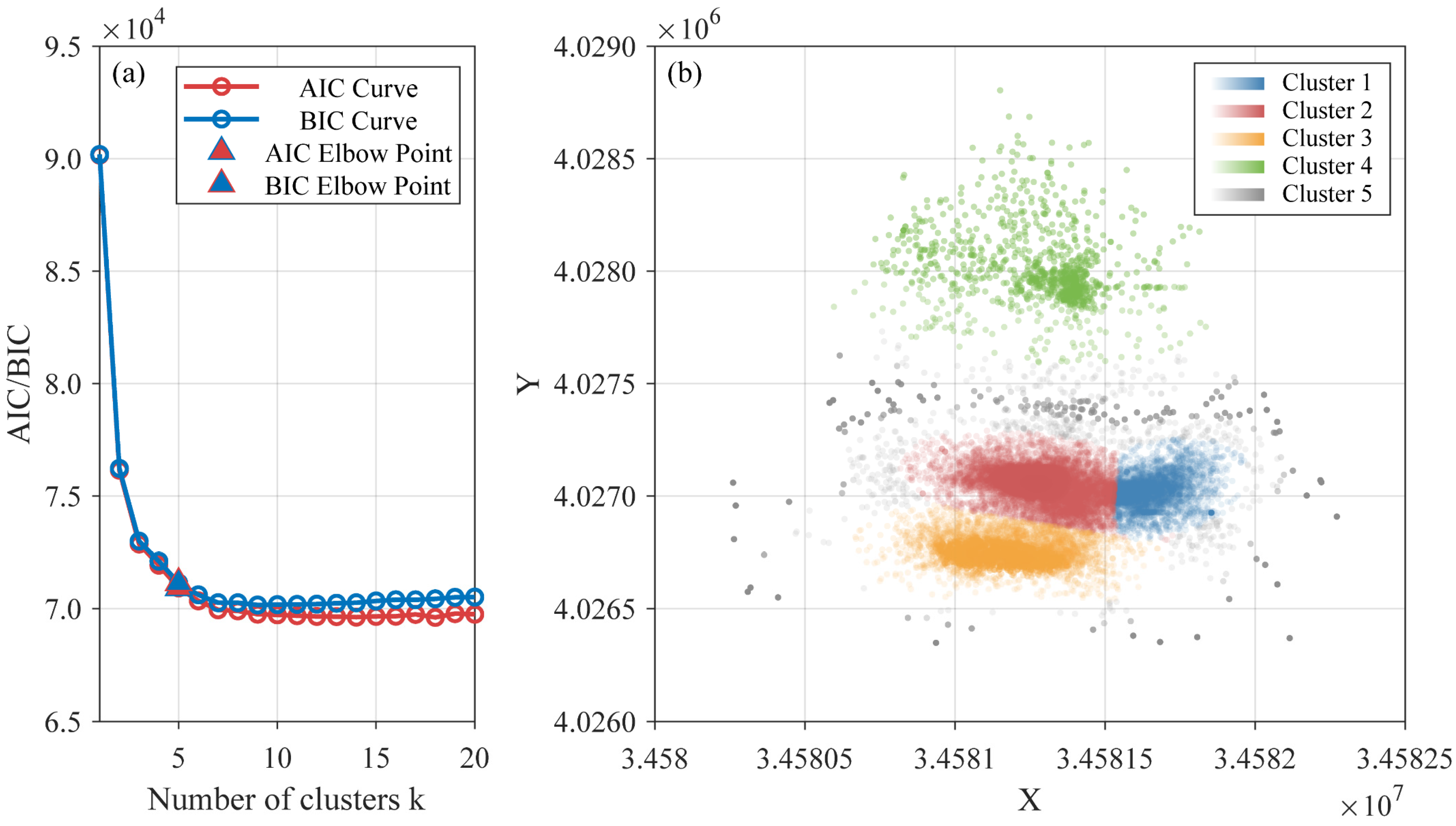
2.2. Clustering Method
2.3. b-Value Estimation Method
3. Results
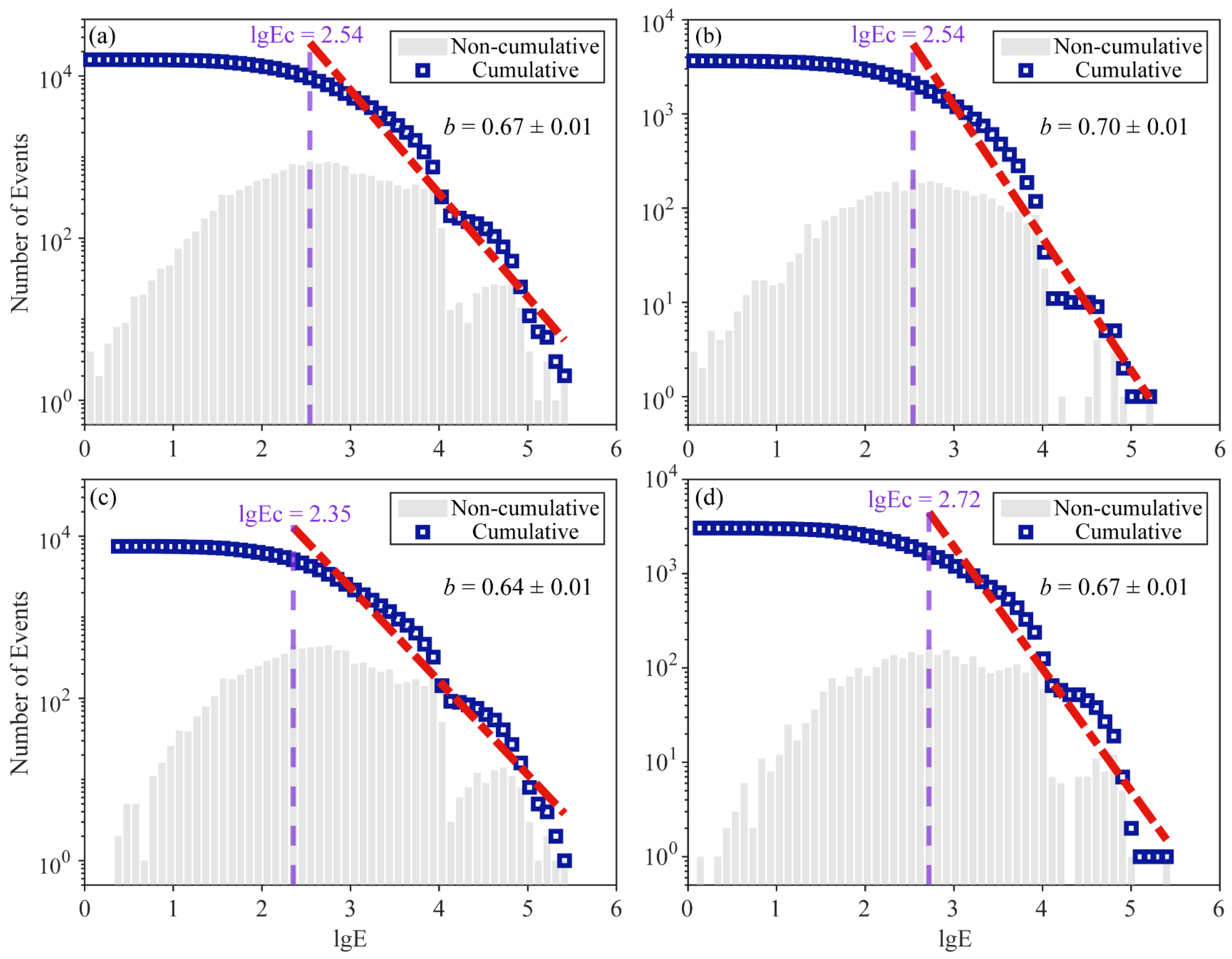
3.1. Spatial Characteristics of b-Values
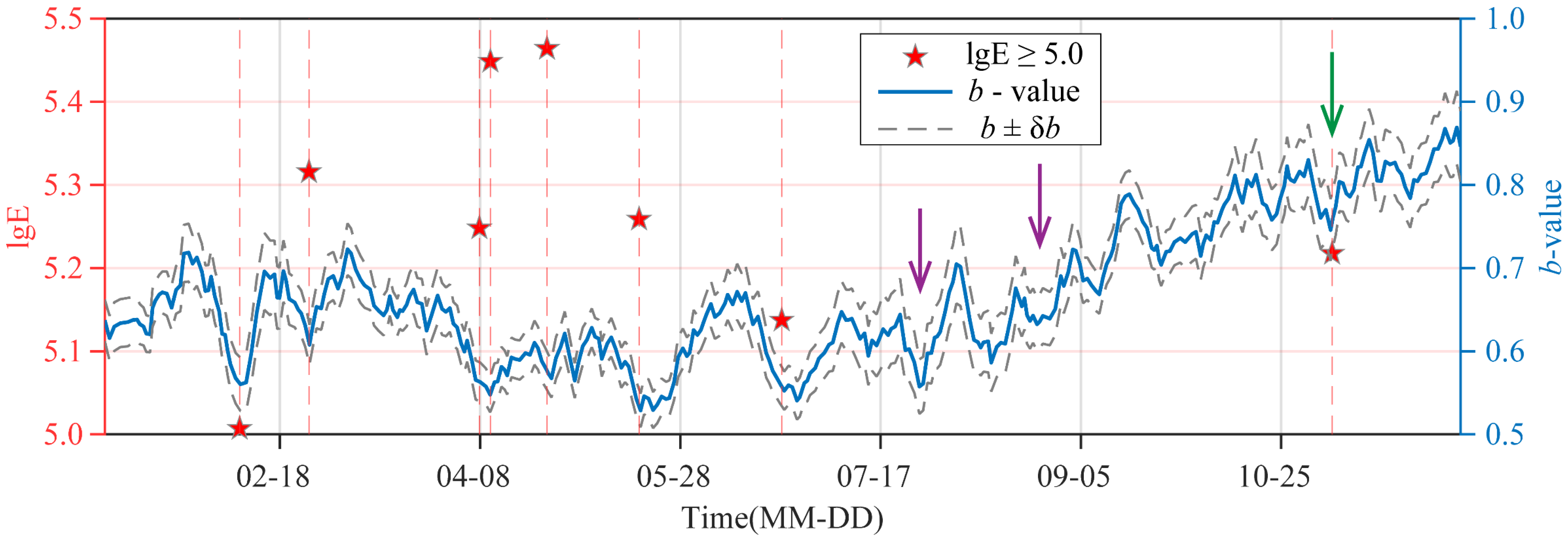
3.2. Temporal Evolution of b-Values
4. Discussion
4.1. Application of Clustering Analysis in b-Value Estimation
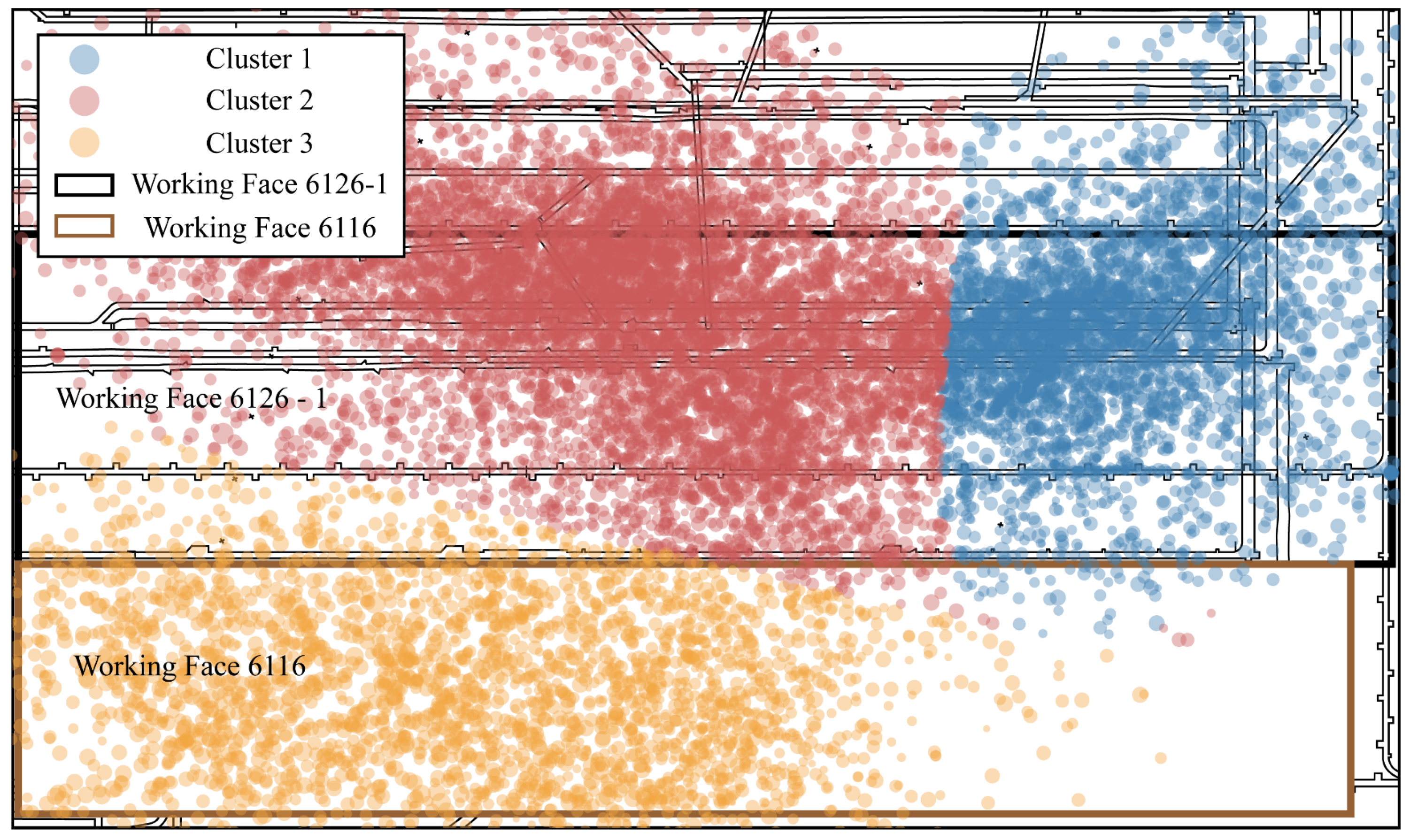
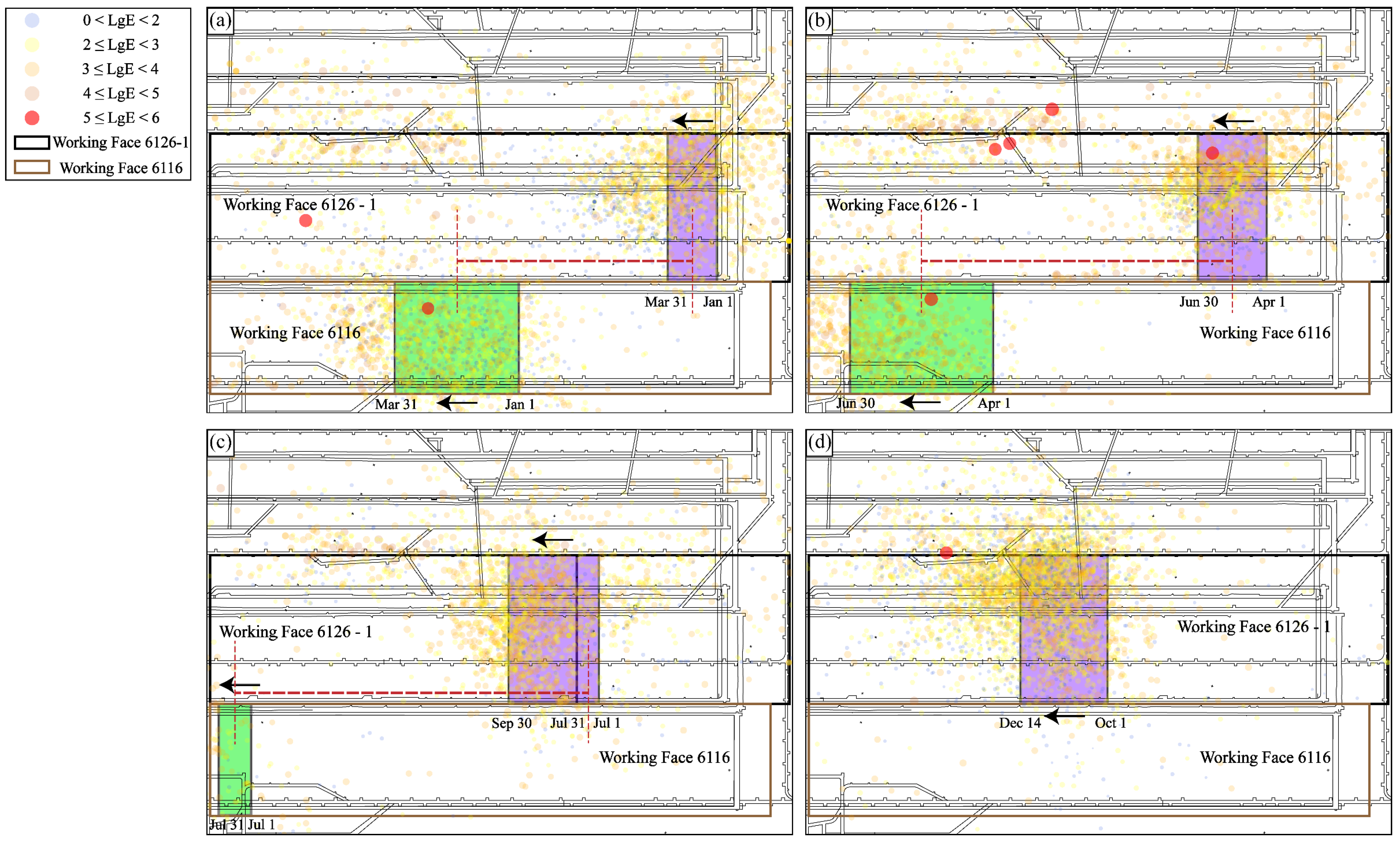
4.2. Spatial Distribution Patterns of Mining-Induced Seismicity
4.3. Challenges in b-Value Interpretation and the Integrated Approach to Hazard Assessment
4.4. Limitations and Future Research Directions
5. Conclusions
- Spatial clustering effectively reveals the heterogeneous distribution of mining-induced seismic hazards. The GMM-based clustering divided the mining area into several regions with distinct stress states, each exhibiting significantly different b-values. Low b-value regions (e.g., Cluster 2 with a b-value of 0.64) indicate areas of high stress concentration and elevated potential for high-energy seismic events, while high b-value regions (e.g., Cluster 1 with a b-value of 0.70) suggest relatively uniform stress release and lower seismic risk. This refined b-value analysis based on clustering overcomes the limitations of uniform b-value estimation across the entire mine and provides a new approach for localized seismic hazard assessment.
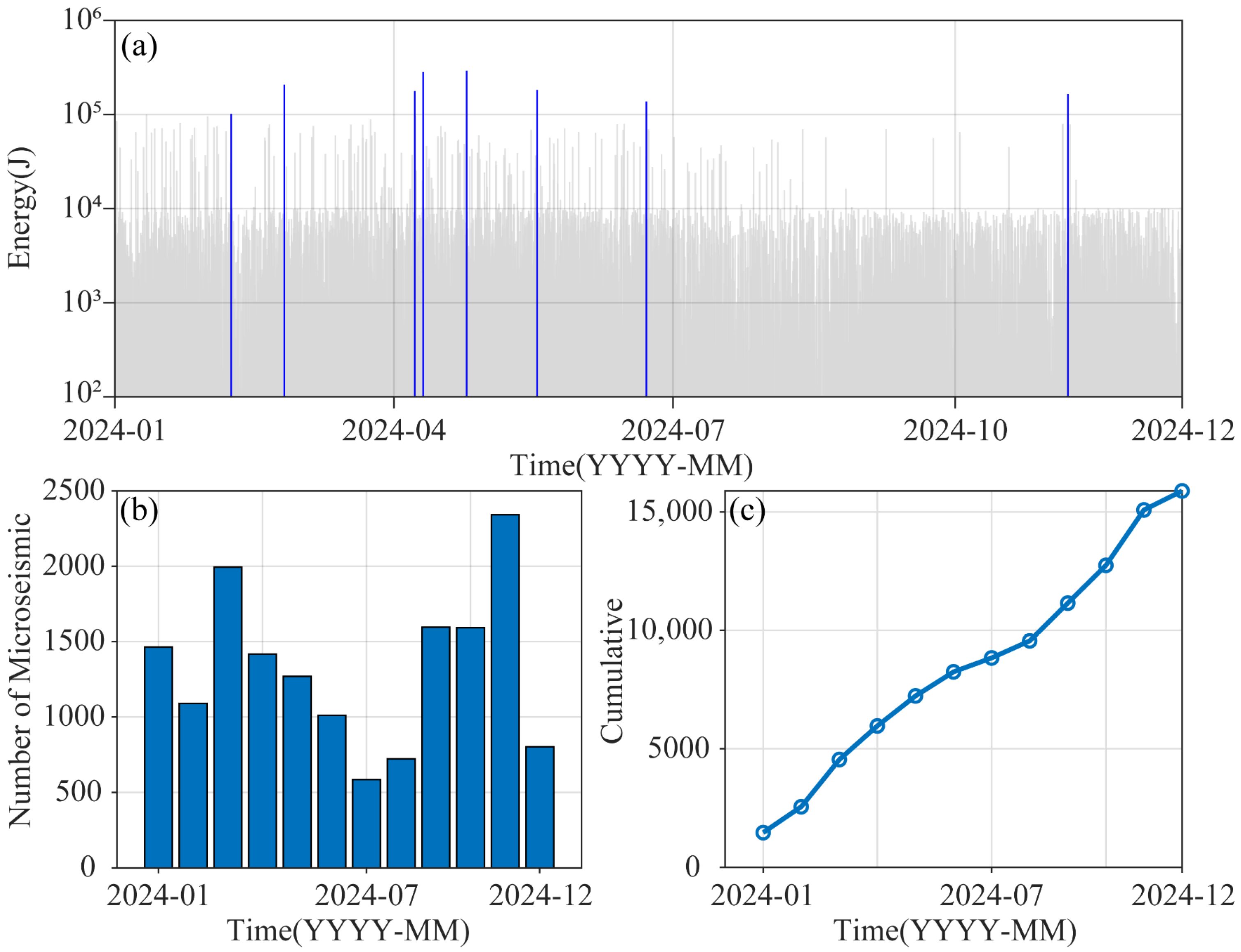
- The temporal evolution of b-values has clear early-warning implications for high-energy seismic events. Sliding window analysis shows that b-values fluctuate within the range of 0.53 to 0.87 in stages. When the b-value sharply dropped to 0.6 or below, the probability of high-energy seismic events significantly increases. Among the eight strong seismic events with lgE greater than 5.0 during the study period, seven occurred when the b-value was below 0.6, all located at troughs in the b-value curve. This cycle of “b-value decline—strong seismic event—b-value recovery” clearly reflects the dynamic process of stress accumulation and release in the mining area, serving as an important indicator for short-term seismic warnings.
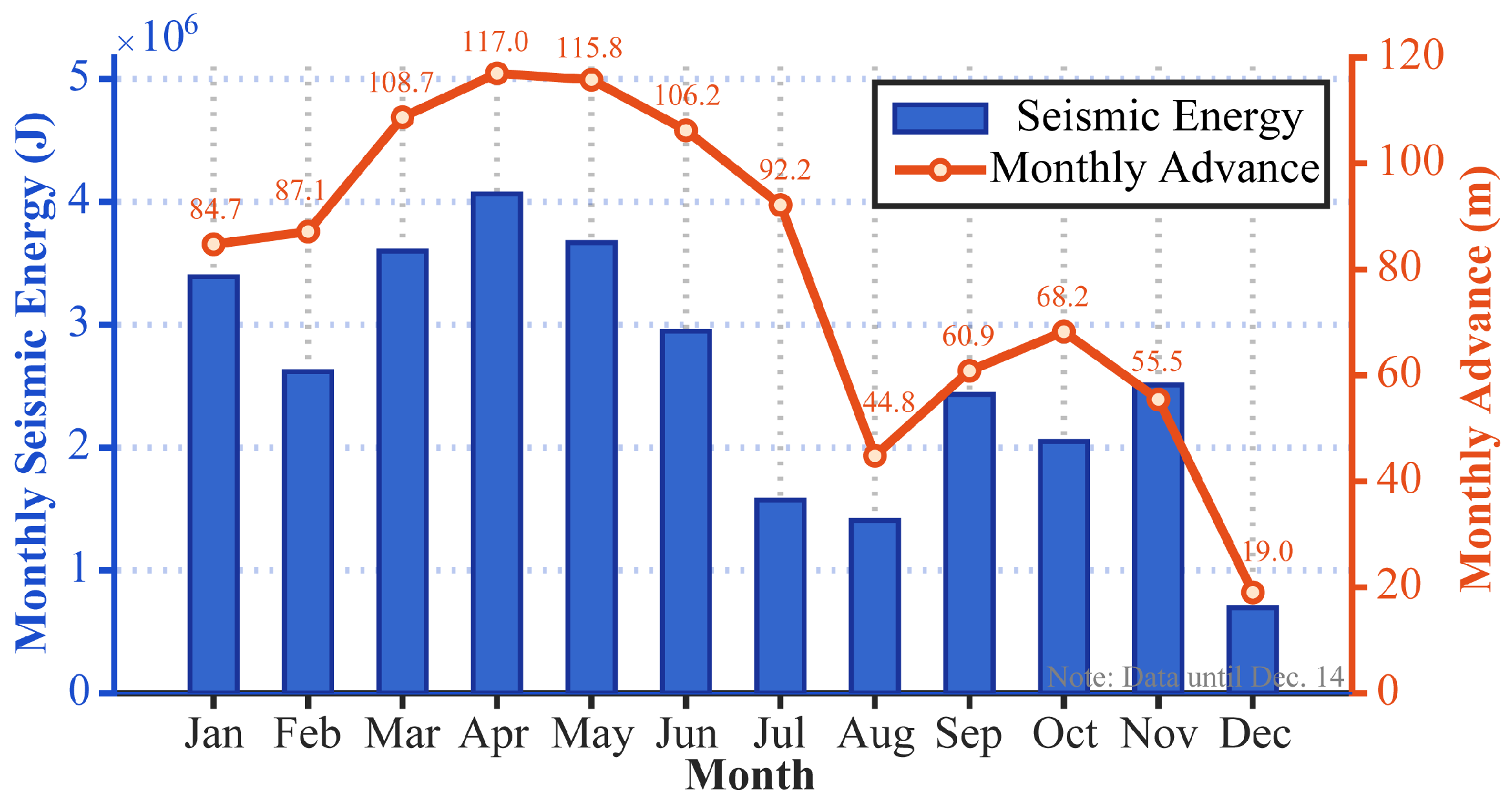
- Mining disturbance is the dominant factor driving mining-induced seismic activity. The spatial migration of seismic events closely follows the advancement of the working faces, and a strong positive correlation is observed between monthly mining progress and monthly seismic energy release. After the cessation of mining at the working face 6116, seismic activity in that area declined markedly, further confirming the controlling effect of mining operations. This understanding suggests that seismic hazard can be mitigated by optimizing mining intensity and advancing rates.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SOS | Seismological Observation System |
| GMM | Gaussian Mixture Model |
| G–R | Gutenberg–Richter |
| EM | Expectation-Maximization |
| AIC | Akaike Information Criterion |
| BIC | Bayesian Information Criterion |
References
- Hudyma, M.; Potvin, Y.H. An engineering approach to seismic risk management in hardrock mines. Rock Mech. Rock Eng. 2010, 43, 891–906. [Google Scholar] [CrossRef]
- Gibowicz, S.J. Seismicity induced by mining. In Advances in Geophysics; Elsevier: Amsterdam, The Netherlands, 1990; Volume 32, pp. 1–74. [Google Scholar]
- Gibowicz, S.J. Seismicity induced by mining: Recent research. Adv. Geophys. 2009, 51, 1–53. [Google Scholar]
- Zhu, J.-B.; Ma, B.-W.; Xie, H.-P.; Gao, F.; Zhou, H.-W.; Zhou, C.-T.; Zheng, F.-R. Differences and connections between mining seismicity and coal bursts in coal mines and preliminary study on coal bursts induced by mining seismicity. J. China Coal Soc. 2022, 47, 3396–3409. [Google Scholar]
- Ayad, A.; Bakkali, S. Economic impact of derangements on mining process—Case study: Sidi Chennane. J. Min. Environ. 2022, 13, 989–996. [Google Scholar]
- Dou, L.-M.; Chen, T.-J.; Gong, S.-Y.; He, H.; Zhang, S.-B. Rockburst hazard determination by using computed tomography technology in deep workface. Saf. Sci. 2012, 50, 736–740. [Google Scholar] [CrossRef]
- Ge, M. Efficient mine microseismic monitoring. Int. J. Coal Geol. 2005, 64, 44–56. [Google Scholar] [CrossRef]
- Yang, C.-X.; Luo, Z.-Q.; Hu, G.-B.; Liu, X.-M. Application of a microseismic monitoring system in deep mining. J. Univ. Sci. Technol. Beijing Miner. Metall. Mater. 2007, 14, 6–8. [Google Scholar] [CrossRef]
- Li, S.-J.; Feng, X.-T.; Li, Z.-H.; Chen, B.-R.; Zhang, C.-Q.; Zhou, H. In situ monitoring of rockburst nucleation and evolution in the deeply buried tunnels of Jinping II hydropower station. Eng. Geol. 2012, 137, 85–96. [Google Scholar] [CrossRef]
- Gutenberg, B.; Richter, C.F. Earthquake magnitude, intensity, energy, and acceleration. Bull. Seismol. Soc. Am. 1942, 32, 163–191. [Google Scholar] [CrossRef]
- Toda, S.; Stein, R.S.; Reasenberg, P.A.; Dieterich, J.H.; Yoshida, A. Stress transferred by the 1995 Mw = 6.9 Kobe, Japan, shock: Effect on aftershocks and future earthquake probabilities. J. Geophys. Res. Solid Earth 1998, 103, 24543–24565. [Google Scholar] [CrossRef]
- Wyss, M.; Sammis, C.G.; Nadeau, R.M.; Wiemer, S. Fractal dimension and b-value on creeping and locked patches of the San Andreas fault near Parkfield, California. Bull. Seismol. Soc. Am. 2004, 94, 410–421. [Google Scholar] [CrossRef]
- Urbancic, T.; Trifu, C.; Long, J.; Young, R. Space-time correlations of b values with stress release. Pure Appl. Geophys. 1992, 139, 449–462. [Google Scholar] [CrossRef]
- Boettcher, M.S.; McGarr, A.; Johnston, M. Extension of Gutenberg-Richter distribution to Mw −1.3, no lower limit in sight. Geophys. Res. Lett. 2009, 36, 1–5. [Google Scholar] [CrossRef]
- Ma, X.; Westman, E.; Slaker, B.; Thibodeau, D.; Counter, D. The b-value evolution of mining-induced seismicity and mainshock occurrences at hard-rock mines. Int. J. Rock Mech. Min. Sci. 2018, 104, 64–70. [Google Scholar] [CrossRef]
- Huang, L.; Zhao, A.-H.; Wu, Q.-J.; Xu, Z.-Y.; Pan, J.-T.; Zhang, F.-X.; Yao, Z.-X. Characteristics of seismic b-value of Changning shale gas region, Sichuan, from a dense seismic array. Acta Seismol. Sin. 2024, 46, 825–843. [Google Scholar]
- Wu, A.-X.; Wu, L.-C.; Liu, X.-H.; Wang, C.-L.; Huang, W.-S.; Zhu, Q.-J. Space-time distribution of microseismic activities in mines. Chin. J. Eng. 2012, 34, 609–613. [Google Scholar]
- Hudyma, M.R. Analysis and Interpretation of Clusters of Seismic Events in Mines; University of Western Australia Perth: Crawley, Australia, 2008. [Google Scholar]
- Cheng, J.-L. Cluster Analysis of Monitoring Data of Coal Mine Microseism. Master’s Thesis, China University of Mining and Technology, Xuzhou, China, 2020. [Google Scholar]
- Luo, F.-Z. Study on Mining Seismic Law of Protective Layeron Deep Giant Thick Coalbed Oil Shale. Master’s Thesis, China University of Mining and Technology, Xuzhou, China, 2023. [Google Scholar]
- Lv, C.-G.; Dou, L.-M.; He, J.; Shan, S.-P.; Liu, B.; Guo, X.-Q. Development and use of SOS microseismic monitoring system at Taoshan coal mine. China Coal 2010, 36, 86–90. [Google Scholar]
- Zhang, P. Research on Prediction Method of Mine Earthquake in Time SEQUENCE based on Clustering Analysis. Master’s Thesis, China University of Mining and Technology, Xuzhou, China, 2023. [Google Scholar]
- Yang, L. Study on the Early Warning of Rockburst Event of a Coal Mine in Hegang Mining Area Based on Mine Earthquake and Microseismic Monitoring. Master’s Thesis, Institute of Engineering Mechanics, China Earthquake Administration, Harbin, China, 2022. [Google Scholar]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. Ser. B (Methodol.) 1977, 39, 1–22. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 2003, 19, 716–723. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Kanamori, H. The energy release in great earthquakes. J. Geophys. Res. 1977, 82, 2981–2987. [Google Scholar] [CrossRef]
- Iwata, T. Estimation of completeness magnitude considering daily variation in earthquake detection capability. Geophys. J. Int. 2013, 194, 1909–1919. [Google Scholar] [CrossRef]
- Shi, X.-Y.; Wang, X.-Q.; Qiu, Y.-R.; Yuan, X.-X. Analysis of the minimum magnitude of completeness for earthquake catalog in China Seismic Experimental Site. Chin. J. Geophys. 2020, 63, 3683–3697. [Google Scholar]
- Wen, S.-L.; Liu, X.-Z.; Qin, M.-Z.; Liu, B.-Y.; Kang, B.-L.; Wu, B.-C. Completeness of the earthquake catalog of the 2023 Jishishan MS6.2 earthquake in Gansu Province. China Earthq. Eng. J. 2024, 46, 924–931. [Google Scholar]
- Woessner, J.; Wiemer, S. Assessing the quality of earthquake catalogues: Estimating the magnitude of completeness and its uncertainty. Bull. Seismol. Soc. Am. 2005, 95, 684–698. [Google Scholar] [CrossRef]
- Aki, K. Maximum likelihood estimate of b in the formula log N= a-bM and its confidence limits. Bull. Earthq. Res. Inst. Tokyo Univ. 1965, 43, 237–239. [Google Scholar]
- Shi, Y.-L.; Bolt, B.A. The standard error of the magnitude-frequency b value. Bull. Seismol. Soc. Am. 1982, 72, 1677–1687. [Google Scholar] [CrossRef]
- Nava, F.; Márquez-Ramírez, V.; Zúñiga, F.; Ávila-Barrientos, L.; Quinteros, C. Gutenberg-Richter b-value maximum likelihood estimation and sample size. J. Seismol. 2017, 21, 127–135. [Google Scholar] [CrossRef]
- Aiken, C.; Meng, X.; Hardebeck, J. Testing for the ‘predictability’of dynamically triggered earthquakes in The Geysers geothermal field. Earth Planet. Sci. Lett. 2018, 486, 129–140. [Google Scholar] [CrossRef]
- Rundle, J.B.; Turcotte, D.L.; Shcherbakov, R.; Klein, W.; Sammis, C. Statistical physics approach to understanding the multiscale dynamics of earthquake fault systems. Rev. Geophys. 2003, 41, 1–30. [Google Scholar] [CrossRef]
- Huang, Q.-H. Seismicity changes prior to the Ms8. 0 Wenchuan earthquake in Sichuan, China. Geophys. Res. Lett. 2008, 35, 1–5. [Google Scholar] [CrossRef]
- Wen, X.-Z.; Ma, S.-L.; Xu, X.-W.; He, Y.-N. Historical pattern and behavior of earthquake ruptures along the eastern boundary of the Sichuan-Yunnan faulted-block, southwestern China. Phys. Earth Planet. Inter. 2008, 168, 16–36. [Google Scholar] [CrossRef]
- Mousavi, S.M.; Ogwari, P.O.; Horton, S.P.; Langston, C.A. Spatio-temporal evolution of frequency-magnitude distribution and seismogenic index during initiation of induced seismicity at Guy-Greenbrier, Arkansas. Phys. Earth Planet. Inter. 2017, 267, 53–66. [Google Scholar] [CrossRef]
- Maity, D.; Ciezobka, J. Using microseismic frequency-magnitude distributions from hydraulic fracturing as an incremental tool for fracture completion diagnostics. J. Pet. Sci. Eng. 2019, 176, 1135–1151. [Google Scholar] [CrossRef]
- Zorn, E.; Kumar, A.; Harbert, W.; Hammack, R. Geomechanical analysis of microseismicity in an organic shale: A West Virginia Marcellus Shale example. Interpretation 2019, 7, T231–T239. [Google Scholar] [CrossRef]
- Woodward, K.; Wesseloo, J.; Potvin, Y. A spatially focused clustering methodology for mining seismicity. Eng. Geol. 2018, 232, 104–113. [Google Scholar] [CrossRef]
- MacQueen, J. Some methods for classification and analysis of multivariate observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability; University of California Press: Oakland, CA, USA, 1967; Volume 1, pp. 281–298. [Google Scholar]
- Ester, M.; Kriegel, H.-P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the KDD; AAAI Press: Menlo Park, CA, USA, 1996; pp. 226–231. [Google Scholar]
- Novianti, P.; Setyorini, D.; Rafflesia, U. K-Means cluster analysis in earthquake epicenter clustering. Int. J. Adv. Intell. Inform. 2017, 3, 81–89. [Google Scholar] [CrossRef]
- Irwansyah, E.; Winarko, E. Spatial data clustering and zonation of earthquake building damage hazard area. EPJ Web Conf. 2014, 68, 00005. [Google Scholar] [CrossRef]
- Cesca, S. Seiscloud, a tool for density-based seismicity clustering and visualization. J. Seismol. 2020, 24, 443–457. [Google Scholar] [CrossRef]
- Wang, J.; Zuo, Y.-Y.; Dong, L.-J.; Yan, X.-H. Spatiotemporal clustering of microseismic signals in mining areas: A case study of the Baoji lead-zinc mine in Shaanxi, China. Eng. Geol. 2025, 352, 108057. [Google Scholar] [CrossRef]
- Wojtecki, Ł.; Pakosz, R.; Apel, D.B.; Mendecki, M.J. Variability and Trends in Selected Seismological Parameters During Longwall Mining of a Coal Seam Disrupted by a Rockburst. Appl. Sci. 2025, 15, 8897. [Google Scholar] [CrossRef]
- Ma, S.-L.; Zhang, M.-W.; Ma, L.; Tian, Z.-C.; Li, X.; Su, Z.-H. Numerical simulation study on the evolution characteristics of the stress induced by mining in deep adjacent working faces. Geoenviron. Disasters 2023, 10, 17. [Google Scholar] [CrossRef]
- Zhou, K.-Y.; Deng, Z.; Kan, J.-L.; Dou, L.-M.; Li, J.-Z.; Duan, M.-K.; Kong, P. Determination of the advanced mining influence range in coal mines based on the statistical analysis of mining-induced seismicity. Appl. Sci. 2024, 14, 7737. [Google Scholar] [CrossRef]
- Das, R.; Das, A. Limitations of Mw and M Scales: Compelling evidence advocating for the das magnitude scale (Mwg)—A critical review and analysis. Indian Geotech. J. 2025, 1–19. [Google Scholar] [CrossRef]
- Das, R.; Sharma, M.L.; Wason, H.R.; Choudhury, D.; Gonzalez, G. A seismic moment magnitude scale. Bull. Seismol. Soc. Am. 2019, 109, 1542–1555. [Google Scholar] [CrossRef]

| Energy Range (J) | Number of Events | Percentage (%) |
|---|---|---|
| <101 | 182 | 1.15 |
| 101–102 | 2732 | 17.20 |
| 102–103 | 7750 | 48.79 |
| 103–104 | 5010 | 31.54 |
| 104–105 | 202 | 1.27 |
| >105 | 8 | 0.05 |
| Cluster | Number of Events | b-Value | lgEC | Average Energy (J) | Events > 105 J |
|---|---|---|---|---|---|
| Entire mine | 15,884 | 0.67 | 2.54 | 1948.45 | 8 |
| 1 | 3660 | 0.70 | 2.54 | 1437.79 | 1 |
| 2 | 7474 | 0.64 | 2.35 | 1859.83 | 5 |
| 3 | 3041 | 0.67 | 2.72 | 2575.94 | 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Wang, J.; Yin, X.; Liang, X. Quantitative Hazard Assessment of Mining-Induced Seismicity Using Spatiotemporal b-Value Dynamics from Microseismic Monitoring. Appl. Sci. 2025, 15, 10073. https://doi.org/10.3390/app151810073
Wang H, Wang J, Yin X, Liang X. Quantitative Hazard Assessment of Mining-Induced Seismicity Using Spatiotemporal b-Value Dynamics from Microseismic Monitoring. Applied Sciences. 2025; 15(18):10073. https://doi.org/10.3390/app151810073
Chicago/Turabian StyleWang, Hao, Jianjun Wang, Xinxin Yin, and Xiaonan Liang. 2025. "Quantitative Hazard Assessment of Mining-Induced Seismicity Using Spatiotemporal b-Value Dynamics from Microseismic Monitoring" Applied Sciences 15, no. 18: 10073. https://doi.org/10.3390/app151810073
APA StyleWang, H., Wang, J., Yin, X., & Liang, X. (2025). Quantitative Hazard Assessment of Mining-Induced Seismicity Using Spatiotemporal b-Value Dynamics from Microseismic Monitoring. Applied Sciences, 15(18), 10073. https://doi.org/10.3390/app151810073





