Deep Neural Network-Based Alignment of Virtual Reality onto a Haptic Device for Visuo-Haptic Mixed Reality

Abstract

Precise alignment between virtual reality (VR) and haptic interfaces is essential for delivering an immersive visuo-haptic mixed reality experience. Existing methods typically depend on markers, external trackers, or cameras, which can be intrusive and hinder usability. In addition, previous network-based approaches generally rely on image data for alignment. This paper introduces a deep neural network-based alignment method that eliminates the need for such external components. Unlike existing methods, our approach is designed based on coordinate transformation and leverages a network model for alignment. The proposed method utilizes the head-mounted display (HMD) position, fingertip position obtained via hand tracking, and the six-degrees-of-freedom (6-DOF) pose of a haptic device’s end-effector as inputs to a neural network model. A shared multi-layer perceptron and max pooling layer are employed to extract global feature vectors from the inputs, ensuring permutation invariance. The extracted feature vectors are then processed through fully connected layers to estimate the pose of the haptic device’s base. Experimental results show a mean positional error of 2.718 mm and the mean rotation error of 0.5330°, which equates to 1.3% relative to the haptic device’s maximum length. The proposed method demonstrates robustness against noise, demonstrating its applicability across various domains, including medical simulations, virtual prototyping, and interactive training environments.

1. Introduction

The rapid advancement of head-mounted display (HMD) devices has enabled the development of diverse applications that facilitate interaction with virtual objects through haptic devices in virtual reality (VR) and augmented reality (AR) [1,2,3,4]. In the interactive simulations, virtual objects and the HMD are positioned based on the world coordinate system defined within the virtual reality. When the user moves their head, the HMD’s pose in the world coordinate system is updated accordingly. An image of the virtual scene is generated using the HMD’s pose and a virtual camera and presented to the user. As a result, the user perceives virtual objects as if the objects were situated directly in front of them. Similarly, a haptic device must be spatially aligned in the same world coordinate system of virtual reality to enable interaction between the user in the real world and virtual objects in virtual reality. Estimating the six-degrees-of-freedom (6-DOF) of a haptic device is, therefore, essential for spatial alignment. Misalignment between the virtual environment and the haptic device can substantially affect users’ perception of stiffness [5]. This issue is particularly critical in applications where haptic feedback is essential, such as medical training simulations. In such cases, perceptual inconsistencies—referred to as cognitive stiffness distortion—can lead to incorrect stiffness perception, ultimately diminishing the effectiveness of the training [6]. However, existing methods for aligning haptic devices with virtual environments often rely on external trackers, cameras, or external markers, which can limit system portability and usability. Moreover, few studies have researched markerless approaches that estimate the 6-DOF pose of a haptic device. The kinematics of robots or those estimated from images are primarily utilized. However, the application may be limited depending on the image resolution and the availability of the robot’s kinematic data. This paper proposes an alignment method without relying on additional hardware or markers.

Several methods have been proposed to align virtual reality on haptic devices precisely using manufacturer-provided controllers or hand-tracking systems [7]. This method can be used when the manufacturer supports the required functionalities. The accuracy of hand-tracking approaches relies on hand size and shape, and delays in recognizing hand movements. Controller-based approaches may introduce errors due to variations in movement speed and rotation direction. Alternatively, alignment can be achieved through external tracking systems, such as QR codes, magnetic trackers, or camera-based external trackers, rather than using the HMD’s internal tracking controller or hand tracking functionality [8,9,10,11,12,13,14]. Hibiki et al. proposed a calibration approach that combines a fiducial marker with a depth camera to align the MR coordinate system with a robot coordinate system [13]. Shao et al. developed a marker-based calibration method using feature points extracted from point cloud data to register physical and virtual objects [14]. Despite their usefulness, these approaches increase system volume and depend heavily on accurate physical marker detection. Marker tracking is sensitive to environmental factors, such as lighting changes and occlusions, and often fails under such conditions. Furthermore, they are unsuitable when markers cannot be attached due to object size, material, or safety concerns.

CNN-based solutions, such as HoloYolo, have been introduced [15] to overcome the limitations of marker-based systems. However, CNN-based alignment methods have a problem in that the estimation accuracy is highly dependent on the resolution of the input image because the estimation relies on the image resolution. Additionally, such methods may fail to detect the target object for alignment in cases where it is occluded, lacks sufficient visual contrast, or is not clearly distinguishable in the image. 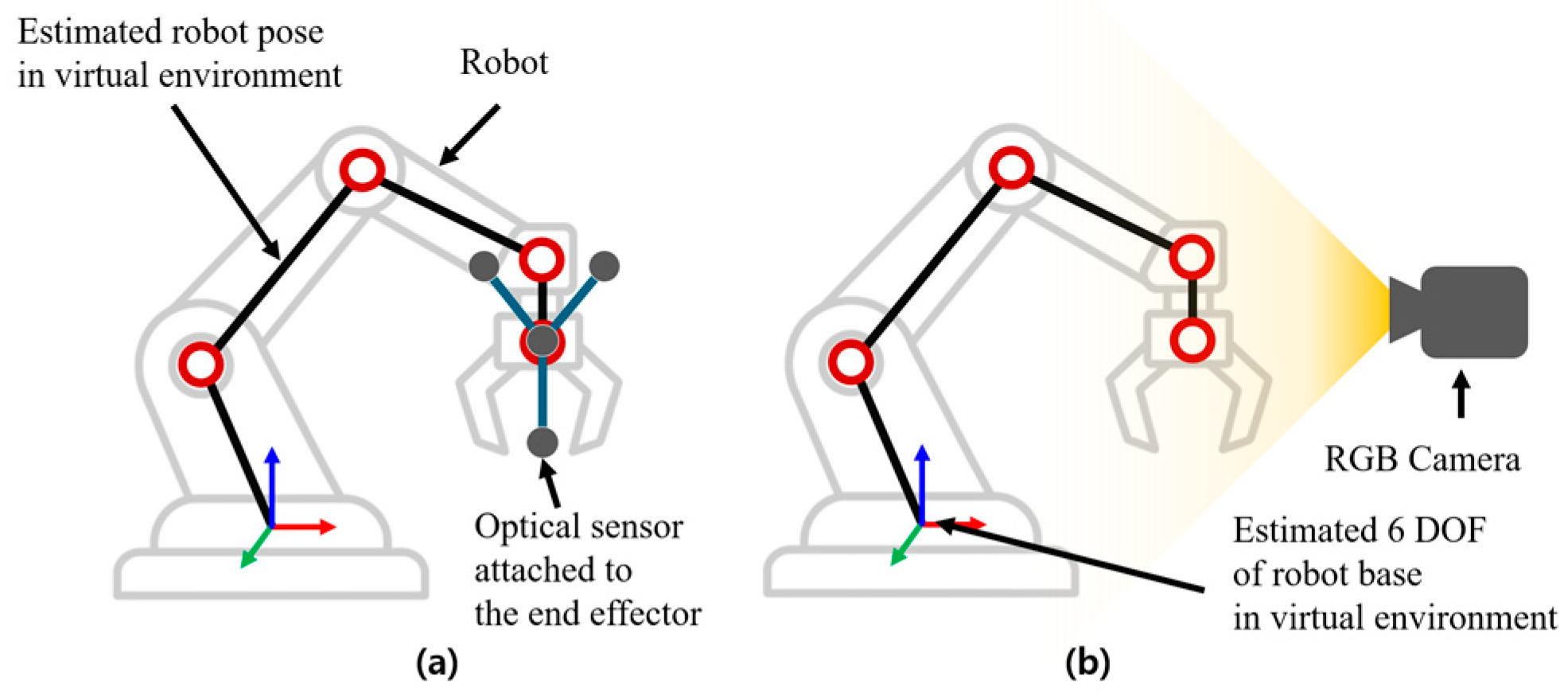Methods using the kinematics of a robot arm for alignment have also been proposed (Figure 1) [16,17,18]. However, these methods require precise robot arm kinematics, making them difficult to apply to soft actuators. Despite using kinematic models, they still depend on external sensors or camera images. Additionally, even with known kinematics, estimating the 6-DOF pose of the robot base relative to the HMD remains necessary.

Yang et al. analyzed the causes of misregistration between a virtual environment and physical environment in Video See Through (VST) AR and proposed a transformation matrix-based correction method to address the misregistration [19]. All components, including HMD, camera, virtual object, and robot, are transformed and aligned within a common world coordinate system. One limitation of this study is the lack of analysis on how alignment accuracy is affected by the depth of the target within the user’s view. Points within the shared workspace may exhibit varying alignment errors depending on their spatial location. Previous studies on visuo-haptic alignment have predominantly relied on external tracking systems or fiducial markers, with limited exploration of markerless, vision-based approaches that can seamlessly integrate with robotic kinematic information.

A study has compared various augmented reality systems used in actual surgical applications [20]. The study analyzed registration errors in surgeries utilizing HMDs and AR technologies. A total of 15 studies were reviewed, focusing on three types of registration methods: pattern marker, surface marker, and manual alignment. Differences in the generation of the HMD devices used—specifically variations in HoloLens hardware specifications—further complicate direct comparison.

This paper presents a neural network-based alignment method for visuo-haptic mixed reality that can align the virtual reality onto a haptic device without the need for external markers. The network model is designed based on the concept of coordinate transformation, rather than performing direct coordinate transformations. Moreover, the network-based method improves accessibility by eliminating the need for additional equipment such as markers or external cameras. The network model uses input data composed of the HMD’s position, the fingertip position acquired via hand tracking, and the end-effector position of the haptic device. The network model accepts between six and nine inputs to enhance robustness against noise introduced by hand tracking errors. The network model then extracts feature vectors from these inputs to estimate the 6-DOF pose of the haptic device’s base. The network model reliably estimates the pose of the haptic device’s base and enables accurate alignment of virtual reality onto a haptic device by utilizing the user’s multiple inputs. The proposed approach is limited by its reliance on a QR code for ground truth acquisition during training. Once the training data is acquired, the QR code is not required during actual use. Crucially, the alignment process is performed only once during initialization. During these steps, the user wearing the HMD is required to look at the fingertip of the hand holding the haptic device’s pen. After the initial alignment, the user can operate freely without looking at the fingertip.

Section 2.1 defines the coordinate systems, while Section 2.2 details the network model architecture. Section 2.3 and Section 2.4 describe the data collection and generation process used for training. Section 3 presents the training procedure and experiment. The analyses of the experimental results are described in Section 4.

2. Method

The proposed method is based on the following idea: when a user starts VR by wearing HMD, the HMD is initialized at the origin of the VR world coordinate system. As a result, the pose of the HMD is known with respect to the world coordinate system. The pose of the haptic device can be estimated in the world coordinate system by applying sequential transformations from the HMD to the fingertip, pen, and ultimately to the haptic device. 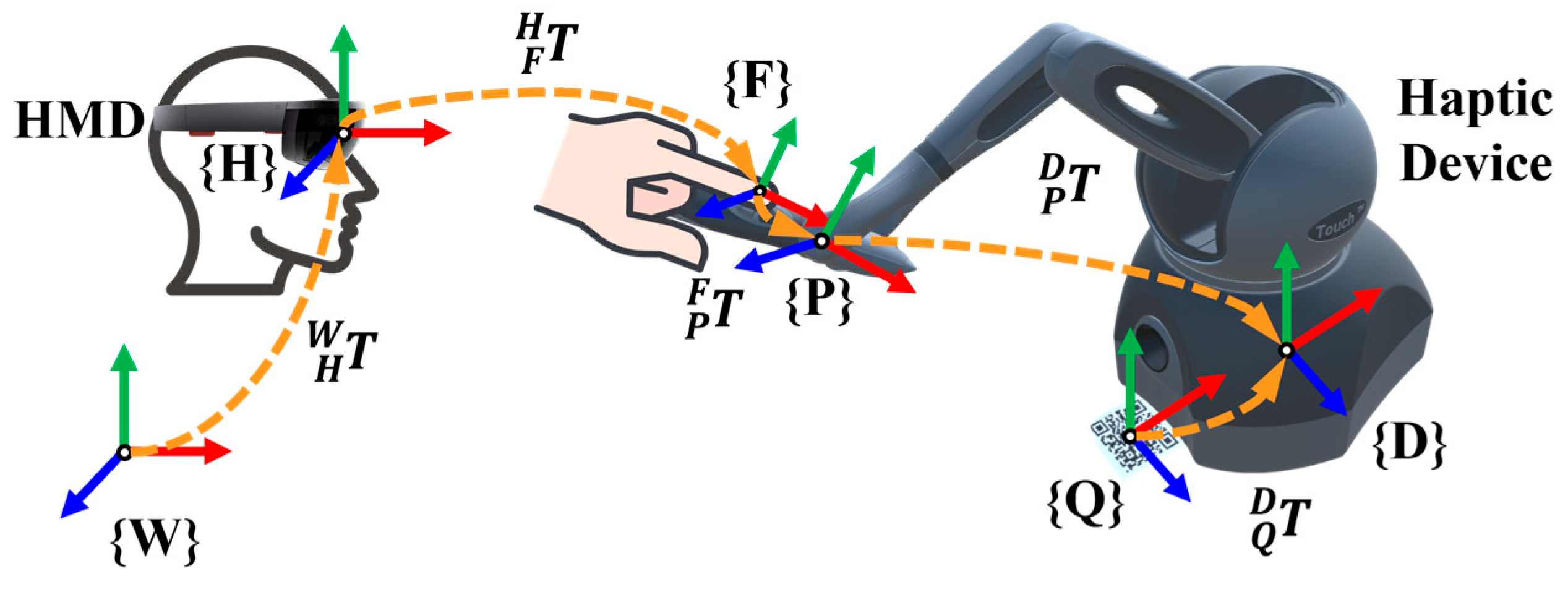When a user holds and manipulates the haptic device’s pen as shown in Figure 2, the tip of the user’s index finger remains fixed at a specific position on the pen. Users are instructed to press a designated button on the pen to give an input while maintaining consistent finger placement. Consequently, as long as the relative rotation between the fingertip and the pen remains constant, the pose of the haptic device’s pen can be estimated by the fingertip’s pose using the HMD’s tracking functionality. The 6-DOF pose of the haptic device’s base can then be estimated by referencing the pen’s pose in the device’s coordinate system. However, a remarkable challenge arises from the individual variability in how users grab the pen. While the fingertip may be fixed at the button location, the relative rotation between the fingertip and the pen often varies across users. This variability introduces inconsistencies that limit the effectiveness of deterministic kinematic approaches for accurately estimating the device’s pose.

We present a network model designed to estimate the 6-DOF pose of a haptic device’s base using the position of the HMD, the fingertip position, and the 6-DOF pose of the pen relative to the haptic device’s base.

2.1. Coordinate System

Figure 2 shows all coordinate systems and transformation matrices. The coordinate systems {W}, {H}, and {D} represent the virtual reality world, the HMD, and the haptic device, respectively. The coordinate systems {F}, {P}, and {Q} correspond to the fingertip, the haptic device’s pen, and the QR code. Coordinate transformations enable alignment of the virtual reality onto the haptic device without external sensors, as shown in Figure 2. The transformation matrix from world coordinate {W} to the haptic device coordinate {D}, denoted as ${}_D{}^{W}T$, can be computed by:

$${}_D{}^{W}T={}_H{}^{W}T\ast {}_F{}^{H}T\ast {}_P{}^{F}T\ast {}_D{}^{P}T$$

(1)

However, the transformation matrix ${}_P{}^{F}T$ varies depending on the user’s grip due to differences in fingertip angles, making it impossible to fix in advance. Additionally, this method is susceptible to noise from hand-tracking [21]. To overcome these challenges, we utilize a neural network model that compensates for hand-tracking noise and the variability in relative rotation between the fingertip and the pen. The network model estimates the 6-DOF pose of the haptic device’s base in the {W}, despite the presence of hand-tracking noise and relative rotation inconsistencies.

2.2. Network Model

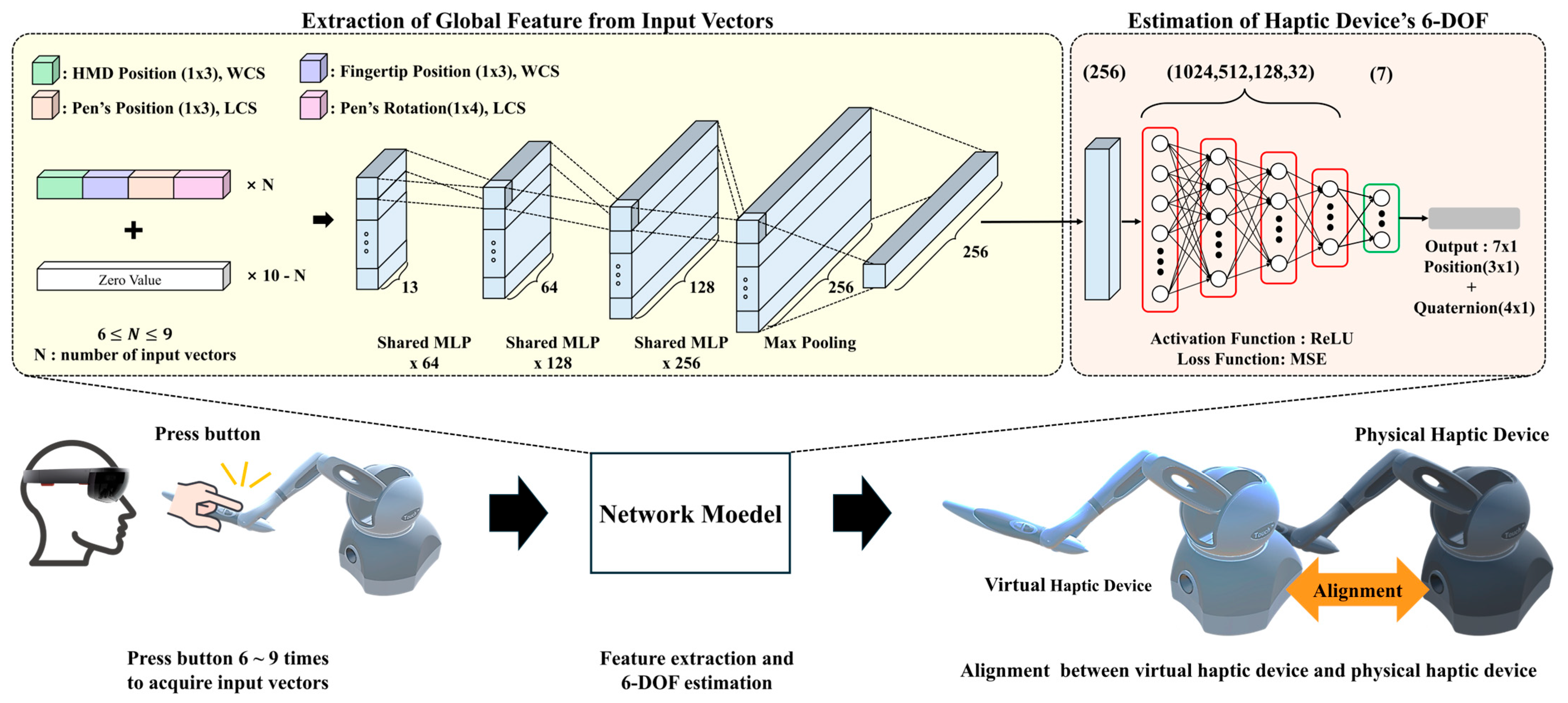
This paper proposes a neural network-based approach for estimating the 6-DOF pose of a haptic device’s base under conditions where the relative rotation between the fingertip and the pen is not consistent. The network model uses shared-MLPs and a DNN composed of fully connected layers and ReLU activations. The detailed parameters, such as the number of layers, were set based on those that yielded the best experimental results. The overall flow and structure of the network model are shown in Figure 3. The network model uses vertical concatenation between 6 and 9 input vectors to robustly estimate the 6-DOF pose of the haptic device’s base under conditions of limited transformation and high noise on acquired fingertip data. When the user presses the button on the haptic device’s pen, an input vector (1 × 13) is collected. This vector includes the position of the HMD (1 × 3), the position of the fingertip (1 × 3) in the world coordinate system, and the 3-DOF position and quaternion of the pen relative to the haptic device’s base (1 × 7), as shown in Figure 3. Also, the dimension of the input vector $x$ can be represented by the following equation:

$$x=\left[P_{HMD}, P_{Finger}, P_{Pen}, Q_{Pen}\right]\in {\mathbb{R}}^{1\times 13}$$

(2)

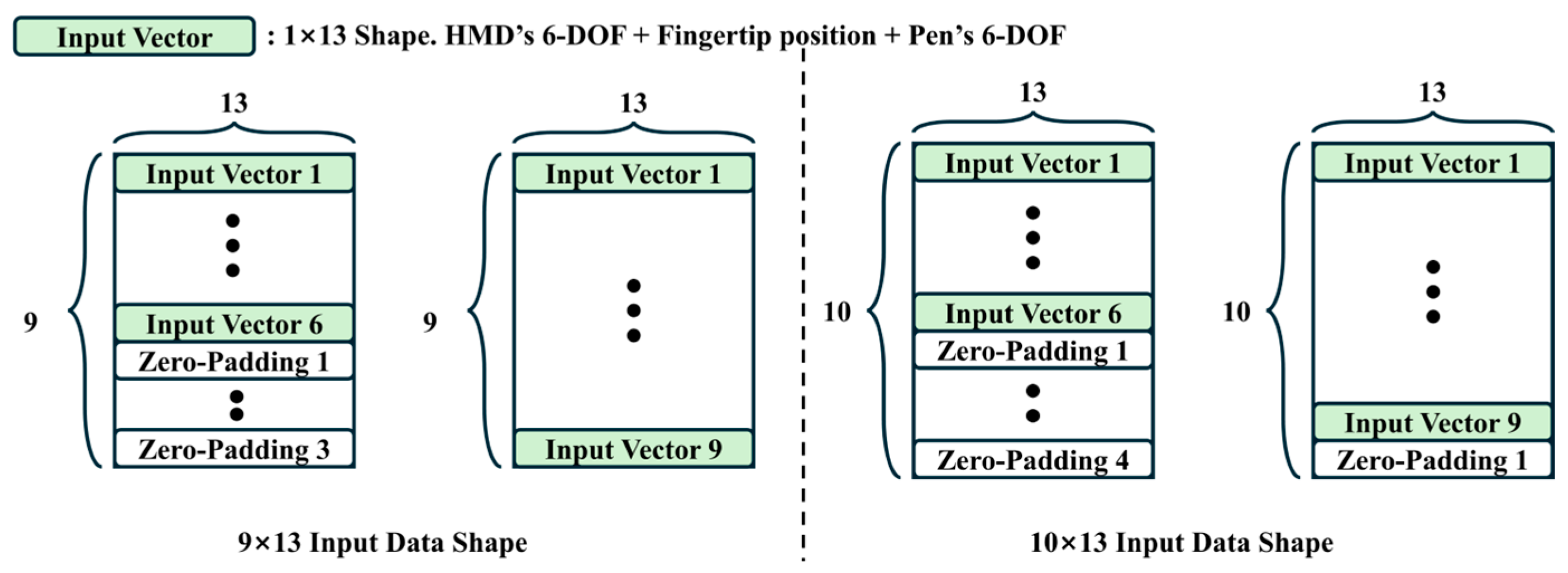
where $P$ and $Q$ are position and quaternion, respectively. As shown in the upper left part of Figure 2, a set of N input vectors (where 6 ≤ N ≤ 9) is vertically concatenated with (10-N) zero-padding vectors to form a single input data, which is then used as the input to the network. The value of N is randomly set between 6 and 9 during data generation, and the N is determined by how many times the user presses the button to acquire input vectors in practical use.

The rotation of HMD is excluded from the input, since the rotation of the HMD is already included during the coordinate transformation from the world to the fingertip. The rotation of the fingertip is also omitted due to inconsistencies in its relative rotation concerning the pen.

In this study, we compensate for the lack of rotation of a fingertip by utilizing multiple inputs. The network model is trained to estimate the 6-DOF pose of the haptic device’s base using various input vectors, including user’s fingertip position, HMD position, and the pen’s 6-DOF pose data. The network model takes more than 6 inputs to compensate for the limited rotation information. Furthermore, the fingertip pose data, acquired via image sensors and tracking systems, are inherently noisy [21]. Relying on only concatenation of 6 vectors to estimate the 6-DOF pose of the haptic device’s base increases the system’s sensitivity to this noise.

The presented approach mitigates the effects of sensor noise and the absence of fingertip rotation by utilizing 6 or more input vectors, offering flexibility in the number of input vectors. The minimum number of input vectors is set to 6 because estimating the 6-DOF pose requires at least 6 values. Although the current implementation uses a maximum of 9 input vectors, the architecture can be extended to accommodate additional input vectors if needed. The network model utilizes a vertical concatenation of 6 to 9 input vectors of size 1 × 13 as input data. Since the number of input vectors varies, the input dimensionality is inconsistent (Figure 4). To standardize the input data’s dimension, zero-padding is applied, filling the empty space with zeros. If the maximum dimension is set to 9 × 13, zero-padding is not applied in the case of 9 vectors, which introduces inconsistency in data representation compared to fewer vectors. These variations can lead to unstable training behavior, as the model may learn to treat padded and unpadded inputs differently (Figure 4).

These inconsistencies can negatively impact model training. To ensure uniformity and improve training stability, the input data’s dimension is fixed at 10 × 13, one row larger than the maximum number of input vectors, thereby enforcing consistent zero-padding across all cases. The dimension of input data can be represented as the following equation:

$$\begin{gathered} X_{input}={\left[x_1^T,x_2^T, \dots , x_N^T, {\mathbb{O}}_1^T, {\mathbb{O}}_2^T, \dots , {\mathbb{O}}_{10-N}^T\right]}^T\in {\mathbb{R}}^{10\times 13}, \\ where 6\le N\le 9,{\mathbb{O}}_i\in {\mathbb{R}}^{1\times 13} \end{gathered}$$

(3)

The input data is a vertical concatenation of unordered input vectors of size 1 × 13, similar to point cloud data. Since there are N! possible permutations for N vectors, where N denotes the number of used input vectors, the same set of input vectors can result in N! different concatenation orders. This variation can result in different estimation accuracy depending on the order and degrade network performance. To address this issue, we adopt the shared multi-layer-perceptron (shared-MLP) structure and max pooling from PointNet [22]. The shared-MLP and max-pooling are employed to capture features of input vectors consistently and achieve the permutation invariance of input vectors, respectively. This architecture enables the model to achieve permutation invariance, making it robust to the ordering of input vectors.

The network model comprises two main components: a feature extraction part that derives a global feature vector from the input data and an estimation part that estimates the 6-DOF pose of the haptic device’s base using the extracted feature vectors (Figure 3). The feature extraction part of the network model processes the input data, which is reshaped to 10 × 13 × 1, to extract a global feature. The reshaped input data first passed through a series of shared-MLP. Each shared-MLP layer applies the same MLP to each input vector of the input data. The first, second, and third layers use 64, 128, and 256 units, respectively, expanding each 13-dimensional input vector to a 256-dimensional representation. This results in a 10 × 256 feature map. Next, a max pooling layer with a pooling of size 10 × 1 is applied column-wise (i.e., along the vertical axis, as vectors are stacked vertically) to aggregate the features, producing a global feature vector regardless of the order of the vectors. This output is then flattened into a 1 × 256 vector for the pose estimation.

The estimation network model has the structure of a fully connected network model and consists of a total of 5 dense layers. The dense layers consist of one input layer, three hidden layers, and one output layer in sequence. The ReLU activation function is applied to all layers except the output layer. The first dense layer is an input layer with 1024 neurons and receives the 1 × 256 input vector. The subsequent hidden layers contain 512, 128, and 32 neurons, respectively. The final layer is an output layer with seven neurons that outputs positions ($x,y,z$) and rotations in quaternion form ($q_w,q_x,q_y,q_z$). Loss is defined as the error between the estimated pose of the haptic device’s base and ground truth:

$$\begin{gathered} L={\displaystyle \frac{1}{N}}{\sum }_i^N{\left({\widehat{y}}_{estimated,i}-y_{ground turth,i}\right)}^2, \mathrm{where} N \mathrm{is} \mathrm{the} \mathrm{number} \mathrm{of} \mathrm{input} \mathrm{data}, \\ {y}_{ground truth},{\widehat{y}}_{estimated}=[x_{position}, y_{position}, z_{position}, q_w, q_x, q_y, q_z] \end{gathered}$$

(4)

2.3. Data Collection

It is essential to acquire both input data and the ground truth representing the 6-DoF pose of the haptic device’s base for training the network model. Leveraging the spatial awareness functionality of the HoloLens 2 (Microsoft, Redmond, Washington, DC, USA), we measured the position of the HMD and the user’s fingertip within the world coordinate system of the virtual reality. Simultaneously, the 6-DOF pose of the pen relative to the local coordinate system of a haptic device is obtained within the haptic device’s coordinate system.

We acquired a large number of vectors and corresponding ground truth to generate training data. From the acquired data, sequences of 6, 7, 8, and 9 concatenated vectors were generated for both training and validation. The 6-DOF pose of the pen relative to the haptic device’s base, the position of the HMD, and the position of the user’s index fingertip in the world coordinates are periodically sampled while the user manipulates the pen in various poses.

The 6-DOF pose of the haptic device’s base in world coordinates is used as the ground truth. The HoloLens 2’s QR code tracking functionality is employed, using a transformation matrix ${}_D{}^{Q}T$ to compute the 6-DOF pose of the haptic device’s base. A custom mounting plate was 3D printed to maintain the relative position between the QR code and the haptic device (Figure 2). After fixing the haptic device and QR code on the plate, HoloLens 2 captures the QR code to determine the 6-DOF pose of the haptic device’s base in the world coordinate system. However, the QR code recognition of the HoloLens 2 is subject to errors depending on the size and distance of the code. In a single-frame detection, the measured size can deviate from the actual size by up to 1%, and during continuous detection, the detected position of the code can fluctuate by up to ±2.5 mm [23]. QR code was tracked while the QR code and device were in a static state at a very close range, since obtaining ground truth using QR code tracking has inherent limitations due to its own measurement errors. QR code was tracked in an environment free of obstacles, since tracking is not possible when the QR code is occluded. A specific button on the haptic device was pressed to get the QR code’s position and orientation values. In this experiment, a QR code with a size of 3 cm was used. QR code tracking is only used for obtaining the ground truth and was performed only once during the data collection process. QR code is not required during the initial alignment and realignment. The QR code was used for ground truth acquisition in this study, but any method capable of estimating the 6-DOF pose can also be employed. When a user initiates an interactive simulation, the HMD is positioned at the origin (0, 0, 0) in the world coordinate system. The position of HMD in the world coordinate is collected near the origin. However, the position of the fingertip may vary depending on the user. Therefore, the estimation accuracy decreases due to the differences between users. To ensure the network model can perform effectively across various users, data augmentation is applied by introducing positional biases while collecting data in world coordinate data. There were limitations in collecting data from diverse participants, and we collected data from a single user and applied systematic data augmentation. Data augmentation was applied to enable the network model to generalize to multiple users by reflecting individual differences such as height of head and arm length. Specifically, biases ranging from −0.2 to 0.2 m along the x and z axes, and from 0 to 0.2 m along the y axis, are added in increments of 0.1 m. This configuration yields 75 (5 × 3 × 5) combinations. One combination ($x=0.2, y=0, z=-0.2$) was excluded due to a data omission, resulting in 74 augmented variations. These bias values were determined empirically. Each of these biases is applied during the augmentation process.

2.4. Data Generation

The network model takes as input a concatenation of 6 to 9 input vectors, each of size 1 × 13, extracted from the collected dataset. These input vectors are selected based on a minimum distance threshold: only those in which the distance between fingertip positions exceeds 3.2 cm are retained. This approach reduces data density and allows the model to capture global features.

Data generation method also applied zero-padding. A varying number of input vectors results in different shapes of input data. Zero-padding is applied to standardize the dimensions of input data. For each 6-DOF configuration of a single haptic device’s base, 10,000 datasets are generated. Given that this process is performed for 74 distinct haptic devices’ bases, the final dataset size is 740,000 × 10 × 13 (Figure 5).

After data generation, a scaling procedure is applied. The position data for both the fingertips and the HMD are recorded in the world coordinate system, while the position in the local coordinate system of the haptic device is collected within the range of the haptic device’s workspace. Rotational data is represented using quaternions, which inherently have a fixed magnitude of 1, restricting each element’s value to the range (−1, 1). To unify the position and rotational data scales, uniaxial normalization is applied. The largest range of position data is set from −1 to 1, which corresponds to the range of quaternions. The largest range of the haptic device’s workspace is the width, 431 mm. The computed scale value is 4.640 (2/0.431), which scales the range to −1 to 1. The computed scale value is multiplied by the position data of the fingertip, HMD, and haptic device’s pen.

3. Experiment

3.1. Experiment Environment

The network model was tested on a Windows 10 operating system (Microsoft, Redmond, Washington, DC, USA) equipped with an NVIDIA RTX 3090 Ti GPU (NVIDIA, Santa Clara, CA, USA). Data acquisition was conducted using the HoloLens 2 and Touch 3D (3D Systems, Rock Hill, SC, USA). All acquired data, except the pen’s 6-DOF information, was referenced in Unity (2020.3.42f1)’s world coordinate system. The pen’s 6-DOF data were represented in the local coordinate system of the haptic device. The fingertip is fixed on a specific button of the pen. As the user provides input through the button, its position is standardized.

3.2. Experiment on Noise-Free Data

A total of 740,000 data were split into training and testing sets in a 4:1 ratio. The size of the input data for training the network model is 592,000 × 10 × 13, and the size of the corresponding ground truth data is 592,000 × 7. Model performance was evaluated using three key metrics: overall Euclidean distance error, per-axis Euclidean distance error, and per-axis rotation error. For each metric, the minimum, maximum, mean, 50th percentile (median), and 99.9th percentile values were calculated. The median indicates that 50% of the data exhibited errors below the stated threshold, while the 99.9th percentile indicates that 99.9% of the data fall below the specified error. During testing, input data had a size of 148,000 × 10 × 13, with a ground truth data of size 148,000 × 7.

The average Euclidean distance error was 2.178 mm, ranging from a minimum of 0.02208 mm to a maximum of 17.78 mm. Despite the high maximum, 50% of the errors were under 1.760 mm, and 99.9% were below 11.69 mm (

Table 1. Euclidean distance error, absolute distance error for each axis, absolute rotation error for each axis.

	Min	Mean	Max	Under 50%	Under 99.9%
Distance error (mm)	0.022	2.178	17.783	1.760	11.692
Distance x-axis error (mm)	0	0.629	4.210	0.466	2.933
Distance y-axis error (mm)	0	0.678	2.848	0.5912	2.213
Distance z-axis error (mm)	0	1.713	17.670	1.117	11.644
Rotation x-axis error (degree)	$2.481\times {10}^{-6}$	0.533	2.340	0.420	2.238
Rotation y-axis error (degree)	$1.821\times {10}^{-6}$	0.288	1.039	0.239	0.980
Rotation z-axis error (degree)	$1.027\times {10}^{-6}$	0.086	0.170	0.085	0.162

).

Axis-specific root mean square error (RMSE) values for distance errors were 0.8496 mm (x-axis), 0.8418 mm (y-axis), and 2.449 mm (z-axis). The x-axis errors ranged from 0 mm to 4.210 mm, the y-axis from 0 mm to 2.848mm, and the z-axis from 0 mm to 17.67 mm (Table 1).

Rotation errors were evaluated by converting both predicted and ground truth quaternions into Euler angles and computing per-axis differences. The angular difference between predicted and ground truth values was normalized to the range of −180 ° to +180°, and absolute values were used to quantify the error magnitudes. RMSE values for rotational errors were 0.7307° (x-axis), 0.3675° (y-axis), and 0.09216° (z-axis). The x-axis rotation error ranged from $2.481\times {10}^{-6}°$ to 2.340°, the y-axis from $1.821\times {10}^{-6}°$ to 1.039°, and the z-axis from 1.027° to 0.1696° (Table 1).

The performance of the network model was compared with other registration methods. The analysis was based on a review paper [20] that categorized various registration techniques. The comparison results are summarized in

Table 2. Comparison with other methods.

Method (The Number of Paper)	Mean Error (mm)
Pattern Marker (11)	2.6
Surface Marker (4)	3.8
Manual Alignment (3)	2.2
Ours	2.718

.

3.3. Experiment on the Number of Vectors

The training and testing datasets comprised 6 to 9 vectors. To assess the impact of the number of vectors on performance, the RMSE for distance and rotational error along each axis was evaluated. The experimental results are shown in

Table 3. Distance RMSE and RMSE for each axis according to the number of input vectors.

The Number of Vectors	6	7	8	9
Distance error (mm)	2.722	2.743	2.720	2.717
Distance x-axis error (mm)	0.849	0.854	0.847	0.848
Distance y-axis error (mm)	0.844	0.842	0.8434	0.837
Distance z-axis error (mm)	2.445	2.467	2.443	2.442

and

Table 4. Rotation RMSE for each axis according to the number of input vectors.

The Number of Vectors	6	7	8	9
Rotation x-axis error (degree)	0.730	0.733	0.732	0.727
Rotation y-axis error (degree)	0.367	0.368	0.368	0.368
Rotation z-axis error (degree)	0.092	0.092	0.092	0.092

.

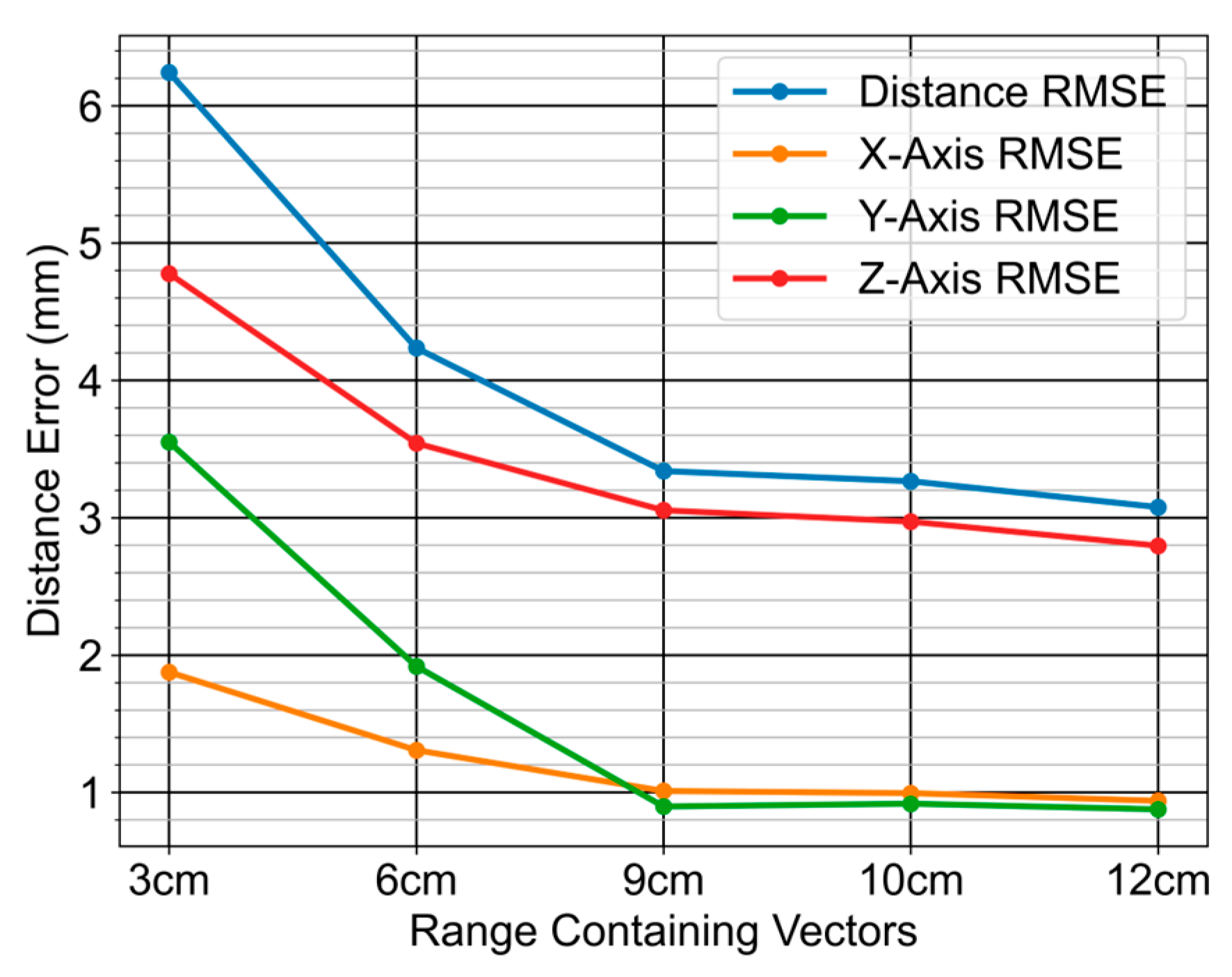
3.4. Experiment on Vector’s Clustered by Range

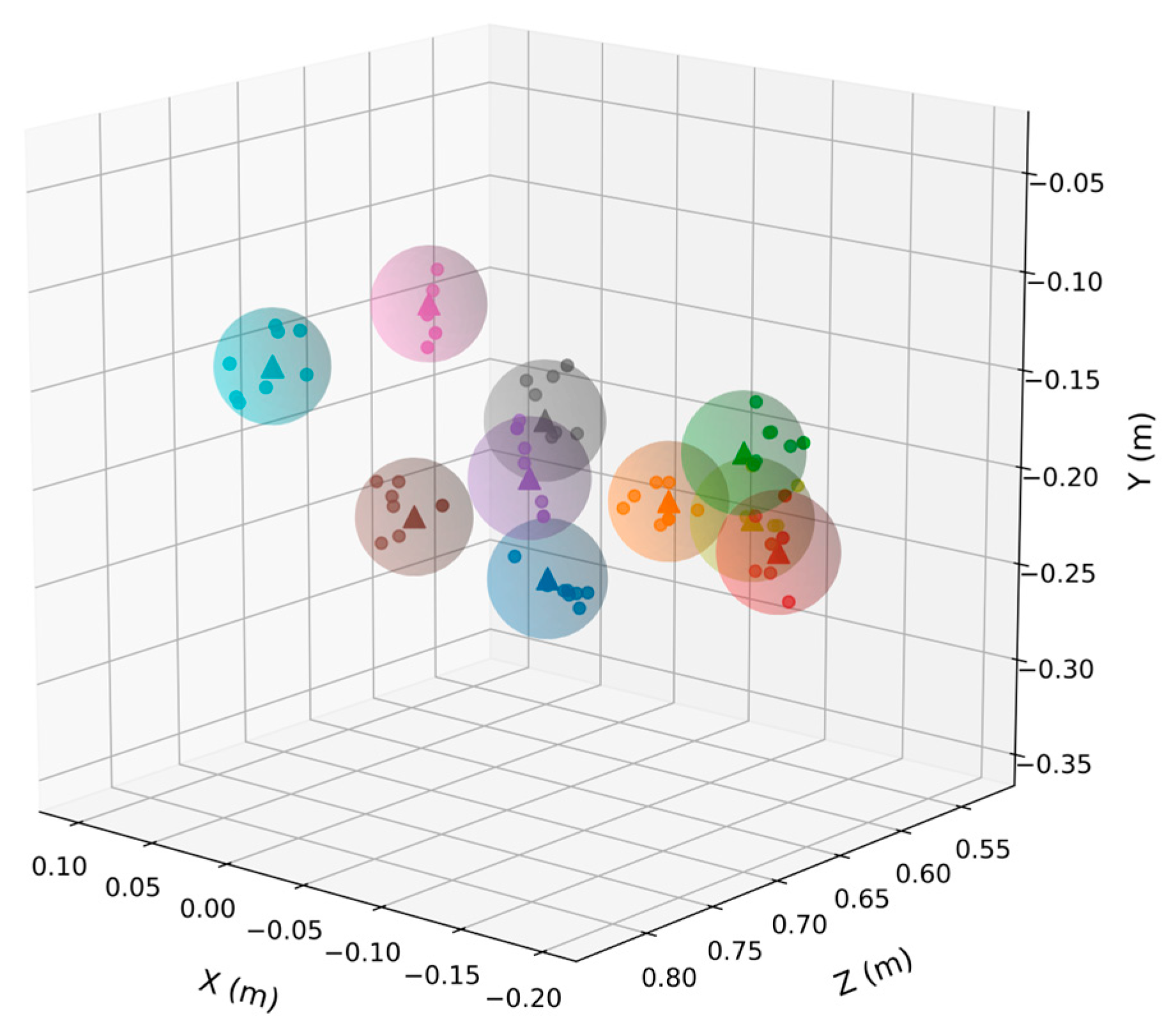
The training dataset was constructed using vectors, each separated by a minimum distance of approximately 3.2 cm. This value represents the combined diameter of the pen and the finger placed on the button during data generation. To evaluate the impact of vector range on the performance of the network model, experiments were conducted using clusters of vectors positioned at distances of 3 cm, 6 cm, 9 cm, 10 cm, and 12 cm. R Ranges were chosen, starting from 3 cm—which is smaller than the 3.2 cm criterion used during training—and progressively increasing to approximately two times, three times and beyond within the minimum workspace range of the haptic device (165 mm). For each experiment, a single reference vector and datasets were generated by clustering 6 to 9 vectors within the specified distance range from the reference vector (Figure 6). The experimental results are shown in Figure 7 and

Table 5. Rotation RMSE for each axis according to the range of clustered vectors.

	3 cm	6 cm	9 cm	10 cm	12 cm
Rotation x-axis error (degree)	0.749	0.740	0.738	0.737	0.736
Rotation y-axis error (degree)	0.392	0.379	0.372	0.373	0.371
Rotation z-axis error (degree)	0.094	0.093	0.093	0.093	0.093

.

3.5. Experiment on Data with Noise

The finger tracking functionality of the HoloLens 2, used in this experiment, does not always provide accurate tracking of the index fingertip’s position [21]. Figure 8 shows both accurate and inaccurate tracking results.

In Figure 8a, the tracking may appear incorrect due to the perspective of the HoloLens 2 camera; however, the fingertip is accurately tracked from the user’s view. This discrepancy arises because the HoloLens 2 camera is positioned higher than the human eye, which causes the tracked hand to appear higher in the captured image. In contrast, Figure 8b clearly shows a noticeable discrepancy between the real hand and the tracked hand.

The network model’s robustness was evaluated by adding artificial noise to the input vectors, simulating fingertip tracking errors. Based on empirical observations, finger tracking error was estimated to be around 1 cm. We also tested with 2 cm and 3 cm perturbations to account for larger deviations. Noise is artificially added to the input vectors. Data is generated by varying the number of noise (1 to 5) and the distance errors from the original fingertip (1 cm to 3 cm). We conducted a total of 15 experiments by combining the number of noises and magnitudes of noise.

In most cases, the results were consistent with those obtained in experiment on noise-free data (

Table 6. Distance RMSE and RMSE for each axis according to the number of noises and their magnitude.

The Number of Noise/ Noise Magnitude (cm)	Distance RMSE (mm)	RMSE x-axis (mm)	RMSE y-axis (mm)	RMSE z-axis (mm)
1/1	2.732	0.851	0.842	2.456
1/2	2.750	0.850	0.842	2.476
1/3	2.879	0.854	0.838	2.618
2/1	2.750	0.850	0.846	2.475
2/2	2.866	0.848	0.840	2.605
2/3	3.011	0.857	0.838	2.763
3/1	2.756	0.858	0.841	2.481
3/2	2.941	0.854	0.838	2.687
3/3	3.129	0.867	0.835	2.888
4/1	2.768	0.858	0.840	2.494
4/2	2.995	0.860	0.838	2.744
4/3	3.297	0.863	0.833	3.071
5/1	2.797	0.848	0.840	2.530
5/2	3.048	0.855	0.836	2.803
5/3	3.331	0.864	0.830	3.108
Result with Noise-free Data	2.726	0.850	0.842	2.449

and

Table 7. Rotation RMSE for each axis according to the number of noises and their magnitude.

The Number of Noise/Noise Magnitude (cm)	RMSE x-axis (Degree)	RMSE y-axis (Degree)	RMSE z-axis (Degree)
1/3	0.731	0.367	0.092
2/3	0.731	0.368	0.092
3/3	0.733	0.368	0.092
4/3	0.732	0.368	0.092
5/3	0.731	0.368	0.092
Result with Noise-free Data	0.731	0.368	0.092

). As shown in Table 6, the RMSE remained essentially unchanged regardless of the noise level or intensity. The rotation RMSE values for each axis exhibited only minor deviations compared to the noise-free experiments. While the distance RMSE occasionally matched or exceeded the values observed without noise, the maximum recorded error was just 0.6050 mm. In some cases, the RMSE for the x-axis, y-axis, and z-axis distances increased slightly, with maximum errors of 0.01718 mm, 0.003944 mm, and 0.6585 mm, respectively. Rotation RMSE for each axis was also slightly higher than those in the noise-free experiments, but the maximum error recorded was 0.002702° for the x-axis, $7.784\times {10}^{-4}°$ for the y-axis, and $1.298\times {10}^{-4}°$ for the z-axis.

3.6. Comparison with the Results Obtained Using a Deterministic Approach

An experiment was conducted to evaluate the performance of the network model in comparison with a deterministic approach. In the deterministic method, the 6-DOF pose of the haptic device’s base is computed through coordinate transformation that computes the transformation matrix ${}_D{}^{W}T$. ${}_D{}^{W}T$ denotes the transformation matrix from world coordinate {W} to the haptic device coordinate {D}, as shown in Figure 2 and Equation (1). The same assumption is maintained: the user’s fingertip is placed on the haptic device’s pen. The pen’s position and rotation are captured from the fingertip’s position and rotation when the user presses the haptic device button. The pen’s rotation is assumed to be identical to the fingertip’s rotation and the pen’s position is determined by the relative positional difference between the center of a pen and fingertip.

The position of the haptic device’s base is computed via coordinate transformation. When the user wears HMD and starts an interactive simulation, the HMD is placed at the origin of the {W}. And rotation expressed as a quaternion is set to (0,0,0,1). The 6-DOF pose of the index fingertip within the {H} is obtained through the HoloLens 2 hand-tracking system. The 6-DOF pose of the index fingertip in {W} can be obtained using a transformation matrix from {W} to {F}. The transformation matrix from {W} to {D}, denoted as ${}_D{}^{W}T$, can be computed by Equation (1). Ground truth is obtained by the transformation from {W} to {D} as follows:

$${{}_D{}^{W}T}_{ground truth}={}_H{}^{W}T\ast {}_Q{}^{H}T\ast {}_D{}^{Q}T$$

(5)

${}_Q{}^{H}T$ and ${}_D{}^{Q}T$ represent a transformation matrix from {H} to {Q} and from {Q} to {D}, respectively.

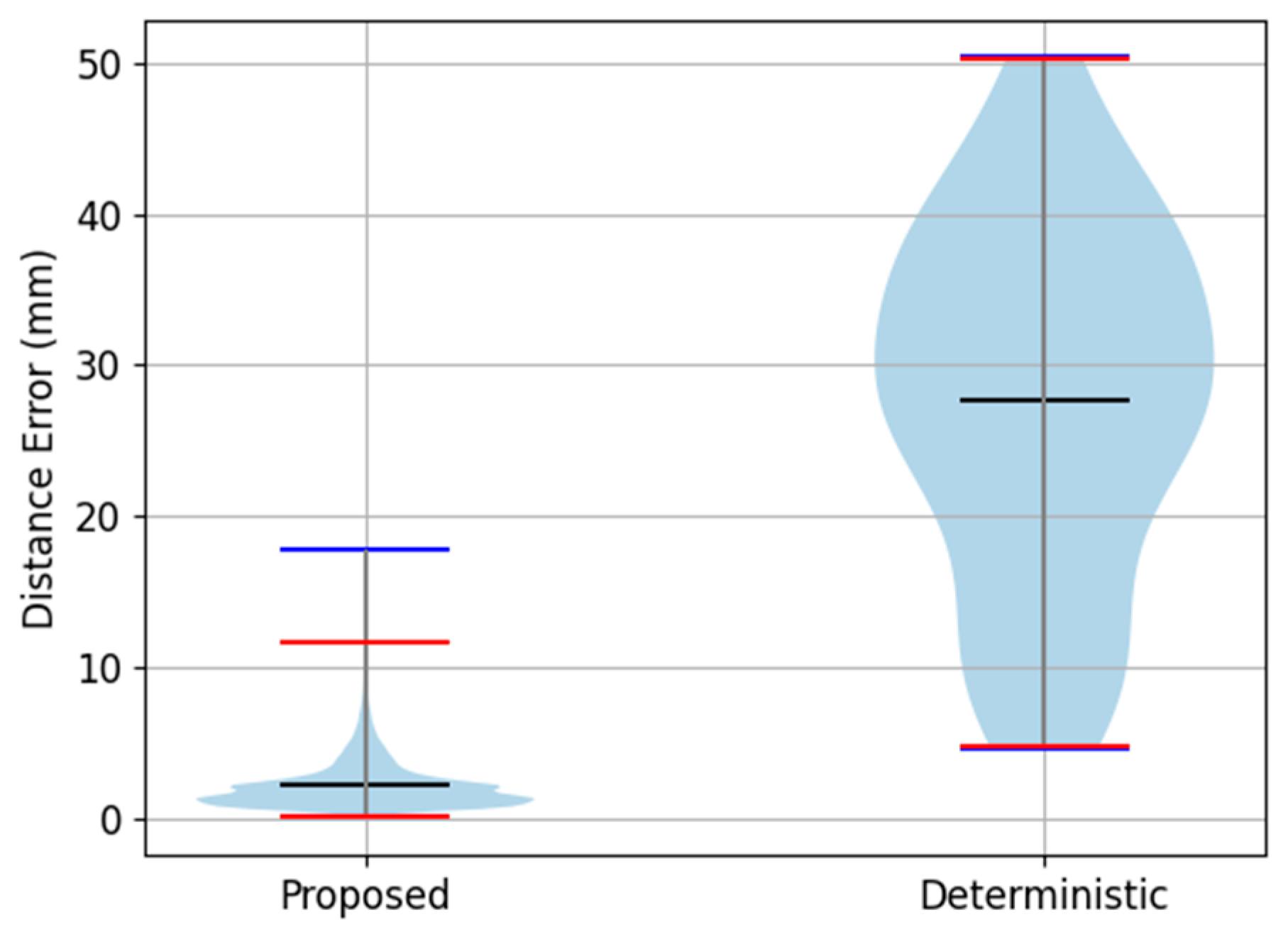
The errors were evaluated against the ground truth. The results confirmed that the network model achieved better performance in terms of distance error, per-axis distance error, and per-axis rotation error for each axis.

Table 8. Comparison of the results of a network model and a deterministic approach.

	Network Model	Deterministic Approach
Distance RMSE (mm)	2.726	30.854
RMSE x-axis (mm)	0.850	23.778
RMSE y-axis (mm)	0.842	16.228
RMSE z-axis (mm)	2.449	12.084
RMSE x-axis (degree)	0.731	17.817
RMSE y-axis (degree)	0.368	4.648
RMSE z-axis (degree)	0.092	4.465

presents the comparative results, while Figure 9 shows the distance error distribution.

In Figure 9, blue lines denote the maximum and minimum error values, whereas red lines represent the 0.1% to 99.9% error range. The blue lines represent the minimum and maximum error range. The black lines represent the mean value. The network model’s maximum error remained below 2 cm, whereas the deterministic method exhibited a maximum error exceeding 5 cm. Notably, the deterministic approach’s mean error surpassed the network model’s maximum error.

3.7. Application

Figure 10 shows the alignment results of the virtual reality on the haptic device using the network model. Figure 10a shows the initial state before alignment. A virtual cube is placed at the position of a QR code attached to the plate to visualize the alignment result. The plate was printed to fix the relative position between haptic device and QR code. The virtual haptic device must be placed behind the virtual cube if the alignment is precise between the haptic device and virtual reality. Users press a button 6 to 9 times to align the virtual reality on the haptic device. An input vector is collected each time the button is pressed. The red spheres in Figure 10b represent fingertip positions, visualizing the acquired points. The network model concatenates these input vectors to estimate the 6-DOF pose of the haptic device’s base. The aligned configuration is shown in Figure 10c, where the haptic device body is positioned behind the virtual object, replicating the real-world setup. After alignment, the user can interact with the virtual object via the haptic device. The light blue sphere, representing the user’s fingertip, is positioned on the pen, indicating successful alignment. Figure 10d shows the alignment result captured through the HMD.

Although the alignment may appear inaccurate due to the perspective difference between the HMD camera and the user’s actual viewpoint (Figure 11), the virtual reality observed through the user’s eye is correctly aligned with the haptic device.

4. Discussion

Experiment 3.2 evaluated the accuracy of the network model. Experiments 3.3 and 3.4 investigated the effects of the number and range of input vectors on network model performance, respectively. Experiment 3.5 assessed the robustness of the network model against noise, while Experiment 3.6 compared the deterministic approach with our proposed network model.

In Experiments 3.2 through 3.5, the distance RMSE of the z-axis was higher than that of RMSE for position along the z-axis and was higher than that for the other axes. This is attributed to the smaller variance in the z-axis, which corresponds to the shortest workspace within which the haptic device’s pen operates as the user manipulates the pen. Similarly, the RMSE for rotation about the x-axis was higher than for other rotational axes due to its smaller variance. The roll rotation (x-axis) has the narrowest range, explaining the increased error in this dimension. These limitations could impact the real-world usability of the system. To improve the robustness of the system in practical use, users should be guided to actively move the haptic device along the z-axis, which corresponds to the depth direction, in order to collect data over a wider range. Similarly, for roll-axis rotation, users should be encouraged to manipulate the pen with more varied rotational angles to generate a more diverse set of training data. Providing such guidelines during data acquisition can help reduce estimation errors and improve model generalization.

The experiment on noise free data showed that the network model performs well under ideal conditions. Furthermore, our approach was evaluated in comparison with conventional marker-based and manual alignment methods. Prior studies have reported registration errors from 2.2 mm to 3.8 mm, whereas our method achieved an error of approximately 2.7 mm. Although slightly less accurate than manual registration, our approach offers sufficient performance to be applicable to alignment.

The experiment on the number of input vectors showed no significant performance differences when varying the number of input vectors. At least six input vectors are required to estimate the 6-DOF pose of the haptic device’s base. In the absence of noise, six input vectors are sufficient to achieve satisfactory accuracy. In our experiments, the input vectors were evenly distributed and largely free of noise. Therefore, increasing the number of input vectors did not lead to notable improvements in accuracy. In practical applications prone to noise or sensor disturbances, using more than six input vectors can enhance robustness and reduce estimation errors. Therefore, allowing flexibility in the number of vectors is a valuable design strategy, particularly in environments with suboptimal measurement conditions.

In the experiment on the range of vectors, the error decreases as the range increases. This implies that greater spacing between input vectors allows for better feature extraction. During training, only vector combinations with a minimum separation of 3.2 cm were used as input data. If the network model was trained on a poorly distributed set of vectors, its estimation accuracy could be further improved by optimizing the distribution of these vectors. Therefore, ensuring sufficient spatial separation between input vectors should be considered a practical guideline when designing data collection strategies for pose estimation systems, and users should be guided to maintain such separation during actual operation to ensure consistent performance.

In the experiment on data with noise, the results were comparable to the results of tests without noise. The network model applies the same filters to all input vectors in input data using a shared-MLP structure. The network extracts global features by applying max pooling to select the highest feature values through max pooling. As the network model captures global features of the input vectors, the presence of noise in some input vectors does not substantially affect the overall feature representation or estimation accuracy. In practical use, noise may arise from errors in fingertip tracking by the HMD or other external factors. However, the network model has demonstrated robustness to such noise, suggesting strong potential for reliable application in real-world environments.

The comparative experiment between the deterministic approach and the network model demonstrates that the latter achieves higher accuracy in both position and rotation estimation. Several factors contribute to the limitations of the deterministic approach. Firstly, finger tracking via the HoloLens 2 is inconsistent, leading to unstable measurements of relative position between the fingertip and the pen. This variability violates the deterministic model’s core assumption that this relative position remains constant during operation. Secondly, when the user presses the button to initiate alignment, oscillation and movements of the hand occur, further degrading the accuracy of fingertip tracking. Moreover, the relative rotation between the fingertip and pen changes depending on the user’s grip. As a result, the deterministic approach processes inherently noisy data when computing the 6-DOF pose of the haptic device’s base. While the network model also operates on noisy input data, its architecture—featuring shared-MLPs combined with max-pooling layers—effectively suppresses noise and extracts robust global features, enabling more reliable and accurate pose estimation under variable conditions.

Although the network model demonstrated satisfactory performance in evaluation experiments, several limitations remain. First, the QR code used to obtain ground truth data introduces its own measurement errors. Second, if the user’s hand moves excessively during input, accurate finger tracking cannot be ensured, which negatively affects the 6-DOF pose estimation results. Furthermore, during the initialization process for finger tracking, the user must keep their fingers visible until all input vectors are collected. If the fingers are occluded at any point, tracking fails, and the corresponding input vectors cannot be acquired.

5. Conclusions

This paper presents a neural network-based method for estimating the 6-DOF pose of the haptic device’s base without relying on markers, external trackers, or cameras. The method leverages shared MLPs and max-pooling techniques to estimate the base position using as few as six to nine user input vectors, demonstrating resilience to input noise. The approach can be scaled to incorporate more than nine input vectors to improve noise tolerance further. Experimental results show that introducing up to three 5 mm noise sources increased the estimation error by approximately 0.6 mm. However, when user inputs were densely clustered, performance degradation was observed, with the maximum error reaching 6.24 mm. This highlights the importance of distributed inputs. On average, the distance error was 2.718 mm, and the rotational error was 0.5330°, equivalent to 1.3% of the haptic device’s maximum length. The maximum observed errors were 17.78 mm in distance and 2.340° in rotation, corresponding to 8% of the haptic device’s maximum length. Although the proposed method demonstrated accurate and robust performance, several limitations remain. First, the proposed method requires markers to obtain ground truth data. In addition, if the user’s hand moves excessively while pressing the input button, estimation accuracy decreases, and the hand must remain visible without occlusion throughout the input process. Future work includes evaluating the method’s performance through user studies. Furthermore, we plan to explore markerless approaches for ground truth acquisition, employing point clouds as ground truth.

The proposed method enables the alignment of virtual reality onto the haptic device using an HMD with finger tracking capabilities. The haptic device can be of any ground type. Ground truth values can be obtained through various methods, such as QR code, magnetic sensors, or other suitable techniques. This alignment process needs to be performed only once during the initial setup and can be applied to various grounded haptic devices, thus offering an efficient solution for visuo-haptic mixed reality applications. Although the proposed method requires an external marker, such as a QR code, during the initial training phase, it enables accurate and efficient alignment of virtual reality to the same haptic device without the need for markers once the training is completed.