APMEG: Quadratic Time–Frequency Distribution Analysis of Energy Concentration Features for Unveiling Reliable Diagnostic Precursors in Global Major Earthquakes Towards Short-Term Prediction

Featured Application

Usage of Energy concentration on Time–Frequency Distributions of earthquake datasets to obtain diagnostic precursors.

Abstract

Earthquake prediction remains a significant challenge in seismology, and advancements in signal processing techniques have opened new avenues for improving prediction accuracy. This paper explores the application of Time–Frequency Distributions (TFDs) to seismic signals to identify diagnostic precursory patterns of major earthquakes. TFDs provide a comprehensive analysis of the non-stationary nature of seismic data, allowing for the identification of precursory patterns based on energy concentration features. Current earthquake prediction models primarily focus on long-term forecasts, predicting events by identifying a cycle in historical data, or on nowcasting, providing alerts seconds after a quake has begun. However, both approaches offer limited utility for disaster management, compared to short-term earthquake prediction methods. This paper proposes a new possible precursory pattern of major earthquakes, tested through analysis of recent major earthquakes and their respective prior minor earthquakes for five earthquake-prone countries, namely Türkiye, Indonesia, the Philippines, New Zealand, and Japan. Precursors in the time–frequency domain have been consistently identified in all datasets within several hours or a few days before the major earthquakes occurred, which were not present in the observation and analysis of the earthquake catalogs in the time domain. This research contributes towards the ongoing efforts in earthquake prediction, highlighting the potential of quadratic non-linear TFDs as a significant tool for non-stationary seismic signal analysis. To the best of the authors’ knowledge, no similar approach for consistently identifying earthquake diagnostics precursors has been proposed, and, therefore, we propose a novel approach in reliable earthquake prediction using TFD analysis.

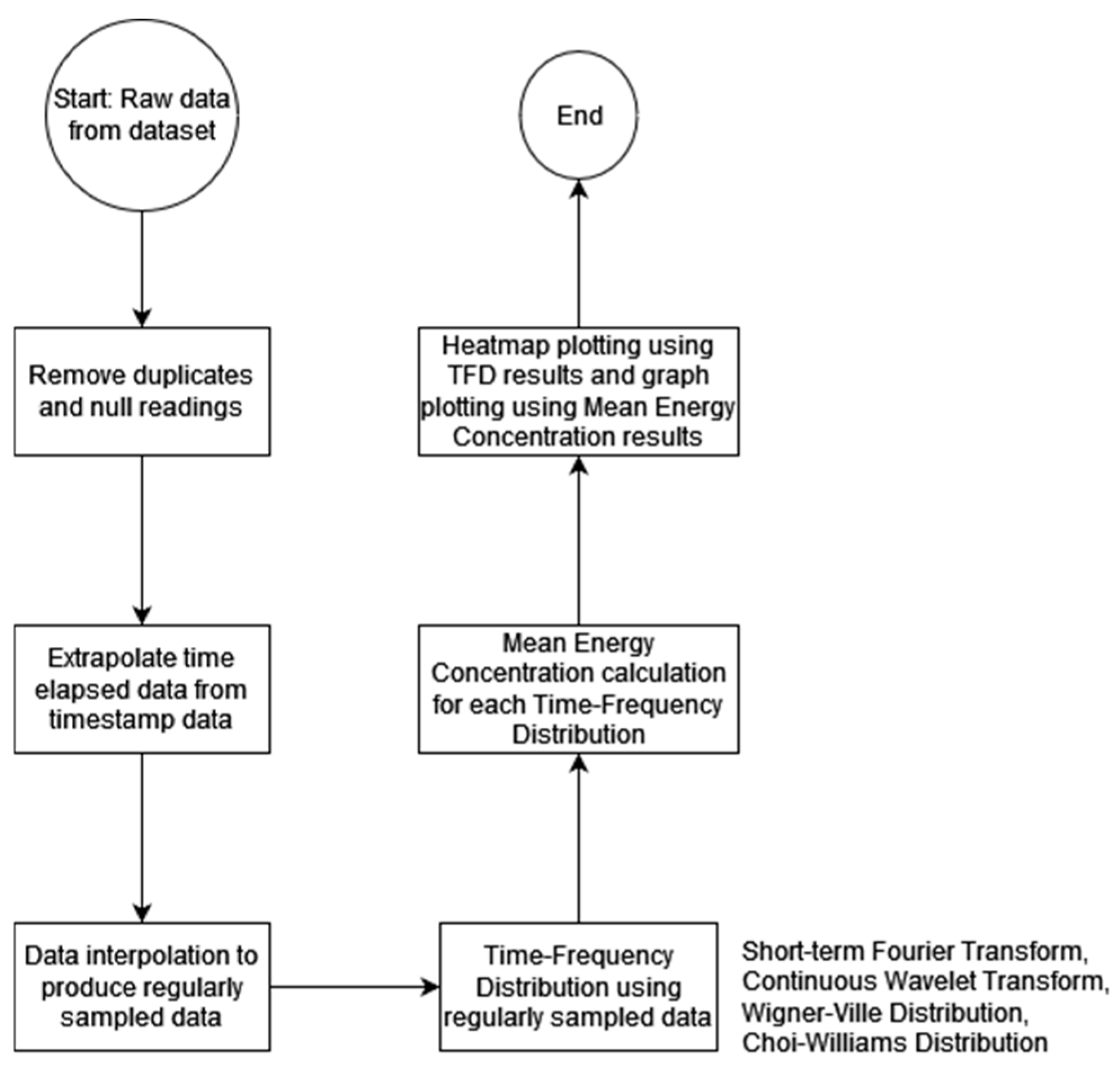
1. Introduction

In recent years, the world has seen devastating earthquakes in various regions, namely the Turkey–Syria earthquake in 2023, the Noto earthquake on New Year’s Day in 2024, the Southern Peru earthquake in the middle of 2024, and most recently, the Myanmar–Thailand earthquake in 2025.

Earthquakes are crucial for releasing energy accumulated in the Earth’s brittle outer layer, the lithosphere, through the movement of adjacent sections of the Earth’s crust driven by tectonic stresses [1]. This energy is measured in Mw or the Moment Magnitude Scale, which is the most popular metric used by seismologists worldwide to measure an earthquake in terms of energy released. Mw is derived from the seismic moment of an earthquake, calculated as the product of the fault displacement and the force required to cause the movement. This scale is logarithmic, where a one-unit increase in magnitude represents a tenfold increase in amplitude on a seismogram and approximately 31.6 times more energy release [2].

An early and accurate prediction of earthquake occurrences would lead to better disaster management and preparations for structural damage control, which reduces injuries and deaths caused by earthquakes, as well as economic losses [3,4,5]. As such, earthquake prediction is thought to be the ‘holy grail’ of seismology, as it is nearly impossible given the various factors and margin of error in time, place, and magnitude [6,7]. The Geological Society of the United Kingdom in Earthquake Briefing, a policy document, mentions that currently, deterministically predicting the specific timing and location of earthquakes is not achievable; however, the identification of a ‘diagnostic precursor’ would be essential to enable such predictions [8]. Vladimir Keilis-Borok, the founding director of the International Institute of Earthquake Prediction Theory and Mathematical Geophysics, Russian Academy of Sciences, in his seminal paper entitled Earthquake Prediction, stated that “Earthquake prediction is necessary to undertake disaster preparedness measures, reducing the damage from earthquakes. This requires that the accuracy of prediction be known, but, contrary to common belief, a timely prediction of low accuracy may be useful” [9]. Perhaps due to these glimpses of hope and optimistic sentiments, there are now many detection and early warning systems for earthquakes using big data through a network of seismic monitoring stations around the world [10,11], including a network of smartphones used by the participating population [12]. China, for example, currently launched the largest Earthquake Early Warning system (EEW) in the world, named the National System for Fast Seismic Intensity Report and Earthquake Early Warning, comprising about 2000 seismic stations, 3200 strong-motion stations, and 10,000 micro-electro-mechanical system (MEM) stations [13]. While EEWs are crucial in enhancing survivability and reducing injuries by alerting the masses, effectiveness is hindered by the alert time window, which is only several seconds before the earthquake shock reaches the masses. Short-term prediction systems, meanwhile, aim to predict major earthquake events in a location with a longer time window, i.e., hours prior. However, reliable short-term prediction systems for earthquakes remain a challenge, receiving critical responses [14,15] due to the impact of such a prediction system. Based on the state-of-the-art literature reviews, the key to predicting seismic events lie in big data, signal processing, and machine learning, including neural networks [16,17,18,19]. Among approaches performed previously are an analysis on changes in horizontal positioning of geodetic stations [20,21], as well as an analysis on FM radio wave-based signals [17].

Disturbingly, most of the earth’s fault lines that cause earthquakes have yet to experience their largest possible earthquake along their individual fault lines [22]. The analyzed 2023 Turkey–Syria earthquake, 2018 Sulawesi earthquake, 2022 Luzon earthquake, 2016 Kaikōura earthquake, and 2024 Noto earthquake are the most recent major earthquakes from these earthquake-prone countries that saw earthquakes of magnitudes 7 and greater, in which the destruction of physical structures caused by the disaster are almost guaranteed [23]; the 2023 Turkey–Syria earthquake saw the largest earthquake of the region. As for the selected earthquake incidents, reports estimate the total casualty of over 56,000 deaths, and total structural damages and immediate production capacity losses are estimated upwards of USD 101 billion, where the latest Noto earthquake losses alone are estimated to cost USD 17 billion [24,25,26,27,28,29,30].

As these seismic movements or waves can be measured and recorded, with the intensity of the waves noted as magnitude, the recorded waves are essentially a time-series function describing the occurrences of earthquakes and their respective magnitudes. In a research study conducted in 2023 aimed to answer the question “do catalogues of smaller earthquakes contain information about future larger earthquakes?”, John B. Rundle concluded, “that catalogues contain significant information on predictability of future large earthquakes” [31], consistent with his other related research [32,33]. This sentiment is also shared by other researchers [34]. As an earthquake can also be described as the dissipation of accumulated energy from tectonic stress in the lithosphere [1], Time–Frequency Distributions (TFDs) analysis, with its energy concentration feature to describe the variation of energy over time, may prove to be useful to understand earthquakes [35]. TFDs are used in signal processing to analyze and characterize signals in the time and frequency domains simultaneously and have been used to analyze earthquake motion measured using accelerograms [36,37,38]. In this research, we propose to analyze earthquake records using the TFD method. While analyzing seismic data using TFD in the form of Short-Time Fourier Transform (STFT) and Wavelet Transform (WT) has been performed previously to obtain geological and stratigraphic information [39] as well as for earthquake pattern recognition and detection [40,41], this research introduces the calculation of mean energy concentration, as well as the utilization of Cohen’s class TFD, specifically Wigner–Ville (WVD) and Choi–Williams (CWD) distributions, aiming to seek major earthquake precursory patterns in the analyzed results for the purpose of timely short-time earthquake prediction. This method of combining Cohen’s class TFDs and the calculation of mean energy concentration has been shown to be able to successfully identify precursory patterns to arrhythmia and ischemia occurrences based on electrocardiogram (ECG) datasets with high accuracy [42,43].

2. Materials and Methods

2.1. Data Sources

Datasets of the Turkey–Syria (2023), Sulawesi (2018), Luzon (2022), Kaikōura (2016), and Noto (2024) major earthquakes were used for the analysis conducted in this research [44,45,46,47,48]. The chosen earthquakes have a similarity in that the major earthquakes reported have Mw magnitudes of 7 or greater, as they are destructive and thus are more important to predict, and it has been found previously that such earthquakes have precursors [20,21]. The datasets selected to be analyzed span one month, inclusive of the major earthquakes, since this research focuses on short-term prediction in the range of hours and days before the earthquake occurrences. It is noted that the datasets used in this research are sampled using geophonic sensors. For this research, we will only be focusing on the timestamp and magnitude data as the time-series function to undergo Time–Frequency Distributions (TFDs). The earthquakes that are selected to be part of the analysis are the latest major earthquakes of each region or country, and the minor earthquakes spanning 1 month before the respective major earthquakes. It is noted that the dataset obtained for the five countries is incomplete with irregular samples; thus, a data interpolation method is required to obtain a regularly sampled time-series function for analysis. This is especially so for Noto, Kaikōura, and Luzon earthquake catalogs, as the threshold set for an earthquake to be recorded in their respective catalogues is Mw 3.0.

2.2. Data Interpolation

While the average sampling period can be calculated from observing the summary of each dataset (refer

Table 1. Summary of dataset to be processed.

Earthquake	Number of Samples	Average Sampling Period (s)
Turkey–Syria	9399	275.681
Sulawesi	2709	924.244
Luzon	1801	1485.441
Kaikōura	7767	332.316
Noto	554	4653.032

), all datasets appear to show irregular sampling, which is not meeting a crucial criterion for applying the key function for TFDs—Fast Fourier Transform (FFT)—i.e., the time-series data provided must be, or is assumed to be, regularly sampled [49]. Therefore, a data interpolation method is used to estimate and produce regularly sampled data based on each dataset. The interpolation method used is linear interpolation, which is achieved by estimating values between two adjacent points using a straight line. As earthquake occurrences are not a high-frequency phenomenon, losing high-frequency information due to linear data interpolation can be considered to have a minimal impact on the analysis result’s reliability, if not negligible. The linear interpolation formula used to determine the magnitude Mw of the interpolated data at a time T with the known discrete magnitude and time before T (Mw₀, T₀) and after T (Mw₁, T₁) is as follows [50]:

$$Mw= {\displaystyle \frac{{Mw}_0\left(T_1- T\right) + {Mw}_1\left(T- T_0\right)}{T_1- T_0}}.$$

(1)

2.3. Time–Frequency Distributions (TFDs)

Time–frequency analysis is mainly achieved by formulating a function that represents the input signal in both the time and frequency spectra simultaneously, instead of either within the time or frequency domains. This function or process can then be changed to suit the various use cases that contain a time-varying spectrum [51]. There is no objective representation for signal energy changes over time and frequency, and this resulted in several proposals [52]. These proposals can be summarized in the following process, as shown in Figure 1.

2.4. Short-Time Fourier Transform (STFT)

The Short-Time Fourier Transform (STFT), also known as spectrogram distribution, is a signal processing method used to analyze multi-component signals. The key idea of this method is to apply FFT over a fixed-width window moving over time, resulting in the change of spectrum of a signal over each frame.

2.5. Wigner–Ville Distribution (WVD)

One of the most significant and well-known representations of signal energy distribution is the quadratic class, or Cohen’s class [52]. However, Cohen’s class distribution is hampered by unwanted cross-terms between frequency components [54]. The Wigner–Ville distribution (WVD) belongs to this non-linear TFD category, with its calculation for a continuous signal on a specific frequency $\omega$ given in (2) [55]. WVD covers most mathematical properties involved in analysis; real-valued, maintains time and shifting frequencies, and satisfies marginal features that generate an instantaneous power and power spectrum.

$${WV}_{t,\omega }={\displaystyle \frac{1}{2\pi }} \int x\left( t+{\displaystyle \frac{\tau }{2}}\right) x^{*}\left( t-{\displaystyle \frac{\tau }{2}}\right) e^{-j\omega \tau } d\tau$$

(2)

where x(t) is the interpolated magnitude signal in a time-series with a constant sampling rate, with x*(t) being its conjugate, and $\omega$ is a desired single frequency band.

To mitigate the issue of unwanted cross-terms between frequency components, the input signal, i.e., interpolated earthquake data, was “converted to complex-valued analytic signal by removing negative frequency auto-terms” before applying WVD [56].

2.6. Choi–Williams Distribution (CWD)

One of the best methods from Cohen’s Class of non-linear time–frequency for reducing cross-terms to the minimum is the Choi–Williams class kernel, with the distribution on a specific frequency $\omega$ of a discrete signal x(n) expressed as Equation (3) [57].

$${CWD}_{n,\omega }={\sum }_{k={\displaystyle \frac{N}{2}}}^{{\displaystyle \frac{N}{2}}-1}{e}^{-i2\omega k}{\sum }_{m=-{\displaystyle \frac{M}{2}}}^{{\displaystyle \frac{M}{2}}}\sqrt{{\displaystyle \frac{\sigma }{4\pi k^2}}}{e}^{-{\displaystyle \frac{{\left(m-n\right)}^2}{4k^2}}}x\left(m+k\right)x^{*}(m-k)$$

(3)

2.7. Continuous Wavelet Transform (CWT)

Continuous Wavelet Transform is able to represent a signal without constant windowing as compared to STFT, and thus has few tradeoffs between resolution and computation time [58]. CWT utilizes a group of functions called wavelets, which are generated by shifting and scaling a mother wavelet function. The CWT of a signal x(t) can be defined as follows [58]:

$$W_{a, b} ={\int }_{-\infty }^{+ \infty }x\left(t\right) {{\psi }_{a,b}}^{*}\left(t\right) dt,$$

(4)

where

$${\psi }_{a, b}={\displaystyle \frac{1}{\sqrt{a}}} \psi \left({\displaystyle \frac{t-b}{a}}\right).$$

2.8. Mean Energy Concentration

The mean energy concentration of TFDs refers to the distribution of energy across the time and/or frequency axes in the TFD representation and provides insights into the dominant time–frequency regions where the signal’s energy is concentrated. As earthquakes are essentially energy released by the lithosphere, the mean energy concentration of TFDs would be an appropriate measurement to reflect the nature of earthquakes [59]. For this research, we will be focusing on the mean energy concentration on the time axis of the TFD representation of the earthquake datasets for any precursory behavior prior to the major earthquakes that are not apparent in the raw earthquake catalogues.

2.9. Analysis Procedure

The analysis procedure performed on the earthquake datasets providing the results for this research are shown in Figure 2.

3. Results

Each data point is linearly interpolated to preserve the low-frequency content. This allows the interpolated data to be analyzed using the time–frequency analysis methods of STFT, WVD, CWD, and CWT, as a constant sampling rate of a signal is a prerequisite for these discrete time–frequency analyses. It is noted that the datasets for these earthquakes have varying ranges of samples, and, therefore, several parameters are adjusted, namely the resampling rate for interpolation of data, the window sizes to optimize both time and frequency resolution for STFT, and the time slots used for mean energy concentration calculation. The estimated time of occurrence for each major earthquake is noted and set as the origin time (0 h) for better visualization and comprehension, and marked with a yellow-tinted region. Figure 3 and Figure 4 visualize the comparisons for the interpolated data against the STFT, CWD, WVD, and CWT sets for the Turkey–Syria and Sulawesi earthquakes. Other earthquake mean energy concentration comparisons are visualized in Figure A1, Figure A2 and Figure A3 in Appendix A.

4. Discussion

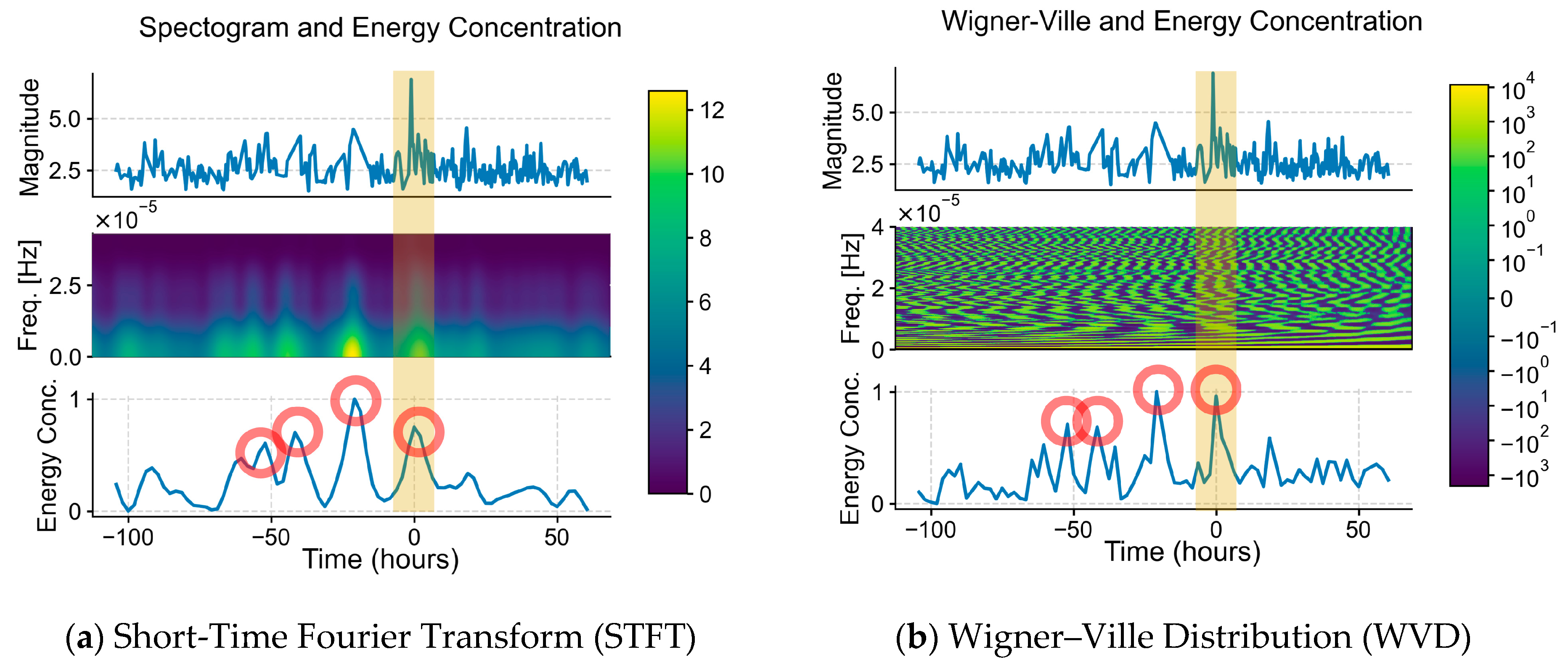
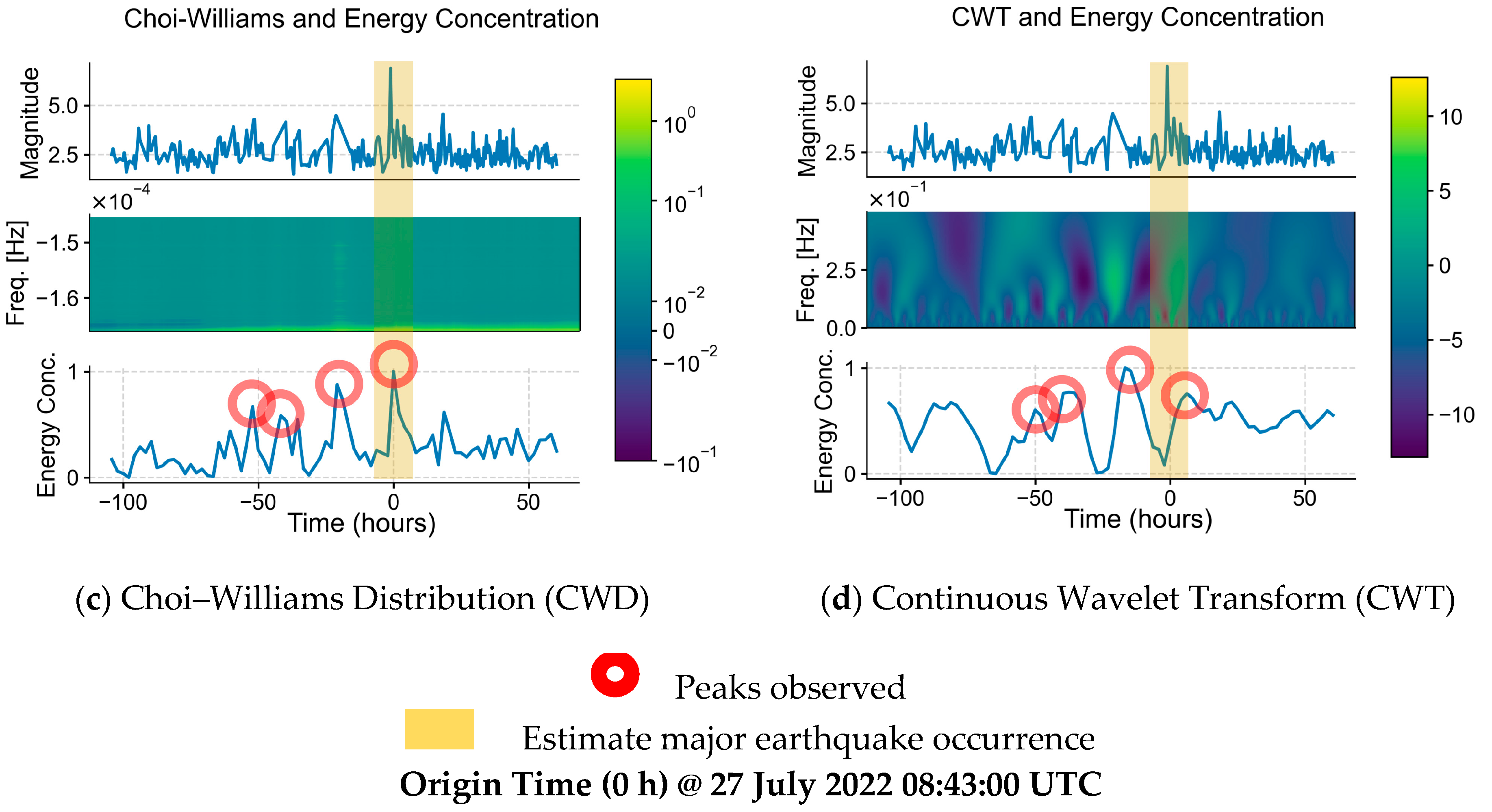
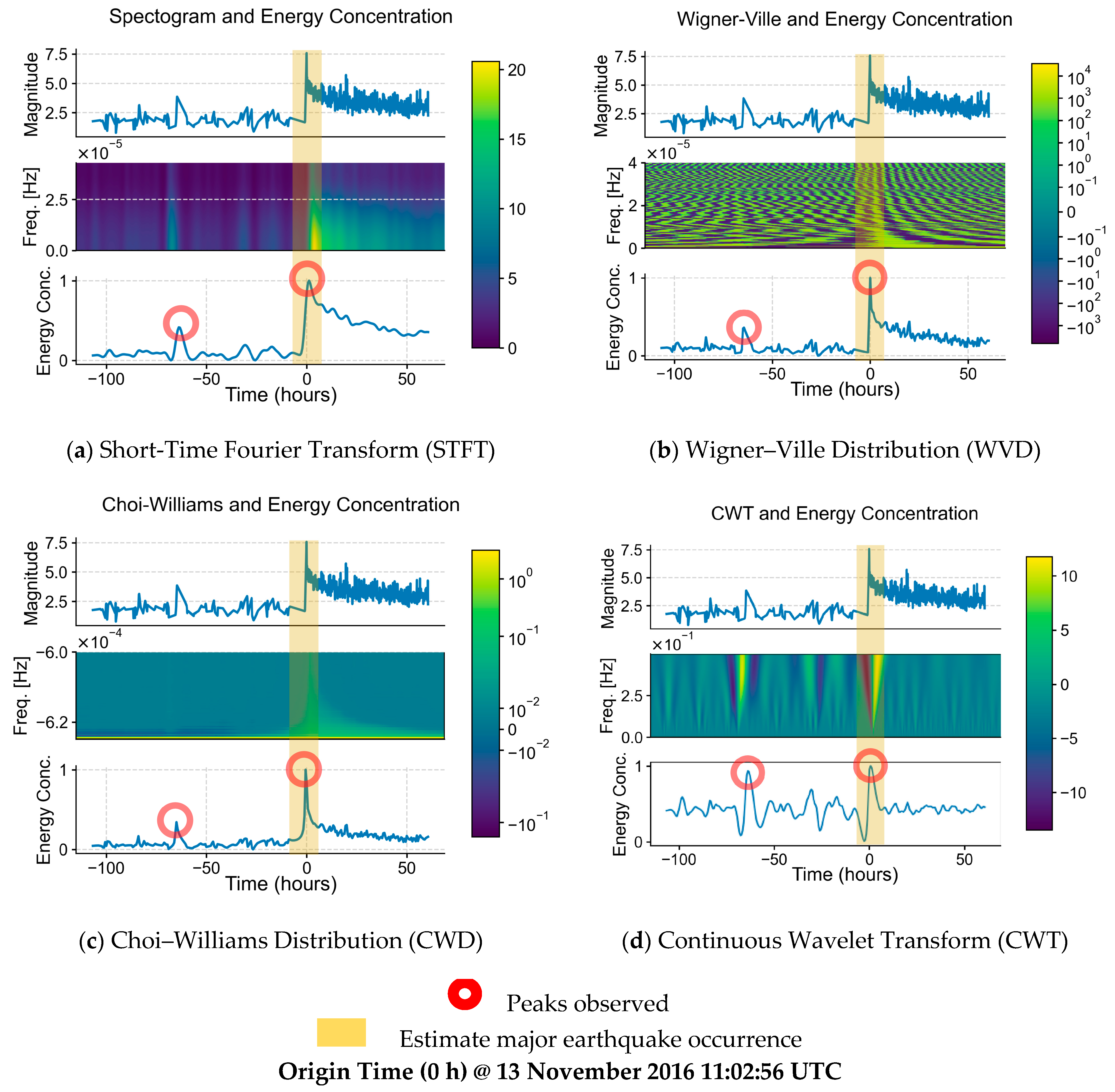
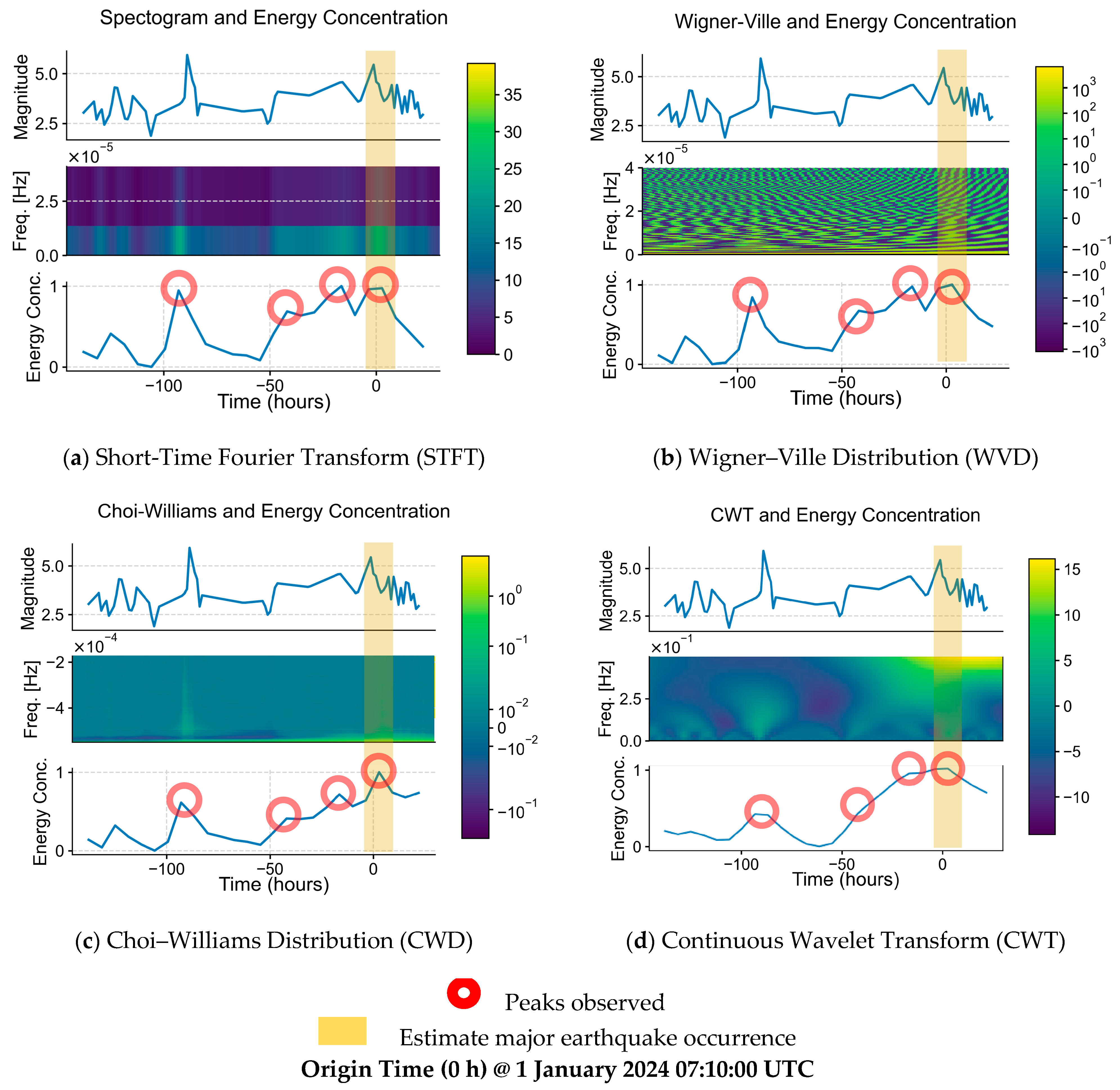
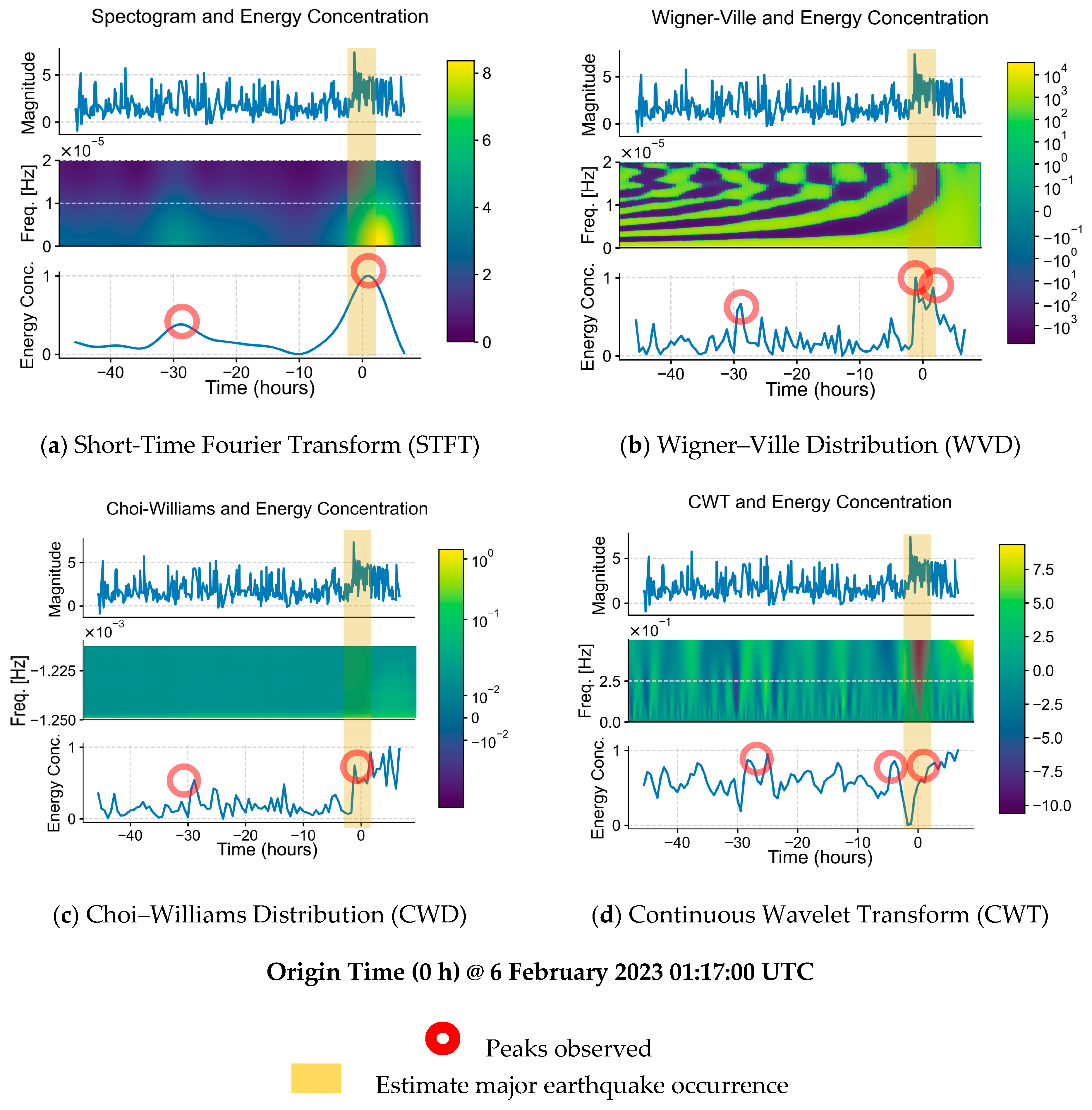
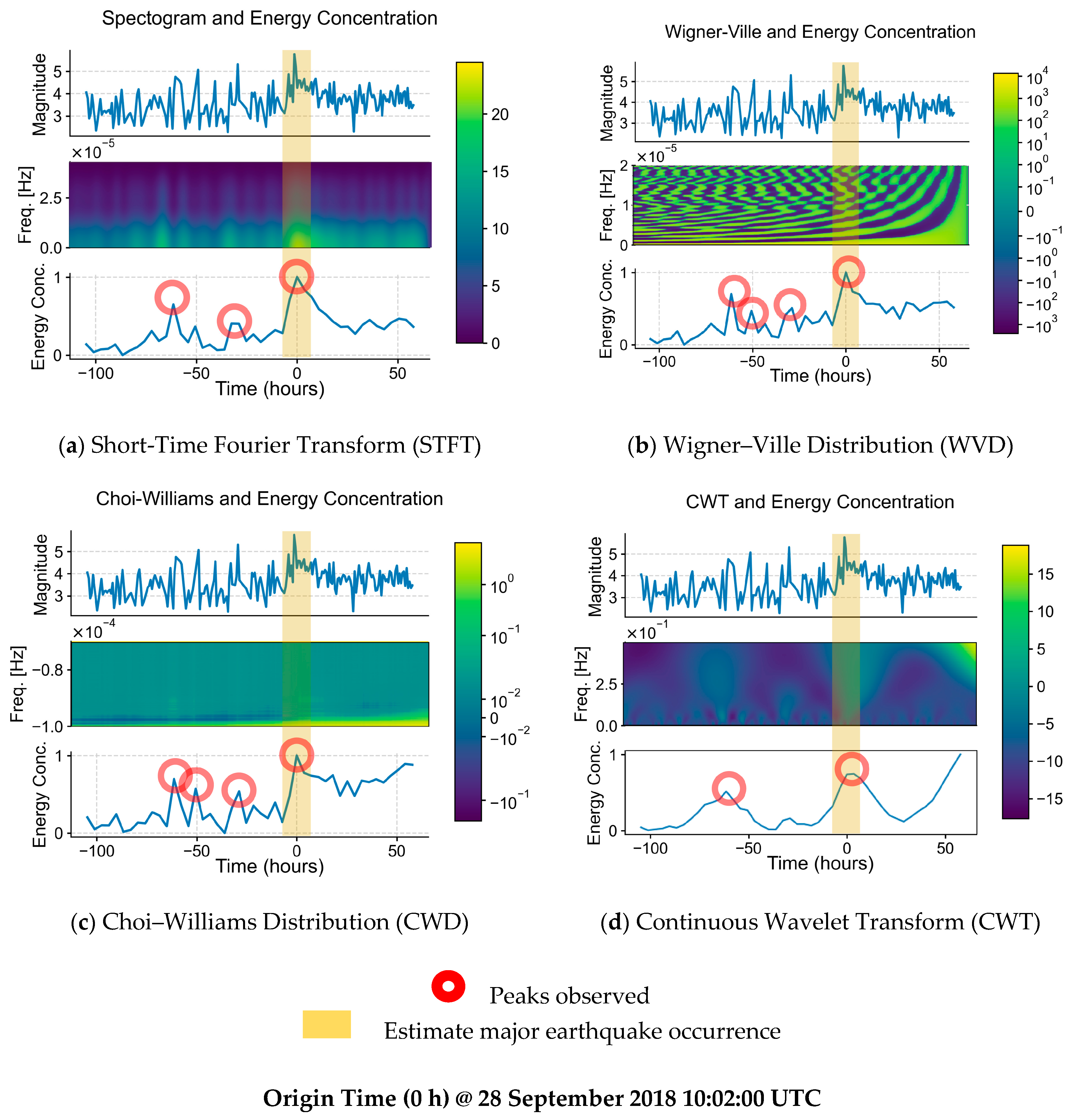
From the TFD visualizations of the earthquakes, it can be said that the TFD methods were able to provide spectral information of the earthquakes, as well as the frequency variations over time, providing more insight into the earthquakes. Each of the mean energy concentration results was also able to correctly show the estimated time when the major earthquakes occurred, marking them with a peak.

As the intention of this research is to ultimately prove the possibility of diagnostic precursory patterns of major earthquakes through the means of TFD, the authors believe that the research at the current stage is insufficient to provide a practical and absolute threshold for peaks, especially for the real-time analysis of earthquake signals, and requires further research. However, for the purpose of this research’s analyses, the threshold for peaks—both major and minor—is defined statistically as the sum of the mean and two standard deviations of the energy concentration of respective TFDs and earthquakes spanning from 1 week prior to the major earthquake. This definition is not concrete yet, as they are values that change over time and differ between regions, TFDs, and a range of input values, e.g., 1 month instead of 1 week prior to the major earthquake.

On observation of the comparisons of the earthquake data, heatmap, and the mean energy concentration derived from the respective TFDs, with the definition of the major and minor peaks stated above, it is seen that there are a few minor peaks visualized in the mean energy concentration graphs, marked with red circles, which were initially barely, if not unnoticeable, in the earthquake signals. The elapsed time in seconds of the peaks since the first sample timestamp of each dataset was noted, and the estimated timestamps in UTC are calculated and tabulated in

Table 2. Summary of mean energy concentration peaks and corresponding earthquakes of the Turkey–Syria earthquake.

Earthquake	Mean Energy Peak Timestamp (UTC)	Mean Energy Concentration
Minor EQ 1	4 February 2023 21:32:44	44.04% (STFT),
		54.59% (CWD),
		64.93% (WVD)
Major EQ	6 February 2023 03:32:44 (STFT), 6 February 2023 01:19:24 (CWD, WVD)	100% (STFT),
		74.69% (CWD),
		96.05% (WVD)

,

Table 3. Summary of mean energy concentration peaks and corresponding earthquakes of the Sulawesi earthquake.

Earthquake	Mean Energy Peak Timestamp (UTC)	Mean Energy Concentration
Minor EQ 1	25 September 2018 23:08:33	69.75% (STFT),
		69.91% (CWD),
		70.07% (WVD),
		51.23% (CWT)
Minor EQ 2	27 September 2018 04:01:53 (STFT), 27 September 2018 07:38:44 (CWD, WVD)	51.22% (STFT),
		53.85% (CWD),
		51.06% (WVD)
Major EQ	28 September 2018 12:31:53	100% (STFT, CWD, WVD)
		73.63% (CWT)

,

Table 4. Summary of mean energy concentration peaks and corresponding earthquakes of the Luzon earthquake.

Earthquake	Mean Energy Peak Timestamp (UTC)	Mean Energy Concentration
Minor EQ 1	25 July 2022 04:37:00	60.51% (STFT),
		66.94% (CWD),
		71.01% (WVD),
		72.44% (CWT)
Minor EQ 2	25 July 2022 15:02:00	70.30% (STFT),
		58.35% (CWD),
		68.48% (WVD),
		68.08% (CWT)
Minor EQ 3	26 July 2022 11:52:00	100% (STFT, WVD, CWT),
		87.63% (CWD)
Major EQ	27 July 2022 08:42:00	75.04% (STFT),
		100% (CWD),
		96.16% (WVD),
		75.45% (CWT)

,

Table 5. Summary of mean energy concentration peaks and corresponding earthquakes of the Kaikōura Earthquake.

Earthquake	Mean Energy Peak Timestamp (UTC)	Mean Energy Concentration
Minor EQ 1	10 November 2016 18:47:35 (STFT)	41.63% (STFT),
	10 November 2016 17:40:55 (CWD)	34.02% (CWD),
	10 November 2016 18:14:15 (WVD)	36.07% (WVD),
	10 November 2016 18:47:35 (CWT)	93.29% (CWT)
Major EQ	13 November 2016 11:47:35 (STFT)	100%
	13 November 2016 10:07:35 (CWD)
	13 November 2016 10:40:55 (WVD)
	13 November 2016 11:14:15 (CWT)

and

Table 6. Summary of mean energy concentration peaks and corresponding earthquakes of the Noto earthquake.

Earthquake	Mean Energy Peak Timestamp (UTC)	Mean Energy Concentration
Minor EQ 1	28 December 2023 03:48:20	94.53% (STFT),
		61.00% (CWD),
		84.12% (WVD),
		41.56% (CWT)
Minor EQ 2	30 December 2023 06:55:00	68.67% (STFT),
		40.78% (CWD),
		67.02% (WVD)
Minor EQ 3	31 December 2023 08:28:20	100% (STFT),
		71.58% (CWD),
		97.76% (WVD),
		93.89% (CWT)
Major EQ	1 January 2024 03:38:20	97.35% (STFT),
		100% (CWD, WVD, CWT)

.

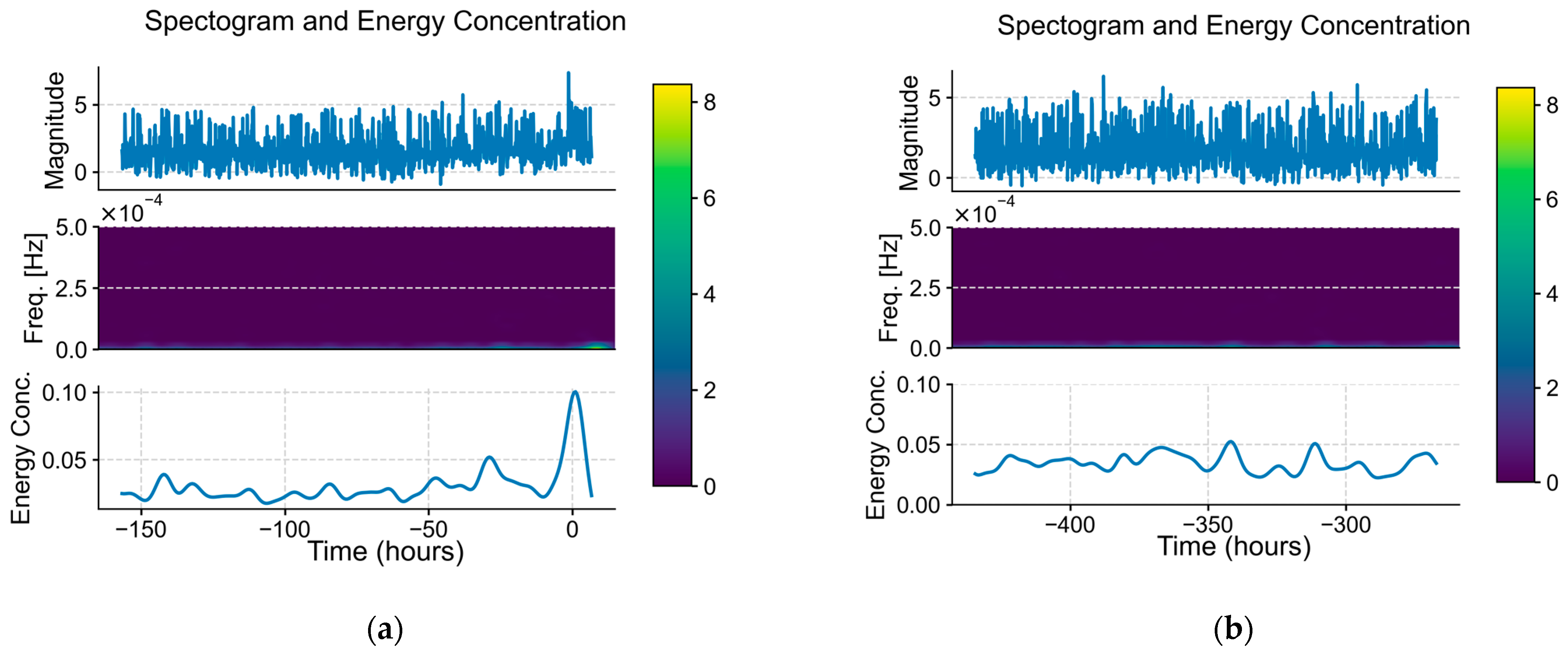
A control is taken such that a different 1-week window from the Turkey–Syria earthquake dataset, with similar seismicity but without a major earthquake. The same process of TFD analysis and mean energy concentration calculation was conducted on the control, and the results (Figure 5) show that no similar pattern—following the definition of the sum of the mean and two standard deviations—could be observed.

It is shown that for all major earthquakes in question, there is at least one minor earthquake occurring between 11 and 66 h prior. This timeframe is consistent with results from different approaches [17,20,21]. On the raw earthquake data, it is noted that lower magnitude level earthquakes are significantly more common compared to higher magnitude level earthquakes (

Table 7. Summary of the raw earthquake signals collected from datasets.

Earthquake	Percentage Between Mw 1.0–4.0	Percentage Mw > 4.0
Turkey–Syria	58.94	8.715
Sulawesi	69.62	30.38
Luzon	97.08	2.96
Kaikōura	93.83	5.71
Noto	79.57	20.43

). It is also noted that earthquakes of magnitudes 4.0 to 5.0 are consciously noticeable, and magnitudes 5.0 to 6.0 are noticeable; however, incidents or injuries caused by these magnitudes are not common [23].

Observing the percentage of minor earthquakes recorded against the percentage of major earthquakes recorded (Table 7), the ratio of recorded minor earthquakes to major earthquakes is staggeringly high. This indicates that the occurrences of minor earthquakes alone do not constitute a precursor to the occurrence of major earthquakes, and as such, observing the time-series data of earthquake signals is insufficient to predict major earthquakes.

In support of this research’s proposed method, the mean energy concentration of the TFD data of the earthquake signals provides possible hints towards the major earthquake occurrences, with peaks corresponding to some of the minor earthquakes. However, it is also noted that not all recorded minor earthquakes have a corresponding mean energy concentration peak, as seen from the overwhelming number of minor earthquakes with magnitudes 1 to 4, compared to only a few mean energy concentration peaks. In other words, the occurrence or lack of minor earthquakes within a timeframe is not the sole factor contributing to the mean energy concentration of that timeframe, but the mean energy concentration is indicative of a signal or data pattern that could indicate a major earthquake.

While the number of major earthquakes analyzed in this research is currently insufficient for rigorous statistical analysis, it can be said that there are no false negative occurrences thus far.

4.1. Necessity of Data Interpolation

To demonstrate the reliability of the data interpolation method for this research’s use case, especially in regards of preservation of the frequency content, a comparison between the time and frequency domains of the dataset before and after interpolation is conducted. Non-Uniform Fast Fourier Transform (NUFFT) is a variation of FFT that enables the calculation of the frequency domain of an unevenly spaced time signal [60]. 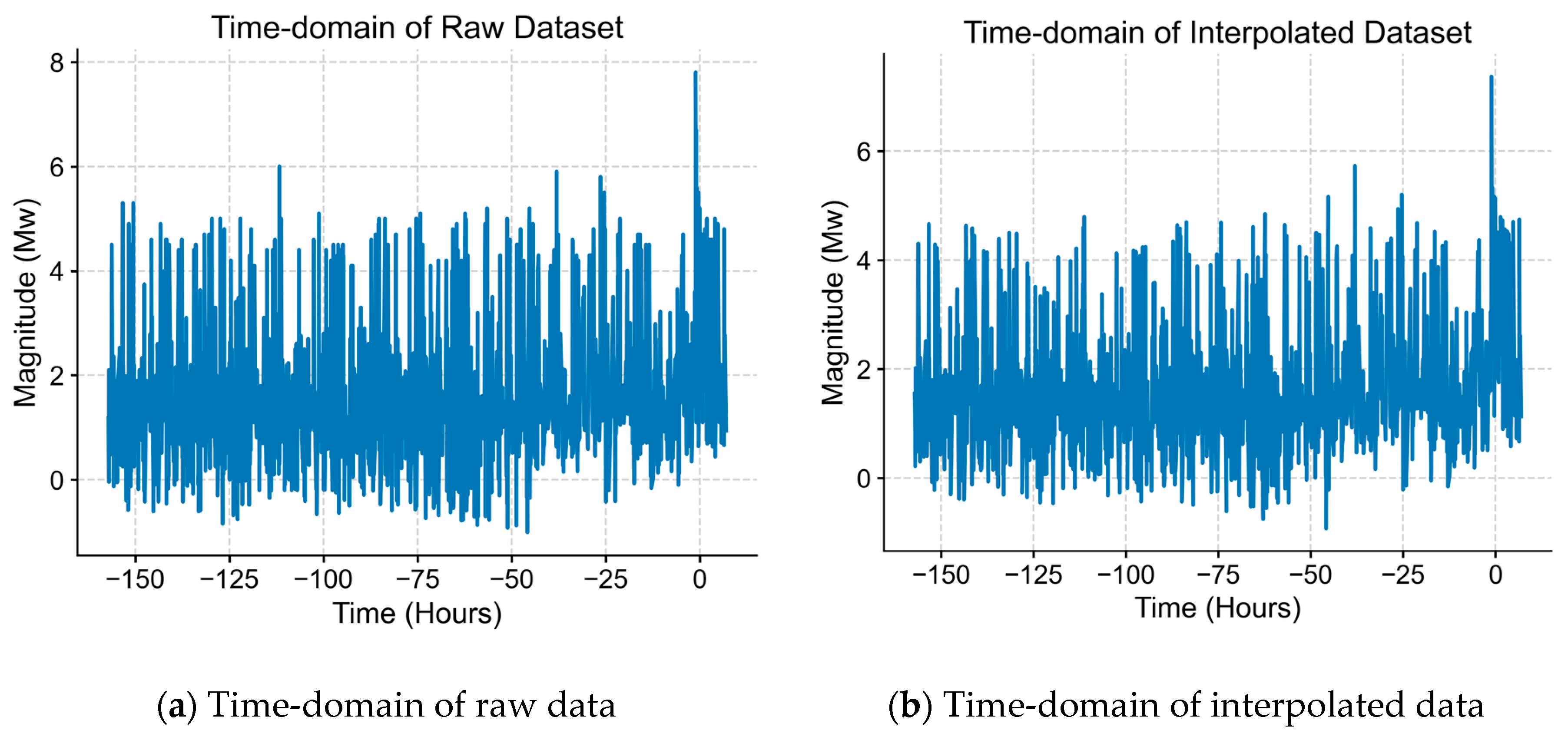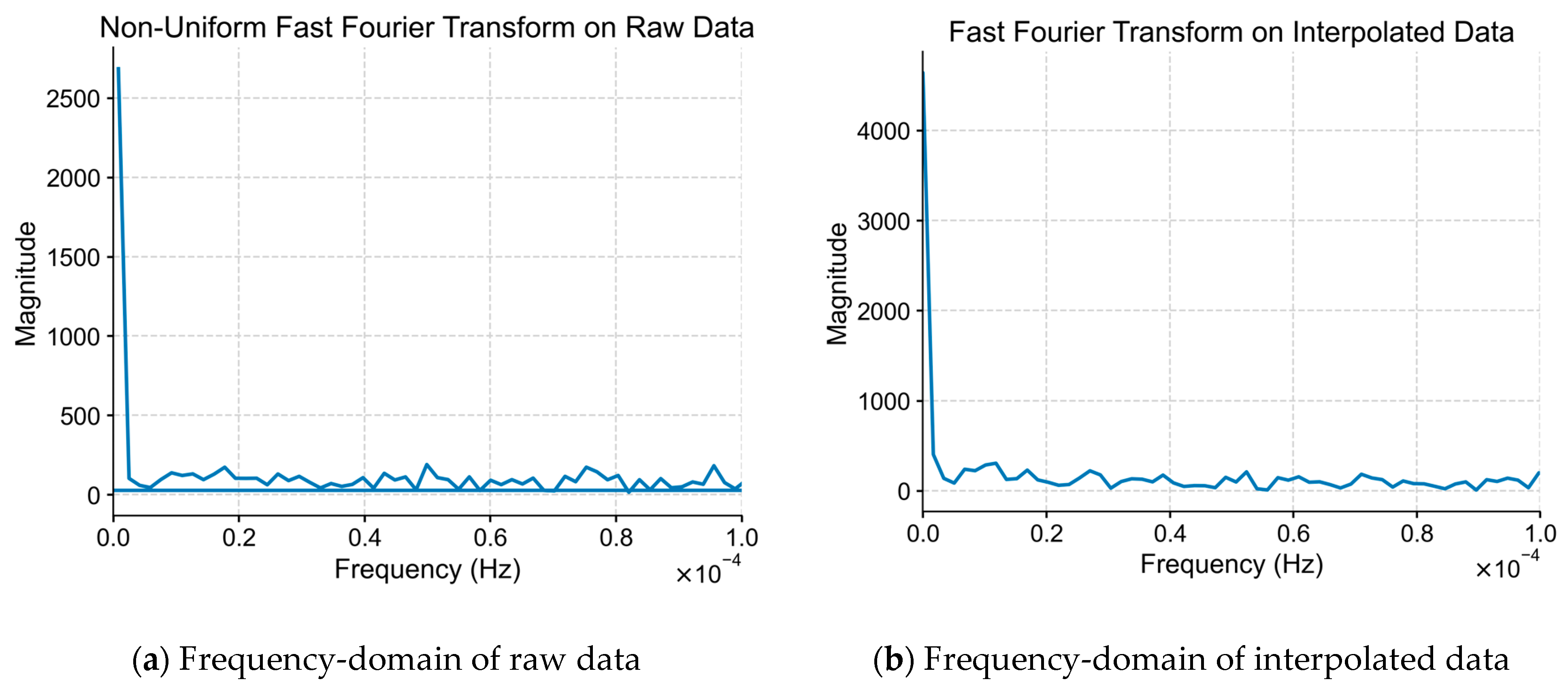Figure 6 and Figure 7 show the comparison in time domain and frequency domain between the NUFFT of raw dataset of the Turkey–Syria earthquake and FFT of interpolated data of the same earthquake, which, in turn, shows that the frequency content of the interpolated data is mostly similar to the raw data, having similar spectral characteristics with minimal distortion especially for the sub-1 Hz frequency range.

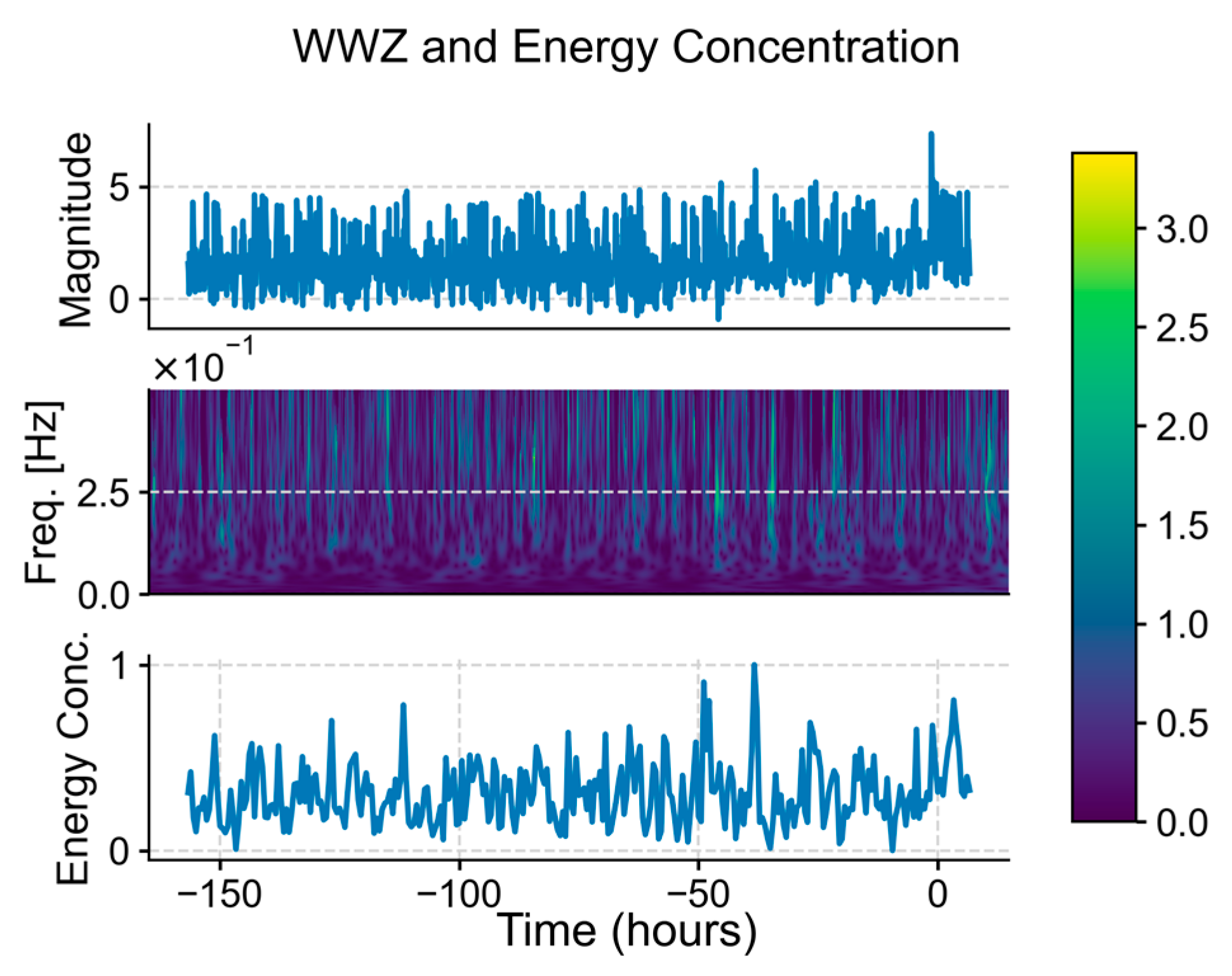
While TFD methods such as Weighted Wavelet Z (WWZ) and Least-Squares Wavelet Analysis (LSWA) account for unevenly spaced data [61], such methods require a new parameter “weight”, which can only be assumed from our dataset unless a proper derivation of the said parameter from the current dataset is available. Without the weight parameter, such methods cannot be considered accurate or viable. In our example, using WWZ with equal weight on all readings of the Turkey–Syria earthquake (Figure 8), we found that it was unable to point out the major earthquake itself compared to the other TFD methods.

On the other hand, linear interpolation (and other simple interpolation) methods also provide a better computational accessibility, especially for complex TFDs (WVD and CWD), as opposed to zero-insertion, where values in between existing data are usually assumed to be zero to an arbitrary resolution, which causes a drastic leap in processing cost and time in our use case, as the resolution in question that can work is 1 s, i.e., inserting zero every second if there is no reading.

4.2. Endpoint Effect

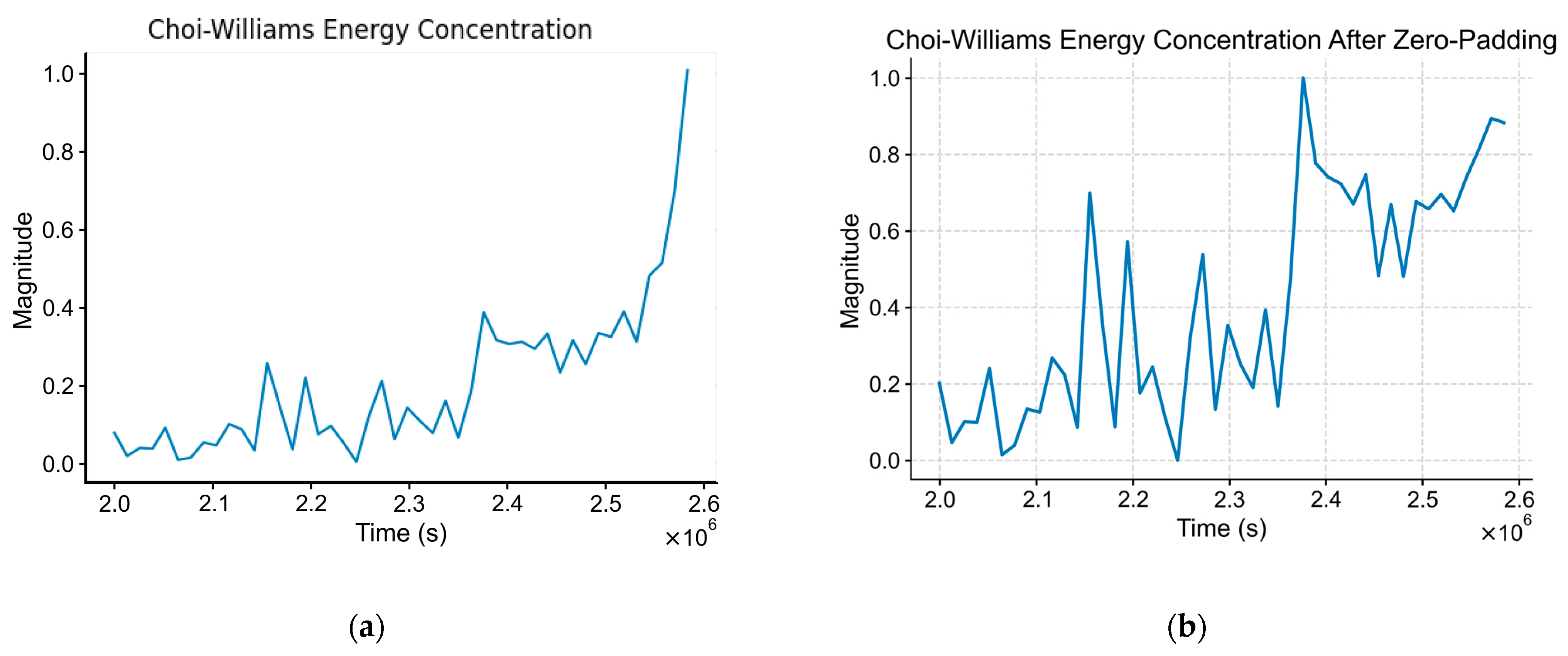
It is worth noting that the earthquake catalog for the Sulawesi earthquake spanned until 29 September 2018 23:54:50 UTC, which is relatively close to the main shock at around 28 September 2018 10:02:00 UTC. This may cause an error during the TFD process known as the endpoint effect, which causes distorted or inaccurate representations of the signal’s time–frequency content near the edges of the analyzed signal [62]. For this reason, the input signal for the Sulawesi earthquake analysis was zero-padded at the endpoint to artificially increase the span of the dataset in order to reduce the endpoint effect. The effectiveness of this method is shown in Figure 9, where the energy concentration at the endpoint of the post-zero-padded input signal showed less compared to without zero-padding, while the rest of the energy concentration features remained the same.

4.3. TFD Comparisons

Among the visualized results (STFT, CWD, WVD, CWT), STFT visualization is the easiest to understand intuitively, followed by CWT, and is more suitable for viewing, while CWD and WVD showed more well-defined mean energy concentration visualizations. In terms of accuracy, CWD shows a more accurate-to-reality graph of mean energy concentration, correctly placing all major peaks at 100% mean energy concentration, as opposed to STFT and WVD (see Figure A1c as opposed to Figure A1a,b), while CWT, although having some similar features in its mean energy concentration graph with STFT, CWD, and WVD such as the presence of minor peaks and major peaks, seems to be the most different from the rest. This can be attributed to the fact that CWT does not produce a time–frequency domain result of the input signal, but rather a time-scale output.

The fundamentals of earthquakes lie in the complex interactions of the Earth’s lithosphere at plate boundaries, and understanding these interactions is the key to studying earthquake mechanisms and potentially predicting their occurrence [63,64]. Due to the non-linear nature of lithosphere dynamics causing non-stationary, time-varying, and multi-spectral earthquake motion, non-linear TFDs (WVD, CWD) prove to be more effective as compared to linear TFD (STFT), showing more well-defined mean energy concentration visualization. Of the Cohen’s class TFDs used, it can be concluded that CWD is more effective and accurate between the two. This conclusion is expected as CWD does have advantages over WVD in multi-component signal analysis [65]. A summary of the CWD TFDs results across all earthquake datasets is shown in

Table 8. Summary of mean energy concentration calculated via Choi–Williams distribution peaks and corresponding earthquakes.

Earthquake	No. of Peaks	Estimate Time Between Neighboring Peaks
Turkey–Syria	2	13 h
Sulawesi	3	30 h
Luzon	4	23 h
Kaikōura	2	60 h
Noto	4	20 h

.

4.4. Limitations and Further Research

This research employs only the magnitude and timestamp of the earthquake datasets in the investigated regions to form a time-series signal in the method of analysis, and, therefore, can be used to estimate the time, magnitude, and the region of major earthquake, which fall short of the strict classification of earthquake prediction (time, size, and location) [66]. Various other measured parameters have yet to be included in the calculation.

In addition, the number of datasets analyzed in this research is yet to be sufficient for rigorous statistical testing to account for false positives, true negatives, and false negatives, and, thus, warrants further research, especially in collaboration with geostations to obtain unfiltered datasets spanning years.

The time window between the precursor pattern to the major earthquake found in this research ranges between 11 and 66 h, which perhaps is acceptable for a prediction timeframe, providing enough time for authorities to warn the public; however, the authors believe that the accuracy of the time window can be further improved with more complete data at a higher and regular sampling rate to achieve the criteria of earthquake prediction. Furthermore, the authors believe that the currently used Mw scale may not be suitable especially for analysis of minor earthquakes associated with major earthquakes and therefore recommend the usage of magnitude scales in datasets that have better precision for minor earthquakes especially with Mw < 7.5, such as the Mwg or the Das scale, which provides improved accuracy through the integration of global seismic data [67]. This suggested change addresses the current limitations of the Mw scale for precision of minor earthquakes and would enhance the reliability of the precursor detection while maintaining an energy-based framework for analysis. The authors also believe that deep learning-based methods in combination with the proposed TFDs analysis would be able to provide a prediction process with enhanced efficiency and efficacy, possibly solving the issue of sparse data in our proposed process [68].

5. Conclusions

In this study, we have explored the utilization of Time–Frequency Distributions (TFDs) on seismic signals, demonstrating the effectiveness of TFD-based techniques and enabling the identification of patterns leading to major earthquakes. Notably, non-linear quadratic Cohen’s class TFDs, especially the Choi–Williams Distribution (CWD), prove to be more effective and accurate in analyzing earthquake records as they are non-stationary, multi-spectral, and time-varying in nature.

Through experimentation on real-world earthquakes, the results indicate that TFD-based techniques show great potential in enabling short-term prediction of seismic events with Mw above 6.0. The usage of TFDs provides valuable insights into the dynamics of earthquakes, while the identification of diagnostic precursor patterns enables improved prediction capabilities. This information can aid in the development of advanced prediction models and early warning systems, and, consequently, proactive measures for disaster and potentially reduce human and economic losses caused by earthquakes. With a reliable prediction method, countries expecting a major earthquake in the upcoming years, such as Japan [69] and the Philippines [70], would be able to better prepare their citizens and crisis teams.

A similar sentiment extends to smaller earthquakes, containing insight into future larger earthquakes [31,32,33,34]. This paper concludes that the analysis of earthquake records using TFDs opens new possibilities in earthquake short-term prediction, a possibility that many considered to be impossible previously. The advancements made in this study contribute to the growing body of knowledge in seismology.