Performance of Fault-Controlled Hydrothermal System: Insights from Multi-Field Coupled Rock Mechanics Analysis
Abstract
1. Introduction
2. Model Description
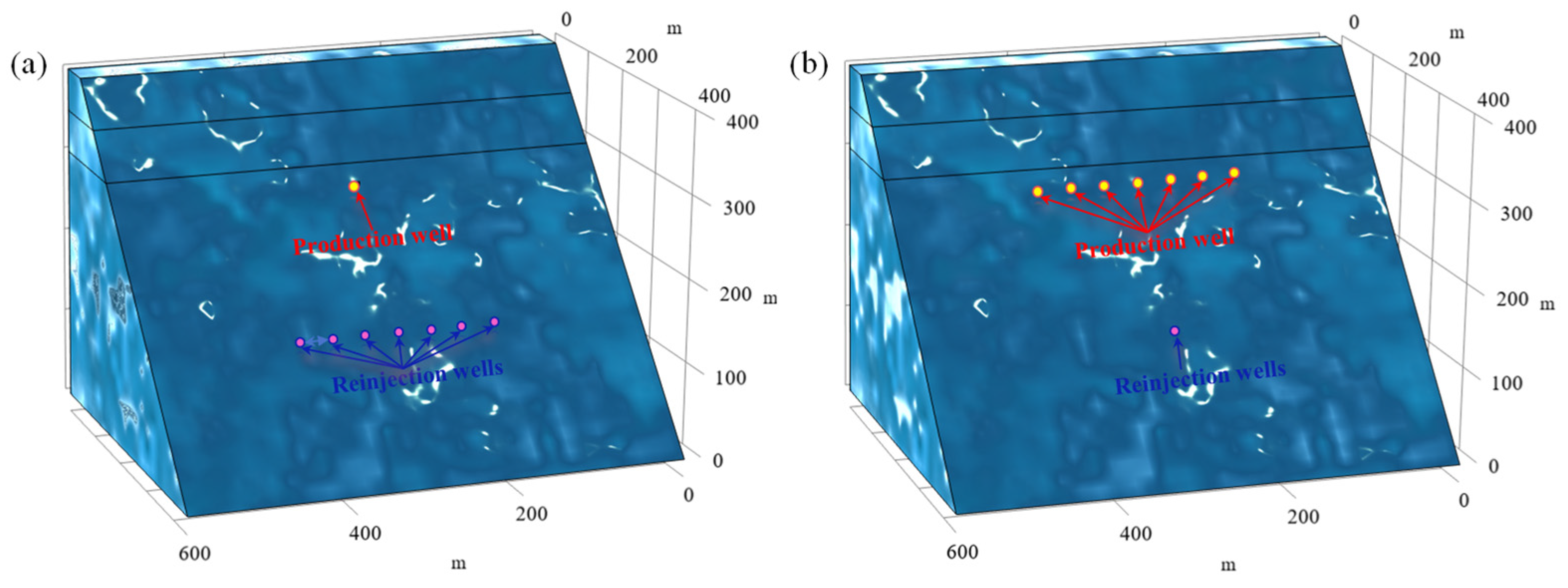
2.1. Geometric Model
2.2. Model Definition and Assumption
2.3. THM Coupling Mathematical Model of Fault-Aquifer
2.3.1. Seepage Control Equations
2.3.2. Mechanical Constitutive and Porosity Evolution Equations
2.3.3. Control Equations of Thermal Transfer
2.3.4. Evaluation Equation of the Thermal Recovery Performance
2.3.5. Evaluation Equation of Fault Stability
2.3.6. Parameter Analysis and Discussion
2.4. Boundary Conditions and Initial Conditions
2.4.1. Boundary Conditions
2.4.2. Initial Conditions
2.4.3. Mesh Generation
2.4.4. Computer Implementation
2.5. Parameters of the Numerical Model
2.6. Model Verification
3. Results
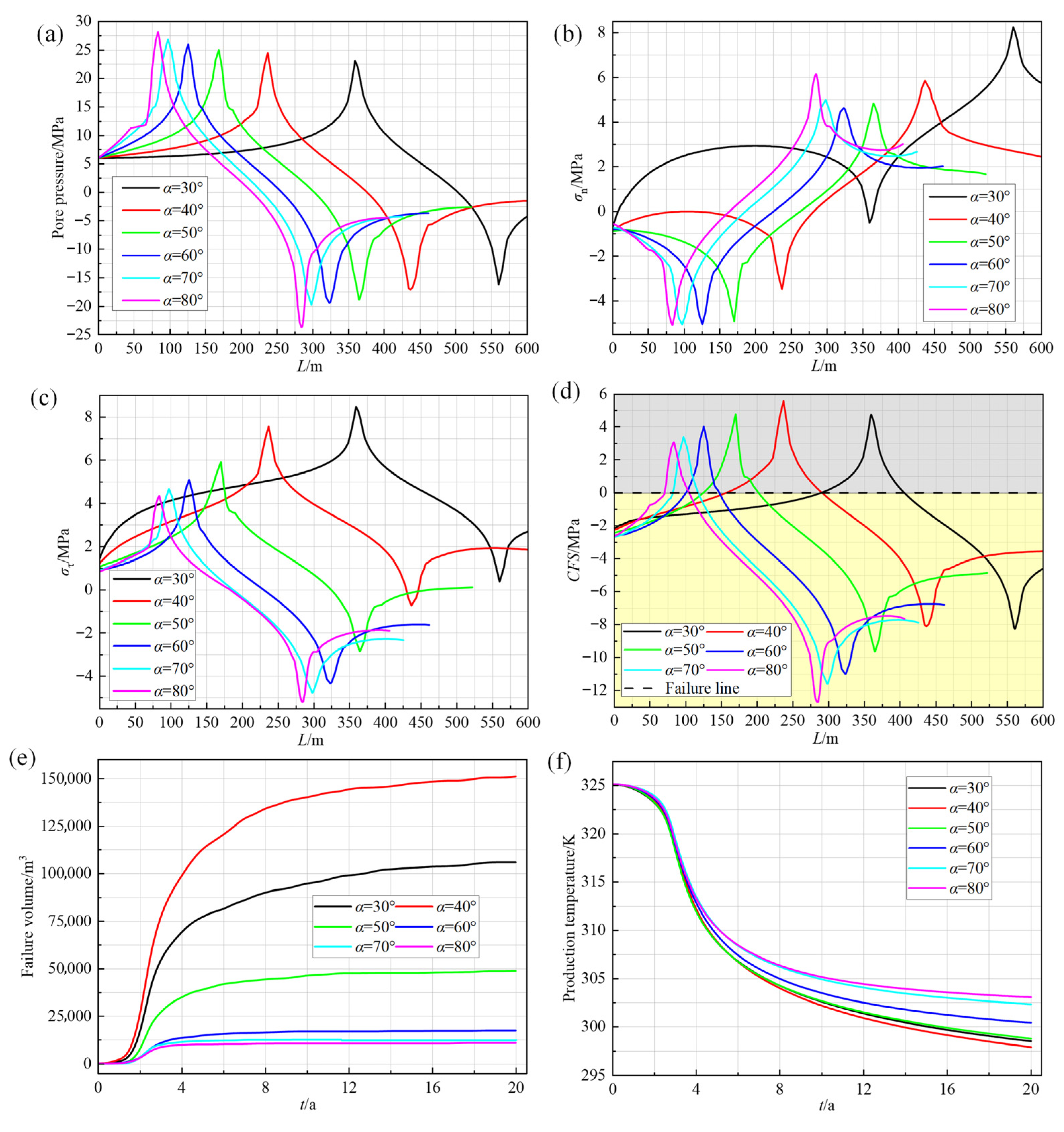
3.1. Evolution of Seepage-Stress-Temperature Characteristics of Fault Rock Mass Under Equilibrium Reinjection/Production
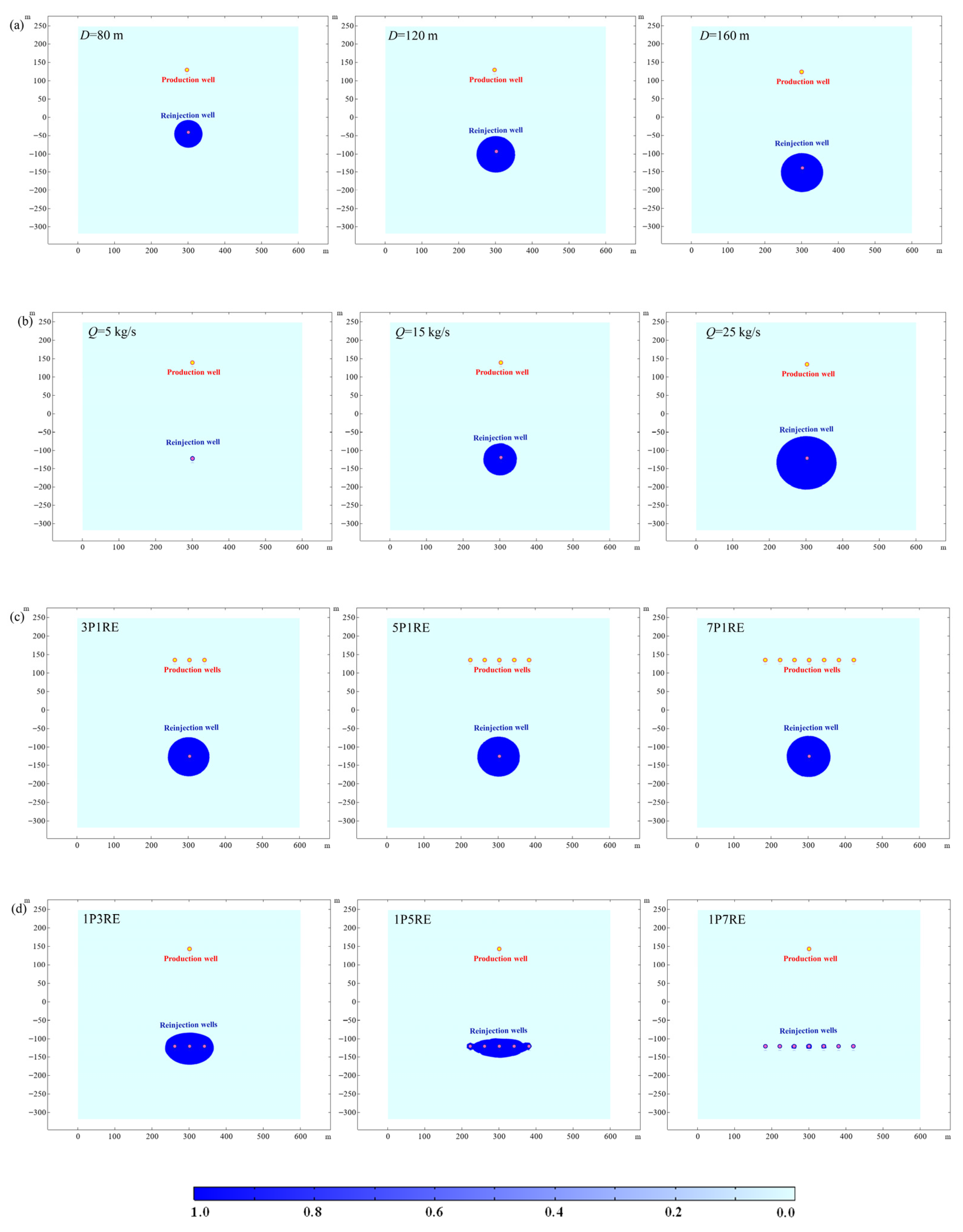
3.2. The Influence of Well Parameters on Fault Stability
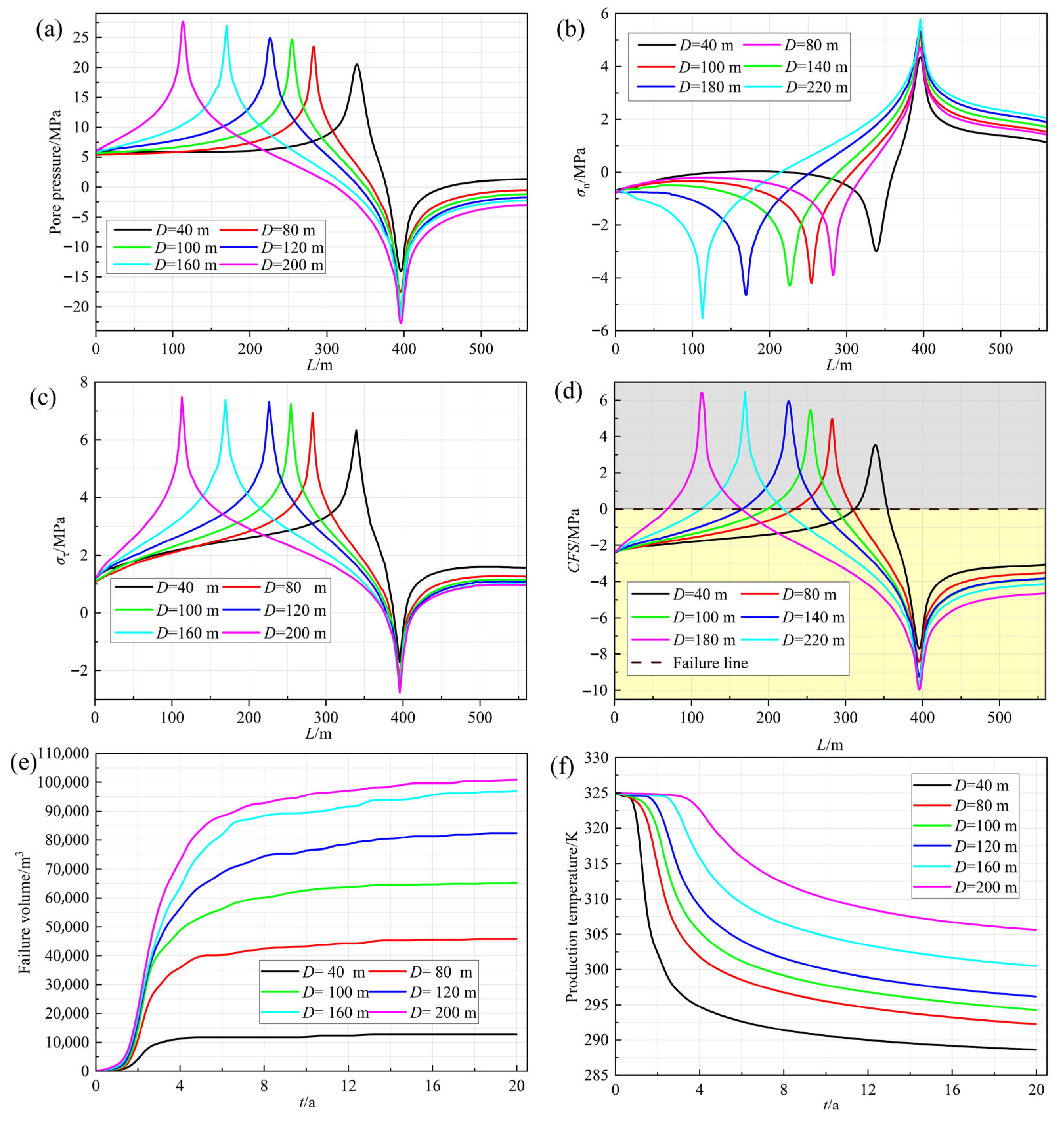
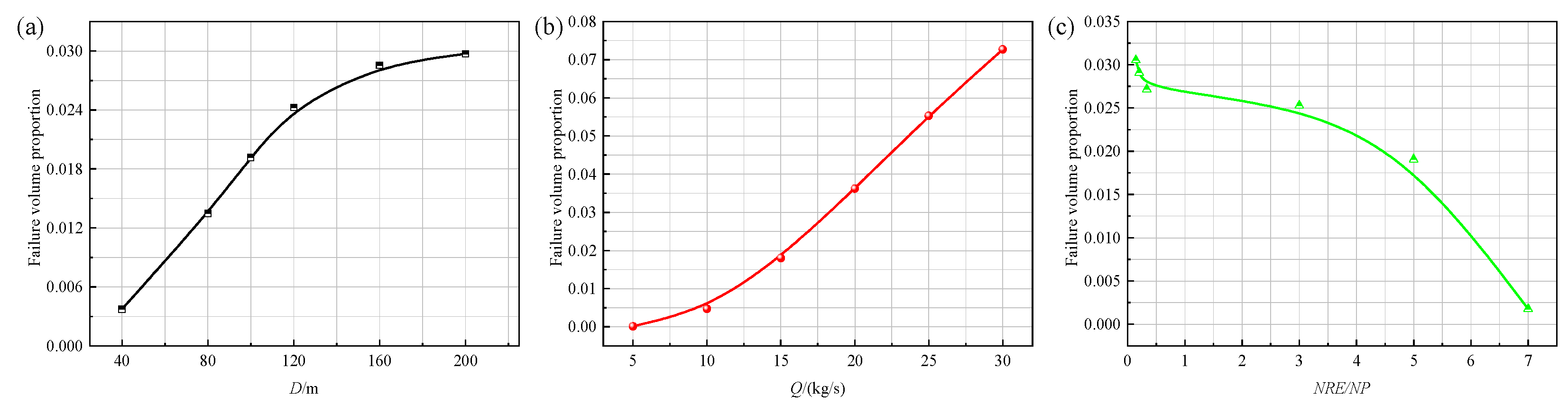
3.2.1. Well Spacing
3.2.2. Production/Reinjection Flow Rate
3.2.3. Number of Production/Reinjection Sub-Wells
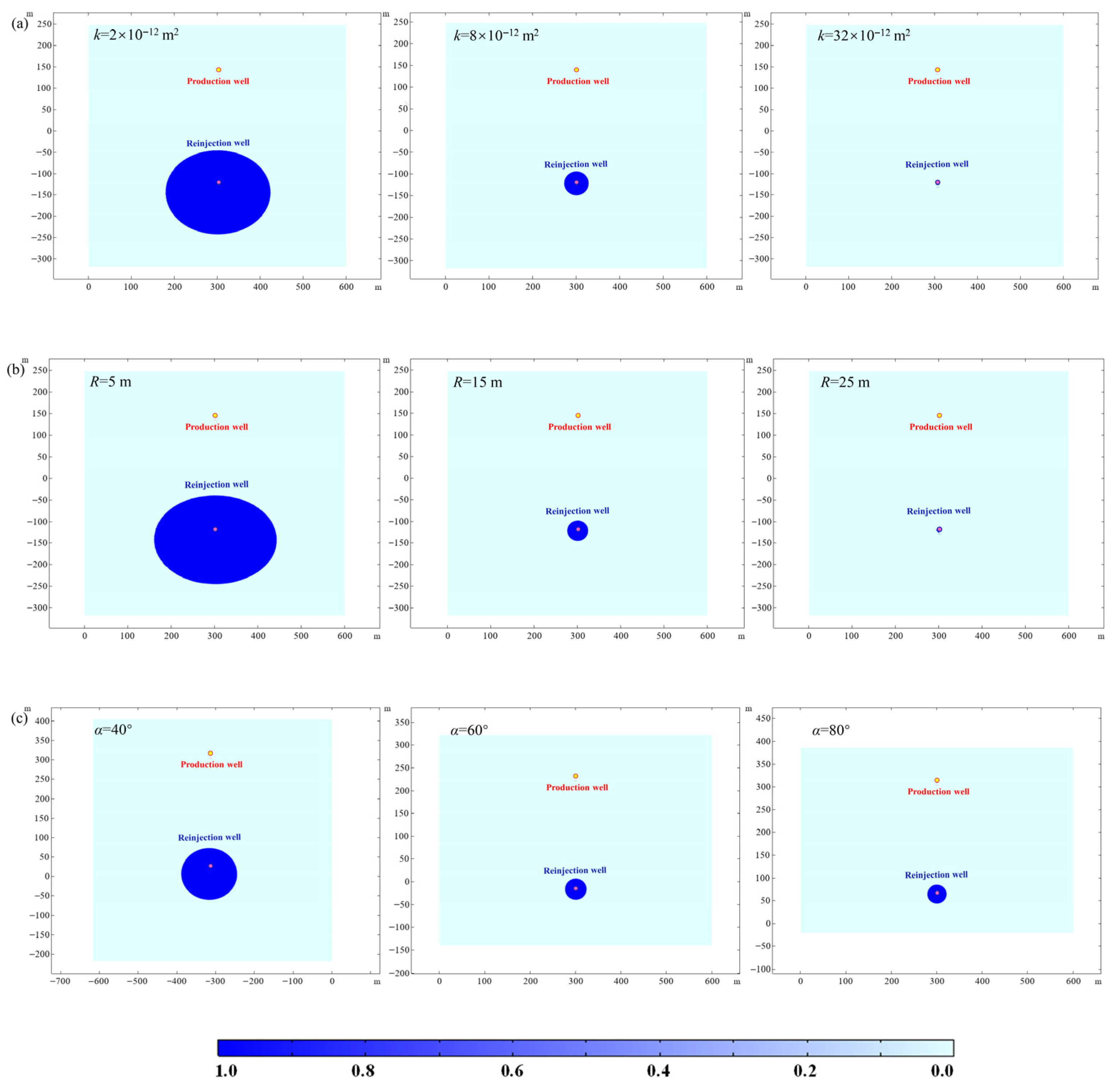
3.3. The Influence of Fault Parameters on Fault Stability
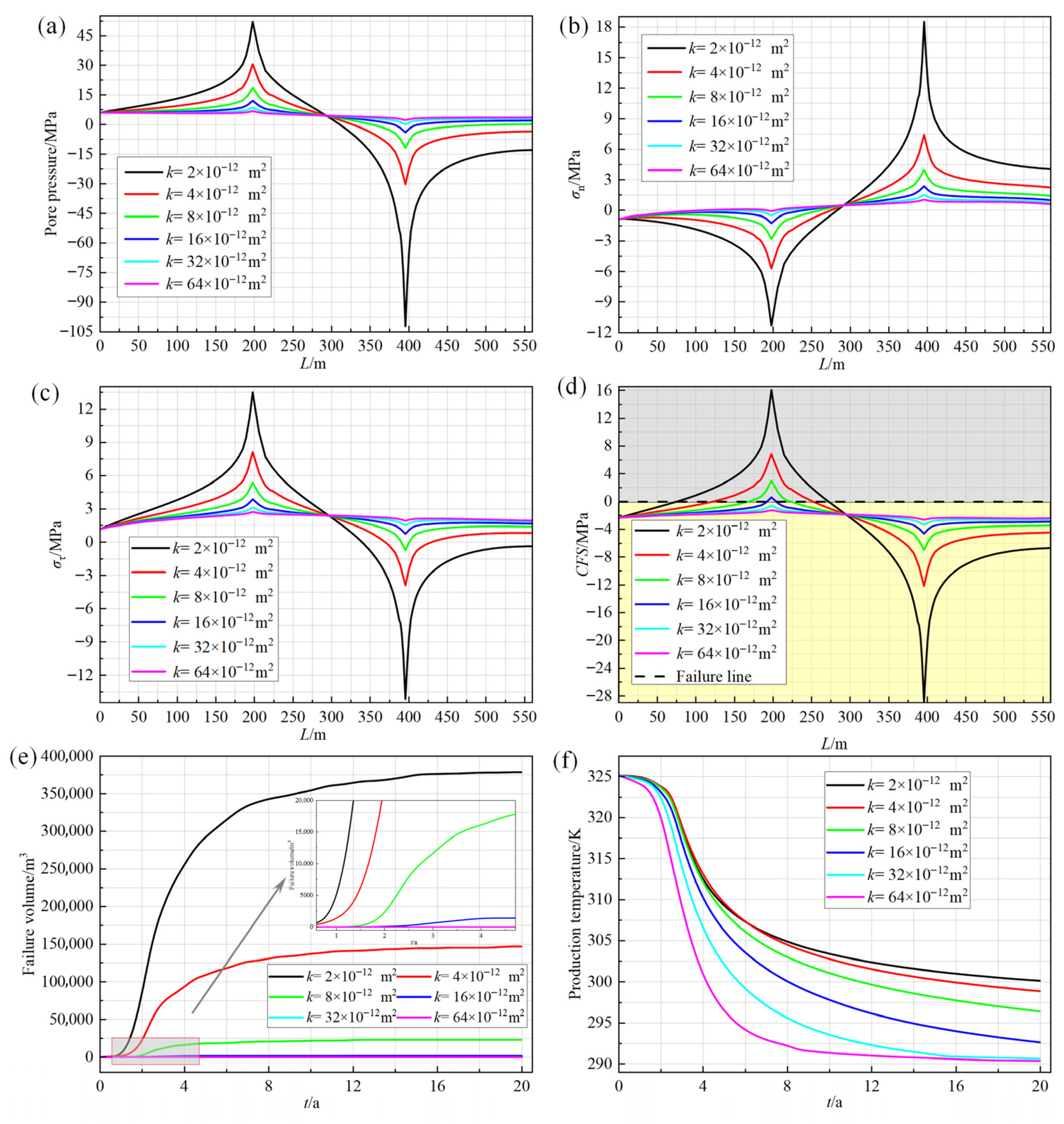
3.3.1. Initial Permeability of Fault
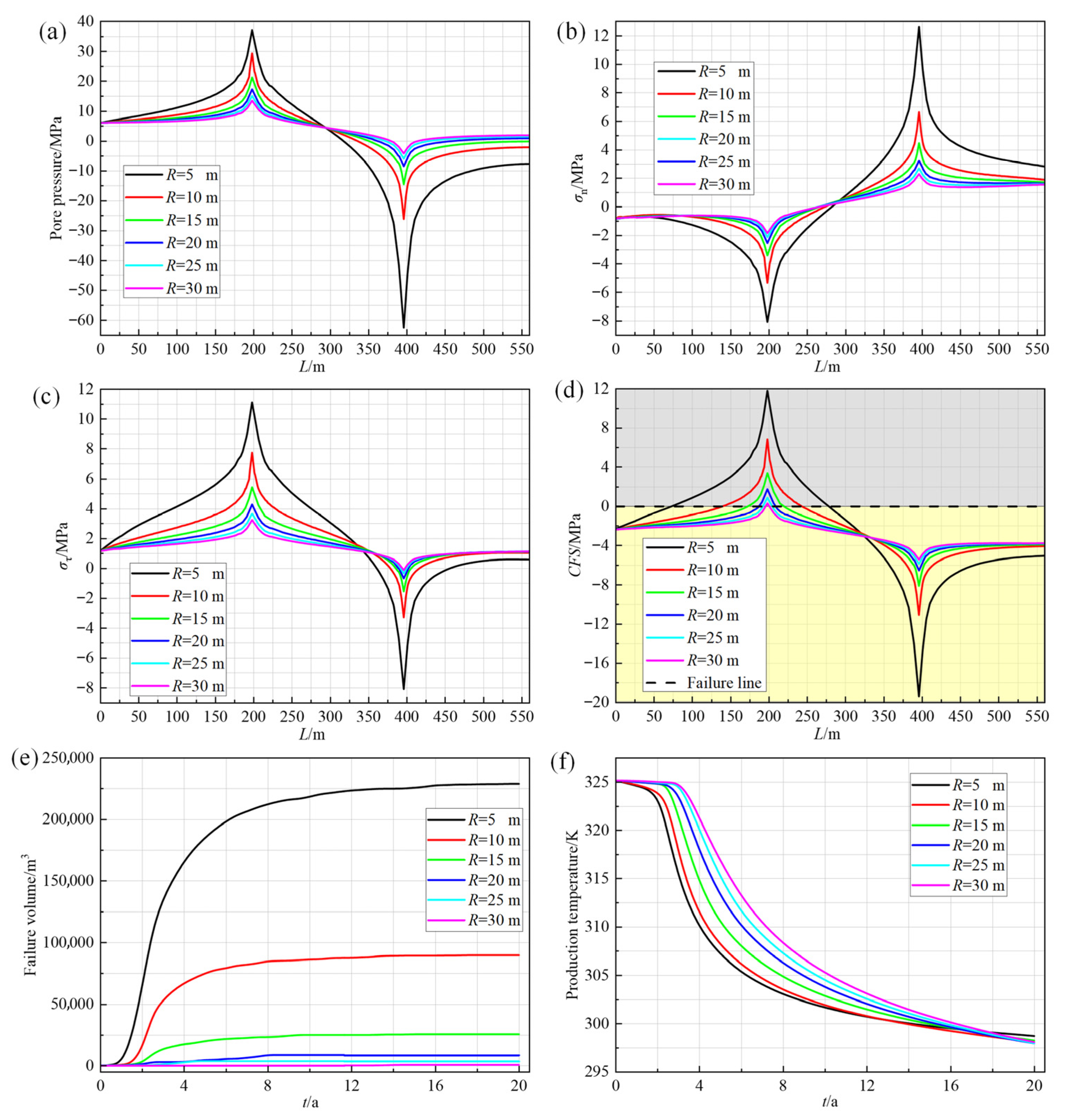
3.3.2. Fault Thickness
3.3.3. Fault Dip-Angle
4. Discussion
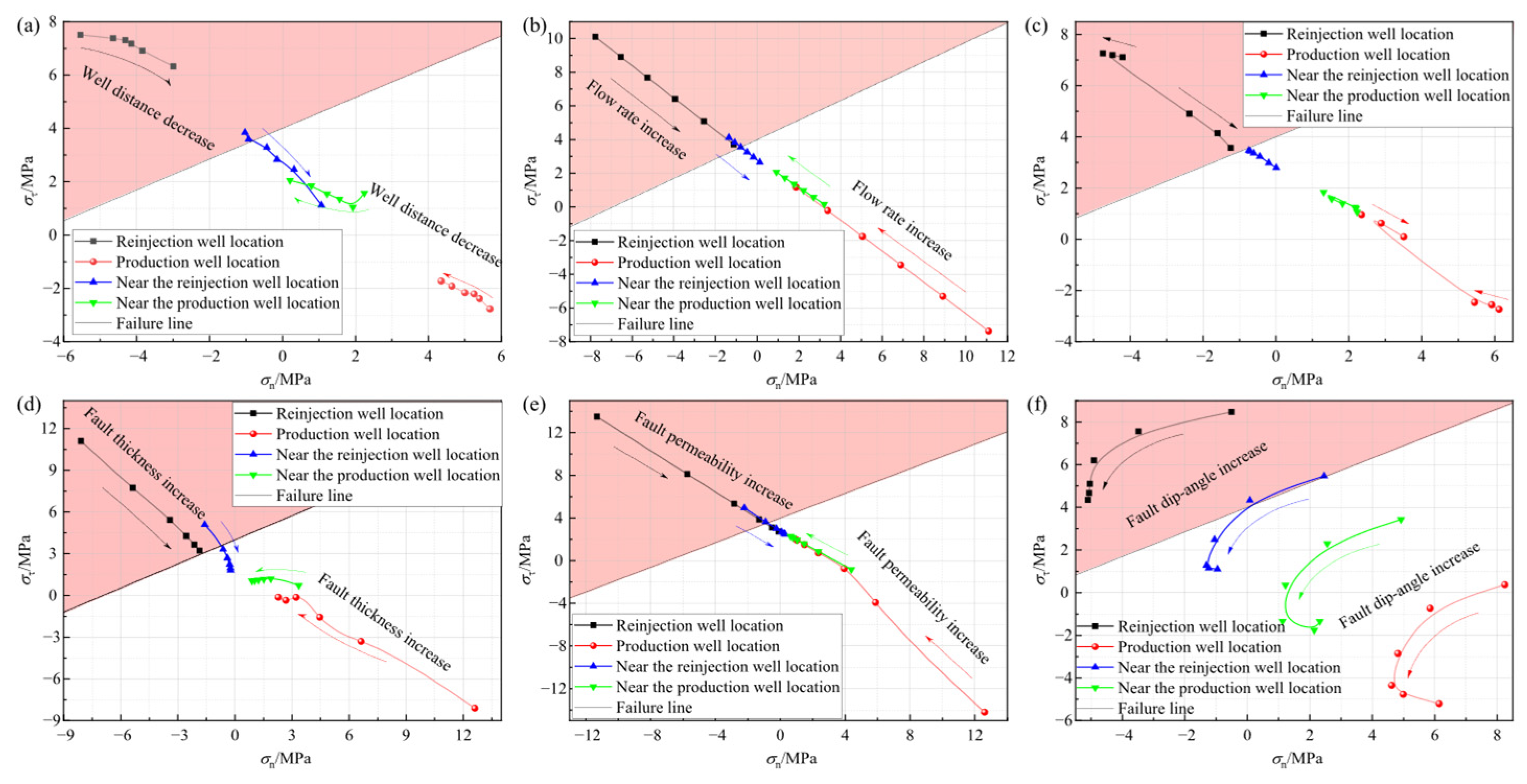
4.1. The Stress Path of Fault Rock Mass Under Different Fault and Well Parameters
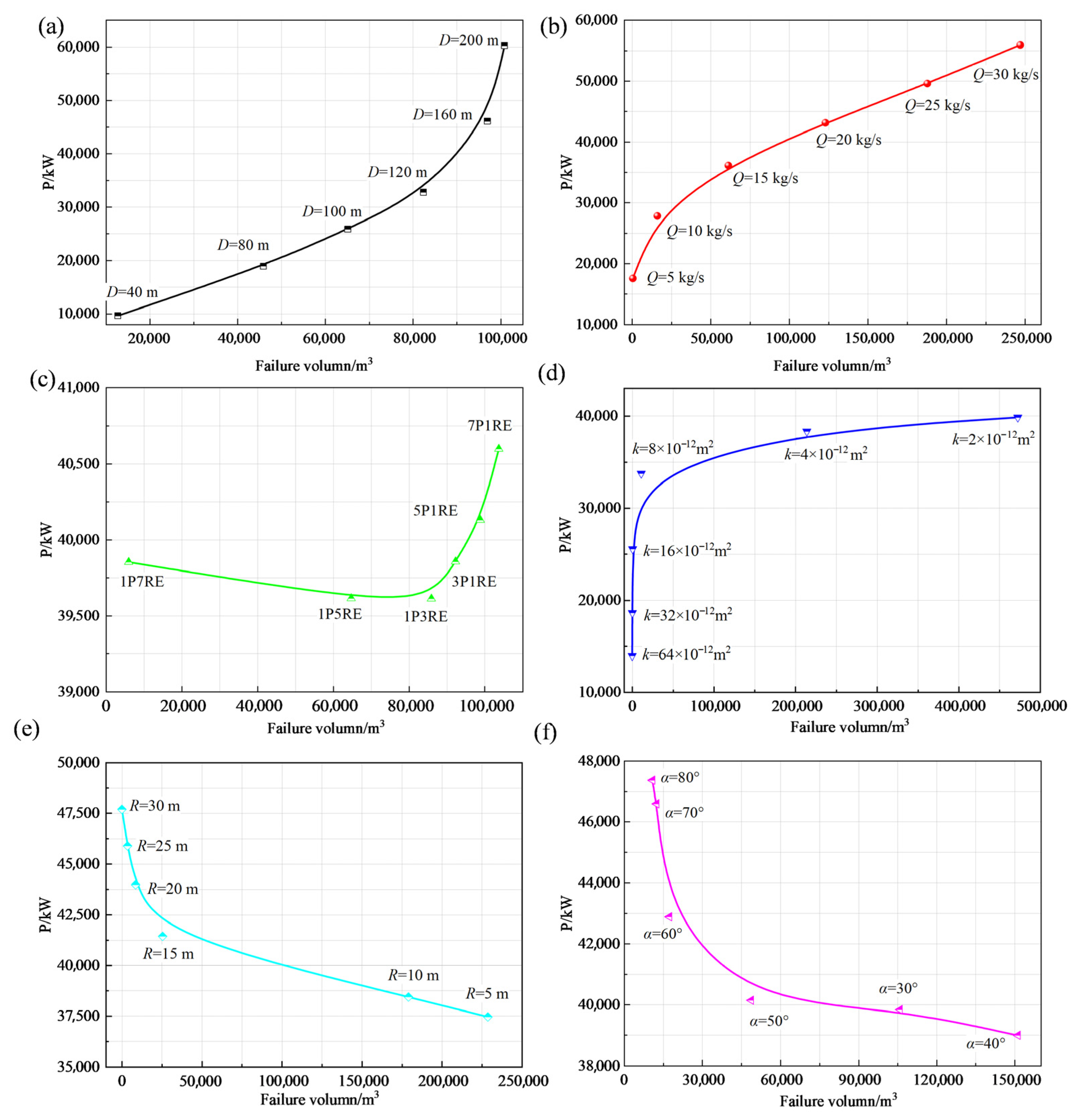
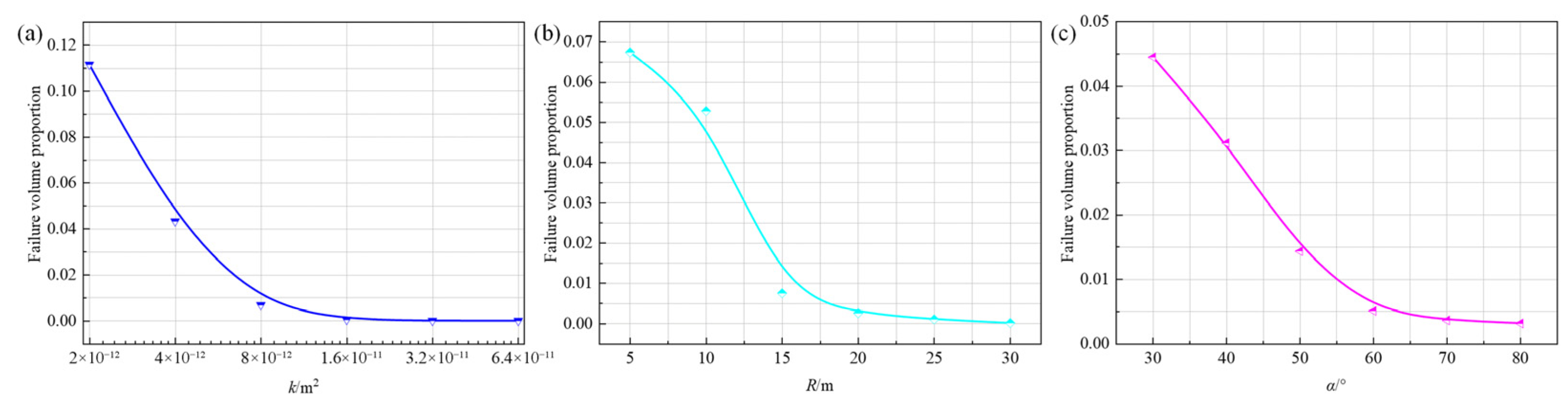
4.2. Relationship Between the Failure Volume and Thermal Recovery Performance
4.3. Relationship Between the Fault Parameters and Failure Zone
4.4. Relationship Between Production Well Parameters and Failure Zone
4.5. Comparison of Key Findings with Previous Studies
4.6. Future Work and Perspective
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FHS | Fault-controlled hydrothermal system |
| THM | Thermo-Hydro-Mechanical |
| TRP | Thermal recovery performance |
| EGS | Enhanced geothermal systems |
| CFS | Coulomb failure stress |
References
- Barbier, E. Geothermal energy technology and current status: An overview. Renew. Sustain. Energy Rev. 2002, 6, 3–65. [Google Scholar] [CrossRef]
- Liu, T.; Xu, G.; Cai, P.; Tian, L.H.; Huang, Q.L. Development forecast of renewable energy power generation in China and its influence on the GHG control strategy of the country. Renew. Energy 2011, 36, 1284–1292. [Google Scholar] [CrossRef]
- Bertani, R. Geothermal power generation in the world 2010–2014 update report. Geothermics 2016, 60, 31–43. [Google Scholar] [CrossRef]
- Soltani, M.; Kashkooli, F.M.; Souri, M.; Rafiei, B.; Jabarifar, M.; Gharali, K.; Nathwani, J.S. Environmental, economic, and social impacts of geothermal energy systems. Renew. Sustain. Energy Rev. 2021, 140, 110750. [Google Scholar] [CrossRef]
- Yang, W.F.; Xiao, C.L.; Jia, Z.L.; Liang, X.J.; Feng, B. Evaluation of the viability of exploitation of hydrothermal resources in the Southern Songliao Basin (China) by integrating resource, demand, and economy. Geothermics 2024, 120, 103022. [Google Scholar] [CrossRef]
- Luo, J.; Xue, W.; Lu, X.S. Characterization of the hydrothermal potential for the cap strata of Yangzte Block (YB), China. Geothermics 2021, 96, 102148. [Google Scholar] [CrossRef]
- An, Q.S.; Wang, Y.Z.; Zhao, J.; Luo, C.; Wang, Y. Direct utilization status and power generation potential of low-medium temperature hydrothermal geothermal resources in Tianjin, China: A review. Geothermics 2016, 64, 426–438. [Google Scholar] [CrossRef]
- Li, Q.; Li, X.B.; Yin, T.B. Factors affecting pore structure of granite under cyclic heating and cooling: A nuclear magnetic resonance investigation. Geothermics 2021, 96, 102198. [Google Scholar] [CrossRef]
- Hou, W.T.; Ma, D.; Liu, X.W.; Zhang, J.X. Experimental study on hydraulic and mechanical properties of fault rock under the thermal-hydraulic-mechanical coupling. Geothermics 2024, 119, 102975. [Google Scholar]
- Konrad, F.; Savvatis, A.; Degen, D.; Wellmann, F.; Einsiedl, F.; Zosseder, K. Productivity enhancement of geothermal wells through fault zones: Efficient numerical evaluation of a parameter space for the Upper Jurassic aquifer of the North Alpine Foreland Basin. Geothermics 2021, 95, 102119. [Google Scholar] [CrossRef]
- Duwiquet, H.; Magri, F.; Lopez, S.; Guillon, T.; Arbaret, L.; Bellanger, M.; Guillou-Frottier, L. Tectonic Regime as a Control Factor for Crustal Fault Zone (CFZ) Geothermal Reservoir in an Amagmatic System: A 3D Dynamic Numerical Modeling Approach. Nat. Resour. Res. 2022, 31, 3155–3172. [Google Scholar] [CrossRef]
- Kivi, I.R.; Vilarrasa, V.; Kim, K.; Yoo, H.; Min, K. On the role of poroelastic stressing and pore pressure diffusion in discrete fracture and fault system in triggering post-injection seismicity in enhanced geothermal systems. Int. J. Rock Mech. Min. Sci. 2024, 175, 105673. [Google Scholar] [CrossRef]
- Jeanne, P.; Rutqvist, J.; Dobson, P.F.; Walters, M.; Hartline, C.; Garcia, J. The impacts of mechanical stress transfers caused by hydromechanical and thermal processes on fault stability during hydraulic stimulation in a deep geothermal reservoir. Int. J. Rock Mech. Min. Sci. 2014, 72, 149–163. [Google Scholar] [CrossRef]
- Gan, Q.; Lei, Q.H. Induced fault reactivation by thermal perturbation in enhanced geothermal systems. Geothermics 2020, 86, 101814. [Google Scholar] [CrossRef]
- Yu, P.L.; Dempsey, D.; Archer, R. A three-dimensional coupled thermo-hydro-mechanical numerical model with partially bridging multi-stage contact fractures in horizontal-well enhanced geothermal system. Int. J. Rock Mech. Min. Sci. 2021, 143, 104787. [Google Scholar] [CrossRef]
- Wu, Z.J.; Cui, W.J.; Weng, L.; Liu, Q.S. Modeling geothermal heat extraction-induced potential fault activation by developing an FDEM-based THM coupling scheme. Rock Mech. Rock Eng. 2023, 56, 3279–3299. [Google Scholar] [CrossRef]
- Ji, Y.L.; Yoon, J.S.; Zang, A.; Wu, W. Mitigation of injection-induced seismicity on undrained faults in granite using cyclic fluid injection: A laboratory study. Int. J. Rock Mech. Min. Sci. 2021, 146, 104881. [Google Scholar] [CrossRef]
- Sabah, M.; Ameri, M.J.; Hofmann, H.; Ebrahimi, M. Numerical modeling of injection-induced earthquakes based on fully coupled thermo-poroelastic boundary element method. Geothermics 2022, 105, 102481. [Google Scholar]
- Ishii, E. A conventional straddle-sliding-packer system as a borehole extensometer: Monitoring shear displacement of a fault during an injection test. Eng. Geol. 2020, 275, 105748. [Google Scholar] [CrossRef]
- Gan, Q.; Feng, Z.J.; Zhou, L.; Li, H.L.; Liu, J.; Elsworth, D. Down-dip circulation at the united downs deep geothermal power project maximizes heat recovery and minimizes seismicity. Geothermics 2021, 96, 102204. [Google Scholar] [CrossRef]
- Li, X.Y.; Lei, X.L.; Li, Q. Fault nucleation of tight sandstone by investigation of mechanical, acoustic, and hydraulic responses. Eng. Geol. 2021, 292, 106254. [Google Scholar] [CrossRef]
- Zhao, C.X.; Liu, J.F.; Dai, H.Y.; Huang, H.Y.; Shi, X.C. Frictional evolution process and stability properties of Longmaxi shale under fluid injection. Energy 2024, 294, 130910. [Google Scholar] [CrossRef]
- Jing, J.; Yang, Y.L.; Cheng, J.M.; Ding, Z.J.; Wang, D.D.; Jing, X.W. Analysis of the effect of formation dip angle and injection pressure on the injectivity and migration of CO2 during storage. Energy 2023, 280, 128021. [Google Scholar] [CrossRef]
- Soltanzadeh, H.; Hawkes, C.D. Assessing fault reactivation tendency within and surrounding porous reservoirs during fluid production or injection. Int. J. Rock Mech. Min. Sci. 2009, 46, 1–7. [Google Scholar] [CrossRef]
- Schwartzkopff, A.K.; Sainoki, A.; Elsworth, D. Numerical simulation of mixed aseismic/seismic fault-slip induced by fluid injection using coupled X-FEM analysis. Int. J. Rock Mech. Min. Sci. 2021, 147, 104871. [Google Scholar] [CrossRef]
- Daniilidis, A.; Saeid, S.; Doonechaly, N.G. The fault plane as the main fluid pathway: Geothermal field development options under subsurface and operational uncertainty. Renew. Energy 2021, 171, 927–946. [Google Scholar] [CrossRef]
- Daniilidis, A.; Nick, H.M.; Bruhn, D.F. Interference between geothermal doublets across a fault under subsurface uncertainty; implications for field development and regulation. Geothermics 2021, 91, 102041. [Google Scholar] [CrossRef]
- Duan, H.Y.; Ma, D.; Zou, L.C.; Xie, S.J.; Liu, Y. Co-exploitation of coal and geothermal energy through water-conducting structures: Improving extraction efficiency of geothermal well. Renew. Energy 2024, 228, 120666. [Google Scholar]
- Zimmerman, R.W.; Al-Yaarubi, A.; Pain, C.C.; Grattoni, C.A. Non-linear regimes of fluid flow in rock fractures. Int. J. Rock Mech. Min. Sci. 2004, 41, 384. [Google Scholar]
- Ma, D.; Miao, X.X.; Chen, Z.Q.; Mao, X.B. Experimental investigation of seepage properties of fractured rocks under different confining pressures. Rock Mech. Rock Eng. 2013, 46, 1135–1144. [Google Scholar] [CrossRef]
- Lee, D.J.; Chen, G.W.; Liao, Y.C.; Hsieh, C.C. On the free-settling test for estimating activated sludge floc density. Water Res. 1996, 30, 541–550. [Google Scholar] [CrossRef]
- Ma, D.; Duan, H.Y.; Zhang, J.X. Solid grain migration on hydraulic properties of fault rocks in underground mining tunnel: Radial seepage experiments and verification of permeability prediction. Tunn. Undergr. Space Technol. 2022, 126, 104525. [Google Scholar] [CrossRef]
- Taghipour, M.; Ghafoori, M.; Lashkaripour, G.R.; Moghaddas, N.H.; Molaghab, A. A geomechanical evaluation of fault reactivation using analytical methods and numerical simulation. Rock Mech. Rock Eng. 2021, 54, 695–719. [Google Scholar]
- Hyman, J.D.; Sweeney, M.R.; Frash, L.P.; Carey, J.W.; Viswanathan, H.S. Scale-bridging in three-dimensional fracture networks: Characterizing the effects of variable fracture apertures on network-scale flow channelization. Geophys. Res. Lett. 2021, 48, e2021GL094400. [Google Scholar]
- Kang, P.K.; Lei, Q.H.; Dentz, M.; Juanes, R. Stress-induced anomalous transport in natural fracture networks. Water Resour. Res. 2019, 55, 4163–4185. [Google Scholar] [CrossRef]
- Gu, S.H.; Liu, Y.T.; Chen, Z.X. Numerical study of dynamic fracture aperture during production of pressure-sensitive reservoirs. Int. J. Rock Mech. Min. Sci. 2014, 70, 229–239. [Google Scholar] [CrossRef]
- Xu, H.R.; Cheng, J.R.; Zhao, Z.H.; Lin, T.Y.; Liu, G.H.; Chen, S.C. Coupled thermo-hydro-mechanical-chemical modeling on acid fracturing in carbonatite geothermal reservoirs containing a heterogeneous fracture. Renew. Energy 2021, 172, 145–157. [Google Scholar] [CrossRef]
- Huang, N.; Liu, R.C.; Jiang, Y.J.; Cheng, Y.F.; Li, B. Shear-flow coupling characteristics of a three-dimensional discrete fracture network-fault model considering stress-induced aperture variations. J. Hydrol. 2019, 571, 416–424. [Google Scholar] [CrossRef]
- Igbokwe, O.A.; Timothy, J.J.; Kumar, A.; Yan, X.; Mueller, M.; Verdecchia, A.; Meschke, G.; Immenhauser, A. Impact of stress regime change on the permeability of a naturally fractured carbonate buildup (Latemar, the Dolomites, northern Italy). Solid Earth 2024, 15, 763–787. [Google Scholar] [CrossRef]
- Yan, J.H.; Ma, D.; Gao, X.F.; Duan, H.Y.; Li, Q.; Hou, W.T. Geothermal energy production potential of karst geothermal reservoir considering mining-induced stress. Int. J. Min. Sci. Technol. 2025, 35, 1153–1170. [Google Scholar] [CrossRef]
- Baghbanan, A.; Jing, L.R. Stress effects on permeability in a fractured rock mass with correlated fracture length and aperture. Int. J. Rock Mech. Min. Sci. 2008, 45, 1320–1334. [Google Scholar] [CrossRef]
- Sainoki, A.; Mitri, H.; Chinnasane, D. Characterization of aseismic fault-slip in a deep hard rock mine through numerical modelling: Case study. Rock Mech. Rock Eng. 2017, 50, 2709–2729. [Google Scholar] [CrossRef]
- Azarfar, B.; Ahmadvand, S.; Sattarvand, J.; Abbasi, B. Stability analysis of rock structure in large slopes and open pit mine: Numerical and experimental fault modeling. Rock Mech. Rock Eng. 2019, 52, 4889–4905. [Google Scholar] [CrossRef]
- Li, Q.; Li, X.B.; Yin, T.B. Effect of microwave heating on fracture behavior of granite: An experimental investigation. Eng. Fract. Mech. 2021, 250, 107758. [Google Scholar] [CrossRef]
- Zhang, X.; Huang, Z.W.; Li, G.S.; Wu, X.G.; Wang, T.Y.; Zhou, X.X. Enhancing reservoir stimulation and heat extraction performance for fractured geothermal reservoirs: Utilization of novel multilateral wells. Energy 2024, 291, 130410. [Google Scholar] [CrossRef]
- Liang, X.; Xu, T.F.; Feng, B.; Jiang, Z.X. Optimization of heat extraction strategies in fault-controlled hydro-geothermal reservoirs. Energy 2018, 164, 853–870. [Google Scholar] [CrossRef]
- Cappa, F.; Guglielmi, Y.; Nussbaum, C.; Birkholzer, J. On the relationship between fault permeability increases, induced stress perturbation, and the growth of aseismic slip during fluid injection. Geophys. Res. Lett. 2018, 45, 11012–11020. [Google Scholar] [CrossRef]
- Hosseini, N.; Priest, J.A.; Eaton, D.W. Extended-fem analysis of injection-induced slip on a fault with rate-and-state friction: Insights into parameters that control induced seismicity. Rock Mech. Rock Eng. 2023, 56, 4229–4250. [Google Scholar] [CrossRef]
- Parisio, F.; Vilarrasa, V.; Wang, W.; Kolditz, O.; Nagel, T. The risks of long-term re-injection in supercritical geothermal systems. Nat. Commun. 2019, 10, 4391. [Google Scholar] [CrossRef] [PubMed]
- Kamila, Z.; Kaya, E.; Zarrouk, S.J. Reinjection in geothermal fields: An updated worldwide review 2020. Geothermics 2021, 89, 101970. [Google Scholar] [CrossRef]
- Hou, W.T.; Yan, J.H.; Ma, D.; Su, H.M.; Li, Q. Effects of extraction well assisted by the fault on thermal recovery performance in hydrothermal system. Case Stud. Therm. Eng. 2025, 69, 105962. [Google Scholar] [CrossRef]
- Yan, J.H.; Ma, D.; Gao, X.F.; Li, Q.; Hou, W.T. Fault zone mechanical response under co-exploitation of mine and geothermal energy: The combined effect of pore pressure and mining-induced stress. Int. J. Coal Sci. Technol. 2025, 12, 33. [Google Scholar]
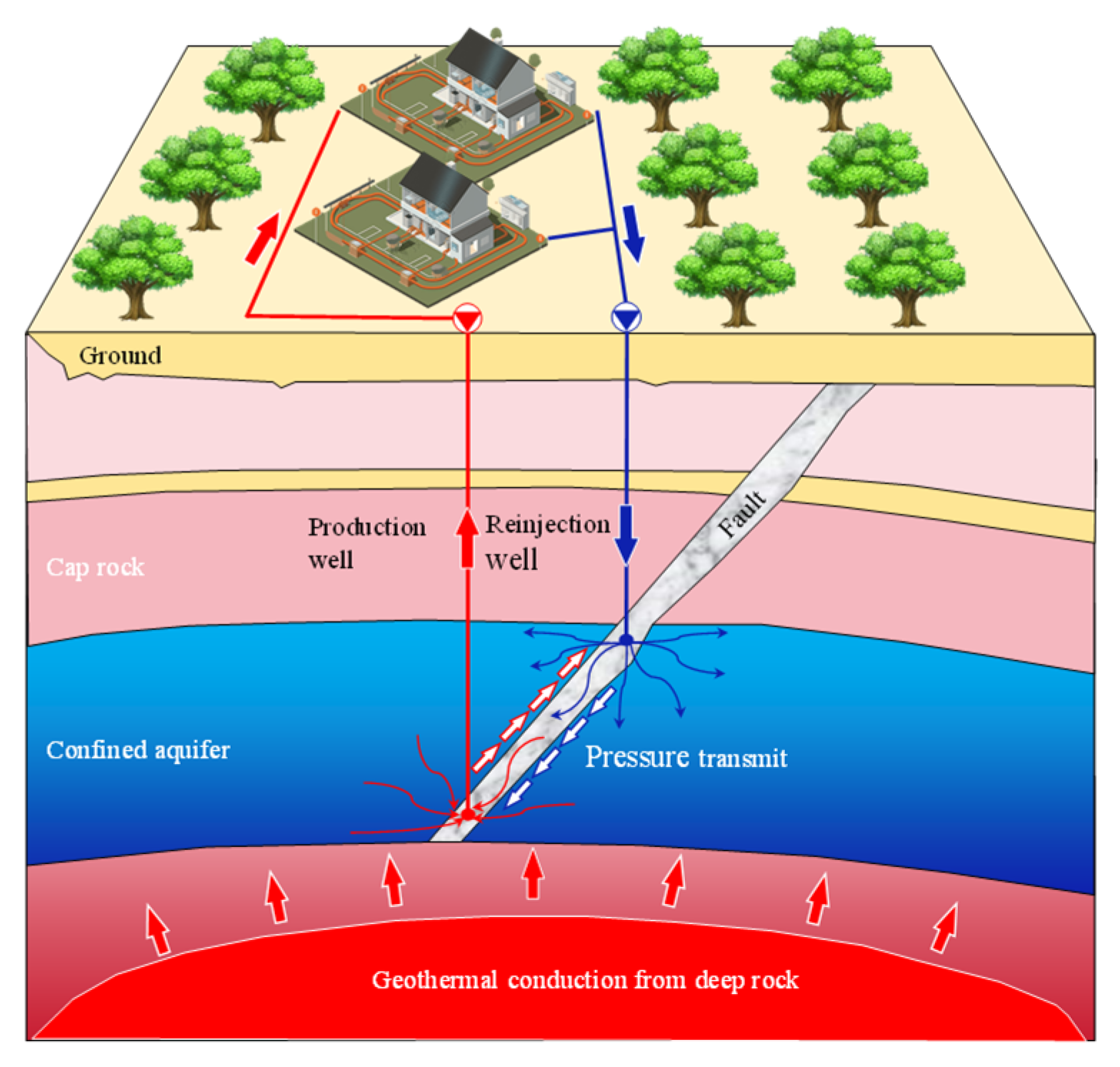
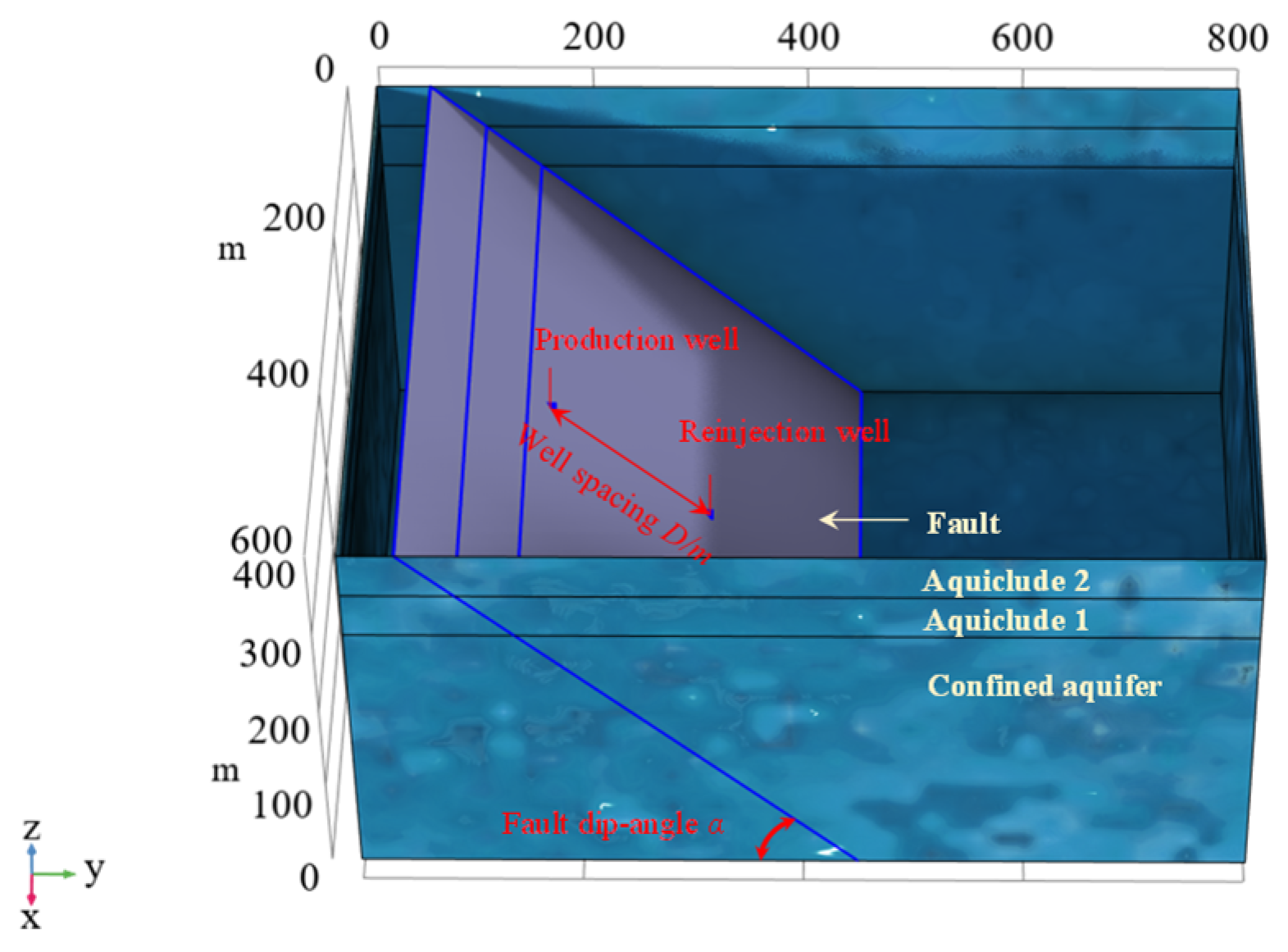
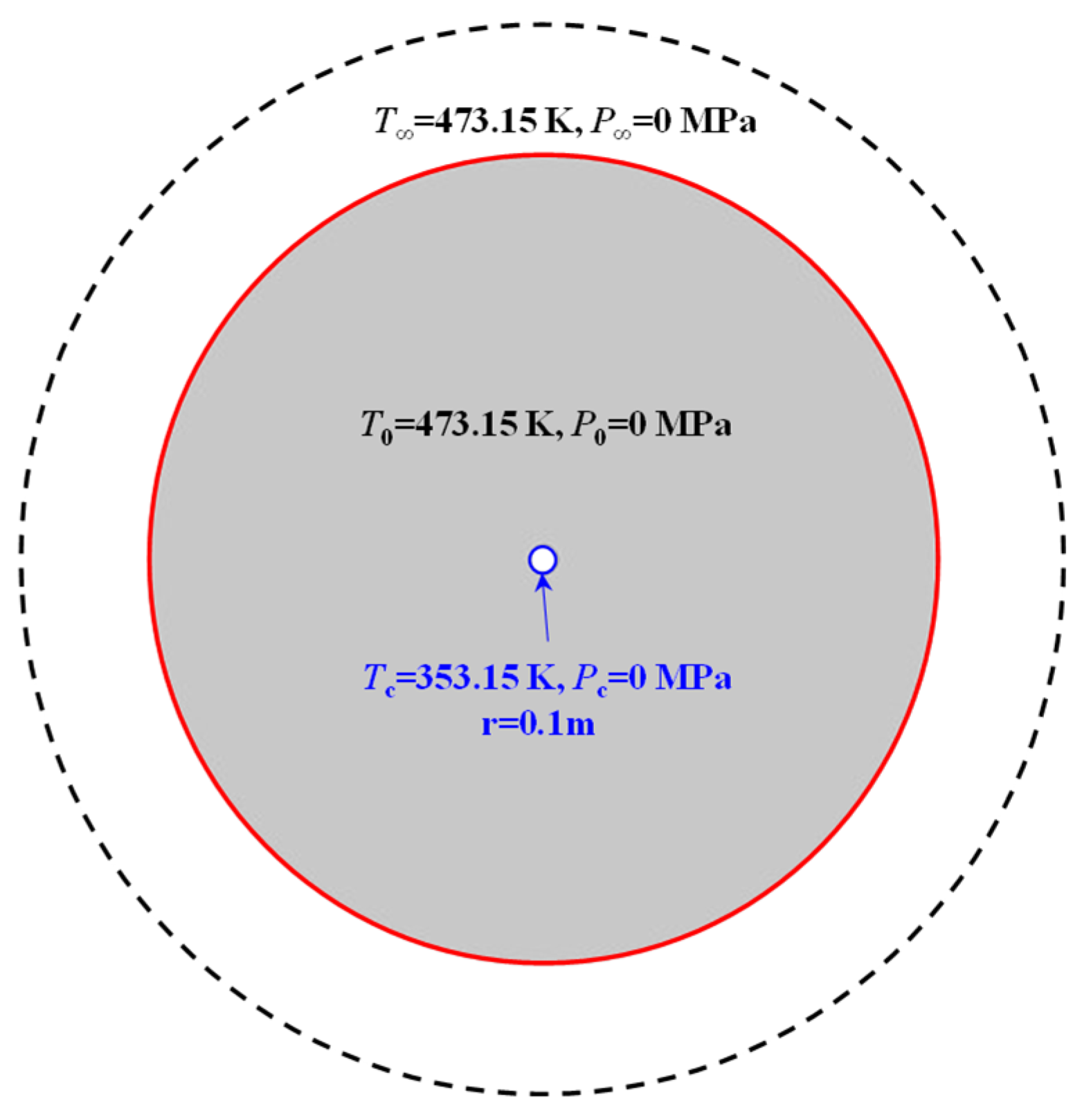


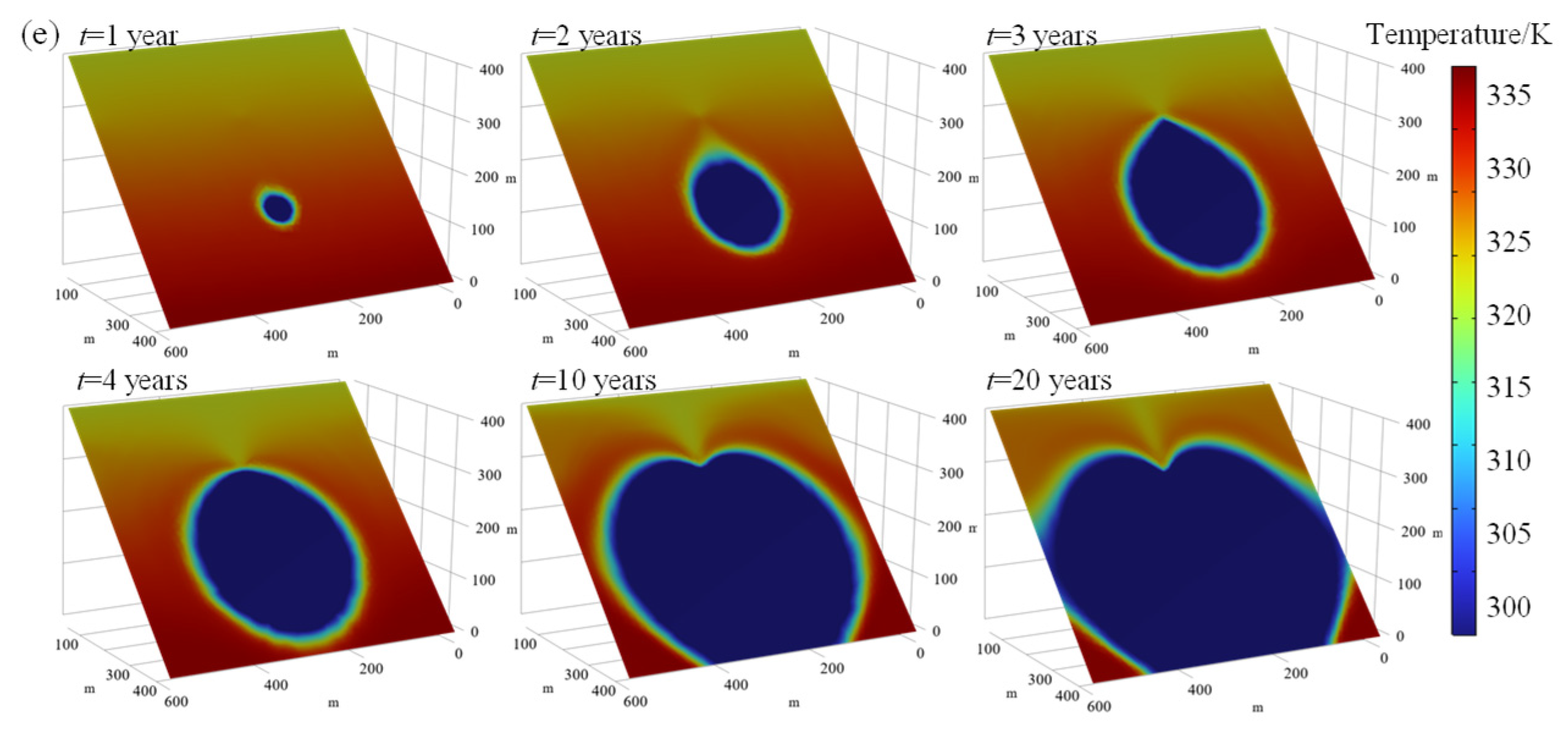




| Parameters | Fault | Aquiclude 2 | Aquiclude 1 | Confined Aquifer |
|---|---|---|---|---|
| Young modulus K∙GPa−1 | 2 | 60 | 60 | 60 |
| Poisson’s ratio ν | 0.2 | 0.3 | 0.3 | 0.3 |
| Initial Porosity φ0 | 0.2 | 0.05 | 0.05 | 0.12 |
| Initial Permeability k0∙m−2 | 5.0 × 10−12 | 1.0 × 10−16 | 1.0 × 10−16 | 1.0 × 10−14 |
| Thermal Conductivity λ∙(W∙(m∙K)−1)−1 | 1.3 | 2.3 | 2.3 | 2.3 |
| Specific thermal capacity C∙(J/kg∙K)−1 | 650 | 850 | 850 | 850 |
| Density ρ∙(kg∙m−3)−1 | 2200 | 2600 | 2600 | 2600 |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Density | 2700 kg∙m−3 | Initial permeability | 4.053 × 10−7 m2 |
| Thermal conductivity | 790 J∙(kg∙K)−1 | Initial porosity rate | 0.01 |
| Specific heat capacity | 2.4 W∙(m∙K)−1 | M1 | 1.0 × 10−7 |
| Young modulus | 37.5 GPa | αT | 3 × 10−6 K−1 |
| Poisson’s ratio | 0.25 |
| Parameters | Value |
|---|---|
| Well distance D/m | 40, 80, 100, 120, 160, 200 |
| Production/reinjection flow rate Q/kg∙s−1 | 5, 10, 15, 20, 25, 30 |
| Number of production/reinjection wells | 1P3RE, 1P5RE, 1P7RE, 3P1RE, 5P1RE, 7P1RE |
| Parameters | Value |
|---|---|
| Initiation permeability of fault k/1 × 10−12 m2 | 2, 4, 8, 16, 32, 64 |
| Fault spacing R/m | 5, 10, 15, 20, 25, 30 |
| Fault dip-angle/° | 30, 40, 50, 60, 70, 80 |
| Comparative Item | This Study | Hou et al. (2025) [51] | Yan et al. (2025) [52] | Daniilidis et al. (2021) [26] | Gan et al. (2020) [14] | Remarks |
|---|---|---|---|---|---|---|
| Model Type | THM | HM | HM | THM | THM | This study incorporates nonlinear flow. |
| Controlling factors of heat extraction efficiency | Flow rate, well spacing, fault thickness, etc. | Flow rate, well spacing, et al. | Well spacing | Flow rate, well spacing and permeability | — | This study reveals that the thickness and dip angle of the fault are also important factors. |
| Main factors of fault stability disturbance | Flow velocity, well spacing, fault thickness, etc. | Well spacing | Well spacing | — | Recharge temperature and flow rate. | This study reveals that the thickness and dip angle of the fault itself are also important factors for fault stability. |
| The relationship between fault stability and heat recovery efficiency | Increasing well spacing and flow rate improves heat extraction efficiency but raises instability risks. Higher fault permeability and thickness enhance efficiency and safety. | — | — | — | — | This study reveals the relationship between fault stability and heat recovery efficiency. |
| Key Finding | The results show that artificial methods to enhance heat extraction efficiency may compromise fault stability, whereas natural faults offer better efficiency and safety. | Recharge temperature is the main factors. | Well spacing is the main factor affecting fault instability | Well spacing is the main factor affecting fault instability | Recharge flow rate is the main factor affecting the stability of faults. | This study comprehensively addresses fault stability and heat extraction efficiency, offering guidance for fault geothermal system parameters. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, B.; Gong, X.; Li, Q.; Liu, Y.; Yan, J. Performance of Fault-Controlled Hydrothermal System: Insights from Multi-Field Coupled Rock Mechanics Analysis. Appl. Sci. 2025, 15, 10064. https://doi.org/10.3390/app151810064
Cheng B, Gong X, Li Q, Liu Y, Yan J. Performance of Fault-Controlled Hydrothermal System: Insights from Multi-Field Coupled Rock Mechanics Analysis. Applied Sciences. 2025; 15(18):10064. https://doi.org/10.3390/app151810064
Chicago/Turabian StyleCheng, Bo, Xiaofei Gong, Qiang Li, Yong Liu, and Jinghong Yan. 2025. "Performance of Fault-Controlled Hydrothermal System: Insights from Multi-Field Coupled Rock Mechanics Analysis" Applied Sciences 15, no. 18: 10064. https://doi.org/10.3390/app151810064
APA StyleCheng, B., Gong, X., Li, Q., Liu, Y., & Yan, J. (2025). Performance of Fault-Controlled Hydrothermal System: Insights from Multi-Field Coupled Rock Mechanics Analysis. Applied Sciences, 15(18), 10064. https://doi.org/10.3390/app151810064





