CPT-Based Shear Wave Velocity Correlation Model for Soft Soils with Graphical Assessment
Abstract
Featured Application
Abstract
1. Introduction
2. Field-Measured Data
3. Development of a Shear Wave Velocity Regression Model for Soils Based on the CPT Data
3.1. Regression Model Form
3.2. Regression Analysis
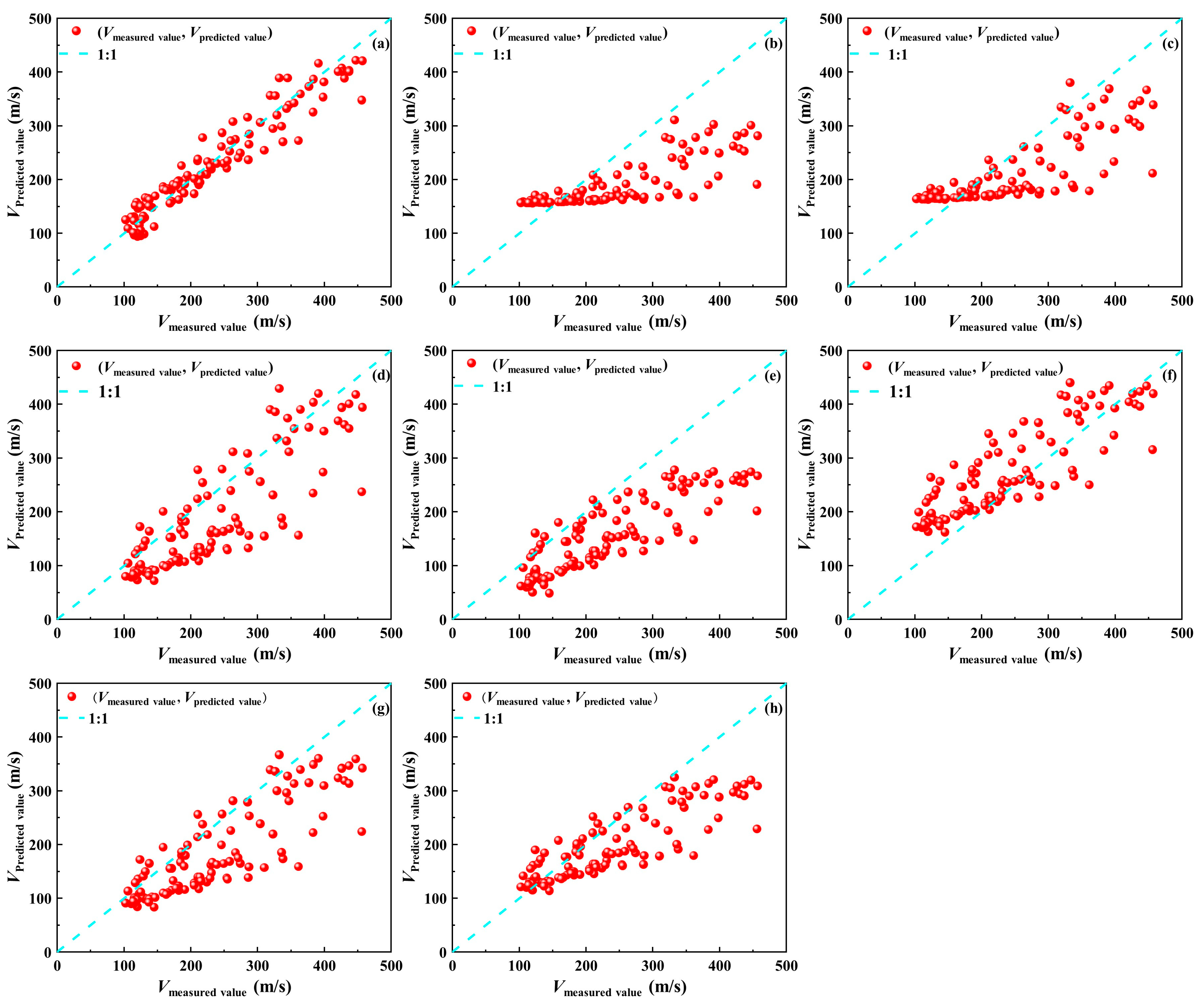
4. Regression Model Evaluation
4.1. Comparative Analysis with Existing Regression Models
4.1.1. Sandy Soil
4.1.2. Clay
4.1.3. General Soil
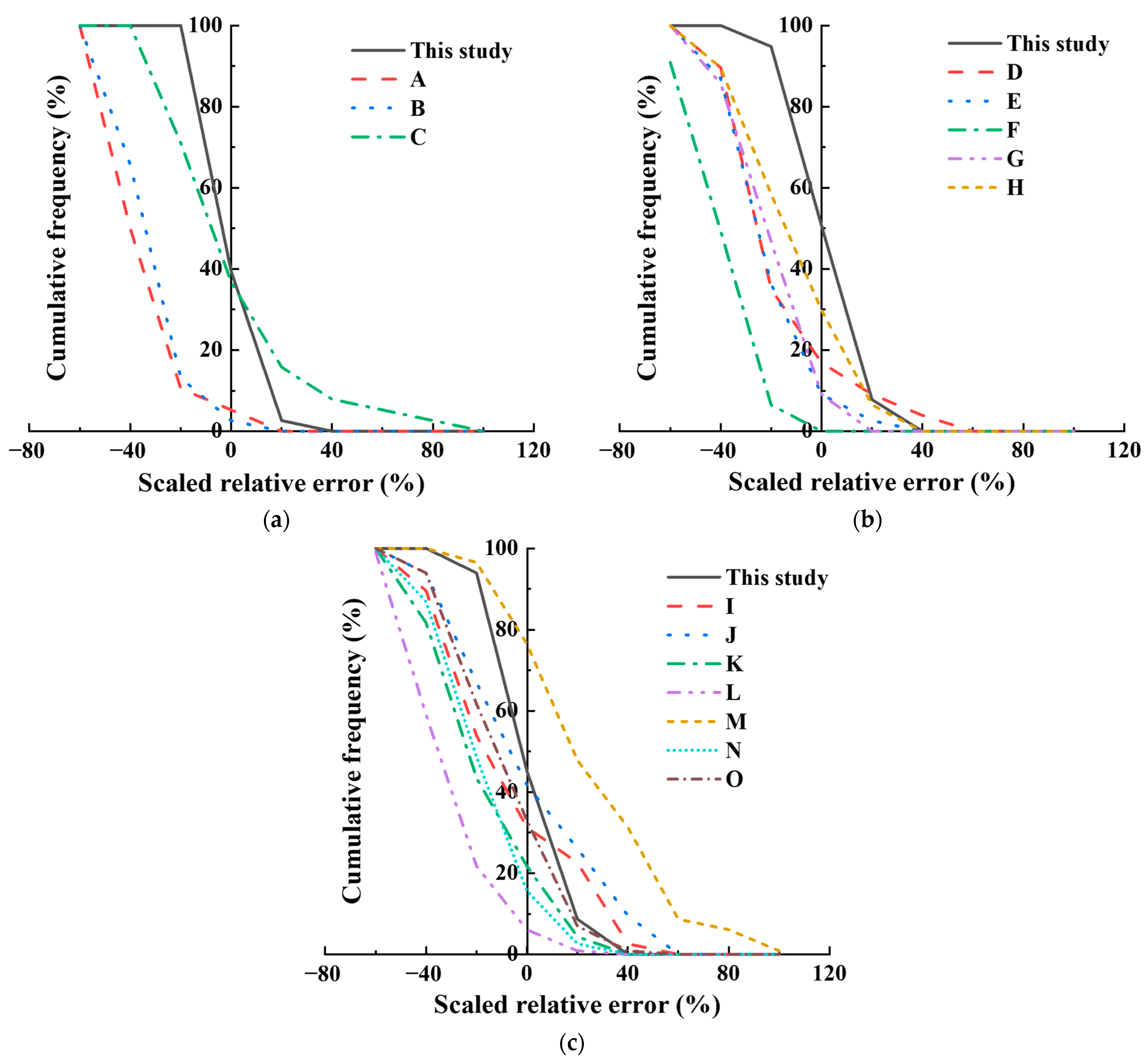
4.2. Graphical Analysis
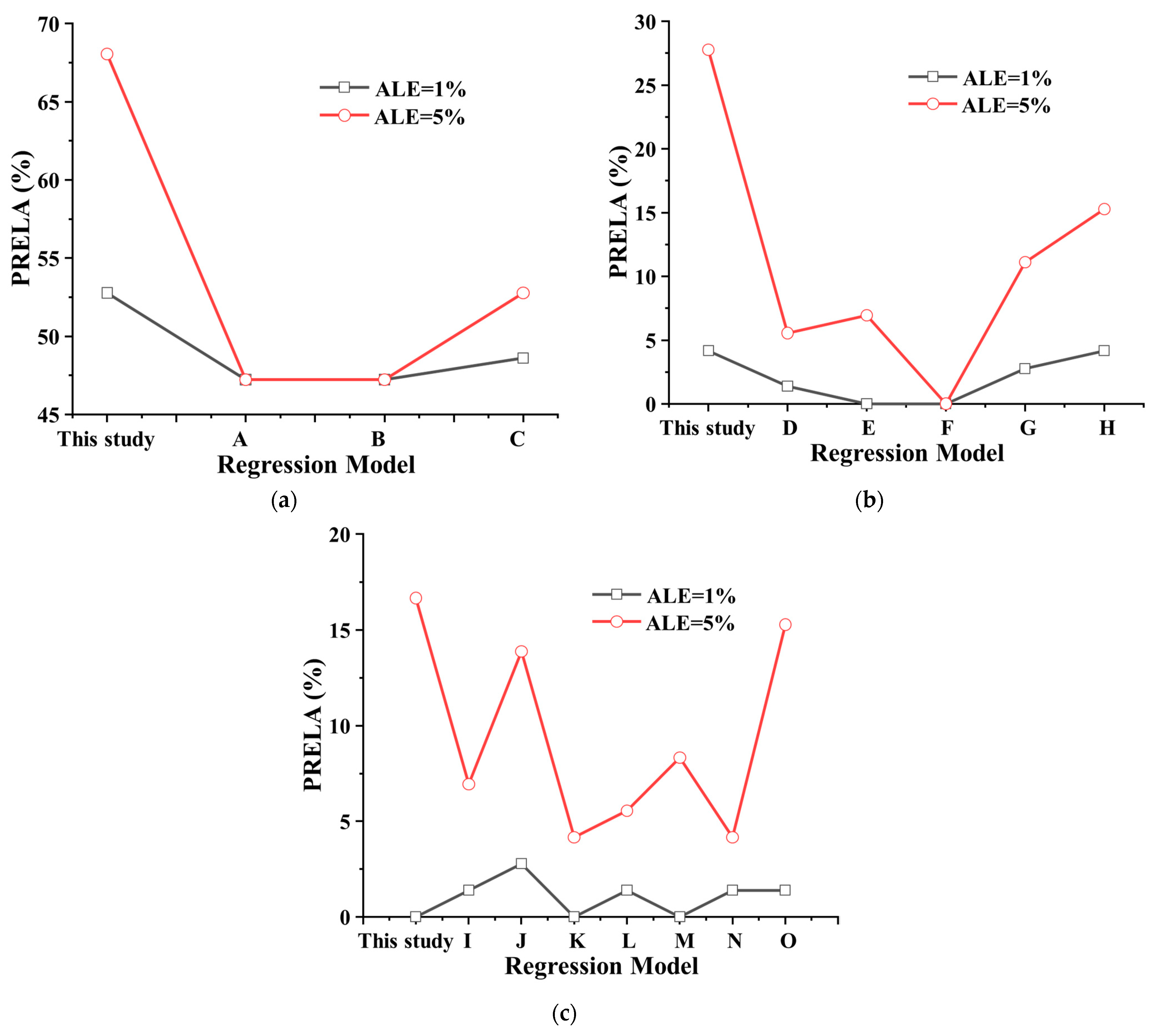
4.2.1. Evaluation Metric Establishment
4.2.2. Evaluation Methods Based on Cumulative Frequency Curves
4.3. The Statistical Assessment Method
5. Conclusions
- (1)
- Existing regression models of shear wave velocity Vs and cone penetration resistance Ps were collected and analyzed, and the regression models of shear wave velocity Vs and cone penetration resistance Ps with burial depth H were established. It is found that the existing regression model of shear wave velocity Vs and cone penetration resistance Ps is not applicable to the prediction of shear wave velocity in soft soil layers.
- (2)
- The regression models of shear wave velocity Vs and cone penetration resistance Ps versus burial depth H for three types of soils are developed, and the evaluation of the new models is assessed by existing regression models, graphical analysis, and statistical assessment methods. At ALE = 5%, the PRELA of sandy, clay, and general soils are 68.06%, 27.78%, and 16.67%, respectively. The predicted shear wave velocity Vs of the newly proposed model in sandy, clay, and general soils agrees best with the monitoring values.
- (3)
- The new model has higher applicability and accuracy in Shanghai, which can provide a more reliable theoretical basis for engineering geological evaluation and seismic design.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ohta, Y.; Goto, N. Empirical shear wave velocity equations in terms of characteristic soil indexes. Earthq. Eng. Struct. Dyn. 1978, 6, 167–187. [Google Scholar] [CrossRef]
- Li, Z.-H.; Xie, J.-J.; Li, K.-W.; Wen, Z.-P.; Li, X.-J.; Wang, Z.-C.; Xu, H.-T.; Zhao, X.-F.; Zhang, N. Empirical extrapolation model of site shear wave velocity and its applicability in Shandong Province. Seismol. Geol. 2024, 46, 934–954. (In Chinese) [Google Scholar]
- Olutoki, J.O.; Zhao, J.G.; Siddiqui, N.A.; Elsaadany, M.; Haque, A.E.; Akinyemi, O.D.; Said, A.H.; Zhao, Z. Shear wave velocity prediction: A review of recent progress and future opportunities. Energy Geosci. 2024, 5, 100338. [Google Scholar] [CrossRef]
- Bekdaş, G.; Aydın, Y.; Işıkdağ, U.; Nigdeli, S.M.; Hajebi, D.; Kim, T.-H.; Geem, Z.W. Shear Wave Velocity Prediction with Hyperparameter Optimization. Information 2025, 16, 60. [Google Scholar] [CrossRef]
- Wang, J.-Y.; Tao, X.-S.; Wang, C.; Shao, B.; Xu, Y. Correlation analysis between shear wave velocity and soil layer depth in urban area of Yancheng City. J. Disaster Prev. Mitig. Eng. 2024, 44, 1193–1201. (In Chinese) [Google Scholar]
- Zheng, M.; Huang, Y.-M.; Liang, J.-W.; He, S.-Y.; Li, X.-D.; Chen, H.-W.; Su, B.; Su, X.-M.; Xie, C. Correlation analysis of shear wave velocity and burial depth in rock and soil in the Yulin Area. Earthquake 2024, 44, 78–93. (In Chinese) [Google Scholar]
- Lu, D.W.; Sun, Y.H.; Liu, H.S. Reliability evaluation of empirical formula between shear wave velocity and depth of conventional soils. J. Jilin Univ. (Earth Sci. Ed.) 2024, 54, 546–557. (In Chinese) [Google Scholar]
- Xu, Y.; Wu, Q.; Fang, Y.; Chen, G.-X. Evaluation method of shear wave velocity of various marine soils in the Lingdingyang Bay. J. Disaster Prev. Mitig. Eng. 2023, 43, 956–964. (In Chinese) [Google Scholar]
- Parvizi, S.; Kharrat, R.; Asef, M.R.; Jahangiry, B.; Hashemi, A. Prediction of the shear wave velocity from compressional wave velocity for Gachsaran Formation. Acta Geophys. 2015, 63, 1231–1243. [Google Scholar] [CrossRef]
- Oloruntobi, O.; Butt, S. The shear-wave velocity prediction for sedimentary rocks. J. Nat. Gas Sci. Eng. 2020, 76, 103084. [Google Scholar] [CrossRef]
- Omovie, S.J.; Castagna, J.P. Estimation of shear-wave velocities in unconventional shale reservoirs. Geophys. Prospect. 2021, 69, 1316–1335. [Google Scholar] [CrossRef]
- Kim, J.; Kim, B.; Cho, H. Shear wave velocity estimation in Korea using P-wave seismograms. KSCE J. Civ. Eng. 2020, 24, 3650–3658. [Google Scholar] [CrossRef]
- Ismail, A.; Azadbakht, S.; Rashid, H.M.A.; Yasin, Q.; Liu, B.; Ijaz, W. Statistical and machine learning hybridization for predicting shear wave velocity in tight sand reservoirs: A case study. Geoenergy Sci. Eng. 2023, 231, 212420. [Google Scholar] [CrossRef]
- Nasrnia, B.; Falahat, R. Studying the Accuracy and Generalizability of Different Estimation Methods of Shear Wave Velocity. Arab. J. Sci. Eng. 2024, 50, 14961–14975. [Google Scholar] [CrossRef]
- Liu, Y.; Gao, C.; Zhao, B. Shear-wave velocity prediction based on the CNN-BiGRU integrated network with spatiotemporal attention mechanism. Processes 2024, 12, 1367. [Google Scholar] [CrossRef]
- Hazbeh, O.; Rajabi, M.; Tabasi, S.; Lajmorak, S.; Ghorbani, H.; Radwan, A.E.; Alvar, M.A.; Molaei, O. Determination and investigation of shear wave velocity based on one deep/machine learning technique. Alex. Eng. J. 2024, 92, 358–369. [Google Scholar] [CrossRef]
- Feng, G.; Zeng, H.-H.; Xu, X.-R.; Tang, G.-Y.; Wang, Y.-X. Shear wave velocity prediction based on deep neural network and theoretical rock physics modeling. Front. Earth Sci. 2023, 10, 1025635. [Google Scholar] [CrossRef]
- Cai, R.; Peng, T.; Luo, D.-L.; Zhou, Y.-D.; Yin, X.-X.; Guo, P.; Peng, J.-C. Correlation between the shear wave velocity and the soil depth in Chengdu Region. J. Seismol. Res. 2022, 45, 498–508. (In Chinese) [Google Scholar]
- Zhang, X.; Zhang, H.; Yun, M.; Wang, F. Research on shear-wave velocity profile VS30 estimation model in Xiong’an New District. Technol. Earthq. Disaster Prev. 2022, 17, 401–408. (In Chinese) [Google Scholar]
- Zekkos, D.; Sahadewa, A.; Woods, R.D.; Stokoe, K.H. Development of model for shear-wave velocity of municipal solid waste. J. Geotech. Geoenviron. Eng. 2014, 140, 04013030. [Google Scholar] [CrossRef]
- Damm, J.C.; Lewis, M.R.; Stokoe, K.H.; Moore, D.P. Comparison of in situ and laboratory shear wave velocity measurements in compacted backfill. Geotech. Test. J. 2013, 36, 515–523. [Google Scholar] [CrossRef]
- Tsiambaos, G.; Sabatakakis, N. Empirical estimation of shear wave velocity from in situ tests on soil formations in Greece. Bull. Eng. Geol. Environ. 2011, 70, 291–297. [Google Scholar] [CrossRef]
- Mayne, P.W.; Rix, G.J. Correlations between shear wave velocity and cone tip resistance in natural Clays. Soils Found. 1995, 35, 107–110. [Google Scholar] [CrossRef]
- Dikmen, U. Statistical correlations of shear wave velocity and penetration resistance for soils. J. Geophys. Eng. 2009, 6, 61–72. [Google Scholar] [CrossRef]
- Robertson, P.K.; Campanella, R.G. Interpretation of cone penetration tests. Part I: Sand. Can. Geotech. J. 1983, 20, 718–733. [Google Scholar] [CrossRef]
- Fear, C.E.; Robertson, P.K. Estimating the undrained strength of sand: A theoretical framework. Can. Geotech. J. 1995, 32, 859–870. [Google Scholar] [CrossRef]
- Karray, M.; Lefebvre, G.; Ethier, Y.; Bigras, A. Influence of particle size on the correlation between shear wave velocity and cone tip resistance. Can. Geotech. J. 2011, 48, 599–615. [Google Scholar] [CrossRef]
- Brignoli, E.M.; Gotti, M.; Stokoe, K.H. Measurement of shear waves in laboratory specimens by means of piezoelectric transducers. Geotech. Test. J. 1996, 19, 384–397. [Google Scholar] [CrossRef]
- Ansal, A.; Iyisan, R.; Güllü, H. Microtremor Measurements for the Microzonation of Dinar. Pure Appl. Geophys. 2001, 158, 2525–2541. [Google Scholar] [CrossRef]
- Ansal, A.; Iyisan, R.; Yldrm, H. The cyclic behaviour of soils and effects of geotechnical factors in microzonation. Soil Dyn. Earthq. Eng. 2001, 21, 445–452. [Google Scholar] [CrossRef]
- Tun, M.; Ayday, C. Investigation of correlations between shear wave velocities and CPT data: A case study at Eskisehir in Turkey. Bull. Eng. Geol. Environ. 2018, 77, 225–236. [Google Scholar] [CrossRef]
- Madiai, C.; Simoni, G. Shear wave velocity-penetration resistance correlation for Holocene and Pleistocene soils of an area in central Italy. In Geotechnical and Geophysical Site Characterization, Proceedings of the Second International Conference on Site Characterization, ISC-2, Porto, Portugal, 19–22 September 2004; IOS Press: Amsterdam, The Netherlands, 2004; Available online: https://www.researchgate.net/publication/237326403 (accessed on 22 July 2025).
- Hegazy, Y.A.; Mayne, P.W. A global statistical correlation between shear wave velocity and cone penetration data. In Site and Geomaterial Characterization; ASCE: Reston, VA, USA, 2006; pp. 243–248. [Google Scholar] [CrossRef]
- Tong, L.Y.; Che, H.B.; Zhang, M.F.; Li, H.J. Review of shear-wave velocity prediction equations based on piezocone penetration test data: Example from Yangtze River floodplain deposits at Nanjing, Jiangsu Province, China. Q. J. Eng. Geol. Hydrogeol. 2018, 51, 229–246. [Google Scholar] [CrossRef]
- Zhang, D.-M.; Chen, H.-H.; Xie, X.-C.; Chen, S.-R.; Chen, Z.-G.; Li, J.-P. Multiscale responses of gap-graded soil under the combined effect of train vibration and seepage erosion. Transp. Geotech. 2025, 55, 101669. [Google Scholar] [CrossRef]
- Liu, Z.; Fan, S.; Liu, S.-L.; Zhao, A.-R.; Liu, L. Research on prediction of pigment concentration in color painting based on BOA-FRNN spectral model. Spectrosc. Spect. Anal. 2025, 45, 322–331. (In Chinese) [Google Scholar]
- Grima, A.; Babuška, R. Fuzzy model for the prediction of unconfined compressive strength of rock samples. Int. J. Rock Mech. Min. Sci. 1999, 36, 339–349. [Google Scholar] [CrossRef]
- Briaud, J.-L.; Tucker, L.-M. Measured and predicted axial response of 98 piles. J. Geotech. Eng. 1988, 114, 984–1001. [Google Scholar] [CrossRef]
- Hu, Q.-Z.; Lu, H.-P.; Yang, Y.-N.; Cheng, N. Dynamic comprehensive measure model based on information degree and order exponent. Syst. Eng. Electron. 2011, 33, 816–820. (In Chinese) [Google Scholar]
- Orr, T.L.; Cherubini, C. Use of the ranking distance as an index for assessing the accuracy and precision of equations for the bearing capacity of piles and at-rest earth pressure coefficient. Can. Geotech. J. 2003, 40, 1200–1207. [Google Scholar] [CrossRef]
- Huang, Z.-K.; Zeng, N.-C.; Zhang, D.-M.; Argyroudis, S.; Mitoulis, S.-A. Resilience Models for Tunnels Recovery After Earthquakes. Engineering 2025, 6, 28. [Google Scholar] [CrossRef]
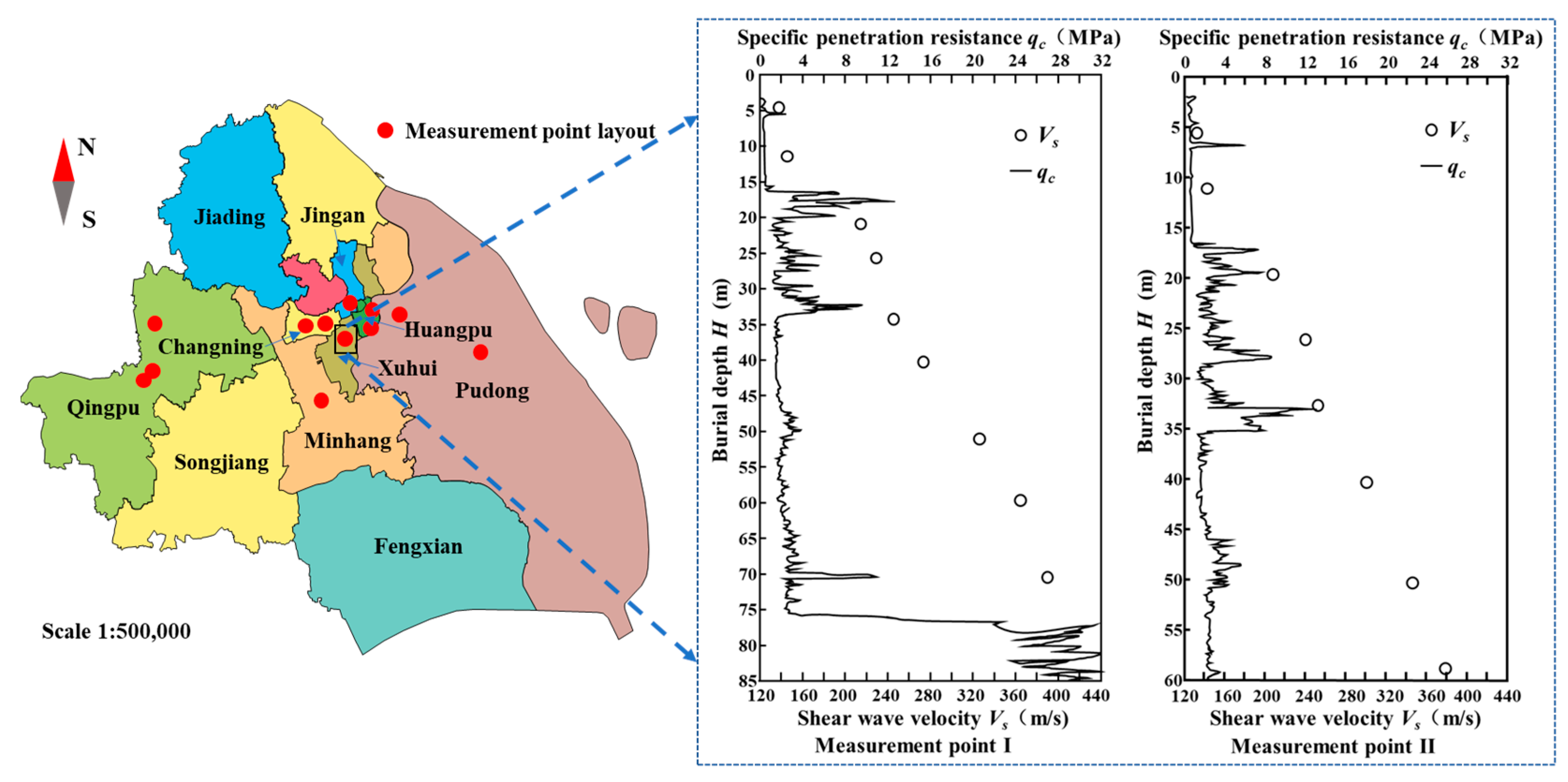
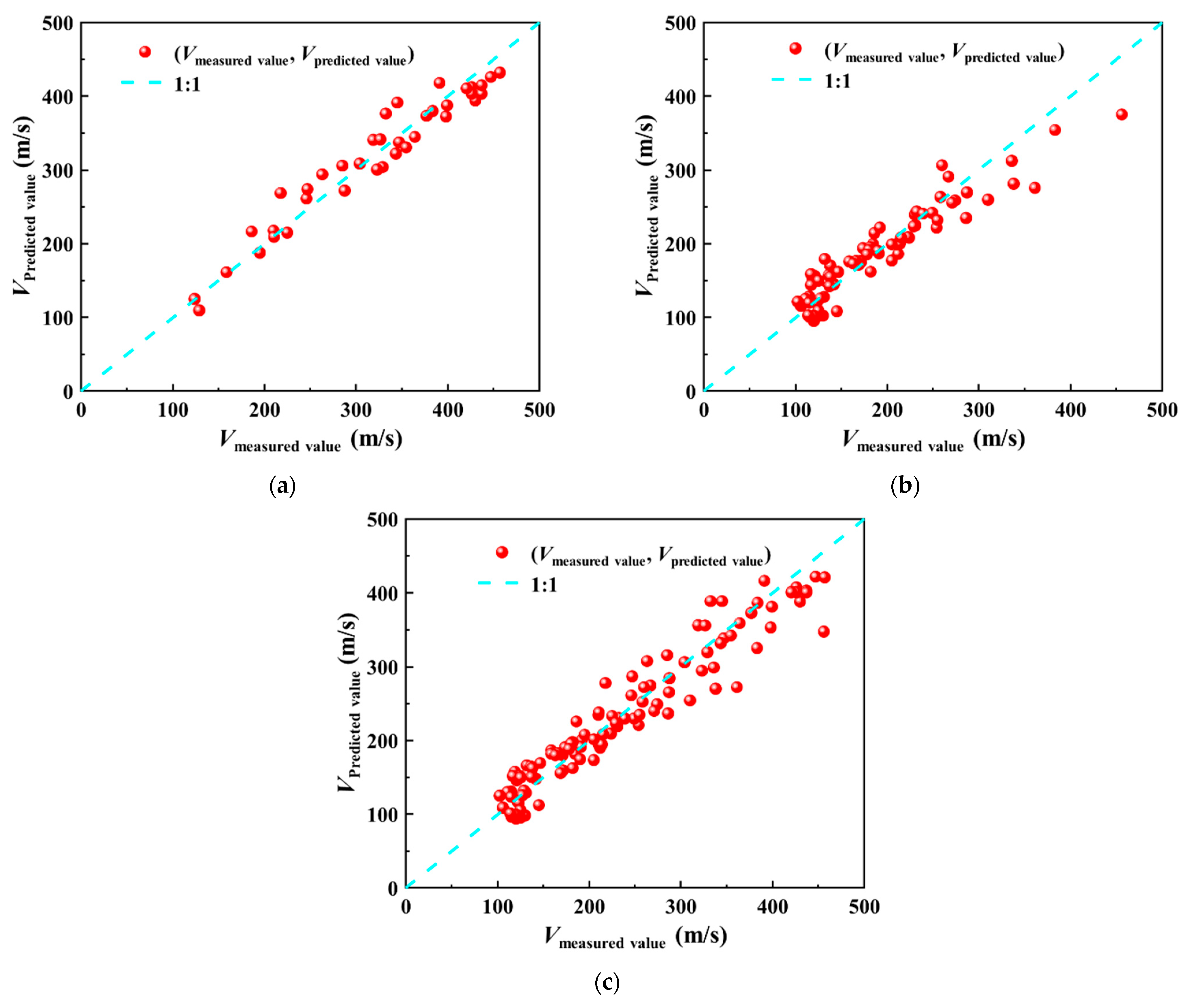
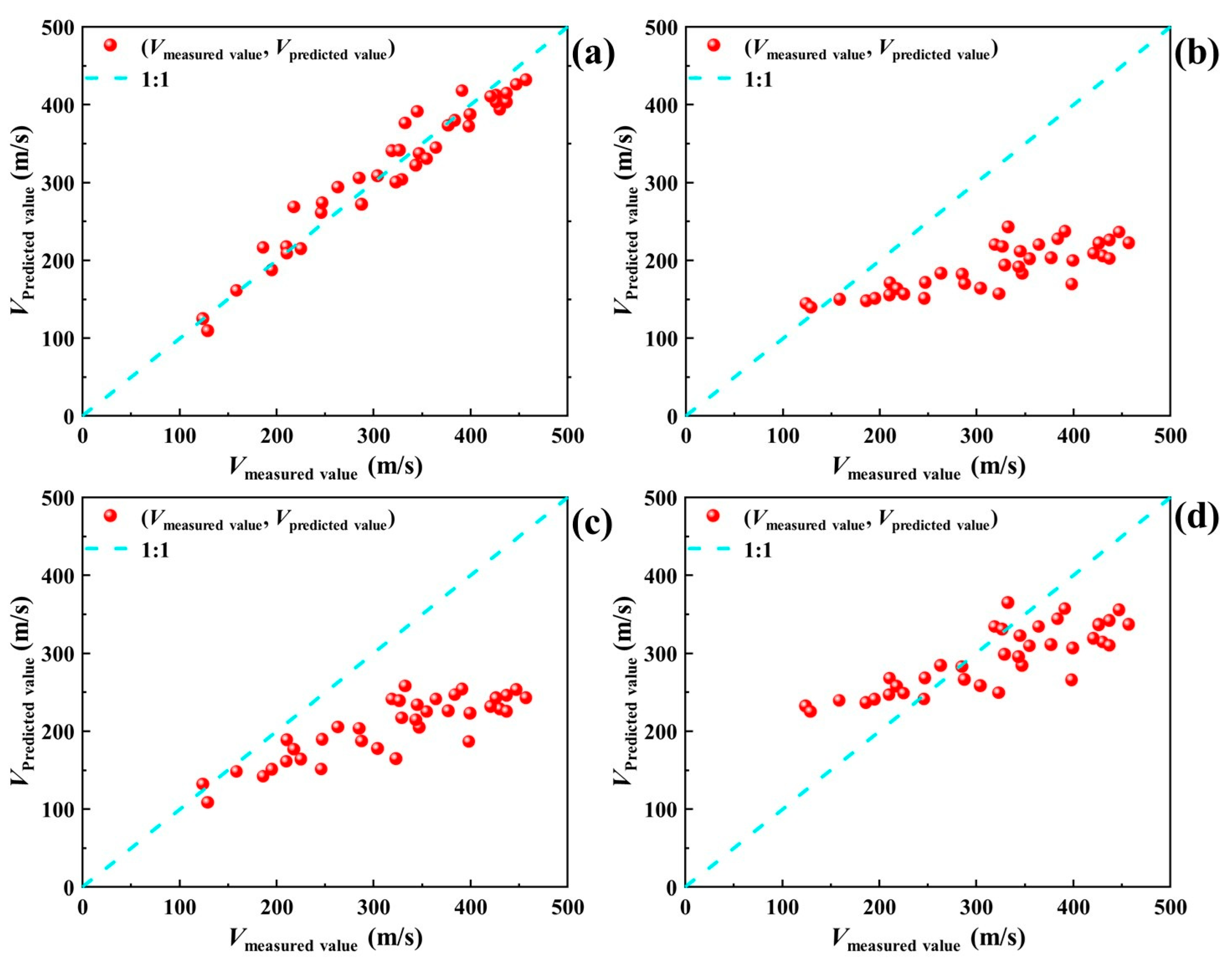
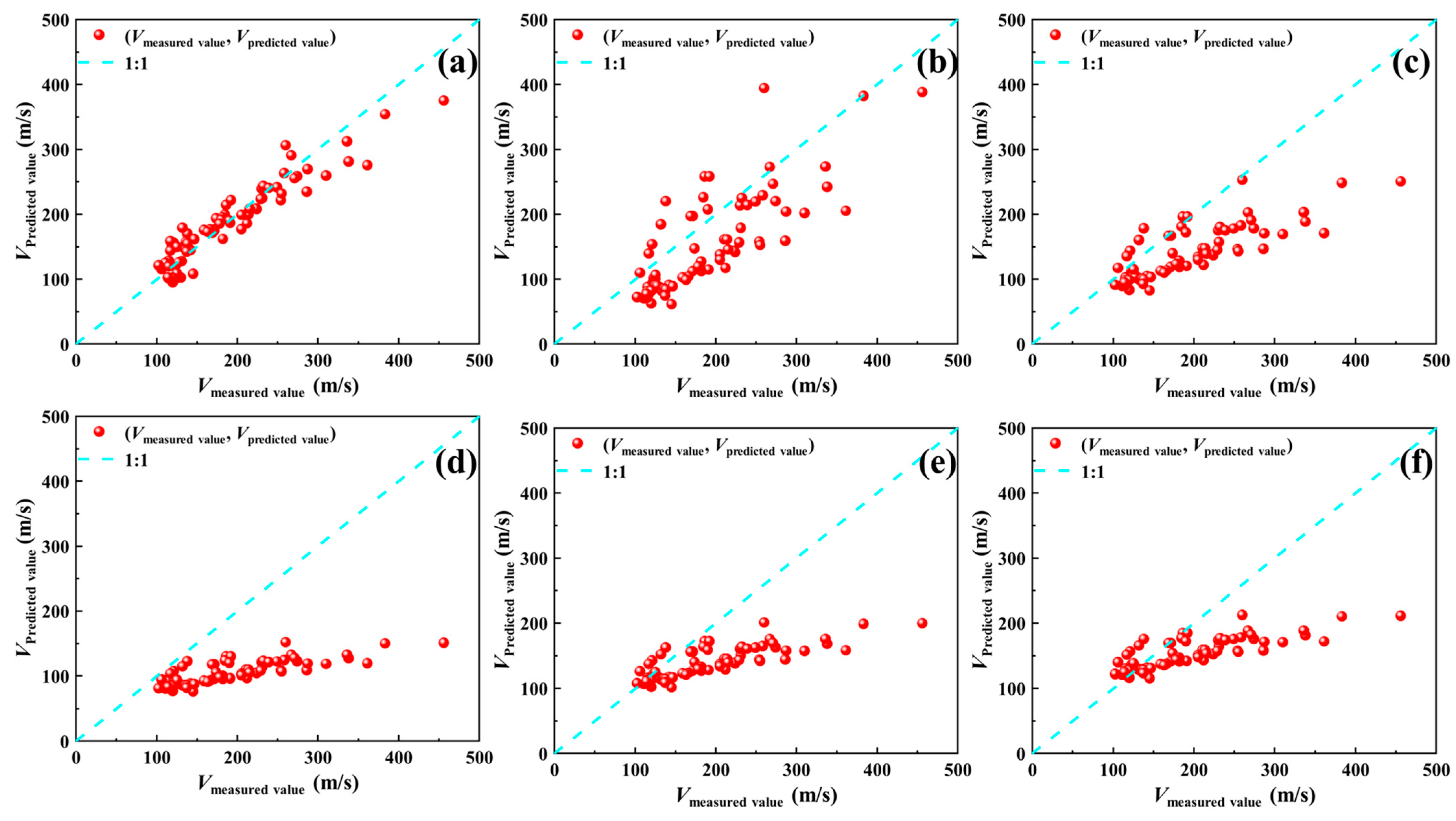

| Soil Type | No. | Regression Model Form | References |
|---|---|---|---|
| Sandy soil | A | Stokoe (1983) [20] | |
| B | Stokoe (1983) [21] | ||
| C | Iyisan (1996) [22] | ||
| Clay | D | Mayne and Rix (1995) [23] | |
| E | Iyisan (1996) [24] | ||
| F | Robertson et al. (1992) [25] | ||
| G | Fear and Robertson (1995) [26] | ||
| H | Karray (2011) [27] | ||
| General soil | I | Barrow and Stokoe (1983) [28] | |
| J | Iyisan and Ansal (1993) [29] | ||
| K | Iyisan and Ansal (1993) [30] | ||
| L | Tun (2003) [31] | ||
| M | Madiai and Simoni (2004) [32] | ||
| N | Hegazy and Mayne (2001) [33] | ||
| O | Tong (2017) [34] |
| Soil Type | No. | RMSE | K | RI | RD | ||
|---|---|---|---|---|---|---|---|
| %<1 | Mean | SD | |||||
| Sandy soil | X | 23.147 | 52.778 | 1.003 | 0.082 | 0.079 | 0.082 |
| A | 146.377 | 47.222 | 0.639 | 0.163 | 0.705 | 0.396 | |
| B | 129.880 | 47.222 | 0.675 | 0.130 | 0.595 | 0.350 | |
| C | 68.860 | 48.611 | 0.993 | 0.272 | 0.280 | 0.272 | |
| Clay | Y | 25.621 | 4.167 | 1.009 | 0.137 | 0.135 | 0.137 |
| D | 60.609 | 1.389 | 0.797 | 0.246 | 0.540 | 0.319 | |
| E | 69.176 | 0 | 0.769 | 0.169 | 0.493 | 0.286 | |
| F | 103.624 | 0 | 0.597 | 0.140 | 0.785 | 0.427 | |
| J | 75.591 | 2.778 | 0.790 | 0.185 | 0.504 | 0.280 | |
| H | 67.362 | 4.167 | 0.873 | 0.210 | 0.416 | 0.246 | |
| General soil | Z | 28.451 | 0 | 1.007 | 0.132 | 0.132 | 0.132 |
| I | 84.046 | 1.389 | 0.907 | 0.276 | 0.448 | 0.291 | |
| J | 68.313 | 2.788 | 0.983 | 0.275 | 0.341 | 0.276 | |
| K | 70.834 | 0 | 0.799 | 0.219 | 0.529 | 0.297 | |
| L | 95.699 | 1.389 | 0.673 | 0.173 | 0.667 | 0.370 | |
| M | 62.252 | 0 | 1.243 | 0.290 | 0.423 | 0.378 | |
| N | 72.494 | 1.389 | 0.797 | 0.184 | 0.482 | 0.274 | |
| O | 68.542 | 1.389 | 0.893 | 0.205 | 0.368 | 0.231 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Huang, Z.; Huang, Q.; Wang, Q. CPT-Based Shear Wave Velocity Correlation Model for Soft Soils with Graphical Assessment. Appl. Sci. 2025, 15, 10065. https://doi.org/10.3390/app151810065
Chen H, Huang Z, Huang Q, Wang Q. CPT-Based Shear Wave Velocity Correlation Model for Soft Soils with Graphical Assessment. Applied Sciences. 2025; 15(18):10065. https://doi.org/10.3390/app151810065
Chicago/Turabian StyleChen, Huihao, Zhongkai Huang, Qiang Huang, and Qiang Wang. 2025. "CPT-Based Shear Wave Velocity Correlation Model for Soft Soils with Graphical Assessment" Applied Sciences 15, no. 18: 10065. https://doi.org/10.3390/app151810065
APA StyleChen, H., Huang, Z., Huang, Q., & Wang, Q. (2025). CPT-Based Shear Wave Velocity Correlation Model for Soft Soils with Graphical Assessment. Applied Sciences, 15(18), 10065. https://doi.org/10.3390/app151810065






