Modeling and Finite-Element Performance Analysis of Selenol-Functionalized Carbon Nanotube/Natural Rubber Composites for Aircraft Tire Applications
Abstract
1. Introduction
1.1. Tread Rubber Composition
1.2. Aircraft Tire Modeling
2. Materials and Methods
2.1. Preparation of Selenol-Functionalized Carbon Nanotube/Natural Rubber Composites
2.2. Experimental Instrumentation
2.3. Scanning Electron Microscopy (SEM) Characterization
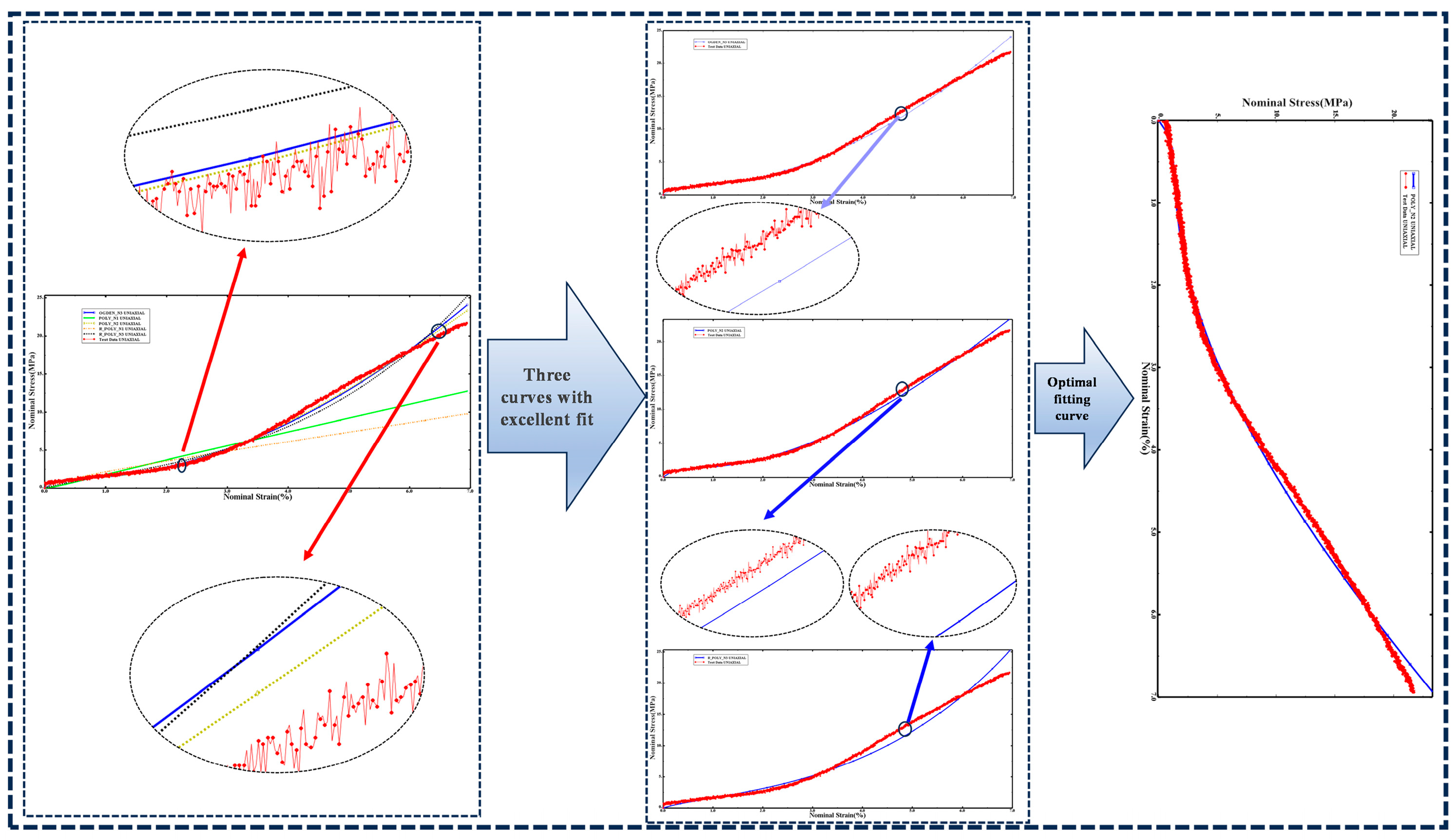
2.4. Experimental Data Fitting for Rubber Constitutive Models
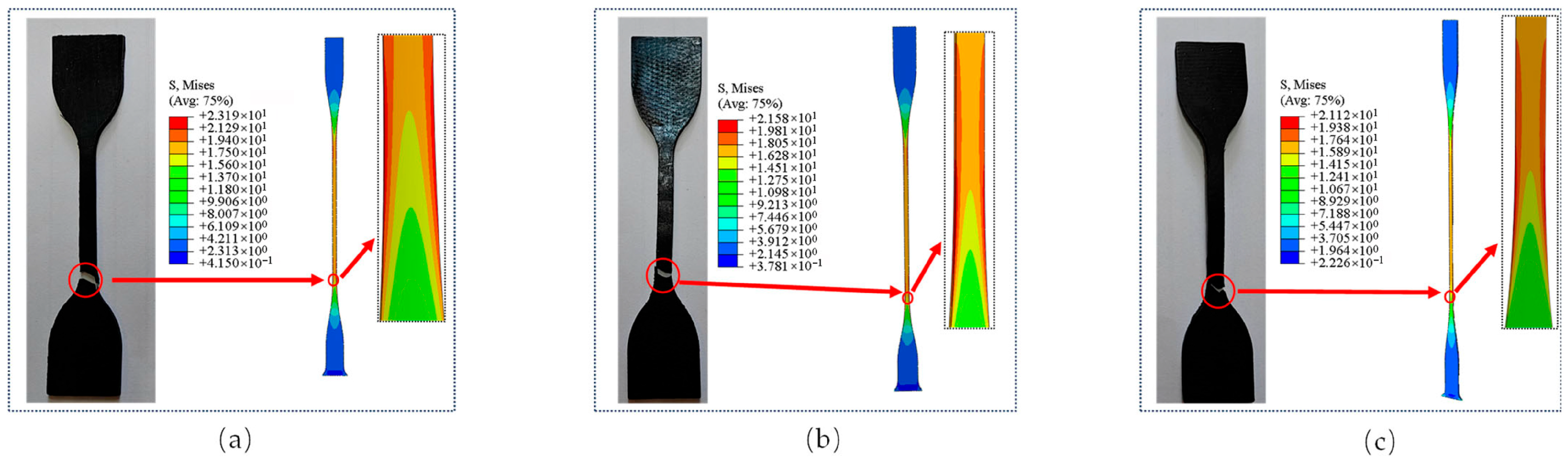
2.5. Abaqus Simulation of Uniaxial Tensile Testing
2.6. Material Properties
2.7. 2D Tire Model Construction
2.8. Mesh Properties and Boundary Conditions of the 2D Finite Element Model
2.9. 3D Static Load Footprint Simulation of Aircraft Tire
2.10. Effective Contact Area in Normal Direction
2.11. Deflection and Radial Stiffness Characteristics
3. Result and Discussion
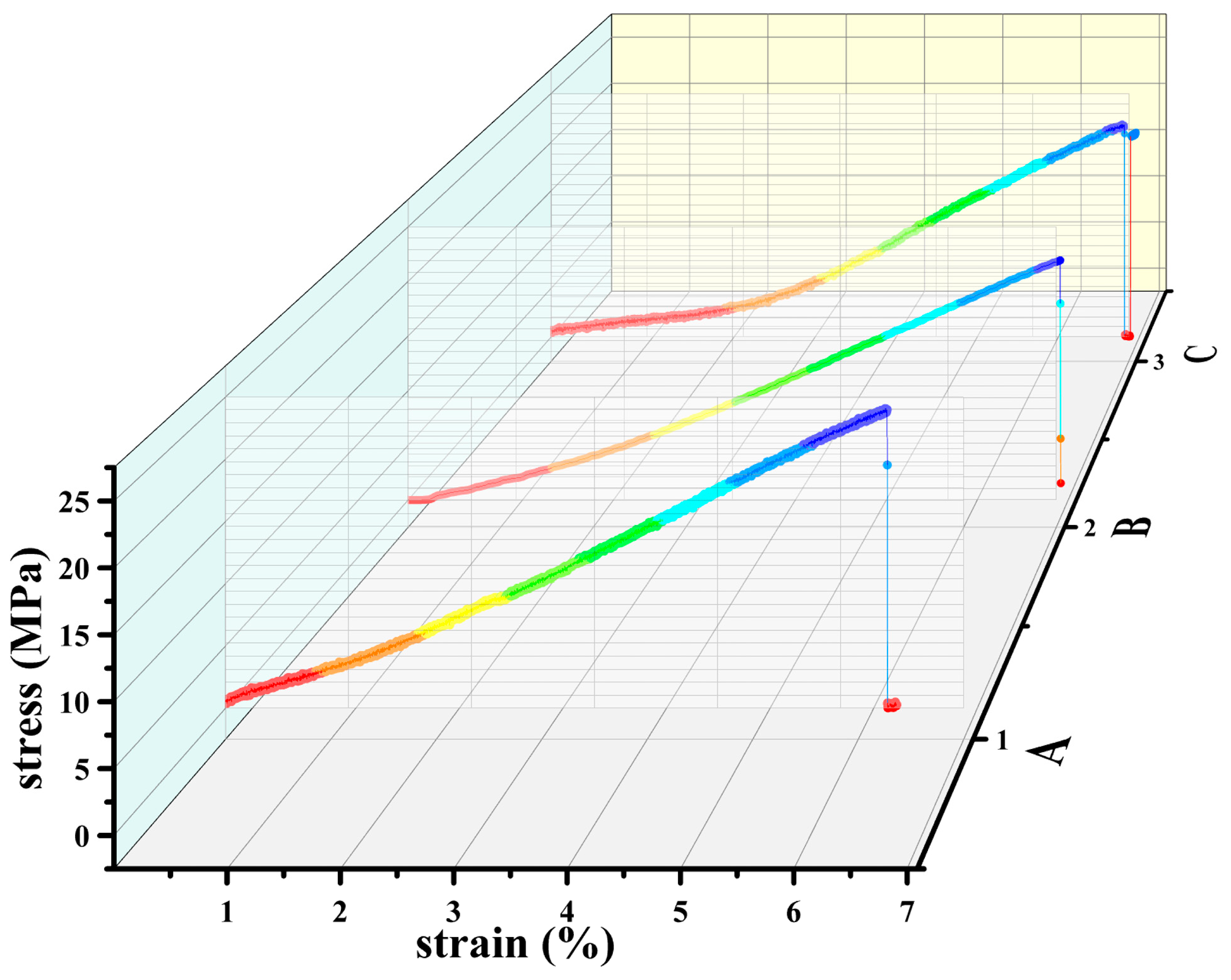
3.1. Comparative Performance Testing of Carbon Nanotube Composites
3.2. Constitutive Model Calibration via Experimental Data Fitting
3.3. Constitutive Model Validation Through Simulated Tensile Testing
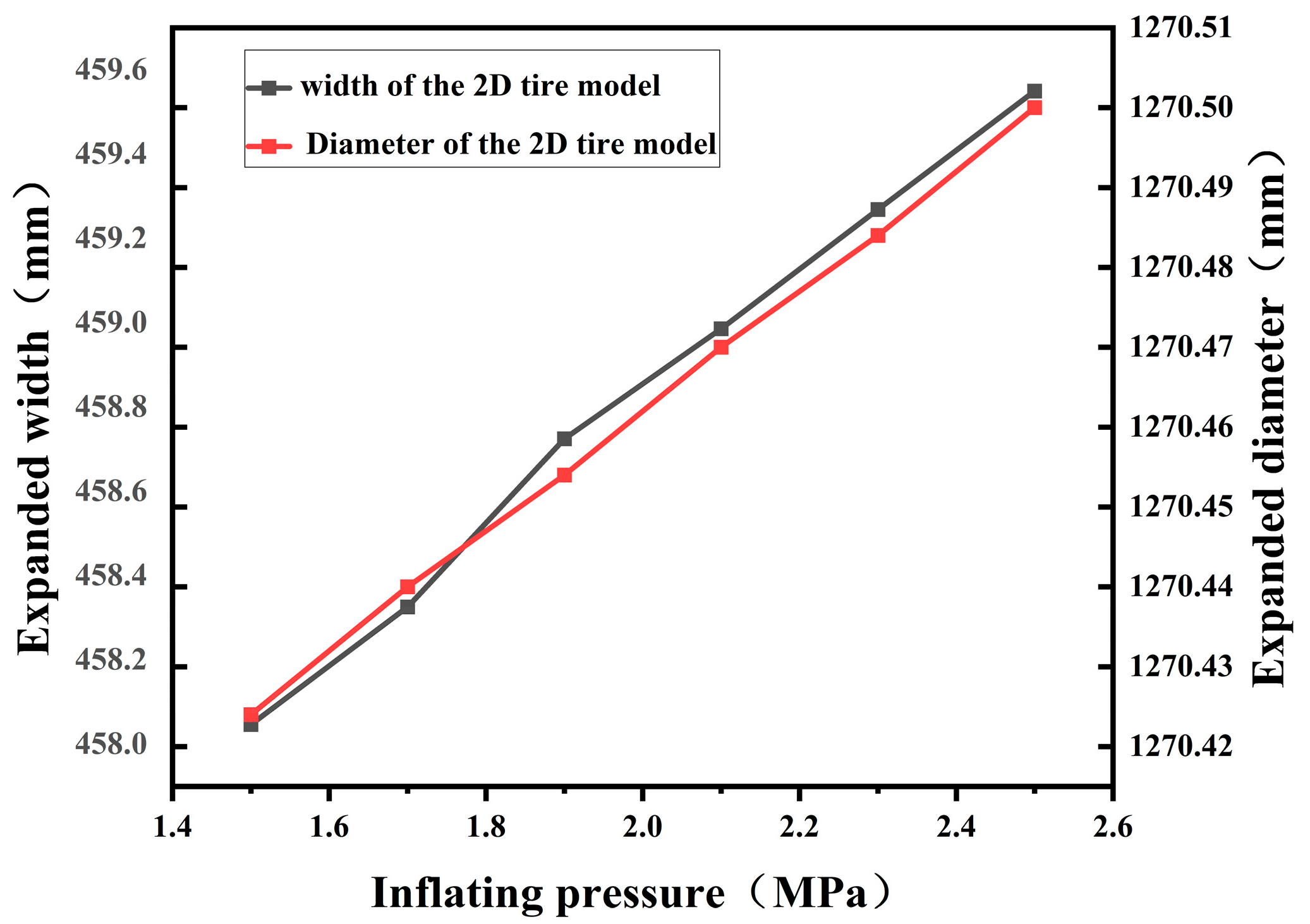
3.4. Inflation Simulation Analysis
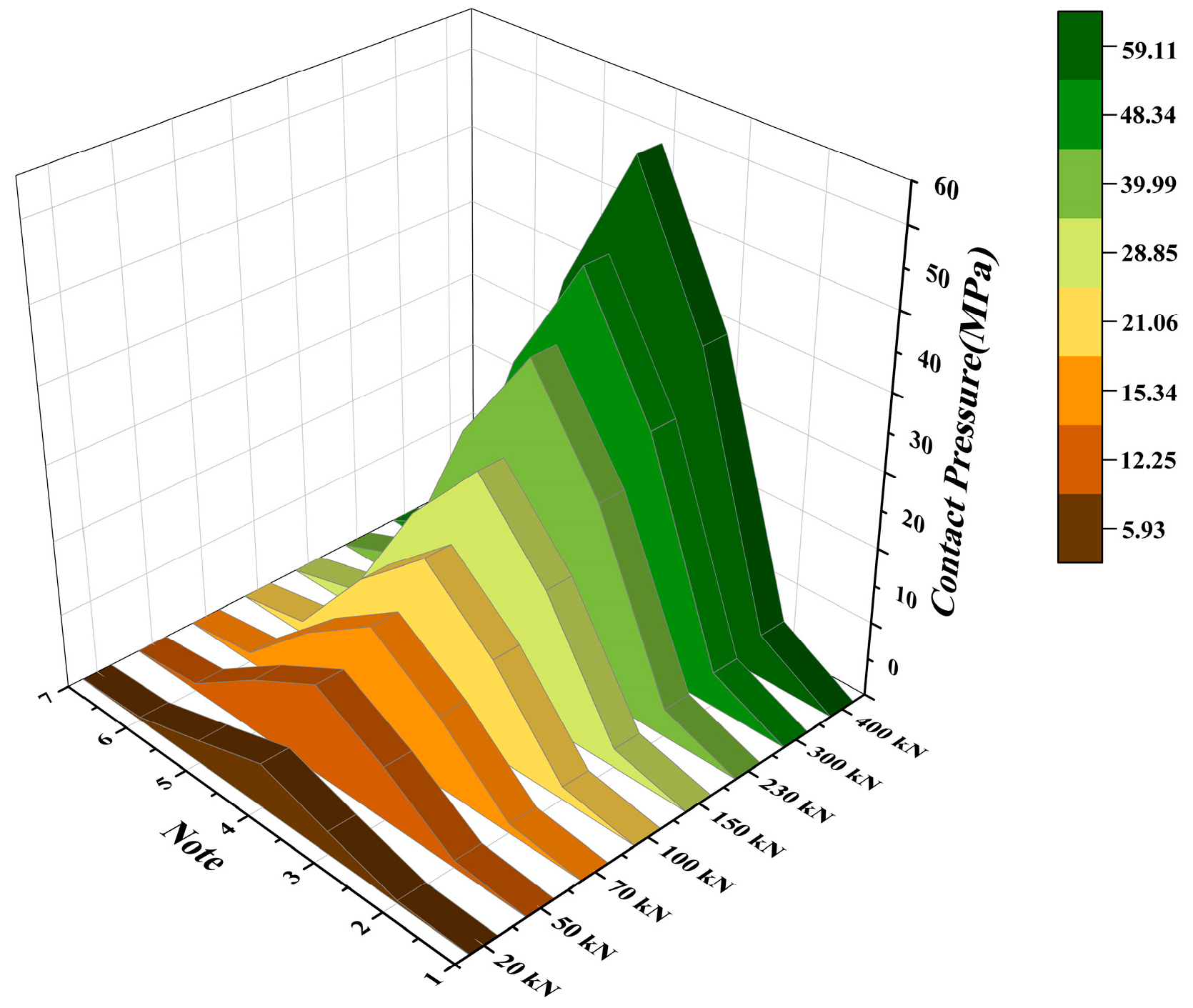
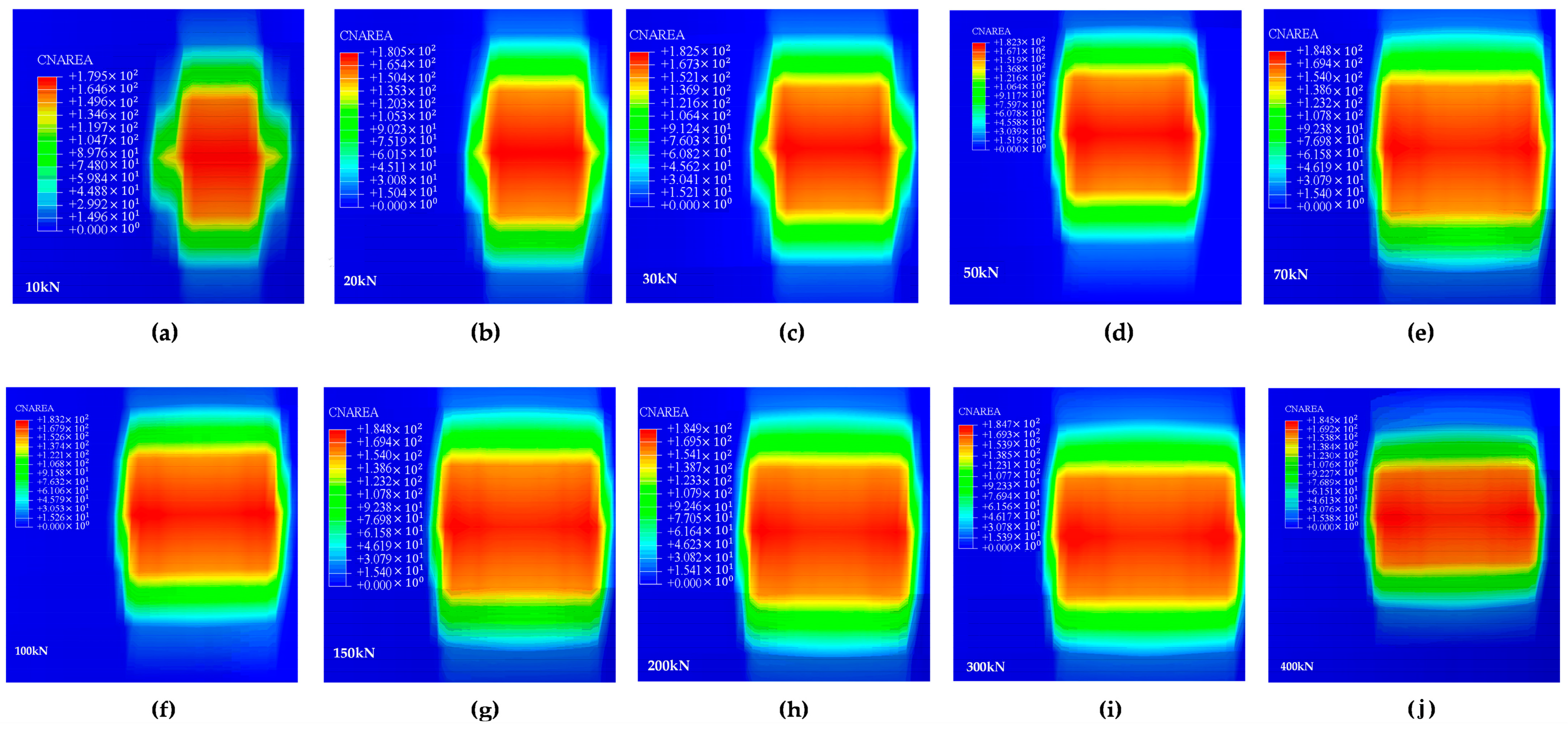
3.5. Tire Footprint Analysis
3.6. Analysis of Effective Normal Contact Area
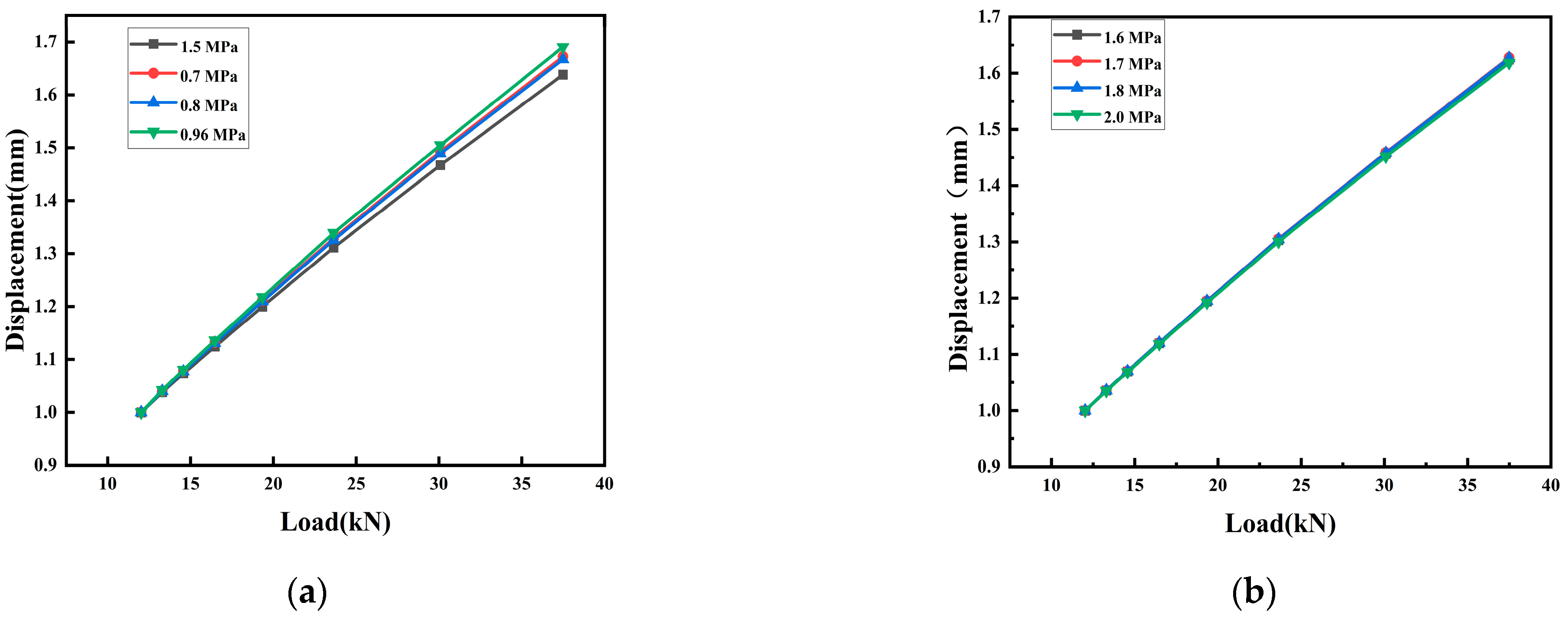
3.7. Deflection and Radial Stiffness Characteristics Analysis
4. Conclusions
4.1. Superiority of the Proposed Material and Mechanism Analysis
4.2. Validation of a Robust Predictive Model
4.3. Performance Advantages in Application Scenarios
4.4. Limitations and Competitive Analysis
4.5. Prospective Applications
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Rohacs, J.; Kale, U.; Rohacs, D. Radically new solutions for reducing the energy use by future aircraft and their operations. Energy 2022, 239, 122420. [Google Scholar] [CrossRef]
- Le Clainche, S.; Ferrer, E.; Gibson, S.; Cross, E.; Parente, A.; Vinuesa, R. Improving aircraft performance using machine learning: A review. Aerosp. Sci. Technol. 2023, 138, 108354. [Google Scholar] [CrossRef]
- Qu, J.; Wang, R.; Huang, F.; Huang, H.; Ren, R.; Wang, Y.; Ding, Y.; Wang, Y. Wear particle matter emission of rubber reinforced by graphene and carbon nanotube hybrid fillers against a rolling-contact concrete surface. Wear 2024, 544–545, 205318. [Google Scholar] [CrossRef]
- Lian, C.; Yi, Y.; Wang, P.; Zhao, S.; Zhou, C.; Zhang, T.; Xue, Z.; Zhang, K.; Yue, Z. Experimental and numerical research of aircraft tire debris impact on landing gear brake pipe. Aerosp. Sci. Technol. 2024, 155, 109546. [Google Scholar] [CrossRef]
- Chen, D.; Wu, J.; Wang, Y.; Su, B.; Liu, Y. High-speed tribology behaviors of aircraft tire tread rubber in contact with pavement. Wear 2021, 486–487, 204071. [Google Scholar] [CrossRef]
- Wu, J.; Chen, L.; Wang, Y.; Su, B.; Cui, Z.; Wang, D. Effect of temperature on wear performance of aircraft tire tread rubber. Polym. Test. 2019, 79, 106037. [Google Scholar] [CrossRef]
- Alroqi, A.A.; Wang, W.; Zhao, Y. Aircraft Tire Temperature at Touchdown with Wheel Prerotation. J. Aircr. 2017, 54, 926–938. [Google Scholar] [CrossRef]
- Ma, Z.; Lu, H.; Liu, C.; Rui, X. Study on the camber angle of an aircraft radial tire: Stress, contact, damage, and modal behaviors. Int. J. Non-Linear Mech. 2025, 175, 105118. [Google Scholar] [CrossRef]
- Teng, F.; Wu, J.; Su, B.; Wang, Y. A cross-scale analysis of the high sliding friction mechanism of the tread rubber under severe working conditions. Wear 2025, 578–579, 206144. [Google Scholar] [CrossRef]
- Lei, K.; Wu, J.; Ren, Z.; Deng, W.; Wang, C. Static Mechanical Characteristics Analysis of Aircraft Tire Under Extreme Weather Conditions. Int. J. Aeronaut. Space Sci. 2024, 25, 979–989. [Google Scholar] [CrossRef]
- Ge, C.; Liu, P.; Qu, Q.; Hu, T.; Zhang, J. Effect of aircraft tire wear on water spray and water displacement drag. Aerosp. Sci. Technol. 2024, 147, 109006. [Google Scholar] [CrossRef]
- Shen, Z.; Wang, Q.; Li, P.; Li, X.; Li, F. Heat build-up and thermo-mechanical fatigue life optimization of aircraft tire using deformation index concept. Int. J. Fatigue 2025, 193, 108815. [Google Scholar] [CrossRef]
- Sattayanurak, S.; Sahakaro, K.; Kaewsakul, W.; Dierkes, W.K.; Reuvekamp, L.A.E.M.; Blume, A.; Noordermeer, J.W.M. Synergistic effect by high specific surface area carbon black as secondary filler in silica reinforced natural rubber tire tread compounds. Polym. Test. 2020, 81, 106173. [Google Scholar] [CrossRef]
- Manikkavel, A.; Kumar, V.; Park, S.-S. MWCNT-reinforced silicone’s dual response to human and mechanical motion: Exploring strain sensing behavior and practical applications. Colloids Surf. A Physicochem. Eng. Asp. 2024, 688, 133536. [Google Scholar] [CrossRef]
- Gao, X.; Yang, J.; Shao, J.; Zhu, H.; Xu, J.; Haruna, S.I. Regulation of carbon nanotubes on internal humidity of concrete with recycled tire rubber: Mechanism analysis and modeling. J. Build. Eng. 2024, 82, 108253. [Google Scholar] [CrossRef]
- Wang, M.; Li, Y.; Qian, C.; Wang, S.; Liu, D. Relationship between the aging thermal oxygen and mechanical properties of nitrile butadiene rubber reinforced by RD-loaded carboxylated carbon nanotubes. Appl. Surf. Sci. 2024, 655, 159569. [Google Scholar] [CrossRef]
- Sari, H.C.; Mubarok, F.A.; Firdaus, M.; Zulfa, I.L.; Fauzi, A.; Rajaelo, W.O.N.F.; Sulistyowati, A.; Ivansyah, A.L.; Muttaqien, F. Computational molecular design to assist modification of single—Walled carbon nanotubes with B, N, Al, Si, P, and S dopant atoms for Cl2 gas sensor application. Surf. Sci. 2023, 731, 122264. [Google Scholar] [CrossRef]
- He, Z.; Xu, J.; Huang, J.; Song, Y.; Li, H.; Man, J.; Liu, T.; Guo, D. Study on the lateral constitutive model for aged laminated rubber bearings considering frictional sliding. Eng. Struct. 2025, 340, 120724. [Google Scholar] [CrossRef]
- Qian, C.; Wang, S.; Li, Y.; Nie, R.; Song, S. Comparative study on thermal-oxygen aging and tribological properties of carbon nanotubes and graphene sheet reinforced hydrogenated nitrile rubber composite materials. J. Mater. Res. Technol. 2024, 29, 2608–2619. [Google Scholar] [CrossRef]
- Lawal, S.A.; Medupin, R.O.; Yoro, K.O.; Ukoba, K.O.; Okoro, U.G.; Adedipe, O.; Abutu, J.; Tijani, J.O.; Abdulkareem, A.S.; Ndaliman, M.B.; et al. Nano-titania and carbon nanotube-filled rubber seed oil as machining fluids. Mater. Chem. Phys. 2024, 316, 129126. [Google Scholar] [CrossRef]
- Yang, C.; Li, W.; Li, Q.; Ma, K.; Zhang, L.; Zhu, M.; Lu, S. Use of non-covalently modified SWCNTs for enhancing the properties of BMI composites with a low loading. Diam. Relat. Mater. 2023, 137, 110089. [Google Scholar] [CrossRef]
- Strozzi, M.; Elishakoff, I.E.; Manevitch, L.I.; Gendelman, O.V. Applicability and limitations of Donnell shell theory for vibration modelling of double-walled carbon nanotubes. Thin Walled Struct. 2022, 178, 109532. [Google Scholar] [CrossRef]
- Ghavanloo, E.; Fazelzadeh, S.A. Vibration characteristics of single-walled carbon nanotubes based on an anisotropic elastic shell model including chirality effect. Appl. Math. Model. 2012, 36, 4988–5000. [Google Scholar] [CrossRef]
- Guo, H.; Bastien, C.; Blundell, M.; Wood, G. Development of a detailed aircraft tyre finite element model for safety assessment. Mater. Des. 2014, 53, 902–909. [Google Scholar] [CrossRef]
- Behroozi, M.; Olatunbosun, O.A.; Ding, W. Finite element analysis of aircraft tyre—Effect of model complexity on tyre performance characteristics. Mater. Des. 2012, 35, 810–819. [Google Scholar] [CrossRef]
- Jiang, B.; Wang, H. An integrated analytical model for friction characteristics of aircraft tire on wet runway pavement. Tribol. Int. 2023, 185, 108501. [Google Scholar] [CrossRef]
- Wood, G.; Blundell, M.; Sharma, S. A low parameter tyre model for aircraft ground dynamic simulation. Mater. Des. 2012, 35, 820–832. [Google Scholar] [CrossRef]
- Jin, J.X. Finite Element Modeling and Static Performance Analysis of Aircraft Tire. Master’s Thesis, Jilin University, Changchun, China, 2022. [Google Scholar]
- Yang, P.; Lei, P.; Liu, B.; Gao, H. Construction of Isotropic Compressible Hyperelastic Constitutive Models Based Solely on Uniaxial Tests. J. Mech. Phys. Solid 2025, 200, 106150. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, L.; Zhang, L.; Li, F. How to effectively perform equibiaxial tension for rubber materials? Polymer 2025, 324, 128256. [Google Scholar] [CrossRef]
- Thorat, R.V.; Anas, M.; Nayek, R.; Chatterjee, S. System identification and reliability assessment of hyperelastic materials via an efficient sparsity-promoting variational Bayesian approach. Probabilistic Eng. Mech. 2025, 80, 103763. [Google Scholar] [CrossRef]
- Liu, H.-Y.; Qiu, L.-C. Three dimensional large deformation and fracture simulation of soft materials using non-ordinary state-based peridynamics with Mooney–Rivlin model. Constr. Build. Mater. 2025, 490, 142574. [Google Scholar] [CrossRef]
- Jing, C.; Jing, W.; Huang, Y.; Qi, L.; Fan, Y. Analysis of interaction between aircraft tire and slush-contaminated pavement. Cold Reg. Sci. Technol. 2025, 240, 104607. [Google Scholar] [CrossRef]
- Hu, Y.; Sun, B.; Wang, X.; Tan, Q.; He, Q.; Wang, J. Simulation Analysis for Mechanical Properties of Radial Aircraft Tires Under Static Load Conditions. J. Nav. Aviat. Univ. 2025, 40, 1–9. [Google Scholar]
- Han, D.; Zhu, G.; Hu, H.; Li, L. Dynamic simulation analysis of the tire-pavement system considering temperature fields. Constr. Build. Mater. 2018, 171, 261–272. [Google Scholar] [CrossRef]
- Park, S.; Yoo, W.; Cho, J.; Kang, B. Pressure-sensing pad test and computer simulation for the pressure distribution on the contact patch of a tyre. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2007, 221, 25–31. [Google Scholar] [CrossRef]
- George, S.; Brady, H.R.C.; Vaccari, J.A. Materials Handbook: A Concise Desktop Reference; Springer: New York, NY, USA, 2002. [Google Scholar]
- GB/T 9746-2013; Series of Aircraft Tyres. General Administration of Quality Supervision, Inspection and Quarantine. Standards Press of China: Beijing, China, 2013.



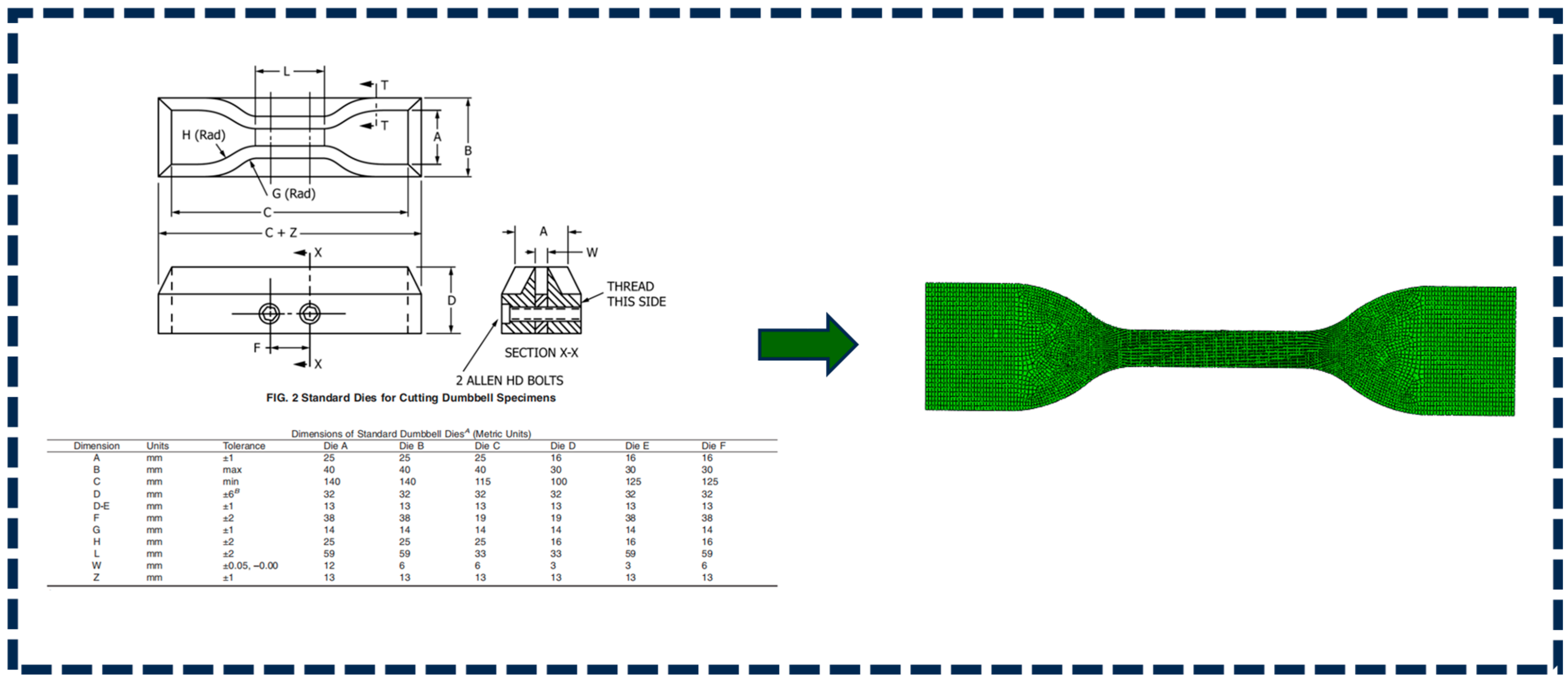
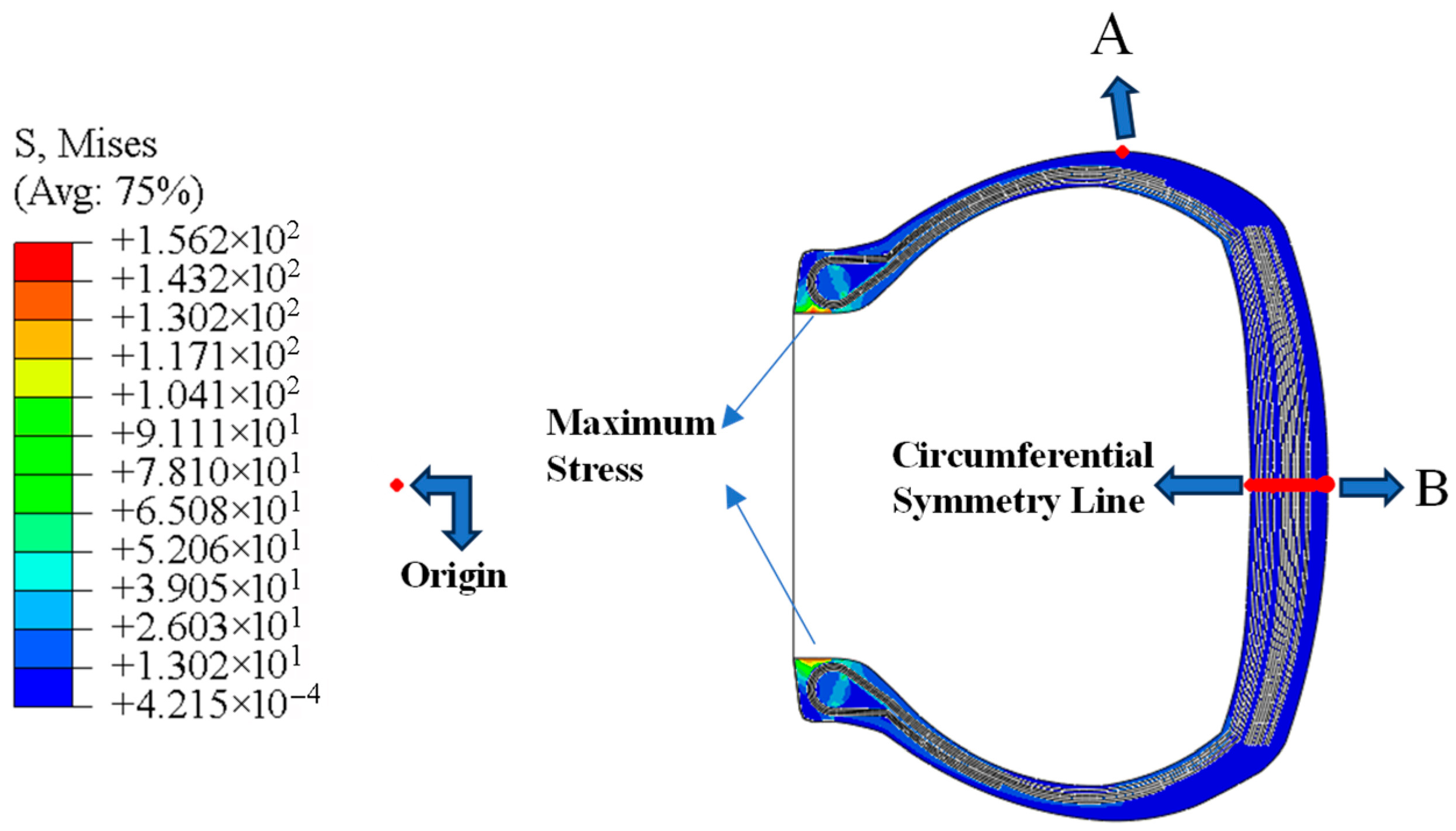
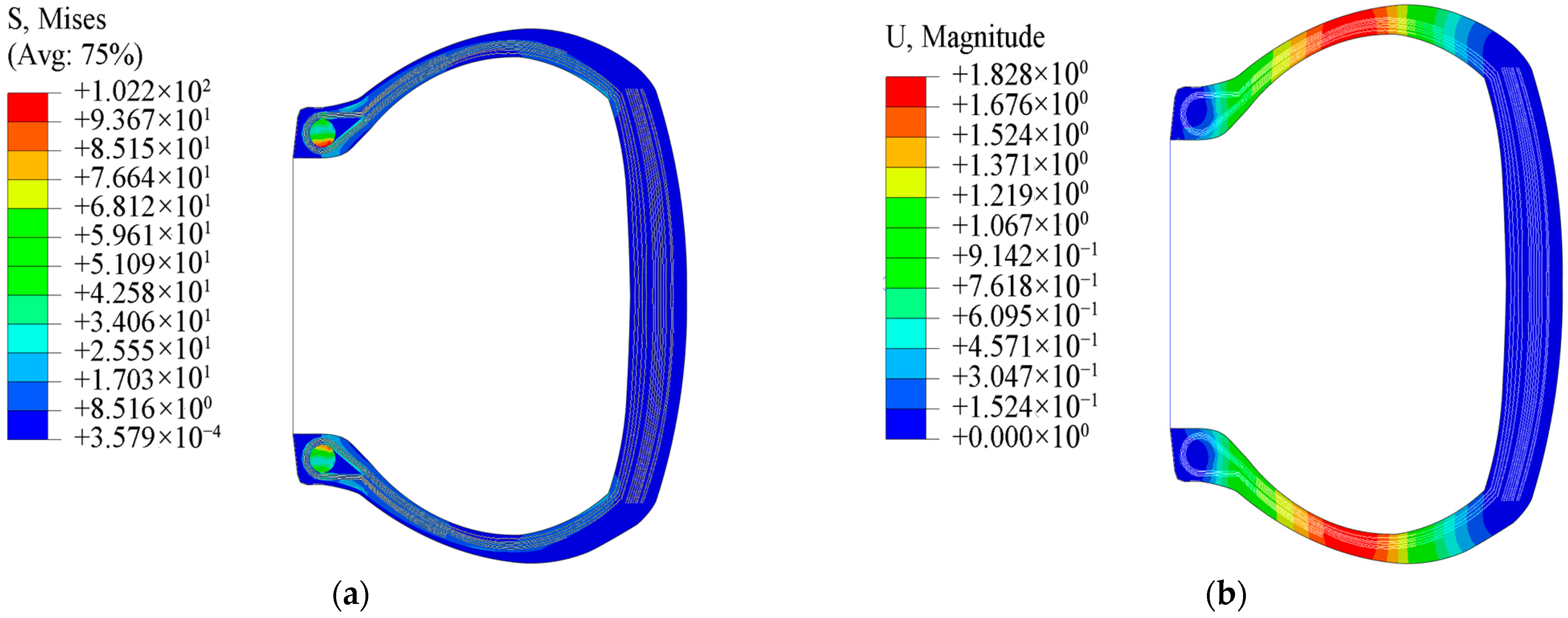
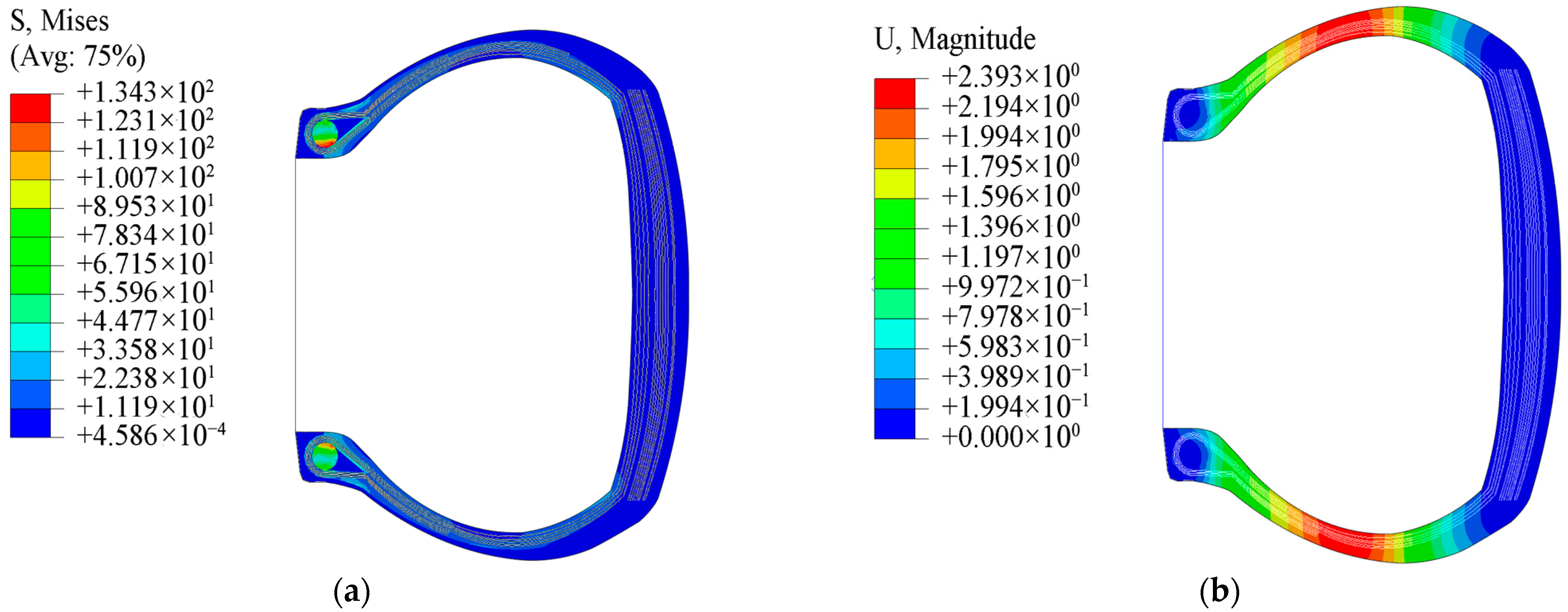






| Raw Materials | A | B | C |
|---|---|---|---|
| NR | 100 | 100 | 100 |
| ZnO | 5 | 5 | 5 |
| SA | 2 | 2 | 2 |
| Sulfur | 3 | 3 | 3 |
| Accelerator CZ | 1 | 1 | 1 |
| Carbon black | 50 | 50 | 50 |
| Carbon nanotubes | 0 | 0.06 | 0 |
| Selenol-functionalized carbon nanotubes | 0.06 | 0 | 0 |
| Material Designations | Mooney–Rivlin Model Parameters | ||
|---|---|---|---|
| C10 | C01 | D1 | |
| Apex Filler | −12.6578 | 17.5212 | 0.000 |
| Sidewall Compound | 0.3932 | 0.2798 | 0.000 |
| Material Designations | Yeoh Model Parameters | |||
|---|---|---|---|---|
| C10 | C20 | C30 | D1 | |
| Carcass | 583.843 | 2671.68 | −5107.4 | 3.67 × 10−4 |
| Belt | 601.288 | 1928.09 | 18,956.8 | 3.56 × 10−4 |
| Material Designations | Parameters for Polynomial Hyperelastic Model (N = 2) | ||||||
|---|---|---|---|---|---|---|---|
| C10 | C01 | C20 | C11 | C02 | D1 | D2 | |
| Tread | −2.05106 | 3.38092 | −0.007145 34 | 0.120132 | 0.408546 | 0.000 | 0.000 |
| Bead Heel | −2.05106 | 3.38092 | −0.007145 34 | 0.120132 | 0.408546 | 0.000 | 0.000 |
| Component | Single-Cord Cross-Sectional Area (mm2) | Cord Spacing (mm) | Orientation Angle (°) |
|---|---|---|---|
| Bead Reinforcement Cords 1 | 1 | 0.2 | 0 |
| Bead Reinforcement Cords 2 | 1 | 0.2 | 0 |
| Belt Reinforcement Cords 1 | 1.5 | 0.2 | −75 |
| Belt Reinforcement Cords 2 | 1.5 | 0.2 | 75 |
| Belt Reinforcement Cords 3 | 1.5 | 0.2 | −75 |
| Belt Reinforcement Cords 4 | 1.5 | 0.2 | 75 |
| Belt Reinforcement Cords 5 | 1.5 | 0.2 | −75 |
| Belt Reinforcement Cords 6 | 1.5 | 0.2 | 75 |
| Carcass Cords 1 | 1.5 | 0.2 | 90 |
| Carcass Cords 2 | 1.5 | 0.2 | 90 |
| Carcass Cords 3 | 1.5 | 0.2 | 90 |
| Carcass Cords 4 | 1.5 | 0.2 | 90 |
| Material | Young’s Modulus (MPa) | Poisson’s Ratio | Density (g/cm3) |
|---|---|---|---|
| Reinforcement Cord | 90,000 | 0.3 | 1.25 |
| Bead Wire Bundle | 209,000 | 0.3 | 7.8 |
| Maximum Expanded Dimensions (mm)/ Inflation Pressure (MPa) | Nominal Diameter | Nominal Width | Expanded Diameter | Expanded Width |
|---|---|---|---|---|
| 1.5 | 1270 | 455 | 1270.424 | 458.047 |
| 1.7 | 1270 | 455 | 1270.440 | 458.326 |
| 1.9 | 1270 | 455 | 1270.454 | 458.725 |
| 2.1 | 1270 | 455 | 1270.470 | 458.986 |
| 2.3 | 1270 | 455 | 1270.484 | 459.269 |
| 2.5 | 1270 | 455 | 1270.500 | 459.550 |
| Sample ID/Physical Properties | A | B | C |
|---|---|---|---|
| 300% Modulus | 10.24 MPa | 7.99 MPa | 5.49 MPa |
| 500% Modulus | 18.31 MPa | 15.63 MPa | 13.20 MPa |
| Tensile Strength | 23.22 MPa | 22.00 MPa | 21.10 MPa |
| Elongation at Break | 630% | 690% | 700% |
| Tear Strength | 58.73 kN/m | 50.32 kN/m | 70.35 kN/m |
| Poisson’s Ratio | 0.50 | 0.44 | 0.35 |
| Young’s Modulus | 3.82 MPa | 3.32 MPa | 3.16 MPa |
| Shore Hardness | 74.8 | 70.9 | 75.00 |
| Material/ Coefficient | C10 | C01 | C20 | C11 | C02 | D1 |
|---|---|---|---|---|---|---|
| A | −2.055 | 3.3809 | −0.007 | 0.12013 | 0.40854 | 0.00 |
| 10,579 | 1519 | 14,534,425 | 2238 | 6221 | 000 |
| Material/ Property | Experimental Peak Stress (MPa) | Experimental Elongation (mm) | Simulated Peak Stress (MPa) | Simulated Elongation (mm) |
|---|---|---|---|---|
| A | 23.22 | 207.90 | 23.19 | 207.90 |
| B | 22.00 | 227.70 | 21.58 | 227.70 |
| C | 21.10 | 231.00 | 21.12 | 231.00 |
| Tire pressure (MPa) | 0.7 | 0.8 | 0.96 | 1.5 | 1.6 | 1.7 | 1.8 | 2.0 |
| Radial stiffness (kN/mm) | 22.8 | 22.4 | 22.4 | 22.1 | 22.9 | 22.9 | 22.9 | 23.0 |
| Material/ Coefficient | C10 | C01 | C20 | C11 | C02 | D1 |
|---|---|---|---|---|---|---|
| B | −4.1566 | 6.24915 | 0.002259 | −0.0011 | 1.49315548 | 0.00 |
| 3236 | 683 | 189,504 | 44,195,275 | 000 |
| Material/ Coefficient | C10 | C01 | C20 | C11 | C02 | D1 |
|---|---|---|---|---|---|---|
| C | −1.2398 | 2.483 | −0.0073 | 0.1440 | 0.1038 | 0.00 |
| 2782 | 83,257 | 87,508,920 | 69,996 | 31,821 | 000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, M.; Du, T.; Shi, J.; Huang, C.; Xu, C.; Wei, Z. Modeling and Finite-Element Performance Analysis of Selenol-Functionalized Carbon Nanotube/Natural Rubber Composites for Aircraft Tire Applications. Appl. Sci. 2025, 15, 10053. https://doi.org/10.3390/app151810053
Xu M, Du T, Shi J, Huang C, Xu C, Wei Z. Modeling and Finite-Element Performance Analysis of Selenol-Functionalized Carbon Nanotube/Natural Rubber Composites for Aircraft Tire Applications. Applied Sciences. 2025; 15(18):10053. https://doi.org/10.3390/app151810053
Chicago/Turabian StyleXu, Mingyao, Tianfeng Du, Jinwei Shi, Chen Huang, Chen Xu, and Zhuoqun Wei. 2025. "Modeling and Finite-Element Performance Analysis of Selenol-Functionalized Carbon Nanotube/Natural Rubber Composites for Aircraft Tire Applications" Applied Sciences 15, no. 18: 10053. https://doi.org/10.3390/app151810053
APA StyleXu, M., Du, T., Shi, J., Huang, C., Xu, C., & Wei, Z. (2025). Modeling and Finite-Element Performance Analysis of Selenol-Functionalized Carbon Nanotube/Natural Rubber Composites for Aircraft Tire Applications. Applied Sciences, 15(18), 10053. https://doi.org/10.3390/app151810053






