Multi-Source Energy Storage Day-Ahead and Intra-Day Scheduling Based on Deep Reinforcement Learning with Attention Mechanism

Abstract

With the rapid integration of high-penetration renewable energy, its inherent uncertainty complicates power system day-ahead/intra-day scheduling, leading to challenges like wind curtailment and high operational costs. Existing methods either rely on inflexible physical models or use deep reinforcement learning (DRL) without prioritizing critical variables or synergizing multi-source energy storage and demand response (DR). This study develops a multi-time scale coordination scheduling framework to balance cost minimization and renewable energy utilization, with strong adaptability to real-time uncertainties. The framework integrates a day-ahead optimization model and an intra-day rolling model powered by an attention-enhanced DRL Actor–Critic network—where the attention mechanism dynamically focuses on critical variables to correct real-time deviations. Validated on an East China regional grid, the framework significantly enhances renewable energy absorption and system flexibility, providing a robust technical solution for the economical and stable operation of high-renewable power systems.

1. Introduction

Against the backdrop of global energy transition and the urgent need to address environmental challenges, accelerating the integration of renewable energy has become a critical strategy for sustainable development. However, the inherent uncertainty of renewable energy sources such as wind power introduces significant complexities to power system scheduling, posing challenges to the stable and economic operation of the grid [1]. Effectively accommodating fluctuations in renewable energy output while coordinating multiple resources—including conventional generators, energy storage systems, and demand response programs—to achieve optimal interaction remains a key issue in modern power system operation.

To tackle the aforementioned challenges, artificial intelligence (AI) methods—especially deep reinforcement learning (DRL)—have emerged as promising alternatives to traditional model-based approaches, thanks to their data-driven adaptability in handling dynamic uncertainties without over-reliance on precise physical models [2]. Recent explorations of AI in real-time optimal power flow [3] not only expand its application scope in power systems but also provide technical references for AI-driven scheduling optimization.

Research on optimal power system scheduling has received extensive attention. For microgrid scenarios involving multi-energy resources, reference [4] proposed a day-ahead economic optimal scheduling method considering time-of-use electricity prices. At the building scale, reference [5] developed a day-ahead optimization model for smart homes with photovoltaic–thermal (PVT) systems, integrating battery/boiler storage and load scheduling to balance cost and comfort. Extending to integrated energy systems, reference [6] proposed a data-driven distributed robust self-scheduling method for integrated energy production units participating in day-ahead electricity–gas joint markets. Reference [7] constructed a battery charging–discharging model and derived an economic scheduling strategy for systems with energy storage using dynamic programming. Reference [8] characterized the uncertainty of new energy generation based on fuzzy sets, adopted a distributed robust optimization method to handle chance constraints, and managed the energy of islanded microgrids. Reference [9] addressed the uncertainty in renewable energy and load forecasting by building a two-stage robust optimization model with uncertainty adjustment parameters, which was solved using the column-and-constraint generation algorithm. Reference [10] considered the uncertainty of wind power in the uncertainty set, iteratively solved the adaptive robust optimization model using the column constraint generation algorithm, and ensured the feasibility of the scheduling strategy through a two-level robustness solution. However, most of these studies are confined to day-ahead scheduling and fail to consider real-time fluctuations or prediction errors; more critically, they rely heavily on precise physical models—computational efficiency declines sharply as system scale expands (e.g., multi-source energy storage integration), making them unsuitable for dynamic intra-day scenarios.

To better adapt to the dynamic characteristics of renewable energy and load fluctuations across different time horizons, research has increasingly focused on multi-time scale scheduling frameworks. Reference [11] proposed a two-stage scheduling model for integrated energy systems (IESs) based on distributionally robust adaptive MPC, improving day-ahead–intra-day coordination via dual-loop feedback. Reference [12] considered the participation of distributed renewable energy and distributed energy storage in microgrid scheduling, establishing an intra-day optimal scheduling model for active distribution networks based on improved deep reinforcement learning. Reference [13] analyzed the power and energy balance mechanism of multi-interactive distribution networks with source-grid–load-storage coordination, and constructed a source-grid–load-storage coordinated optimal scheduling model. Reference [14] proposed a four-stage scheduling model (day-ahead, intra-day, ultra-short-term, and ultra-ultra-short-term) optimized via Gurobi, incorporating buffer boundaries for global coordination. Reference [15] developed a multi-time scale rolling scheduling model based on “robust plans” and “robust operation zones” using robust optimization. While these models improve temporal coordination, they still depend on predefined physical constraints and neglect demand-side flexibility, limiting their ability to handle high-renewable penetration.

With the advancement of artificial intelligence, DRL chen2024model has emerged as a promising solution for uncertain environments [16,17], leveraging its adaptability and flexibility in dynamic scenarios [18,19]. Reference [20] adopted the deep Q-learning algorithm for optimal scheduling of energy management, and the simulation results showed that the use of reinforcement learning algorithms can improve energy utilization and scheduling performance. Reference [21] employed a two-layer RL model, where the upper layer considers the energy state of the entire scheduling cycle to generate charging and discharging strategies for energy storage, and the lower layer only considers the current operating cost, using mixed-integer linear programming to solve the current scheduling actions and operating costs. Reference [22] considered energy storage systems and realized robust economic scheduling of virtual power plants using the deep deterministic policy gradient algorithm based on scenario datasets generated by generative adversarial networks. Reference [23] evaluated seven DRL algorithms for energy management, highlighting their potential in complex scheduling scenarios.

Beyond electrochemical and pumped hydro storage, reference [24] integrated tidal range power stations into day-ahead scheduling, demonstrating flexible coordination of renewable energy with unique storage characteristics. Reference [25] further explored gravity energy storage (GES) in day-ahead scheduling, using distributionally robust optimization to handle price uncertainty. However, the above studies have two critical limitations: (1) they rarely consider the synergistic coordination of multi-source energy storage (e.g., pumped hydro storage + electrochemical storage) and dual-type demand response (price-based + incentive-based); (2) they lack mechanisms to prioritize critical state variables (e.g., wind power forecasts, energy storage state of charge), leading to suboptimal decision-making in multi-variable, multi-time scale scenarios.

The limitations of existing methods directly affect practical operation of high-renewable power systems: traditional day-ahead models cannot adjust to sudden wind surges; over-reliance on conventional generator ramping increases fuel/penalty costs; and poor multi-source coordination raises grid instability risks. For grids like East China’s (plagued by renewable integration challenges), these issues hinder carbon reduction and grid stability—urgently requiring a more adaptive framework.

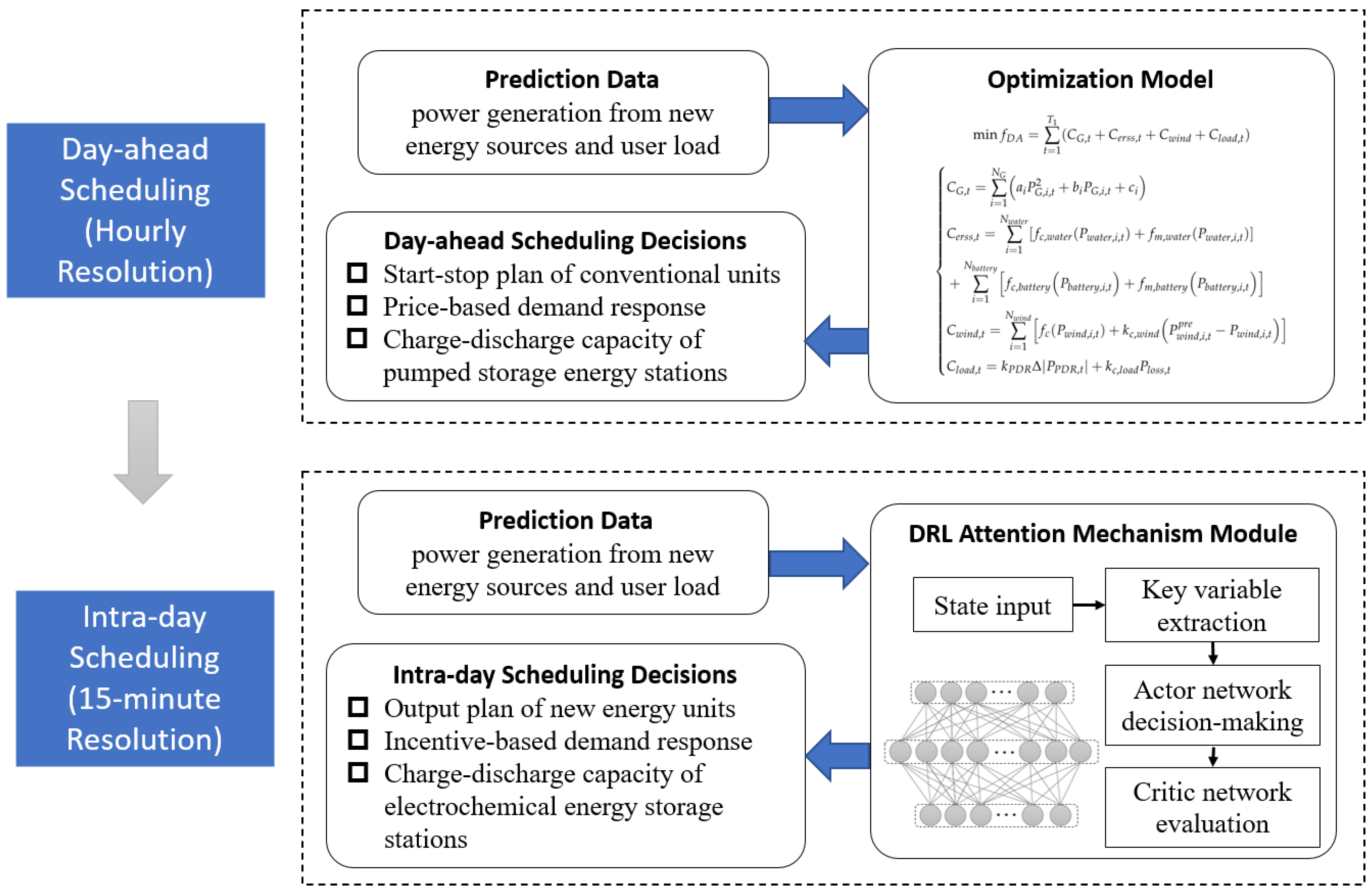
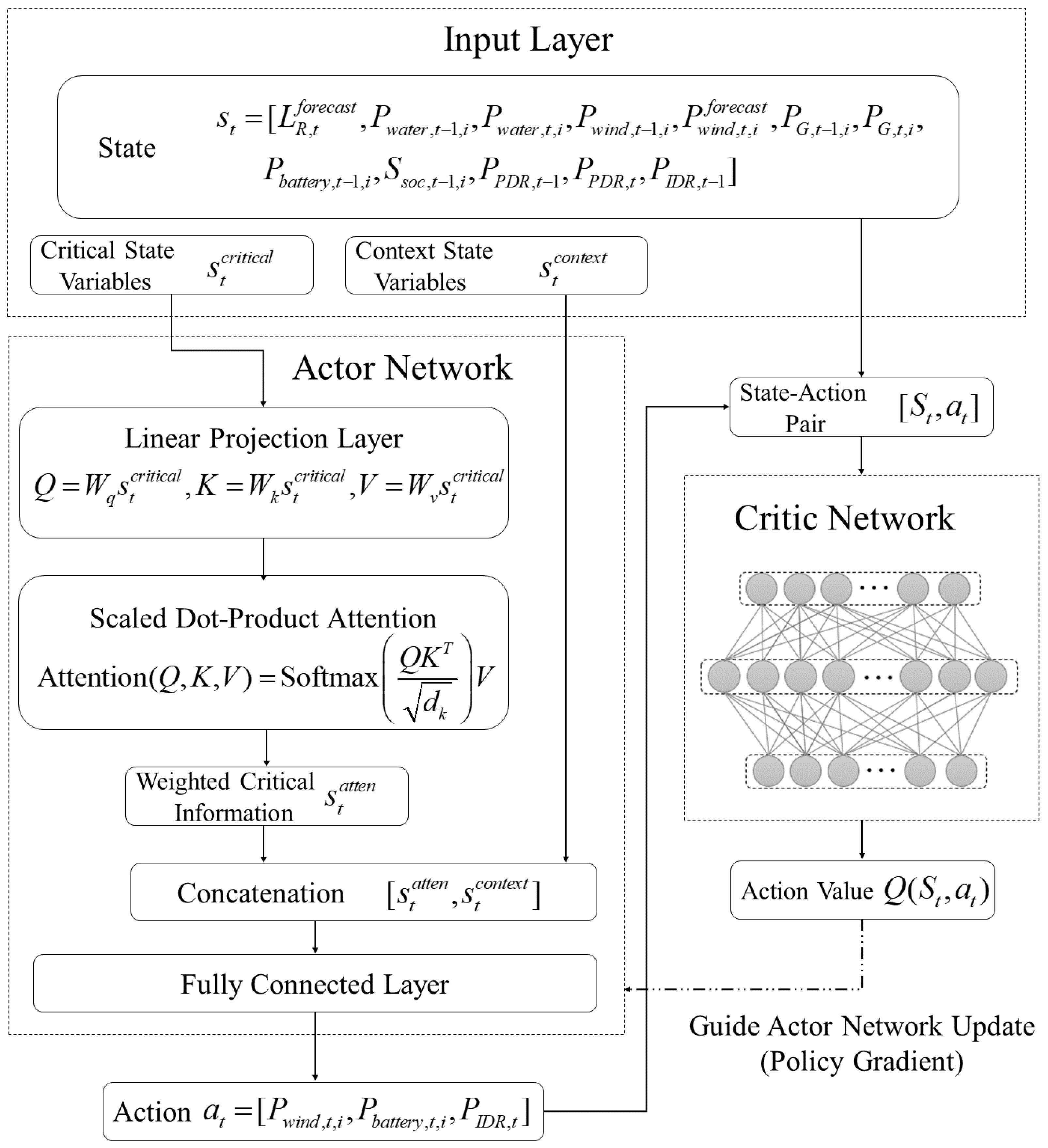
To address the above gaps, this study develops a multi-time scale coordination scheduling framework integrated with attention-enhanced DRL, balancing cost minimization and renewable utilization while improving real-time adaptability. The proposed framework combines two core stages: Day-ahead scheduling (hourly resolution), which optimizes conventional generators, pumped hydro storage, electrochemical energy storage, and price-based demand response (PDR) to minimize total operational costs; and intra-day rolling scheduling (15 min resolution, 4 h horizon), which adjusts wind power, battery operation, and incentive-based demand response (IDR) in real time. Notably, the intra-day stage uses an attention-based Actor–Critic DRL algorithm—dynamically weighting critical variables (e.g., wind forecast errors, storage SOC) to correct deviations, overcoming the lack of targeted decision-making in existing DRL methods.

The rest of the paper is organized as follows. The multi-time scale coordination scheduling model is proposed in Section 2. Section 3 presents the reinforcement learning-based optimization framework. Section 4 verifies the effectiveness and advantages of the proposed method with simulation results. Finally, the conclusion of this paper is presented in Section 5.

2. Multi-Time Scale Coordination Scheduling Model

Figure 1 systematically outlines the two core stages of the framework—day-ahead scheduling and intra-day rolling scheduling—including their respective input, core optimization models, and key decision outputs, while also reflecting the integration of the attention-enhanced DRL mechanism in the intra-day dynamic adjustment process.

2.1. Day-Ahead Scheduling Optimization Model

The developed day-ahead optimization framework synergistically combines wind power forecasts with load demand predictions to achieve dual objectives of cost minimization and renewable energy utilization maximization. By coordinating the dispatch of conventional generators, pumped hydro storage, electrochemical energy storage systems, and demand response (DR), the model achieves the lowest total system operating cost while enhancing renewable energy utilization.

2.1.1. Objective Function

The proposed day-ahead scheduling model addresses two critical challenges in modern power systems: maximizing renewable energy integration and maintaining grid reliability under contingency conditions. Specifically, the optimization framework simultaneously minimizes total system operating costs while accounting for penalty costs associated with wind curtailment and emergency load shedding. By incorporating these penalty mechanisms, the model achieves a threefold optimization objective: economic efficiency through optimal resource dispatch, enhanced utilization of wind power generation by minimizing curtailment, and guaranteed power supply reliability during emergency operations through controlled load shedding strategies. This comprehensive approach effectively balances cost-effectiveness with operational resilience in renewable-rich power systems.

$$min{f}_{DA}=\sum _{t=1}^{T_1}\left(C_{G,t}+C_{erss,t}+C_{wind}+C_{load,t}\right)$$

(1)

$$\left\{\begin{array}{c}{C}_{G,t}=\sum _{i=1}^{N_G}\left(a_i{P}_{G,i,t}^2+b_i{P}_{G,i,t}+c_i\right)\hfill \\ C_{erss,t}=\sum _{i=1}^{N_{water}}\left[f_{c,water}\left(P_{water,i,t}\right)+f_{m,water}\left(P_{water,i,t}\right)\right]\hfill \\ +\sum _{i=1}^{N_{battery}}\left[f_{c,battery}\left(P_{battery,i,t}\right)+f_{m,battery}\left(P_{battery,i,t}\right)\right]\hfill \\ C_{wind,t}=\sum _{i=1}^{N_{wind}}\left[f_c\left(P_{wind,i,t}\right)+k_{c,wind}\left(P_{wind,i,t}^{pre}-P_{wind,i,t}\right)\right]\hfill \\ C_{load,t}=k_{PDR}\Delta \left|P_{PDR,t}\right|+k_{c,load}{P}_{loss,t}\hfill \end{array}\right.$$

(2)

where $f_{DA}$ is the objective function of the day-ahead scheduling optimization model, representing the system operation cost; $T_1$ represents the number of time intervals in a day (24 h, hourly resolution); $C_{G,t}$, $C_{erss,t}$, $C_{wind,t}$, and $C_{load,t}$ represent the cost functions of conventional units, energy storage power stations (ERSS, including pumped hydro storage and electrochemical energy storage), wind turbines, and user loads, respectively; $N_G$ is the number of conventional units; $P_{G,i,t}$ is the power generation of the i-th conventional unit at time t; $a_i$, $b_i$, and $c_i$ are the quadratic, linear, and constant cost coefficients of the i-th conventional unit, respectively; $N_{water}$ and $N_{battery}$ are the numbers of pumped hydro storage stations and electrochemical energy storage stations, respectively; $P_{water,i,t}$ and $P_{battery,i,t}$ are the output of pumped hydro storage stations and electrochemical energy storage stations, i at time t, respectively; $f_c\left(P_{water,i,t}\right)$ and $f_c\left(P_{battery,i,t}\right)$ are the cost function of the pumped hydro storage stations and electrochemical energy storage stations, respectively; $f_m\left(P_{water,i,t,}\right)$ and $f_m\left(P_{battery,i,t,}\right)$ are the maintenance cost function of the pumped hydro storage stations and electrochemical energy storage stations, respectively; $N_{wind}$ represents the number of distributed new energy units; $P_{wind,i,t}$ represents the output of the i-th wind turbine at time t; $f_{c,wind}\left(P_{wind,i,t}\right)$ represents the cost function of the wind turbine at time t; $k_{c,wind}$ represents the wind curtailment penalty cost coefficient; $P_{wind,t}^{pre}$ represents the predicted output of wind power at time t; $k_{PDR}$ is the cost coefficients of PDR; $\Delta |P_{PDR,t}|$ is the call volume of PDR at time t; $k_{c,load}$ is the load loss penalty coefficient; $P_{loss,t}$ is the power loss of the load at time t.

2.1.2. Constraints

The day-ahead scheduling model incorporates comprehensive operational constraints to ensure physical feasibility and system reliability. These constraints govern the balanced operation of conventional generation units, renewable energy sources, energy storage systems, and demand response resources while maintaining network security.

The power balance constraint ensures generation–load equilibrium at each time interval, accounting for both fixed and price-responsive demand components:

$$\begin{array}{c}\hfill L_{R,t}+\Delta P_{PDR,t}+\Delta P_{IDR,t}=\sum _i^{N_G}{P}_{G,i,t}+\sum _i^{N_{DC}}{P}_{wind,i,t}+\sum _i^{N_{water}}{P}_{water,i,t}+\sum _i^{N_{battery}}{P}_{battery,i,t}+P_{loss,t}\end{array}$$

(3)

where $L_R$ is the part of the load that does not change with the electricity price; $\Delta P_{PDR,t}$ is the change in PDR at time t; and $\Delta P_{IDR,t}$ is the change in IDR at time t.

Conventional generation units are subject to technical operating limits. The output of each thermal unit must remain within its designated capacity range:

$$P_{G,i}^{min}\le P_{G,i,t}\le P_{G,i}^{max}$$

(4)

where $P_{G,i}^{min}$ and $P_{G,i}^{max}$ are the upper and lower limits of the output of the i-th conventional unit, respectively.

Additionally, ramping capabilities constrain inter-temporal output variations to ensure feasible dispatch transitions:

$$-R_i^{dn}\le P_{G,i,t}-P_{G,i,t-1}\le R_i^{up}$$

(5)

where $R_i^{up}$ and $R_i^{dn}$ represent the maximum allowable upward and downward power adjustments per time interval.

Renewable energy integration follows forecast availability constraints, requiring wind power output to not exceed predicted generation potential:

$$0\le P_{wind,i,t}\le P_{wind,i,t}^{pre}$$

(6)

The output of new energy power generation should be less than the predicted value.

Energy storage systems, including both pumped hydro and electrochemical storage, operate under distinct technical constraints. Pumped hydro storage must maintain reservoir water volume within operational limits while respecting pumping/discharge rate constraints:

$$\left\{\begin{array}{c}{P}_{water,t}^{min}\le P_{water,t}\le P_{water,t}^{max}\hfill \\ V_{Pump}^{min}\le V_{water}\le V_{Pump}^{max}\hfill \\ \left|P_{water,t}-P_{water,t-1}\right|\le \Delta P_R,\hfill \end{array}\right.$$

(7)

where $P_{water,t}^{min}$ and $P_{water,t}^{max}$ represent the upper and lower limits of the power input and output of the pumped storage power station, respectively; $V_{Pump}^{min}$ and $V_{Pump}^{max}$ represent the upper and lower limits of the water storage of the pumped storage power station; and $\Delta P_R$ represents the ramp rate of the pumped storage power station.

Electrochemical storage systems are constrained by power converter ratings and state-of-charge (SOC) boundaries:

$$\left\{\begin{array}{c}{P}_{elec,t}^{cha}\le P_{elec,t}\le P_{elec,t}^{dis}\hfill \\ S_{SOCmin}\le S_{SOC,t}\le S_{SOCmax}\hfill \end{array}\right.$$

(8)

where $P_{elec,t}^{cha}$ and $P_{elec,t}^{dis}$ are the rated charging power and rated discharging power of the inverter, respectively; $S_{SOC,t}$ is the state of charge of the energy storage power station; upper and lower limits; and $S_{SOCmax}$ and $S_{SOCmin}$ are the upper and lower limits of the state of charge of the energy storage power station.

Transmission network security is enforced through line flow limits derived from DC power flow assumptions:

$$-P_{ij}^{max}\le B_{ij}\left({\theta }_{i,t}-{\theta }_{j,t}\right)\le P_{ij}^{max}$$

(9)

where $P_{ij}^{max}$ is the maximum transmission power of the transmission line between nodes $ij$; $B_{ij}$ is the susceptance between nodes i; and ${\theta }_{i,t}$ is the phase angle of node i at time t.

Flexibility requirements ensure adequate adjustment capabilities from both conventional and storage resources:

$$\left\{\begin{array}{c}\left|P_{G,i,t}-P_{G,i,t,base}\right|\le {\psi }_i\hfill \\ \left|P_{erss,t}-P_{erss,t,base}\right|\le {\psi }_{erss}\hfill \end{array}\right.$$

(10)

where ${\psi }_i$ and ${\psi }_{erss}$ are the flexible adjustment capabilities of conventional units and ERSS, respectively. $P_{G,i,t,base}$ and $P_{erss,t,base}$ are the baseline scheduled outputs of conventional units and ERSS, respectively.

Demand response programs operate within predefined participation limits. Price-based DR follows continuous adjustment bounds:

$$P_{PDR}^{min}\le P_{PDR,t}\le P_{PDR}^{max}$$

(11)

where $P_{PDR}^{min}$ and $P_{PDR}^{max}$ are the lower and upper limits of the PDR load call volume, respectively.

The day-ahead scheduling solution provides key operational parameters for subsequent intra-day coordination, including committed conventional unit outputs, pumped storage schedules, and activated demand response quantities. These predetermined values serve as boundary conditions for finer-time scale operational decisions while maintaining overall system optimization objectives.

2.2. Intra-Day Rolling Scheduling Optimization Model

The intra-day rolling optimization framework establishes a dynamic decision-making process to address real-time operational challenges in renewable-integrated power systems. Building upon the day-ahead scheduling results, this approach combines ultra-short-term forecasting with adaptive optimization to maintain system balance while accommodating renewable generation variability. The model solves for optimal control sequences using 15 min resolution forecast data for wind power and load demand across a rolling 4 h horizon.

The objective function maintains consistency with the day-ahead optimization while focusing on adjustable operational costs:

$$min{f}_{ID}=\sum _{t=1}^{T_2}{C}_{G,t}+C_{erss,t}+C_{wind,t}+C_{load,t}$$

(12)

where $T_2$ represents the number of time intervals in the 4 h rolling horizon (15 min resolution, 16 intervals) and the load cost component now exclusively considers IDR activation:

$$\begin{array}{c}{C}_{load,t}=k_{IDR}\Delta \left|P_{IDR,t}\right|+k_{c,load}{P}_{loss,t}\end{array}$$

(13)

where $k_{IDR}$ is the cost coefficient of IDR; $\Delta |P_{IDR,t}|$ is the call volume of IDR at time t. IDR refers to a demand-side management mechanism where users receive direct financial incentives (e.g., subsidies or rebates) to adjust their electricity consumption in response to grid operational needs, such as peak shaving or renewable energy absorption.

The constraint set largely mirrors the day-ahead model with additional provisions for IDR flexibility. IDR maintains separate capacity limits for load increase and decrease:

$$\left\{\begin{array}{c}0\le P_{IDR,t}^{+}\le P_{IDR}^{+,max}\hfill \\ 0\le P_{IDR,t}^{-}\le P_{IDR}^{-,max}\hfill \end{array}\right.$$

(14)

where $P_{IDR,t}^{+}$ and $P_{IDR,t}^{-}$ are the increased load volume and decreased load volume of IDR, respectively.

The optimization process takes the day-ahead scheduled states as fixed parameters, including conventional unit commitments, pumped storage operations, and PDR allocations. Within this framework, the model determines optimal wind farm dispatch schedules, battery storage operations, and IDR activation levels to maintain system balance.

3. Reinforcement Learning-Based Optimization Framework

This study proposes a novel hierarchical optimization framework for power system dispatch that combines conventional optimization with reinforcement learning. The framework operates across two distinct time scales to address both planning and real-time operational challenges. In the day-ahead stage, a deterministic optimization problem is solved using hourly forecast data to establish baseline schedules for thermal units, pumped hydro storage, and PDR resources. These day-ahead commitments then serve as fixed parameters for the subsequent intra-day optimization phase.

The intra-day scheduling operates on a rolling 4 h horizon with 15 min resolution, employing reinforcement learning to adjust for forecast errors and real-time system conditions. This stage focuses on optimizing three key adjustable parameters: wind power output adjustments, battery storage charge/discharge commands, and IDR activations. The reinforcement learning agent interacts with a simulated power system environment, receiving state observations and reward signals to continuously improve its dispatch policy.

3.1. State Space and Action Set

The state space includes six dimensions: system load, wind power, current output state of conventional units, current output status of pumped storage units, state of charge of electrochemical energy storage at the previous moment, and reducible load reduction. The system state at the current time t is as follows:

$$\begin{array}{cc}\hfill s_t=& [L_{R,t}^{forecast},P_{water,t-1,i},P_{water,t,i},P_{wind,t-1,i},P_{wind,t,i}^{forecast},P_{G,t-1,i},\hfill \\ \hfill & P_{G,t,i},P_{battery,t-1,i},S_{soc,t-1,i},P_{PDR,t-1},P_{PDR,t},P_{IDR,t-1}]\hfill \end{array}$$

(15)

where $L_{R,t}^{forecast}$ is the load forecast value at the current time; $P_{water,t-1,i}$ and $P_{water,t,i}$ are the power of the i-th pumped storage unit at the previous moment and the current time, respectively. $P_{wind,t-1,i}$ and $P_{wind,t,i}^{forecast}$ are the actual output of wind power at the previous moment and the forecast value at the current moment, respectively; $P_{G,t-1,i}$ and $P_{G,t,i}$ are the power of the i-th conventional unit at the previous moment and the current time, respectively. $P_{battery,t-1,i}$ is the power of the i-th electrochemical energy storage at the previous moment. $S_{soc,t-1,i}$ is the actual state of charge of the electrochemical energy storage at the previous moment. $P_{PDR,t-1}$ and $P_{PDR,t}$ are the power of PDR at the previous moment and the current time, respectively.

The action space includes three dimensions: wind turbine output adjustment, charge/discharge power of electrochemical energy storage, and reducible load reduction. The action space at the current time t is as follows:

$$a_t=[P_{wind,t,i},P_{battery,t,i},P_{IDR,t}]$$

(16)

3.2. Reward Function

The reward function is an evaluation in the process of action network updating. During the model training process, the agent inputs action values to the power system. The system simulates operation according to the scheduling strategy and feeds back the reward function and the next state. The reward function reflects the quality of the agent’s output actions, thereby guiding the direction of strategy updating. The reward function mainly reflects two aspects: reducing the system operating cost and minimizing the penalty for system operation exceeding limits. The penalty function is as follows:

$$\left\{\begin{array}{c}{F}_{all,t}={\alpha }_5{F}_{unb,t}+{\alpha }_6{F}_{wind,t}+{\alpha }_7{F}_{elec,t}+{\alpha }_{8}Fsoc,t+{\alpha }_9{F}_{line,t}\hfill \\ +{\alpha }_{10}{F}_{adjust,t}+{\alpha }_{11}{F}_{IDR,t}\hfill \\ R_t=\left\{\begin{array}{cc}{F}_{all,t},\hfill & \hfill F_{all,t}\le 0\\ {\alpha }^{+}-{\alpha }_1{C}_{G,t}-{\alpha }_2{C}_{erss,t}-{\alpha }_3{C}_{wind}-{\alpha }_4{C}_{load,t},\hfill & \hfill F_{all,t}>0\end{array}\right.\hfill \end{array}\right.$$

(17)

where $F_{unb,t}$ is the power imbalance penalty quantifying deviation from generation–load equilibrium, $F_{wind,t}$ is the wind curtailment penalty for underutilized renewable generation, $F_{elec,t}$ is the battery storage violation penalty for exceeding power ratings, $F_{soc,t}$ is the SOC boundary violation penalty for energy storage, $F_{line,t}$ is the transmission line overload penalty for exceeding thermal limits, $F_{adjust,t}$ is the regulation capacity violation penalty for exceeding ramping capabilities, and $F_{IDR,t}$ is the IDR deviation penalty. The coefficients ${\alpha }_1$ through ${\alpha }_{11}$ serve to normalize the dimensional units of all reward and penalty terms and establish the proportional relationships between different components. The parameter ${\alpha }^{+}=100$ ensures that the reward value under non-violation conditions is always greater than that under violation conditions.

$$F_{unb,t}={\left|L_{R,t}+\Delta P_{PDR,t}+\Delta P_{IDR,t}-\left(\sum P_{G,i,t}+\sum P_{wind,i,t}+\sum P_{water,i,t}+\sum P_{battery,i,t}\right)\right|}^2$$

(18)

$$F_{wind,t}=\sum _{i=1}^{N_{DC}}max(0,P_{wind,i,t}^{pre}-P_{wind,i,t})$$

(19)

$$F_{elec,t}=\sum _{i=1}^{N_{battery}}\left[max(0,P_{battery,i,t}-P_{elec}^{dis})+max(0,P_{elec}^{cha}-P_{battery,i,t})\right]$$

(20)

$$F_{soc,t}=\sum _{i=1}^{N_{battery}}\left[max(0,SO{C}_{i,t}-SO{C}^{max})+max(0,SO{C}^{min}-SO{C}_{i,t})\right]$$

(21)

$$F_{line,t}=\sum _{ij}^{N_l}max\left(0,{\displaystyle \frac{|B_{ij}({\theta }_{i,t}-{\theta }_{j,t})|}{P_{ij}^{max}}}-1\right)$$

(22)

$$F_{adjust,t}=\sum _{i=1}^{N_G}max(0,|P_{G,i,t}-P_{G,i,t,base}|-{\psi }_i)+\sum _{j=1}^{N_{erss}}max(0,|P_{erss,j,t}-P_{erss,j,t,base}|-{\psi }_{erss})$$

(23)

$$F_{IDR,t}=max(0,P_{IDR,t}^{+}-P_{IDR}^{+,max})+max(0,P_{IDR,t}^{-}-P_{IDR}^{-,max})$$

(24)

3.3. Attention-Based Actor Network

The Actor–Critic framework is a powerful reinforcement learning approach that combines the strengths of policy-based and value-based methods [26]. In this paper, we adopt the Actor–Critic framework to solve the intra-day rolling scheduling problem, where the Actor network is responsible for generating control actions, and the Critic network evaluates the quality of these actions, as shown in Figure 2.

Actor–Critic methods are used, whose approach is to learn a value function $Q(S,a)$ to approximate the expected return value in

$$Q(S,a)\Rightarrow \mathbb{E}\left[\sum _{t^{\prime }=t}^T{\gamma }^{\prime -t}{R}_t(S^{\prime },a^{\prime })\right]$$

(25)

The Critic network is updated to minimize the mean squared error between the predicted Q-value and the target Q-value:

$$L\left(\psi \right)={\mathbb{E}}_{(s,a,r,s^{\prime })\sim \mathcal{D}}\left[{(Q_{\psi }(s,a)-y_i)}^2\right]$$

(26)

where the target value $y_i$ is computed using the target networks:

$$y_i=r+\gamma Q_{\overline{\psi }}(s^{\prime },{\pi }_{\overline{\theta }}\left(s^{\prime }\right))$$

(27)

To enhance the Actor network’s ability to focus on critical state variables, such as wind power output, energy storage state, and reducible load, this paper introduces a multi-head attention mechanism [27] into the Actor network. The attention mechanism adaptively weights these key inputs based on their relevance to the current decision-making process. The proposed architecture enhances the Actor network’s state processing capability through an attention mechanism. This design focuses computational resources on critical power system variables while maintaining efficient operation. The complete state representation combines temporal system measurements and forecast data in Equation (15). The attention mechanism operates on carefully selected critical variables that most significantly impact dispatch decisions:

$$s_t^{critical}=\left[P_{wind,t-1,i},P_{wind,t,i}^{forecast},P_{battery,t-1,i},S_{soc,t-1,i},P_{IDR,t-1}\right]$$

(28)

while the remaining variables form the context set:

$$s_t^{context}=\left[L_{R,t}^{forecast},P_{water,t-1,i},P_{water,t,i},P_{G,t-1,i},P_{G,t,i},P_{PDR,t-1},P_{PDR,t}\right]$$

(29)

The attention transformation follows the standard scaled dot-product formulation:

$$\mathrm{Attention}(Q,K,V)=\mathrm{Softmax}\left({\displaystyle \frac{Q{K}^T}{\sqrt{d_k}}}\right)V$$

(30)

with the query, key, and value matrices derived through learned linear projections:

$$Q=W_q{s}_t^{critical},K=W_k{s}_t^{critical},V=W_v{s}_t^{critical}$$

(31)

where $W_q\in {\mathbb{R}}^{d\times d_k}$, $W_k\in {\mathbb{R}}^{d\times d_k}$, and $W_v\in {\mathbb{R}}^{d\times d_v}$ are trainable weight matrices. The network architecture then combines the processed representations:

$$a_t={\pi }_{\theta }\left(s_t\right)=\mathrm{Tan}\mathrm{h}\left(W_2·\mathrm{ReLU}(W_1·[s_t^{attn};s_t^{context}]+b_1)+b_2\right)$$

(32)

The complete system automatically learns to allocate attention weights to variables like wind power forecast errors and storage SOC levels that prove most relevant for optimal dispatch decisions. The Tanh activation ensures generated actions remain within normalized bounds for subsequent scaling to actual control signals. Through end-to-end training, the attention mechanism develops specialized sensitivity to critical operational constraints without requiring manual feature engineering.

The Actor network is updated using the policy gradient:

$${\nabla }_{\theta }J\left(\theta \right)={\mathbb{E}}_{s\sim \mathcal{D}}\left[{\nabla }_{\theta }log{\pi }_{\theta }\left(a\right|s)·A^{\pi }(s,a)\right]$$

(33)

where the advantage function $A^{\pi }(s,a)$ is approximated as:

$$A^{\pi }(s,a)=\alpha log{\pi }_{\theta }\left(a\right|s)-Q_{\psi }(s,a)+b(s,a_{-i})$$

(34)

where $b(s,a_{-i})$ is a baseline function that reduces variance in policy gradient estimation, computed as:

$$b(s,a_{-i})={\mathbb{E}}_{a\sim \pi \left(s\right)}\left[Q_{\psi }(s,(a,a_{-i}))\right]$$

(35)

4. Case Study

Tackling the critical issue of constrained renewable energy absorption, this study selects a regional power grid in East China—plagued by significant new energy integration hurdles—as a real-world testbed to validate its proposed scheduling framework. The grid’s infrastructure includes six traditional thermal units stationed at nodes 1, 2, 5, 8, 11, and 13, with detailed parameters documented in

Table 1. Parameters of conventional units.

Unit Number	Node	${\mathit{P}}_{\mathit{max}}/\mathbf{MW}$	${\mathit{P}}_{\mathit{min}}/\mathbf{MW}$	$\mathit{a}/{\left(\mathbf{Yuan}/(\mathbf{MW}\right)}^2)$
1	1	200	50	0.0375
2	2	80	20	0.175
3	5	50	15	0.625
4	8	35	10	0.0834
5	11	30	10	0.25
6	13	40	12	0.25
Unit Number	$b/(\mathrm{Yuan}/\mathrm{MW})$	$c/\mathrm{Yuan}$	$R_u/R_d$/(MW/h)	$T_S/T_D$/h
1	20	372.5	72	2
2	17.5	352.3	48	2
3	10	316.5	30	2
4	32.5	329.2	21	2
5	30	276.4	18	2
6	30	232.2	24	2

. Node 2 hosts a 400 MW wind farm alongside a 50 MW/200 MW·h electrochemical storage system, while node 8 accommodates a 100 MW/400 MW·h pumped storage facility [28].

Operational assumptions are set as follows: PDR adjustments are capped at 10% of total load, and IDR deployment does not exceed 5% of total load. For streamlined calculations, fixed compensation cost coefficients for IDR are employed, as specified in

Table 2. Compensation cost coefficients of DR.

DR Type	Compensation Cost Coefficient/(Yuan/(MW·h))
PDR	225
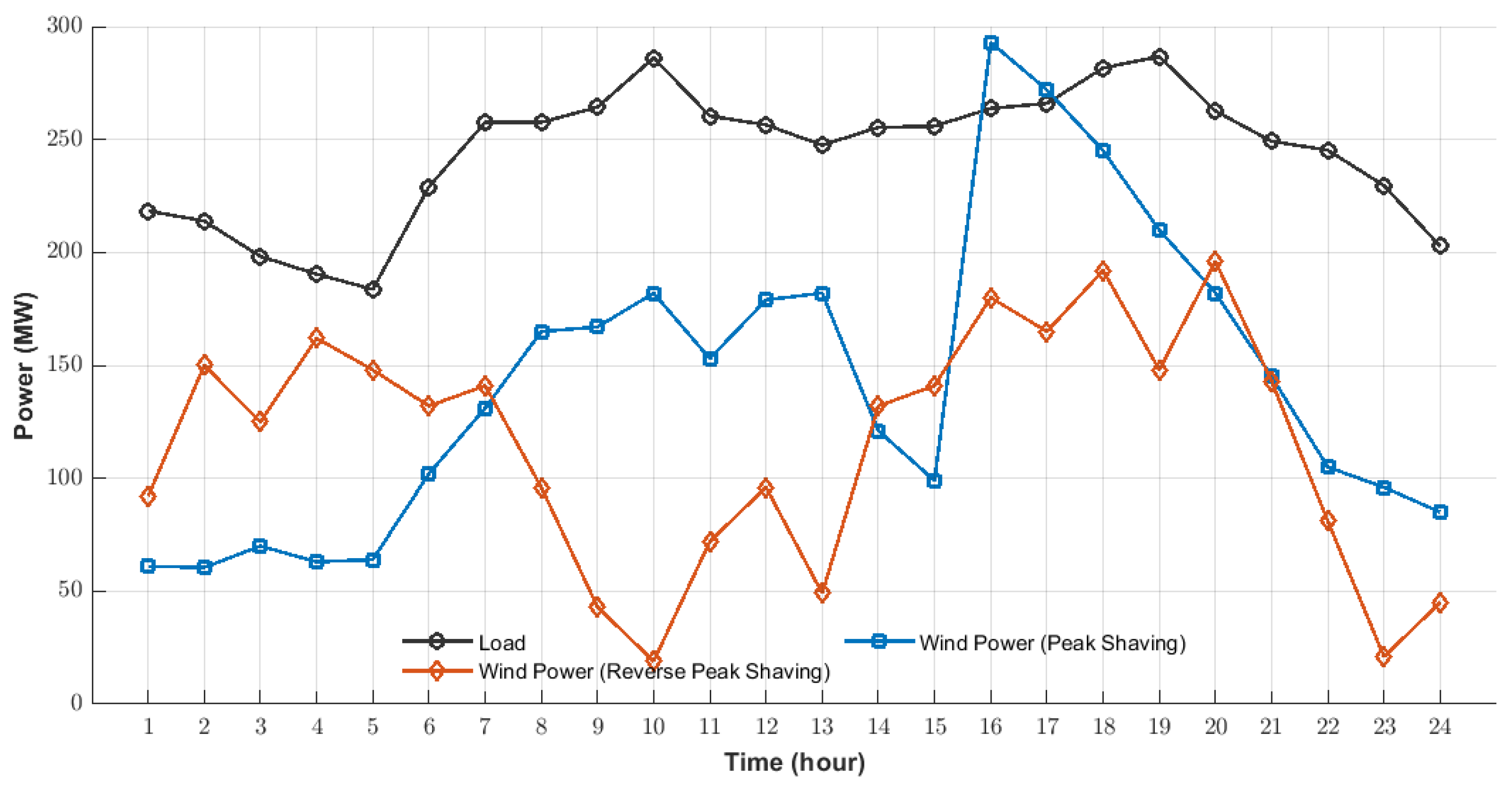
IDR	150

. Load and wind power dynamics are visualized in Figure 3, which captures load fluctuations alongside wind power variations under both scenarios. To ensure the reproducibility of the DRL implementation, detailed parameters of the training process and computational setup are specified as follows: the learning rate is set to 0.001 for both the Actor and Critic networks to balance training convergence speed and stability; the Adam optimizer is adopted, with momentum parameters ${\beta }_1$ = 0.9 and ${\beta }_2$ = 0.9 to adaptively adjust the learning rate for different parameters; the discount factor $\gamma =0.95$ is used to emphasize short-term operational rewards while retaining consideration for long-term system stability; training is terminated when the average reward of 20 consecutive episodes stabilizes within a 2% fluctuation range, ensuring the learned policy is robust and convergent; and experiments are conducted on a server equipped with an Intel Core i5-11400F and 16 GB RAM with the software environment built using Python 3.8 and PyTorch 1.10 to provide sufficient computational resources for DRL model training and inference. The DRL model undergoes offline training only once. The training is conducted using sufficient historical operational data, which covers typical seasonal, daily, and load fluctuation scenarios.

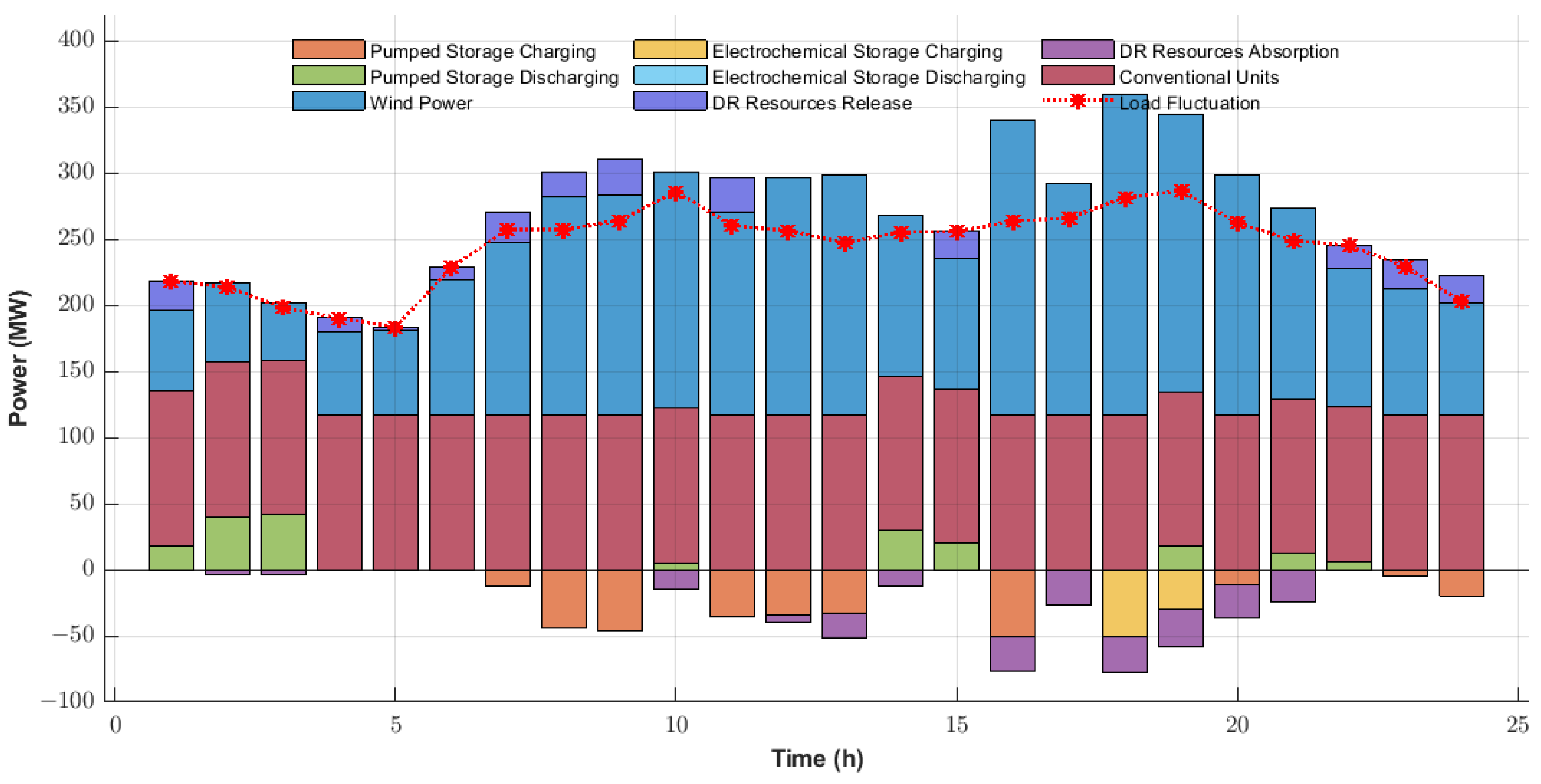
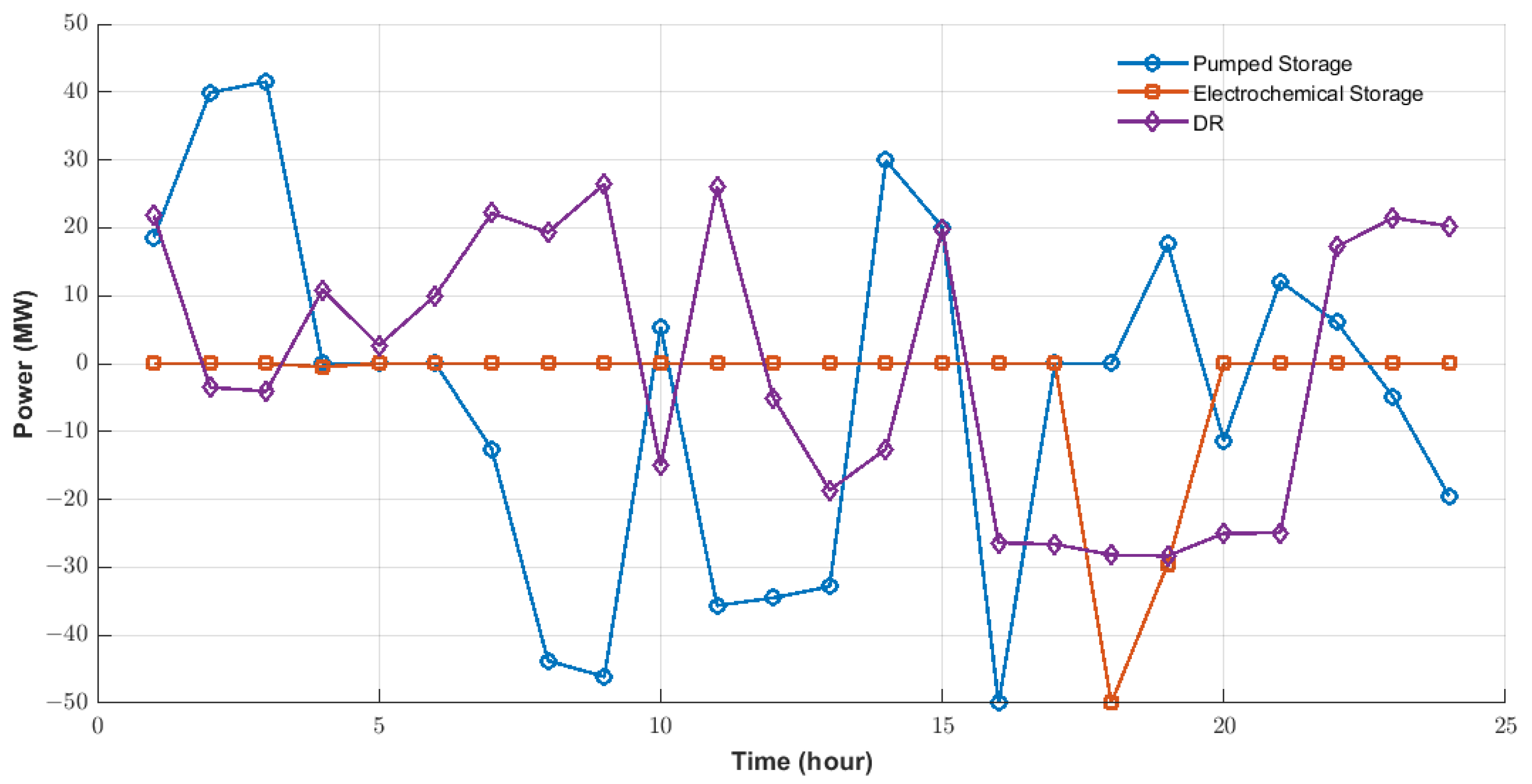
Scheduling schemes for both scenarios are detailed in Figure 4 and Figure 5, where each curve represents the cumulative output of preceding components plus the contribution of the current unit or DR resource. Notably, the red curve (denoting load fluctuations) maintains balance with the combined outputs of conventional units, storage systems, and wind power across all periods. Meanwhile, Figure 6 and Figure 7 illustrate the operational plans for pumped storage, electrochemical storage, and demand response resources across the two scenarios. A closer look at DR resource behavior reveals distinct diurnal roles: daytime usage focuses on peak shaving and damping wind power volatility, while nighttime operations shift to valley filling. This division aligns with the contrasting patterns observed in wind power and load interactions. In reverse peak shaving scenarios, wind power generation surges during early morning (2:00–6:00) and evening (16:00–21:00)—periods when non-DR loads are low. Here, active DR resource activation and storage charging effectively boost wind power absorption. Conversely, during peak shaving, wind power output aligns more closely with load curves, peaking at midday (10:00–14:00) and afternoon (16:00–19:00). The high non-DR load during these windows reduces the need for DR resources compared to reverse peak shaving at the same times.

From the perspective of practical applicability, the proposed framework aligns well with the operational characteristics of the East China regional grid—where wind power is concentrated in coastal areas and load peak–valley differences are high. As shown in Figure 5 and Figure 7, the framework activates IDR and charges electrochemical storage to absorb surplus wind power. Regarding computational scalability, the attention mechanism’s ability to prioritize critical variables reduces redundant calculations.

The framework’s design allows straightforward extension to solar PV integration. PV’s uncertainty can be incorporated by adding “PV forecast error” to the attention mechanism’s critical variable set (Equation (28) in Section 3.3). For dynamic demand response, replacing the fixed DR participation rate with a “user response elasticity model” would further enhance performance.

To explore the practical effectiveness of dual energy storage systems in improving wind power utilization, reducing curtailment rates, and saving costs, this study designed comparative experiments targeting two typical scenarios: wind power peak shaving and reverse peak shaving. By constructing three differentiated operational schemes, the research systematically analyzed the impact mechanisms of energy storage integration forms and scheduling time scales on overall performance: The first scheme is the “no-storage benchmark mode”, which relies entirely on day-ahead scheduling plans without incorporating any energy storage equipment or implementing dynamic adjustments across multiple time scales such as intra-day, serving as a basic reference. The second scheme is the “single pumped storage mode”, which, while retaining the day-ahead scheduling framework, only introduces pumped storage stations for regulation, focusing on examining the operational boundaries of a single energy storage type. The third scheme, the “hybrid energy storage multi-scale mode”, represents the core strategy proposed in this study. It combines pumped storage with electrochemical energy storage and embeds a day-ahead-intra-day coordinated multi-time scale scheduling architecture to achieve complementary advantages of different energy storage characteristics. The DRL architecture, specifically the attention-based Actor–Critic network, is applied to all three schemes.

The experimental results (as shown in

Table 3. Comparison of different scheduling schemes.

Scenario	Scheduling Scheme	Cost/CNY 10,000	Curtailment Rate/%
Scenario 1	Scheme 1	123.95	12.40
	Scheme 2	118.27	8.09
	Scheme Without Attention	116.63	6.53
	Proposed Scheme	115.79	5.76
Scenario 2	Scheme 1	120.54	7.91
	Scheme 2	116.35	2.05
	Scheme Without Attention	113.59	1.30
	Proposed Scheme	112.46	1.12

) clearly demonstrate the performance differences among the three schemes. The “no-storage benchmark mode” has obvious shortcomings in wind power absorption, especially in reverse peak shaving scenarios. During the high wind power periods, the limited call volume of demand response resources fails to match the large-scale wind power output, leading to severe curtailment and insufficient system flexibility to meet fluctuations. The “single pumped storage mode”, although an improvement over the benchmark scheme, is constrained by the inherent slow adjustment speed of pumped storage. It struggles to quickly respond to instantaneous fluctuations in wind power and load during reverse peak shaving, resulting in nearly identical curtailment rates in peak shaving and reverse peak shaving scenarios, with limited optimization effects.

In contrast, the “hybrid energy storage multi-scale mode” exhibits significant advantages: the rapid response capability of electrochemical energy storage can compensate for the lag in pumped storage adjustment, while the large-capacity characteristic of pumped storage can support energy balance over long time scales, forming efficient synergy. Combined with the refined regulation of demand response resources, this mode not only drastically reduces curtailment rates in both scenarios but also achieves a moderate reduction in system operation costs by minimizing unnecessary power redundancy and adjustment losses.To isolate the impact of the attention mechanism, a head-to-head comparison with the “DRL without attention” model is performed. The attention-enhanced model reduces wind curtailment and lowers operational costs. This improvement is attributed to the attention mechanism’s ability to weight wind power forecast errorsand energy storage SOC more heavily than other variables, enabling proactive correction of prediction deviations that would otherwise lead to curtailment or load shedding.

To evaluate the robustness of the framework under parameter fluctuations, sensitivity tests are conducted on key variables affecting scheduling outcomes. Focusing on IDR compensation costs—a critical parameter in demand response programs—we simulate adjustments within a 10% range (consistent with practical policy and subsidy variation ranges of 8–12%), modifying the baseline IDR cost (150 CNY/(MW·h)) to 135 CNY/(MW·h) and 165 CNY/(MW·h). The results indicate that even with 10% cost variations, the total operational cost changes by only 0.8–1.2% This stability arises from the framework’s “baseline + dynamic supplement” DR coordination: when IDR costs increase, the system automatically reduces IDR activation and increases battery discharge to maintain balance, avoiding over-reliance on expensive demand response. Conversely, lower IDR costs trigger increased IDR utilization, reducing energy storage cycling losses. This adaptive adjustment mechanism eliminates the need for precise parameter calibration, enhancing practical applicability.

The superiority of the proposed framework stems from three synergistic mechanisms: (1) the attention mechanism dynamically prioritizes critical variables (e.g., wind power forecast errors and energy storage SOC), enabling the agent to allocate computational focus to high-impact factors during decision-making; (2) hybrid energy storage (pumped hydro + electrochemical) leverages the high capacity of pumped storage and rapid response of batteries, reducing reliance on conventional generator ramping; and (3) coordinated DR scheduling (day-ahead PDR + intra-day IDR) enhances demand-side flexibility, with PDR establishing cost-effective baselines and IDR addressing real-time mismatches.

In summary, integrating dual energy storage technologies with a multi-time scale scheduling framework can more effectively address the uncertainty in new energy generation forecasts compared to a single pumped storage scheme. It establishes a more flexible and reliable balancing mechanism for the “source-grid-load-storage” system, thereby significantly enhancing new energy absorption capacity and providing strong support for the economical and stable operation of power grids with high proportions of renewable energy.

5. Conclusions

This study develops a multi-time scale coordination scheduling framework integrated with reinforcement learning to address the challenges of renewable energy integration in power systems. The framework combines day-ahead and intra-day rolling scheduling to balance cost efficiency and adaptability: the day-ahead model establishes optimal baselines for conventional generators, pumped hydro storage, and PDR to minimize operational costs, while the intra-day model adjusts to real-time fluctuations using electrochemical storage and IDR. The reinforcement learning-based intra-day optimization, featuring an attention-based Actor–Critic network, effectively handles wind power uncertainty by prioritizing critical variables such as wind forecasts and storage states, enhancing decision precision. Integrating hybrid energy storage (pumped hydro + electrochemical) and coordinated demand response significantly improves performance: compared to traditional schemes, it reduces wind curtailment rates and lowers operational costs. Case studies on an East China regional grid validate the framework’s practicality across typical scenarios, demonstrating its ability to mitigate source–load mismatches, especially during reverse peak conditions.

This study still has limitations that point to clear opportunities for future research: it currently focuses solely on wind power without incorporating solar PV, and uses a fixed demand response participation rate that fails to reflect the dynamic response characteristics of users in practice. Future work will integrate solar PV into the framework—by adding PV forecast error to the attention mechanism’s critical variables to optimize decision-making—and construct a dynamic demand response model based on user response elasticity, while further verifying the framework on large-scale power grids to enhance its universality and practical value.