Preliminary Design and Parametric Study of Minimum-Weight Steel Tied-Arch Bridges Obtained According to a Maximum Allowable Deflection Criterion
Abstract
Featured Application
Abstract
1. Introduction
1.1. Preliminary In-Plane Design of Arch Bridges
1.2. Research Objectives
- Developing a method for the preliminary design of an arch bridge that verifies that, at a selected checkpoint at the deck, the maximum deflection δD is smaller than the maximum allowable deflection at the same point, δlim, under a given SLC.
- Simplifying the design process by reducing the number of geometrical variables used to define the cross-sections.
- Minimizing the weight of the bridge since, in general, the cost will be lower for a smaller amount of material.
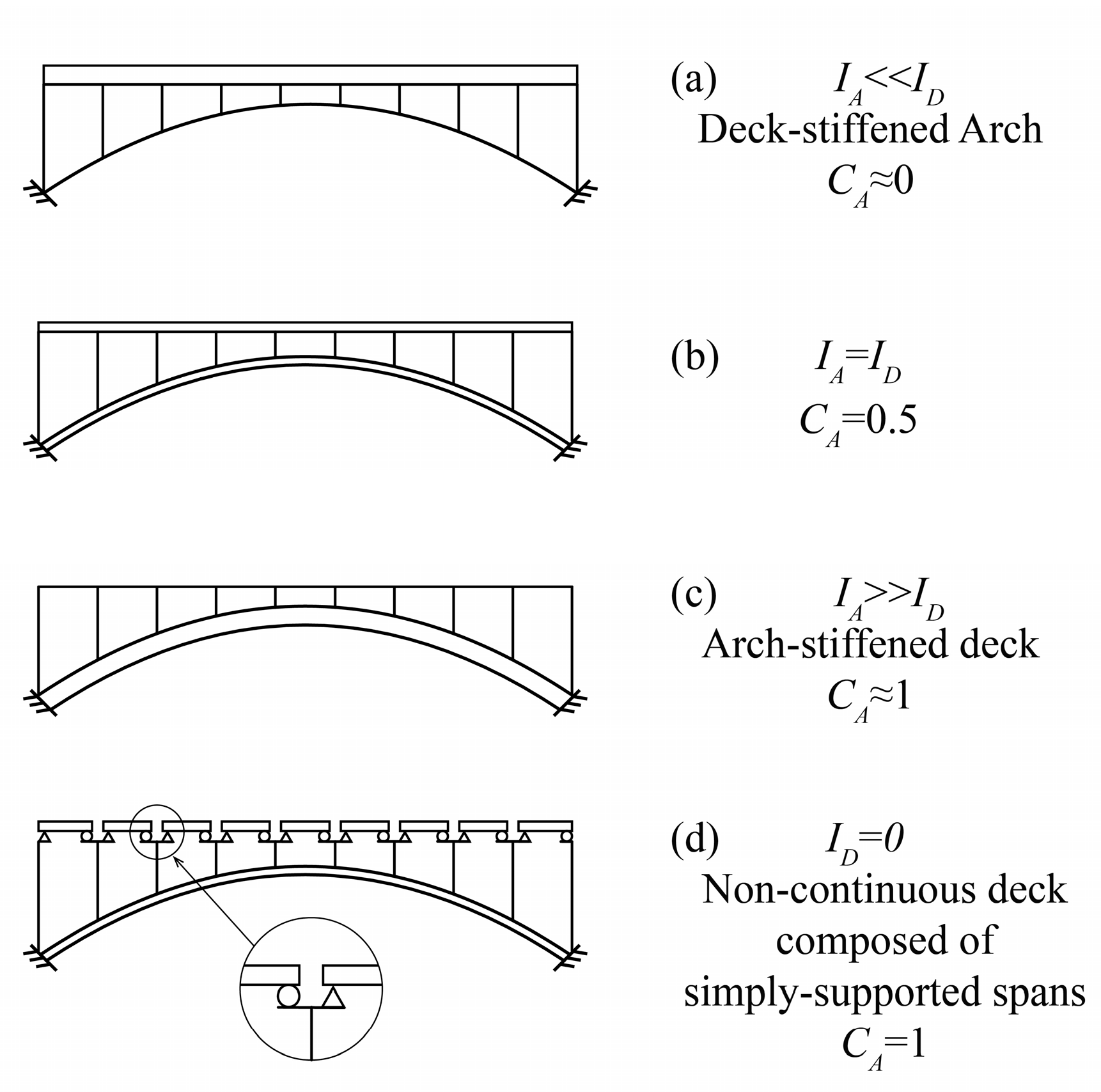
- Ensuring the usefulness of the method for designers. To achieve this goal, the input data must consist of variables commonly used in preliminary design. In particular, it should enable designers to select the relative flexural stiffness of the arch and deck, since this has a significant impact on arch bridge design (see Stavridis [1], Manterola-Armisén [4], or Menn [7]).
- Realizing parametric studies to illustrate the effect of the main variables on preliminary design.
- Developing an approximate analytical formulation to allow manual calculations of tied-arch bridges with vertical hangers, aiming to speed up the conceptual design step.
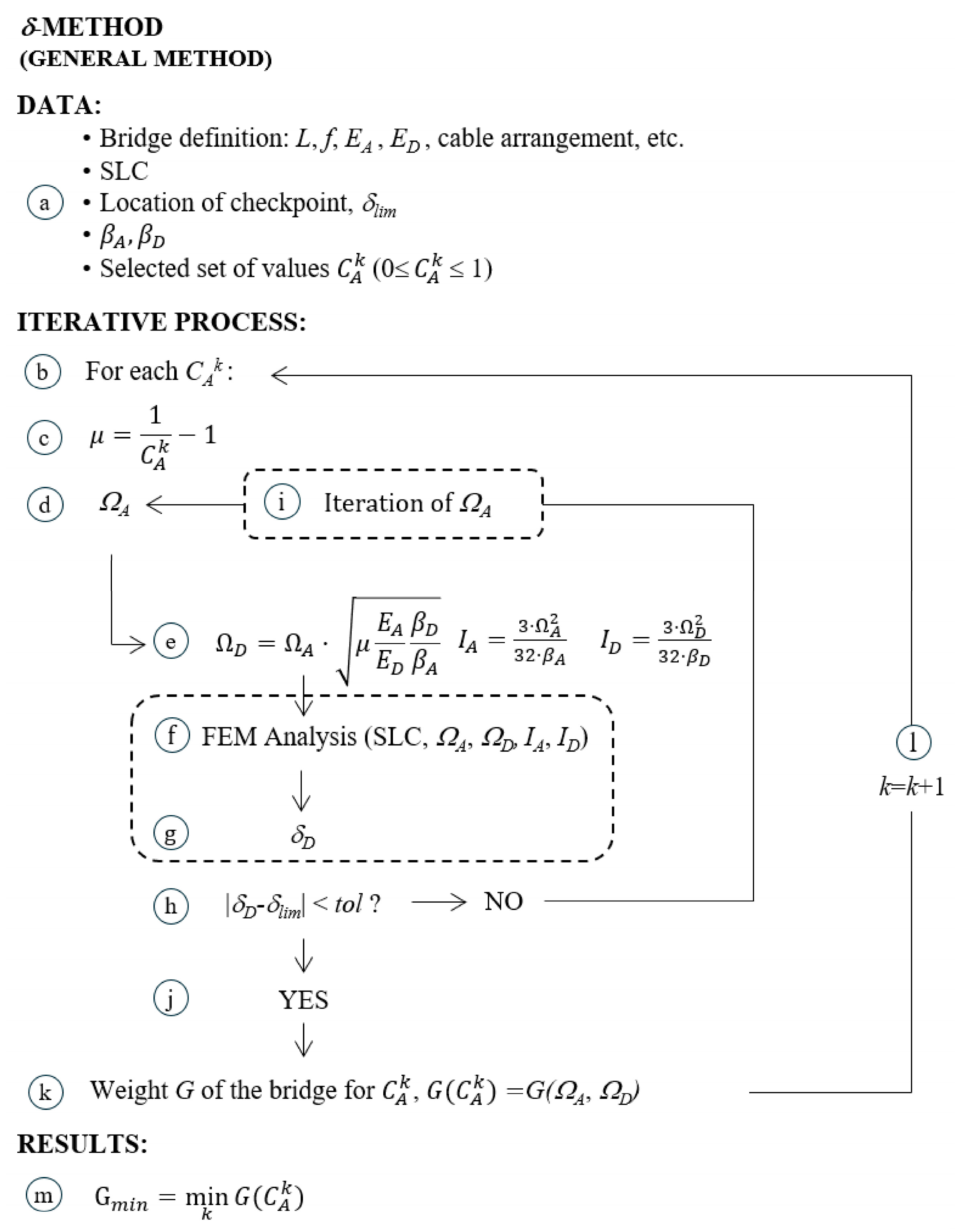
1.3. The δ-Method
1.4. Structure of the Paper
2. Preliminary In-Plane Design Approach
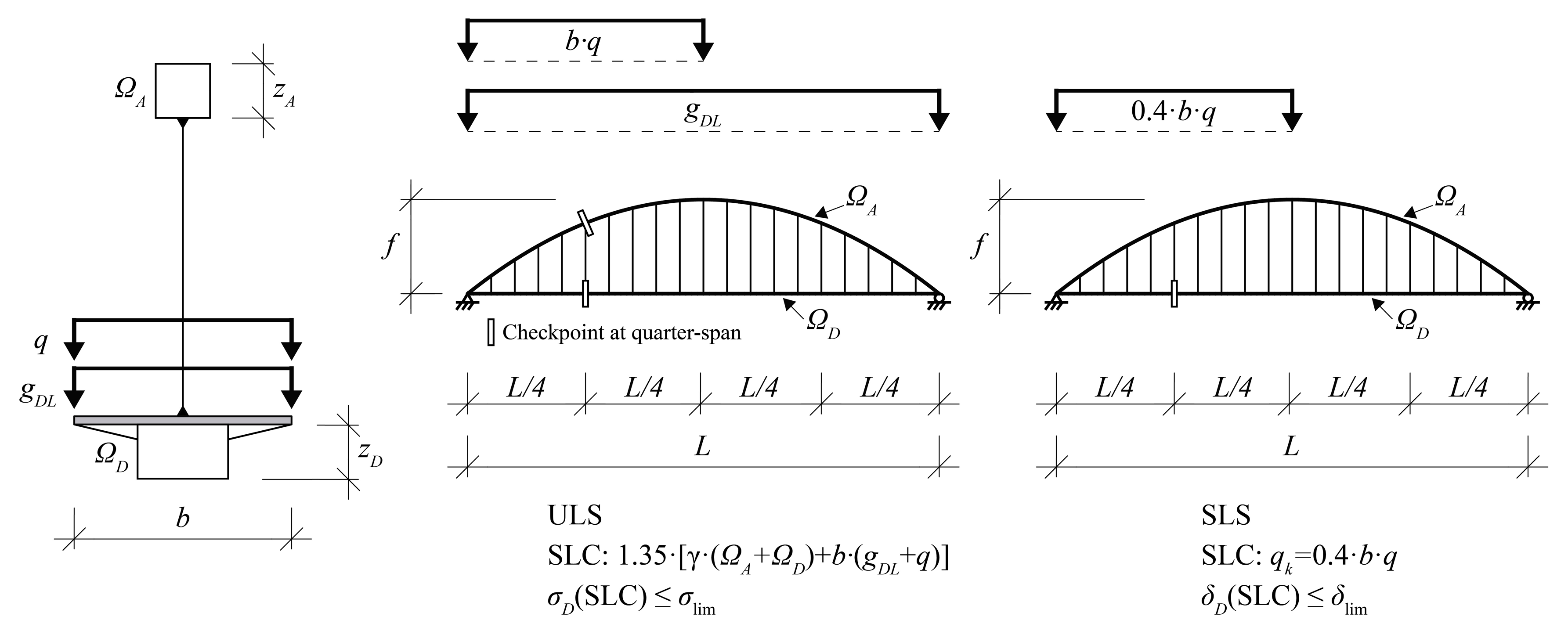
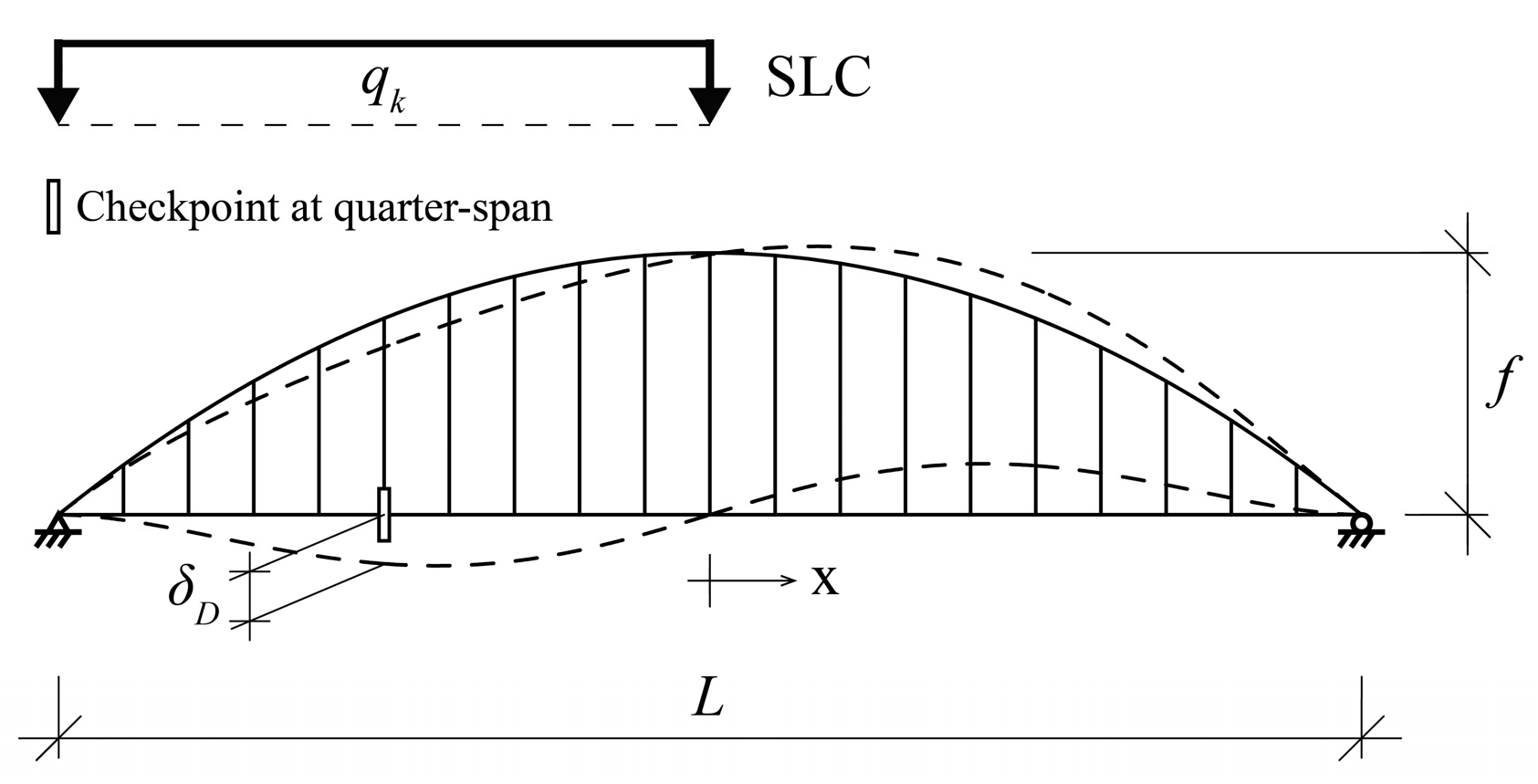
2.1. Maximum Deflection Criterion
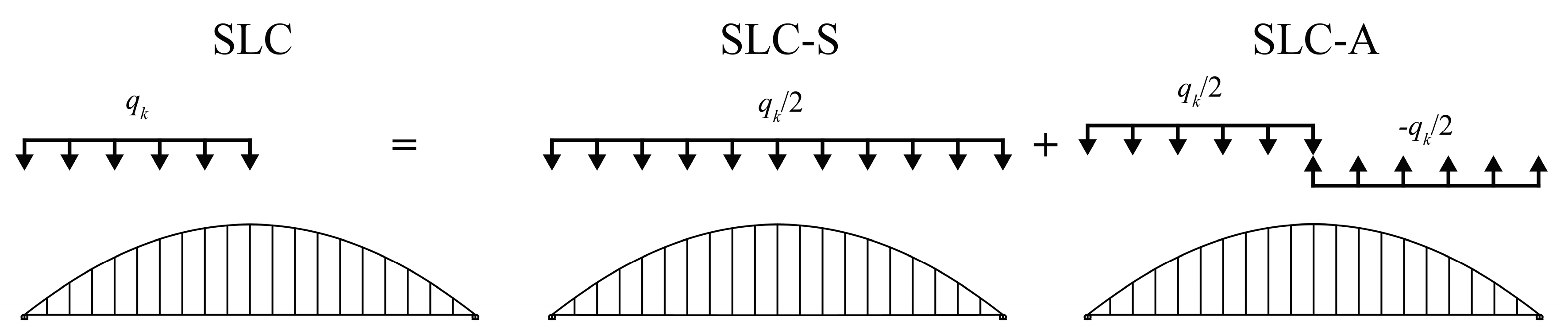
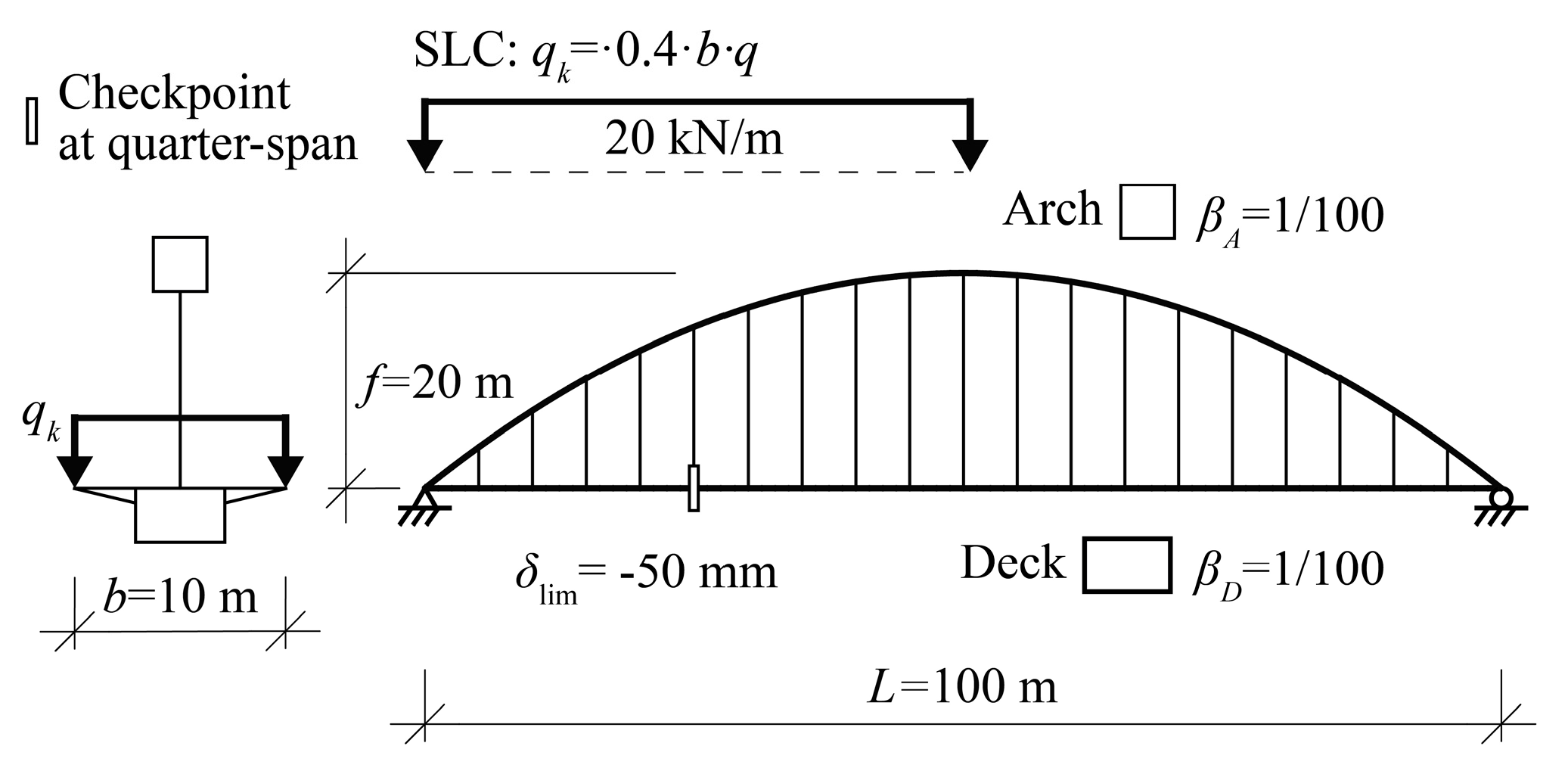
2.2. Definition of SLC and Checkpoints
2.3. Arch–Deck Interaction
2.4. Doubly Symmetric Cross-Sections
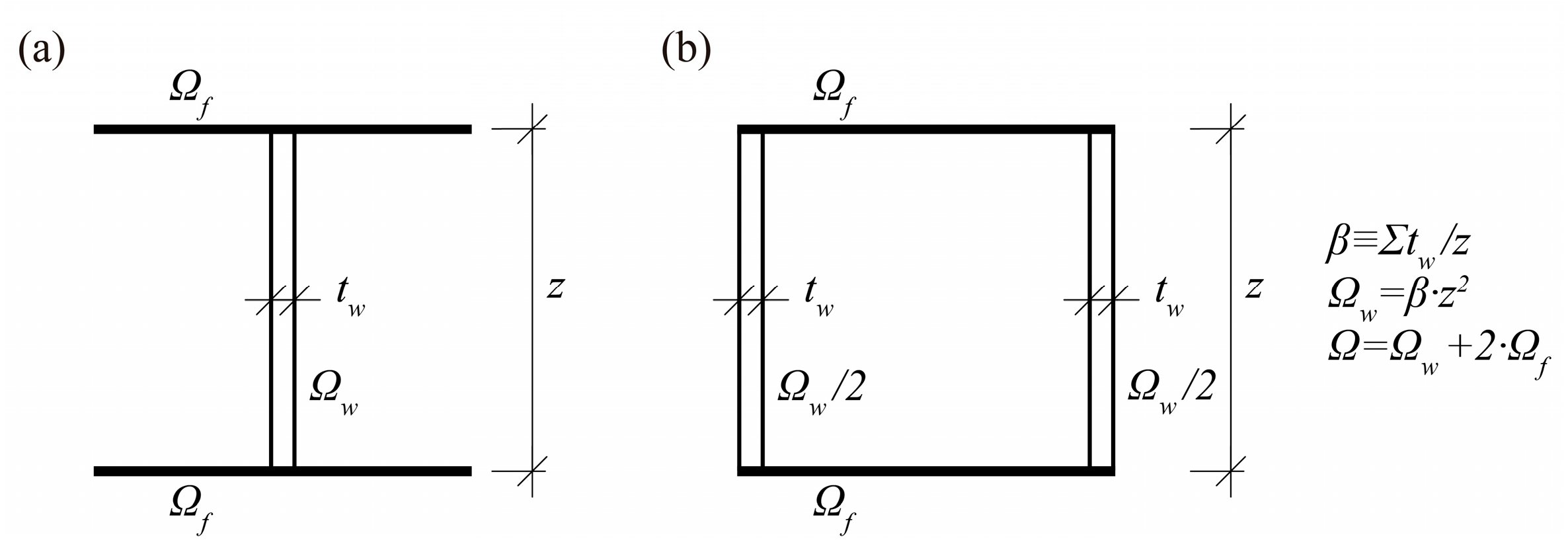
2.5. Mechanical Properties of Cross-Sections
- The cross-section area, Ω.
- The distance between the center lines of the flanges, z. The flange thickness is assumed to be small compared to z, which means that, in practical terms, z coincides with the cross-section depth, and, thus, the area of each flange Ωf, is concentrated at each end of the web.
- The geometrical slenderness of the web (or webs) of the cross-section, β, which is very relevant in the classification and behavior of steel cross-sections (see Eurocode 1 [14]). Equation (3) defines β for both the box and H-section cross-sections shown in Figure 4, regardless of the number of webs:
2.6. Scope of the Method
3. The δ-Method: General Case
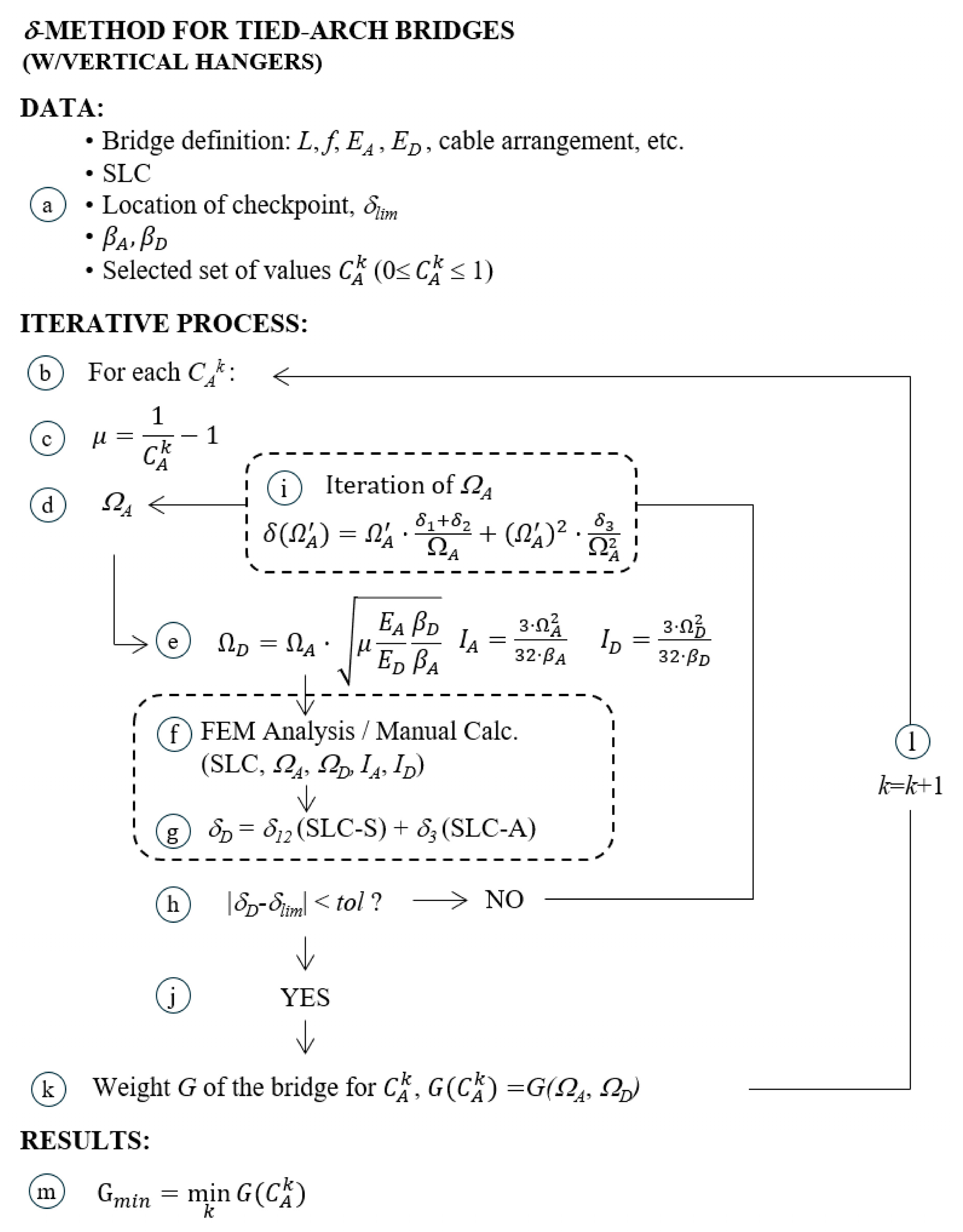
4. Method for Tied-Arch Bridges with Vertical Hangers
4.1. SLC and Location of Checkpoints
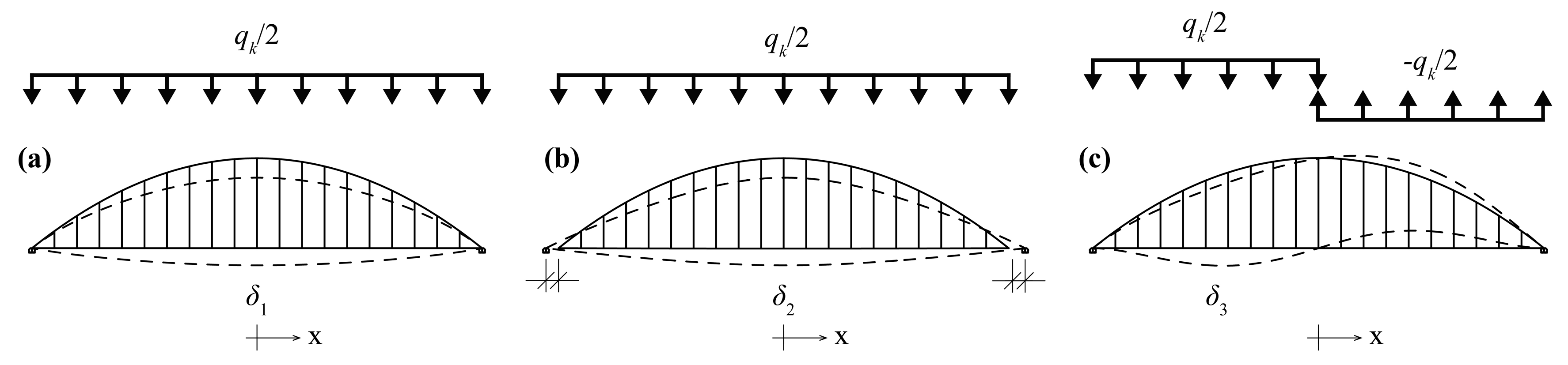
4.2. Theoretical Formulation of Deflections for Tied-Arch Bridges with Vertical Hangers
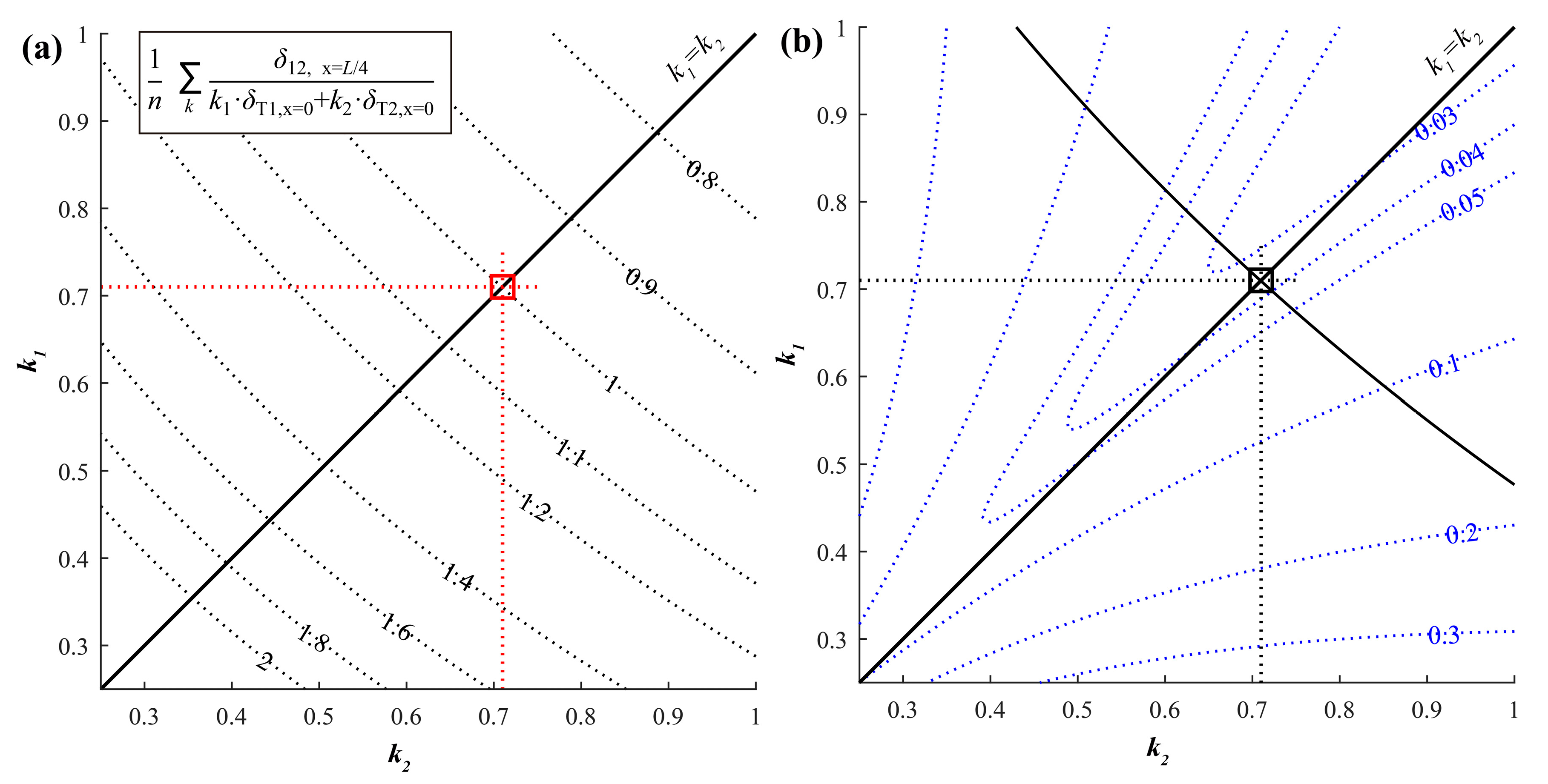
4.3. Correction of Area Between Iterations
4.4. Flowchart
5. Example of Application
5.1. Tied Arch with Vertical Hangers
5.2. Comparison with Real Bridges
5.3. Influence of the SLC
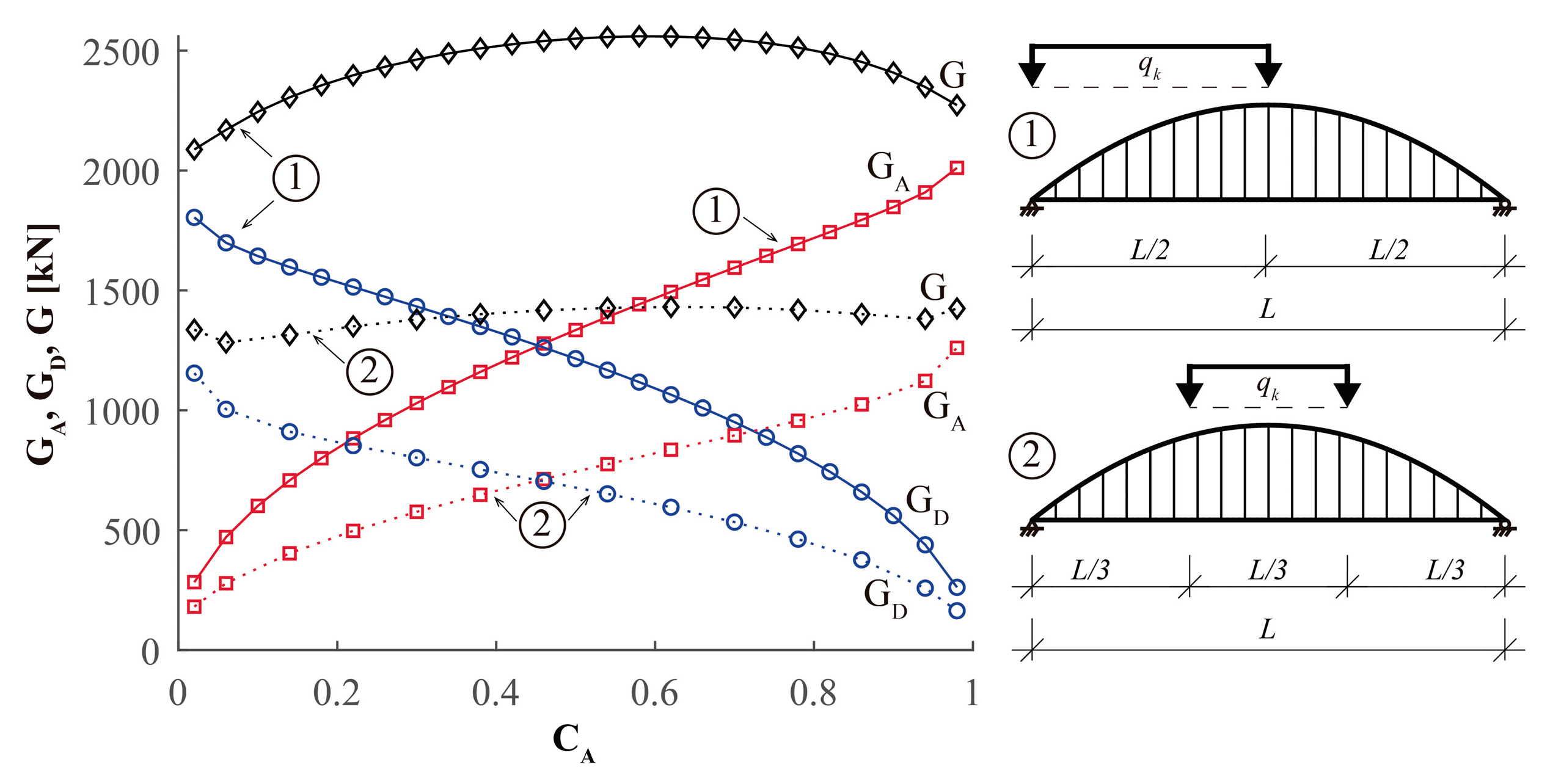
6. Preliminary Parametric Studies
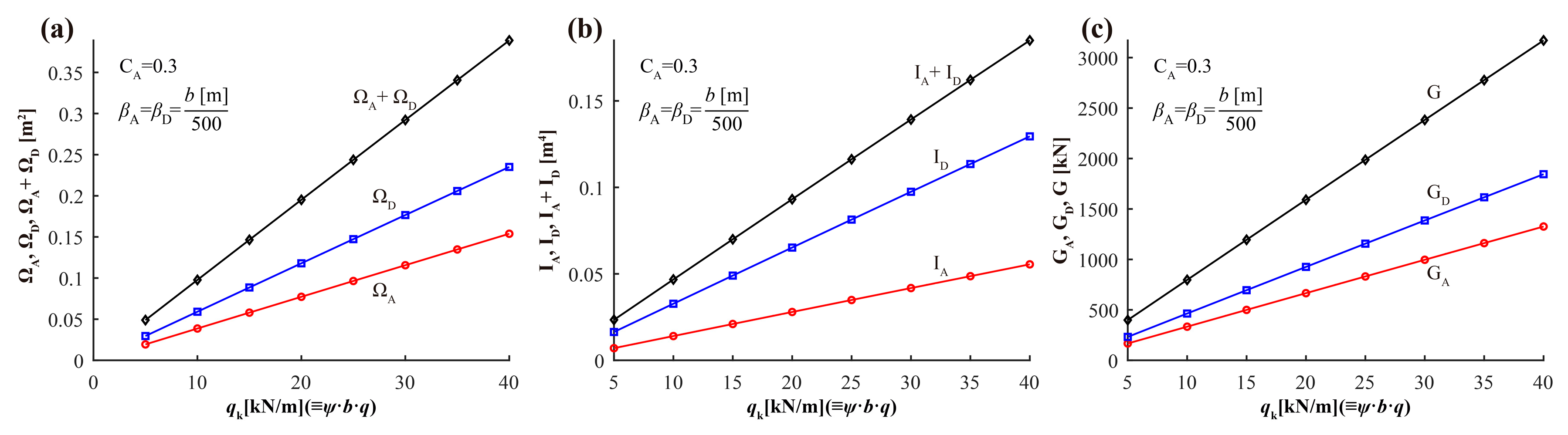
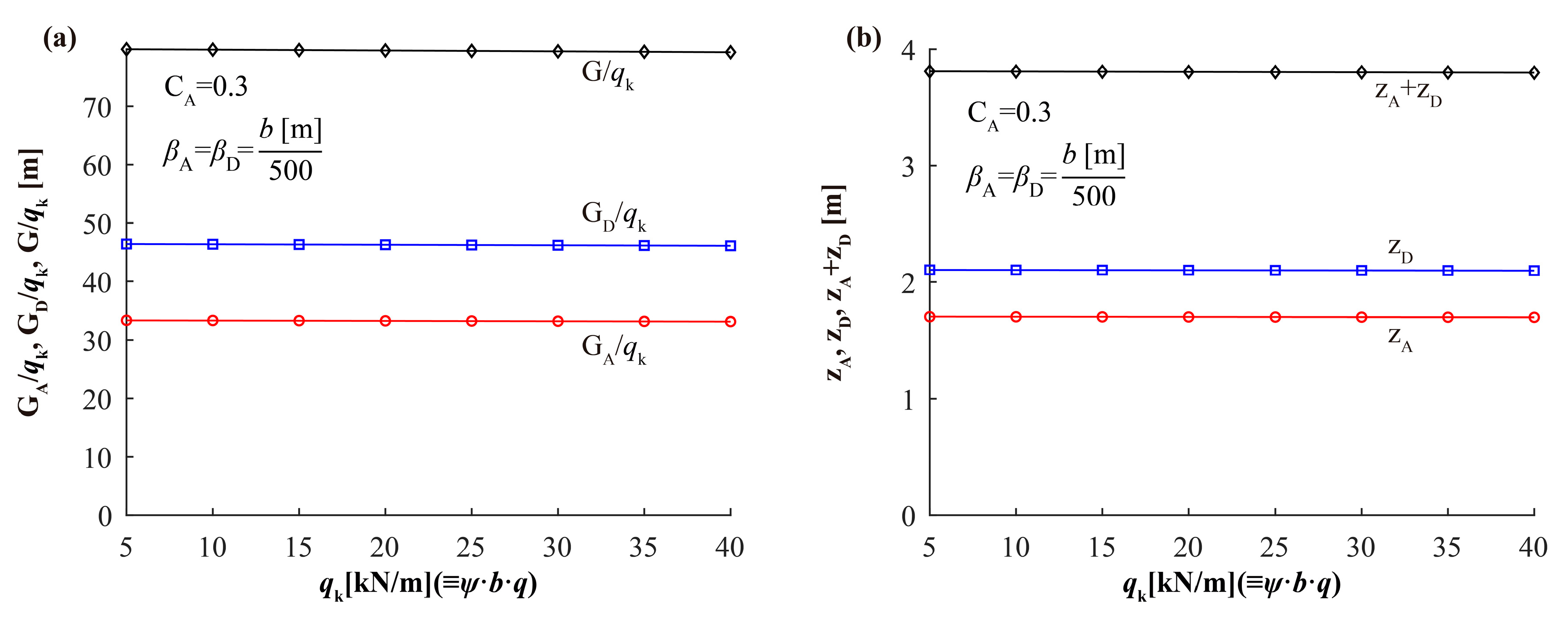
6.1. Effect of the Load qk
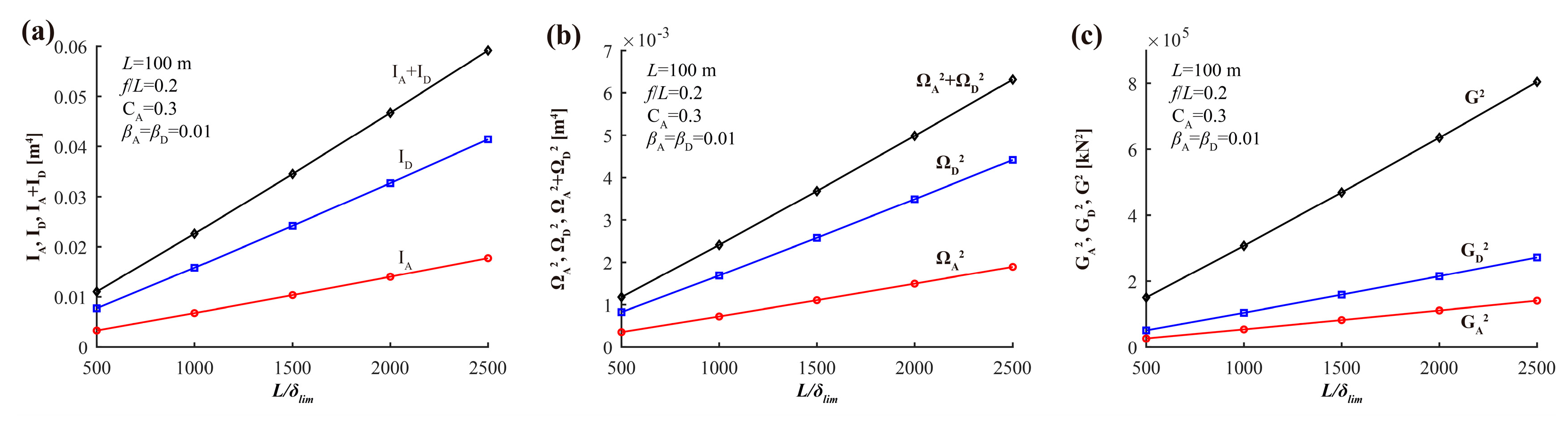
6.2. Effect of δlim
7. Parametric Studies
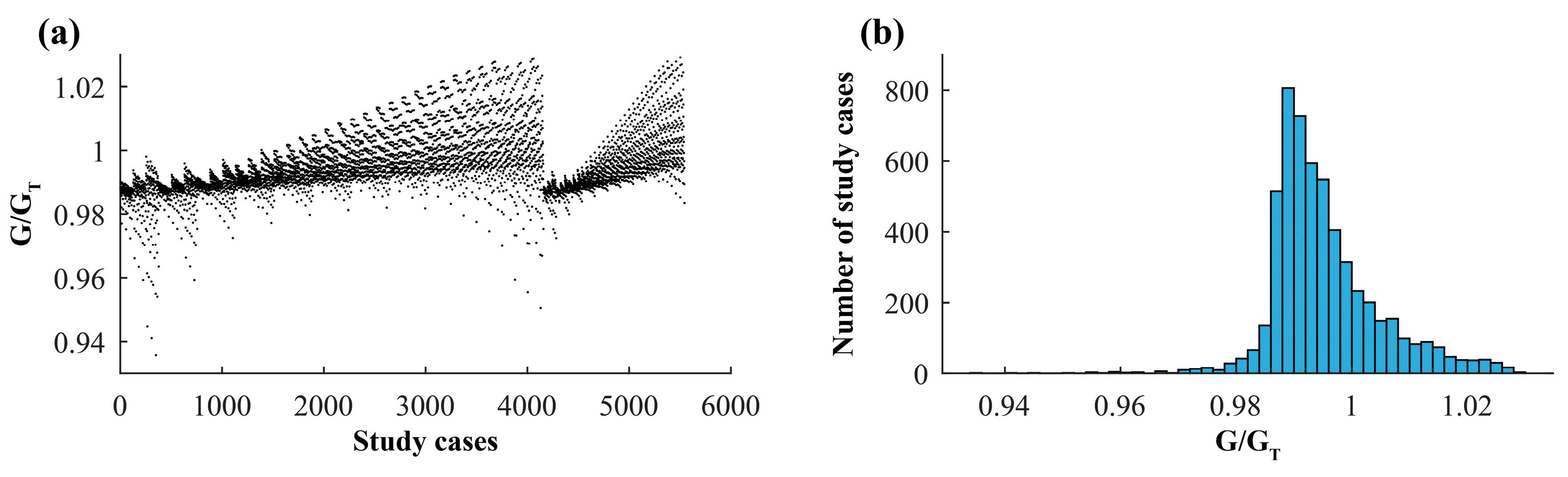
7.1. Relationship Between Inertia, Area, and Weight and Span
7.2. Effect of the Web Slenderness
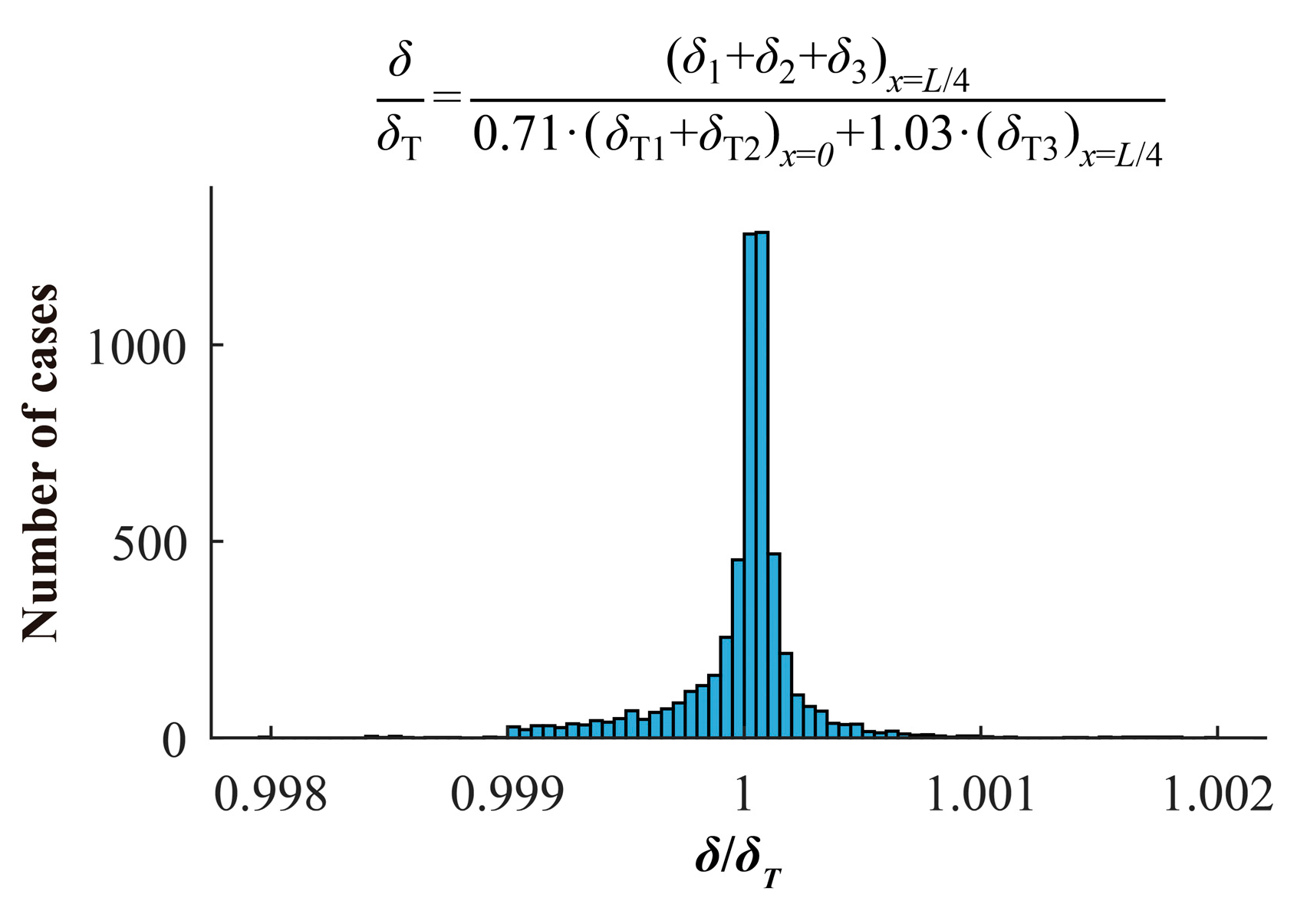
8. Manual Calculation of Tied-Arch Bridges
9. Conclusions
9.1. Conclusions from Parametric Studies
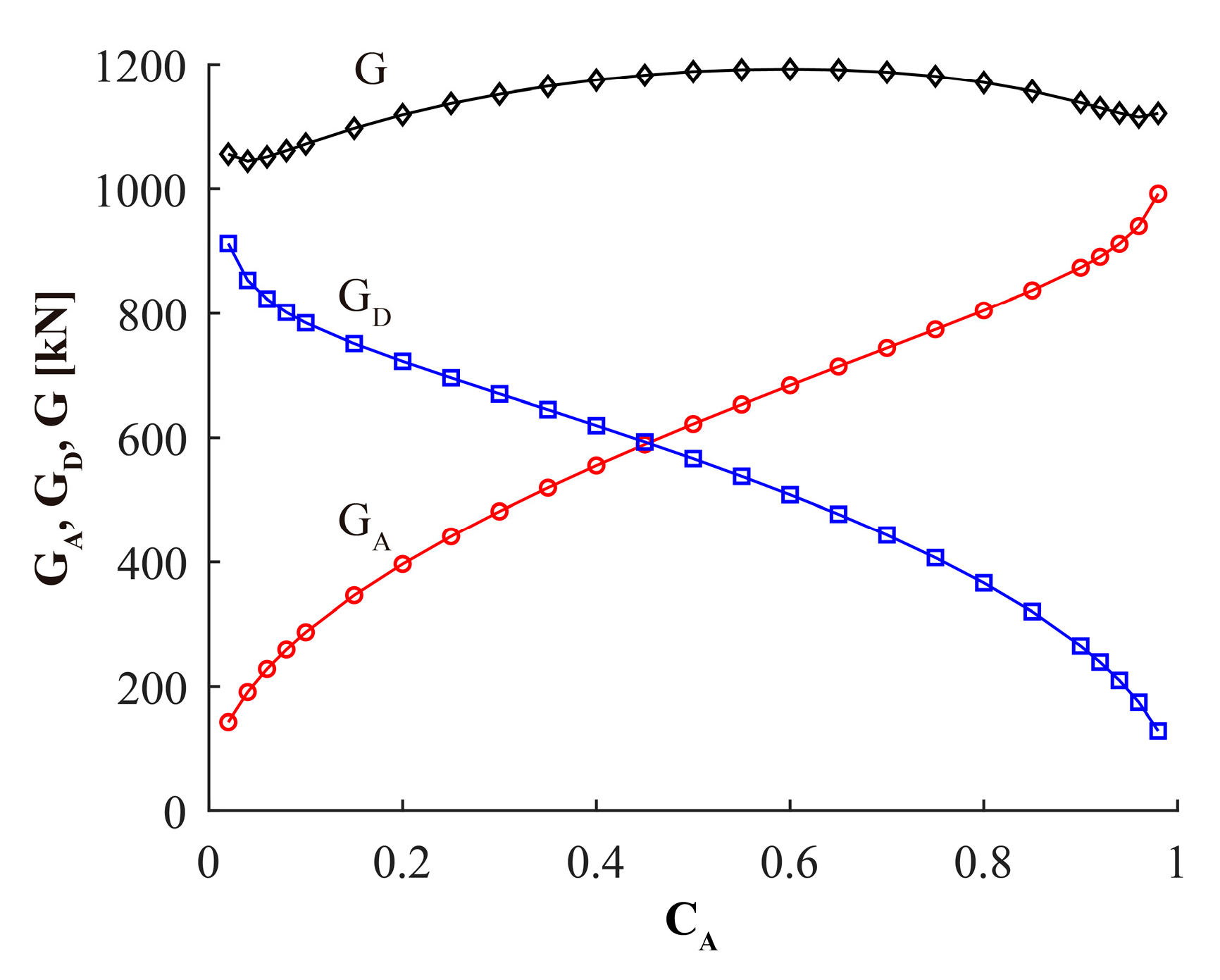
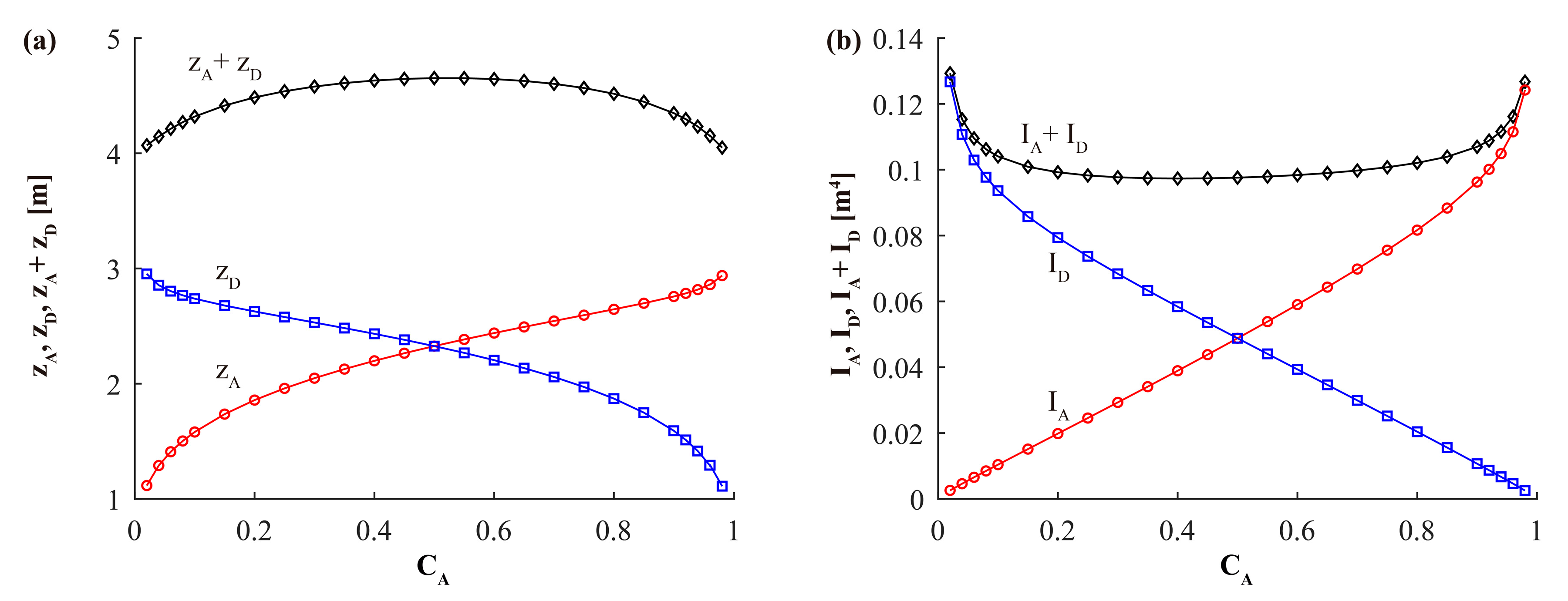
- Minimum-weight bridges usually are obtained for very low CA values, i.e., for arches with very low bending stiffness, which are practically deck-stiffened arches. The reason for this is that G depends both on the length of the arch, LA, and the span of the deck, L, and, consequently, the algorithm tends to penalize heavy arch cross-sections rather than heavy deck cross-sections, as LA > L. This trend is confirmed in the remaining parametric studies carried out.
- When the web thickness (tw = β·z) is proportional to the value of qk (which is the value of the UDL used for the SLC), the area of the cross-sections, Ω; their inertias, I; and the weight of the bridge, G, are directly proportional to qk. In this case, the ratios G/qk and z/qk for the arch and the deck are constant for any value of qk.
- Regarding δlim, the relationship between L/δlim and IA and ID can be considered linear. The same thing happens for ΩA2 and ΩD2 or GA2 and GD2.
- The parametric study has shown that IA or ID, ΩA or ΩD, and G are directly proportional to L3, L3/2, and L5/2, respectively, for all the studied values of f/L.
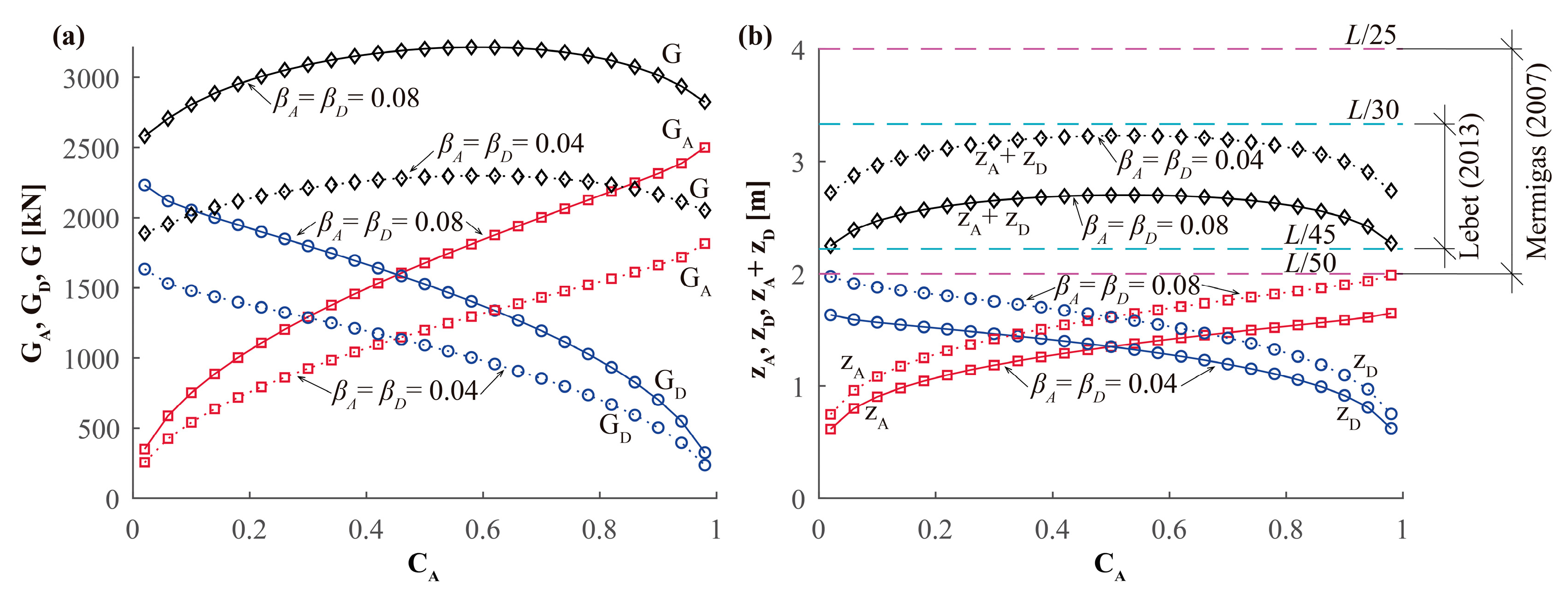
- Regarding the influence of the f/L ratio on G, in the studied bridges, the value of G/L5/2 is lower for f/L values between 0.15 and 0.2, and G increases for both shallower and deeper arches.
- In the same example, the smaller the L value, the higher the ratio G/L5/2.
- Cross-sections with the thinnest possible web (with low values of βA and βD) should be used to minimize the bridge weight.
- Thicker webs (with higher values of βA and βD) should be used to reduce the depths of the cross-sections.
9.2. Design Recommendations
- Use rise–span ratios f/L between 1/5 and 1/7, with f/L being more than 1/10;
- Use sections with very different stiffness levels in the arch and deck, preferably with very flexible arches;
- Use the thinnest possible web thickness, β, to achieve higher stiffness with less material, with β being more than 1/100.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| b | Loaded deck width (Figure 1) |
| CA | Contribution of the arch to the global flexural stiffness of the bridge (Section 2.3, Equation (1)) |
| EA, ED | Young’s modulus for the materials of the arch and the deck |
| f | Rise of the arch (Figure 1) |
| FEM | Finite elements method |
| gDL | Superimposed dead load (Figure 1) |
| GA, GD, G | Arch, deck, and bridge weight. |
| I | Inertia (second moment of area) of a cross-section (Section 2.5, Equation (4)) |
| IA, ID | Second moment of area (inertia) of the arch and deck cross-sections (Section 3, Equations (11) and (12)) |
| Imax | Maximum second moment for a given area and web slenderness (Section 2.5, Equation (9)) |
| k1, k2, k3 | Correction coefficients of theoretical formulation (Section 8). |
| L | Bridge span (Figure 1) |
| LA | Length of the arch |
| NA, ND | Axial force at crown of the arch and at the deck (Section 4.2, Equation (20)) |
| q | Live load |
| qk | Live load used for the SLC in the δ-method |
| SLC | Simplified load combination used for the preliminary design stage (Section 1.1 and Section 2.2) |
| SLC-A, SLC-S | Symmetric and antisymmetric load combinations in which the SLC is decomposed (Section 4, Figure 8) |
| tw | Web thickness (Figure 4) |
| tol | Tolerance of iterative process (Section 2.1, Figure 7) |
| UDL | Uniformly distributed load |
| z | Web depth, approximately equal to cross-section depth (Figure 4) |
| zA, zD | Arch and deck web depth |
| zI | For a given area, web depth that maximizes the second moment of area (Section 2.5, Equation (8)) |
| β | Geometrical slenderness of the web(s) (Section 2.5, Equation (3)) |
| βA, βD | Geometrical slenderness of the web of the arch and deck |
| γ | Density of the arch and deck materials |
| δ | Vertical deflection at the arch |
| δ1, δ2, δ3 | Deflections, calculated with FEM, due to axial shortening of the arch, axial elongation of the deck, and a UDL q acting upon half of the deck |
| δD | Total deflection (δ1 + δ2 + δ3) at the deck checkpoint |
| δlim | Maximum allowable deflection at the deck checkpoint |
| δT1, δT2, δT3 | Values of δ1, δ2, δ3, calculated with theoretical formulae (Figure 9, Equations (18), (19), and (21) |
| μ | Auxiliary coefficient (Equation (10)) |
| Ω | Area of a cross-section (Figure 4) |
| ΩA, ΩD | Area of the arch and deck cross-sections |
| Ωf, Ωw | Areas of one flange and the web of the cross-section (Figure 4) |
References
- Stavridis, L. Structural Systems: Behaviour and Design; Thomas Telford: London, UK, 2010. [Google Scholar]
- Granata, M.F.; Arici, M.; Longo, G.; Recupero, A. Steel and composite tied-arch bridges: A conceptual approach to structural design. Proc. Inst. Civ. Eng.-Bridge Eng. 2021, 174, 281–298. [Google Scholar] [CrossRef]
- Mermigas, K.K.; Wang, H. Comparative Study of the Proportions and Efficiency of Steel Arch Bridges. In Proceedings of the 5th International Conference on Arch Bridges, Funchal, Portugal, 12–14 September 2007. [Google Scholar]
- Manterola-Armisén, J. Puentes (Bridge Engineering); Colegio de Ingenieros de Caminos, Canales y Puertos: Madrid, Spain, 2006; pp. 897–988. (In Spanish) [Google Scholar]
- Lebet, J.P.; Hirt, M.A. Steel Bridges; EPFL Press: Lausanne, Switzerland, 2013; pp. 461–488. [Google Scholar]
- Leonhardt, F. Bridges/Brücken; The Architectural Press: London, UK, 1982; pp. 38–43. [Google Scholar]
- Menn, C. Prestressed Concrete Bridges; Birkhäuser Verlag: Vienna, Austria, 1989; pp. 382–394. [Google Scholar]
- Salonga, J.; Gauvreau, P. Comparative Study of the Proportions, Form, and Efficiency of Concrete Arch Bridges. J. Bridge Eng. 2014, 19, 04013010. [Google Scholar] [CrossRef]
- Korus, K.; Salamak, M.; Jasiński, M. Optimization of geometric parameters of arch bridges using visual programming FEM components and genetic algorithm. Eng. Struct. 2021, 241, 112465. [Google Scholar] [CrossRef]
- Jorquera-Lucerga, J.J. Form-Finding of Funicular Geometries in Spatial Arch Bridges through Simplified Force Density Method. Appl. Sci. 2018, 8, 2553. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhang, T.; Wang, W. A form-finding method for spatial arch bridges based on inverse hanging method. Structures 2022, 46, 64–72. [Google Scholar] [CrossRef]
- Haaijer, G. Economy of High Strength Steel Structural Members. Trans. Am. Soc. Civ. Eng. 1963, 128, 820–842. [Google Scholar] [CrossRef]
- Eurocode 1: Actions on Structures-Part 2: Traffic Loads on Bridges; CEN: Brussels, Belgium, 2003.
- Eurocode 3: Design of Steel Structures; CEN: Brussels, Belgium, 2005.
- Argüelles Álvarez, R. Estructuras de Acero: Cálculo (Steel Structures: Analysis), 2nd ed.; Bellisco, Ediciones Técnicas y Científicas: Madrid, Spain, 2005. (In Spanish) [Google Scholar]
- Prendes Gero, M.B.; Bello García, A.; del Coz Díaz, J.J. Design optimization of 3D steel structures: Genetic algorithms vs. classical techniques. J. Constr. Steel Res. 2006, 62, 1303–1309. [Google Scholar] [CrossRef]
- Liu, X.; Yi, W.J.; Li, Q.S.; Shen, P.S. Genetic evolutionary structural optimization. J. Constr. Steel Res. 2008, 64, 305–311. [Google Scholar] [CrossRef]
- Saka, M.P.; Geem, Z.W.; Shen, P.S. Mathematical and Metaheuristic Applications in Design Optimization of Steel Frame Structures: An Extensive Review. Math. Probl. Eng. 2013, 271031. [Google Scholar] [CrossRef]
- Billington, D.P. Robert Maillart’s Bridges: The Art of Engineering; Princeton University Press: Princeton, NJ, USA, 1979. [Google Scholar]
- Jorquera-Lucerga, J.J.; García-Guerrero, J.M. Predimensionamiento gráfico multicriterio en el plano de secciones metálicas bisimétricas (Graphical Multi-Criteria in-Plane Preliminary Sizing of Bisymmetrical All-Metal Cross-Sections). Inf. Constr. 2021, 73, e418. (In Spanish) [Google Scholar] [CrossRef]
- García-Guerrero, J.M. El Puente Arco Espacial Como una Evolución Tipológica (The Spatial Arch Bridge as a Typological Evolution). Ph.D. Thesis, Technical University of Cartagena, Cartagena, Spain, 2018. (In Spanish). [Google Scholar]
- Park, G.; Hewson, N. ICE Manual of Bridge Engineering, 2nd ed.; Thomas Telford: London, UK, 2008. [Google Scholar]
- Tveit, P. Considerations for Design of Network Arches. J. Struct. Eng. 1987, 113, 2189–2207. [Google Scholar] [CrossRef]
- Romeijn, A.; Bouras, C. Investigation of the arch in-plane buckling behaviour in arch bridges. J. Constr. Steel Res. 2008, 64, 1349–1356. [Google Scholar] [CrossRef]
- Chengyi, C.; Genshu, T.; Lei, Z. In-plane nonlinear buckling analysis of circular arches considering shear deformation. J. Constr. Steel Res. 2020, 164, 105762. [Google Scholar] [CrossRef]
- Tang, Z.; Zhang, W.; Yu, J.; Pospíšil, S. Prediction of the elastoplastic in-plane buckling of parabolic steel arch bridges. J. Constr. Steel Res. 2020, 168, 105988. [Google Scholar] [CrossRef]
- Strasky, J. Stress Ribbon and Cable Supported Pedestrian Bridges, 2nd ed.; ICE Publishing: London, UK, 2011. [Google Scholar]
- Ministerio de Fomento de España. Instrucción Sobre las Acciones a Considerar en el Proyecto de Puentes de Carretera, (IAP-11); Ministerio de Fomento: Madrid, Spain, 2011. [Google Scholar]
- AN/UNE-EN 1990; Anejo Nacional Para el Eurocódigo 0: Bases de Cálculo de Estructuras y Anejo A2: Aplicación a Puentes. Ministerio de Transportes y Movilidad Sostenible: Madrid, Spain. (In Spanish)
- Nettleton, D.A. Arch Bridges; U.S. Department of Transportation: Washington, DC, USA, 1977. [Google Scholar]
- Buchholdt, H.A. An Introduction to Cable Roof Structures, 2nd ed.; Thomas Telford: London, UK, 1999. [Google Scholar]
- The MathWorks Inc. Matlab; R2017; The MathWorks Inc.: Madrid, Spain, 2017. [Google Scholar]
- Computers and Structures, Inc. Analysis Reference Manual for SAP2000® v 26; CSI: Berkeley, CA, USA, 2024. [Google Scholar]


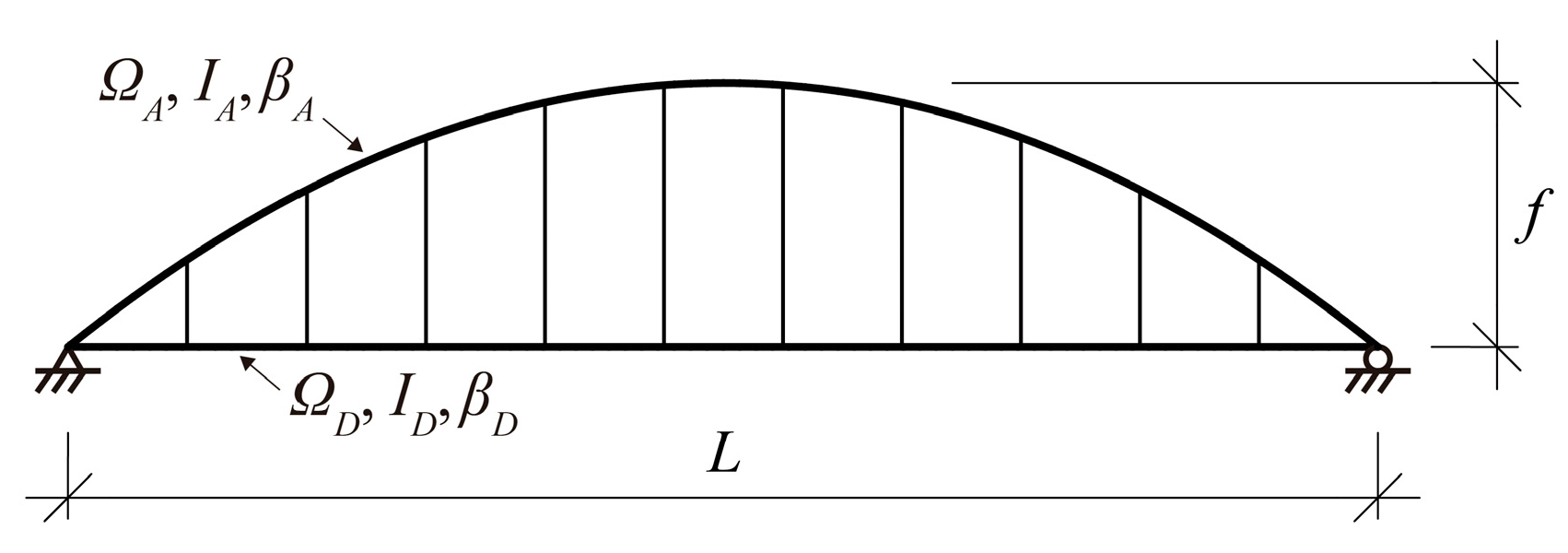
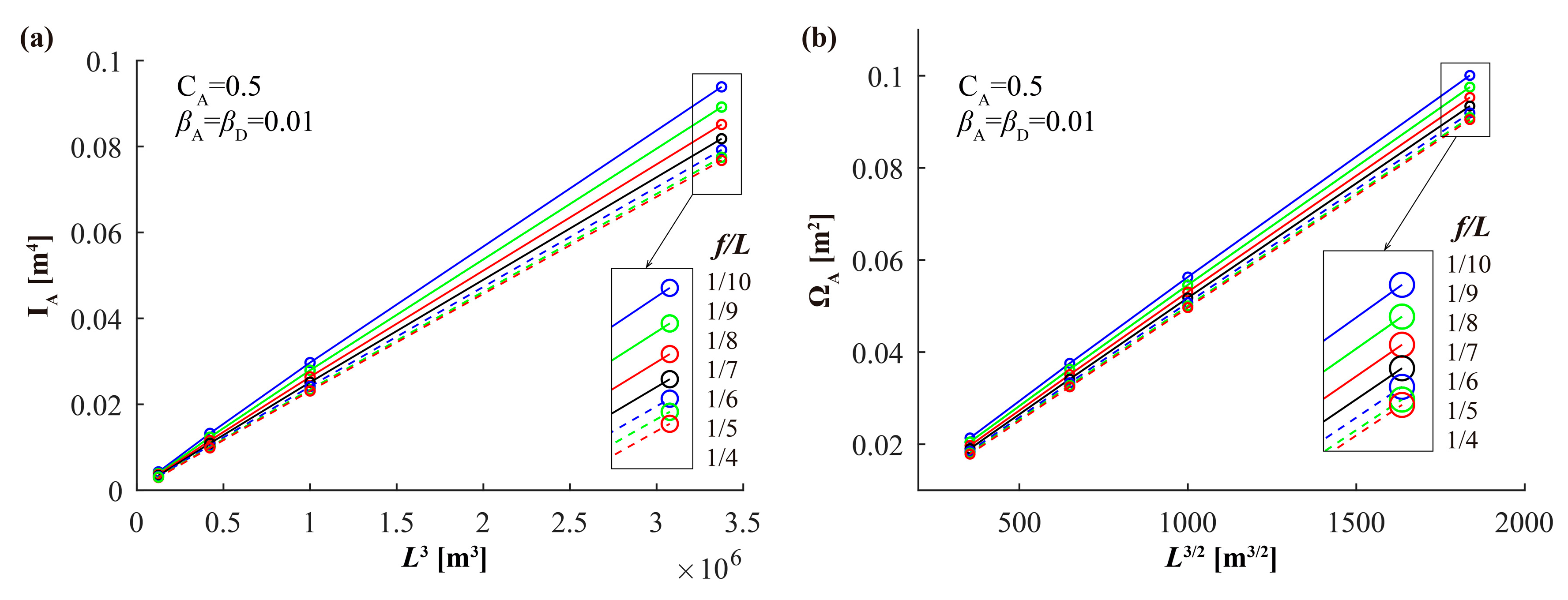
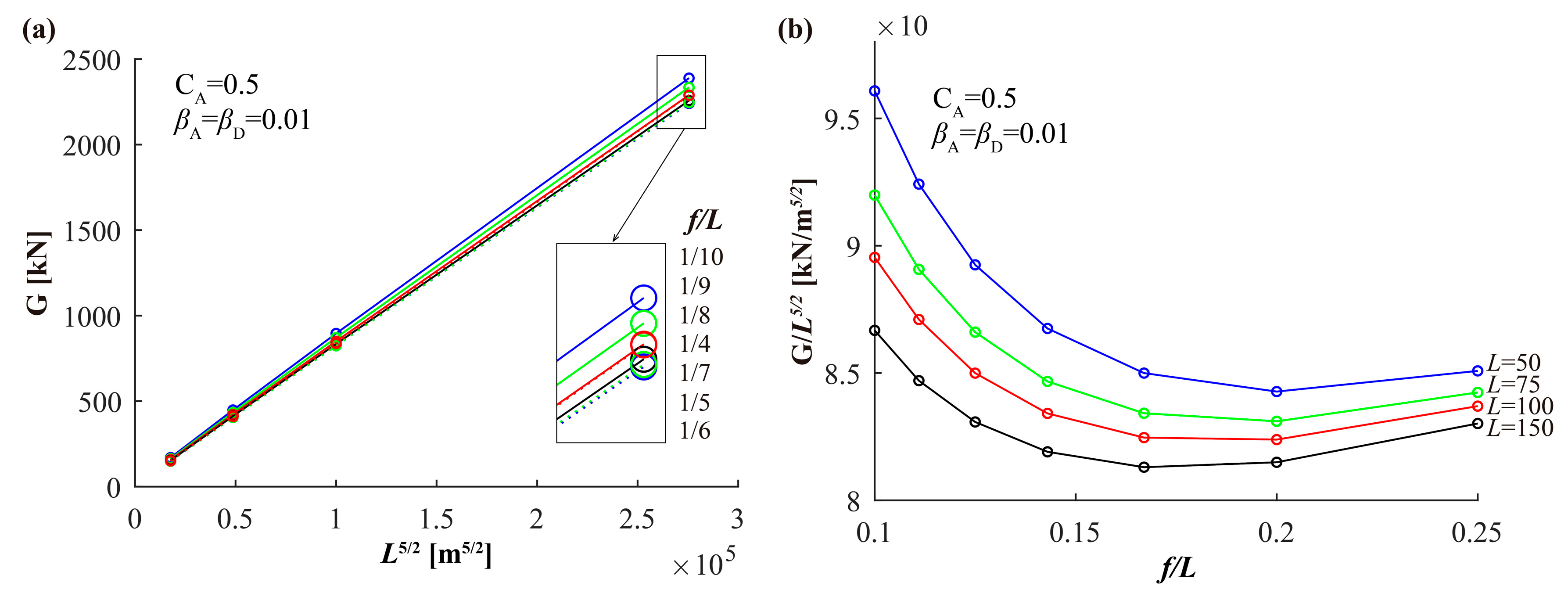

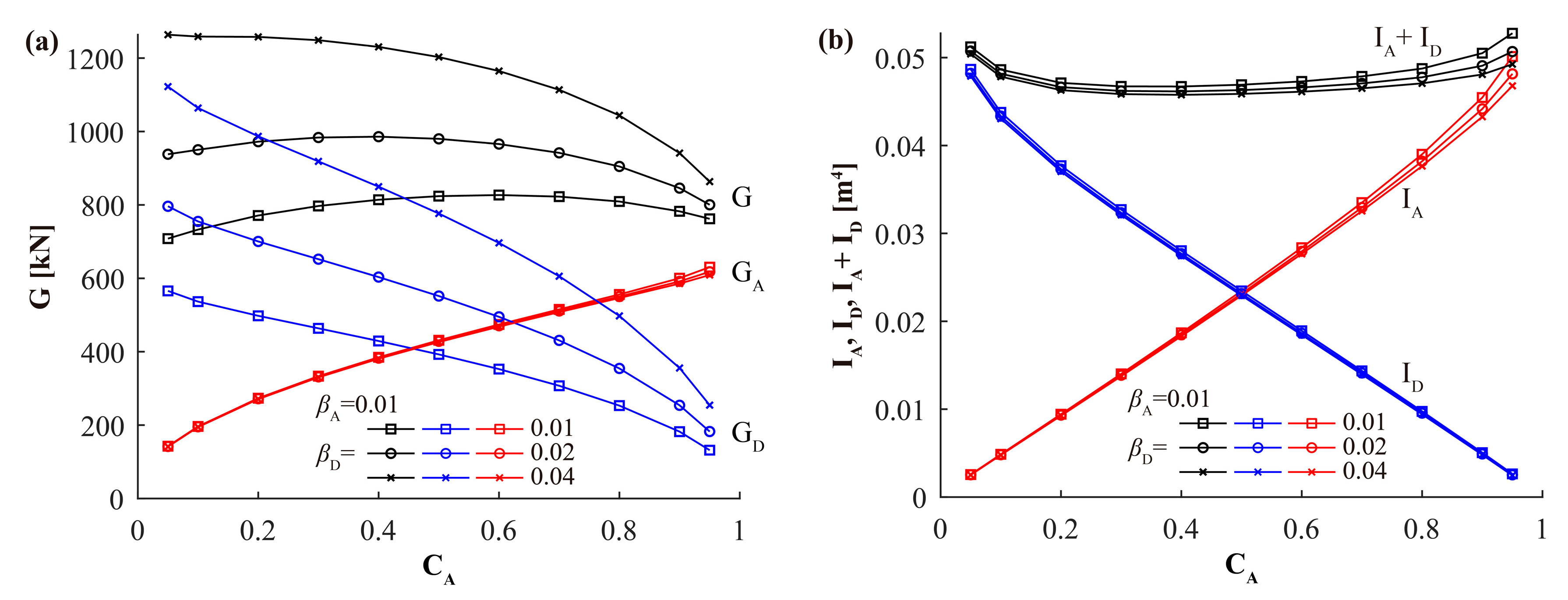
| Symbol | Units | Values | ni |
|---|---|---|---|
| L | m | 50 75 100 150 | 4 |
| f/L | - | 0.25 0.2 0.167 0.143 0.125 0.111 0.10 | 7 |
| CA | - | 0.05 0.10 0.20 0.30 0.40 0.45 0.50 0.55 0.60 0.65 0.70 0.75 0.80 0.85 0.90 0.95 | 11 |
| βA | - | 1/25 1/50 1/100 | 3 |
| βD | - | 1/25 1/50 1/100 | 3 |
| qk | kN/m | 10 | 1 |
| δlim | m | L/500 L/2000 | 2 |
| Total n models = P(ni) | 5544 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jorquera-Lucerga, J.J.; García-Guerrero, J.M. Preliminary Design and Parametric Study of Minimum-Weight Steel Tied-Arch Bridges Obtained According to a Maximum Allowable Deflection Criterion. Appl. Sci. 2025, 15, 10022. https://doi.org/10.3390/app151810022
Jorquera-Lucerga JJ, García-Guerrero JM. Preliminary Design and Parametric Study of Minimum-Weight Steel Tied-Arch Bridges Obtained According to a Maximum Allowable Deflection Criterion. Applied Sciences. 2025; 15(18):10022. https://doi.org/10.3390/app151810022
Chicago/Turabian StyleJorquera-Lucerga, Juan José, and Juan Manuel García-Guerrero. 2025. "Preliminary Design and Parametric Study of Minimum-Weight Steel Tied-Arch Bridges Obtained According to a Maximum Allowable Deflection Criterion" Applied Sciences 15, no. 18: 10022. https://doi.org/10.3390/app151810022
APA StyleJorquera-Lucerga, J. J., & García-Guerrero, J. M. (2025). Preliminary Design and Parametric Study of Minimum-Weight Steel Tied-Arch Bridges Obtained According to a Maximum Allowable Deflection Criterion. Applied Sciences, 15(18), 10022. https://doi.org/10.3390/app151810022






