Research on the Internal Flow Characteristics of Single- and Coaxial-Nozzle Ejectors for Hydrogen Recirculation in PEMFC
Abstract
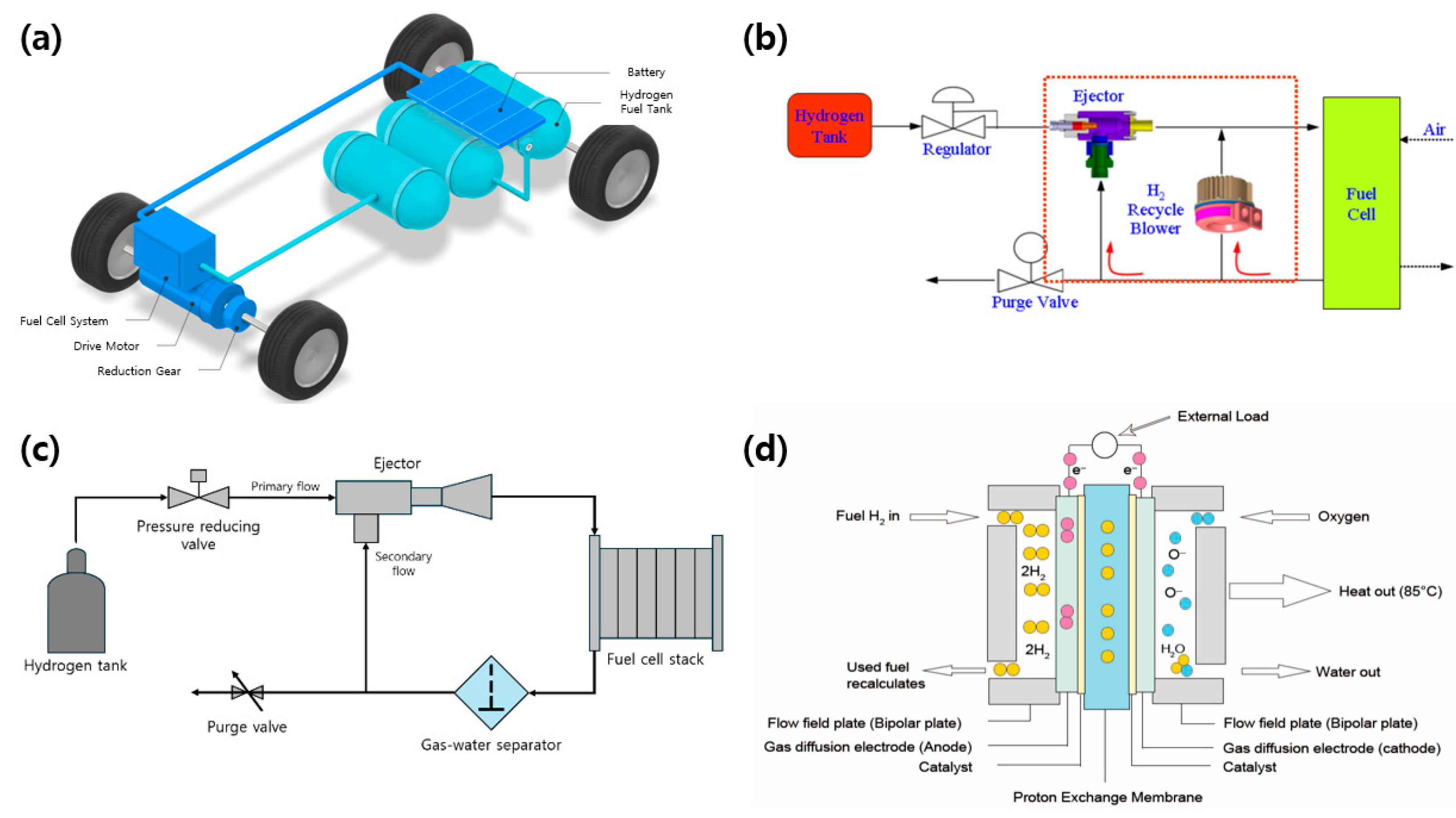
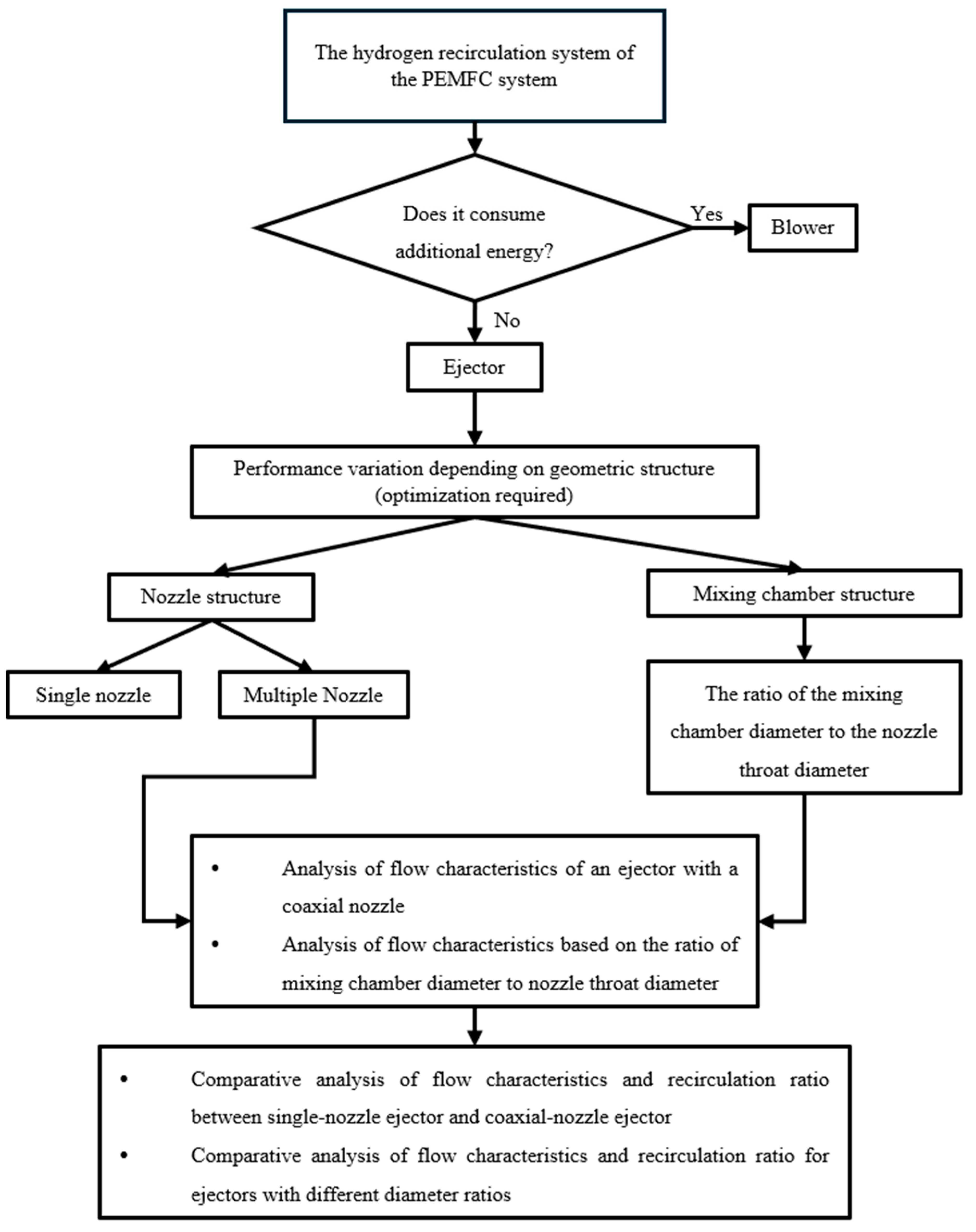
1. Introduction
2. Analysis of Internal Flow Characteristics of Hydrogen Recirculation Ejectors
2.1. Modeling of Single- and Coaxial-Nozzle Ejectors
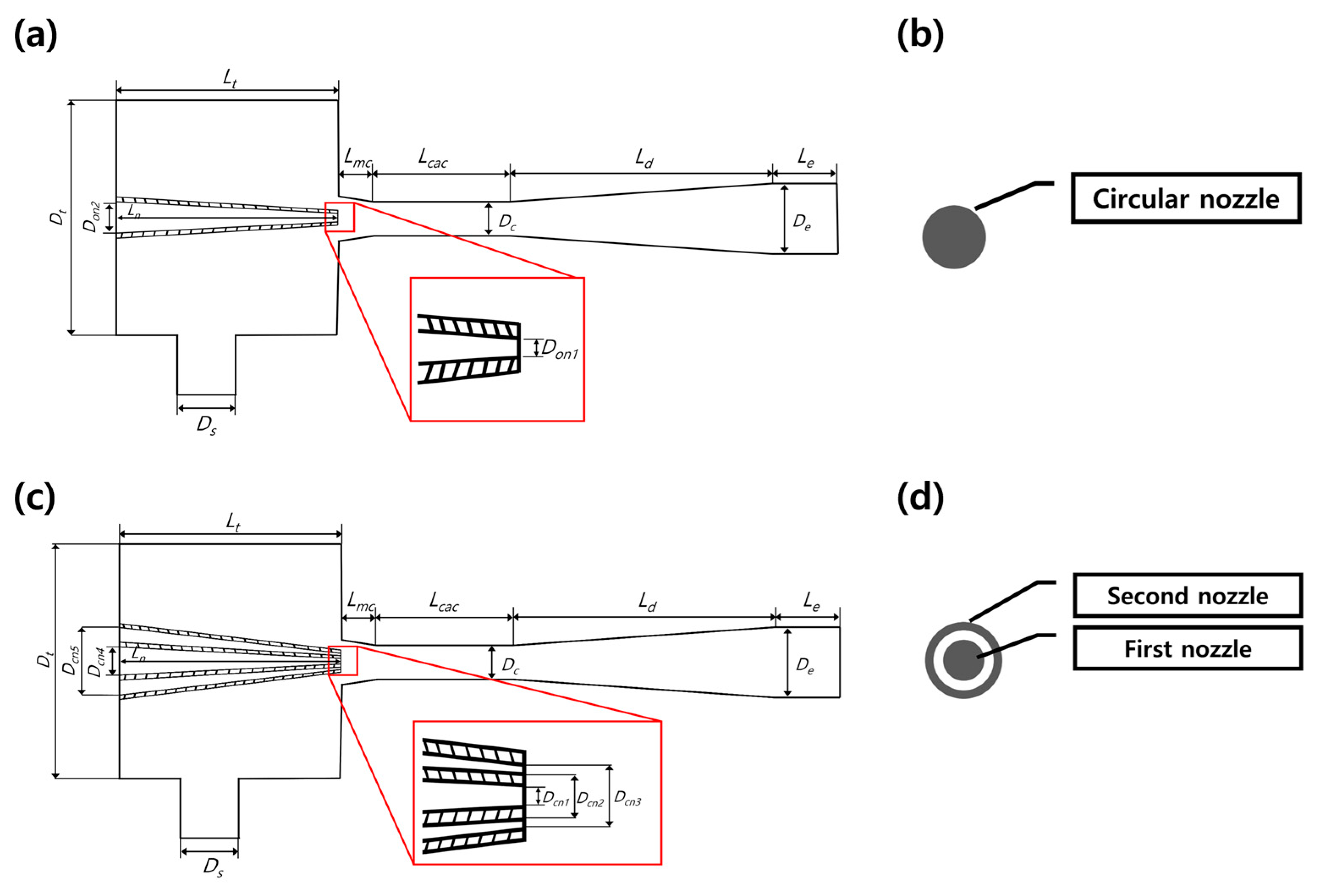
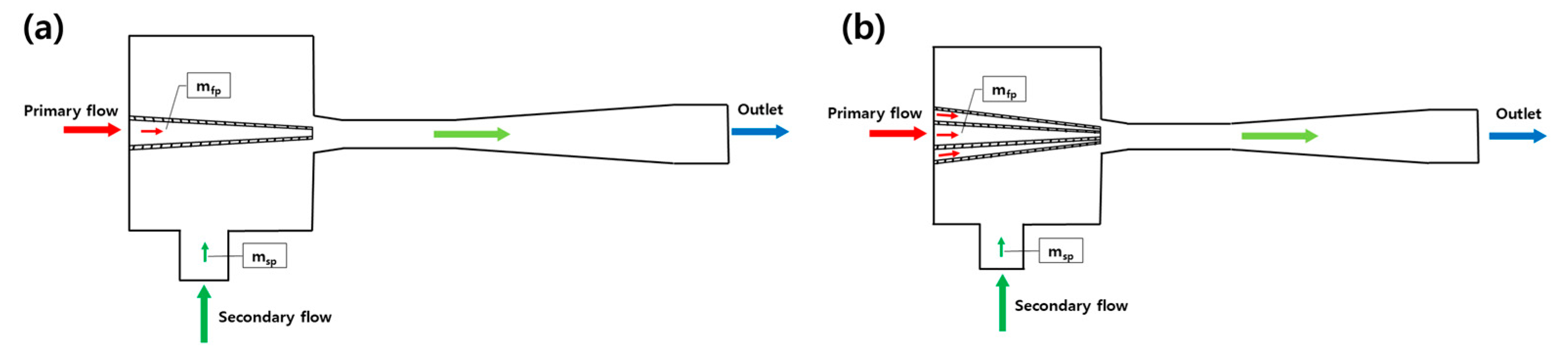
2.1.1. Geometric Modeling
2.1.2. Numerical Modeling
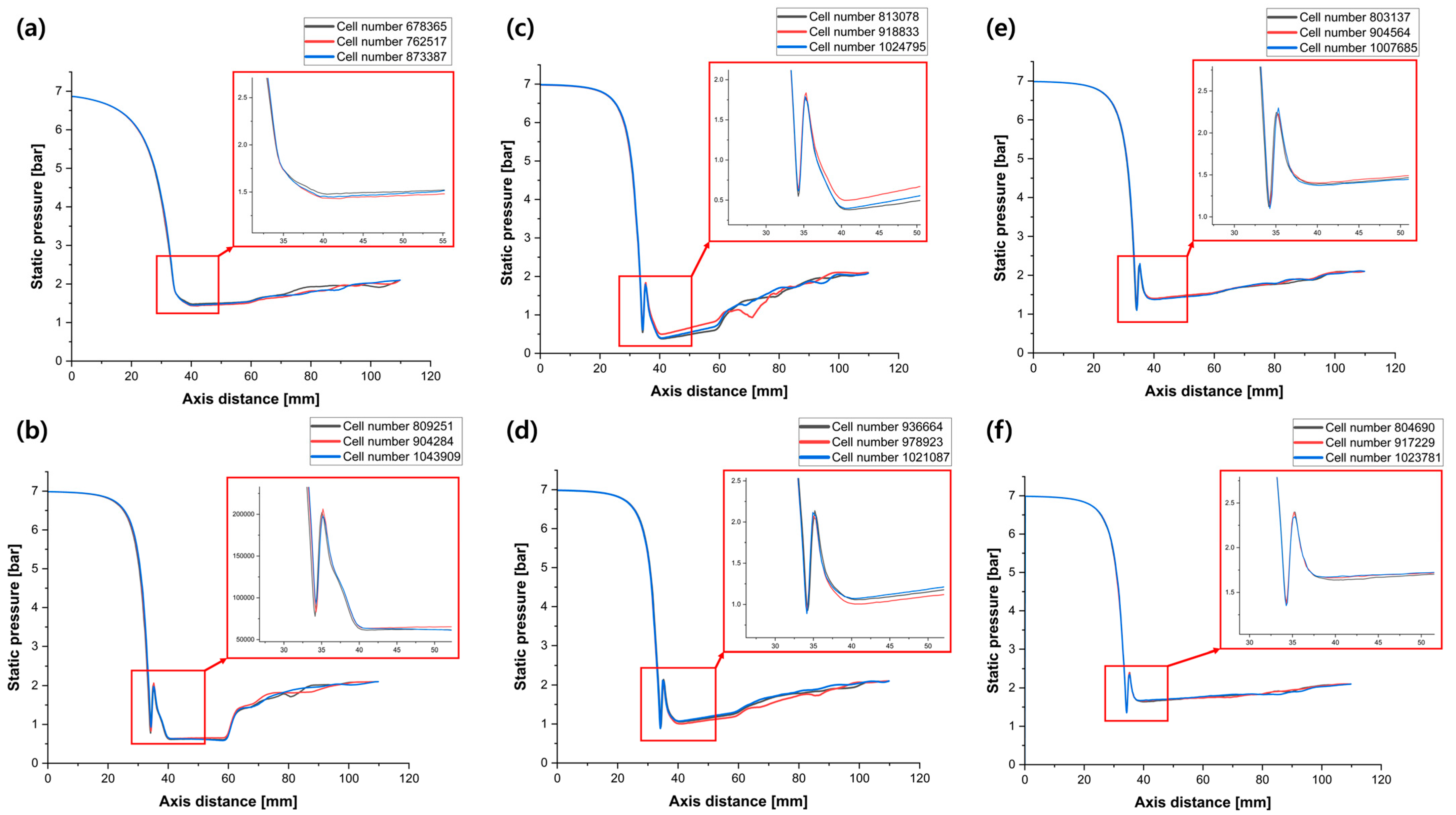
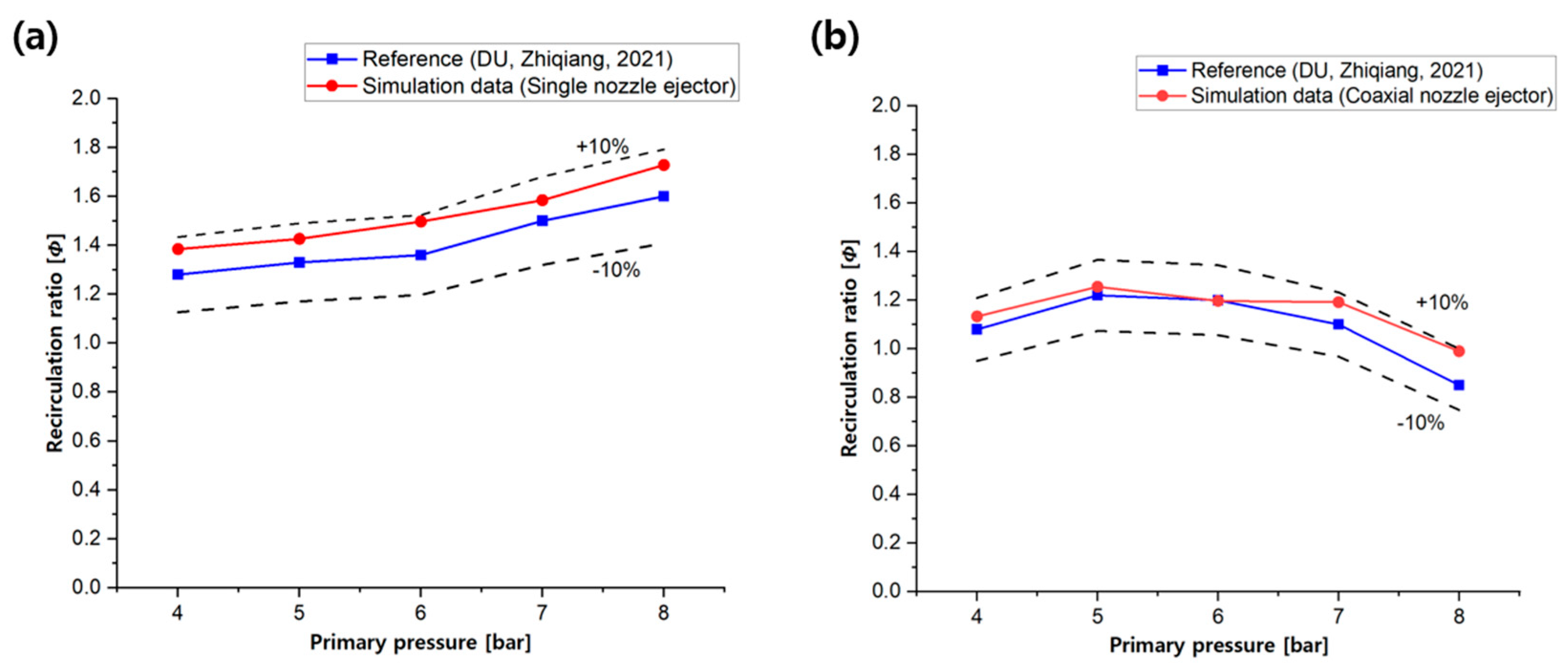
2.2. Validation of the Ejector Analysis Model
3. Analysis Results and Discussion
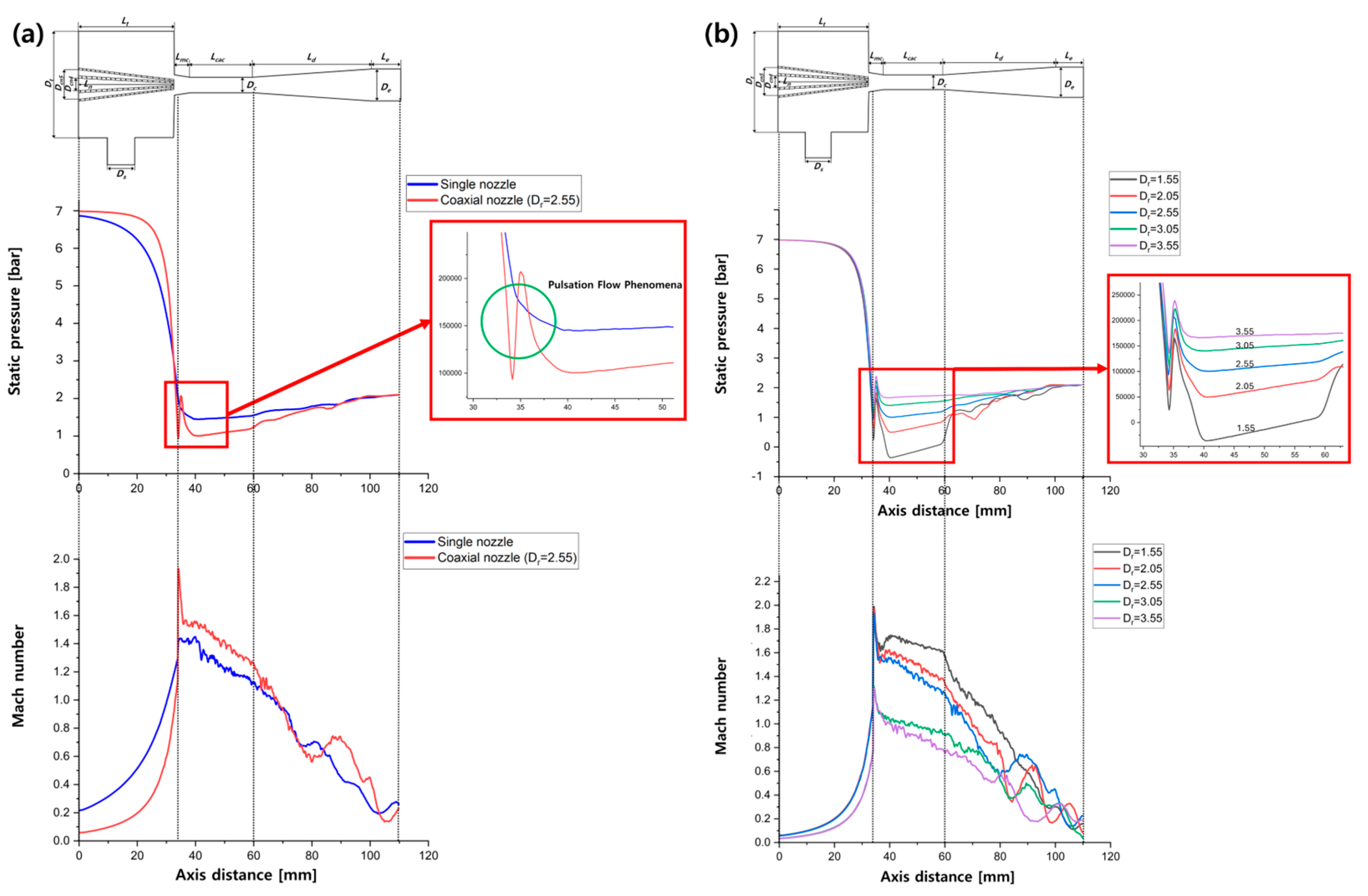
3.1. Flow Characteristics of Single- and Coaxial-Nozzle Ejectors
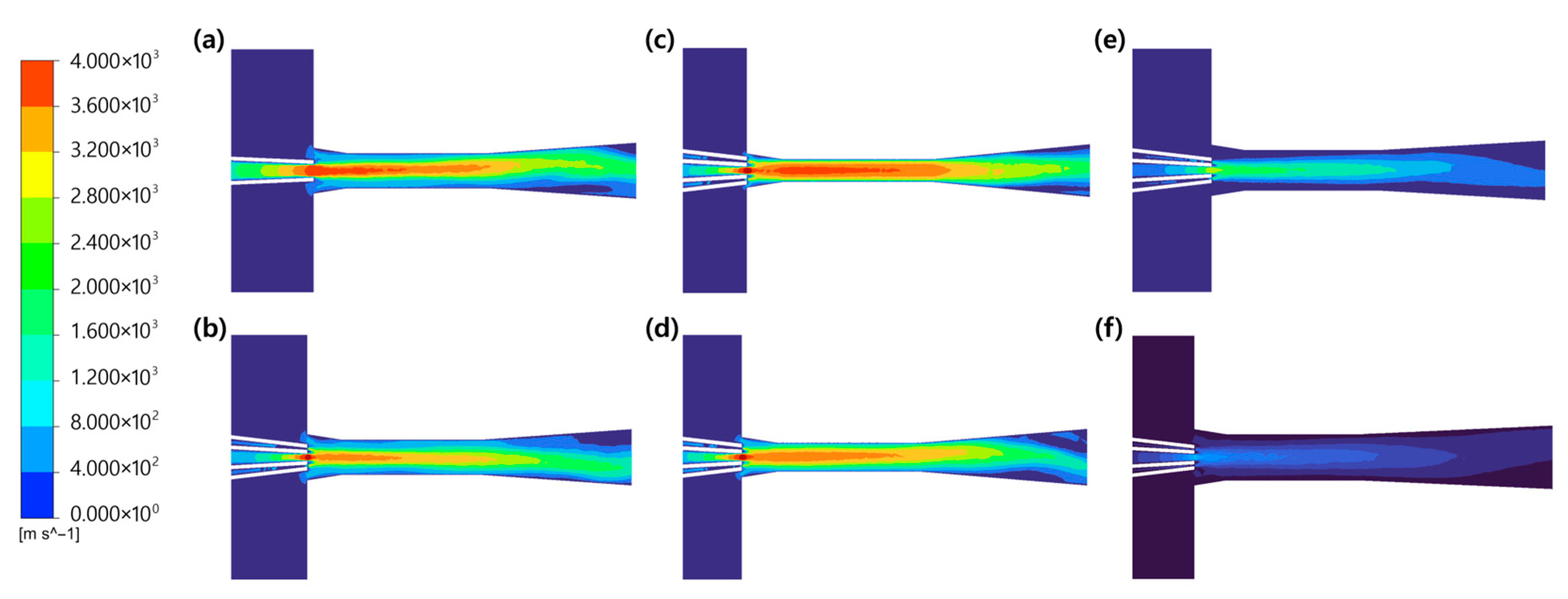
3.2. Velocity Distribution in Single- and Coaxial-Nozzle Ejectors
3.3. Recirculation Ratio in Single- and Coaxial-Nozzle Ejectors
4. Conclusions
- (1)
- Unlike single-nozzle ejectors, coaxial-nozzle ejectors exhibited supersonic flow acceleration near the nozzle exit as the two flow streams converged, accompanied by the formation of shock waves and observable pressure pulsations. These flow characteristics contribute to a decrease in the recirculation ratio.
- (2)
- For coaxial-nozzle ejectors with lower diameter ratios, the flow was more intensely accelerated, resulting in stronger vortices and shock waves. Although larger pressure drops were observed, these flow characteristics led to a reduction in the recirculation ratio. The ejectors with the diameter ratios of 1.55 and 2.05 showed relatively low and stable recirculation performance across the entire range of primary flow pressures, with the recirculation ratios of approximately 0.5 and 1.0, respectively.
- (3)
- For higher diameter ratios, the flow acceleration weakened, and the flow field became relatively stable. The ejector with a diameter ratio of 3.05 achieved a recirculation ratio above 1.5 when the primary flow pressure exceeded 5 bar, whereas the ejector with a diameter ratio of 3.55 achieved the highest recirculation ratio at pressures above 6 bar. Both the ejectors outperformed the single-nozzle ejector under high-output conditions.
- (4)
- The ratio of the mixing-chamber diameter to the nozzle-throat diameter significantly affected the recirculation ratio. A comparison of the relationship between the primary flow pressure and recirculation ratio revealed that optimal geometric conditions exist within the operating range.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ministry of Land, Infrastructure and Transport. Vehicle Registration Statistics in South Korea. Available online: https://www.molit.go.kr/USR/NEWS/m_71/dtl.jsp?lcmspage=1&id=95086498 (accessed on 24 August 2025).
- Hyundai Motor Group. The Path to a Hydrogen Society: How Is the World Moving? Available online: https://www.hyundai.co.kr/amp/CONT0000000000000865 (accessed on 24 August 2025).
- Hyundai Motor Group. The Principle of Hydrogen Fuel Cell Vehicles Driving the Future. Available online: https://www.hyundai.co.kr/story/CONT0000000000005046 (accessed on 24 August 2025).
- Top TiTechs. How Is the Generated Water Controlled in Proton Exchange Membrane Fuel Cells (PEMFC)? Available online: https://toptitechs.com/how-is-the-generated-water-controlled-in-proton-exchange-membrane-fuel-cells-pemfc/ (accessed on 24 August 2025).
- Wang, C.; Wang, L. Investigation of fluid characteristic and performance of an ejector by a wet steam model. Entropy 2023, 25, 85. [Google Scholar] [CrossRef] [PubMed]
- Dong, J.-M.; Song, H.; Yu, M.-Q.; Wang, W.-N.; Pan, X.-X. Numerical investigation of miniature ejector refrigeration system embedded with a capillary pump loop. Micromachines 2017, 8, 235. [Google Scholar] [CrossRef] [PubMed]
- Yan, J.; Shu, Y.; Wang, C. Effect of back pressure on performances and key geometries of the second stage in a highly coupled two-stage ejector. Entropy 2022, 24, 1847. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Xu, S.; Xing, C. Numerical and experimental investigation on an ejector designed for an 80 kW polymer electrolyte membrane fuel cell stack. J. Power Sources 2019, 415, 25–32. [Google Scholar] [CrossRef]
- Ding, G.; Cao, X.; Chen, J.; Zhang, Y.; Bian, J. Impact of the expansion ratio on the properties of hydrogen recirculation ejectors. Appl. Energy 2024, 374, 124026. [Google Scholar] [CrossRef]
- Nikiforow, K.; Koski, P.; Karimmäki, H.; Ihonen, J.; Alopaeus, V. Designing a hydrogen gas ejector for 5 kW stationary PEMFC system–CFD-modeling and experimental validation. Int. J. Hydrogen Energy 2016, 41, 14952–14970. [Google Scholar] [CrossRef]
- Yin, Y.; Fan, M.; Jiao, K.; Du, Q.; Qin, Y. Numerical investigation of an ejector for anode recirculation in proton exchange membrane fuel cell system. Energy Convers. Manag. 2016, 126, 1106–1117. [Google Scholar] [CrossRef]
- Bian, J.; Zhang, Y.; Liu, Y.; Gong, L.; Cao, X. Structural optimization of hydrogen recirculation ejector for proton exchange membrane fuel cells considering the boundary layer separation effect. J. Clean. Prod. 2023, 397, 136535. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, L.; Zhang, H.; Jia, L. Optimization of ejector structure for the PEMFC hydrogen recirculation system. In Proceedings of the 2020 Chinese Automation Congress (CAC), Shanghai, China, 6–8 November 2020; pp. 2954–2959. [Google Scholar] [CrossRef]
- Han, J.; Feng, J.; Hou, T.; Peng, X. Performance investigation of a multi-nozzle ejector for proton exchange membrane fuel cell system. Int. J. Energy Res. 2020, 45, 3031–3048. [Google Scholar] [CrossRef]
- Xue, H.; Wang, L.; Zhang, H.; Jia, L.; Ren, J. Design and Investigation of Multi-Nozzle Ejector for PEMFC Hydrogen Recirculation. Int. J. Hydrogen Energy 2020, 45, 14500–14516. [Google Scholar] [CrossRef]
- Chen, L.; Xu, K.; Yang, Z.; Yan, Z.; Zhai, C.; Dong, Z. Optimal design of a novel nested-nozzle ejector for PEMFC’s hydrogen supply and recirculation system. Int. J. Hydrogen Energy 2023, 48, 27330–27343. [Google Scholar] [CrossRef]
- Du, Z.; Liu, Q.; Wang, X.; Wang, L. Performance investigation on a coaxial-nozzle ejector for PEMFC hydrogen recirculation system. Int. J. Hydrogen Energy 2021, 46, 38026–38039. [Google Scholar] [CrossRef]
- Chong, D.; Hu, M.; Chen, W.; Wang, J.; Liu, J.; Yan, J. Experimental and numerical analysis of supersonic air ejector. Appl. Energy 2014, 130, 679–684. [Google Scholar] [CrossRef]
- Zhang, K.; Shen, S.; Yang, Y. Numerical investigation on performance of the adjustable ejector. Int. J. Low-Carbon Technol 2010, 5, 51–56. [Google Scholar] [CrossRef]
- Zhu, Y.; Jiang, P. Experimental and numerical investigation of the effect of shock wave characteristics on the ejector performance. Int. J. Refrig. 2014, 40, 31–42. [Google Scholar] [CrossRef]
- Croquer, S.; Lamberts, O.; Poncet, S.; Moreau, S.; Bartosiewicz, Y. Large Eddy Simulation of a supersonic air ejector. Appl. Therm. Eng. 2022, 209, 118177. [Google Scholar] [CrossRef]
- Mazzelli, F.; Little, A.B.; Garimella, S.; Bartosiewicz, Y. Computational and experimental analysis of supersonic air ejector: Turbulence modeling and assessment of 3D effects. Int. J. Heat Fluid Flow 2015, 56, 305–316. [Google Scholar] [CrossRef]
- Li, Y.; Niu, C.; Shen, S.; Mu, X.; Zhang, L. Turbulence Model Comparative Study for Complex Phenomena in Supersonic Steam Ejectors with Double Choking Mode. Entropy 2022, 24, 1215. [Google Scholar] [CrossRef] [PubMed]


| Single-Nozzle Ejector [5] | Multi-Nozzle Ejector [15] | Coaxial-Nozzle Ejector | |
| Structural Diagram |  | 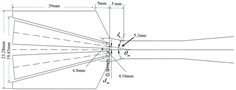 | 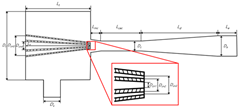 |
| Characteristics |
|
|
|
| Disadvantages |
|
|
|
| Parameter | Value [mm] |
|---|---|
| Single-Nozzle Exit Diameter, Don1 | 2.04 |
| Single-Nozzle Inlet Diameter, Don2 | 5.00 |
| First-Nozzle Exit Diameter, Dcn1 | 1.12 |
| Second-Nozzle Inner Exit Diameter, Dcn2 | 2.20 |
| Second-Nozzle Outer Exit Diameter, Dcn3 | 2.78 |
| Nozzle Length, Ln | 34.00 |
| First-Nozzle Inlet Diameter, Dcn4 | 5.00 |
| Second-Nozzle Inlet Diameter, Dcn5 | 10.80 |
| Uniform Pressure Mixing-Chamber Length, Lmc | 5.00 |
| Uniform Cross-Section Mixing-Chamber Diameter, Dc | 5.20 |
| Uniform Cross-Section Mixing-Chamber Length, Lcac | 20.80 |
| Diffuser Diameter, De | 10.80 |
| Diffuser Length, Ld | 40.00 |
| Suction Chamber Diameter, Dt | 36.00 |
| Suction Chamber Length, Lt | 30.00 |
| Secondary Flow Inlet Diameter, Ds | 9.00 |
| Diameter Ratio (Dr = Dc/Dn) [mm] | Mixing-Chamber Diameter (Dc) [mm] | Nozzle-Throat Diameter (Dn) [mm] |
|---|---|---|
| 1.55 | 3.15 | 2.04 |
| 2.05 | 4.17 | 2.04 |
| 2.55 | 5.20 | 2.04 |
| 3.05 | 6.21 | 2.04 |
| 3.55 | 7.23 | 2.04 |
| Power Output [kW] | Voltage [V] | Single-Cell Voltage [V] | Current [A] | Ejector Primary Flow Rate [g/s] | Ejector Primary Flow Pressure [kPa] |
|---|---|---|---|---|---|
| 84 | 282 | 0.65 | 300 | 1.36 | 819 |
| 70 | 291 | 0.67 | 240 | 1.097 | 660 |
| 60 | 300 | 0.689 | 200 | 0.914 | 550 |
| 48.3 | 322 | 0.74 | 150 | 0.685 | 413 |
| 33.7 | 337 | 0.77 | 100 | 0.46 | 277 |
| 17.9 | 358 | 0.82 | 50 | 0.229 | 138 |
| Parameter | Unit | Value |
|---|---|---|
| Primary Flow Pressure | bar | 4, 5, 6, 7, 8 |
| Secondary Flow Pressure | bar | 1.9 |
| Outlet Pressure | bar | 2.1 |
| Primary Flow Temperature | K | 293 |
| Secondary Flow Temperature | K | 338 |
| Flow Temperature at Outlet | K | 308 |
| Diameter Ratio (Dr) | 1.55 | 2.05 | 2.55 | 3.05 | 3.55 | Single-Nozzle Ejector | |
|---|---|---|---|---|---|---|---|
| Comparison Item | |||||||
| Primary Minimum Static Pressure [bar] | 0.247 | 0.631 | 1.010 | 1.109 | 1.358 | 1.452 | |
| Maximum Pressure Between Primary and Secondary Minima [bar] | 1.652 | 1.837 | 2.032 | 2.228 | 2.394 | - | |
| Secondary Minimum Static Pressure [bar] | −0.359 | 0.498 | 1.005 | 1.404 | 1.662 | - | |
| Mach Number at Primary Static Pressure Minimum | 1.989 | 1.954 | 1.919 | 1.317 | 1.301 | 1.450 | |
| Mach Number at Secondary Static Pressure Minimum | 1.747 | 1.583 | 1.507 | 1.021 | 1.015 | - | |
| Diameter Ratio | Coaxial-Nozzle Ejector | Single-Nozzle Ejector | |||||
|---|---|---|---|---|---|---|---|
| Primary Flow Pressure [bar] | 1.55 | 2.05 | 2.55 | 3.05 | 3.55 | ||
| 4 | 0.538 | 1.008 | 1.133 | 1.087 | 0.446 | 1.384 | |
| 5 | 0.533 | 1.017 | 1.255 | 1.438 | 1.215 | 1.426 | |
| 6 | 0.570 | 1.086 | 1.197 | 1.529 | 1.591 | 1.497 | |
| 7 | 0.559 | 1.066 | 1.192 | 1.729 | 1.743 | 1.584 | |
| 8 | 0.579 | 1.001 | 1.026 | 1.769 | 1.842 | 1.728 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, J.; Won, S.; Lee, J. Research on the Internal Flow Characteristics of Single- and Coaxial-Nozzle Ejectors for Hydrogen Recirculation in PEMFC. Appl. Sci. 2025, 15, 9845. https://doi.org/10.3390/app15179845
Han J, Won S, Lee J. Research on the Internal Flow Characteristics of Single- and Coaxial-Nozzle Ejectors for Hydrogen Recirculation in PEMFC. Applied Sciences. 2025; 15(17):9845. https://doi.org/10.3390/app15179845
Chicago/Turabian StyleHan, Jaewoong, Seongjae Won, and Jinwook Lee. 2025. "Research on the Internal Flow Characteristics of Single- and Coaxial-Nozzle Ejectors for Hydrogen Recirculation in PEMFC" Applied Sciences 15, no. 17: 9845. https://doi.org/10.3390/app15179845
APA StyleHan, J., Won, S., & Lee, J. (2025). Research on the Internal Flow Characteristics of Single- and Coaxial-Nozzle Ejectors for Hydrogen Recirculation in PEMFC. Applied Sciences, 15(17), 9845. https://doi.org/10.3390/app15179845






