Research on the Lightweight Design of Aviation Generator Rear Cover Utilizing Topology Optimization

Abstract

Topology optimization serves as a critical method for promoting lightweight structural design. Traditional methods predominantly focus on mechanical performance evaluation, often neglecting the critical correlation between modal characteristics and structural stiffness. The Evolutionary Structural Optimization (ESO) method is extensively employed in topology optimization; however, iterative oscillations lead to issues such as grid divergence and diminished solution quality. To address issues such as iterative oscillations and mesh divergence in the traditional Evolutionary Structural Optimization (ESO) method, this study applies a Simp Evolutionary Structural Optimization (SI-ESO) methodology. This method integrates intermediate density parameters and penalty factors into the progressive structural optimization process, thereby significantly enhancing iterative convergence and model quality. This work applied the optimized SI-ESO method to the lightweight redesign of an aviation generator’s rear cover, with validation conducted through additive manufacturing. Subsequently, the back cover of an aviation generator was redesigned and fabricated utilizing additive manufacturing technology. Empirical results indicate that under maximum stress conditions and employing the same additive process, the maximum deformation of the SI-ESO-optimized model is reduced compared to that of the ESO-designed model. Compared with the original design, the SI-ESO-optimized model achieved a 31% weight reduction, while relative to the ESO-optimized model, it exhibited a 27% lower maximum stress and a 10.53% higher first-order frequency, demonstrating both lightweighting and enhanced structural stiffness.

1. Introduction

The pursuit of lightweight design is a fundamental and perpetual objective in the aviation industry, driven by the direct correlation between reduced structural mass and enhanced operational performance. Significantly, lowering the weight of aircraft components leads to improved fuel efficiency and a substantial decrease in carbon emissions over the operational lifespan [1]. The implementation of lightweight design principles for aviation components not only enhances structural performance but also significantly improves aircraft fuel efficiency. China has proposed the “dual carbon” goals, which introduce new requirements and challenges for energy conservation and emission reduction within the aviation industry. Consequently, the lightweight design of aircraft components has emerged as a research hotspot in the aviation sector. The application of topology optimization to the lightweight design of components not only optimizes the material distribution of the structure and enhances performance but also reduces material costs and resource consumption, thereby achieving component lightweighting while fulfilling functional requirements. Therefore, components designed via topology optimization are progressively becoming an emerging trend in the design of aviation components. Topology optimization employs mathematical methods to determine the optimal structural design. By modifying the material distribution within a structure, it allows for a reduction in material usage while satisfying mechanical requirements, thus achieving the objective of lightweight design. In research concerning the optimization of components using topology optimization, Matsui et al. [2] proposed a multi-scale topological optimization method for the microstructure geometry and performance requirements in additive manufacturing. They utilized the fast Fourier transform as the basis for traditional finite element analysis in two-dimensional and three-dimensional optimization analyses to obtain a material distribution that matches the force-bearing structure. In the local optimization analysis of parts, to improve component stiffness and prevent structural deformation, Zhang et al. [3] applied topology optimization technology to the design process of variable-density lattice structures. Based on actual load conditions, they designed an optimal variable-density lattice structure to achieve superior performance. The optimal parameters for this design were determined through orthogonal experiments, resulting in enhanced lightweight characteristics for the rocker arm. Wang et al. [4] employed a topological optimization method based on subset simulation to refine the design of the leading-edge ribs for a specific type of aircraft wing. By integrating advanced sensitivity filtering techniques with subset simulation, they established a novel topological optimization approach that demonstrates convergence, eliminates chessboard patterns, and ensures grid independence, thereby enhancing the overall optimization quality. Munk et al. [5] elucidated and addressed the optimization problem using the Bidirectional Evolutionary Structural Optimization (BESO) method, a notable advancement over simpler evolutionary approaches. This approach significantly reduces maximum stress levels, leading to notable increases in fatigue life while potentially compensating for the inherent degradation in fatigue performance associated with additively manufactured metal structures. The aforementioned research indicates that adopting topology optimization and its refined methodologies has markedly improved component performance while reducing structural weight. This provides valuable reference points for further studies on topology optimization designs applicable to other aviation components. ESO is another topological optimization technique that systematically removes material from low-stress regions to promote a more uniform stress distribution and mitigate stress concentration issues. It is particularly well-suited for optimizing components characterized by continuous structures [6]. However, this classic method suffers from several inherent drawbacks. When the ESO method removes inefficient material, it can cause abrupt changes in the force transmission path. This may result in mesh distortion and iterative oscillations, leading to issues such as diminished optimization quality and grid divergence. In response to these limitations, various improvements have been proposed. For instance, Liu et al. [7] improved the sensitivity weight coefficient of the ESO method and proposed using the sensitivity weight of void elements to globally rank the sensitivity of all partitioned elements. By multiplying the sensitivity of void elements by this weight coefficient, the importance of these elements is reduced, thereby decreasing the degree of oscillation during the iterative process. Furthermore, an adaptive dynamic evolution rate (ER) was introduced to accelerate the convergence toward stable topological results. However, the problem of solution quality degradation caused by grid divergence during the iterative process remained unresolved. Topology optimization analysis is conducted using the discretized mesh elements as minimum units. Therefore, the quality of the mesh elements plays a critical role in the effectiveness of topology optimization. During the ESO process, binarization is applied to the grid cells, and inefficient material is deleted, which can readily lead to force-flow divergence during transmission. These regions of force-flow divergence generate structurally ambiguous areas, often termed “gray regions,” when material is assigned. These gray regions intensify model oscillation and degrade the quality of mesh elements, thereby compromising the topological optimization outcome. The challenge of this study lies in concurrently ensuring the quality of grid elements while mitigating their iterative divergence. To enhance the quality of topological optimization, it is necessary to re-evaluate the gray regions during the optimization process to reduce the dispersion of grid elements. To move beyond incremental fixes and address the root cause of these issues, a different paradigm is needed. By integrating the Solid Isotropic Material with Penalization (SIMP) method into the ESO framework [8], the issues of grid element divergence and iterative oscillation are addressed simultaneously, leading to an improvement in the quality of the grid elements.

Current research predominantly employs a single topological design approach for component optimization and omits a modal analysis process during optimization. Transitional topology optimization can lead to a decrease in stiffness, which in turn compromises performance. The ESO method achieves optimization of material distribution by progressively removing inefficient and ineffective elements. Its core advantages lie in algorithmic simplicity and high computational efficiency, making it relatively suitable for the optimal design of simple model structures. The disadvantages of ESO are that its unidirectional removal mechanism can easily lead to the erroneous deletion of material in critical load-bearing regions, and it possesses inherent defects such as the checkerboard pattern and mesh dependency. The BESO method introduces an element restoration mechanism to the ESO framework, enhancing global optimization capabilities through a bidirectional adjustment of the topology. Its improved algorithm significantly suppresses local optima problems through a two-step iterative strategy, but it has higher complexity and its convergence speed is constrained by the number of iterations, leading to iterative oscillation phenomena in components with complex structures, which affects the stability of the optimization results. By combining SIMP with SI-ESO, a penalty factor is introduced to transform material density into a design variable, and the variable-density method is employed to achieve topological optimization. A penalty exponent is utilized to apply a non-linear penalty to intermediate densities, thereby driving the mesh element densities to converge towards 0 or 1. This approach is suitable for the structural optimization of complex structures or in cases requiring high-precision solutions. Furthermore, the use of a sensitivity filtering method can effectively suppress gray-scale elements and improve the definition of the model boundary. The resulting optimized designs perform well in static mechanical analysis, yet paradoxically exhibit reduced stiffness, leading to suboptimal outcomes in terms of stiffness optimization. Specific issues include the following: First, existing topological optimization research is often limited to a singular design mode focused on mechanical performance, frequently neglecting the crucial role of modal analysis. Consequently, components designed in this manner may not achieve optimal stiffness. Second, for continuous structural parts such as the aviation generator’s rear cover, the commonly used ESO method presents practical limitations. These include insufficient model convergence during iteration, the mesh divergence trend caused by BESO’s direct removal of low-sensitivity areas in grid cells, and resulting poor mesh quality. Third, in the context of additive manufacturing, a significant gap exists in establishing suitable laser printing parameters for components like the aviation generator’s rear cover. While parameters are typically determined based on stress conditions, the lack of specific guidance for this component leads to suboptimal forming quality. In response to the aforementioned issues, this study enhances the topological optimization quality of the aviation generator’s rear cover from a design perspective and improves the additive manufacturing forming quality of the topologically optimized aviation generator’s rear cover from a manufacturing perspective. This has positive practical significance for the high-performance, lightweight design of aircraft components and for improving the fuel efficiency of aircraft. The main innovations and contributions of this study are as follows:

• This study presents a practical design workflow that integrates topology optimization with modal analysis for a real-world aerospace component. By incorporating modal frequency as a design constraint, this approach simultaneously enhances component stiffness and achieves significant weight reduction. The influence of the penalty factor value on the effectiveness of model optimization was investigated to determine the appropriate value for the present model.
• An improved SI-ESO method is developed to overcome the limitations of traditional ESO, such as mesh divergence and poor convergence. This method effectively reduces mesh oscillation and improves model quality, enabling weight reduction while preserving original mechanical properties. The optimization method combining SIMP and ESO yields a more uniform material distribution in the model during the forming simulation. Its relatively continuous topological configuration facilitates the simulation of actual processing conditions in manufacturing simulations, thereby avoiding the generation of sharp or rough structures that are unprintable.
• Optimal laser parameters for the additive manufacturing of the aviation generator’s rear cover were determined through systematic comparative experiments. This research establishes a clear process–parameter–quality relationship, significantly improving the forming quality of the final component.
• To more intuitively illustrate the technical rationale and overall process adopted in this study to address the aforementioned problems, we constructed the general technical roadmap as shown in Figure 1. Topological optimization combined with modal analysis was used to determine the stress and resonance thresholds of the aviation generator’s rear cover, and the optimization region was then defined according to its service functions. Comparative tests on mesh element sizes were conducted to determine a suitable optimization threshold. After the topological optimization design, the weight of the component was reduced and the maximum stress it sustained decreased under the original load conditions. The surface of the topologically optimized aviation generator’s rear cover was rough, and it underwent a smoothing treatment before laser additive manufacturing. Prior to manufacturing, simulation analysis was performed using Simufact Additive process software (Version 1.0; Simufact Engineering GmbH, Hamburg, Germany) to investigate the effects of different support strategies, laser power, and laser spot size on the maximum deformation of the model. The processing parameters were thereby determined, and the physical fabrication of the aviation generator’s rear cover using additive manufacturing was subsequently completed.

2. Structural and Modal Analysis

2.1. Load Conditions

The rear cover shell of the aviation generator is positioned on the generator’s exterior surface, with dimensional specifications of 162 mm in length, 136 mm in width, and 85 mm in height. Fabricated from aluminum alloy material, the structural component weighs 450 g and is subjected to a self-weight load (F) of 4.5 Newtons applied at a fixed hole constraint; this force vector is oriented perpendicularly at a 90° angle relative to the shell’s horizontal plane. The generator’s bearing assembly interfaces with the housing through a slip ring end bearing configuration [9,10]. The shaft and slip ring are smoothly integrated for rotation without impacting the rear cover of the generator. Its loading conditions are illustrated in Figure 2.

2.2. Mechanical Analysis

Mechanical analysis was performed on the original aero-generator rear cover model to evaluate its structural behavior under load conditions. This investigation provides crucial insights into stress distribution patterns across the rear cover during load application, establishing essential baseline data for subsequent topology optimization processes. The analysis procedure involves several critical steps: configuring the mechanical analysis module within Ansys software(Version 2022; ANSYS, Inc., Pittsburgh, PA, USA), importing the aero generator’s rear cover model, applying relevant load conditions, and specifying the appropriate stress analysis type for accurate mechanical evaluation [11].

Under self-gravity loading, the analysis revealed that the maximum stress on the generator’s rear cover reached approximately 0.635 MPa. Stress concentrations at constraint locations remained minimal. Potential areas for material removal from the generator’s rear cover are predominantly located at the interface between the upper and lower sections, where stress values consistently remain low [12,13]. Furthermore, these results indicate that regions of non-stressed volume in the rear cover model are substantial and present opportunities for material reduction. Therefore, structural optimization analyses should be performed on these specific sections of the model.

2.3. Modal Analysis

Modal analysis is a fundamental computational mechanics methodology for characterizing the inherent vibrational properties of structural systems. This approach determines critical vibration parameters, including the first-order natural frequency, modal shapes, and associated dynamic characteristics under operational loading conditions [14]. The principle of resonance dictates that when the frequency of external excitation approaches a structure’s natural frequency, the vibrational response amplifies significantly, reaching its maximum at the resonant frequency threshold. According to fundamental vibration theory, a direct proportionality exists between a structure’s modal frequency and its stiffness characteristics. This investigation integrates mechanical analysis with modal analysis to establish critical design references, ensuring that component stiffness in topologically optimized structures is not compromised. Modal analysis results are systematically incorporated into the topology optimization process, achieving the dual objectives of weight reduction and structural stiffness preservation.

The rear cover of an aircraft generator is a critical component for overall generator functionality, primarily securing and supporting the rotor and terminals to ensure stable rotor operation and protect internal rotor and winding connections. During operation, the rear cover experiences vibrations induced by generator excitation. When vibration frequencies of both the generator and its rear cover are closely aligned, resonance may occur, potentially leading to accelerated wear, deformation, or even failure of components within both the rear cover and generator. This phenomenon can substantially compromise structural integrity and operational longevity. Additionally, the considerable mass of aviation generator rear cover assemblies imposes extra operational burdens. Optimized lightweight designs can effectively reduce these operational loads, enhancing system reliability and extending service life [15,16,17,18].

This phenomenon can substantially compromise the structural integrity and operational longevity of the components. Furthermore, it is crucial to recognize that the rear cover assembly of aviation generators typically exhibits considerable mass, which imposes additional operational burdens on the generator system. The implementation of optimized lightweight designs can effectively reduce these operational loads, thereby enhancing system reliability and extending service life [19]. To address potential resonance phenomena between these critical components, a comprehensive analysis of their natural frequency characteristics must be conducted, complemented by empirical vibration frequency data collected from various generator configurations. For example, in small twin-engine aviation generator systems coupled with specific rear cover designs, the observed vibration frequency spectrum typically ranges from 50 Hz to 133 Hz. The modal analysis methodology will be developed based on fundamental stress analysis principles, employing tetrahedral mesh generation for accurate modeling while implementing appropriate boundary conditions to determine third-order modal frequency characteristics. Of particular significance is the first-order modal frequency [20], which exerts a more substantial influence on potential resonance occurrences and will therefore receive prioritized attention during the analytical process. Following the completion of mechanical evaluations on our computational model, which will be imported into Ansys’ modal analysis module, we established appropriate boundary conditions prior to executing modal analyses and subsequently exporting the solution data. The systematic workflow for conducting modal analysis is graphically represented in Figure 3.

The first three frequencies of the modal analysis based on ESO are shown in

Table 1. Modal frequency.

Modal	Frequencies (Hz)
First order	2221
Second order	3130
Third order	3353

below.

The first-order natural frequency of the rear cover model of the aviation generator is 2221 Hz. Its relatively high natural frequency provides a large space for topological optimization. When optimizing, the influence of the topological structure on the stiffness of the components should be fully considered [21].

3. Topology Optimization of the Aviation Generator Rear Cover

3.1. ESO Topology Optimization Algorithm

Following the execution of mechanical and modal analyses, the resultant data forms the basis for topological optimization, which is implemented through the ESO methodology. The ESO algorithm employs finite element mesh analysis to assess the stress distribution within the model, thereby determining the elimination of specific elements based on their stress states. In the context of finite element analysis, mesh elements function as both computational entities and stress transfer mechanisms. These elements discretize the model into a finite number of components, thereby defining the computational domain for topological optimization [22]. Consequently, the quality of these mesh elements exerts a substantial influence on the efficacy of topological optimization processes. The iterative procedure persists until the volume response criteria are satisfied. The optimization objective is consistently defined as compliance minimization (equivalent to stiffness maximization), and structural lightweighting is realized under the imposed volume constraint. Compliance is the inverse measure of stiffness, and minimizing compliance means increasing the rigidity of the structure, thereby making it more resistant to deformation. The formulation is given as follows [23]:

$$C_x=U^{T}KU=\sum _{k=0}^n{K}_e{u}_e{u}_e^T$$

(1)

In the formula, $C_x$ represents the compliance of the structure, $U$ represents the magnitude of displacement, $K$ represents the stiffness matrix, and $u_e$ and $K_e$ are the displacement vector and stiffness matrix of the e-th element, respectively. The weight reduction objective of the structure is taken as the function index, and the structure volume is used as the constraint condition [24].

The volume constraints of the progressive structure optimization method are as follows:

$$V=\sum _{e=1}^n{v}_e\le V_{target}$$

(2)

Among them, $v_e$ is the volume of unit $e$, and $V_{target}$ is the target volume.

Progressive structural optimization is carried out by deleting the cell regions with low stress or low strain capacity. The calculation formula for the grid threshold of the deleted cells is as follows:

$${\alpha }_e={\displaystyle \frac{{\sum }_{k=0}^n{K}_e{u}_e{u}_e^T}{C}}$$

(3)

In this formula, ${\alpha }_e$ is the optimized proportion of the total stiffness of the cell. When the value of ${\alpha }_e$ is less than a certain threshold, the grid cells are deleted. In terms of the sensitivity of the execution of deleting grid cells, the absolute value of the sensitivity is determined by the following formula [25].

$${\displaystyle \frac{\partial C}{\partial x_e}}=-K_e{u}_e{u}_e^T$$

(4)

The determination of inefficient cells in the ESO algorithm depends on the sensitivity of the objective function to the density of this cell. In this formula, $x_e$ represents the density sensitivity threshold, which ranges from 0 to 1. Grid cells with values lower than this are deleted. The optimization process of the progressive structural optimization method is as follows. After defining the optimized design area, set $V_{target}$ and the number $\beta$ of grid elements deleted in each iteration process, solve the displacement balance equation $KU=F$, obtain the displacement and stress-strain of the iteration process, and analyze the sensitivity value of the grid elements according to the magnitude of the stress-strain. Arrange the grid retention cells in order of ${\alpha }_e$, and delete the first n cells according to the sensitivity threshold so that the total product after deletion satisfies ${\sum }_{i=1}^n{v}_i\le V_c$. In the formula, $V_c$ is the target response after deleting the redundant units [26]. After this operation is completed, one round of iteration is completed. After the iteration is completed, check the convergence of the structure. If the volume of $V_c$ is less than $V_{target}$, terminate the iteration and output the topological optimization result.

3.2. Improve the ESO Topology Optimization Algorithm

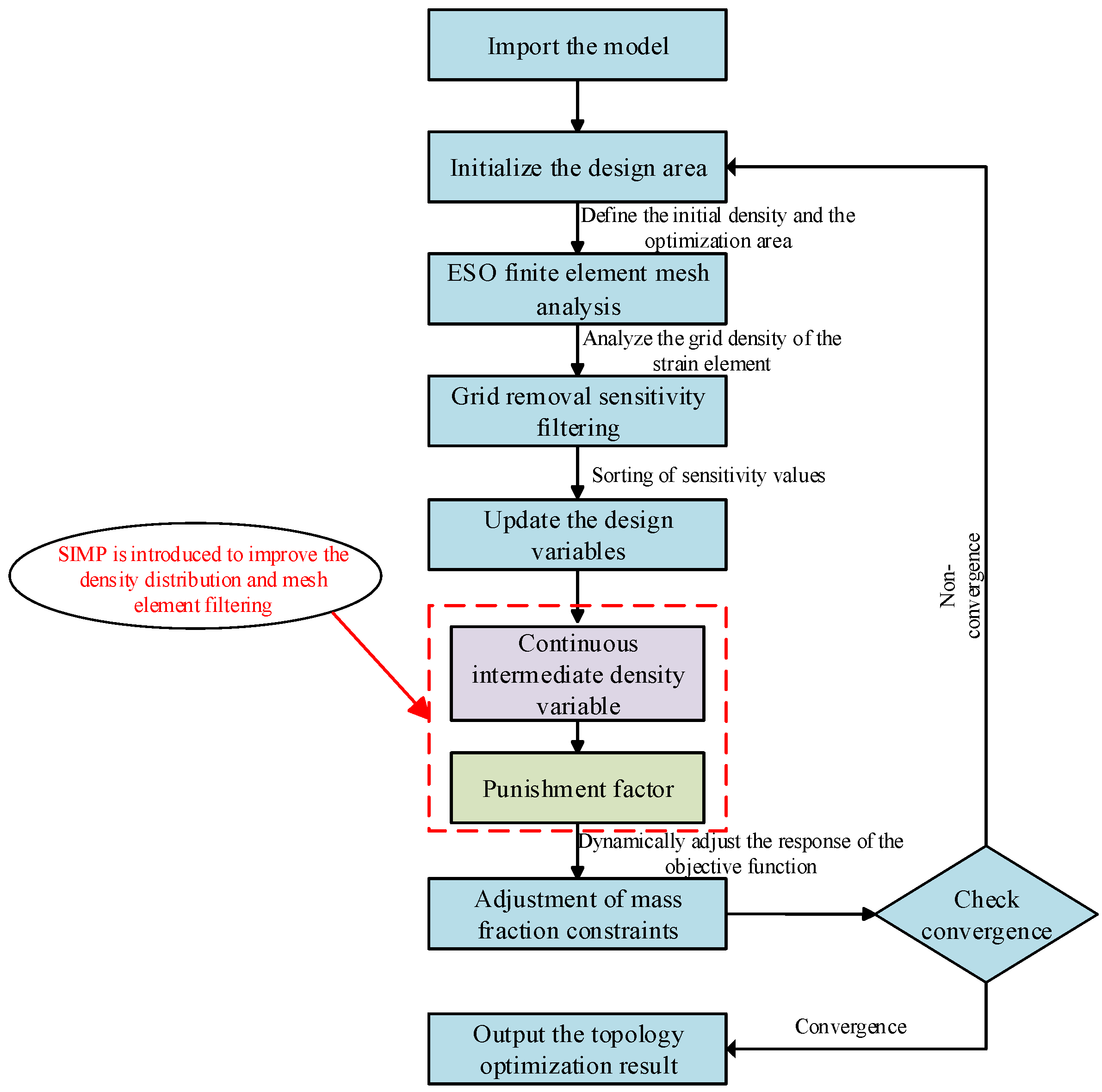
Since the ESO method directly removes inefficient mesh elements, this operation tends to increase structural divergence and degrade element quality. The SIMP (Solid Isotropic Material with Penalization) method introduces continuous intermediate density variables and penalty factors [27] during the ESO process. Integrated with ESO’s finite element analysis, it performs sensitivity analysis and filtering for mesh element removal. The filtered objective function is sorted in descending order of sensitivity to update the design variables. Mesh elements with sensitivity below the threshold are eliminated, and the mass fraction is adjusted according to target constraints. Once the mass fraction satisfies the response constraint, convergence is verified. The optimization process of the enhanced SI-ESO is illustrated in Figure 4 below.

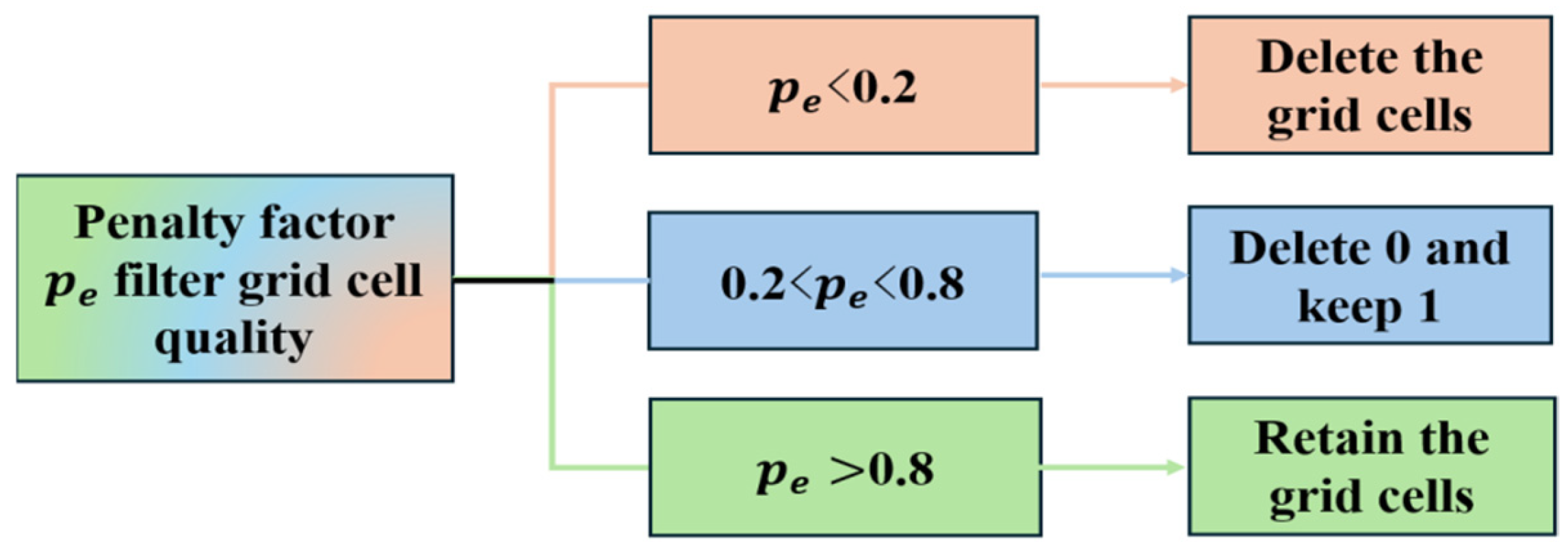
The introduction of SIMP in the SI-ESO algorithm improves the convergence of the progressive structure optimization method in the process of discrete model mesh cells. SIMP consists of an intermediate density interpolation model and a penalty factor. The ESO method categorizes the grid cells of the model into two groups: those assigned a value of 0 and those assigned a value of 1 [28]. All grid cells designated as 0 are eliminated, while all grid cells classified as 1 through discrete evaluations are preserved. However, certain meshes exhibiting intermediate densities and relatively low sensitivity values still play a crucial role in maintaining structural integrity and must be retained. The removal of these meshes could result in divergence within the model’s mesh structure. Grid cell densities that fall between 0 and 1 represent intermediate densities, commonly referred to as fuzzy regions. These intermediate densities encompass both the grid density cells that should be deleted and those that need to be retained. The SIMP approach introduces the concept of intermediate density and applies penalty factors to re-evaluate the grid cells initially judged as 0 in ESO. The functionality of the intermediate density unit is illustrated in Figure 5.

Mesh elements designated as 0 in the ESO process are re-evaluated using a penalty factor, which mitigates the sensitivity of the filtering mechanism. Within the SIMP penalty factor model, specific mesh elements possessing intermediate density values are subjected to penalization. This approach discretizes the design domain into a finite number of mesh elements, thereby accelerating the convergence of element densities towards either 0 or 1. Each mesh element is normalized by the parameter $p_e$, yielding a continuous value ranging from 0 (denoting removable elements) to 1 (indicating elements that must be preserved). The computational formulation for the penalty factor within the SIMP framework is presented as follows.

$${\displaystyle \frac{\partial C}{\partial p_e}}={-p\rho }_e^{p-1}{K}_e{u}_e{u}_e^T$$

(5)

When the penalty factor $p_e$ approaches 0, $\frac{\partial C}{\partial p_e}$ − $p·0^{p-1}$ approaches 0, and the influence of cells with intermediate density on the objective function also tends to 0. At this time, SI-ESO improves the efficiency of removing grid cells with lower intermediate density ($p_e<0.2)$. When $p_e$ approaches 1, It indicates that the quality of the grid cells is relatively high and can be directly retained. When ${0.2<p}_e<0.8$, the grid cells within this range gradually converge to 0 or 1. In simple terms, the penalty factor serves to reclassify the intermediate density regions identified in the ESO algorithm as non-zero or non-one into three categories of grid density cells: high, medium, and low. Subsequently, through a process of gradual convergence, the medium- and high-density grid cells are assigned a value of 1, while the low-efficiency grid cells are designated as 0. This approach enhances the efficiency of processing intermediate density grid cells [29]. The impact of the penalty factor $p_e$ is illustrated in Figure 6.

In contrast to the direct elimination of inefficient elements in ESO, the penalty factor mechanism preserves mesh elements exhibiting stress effects by facilitating the removal of inefficient intermediate density elements. This approach drives the density of mesh elements towards either 0 or 1, thereby enhancing the quality of elements within the evolutionary topology optimization framework. Subsequently, the convergence of optimization results is verified, and the convergence formulation is presented as follows.

$${\displaystyle \frac{C_k-C_{k-1}}{C_k}}<\epsilon$$

(6)

When the convergence rate falls below the threshold ε, which represents the rate of change in the objective function, it indicates the convergence of the topological structure, thereby facilitating the generation of the topologically optimized configuration. The enhanced SI-ESO algorithm exhibits substantial improvements in both mesh convergence and element quality. Through the execution of 100 iterations of model optimization experiments, a comprehensive analysis was conducted on the mesh divergence and quality throughout the iterative process of the SI-ESO algorithm [30].

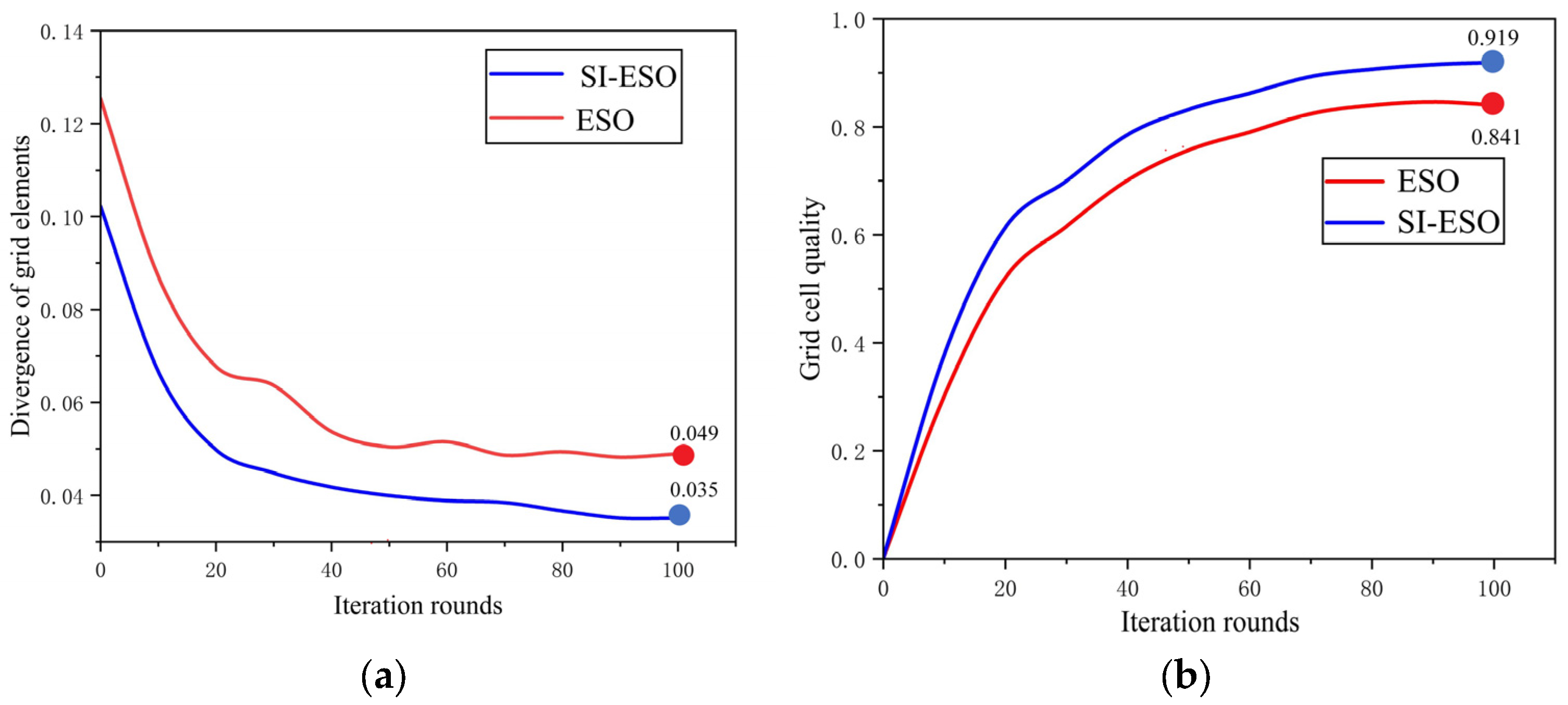
Figure 7a presents a comparison of mesh divergence between the SI-ESO and ESO methods after 100 iterations. The results, along with the characteristics of SIMP, indicate that the penalty factor filtering in SI-ESO effectively eliminates meshes associated with intermediate density elements. This process encourages the element densities to converge towards a binary distribution—either 0 or 1—thereby minimizing the fuzzy density regions typically produced by intermediate densities. In contrast, such regions are retained in the ESO algorithm, which contributes to increased divergence among mesh elements in that method. Consequently, SI-ESO mitigates this divergent behavior during its iterative modeling process by eliminating the need to compute mesh cells within blurred areas, resulting in enhanced convergence speed and improved computational efficiency compared to ESO [31]. Additionally, SI-ESO reduces iterative oscillations and mesh dispersion caused by direct material removal, leading to a more stable iteration process.

Figure 7b presents a comparative analysis of cell quality between SI-ESO after 100 iterations. The grid cell quality attained through SI-ESO demonstrates significant superiority over that achieved via ESO. The penalty factor implemented in SI-ESO facilitates a binarized density distribution for grid cells while effectively reducing fuzzy regions; these areas would otherwise be occupied by low-quality sawtooth cells during material distribution computations. Moreover, the sensitivity filtering mechanism integrated into the SI-ESO algorithm mitigates shape distortion and reduces sharp edge meshes caused by abrupt cell deletions [32], which are characteristic of ESO. These enhancements result in smoother and more distinct structural transitions within material distributions. Consequently, it is evident that SI-ESO consistently produces higher-quality mesh cells compared to its counterpart.

The introduction of the penalty factor aims to drive the determination result of the grid cell density closer to either 0 or 1, thereby enhancing the clarity of the optimization outcome. When performing optimization analysis under identical conditions, a larger penalty factor $\mathsf{\rho }$ results in fewer intermediate density elements during topological optimization. Consequently, more elements approach 0 or 1, leading to a superior optimization effect. For structures intended for additive manufacturing, the $\mathsf{\rho }$ value should be set to no less than 3. This is because when $\mathsf{\rho }<3$, excessive intermediate density regions fail to accurately represent the mechanical transfer path, complicating the manufacturing and processing of the optimized structure. A grid generation experiment was conducted to compare the impact of different penalty factors on the model’s display effect, with the results illustrated in Figure 8 below.

It can be seen from the results in Figure 8 that the division effect of the grid cells with $\mathsf{\rho }$ = 3 is smoother and more refined than that with $\mathsf{\rho }=4$, and the quality of the grid cells is higher. When $\mathsf{\rho }=4$, the grid undergoes sharp mutations, resulting in a sharp serrated structure. The cause of this phenomenon is the sensitivity failure caused by excessive punishment. The calculated sensitivity value has an excessive error compared with the change in structural flexibility after the deletion of the element, resulting in the failure of the checkerboard element suppression. The rapid disappearance of the intermediate density elements causes changes in the material distribution of the mesh elements, generating serrated mesh elements at the transition parts and edges of the model structure. The iterative process of $\mathsf{\rho }=3$ gradually converges to 0 or 1, avoiding the rapid deletion of intermediate density elements. The division of grid elements is smoother, reducing jagged edge grids. The performance in controlling the smoothness of intermediate density elements and grid elements is more balanced. Therefore, from the application experience and actual effect, when the penalty factor $\mathsf{\rho }$ is taken as 3, the effect on the division of grid elements is better [33].

As the $\mathsf{\rho }$ value increases, the optimization results tend to increase towards the element density of 0 or 1. When $\mathsf{\rho }$ is taken as 4, due to the intermediate density element approaching 0 or 1 too quickly, the penalty sensitivity is slightly higher, causing a change in the global stiffness matrix and resulting in a decrease in the element density. The decrease in the element density will affect the model stiffness and lead to a decrease in the model stiffness [34]. When $\mathsf{\rho }$ is taken as 5, the model shows a relatively obvious structural dispersion phenomenon due to the overly steep penalty sensitivity, which makes it difficult for some structures to converge. The modal frequencies corresponding to different $\mathsf{\rho }$ values are shown in

Table 2. Effects of different penalty factors on modal frequency.

Penalty Factor	Modal Frequency (Hz)
$\rho$ = 3	2516
$\rho$ = 4	2115
$\rho$ = 5	1821

.

When the value of $\mathsf{\rho }$ is 3, the density of the intermediate element and the modal frequency are significantly greater than those of the elements when $\mathsf{\rho }$ is 4 and 5. The higher the modal frequency, the higher the stiffness of the model. Therefore, in the optimization of the rear cover of the aviation generator, it is more appropriate to set the penalty factor to 3.

3.3. Quality Response Analysis

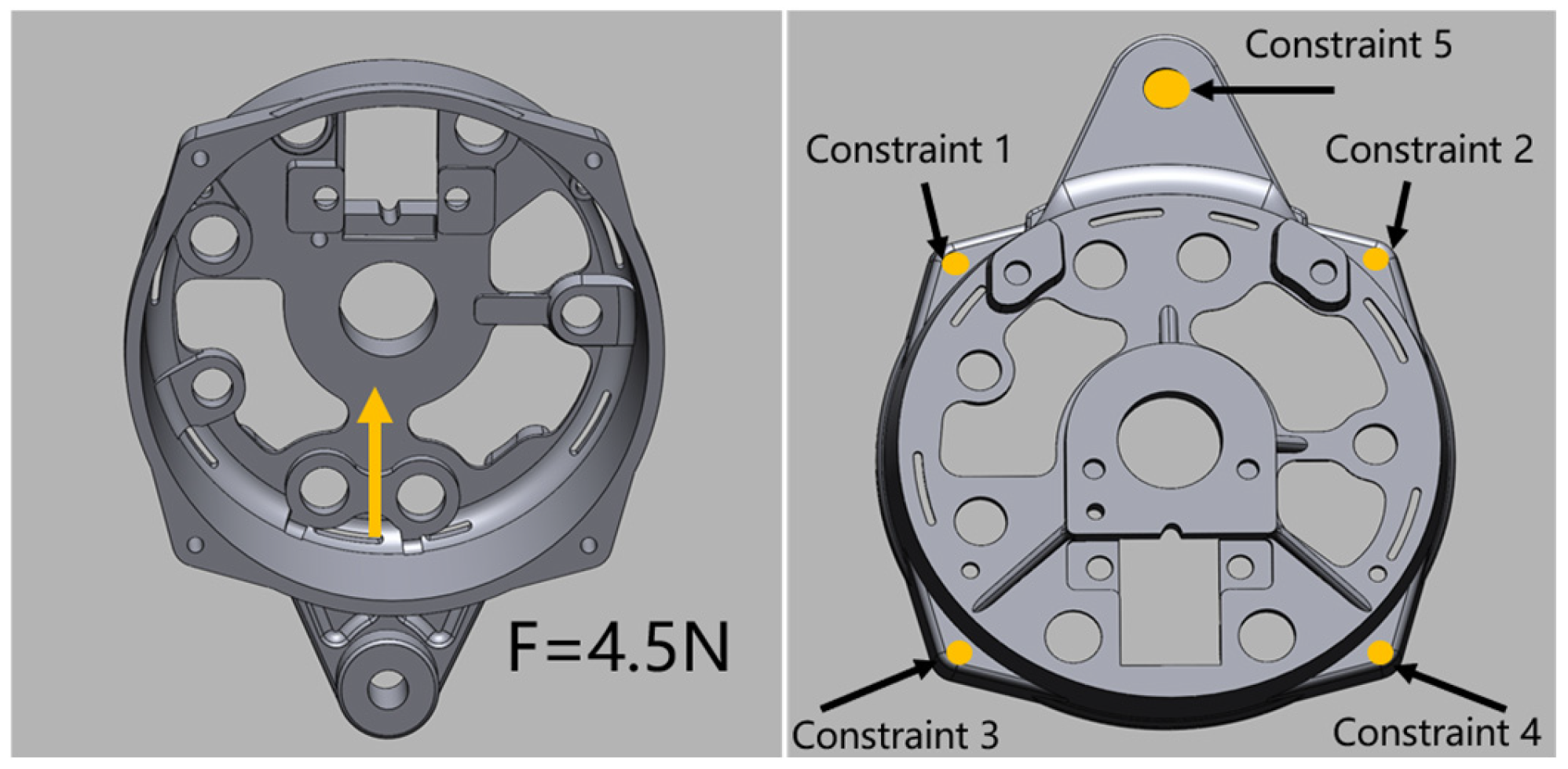
The rear cover of the aviation generator sustains its own weight during operational conditions. The combined effects of the fixing forces at the five bolt holes and the external vibrational excitation generated by the system collectively represent the actual working conditions. The primary objective of topology optimization is weight reduction. Consequently, topology optimization is systematically performed by sequentially reducing the mass fraction by 10% increments within the constraints of available computational resources. Through comparative analysis of the topological optimization outcomes obtained under various mass fraction constraints, the results are illustrated in Figure 9.

From the perspective of topological optimization results, when the mass fraction is maintained at 90%, the base part and the triangular hole region of the generator rear cover exhibit minimal optimization. The optimization outcomes are conservative, with negligible weight reduction effects. When the mass fraction is reduced to 80%, a moderate weight reduction is observed in the base and triangular hole regions. However, the discontinuous structure in the base part may induce stress concentration, adversely affecting subsequent reconstruction models and additive manufacturing processes. Based on the mechanical analysis presented earlier, the base part experiences minimal stress, yet the material removal during optimization remains insufficient, indicating further optimization potential. At a mass fraction of 70%, the boundaries of the four bolt holes in the base are clearly defined after topological optimization, resulting in a structurally complete and stable configuration that facilitates subsequent reconstruction. Therefore, the topological optimization model of the aviation generator rear cover under the constraint of retaining 70% of the mass response was selected as the subsequent research object.

After the topological optimization is completed, the surface of the model is very rough. The rough surface cannot establish mesh elements for stress analysis and needs to be smoothed before stress analysis can be carried out [35]. The mesh is redivided by using methods such as patching and surface fitting. The mesh division for redrawing is set to 0.3 mm, which can achieve the best smoothing effect for the rear cover model. The flattened model retains the structural features of the model after topological optimization while having a smoother surface. The reconstructed model is shown in Figure 10.

3.4. Comparison of Stress and Natural Frequency Optimized by ESO and SI-ESO

To validate the superior mechanical integrity of the SI-ESO-optimized rear cover model, a comparative performance analysis was conducted. The model was assessed under operational conditions, which included its gravitational load and fixed constraints at the five circular holes, while being subjected to external excitation frequencies ranging from 50 to 133 Hz. The analysis confirmed that the SI-ESO-optimized model satisfies all performance requirements, demonstrating its enhanced suitability for normal operational conditions compared to baseline methods.

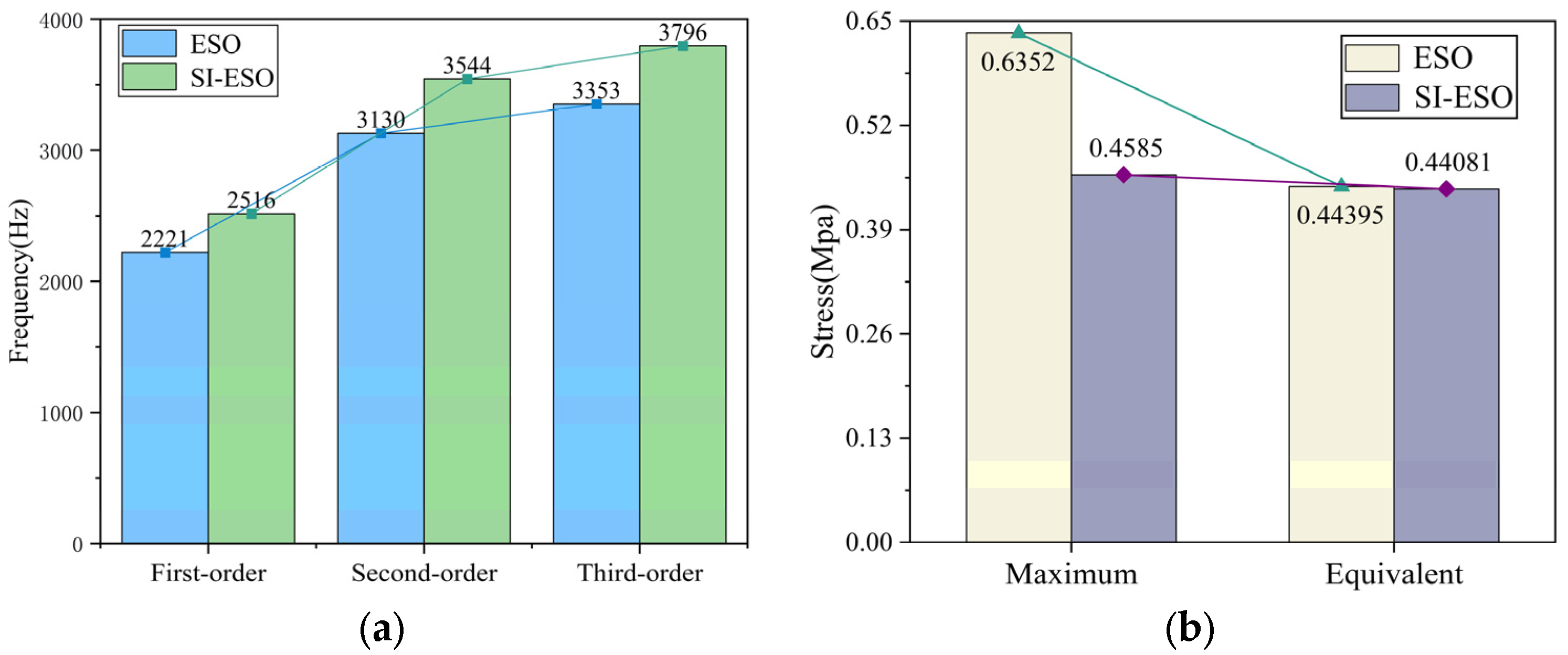
A comparative stress analysis was conducted to evaluate the performance of the SI-ESO-optimized model against the ESO-optimized model. The results demonstrated a significant performance enhancement with the proposed SI-ESO method. Under gravitational load, the maximum stress in the SI-ESO model was approximately 0.460 MPa. This value represents a 27% reduction (0.175 MPa) relative to the stress exhibited by the ESO-optimized model under identical conditions. Moreover, the equivalent stress was measured at 0.440 MPa, also indicating a marginal decrease. These comparative findings, presented in Figure 11, confirm the structural improvements achieved by the SI-ESO algorithm over the conventional ESO approach.

Figure 11 demonstrates that the optimization and reconstruction process resulted in material removal, consequently reducing the equivalent stress value. The maximum stress concentration was identified at the reinforcing ribs’ locations, which improved stress distribution and increased the natural frequency. The SI-ESO algorithm’s optimization of intermediate density variables enabled smoother material transitions and alleviated stress concentrations caused by abrupt geometric features. Furthermore, the penalty factor effectively moderated penalty intensity in high-stress regions, permitting enhanced material retention for more uniform stress distribution and achieving a balanced dynamic load across the model.

The uniformly distributed dynamic load reduces local stress interference on modal frequency while simultaneously enhancing natural frequency and reducing maximum stress values. Significantly, the equivalent stress value of the optimized rear cover model maintained stability, successfully achieving lightweight design objectives without compromising mechanical integrity, thus meeting the lightweight requirements for the aero generator’s rear cover model [36]. Modal verification experiments were conducted on the first three vibration frequencies, with detailed results presented in

Table 3. Mode frequency.

Modal	Modal 1 (ESO) Hz	Modal 2 (SI-ESO) Hz	Experimental Modal Hz	Error%
First order	2221	2516	2455	2.42
Second order	3130	3544	3413	3.69
Third order	3353	3796	3621	4.61

.

Given that the modal frequency is directly proportional to the stiffness of structural components, an increase in structural stiffness consequently leads to a corresponding elevation in modal frequency. The first-order modal frequency exerts the most significant influence on stiffness, which is predominantly determined by material distribution. The SI-ESO method facilitates the binarization of density distribution in grid cells, reduces the transitional density regions, clarifies the stress distribution pattern, and enhances structural stiffness. The introduction of continuous intermediate density variables in SI-ESO optimizes material distribution. In simulation mode, the first-order natural frequency threshold demonstrated a 13% increase, while experimental results showed a 10.53% enhancement, surpassing the modal frequency obtained through ESO analysis. The maximum third-order error of the SI-ESO optimization method remains within 5%, primarily attributable to manufacturing precision and modal truncation errors. All third-order errors fall within acceptable tolerance ranges. Free vibration mode experiments confirm that the finite element model exhibits high accuracy in modal analysis, effectively expanding the resonance frequency range and significantly improving the stiffness of designed components.

Comparative experiments were established to evaluate the improvements of the SI-ESO method over other optimization approaches. The data in

Table 4. Comparison of different optimization methods.

Method	Modal (Hz)	Stress (Mpa)
BESO	1961	0.723
MMA	2115	0.579
SI-ESO	2516	0.458

indicate that the first-order modal frequencies for both the BESO and MMA methods are lower than that of the SI-ESO method. During optimization, the BESO and MMA methods indirectly influence the modal frequencies by adjusting the overall mass and stiffness distribution. In contrast, the SI-ESO method refines the mesh optimization elements, creating a smoother material transition between them. This allows for a better adjustment of local material distribution to optimize the stiffness and mass distribution of the structure, thereby enhancing the modal frequency. Simultaneously, it enables a more uniform material mass distribution in the designed model and reduces sawtooth-like sharp features, which leads to a decrease in the model’s stress values.

4. Additive Manufacturing and Performance Comparison Experiments of the Optimized Model

4.1. Simulation of Additive Manufacturing Process

Initially, both the rear cover model of the aero generator and the base plate underwent meshing procedures. The selected mesh configuration for these components employs tetrahedral elements, which are particularly suited for handling the complex structural characteristics of the model while ensuring effective coverage of edge regions. This discretized grid serves as the fundamental framework for all subsequent process simulations, including support structure generation, thermal stress transfer analysis, and deformation calculations. The grid parameters are specifically configured with a 1 mm element size for the aviation generator’s rear cover model, complemented by a single-layer powder height of 0.03 mm. Upon completion of the grid division, process parameters are established within the Database section of the Manufacturing TAB. Coupled with printing parameters from additive manufacturing equipment,

Table 5. Simulation parameters.

Layer Thickness	Laser Efficiency	Scanning Width	Materials	Scanning Rate
0.03 mm	0.5	50 mm	AlSi10 Mg	0.1 m/s

below presents the process simulation parameters specific to the aviation generator’s rear cover.

Following the parameter configuration, the influence of laser power on the overall deformation of the model was investigated. Based on the forming simulation results, a laser power of 150 W yielded the minimum model deformation. The maximum overall deformation of the aero-generator rear cover was 0.54 mm, with a deformation of 0.33 mm in the z-direction. The results of the Selective Laser Melting (SLM) process simulation are presented in Figure 12.

Laser power is crucial to forming quality, as it directly influences melting characteristics, thermal stress, and residual stress during material formation. The laser energy source causes the metal to melt layer by layer, followed by rapid cooling and solidification. Throughout this process, varying cooling rates across different regions can lead to significant residual stresses being generated. These residual stresses are released through alterations in material distribution, which may result in deformation of components as they cool [37]. The impact of laser power wattage on forming quality is illustrated in

Table 6. The influence of laser power on deformation.

Laser power (W)	100	150	200
Maximum deformation (mm)	0.82	0.54	1.1
Z-direction deformation (mm)	0.55	0.33	0.72

below.

When the laser power was set at 100 W, the insufficient energy resulted in the metal material failing to reach the appropriate spraying temperature, which caused a gradual increase in model deformation up to 0.82 mm. In conditions of inadequate laser power, the energy per unit area is unable to completely melt the powder supplied by the feeding system. This leads to incomplete melting of the powder, making it challenging to establish a robust metal bonding zone and consequently diminishing the quality of the cladding layer. These incompletely melted powders may undergo deformation during subsequent stacking processes due to weak interlayer bonding. Additionally, insufficient laser power can result in either a thin cladding layer or an unevenly formed cladding layer. The inconsistency in bonding strength across layers during later accumulation processes increases susceptibility to stress concentration, causing components to deform under force imbalances. Residual stress also contributes significantly to increased deformation; when heat input is inadequate, material cooling rates accelerate. This will lead to an increase in residual stress, as the material cannot fully release the internal stress during the rapid cooling process, causing deformation of the components [38].

At a laser power setting of 200 W, an enhanced amount of heat is introduced into the material, subsequently reducing its solidification rate after melting occurs. Consequently, molten material does not solidify rapidly upon cessation of laser activity, leading to thermal stress and component deformation. The elevated power level shortens melting times; therefore, residual stresses induced by rapid heating and cooling are exacerbated as well, resulting in total displacement deformations reaching up to 1.1 mm and specifically 0.72 mm along the Z-direction. Given that this power level is relatively high for achieving optimal quality in aviation generator rear covers, it becomes apparent that lower heat input would be more advantageous for this application. In contrast, utilizing a laser power setting of 150 W appears more suitable regarding effective heat input management.

The spot size of the laser light source significantly influences forming quality as well. By affecting energy density distribution within the laser beam, spot size alters both heat range and temperature uniformity at melting points. A larger spot diameter results in a greater temperature differential between its center and edges, thereby creating a pronounced temperature gradient. Therefore, it is essential to determine an optimal laser spot size through simulation studies [39]. Commonly utilized spot sizes range from 50 μm to 200 μm; spots exceeding 150 μm are classified as large-sized spots. In our study, four groups with varying diameters—namely 50 μm, 100 μm, 150 μm, and 200 μm—were established for simulation under conditions where laser power was maintained at 150 W. The findings are summarized in

Table 7. The influence of laser spot on deformation.

Laser power (W)	150	150	150	150
Spot diameter (μm)	50	100	150	200
Maximum deformation (mm)	0.84	0.77	0.91	1.08

below; it can be observed that among these parameters (specifically for configuration denoted as “150 w + 100 μm”), there exists minimal deformation during component formation.

It can be observed from the results presented in Table 6 that a smaller spot size (50 μm) significantly increases the energy density of the melting zone. The laser power density is inversely proportional to the spot size. A smaller spot size leads to rapid heat accumulation, resulting in a swift rise in temperature within the melting zone and creating a steep temperature gradient. During the subsequent rapid cooling process following laser removal, differences in cooling shrinkage of the molten metal intensify, leading to higher residual stress and increased deformation.

The 100 μm spot size achieves an optimal balance between energy density and heat input [40]. The resulting melting area exhibits a more favorable width-to-depth ratio, with reduced anisotropic shrinkage during solidification. The uniform distribution of laser energy contributes to a more balanced residual stress distribution. This configuration not only ensures complete melting while avoiding unfused defects but also allows for better control over the extent of the heat-affected zone, thereby reducing both temperature gradients and thermal stress-induced deformation [41]; this has been evidenced by achieving a maximum deformation of 0.77 mm across several comparative datasets.

In contrast, larger spot sizes (>150 μm) result in wide dispersion of laser energy, which leads to insufficient heat density at the edges of the molten area. Consequently, it becomes necessary to extend laser irradiation time to provide adequate heating; however, sufficient heat is already present at the center of such spots. Prolonged exposure may cause excessive temperatures in this central region, extending its duration at elevated temperatures. Heat transfer occurs slowly towards the edge areas of these larger spots, causing uneven thermal expansion and phase transformation effects. Ultimately, this generates greater contraction stresses that contribute to increased deformation levels. The simulation results illustrating these forming effects are depicted in Figure 13.

The laser power at 100 W and 200 W was studied in combination with the spot size parameter and compared with 150 W. The results are shown in Figure 14 below.

The experimental data illustrated in Figure 14 demonstrate that the impact of laser spot size on maximum deformation is more pronounced under power conditions of 100 W and 200 W compared to all spot sizes at 150 W. Specifically, at 100 W power level, the enlargement of spot size fails to deliver adequate energy for complete powder melting, leading to defect formation including porosity and aggravated localized deformation. In contrast, at 200 W power level, the expansion of spot size for energy distribution results in an excessively deep or wide molten pool, which amplifies heat diffusion into the substrate, consequently extending the heat-affected zone and augmenting overall deformation. Through comprehensive simulation experiments, the optimal process parameter combination has been identified as 150 W power with a 100 μm spot size. Based on these findings, we have adopted this specific laser parameter configuration—150 W power and 100 μm spot size—for the fabrication of the physical component corresponding to the aviation generator rear cover [42].

4.2. Effects of Additive Manufacturing on the Component

The aviation generator rear cover, designed using the SI-ESO topology optimization methodology, was fabricated via laser additive manufacturing with a BLT A300 printer from Xi’an Bright Laser Technologies Co., Ltd. (Xi’an, Shaanxi, China; website: https://www.xa-blt.com/en/, accessed on 5 September 2025). Initially, the digital model was imported and processed using the proprietary slicing software integrated with the BLT A300 printer. This software then automatically generated the precise printing trajectory and corresponding control code. The printed components inherently include both external and internal support structures, as illustrated in Figure 15a,b. Upon completion of the printing process, these auxiliary support structures require meticulous removal. The components designed through both ESO and SI-ESO optimization approaches are manufactured using SLM technology, with their respective formations depicted in Figure 15c,d.

Based on the preceding mechanical simulation analysis, the maximum stress values for models optimized using the ESO and SI-ESO methods were determined to be 0.635 MPa and 0.46 MPa, respectively, with corresponding deformation values of 0.104 mm and 0.057 mm. To facilitate comprehensive performance comparison, simulations were conducted for both the ESO model at 0.46 MPa and the SI-ESO model under 0.635 MPa loading conditions. Dynamic pressure was systematically applied to the upper surface of the physical specimen, with precisely controlled pressures of 0.635 MPa and 0.46 MPa administered to analyze maximum deformation characteristics. Given the total force-bearing area of the upper surface measuring 13 square centimeters, the pressure conversion formula (F = P × A) was implemented. Through this calculation, it was established that 0.635 MPa corresponds to an applied force of 826 N, while 0.46 MPa equates to 598 N. The resultant maximum deformation following pressure application is graphically represented in Figure 16.

Under the same force conditions, the deformation of the physical object designed and manufactured by SI-ESO is less than that of the physical object designed and manufactured by ESO. Compared with ESO, the SI-ESO method reduces low-quality serrated elements and improves the uniformity of material distribution. This makes the force path clearer, and the force transmission path between the grid elements becomes more continuous, which reduces the bending or torsional deformation of the model. The model has higher rigidity and thus better mechanical properties. Consequently, the slope of the force-versus-deformation curve for the manufactured object after SI-ESO optimization is smaller than that of the ESO one, and the change is gentler. The maximum deformation from the simulation and the experiment are shown in

Table 8. Simulation and experimental variables.

Parameters	ESO Simulation Deformation	ESO Experimental Deformation	SI-ESO Simulation Deformation	SI-ESO Experimental Deformation
598 N	0.075 mm	0.073 mm	0.057 mm	0.061 mm
826 N	0.104 mm	0.107 mm	0.079 mm	0.082 mm

.

Components produced via additive manufacturing inherently include support structures, burrs, and excess material that must be removed through post-processing. The final prototype of the aviation generator rear cover was obtained through a series of machining and grinding operations. The SI-ESO-optimized additively manufactured component weighs 310 g, demonstrating the effectiveness of the topology optimization design that targeted a 30% weight reduction. A comparative analysis with the original 450 g component reveals an actual weight reduction of approximately 31%, which closely aligns with the simulation data. The optimized generator rear cover successfully fulfills the lightweight design requirements [43], and the detailed weight reduction metrics are presented in

Table 9. Optimal results.

Parameters	Prototype Weight/g	ESO Optimizes Weight/g	SI-ESO Optimizes Weight/g	Weight Loss Ratio/%
Weight	450	322	310	31%

.

4.3. Extreme Performance Test

To comprehensively investigate its ultimate load-bearing capacity, an experimental study was conducted on the mechanical performance of the component under extreme loading conditions at a controlled compression rate of 0.1 mm/min. The resulting load–displacement curve, obtained by applying a perpendicular downward pressure (90° loading angle) to the upper surface, is illustrated in Figure 17. A comparative analysis of the curve data reveals that the SI-ESO component exhibits a superior load-bearing capacity and greater deformation tolerance compared to the ESO component. Notably, as the compression displacement approached 1 mm, the load-bearing capacity of the ESO component degraded significantly, whereas the SI-ESO specimen maintained its structural load-bearing capacity during this deformation stage. The compression test results conclusively demonstrate that, relative to the ESO component, the SI-ESO aviation generator rear cover possesses superior deformation resistance and enhanced structural stiffness.

5. Conclusions

This study employs an improved topological optimization algorithm, namely SI-ESO, which introduces a penalty function factor and intermediate density variables into the traditional ESO framework. This modification effectively mitigates the issue of mesh element discretization during iteration, thereby enhancing mesh quality, increasing the model’s natural frequency, and reducing maximum stress. Through comparative experiments, a mass retention of 70% was identified as the optimal target. The resulting topology-optimized model, when compared to the baseline ESO design under identical constraints, achieved a 27% reduction in maximum stress, a 0.003 MPa decrease in equivalent stress, and a 10.53% increase in its first-order natural frequency. Furthermore, after determining the optimal laser parameters for the aviation generator rear cover, a prototype fabricated via laser additive manufacturing realized a 31% weight reduction. Mechanical compression tests demonstrated that the SI-ESO-optimized part exhibits superior structural stability and load-bearing capacity under high-load conditions. These findings indicate that the proposed methodology can successfully achieve significant lightweighting while fulfilling the specified functional requirements. The results from the prototype validation provide strong evidence for the method’s potential, offering valuable insights for the advanced design and manufacturing of aviation components. Future research will address mesh dependency through systematic convergence studies and evaluate manufacturing tolerance effects on optimized structures. Additionally, the dynamic response and fatigue performance under vibratory loads will be investigated to validate long-term reliability in operational conditions.