Contextual Feature Expansion with Superordinate Concept for Compositional Zero-Shot Learning
Abstract
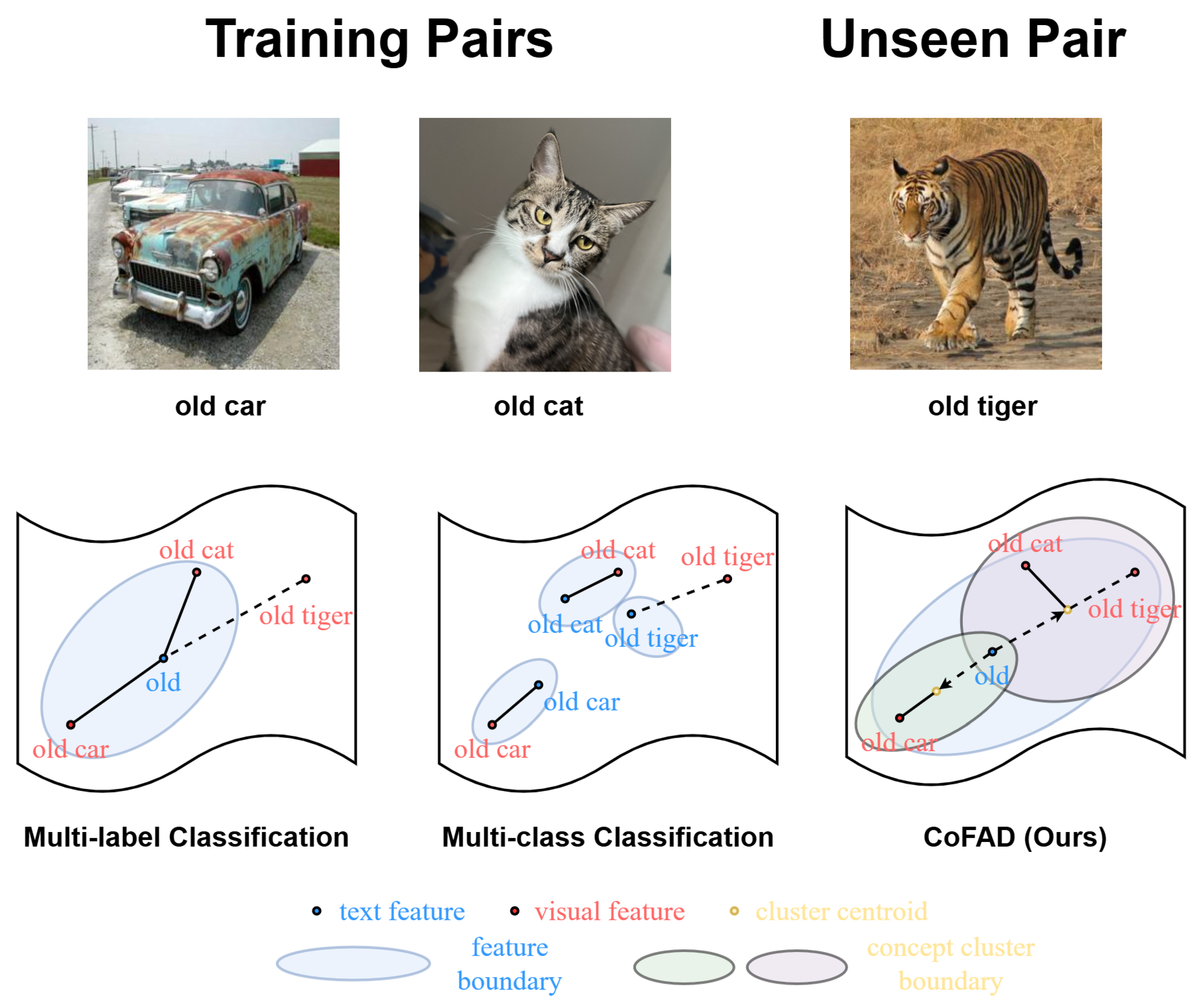
1. Introduction
- Novel Model Architecture: We introduce the CoFAD model, which extends contextual feature boundaries through concept-oriented learning.
- State-of-the-Art Performance: Experimental results on benchmark datasets establish CoFAD as SOTA in open-world scenarios, while maintaining strong performance in closed-world settings.
- Enhanced Computational Efficiency: CoFAD achieves remarkable efficiency, utilizing significantly less GPU memory and reducing training times by up to 50× compared to SOTA models.
2. Related Work
3. Preliminaries
3.1. Problem Formulation
3.2. Construct Prompt and Backbone
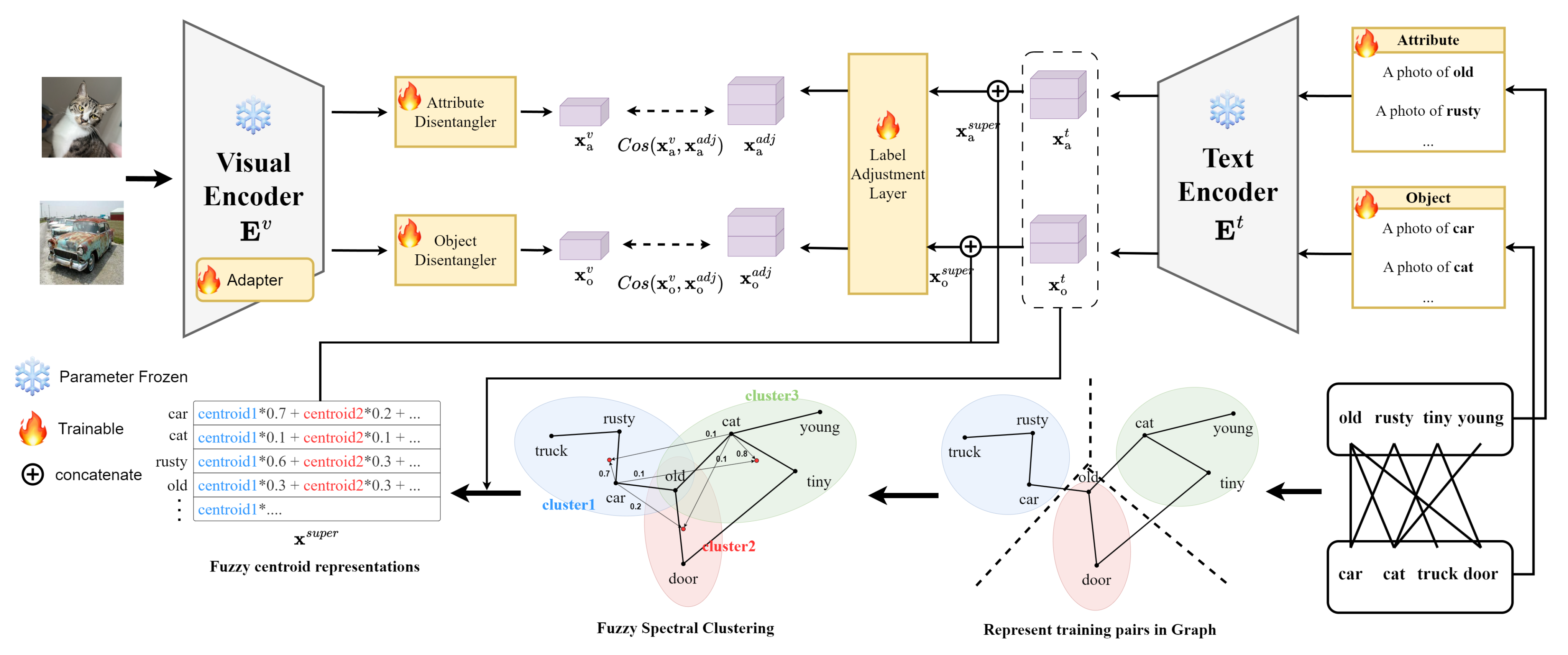
4. Methodology
4.1. Fuzzy Spectral Clustering
4.2. Feasibility Score
4.3. Label Adjustment
4.4. Training and Inference
5. Experiments
5.1. Experimental Setup
- MIT-States, collected via older search engines, includes diverse compositions without distinguishing between living and non-living entities, such as “Burnt Wood” or “Tiny Cat.” It contains 115 attributes and 245 objects, with 26,114 out of 28,175 compositions being non-existent labels (≈93%).In addition, because it is compiled from web-scraped and automatically annotated images, MIT-States contains numerous mislabeled instances, occlusions, and low-quality samples—conditions that closely resemble the imperfections typically observed in large-scale real-world corpora.
- UT-Zappos focuses on fine-grained images of shoes, such as “Suede Slippers” or “Cotton Sandals.” It includes 16 attributes and 12 objects, with 76 out of 192 compositions being non-existent labels (≈40%). Due to the extremely subtle inter-class differences (e.g., “Leather Boots” vs. “Suede Boots”), even human annotators often struggle to differentiate categories, making this dataset an effective stand-in for noisy or ambiguous inputs.
- C-GQA, built on the Stanford GQA dataset [24], shares similar primitives with MIT-States but includes a significantly larger number of labels. It comprises 413 attributes and 674 objects, resulting in nearly 280,000 possible compositions. However, only 7555 compositions are valid, with approximately 97% being non-existent pairs. This extreme imbalance mirrors the combinatorial explosion and sparsity of feasible compositions that occur in real-world knowledge graphs and retrieval-based applications.
5.2. Metrics
5.3. Implementation Details
5.4. Comparison with State-of-the-Arts
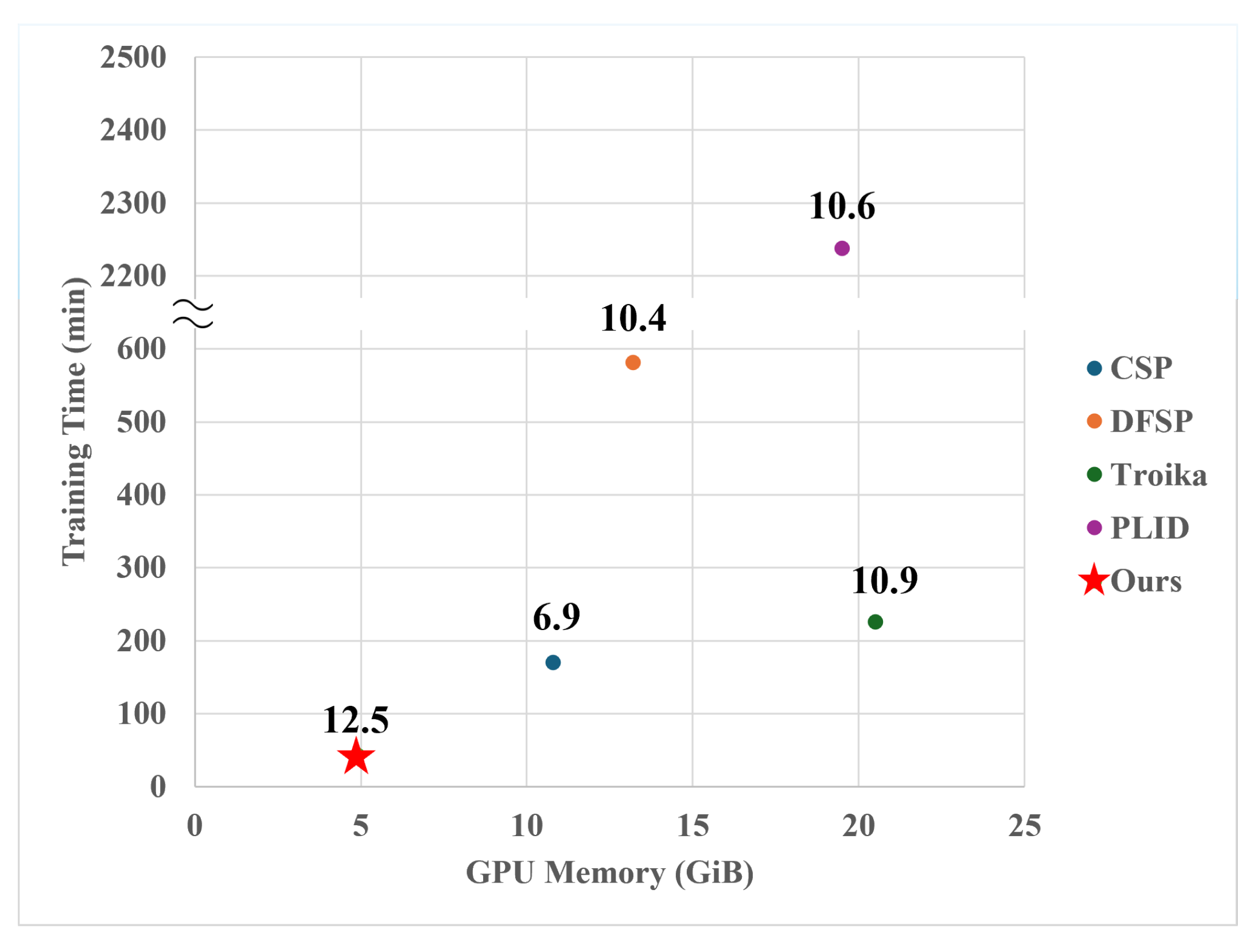
5.5. Cost Efficiency
5.6. Discussion
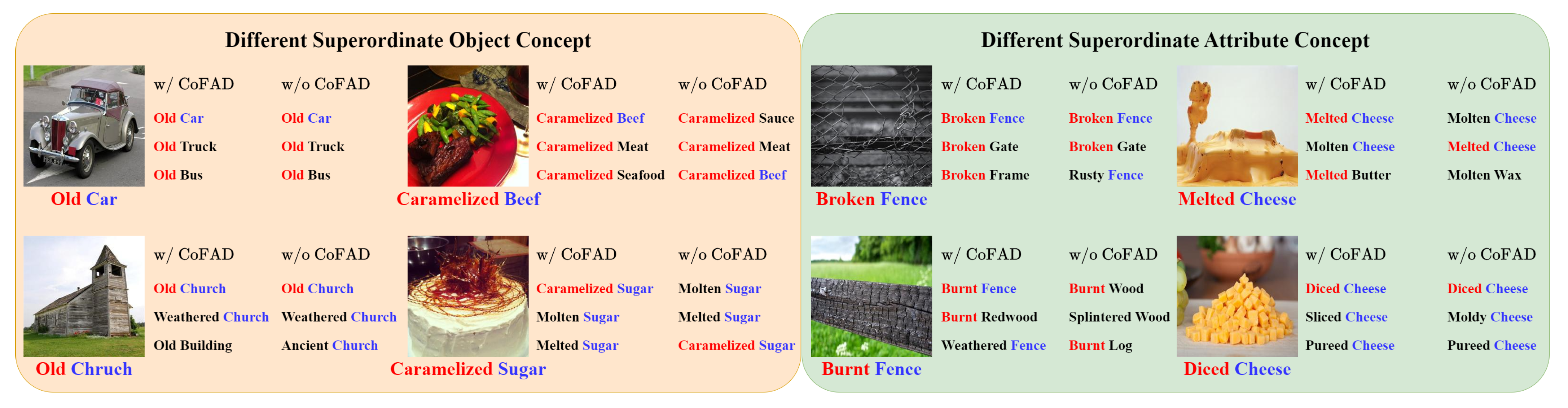
5.7. Qualitative Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rosch, E.; Mervis, C.B.; Gray, W.D.; Johnson, D.M.; Boyes-Braem, P. Basic objects in natural categories. Cogn. Psychol. 1976, 8, 382–439. [Google Scholar] [CrossRef]
- Rosch, E. Principles of categorization. In Cognition and Categorization/Erlbaum; Routledge: Abingdon, UK, 1978. [Google Scholar]
- Misra, I.; Gupta, A.; Hebert, M. From red wine to red tomato: Composition with context. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1792–1801. [Google Scholar]
- Nagarajan, T.; Grauman, K. Attributes as operators: Factorizing unseen attribute-object compositions. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 169–185. [Google Scholar]
- Purushwalkam, S.; Nickel, M.; Gupta, A.; Ranzato, M. Task-driven modular networks for zero-shot compositional learning. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Rpublic of Korea, 27 October–2 November 2019; pp. 3593–3602. [Google Scholar]
- Li, Y.L.; Xu, Y.; Mao, X.; Lu, C. Symmetry and group in attribute-object compositions. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11316–11325. [Google Scholar]
- Naeem, M.F.; Xian, Y.; Tombari, F.; Akata, Z. Learning graph embeddings for compositional zero-shot learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 953–962. [Google Scholar]
- Mancini, M.; Naeem, M.F.; Xian, Y.; Akata, Z. Learning graph embeddings for open world compositional zero-shot learning. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 46, 1545–1560. [Google Scholar] [CrossRef] [PubMed]
- Karthik, S.; Mancini, M.; Akata, Z. Revisiting visual product for compositional zero-shot learning. In Proceedings of the NeurIPS 2021 Workshop on Distribution Shifts: Connecting Methods and Applications, Virtual, 6–14 December 2021. [Google Scholar]
- Kim, S.; Lee, S.; Choi, Y.S. Focusing on valid search space in Open-World Compositional Zero-Shot Learning by leveraging misleading answers. IEEE Access 2024, 12, 165822–165830. [Google Scholar] [CrossRef]
- Anwaar, M.U.; Pan, Z.; Kleinsteuber, M. On leveraging variational graph embeddings for open world compositional zero-shot learning. In Proceedings of the 30th ACM International Conference on Multimedia, Lisbon, Portugal, 10–14 October 2022; pp. 4645–4654. [Google Scholar]
- Karthik, S.; Mancini, M.; Akata, Z. Kg-sp: Knowledge guided simple primitives for open world compositional zero-shot learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 9336–9345. [Google Scholar]
- Li, X.; Yang, X.; Wei, K.; Deng, C.; Yang, M. Siamese contrastive embedding network for compositional zero-shot learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 9326–9335. [Google Scholar]
- Huang, S.; Gong, B.; Feng, Y.; Zhang, M.; Lv, Y.; Wang, D. Troika: Multi-path cross-modal traction for compositional zero-shot learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 24005–24014. [Google Scholar]
- Li, Y.; Liu, Z.; Chen, H.; Yao, L. Context-based and Diversity-driven Specificity in Compositional Zero-Shot Learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 17037–17046. [Google Scholar]
- Isola, P.; Lim, J.J.; Adelson, E.H. Discovering states and transformations in image collections. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1383–1391. [Google Scholar]
- Yu, A.; Grauman, K. Fine-grained visual comparisons with local learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 192–199. [Google Scholar]
- Hao, S.; Han, K.; Wong, K.Y.K. Learning attention as disentangler for compositional zero-shot learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 15315–15324. [Google Scholar]
- Mancini, M.; Naeem, M.F.; Xian, Y.; Akata, Z. Open world compositional zero-shot learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19–25 June 2021; pp. 5222–5230. [Google Scholar]
- Radford, A.; Kim, J.W.; Hallacy, C.; Ramesh, A.; Goh, G.; Agarwal, S.; Sastry, G.; Askell, A.; Mishkin, P.; Clark, J.; et al. Learning transferable visual models from natural language supervision. In Proceedings of the International Conference on Machine Learning PMLR, Online, 18–24 July 2021; pp. 8748–8763. [Google Scholar]
- Nayak, N.V.; Yu, P.; Bach, S.H. Learning to compose soft prompts for compositional zero-shot learning. arXiv 2022, arXiv:2204.03574. [Google Scholar]
- Houlsby, N.; Giurgiu, A.; Jastrzebski, S.; Morrone, B.; De Laroussilhe, Q.; Gesmundo, A.; Attariyan, M.; Gelly, S. Parameter-efficient transfer learning for NLP. In Proceedings of the International Conference on Machine Learning PMLR, Long Beach, CA, USA, 9–15 June 2019; pp. 2790–2799. [Google Scholar]
- Von Luxburg, U. A tutorial on spectral clustering. Stat. Comput. 2007, 17, 395–416. [Google Scholar] [CrossRef]
- Hudson, D.A.; Manning, C.D. Gqa: A new dataset for real-world visual reasoning and compositional question answering. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 6700–6709. [Google Scholar]
- Zhang, T.; Liang, K.; Du, R.; Sun, X.; Ma, Z.; Guo, J. Learning invariant visual representations for compositional zero-shot learning. In Proceedings of the European Conference on Computer Vision; Springer: Cham, Switzerland, 2022; pp. 339–355. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. Pytorch: An imperative style, high-performance deep learning library. Adv. Neural Inf. Process. Syst. 2019, 32. [Google Scholar] [CrossRef]
- Zhou, K.; Yang, J.; Loy, C.C.; Liu, Z. Learning to prompt for vision-language models. Int. J. Comput. Vis. 2022, 130, 2337–2348. [Google Scholar] [CrossRef]
- Xu, G.; Kordjamshidi, P.; Chai, J. Prompting large pre-trained vision-language models for compositional concept learning. arXiv 2022, arXiv:2211.05077. [Google Scholar]
- Wang, H.; Yang, M.; Wei, K.; Deng, C. Hierarchical prompt learning for compositional zero-shot recognition. In Proceedings of the Thirty-Second International Joint Conference on Artificial Intelligence, Macao, China, 19–25 August 2023; pp. 1470–1478. [Google Scholar]
- Xu, G.; Chai, J.; Kordjamshidi, P. GIPCOL: Graph-Injected Soft Prompting for Compositional Zero-Shot Learning. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2024; pp. 5774–5783. [Google Scholar]
- Lu, X.; Guo, S.; Liu, Z.; Guo, J. Decomposed soft prompt guided fusion enhancing for compositional zero-shot learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 23–24 June 2023; pp. 23560–23569. [Google Scholar]
- Bao, W.; Chen, L.; Huang, H.; Kong, Y. Prompting language-informed distribution for compositional zero-shot learning. In Proceedings of the 18th European Conference on Computer Vision, Milan, Italy, 29 September–4 October 2024; Springer: Cham, Switzerland, 2025; pp. 107–123. [Google Scholar]
- Saini, N.; Pham, K.; Shrivastava, A. Disentangling visual embeddings for attributes and objects. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 13658–13667. [Google Scholar]
| Dataset | Training | Validation | Test | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| UT-Zappos | 16 | 12 | 192 | 83 | 23 k | 15 | 15 | 3 k | 18 | 18 | 3 k |
| MIT-States | 115 | 245 | 28,175 | 1262 | 30 k | 300 | 300 | 10 k | 400 | 400 | 13 k |
| CGQA | 413 | 674 | 278,362 | 5592 | 27 k | 1040 | 1252 | 7 k | 888 | 923 | 5 k |
| Models | MIT | UT-Zappos | C-GQA | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S | U | HM | AUC | S | U | HM | AUC | S | U | HM | AUC | |
| w/o CLIP | ||||||||||||
| SymNet [6] | 21.4 | 7.0 | 5.8 | 0.8 | 53.3 | 44.6 | 34.5 | 18.5 | 26.7 | 2.2 | 3.3 | 0.43 |
| CGE [7] | 32.4 | 5.1 | 6.0 | 1.0 | 61.7 | 47.7 | 39.0 | 23.1 | 32.7 | 1.8 | 2.9 | 0.47 |
| CompCos [19] | 25.4 | 10 | 8.9 | 1.6 | 59.3 | 46.8 | 36.9 | 21.3 | 28.4 | 1.8 | 2.8 | 0.39 |
| VisProd++ [9] | 28.1 | 7.5 | 7.3 | 1.2 | 62.5 | 51.5 | 41.8 | 26.5 | 28.0 | 2.8 | 4.5 | 0.75 |
| KG-SP [12] | 28.4 | 7.5 | 7.4 | 1.3 | 61.8 | 52.1 | 42.3 | 26.5 | 31.5 | 2.9 | 4.7 | 0.78 |
| Co-CGE [8] | 30.3 | 11.2 | 10.7 | 2.3 | 61.2 | 45.8 | 40.8 | 23.3 | 32.1 | 3.0 | 4.8 | 0.78 |
| CLIP [20] | 30.1 | 14.3 | 12.8 | 3.0 | 15.7 | 20.6 | 11.2 | 2.2 | 7.5 | 4.6 | 4.0 | 0.3 |
| CoOp [27] | 34.6 | 9.3 | 12.3 | 2.8 | 52.1 | 31.5 | 28.9 | 13.2 | 21.0 | 4.6 | 5.5 | 0.7 |
| PromptVL [28] | 48.5 | 16.0 | 17.7 | 6.1 | 64.6 | 44.0 | 37.1 | 21.6 | - | - | - | - |
| CSP [21] | 46.3 | 15.7 | 17.4 | 5.7 | 64.1 | 44.1 | 38.9 | 22.7 | 28.7 | 5.2 | 6.9 | 1.2 |
| HPL [29] | 46.4 | 18.9 | 19.8 | 6.9 | 63.4 | 48.1 | 40.2 | 24.6 | 30.1 | 5.8 | 7.5 | 1.4 |
| GIPCOL [30] | 48.5 | 16.0 | 17.9 | 6.3 | 65.0 | 45.0 | 40.1 | 23.5 | 31.6 | 5.5 | 7.3 | 1.3 |
| DFSP(i2t) [31] | 47.2 | 18.2 | 19.1 | 6.7 | 64.3 | 53.8 | 41.2 | 26.4 | 35.6 | 6.5 | 9.0 | 2.0 |
| DFSP(BiF) [31] | 47.1 | 18.1 | 19.2 | 6.7 | 63.5 | 57.2 | 42.7 | 27.6 | 36.4 | 7.6 | 10.6 | 2.4 |
| DFSP(t2i) [31] | 47.5 | 18.5 | 19.3 | 6.8 | 66.8 | 60.0 | 44.0 | 30.3 | 38.3 | 7.2 | 10.4 | 2.4 |
| PLID [32] | 49.1 | 18.7 | 20.0 | 7.3 | 67.6 | 55.5 | 46.6 | 30.8 | 39.1 | 7.5 | 10.6 | 2.5 |
| Troika [14] | 48.8 | 18.7 | 20.1 | 7.2 | 66.4 | 61.2 | 47.8 | 33.0 | 40.8 | 7.9 | 10.9 | 2.7 |
| CDS-CZSL [15] | 49.4 | 21.8 | 22.1 | 8.5 | 64.7 | 61.3 | 48.2 | 32.3 | 37.6 | 8.2 | 11.6 | 2.7 |
| CoFAD (ours) | 45.5 | 21.6 | 20.2 | 7.3 | 67.4 | 59.7 | 50.1 | 34.0 | 44.6 | 9.1 | 12.5 | 3.4 |
| Models | UT-Zappos | C-GQA | ||||||
|---|---|---|---|---|---|---|---|---|
| S | U | HM | AUC | S | U | HM | AUC | |
| CSP | 64.2 | 66.2 | 46.6 | 33.0 | 28.8 | 26.8 | 20.5 | 6.2 |
| HPL | 63.0 | 68.8 | 48.2 | 35.0 | 30.8 | 28.4 | 22.4 | 7.2 |
| GIPCOL | 65.0 | 68.5 | 48.8 | 36.2 | 31.9 | 28.4 | 22.5 | 7.1 |
| DFSP(t2i) | 66.7 | 71.7 | 47.2 | 36.0 | 38.2 | 32.0 | 27.1 | 10.5 |
| PLID | 67.3 | 68.8 | 52.4 | 38.7 | 38.8 | 33.0 | 27.9 | 11.0 |
| Troika | 66.8 | 73.8 | 54.6 | 41.7 | 41.0 | 35.7 | 29.4 | 12.4 |
| CDS-CZSL | 63.9 | 74.8 | 52.7 | 39.5 | 38.3 | 34.2 | 28.1 | 11.1 |
| CoFAD | 66.3 | 72.7 | 54.2 | 40.7 | 45.4 | 29.2 | 28.0 | 11.5 |
| 67.1 | 71.6 | 54.2 | 41.1 | 44.6 | 29.5 | 28.6 | 11.5 | |
| 30.3 | 34.3 | 24.3 | 8.6 | 32.0 | 13.3 | 13.7 | 3.3 | |
| 65.1 | 67.3 | 48.9 | 35.8 | 37.7 | 27.3 | 25.3 | 9.2 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.; Choi, Y.S. Contextual Feature Expansion with Superordinate Concept for Compositional Zero-Shot Learning. Appl. Sci. 2025, 15, 9837. https://doi.org/10.3390/app15179837
Kim S, Choi YS. Contextual Feature Expansion with Superordinate Concept for Compositional Zero-Shot Learning. Applied Sciences. 2025; 15(17):9837. https://doi.org/10.3390/app15179837
Chicago/Turabian StyleKim, Soohyeong, and Yong Suk Choi. 2025. "Contextual Feature Expansion with Superordinate Concept for Compositional Zero-Shot Learning" Applied Sciences 15, no. 17: 9837. https://doi.org/10.3390/app15179837
APA StyleKim, S., & Choi, Y. S. (2025). Contextual Feature Expansion with Superordinate Concept for Compositional Zero-Shot Learning. Applied Sciences, 15(17), 9837. https://doi.org/10.3390/app15179837






