MNATS: A Multi-Neighborhood Adaptive Tabu Search Algorithm for the Distributed No-Wait Flow Shop Scheduling Problem
Abstract
1. Introduction
- (1)
- A Balance–Lookahead NEH (BL-NEH) initializer is proposed to generate higher-quality initial solutions under no-wait and distributed constraints.
- (2)
- An Adaptive Neighborhood Local Search (ANLS) is designed to dynamically coordinate multiple operators, balancing exploration and exploitation to improve local search efficiency.
- (3)
- An Adaptive Tabu-Guided Perturbation (ATP) is introduced to strengthen global search by adjusting perturbation strength based on search history, enabling the algorithm to escape local optima and maintain diversity.
2. Related Works
2.1. Overview of FSP and Its Variants
2.2. Application of Evolutionary Algorithms in FSP
2.3. Specific Related Research on DNWFSP
3. Problem Formulation
- (1)
- Job Assignment Constraint
- (2)
- No-wait constraint
- (3)
- Inter-Job Start Time Constraint
- (4)
- Completion Time Definition
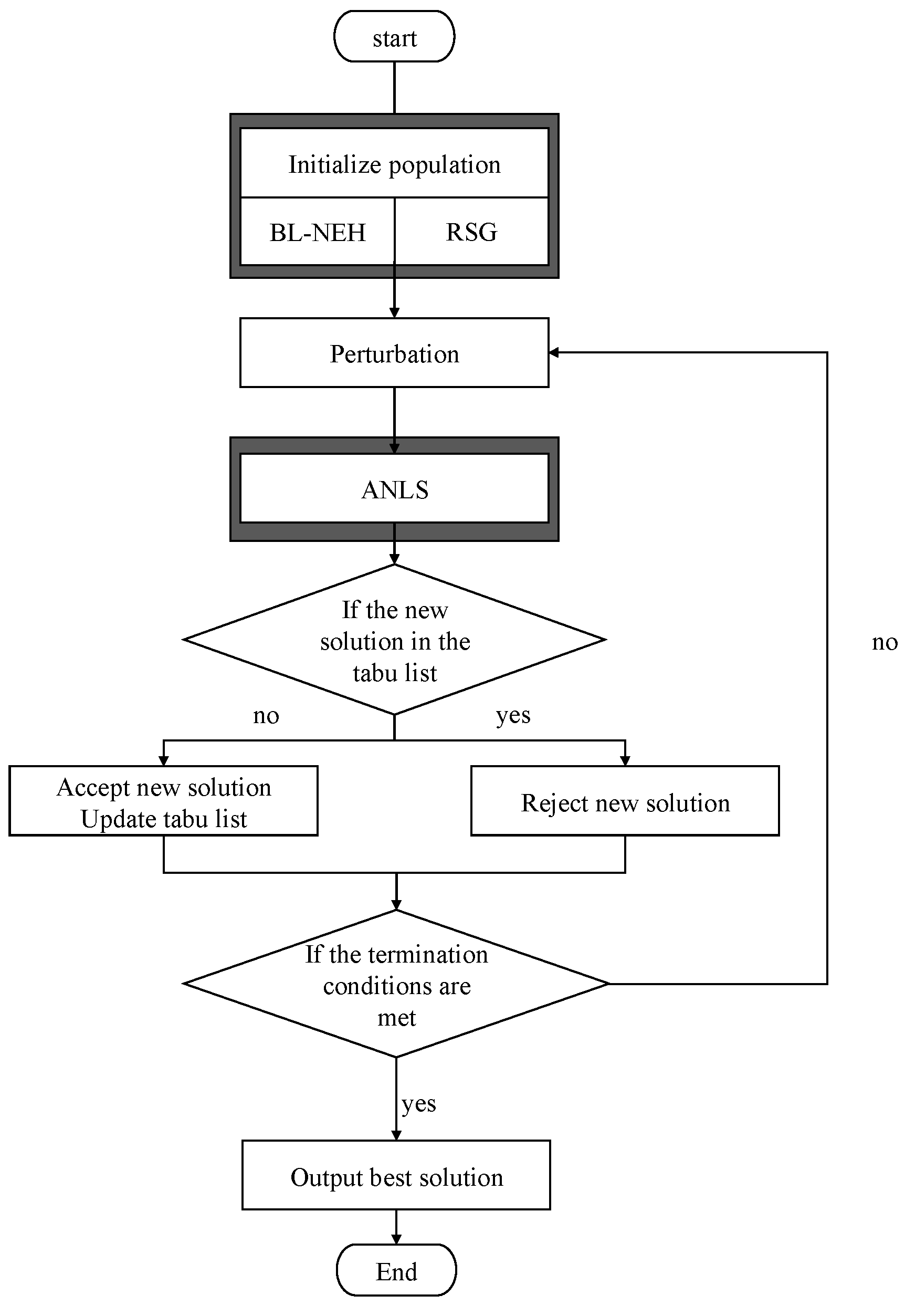
4. MNATS
4.1. Population Initialization
- (1)
- Job Balance Factor:The balance factor measures the uniformity of a job’s processing times across machines, defined as the ratio of its minimum to maximum processing time. Jobs with highly unbalanced times are more likely to create bottlenecks, since the critical machine dominates completion. By contrast, jobs with higher balance factors are less prone to cause congestion. Prioritizing such jobs helps construct more stable schedules under no-wait constraints, and preliminary tests confirmed that this simple min/max ratio is both effective and computationally inexpensive.
- (2)
- Lookahead Evaluation:When constructing the schedule, BL-NEH not only considers the immediate makespan impact of each job insertion but also estimates the influence on subsequent jobs. At each candidate position, it simulates the scheduling of a subset of unscheduled jobs by calculating their average processing times. Half of this minimum average is used as a lower bound for costs. The insertion position with the lowest combined sum of the current makespan and this estimate is selected.
| Algorithm 1: BL-NEH |
| Input: J—set of job; P—processing times Output: X—High-quality initial solution 1: Begin 2: For each job i in J Do 3: 4: Bi = minPik/maxPik 5: Qi = Ti⋅(1 + Bi) 6: End For 7: Sort jobs in descending order of Qi→ [j1, j2, …, jn] 8: S = [j1] 9: For i = 2 to n Do 10: For each possible position pos in S Do 11: Insert ji at pos to form S′ 12: cost(S′) = Cmax(S′) + lookahead_increment(S′, remaining jobs) 13: End For 14: Choose pos* with minimal cost(S′) 15: Insert ji at pos* in S 16: End For 17: X = ∅ 18: For i = 1 to n Do 19: For j = 1 to f Do 20: Evaluate insertion of Si in all positions of factory j 21: End For 22: Select factory j* and position pos* with minimal makespan 23: Insert Si into X at pos* in factory j* 24: End For 25: End |
| Algorithm 2: RSG |
| Input: n—number of jobs f—number of factories Output: X—a constructed solution 1: Begin 2: S = Randomly sort all jobs 3: Initialize X as empty job sequences for all factories 4: For i = 1 to n Do 5: For j = 1 to f Do 6: Test inserting job Si at the end of factory j 7: Compute Cmax (Xj) after insertion 8: End For 9: Select factory j* with minimal makespan 10: Insert job Si at end of j* 11: End For 12: End |
4.2. ANLS
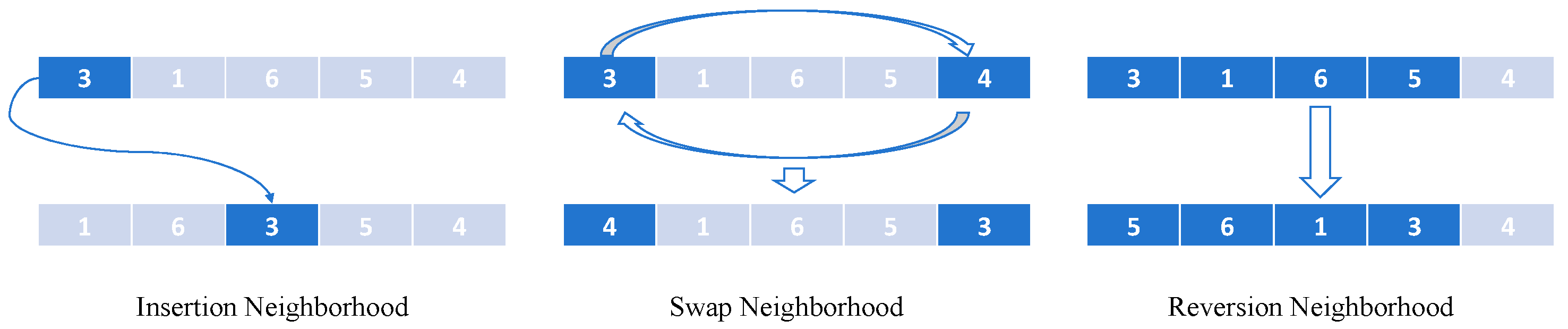
- -
- Insertion Neighborhood: Remove a job from its current position and insert it into another position within the same factory.
- -
- Swap Neighborhood: Swap the positions of two distinct jobs within the same factory.
- -
- Reversion Neighborhood: Reverse the order of a consecutive subsequence of jobs within the same factory.
| Algorithm 3: ANLS-Insert Search |
| Input: π—current solution set X—a newly generated solution to be improved Output: Xnew—a constructed solution 1: Begin 2: Xbest = Select solution from π with minimal makespan 3: Seq = Job sequence of Xbest 4: For i = 1 to length(Seq) Do 5: job = Seq [i] 6: X′ = Remove job from X 7: For pos = 1 to length(Seq) Do 8: If pos ≠ i then 9: Insert job at position pos 10: If Cmax(X′) < Cmax(X) then 11: Xnew = X′ 12: End If 13: End If 14: End For 15: End For 16: End |
| Algorithm 4: ANLS—Swap Search |
| Input: π—current solution set X—a newly generated solution to be improved Output: Xnew—a constructed solution 1: Begin 2: Xnew = X 3: For each factory F in X Do 4: Seq = Job sequence of F 5: For i = 1 to length(Seq) − 1 Do 6: For j = i + 1 to length(Seq) Do 7: Seq′ = Swap Seq [i] and Seq [j] 8: X′ = X with Seq′ for factory F 9: If Cmax(X’) < Cmax (Xnew) then 10: Xnew = X′ 11: End If 12: End For 13: End For 14: End For 15: End |
| Algorithm 5: ANLS—Reverse Search |
| Input: π—current solution set X—a newly generated solution to be improved Output: Xnew—a constructed solution 1: Begin 2: Xnew = X 3: For each factory F in X Do 4: Seq = Job sequence of F 5: For i = 1 to length(Seq) − 1 Do 6: For j = i + 1 to length(Seq) Do 7: Seq′ = Seq 8: Reverse Seq′ [i..j] // reverse the subsequence between positions i and j 9: X′ = X with Seq′ for factory F 10: If Cmax(X′) < Cmax (Xnew) then 11: Xnew = X′ 12: End If 13: End For 14: End For 15: End For 16: End |
| Algorithm 6: ANLS |
| Input: π—current solution set X—a newly generated solution to be improved Output: Xnew—a constructed solution 1: Begin 2: Xnew = X 3: Ntypes = {Insert, Swap, Reverse} 4: k = 1 5: While k ≤ length(Ntypes) Do 6: N = Ntypes [k] 7: Xtemp = Apply neighborhood search N to Xnew 8: If Xtemp not in tabu list T and Cmax (Xtemp) < Cmax (Xnew) then 9: Xnew = Xtemp 10: Update Tabu List T with Xtemp 11: k = 1 // reset to Insert next round 12: Break 13: Else 14: k = k + 1 // try next operator 15: End If 16: End While 17: End |
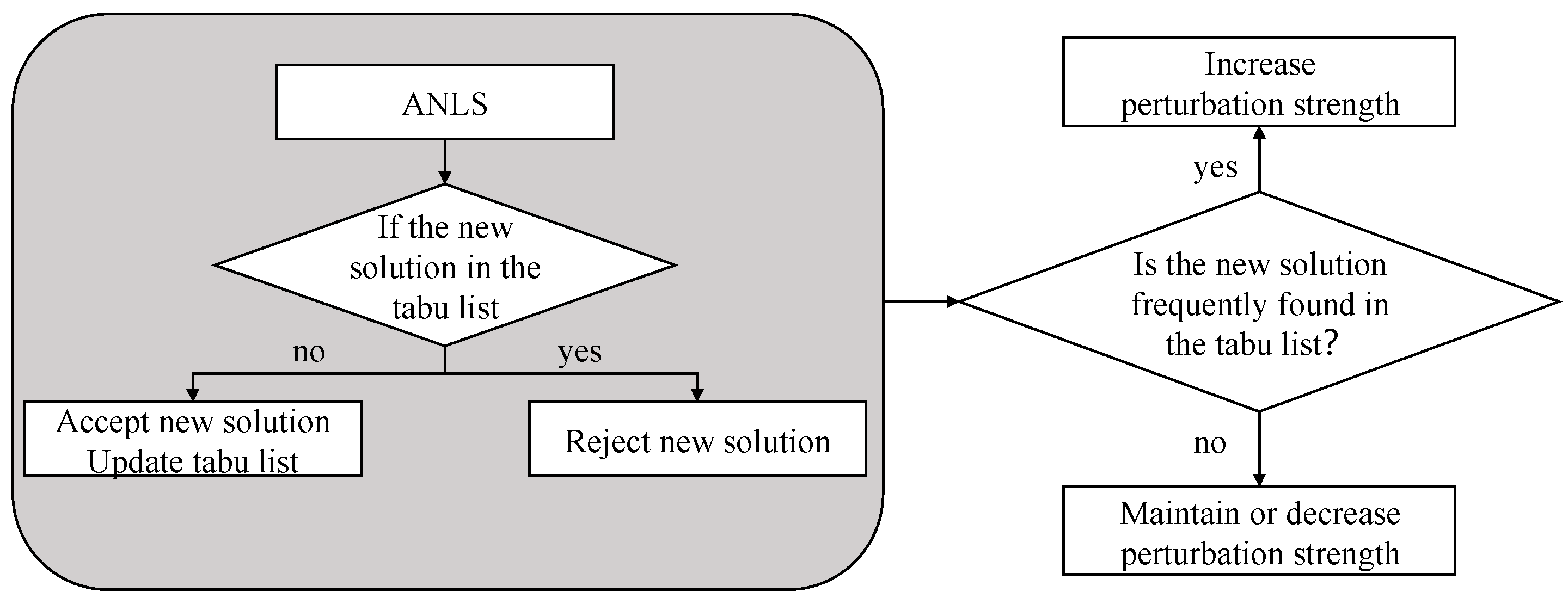
4.3. ATP
| Algorithm 7: ATP |
| Input: π—current solution set X—a newly generated solution to be improved T—tabu list r—perturbation intensity κ—max swap size l—max perturbation size Output: Xnew—a constructed solution 1: Begin 2: Xnew = X 3: Identify the key factory F* 4: C = ∅; skipped = 0; i = 1 5: While i ≤ r × l Do 6: Randomly select k ∈ {1, …, κ × r} 7: Randomly pick k jobs from F* and k jobs from another factory F′ 8: Xtemp = Exchange these jobs between F* and F′ 9: If hash(Xtemp) ∈ T then 10: skipped = skipped + 1; i = i + 1; Continue 11: End If 12: Evaluate Cmax(Xtemp) 13: C = C ∪ {Xtemp} 14: i = i + 1 15: End While 16: Xnew = getmin Cmax(C) 17: hit_rate = skipped/r × l 18: intensity adaptation (hit_rate) 19: Update T with Xnew 20: Return Xnew 21: End |
4.4. Acceptance Criterion
4.5. Computational Complexity
5. Experiments
5.1. Experimental Setup
5.2. Experimental Evaluation Metrics
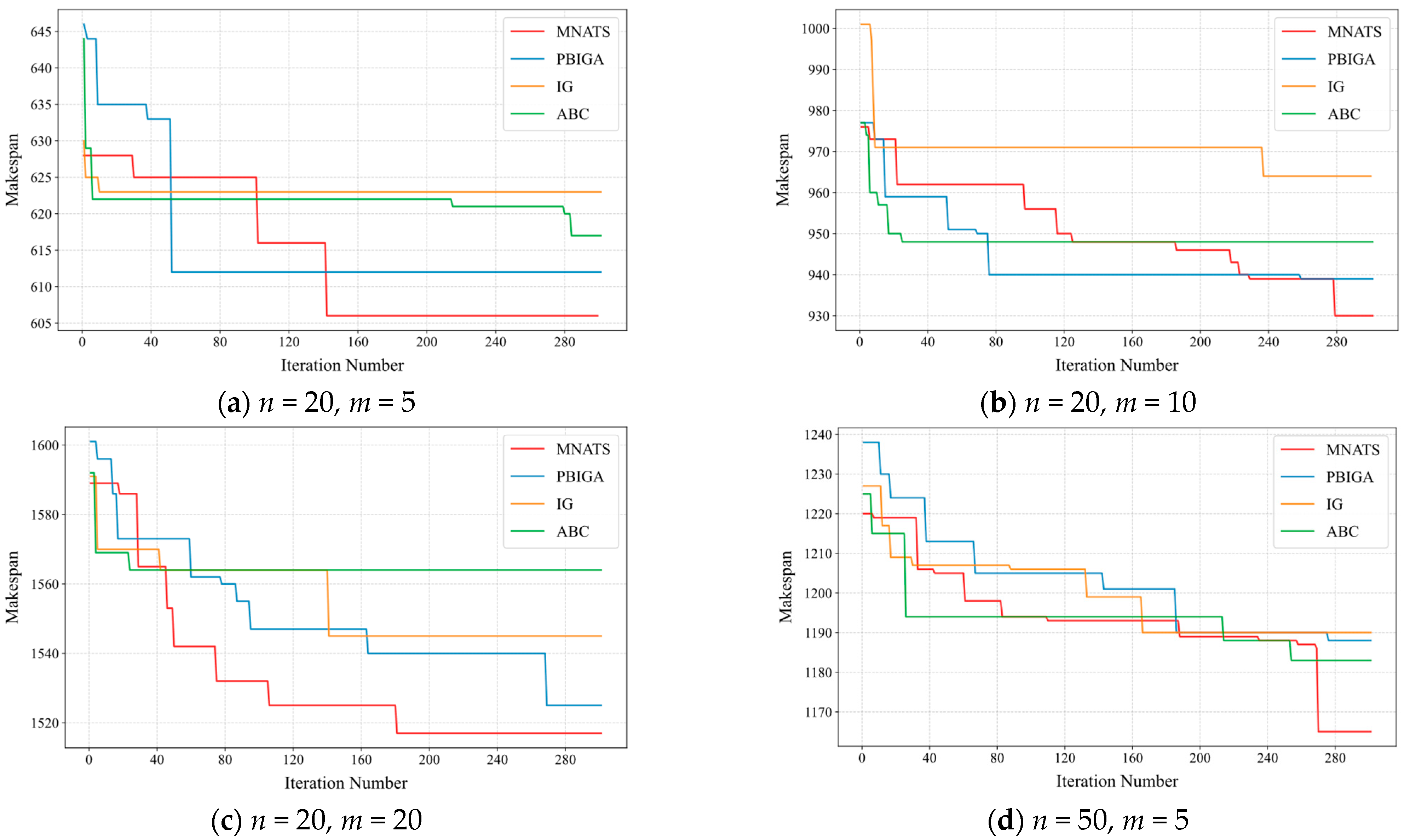
5.3. Comparative Experiment
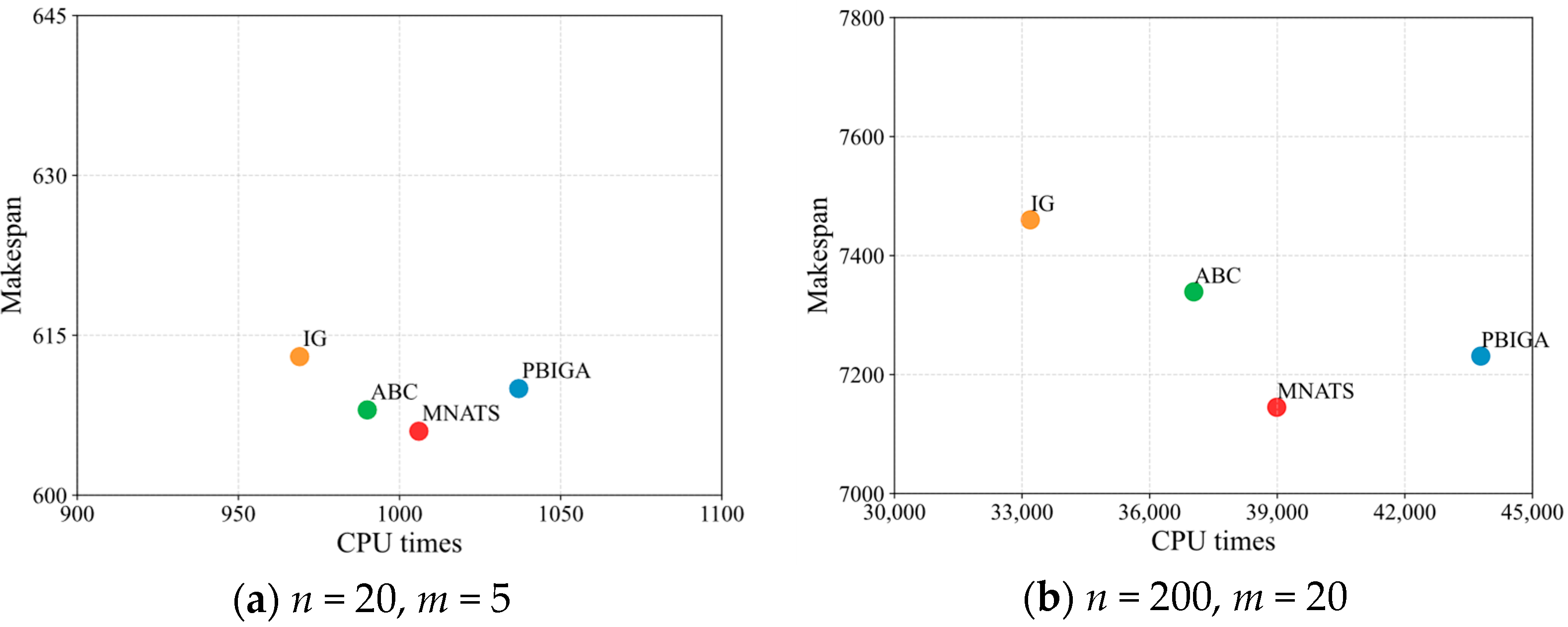
5.4. Runtime Analysis
5.5. Ablation Experiments
- MNATS w/o BL-NEH: Removes the BL-NEH module and uses traditional NEH initialization.
- MNATS ANLS-Insert/ANLS-Swap/ANLS-Reverse: Retains only one neighborhood operator in ANLS to evaluate the contribution of each neighborhood separately.
- MNATS w/o ATP: Removes the tabu list and uses a fixed perturbation strength.
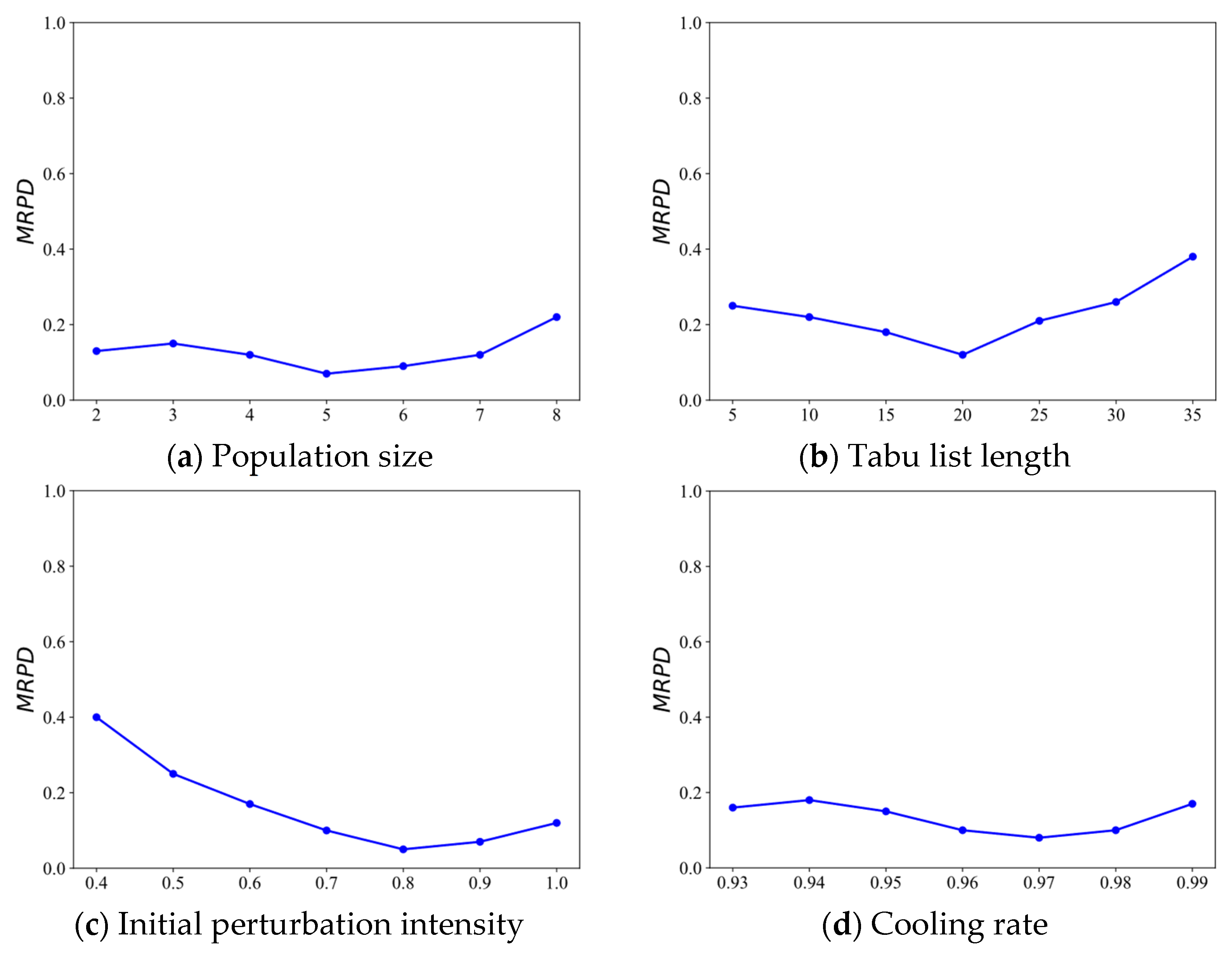
5.6. Sensitivity Analysis of Key Parameters
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lin, S.W.; Ying, K.C. Minimizing makespan for solving the distributed no-wait flowshop scheduling problem. Comput. Ind. Eng. 2016, 99, 202–209. [Google Scholar] [CrossRef]
- Aldowaisan, T.; Allahverdi, A. Minimizing total tardiness in no-wait flowshops. Found. Comput. Decis. Sci. 2012, 37, 149–162. [Google Scholar] [CrossRef]
- Rajendran, C. A no-wait flowshop scheduling heuristic to minimize makespan. J. Oper. Res. Soc. 1994, 45, 472–478. [Google Scholar] [CrossRef]
- Hall, N.G.; Sriskandarajah, C. A survey of machine scheduling problems with blocking and no-wait in process. Oper. Res. 1996, 44, 510–525. [Google Scholar] [CrossRef]
- Garey, M.R.; Johnson, D.S.; Sethi, R. The complexity of flowshop and jobshop scheduling. Math. Oper. Res. 1976, 1, 117–129. [Google Scholar] [CrossRef]
- Wang, B.; Han, K.; Spoerre, J.; Zhang, C. Integrated product, process and enterprise design: Why, what and how? In Integrated Product, Process and Enterprise Design; Springer: Boston, MA, USA, 1997; pp. 1–20. [Google Scholar]
- Kahn, K.B. The PDMA Handbook of New Product Development; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Tseng, L.Y.; Lin, Y.T. A hybrid genetic algorithm for no-wait flowshop scheduling problem. Int. J. Prod. Econ. 2010, 128, 144–152. [Google Scholar] [CrossRef]
- Zhang, W.; Geng, H.; Li, C.; Gen, M.; Zhang, G.; Deng, M. Q-learning-based multi-objective particle swarm optimization with local search within factories for energy-efficient distributed flow-shop scheduling problem. J. Intell. Manuf. 2023, 36, 185–208. [Google Scholar] [CrossRef]
- Komaki, M.; Malakooti, B. General variable neighborhood search algorithm to minimize makespan of the distributed no-wait flow shop scheduling problem. Prod. Eng. 2017, 11, 315–329. [Google Scholar] [CrossRef]
- Allali, K.; Aqil, S.; Belabid, J. Distributed no-wait flow shop problem with sequence dependent setup time: Optimization of makespan and maximum tardiness. Simul. Model. Pr. Theory 2022, 116, 102455. [Google Scholar] [CrossRef]
- Nawaz, M.; Enscore, E.E., Jr.; Ham, I. A heuristic algorithm for the m-machine, n-job flow-shop sequencing problem. Omega 1983, 11, 91–95. [Google Scholar] [CrossRef]
- Zeng, Q.-Q.; Li, J.-Q.; Li, R.-H.; Huang, T.-H.; Han, Y.-Y.; Sang, H.-Y. Improved NSGA-II for energy-efficient distributed no-wait flow-shop with sequence-dependent setup time. Complex Intell. Syst. 2022, 9, 825–849. [Google Scholar] [CrossRef]
- Aggoune, R. Minimizing the makespan for the flow shop scheduling problem with availability constraints. Eur. J. Oper. Res. 2004, 153, 534–543. [Google Scholar] [CrossRef]
- Koulamas, C.; Kyparisis, G.J. Two-stage no-wait proportionate flow shop scheduling with minimal service time variation and optional job rejection. Eur. J. Oper. Res. 2022, 305, 608–616. [Google Scholar] [CrossRef]
- Utama, D.M.; Umamy, S.Z.; Al-Imron, C.N. No-wait flow shop scheduling problem: A systematic literature review and bibli-ometric analysis. RAIRO-Oper. Res. 2024, 58, 1281–1313. [Google Scholar] [CrossRef]
- Wang, S.-Y.; Wang, L.; Liu, M.; Xu, Y. An effective estimation of distribution algorithm for solving the distributed permutation flow-shop scheduling problem. Int. J. Prod. Econ. 2013, 145, 387–396. [Google Scholar] [CrossRef]
- Becker, T.; Neufeld, J.; Buscher, U. The distributed flow shop scheduling problem with inter-factory transportation. Eur. J. Oper. Res. 2024, 322, 39–55. [Google Scholar] [CrossRef]
- Miyata, H.H.; Nagano, M.S. An iterated greedy algorithm for distributed blocking flow shop with setup times and maintenance operations to minimize makespan. Comput. Ind. Eng. 2022, 171, 108366. [Google Scholar] [CrossRef]
- Avci, M.; Avci, M.G.; Hamzadayı, A. A branch-and-cut approach for the distributed no-wait flowshop scheduling problem. Comput. Oper. Res. 2022, 148, 106009. [Google Scholar] [CrossRef]
- Bäck, T.; Schwefel, H.-P. An Overview of Evolutionary Algorithms for Parameter Optimization. Evol. Comput. 1993, 1, 1–23. [Google Scholar] [CrossRef]
- Hussain, K.; Salleh, M.N.M.; Cheng, S.; Shi, Y. Metaheuristic research: A comprehensive survey. Artif. Intell. Rev. 2018, 52, 2191–2233. [Google Scholar] [CrossRef]
- Ruiz, R.; Maroto, C.; Alcaraz, J. Two new robust genetic algorithms for the flowshop scheduling problem. Omega 2006, 34, 461–476. [Google Scholar] [CrossRef]
- Engelbrecht, A.P.; Grobler, J.; Langeveld, J. Set based particle swarm optimization for the feature selection problem. Eng. Appl. Artif. Intell. 2019, 85, 324–336. [Google Scholar] [CrossRef]
- Chen, R.M.; Lo, S.T.; Wu, C.L.; Lin, T.H. An effective ant colony optimization-based algorithm for flow shop scheduling. In Proceedings of the 2008 IEEE Conference on Soft Computing in Industrial Applications, Muroran, Japan, 25–27 June 2008; IEEE: Piscataway, NJ, USA; pp. 101–106. [Google Scholar]
- Zhang, W.; Wang, Y.; Yang, Y.; Gen, M. Hybrid multiobjective evolutionary algorithm based on differential evolution for flow shop scheduling problems. Comput. Ind. Eng. 2019, 130, 661–670. [Google Scholar] [CrossRef]
- Engin, O.; Güçlü, A. A new hybrid ant colony optimization algorithm for solving the no-wait flow shop scheduling prob-lems. Appl. Soft Comput. 2018, 72, 166–176. [Google Scholar] [CrossRef]
- Nejjarou, O.; Aqil, S.; Lahby, M. Hybrid meta-heuristic solving no-wait flow shop scheduling minimizing maximum tardiness. Evol. Intell. 2024, 17, 3935–3959. [Google Scholar] [CrossRef]
- Han, X.; Han, Y.; Chen, Q.; Li, J.; Sang, H.; Liu, Y.; Pan, Q.; Nojima, Y. Distributed flow shop scheduling with sequence-dependent setup times using an improved iterated greedy algorithm. Complex Syst. Model. Simul. 2021, 1, 198–217. [Google Scholar] [CrossRef]
- Lu, C.; Huang, Y.; Meng, L.; Gao, L.; Zhang, B.; Zhou, J. A Pareto-based collaborative multi-objective optimization algorithm for energy-efficient scheduling of distributed permutation flow-shop with limited buffers. Robot. Comput. Manuf. 2022, 74, 102277. [Google Scholar] [CrossRef]
- Khurshid, B.; Maqsood, S.; Khurshid, Y.; Naeem, K.; Khalid, Q.S. A hybridization of evolution strategies with iterated greedy algorithm for no-wait flow shop scheduling problems. Sci. Rep. 2024, 14, 1–22. [Google Scholar] [CrossRef] [PubMed]
- Pan, Y.; Gao, K.; Li, Z.; Wu, N. A novel evolutionary algorithm for scheduling distributed no-wait flow shop problems. IEEE Trans. Syst. Man, Cybern. Syst. 2024, 54, 3694–3704. [Google Scholar] [CrossRef]
- Li, H.; Li, X.; Gao, L. A discrete artificial bee colony algorithm for the distributed heterogeneous no-wait flowshop scheduling problem. Appl. Soft Comput. 2021, 100, 106946. [Google Scholar] [CrossRef]
- Zhu, N.; Zhao, F.; Yu, Y.; Wang, L. A cooperative learning-aware dynamic hierarchical hyper-heuristic for distributed heterogeneous mixed no-wait flow-shop scheduling. Swarm Evol. Comput. 2024, 90, 101668. [Google Scholar] [CrossRef]
- Zhang, X.-J.; Li, J.-Q.; Liu, X.-F.; Tian, J.; Duan, P.-Y.; Tan, Y.-Y. A hybrid whale optimization algorithm for distributed no-wait flow-shop scheduling problem with batch delivery. J. Intell. Fuzzy Syst. 2024, Preprint, 1–14. [Google Scholar] [CrossRef]
- An, Y.; Chen, X.; Gao, K.; Li, Y.; Zhang, L. Multiobjective flexible job-shop rescheduling with new job insertion and machine preventive maintenance. IEEE Trans. Cybern. 2022, 53, 3101–3113. [Google Scholar] [CrossRef]
- Li, J.-Q.; Pan, Q.-K.; Wang, F.-T. A hybrid variable neighborhood search for solving the hybrid flow shop scheduling problem. Appl. Soft Comput. 2014, 24, 63–77. [Google Scholar] [CrossRef]
- Taillard, E. Benchmarks for basic scheduling problems. Eur. J. Oper. Res. 1993, 64, 278–285. [Google Scholar] [CrossRef]
- Avci, M. An effective iterated local search algorithm for the distributed no-wait flowshop scheduling problem. Eng. Appl. Artif. Intell. 2023, 120, 105921. [Google Scholar] [CrossRef]
- Shao, W.; Pi, D.; Shao, Z. Optimization of makespan for the distributed no-wait flow shop scheduling problem with iterated greedy algorithms. Knowl.-Based Syst. 2017, 137, 163–181. [Google Scholar] [CrossRef]
- Zhao, F.; Xu, Z.; Wang, Q. A population-based iterated greedy algorithm for distributed no-wait flow-shop scheduling problem. In Proceedings of the 2023 26th International Conference on Computer Supported Cooperative Work in Design (CSCWD), Rio de Janeiro, Brazil, 24–26 May 2023; pp. 715–720. [Google Scholar]
- Zhao, F.; Yin, F.; Wang, L.; Yu, Y. A co-evolution algorithm with dueling reinforcement learning mechanism for the energy-aware distributed heterogeneous flexible flow-shop scheduling problem. IEEE Trans. Syst. Man, Cybern. Syst. 2024, 55, 1794–1809. [Google Scholar] [CrossRef]
- Huang, J.-P.; Gao, L.; Li, X.-Y. An end-to-end deep reinforcement learning method based on graph neural network for distributed job-shop scheduling problem. Expert Syst. Appl. 2023, 238, 121756. [Google Scholar] [CrossRef]
- Wu, X.; Yan, X.; Guan, D.; Wei, M. A deep reinforcement learning model for dynamic job-shop scheduling problem with uncertain processing time. Eng. Appl. Artif. Intell. 2024, 131, 107790. [Google Scholar] [CrossRef]
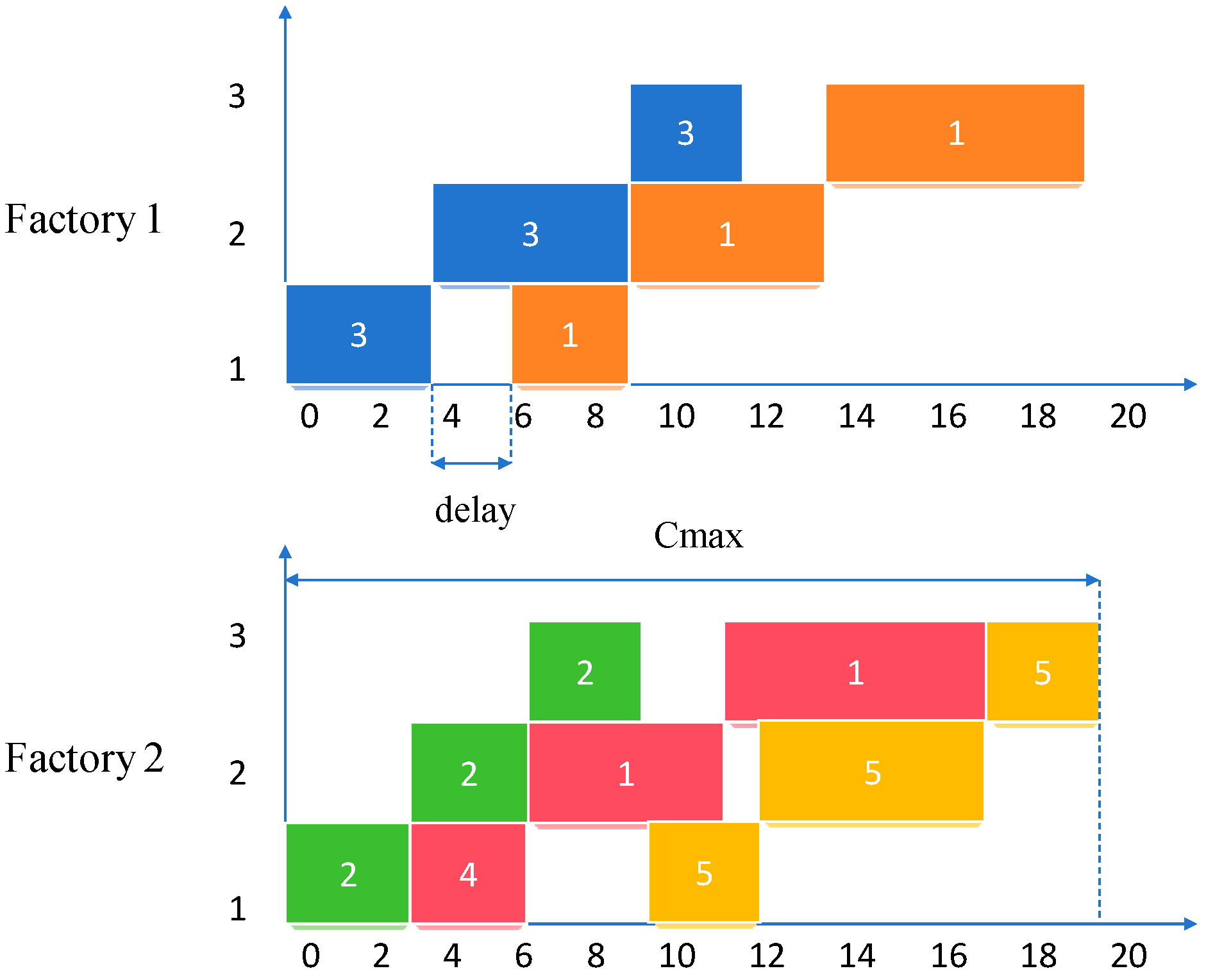
| Symbols | Description |
|---|---|
| Parameters and Sets | |
| π | Solution |
| i | Index for jobs, where |
| j | Index for factories, where |
| k | Index for machines, where |
| J = {J1, J2, …, Jn} | Set of jobs, containing n jobs |
| F = {F1, F2, …, Ff} | Set of factories, with a total of f factories |
| M = {M1, M2, …, Mm} | Set of machines in each factory, with m processing stages |
| Pi,k | Processing time of job Ji on machines k |
| πij | The i-th job in the processing sequence of factory Fj |
| Cmax | Maximum completion time among all jobs in all factories |
| The delay between the start time of job πi−1 ,j and job πij on the first machine | |
| xi,j | Binary variable: xi,j = 1 if job Ji is assigned to factory Fj; otherwise xi,j = 0 |
| Parameter Setting | |
|---|---|
| Population size | 5 |
| Tabu list length | 20 |
| Initial perturbation intensity | 0.8 |
| Cooling rate | 0.97 |
| Iteration Times | f | IG | ABC | PBIGA | MNATS |
|---|---|---|---|---|---|
| 100 | 2 | 4.23 ± 0.28 | 3.81 ± 0.25 | 1.54 ± 0.14 | 1.67 ± 0.12 |
| 3 | 4.15 ± 0.27 | 3.52 ± 0.22 | 2.28 ± 0.19 | 1.58 ± 0.11 | |
| 4 | 4.02 ± 0.30 | 3.33 ± 0.23 | 1.91 ± 0.16 | 1.95 ± 0.14 | |
| 5 | 3.88 ± 0.26 | 3.15 ± 0.20 | 2.55 ± 0.21 | 2.31 ± 0.17 | |
| 6 | 4.74 ± 0.33 | 3.47 ± 0.24 | 2.19 ± 0.18 | 2.67 ± 0.15 | |
| 200 | 2 | 3.12 ± 0.25 | 2.75 ± 0.19 | 0.89 ± 0.10 | 0.55 ± 0.08 |
| 3 | 3.98 ± 0.27 | 3.43 ± 0.21 | 1.47 ± 0.12 | 0.53 ± 0.07 | |
| 4 | 3.76 ± 0.29 | 3.11 ± 0.20 | 1.22 ± 0.11 | 0.67 ± 0.09 | |
| 5 | 3.53 ± 0.28 | 2.79 ± 0.18 | 1.56 ± 0.14 | 0.51 ± 0.08 | |
| 6 | 3.30 ± 0.26 | 2.47 ± 0.17 | 1.10 ± 0.10 | 0.85 ± 0.09 | |
| 300 | 2 | 2.67 ± 0.23 | 2.06 ± 0.16 | 0.52 ± 0.09 | 0.14 ± 0.04 |
| 3 | 2.81 ± 0.22 | 1.91 ± 0.15 | 0.88 ± 0.08 | 0.12 ± 0.03 | |
| 4 | 2.87 ± 0.24 | 1.41 ± 0.12 | 0.63 ± 0.07 | 0.11 ± 0.03 | |
| 5 | 2.93 ± 0.25 | 1.53 ± 0.13 | 0.74 ± 0.07 | 0.19 ± 0.05 | |
| 6 | 3.04 ± 0.26 | 1.58 ± 0.14 | 0.72 ± 0.08 | 0.22 ± 0.05 |
| Comparison | Z-Statistic | p-Value |
|---|---|---|
| IG vs. MNATS | −7.489 | p < 0.01 |
| ABC vs. MNATS | −6.503 | p < 0.01 |
| PBIGA vs. MNATS | −7.574 | p < 0.01 |
| f | MNATS | IG | ABC | PBIGA |
|---|---|---|---|---|
| 2 | 1.00 | 0.71 | 0.72 | 1.23 |
| 3 | 1.00 | 0.76 | 0.81 | 1.37 |
| 4 | 1.00 | 0.78 | 0.94 | 1.56 |
| 5 | 1.00 | 0.70 | 0.78 | 1.44 |
| 6 | 1.00 | 0.71 | 0.83 | 1.39 |
| f | MNATS | w/o BL-NEH | w/o ATP | ANLS-Insert | ANLS-Swap | ANLS-Reverse |
|---|---|---|---|---|---|---|
| 2 | 0.17 ± 0.02 | 0.32 ± 0.03 | 0.41 ± 0.06 | 0.29 ± 0.02 | 0.59 ± 0.05 | 0.66 ± 0.07 |
| 3 | 0.15 ± 0.02 | 0.35 ± 0.05 | 0.58 ± 0.05 | 0.31 ± 0.02 | 0.62 ± 0.07 | 0.71 ± 0.06 |
| 4 | 0.19 ± 0.02 | 0.43 ± 0.04 | 0.72 ± 0.05 | 0.34 ± 0.03 | 0.67 ± 0.05 | 0.74 ± 0.05 |
| 5 | 0.23 ± 0.03 | 0.38 ± 0.05 | 0.64 ± 0.07 | 0.37 ± 0.04 | 0.70 ± 0.06 | 0.79 ± 0.07 |
| 6 | 0.25 ± 0.03 | 0.37 ± 0.04 | 0.56 ± 0.04 | 0.39 ± 0.03 | 0.73 ± 0.05 | 0.81 ± 0.07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Zhao, W.; Zhao, H.; Bian, X. MNATS: A Multi-Neighborhood Adaptive Tabu Search Algorithm for the Distributed No-Wait Flow Shop Scheduling Problem. Appl. Sci. 2025, 15, 9840. https://doi.org/10.3390/app15179840
Zhang Z, Zhao W, Zhao H, Bian X. MNATS: A Multi-Neighborhood Adaptive Tabu Search Algorithm for the Distributed No-Wait Flow Shop Scheduling Problem. Applied Sciences. 2025; 15(17):9840. https://doi.org/10.3390/app15179840
Chicago/Turabian StyleZhang, Zhaohui, Wanqiu Zhao, Hong Zhao, and Xu Bian. 2025. "MNATS: A Multi-Neighborhood Adaptive Tabu Search Algorithm for the Distributed No-Wait Flow Shop Scheduling Problem" Applied Sciences 15, no. 17: 9840. https://doi.org/10.3390/app15179840
APA StyleZhang, Z., Zhao, W., Zhao, H., & Bian, X. (2025). MNATS: A Multi-Neighborhood Adaptive Tabu Search Algorithm for the Distributed No-Wait Flow Shop Scheduling Problem. Applied Sciences, 15(17), 9840. https://doi.org/10.3390/app15179840






