Multi-Objective Optimization with Server Load Sensing in Smart Transportation
Abstract
1. Introduction
- A three-tier cloud–edge–device collaborative IoV architecture is proposed, utilizing V2X-enabled multihop vehicular communication.
- Comprehensive system models are developed that integrate delay, energy consumption, and edge caching, along with a load-aware dynamic pricing mechanism that balances QoS and cost-effectiveness through economic cost quantification.
- An Adaptive Distributed Population-enhanced NSGA-III (ADP-NSGA-III) algorithm is designed, incorporating adaptive reference vector adjustment and distributed population management to address the QoS-cost paradox in conventional cloud–edge resource scheduling via the tri-objective optimization of delay, energy consumption, and resource pricing.
2. Related Work
2.1. Multi-Layer Resource Scheduling for Telematics with Cloud–Edge–End Collaboration
2.2. Multi-Objective Optimization and Resource Pricing
3. System Modeling
3.1. Three-Tier Communication Architecture for Cloud–Edge–End Collaboration
- The cloud server can provide services to any service unit within the scenario, while the edge server and the intelligent Internet-connected vehicle-mounted terminal can only serve units within their respective signal coverage areas.
- The communication mode between the intelligent Internet connected vehicle mounted terminal and the cloud server is V2C (Vehicle-to-Cloud), between the vehicle mounted terminal and the edge server is V2E (Vehicle-to-Edge), and between vehicle-mounted terminals is V2V (Vehicle-to-Vehicle).
- During task execution, both the vehicle and the edge server have stable computing power. However, the vehicle computing power is significantly lower than that of the edge server, and once servers reach their maximum load, they cannot continue processing tasks.
- The three-layer cloud–edge–end collaborative communication architecture proposed in this paper enables dynamic resource allocation among cloud servers, vehicles, and edge servers.
- The scenario considered in this paper is an idealized quasi-dynamic scenario, where the time at which the intelligent Internet-connected vehicle terminal passes through the edge server is divided into time slots, with each time slot having a duration of t.
- The mobility of vehicles is simulated using a random walk model, in which the direction and speed of each vehicle are random. The simulation is based on the generation of random trajectory, and the movement of vehicles is discretized using time steps.
- Task generation is based on a “quasi-dynamic” scenario, using a uniform distribution to generate task sizes, randomly and uniformly selecting task sizes within the range of 10 MB to 100 MB.
3.2. Communication Model
3.3. Edge Caching Model
3.4. Delay Modeling and Energy Modeling
3.4.1. Tasks Are Executed Locally
3.4.2. Tasks Are Executed in Other Vehicles
3.4.3. Tasks Are Executed at the Edge Server
3.4.4. Tasks Are Executed at the Cloud Server
3.5. Resource Dynamic Pricing Model Based on Load Balancing Awareness
3.6. Delay Modeling and Energy Modeling
4. NSGA-III Based Optimization Scheme
4.1. Coding
4.2. Adaptation Evaluation Function
4.3. ADP-NSGA-III Algorithm Design
4.3.1. Reference Vector Dynamic Response Mechanism
4.3.2. Population Delimitation Mechanisms Based on Partitioning Strategies
4.3.3. ADP-NSGA-III Algorithm
| Algorithm 1 AD-NSGA-III algorithm. |
| Require: input Population size N, maximum number of iterations , number of reference vectors H, migration rate , crossover probability , mutation probability F Ensure: output Pareto optimal solution set
|
4.3.4. Complexity Analysis of ADP-NSGA-III Algorithm
5. Simulation Experiment and Analysis
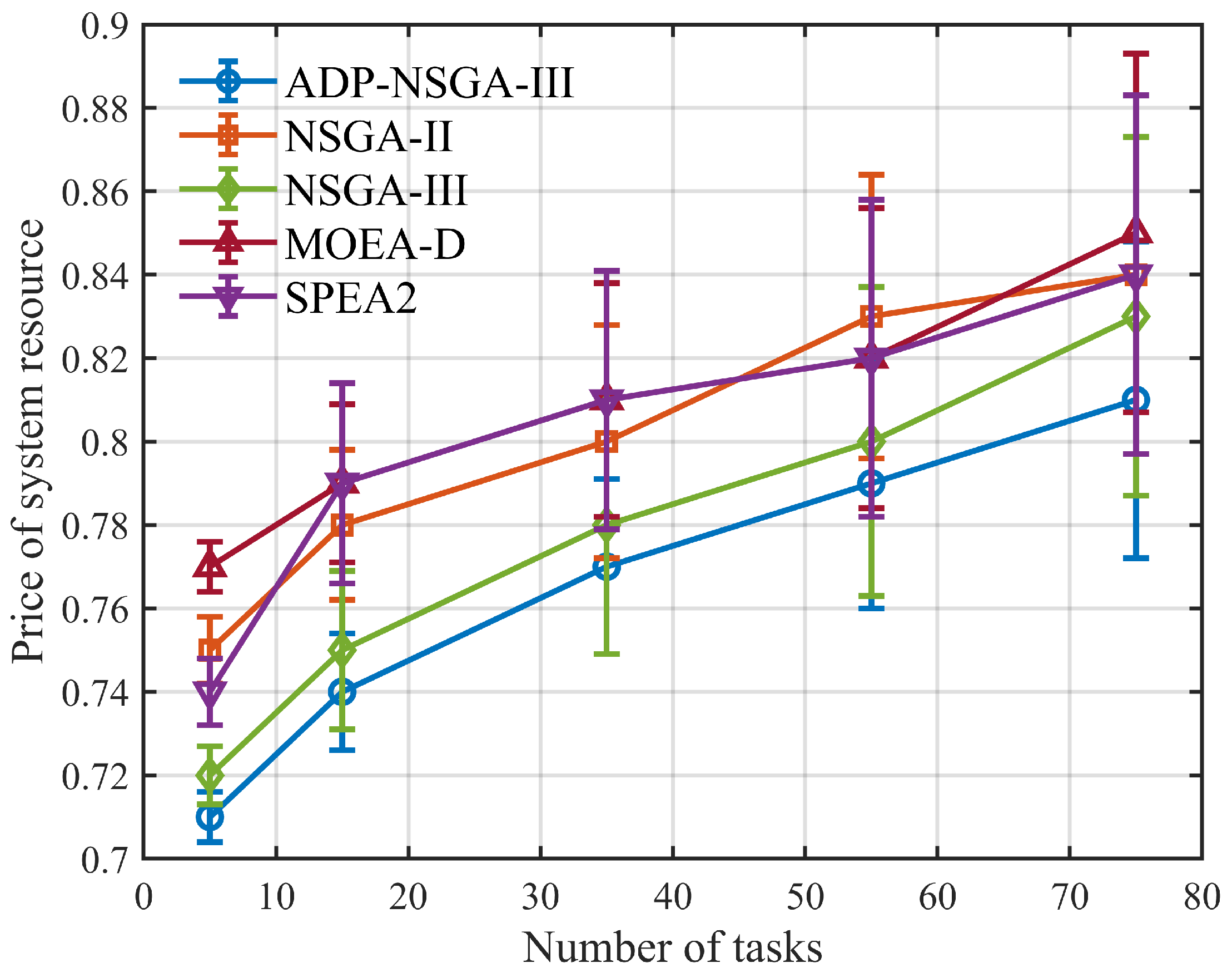
Experimental Design and Analysis of Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, H.; Jin, J.; Ma, H.; Xing, L. Hybrid Cooperative Cache Based on Temporal Convolutional Networks in Vehicular Edge Network. Sensors 2023, 23, 4619–4633. [Google Scholar] [CrossRef]
- Tian, A.; Feng, B.; Zhou, H.; Huang, Y.; Sood, K.; Yu, S.; Zhang, H. Efficient Federated DRL-Based Cooperative Caching for Mobile Edge Networks. IEEE Trans. Netw. Serv. Manag. 2023, 20, 246–260. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, N.; Wu, H.; Tang, C.; Li, R. A Fast and Efficient Task Offloading Algorithm in Heterogeneous Edge Cloud Computing Environments. IEEE Internet Things J. 2023, 10, 3165–3178. [Google Scholar] [CrossRef]
- Bi, X.; Zhao, L. Collaborative Caching Strategy for RL-Based Content Downloading Algorithm in Clustered Vehicular Networks. IEEE Internet Things J. 2023, 10, 9585–9596. [Google Scholar] [CrossRef]
- Gul-E-Laraib; Uz, S.K.; Maqsood, T.; Rehman, F.; Saad, M.; Amir, K.M.; Neelam, G.; Algarni, A.D.; Hela, E. Content Caching in Mobile Edge Computing Based on User Location and Preferences Using Cosine Similarity and Collaborative Filtering. Electronics 2023, 12, 284–302. [Google Scholar] [CrossRef]
- Cui, Y.; Yang, X.; He, P.; Wang, R.; Wu, D. URLLC-eMBB hierarchical network slicing for Internet of Vehicles: An AoI-sensitive approach. Veh. Commun. 2023, 43, 100648. [Google Scholar] [CrossRef]
- Zhu, S.; Song, Z.; Huang, C.; Zhu, H.; Qiao, R. Dependency-aware cache optimization and offloading strategies for intelligent transportation systems. J. Supercomput. 2025, 81, 45. [Google Scholar] [CrossRef]
- Feng, B.; Feng, C.; Feng, D.; Feng, D.; Wu, Y.; Xia, X.G. Proactive Content Caching Scheme in Urban Vehicular Networks. IEEE Trans. Commun. 2023, 71, 4165–4180. [Google Scholar] [CrossRef]
- Yin, S.; Sun, Y.; Xu, Q.; Sun, K.; Li, Y.; Ding, L.; Liu, Y. Multi-harmonic sources identification and evaluation method based on cloud-edge-end collaboration. Int. J. Electr. Power Energy Syst. 2024, 156, 109681. [Google Scholar] [CrossRef]
- Cai, J.; Liu, W.; Huang, Z.; Yu, F.R. Task decomposition and hierarchical scheduling for collaborative cloud-edge-end computing. IEEE Trans. Serv. Comput. 2024, 17, 4368–4382. [Google Scholar] [CrossRef]
- Li, B.; Yang, Y. Distributed fault detection for large-scale systems: A subspace-aided data-driven scheme with cloud-edge-end collaboration. IEEE Trans. Ind. Inform. 2024, 20, 12200–12209. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, C.; Lan, S.; Zhu, L.; Zhang, Y. End-edge-cloud collaborative computing for deep learning: A comprehensive survey. IEEE Commun. Surv. Tutor. 2024, 26, 2647–2683. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, Y. Task Offloading Optimization for Multi-objective Based on Cloud-Edge-End Collaboration in Maritime Networks. Future Gener. Comput. Syst. 2025, 164, 107588. [Google Scholar] [CrossRef]
- Zhang, T.; Wu, F.; Chen, Z.; Chen, S. Optimization of Edge–Cloud Collaborative Computing Resource Management for Internet of Vehicles Based on Multiagent Deep Reinforcement Learning. IEEE Internet Things J. 2024, 11, 36114–36126. [Google Scholar] [CrossRef]
- Geng, J.; Qin, Z.; Jin, S. Dynamic Resource Allocation for Cloud-Edge Collaboration Offloading in VEC Networks With Diverse Tasks. IEEE Trans. Intell. Transp. Syst. 2024, 25, 21235–21251. [Google Scholar] [CrossRef]
- Wu, J.; Tang, M.; Jiang, C.; Gao, L.; Cao, B. Cloud-Edge–End Collaborative Task Offloading in Vehicular Edge Networks: A Multilayer Deep Reinforcement Learning Approach. IEEE Internet Things J. 2024, 11, 36272–36290. [Google Scholar] [CrossRef]
- Sun, Z.; Sun, G.; Liu, Y.; Wang, J.; Cao, D. BARGAIN-MATCH: A Game Theoretical Approach for Resource Allocation and Task Offloading in Vehicular Edge Computing Networks. IEEE Trans. Mob. Comput. 2024, 23, 1655–1673. [Google Scholar] [CrossRef]
- Liu, M.; Pan, L.; Liu, S. Collaborative Storage for Tiered Cloud and Edge: A Perspective of Optimizing Cost and Latency. IEEE Trans. Mob. Comput. 2024, 23, 10885–10902. [Google Scholar] [CrossRef]
- Nouruzi, A.; Mokari, N.; Azmi, P.; Jorswieck, E.A.; Erol-Kantarci, M. Smart Dynamic Pricing and Cooperative Resource Management for Mobility-Aware and Multi-Tier Slice-Enabled 5G and Beyond Networks. IEEE Trans. Netw. Serv. Manag. 2024, 21, 2044–2063. [Google Scholar] [CrossRef]
- Tan, J.; Khalili, R.; Karl, H. Multi-Objective Optimization Using Adaptive Distributed Reinforcement Learning. IEEE Trans. Intell. Transp. Syst. 2024, 25, 10777–10789. [Google Scholar] [CrossRef]
- Zhu, S.; Song, Z.; Zhu, H.; Rui, Q. Efficient Slicing Scheme and Cache Optimization Strategy for Structured Dependent Tasks in Intelligent Transportation Scenarios. Ad Hoc Netw. 2025, 168, 103699. [Google Scholar]
- Wang, B.; Guo, Q.; Xia, T.; Li, Q.; Liu, D.; Zhao, F. Cooperative IoT Data Sharing with Heterogeneity of Participants Based on Electricity Retail. IEEE Internet Things J. 2024, 11, 4956–4970. [Google Scholar] [CrossRef]
- Zhu, S.; Wang, Y.; Chen, H.; Zha, H. A Novel Internet of Vehicles’s Task Offloading Decision Optimization Scheme for Intelligent Transportation System. Wirel. Pers. Commun. 2024, 137, 2359–2379. [Google Scholar] [CrossRef]
- Asghari, A.; Sohrabi, M.K. Bi-objective Cloud Resource Management for Dependent Tasks Using Q-learning and NSGA-III. J. Ambient Intell. Humaniz. Comput. 2024, 15, 197–217. [Google Scholar] [CrossRef]
- Mahmed, A.N.; Kahar, M.N.M. Simulation for Dynamic Patients Scheduling Based on Many Objective Optimization and Coordinator. Informatica 2024, 48, 91–106. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, H.L.; Chen, L. Variable Universe Fuzzy Logic Controller-Based Constrained Multi-Objective Evolutionary Algorithm. SSRN 2024. ssrn:4931444. [Google Scholar]
- Rawat, R.; Rajavat, A. Illicit Events Evaluation Using NSGA-2 Algorithms Based on Energy Consumption. Informatica 2024, 48, 77–96. [Google Scholar] [CrossRef]
- Gu, Q.; Li, K.; Wang, D.; Liu, D. A MOEA/D with Adaptive Weight Subspace for Regular and Irregular Multi-objective Optimization Problems. Inf. Sci. 2024, 661, 120143. [Google Scholar] [CrossRef]
- Wang, H.; Du, Y.; Chen, F. A Hybrid Strategy Improved SPEA2 Algorithm for Multi-Objective Web Service Composition. Appl. Sci. 2024, 14, 4157. [Google Scholar] [CrossRef]
- Xu, Y.; Ma, J.; Yuan, J. Application of SPEA2-MMBB for Distributed Fault Diagnosis in Nuclear Power System. Processes 2024, 12, 2620. [Google Scholar] [CrossRef]












| Model Symbol | Symbol Meaning |
|---|---|
| Parameters | Symbolic | Numerical Value |
|---|---|---|
| Amount of data of | 10∼100 MB | |
| Required computing resources of | 60∼100 mips | |
| Computing Resources of Cloud Server | 800 mips | |
| Computing resources of | 180∼280 mips | |
| Computing resources of | 60∼120 mips | |
| Computational power of | 100∼160 W | |
| Computational power of cloud servers | 400 W | |
| Computational power of | 200 W | |
| Transmission power of | 30 W | |
| Gaussian white noise power | −70 dBm | |
| Cache resources for | 3000 MHz | |
| Communication bandwidth of Cloud Servers | 400 MHz | |
| Communication bandwidth of | 100 MHz | |
| Population size | N | 100 |
| Maximum number of iterations | 500 | |
| Initial number of reference vectors | V | 6 |
| Crossover probability | From 0.9 to no less than 0.1 | |
| Differential coefficient of variation | F | From 0.9 to 0.1 |
| Number of subpopulations | 42 |
| Algorithm Variant | ARV | DSP | Migration | IGD (Mean ± Std) | HV (Mean ± Std) |
|---|---|---|---|---|---|
| ADP-NSGA-III | Yes | Yes | Yes | 0.037 ± 0.002 | 0.815 ± 0.009 |
| Without Adaptive Reference Vector | No | Yes | Yes | 0.041 ± 0.003 | 0.805 ± 0.010 |
| Without Distributed Subpopulations | Yes | No | Yes | 0.040 ± 0.003 | 0.800 ± 0.012 |
| Without Migration Strategy | Yes | Yes | No | 0.039 ± 0.002 | 0.810 ± 0.011 |
| NSGA-III | No | No | No | 0.050 ± 0.004 | 0.770 ± 0.013 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Y.; Song, Z.; Zhang, Q. Multi-Objective Optimization with Server Load Sensing in Smart Transportation. Appl. Sci. 2025, 15, 9717. https://doi.org/10.3390/app15179717
Yu Y, Song Z, Zhang Q. Multi-Objective Optimization with Server Load Sensing in Smart Transportation. Applied Sciences. 2025; 15(17):9717. https://doi.org/10.3390/app15179717
Chicago/Turabian StyleYu, Youjian, Zhaowei Song, and Qinghua Zhang. 2025. "Multi-Objective Optimization with Server Load Sensing in Smart Transportation" Applied Sciences 15, no. 17: 9717. https://doi.org/10.3390/app15179717
APA StyleYu, Y., Song, Z., & Zhang, Q. (2025). Multi-Objective Optimization with Server Load Sensing in Smart Transportation. Applied Sciences, 15(17), 9717. https://doi.org/10.3390/app15179717






