Electromagnetic and NVH Characteristic Analysis of Eccentric State for Surface-Mounted Permanent Magnet Synchronous Generators in Wave Power Applications
Abstract
Featured Application
Abstract
1. Introduction
2. Analysis Model of the Outer Rotor SPMSG with Rotor Eccentricity
3. Electromagnetic Analysis
3.1. Back-EMF Characteristics
3.2. Torque Characteristics with FFT-Based Harmonic Components
3.3. Electromagnetic Force Characteristic
4. Mechanical and NVH Analysis
4.1. Modal Analysis
4.2. Rotor Dynamics
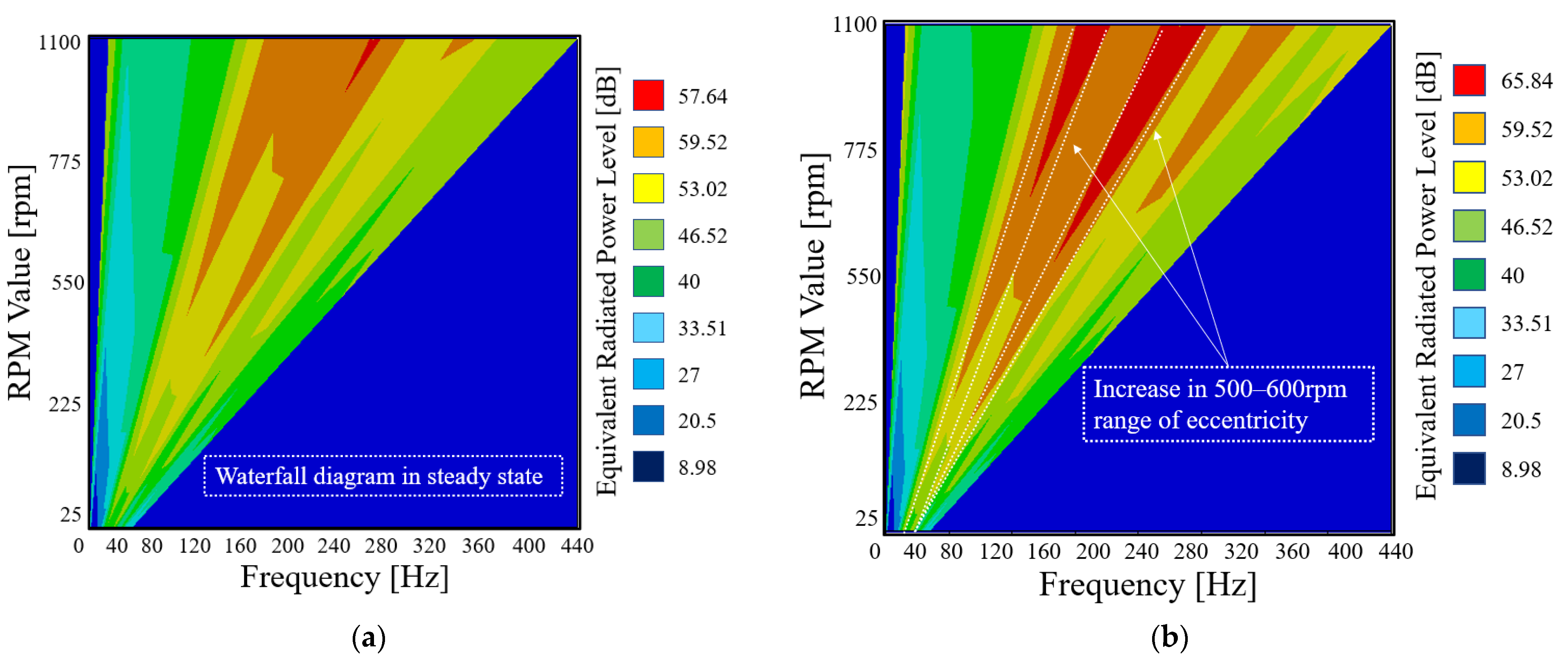
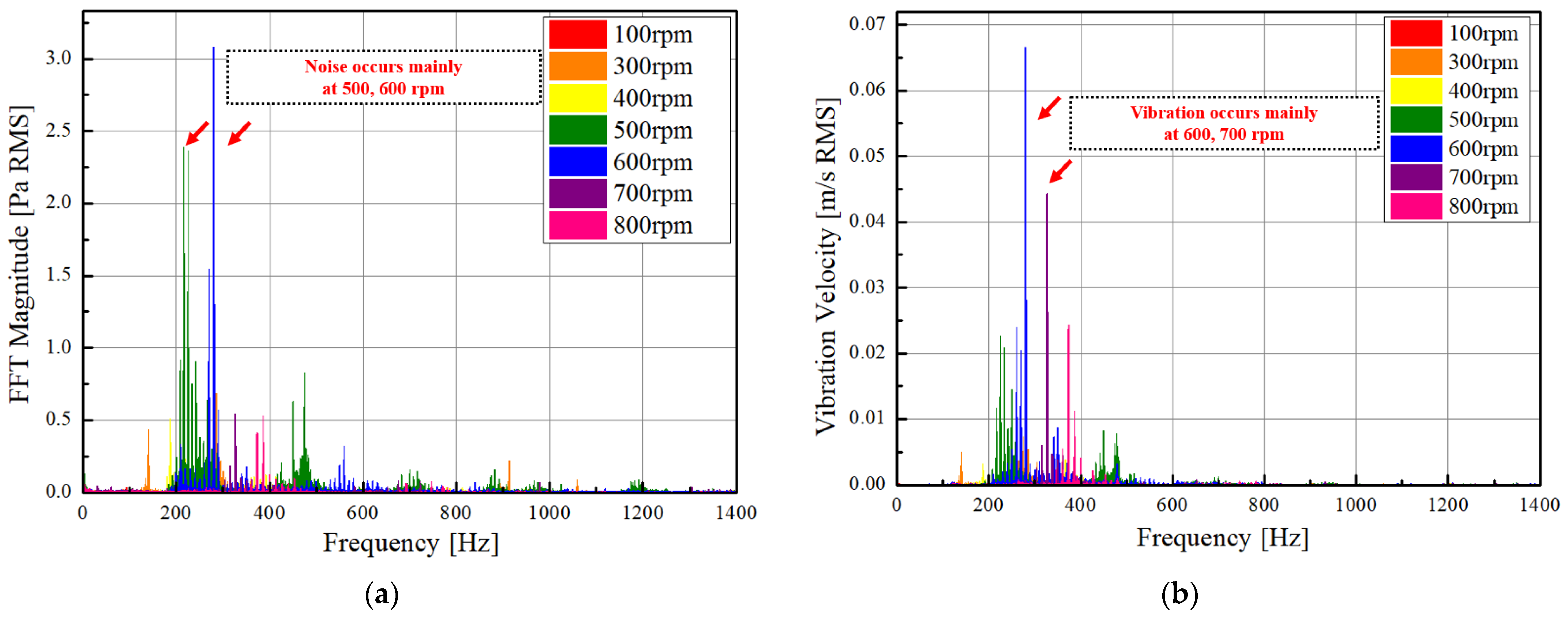
4.3. Coupled Electromagnetic–Mechanical NVH Evaluation
5. Experimental Setup and Validation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dutta, R.; Rahman, M.F.; Chong, L. Winding Inductances of an Interior Permanent Magnet Machine with Fractional Slot Concentrated Winding. IEEE Trans. Magn. 2012, 48, 4842–4849. [Google Scholar] [CrossRef]
- Zou, J.; Lan, H.; Xu, Y.; Zhao, B. Analysis of Global and Local Force Harmonics and Their Effects on Vibration in Permanent Magnet Synchronous Machines. IEEE Trans. Energy Convers. 2017, 32, 1523–1532. [Google Scholar] [CrossRef]
- Dong, J.; Huang, Y.; Jin, L.; Lin, H. Comparative Study of Surface-Mounted and Interior Permanent-Magnet Motors for High-Speed Applications. IEEE Trans. Appl. Supercond. 2015, 26, 5200304. [Google Scholar] [CrossRef]
- Bang, T.-K.; Shin, K.-H.; Lee, J.-I.; Lee, H.-K.; Cho, H.-W.; Choi, J.-Y. Electro-Mechanical Characteristics Analysis and Experimental Study of PMSM According to Rotor Eccentricity. IEEE Trans. Magn. 2022, 58, 2. [Google Scholar] [CrossRef]
- Yang, H.; Chen, Y. Influence of Radial Force Harmonics with Low Mode Number on Electromagnetic Vibration of PMSM. IEEE Trans. Energy Convers. 2014, 29, 38–45. [Google Scholar] [CrossRef]
- Ahn, J.-H.; Han, C.; Kim, C.-W.; Choi, J.-Y. Rotor Design of High-Speed Permanent Magnet Synchronous Motors Considering Rotor Magnetic and Sleeve Materials. IEEE Trans. Appl. Supercond. 2015, 28, 3. [Google Scholar]
- Zhu, Z.Q.; Liu, Y.; Howe, D. Minimizing the Influence of Cogging Torque on Vibration of PM Brushless Machines by Direct Torque Control. IEEE Trans. Magn. 2006, 42, 3512–3514. [Google Scholar] [CrossRef]
- Torregrossa, D.; Peyraut, F.; Fahimi, B.; M’bOua, J.; Miraoui, A. Multiphysics Finite-Element Modeling for Vibration and Acoustic Analysis of Permanent Magnet Synchronous Machine. IEEE Trans. Energy Convers. 2011, 26, 490–500. [Google Scholar] [CrossRef]
- Huo, M.; Wang, S.; Xiu, J.; Cao, S. Effect of Magnet/Slot Combination on Triple-Frequency Magnetic Force and Vibration of Permanent Magnet Motors. J. Sound Vib. 2013, 332, 5965–5980. [Google Scholar] [CrossRef]
- Beccue, P.; Neely, J.; Pekarek, S.; Stutts, D. Measurement and Control of Torque Ripple-Induced Frame Torsional Vibration in a Surface Mount Permanent Magnet Machine. IEEE Trans. Power Electron. 2005, 20, 182–191. [Google Scholar] [CrossRef]
- Huang, Z.; Fang, J. Multiphysics Design and Optimization of High-Speed Permanent Magnet Electrical Machines for Air Blower Applications. IEEE Trans. Ind. Electron. 2016, 63, 2766–2774. [Google Scholar] [CrossRef]
- Zhu, Z.Q.; Howe, D. Influence of Design Parameters on Cogging Torque in Permanent Magnet Machines. IEEE Trans. Energy Convers. 2000, 15, 407–412. [Google Scholar] [CrossRef]
- Bang, T.-K.; Shin, K.-H.; Lee, Y.-G.; Lee, J.-I.; Lee, H.-K.; Cho, H.-W.; Choi, J.-Y. Comparative Study of NVH of Permanent Magnet Machines According to Rotor Eccentricity with Fractional Pole/Slot Combinations. IEEE Trans. Appl. Supercond. 2022, 32, 6. [Google Scholar] [CrossRef]
- Kim, D.-Y.; Park, M.-R.; Sim, J.-H.; Hong, J.-P. Advanced Method of Selecting Number of Poles and Slots for Low-Frequency Vibration Reduction of Traction Motor for Elevator. IEEE/ASME Trans. Mechatronics 2017, 22, 1554–1562. [Google Scholar] [CrossRef]
- Cieras, J.F.; Wang, C.; Lai, J. Noise of Poly-Phase Electric Motors; Taylor & Francis: New York, NY, USA, 2006. [Google Scholar]
- Damiano, A.; Floris, A.; Fois, G.; Marongiu, I.; Porru, M.; Serpi, A. Design of a High-Speed Ferrite-Based Brushless DC Machine for Electric Vehicles. IEEE Trans. Ind. Appl. 2017, 53, 4279–4287. [Google Scholar] [CrossRef]
- Musuroi, S.; Sorandaru, C.; Greconici, M.; Olarescu, V.; Weinman, M. Low-Cost Ferrite Permanent Magnet Assisted Synchronous Reluctance Rotor: An Alternative for Rare Earth Permanent Synchronous Motors. In Proceedings of the 39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013; pp. 2966–2970. [Google Scholar]
- Huo, Q.; Han, J.; Wei, P. PMSM Servo Control System Design Based on Fuzzy PID. In Proceedings of the International Conference on Cybernetics, Robotics and Control, Chengdu, China, 21–23 August 2017; pp. 85–88. [Google Scholar]
- Zhang, W.; He, Y.L.; Dai, D.R.; Liu, Z.H.; Xu, M.X.; Gyselinck, J.; Zhang, F.; Gerada, D. UMF and Vibration Analysis for Eccentricity Detection in Permanent Magnet Synchronous Generators. IEEE Trans. Transp. Electr. 2025, in press.
- Wang, J.; Wang, Y. Electromagnetic Torque Analysis and Structure Optimization of Interior Permanent Magnet Synchronous Machine with Air-Gap Eccentricity. Energies 2023, 16, 1665. [Google Scholar] [CrossRef]
- Perez, R.; Cros, J.; Picard, M. Real-Time Modeling of Static, Dynamic and Mixed Eccentricity in Permanent Magnet Synchronous Machines. Machines 2025, 13, 120. [Google Scholar] [CrossRef]
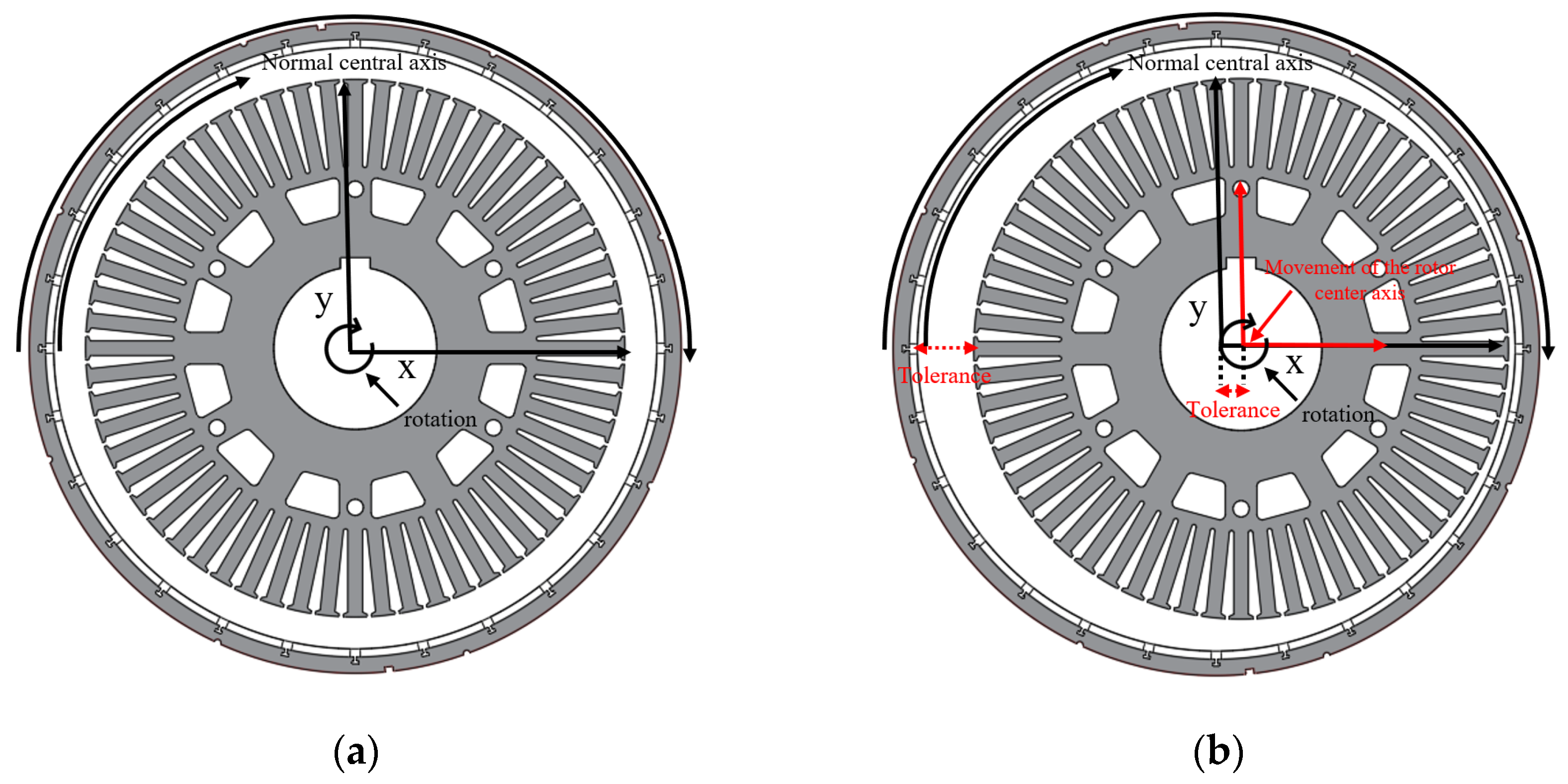
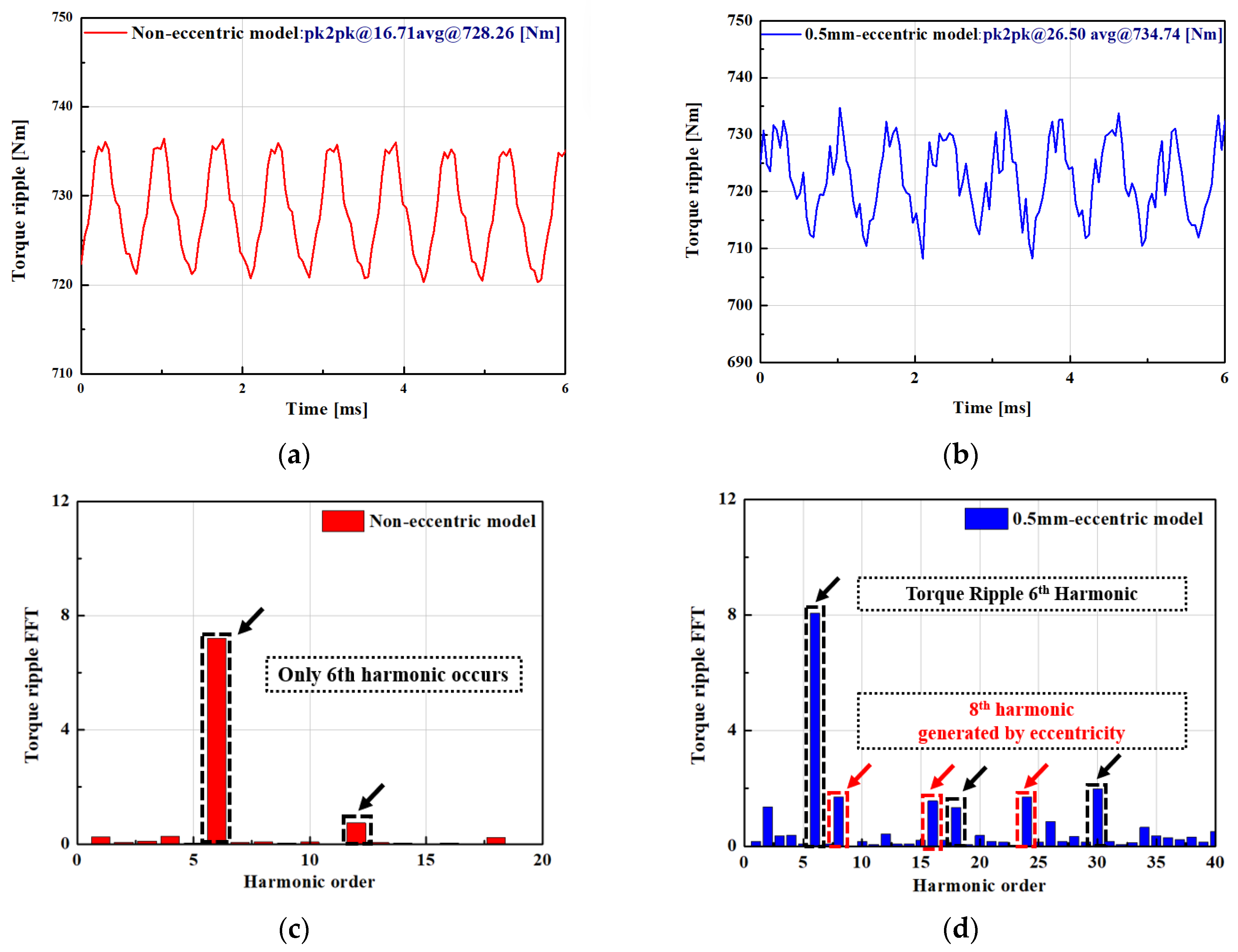
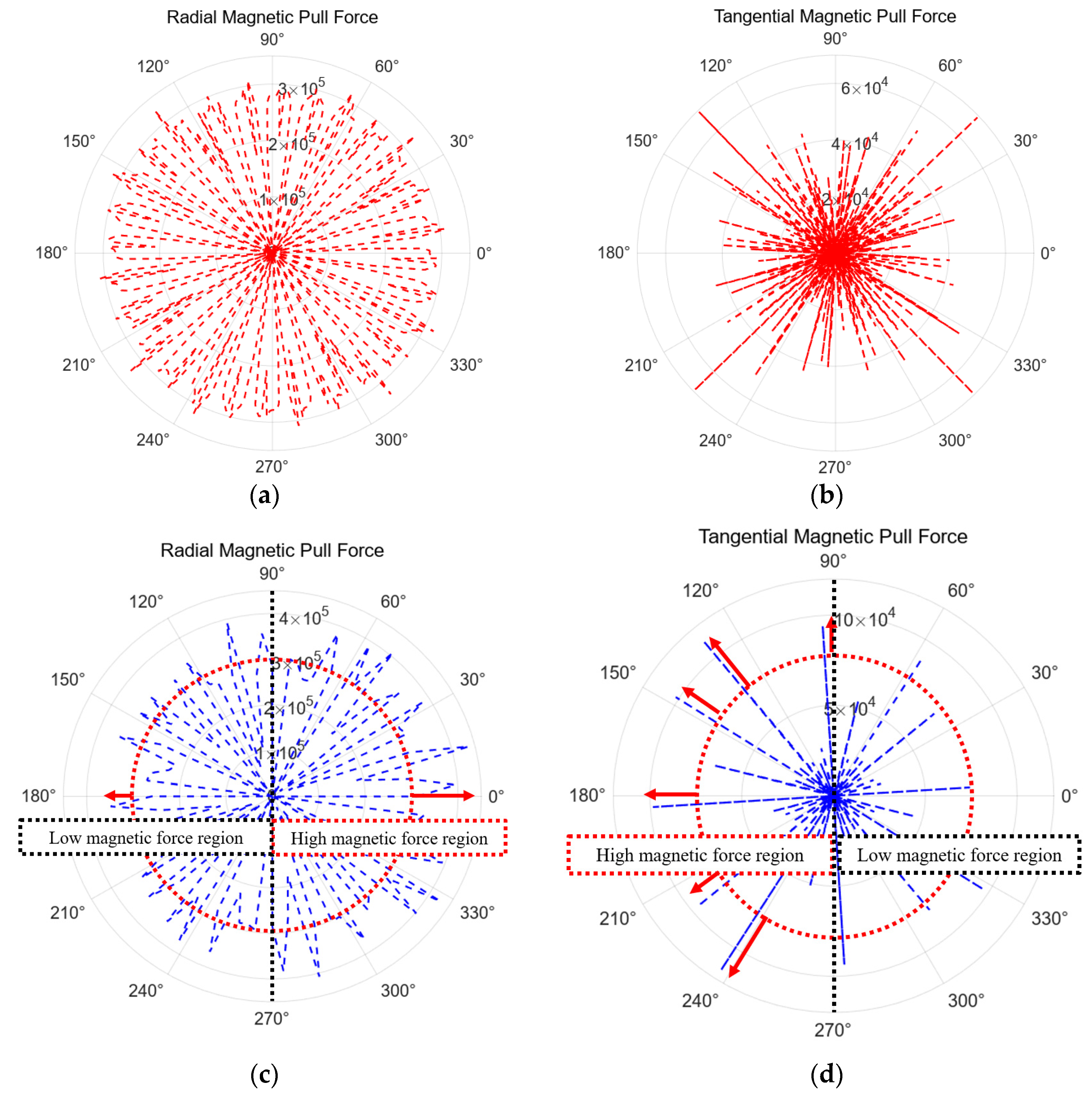
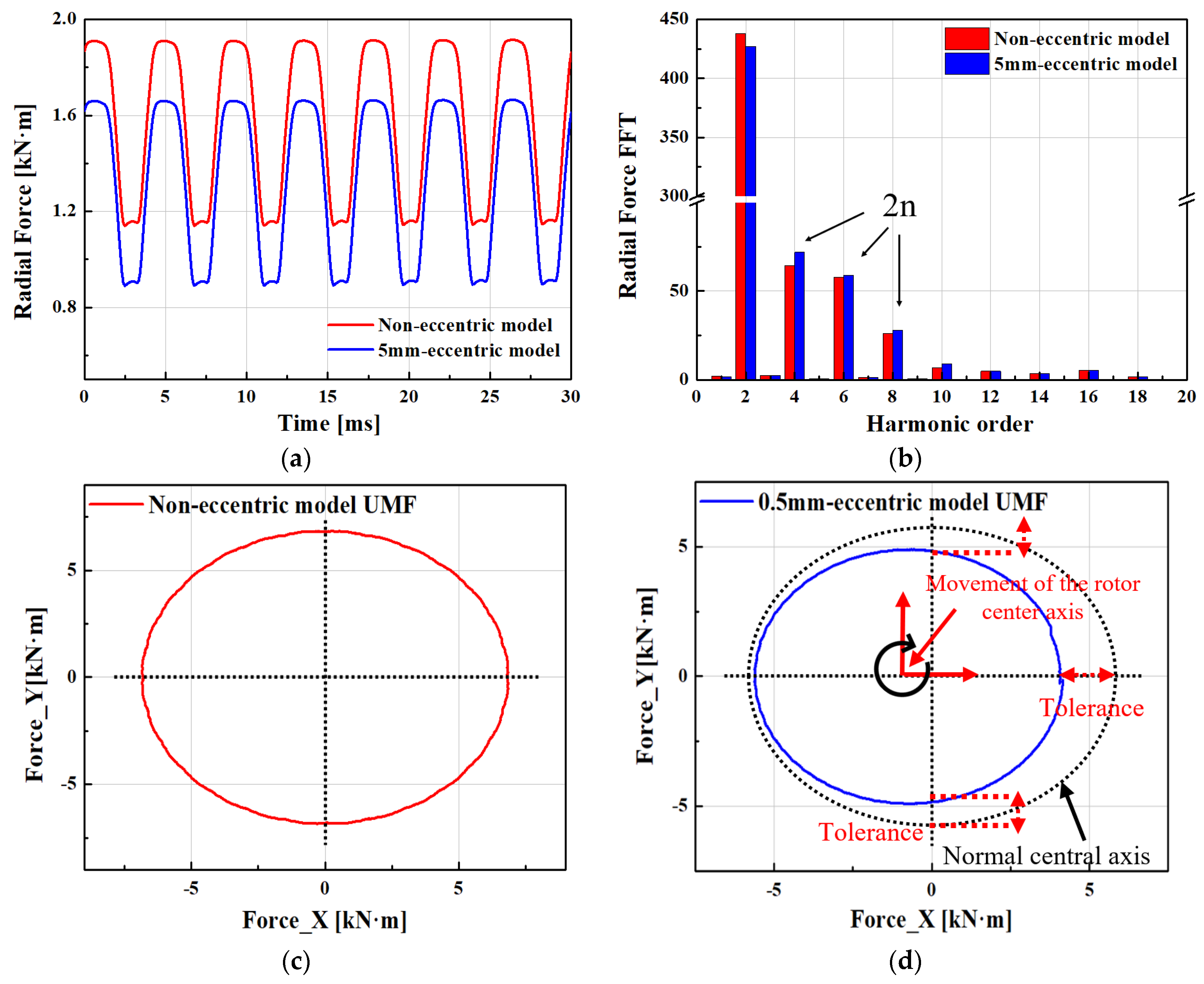
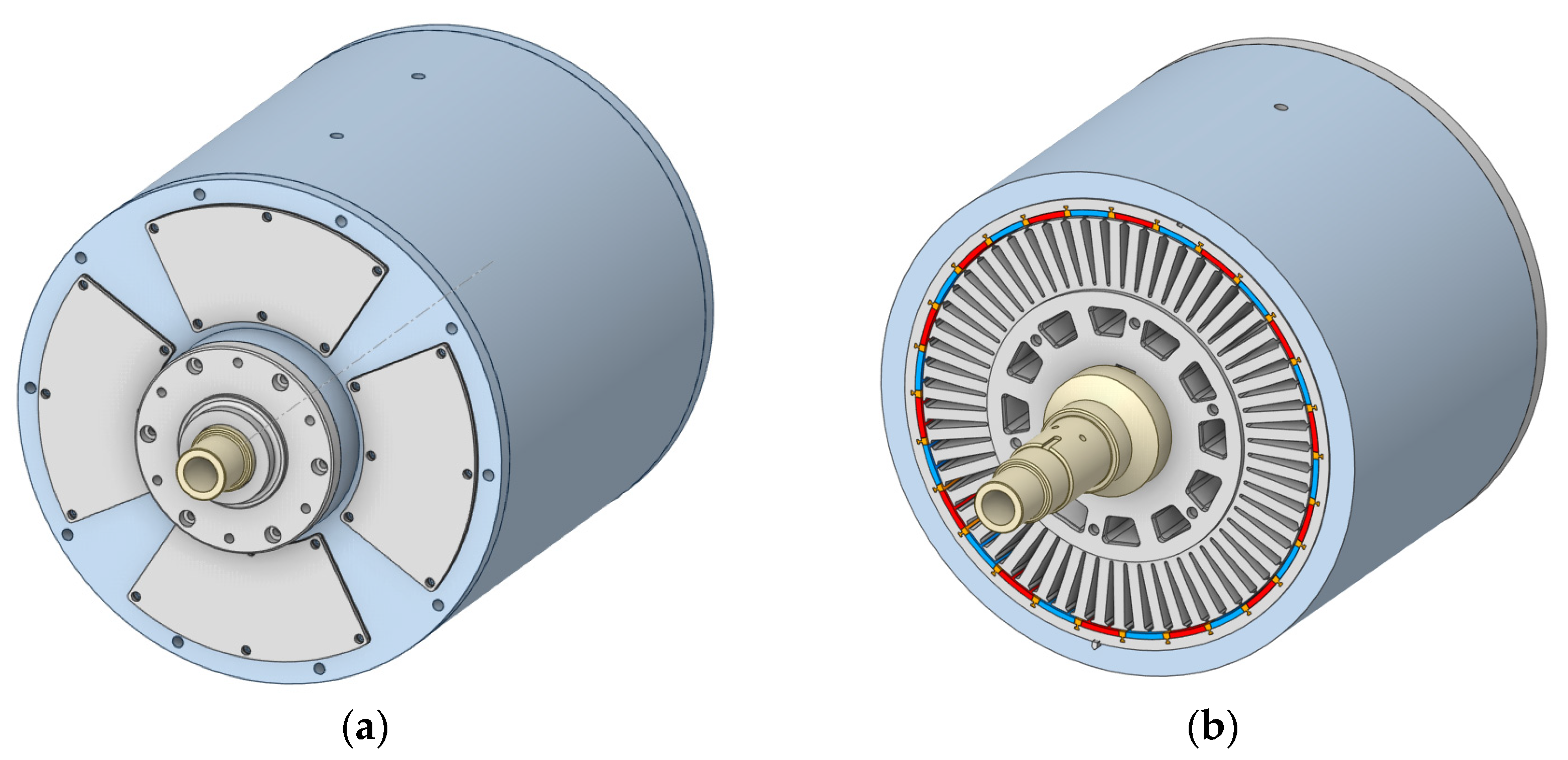
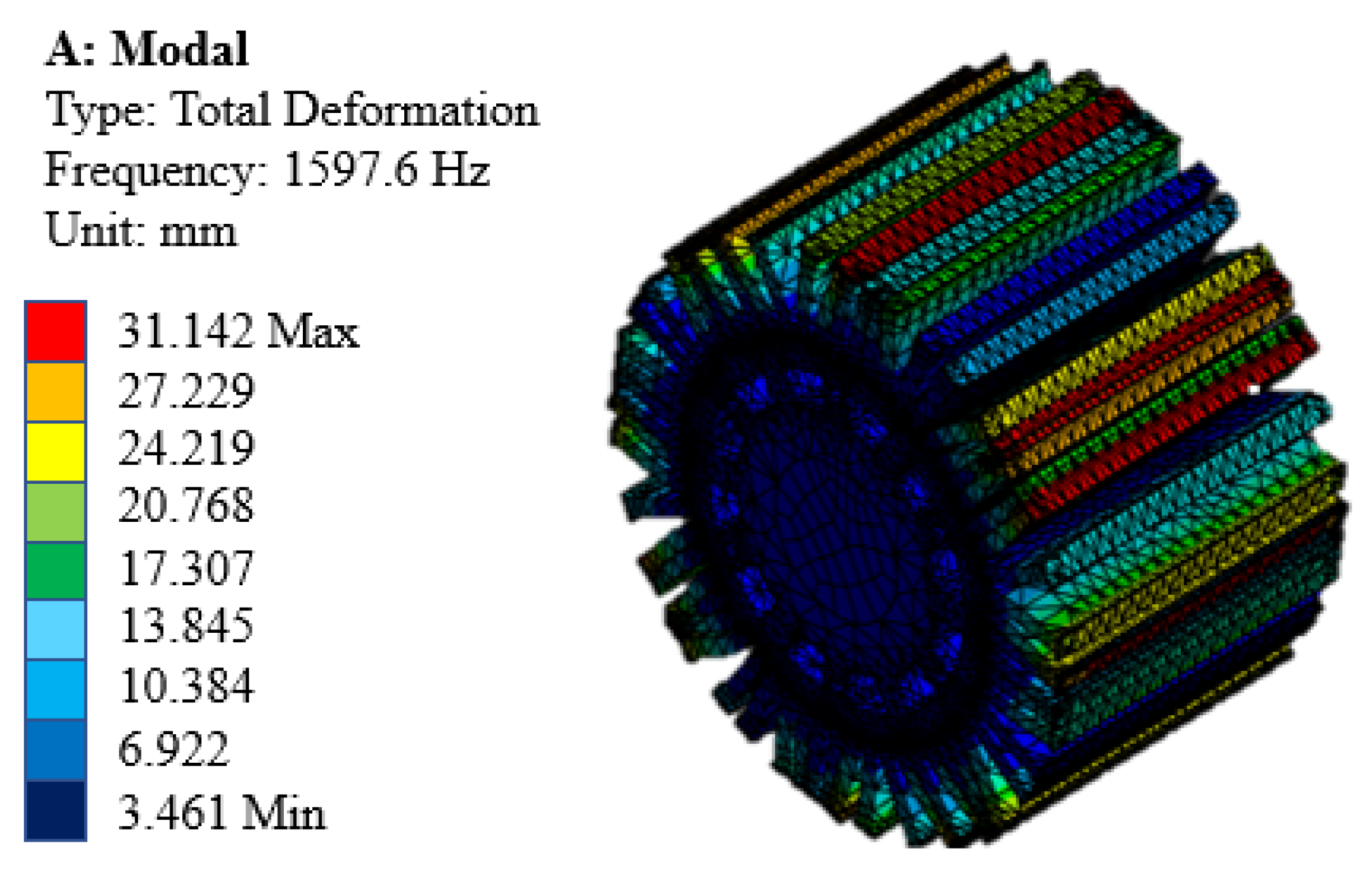
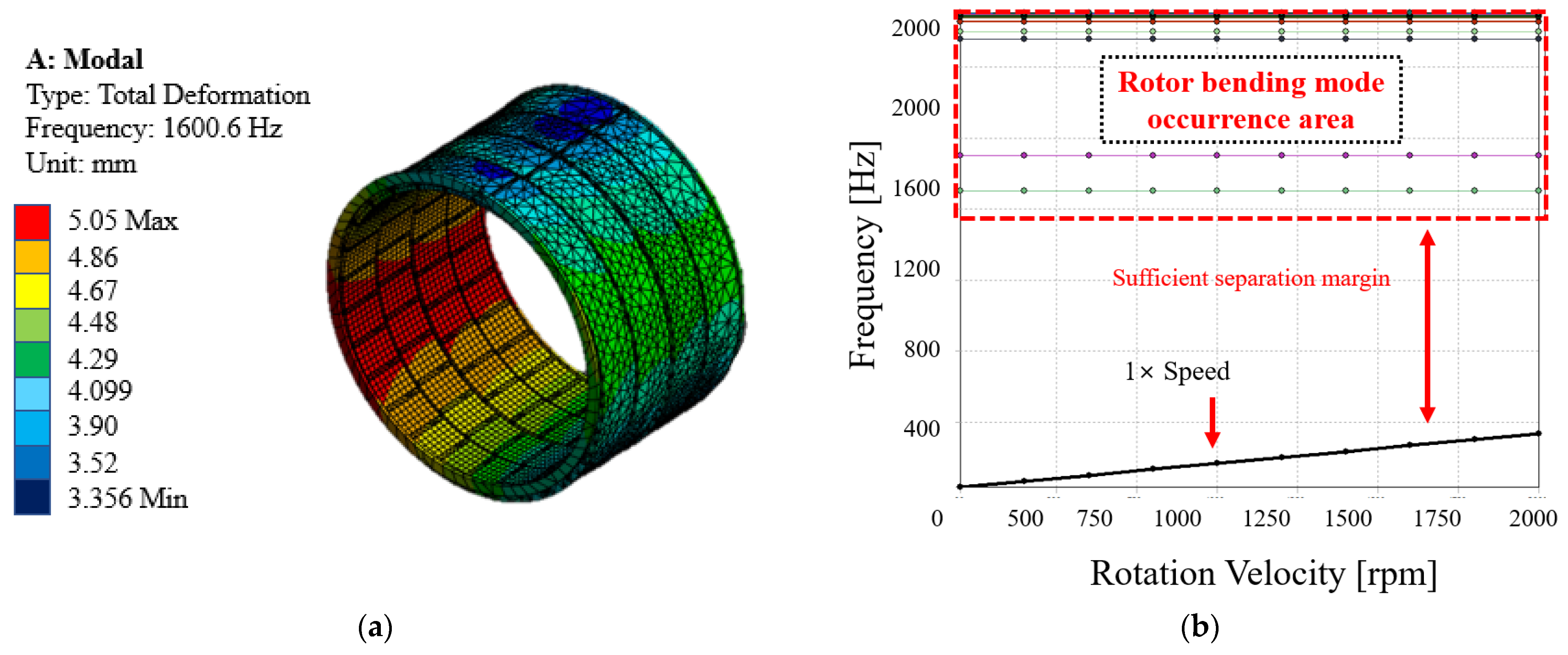
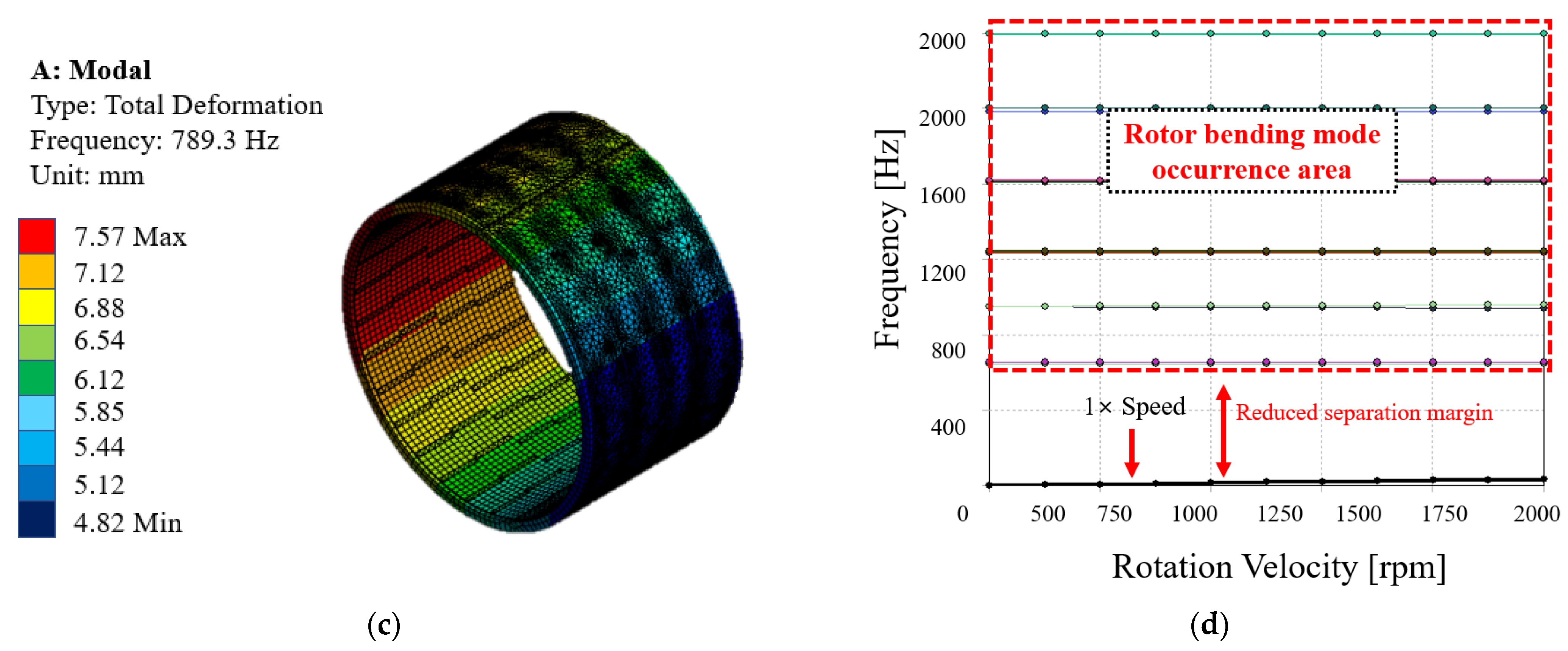

| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Inner diameter of rotor | 444 mm | Number of poles | 28 |
| Outer diameter of rotor | 480 mm | Number of slots | 60 |
| Inner diameter of stator | 111.8 mm | Number of turns | 4 |
| Outer diameter of stator | 440 mm | Current density | 5 A/mm2 |
| Stack | 280 mm | Magnet material | N45SH |
| Pole arc ratio | 0.85 | Core material | 35JN270 |
| Parameters | Eccentricity | Non-Eccentricity | Unit |
|---|---|---|---|
| Back-EMF | 861.5 | 859.17 | V |
| Back-EMF THD | 21.07 | 21.22 | % |
| Power | 77.09 kW | 74.85 | kW |
| Torque | 669.24 Nm | 665.77 | Nm |
| Torque ripple | 12.7 | 15.1 | % |
| Core loss | 3.84 kW | 5.65 | kW |
| Eddy current loss | 0.53 | 0.9 | kW |
| Efficiency | 94.03 | 91.2 | % |
| Parameters | Value |
|---|---|
| SPL in normal state | 59 dB |
| SPL in eccentric state | 65.84 dB |
| Increase in dB | +6.84 dB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, W.-S.; Kim, Y.-S.; Choi, Y.-T.; Shin, K.-H.; Choi, J.-Y. Electromagnetic and NVH Characteristic Analysis of Eccentric State for Surface-Mounted Permanent Magnet Synchronous Generators in Wave Power Applications. Appl. Sci. 2025, 15, 9697. https://doi.org/10.3390/app15179697
Jung W-S, Kim Y-S, Choi Y-T, Shin K-H, Choi J-Y. Electromagnetic and NVH Characteristic Analysis of Eccentric State for Surface-Mounted Permanent Magnet Synchronous Generators in Wave Power Applications. Applied Sciences. 2025; 15(17):9697. https://doi.org/10.3390/app15179697
Chicago/Turabian StyleJung, Woo-Sung, Yeon-Su Kim, Yeon-Tae Choi, Kyung-Hun Shin, and Jang-Young Choi. 2025. "Electromagnetic and NVH Characteristic Analysis of Eccentric State for Surface-Mounted Permanent Magnet Synchronous Generators in Wave Power Applications" Applied Sciences 15, no. 17: 9697. https://doi.org/10.3390/app15179697
APA StyleJung, W.-S., Kim, Y.-S., Choi, Y.-T., Shin, K.-H., & Choi, J.-Y. (2025). Electromagnetic and NVH Characteristic Analysis of Eccentric State for Surface-Mounted Permanent Magnet Synchronous Generators in Wave Power Applications. Applied Sciences, 15(17), 9697. https://doi.org/10.3390/app15179697






