Hybrid Hourly Solar Energy Forecasting Using BiLSTM Networks with Attention Mechanism, General Type-2 Fuzzy Logic Approach: A Comparative Study of Seasonal Variability in Lithuania
Abstract
1. Introduction
1.1. Photovoltaic Forecasting Challenges
1.2. State-of-the-Art Review
1.3. Research Gaps and Motivation
1.4. Research Contributions and Theoretical Significance
2. Theoretical Background
2.1. Preprocessing Techniques
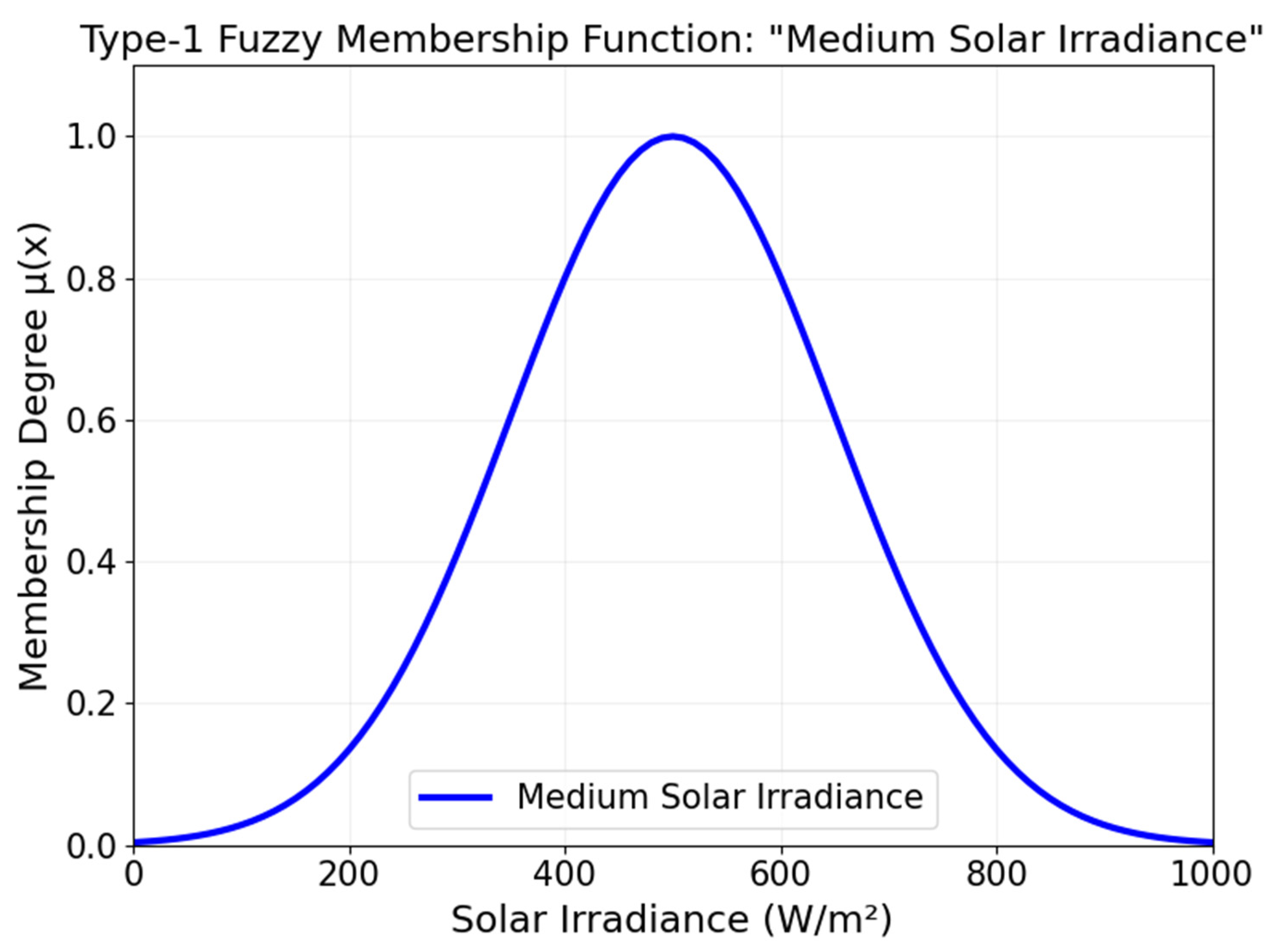
2.1.1. General Type-2 Fuzzy Logic Systems
2.1.2. Time to Vector
2.1.3. Variational Mode Decomposition (VMD)
2.1.4. Sine-Cosine Transformation
2.1.5. Attention Mechanism
2.2. Main Forecasting Models
2.2.1. Bidirectional Long Short-Term Memory (BiLSTM)
2.2.2. Sample Convolution and Interactive Neural Networks (SCINet)
- (odd-indexed elements)
- (even-indexed elements)
2.3. Evaluation Metrics
- Normalized Root Mean Squared Error (nRMSE%): Based on maximum observed power, emphasizing larger errors
- Normalized Mean Absolute Error (NMAE%): Based on plant capacity, providing a reliable accuracy measure
- Weighted Mean Absolute Error (WMAE%): Based on total energy production, accounting for generation-weighted errors
3. Proposed Model Architecture
3.1. Forecasting Scope and Temporal Framework
3.2. Data Description and Implementation Details
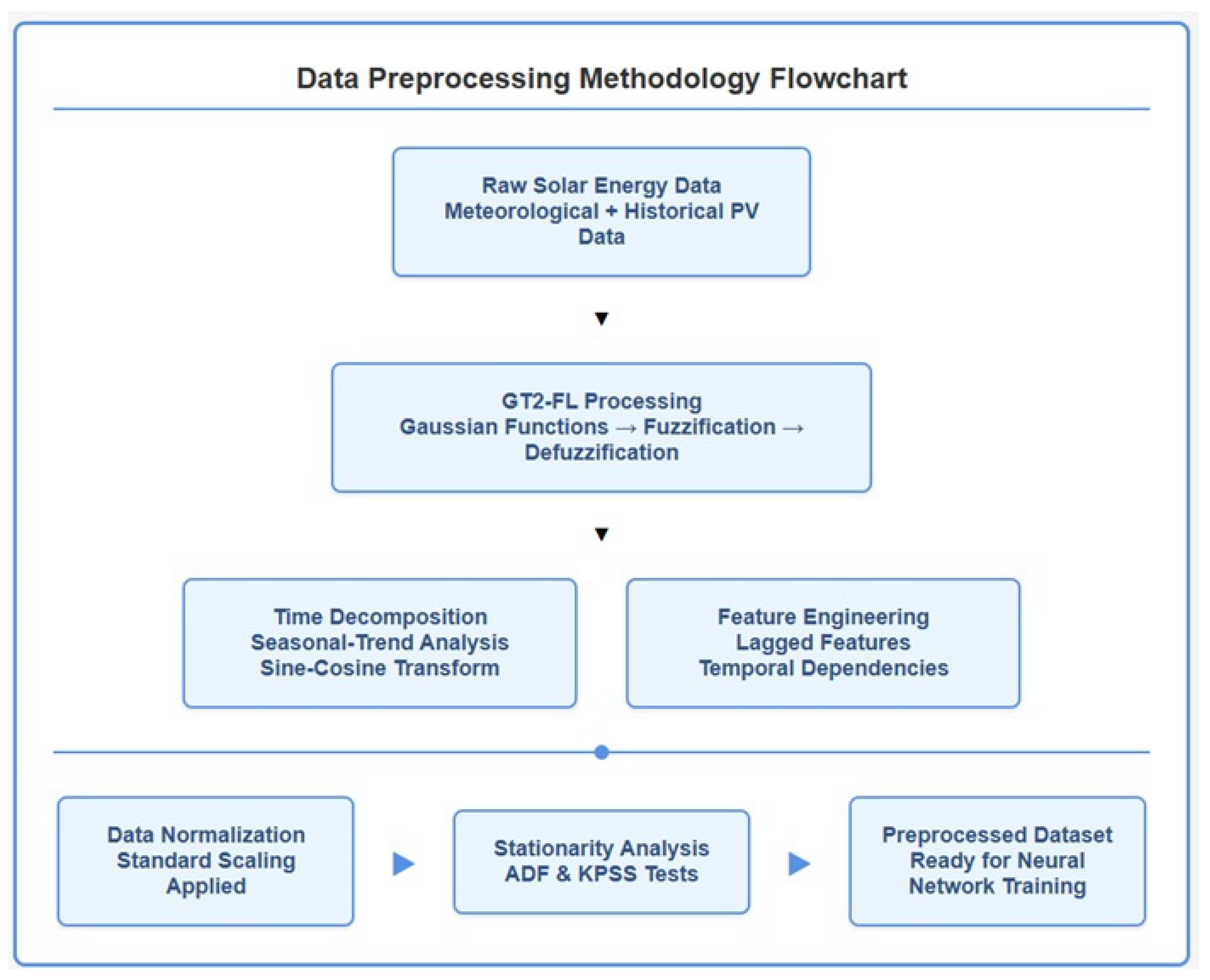
3.3. Data Preprocessing Pipeline
3.3.1. Fuzzification and Defuzzification
3.3.2. Temporal Feature Engineering and Preprocessing Workflow
- Time Series Decomposition: Solar power data is decomposed into trend, seasonal, and residual components using additive decomposition
- Cyclical Feature Encoding: Time-related variables undergo sine-cosine transformations to preserve the periodic nature and enable the recognition of recurring patterns.
- Lagged Features: Historical data from previous time steps are incorporated to capture temporal dependencies, using actual measurements rather than predicted values during rolling forecasting.
- Normalization: Standard scaling ensures all features operate on comparable scales, preventing numerical instability during training.
3.3.3. Stationarity and Statistical Analysis
3.3.4. Meteorological Impact Integration
3.4. Hybrid Model Architectures
3.4.1. BiLSTM-Based Models with Attention Mechanism
- BiLSTM with Time2Vec Integration
- BiLSTM with VMD Integration
3.4.2. SCINet-Based Models with Self-Attention Mechanism
- SCINet with Time2Vec Integration
- SCINet with VMD Integration
3.5. Rolling Forecasting Strategy
3.6. Model Training and Evaluation
4. Result
4.1. Comparison of Neural Network Architectures
- Model 1 (BiLSTM with Time2Vec): This model utilizes bidirectional LSTM layers with Time2Vec temporal encoding. The architecture integrates attention mechanisms between LSTM layers and features residual connections to enhance gradient flow.
- Model 2 (BiLSTM with VMD): This model enhances the BiLSTM architecture with VMD-based feature extraction. It combines mode decomposition with bidirectional LSTM layers and attention mechanisms for comprehensive temporal pattern capture.
- Model 3 (SCINet with Time2Vec): An input layer processes 24-h sequences with Time2Vec encoding, followed by spatial attention mechanisms and SCINet blocks for capturing temporal dependencies. The model employs convolutional layers with spatial attention and residual connections, culminating in global mean pooling and dense layers for prediction.
- Model 4 (SCINet with VMD): This architecture builds upon SCINet by incorporating VMD for signal processing. It maintains self-attention and SCINet blocks while leveraging decomposed signal components for enhanced feature extraction.
4.2. Performance Evaluation Metrics
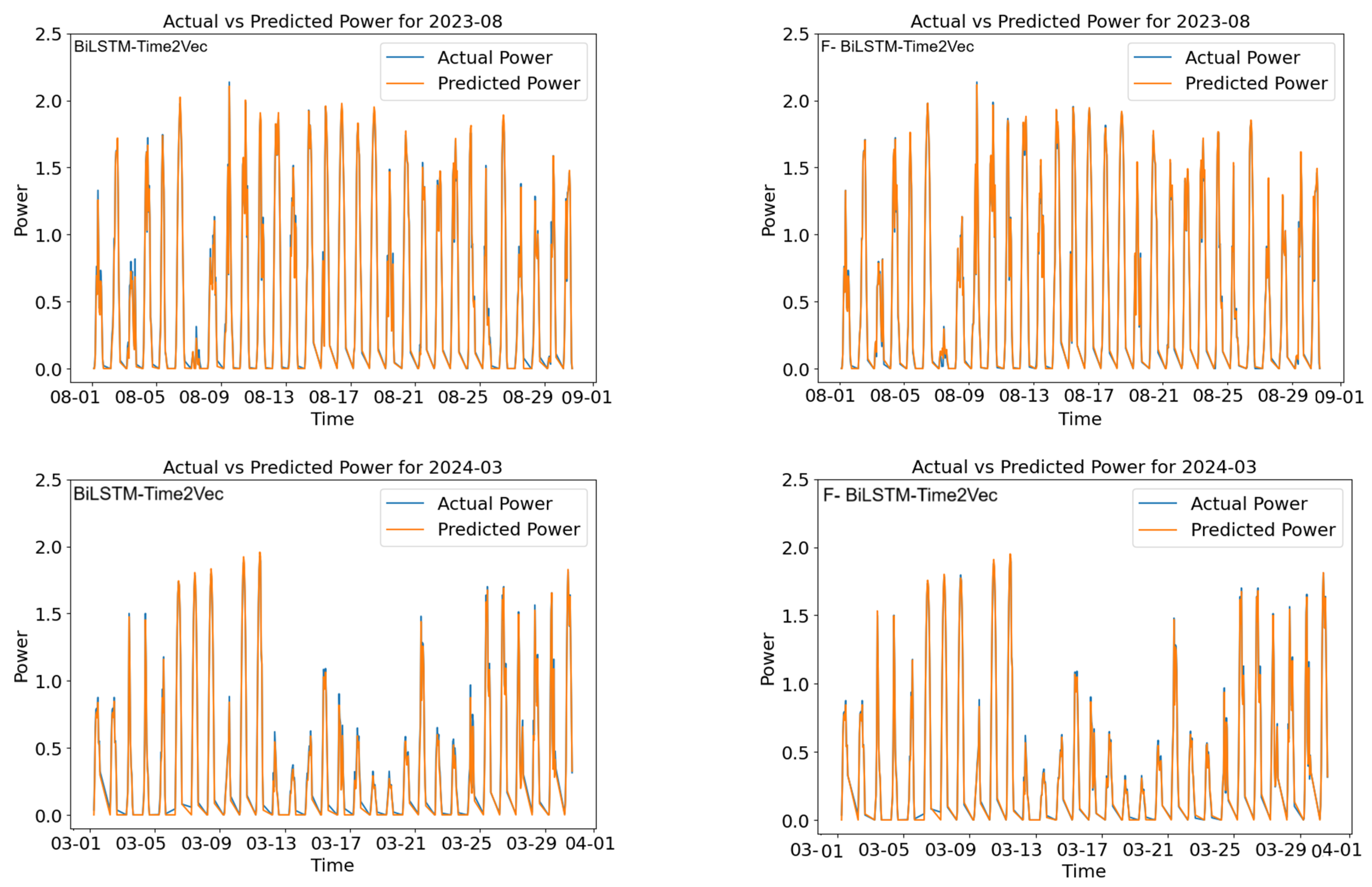
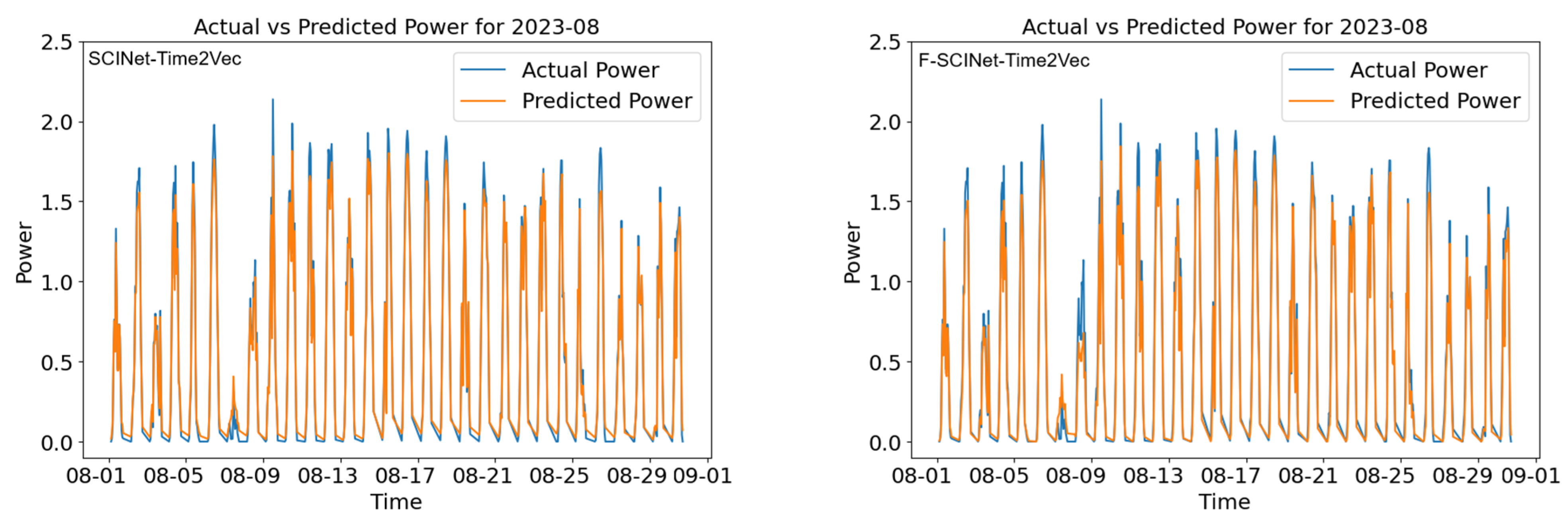
4.3. Comparing Fuzzified and Non-Fuzzified Versions of Each Architecture
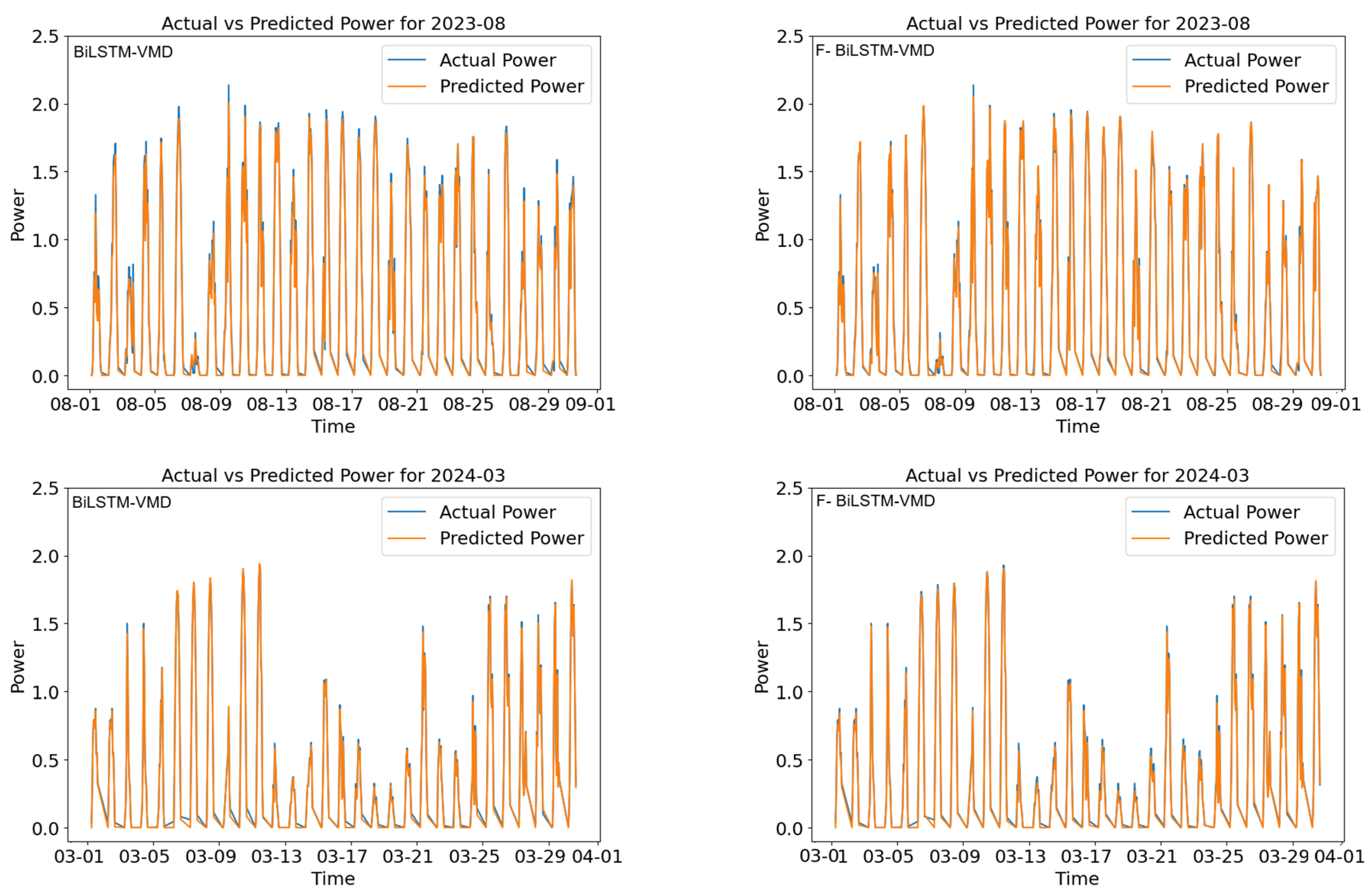
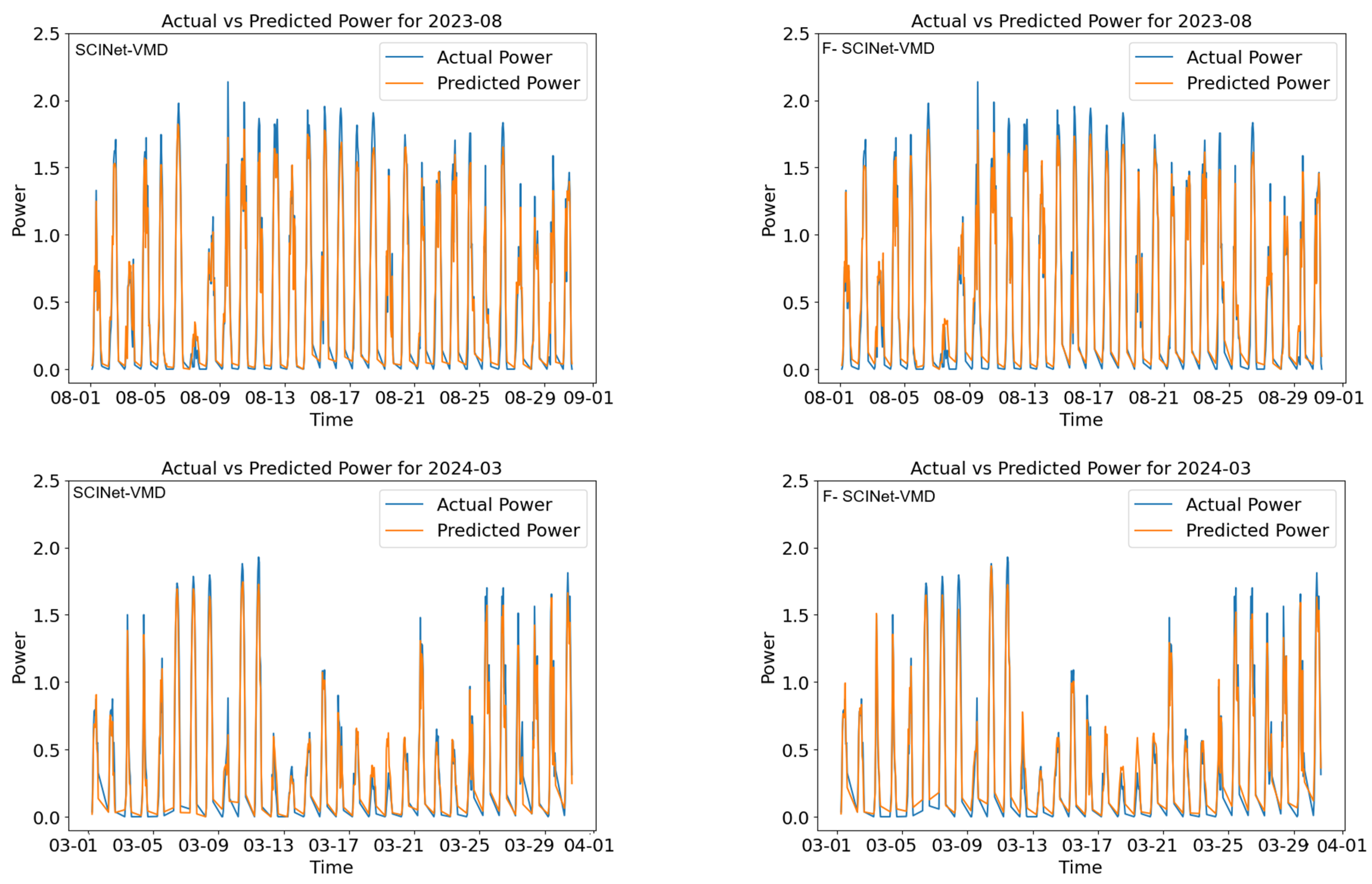
4.4. Seasonal Performance
4.5. Structural Advantages of the Hybrid Approach
4.6. Statistical Significance Analysis
- Descriptive Statistics: F-BiLSTM-Time2Vec demonstrated the most consistent performance with the lowest mean nRMSE of 1.256% ± 0.464%, followed by F-BiLSTM-VMD (1.571% ± 0.660%) and BiLSTM-Time2Vec (1.733% ± 0.521%). SCINet-based architectures exhibited significantly higher error rates with greater variability (F-SCINet-Time2Vec: 4.393% ± 2.783%).
- Statistical Testing: Using F-BiLSTM-Time2Vec as a reference, paired t-tests revealed statistically significant differences across all competing models (p < 0.001). Cohen’s d calculations showed large effect sizes: BiLSTM-Time2Vec (d = 1.663), F-BiLSTM-VMD (d = 0.994), and BiLSTM-VMD (d = 2.582), indicating practically significant improvements beyond statistical significance.
- Non-parametric Validation: Shapiro–Wilk tests revealed non-normal distributions across models, necessitating Wilcoxon signed-rank tests for validation. These confirmed the parametric results (p < 0.001 for all comparisons), strengthening confidence in our conclusions despite non-normal data distributions.
- Time Series Considerations: Lag-1 autocorrelation analysis showed no significant temporal dependency (r = 0.374, p = 0.115), validating the independence assumption. One-way Analysis of Variance (ANOVA) confirmed substantial model differences (F = 11.85, p < 0.001).
4.7. Architectural Comparison and Computational Considerations
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviation | Full Form |
| ADF | Augmented Dickey–Fuller |
| AI | Artificial Intelligence |
| ANN | Artificial Neural Network |
| ANOVA | Analysis of Variance |
| API | Application Programming Interface |
| ARIMA | Autoregressive Integrated Moving Average |
| BiGRU | Bidirectional Gated Recurrent Unit |
| BiLSTM | Bidirectional Long Short-Term Memory |
| CEEMDAN | Complete Ensemble Empirical Mode Decomposition with Adaptive Noise |
| CNN | Convolutional Neural Network |
| CPV | Concentrated Photovoltaic |
| CSP | Concentrated Solar Power |
| DHI | Diffuse Horizontal Irradiance |
| DL | Deep Learning |
| DNN | Deep Neural Network |
| DNI | Direct Normal Irradiance |
| EMD | Empirical Mode Decomposition |
| EU | European Union |
| F&W | Fall and Winter |
| FL | Fuzzy Logic |
| FOU | Footprint of Uncertainty |
| GAN | Generative Adversarial Network |
| GHG | Greenhouse Gas |
| GHI | Global Horizontal Irradiance |
| GRU | Gated Recurrent Unit |
| GT2-FL | General Type-2 Fuzzy Logic |
| IMF | Intrinsic Mode Function |
| KPSS | Kwiatkowski-Phillips-Schmidt-Shin |
| LHMT | Lithuanian Hydrometeorological Service |
| LSTM | Long Short-Term Memory |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percentage Error |
| MRE | Mean Relative Error |
| NARX | Non-linear Autoregressive Exogenous |
| NMAE | Normalized Mean Absolute Error |
| nRMSE | Normalized Root Mean Square Error |
| PSO | Particle Swarm Optimization |
| PV | Photovoltaic |
| RE | Renewable Energy |
| RMSE | Root Mean Square Error |
| RNN | Recurrent Neural Network |
| S&S | Spring and Summer |
| SCINet | Sample Convolution and Interactive Neural Network |
| SVM | Support Vector Machine |
| T1-FL | Type-1 Fuzzy Logic |
| T1-FS | Type-1 Fuzzy Set |
| T2-FL | Type-2 Fuzzy Logic |
| T2-FS | Type-2 Fuzzy Set |
| TCN | Temporal Convolutional Network |
| Time2Vec | Time to Vector |
| TWh | Terawatt hours |
| UHD | Ultra High Definition |
| VMD | Variational Mode Decomposition |
| WMAE | Weighted Mean Absolute Error |
| WOA | Whale Optimization Algorithm |
References
- Paramati, S.R.; Shahzad, U.; Doğan, B. The role of environmental technology for energy demand and energy efficiency: Evidence from OECD countries. Renew. Sustain. Energy Rev. 2022, 153, 111735. [Google Scholar] [CrossRef]
- Paraschiv, L.S.; Paraschiv, S. Contribution of renewable energy (hydro, wind, solar and biomass) to decarbonization and transformation of the electricity generation sector for sustainable development. Energy Rep. 2023, 9, 535–544. [Google Scholar] [CrossRef]
- Foley, A.M.; McIlwaine, N.; Morrow, D.J.; Hayes, B.P.; Zehir, M.A.; Mehigan, L.; Papari, B.; Edrington, C.S.; Baran, M. A critical evaluation of grid stability and codes, energy storage and smart loads in power systems with wind generation. Energy 2020, 205, 117671. [Google Scholar] [CrossRef]
- Simsek, Y.; Santika, W.G.; Anisuzzaman, M.; Urmee, T.; Bahri, P.A.; Escobar, R. An analysis of additional energy requirement to meet the sustainable development goals. J. Clean. Prod. 2020, 272, 122646. [Google Scholar] [CrossRef]
- Eurostat. Renewable Energy Statistics. Available online: https://ec.europa.eu/eurostat/statistics-explained/index.php?title=Renewable_energy_statistics (accessed on 4 July 2025).
- Sharma, N.; Sharma, P.; Irwin, D.; Shenoy, P. Predicting solar generation from weather forecasts using machine learning. In Proceedings of the IEEE International Conference on Smart Grid Communications (SmartGridComm), Brussels, Belgium, 17–20 October 2011; pp. 528–533. [Google Scholar] [CrossRef]
- Nwagu, C.N.; Ujah, C.O.; Kallon, D.V.; Aigbodion, V.S. Integrating solar and wind energy into the electricity grid for improved power accessibility. Unconv. Resour. 2025, 5, 100129. [Google Scholar] [CrossRef]
- Cocco, D.; Migliari, L.; Petrollese, M. A hybrid CSP–CPV system for improving the dispatchability of solar power plants. Energy Convers. Manag. 2016, 114, 312–323. [Google Scholar] [CrossRef]
- Rodríguez, F.; Fleetwood, A.; Galarza, A.; Fontán, L. Predicting solar energy generation through artificial neural networks using weather forecasts for microgrid control. Renew. Energy 2018, 126, 855–864. [Google Scholar] [CrossRef]
- Moser Baer Solar. Solar PV Monitoring: Maximizing Performance Through Real-Time Analytics. Available online: https://www.moserbaersolar.com/maintenance-and-performance-optimization/solar-pv-monitoring-maximizing-performance-through-real-time-analytics/ (accessed on 4 July 2025).
- Rodriguez, J.; Pontt, J.; Correa, P.; Lezana, P.; Cortes, P. Predictive power control of an AC/DC/AC converter. In Proceedings of the 40th IAS Annual Meeting Conference Record of the Industry Applications Conference, Hong Kong, China, 2–6 October 2005; pp. 934–939. [Google Scholar]
- Narkutė, V. Forecast of Energy Produced by Solar Power Plants. Ph.D. Thesis, Vilniaus Universitetas, Vilnius, Lithuania, 2022. [Google Scholar]
- Mellit, A.; Massi Pavan, A.; Ogliari, E.; Leva, S.; Lughi, V. Advanced methods for photovoltaic output power forecasting: A review. Appl. Sci. 2020, 10, 487. [Google Scholar] [CrossRef]
- Sobri, S.; Koohi-Kamali, S.; Rahim, N.A. Solar photovoltaic generation forecasting methods: A review. Energy Convers. Manag. 2018, 156, 459–497. [Google Scholar] [CrossRef]
- Kudo, M.; Takeuchi, A.; Nozaki, Y.; Endo, H.; Sumita, J. Forecasting electric power generation in a photovoltaic power system for an energy network. Electr. Eng. Jpn. 2009, 167, 16–23. [Google Scholar] [CrossRef]
- Sen, Z. Fuzzy algorithm for estimation of solar irradiation from sunshine duration. Sol. Energy 1998, 63, 39–49. [Google Scholar] [CrossRef]
- Gautam, N.K.; Kaushika, N.D. A model for the estimation of global solar radiation using fuzzy random variables. J. Appl. Meteorol. Climatol. 2002, 41, 1267–1276. [Google Scholar] [CrossRef]
- Rizwan, M.; Jamil, M.; Kirmani, S.; Kothari, D.P. Fuzzy logic-based modeling and estimation of global solar energy using meteorological parameters. Energy 2014, 70, 685–691. [Google Scholar] [CrossRef]
- Nalbant, K.G.; Özdemir, Ş.; Özdemir, Y. Evaluating the campus climate factors using an interval type-2 fuzzy ANP. Sigma J. Eng. Nat. Sci. 2024, 42, 89–98. [Google Scholar] [CrossRef]
- Mendel, J.M.; John, R.B. Type 2-Fuzzy sets made simple. IEEE Trans. Fuzzy Syst. 2002, 10, 117–127. [Google Scholar] [CrossRef]
- Hinton, G.E.; Osindero, S.; Teh, Y. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef]
- Jlidi, M.; Hamidi, F.; Barambones, O.; Abbassi, R.; Jerbi, H.; Aoun, M.; Karami-Mollaee, A. An artificial neural network for solar energy prediction and control using Jaya-SMC. Electronics 2023, 12, 592. [Google Scholar] [CrossRef]
- Zhidan, L.; Wei, G.; Qingfu, L.; Zhengjun, Z. A hybrid model for financial time-series forecasting based on mixed methodologies. Expert Syst. 2021, 38, e12633. [Google Scholar]
- Ni, Z.; Zhang, C.; Karlsson, M.; Gong, S. A study of deep learning-based multi-horizon building energy forecasting. Energy Build. 2024, 303, 113810. [Google Scholar] [CrossRef]
- Bai, S.; Kolter, J.Z.; Koltun, V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar] [CrossRef]
- Li, Y.; Song, L.; Zhang, S.; Kraus, L.; Adcox, T.; Willardson, R.; Komandur, A.; Lu, N. A TCN-based hybrid forecasting framework for hours-ahead utility-scale PV forecasting. IEEE Trans. Smart Grid 2023, 14, 4073–4085. [Google Scholar] [CrossRef]
- Kong, X.; Du, X.; Xu, Z.; Xue, G. Predicting solar radiation for space heating with thermal storage system based on temporal convolutional network-attention model. Appl. Therm. Eng. 2023, 219, 119574. [Google Scholar] [CrossRef]
- Liu, M.; Qin, H.; Cao, R.; Deng, S. Short-term load forecasting based on improved TCN and DenseNet. IEEE Access 2022, 10, 115945–115957. [Google Scholar] [CrossRef]
- Limouni, T.; Yaagoubi, R.; Bouziane, K.; Guissi, K.; Baali, E.H. Accurate one step and multistep forecasting of very short-term PV power using LSTM-TCN model. Renew. Energy 2023, 205, 1010–1024. [Google Scholar]
- Zhao, Y.; Peng, X.; Tu, T.; Li, Z.; Yan, P.; Li, C. WOA-VMD-SCINet: Hybrid model for accurate prediction of ultra-short-term Photovoltaic generation power considering seasonal variations. Energy Rep. 2024, 12, 3470–3487. [Google Scholar] [CrossRef]
- Huang, X.; Li, Q.; Tai, Y.; Chen, Z.; Liu, J.; Shi, J.; Liu, W. Time series forecasting for hourly photovoltaic power using conditional generative adversarial network and Bi-LSTM. Energy 2022, 246, 123403. [Google Scholar] [CrossRef]
- Zhang, C.; Peng, T.; Nazir, M.S. A novel integrated photovoltaic power forecasting model based on variational mode decomposition and CNN-BiGRU considering meteorological variables. Electr. Power Syst. Res. 2022, 213, 108796. [Google Scholar] [CrossRef]
- Trong, T.N.; Son, H.V.X.; Dinh, H.D.; Takano, H.; Duc, T.N. Short-term PV power forecast using hybrid deep learning model and Variational Mode Decomposition. Energy Rep. 2023, 9, 712–717. [Google Scholar] [CrossRef]
- Wang, X.; Ma, W. A hybrid deep learning model with an optimal strategy based on improved VMD and transformer for short-term photovoltaic power forecasting. Energy 2024, 295, 131071. [Google Scholar] [CrossRef]
- Peng, S.; Zhu, J.; Wu, T.; Yuan, C.; Cang, J.; Zhang, K.; Pecht, M. Prediction of wind and PV power by fusing the multi-stage feature extraction and a PSO-BiLSTM model. Energy 2024, 298, 131345. [Google Scholar] [CrossRef]
- Voyant, C.; Notton, G.; Kalogirou, S.; Nivet, M.L.; Paoli, C.; Motte, F.; Fouilloy, A. Machine learning methods for solar radiation forecasting: A review. Renew. Energy 2017, 105, 569–582. [Google Scholar] [CrossRef]
- Chaturvedi, D.K.; Isha, I. Solar power forecasting: A review. Int. J. Comput. Appl. 2016, 140, 28–50. [Google Scholar] [CrossRef]
- Rana, M.; Rahman, A. Multiple steps ahead solar photovoltaic power forecasting based on univariate machine learning models and data re-sampling. Sustain. Energy Grids Netw. 2020, 21, 100286. [Google Scholar] [CrossRef]
- Wang, K.; Qi, X.; Liu, H. A comparison of day-ahead photovoltaic power forecasting models based on deep learning neural network. Appl. Energy 2019, 251, 113315. [Google Scholar] [CrossRef]
- Gao, M.; Li, J.; Hong, F.; Long, D. Day-ahead power forecasting in a large-scale photovoltaic plant based on weather classification using LSTM. Energy 2019, 187, 115838. [Google Scholar] [CrossRef]
- Qing, X.; Niu, Y. Hourly day-ahead solar irradiance prediction using weather forecasts by LSTM. Energy 2018, 148, 461–468. [Google Scholar] [CrossRef]
- Cabello-López, T.; Carranza-García, M.; Riquelme, J.C.; García-Gutiérrez, J. Forecasting solar energy production in Spain: A comparison of univariate and multivariate models at the national level. Appl. Energy 2023, 350, 121645. [Google Scholar] [CrossRef]
- Gao, B.; Huang, X.; Shi, J.; Tai, Y.; Zhang, J. Hourly forecasting of solar irradiance based on CEEMDAN and multi-strategy CNN-LSTM neural networks. Renew. Energy 2020, 162, 1665–1683. [Google Scholar] [CrossRef]
- Liu, M.; Zeng, A.; Chen, M.; Xu, Z.; Lai, Q.; Ma, L.; Xu, Q. Scinet: Time series modeling and forecasting with sample convolution and interaction. Adv. Neural Inf. Process. Syst. 2022, 35, 5816–5828. [Google Scholar]
- Li, F.F.; Wang, S.Y.; Wei, J.H. Long term rolling prediction model for solar radiation combining empirical mode decomposition (EMD) and artificial neural network (ANN) techniques. J. Renew. Sustain. Energy 2018, 10, 1. [Google Scholar] [CrossRef]
- Lanbaran, N.M.; Celik, E.; Yigider, M. Evaluation of investment opportunities with interval-valued fuzzy TOPSIS method. Appl. Math. Nonlinear Sci. 2020, 5, 461–474. [Google Scholar] [CrossRef]
- Melin, P.; Castillo, O. A review on Type 2-Fuzzy logic applications in clustering, classification and pattern recognition. Appl. Soft Comput. 2014, 21, 568–577. [Google Scholar] [CrossRef]
- Mittal, K.; Jain, A.; Vaisla, K.S.; Castillo, O.; Kacprzyk, J. A comprehensive review on type 2 fuzzy logic applications: Past, present and future. Eng. Appl. Artif. Intell. 2020, 95, 103916. [Google Scholar] [CrossRef]
- Juang, C.-F.; Huang, R.-B.; Lin, Y.-Y. A recurrent self-evolving interval Type 2-Fuzzy neural network for dynamic system processing. IEEE Trans. Fuzzy Syst. 2009, 17, 1092–1105. [Google Scholar] [CrossRef]
- Geng, D.; Wang, B.; Gao, Q. A hybrid photovoltaic/wind power prediction model based on Time2Vec, WDCNN and BiLSTM. Energy Convers. Manag. 2023, 291, 117342. [Google Scholar] [CrossRef]
- Zosso, D.; Dragomiretskiy, K.; Bertozzi, A.L.; Weiss, P.S. Two-dimensional compact variational mode decomposition: Spatially compact and spectrally sparse image decomposition and segmentation. J. Math. Imaging Vis. 2017, 58, 294–320. [Google Scholar] [CrossRef]
- Guermoui, M.; Fezzani, A.; Mohamed, Z.; Rabehi, A.; Ferkous, K.; Bailek, N.; Ghoneim, S.S.M. An analysis of case studies for advancing photovoltaic power forecasting through multi-scale fusion techniques. Sci. Rep. 2024, 14, 6653. [Google Scholar] [CrossRef] [PubMed]
- Efimov, V.M.; Reznik, A.L.; Bondarenko, Y.V. Increasing the sine-cosine transformation accuracy in signal approximation and interpolation. Optoelectron. Instrum. Data Process. 2008, 44, 218–227. [Google Scholar] [CrossRef]
- Niu, Z.; Zhong, G.; Yu, H. A review on the attention mechanism of deep learning. Neurocomputing 2021, 452, 48–62. [Google Scholar] [CrossRef]
- Lin, J.; Ma, J.; Zhu, J.; Cui, Y. Short-term load forecasting based on LSTM networks considering attention mechanism. Int. J. Electr. Power Energy Syst. 2022, 137, 107818. [Google Scholar] [CrossRef]
- Yang, M.; Wang, J. Adaptability of financial time series prediction based on BiLSTM. Procedia Comput. Sci. 2022, 199, 18–25. [Google Scholar] [CrossRef]
- Parri, S.; Teeparthi, K. VMD-SCINet: A hybrid model for improved wind speed forecasting. Earth Sci. Inform. 2024, 17, 329–350. [Google Scholar] [CrossRef]
- Dong, P.; Zuo, Y.; Chen, L.; Li, S.; Zhang, L. VSNT: Adaptive Network Traffic Forecasting via VMD and Deep Learning with SCI-Block and Attention Mechanism. In Proceedings of the 2023 IEEE International Conference on Parallel and Distributed Processing with Applications, Big Data and Cloud Computing, Sustainable Computing and Communications, Social Computing and Networks (ISPA/BDCloud/SocialCom/SustainCom), Haikou, China, 21–23 December 2023; pp. 104–109. [Google Scholar]
- Leva, S.; Dolara, A.; Grimaccia, F.; Mussetta, M.; Ogliari, E. Analysis and validation of 24 hours ahead neural network forecasting of photovoltaic output power. Math. Comput. Simul. 2017, 131, 88–100. [Google Scholar] [CrossRef]
- Arltová, M.; Fedorová, D. Selection of Unit Root Test on the Basis of Length of the Time Series and Value of AR (1) Parameter. Stat. Stat. Econ. J. 2016, 96, 4–17. [Google Scholar]
- Musbah, H.; Aly, H.H.; Little, T.A. A proposed novel adaptive DC technique for non-stationary data removal. Heliyon 2023, 9, 3. [Google Scholar] [CrossRef] [PubMed]





| Approach Category | Key Methods | Limitations | Best Performance | Reference |
|---|---|---|---|---|
| Statistical Models | ARIMA, SVM, Random Forest | Limited handling of non-linear patterns | 15% MRE (Random Forest), 17.70% MAPE (ARIMA) | [36,37,38] |
| Classical Neural Networks | ANN, CNN, DNN | Difficulty with temporal dependencies | R2 = 0.93 (ANN monthly), R = 0.92 (NARX NN) | [22,39] |
| Recurrent Architectures | LSTM, BiLSTM, GRU | Computational complexity, gradient issues | 5% nRMSE (LSTM), 7% nMAE (LSTM), 8% nMAE (GRU) | [24,40,41] |
| Hybrid Deep Learning | CNN-LSTM, TCN-DenseNet | High computational requirements | 23.38% MAPE reduction (TCN-DN), 38.49% error rate (CEEM-CNN-LSTM) | [28,42,43] |
| Advanced Architectures | SCINet, Transformer | Complex hyperparameter tuning | 13.7% MAE (VMD-Transformer), 0.619–1.149 kW RMSE (WOA-VMD-SCINet) | [33,34,44] |
| Signal Processing | VMD, EMD, CEEMDAN | Preprocessing complexity | 93.0% correlation (monthly), 69.8% correlation (daily), 29.05% RMSE, 4.157 RMSE | [32,43,45] |
| Parameter Category | Parameter | Value |
|---|---|---|
| Data Configuration | Look Back Window | 24 |
| Forecast Horizon | 1 | |
| Training Period | 1 January 2023 08:00–5 August 2023 18:00 | |
| Validation Period | 6 August 2023 03:00–15 June 2024 19:00 | |
| Testing Period | 16 June 2024 02:00–31 August 2024 17:00 | |
| Training Parameters | Batch Size | 42 |
| Learning Rate | 1.00 × 10−3 | |
| Weight Decay | 1.00 × 10−5 | |
| Loss Function Epochs | 0.4MSE + 0.3MAE + 0.3Huber 100 | |
| Architecture | Main Units | [512, 256, 128, 64] |
| Time2Vec Models | kernel_size = 64, Dropout: LSTM 0.2, Dense 0.1 | |
| VMD Models | K = 3 modes, Dropout: LSTM 0.2, Dense 0.1 |
| Date | F- BiLSTM-Time2Vec | BiLSTM-Time2Vec | F-BiLSTM-VMD | BiLSTM-VMD | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| nRMSE | NMAE | WMAE | nRMSE | NMAE | WMAE | nRMSE | NMAE | WMAE | nRMSE | NMAE | WMAE | |
| S&S | ||||||||||||
| 2023-04 | 1.0995 | 0.7467 | 3.2800 | 1.2082 | 0.8457 | 3.7149 | 1.2012 | 0.8110 | 3.5623 | 1.9509 | 1.3322 | 5.8516 |
| 2023-05 | 1.3551 | 0.9453 | 2.7461 | 1.2352 | 0.8606 | 2.5002 | 1.1321 | 0.7785 | 2.2615 | 2.1012 | 1.5118 | 4.3918 |
| 2023-06 | 1.1948 | 0.8375 | 2.8634 | 1.3627 | 0.9362 | 3.2006 | 1.2164 | 0.8207 | 2.8061 | 1.9619 | 1.3692 | 4.6813 |
| 2023-07 | 1.1574 | 0.8170 | 2.8759 | 1.5974 | 1.1387 | 4.0082 | 1.2951 | 0.9215 | 3.2438 | 1.9152 | 1.3519 | 4.7586 |
| 2023-08 | 0.9719 | 0.6816 | 2.6613 | 1.6710 | 1.1600 | 4.5291 | 1.5871 | 1.0900 | 4.2557 | 2.1316 | 1.5195 | 5.9327 |
| 2023-09 | 1.0987 | 0.7432 | 2.4083 | 2.2094 | 1.6347 | 5.2975 | 1.6899 | 1.1565 | 3.7477 | 2.9258 | 2.1495 | 6.9659 |
| 2024-04 | 1.2697 | 0.8714 | 4.5141 | 1.6860 | 1.2171 | 6.3050 | 1.5477 | 1.0748 | 5.5677 | 2.3897 | 1.6987 | 8.7997 |
| 2024-05 | 1.1912 | 0.8233 | 2.5346 | 1.2658 | 0.8803 | 2.7101 | 1.1764 | 0.8029 | 2.4719 | 2.1061 | 1.5092 | 4.6463 |
| 2024-06 | 1.1514 | 0.7842 | 3.0696 | 1.4826 | 1.0134 | 3.9670 | 1.3484 | 0.9017 | 3.5297 | 1.9505 | 1.3389 | 5.2409 |
| 2024-07 | 1.6030 | 0.9706 | 3.7529 | 2.0055 | 1.2217 | 4.7240 | 1.5110 | 1.0423 | 4.0302 | 2.2931 | 1.5486 | 5.9878 |
| 2024-08 | 0.9720 | 0.7169 | 2.4385 | 1.5632 | 1.0999 | 3.7412 | 1.5014 | 1.0646 | 3.6210 | 2.1073 | 1.5156 | 5.1549 |
| F&W | ||||||||||||
| 2023-01 | 0.9410 | 0.4999 | 28.4122 | 1.3034 | 0.7086 | 40.2726 | 1.2342 | 0.7069 | 40.1770 | 1.5645 | 0.8865 | 50.3838 |
| 2023-02 | 1.0867 | 0.7183 | 8.0396 | 1.7122 | 1.1475 | 12.8430 | 1.4119 | 0.9855 | 11.0305 | 2.0110 | 1.3836 | 15.4861 |
| 2023-03 | 0.8935 | 0.6154 | 3.1645 | 1.6153 | 1.2130 | 6.2379 | 1.1976 | 0.8437 | 4.3386 | 2.0256 | 1.4361 | 7.3851 |
| 2023-10 | 2.1331 | 1.4092 | 10.7094 | 2.7625 | 1.8522 | 14.0767 | 2.7239 | 1.7460 | 13.2694 | 3.7712 | 2.4648 | 18.7321 |
| 2023-11 | 2.7027 | 1.7211 | 36.1714 | 3.0977 | 1.9351 | 40.6689 | 3.8945 | 2.3198 | 48.7539 | 4.4511 | 2.6487 | 55.6667 |
| 2023-12 | 1.5820 | 0.6387 | 87.4059 | 2.3255 | 0.9315 | 127.4846 | 1.7999 | 0.7049 | 96.4637 | 1.8740 | 0.7226 | 98.8857 |
| 2024-01 | 0.6196 | 0.2542 | 12.3043 | 1.1701 | 0.4833 | 23.3938 | 0.9579 | 0.4090 | 19.7990 | 1.2848 | 0.5376 | 26.0215 |
| 2024-02 | 1.0537 | 0.7018 | 9.5734 | 1.8725 | 1.2583 | 17.1650 | 1.6827 | 1.1407 | 15.5608 | 2.2131 | 1.5262 | 20.8197 |
| 2024-03 | 1.0447 | 0.7087 | 3.5622 | 1.5149 | 1.1040 | 5.5493 | 1.3168 | 0.9199 | 4.6240 | 2.1507 | 1.5578 | 7.8308 |
| Averages | ||||||||||||
| Ave of S&S | 1.1877 | 0.8125 | 3.0132 | 1.5715 | 1.0917 | 4.0634 | 1.3824 | 0.9513 | 3.5543 | 2.1667 | 1.5314 | 5.6738 |
| Ave of F&W | 1.3397 | 0.8075 | 22.1492 | 1.9305 | 1.1815 | 31.9658 | 1.8022 | 1.0863 | 28.2241 | 2.3718 | 1.4627 | 33.4679 |
| Entire Ave | 1.2561 | 0.8103 | 11.6244 | 1.7331 | 1.1321 | 16.6195 | 1.5713 | 1.0120 | 14.6557 | 2.2590 | 1.5005 | 18.1812 |
| Test Set | 1.5320 | 0.8340 | 3.0990 | 2.6973 | 1.3392 | 4.9780 | 1.724 | 1.0630 | 3.9520 | 2.9962 | 1.4470 | 3.625 |
| Date | F-SCINet-Time2Vec | SCINet-Time2Vec | F-SCINet-VMD | SCINet-VMD | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| nRMSE | NMAE | WMAE | nRMSE | NMAE | WMAE | nRMSE | NMAE | WMAE | nRMSE | NMAE | WMAE | |
| S&S | ||||||||||||
| 2023-04 | 4.1863 | 2.4873 | 10.9255 | 3.7030 | 2.2168 | 9.7375 | 4.5508 | 3.2229 | 14.1568 | 4.3533 | 3.1900 | 14.0123 |
| 2023-05 | 4.9930 | 3.2968 | 9.5777 | 4.1448 | 2.7157 | 7.8893 | 5.0733 | 3.5023 | 10.1745 | 5.0824 | 3.6188 | 10.5131 |
| 2023-06 | 4.4851 | 2.8912 | 9.8848 | 3.8973 | 2.4807 | 8.4814 | 4.2367 | 2.8235 | 9.6533 | 4.5913 | 3.0199 | 10.3247 |
| 2023-07 | 4.3423 | 2.8022 | 9.8638 | 3.6288 | 2.3615 | 8.3125 | 3.8229 | 2.6315 | 9.2630 | 4.6475 | 3.1405 | 11.0545 |
| 2023-08 | 4.0035 | 2.5730 | 10.0455 | 3.7268 | 2.4104 | 9.4109 | 4.8280 | 3.3020 | 12.8918 | 5.1443 | 3.4783 | 13.5801 |
| 2023-09 | 3.4453 | 2.2114 | 7.1663 | 3.1122 | 2.0243 | 6.5599 | 6.7737 | 4.4505 | 14.4223 | 6.4818 | 4.3321 | 14.0388 |
| 2024-04 | 3.5722 | 2.1741 | 11.2625 | 3.5196 | 2.2200 | 11.5001 | 5.7042 | 3.7965 | 19.6668 | 5.5777 | 3.6967 | 19.1496 |
| 2024-05 | 4.9638 | 3.1574 | 9.7207 | 4.5764 | 2.7809 | 8.5617 | 5.2325 | 3.5183 | 10.8317 | 5.0154 | 3.4181 | 10.5233 |
| 2024-06 | 4.1457 | 2.5733 | 10.0731 | 3.7812 | 2.3378 | 9.1512 | 4.6228 | 3.0239 | 11.8367 | 4.7279 | 3.0874 | 12.0855 |
| 2024-07 | 4.5398 | 2.7464 | 10.6194 | 4.3067 | 2.5460 | 9.8448 | 6.1678 | 3.9366 | 15.2219 | 5.8850 | 3.9495 | 15.2718 |
| 2024-08 | 3.8082 | 2.4527 | 8.3424 | 3.4340 | 2.1947 | 7.4648 | 5.2756 | 3.5145 | 11.9539 | 5.7736 | 3.9082 | 13.2930 |
| F&W | ||||||||||||
| 2023-01 | 1.4482 | 1.1512 | 65.4267 | 1.5671 | 1.2267 | 69.7188 | 1.1467 | 0.8738 | 49.6618 | 1.7574 | 1.3434 | 76.3508 |
| 2023-02 | 2.4027 | 1.3478 | 15.0857 | 2.3943 | 1.4760 | 16.5199 | 2.3086 | 1.5976 | 17.8814 | 2.7894 | 2.0555 | 23.0055 |
| 2023-03 | 3.5334 | 2.0916 | 10.7560 | 3.1646 | 1.8918 | 9.7283 | 3.5082 | 2.4037 | 12.3609 | 3.8249 | 2.6719 | 13.7398 |
| 2023-10 | 14.6823 | 8.5658 | 65.0988 | 16.5972 | 9.3639 | 71.1646 | 10.6315 | 6.4674 | 49.1510 | 9.9314 | 6.1672 | 46.8697 |
| 2023-11 | 8.0100 | 4.1350 | 86.9027 | 8.9692 | 4.4608 | 93.7511 | 5.8113 | 3.6476 | 76.6612 | 5.5910 | 3.7098 | 77.9664 |
| 2023-12 | 1.9130 | 0.7307 | 100.0000 | 1.9130 | 0.7307 | 100.0000 | 4.6434 | 3.3954 | 464.6711 | 5.8990 | 4.4411 | 607.7771 |
| 2024-01 | 2.7605 | 2.0812 | 100.7387 | 2.9707 | 2.1891 | 105.9653 | 2.9437 | 1.9604 | 94.8939 | 3.5564 | 2.4776 | 119.9293 |
| 2024-02 | 2.6717 | 1.5802 | 21.5573 | 2.4559 | 1.4407 | 19.6538 | 3.9645 | 2.2521 | 30.7230 | 4.0916 | 2.6434 | 36.0611 |
| 2024-03 | 3.9556 | 2.5313 | 12.7243 | 3.6999 | 2.3810 | 11.9686 | 4.7269 | 3.1850 | 16.0101 | 4.5084 | 3.1120 | 15.6431 |
| Averages | ||||||||||||
| Ave of S&S | 4.2259 | 2.6696 | 9.7711 | 3.8028 | 2.3899 | 8.8104 | 5.1171 | 3.4293 | 12.7339 | 5.2073 | 3.5309 | 13.0770 |
| Ave of F&W | 4.5975 | 2.6905 | 53.1434 | 4.8591 | 2.7956 | 55.3856 | 4.4094 | 2.8648 | 90.2238 | 4.6611 | 3.1802 | 113.0381 |
| Entire Ave | 4.3931 | 2.6790 | 29.2886 | 4.2781 | 2.5725 | 29.7692 | 4.7987 | 3.1753 | 47.6044 | 4.9615 | 3.3731 | 58.0595 |
| Test Set | 4.5310 | 2.6331 | 9.7862 | 4.4300 | 2.5432 | 9.4501 | 5.5860 | 3.6263 | 13.4751 | 5.8334 | 3.7504 | 13.9360 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohammadi Lanbaran, N.; Naujokaitis, D.; Kairaitis, G.; Radziukynas, V. Hybrid Hourly Solar Energy Forecasting Using BiLSTM Networks with Attention Mechanism, General Type-2 Fuzzy Logic Approach: A Comparative Study of Seasonal Variability in Lithuania. Appl. Sci. 2025, 15, 9672. https://doi.org/10.3390/app15179672
Mohammadi Lanbaran N, Naujokaitis D, Kairaitis G, Radziukynas V. Hybrid Hourly Solar Energy Forecasting Using BiLSTM Networks with Attention Mechanism, General Type-2 Fuzzy Logic Approach: A Comparative Study of Seasonal Variability in Lithuania. Applied Sciences. 2025; 15(17):9672. https://doi.org/10.3390/app15179672
Chicago/Turabian StyleMohammadi Lanbaran, Naiyer, Darius Naujokaitis, Gediminas Kairaitis, and Virginijus Radziukynas. 2025. "Hybrid Hourly Solar Energy Forecasting Using BiLSTM Networks with Attention Mechanism, General Type-2 Fuzzy Logic Approach: A Comparative Study of Seasonal Variability in Lithuania" Applied Sciences 15, no. 17: 9672. https://doi.org/10.3390/app15179672
APA StyleMohammadi Lanbaran, N., Naujokaitis, D., Kairaitis, G., & Radziukynas, V. (2025). Hybrid Hourly Solar Energy Forecasting Using BiLSTM Networks with Attention Mechanism, General Type-2 Fuzzy Logic Approach: A Comparative Study of Seasonal Variability in Lithuania. Applied Sciences, 15(17), 9672. https://doi.org/10.3390/app15179672






