Abstract
As the complexity and functional integration of mechanism systems continue to increase in modern practical engineering, the challenges of changing environmental conditions and extreme working conditions are becoming increasingly severe. Traditional uncertainty-based design optimization (UBDO) has exposed problems of low efficiency and slow convergence when dealing with nonlinear, high-dimensional, and strongly coupled problems. In response to these issues, this paper proposes an UBDO framework that integrates an efficient intelligent optimization algorithm with an excellent surrogate model. By fusing butterfly search with Levy flight optimization, an improved chicken swarm algorithm is introduced, aiming to address the imbalance between global exploitation and local exploration capabilities in the original algorithm. Additionally, Bayesian optimization is employed to fit the limit-state evaluation function using a BP neural network, with the objective of reducing the high computational costs associated with uncertainty analysis through repeated limit-state evaluations in uncertainty-based optimization. Finally, a decoupled optimization framework is adopted to integrate uncertainty analysis with design optimization, enhancing global optimization capabilities under uncertainty and addressing challenges associated with results that lack sufficient accuracy or reliability to meet design requirements. Based on the results from engineering case studies, the proposed UBDO framework demonstrates notable effectiveness and superiority.
1. Introduction
With the continuous advancement of science and technology, the complexity of engineering structures has further increased, posing more stringent requirements for structural design under variable environments and extreme operating conditions [1,2,3]. Traditional design methods are difficult to meet the comprehensive requirements of high precision, high efficiency, and high reliability for complex systems in today’s engineering [4,5]. The development of advanced intelligent design optimization methods and intelligent computing technology has provided new development ideas for the research on uncertainty-based design optimization (UBDO) of structures [6,7,8]. Establishing efficient and accurate reliability analysis models, as well as developing intelligent optimization algorithms with enhanced global convergence capabilities, has gradually become a powerful support for improving the safety of modern mechanical structures and reducing design risks [9,10,11].
In recent years, a variety of excellent UBDO methods have been developed and applied across different engineering fields. Meng et al. [12] proposed an optimization framework considering uncertainties, composed of four nested optimization loops, employing two improved gradient-based methods for optimization. However, while gradient-based optimization methods exhibit certain advantages, the performance and generalization capabilities of these methods may be influenced by the iteration step size and direction. Mierlo et al. [13] introduced a robust optimization method considering uncertainties based on Gaussian process surrogates, achieving superior optimization convergence results with the assistance of novel learning functions. Farahmand et al. [14] presented a solution approach for problems based on enhanced metaheuristic algorithms. Experimental results demonstrate that the flexibility, efficiency, and ability to effectively explore the entire search space inherent in metaheuristic algorithms play a crucial auxiliary role in enhancing the reliability of optimization designs, highlighting the application potential of metaheuristic algorithms in UBDO. From these studies, it can be observed that metaheuristic algorithms exhibit significant advantages over gradient-based optimization methods. Furthermore, there remains a high demand for more advanced metaheuristic algorithms.
In the related research on UBDO of various engineering structures, intelligent optimization algorithms have gradually become a common optimization method in the field of engineering structure optimization due to their powerful nonlinear processing capabilities and global search advantages [15,16,17]. These algorithms solve complex optimization problems in engineering by simulating biological behaviors or physical phenomena in nature [18]. Particle swarm optimization (PSO) algorithms [19], Genetic algorithms (GA) [20], ant colony algorithms [21] and Butterfly Optimization Algorithms (BOA) [22] are commonly used by researchers. In recent years, scholars have conducted innovative research and applications of intelligent optimization algorithms in related fields. Meng et al. [23] proposed a support vector regression modeling strategy based on intelligent optimization for fatigue problems of offshore wind turbine support structures, which was used to build a high-precision approximate model. Ghasemi et al. [24] simulated the population growth and spread of IVY plants, proposing a novel bionic algorithm variant, the IVY Algorithm (IVYA). In the comparison of 26 classic test functions, the IVYA proved its effectiveness compared with other optimization algorithms. Zhu et al. [25] proposed a path planning algorithm inspired by insect behavior, which enhances the algorithm’s performance by incorporating quantum computing methods and a hybrid strategy of multiple tactics. To improve the algorithm’s global optimization capability, a merit set strategy was adopted to ensure a more uniform distribution of the initial insect population. The study employed test functions and practical engineering case examples to validate and compare the proposed algorithm, demonstrating its superiority in terms of convergence speed and accuracy. Inspired by various natural behaviors of a certain bird species, Wang et al. [26] proposed another metaheuristic algorithm. To achieve a favorable balance between exploring global solutions and exploiting local information, the algorithm also incorporates the Cauchy mutation strategy and the Leader strategy. Previous studies indicate that intelligent optimization algorithms exhibit strong global search capabilities and adaptability, showing promising applications in solving UBDO problems of engineering structures [27,28]. However, existing UBDO approaches struggle to strike a dynamic balance between computational efficiency and robustness, and the employed metaheuristic algorithms may exhibit performance deficiencies when confronted with diverse problem types. Consequently, when dealing with increasingly complex engineering structures, there remains an urgent need for metaheuristic algorithms capable of efficiently and robustly handling problems with varying degrees of nonlinearity.
Intelligent optimization algorithms can improve the accuracy of the UBDO process for engineering structures [29,30]. However, in the case of high-dimensional variable space, high computational complexity, and difficulty in obtaining simulation data, the UBDO process faces extremely high computational costs [31,32,33]. To solve such problems, researchers have proposed a method to introduce a surrogate model to replace traditional numerical simulation, thereby significantly improving optimization efficiency and accuracy [34,35]. Yu et al. [36] proposed an efficient UBDO method for monopile-supported offshore wind turbine structures. To enhance computational efficiency, a surrogate model was constructed using the radial basis function neural network. Allahvirdizadeh et al. [37] used adaptive training of the Kriging metamodel as a surrogate model for the computational model of the decoupled UBDO problem to reduce the computational cost. At the same time, a new stopping criterion was proposed to reduce the generalization error of the trained metamodel, thereby reducing the estimated failure probability. Fu et al. [38] investigated a hierarchical hybrid sequential optimization and reliability assessment strategy under multi-source uncertainties. Building upon intelligent optimization algorithms, they proposed an adaptive collaborative optimization approach, thereby extending and refining the theoretical framework of UBDO under multi-source uncertainties. From the UBDO methods applied to related engineering structures studied by previous researchers, various surrogate models can significantly reduce the computational cost and have great room for development in practical engineering applications [39,40,41]. In addition, various advanced models and technologies are also widely used in the safety and reliability assessment of actual engineering structures [42,43,44]. The surrogate model of Bayesian Optimization Back Propagation (BO-BP) neural network has attracted wide attention in reliability analysis due to its powerful nonlinear fitting ability and uncertainty quantification advantages [45,46]. However, as engineering structures gradually become more complex, the development of intelligent optimization algorithms with enhanced global convergence capabilities and the establishment of efficient and accurate reliability analysis models have increasingly become powerful tools for improving the safety of modern mechanical structures and reducing design risks.
Nevertheless, traditional UBDO methods still suffer from issues of low efficiency, slow convergence, and insufficient accuracy when dealing with nonlinear, high-dimensional, and highly coupled problems. Furthermore, existing UBDO research still lacks surrogate models capable of balancing high fitting accuracy with computational efficiency, making it difficult to meet the design requirements of complex engineering structures in terms of high precision, high efficiency, and high reliability. To address these challenges, this study proposes a novel UBDO method that integrates an improved Chicken Swarm Optimization (CSO) algorithm with a BO-BP neural network. This approach has achieved promising results in addressing optimization problems for engineering structures. By introducing the butterfly optimization adaptive mutation and local search strategy, the convergence stability and optimization accuracy of the improved optimization algorithm (BLCSO) have been effectively enhanced. Through improvements to the optimization algorithm, this study aims to reduce the computational difficulty of obtaining the optimal solution for the UBDO problem and enhance the accuracy of the optimal solution. Addressing the computational efficiency issues that may arise during the optimization process using metaheuristic algorithms—due to multiple calls to complex nonlinear constraint functions—this research proposes the BO-BP model. By leveraging BO, the number of iterations required to establish a surrogate model is reduced, while improving the model’s fitting accuracy. Ultimately, a comprehensive UBDO framework is constructed by integrating the BLCSO algorithm with the BO-BP model, and the effectiveness and efficiency of the proposed framework are validated through applications to complex engineering problems.
The contents of other parts of this study are as follows: Section 2 introduces the optimization algorithms CSO and BOA involved in this study, and also provides a brief overview of the BP neural network model. Section 3 elaborates in detail on the computational steps of the BLCSO algorithm and the UBDO algorithm (BLCSO-BO-BP) that integrates BLCSO with the BO-BP model. Section 4 evaluates the BLCSO algorithm and further tests the proposed BLCSO-BO-BP using engineering examples. Section 5 offers a concise summary of the research conducted in this study.
2. Basic Methods and Models
2.1. Optimization Algorithm
2.1.1. Chicken Swarm Optimization Algorithm
The CSO algorithm is a type of bionic intelligent algorithm, and its design is inspired by the foraging behavior and social hierarchy characteristics of poultry groups [47]. This algorithm divides the chicken swarm into multiple subgroups, with each subgroup following a composition pattern of “1 rooster + N hens + M chicks”. Here, the values of N and M are dynamically adjusted based on the total swarm size and the preset ratio parameter of hens to chicks. Within the swarm, there exists a hierarchical learning mechanism, where higher-ranking individuals exert behavioral guidance on lower-ranking ones, while collaborative and competitive relationships exist among individuals of the same rank. Additionally, competitive dynamics are also present among different subgroups. This dual-competition mechanism effectively enhances the algorithm’s global search capability.
The position update formula for roosters in the chicken swarm is as follows:
where represents the location coordinate of individual in the dimension at the -th iteration; denotes a Gaussian distribution function with a mean of 0 and a standard deviation of ; k represents the number of any rooster individual, and ; denotes individual i’s fitness value; denotes the fitness value of the individual, and denotes an infinitesimal positive number to prevent the denominator from taking a value of 0.
The position update of hens follows the formula indicated as Equations (3)–(5).
where means a random number uniformly distributed between [0, 1]; denotes the individual number of the mate rooster of the -th hen, is the individual number of any randomly selected rooster or hen, and ; serves as the influence factor associated with its partner rooster, and functions as the influence factor related to other roosters or hens. denotes individual ’s fitness value, denotes individual ’s fitness value.
The position update formula for chicks is described as follows:
where represents the location of the mother of the -th chick in the dimension at the -th iteration. The chick’s position is associated with both its own position and the position of the mother hen. The learning factor is the degree to which the chick is influenced by its mother hen. The value of is obtained through random sampling.
At the initial stage of the algorithm, the individuals in the population are initialized as follows:
where denotes the -th chicken in all of the population, , represents the -th dimension of the population, , signifies the individuals within the -th dimension of the -th chicken. signifies a random number in the interval to ensure that the variable values stay within their specified range. and signifies the upper and lower boundaries of the -th dimension variable, respectively. Subsequently, the fitness value is computed based on the objective function, and the individual possessing the best fitness along with its optimal fitness value is retained.
The pertinent fundamental steps are outlined as follows:
Step 1: Population initialization to initiate the algorithm;
Step 2: The fitness value of each individual is evaluated, followed by sorting them. Subsequently, the roles of roosters, hens, mother hens, and chicks are determined, and the variable is initialized to 1;
Step 3: In the event that mod , update the population hierarchy;
Step 4: The positions of the rooster, hen, and chicks are updated in accordance with the individual update formula;
Step 5: Compute the fitness values of all individuals within the population, update the globally optimal individual, and increment by 1;
Step 6: In the event that the algorithm termination condition is fulfilled, the iteration ceases, and the optimal solution is generated as the output. Otherwise, advance to Step 3.
2.1.2. Butterfly Optimization Algorithm
Inspired by the behaviors of butterflies in nature, Sankalap Arora and Satvir Singh [48] proposed the BOA in 2019, which simulates the foraging and mating behaviors of butterflies for optimization search. This algorithm uses “scent” to simulate fitness values, guiding individuals to move within the solution space through two modes: global search and local search. Specifically, individuals perform rapid directional movement (global search) when perceiving distant signals, and otherwise engage in random movement (local search).
Within the BOA, the scent emitted by the butterfly is denoted by , and is associated with the variation in fitness. When a butterfly possessing a relatively weaker moves towards a butterfly with a stronger , the value of escalates at a faster rate than . Consequently, the scent is expressed as a function of the intensity of the stimulus:
where is the sensory factor, which refers to taste. Parameter is a power index that depends on and controls the behavior of the algorithm. Where . When , it implies that the fragrance released by any butterfly is imperceptible to other butterflies. When , it implies that the fragrance concentration dispersed by a butterfly is discernible to other butterflies possessing an equivalent ability.
The BOA is principally partitioned into three stages:
The first stage is the initial stage, including initializing the population, parameters, objective function, etc.
The second stage is the iteration stage. In each iteration, the butterflies will fly to a new position and recalculate their fitness values through the function;
Upon a butterfly’s perception of the scent released by another butterfly, it will migrate towards the source of the scent. This stage is formally termed the global search stage. The equation that characterizes the global search stage is presented below:
where denotes the solution vector associated with the -th butterfly during the -th iteration. represents the optimal solution within the present iteration. represents the -th butterfly’s scent, and is a randomly generated number between 0 and 1.
In an alternative scenario, if a butterfly is unable to detect the scent emitted by other individuals, it will execute a random movement. This stage is formally termed the local search stage. The mathematical expression for the local search stage is as follows:
where and denote the -th and -th butterflies, which have been randomly selected from the solution space.
During the foraging and mating activities of butterflies, the transition between the global search and the local search is accomplished through a switching probability denoted as . In every iteration step, a value is generated at random based on Equation (16). Then, is juxtaposed with the switch probability to ascertain whether the ongoing search cons. In the original BOA, is typically set to 0.8 [48].
The third stage is the termination stage. When the algorithm reaches the upper limit of iterations, it performs a comprehensive search and then outputs the current optimal solution, which is the best result obtained up to that point in the algorithm.
2.1.3. A Summary of the Strengths and Weaknesses of Original Optimization Algorithms
The CSO algorithm distinguishes itself from traditional evolutionary optimization methods (such as GA, immune optimization algorithms, differential evolution algorithms, etc.) in that its population iteration and update mechanism does not rely on biological operations like genetic inheritance or gene recombination to generate the next generation of the population. Consequently, it requires less memory and runtime, effectively reducing computational complexity. By fully leveraging the information shared among individuals with different roles within the swarm (roosters, hens, and chicks) during foraging, each type of individual employs distinct search strategies, enabling more efficient exploration in complex search spaces. Additionally, through the collaborative search mechanism among individuals with different roles, the algorithm facilitates cross-dimensional information sharing in complex optimization scenarios, ultimately converging towards the global optimum.
However, due to the relatively weak search capability of hens in the CSO algorithm, it is prone to being attracted by local optimal solutions. Consequently, this may result in insufficient search precision when the algorithm approaches the optimal solution. Additionally, the random mutation process in the CSO algorithm is blind and fails to effectively enhance population diversity. For individuals with high fitness, random mutation may disrupt their advantageous traits, leading to a decline in individual quality, population degradation, and reduced diversity. Therefore, enhancing the CSO algorithm’s ability to converge to the optimal solution as quickly as possible in the later stages of optimization, and improving the efficiency and accuracy of population mutation during the search process, have become significant research directions in this field.
The BOA utilizes the concept of “scent” to guide individuals in moving through the solution space. This mechanism enables the algorithm to swiftly locate regions with potential high-quality solutions during the global search phase. Furthermore, the relatively simple structure of the BOA facilitates its application and extension. However, due to the randomness inherent in its local search phase, the algorithm may exhibit slower convergence when addressing complex high-dimensional problems. When confronted with complex optimization challenges, although BOA can conduct local searches through random movements, this strategy may still lack an effective mechanism for escaping local optima compared to advanced optimization algorithms.
To this end, this study proposes an effective strategy that combines BOA and CSO. By leveraging BOA’s capability of rapid convergence towards the optimal solution in the later stages of iteration, it can compensate for the performance deficiencies of the CSO algorithm during its late-stage iterations. Additionally, since the CSO algorithm comprises multiple sub-populations with distinct roles, integrating it with BOA’s more efficient population search capability can further enhance the overall optimization performance.
2.2. BP Neural Network Model
BP neural network is a network structure that calculates forward, propagates errors backward and corrects them, thereby reducing the errors along the gradient direction. After multiple training and learning, BP neural network can obtain stable and reliable output results [49,50]. Currently, owing to the pro-found exploration of BP neural network theory and the swift advancement of electronic computers, this theory has found extensive application across various domains, including pattern recognition, intelligent robotics, biology, medicine, prediction and estimation, as well as risk assessment.
The principal architecture of the BP neural network comprises an input layer, a hidden layer, and an output layer, as illustrated in Figure 1. The input layer is composed of input units. The significance and quantity of these input units are ascertained based on the actual engineering scenario. For structural reliability analysis, the input units are generally random variables of the structure. The output layer is com-posed of the outcomes generated by the neural network. For structural reliability analysis, the output layer is generally a safety margin. The hidden layer lies between the input and output layers, acting as a link be-tween them. The quantity of layers and neurons within the hidden layer dictates the intricacy of the neural network. In the case of a neural network lacking a hidden layer, it is only capable of addressing straight-forward linear problems. For a neural network with 1–3 hidden layers, most nonlinear problems can be solved. The neural network’s calculation accuracy mainly relies on the neurons in the hidden layer. Nevertheless, there exists no credible research that can precisely ascertain the quantity of neurons within the hidden layer. Typically, the number of neurons in the hidden layer may be roughly estimated through the subsequent empirical formula. This study utilizes the BO algorithm to determine the ideal count of neurons in the hidden layer.
where represents the quantity of neurons within the hidden layer, denotes the number of neurons in the input layer, signifies the count of neurons in the output layer, and is a constant value falling within the range of 1 to 10.
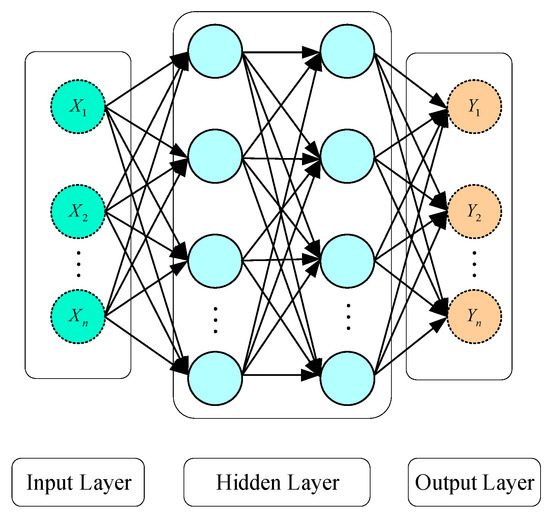
Figure 1.
Main structure of BP neural network.
The BP neural network primarily establishes the internal rules governing the relationship between input features and output features by means of two sequential processes: forward propagation and backward propagation. The BP neural network’s forward transmission multiplies the output of each neuron in the last layer by the matching inter-layer weight and then perform a linear operation to obtain the parameter , as shown in Equation (13). Then, substitute the parameter into the activation function , introduce nonlinearity, and finally pass the result to the next neuron, as shown in Figure 2.
where is the input to the neuron within this layer subsequent to the linear operation; stands for the -th weight of the neuron in this layer; signifies the output value of the neuron in the prior layer, and this value is transmitted as the input of the neuron in this layer; is the neuron’s bias in this layer; is the activation function, which can be selected from Sigmoid, Tanh, ReLU and Leaky_ReLU according to the different functions of the neural network.
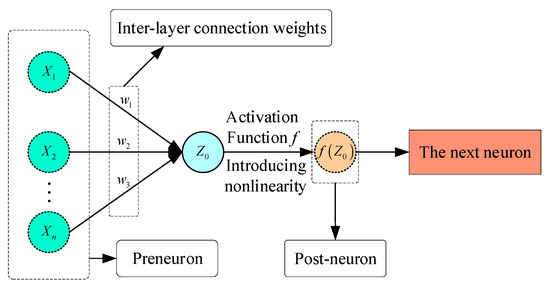
Figure 2.
BP neural network feedforward transmission.
The backward propagation in the BP neural network denotes the procedure of fine-tuning the weights and biases of every neuron within the BP neural network by employing certain techniques (e.g., the gradient descent method). The objective is to diminish the discrepancy between the output value (the predicted value) and the actual value, consequently accomplishing the optimization of the computational accuracy of the BP neural network. The adjustment approach for weights and biases is illustrated in Equation (14).
where and are the weights and biases before updating; and are the weights and biases after updating, respectively; is the learning rate, which controls the step size of gradient descent; is the loss function.
In this context, we opt for the Mean Square Error, which exhibits strong adaptability, excellent stability, and rapid convergence speed, to serve as the loss function for the BP neural network:
where is the actual value and is the predicted value of the neural network.
For the activation function in the BP neural network, this paper chooses the Leaky ReLU function with high computational efficiency, fast convergence speed, no saturation mechanism, and no “dead ReLU” problem:
where is a very small constant, which can be taken as 0.01.
The training process of BP neural network is essentially an optimization process, so it is particularly important to choose a suitable optimization algorithm. The conventional gradient descent algorithm exhibits inadequate optimization capability and is highly susceptible to being trapped in local optimal solutions. Therefore, this study uses the Adaptive Moment Estimation (Adam) algorithm instead of the gradient descent method. The Adam algorithm integrates the merits of the RMSProp method and the momentum algorithm. It not only uses the moving average of the gradient instead of the negative gradient direction as the update direction of the parameters, but also adaptively adjusts the learning rate for different parameters.
3. UBDO Based on BLCSO and BO-BP Neural Network Model
3.1. Improved CSO Based on Butterfly Optimization Strategy
3.1.1. Dynamic Multi-Population Partitioning Strategy
- (1)
- Rooster search strategy integrating butterfly algorithm
For the purpose of augmenting the global optimization performance of roosters, a dual-population crossover optimization strategy centered on roosters and butterflies was formulated. This strategy leverages the remarkable robustness and global search proficiency of the population in the BOA. This strategy uses a random number to determine the update between the two populations, that is, when the random number is less than , the population is updated using Equation (9), otherwise it is updated using Equation (1). To examine the performance differences in the algorithm in solving complex optimization problems when the parameter takes on various values, this study conducted a parameter sensitivity analysis, the details of which are included in Appendix A. The results of the sensitivity analysis indicate that when = 0.7, the algorithm achieves a favorable balance between global and local search.
This fusion strategy can break the single optimization mode of roosters within the population, greatly enhance the global optimization ability of roosters, increase the randomness of algorithm optimization, and avoid getting trapped in local optimality.
During the process of updating the rooster position within the BLCSO framework, the CSO algorithm is amalgamated with the BOA. The fused rooster position update as:
- (2)
- Hen search strategy based on Levy flight
The term “Levy walk” was first proposed by French mathematician Paul Levy to simulate the process of organisms in nature looking for food in an uncertain environment. Levy flight is a mathematical method that provides random factors that obey the Levy distribution. Its essence is a long-term short-distance back-and-forth search interspersed with occasional long-distance searches. This feature can be used to form a Levy flight mechanism to ensure that the population fully explores the solution space and improves the global optimization ability.
The mathematical expression for the Levy flight is presented as follows:
where represents the flight step length. , variance are:
where is the function and is the parameter, which is usually 1.5.
As can be seen from the aforementioned formula, the adopted Levy flight strategy adjusts step sizes by generating random numbers. Figure 3 illustrates the probability density function and random walk path of Levy flight when . By comparing it with the Gaussian distribution, it is evident that Levy flight exhibits pronounced characteristics of a heavy-tailed stable distribution, with its random walk step sizes comprising numerous small steps interspersed with occasional large jumps.
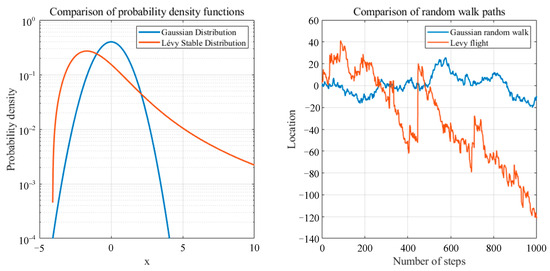
Figure 3.
Schematic Diagram of the Heavy-Tailed Stable Distribution Characteristics of Levy Flight.
Traditional random walks usually have only small step lengths and short distances of movement, with a relatively limited search range and unable to explore the search space extensively. In contrast, the Levy flight step size satisfies the heavy-tailed stable distribution and has the probability of long-range movement. This distribution method enables Levy flight to perform both detailed local searches and quickly explore new areas through long-distance jumps during the search process, thus a good balance between global and local searches is attained. Therefore, in the improved swarm optimization algorithm, the Levy flight strategy is employed for global detection, so that the swarm is widely distributed in the search space.
During the latter phase of algorithm iteration, hens exhibit a tendency to be trapped in local optimality. With the aim of enhancing the local optimization capability of the algorithm, a part of individuals is selected from the hens to learn from the optimal individuals, and the Levy flight strategy is incorporated for perturbation. The mathematical expression is shown in Equation (21).
where denotes the individual that possesses the highest fitness value within the population.
If , the -th individual is within the hen population occupies a position characterized by low fitness, and Equation (21) is utilized to perform the position update of the -th hen in every iteration. Where . Levy flight can help the algorithm to effectively explore a large range of search space, while considering small-scale detailed search and occasional long-distance jumps, thereby preventing the hen from being trapped in the local optimal solution and enhancing its search capability. When the hen’s sense that the roosters have found a better food source, they will flock in in large numbers, making the population density around the roosters too high, making it easy to get stuck in a local optimum. In the original CSO algorithm, during the later stages of iteration, when hens perceive that roosters have discovered better food sources, they tend to flock in large numbers, which can easily lead to local optima. Therefore, in this study, by incorporating Levy flight step sizes into the hens’ position update formula and combining it with learning from the optimal individual, the influence of roosters on the search behavior of the hen population can be reduced to a certain extent, thereby expanding the search space of the entire population.
The BLCSO hen position update formula is:
- (3)
- The overall computational procedure of the BLCSO algorithm
The BLCSO algorithm can avoid the problem of traditional CSO algorithm falling into local optimality. First, the tent mapping of the initial population is initialized. Secondly, in the context of rooster position updating, the BOA and the CSO algorithm are amalgamated, and the BOA optimizer is utilized to achieve global optimization. Finally, considering the drawback that the CSO algorithm is susceptible to getting trapped in local optimality, a hen update strategy incorporating Levy flight is put forward to augment the algorithm’s global optimization capability.
Figure 4 displays the overall flow chart, and the following provides a clear breakdown of the specific steps:
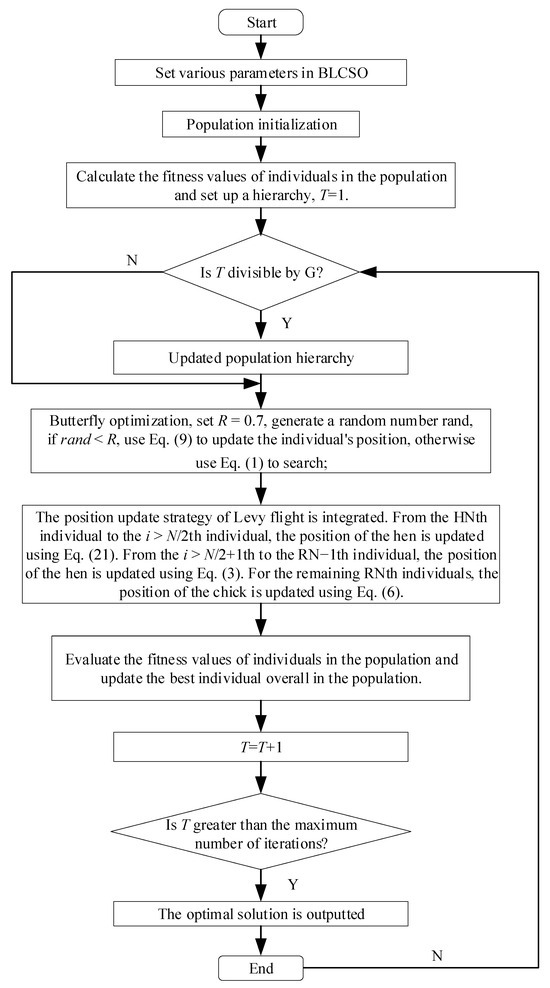
Figure 4.
Flow chart of BLCSO algorithm.
Step 1: (Parameter setting): Configure the parameters of the BLCSO algorithm, which encompasses setting the population size denoted as , the dimension of the search space labeled as , the maximum iteration count represented by , the quantities of roosters, hens, mother hens, and chicks, the sensing form , the power index , the update generation , among others. Subsequently, initialize the population using the tent mapping chaotic map;
Step 2: (Initialization): Compute the fitness value of every individual within the flock, arrange them in ascending order, ascertain the roles of roosters, hens, chicks, and mother hens, and record the optimal position along with the corresponding optimal fitness value of each individual. Then, initialize the iteration counter by setting the number of iterations ;
Step 3: (System update): Evaluate whether the quantity of iterations fulfills the criteria for the update of population roles. If so, update the role; otherwise, go to Step 4;
Step 4: (Position update of butterfly optimizer): Set , generate a random number , if , use Equation (9) to update the individual’s position, otherwise use Equation (1) to search;
Step 5: (Improved hen position update and chick position update by integrating Levy flight): In the HN-th individual to -th individual, update the hen position using Equation (21), for to −1-th individual, use Equation (3) to update the hen individual position, and for the remaining individuals, use Equation (6) to update the chick position;
Step 6: (Population update of the generation): Update the global optimal individual and recalculate the fitness values of individuals in the flock, record ;
Step 7: (Terminate verification): Has the iteration process reached the stage where the maximum number of iterations has been exhausted? If the condition is met, proceed to output the optimal solution; otherwise, head back to Step 3. It should be noted that the algorithm’s optimization will cease iterating only when the maximum number of iterations is reached.
3.1.2. Complexity Calculation of the BLCSO Algorithm
Time complexity can be measured by the runtime consumption and, to a certain extent, reflects the performance of an algorithm. The original CSO algorithm involves steps such as population initialization, role-based grouping of roosters, hens, and chicks, position updates, and fitness evaluations.
Assuming the population size is and the dimensionality of the solution space is , the time required for population initialization is . Fitness evaluation has a time complexity of per iteration. During the grouping phase, assuming that re-grouping based on fitness occurs in each iteration and requires sorting, the time complexity is . When updating positions, the update rules differ for roosters, hens, and chicks. Assuming there are roosters, hens, and chicks, and considering that hens and chicks involve following roosters and other hens, the complexity may be higher for them. However, overall, the position update for each individual remains , so the time complexity of the entire position update step is . Combining these factors, the overall time complexity of the CSO algorithm is .
The proposed BLCSO algorithm introduces BOA search and Levy step size adjustment into the CSO algorithm. These two adjustment strategies solely modify the displacements of roosters and hens during the iterative process, without altering the initialization positions, fitness values, or the time complexity of position updates. Therefore, the overall time complexity of BLCSO remains . This indicates that the improved CSO algorithm does not affect the time complexity, and its computational efficiency remains undegraded.
3.1.3. Convergence Analysis of the BLCSO Algorithm
To demonstrate the global convergence of the BLCSO algorithm, this study employs a Markov chain model combined with the convergence criteria for stochastic algorithms to conduct the analysis. The proof is divided into two steps: first, proving that the BLCSO algorithm possesses Markovian properties, and second, demonstrating that the algorithm can converge to the global optimal solution.
Step 1: Prove that the BLCSO algorithm exhibits Markovian properties.
To prove this conclusion, the following definitions are first presented.
- 1.
- Markov Model: Within the probability space , consider a one-dimensional countable set of random variables , where each random variable takes values , with satisfying:
- 2.
- Definition of chicken states and state space: The position of each chicken in the flock constitutes its individual state, and the set of all possible states of this chicken forms its state space, denoted as , where represents the feasible solution space.
- 3.
- Definition of flock states and state space: The states of all chickens in the population constitute the flock state, denoted as , where represents the state of the -th chicken, and is the total number of individuals in the flock. The set composed of all possible states in the flock forms the flock state space, denoted as .
- 4.
- Equivalence of flock states:
For and , denote:
where represents the indicator function of event , and denotes the number of chicken states included in the flock state .
If there exist two flocks such that for any , , then and are said to be equivalent, denoted as .
- 5.
- Equivalence classes of flock states: A population state partitioning model can be constructed based on the state equivalence relation. Let the universal set of population states be denoted as . Then, the corresponding set of equivalence classes for population states can be formally defined as , which possesses the following properties:
- For any equivalence class within the flock, any two states within it satisfy a complete equivalence relation: ;
- There are no overlapping states between different equivalence classes, that is, , .
- 6.
- For any two states of an individual, if there exists a transition operator such that the state transition of the individual satisfies , then the individual transition probability in the chicken swarm algorithm is given by:
Proof.
According to Definition (5) and the operational mechanism of the chicken swarm, the one-step transition probability of a rooster is as follows:
The one-step transition probability for a hen is:
The one-step transition probability for a chick is:
Then, if transferring the flock state from to is denoted as , where , , and , the transition probability of the flock state moving from to in one step is:
It can thus be seen that the transition probability of any chicken’s state is solely dependent on the state at time , namely, the random numbers , , in the algorithm at that moment, as well as the current positions of randomly selected individuals in various roles within the chicken swarm. Therefore, all transition probabilities for chickens in the swarm exhibit this property, indicating that the BLCSO algorithm possesses Markovian characteristics. Consequently, the state sequence of the chicken swarm in BLCSO, , constitutes a finite homogeneous Markov chain. □
Step 2: Prove that the BLCSO algorithm possesses global convergence.
First, the following definitions are made.
- 1.
- The global optimal solution to the optimization problem is denoted as , and the set of optimal solutions is , with .
- 2.
- If for any initial state , it holds that , then the algorithm is said to converge in probability to the global optimal solution.
Proof.
During the iterative process of the BLCSO algorithm, it is necessary to continuously update the optimal positions of individuals.
Considering that in the BLCSO algorithm, the chicken swarm state forms a finite homogeneous Markov chain, and within a given state space, the number of optimal solutions is monotonically non-decreasing. Therefore, the probability that the BLCSO algorithm fails to find the optimal solution after an infinite number of consecutive searches is zero. In other words, after a certain number of iterations, the state sequence of the chicken swarm will enter the optimal solution set , and the chicken swarm algorithm will converge to the global optimum. The following equality holds:
where represents the optimal fitness value of , and denotes the global optimal value. □
Based on the aforementioned proof, it can be concluded that the BLCSO algorithm exhibits global convergence.
3.2. The UBDO Framework Integrating Neural Networks with Novel Optimization Algorithms
3.2.1. BO-BP Neural Network Model
The BO algorithm is an algorithm that finds the optimal value by constructing the posterior probability of the output of a black box function when a limited number of sample points are known. Currently, the BO algorithm is a very important method in the field of hyperparameter optimization. Through the application of the BO algorithm, this study optimizes the parameters and hyperparameters of the BP neural network surrogate model. The primary purpose is to curb the detrimental effect of initial state randomness on the training and substantially enhance the model’s fitting accuracy, which is crucial for achieving high-quality modeling results.
The problem of optimizing the parameters and hyperparameters of the BP neural network can be mathematically represented by Equation (35):
where denotes the hyperparameter to be optimized, is the objective function, is the ideal hyperparameter combination, and is the feasible hyperparameter domain.
where denotes the actual value and denotes the predicted value.
where refers to the posterior probability obtained by the current probability surrogate model. denotes the optimal value among the current samples.
The parameters to be optimized in this paper are the initial weight and the initial bias ; the hyperparameters subject to optimization encompass the quantity of neurons within the hidden layer, the number of iterative optimization steps for the BP neural network, the initial value assigned to the learning rate, the interval for dynamic learning rate descent, and the gradient for dynamic learning rate descent. This study selects the Mean Absolute Percentage Error of the BP neural network validation set is utilized as the objective function of the BO algorithm for the purpose of assessing the model’s performance, as shown in Equation (36). The target MAPE (Mean Absolute Percentage Error) value is set to 5%. The maximum number of iterations is set to 1000. The TPE (Tree-structured Parzen Estimator) model with fast calculation speed is selected as the probabilistic surrogate model (probabilistic surrogate model) to replace the objective function for iterative optimization of parameters and hyperparameters; the expected improvement function (Expected Improvement, EI) is selected as the acquisition function (acquisition function) to determine the location of the optimal sample point, as shown in Equation (37).
BO-BP neural network model’s code flow [49] is as follows:
| BO-BP neural network agent model |
| Input: |
| Output: Ideal parameters and hyperparameter combination |
| 1. Initial dataset →D |
| 2. for |
| 3. |
| 4. |
| 5. |
| 6. |
| 7. end for |
The BO-BP neural network agent model construction process is as follows:
- (1)
- Determine the objective function, the feasible domain of parameters and hyperparameters, the acquisition function , and the probabilistic surrogate model .
- (2)
- Generate the initial dataset : First, perform random sampling within the feasible domain of parameters and hyperparameters, and substitute the samples you obtained into the objective function to work out the target value, that is, . Therefore, the initial dataset is obtained.
- (3)
- Specify the quantity of iterations . This quantity denotes the number of instances the objective function is executed. Since the objective function requires a lot of computation, the number of iterations cannot be too large.
- (4)
- Calculate the posterior probability of the data sample based on the selected probabilistic surrogate model and the generated dataset .
- (5)
- Based on the posterior probability distribution obtained by the probabilistic surrogate model, the acquisition function is used to select the next most promising parameter and hyperparameter combination .
- (6)
- Substitute the most promising parameter and hyperparameter combination into the objective function to calculate the target value that is, .
- (7)
- Add the new data sample to the dataset as a surrogate model for the historical information update probability.
- (8)
- Repeat steps (4) to (7) until the iteration is completed and the optimal combination of parameters and hyperparameters is output.
Compared to traditional hyperparameter optimization methods, such as grid search, random search, and GA, BO-BP demonstrates advantages in terms of optimization efficiency, global search capability, and adaptability. By constructing a probabilistic surrogate model of the hyperparameters and the objective function MAPE (Mean Absolute Percentage Error), BO-BP efficiently infers the optimal region using existing evaluation results, enabling the identification of hyperparameter combinations close to the global optimum with only a small number of iterations. The probabilistic surrogate model built on the Gaussian process can capture the nonlinear characteristics of the objective function, guiding the search to concentrate on the global optimal region and achieving faster convergence compared to other metaheuristic algorithms. Additionally, BO can automatically search for the optimal structure, reducing the need for manual intervention.
3.2.2. UBDO Framework
The proposed BO-BP neural network is employed for uncertainty analysis using the first-order reliability method, serving as a substitute for time-consuming constraint functions. Its main purpose is to mitigate the drawbacks of traditional methods, such as substantial computational expenses and sluggish convergence velocities, especially in the context of high-dimensional nonlinear problems. Combining the BO-BP algorithm with the BLCSO algorithm mentioned above, a new double-loop optimization design framework for structural reliability is established, and its overall process is shown in Figure 5.
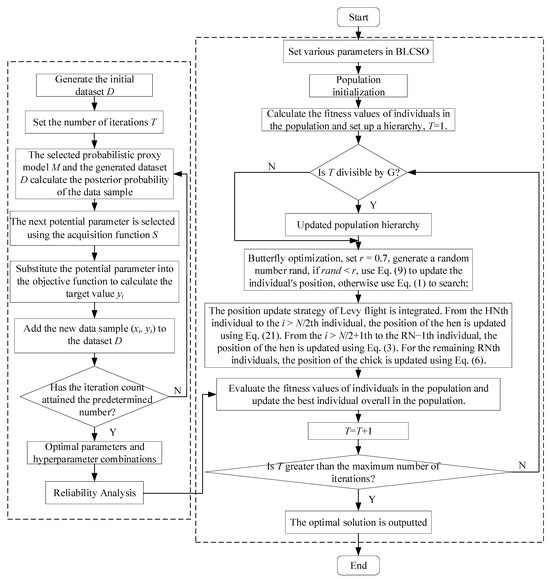
Figure 5.
Flowchart of Uncertainty design optimization method.
4. Example Study Verification
4.1. Verification Based on Test Functions
To verify the advantages of the proposed BLCSO optimization algorithm over other optimization algorithms, the proposed BLCSO is compared with nine notable metaheuristic algorithms, namely PSO, Grey Wolf Optimizer (GWO) [51], Harris Hawks Optimization (HHO) [52], GA [20], Sparrow Search Algorithm (SSA) [53], and the original CSO. Table 1 meticulously details the relevant parameters for each algorithm.

Table 1.
The parameter of metaheuristic algorithm.
To evaluate the performance of the algorithm, 30 repeated experiments were conducted on the CEC2017 function suite [10]. The CEC2017 test functions encompass unimodal functions, multimodal functions, composite functions, irregular functions, and rotated functions, among others. Among them, unimodal benchmark functions feature a single optimal solution without local optima, enabling the assessment of the algorithm’s convergence speed and accuracy. Multimodal benchmark functions contain multiple local optima, effectively testing the algorithm’s global search capability and computational precision. Composite and irregular functions, with higher complexity and greater resemblance to real-world engineering functions, can effectively evaluate the algorithm’s ability to handle highly nonlinear and high-dimensional problems. To further assess the algorithm’s performance, the population size for different heuristic algorithms was set to = 100, and the number of iterations was set to = 1000. The computational results of different algorithms on the benchmark test functions are included in Appendix B. One representative function from each category was selected for graphical illustration, as shown in Figure 6.
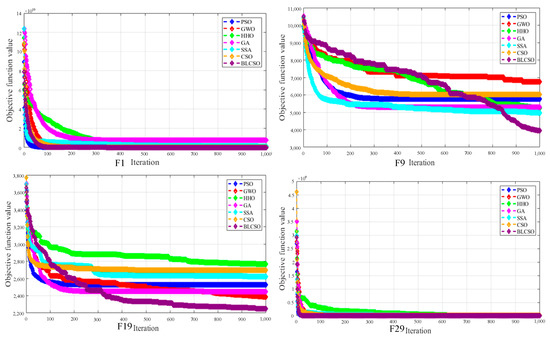
Figure 6.
Comparison of Iterative Processes among Different Optimization Algorithms.
From the comparative results, it can be observed that BLCSO generally performs the best across almost all test functions, not only achieving the optimal optimization results but also demonstrating the highest stability. Compared to the latest optimization algorithms, the proposed optimization method exhibits significant superiority. During the long-term optimization iteration process, BLCSO demonstrates superior global iterative capability and exhibits a higher propensity to converge to the optimal solution.
To eliminate the impact of random factors during the evaluation process, statistical significance tests were added to further examine the performance of the BLCSO algorithm. The table in Appendix B presents the results of comparing the optimal solutions obtained by different algorithms and the BLCSO algorithm using the Wilcoxon signed-rank test. The results reveal that, for most test functions, the Wilcoxon test yields p-values substantially smaller than 0.05, and the Cliff’s delta effect size is less than −0.474. This indicates a statistically significant difference in performance between the BLCSO algorithm and other algorithms, with the BLCSO algorithm capable of obtaining smaller optimal solution values and demonstrating superior performance.
4.2. Validation of Uncertainty Optimization Case Studies
4.2.1. Mathematical Example
This example uses a mathematical example with two optimization variables, and its optimization model is as follows:
where represents the random variable ’s mean value. The limit-state function of this example is as follows:
Among them, both optimization variables obey normal distribution, .
Table 2 presents the optimization iteration data of the method proposed in this paper. It can be observed that the proposed method achieves the optimal solution after 7 iterations, with the number of newly added sample points being 58.

Table 2.
The iteration process of this method in the mathematical example.
Table 3 presents the optimization design methods based on the Kriging model (Kriging-method), Response Surface Methodology model (RSM-method), Support Vector Regression model (SVR-method), and Radial Basis Function model (RBF-method). These methods also employ a bi-level optimization strategy, with the BLCSO (a specific optimization algorithm) strategy adopted for the optimization process.

Table 3.
Contrast of the optimization results yielded by various methods in the mathematical example.
Additionally, the results of individual ablation experiments are provided: “BLCSO-None BP” denotes the optimization design results obtained using the BLCSO strategy without employing a surrogate model; “BLCSO-BP” represents the optimization design results based on a BP (Backpropagation) neural network model without BO; “CSO-BO-BP” indicates the optimization design results using a BP neural network model with BO but employing the original CSO (another optimization algorithm) instead of the BLCSO algorithm; “BLSO-PSO-BP” denotes a UBDO framework that integrates a BP model optimized by PSO with the BLCSO algorithm and “BLCSO-BO-BP” refers to the proposed optimization design results that utilize both the BLCSO algorithm and the BO-BP neural network model.
From the computational results, it can be observed that the BLCSO-BO-BP approach incurs the least computational cost compared to other surrogate models. Among the optimization design methods employing different surrogate models, the method based on the RSM model utilizes 67 sample points. In contrast, the optimization design methods based on the proposed BO-BP model, namely CSO-BO-BP and BLCSO-BO-BP, require a smaller number of sample points. Specifically, the computational cost of BLCSO-BO-BP is reduced by 13.43%. Compared to the BP model optimized by the PSO algorithm, the BP model optimized by BO demonstrates superior performance. Furthermore, when comparing the accuracy and reliability of different optimization design results, it is evident that the proposed method exhibits higher accuracy while maintaining reliability.
With the aim of more vividly illustrating the change in the objective function value across each iteration process, Figure 7 illustrates the iteration curve of the objective function for this specific case.
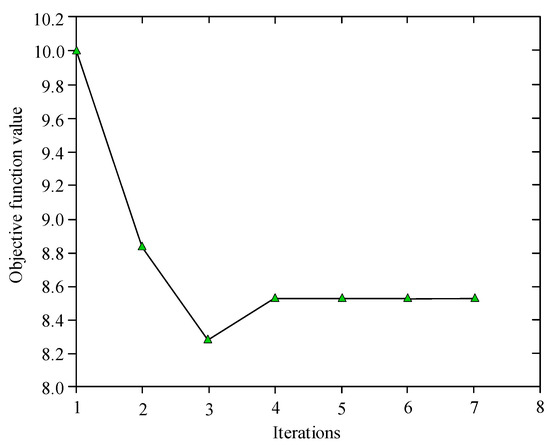
Figure 7.
Objective function iteration process in the mathematical example.
4.2.2. The 10-Rod Truss Structure
The 10-rod truss structure in this example is derived from engineering applications, and its structure is shown in Figure 8. The 10 rods are made of aluminum alloy and can be divided into three groups: the first group consists of 4 rods, placed horizontally; the second group consists of 4 rods, placed at a 45-degree angle; the third group consists of 2 rods, placed vertically.
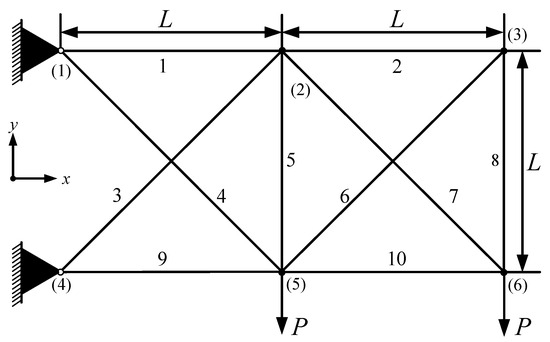
Figure 8.
The 10-bar truss structure.
Within the 10-bar truss structure presented in this section, the elastic modulus of the bar is 107 psi, and there are two concentrated external loads at nodes (5) and (6), both of which are 105 1b. The cross-sectional area of the bar obeys the normal distribution, and the mean is 3in2. The optimization model is:
where represents the vertical displacement of node (6).
Table 4 shows the optimization results of the 10-bar truss structure. From the data in the table, it can be found that after 10 iterations, an ideal optimization result was obtained. A total of 876 new sample points was added during the optimization process. Figure 9 presents the iteration curve of the objective function in this computational example, visually demonstrating the variation in the objective function value.

Table 4.
The selection process of this method in the example of the 10-rod truss structure.
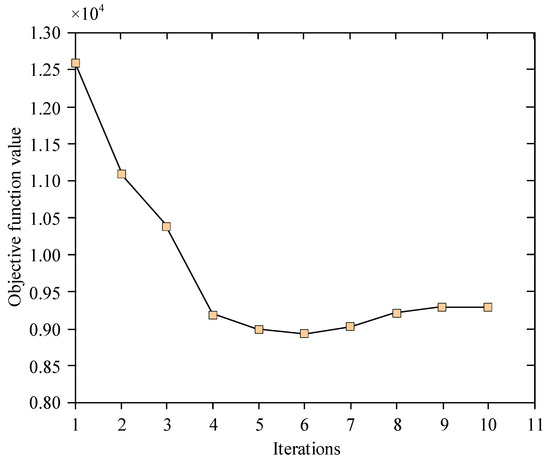
Figure 9.
Objective function iteration process in the example of the 10-rod truss structure.
Table 5 presents the optimization design results of different methods for the 10-rod truss structure. From the results, it can be observed that the number of limit-state evaluations invoked by the BO-BP model is significantly fewer than those based on Kriging and RSM models, while achieving higher accuracy. Furthermore, in terms of computational accuracy, the BLCSO-BO-BP method obtains a smaller objective function value while satisfying reliability constraints. In comparison, although the CSO-BO-BP method also yields optimization results with higher reliability, the value of the optimal solution is larger. Additionally, compared to BLCSO-BP, the proposed BLCSO-BO-BP method requires fewer limit-state evaluations and demonstrates higher accuracy.

Table 5.
Contrast of the optimization results yielded by various methods in the example of the 10-rod truss structure.
4.2.3. Cantilever Beam Structure
This example uses a cantilever beam structure with a rectangular cross-section, as shown in Figure 10. Its optimization model is shown in Equation (41):
where and are optimization variables, and . is a random variable, and represent external loads, represents material strength, and represents elastic modulus. The distribution type of is normal distribution, with a mean of and a standard deviation of .
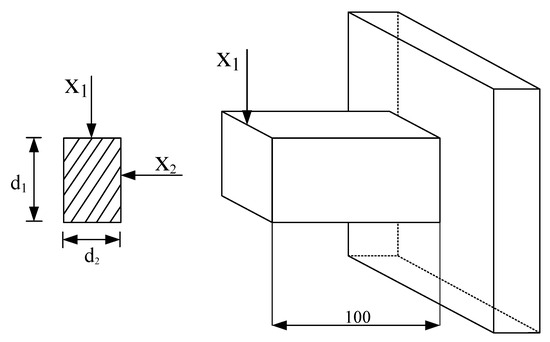
Figure 10.
Cantilever beam structure.
Table 6 shows the cantilever beam structure’s optimization results. From the data in the table, it can be found that after 7 iterations, an ideal optimization result was obtained. The overall count of new sample points demanded in the course of calculation was 603.

Table 6.
The iteration process of this method in the example of the cantilever beam structure.
Table 7 presents the computational results of different optimization design methods for this case study. It can be observed that other surrogate models have invoked more than 1000 limit-state evaluations, whereas the proposed BLCSO-BO-BP method has only required 603 evaluations. Furthermore, compared to the optimization design method based on CSO, the BLCSO-BO-BP method achieves a smaller objective function value while satisfying reliability constraints. Therefore, the proposed method demonstrates outstanding effectiveness and superiority.

Table 7.
Comparison of optimization results of different methods in the example of the cantilever beam structure.
With the aim of presenting the variation in the objective function value in each iteration process in a more intuitive manner, Figure 11 illustrates the iteration curve of the objective function pertaining to the cantilever beam structure.
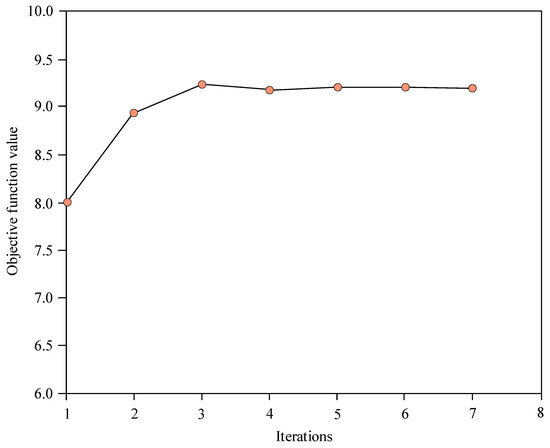
Figure 11.
Objective function iteration process in the example of the cantilever beam structure.
4.2.4. Vehicle Side Impact
As illustrated in Figure 12, this case study focuses on the structural design for vehicle side impact. In this example, seven random design variables and four levels of random design parameters that follow a normal distribution are considered, with their statistical parameters presented in Table 8. In this computational example, the vehicle side impact protection guidelines specified by the European Enhanced Vehicle-safety Committee (EEVC) were adopted as the safety standards. According to these guidelines: the allowable value for passenger abdominal load is set at 1 kN, the allowable values for rib deflection (upper, middle, and lower) are set at 32 mm, the allowable values for the viscous criterion (upper, middle, and lower) are set at 0.32 m/s, the allowable value for the public combined force is set at 4.0 kN, and the allowable values for velocity at the midpoint of the B-pillar and at the B-pillar location on the front door are set at 9.9 mm/ms and 15.69 mm/ms, respectively.
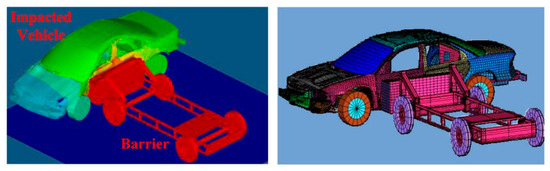
Figure 12.
Schematic Diagram of Vehicle Side Impact Structure [54].

Table 8.
Statistical Information of Random Variables and Parameters in Vehicle Side Impact Cases.
Based on the above description, the mathematical optimization model for this case is formulated as follows:
Among them, the expression of the objective function is obtained through finite element analysis and response surface methodology. Additionally, the performance functions in the probabilistic constraint functions are derived using the same approach, specifically represented as:
Table 9 summarizes the optimization design results for vehicle side impact structures obtained using different optimization design methods.

Table 9.
Comparison of optimization results of different methods in the example of the vehicle side impact.
From the aforementioned computational results, it can be observed that different optimization methods have all yielded final optimized outcomes. Among various surrogate models, BO-BP requires the smallest total number of sample points. In comparison, BLCSO-BO-BP reduces the computational cost by 37.16% compared to the commonly used Kriging model. Furthermore, when comparing CSO with BLCSO, it is evident that under the condition of employing the same surrogate model, the latter demonstrates superior optimization capability, resulting in more reliable and excellent design solutions. In summary, the proposed BLCSO-BO-BP in this study exhibits certain effectiveness and superiority.
5. Conclusions
In this study, for the UBDO research of practical engineering problems, a framework incorporating the BLCSO and BO-BP neural network models is proposed. By applying the butterfly optimization strategy and the Levy flight mechanism, the local search ability and global search ability of the CSO algorithm are effectively balanced, resulting in a more robust search performance. At the same time, the adoption of the BO-BP neural network model serves to diminish the computational cost of overall UBDO, paving the way for an efficient and accurate structural design while enhancing the overall design quality. Finally, the proposed method was validated through 29 test functions and four engineering examples. From the comparison among different optimization algorithms, it can be observed that BLCSO achieves significant improvements in computational accuracy and robustness compared to the original CSO, and demonstrates highly competitive performance relative to other state-of-the-art optimization algorithms. The results from the engineering examples reveal that BLCSO-BO-BP exhibits higher computational accuracy and lower computational cost. Furthermore, the ablation experiment results indicate that the BO-BP model achieves a substantial enhancement in computational efficiency compared to the BP model, while BLCSO demonstrates superior computational accuracy over CSO.
However, the surrogate model adopted in this study solely relies on a data-driven approach. With the advancement of science and technology, incorporating physical information into the development of surrogate models represents a promising new direction. Therefore, subsequent research will focus on integrating more advanced surrogate models to devise novel UBDO strategies. In addition, as engineering problems become increasingly complex, high-dimensional problems and highly nonlinear problems have gradually emerged as challenging issues. More effective solutions need to be proposed for problems of high complexity and engineering problems involving large-scale datasets. These will also be the focal points of subsequent research.
Author Contributions
Conceptualization, Q.J., R.L. and S.J.; Methodology, Q.J., R.L. and S.J.; Validation, Q.J., R.L. and S.J.; Formal analysis, Q.J., R.L. and S.J.; Resources, Q.J., R.L. and S.J.; Writing—original draft, Q.J., R.L. and S.J.; Writing—review and editing, Q.J., R.L. and S.J.; Funding acquisition, Q.J., R.L. and S.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
To evaluate the optimization performance of the BL-COA algorithm when different values of are selected, this study conducted tests using various benchmark functions. These benchmark functions encompass Unimodal Functions, Multimodal Functions, and Composite Functions. The expressions of these benchmark functions are provided in the Table A1, where the dimension of the test function.

Table A1.
Information on the test functions.
Table A1.
Information on the test functions.
| Function | Range | |
|---|---|---|
| 30 | [−5.12, 5.12] D | |
| 30 | [−2.048, 2.048] D | |
| 30 | [−32.768, 32.768] D | |
| 10 | [−5.12, 5.12] D | |
| 30 | [−600, 600] D | |
| 50 | [−500, 500] D |
The value range of the parameter r is set from 0 to 1, with a step size of 0.1. For each value of , to evaluate the algorithm’s stability, the population size of the algorithm is set to 50, and the maximum number of iterations is set to 100. Thirty independent optimization experiments are conducted. Table A2 presents the convergence speed, as well as the minimum, maximum, average, and standard deviation of the optimal solutions obtained from multiple experiments. Use bold in the table to highlight the calculation results when = 0.7.

Table A2.
Results of sensitivity experiments.
Table A2.
Results of sensitivity experiments.
| Functions | r | The minimum Value of the Optimal Solution | The Average Value of the Optimal Solutions | The Maximum Value of the Optimal Solution | The Standard Deviation of the Optimal Solutions | Convergence Speed (s) |
|---|---|---|---|---|---|---|
| F1 | 0.1 | 1.2674 × 10−35 | 2.6401 × 10−33 | 1.2571 × 10−32 | 4.1469 × 10−33 | 0.029508 |
| 0.2 | 0.00015681 | 0.002091 | 0.0047768 | 0.001546 | 0.12979 | |
| 0.3 | 2.071 × 10−214 | 9.0618 × 10−69 | 9.0618 × 10−68 | 2.8656 × 10−68 | 0.030281 | |
| 0.4 | 6.051 × 10−35 | 2.5161 × 10−25 | 2.5156 × 10−24 | 7.9549 × 10−25 | 0.022371 | |
| 0.5 | 0.25392 | 0.52169 | 0.74901 | 0.13485 | 0.015554 | |
| 0.6 | 4.2816 × 10−7 | 3.8951 × 10−6 | 7.0286 × 10−6 | 1.9831 × 10−6 | 0.030294 | |
| 0.7 | 0 | 2.2684 × 10−125 | 1.7343 × 10−124 | 5.5562 × 10−125 | 0.026011 | |
| 0.8 | 3.3767 × 10−35 | 1.1359 × 10−33 | 8.1204 × 10−33 | 2.4834 × 10−33 | 0.028445 | |
| 0.9 | 1.6341 × 10−37 | 7.7333 × 10−25 | 6.0758 × 10−24 | 1.8921 × 10−24 | 0.021513 | |
| 1 | 6.9763 × 10−7 | 2.2024 × 10−6 | 5.8204 × 10−6 | 1.6029 × 10−6 | 0.028347 | |
| F2 | 0.1 | −418.33 | −415.76 | −405.75 | 3.7741 | 0.018862 |
| 0.2 | −418.33 | −412.94 | −409.25 | 4.2267 | 0.046129 | |
| 0.3 | −418.33 | −417.56 | −416.14 | 0.7413 | 0.01932 | |
| 0.4 | −418.33 | −413.42 | −410.14 | 4.2303 | 0.0077923 | |
| 0.5 | −418.33 | −415.87 | −410.13 | 3.9568 | 0.013134 | |
| 0.6 | −418.33 | −417.07 | −410.14 | 2.4965 | 0.02676 | |
| 0.7 | −418.33 | −418.33 | −418.33 | 9.5296 × 10−5 | 0.018653 | |
| 0.8 | −418.33 | −418.33 | −418.32 | 0.0044498 | 0.066814 | |
| 0.9 | −418.33 | −417.8 | −416.14 | 0.76649 | 0.01952 | |
| 1 | −418.33 | −416.96 | −410.14 | 2.4589 | 0.026582 | |
| F3 | 0.1 | −2.6097 | −2.2255 | −1.8999 | 0.24426 | 0.009646 |
| 0.2 | −2.7176 | −2.7155 | −2.7092 | 0.0024518 | 0.046611 | |
| 0.3 | −2.718 | −2.7156 | −2.7128 | 0.0017583 | 0.046178 | |
| 0.4 | −2.7179 | −2.7156 | −2.7132 | 0.001481 | 0.046432 | |
| 0.5 | −2.7183 | −2.7183 | −2.7183 | 7.0086 × 10−7 | 0.014749 | |
| 0.6 | −2.7183 | −2.7183 | −2.7183 | 2.2083 × 10−7 | 0.021694 | |
| 0.7 | −2.7183 | −2.7183 | −2.7183 | 4.6811 × 10−16 | 0.028963 | |
| 0.8 | −2.7183 | −2.7183 | −2.7183 | 4.6811 × 10−16 | 0.02057 | |
| 0.9 | −2.7183 | −2.7183 | −2.7183 | 3.7855 × 10−12 | 0.020766 | |
| 1 | −2.7177 | −2.7152 | −2.707 | 0.0032081 | 0.046641 | |
| F4 | 0.1 | 4.7243 × 10−7 | 0.00011708 | 0.00070876 | 0.00021327 | 0.046361 |
| 0.2 | 0 | 2.2273 | 10.945 | 4.1622 | 0.020712 | |
| 0.3 | 4.3039 × 10−8 | 3.8361 | 7.3024 | 2.2435 | 0.014527 | |
| 0.4 | 1.4924 × 10−6 | 0.11326 | 1.0379 | 0.32613 | 0.045362 | |
| 0.5 | 0.067671 | 0.00016892 | 0.0009582 | 0.00029693 | 0.021115 | |
| 0.6 | 0 | 6.0606 × 10−5 | 0.00028943 | 9.3136 × 10−5 | 0.0091597 | |
| 0.7 | 0 | 0 | 0 | 0 | 0.014531 | |
| 0.8 | 0 | 1.6538 × 10−6 | 0.00013503 | 2.0429 × 10−6 | 0.028017 | |
| 0.9 | 6.8531 × 10−6 | 0.00020814 | 0.0010683 | 0.00031516 | 0.019713 | |
| 1 | 1.4704 × 10−6 | 0.00028076 | 0.0016492 | 0.00054483 | 0.067671 | |
| F5 | 0.1 | 0.43399 | 0.71257 | 0.95111 | 0.19868 | 0.00983 |
| 0.2 | 0.015268 | 0.082615 | 0.17984 | 0.056173 | 0.014997 | |
| 0.3 | 0.0038319 | 0.096991 | 0.27921 | 0.092249 | 0.046197 | |
| 0.4 | 0.002467 | 0.024119 | 0.081303 | 0.027423 | 0.021265 | |
| 0.5 | 0.0024663 | 0.0068887 | 0.024551 | 0.0077457 | 0.028851 | |
| 0.6 | 0.0024696 | 0.0069524 | 0.036808 | 0.01062 | 0.068428 | |
| 0.7 | 0.0024663 | 0.0044396 | 0.0098544 | 0.0027945 | 0.02841 | |
| 0.8 | 0.0024663 | 0.0056693 | 0.014762 | 0.0040234 | 0.040013 | |
| 0.9 | 0.0024696 | 0.013298 | 0.041803 | 0.013017 | 0.0207 | |
| 1 | 0.0056531 | 0.072293 | 0.26635 | 0.077289 | 0.020923 | |
| F6 | 0.1 | 12,880 | 13,971 | 14,647 | 596.08 | 0.20069 |
| 0.2 | 8749.5 | 10,715 | 11,564 | 845.16 | 0.11394 | |
| 0.3 | 9231.3 | 11,289 | 12,765 | 986.73 | 0.025697 | |
| 0.4 | 10,053 | 12,516 | 17,438 | 1965.6 | 0.048951 | |
| 0.5 | 7273.4 | 8865.6 | 10,498 | 1089.2 | 0.043216 | |
| 0.6 | 5447.8 | 9140.3 | 11,694 | 1888.9 | 0.041474 | |
| 0.7 | 2554.7 | 8678.2 | 9758.6 | 927.63 | 0.032363 | |
| 0.8 | 7341.4 | 9150.9 | 9776 | 768.61 | 0.04254 | |
| 0.9 | 9398.3 | 11,396 | 13,030 | 1183.2 | 0.025367 | |
| 1 | 8641.8 | 9979.2 | 11,260 | 831.14 | 0.11218 |
Appendix B
The following table presents the test results for the CEC2017 function suite. The provided data encompass the mean, standard deviation, p-value, Cliff’s delta value, and ranking of the optimal solutions obtained by different optimization algorithms.

Table A3.
Results for the CEC2017 function suite.
Table A3.
Results for the CEC2017 function suite.
| Function | Indicator | PSO | GWO | HHO | GA | SSA | CSO | BLCSO |
|---|---|---|---|---|---|---|---|---|
| F1 | Ave | 2.6948 × 106 | 11150 | 1.1609 × 107 | 7.453 × 109 | 1.2153 × 109 | 8.3445 × 107 | 3960.1 |
| Std | 2.7113 × 106 | 5486.7 | 2.438 × 106 | 5.8434 × 109 | 8.4496 × 108 | 4.046 × 107 | 4204.3 | |
| p-valve | 2 × 10−6 | 2 × 10−6 | 2 × 10−6 | 2 × 10−6 | 2 × 10−6 | 2 × 10−6 | -- | |
| Cliff’s delta | −1.000 | −1.000 | −1.000 | −1.000 | −1.000 | −1.000 | -- | |
| Rank | 3 | 2 | 4 | 7 | 6 | 5 | 1 | |
| F2 | Ave | 12,477 | 52,701 | 25,599 | 1.2014 × 105 | 2.372 × 105 | 41,642 | 12,879 |
| Std | 6581.8 | 12,254 | 8994.4 | 40,918 | 52,094 | 4050.7 | 4907.9 | |
| p-valve | 0.7343 | 2 × 10−6 | 9 × 10−6 | 2 × 10−6 | 1.7 × 10−6 | 0.0064 | -- | |
| Cliff’s delta | −0.009 | −0.996 | −0.824 | −1.000 | −1.000 | −0.436 | -- | |
| Rank | 1 | 5 | 3 | 6 | 7 | 4 | 2 | |
| F3 | Ave | 540.11 | 570.99 | 575.94 | 982.32 | 499.08 | 663.63 | 476.68 |
| Std | 12.776 | 51.759 | 63.045 | 384.98 | 17.736 | 42.514 | 9.8982 | |
| p-valve | 1.7 × 10−6 | 2.9 × 10−6 | 5.2 × 10−6 | 1.2 × 10−5 | 2.8 × 10−5 | 1.7 × 10−6 | -- | |
| Cliff’s delta | −1.000 | −0.933 | −0.924 | −0.836 | −0.762 | −1.000 | -- | |
| Rank | 3 | 4 | 5 | 7 | 2 | 6 | 1 | |
| F4 | Ave | 655.13 | 634.42 | 736.12 | 720.25 | 755.18 | 797.68 | 629.43 |
| Std | 29.004 | 63.974 | 43.668 | 58.041 | 59.344 | 87.691 | 21.356 | |
| p-valve | 0.00039 | 0.44 | 1.9 × 10−6 | 5.8 × 10−6 | 2.4 × 10−6 | 2.6 × 10−6 | -- | |
| Cliff’s delta | −0.567 | −0.027 | −0.958 | −0.893 | −0.936 | −0.933 | -- | |
| Rank | 3 | 2 | 5 | 4 | 6 | 7 | 1 | |
| F5 | Ave | 645.55 | 604.44 | 662.85 | 623.39 | 647.5 | 674.67 | 608.1 |
| Std | 6.1205 | 1.1778 | 2.9074 | 11.993 | 11.105 | 11.994 | 1.6554 | |
| p-valve | 1.7 × 10−6 | 1.7 × 10−6 | 1.7 × 10−6 | 1.2 × 10−5 | 1.7 × 10−6 | 1.7 × 10−6 | -- | |
| Cliff’s delta | −1.000 | 0.922 | −1.000 | −0.840 | −1.000 | −1.000 | -- | |
| Rank | 4 | 1 | 6 | 3 | 5 | 7 | 2 | |
| F6 | Ave | 941.36 | 907.42 | 1277.7 | 983 | 1228.3 | 1291.7 | 878.84 |
| Std | 39.698 | 32.512 | 113.08 | 98.178 | 95.887 | 140.18 | 51.132 | |
| p-valve | 3.4 × 10−5 | 0.0032 | 1.7 × 10−6 | 5.3 × 10−5 | 1.7 × 10−6 | 1.7 × 10−6 | -- | |
| Cliff’s delta | −0.722 | −0.462 | −1.000 | −0.729 | −1.000 | −0.984 | -- | |
| Rank | 3 | 2 | 6 | 4 | 5 | 7 | 1 | |
| F7 | Ave | 922.63 | 976.41 | 968.35 | 975.11 | 1044.4 | 896.27 | 872.42 |
| Std | 20.547 | 12.266 | 26.826 | 42.983 | 50.973 | 26.261 | 19.587 | |
| p-valve | 2.6 × 10−6 | 1.7 × 10−6 | 1.7 × 10−6 | 1.9 × 10−6 | 1.7 × 10−6 | 0.00031 | -- | |
| Cliff’s delta | −0.931 | −1.000 | −0.996 | −0.951 | −0.998 | −0.571 | -- | |
| Rank | 3 | 6 | 4 | 5 | 7 | 2 | 1 | |
| F8 | Ave | 7298.5 | 5887.3 | 5318.2 | 9601.8 | 3866.5 | 2155.2 | 2049 |
| Std | 942.08 | 1833.7 | 178.37 | 2273.2 | 1806.6 | 969.72 | 1478.8 | |
| p-valve | 1.7 × 10−6 | 2.9 × 10−6 | 1.7 × 10−6 | 1.7 × 10−6 | 0.00021 | 0.29 | -- | |
| Cliff’s delta | −1.000 | −0.904 | −1.000 | −0.996 | −0.611 | −0.124 | -- | |
| Rank | 6 | 5 | 4 | 7 | 3 | 2 | 1 | |
| F9 | Ave | 5757.5 | 6756 | 5254 | 5285.1 | 4975 | 6017.1 | 3945 |
| Std | 494.77 | 291.87 | 709.68 | 478.02 | 379.36 | 684.34 | 252.38 | |
| p-valve | 1.7 × 10−6 | 1.7 × 10−6 | 2.9 × 10−6 | 1.9 × 10−6 | 1.9 × 10−6 | 1.7 × 10−6 | -- | |
| Cliff’s delta | −1.000 | −1.000 | −0.924 | −0.976 | −0.971 | −0.991 | -- | |
| Rank | 5 | 7 | 3 | 4 | 2 | 6 | 1 | |
| F10 | Ave | 1331.2 | 1390.3 | 1322.6 | 1758.6 | 1270.3 | 5157.5 | 1248.9 |
| Std | 44.563 | 48.162 | 42.595 | 269.39 | 65.073 | 1132.4 | 42.233 | |
| p-valve | 4.7 × 10−6 | 1.7 × 10−6 | 7 × 10−6 | 2.6 × 10−6 | 0.043 | 1.7 × 10−6 | -- | |
| Cliff’s delta | −0.851 | −0.973 | −0.811 | −0.933 | −0.231 | −1.000 | -- | |
| Rank | 4 | 5 | 3 | 6 | 2 | 7 | 1 | |
| F11 | Ave | 4.0014 × 106 | 1.1835 × 108 | 3.035 × 107 | 4.2306 × 107 | 2.7555 × 106 | 2.1966 × 108 | 2.0016 × 105 |
| Std | 1.7018 × 106 | 1.018 × 108 | 2.0077 × 107 | 7.0855 × 107 | 1.5392 × 106 | 1.0772 × 108 | 2.2045 × 105 | |
| p-valve | 1.9 × 10−6 | 1.6 × 10−5 | 5.8 × 10−6 | 0.0044 | 3.5 × 10−6 | 1.9 × 10−6 | -- | |
| Cliff’s delta | −0.933 | −0.800 | −0.933 | −0.467 | −0.933 | −0.933 | -- | |
| Rank | 3 | 6 | 4 | 5 | 2 | 7 | 1 | |
| F12 | Ave | 45,729 | 1.2644 × 105 | 4.5846 × 105 | 9.2591 × 105 | 21,206 | 5.3441 × 105 | 28,735 |
| Std | 31,092 | 37090 | 1.3208 × 105 | 1.9676 × 106 | 11,899 | 4.6919 × 105 | 12,156 | |
| p-valve | 0.0036 | 1.9 × 10−6 | 1.7 × 10−6 | 0.024 | 0.098 | 3.4 × 10−5 | -- | |
| Cliff’s delta | −0.389 | −0.964 | −1.000 | −0.322 | 0.280 | −0.800 | -- | |
| Rank | 3 | 4 | 5 | 7 | 1 | 6 | 2 | |
| F13 | Ave | 86,655 | 2.4615 × 105 | 1.3344 × 105 | 30,987 | 5773.6 | 1.1669 × 106 | 3216.9 |
| Std | 55,422 | 2.1085 × 105 | 1.2696 × 105 | 27,317 | 3860.4 | 7.3443 × 105 | 3471.8 | |
| p-valve | 5.8 × 10−6 | 1.6 × 10−5 | 4.1 × 10−5 | 3.7 × 10−5 | 0.0024 | 4.3 × 10−6 | -- | |
| Cliff’s delta | −0.933 | −0.800 | −0.800 | −0.756 | −0.429 | −0.933 | -- | |
| Rank | 4 | 6 | 5 | 3 | 2 | 7 | 1 | |
| F14 | Ave | 18,292 | 50,617 | 35,615 | 1.0176 × 106 | 7945.9 | 62,452 | 7459.3 |
| Std | 10,716 | 27,787 | 12,378 | 1.9419 × 106 | 3798.7 | 26,804 | 4263.2 | |
| p-valve | 6.9 × 10−5 | 5.8 × 10−6 | 1.9 × 10−6 | 0.01 | 0.25 | 2.1 × 10−6 | -- | |
| Cliff’s delta | −0.696 | −0.924 | −0.940 | −0.400 | −0.131 | −0.933 | -- | |
| Rank | 3 | 5 | 4 | 7 | 2 | 6 | 1 | |
| F15 | Ave | 2666.4 | 3242.6 | 3088.4 | 3142.2 | 2557 | 3533.5 | 2273.4 |
| Std | 247.5 | 479.41 | 377.89 | 389.89 | 134.76 | 656.39 | 152.23 | |
| p-valve | 5.8 × 10−6 | 2.4 × 10−6 | 2.4 × 10−6 | 1.9 × 10−6 | 3.9 × 10−6 | 2.6 × 10−6 | -- | |
| Cliff’s delta | −0.873 | −0.936 | −0.940 | −0.940 | −0.871 | −0.933 | -- | |
| Rank | 3 | 6 | 4 | 5 | 2 | 7 | 1 | |
| F16 | Ave | 2165.7 | 2077.9 | 2395.5 | 2465 | 2555.2 | 2512.8 | 2065.5 |
| Std | 261.02 | 59.968 | 299.12 | 248.41 | 249.73 | 265.94 | 103.28 | |
| p-valve | 0.02 | 0.18 | 3.1 × 10−5 | 5.2 × 10−6 | 2.4 × 10−6 | 3.9 × 10−6 | -- | |
| Cliff’s delta | −0.271 | −0.167 | −0.753 | −0.884 | −0.927 | −0.911 | -- | |
| Rank | 3 | 2 | 4 | 5 | 7 | 6 | 1 | |
| F17 | Ave | 2.3416 × 106 | 2.0959 × 106 | 6.1878 × 105 | 7.125 × 105 | 7.069 × 106 | 5.9273 × 105 | 82,689 |
| Std | 5.5303 × 105 | 1.9468 × 106 | 2.919 × 105 | 7.4786 × 105 | 5.4647 × 106 | 5.3013 × 105 | 18,258 | |
| p-valve | 1.7 × 10−6 | 4.1 × 10−5 | 2.6 × 10−6 | 0.00024 | 1.2 × 10−5 | 4.4 × 10−5 | -- | |
| Cliff’s delta | −1.000 | −0.800 | −0.933 | −0.549 | −0.800 | −0.747 | -- | |
| Rank | 6 | 5 | 3 | 4 | 7 | 2 | 1 | |
| F18 | Ave | 28,290 | 2.4408 × 105 | 3.1424 × 105 | 3.8196 × 106 | 7.4957 × 106 | 9.436 × 105 | 4762.1 |
| Std | 19,780 | 53,198 | 1.8894 × 105 | 4.6224 × 106 | 4.5621 × 106 | 7.145 × 105 | 4389.2 | |
| p-valve | 2.2 × 10−5 | 1.7 × 10−6 | 3.9 × 10−6 | 0.00033 | 3.9 × 10−6 | 1.2 × 10−5 | -- | |
| Cliff’s delta | −0.809 | −1.000 | −0.933 | −0.533 | −0.933 | −0.831 | -- | |
| Rank | 2 | 3 | 4 | 6 | 7 | 5 | 1 | |
| F19 | Ave | 2526.5 | 2386.2 | 2767 | 2449.3 | 2620 | 2694.3 | 2250.3 |
| Std | 231.6 | 148.13 | 245.7 | 234.24 | 238.29 | 313.55 | 51.841 | |
| p-valve | 2 × 10−5 | 0.00011 | 1.9 × 10−6 | 0.00021 | 5.2 × 10−6 | 7.7 × 10−6 | -- | |
| Cliff’s delta | −0.811 | −0.642 | −0.933 | −0.611 | −0.916 | −0.893 | -- | |
| Rank | 4 | 2 | 7 | 3 | 5 | 6 | 1 | |
| F20 | Ave | 2453 | 2488.3 | 2553.5 | 2460.5 | 2500.8 | 2550.4 | 2396.9 |
| Std | 55.299 | 12.039 | 39.853 | 40.851 | 45.704 | 84.677 | 42.472 | |
| p-valve | 0.00017 | 1.7 × 10−6 | 1.7 × 10−6 | 2.2 × 10−5 | 2.9 × 10−6 | 2.9 × 10−6 | -- | |
| Cliff’s delta | −0.624 | −0.987 | −0.996 | −0.769 | −0.922 | −0.909 | -- | |
| Rank | 2 | 4 | 7 | 3 | 5 | 6 | 1 | |
| F21 | Ave | 5069.1 | 4964.9 | 7475.4 | 5617.3 | 3102.5 | 7781.6 | 3428.9 |
| Std | 2418.5 | 626.63 | 358.73 | 2039.8 | 1789.3 | 790.32 | 1321.3 | |
| p-valve | 0.0015 | 1.1 × 10−5 | 1.7 × 10−6 | 7.5 × 10−5 | 0.86 | 1.7 × 10−6 | -- | |
| Cliff’s delta | −0.487 | −0.764 | −1.000 | −0.684 | 0.087 | −0.996 | -- | |
| Rank | 4 | 3 | 6 | 5 | 1 | 7 | 2 | |
| F22 | Ave | 2980.1 | 2829.5 | 3147.2 | 2796.6 | 3042.3 | 3067.9 | 2770.3 |
| Std | 90.326 | 17.923 | 75.85 | 41.128 | 135.32 | 104.51 | 29.821 | |
| p-valve | 1.9 × 10−6 | 2.1 × 10−6 | 1.7 × 10−6 | 0.0024 | 2.1 × 10−6 | 1.7 × 10−6 | -- | |
| Cliff’s delta | −0.942 | −0.929 | −1.000 | −0.440 | −0.933 | −0.984 | -- | |
| Rank | 4 | 3 | 7 | 2 | 5 | 6 | 1 | |
| F23 | Ave | 3093.3 | 3029.3 | 3401.1 | 2971.5 | 3116.7 | 3230.1 | 2920.5 |
| Std | 81.288 | 15.5034 | 79.465 | 24.971 | 103.66 | 99.543 | 83.648 | |
| p-valve | 2.9 × 10−6 | 4.3 × 10−6 | 1.7 × 10−6 | 0.00066 | 3.9 × 10−6 | 1.7 × 10−6 | -- | |
| Cliff’s delta | −0.882 | −0.858 | −1.000 | −0.549 | −0.878 | −0.984 | -- | |
| Rank | 4 | 3 | 7 | 2 | 5 | 6 | 1 | |
| F24 | Ave | 2940 | 2896.8 | 2936.4 | 3169.4 | 2894.4 | 3062.9 | 2995.9 |
| Std | 18.369 | 2.2586 | 28.62 | 209.55 | 28.3295 | 50.951 | 14.57 | |
| p-valve | 1.7 × 10−6 | 1.7 × 10−6 | 2.4 × 10−6 | 0.00028 | 1.7 × 10−6 | 1.2 × 10−5 | -- | |
| Cliff’s delta | 0.971 | 1.000 | 0.853 | −0.558 | 1.000 | −0.842 | -- | |
| Rank | 4 | 1 | 3 | 7 | 2 | 6 | 5 | |
| F25 | Ave | 6237.9 | 5502.4 | 6985 | 5623.7 | 5898.3 | 7441.6 | 4513.5 |
| Std | 642.06 | 142.64 | 2176.7 | 608.53 | 1951.4 | 1689.4 | 155.07 | |
| p-valve | 1.9 × 10−6 | 1.7 × 10−6 | 2.6 × 10−5 | 2.9 × 10−6 | 0.00096 | 3.2 × 10−6 | -- | |
| Cliff’s delta | −0.971 | −1.000 | −0.800 | −0.929 | −0.476 | −0.933 | -- | |
| Rank | 5 | 2 | 6 | 3 | 4 | 7 | 1 | |
| F26 | Ave | 3272.9 | 3228.7 | 3476.2 | 3247.1 | 3278.1 | 3434 | 3235.8 |
| Std | 18.59 | 4.3929 | 104.85 | 15.1 | 10.192 | 80.496 | 14.667 | |
| p-valve | 2.9 × 10−6 | 0.032 | 1.9 × 10−6 | 0.0015 | 1.7 × 10−6 | 1.9 × 10−6 | -- | |
| Cliff’s delta | −0.896 | 0.316 | −0.933 | −0.471 | −0.996 | −0.940 | -- | |
| Rank | 4 | 1 | 7 | 3 | 5 | 6 | 2 | |
| F27 | Ave | 3297.2 | 3299.8 | 3310 | 4510.5 | 3487.3 | 3370.7 | 3243.9 |
| Std | 30.382 | 11.639 | 40.678 | 476.76 | 72.122 | 36.426 | 24.532 | |
| p-valve | 4.7 × 10−6 | 1.7 × 10−6 | 5.2 × 10−6 | 1.9 × 10−6 | 1.7 × 10−6 | 1.7 × 10−6 | -- | |
| Cliff’s delta | −0.860 | −0.982 | −0.878 | −0.962 | −1.000 | −0.996 | -- | |
| Rank | 2 | 3 | 4 | 7 | 6 | 5 | 1 | |
| F28 | Ave | 4228.1 | 4065.4 | 4621.6 | 4027.2 | 3943.7 | 5157 | 3837.9 |
| Std | 307.46 | 141.38 | 92.231 | 271.55 | 173.57 | 502.42 | 187.59 | |
| p-valve | 2.8 × 10−5 | 3.4 × 10−5 | 1.7 × 10−6 | 0.0016 | 0.0057 | 1.9 × 10−6 | -- | |
| Cliff’s delta | −0.756 | −0.722 | −1.000 | −0.482 | −0.384 | −0.964 | -- | |
| Rank | 5 | 4 | 6 | 3 | 2 | 7 | 1 | |
| F29 | Ave | 1.7902 × 105 | 1.2564 × 105 | 2.1557 × 106 | 3.256 × 105 | 8.9325 × 106 | 1.6245 × 107 | 16,244 |
| Std | 1.5375 × 105 | 55,218 | 8.6316 × 105 | 3.3875 × 105 | 9.4394 × 106 | 6.1396 × 106 | 8111.9 | |
| p-valve | 3.4 × 10−5 | 2.4 × 10−6 | 1.9 × 10−6 | 9.7 × 10−5 | 6.3 × 10−5 | 1.9 × 10−6 | -- | |
| Cliff’s delta | −0.800 | −0.933 | −0.933 | −0.667 | −0.667 | −0.933 | -- | |
| Rank | 3 | 2 | 5 | 4 | 6 | 7 | 1 |
References
- Luo, C.; Zhu, S.P.; Keshtegar, B.; Macek, W.; Branco, R.; Meng, D. Active Kriging-based conjugate first-order reliability method for highly efficient structural reliability analysis using resample strategy. Comput. Methods Appl. Mech. Eng. 2024, 423, 116863. [Google Scholar] [CrossRef]
- Meng, D.; Yang, S.; Yang, H.; De Jesus, A.M.; Correia, J.; Zhu, S.P. Intelligent-inspired framework for fatigue reliability evaluation of offshore wind turbine support structures under hybrid uncertainty. Ocean Eng. 2024, 307, 118213. [Google Scholar] [CrossRef]
- Meng, D.; Yang, H.; Yang, S.; Zhang, Y.; De Jesus, A.M.; Correia, J.; Zhu, S.P. Kriging-assisted hybrid reliability design and optimization of offshore wind turbine support structure based on a portfolio allocation strategy. Ocean Eng. 2024, 295, 116842. [Google Scholar] [CrossRef]
- Wang, B.; Zhu, Q. Stability analysis of discrete-time semi-Markov jump linear systems. IEEE Trans. Autom. Control 2020, 65, 5415–5421. [Google Scholar] [CrossRef]
- Yang, X.; Zhu, Q. Stabilization of stochastic retarded systems based on sampled-data feedback control. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 5895–5904. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, H.; Wu, T.; Xu, J.; Jiang, C. A novel reliability-based design optimization method through instance-based transfer learning. Comput. Methods Appl. Mech. Eng. 2024, 432, 117388. [Google Scholar] [CrossRef]
- Meng, D.; Yang, S.; De Jesus, A.M.; Fazeres-Ferradosa, T.; Zhu, S.P. A novel hybrid adaptive Kriging and water cycle algorithm for reliability-based design and optimization strategy: Application in offshore wind turbine monopile. Comput. Methods Appl. Mech. Eng. 2023, 412, 116083. [Google Scholar] [CrossRef]
- Meng, D.; Yang, S.; De Jesus, A.M.; Zhu, S.P. A novel Kriging-model-assisted reliability-based multidisciplinary design optimization strategy and its application in the offshore wind turbine tower. Renew. Energy 2023, 203, 407–420. [Google Scholar] [CrossRef]
- Lai, X.; Chen, Y.; Zhang, Y.; Wang, C. Fast solution of reliability-based robust design optimization by reducing the evaluation number for the performance functions. Int. J. Struct. Integr. 2023, 14, 946–965. [Google Scholar] [CrossRef]
- Yang, S.; Guo, C.; Meng, D.; Guo, Y.; Guo, Y.; Pan, L.; Zhu, S.P. MECSBO: Multi-strategy enhanced circulatory system based optimisation algorithm for global optimisation and reliability-based design optimisation problems. IET Collab. Intell. Manuf. 2024, 6, e12097. [Google Scholar] [CrossRef]
- Huang, Y.; Zhu, Q. pth Moment Exponential Stability of Highly Nonlinear Neutral Hybrid Stochastic Delayed Systems with Impulsive Effect; IEEE: New York, NY, USA, 2025. [Google Scholar]
- Meng, Z.; Li, C.; Hao, P. Unified reliability-based design optimization with probabilistic, uncertain-but-bounded and fuzzy variables. Comput. Methods Appl. Mech. Eng. 2023, 407, 115925. [Google Scholar] [CrossRef]
- van Mierlo, C.; Persoons, A.; Faes, M.G.; Moens, D. Robust design optimisation under lack-of-knowledge uncertainty. Comput. Struct. 2023, 275, 106910. [Google Scholar] [CrossRef]
- Farahmand-Tabar, S.; Shirgir, S. Positron-enabled atomic orbital search algorithm for improved reliability-based design optimization. In Handbook of Formal Optimization; Springer Nature: Singapore, 2024; pp. 389–418. [Google Scholar]
- Ebrahimi, B.; Bataleblu, A.A. Intelligent reliability-based design optimization: Past and future research trends. In Developments in Reliability Engineering; Elsevier: Amsterdam, The Netherlands, 2024; pp. 787–826. [Google Scholar]
- Hu, W.; Cheng, S.; Yan, J.; Cheng, J.; Peng, X.; Cho, H.; Lee, I. Reliability-based design optimization: A state-of-the-art review of its methodologies, applications, and challenges. Struct. Multidiscip. Optim. 2024, 67, 168. [Google Scholar] [CrossRef]
- Yang, S.; Meng, D.; Guo, Y.; Nie, P.; de Jesus, A.M. A reliability-based design and optimization strategy using a novel MPP searching method for maritime engineering structures. Int. J. Struct. Integr. 2023, 14, 809–826. [Google Scholar] [CrossRef]
- Yang, S.; Meng, D.; Wang, H.; Yang, C. A novel learning function for adaptive surrogate-model-based reliability evaluation. Philos. Trans. R. Soc. A 2024, 382, 20220395. [Google Scholar] [CrossRef]
- Abualigah, L.; Sheikhan, A.; Ikotun, A.M.; Zitar, R.A.; Alsoud, A.R.; Al-Shourbaji, I.; Jia, H. Particle Swarm Optimization Algorithm: Review and Applications; Elsevier: Amsterdam, The Netherlands, 2024. [Google Scholar]
- Alhijawi, B.; Awajan, A. Genetic algorithms: Theory, genetic operators, solutions, and applications. Evol. Intell. 2024, 17, 1245–1256. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Wang, J.H.; Wang, Y.; Jia, Z.C.; Sun, Q.; Pei, Q.Y.; Wu, D. Intelligent planning of fire evacuation routes in buildings based on improved adaptive ant colony algorithm. Comput. Ind. Eng. 2024, 194, 110335. [Google Scholar] [CrossRef]
- He, K.; Zhang, Y.; Wang, Y.K.; Zhou, R.H.; Zhang, H.Z. EABOA: Enhanced adaptive butterfly optimization algorithm for numerical optimization and engineering design problems. Alex. Eng. J. 2024, 87, 543–573. [Google Scholar] [CrossRef]
- Meng, D.; Zhu, S.-P. Multidisciplinary Design Optimization of Complex Structures Under Uncertainty, 1st ed.; CRC Press: Boca Raton, FL, USA, 2024; ISBN 9781003464792. [Google Scholar]
- Ghasemi, M.; Zare, M.; Trojovský, P.; Rao, R.V.; Trojovská, E.; Kandasamy, V. Optimization based on the smart behavior of plants with its engineering applications: Ivy algorithm. Knowl.-Based Syst. 2024, 295, 111850. [Google Scholar] [CrossRef]
- Zhu, F.; Li, G.; Tang, H.; Li, Y.; Lv, X.; Wang, X. Dung beetle optimization algorithm based on quantum computing and multi-strategy fusion for solving engineering problems. Expert Syst. Appl. 2024, 236, 121219. [Google Scholar] [CrossRef]
- Wang, J.; Wang, W.C.; Hu, X.X.; Qiu, L.; Zang, H.F. Black-winged kite algorithm: A nature-inspired meta-heuristic for solving benchmark functions and engineering problems. Artif. Intell. Rev. 2024, 57, 98. [Google Scholar] [CrossRef]
- Meng, D.; Yang, S.; Zhang, Y.; Zhu, S.-P. Structural reliability analysis and uncertainties-based collaborative design and optimization of turbine blades using surrogate model. Fatigue Fract. Eng. Mater. Struct. 2019, 42, 1219–1227. [Google Scholar] [CrossRef]
- Meng, Z.; Yıldız, B.S.; Li, G.; Zhong, C.; Mirjalili, S.; Yildiz, A.R. Application of state-of-the-art multiobjective metaheuristic algorithms in reliability-based design optimization: A comparative study. Struct. Multidiscip. Optim. 2023, 66, 191. [Google Scholar] [CrossRef]
- Hamza, F.; Ferhat, D.; Abderazek, H.; Dahane, M. A new efficient hybrid approach for reliability-based design optimization problems. Eng. Comput. 2022, 38, 1953–1976. [Google Scholar] [CrossRef]
- Zadeh, P.M.; Mohagheghi, M. An efficient Bi-level hybrid multi-objective reliability-based design optimization of composite structures. Compos. Struct. 2022, 296, 115862. [Google Scholar] [CrossRef]
- Chun, J. Reliability-based design optimization of structures using complex-step approximation with sensitivity analysis. Appl. Sci. 2021, 11, 4708. [Google Scholar] [CrossRef]
- Lai, X.; Huang, J.; Zhang, Y.; Wang, C.; Zhang, X. A general methodology for reliability-based robust design optimization of computation-intensive engineering problems. J. Comput. Des. Eng. 2022, 9, 2151–2169. [Google Scholar] [CrossRef]
- Meng, X.J.; Zhang, L.X.; Pan, Y.; Liu, Z.M. Reliability-based multidisciplinary concurrent design optimization method for complex engineering systems. Eng. Optim. 2022, 54, 1374–1394. [Google Scholar] [CrossRef]
- Li, X.; Zhu, H.; Chen, Z.; Ming, W.; Cao, Y.; He, W.; Ma, J. Limit state Kriging modeling for reliability-based design optimization through classification uncertainty quantification. Reliab. Eng. Syst. Saf. 2022, 224, 108539. [Google Scholar] [CrossRef]
- Meng, D.; Li, Y.; He, C.; Guo, J.; Lv, Z.; Wu, P. Multidisciplinary design for structural integrity using a collaborative optimization method based on adaptive surrogate modelling. Mater. Des. 2021, 206, 109789. [Google Scholar] [CrossRef]
- Yu, C.; Lv, X.; Huang, D.; Jiang, D. Reliability-based design optimization of offshore wind turbine support structures using RBF surrogate model. Front. Struct. Civ. Eng. 2023, 17, 1086–1099. [Google Scholar] [CrossRef]
- Allahvirdizadeh, R.; Andersson, A.; Karoumi, R. Improved dynamic design method of ballasted high-speed railway bridges using surrogate-assisted reliability-based design optimization of dependent variables. Reliab. Eng. Syst. Saf. 2023, 238, 109406. [Google Scholar] [CrossRef]
- Fu, C.; Liu, J.; Xu, W.; Yu, H. A reliability based multidisciplinary design optimization method with multi-source uncertainties. J. Phys. Conf. Ser. 2020, 1654, 012043. [Google Scholar] [CrossRef]
- Ni, P.; Li, J.; Hao, H.; Zhou, H. Reliability based design optimization of bridges considering bridge-vehicle interaction by Kriging surrogate model. Eng. Struct. 2021, 246, 112989. [Google Scholar] [CrossRef]
- Su, X.; Hong, Z.; Xu, Z.; Qian, H. An improved CREAM model based on Deng entropy and evidence distance. Nucl. Eng. Technol. 2025, 57, 103485. [Google Scholar] [CrossRef]
- Huang, J.; Ai, Q. Key vulnerability parameters for steel pipe pile-supported wharves considering the uncertainties in structural design. Int. J. Ocean Syst. Manag. 2025, 2, 35–51. [Google Scholar] [CrossRef]
- Correia, J.A.; Haselibozchaloee, D.; Zhu, S.P. A review on fatigue design of offshore structures. Int. J. Ocean Syst. Manag. 2025, 2, 1–18. [Google Scholar] [CrossRef]
- Su, X.; Zhong, J.; Hong, Z.; Qian, H.; Pelusi, D. A novel belief entropy and its application in cooperative situational awareness. Expert Syst. Appl. 2025, 286, 128027. [Google Scholar] [CrossRef]
- Yang, S.; Chen, Y. Modelling and analysis of offshore wind turbine gearbox under multi-field coupling. Int. J. Ocean. Syst. Manag. 2025, 2, 52–66. [Google Scholar] [CrossRef]
- Gargama, H.; Chaturvedi, S.K.; Rai, R.N. Genetic Algorithm and Artificial Neural Networks in Reliability-Based Design Optimization. Reliab. Anal. Mod. Power Syst. 2024, 8, 125–141. [Google Scholar]
- Wang, Y.; Sha, W.; Xiao, M.; Qiu, C.W.; Gao, L. Deep-Learning-Enabled Intelligent Design of Thermal Metamaterials (Adv. Mater. 33/2023). Adv. Mater. 2023, 35, 2370237. [Google Scholar] [CrossRef]
- Chen, B.; Cao, L.; Chen, C.; Chen, Y.; Yue, Y. A comprehensive survey on the chicken swarm optimization algorithm and its applications: State-of-the-art and research challenges. Artif. Intell. Rev. 2024, 57, 170. [Google Scholar] [CrossRef]
- Arora, S.; Singh, S. Butterfly optimization algorithm: A novel approach for global optimization. Soft Comput. 2019, 23, 715–734. [Google Scholar] [CrossRef]
- Dong, Z.; Sheng, Z.; Zhao, Y.; Zhi, P. Robust optimization design method for structural reliability based on active-learning MPA-BP neural network. Int. J. Struct. Integr. 2023, 14, 248–266. [Google Scholar] [CrossRef]
- Song, X.; Zou, L.; Tang, M. An improved Monte Carlo reliability analysis method based on BP neural network. Appl. Sci. 2025, 15, 4438. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Zhong, C.; Wang, M.; Dang, C.; Ke, W.; Guo, S. First-order reliability method based on Harris Hawks Optimization for high-dimensional reliability analysis. Struct. Multidiscip. Optim. 2020, 62, 1951–1968. [Google Scholar] [CrossRef]
- Gharehchopogh, F.S.; Namazi, M.; Ebrahimi, L.; Abdollahzadeh, B. Advances in sparrow search algorithm: A comprehensive survey. Arch. Comput. Methods Eng. 2023, 30, 427–455. [Google Scholar] [CrossRef]
- Zhang, Z.; Deng, W.; Jiang, C. A PDF-based performance shift approach for reliability-based design optimization. Comput. Methods Appl. Mech. Eng. 2021, 374, 113610. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).