Abstract
Graph Neural Networks (GNNs) have shown strong performance in link prediction, a core task in graph analysis. However, recent studies reveal their vulnerability to backdoor attacks, which can manipulate predictions stealthily and pose significant yet underexplored security risks. The existing backdoor strategies for link prediction suffer from two key limitations: gradient-based optimization is computationally intensive and scales poorly to large graphs, while single-node triggers introduce noticeable structural anomalies and local feature inconsistencies, making them both detectable and less effective. To address these limitations, we propose a novel backdoor attack framework grounded in the principle of homophily, designed to balance effectiveness and stealth. For each selected target link to be poisoned, we inject a unique path-based trigger by adding a bridge node that acts as a shared neighbor. The bridge node’s features are generated through a context-aware probabilistic sampling mechanism over the joint neighborhood of the target link, ensuring high consistency with the local graph context. Furthermore, we introduce a confidence-based trigger injection strategy that selects non-existent links with the lowest predicted existence probabilities as targets, ensuring a highly effective attack from a small poisoning budget. Extensive experiments on five benchmark datasets—Cora, Citeseer, Pubmed, CS, and the large-scale Physics graph—demonstrate that our method achieves superior performance in terms of Attack Success Rate (ASR) while maintaining a low Benign Performance Drop (BPD). These results highlight a novel and practical threat to GNN-based link prediction, offering valuable insights for designing more robust graph learning systems.
1. Introduction
Graph-structured data [1,2,3] underpins a wide range of real-world applications, including social networks [4], biological interaction networks [5], and recommender systems [6]. Link prediction [7,8,9], a fundamental task in graph learning, aims to infer potential or missing links from existing topology and node features. It plays a crucial role in downstream applications. For example, in co-authorship networks [10,11], it enables the discovery of potential collaborators; in recommender systems [12], it identifies latent associations between users and items; in bioinformatics [13], it helps to predict protein–protein interactions; in knowledge graphs [14], it uncovers new relations; and, in cybersecurity [15], it aids in detecting suspicious connections. The development of GNNs [16,17], which jointly model graph structure and node attributes, has significantly enhanced link prediction performance across these domains.
Although GNNs have achieved significant success in link prediction, their effectiveness largely relies on access to large-scale and high-quality training data. However, recent studies [18,19,20] have shown that GNN models may exhibit serious vulnerabilities when training data is intentionally manipulated or poisoned, which has raised growing concerns about their security in real-world deployments. Among these threats, backdoor attacks [21,22] pose a serious risk by enabling adversaries to covertly manipulate model behavior through the injection of specially crafted triggers during training. Once trained, the backdoored model behaves normally on clean inputs but consistently produces attacker-specified outputs when the triggers are present. Figure 1 illustrates an example of such an attack targeting link prediction. In this context, the attacker may embed covert patterns into the training graph by injecting triggers—such as synthetic nodes and crafted features—so that the backdoored model consistently predicts the existence of links for specific node pairs during inference. For example, in recommendation systems, malicious users can forge false interactions with selected items to ensure that these items are always recommended by the system—regardless of actual user preferences—thereby achieving targeted exposure or economic benefits. Given the widespread adoption of GNN-based link prediction models in sensitive fields such as recommendation systems, biological research, and network security, it is crucial to understand their vulnerability to backdoor attacks. Studying such attacks not only reveals fundamental flaws in the current learning paradigm but also provides important insights for designing more robust and trustworthy graph learning systems.
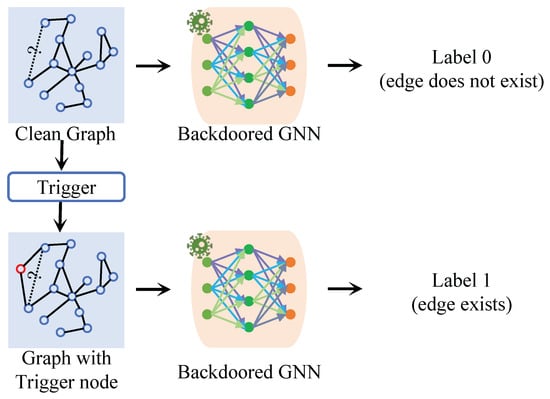
Figure 1.
An example of a backdoor attack targeting the link prediction task. The upper part shows the clean graph: the target edge (dotted line with question mark) is correctly predicted as non-existent (Label 0) by the backdoored GNN. The lower part shows the poisoned case: after injecting a trigger (red node and connections), the same GNN is misled to predict that the target edge exists (Label 1). This example highlights the essence of a backdoor attack: the trigger covertly changes the model’s decision, overriding normal prediction behavior while leaving benign inputs unaffected.
Despite recent advances, research on backdoor attacks specifically targeting GNN-based link prediction remains limited. To date, only two prior works have directly addressed this problem in static graphs. Link-Backdoor [23] initiates this line of research by optimizing complex subgraph triggers via gradient-based methods. While effective in small graphs, it incurs high computational overhead and struggles to scale, resulting in limited attack success and degraded performance on large datasets. More recently, Dai et al. [24] proposed a globally shared single-node trigger whose features are crafted based on globally rare attributes. All poisoned node pairs are connected to this centralized trigger. However, this “one-to-many” design creates structural vulnerability: the trigger node becomes a high-degree outlier, making it easily identifiable through its abnormal connectivity. Moreover, the injected features introduce local heterophily, further amplifying its detectability. As a result, such triggers are susceptible to removal by basic graph anomaly detection techniques, undermining the effectiveness of the attack.
To overcome these limitations, we propose a homophily-driven backdoor attack framework tailored for link prediction. The core idea is to craft a trigger that exploits GNNs’ inherent preference for homophily. For each targeted node pair , we construct a unique path trigger by injecting a bridge node that serves as a common neighbor, thereby introducing structural homophily. The term “unique” here refers not only to the topological independence of each trigger but also to its adaptively synthesized feature. The feature vector of is not statically defined. Instead, it is dynamically generated through a context-aware probabilistic sampling process. We first analyze the joint neighborhood of to obtain the occurrence frequency of each feature dimension, then construct a probability distribution accordingly. Sampling from this distribution yields a feature vector that closely aligns with the local context, ensuring semantic homophily. This design ensures that the trigger conforms to both structural and feature-level patterns, thereby making it more plausible, stealthy, and effective in misleading the model.
To further improve attack efficiency and reduce trigger redundancy, we propose an intelligent trigger injection position selection strategy based on model confidence. Specifically, we leverage a proxy model trained on clean data to estimate the link existence probabilities for all candidate negative edges. Node pairs with the lowest predicted confidence scores (i.e., those the model is most certain are not connected) are selected as attack targets. By injecting triggers into these high-certainty negative samples, the model is forced to override its prior beliefs and internalize a strong generalizable backdoor rule. This confidence-based strategy improves attack effectiveness while reducing the poisoning budget by targeting representative and model-contradictory samples.
Overall, the novelty of this work lies in proposing a homophily-guided backdoor attack framework for GNN-based link prediction, where context-aware path triggers and confidence-driven injection are combined to achieve both high stealthiness and strong attack effectiveness, even on large-scale graphs. The main contributions of this paper can be summarized as follows:
- We propose a novel backdoor attack framework for GNN-based link prediction, theoretically grounded in the principle of homophily, offering a new perspective on attack design.
- We design a context-aware path trigger whose features are synthesized via probabilistic sampling of the local joint neighborhood. This approach adheres to graph homophily, significantly enhancing stealth while maintaining attack effectiveness.
- We introduce a confidence-based trigger injection location selection strategy that identifies the most cognitively representative attack samples. By selecting links that the model is highly confident do not exist, our method encourages the model to override its learned priors and improves both attack efficiency and effectiveness.
- Our overall framework is lightweight, making it applicable in realistic black-box settings. Experiments on five benchmark datasets demonstrate that it outperforms the baselines in ASR while maintaining low BPD.
The remainder of this paper is organized as follows. Section 2 reviews the related work on GNN-based link prediction and backdoor attacks. Section 3 provides the preliminaries and formulates the problem of backdoor attacks on link prediction. Section 4 details our proposed homophily-based backdoor attack framework. Section 5 presents our experimental setup, comprehensive results, and analysis. Finally, Section 6 concludes the paper and discusses potential future work.
2. Related Work
2.1. GNN-Based Link Prediction
Link prediction is a fundamental task in graph data analysis, aiming to predict potential or missing links between nodes in a network [9]. In recent years, methods based on GNNs have become the mainstream approach in this domain. These methods typically follow an encoder–decoder architecture. The encoder, utilizing a GNN, learns a low-dimensional representation (embedding) for each node, which encodes both its own attributes and its complex topological environment. The decoder then uses these node embeddings to compute the probability of a link’s existence between any two nodes, often via a simple function like an inner product.
Among these methods, models like Graph Auto-Encoder (GAE) and Variational Graph Auto-Encoder (VGAE) [25] are classic benchmarks for link prediction. To further improve representation quality, subsequent works introduced adversarial regularization, leading to models like ARGA and ARVGA [26]. These models use a discriminator to constrain the latent distribution of node embeddings, making them more robust. Due to their excellent performance on multiple benchmark datasets, these models are also common targets for evaluating the effectiveness of graph attack algorithms.
2.2. Backdoor Attacks on Graph Classification
Backdoor attacks, as a stealthy and potent type of training-time attack, have been widely studied in the fields of computer vision [27] and natural language processing [28]. In recent years, this threat has also been extended to the domain of graph learning. The existing backdoor attacks on GNNs have predominantly focused on graph classification tasks [29,30,31,32]. The core idea of these attacks is to establish a malicious correlation between a trigger—typically a specific subgraph structure or feature pattern—and a target label by injecting carefully crafted triggers into the training graph.
For instance, Zhang et al. [33] systematically investigated backdoor attacks on graph classification and demonstrated their potential threat. Building on this line of work, Graph Backdoor by Xi et al. [34] further introduced a method for dynamically generating customizable subgraph triggers tailored to individual graphs, also targeting the graph classification task. While these works provide important insights into the vulnerabilities of GNNs, their attack methods and objectives differ significantly from those for link prediction and thus cannot be directly transferred.
2.3. Backdoor Attacks on Link Prediction
To the best of our knowledge, there are only two prior works that directly address backdoor attacks on static graph link prediction, representing two different technical approaches.
The first approach, Link-Backdoor (LB) [23], utilizes a white-box or surrogate-based attack paradigm. The core of this method is a trigger optimization process. It begins by injecting new nodes and forming an initial random subgraph trigger around a target node pair. It then calculates the gradients of an attack loss function with respect to the trigger’s adjacency matrix and the injected nodes’ features. Based on the sign of these gradients, the trigger’s structure and features are iteratively and discretely updated to maximize its deceptive effect on a pre-trained model.
The second approach, Single Node (SN) [24], pursues simplicity and efficiency in a gradient-free manner. This method employs a globally shared single trigger node for all attack instances. The feature vector for this trigger is deterministically constructed by identifying the Top-K globally rarest features across the entire training dataset and creating a corresponding multi-hot vector. During poisoning, this single trigger node is then connected to the endpoints of all selected target pairs.
Different from these works, our method aims to design a trigger that is homophilous with the local graph environment in order to overcome the shortcomings of the existing methods in terms of stealthiness or applicability to large-scale graphs while ensuring attack effectiveness. For clarity, Table 1 contrasts our method with existing backdoor attack methods on link prediction.

Table 1.
Comparison of backdoor attacks on link prediction.
3. Preliminaries and Problem Definition
3.1. Preliminaries
3.1.1. Link Prediction on Graphs
We consider an undirected attributed graph defined as , where is the set of N nodes, is the set of edges, and is the node feature matrix, where each row represents the attribute vector of node . The topological structure of the graph is represented by an adjacency matrix , where if and 0 otherwise. The task of link prediction aims to learn a model that leverages the observed graph structure and node features to predict the likelihood of unobserved links.
3.1.2. Link Prediction with Graph Auto-Encoders
GNN-based link prediction methods commonly adopt an encoder–decoder architecture. A representative framework is the Graph Auto-Encoder (GAE) [25], which uses a Graph Convolutional Network (GCN) [35] as the encoder and an inner product function as the decoder.
GCN Encoder
The encoder computes node embeddings , where each row captures the representation of node . A standard two-layer GCN encoder is defined as
where is the symmetrically normalized adjacency matrix with added self-loops, and , are learnable weight matrices.
Inner Product Decoder
Given embeddings Z, the decoder predicts the likelihood of a link between nodes and using their inner product:
where denotes the sigmoid function, which maps the inner product score to a probability in the range . The model is trained to minimize the Binary Cross-Entropy (BCE) loss between the predicted adjacency matrix and the ground-truth adjacency matrix A.
3.2. Problem Definition
The backdoor attack proposed in this paper targets the link prediction task. The objective is to poison the training data such that the backdoored model incorrectly predicts that a link exists between two unlinked nodes when a specific trigger is present in the graph.
3.2.1. Attacker’s Knowledge and Capabilities
We consider a realistic black-box poisoning scenario, where we assume the attacker has access to the training data but no knowledge of the victim model’s architecture or parameters. This assumption reflects common settings such as open or crowdsourced graphs and provides a solid basis for studying poisoning-based backdoors. While not all deployments offer such access, those cases correspond to different threat models and fall beyond our present scope. Within this setting, the attacker can inject additional nodes, edges, and feature vectors into the training graph to implant hidden behaviors.
Following prior work [24], we assume that node features are binary, i.e., , where each dimension indicates the presence or absence of a discrete attribute.
3.2.2. Backdoor Attack Objective
Let denote the clean training graph, and denote the poisoned graph obtained by injecting trigger nodes and edges. Let denote the set of negative links (i.e., non-existent in the clean graph), and let be the attacker-specified target link set. These links are selected to be associated with triggers and are intended to be predicted as positive by the backdoored model.
The attacker’s objective is to train a backdoored model such that
The first condition represents attack effectiveness: when a trigger is present, the model’s prediction for a target non-existent link must be 1 (representing “link exists”). The second condition represents evasiveness: for any clean input, the backdoored model’s predictions should be indistinguishable from those of a benign model .
4. The Proposed Method
To address the deficiencies of existing link prediction backdoor attacks in terms of stealth, attack cost, and effectiveness on large-scale graphs, we propose a novel backdoor attack framework based on the principle of homophily. Our method aims to implant a backdoor into GNN models in a more natural and deceptive manner by designing a trigger that is highly “homophilous” with the local graph environment. Our framework consists of three main parts: homophily-based trigger design, trigger injection location selection, and, finally, backdoor injection and model training. The overall workflow of our proposed method is illustrated in Figure 2.

Figure 2.
The overall workflow of our proposed backdoor attack framework. Stage 1: Trigger Injection Location Selection. We first train a proxy model on the clean graph. The proxy’s predictions are used to identify a set of M non-existent links (where M is determined by the poisoning rate) with the lowest predicted edge existence probability, which serve as the locations for trigger injection. This stage ensures that the poisoned samples are highly representative and force the model to override its strongest priors. Stage 2: Trigger Injection. For each selected node pair, we introduce a new intermediate node. The features for this node are synthesized by sampling based on the feature information of the target node pair and their respective neighbors. The designed triggers are injected into the graph; the labels of the corresponding target edges are flipped. This stage creates triggers that blend naturally with the local graph context, thereby enhancing stealth. Stage 3: Backdoored Model Implementation. The final backdoored model is obtained by training on the resulting poisoned graph. This stage embeds the backdoor pattern into the model, enabling it to respond to triggers as intended.
4.1. Homophily-Based Trigger Design
Our core innovation lies in the trigger design. Unlike the centralized “honeypot” design of Dai et al. [24], our trigger is “tailor-made” for each target. For each non-existent node pair selected for an attack, we generate a unique trigger that adheres to the principle of homophily in terms of both its topology and its features.
4.1.1. Topological Design: The Path Trigger
For each node pair selected as an attack target, we inject a novel bridge node into the graph and construct a path structure u–ti–v. This path trigger offers a dual topological advantage:
- It makes a common neighbor of u and v.
- It establishes a short path of length 2 connecting u and v.
In the GNN learning paradigm, both common neighbors and short paths are strong structural signals indicating similarity (homophily) and a potential link. Therefore, this topological design allows our trigger to “disguise” itself as a very plausible benign structure indicative of a link.
4.1.2. Feature Synthesis: Probabilistic Sampling
To ensure the bridge node also maintains homophily with its local environment, we propose a context-aware probabilistic sampling mechanism. This process is designed to create a feature vector that reflects the relative importance of features in the local community.
First, for a target pair , we analyze its joint neighborhood , defined as the union of the 1-hop neighborhoods of each node (including themselves):
We then compute a feature count vector , where each element denotes the number of times the l-th feature takes the value 1 among all nodes in the joint neighborhood . To mitigate the dominance of high-frequency features, we first compress the counts using a logarithmic transformation:
Next, we construct the final probability vector for the bridge node . The probability for the l-th feature is derived by normalizing the log-scaled counts and then enforcing a minimum probability floor for all present features:
where is an indicator function, denotes the maximum log-scaled feature count across all d feature dimensions, and is a hyperparameter. We introduce the minimum probability threshold to ensure that any feature dimension observed in the local context is not assigned a vanishingly small probability. This design prevents such dimensions from being overlooked during sampling, thereby preserving semantic consistency and enhancing the homophily of the generated trigger. Finally, the multi-hot feature vector for the bridge node is generated by performing a multivariate Bernoulli trial:
The feature vector synthesized in this manner is a “hybrid” of the features from the two target nodes’ communities, making highly similar in features to its connected nodes u and v, thus well adhering to the principle of homophily.
As each bridge node is generated independently for its associated target pair and its features are synthesized from a locally adapted distribution, triggers across poisoned links exhibit both structural and contextual diversity rather than converging to a shared pattern, thereby enhancing stealthiness and reducing detection risk. In addition, the neighborhood intersection and feature count operations for each poisoned link scale with the degrees of its endpoints (, where and denote the degrees of nodes u and v), meaning that the cost depends only on local neighborhoods and remains modest even for large-scale graphs.
Toy Example
Consider binary node features with dimension . Let u and v each have four distinct neighbors, providing a joint neighborhood of 10 nodes. Suppose the counts of “1” in each feature dimension are . We compute using the natural logarithm (base e), then normalize by (corresponding to the maximum case ), and finally apply a probability floor . Table 2 shows the intermediate values and the final probabilities:

Table 2.
A toy example.
Here, Feature 5 falls below the floor and is lifted to , while Feature 6 does not appear and remains 0. The bridge node feature is then sampled as .
4.2. Trigger Injection Location Selection
Our attack aims to manipulate the backdoored model into predicting the existence of links where none originally exist. Therefore, our attack candidate pool consists exclusively of negative samples (non-existent edges) from the training set. Typically, the training set is constructed such that the number of negative samples satisfies , ensuring class balance during optimization. To maximize attack efficiency, we propose an intelligent injectselection strategy based on a proxy model . The core idea is to force the backdoored model to learn a powerful “override rule” by attacking the links that a clean model is most “certain” do not exist. After training the proxy model on the clean graph, we use it to compute a prediction score for every non-existent link . Based on a predefined poisoning rate p, we then identify the node pairs with the lowest scores as the target set for backdoor injection:
This principled selection of the most confident negative predictions ensures a more potent and efficient backdoor implantation compared to random choice.
It is worth noting that this strategy depends only on the relative ranking of candidate negatives rather than precise probability estimates. Node pairs assigned consistently low scores usually correspond to strong non-links as they exhibit distant topology and distinct feature profiles. Such edges are generally recognized as negatives across different models, which makes the ranking-based selection robust and applicable even when the proxy model is not perfectly aligned with the target model.
4.3. Backdoor Injection and Model Training
For each selected target negative sample in Section 4.2, we first inject a homophily-based trigger as designed in Section 4.1. Then, we flip its label from 0 (non-existent) to 1 (existent) in the training data. The collection of all poisoned samples, along with the original benign samples, constitutes the final poisoned training set, which is used to obtain the final backdoored model . With a small poisoning budget (1% of training edges by default) and each bridge node injected locally without reuse, the modifications remain sparse and confined to 1-hop neighborhoods. As a result, the overall global graph characteristics are largely preserved, which is further supported by the low BPD observed in our experimental results (see Section 5).
The final backdoor injection process is summarized in Algorithm 1.
| Algorithm 1 Proposed Homophily-based Backdoor Attack |
|
4.4. Analysis of the Attack Mechanism
To theoretically understand the effectiveness of our homophily-based backdoor attack, we analyze how the designed trigger jointly manipulates the topological and feature spaces of GNNs to align node embeddings and induce incorrect predictions.
We consider a standard two-layer GCN encoder, whose final node embeddings Z are given by
The decoder predicts the existence of a link via .
4.4.1. Prediction on Benign Samples
In a well-trained clean model, for a non-existent link , the nodes are typically distant in the graph with few, if any, common neighbors. Consequently, their 2-hop neighborhoods have minimal overlap. Under the GCN’s aggregation mechanism, their learned embedding vectors, and , will tend to be orthogonal or directionally dissimilar in the high-dimensional space. This results in their inner product being a small value (negative). Therefore, the model’s predicted link probability will be close to 0, leading to a correct “no link” prediction.
4.4.2. Impact of Trigger Injection
When a trigger is injected, a bridge node is added along with edges and . This alters both the graph structure and the node representations.
Topological Impact
The trigger introduces a 2-hop path , making a shared neighbor of u and v. In the second propagation layer of the GCN, now aggregates messages from , which in turn aggregates from v, effectively introducing mutual information flow.
Feature Impact
The feature vector is synthesized based on the joint neighborhood , ensuring it is homophilous with both u and v. During message passing, acts as a feature relay, promoting alignment between and .
4.4.3. Impact on Prediction and Training
These topological and feature-level interactions increase the inner product , pushing the predicted probability close to 1. Since we flip the label of to 1 in training, the loss becomes small, making the sample easy to fit and requiring minimal gradient updates. This also accounts for the low BPD as the trigger has relatively little interference with the model decision boundaries on benign data.
In summary, the trigger creates a homophily-consistent shortcut in both structure and feature space, exploiting the GNN’s inductive biases to embed a persistent and low-cost backdoor.
5. Experiments
5.1. Experimental Settings
In this section, we detail our experimental settings, including the datasets, target models, evaluation metrics, baselines, and parameter configurations.
5.1.1. Datasets
Our method is evaluated on five widely adopted benchmark datasets—Cora, Citeseer, Pubmed, CS, and Physics—with Physics being a large-scale graph dataset. Table 3 summarizes the key statistics of these datasets.

Table 3.
Statistics of the datasets.
5.1.2. GNN-Based Link Prediction Models
To assess the effectiveness of our attack across different architectures, we target four popular GNN-based models for link prediction:
- GAE [25]: A foundational model that uses a GCN encoder to learn node embeddings and an inner product decoder to reconstruct the adjacency matrix.
- VGAE [25]: A variational extension of GAE, where the encoder learns a probabilistic distribution for each node’s embedding, enhancing robustness.
- ARGA [26]: An adversarially regularized version of GAE that replaces the standard regularizer with a discriminator to better shape the embedding distribution.
- ARVGA [26]: A model that combines the variational aspects of VGAE with the adversarial training of ARGA.
5.1.3. Evaluation Metrics
We use two primary metrics to evaluate the effectiveness and evasiveness of the backdoor attacks, consistent with prior work [23,24]:
- ASR: This metric measures the attack’s effectiveness. It is the ratio of triggered non-existent links that are successfully misclassified as “existent” by the backdoored model. A higher ASR indicates a more effective attack.
- BPD: This metric measures the attack’s evasiveness. It is defined as the difference in the Area Under Curve (AUC) score between a clean model and the backdoored model when evaluated on a benign test set (). A lower BPD indicates a stealthier attack as it has less impact on the model’s normal functionality.
5.1.4. Baselines
We compare our proposed method against the two state-of-the-art backdoor attacks on link prediction discussed in our related work, as well as two classic backdoor attacks originally designed for graph classification:
- Link-Backdoor (LB) [23]: A powerful attack that uses gradient information to optimize a subgraph trigger. We will compare against the results reported in their paper.
- Single Node (SN) [24]: A gradient-free attack that uses a globally shared single node with rare features as a trigger. We will re-implement this method.
- Erdos–Renyi Backdoor (ERB) [33]: An attack that uses a randomly generated Erdos–Renyi graph as a trigger.
- Graph Trojaning Attack (GTA) [34]: A generative attack that uses an optimization algorithm to craft a trigger.
For ERB and GTA, which were originally designed for graph classification, we adapt them to the link prediction task as described in [23]. Specifically, the generated trigger subgraph is modified to connect to and include the two endpoint nodes of the target non-existent link.
5.1.5. Parameter Settings
We split the edges of each dataset into 85% for training, 5% for validation, and 10% for testing. The validation and test edges are entirely unseen during training, which is the standard and default setting for link prediction tasks, ensuring that the evaluation reflects an inductive scenario. The GNN encoders in all models consist of a two-layer GCN with a 128-dimensional hidden layer and a 64-dimensional output embedding layer. During training, we employ an early stopping criterion: training is halted if the validation loss does not decrease for 20 consecutive epochs. All models are trained for 300 epochs unless early stopping is triggered. Table 4 reports the AUC scores of all models trained on the clean datasets. We use GAE as the proxy model when selecting edges. For our attack, unless otherwise specified, we set the poisoning rate to 1% of the total number of existent links in the training set. The minimum sampling probability for present features during trigger synthesis (i.e., the probability floor ) is set to 0.3 by default. All experiments are repeated ten times with different random seeds, and we report the mean and standard deviation of ASR and BPD. For the baselines, we adhere to their default hyperparameter settings.

Table 4.
Benign AUC (%) of four models on five datasets without any backdoor injection.
5.2. Overall Attack Performance
As shown in Table 5, our proposed backdoor attack consistently achieves the highest ASR across all datasets and model architectures while maintaining a low BPD. This demonstrates that our method is effective in implanting targeted backdoor behavior and can maintain the practicality of the model on clean data. The superior performance can be attributed to the design of our homophily-based path trigger, which integrates seamlessly into the graph structure and node feature space, making it inherently difficult to distinguish from benign patterns. Furthermore, the confidence-based trigger injection location selection strategy ensures that the poisoned links introduce strong yet localized supervisory signals, thereby maximizing the attack’s impact with minimal interference.

Table 5.
Overall backdoor performance (% mean ± std) on five datasets. The bold values indicate the best performance.
Compared to existing baselines, our method exhibits clear advantages. Gradient-based methods like LB tend to suffer from scalability issues and reduced effectiveness on large graphs due to their reliance on global optimization procedures. Random or generative approaches such as ERB and GTA show consistently lower ASR and are less reliable as they were not originally designed as backdoor attack methods for link prediction tasks. Although SN performs competitively on small-scale datasets, its effectiveness degrades on larger graphs. This is primarily because the trigger, constructed from global feature frequency statistics, exhibits local heterogeneity with neighboring nodes, thereby reducing its impact.
Notably, our method maintains strong performance even on large-scale datasets such as Physics, where several baselines experience significant degradation. This highlights the scalability and robustness of our local adaptive trigger mechanism, which remains effective across diverse graph sizes and densities.
In summary, the results confirm that our homophily-guided backdoor framework achieves an excellent balance between attack effectiveness and evasiveness and offers clear advantages over existing methods in terms of both generality and scalability.
5.3. Impact of Poisoning Rate
To further understand the robustness and controllability of our attack strategy, we evaluate its performance under varying poisoning rates. Specifically, we vary the proportion of poisoned training edges from 0.2% to 1.4% in increments of 0.2% and report the corresponding ASR and BPD values. The results are summarized in Figure 3.
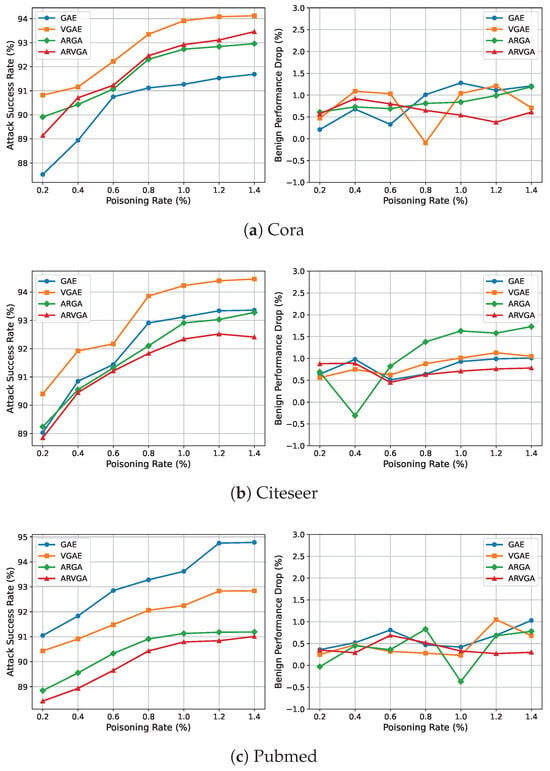
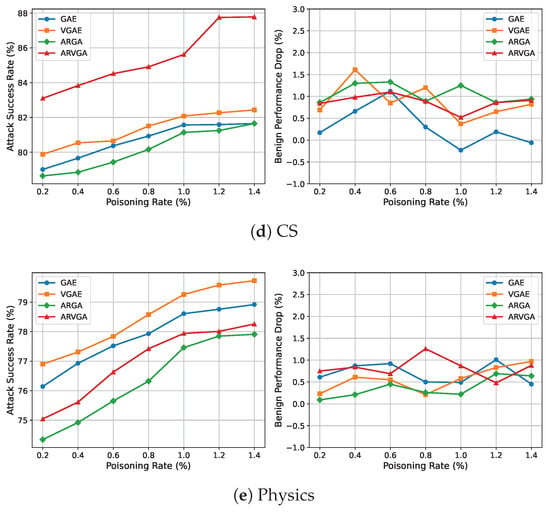
Figure 3.
Impact of poisoning rate on ASR and BPD.
We observe that the ASR increases rapidly at lower poisoning rates (e.g., from 0.2% to 0.6%), and then gradually saturates as the rate increases. This indicates that, owing to our confidence-based trigger injection location selection and consistency-aligned trigger design, strong attack effectiveness can be achieved without requiring excessive poisoning.
The BPD remains consistently low across all poisoning rates. Although it exhibits slight fluctuations due to randomness in the poisoned samples, no clear monotonic trend is observed. This confirms the stability and evasiveness of our method, even as the poisoning intensity varies.
5.4. Impact of Training Data Poisoning
To assess the benefit of poisoning the training data, we compare two settings: injecting the trigger during training versus only applying it at inference time. Since the latter does not modify the training data, we report only the ASR as the evaluation metric.
As shown in Figure 4, incorporating the trigger into the training set leads to a noticeable improvement in ASR across all datasets and models, with increases ranging from approximately 5% to 9%. This demonstrates that our homophily-aware trigger, when introduced during training, effectively guides the model to internalize the backdoor pattern, thereby enhancing the overall attack performance. Nonetheless, the relatively high ASR achieved even without poisoning underscores the robustness and transferability of our trigger design.
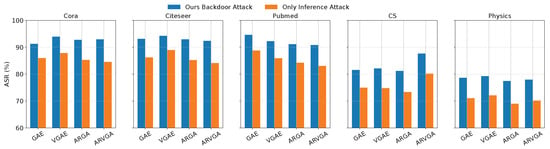
Figure 4.
Comparison of ASR under our backdoor attack and only inference-time trigger injection across five datasets.
5.5. Ablation Studies
To validate the effectiveness of the key components in our proposed attack, we conduct two ablation studies on the Citeseer dataset. We investigate the contributions of our context-aware feature synthesis and our confidence-based target selection strategy, respectively. The results are presented in Table 6.

Table 6.
Ablation study results on the Citeseer dataset (% mean ± std). The bold values indicate the best performance.
5.5.1. Impact of Feature Synthesis
To verify the importance of our context-aware homophily-based feature synthesis, we create a variant, No Feature Synthesis, where the bridge node’s features are replaced with a randomly generated multi-hot vector. To ensure a fair comparison, the number of non-zero features in this random vector is set to the average number of non-zero features per node across the dataset. As shown in Table 6, removing our feature synthesis strategy leads to a precipitous drop in attack performance. The ASR decreases by an average of 10.4% across the four GNN models. This significant degradation confirms that synthesizing trigger features that are homophilous with the local environment is a critical factor for the attack’s success, as opposed to using generic context-free random features.
5.5.2. Impact of Target Selection
To validate our intelligent trigger location selection strategy, we compare our complete method (Full Attack) against the No Confidence-based Selection variant, which uses the same homophilous trigger but injects it into randomly selected non-existent links. The results in Table 6 demonstrate that abandoning the lowest-confidence selection strategy leads to a consistent decrease in ASR across all models, with an average drop of 2.15%. While less dramatic than the feature ablation, this still proves that our principled approach of identifying and poisoning the most challenging negative examples is superior to a naive random strategy and contributes significantly to the attack’s high efficiency.
5.6. Parameter Sensitivity Analysis
In this section, we investigate the impact of a key hyperparameter in our feature synthesis process: the feature sampling probability floor, . This parameter controls the minimum sampling probability for any feature present in the target’s joint neighborhood, thus directly influencing the density and strength of the trigger’s feature signal. A higher leads to a denser, and potentially stronger, trigger feature vector.
To analyze its effect, we conduct an experiment on the Citeseer dataset using the GAE model. We vary the value of from 0.1 to 0.4. The results are presented in Table 7.

Table 7.
Impact of the trigger probability floor () on attack performance for the GAE model on the Citeseer dataset (% mean ± std).
As shown in Table 7, we observe that, as the probability floor increases, the ASR exhibits a consistent upward trend. Specifically, the ASR improves steadily from 91.50% at to 93.68% at . This trend indicates that a denser trigger feature vector, which provides a stronger and less ambiguous signal by ensuring more features from the local context are included, leads to a more effective and reliable backdoor. Notably, the rate of improvement appears to diminish as surpasses 0.25, suggesting that, while a denser trigger is beneficial, there are diminishing returns once the signal becomes sufficiently potent. Meanwhile, the BPD remains consistently low and stable across all tested values, indicating that varying the trigger’s feature density in this range has a negligible impact on the model’s performance on clean data.
5.7. Generalization Across Architectures
To further evaluate the generality of our proposed attack beyond the two-layer GCN encoder analyzed theoretically, we conducted additional experiments on the Citeseer dataset using three alternative architectures: a two-layer GAT, a two-layer GraphSAGE, and a three-layer GCN. We applied our attack, as well as the four baseline models (GAE, VGAE, ARGA, and ARVGA), under the same settings described in Section 5.1.5.
As shown in Table 8, our attack generalizes well across different GNN architectures. On the GAT encoder, the ASR tends to be higher than that on the two-layer GCN, suggesting that attention mechanisms can amplify the influence of our homophily-guided trigger. For GraphSAGE, the ASR is generally lower, which can be attributed to its neighborhood sampling that dilutes localized trigger effects. On the deeper three-layer GCN, the ASR is slightly lower than that of the two-layer version, indicating that increased network depth does not substantially weaken the backdoor. Across all architectures, the BPD remains low and stable, confirming that the attack consistently preserves the model’s utility on clean data.

Table 8.
Attack performance on Citeseer under different GNN architectures (% mean ± std).
5.8. Defense
We evaluate two representative defenses against our attack. Cosine-based graph purification prunes of edges with lowest cosine similarity and adds high-similarity non-edges, aiming to purify the structure before training. Feature-noise defense, following prior work [23], perturbs of node feature entries at inference time (bit-flip for binary attributes). Figure 5 reports the ASR under these settings across all datasets and models.
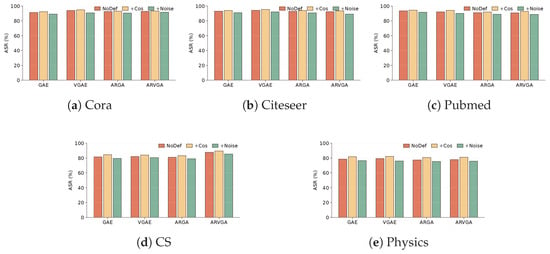
Figure 5.
ASR under two defenses (cosine-based graph purification and feature-noise defense) across five datasets.
The purification strategy consistently raises ASR because its objective—enhancing homophily—is closely aligned with our backdoor design, making the injected path triggers easier to learn. By contrast, feature-noise defense produces a slight reduction in ASR, but the effect remains marginal since random perturbations rarely touch the injected bridge nodes and are quickly smoothed during message passing. Overall, our attack retains high effectiveness under both defenses.
5.9. Embedding Visualization
To further examine whether our attack leaves detectable traces in the latent space, we visualize node embeddings with t-SNE on the Citeseer dataset. As shown in Figure 6, the injected bridge nodes (red) do not form any separate cluster but are scattered across the embedding space. The attacked endpoints (blue) often appear close to these bridge nodes, reflecting the intended local homophily effect, yet they remain distributed across different clusters. Importantly, the overall embedding structure remains consistent with the benign case, making the backdoor visually indistinguishable and difficult to detect through clustering- or visualization-based defenses.
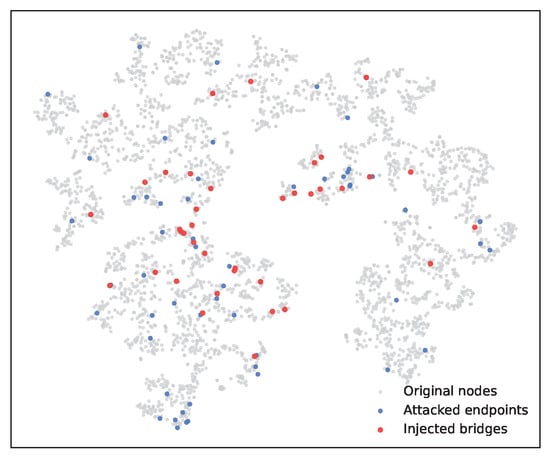
Figure 6.
t-SNE visualization of node embeddings under backdoor attack. Injected bridge nodes (red) scatter across the space without forming a separate cluster, while attacked endpoints (blue) appear near bridges but remain distributed across clusters.
6. Conclusions
In this paper, we presented a novel backdoor attack framework targeting GNN-based link prediction, addressing the key limitations of existing methods in terms of scalability, stealth, and attack effectiveness. Motivated by the principle of homophily, we designed a path-based trigger that introduces both topological and feature-level similarity between target node pairs. To further enhance attack efficiency and reduce poisoning overhead, we proposed a confidence-based trigger injection strategy that selects the most cognitively representative negative links for manipulation.
Extensive experiments on five benchmark datasets and four representative GNN architectures demonstrate that our method consistently achieves superior ASR while maintaining a low BPD. Ablation and sensitivity analyses further verify the robustness and effectiveness of our homophily-aware trigger design and confidence-guided injection mechanism.
In future work, we plan to explore three key directions. First, while our method focuses on path-based triggers, incorporating more complex homophilous motifs may lead to stronger or stealthier attack patterns. Second, we aim to extend our framework to dynamic and heterogeneous graphs, where structural evolution and multi-relational semantics introduce new challenges for both attack and defense. Third, we will investigate defense strategies specifically tailored to detect or mitigate homophily-guided triggers.
We believe this work provides new insights into the security vulnerabilities of GNN-based link prediction and lays a foundation for both adversarial research and robust graph learning in future applications.
Author Contributions
Conceptualization, Y.W., Z.Z., and P.Q.; methodology, Y.W.; software, Y.W.; validation, Y.W.; formal analysis, Y.W.; investigation, Y.W.; resources, Z.Z., Y.Y., and G.W.; data curation, Y.W.; writing—original draft preparation, Y.W.; writing—review and editing, Y.W., Z.Z., and P.Q.; visualization, Y.W.; supervision, Z.Z. and Y.Y.; project administration, Z.Z., Y.Y., and G.W.; funding acquisition, Z.Z., Y.Y., and G.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the NSFC (Grant No. U23B2019) and the National Key R&D Program of China (Grant No. 2024YFE0209000).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The datasets used in our experiments are publicly available and can be accessed from the following URLs: Cora, Citeseer, and Pubmed: https://github.com/kimiyoung/planetoid, (accessed on 28 June 2025); CS, Physics: https://github.com/pyg-team/pytorch_geometric (accessed on 28 June 2025).
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| GNN | Graph Neural Network |
| ASR | Attack Success Rate |
| AUC | Area Under Curve |
| BPD | Benign Performance Drop |
| GAE | Graph Auto-Encoder |
| VGAE | Variational Graph Auto-Encoder |
| ARGA | Adversarially Regularized Graph Auto-Encoder |
| ARVGA | Adversarially Regularized Variational Graph Auto-Encoder |
| GCN | Graph Convolutional Network |
| BCE | Binary Cross-Entropy |
| ERB | Erdos–Renyi Backdoor |
| GTA | Graph Trojaning Attack |
| SN | Single Node |
| LB | Link-Backdoor |
References
- Khemani, B.; Patil, S.; Kotecha, K.; Tanwar, S. A review of graph neural networks: Concepts, architectures, techniques, challenges, datasets, applications, and future directions. J. Big Data 2024, 11, 18. [Google Scholar] [CrossRef]
- Chen, C.; Xu, Z.; Hu, W.; Zheng, Z.; Zhang, J. FedGL: Federated graph learning framework with global self-supervision. Inf. Sci. 2024, 657, 119976. [Google Scholar] [CrossRef]
- Zhang, W.; Zhou, S.; Walsh, T.; Weiss, J.C. Fairness amidst non-IID graph data: A literature review. AI Mag. 2025, 46, e12212. [Google Scholar] [CrossRef]
- Thapliyal, K.; Thapliyal, M.; Thapliyal, D. Social media and health communication: A review of advantages, challenges, and best practices. In Emerging Technologies for Health Literacy and Medical Practice; IGI Global Scientific Publishing: Hershey, PA, USA, 2024; pp. 364–384. [Google Scholar] [CrossRef]
- Wang, Y.F.; Xu, J.Y.; Liu, Z.L.; Cui, H.L.; Chen, P.; Cai, T.G.; Li, G.; Ding, L.J.; Qiao, M.; Zhu, Y.G.; et al. Biological interactions mediate soil functions by altering rare microbial communities. Environ. Sci. Technol. 2024, 58, 5866–5877. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.C.; Zain, A.M.; Zhou, K.Q.; Chen, X.; Zhang, R.M. A review of recommender systems based on knowledge graph embedding. Expert Syst. Appl. 2024, 250, 123876. [Google Scholar] [CrossRef]
- Arrar, D.; Kamel, N.; Lakhfif, A. A comprehensive survey of link prediction methods: D. Arrar et al. J. Supercomput. 2024, 80, 3902–3942. [Google Scholar] [CrossRef]
- Zhang, M.; Chen, Y. Link prediction based on graph neural networks. Adv. Neural Inf. Process. Syst. 2018, 31, 5171–5181. [Google Scholar] [CrossRef]
- Kumar, A.; Singh, S.S.; Singh, K.; Biswas, B. Link prediction techniques, applications, and performance: A survey. Phys. A Stat. Mech. Appl. 2020, 553, 124289. [Google Scholar] [CrossRef]
- Kumar, S. Co-authorship networks: A review of the literature. Aslib J. Inf. Manag. 2015, 67, 55–73. [Google Scholar] [CrossRef]
- Ji, P.; Jin, J.; Ke, Z.T.; Li, W. Co-citation and co-authorship networks of statisticians. J. Bus. Econ. Stat. 2022, 40, 469–485. [Google Scholar] [CrossRef]
- Lakshmi, T.J.; Bhavani, S.D. Link prediction approach to recommender systems. Computing 2024, 106, 2157–2183. [Google Scholar] [CrossRef]
- Long, Y.; Wu, M.; Liu, Y.; Fang, Y.; Kwoh, C.K.; Chen, J.; Luo, J.; Li, X. Pre-training graph neural networks for link prediction in biomedical networks. Bioinformatics 2022, 38, 2254–2262. [Google Scholar] [CrossRef]
- Rossi, A.; Barbosa, D.; Firmani, D.; Matinata, A.; Merialdo, P. Knowledge graph embedding for link prediction: A comparative analysis. ACM Trans. Knowl. Discov. Data 2021, 15, 1–49. [Google Scholar] [CrossRef]
- Yin, J.; Tang, M.; Cao, J.; You, M.; Wang, H.; Alazab, M. Knowledge-driven cybersecurity intelligence: Software vulnerability coexploitation behavior discovery. IEEE Trans. Ind. Inform. 2022, 19, 5593–5601. [Google Scholar] [CrossRef]
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C.; Yu, P.S. A comprehensive survey on graph neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 4–24. [Google Scholar] [CrossRef]
- Corso, G.; Stark, H.; Jegelka, S.; Jaakkola, T.; Barzilay, R. Graph neural networks. Nat. Rev. Methods Prim. 2024, 4, 17. [Google Scholar] [CrossRef]
- Fang, J.; Wen, H.; Wu, J.; Xuan, Q.; Zheng, Z.; Tse, C.K. Gani: Global attacks on graph neural networks via imperceptible node injections. IEEE Trans. Comput. Soc. Syst. 2024, 11, 5374–5387. [Google Scholar] [CrossRef]
- Sun, L.; Dou, Y.; Yang, C.; Zhang, K.; Wang, J.; Yu, P.S.; He, L.; Li, B. Adversarial attack and defense on graph data: A survey. IEEE Trans. Knowl. Data Eng. 2022, 35, 7693–7711. [Google Scholar] [CrossRef]
- Zhu, G.; Chen, M.; Yuan, C.; Huang, Y. Simple and efficient partial graph adversarial attack: A new perspective. IEEE Trans. Knowl. Data Eng. 2024, 36, 4245–4259. [Google Scholar] [CrossRef]
- Li, Y.; Jiang, Y.; Li, Z.; Xia, S.T. Backdoor learning: A survey. IEEE Trans. Neural Netw. Learn. Syst. 2022, 35, 5–22. [Google Scholar] [CrossRef]
- Saha, A.; Subramanya, A.; Pirsiavash, H. Hidden trigger backdoor attacks. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 11957–11965. [Google Scholar] [CrossRef]
- Zheng, H.; Xiong, H.; Ma, H.; Huang, G.; Chen, J. Link-backdoor: Backdoor attack on link prediction via node injection. IEEE Trans. Comput. Soc. Syst. 2023, 11, 1816–1831. [Google Scholar] [CrossRef]
- Dai, J.; Sun, H. A backdoor attack against link prediction tasks with graph neural networks. arXiv 2024, arXiv:2401.02663. [Google Scholar] [CrossRef]
- Kipf, T.N.; Welling, M. Variational graph auto-encoders. arXiv 2016, arXiv:1611.07308. [Google Scholar] [CrossRef]
- Pan, S.; Hu, R.; Long, G.; Jiang, J.; Yao, L.; Zhang, C. Adversarially regularized graph autoencoder for graph embedding. In Proceedings of the 27th International Joint Conference on Artificial Intelligence, Stockholm, Sweden, 13–19 July 2018; AAAI Press: Washington, DC, USA, 2018. IJCAI’18. pp. 2609–2615. [Google Scholar] [CrossRef]
- Li, Y. Poisoning-based backdoor attacks in computer vision. In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; Volume 37, pp. 16121–16122. [Google Scholar] [CrossRef]
- Sheng, X.; Han, Z.; Li, P.; Chang, X. A survey on backdoor attack and defense in natural language processing. In Proceedings of the 2022 IEEE 22nd International Conference on Software Quality, Reliability and Security (QRS), Guangzhou, China, 5–9 December 2022; pp. 809–820. [Google Scholar] [CrossRef]
- Zeng, Y.; Park, W.; Mao, Z.M.; Jia, R. Rethinking the backdoor attacks’ triggers: A frequency perspective. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 11–17 October 2021; pp. 16473–16481. [Google Scholar] [CrossRef]
- Yang, S.; Doan, B.G.; Montague, P.; De Vel, O.; Abraham, T.; Camtepe, S.; Ranasinghe, D.C.; Kanhere, S.S. Transferable graph backdoor attack. In Proceedings of the 25th International Symposium on Research in Attacks, Intrusions and Defenses, Limassol, Cyprus, 26–28 October 2022; pp. 321–332. [Google Scholar] [CrossRef]
- Zheng, H.; Xiong, H.; Chen, J.; Ma, H.; Huang, G. Motif-backdoor: Rethinking the backdoor attack on graph neural networks via motifs. IEEE Trans. Comput. Soc. Syst. 2023, 11, 2479–2493. [Google Scholar] [CrossRef]
- Xu, J.; Xue, M.; Picek, S. Explainability-based backdoor attacks against graph neural networks. In Proceedings of the 3rd ACM Workshop on Wireless Security and Machine Learning, Abu Dhabi, United Arab Emirates, 28 June–2 July 2021; pp. 31–36. [Google Scholar] [CrossRef]
- Zhang, Z.; Jia, J.; Wang, B.; Gong, N.Z. Backdoor attacks to graph neural networks. In Proceedings of the 26th ACM Symposium on Access Control Models and Technologies, Virtual Event, 16–18 June 2021; pp. 15–26. [Google Scholar] [CrossRef]
- Xi, Z.; Pang, R.; Ji, S.; Wang, T. Graph backdoor. In Proceedings of the 30th USENIX Security Symposium (USENIX Security 21), Virtual Event, 11–13 August 2021; pp. 1523–1540. [Google Scholar] [CrossRef]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar] [CrossRef]
- Sen, P.; Namata, G.; Bilgic, M.; Getoor, L.; Galligher, B.; Eliassi-Rad, T. Collective classification in network data. AI Mag. 2008, 29, 93. [Google Scholar] [CrossRef]
- Shchur, O.; Mumme, M.; Bojchevski, A.; Günnemann, S. Pitfalls of graph neural network evaluation. arXiv 2018, arXiv:1811.05868. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).