The Influence of Thermal Stresses on the Load Distribution and Stress–Strain State of Cycloidal Reducers
Abstract
Featured Application
Abstract
1. Introduction
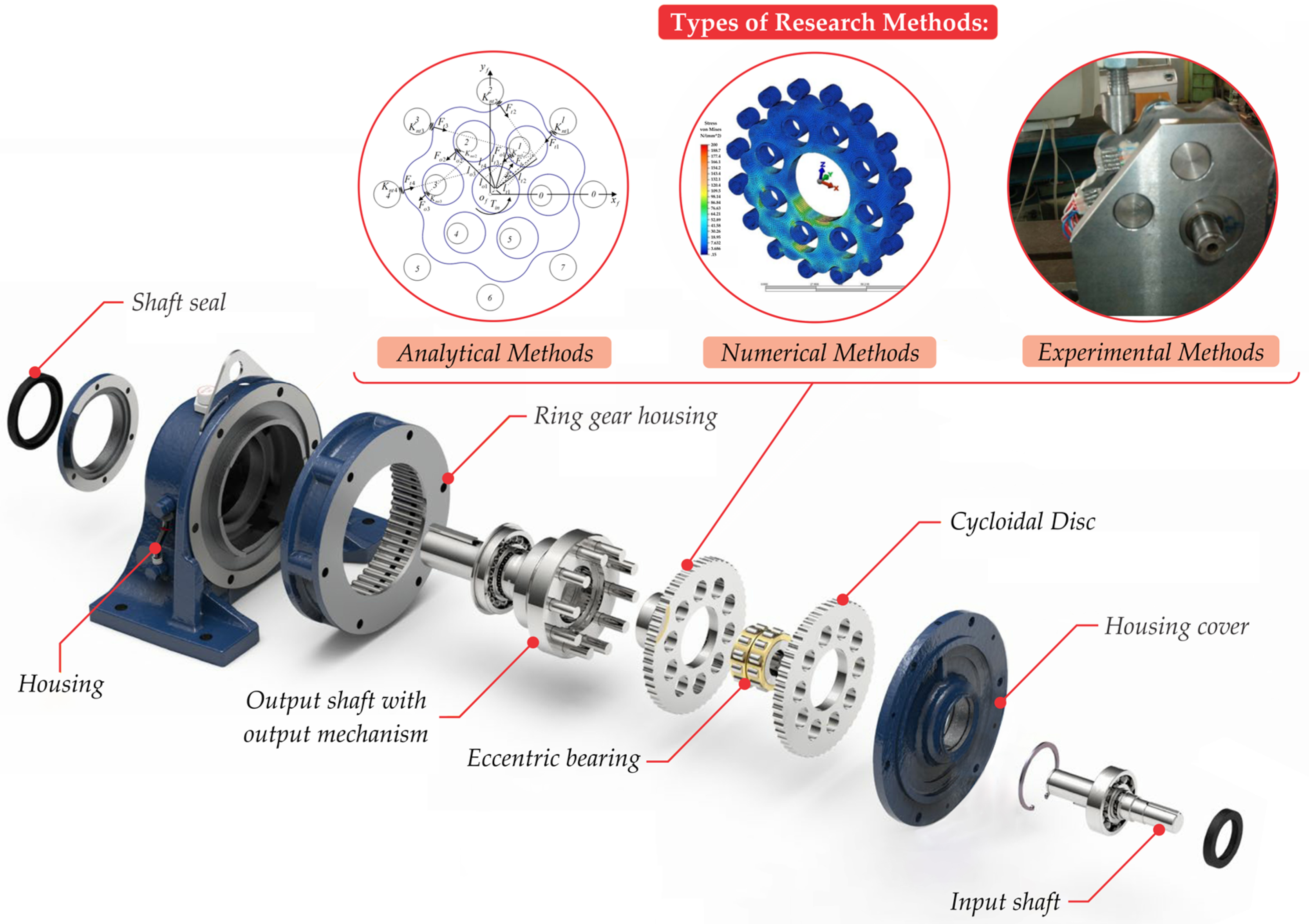
2. Materials and Methods
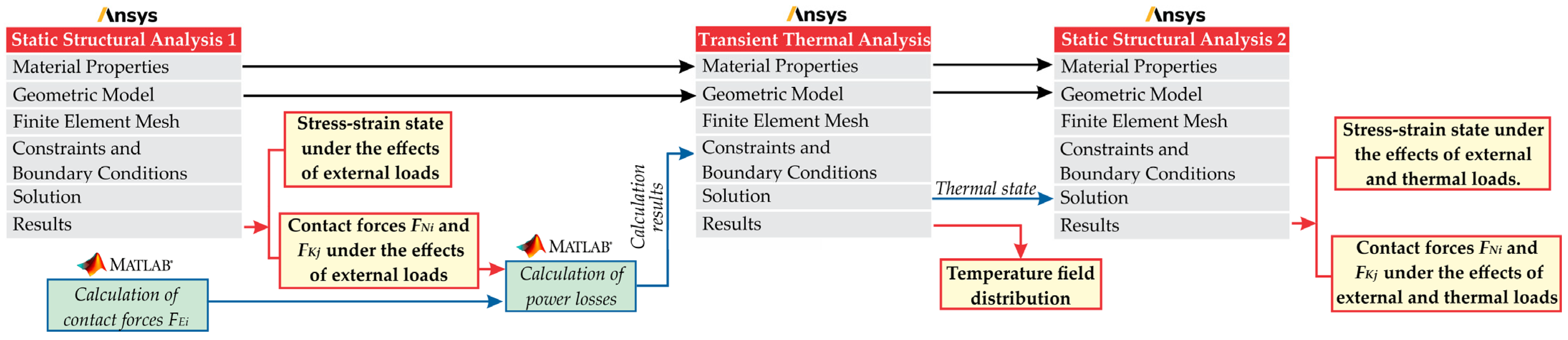
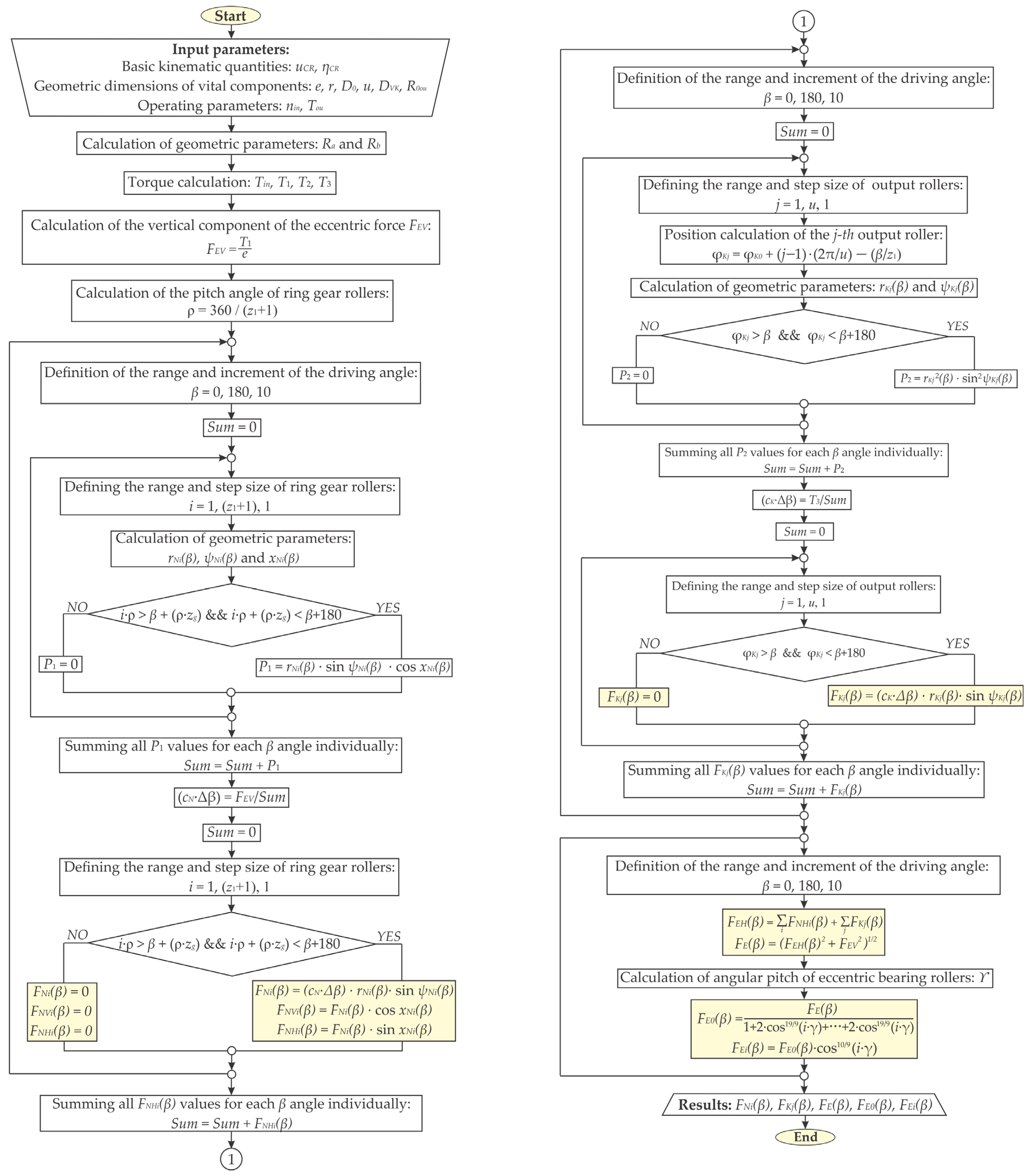
2.1. Numerical–Analytical Methodology
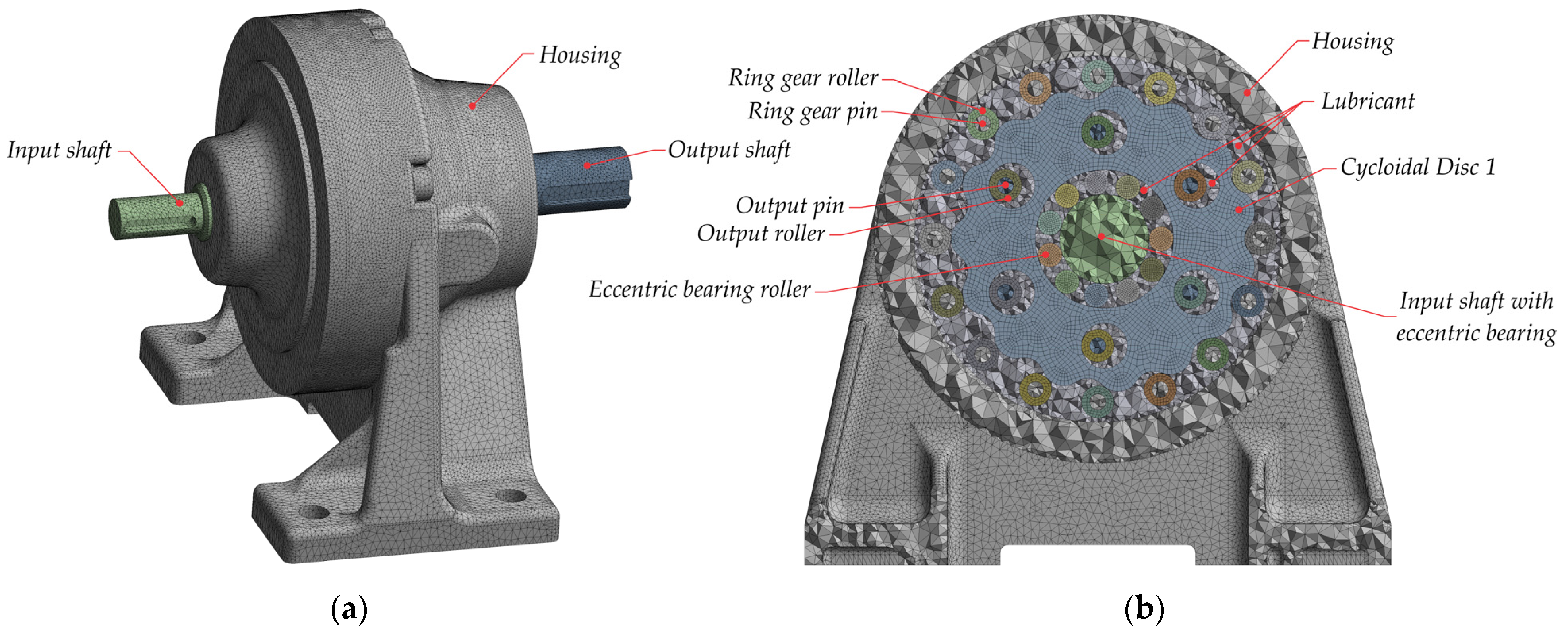
2.1.1. Geometric Model and Material Properties
2.1.2. Finite Element Mesh
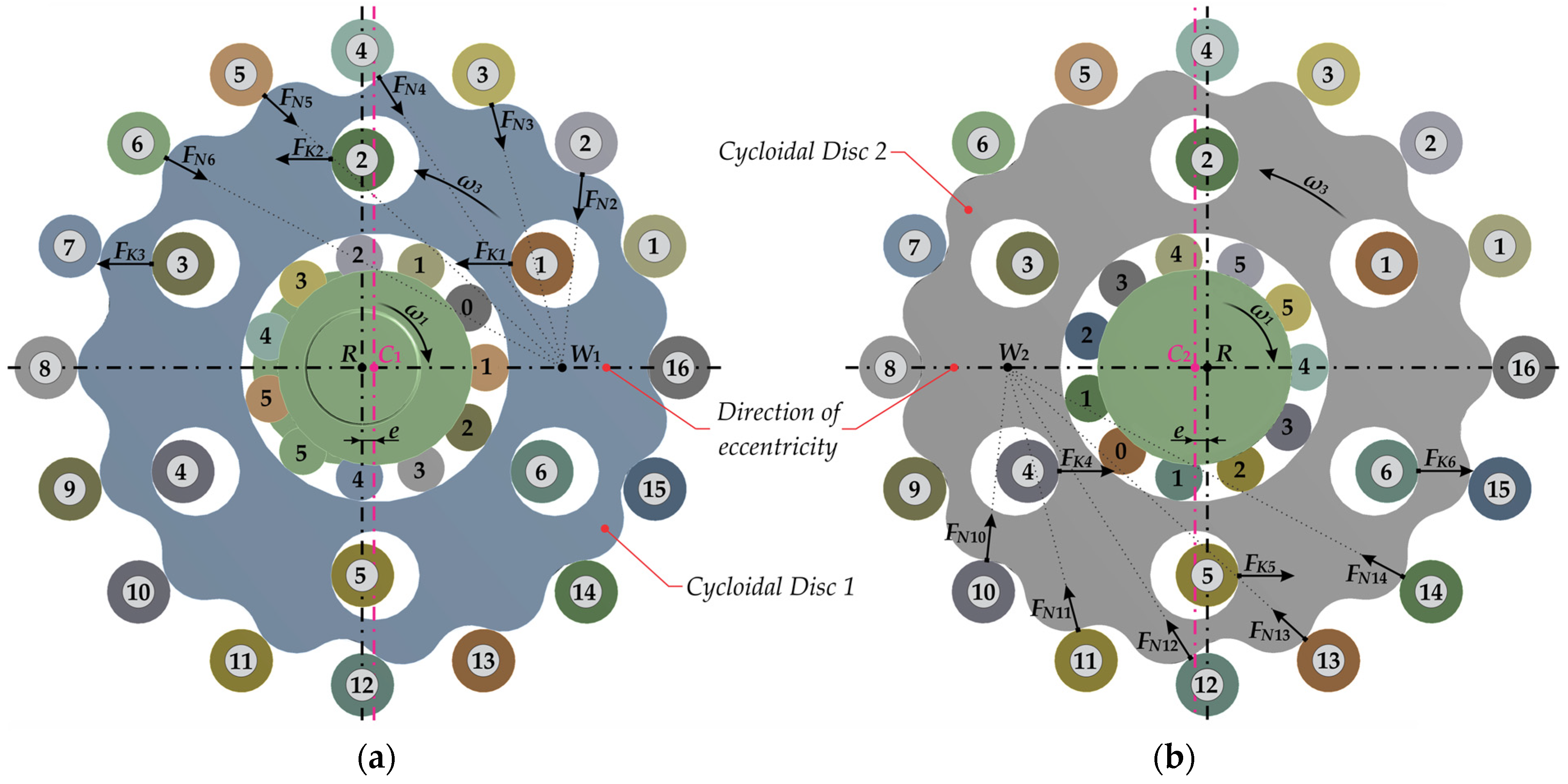
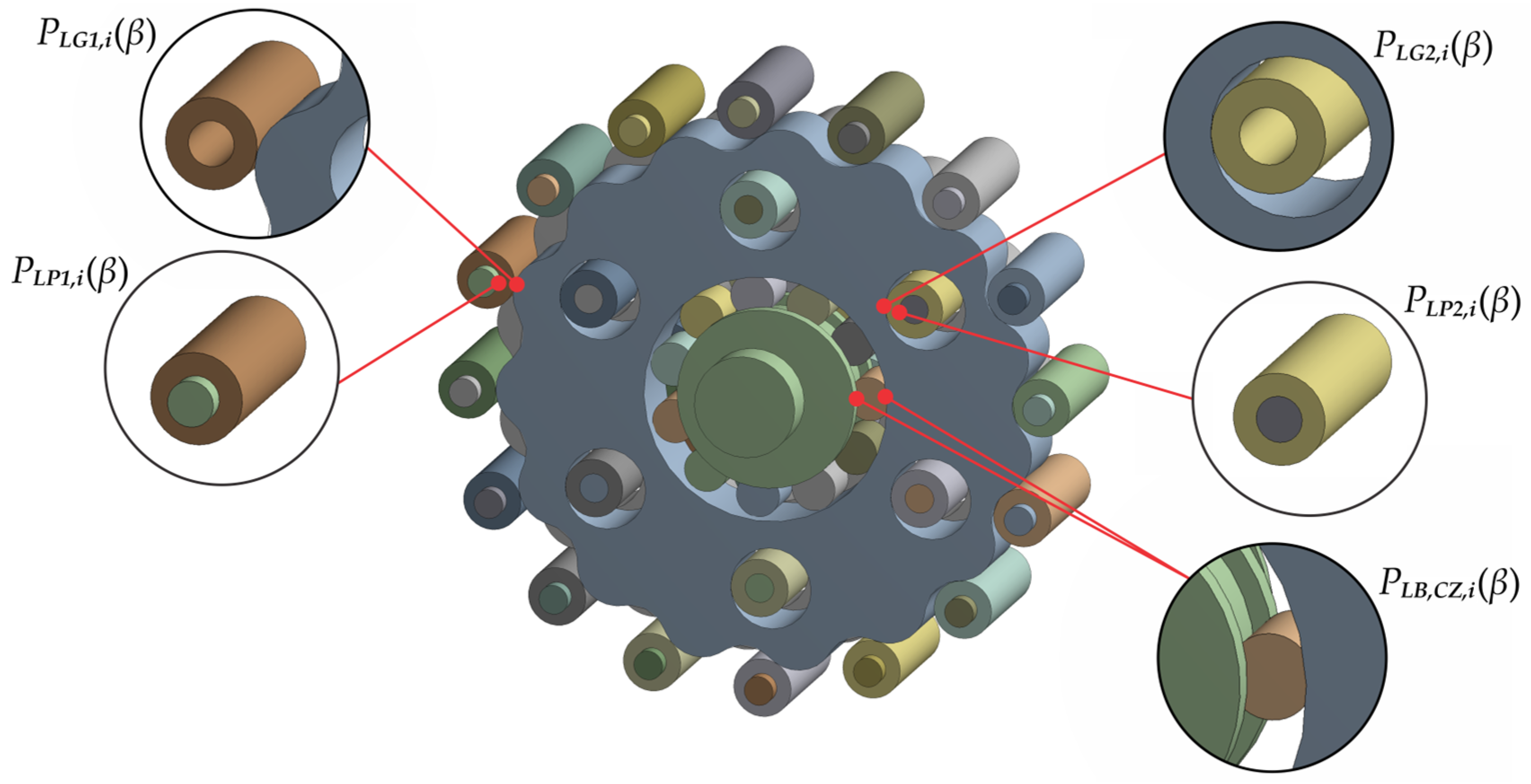
2.1.3. Constraints and Boundary Conditions in Static Structural Analysis
- ▪
- The teeth of the cycloidal disc and the ring gear rollers (normal contact force );
- ▪
- The output rollers and the holes in the cycloidal disc (output contact force).
2.1.4. Constraints and Boundary Conditions in Transient Thermal Analysis
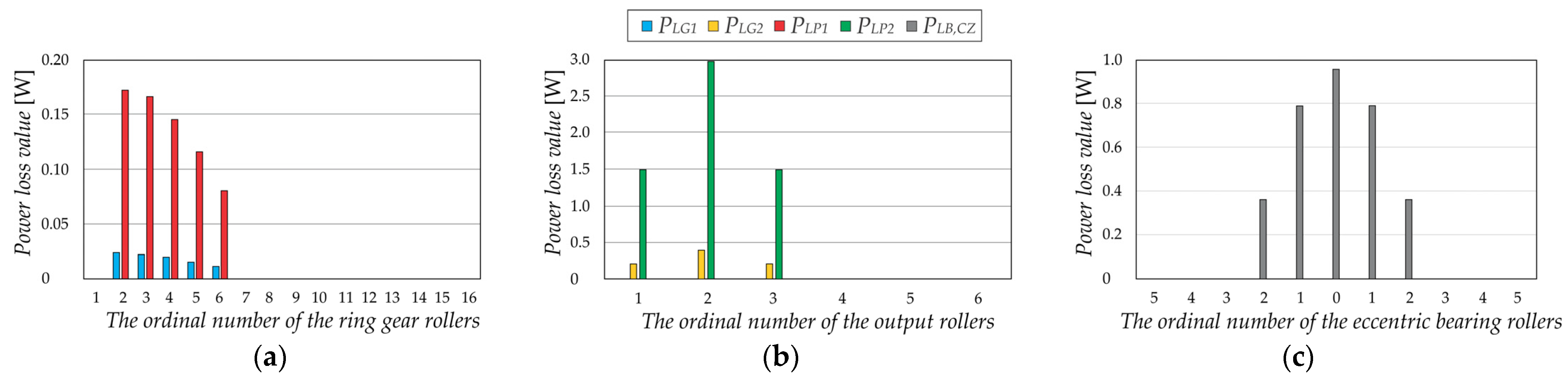
2.1.5. Power Loss Calculation
2.2. Model Validation
2.2.1. Analytical Validation of Contact Forces Without the Effects of the Thermal Stresses
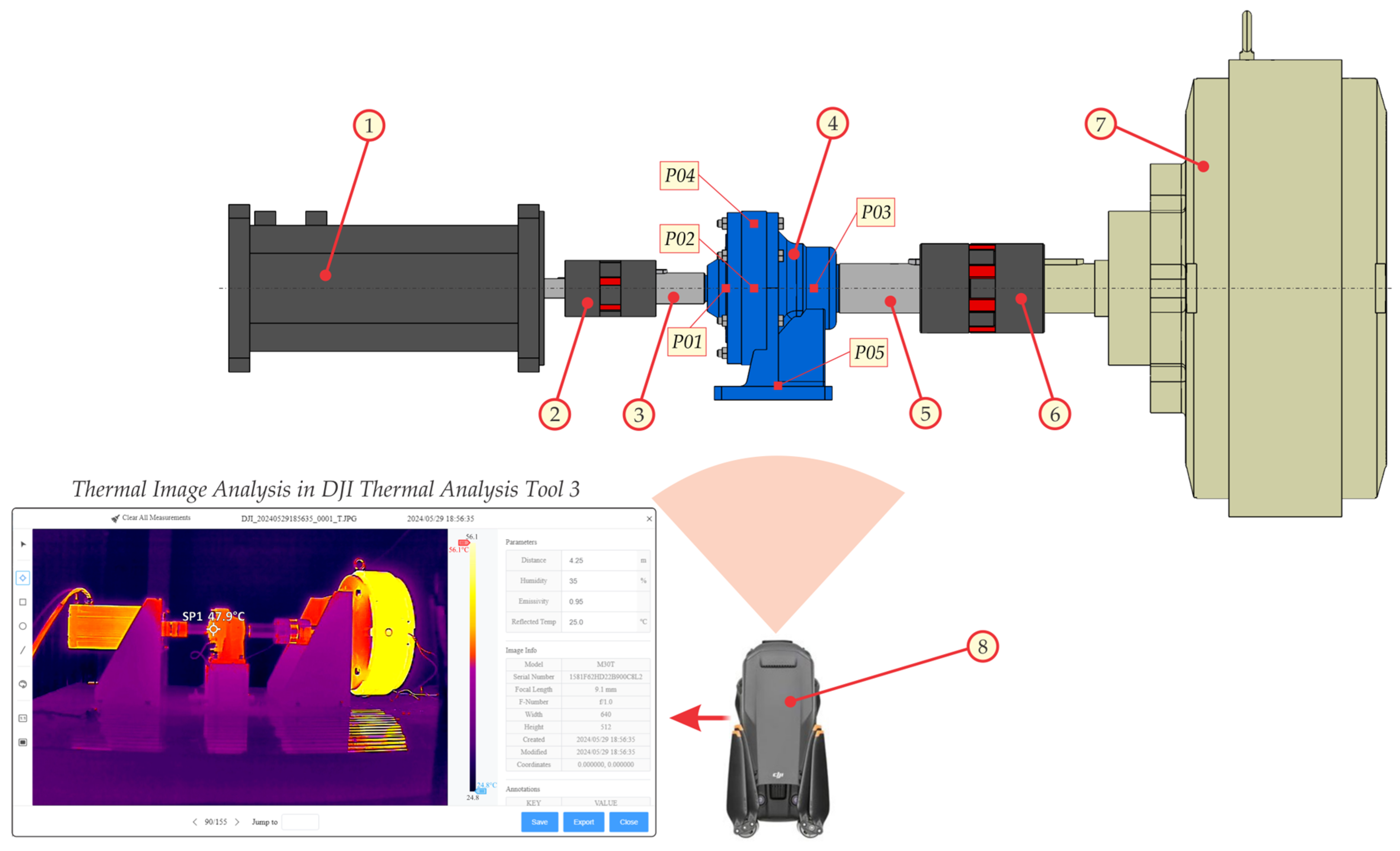
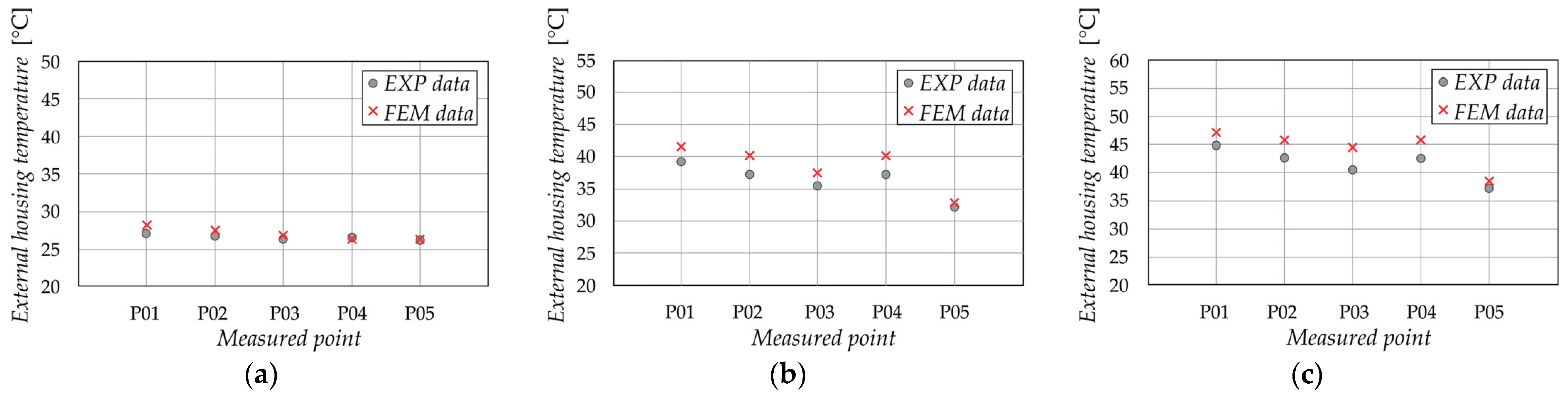
2.2.2. Experimental Validation of Temperature Field Distribution
3. Results and Discussion
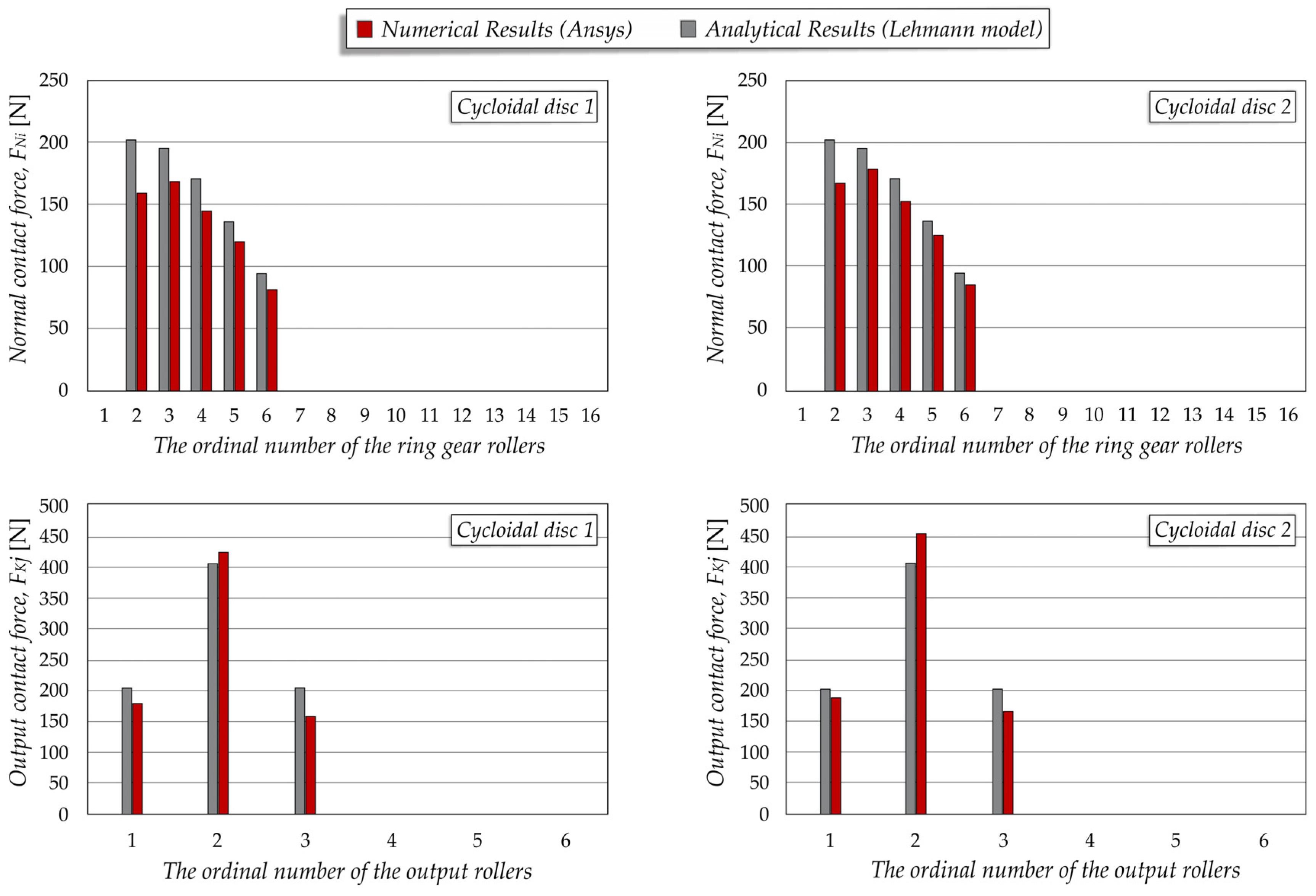
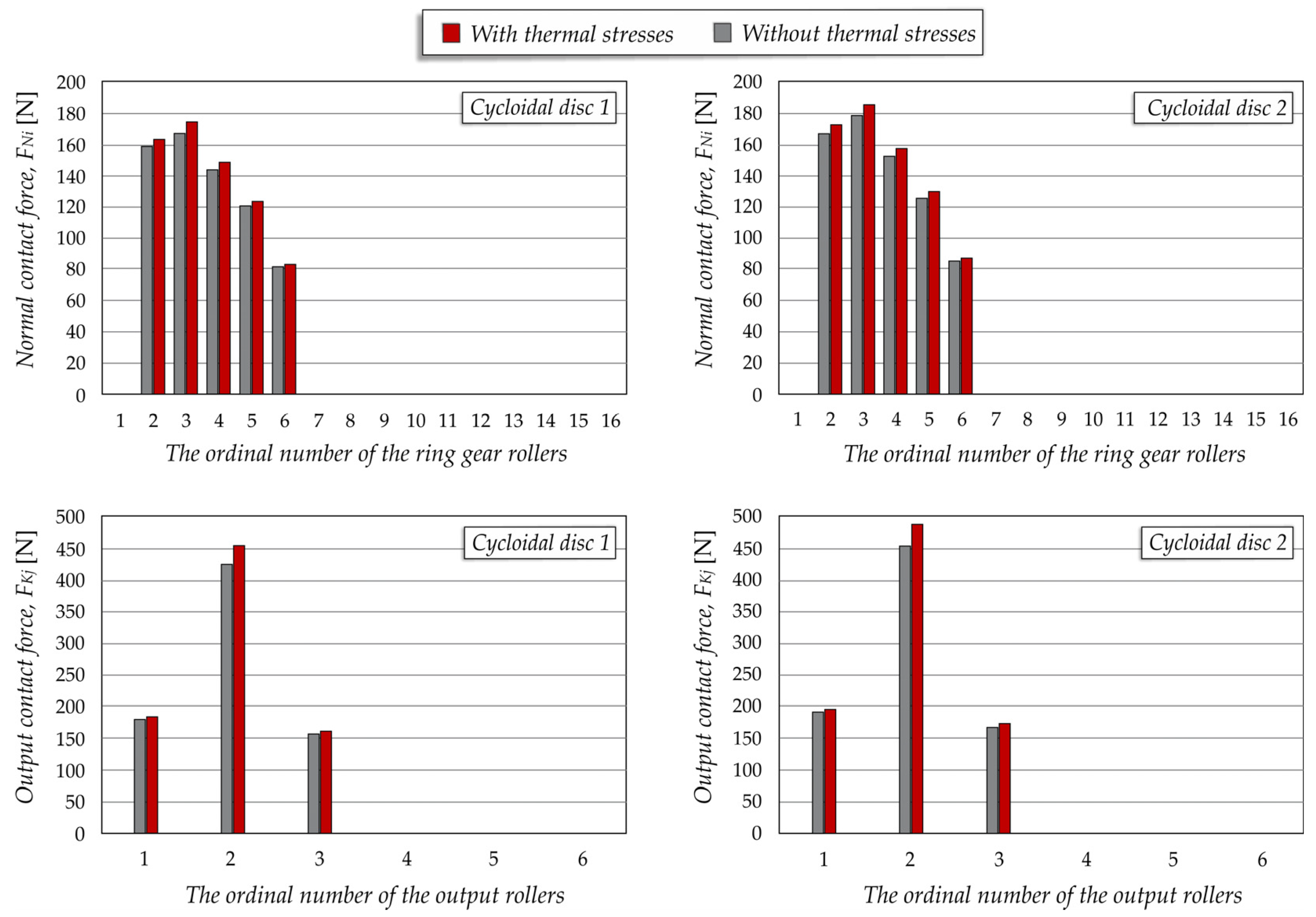
3.1. Contact Forces
3.2. Power Losses
3.3. Temperature Field Distribution on the Outer Surface of the Housing
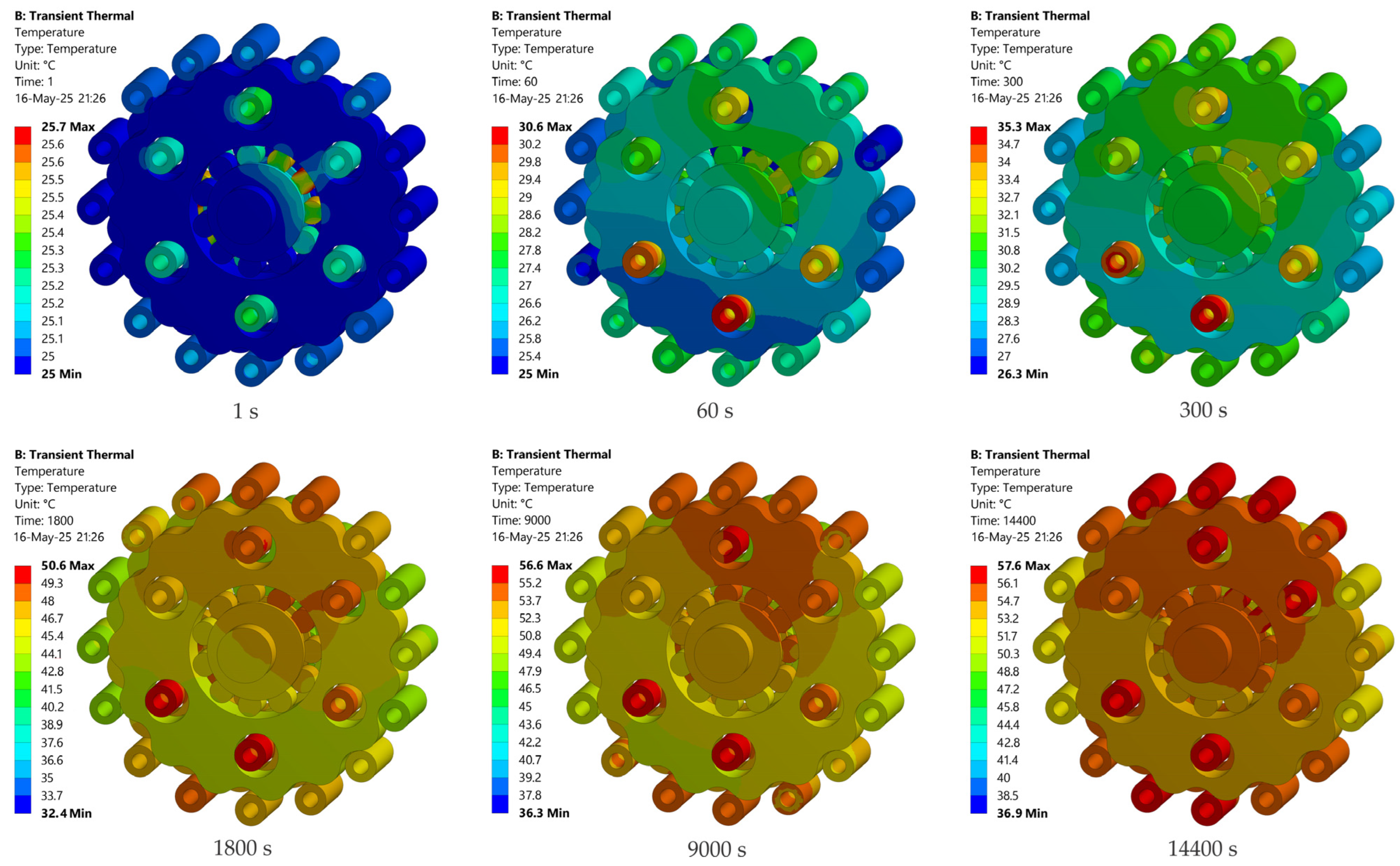
3.4. Distribution of the Temperature Fields on the Internal Elements
3.5. Influence of Thermal Stresses on the Contact Forces
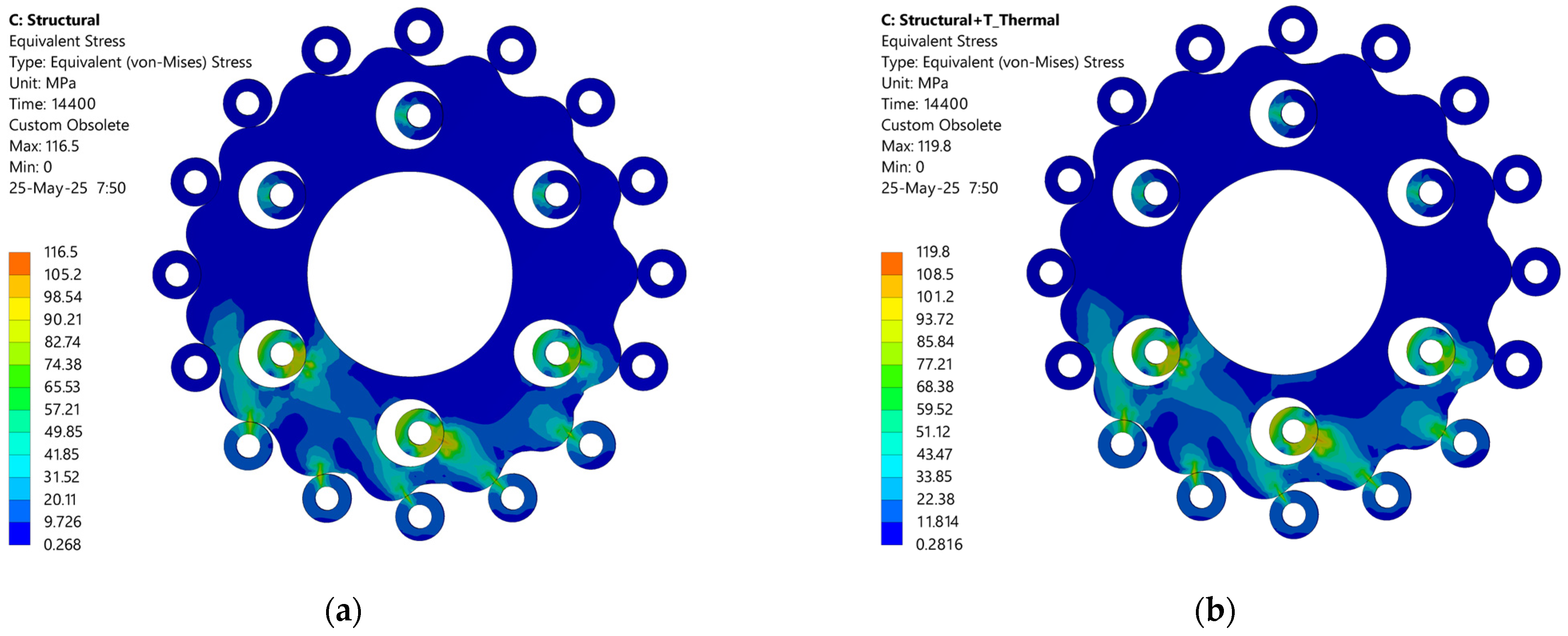
3.6. Influence of Thermal Stresses on the Stress–Strain State
4. Conclusions
- ▪
- Numerical simulations with accurately defined boundary conditions provide reliable predictions of the temperature field distribution.
- ▪
- An uneven load distribution is observed between the cycloidal discs and the corresponding rollers. In the studied case, the contact forces between the ring gear rollers and the teeth of cycloidal disc 2 are 5–6% higher compared to those between the ring gear rollers and the teeth of cycloidal disc 1. The same trend is observed in the contact forces between the output rollers and the holes in the cycloidal disc, with differences ranging from 6–7%.
- ▪
- Thermal stresses lead to an increase in the values of contact forces. In the studied case, the normal contact forces increase by 2–3% on average due to thermal stresses, while the output contact forces increase by an average of 5–8%.
- ▪
- Including thermal stresses in the analysis increases the von Mises stress values by an average of 2.4%.
- ▪
- The stresses on the rollers are higher compared to those on the cycloidal disc, which is attributed to the shape of the roller and the direction of stress propagation.
- ▪
- The von Mises stresses in the contacts between the cycloidal disc 2 and the corresponding rollers are 4.8% higher compared to those in the contacts between the cycloidal disc 1 and the corresponding rollers. This stress distribution is the result of the uneven load distribution between the cycloidal discs.
- ▪
- Infrared thermal (IRT) images show that the maximum temperature is located in the input shaft bearing region, with the temperature increasing and propagating towards the output shaft. This temperature distribution is primarily due to the close proximity of the eccentric bearing, which is one of the main heat sources in the cycloidal reducer.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BLDC | Brushless DC motor |
| DoE | Design of experiments |
| EXP | Experimental |
| FEM | Finite element method |
| IRT | Infrared thermal |
| Nomenclature | |
| Stiffness of the ring gear and output rollers | |
| Specific heat capacity at constant pressure of the ambient air | |
| Ring gear roller diameter | |
| Diameter of the ring gear roller pin | |
| Mean diameter of the bearing | |
| Outer diameter of the cylindrical wall | |
| Diameter of the shaft | |
| Output roller diameter | |
| Diameter of the output roller pin | |
| Eccentricity | |
| Factor dependent on the bearing type and the direction of the load | |
| Contact force between the rolling body of the eccentric bearing and the corresponding rolling raceway located on the line of action of the eccentric force | |
| Contact force between the i-th rolling body of the eccentric bearing and the corresponding rolling raceways | |
| Horizontal component of the eccentric force | |
| Vertical component of the eccentric force | |
| Contact force between the j-th output rollers and the holes in the cycloidal disc (output contact force) | |
| Contact force between the teeth of the cycloidal disc and the i-th ring gear roller (normal contact force) | |
| Horizontal component of the normal contact force | |
| Vertical component of the normal contact force | |
| Gravitational acceleration | |
| Grashof number for the cylindrical wall | |
| Grashof number for a flat vertical wall | |
| Height of the vertical wall | |
| Input speed | |
| Nusselt number | |
| Total power loss due to friction in the bearing elements (eccentric, input, and output shaft bearings) | |
| Total power loss due to interaction between the lubricant and the bearing elements | |
| Power loss due to friction between the i-th rolling body of the input shaft bearing and the corresponding rolling raceways | |
| Power loss due to friction between the i-th rolling body of the output shaft bearing and the corresponding rolling raceways | |
| Power loss due to friction between the i-th rolling body of the eccentric bearing and the corresponding rolling raceways | |
| Total power loss due to interaction between the lubricant and the cycloidal disc | |
| Total power loss due to friction between the ring gear rollers and the cycloidal disc teeth | |
| Power loss due to friction between the i-th ring gear roller and a cycloidal disc tooth | |
| Total power loss due to friction between the output rollers and the holes in the cycloidal disc | |
| Power loss due to friction between the j-th output roller and the holes in the cycloidal disc | |
| Total power loss due to friction between the ring gear rollers and the pins | |
| Power loss due to friction between the i-th ring gear roller and the pin | |
| Total power loss due to friction between the output rollers and the pins | |
| Power loss due to friction between the j-th output roller and the pin | |
| Total power loss due to friction in the radial shaft seals | |
| Prandtl number | |
| Radius of the pitch circle of the ring gear rollers | |
| Pitch circle diameter of output rollers | |
| Radius of the rolling circle | |
| Radius of the base (stationary) circle | |
| Reynolds number | |
| Distance between the line of contact of the j-th output roller and the central axis of the cycloidal disc | |
| Distance between the line of contact of the i-th ring gear roller and the central axis of the cycloidal disc | |
| Driving torque of one cycloidal disc | |
| Torque at the ring gear coming from one cycloidal disc | |
| Output torque also coming from one cycloidal disc | |
| Torque at the input shaft | |
| Torque at the output shaft | |
| Number of output rollers | |
| Transmission ratio | |
| Angle between normal force of i-th ring gear roller and vertical direction | |
| Number of cycloidal disc teeth | |
| Number of ring gear roller pairs closest to the direction of eccentricity that are excluded from the load transfer process | |
| Coefficient of heat transfer by natural convection from the external surface of the cylindrical housing wall to the ambient air | |
| Coefficient of heat transfer by natural convection from the external surface of the vertical housing wall to the ambient air | |
| Coefficient of heat transfer by radiation from the external surface of the housing to the ambient air | |
| Coefficients of heat transfer between the shafts and the ambient air | |
| Drive angle of the cycloidal disc | |
| Coefficient of volumetric expansion | |
| Equivalent thickness of the walls of the housing | |
| Small angular displacement of the cycloidal disc | |
| Emissivity coefficient of the housing surface | |
| Efficiency of the cycloidal reducer | |
| Ambient air temperature | |
| Lubricant temperature | |
| Thermal conductivity coefficient of the ambient air | |
| Dynamic viscosity of the ambient air | |
| Rolling friction coefficient between the ring gear rollers and the cycloidal disc teeth | |
| Rolling friction coefficient between the output rollers and the holes in the cycloidal disc | |
| Sliding friction coefficient between the ring gear rollers and their pins | |
| Sliding friction coefficient between the output rollers and their pins | |
| Kinematic viscosity of the ambient air | |
| Pitch angle of the ring gear roller | |
| Angular pitch of the rolling bodies of the eccentric bearing | |
| Plate inclination angle relative to the vertical plane | |
| Angle of the first output roller relative to the x-axis in the initial position | |
| Position angle of the j-th output roller relative to the x-axis in an arbitrary position | |
| Angle between the direction of action of the output contact force of the j-th output roller and the direction that connects the contact line with the central axis of the cycloidal disc | |
| Angle between the direction of action of the normal contact forces of the i-th ring gear roller and the direction that connects the line of contact and the central axis of the cycloidal disc | |
| Angular velocity of the ring gear rollers | |
| Angular velocity of the output rollers | |
| Angular velocity of the input shaft | |
| Angular velocity of the output shaft | |
| Angular velocity of the shaft |
References
- Kudryavtsev, V.N. Planetarnye Peredachi (Planetary Transmissions); Masinostroenie: Moscow–Leningrad, Russian, 1966. [Google Scholar]
- Lehmann, M. Calculation and Measurement of Forces Acting on Cycloidal Speed Reducer. Ph.D. Thesis, The Technical University of Munich, Munich, Germany, 1976. [Google Scholar]
- Li, X.; Li, C.; Wang, Y.; Chen, B. Analysis of a Cycloid Speed Reducer Considering Tooth Profile Modification and Clearance—Fit Output Mechanism. J. Mech. Des. 2017, 139, 033303. [Google Scholar] [CrossRef]
- Ren, Z.Y.; Mao, S.M.; Guo, W.C.; Guo, Z. Tooth Modification and Dynamic Performance of the Cycloidal Drive. Mech. Syst. Signal Process. 2017, 85, 857–866. [Google Scholar] [CrossRef]
- Xu, L.X. A Dynamic Model to Predict the Number of Pins to Transmit Load in a Cycloidal Reducer with Assembling Clearance. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 4247–4269. [Google Scholar] [CrossRef]
- Artyomov, I.I.; Tcufistov, E.A.; Tchufistov, O.E. Analysis of Static Loading of Meshing in Planetary Cycloid Gear. IOP Conf. Ser. Mater. Sci. Eng. 2020, 734, 012056. [Google Scholar] [CrossRef]
- Bednarczyk, S. Determining Power Losses in the Cycloidal Gear Transmission Featuring Manufacturing Deviations. In Proceedings of the 14th International Scientific Conference: Computer Aided Engineering (CAE 2018), Wrocław, Poland, 20–23 June 2019. [Google Scholar]
- Bednarczyk, S.; Jankowski, L.; Krawczyk, J. The Influence of Eccentricity Changes on Power Losses in Cycloidal Gearing. Tribologia 2019, 3, 19–29. [Google Scholar] [CrossRef]
- Zhang, T.; Li, X.; Wang, Y.; Sun, L. A Semi-Analytical Load Distribution Model for Cycloid Drives with Tooth Profile and Longitudinal Modification. Appl. Sci. 2020, 10, 4859. [Google Scholar] [CrossRef]
- Jiang, N.; Wang, S.; Xie, X.; Yuan, X.; Yang, A.; Zhang, J. A Vectorial Modification Methodology Based on an Efficient and Accurate Cycloid Tooth Profile Model. Precis. Eng. 2022, 73, 435–456. [Google Scholar] [CrossRef]
- Tchufistov, E.A.; Tchufistov, O.E.; Blagojević, M.; Vasić, M. Simulation of motion in a cycloidal gear. Part I. Unloaded gear; Izvestiya vysshikh uchebnykh zavedeniy. Povolzhskiy region. Univ. Proc. Volga Reg. Tech. Sci. 2024, 72, 92–108. [Google Scholar]
- Tchufistov, E.A.; Tchufistov, O.E.; Blagojević, M.; Vasić, M. Simulation of motion in a cycloidal gear. Part II. Loaded gear; Izvestiya vysshikh uchebnykh zavedeniy. Povolzhskiy region. Univ. Proc. Volga Reg. Tech. Sci. 2025, 73, 92–105. [Google Scholar]
- Thube, S.V.; Bobak, T.R. Dynamic analysis of a cycloidal gearbox using finite element method. AGMA Tech. Pap. 2012, 1–13. [Google Scholar]
- Krol, R. Kinematics and Dynamics of two Stage Cycloidal Gearbox. AUTOBUSY–Tech. Eksploat. Syst. Transp. 2018, 220, 523–527. [Google Scholar] [CrossRef]
- Jang, D.J.; Kim, Y.C.; Hong, E.P.; Kim, G.S. Geometry Design and Dynamic Analysis of a Modified Cycloid Reducer with Epitrochoid Tooth Profile. Mech. Mach. Theory 2021, 164, 104399. [Google Scholar] [CrossRef]
- Zakharov, M.N.; Ermolaev, M.M.; Zaitseva, A.V. Nonuniform Load Distribution Between the Satellites of a Cycloid Gear. Russ. Eng. Res. 2020, 40, 720–725. [Google Scholar] [CrossRef]
- Mihailidis, A.; Athanasopoulos, E.; Okkas, E. Flash temperature in cycloid reducers. J. Balk. Tribol. Assoc. 2015, 21, 76–89. [Google Scholar]
- Zah, M.; Lates, D.; Csibi, V. Thermal calculation for planetary cycloidal gears with bolts. Acta Univ. Sapientiae-Electr. Mech. Eng. 2012, 4, 103–110. [Google Scholar]
- Hu, Y.; Li, G.; Zhu, W.; Cui, J. An Elastic Transmission Error Compensation Method for Rotary Vector Speed Reducers Based on Error Sensitivity Analysis. Appl. Sci. 2020, 10, 481. [Google Scholar] [CrossRef]
- Vasić, M.; Blagojević, M.; Banić, M.; Maccioni, L.; Concli, F. Theoretical and Experimental Investigation of the Thermal Stability of a Cycloid Speed Reducer. Lubricants 2025, 13, 70. [Google Scholar] [CrossRef]
- Blagojević, M.; Vasić, M.; Dizdar, S.; Tuka, S.; Josimović, M. The Influence of Thermal Stresses on the Load Distribution in Cycloidal Reducers. In Proceedings of the 3rd International Symposium on Industrial Engineering and Automation—ISIEA 2024, Bolzano, Italy, 19–21 June 2024. [Google Scholar]
- Pastukhov, A.; Timashov, E. Procedure for simulation of stable thermal conductivity of bearing assemblies. Adv. Eng. Lett. 2023, 2, 58–63. [Google Scholar] [CrossRef]
- Blagojević, M. Stress and Strain State of Cyclo Speed Reducers Elements Under Dynamic Loads. Ph.D. Thesis, Faculty of Engineering, University of Kragujevac, Kragujevac, Serbia, 2008. [Google Scholar]
- Miltenović, A.; Banić, M. Thermal analysis of a crossed helical gearbox using FEM. Trans. FAMENA 2020, 44, 67–78. [Google Scholar] [CrossRef]
- Linke, H.; Börner, J.; Hess, R. Cylindrical Gears: Calculation–Materials–Manufacturing; Carl Hanser Verlag GmbH & Company KG: Munich, Germany, 2016. [Google Scholar]
- Niemann, G.; Winter, H. Maschinenelemente, Band 3: Schraubrad-, Kegelrad-, Schnecken-, Ketten-, Riemen-, Reibradgetriebe, Kupplungen, Bremsen, Freiläufe, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1983. [Google Scholar]
- Schaeffler Technologies AG & Co. KG. Wälzlagerpraxis—Handbuch zur Gestaltung und Berechnung von Wälzlagerungen; Vereinigte Fachverlage GmbH: Mainz, Germany, 2015. [Google Scholar]


| Parameter | Units | Value |
|---|---|---|
| Transmission ratio, | – | 15 |
| Eccentricity, | mm | 1.6 |
| Ring gear roller diameter, | mm | 8 |
| Diameter of the ring gear roller pin, | mm | 6 |
| Output roller diameter, | mm | 8 |
| Diameter of the output roller pin, | mm | 6 |
| Number of output rollers, | – | 6 |
| Pitch circle diameter of output rollers, | mm | 26.2 |
| Position | Eccentric | Bearing A | Bearing B | Bearing C | Bearing D | Oil Seals [mm] |
|---|---|---|---|---|---|---|
| Input shaft | 6301 | 6301Z | 17 × 30 × 6 | |||
| Output shaft | 6204Z | 6909 | 30 × 47 × 8 | |||
| Cycloidal disc | 607–YSX |
| Cycloidal Reducer Components | Young’s Modulus [Pa] | Poisson’s Ratio [–] | Density [kg/m3] | Bulk Modulus [Pa] | Shear Modulus [Pa] | Isotropic Thermal Conductivity [W/mK] | Specific Heat [J/kgK] |
|---|---|---|---|---|---|---|---|
| Housing (cast iron GG25) | 95 × 109 | 0.26 | 7100 | 110 × 109 | 41 × 109 | 55 | 460 |
| Cycloidal disc, ring gear roller, Output roller, bearing (bearing steel 100Cr6) | 210 × 109 | 0.30 | 7810 | 160 × 109 | 80 × 109 | 46 | 460 |
| Shaft (medium carbon steel C45) | 210 × 109 | 0.29 | 7850 | 160 × 109 | 80 × 109 | 50 | 470 |
| Name | Thickener Type | Grade | Dropping Point, [°C] | Base Oil Viscosity, [mm2/s] | Viscosity Index | Isotropic Thermal Conductivity [W/mK] | Specific Heat [J/kgK] | |
|---|---|---|---|---|---|---|---|---|
| Unirex N2 | Lithium Complex | NLGI 2 | 210 | 115 | 95 | 95 | 0.272 | 1670 |
| Mesh Parameter | Hex20 (Brick) | Tet10 (Tetrahedron) | Prism15 | Pyramid13 |
|---|---|---|---|---|
| Number of nodes per element | 20 | 10 | 15 | 13 |
| Degrees of freedom per node | 3 (UX, UY, UZ) | |||
| Shape functions | Quadratic displacement | |||
| Jacobian/Integration points | 8 (2 × 2 × 2 Gauss full integration) | 4 (Gauss integration) | 9 (3 × 3 in plane × 1 through height) | 4 (2 × 2 in plane × 1 through height) |
| Element formulation | 3D structural solid, higher-order | |||
| Typical use in mesh | Regular hex mesh regions | Irregular complex geometries | Transitional prismatic regions | Transitional pyramid regions |
| Heat Transfer Mechanism | Location |
|---|---|
| Conduction | Internal elements in contact |
| Internal elements → Lubricant | |
| Lubricant → Internal surface of the housing | |
| Convection | External surface of the housing → Ambient air |
| Foot mount → Ambient air | |
| External parts of the input and the output shaft → Ambient air | |
| Radiation | External surface of the housing → Ambient air |
| Foot mount → Ambient air | |
| External parts of the input and the output shaft → Ambient air |
| Parameter | Unit | Value |
|---|---|---|
| Ambient temperature, | 25 | |
| Coefficient of the rolling friction, , | – | 0.003 |
| Coefficient of the sliding friction, , | – | 0.03 |
| Cycloidal Disc | Type of Load | Maximum von Mises Stress, (MPa) | Maximum Deformation, (mm) |
|---|---|---|---|
| Cycloidal disc 1 | Without thermal load | 110.9 | 0.000324 |
| With thermal load | 113.6 | 0.000342 | |
| Cycloidal disc 2 | Without thermal load | 116.5 | 0.000329 |
| With thermal load | 119.8 | 0.000350 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vasić, M.; Blagojević, M.; Dizdar, S.; Tuka, S. The Influence of Thermal Stresses on the Load Distribution and Stress–Strain State of Cycloidal Reducers. Appl. Sci. 2025, 15, 9607. https://doi.org/10.3390/app15179607
Vasić M, Blagojević M, Dizdar S, Tuka S. The Influence of Thermal Stresses on the Load Distribution and Stress–Strain State of Cycloidal Reducers. Applied Sciences. 2025; 15(17):9607. https://doi.org/10.3390/app15179607
Chicago/Turabian StyleVasić, Milan, Mirko Blagojević, Samir Dizdar, and Smajo Tuka. 2025. "The Influence of Thermal Stresses on the Load Distribution and Stress–Strain State of Cycloidal Reducers" Applied Sciences 15, no. 17: 9607. https://doi.org/10.3390/app15179607
APA StyleVasić, M., Blagojević, M., Dizdar, S., & Tuka, S. (2025). The Influence of Thermal Stresses on the Load Distribution and Stress–Strain State of Cycloidal Reducers. Applied Sciences, 15(17), 9607. https://doi.org/10.3390/app15179607









