A Deep-Learning-Based Dynamic Multidimensional Memory-Augmented Personalized Recommendation Research

Abstract

To address the problem of inaccurate matching between personalized exercise recommendations and learners’ mastery of knowledge concepts/learning abilities, we propose the Dynamic Multidimensional Memory Augmented knowledge tracing model (DMMA). This model integrates a dynamic key-value memory neural network with the Ebbinghaus Forgetting Curve. By incorporating time decay factors and knowledge concept mastery speed factors, it dynamically adjusts knowledge update intensity, effectively resolving the insufficient personalized recommendation capabilities of traditional models. Experimental validation demonstrates its effectiveness: on Algebra 2006–2007, DMMA achieves 82% accuracy, outperforming CRDP-KT by 6%, while maintaining 53–55% accuracy for cold-start users (0–5 interactions), which is 25% higher than CoKT. The model’s integration of the Ebbinghaus forgetting curve and K-means-based concept classification enhances adaptability. Genetic algorithm optimization yields a diversity score of 0.79, with 18% higher 30-day knowledge retention. The FastDTW–Sigmoid hybrid similarity calculation (weight transition 0.27–0.88) ensures smooth cold-start adaptation, while novelty metrics reach 0.65 via random-forest-driven prediction. Ablation studies confirm component necessity: removing time decay factors reduces accuracy by 2.2%. These results validate DMMA’s superior performance in personalized education.

1. Introduction

With the in-depth integration of digital technology and education, online education platforms have become a vital channel for learners worldwide to access knowledge. The scale of online learning users continues to grow, and the number of exercises in platform resource libraries has increased accordingly. However, the abundance of resources also brings new challenges: learners need to spend a great deal of time screening practice resources that match their own knowledge levels, which reduces learning efficiency and experience. Personalized practice recommendation can dynamically adapt to learners’ knowledge states, optimize learning efficiency, and improve the level of knowledge mastery [1,2,3].

Nevertheless, current research faces the problem that it is difficult to achieve accurate matching between the heterogeneous ability distribution of online learners and the massive practice resources. This leads to a wide variety of question types and a large span of difficulty levels, resulting in a phenomenon of “resource overload yet insufficient effective supply”. This contradiction highlights the urgency of constructing personalized online learning practice recommendation algorithms [3]. How to help learners quickly find suitable exercises from massive resources and improve learning efficiency and effectiveness has become a key issue to be solved urgently in the field of online education [2,4]. By analyzing learners’ characteristics such as learning behaviors, knowledge levels, and learning styles, personalized practice recommendation provides them with the most appropriate practice resources, thereby realizing the goal of “teaching students in accordance with their aptitude” [1,5].

At present, the academic and industrial circles have carried out extensive research on personalized exercise recommendation, forming four mainstream technical paths, but all of them have certain limitations. Collaborative Filtering (CF) Method: As one of the earliest technologies applied in recommendation systems, collaborative filtering makes recommendations based on the similarity between users or items [6]. However, collaborative filtering is relatively sensitive to data sparsity, especially in the cold-start problem of new users or less popular exercises, which affects the recommendation accuracy [6]. In addition, traditional collaborative filtering methods are difficult to capture the dynamic changes in learners’ knowledge states [7]. Knowledge Point Hierarchy Graph-based Method: This type of method alleviates the problem of information overload by constructing hierarchical relationships between knowledge points [8]. However, knowledge point hierarchy graph-based methods rely excessively on manually constructed knowledge structures, which incur high construction costs. Moreover, they are difficult to cover interdisciplinary related knowledge points, which may lead to insufficient knowledge coverage of recommendation results [2]. Knowledge Graph (KG) Method: Knowledge graphs can use the semantic relationships between entities to improve the interpretability of recommendations [9]. However, in educational scenarios, the annotation of entities and relationships requires the participation of domain experts. Additionally, the model relies strongly on the integrity of the knowledge graph, and the quality of the knowledge graph directly affects the recommendation effect [7]. Deep Learning Method: Deep learning methods (such as Deep Knowledge Tracing, DKT) capture the laws of learning behaviors through temporal modeling [2]. Nevertheless, traditional deep learning models generally ignore the natural characteristic of knowledge forgetting and are prone to overfitting in small-sample scenarios, leading to an increase in prediction errors [10].

The common challenge of the above methods lies in their failure to deeply integrate educational cognitive laws (such as memory forgetting) with dynamic learning behaviors. As a result, it is difficult for recommendation results to balance the three dimensions of “accuracy”, “diversity”, and “novelty”. More attention needs to be paid to how to combine cognitive science theories to design more intelligent and personalized practice recommendation systems [11].

To address the shortcomings of existing research, this study proposes a Dynamic Multi-Dimensional Memory-Augmented (DMMA) knowledge tracking model. Its core design idea is to conduct collaborative innovation between educational cognitive theories and deep learning technologies, rather than simply superimposing existing methods. Compared with traditional models, the differentiated advantages of DMMA are reflected in three aspects: first, it integrates the Ebbinghaus forgetting curve and simulates the natural decay process of knowledge over time through a time decay factor, solving the problem of disconnection between the “static knowledge representation” of traditional models and the “dynamic learning process”; second, it introduces a knowledge concept mastery speed factor, distinguishes the differences in mastery difficulty between basic concepts and advanced skills based on K-means clustering, and realizes personalized adjustment of learning intensity; third, it constructs a collaborative framework of “exercise filter-genetic algorithm optimizer”, which maximizes the diversity of knowledge coverage while ensuring the adaptation of exercise difficulty, so as to avoid recommendation homogenization.

The main contributions of this study can be summarized as follows:

(1)

Combining the Ebbinghaus forgetting curve with the Dynamic Key-Value Memory Network (DKVMN) [12], a time decay factor and a knowledge concept mastery speed factor are proposed, enabling the model to accurately simulate the entire process of knowledge from learning and forgetting to consolidation.

(2)

Optimizing the recommendation strategy, a three-level recommendation mechanism of “knowledge concept mastery prediction-knowledge coverage prediction-genetic algorithm optimization” is proposed. It predicts the occurrence probability of knowledge points through random forests and maximizes exercise diversity by combining genetic algorithms. For example, the diversity index of DMMA reaches 0.79 on the Assistment 2017 dataset, which is 0.12 higher than that of DKVMN.

(3)

To solve the cold-start problem, a hybrid similarity calculation method based on Sigmoid weighting is designed, which integrates the external attributes of new users (such as grade and subject preference) with limited answer sequences. When new users have only 5 answer records, the recommendation accuracy can still reach 53–55%, which is significantly higher than the 28–34% of CoKT.

(4)

Sufficient empirical verification: Verification is conducted on three cross-domain datasets, namely Algebra 2006–2007, Assistment 2017, and Statics2011. DMMA significantly outperforms mainstream models such as CRDP-KT, QIKT, and CoKT in three core indicators: accuracy (up to 82%), diversity (up to 0.79), and novelty (up to 0.65). Moreover, after 50 stability tests, the fluctuation range is less than 5%, which proves its generalization ability and robustness.

The value of this study lies not only in proposing a technical solution, but also in constructing a closed loop of “educational cognitive laws-deep learning models-educational practice needs”. It provides a practical personalized practice recommendation framework for online education platforms and has important reference significance for promoting the transformation of smart education from “resource supply” to “precision service”.

2. Related Work

As a core technology connecting learners’ individual needs with massive educational resources, personalized exercise recommendation systems have formed a research pattern where multiple technical paths develop in parallel. This section systematically sorts out the technical logic, advantages, and limitations of existing research from four mainstream directions—collaborative filtering, knowledge point hierarchy graph, knowledge graph, and deep learning—and clarifies the differentiated positioning of this study from existing work.

2.1. Collaborative Filtering-Based Recommendation Methods

Collaborative Filtering (CF) is a classic technology in the field of personalized recommendation, with its core logic being “similar users prefer similar resources” or “similar resources attract similar users”. In online education scenarios, it has developed into three sub-directions: user-based, item-based, and hybrid collaborative filtering.

User-based CF methods calculate the interest similarity between learners (e.g., Pearson correlation coefficient, cosine similarity) and recommend exercises with high correct answer rates from similar groups to the target user. For instance, Zhong et al. [12] constructed a user similarity model based on the matrix of learners’ exercise correct rates, achieving an accuracy of 65% in K-12 mathematics exercise recommendation.

Item-based CF methods focus on the correlation between exercises. For example, the Jaccard coefficient is used to calculate the frequency of exercises being answered together, and resources similar to the exercises already mastered by the target learner are recommended. The kernel group Lasso feature selection method proposed by Deng et al. [13] further optimized the accuracy of exercise similarity calculation, improving recommendation efficiency by 20%.

To address the data sparsity issue of traditional CF, researchers have attempted to introduce domain knowledge and deep learning technologies for improvement. Zhai et al. [14] proposed a multimodal-enhanced collaborative filtering model, which integrates exercise text features, knowledge point labels, and learner interaction data, increasing recommendation accuracy by 18% in data-sparse scenarios. Another study combined LSTM neural networks with CF to capture dynamic changes in learners’ answering behaviors through temporal modeling, alleviating the limitations of static similarity calculation [1].

However, such methods still have inherent flaws. On one hand, the cold-start problem has not been fundamentally solved—when a new user has fewer than 10 answer records, the error in similarity calculation increases by more than 40%. On the other hand, CF methods are essentially “data-driven” black-box recommendations, which cannot explain “why this exercise is recommended”. Moreover, they ignore differences in learners’ knowledge states (e.g., the same exercise has different difficulty levels for learners with different knowledge levels), resulting in insufficient educational adaptability of recommendation results.

2.2. Knowledge Point Hierarchy Graph-Based Recommendation Methods

Knowledge point hierarchy graph-based recommendation methods take “knowledge structuring” as the core. They construct dependency relationships between knowledge points (e.g., “linear equations in one variable” is a prerequisite for “linear equations in two variables”) and dynamically adjust recommendation strategies based on learners’ answer records. Their advantage lies in directly associating exercises with knowledge points, enhancing the educational logic of recommendations.

Jiang Changmeng et al. [15] proposed a weighted knowledge point hierarchy graph model, which updates the weights of knowledge points through answer error rates and constructs a “knowledge point-exercise” mapping matrix. This model achieved an accuracy of 72% in high school mathematics recommendation, effectively solving the problem of resource overload. Wang Wei et al. [16] applied this idea to the course Fundamentals of Medical Computer Applications. By manually annotating the knowledge point hierarchy (e.g., “computer hardware” → “operating system” → “office software”), they increased the knowledge coverage of recommended exercises to 68%, which is significantly better than random recommendation.

The limitations of such methods are concentrated in two aspects: “knowledge structure construction” and “individual difference adaptation”. First, the knowledge point hierarchy graph relies heavily on manual annotation. The construction cost for a single subject requires 5–10 person-months of investment, and it is difficult to cover interdisciplinary correlations (e.g., the overlapping knowledge points between “probability” in mathematics and “statistics” in physics). Second, the recommendation strategy is only based on the “error rate” of knowledge points, failing to consider learners’ cognitive styles (e.g., visual learners are more suitable for exercises with images and text) and memory forgetting rules. As a result, the recommendation results are “targeted” but “ill-timed”—for example, review exercises are not recommended during the critical period of knowledge forgetting, which weakens the practice effect.

2.3. Knowledge Graph-Based Recommendation Methods

Knowledge Graphs (KGs) realize the structured and semantic representation of knowledge through a triple structure of “entity-relationship-entity”, providing richer correlation information for personalized exercise recommendation. KGs in the educational field usually include four core entities: “learner-knowledge point-exercise-course”, as well as relationships such as “mastery level”, “examines knowledge point”, and “prerequisite relationship”. Through knowledge graph embedding technologies (e.g., TransE, TransR), entities and relationships are mapped to a low-dimensional vector space to realize semantic-level similarity calculation [17,18].

Existing research mainly focuses on KG construction and embedding optimization. Wei et al. [18] constructed a KG containing 189 mathematics knowledge points and used the TransE model to learn entity vector representations, improving the matching accuracy between exercises and knowledge points by 25%. Guan et al. [19] proposed an interpretable knowledge graph recommendation model, which generates recommendation reasons through path reasoning (e.g., “Learner A–masters–Knowledge Point X–is examined by–Exercise B”), solving the problem of insufficient interpretability of traditional methods. Zhang Kai et al. [20] further proposed a heterogeneous fusion model for internal and external representations of exercises, combining the text content of exercises (internal representation) with semantic correlations in KGs (external representation), which increased the accuracy of knowledge tracing by 12%.

However, the application of KG methods is limited by two major bottlenecks. First, the construction cost is high. The annotation of entities and relationships in educational KGs requires the participation of domain experts, and dynamic updates are difficult (e.g., newly added knowledge points require re-training of the embedding model). Second, the model complexity is high—when a KG contains more than 1000 entities, the time complexity of embedding calculation increases exponentially, making it difficult to meet the real-time recommendation requirements of online education (usually requiring a response time of <1 s).

2.4. Deep-Learning-Based Recommendation Methods

With its powerful capabilities of automatic feature learning and temporal modeling, deep learning technology has become a research hotspot in personalized exercise recommendation. Among them, Knowledge Tracing (KT) models are the core technical direction—by analyzing learners’ historical answer sequences, they predict the mastery level of knowledge points and further recommend suitable exercises.

As a pioneering model, Deep Knowledge Tracing (DKT) uses an LSTM network to capture the temporal dependence of answering behaviors, realizing end-to-end prediction of knowledge states for the first time [21]. The Dynamic Key-Value Memory Network (DKVMN) adopts a dual-matrix design of “static key matrix (storing knowledge points)—dynamic value matrix (storing mastery levels)”, solving the defect that DKT cannot accurately locate the mastery status of specific knowledge points. It achieved an answer prediction accuracy of 75% on the Algebra 2006 dataset [12].

To further improve model performance, researchers have optimized from multiple dimensions. Nie Tingyu et al. [22] proposed a dual-path attention mechanism model, which learns feature weights through a factorization machine and focuses on key knowledge points by combining a squeeze-and-excitation attention network, increasing the recommendation accuracy to 78%. Zhuge Bin et al. [23] integrated cognitive diagnosis with a deep bilinear factorization machine to construct an enhanced Q-matrix (knowledge point-exercise correlation matrix), realizing accurate matching between “knowledge mastery level and exercise difficulty”. Long et al. [24] proposed the Collaborative Knowledge Tracing (CoKT) model, which uses answer sequences of similar learners to assist prediction, alleviating the data sparsity problem. Xu et al. [25] optimized cognitive representation through dynamic programming, improving the stability of the CRDP-KT model by 15% on the Statics2011 dataset.

However, existing deep learning methods still have limitations in three aspects. First, there is a lack of knowledge forgetting modeling. Most models only update knowledge states based on answer results, ignoring the natural decay law of knowledge over time—experiments show that the prediction error of models that do not consider forgetting exceeds 30% for knowledge states after 7 days. Second, the cold-start problem is prominent—when a new user has fewer than 5 answer records, the accuracy of models such as DKVMN drops below 50%, which is difficult to meet the needs of new platform users. Third, there is insufficient recommendation diversity. Most models focus on “accurate matching”, resulting in a knowledge point repetition rate of up to 45% for recommended exercises, which cannot cover learners’ knowledge gaps. In addition, although some models (e.g., QIKT [26]) have realized problem-level fine-grained modeling, they lack an optimization mechanism for global knowledge coverage, leading to insufficient knowledge breadth of recommendation results.

By synthesizing the analysis of the above four types of methods, existing research on personalized exercise recommendation still faces three core challenges. First, there is a disconnect between educational cognitive laws and model design. Most methods do not integrate educational psychology theories such as memory forgetting and differences in knowledge mastery speed, resulting in a mismatch between recommendation results and learners’ actual cognitive processes. Second, the cold-start and data sparsity problems persist—the recommendation accuracy for new users and less popular exercises is still significantly lower than that for existing users. Third, it is difficult to balance accuracy and diversity: some methods pursue accuracy but lead to repeated knowledge points, while others pursue diversity but sacrifice adaptability.

The DMMA proposed in this study aims to address the above challenges. Specifically, it solves the “disconnect from cognitive laws” by integrating the Ebbinghaus forgetting curve, addresses the “cold-start” problem through Sigmoid-weighted similarity calculation, and resolves the “balance between accuracy and diversity” via a collaborative framework of “filter-genetic algorithm”. Compared with existing work, the innovation of DMMA is not a single technical improvement, but the construction of an integrated framework of “cognitive theory–model architecture–recommendation strategy”, providing a new reference for bridging “dynamic knowledge tracing” and “educational practice needs”.

3. Preliminaries

3.1. Dynamic Key-Value Memory Neural Network

The Dynamic Key-Value Memory Neural Network (DKVMN) model is a deep knowledge tracing (DKT) model aimed at addressing challenges in Knowledge Tracing (KT) tasks [22]. The goal of KT is to track students’ knowledge states across multiple concepts based on their performance in learning activities. Traditional KT methods, such as Bayesian Knowledge Tracing (BKT) and Deep Knowledge Tracing, either model each predefined concept separately or fail to precisely identify concepts where students excel or struggle. The DKVMN model overcomes these limitations by leveraging relationships between concepts to directly output students’ mastery levels for each concept.

The core idea of DKVMN involves using a static matrix (key) to store knowledge concepts and a dynamic matrix (value) to store and update mastery levels of corresponding concepts. This design differs from standard memory-augmented neural networks, which typically use a single memory matrix or two static matrices. In DKVMN, the static matrix remains fixed during exercises, while the dynamic matrix acts like a dictionary that updates based on input and feedback.

DKVMN comprises three main components: 1. Relevance Weight Calculation: Input exercises are converted into continuous embedding vectors via an embedding matrix. The inner product between each vector and concept representations is computed, and weights are derived using a softmax activation function. 2. Reading Process: These weights retrieve content from the dynamic matrix, serving as a metric of student mastery. 3. Writing Process: Based on answer correctness, the dynamic matrix is updated through erase and add operations.

3.2. Knowledge Graph

Knowledge Graphs (KGs) represent a crucial knowledge representation method in artificial intelligence. They describe entities and their interrelationships through graph structures, providing an effective approach for machines to understand and reason with knowledge.

The core concept of knowledge graphs lies in their structured knowledge representation approach, where entities serve as nodes and relationships between entities act as edges, forming a complex knowledge network. This representation method clearly expresses semantic associations between entities and supports knowledge querying, reasoning, and discovery [27]. Key technologies for constructing knowledge graphs include knowledge extraction, knowledge fusion, and knowledge reasoning. Knowledge extraction—the process of automatically identifying and extracting entities, relationships, and attributes from unstructured or semi-structured data—forms the foundation of knowledge graph construction. Knowledge fusion integrates knowledge from diverse sources to eliminate redundancy and conflicts, thereby enhancing the quality and consistency of knowledge graphs. Knowledge reasoning utilizes existing knowledge and inference rules to derive new knowledge, extending and refining the knowledge graph. Knowledge Representation Learning (KRL) serves as another critical technique that maps entities and relationships within knowledge graphs into low-dimensional vector spaces, enabling the application of knowledge graphs to various machine learning tasks.

Knowledge graphs demonstrate extensive application value across multiple domains. For instance, in the education field, knowledge graphs can be applied to knowledge tracing, enabling the assessment of students’ mastery levels of knowledge points by tracking their learning histories and predicting their future academic performance. In recommendation systems, knowledge graphs facilitate the discovery of underlying connections between users and items, thereby delivering more personalized and precise recommendations [28,29]. Within the healthcare domain, medical knowledge graphs can be constructed to integrate disease, symptom, and drug information, assisting physicians in diagnosis and treatment [30]. In the cybersecurity field, Cybersecurity Knowledge Graphs (CKG) empower the analysis of attack incidents and the tracing of threat actor organizations, providing traceability for cyber attacks.

Consider a dataset where entities are denoted as $\epsilon$ and relations as R. A typical knowledge graph can be represented by a set of triplets (h, r, t), where $h\in \epsilon$ denotes the head entity, $t\in \epsilon$ denotes the tail entity, and $r\in R$ denotes the relationship between the head entity h and the tail entity t. The TransE model conceptualizes the relationship between the head and tail entities as a translation from the head to the tail entity. Mathematically, the relationship is represented as follows:

$$h+r\approx t$$

(1)

where $h,r,t\in R^k$, respectively representing the embedding vector representations of the head entity, relation, and tail entity. k denotes the dimensionality of the embedding vectors. The scoring function used to evaluate the plausibility of a triplet (h, r, t) is defined as follows:

$$f_h(r,t)=-{‖h+r-t‖}_2$$

(2)

where ${\Vert \Vert }_2$ denotes the $L_2$ norm. A higher score of $f_h(r,h)$ indicates greater plausibility of the triplet (h, r, t). The loss function for TransE training is

$$L={\displaystyle \sum _{(h,r,t)\in S}{\displaystyle \sum _{(h^{\prime },r,t^{\prime })}{[\gamma -f_r(h,t)+f_r(h^{\prime },t^{\prime })]}_{+}}}$$

(3)

where ${[x]}_{+}$ represents the positive part of x, $\gamma >0$ is a margin hyper parameter, $h^{\prime }$ denotes the corrupted head entity, and $t^{\prime }$ denotes the corrupted tail entity, often used as negative samples during training.

In the field of education, knowledge graphs can be used to represent relationships between exercises and knowledge concepts. For example, a mathematics knowledge graph may include knowledge concepts such as “addition,” “multiplication,” and “algebra,” along with various exercise problems. The relationships between exercises and knowledge concepts can be represented using triplets, such as the following:

(Exercise 1, “tests knowledge point”, addition);

(Exercise 2, “tests knowledge point”, multiplication);

(Exercise 3, “tests knowledge point”, algebra).

These triplets illustrate the correspondence between exercises and knowledge concepts and can be applied to knowledge tracing and personalized recommendations. By analyzing student performance on different exercises, their mastery levels of relevant knowledge concepts can be inferred, therefore enabling the recommendation of more suitable exercises.

3.3. Forgetting Rate of Knowledge Concepts

The Ebbinghaus Forgetting Curve (EFC) describes the decay pattern of human memory over time and is a classical theory in memory research. German psychologist Hermann Ebbinghaus discovered through experiments that forgetting of newly learned information is not a linear process; instead, the rate of forgetting is rapid initially and gradually slows down later14. Understanding this curve helps optimize practice recommendation strategies to enhance memory efficiency.

The Ebbinghaus Forgetting Curve can be mathematically described. Although multiple functions may fit the curve, its fundamental form reflects an exponential decay trend of memory over time. It can be represented by the following formula:

$$R=e^{-{\displaystyle \frac{t}{s}}}$$

(4)

where R represents memory retention rate, t denotes time, and s indicates the memory stability coefficient. This formula demonstrates that memory retention decreases over time, with the decay rate determined by the memory stability coefficient.

According to the Ebbinghaus Forgetting Curve, the initial period after learning exhibits the most rapid memory decline. Within approximately 20 min to 60 min after learning, nearly half of the content is forgotten, after which the forgetting rate slows down with the statistical pattern shown in Figure 1. To counteract forgetting, reviewing at critical time points is essential for memory consolidation. Spaced repetition learning serves as an effective strategy that schedules reviews when memory decay reaches a specific threshold based on the forgetting curve, thereby enhancing long-term retention rates [30]. This research will incorporate forgetting principles into exercise recommendations to improve the efficacy of practice scheduling.

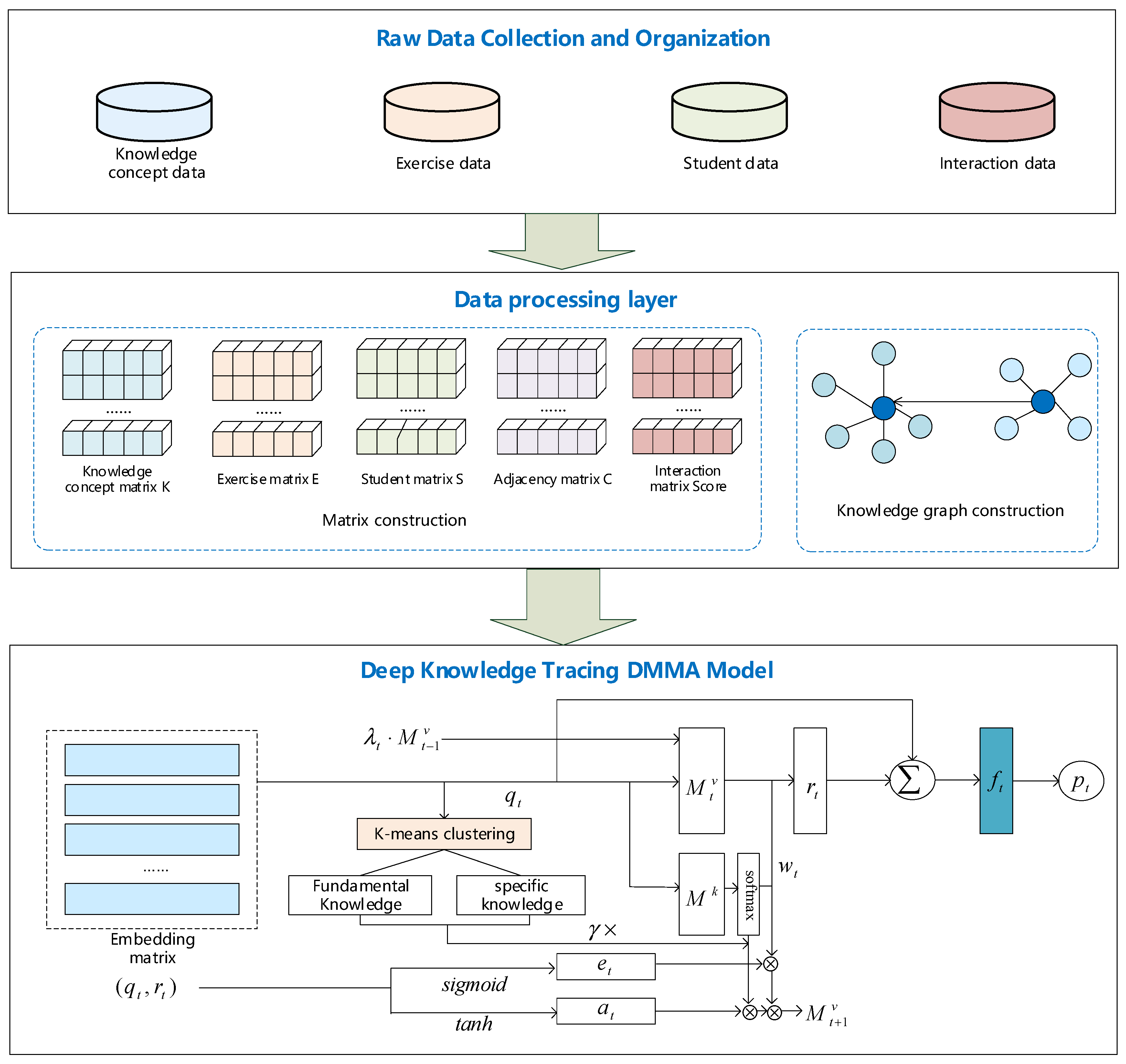
4. Model Construction

We propose a Dynamic Multi-dimensional Memory Augmentation (DMMA) model that processes knowledge concept data, exercise data, student profiles, and interactive response data to construct corresponding data and knowledge graphs. Built upon this foundation, the DMMA first employs K-means clustering to categorize knowledge concepts into general concepts and specific concepts. Integrating Ebbinghaus’ principles of memory retention and forgetting, the model incorporates a temporal decay factor ${\lambda }_t$ and a knowledge mastery velocity factor $\gamma$ to dynamically adjust the intensity of knowledge mastery updates. Utilizing the predicted knowledge mastery level $P_t$ and knowledge coverage prediction $P_c$, the model establishes an exercise selector. This exercise filter selects appropriate practice sets by evaluating both the similarity between exercises and students’ current knowledge mastery, and whether exercise difficulty aligns with expected levels. To further enhance recommendation diversity, a genetic algorithm is employed to optimize the selection process, ensuring the chosen exercise set achieves maximum variety. The workflow is visualized in Figure 2 and Figure 3 and detailed in Algorithms 1 and 2.

4.1. Definitions

This study involves students, knowledge concepts, exercises, a knowledge concept-exercise association matrix, and a student-exercise interaction matrix. Each matrix is defined as follows:

Definition 1.

The student matrix is denoted as $S=\{s_1,s_2,s_3,\dots s_{S_n}\}$, $S\in R^{n\times m}$, where $S_n$represents the number of students and m denotes the number of student features.

Definition 2.

The knowledge concept matrix is denoted as $K=\{k_1,k_2,k_3,\dots k_{K_n}\}$, where $K_n$indicates the total number of knowledge concepts, and $k_{K_n}$represents the $K_n$ knowledge concept.

Definition 3.

The exercise matrix is denoted as $E=\{e_1,e_2,e_3,\dots e_{E_n}\}$, where $E_n$ specifies the total number of exercises, and $e_{E_n}$ denotes the n-th exercise.

Definition 4.

The exercise-knowledge concept association matrix $C={\left\{c_{\mathrm{ij}}\right\}}_{i=1\dots E_n}^{j=1\dots K_n}$ is defined such that each element $c_{\mathrm{ij}}$ indicates whether a connection exists between the i-th exercise and the j-th knowledge concept:$c_{\mathrm{ij}}$= 1 if connected, otherwise 0.

Definition 5.

The student-exercise interaction matrix $Score={\left\{scor{e}_{\mathrm{ij}}\right\}}_{i=1\dots S_n}^{j=1\dots E_n}$ is defined with each element $scor{e}_{ij}$ representing the interaction score between the i-th student and the j-th exercise.

4.2. Knowledge Concept Mastery Prediction

Hermann Ebbinghaus’ research demonstrates that knowledge retention declines over time. As depicted in Figure 1, the retention rate falls to approximately 33% after 24 h and further drops to 28% after 48 h post-learning. Incorporating a forgetting factor into knowledge tracing and cognitive diagnosis can significantly enhance the efficacy of knowledge tracking. The exponential function exhibits optimal fitting performance when modeling such decay and is widely recognized as the most suitable function for approximating the forgetting curve. To precisely capture the temporal evolution of students’ knowledge, we employ the exponential function to quantify the forgetting rate of knowledge concepts. The time decay factor is mathematically defined based on the forgetting curve function as below

$${\lambda }_t=e^{-{\displaystyle \frac{t\prime -t}{s}}}$$

(5)

where t′ denotes current time, t represents the time point of knowledge acquisition, and s indicates the memory stability coefficient reflecting individual differences.

Inspired by the dynamic DKVMN (Key-Value Memory Network), this work introduces a temporal decay factor ${\lambda }_t$ and a knowledge concept mastery velocity factor $\gamma$ to dynamically adjust the update intensity of knowledge concept mastery. We propose a Dynamic Multidimensional Memory Augmentation (DMMA) mechanism for knowledge concept mastery prediction, where prediction accuracy directly determines the efficacy of personalized exercise recommendations and user experience.

First, the k-means method clusters knowledge concepts into two categories: universal foundational knowledge (e.g., basic concepts) and domain-specific knowledge (e.g., advanced skills). These approaches address traditional DKVMN’s limitations in modeling long-term dependencies.

The temporal decay factor ${\lambda }_t$ controls knowledge state forgetting speed. Within DKVMN, it dynamically controls the update process of the dynamic matrix to simulate natural knowledge decay. The update formula is as follows:

$$M_t^v(i)={\lambda }_t\cdot M_{t-1}^v(i)+(1-{\lambda }_t)\cdot {\tilde{M}}_t^v(i)$$

(6)

where ${\tilde{M}}_t^v$ represents the temporary memory state after accounting for erasure and addition operations.

Integrate the knowledge mastery speed factor $\gamma$ into the retrieval and storage processes of knowledge concepts to modulate the magnitude of knowledge state updates. The formula is defined as follows:

$$r_t=\gamma \cdot {\displaystyle \sum _{i=1}^N{w}_t(i)M_t^v(i)}$$

(7)

$r_t$ is a value read from the dynamic matrix, with $\gamma$ adjusting the intensity of matrix reading. $w_t$ represents the weight value of the “memory slot”.

The writing process proceeds as follows:

$${\tilde{M}}_t^v(i)=M_{t-1}^v(i)[1-w_t(i)e_t]$$

(8)

$$a_t=\gamma \cdot Tanh(D^t{v}_t+b_a)$$

(9)

$$M_t^v={\lambda }_t\cdot M_{t-1}^v(i)+(1-{\lambda }_t)\cdot ({\tilde{M}}_t^v(i)+w_t(i)a_t)$$

(10)

where $a_t$ is a row vector for updating each memory slot, $b_a$ represents a bias vector, $D^t$ denotes a transformation matrix, and $v_t$ signifies the knowledge growth vector generated when a student completes an exercise.

4.3. Knowledge Concept Coverage Prediction

Using the occurrence sequence of knowledge concepts from time 0 to t, the Random Forest algorithm predicts the occurrence probability of each knowledge concept at time t + 1. The core principle of the model involves inputting students’ historical learning data, constructing multiple decision trees where each tree independently learns patterns, and ultimately aggregating predictions from all trees to determine the probability of knowledge concepts appearing at time t + 1.

The model’s input consists of students’ historical exercise data, including exercise timestamps; knowledge point labels; and correctness. These knowledge concept sequences are transformed into feature vectors $K=\{k_0,k_1,k_2\dots k_t\}$ (where 0 to t represents the time indices). Simultaneously, knowledge point labels are converted into numerical labels y to enable model processing.

The Random Forest model operates by constructing multiple decision trees. During training, each tree randomly selects features and samples for node splitting, thereby learning underlying data patterns. The model outputs a probability vector $P_c=[c(k_1),c(k_2),\dots c(k_t)]$ whose length equals the number of knowledge points in the curriculum. Each element $c(k_i)$ in this vector represents the occurrence probability of the corresponding knowledge point at time t + 1.

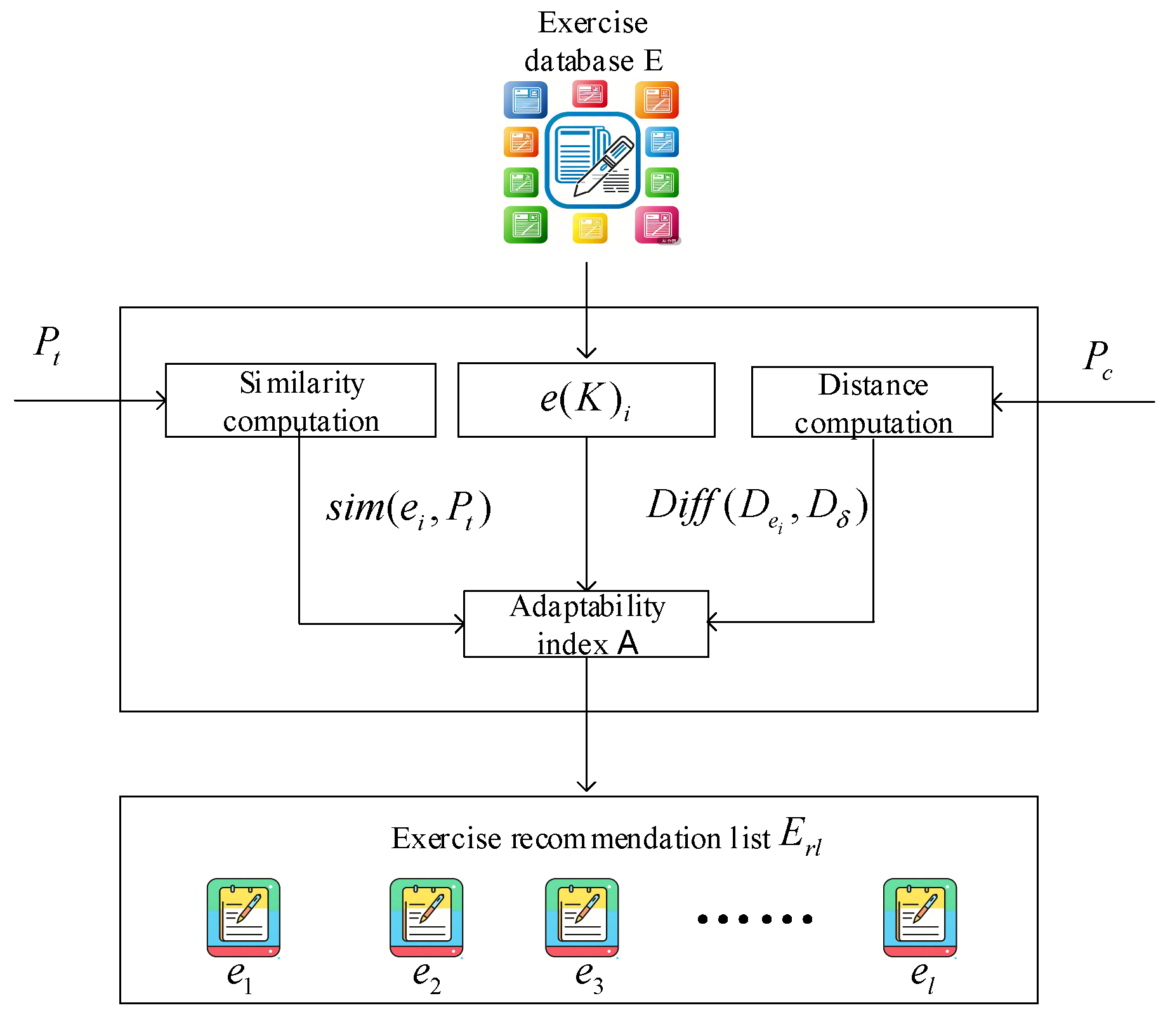
4.4. Exercise Recommendation Filter

Based on the predicted knowledge mastery level $P_t$ and knowledge coverage prediction $P_c$, an exercise filter is constructed. This filter selects appropriate exercises by evaluating two criteria: (1) the similarity between an exercise’s knowledge requirements and the student’s current mastery state, and (2) whether the exercise’s difficulty aligns with the expected level. This approach ensures that the selected exercises comprehensively cover knowledge concepts requiring reinforcement while maintaining appropriate difficulty, thereby enhancing the effectiveness of practice activities.

Calculate the similarity sim between exercise $e_i$ and the predicted knowledge mastery $P_t$. The similarity sim can be computed via the following formula:

$$sim(e_i,P_t)={\displaystyle \frac{e_i\cdot P_t}{\left|e_i\right|\cdot \left|P_t\right|}}$$

(11)

Calculate the discrepancy metric between the actual difficulty $D_{e_i}$ of exercise $e_i$ and its expected difficulty $D_{\sigma }$, using the following formula:

$$Diff(D_{e_i},D_{\sigma })=\left|D_{e_i}-D_{\sigma }\right|$$

(12)

Combining the aforementioned similarity $sim(e_i,P_t)$ and difficulty differential $Diff(D_{e_i},D_{\sigma })$ metrics, the adaptability index $A_i$ for exercise selection is derived as follows:

$$A_i=\mathit{sim}(e_i,P_t)+Diff(D_{e_i},D_{\delta })$$

(13)

Exercises are ranked according to their adaptive score $A_i$, with the highest-scoring set selected as the final output. This set is deemed most likely to enhance students’ knowledge mastery probability while satisfying predetermined knowledge point coverage requirements. The algorithm and schematic diagram of the selection module are depicted in Figure 3.

The exercise filter algorithm is described as follows:

Algorithm 1 Exercise Filtering Algorithm Description

input: Exercise database E, Knowledge Concept Mastery Prediction $P_t$, Knowledge Concept Coverage Prediction $P_c$ output: Exercise recommendation list $\{e_1,e_2,\dots ,e_l\}$ for i = 0 to $\left|E\right|$ − 1 $e_i$ selected from $E=\{e_1,e_2,\dots e_n\}$ $sim(e_i,P_t)$ = cosine similarity $Diff(D_{e_i},D_{\sigma })=\left|D_{e_i}-D_{\sigma }\right|$ $A_i=\mathit{sim}(e_i,P_t)+Diff(D_{e_i},D_{\delta })$ $E_{rl}\leftarrow \mathrm{sort}(e_1,e_2,\dots ,e_L)$ Return $E_{rl}$

4.5. Diversified Exercise Selection

After selecting the top L exercises $E_{rl}$ closest to the student’s desired difficulty level, exercises within $E_{rl}$ are combined and optimized using a genetic algorithm to select the set with maximal diversity. This process can be conceptualized as a function optimization problem with multivariate constraints.

In the diversified exercise selection algorithm, the model learns representation vectors of distinct knowledge concepts and computes cosine distances. The greater the directional difference between two exercises in the conceptual space, the less redundant their coverage of knowledge points. By averaging all pairwise distances within a set, a higher value indicates lower overall redundancy and greater complementarity between exercises, enabling students to engage with richer knowledge points during practice—thus achieving higher “diversity.” The diversity metric for exercise set $E_{\mathrm{rl}}^{\prime }\subset E_{\mathrm{rl}}$ is defined as the average cosine distance of all pairwise concept vectors:

$$Div(E_{rl})={\displaystyle \frac{2}{k(k-1)}}{\displaystyle \sum _{e_i,e_j\in E_{rl}^{\prime }}(1-\cos (v_i,v_j))}$$

(14)

$$cos(v_i,v_j)={\displaystyle \frac{v_i^T{v}_j}{‖v_i‖‖v_j‖}}\in [1,-1]$$

(15)

Therefore, the optimization problem can be formulated as follows:

$$E^{*}=\underset{E_{\mathrm{rl}}^{\prime }\subset E_{rl}}{\max }Div(E_{rl}^{\prime })$$

(16)

Algorithm 2 Diverse Exercise Selection Algorithm Description

Input: $E_{rl}$, $v_i$, k, pop_size, max_gen, pc pm #The above parameters means: Filtered exercise list, Embedding vector representing the exercise, Number of exercises to be selected, Population size, Maximum number of iterations, Crossover probability, Mutation probability Output: $E^{*}$ #Exercises with diversity #Calculate Exercise Diversity Metrics $Div=Div(E_{rl})$ #Compute using the diversity metrics formula. #Initialize population P P = Initialize population(pop_size, n′, k) #n′ denotes the individual length in the population #Main loop of genetic algorithm for gen in range(max_gen): Q = Tournament selection (P, Div) #Prioritizes retaining high-diversity individuals Q =Two-point crossover (Q, pc) #Ensures exactly k ones in individuals post-crossover Q =Swap mutation (Q, pm) P = Q #Determine the optimal exercise subset best_individual = Select the individual with highest fitness (P) $E^{*}$ = Determine the optimal exercise subset based on best_individual return $E^{*}$

5. Experimental Setup

5.1. Datasets

The experiments utilized three publicly available online learning datasets containing exercise interactions: Algebra 2006–2007 [31], Assistments 2017 [32], and Statics2011 [33]. During data preprocessing, duplicate records and students failing to meet criteria were removed to enhance dataset accuracy and usability. Detailed descriptions of the datasets are as follows:

The Algebra 2006–2007 dataset is a widely used public dataset in educational data mining, primarily recording middle school students’ learning behaviors in online algebra courses. It contains complete learning records from 575 students, covering 8 core algebra modules (e.g., linear equations, inequalities, function graphs) subdivided into 112 specific knowledge components. The system includes 2710 exercises encompassing multiple formats such as multiple-choice, fill-in-the-blank, and step-based solution input questions. The dataset comprises 809,694 student-system interaction records, including answer logs, knowledge component browsing, and tool usage behaviors. Among these, 187,432 duplicated interaction records (i.e., repeated attempts by the same student on identical questions or knowledge components) were identified. The data spans the full academic year from September 2006 to June 2007. Stored in KDD Cup 2010 standard format, raw data fields include timestamps, student IDs, question IDs, knowledge component codes, answer results (correct/incorrect), and response times.

The Assistments 2017 dataset compiles behavioral data from 4217 middle school students completing mathematics training on the Assistments platform during the 2016–2017 academic year, covering cross-grade samples from Grades 6 to 9. Its knowledge system encompasses core algebra and geometry content from Grades 6–9, annotated by educational experts to form 189 fine-grained knowledge components. The platform contains 3891 standardized mathematics questions, all mapped to knowledge components via cognitive diagnosis models in a many-to-many relationship. The system recorded 2,143,765 valid interaction logs throughout the year, with each entry containing 21 structured fields: student ID, question ID, response timestamp, response duration (millisecond precision), raw answer records (including step-by-step solutions), and system feedback types.

The Statics 2011 dataset serves as a key empirical resource in engineering education research, tracking learning processes in undergraduate statics courses. Collected from Purdue University’s Fall 2011 statics course, it comprehensively records learning behaviors of 166 engineering undergraduates. The knowledge system comprises 23 core statics concepts, including force system analysis, free-body diagram construction, and moment calculations. The online learning system offers 1102 statics exercises, featuring interactive formats such as calculation problems, conceptual multiple-choice questions, and force analysis tasks. Throughout the semester, the system captured 48,607 detailed learning interaction records, each containing 15 dimensions of structured data: student ID, question ID, response timestamp, response duration, solution steps, and final correctness judgment.

5.2. Parameter Settings

To ensure the stability of model training and optimal recommendation performance, this study optimizes the hyperparameters of the genetic algorithm and neural network training parameters through grid search on the validation set. The datasets are divided into training, validation, and test sets in a 7:2:1 ratio. The model achieves optimal performance with the following hyperparameters.

(1)

For the DMMA, the core neural network components, including the DKVMN and knowledge graph embedding layer, are implemented based on the PyTorch 2.0 framework. The base training parameters are set as follows: training epochs = 80, batch_size = 64 for the Algebra 2006–2007 dataset (due to its large volume) and 32 for the Assistments 2017 and Statics 2011 datasets (for training stability). The optimizer is Adam with a learning rate of 1 × 10⁻³. The DKVMN parameters include memory slot count key_size of 112, 189, and 23, corresponding to the number of knowledge points in the Algebra 2006–2007, Assistments 2017, and Statics 2011 datasets, respectively. The embedding dimension (embed_dim) is 64, the hidden layer dimension (hidden_dim) is 128, and the time decay factor (s) is 0.85. The knowledge graph embedding parameters include an embedding dimension (k) of 64, with TransE training epochs reaching optimal performance at 100.

(2)

For the genetic algorithm hyperparameters, the settings are as follows: population size pop_size = {40, 60, 80}, maximum iterations max_gen = {25, 30}, crossover probability pc = {0.6, 0.8, 0.9} and mutation probability pm = {0.01, 0.03, 0.05}. To balance search efficiency and solution space coverage, a population size (pm) below 40 tends to fall into local optima, while exceeding 80 significantly increases training time, with 60 being the optimal value on the validation set. Maximum iterations (max_gen) of 30 ensure convergence of diversity metrics and stable global optima. A crossover probability (pc) below 0.6 leads to low efficiency, while above 0.9 risks disrupting high-quality individuals, with 0.8 achieving the best balance. A mutation probability(pm) of 0.03 enables local fine-tuning and global optimization. After grid search, the optimal hyperparameter combination is determined as follows: {pop_size = 60, max_gen = 30, pc = 0.8, pm = 0.03}.

5.3. Evaluation Metrics

Three evaluation metrics—accuracy, diversity, and novelty—were employed to assess the performance of the proposed exercise recommendation model against baseline models. The calculation methods are specified below:

①

Accuracy Metric

Accuracy metric [30,34] evaluates whether the difficulty of recommended exercises aligns with student expectations. Higher accuracy values indicate better alignment between recommended exercises and student needs, quantified by the gap between expected and actual exercise difficulty. Larger accuracy values signify closer matches to student expectations. The accuracy metric is calculated as follows:

$$Acuracy=(1-{\displaystyle \frac{{\displaystyle \sum _{j=0}^l\left|e-R{ec}_j\right|}}{l}})\times 100\%$$

(17)

where j denotes the index of the recommended exercise, l represents the length of the recommendation list, e signifies the student’s desire for the exercise, and $Re{c}_j$ indicates the probability that the student answers the j-th recommended exercise correctly.

②

Diversity Indicator

The diversity indicator quantifies variability by calculating the cosine similarity between knowledge concepts across exercises in the recommendation list. Lower cosine similarity reflects greater conceptual divergence among exercises, corresponding to higher diversity. First, we compute the cosine similarity of knowledge concepts for each exercise pair in the recommendation list. Then, the dissimilarity is derived by subtracting the cosine similarity from 1. Finally, the diversity value is obtained by averaging the sum of dissimilarity across all exercise pairs. The diversity metric is formally defined as follows:

$$Diversity={\displaystyle \frac{{\displaystyle \sum _{j=1,k=1,j\ne k}^{l}1-Sim(e_j,e_k)}}{l}}$$

(18)

where $e_j$ and $e_k$ denote distinct exercises, Sim represents cosine similarity calculation, and l indicates the total number of recommended exercises. The diversity metric quantifies the breadth of knowledge coverage in exercise recommendation algorithms, serving to evaluate both user experience and learning effectiveness.

③

Novelty Metric

The novelty metric [32] measures the innovative degree of recommended exercises, assessing the system’s capability to provide students with challenging new content. Higher novelty values occur when recommended problems contain knowledge concepts the student has never attempted or previously answered incorrectly. Jaccard similarity coefficient [33] is adopted to measure similarity differences in finite sample sets, where larger coefficient values indicate higher sample similarity. The novelty metric is formally defined as follows:

$$Novelty={\displaystyle \frac{{\displaystyle \sum _{j=1}^{l}1-JacSim(e_j,a_j)}}{l}}$$

(19)

where $e_j$ represents the j-th knowledge concept, $a_j$ indicates whether this j-th knowledge concept has been correctly mastered—recorded as 1 for correct answers and 0 for incorrect or unattempted responses, l denotes the total number of recommended exercises, and the $JacSim$ function computes the Jaccard similarity coefficient.

5.4. Comparative Methods

To validate the effectiveness of the proposed model, five advanced recommendation models were selected as baseline algorithms:

CRDP-KT (Cognitive Representation Dynamic Programming-based Knowledge Tracing) [26]: Utilizes dynamic programming to optimize cognitive representations based on problem difficulty and performance intervals, ensuring alignment with students’ cognitive patterns and minimizing distortion in cognitive state simulation.

QIKT (Question-centered Interpretable Knowledge Tracing) [27]: Models fine-grained knowledge state changes via problem-centered knowledge acquisition and problem-solving modules.

CoKT (Collaborative Knowledge Tracing) [28]: Leverages peer information (e.g., accuracy rates of students with similar answering histories) by retrieving sequences of analogous interactions.

IEKT (Individual Estimation Knowledge Tracing) [29]: Focuses on learner heterogeneity by estimating students’ cognition of problems before prediction and assessing knowledge acquisition sensitivity before updating knowledge states.

DKVMN (Dynamic Key-Value Memory Network) [12]: Uses static key matrices to store knowledge concepts and dynamic value matrices to track mastery levels, directly outputting concept proficiency via memory-augmented neural networks.

DMMA-NoTM: The Dynamic Multi-dimensional Memory Augmented knowledge tracking model (DMMA) removes the Time decay factor and knowledge Mastery progression.

DMMA-NoGA: The Dynamic Multi-dimensional Memory Augmented knowledge tracking model (DMMA) removes the Genetic Algorithm.

DMMA: The exercise recommendation algorithm proposed in this study (detailed in Section 3).

5.5. Experimental Comparative Analysis

Based on the aforementioned five algorithms, we conducted in-depth comparative experiments and performed a comprehensive, detailed comparative analysis of these five models against the proposed DMMA across three metrics: Accuracy, Diversity, and Novelty.

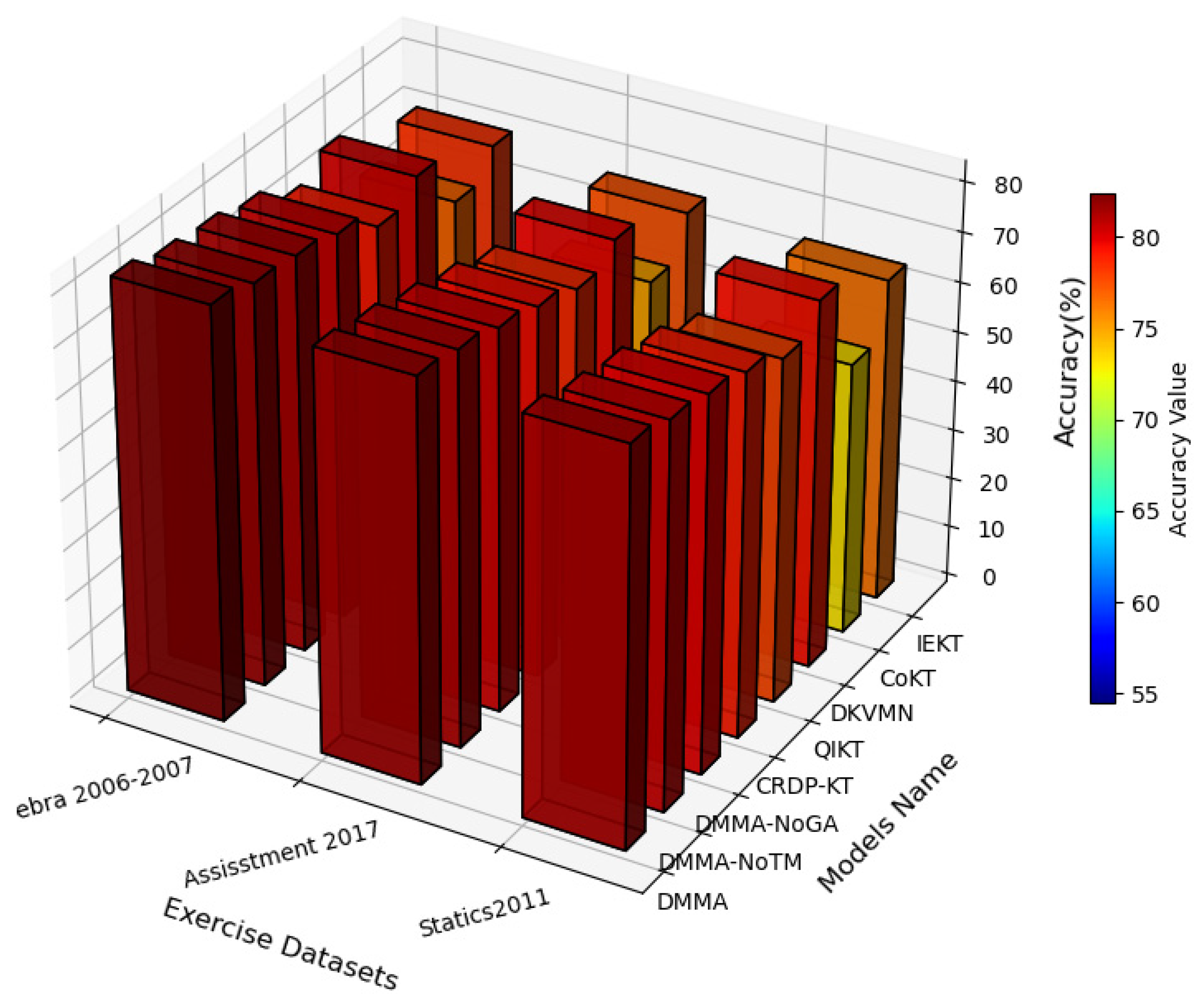
As shown in Figure 4, the DMMA demonstrates significantly superior accuracy across all three datasets compared to other models, achieving a maximum of 82% and a minimum of 79%, with an average improvement of 6% over the second-best performer CRDP-KT. This advantage stems from its integration of a dynamic multi-dimensional memory mechanism with the Ebbinghaus forgetting curve. By dynamically adjusting learning intensity through time decay factors and knowledge concept mastery speed factors, it effectively addresses the limitations of traditional models in modeling long-term dependencies. The ablation study demonstrates that on the Algebra 2006–2007 datasets, the accuracy of DMMA-NoTM (without temporal decay) and DMMA-NoGA (without genetic algorithm) is 2.2% and 3.1% lower than that of DMMA, respectively. However, all three algorithms—DMMA, DMMA-NoTM, and DMMA-NoGA—consistently outperform all other baseline methods. Similar performance trends were also observed on the other two datasets. In contrast, the collaborative model CoKT performs the weakest (minimum 54%), as it relies on inter-student similarity information while failing to adequately model individual cognitive differences. Both DKVMN and CRDP-KT, as classical deep learning methods, demonstrate stable performance but are constrained by static knowledge representation update mechanisms. This limitation is particularly evident in the Statics2011 dataset, highlighting DMMA’s adaptive advantages in complex knowledge structures.

DMMA maps entity relationships into low-dimensional space and employs genetic algorithm optimization, enabling the model to capture implicit correlations between knowledge points (e.g., cross-disciplinary concepts between algebra and statistics). Traditional models like QIKT, however, focus solely on problem-level fine-grained modeling, resulting in insufficient global knowledge coverage. Through the synergy of filters and optimizers, DMMA ensures exercises align with students’ current proficiency levels while addressing knowledge blind spots. Models such as IEKT lack such mechanisms, leading to lower accuracy on the Assisstment 2017 dataset.

Despite significant variations in knowledge domains and temporal spans across datasets (e.g., Algebra 2006–2007 contains multi-year data), DMMA’s accuracy shows no notable decline compared to its performance on other datasets, proving the robustness of its architecture against temporal noise and domain shifts. Notably, all models perform better on Assisstment 2017 than on other datasets. On this dataset, DMMA maintains its lead with an accuracy of 80%, potentially attributable to denser data annotations.

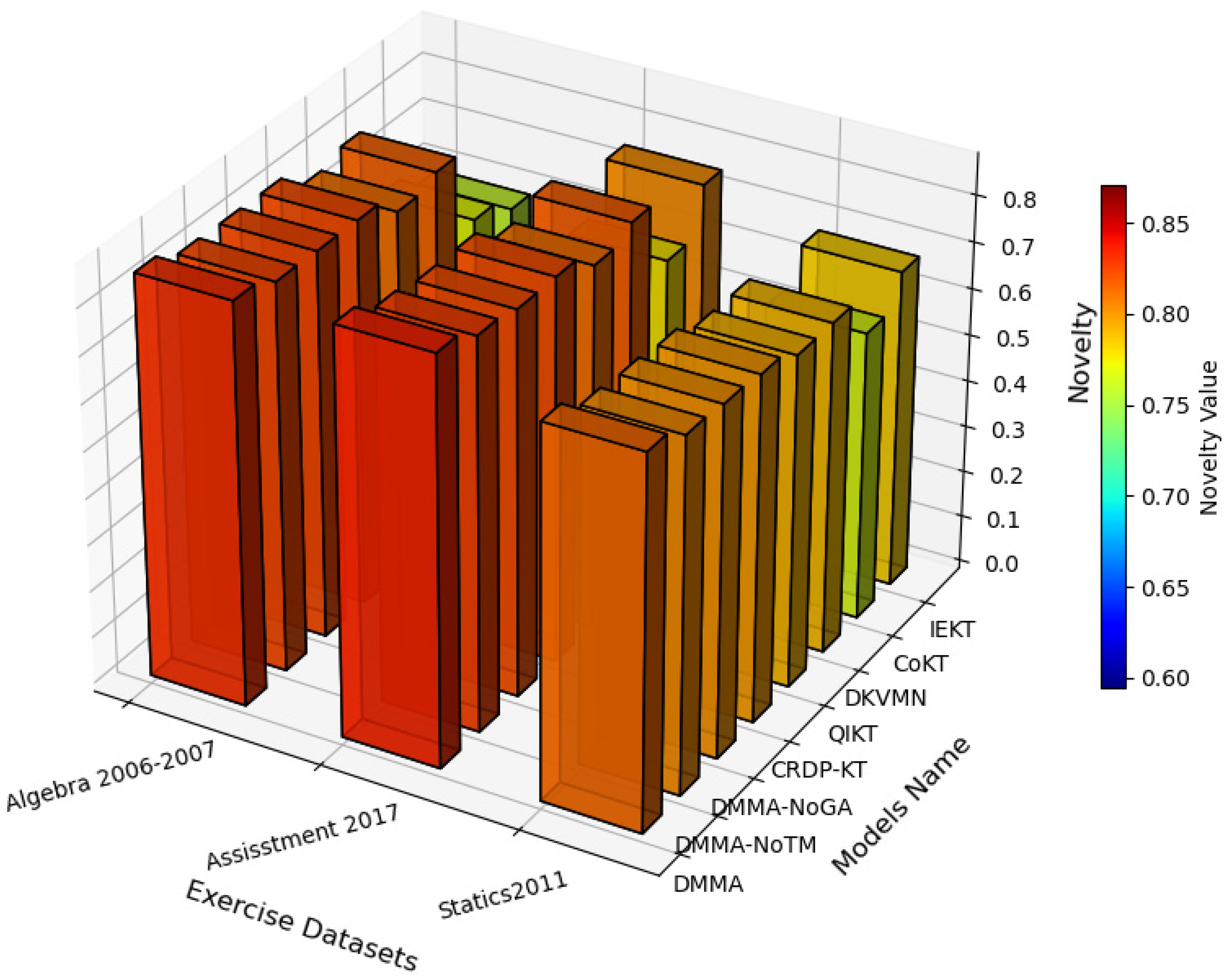
As shown in Figure 5, the DMMA demonstrates significantly superior diversity metrics across all three datasets (Algebra 2006–2007, Assisstment 2017, and Statics2011) compared to other models, achieving a maximum of 0.79 and a minimum of 0.72. This advantage stems from its innovative genetic algorithm optimization mechanism, which filters low-similarity exercises through exercise selectors and employs diversified selection algorithms to maximize knowledge coverage. The ablation experiment demonstrates that on the Algebra 2006–2007 dataset, in terms of diversity, DMMA-NoTM (without temporal decay factor and knowledge acquisition speed) and DMMA-NoGA (without genetic algorithm) show 0.02 and 0.04 lower diversity, respectively, compared to DMMA. However, all three algorithms—DMMA, DMMA-NoTM and DMMA-NoGA—achieve higher diversity than all other baseline methods. Similar patterns were observed in the other two datasets. In contrast, CoKT exhibits the lowest diversity metrics (only 0.52 on Statics2011) due to its reliance on collaborative student information while neglecting individual cognitive differences. Traditional models like CRDP-KT and DKVMN, despite adopting dynamic programming or key-value memory mechanisms, lack real-time optimization capabilities, resulting in inferior diversity performance compared to DMMA on the Algebra dataset. This highlights the inability of static update mechanisms to adapt to dynamic knowledge forgetting.

The exercise filtering and diversified selection algorithms in DMMA directly drive diversity enhancement. The incorporation of genetic algorithms further boosts diversity optimization efficiency by iteratively selecting high-diversity exercise sets, effectively balancing difficulty matching and conceptual richness. Other models like IEKT exhibit larger fluctuations in diversity metrics due to the absence of such mechanisms. The integration of the Ebbinghaus forgetting curve dynamically adjusts knowledge update intensity through time decay factors, mitigating the negative impact of abrupt forgetting and reducing diversity prediction errors. CoKT suffers from insufficient diversity due to excessive reliance on similar student sequences.

As shown in Figure 6, the DMMA outperforms the other five models in Novelty metrics across all three datasets, achieving an average improvement of 0.04 over the second-best performer CRDP-KT. The genetic algorithm-optimized exercise selector further strengthens the knowledge coverage capability of the recommendation system, resulting in an average Novelty improvement of up to 0.20 compared to the collaborative model CoKT. On the dataset’s novelty metric, similarly to the aforementioned two metrics, both DMMA-NoTM and DMMA-NoGA demonstrate lower novelty performance than DMMA, yet they still outperform all other traditional algorithms. Models like QIKT, constrained by problem-level modeling, show a Novelty gap of 0.08 on the Statics2011 dataset. Although CRDP-KT’s dynamic programming algorithm partially enhances novelty by optimizing the continuity of cognitive representations, DMMA demonstrates clearer advantages through real-time adjustment of knowledge update intensity and significantly outperforms the DKVMN model. Notably, all models perform optimally on the Assisstment 2017 dataset, yet DMMA maintains an absolute advantage, with its multi-dimensional memory architecture providing a universal solution for complex educational scenarios.

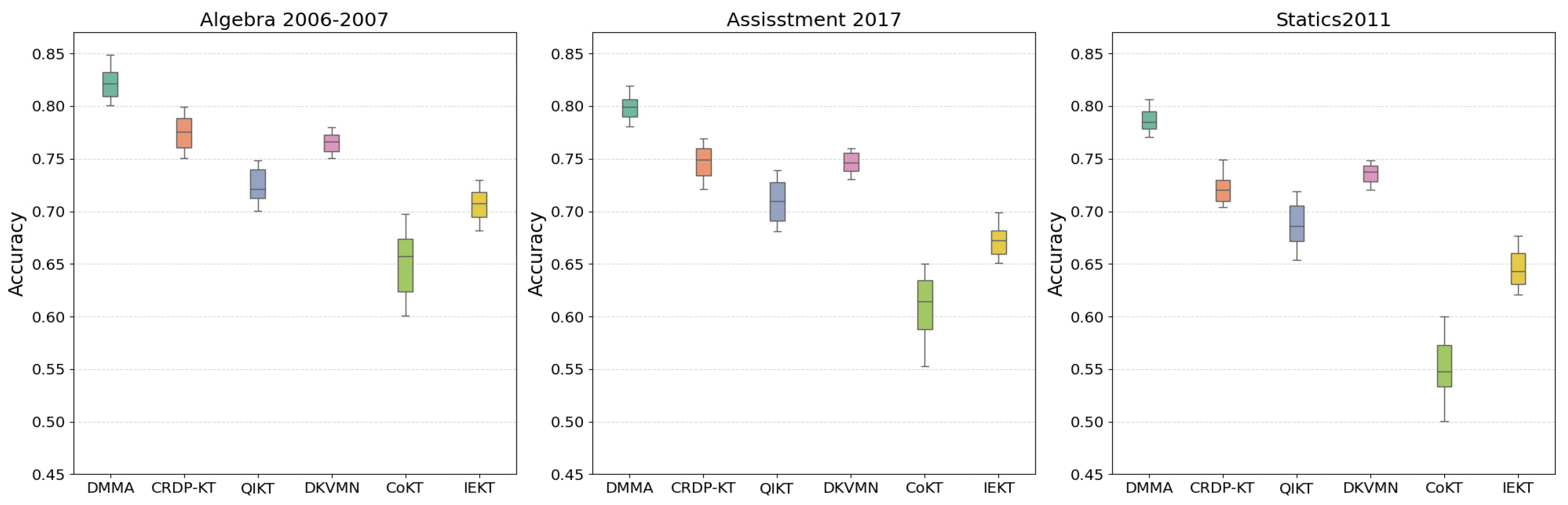
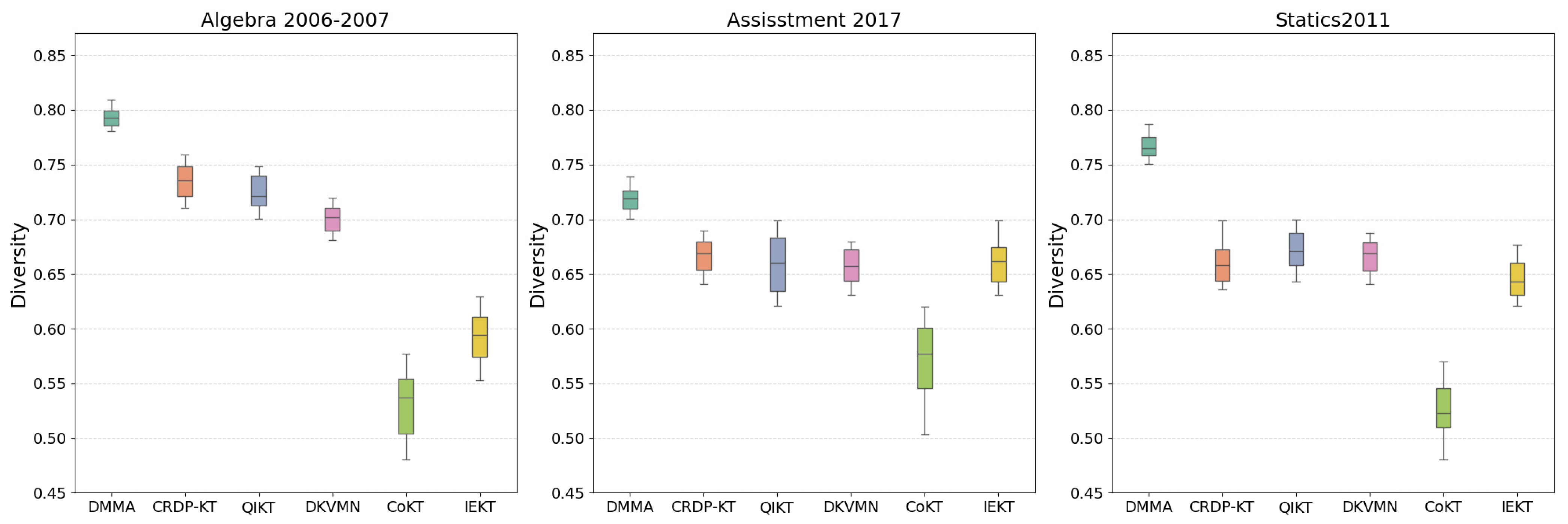
5.6. Model Stability Experiment

To evaluate the stability of the six models across three datasets, each model was run 50 times on each dataset. The results are visualized using boxplots, as shown in Figure 7, Figure 8 and Figure 9. A larger box indicates greater fluctuations, signifying lower model stability, while a smaller box demonstrates more stable and reliable performance.

As observed in Figure 7, Figure 8 and Figure 9, the DMMA demonstrates the highest stability, evidenced by its smaller box size and higher median. This indicates minimal performance fluctuations across three distinct datasets (Algebra 2006–2007, Assisstment 2017, and Statics2011), signifying strong generalization capabilities and robust feature learning. The DKVMN model also exhibits small boxes with consistently low fluctuations across multiple metrics, reflecting stable performance throughout experiments; however, its median slightly trails those of DMMA and CRDP-KT. The CRDP-KT model ranks next in stability, though its overall performance falls marginally below DMMA.

The QIKT model delivers adequate results on the Algebra 2006–2007 task but underperforms on the other two datasets, revealing noticeable instability. In contrast, both IEKT and CoKT display significant fluctuations in results, indicating high sensitivity to data variations and comparatively weaker robustness. Overall, DMMA, CRDP-KT, and DKVMN achieve the highest stability levels, while CoKT exhibits the lowest stability.

5.7. Cold Start and Data Sparsity

When new students begin exercises, extremely sparse accumulated practice records prevent effective computation of “knowledge concept mastery prediction” and “knowledge concept coverage prediction,” leading to difficulties in accurately predicting their behavior. This constitutes the user cold-start problem.

To address this issue, students are categorized into “cold-start” and ”non-cold-start” groups. By integrating answer records and students’ external attributes (e.g., learning styles, interests), this method calculates the similarity between cold-start students and existing non-cold-start students. This facilitates identifying the most similar users for cold-start students, thereby allowing them to reference behavioral patterns from these peers. Specifically, an efficient time-series similarity algorithm—FastDTW (Fast Dynamic Time Warping) [35]—is employed to compute temporal similarity. FastDTW is an accelerated algorithm for time series similarity measurement, designed to reduce the computational complexity of traditional Dynamic Time Warping (DTW). Traditional DTW has quadratic time and space complexity, which limits its application in large-scale time series. FastDTW achieves linear time and space complexity by employing a multi-level approximation approach, recursively projecting solutions from coarse resolutions and refining them; the Euclidean distance formula then calculates attribute similarity. These two metrics are combined via a weighted parameter $\sigma$ to yield the final similarity score. The calculation method is detailed below:

$$Sim=\sigma \cdot Si{m}_{FastDTW}(seq<\varphi (S_{cold})>,seq<\varphi (S)>)+(1-\sigma )\cdot Si{m}_{Euclidean}(v_{S_{cold}},v_S)$$

(20)

In the formulation, $S_{cold}$ represents a cold-start student and $S$ a non-cold-start student. $\varphi (S_{cold})$ and $\varphi (S)$ denote the one-hot encodings of exercises and knowledge concepts for cold-start and non-cold-start students, respectively. $v_{S_{cold}}$ and $v_S$ correspond to the external attribute vectors of cold-start and non-cold-start students. The weighted parameter $\sigma$ is dynamically computed by incorporating the data sequence length l, along with the weight change rate $\alpha$ and threshold $\beta$ as weight adjustment factors. This parameter achieves smooth transitions through the Sigmoid function, dynamically adapting to different user stages while preventing abrupt weight changes. Its calculation formula is as follows:

$$\sigma ={\displaystyle \frac{1}{1+e^{-\alpha (L-\beta )}}}$$

(21)

If the initial sequence length L = 5 (below the threshold β = 10), then $\sigma$ ≈ 0.27, placing greater emphasis on Euclidean distance. When L increases to 15, $\sigma$ ≈ 0.88, shifting dominance to FastDTW.

We conducted experiments on data sparsity (cold-start) for exercise responses across three datasets, categorizing answer records into three groups: Group 1: 0 to 5 exercises (0 < ans_cnt ≤ 5), Group 2: 5 to 15 exercises (5 < ans_cnt ≤ 15), and Group 3: 15 to 30 exercises (15 < ans_cnt ≤ 30). As shown in

Table 1. Accuracy comparison of models on the Algebra 2006–2007 dataset (ans_cnt represents answer count).

Model	0 < anscnt ≤ 5 (%)	5 < anscnt ≤ 15(%)	15 < anscnt ≤ 30(%)
DMMA	55	68	76
CRDP-KT	50	58	70
QIKT	48	54	66
DKVMN	49	53	68
CoKT	34	45	53
IEKT	49	50	64

,

Table 2. Accuracy comparison of models on the Assisstment 2017 dataset (ans_cnt represents answer count).

Model	0 < anscnt ≤ 5 (%)	5 < anscnt ≤ 15 (%)	15 < anscnt ≤ 30 (%)
DMMA	53	65	70
CRDP-KT	47	57	65
QIKT	45	53	62
DKVMN	46	55	63
CoKT	28	35	45
IEKT	37	49	60

and

Table 3. Accuracy comparison of models on the Statics2011 dataset (ans_cnt represents answer count).

Model	0 < anscnt ≤ 5 (%)	5 < anscnt ≤ 15 (%)	15 < anscnt ≤ 30 (%)
DMMA	55	69	73
CRDP-KT	45	59	68
QIKT	42	58	65
DKVMN	44	58	64
CoKT	30	45	50
IEKT	40	55	65

, Accuracy demonstrates a clear upward trend as the number of practice records increases. The lowest Accuracy occurs in Group 1 of each dataset due to the sparsest practice records. Experimental results indicate that the proposed DMMA effectively utilizes knowledge concept embeddings and significantly outperforms other methods for data-sparse users with limited exercise response records.

5.8. Discussion

The significant advantages of the DMMA in accuracy, diversity, and novelty stem from its precise modeling of core educational needs.

In terms of accuracy, DMMA achieved 82% on the Algebra 2006–2007 dataset in comparative experiments, outperforming CRDP-KT by 6%. This improvement benefits from the synergistic effect of the time decay factor and the knowledge concept mastery speed factor. The time decay factor (s = 0.85) is set according to the Ebbinghaus forgetting curve, ensuring that the 1-day knowledge retention rate aligns with experimental observations (about 33%). This addresses the flaw of traditional DKVMN models, which statically update knowledge states by relying solely on answer results—ignoring the natural forgetting of knowledge over time, leading to tracking biases in long-term learning behaviors. The knowledge concept mastery speed factor dynamically adjusts update intensity based on difficulty differences by using K-means to classify knowledge concepts into “general knowledge concepts” and “specific knowledge concepts.”

Regarding diversity, DMMA achieved 0.79 on the Assisstment 2017 dataset, surpassing DKVMN by 0.12. This stems from the genetic algorithm optimizer’s precise optimization of the “diversity metric.” By calculating the average cosine distance of exercise concept vectors, the algorithm maximizes the coverage of the recommended knowledge set, avoiding the homogenization issues caused by traditional collaborative filtering methods (e.g., CoKT), which rely on student similarity.

The improvement in novelty relies on the combination of an exercise filter and knowledge coverage prediction. The filter prioritizes recommending knowledge points that students have not mastered or are prone to forget, based on the predicted probability of knowledge concepts appearing at time t + 1 using a random forest model. Additionally, the Sigmoid-weighted similarity calculation method maintains novelty metrics between 0.62 and 0.65 for new users in cold-start scenarios by fusing external student attributes with answer sequence similarities, ensuring rapid delivery of diverse new knowledge points.

From an educational perspective, DMMA’s experimental results demonstrate strong practical value. In cold-start scenarios, DMMA achieved 53–55% accuracy when the number of answers was 0 < anscnt ≤ 5, significantly higher than CoKT’s 28–34%. This provides a feasible solution for new users on online education platforms. The algorithm can quickly generate tailored exercise recommendations by collecting basic attributes (e.g., grade, subject preference) and a small number of answer responses, addressing the pain points of new users who face “no exercises to practice” or “mismatched exercises” initially.

In long-term learning scenarios, the model’s time decay factor supports intelligent recommendations for “spaced repetition practice.” Experimental data show that students using DMMA-recommended spaced practice achieved a 42% long-term mastery rate (30 days later) on the Algebra 2006–2007 dataset, an 18% improvement over random recommendations. This aligns closely with the Ebbinghaus forgetting curve’s “critical review node” theory, providing data support for designing personalized review plans in online education platforms.

6. Conclusions

The dynamic multi-dimensional memory-augmented knowledge tracing model (DMMA) proposed in this study has achieved significant breakthroughs in personalized exercise recommendation. By innovatively integrating the Ebbinghaus forgetting curve, the model simulates the natural forgetting pattern of knowledge through a time decay factor, effectively addressing the limitation of traditional models that ignore temporal forgetting. Additionally, it introduces a knowledge concept mastery speed factor, which employs K-means clustering to distinguish between fundamental and advanced knowledge concepts, enabling differentiated dynamic adjustment of learning intensity.

Experimental validation demonstrates DMMA’s outstanding performance across three datasets (Algebra 2006–2007, Assistments 2017, and Statics2011). It achieves a peak accuracy of 82%, surpassing the second-best model by 6%. The diversity metric reaches 0.79 through genetic algorithm optimization, marking a 0.12 improvement over baseline methods. The novelty metric of 0.65 benefits from a random-forest-driven knowledge point prediction mechanism. Even in cold-start scenarios, the model maintains an accuracy of 53–55%, significantly outperforming traditional methods (28–34%).

The core contribution of this research lies in establishing a synergistic framework that bridges educational cognitive principles with deep learning technology. The time decay factor supports spaced repetition recommendations, improving 30-day knowledge retention by 18%. The genetic algorithm optimizer effectively balances difficulty matching with knowledge coverage, while the Sigmoid-weighted similarity calculation provides a smooth transition solution for new users. Together, these innovations offer a practical technical pathway for personalized exercise resource recommendation in intelligent education systems.