Dependence of Interface Shear Strength of Sand on Surface Roughness and Particle Size
Abstract
1. Introduction
2. Methods and Materials
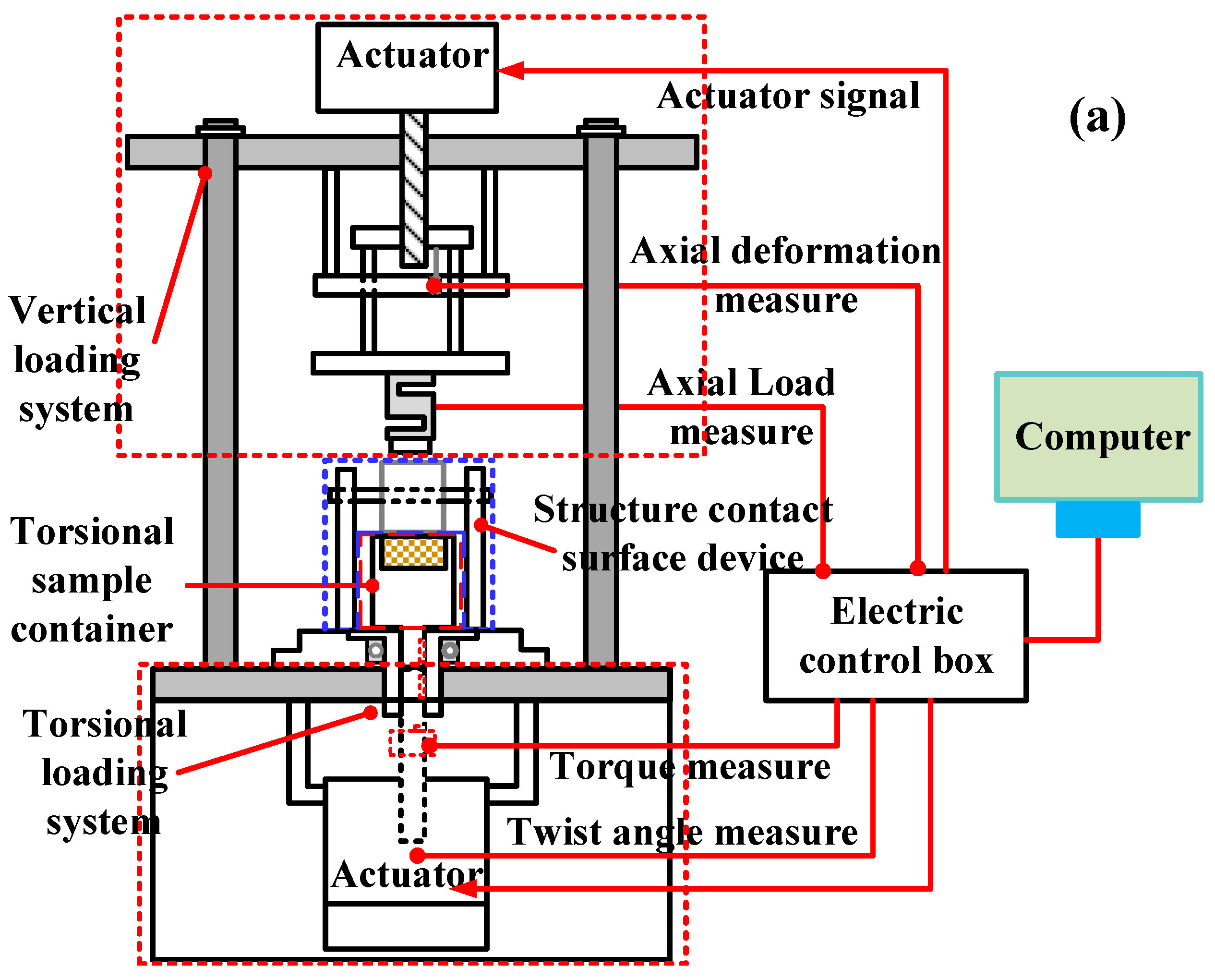
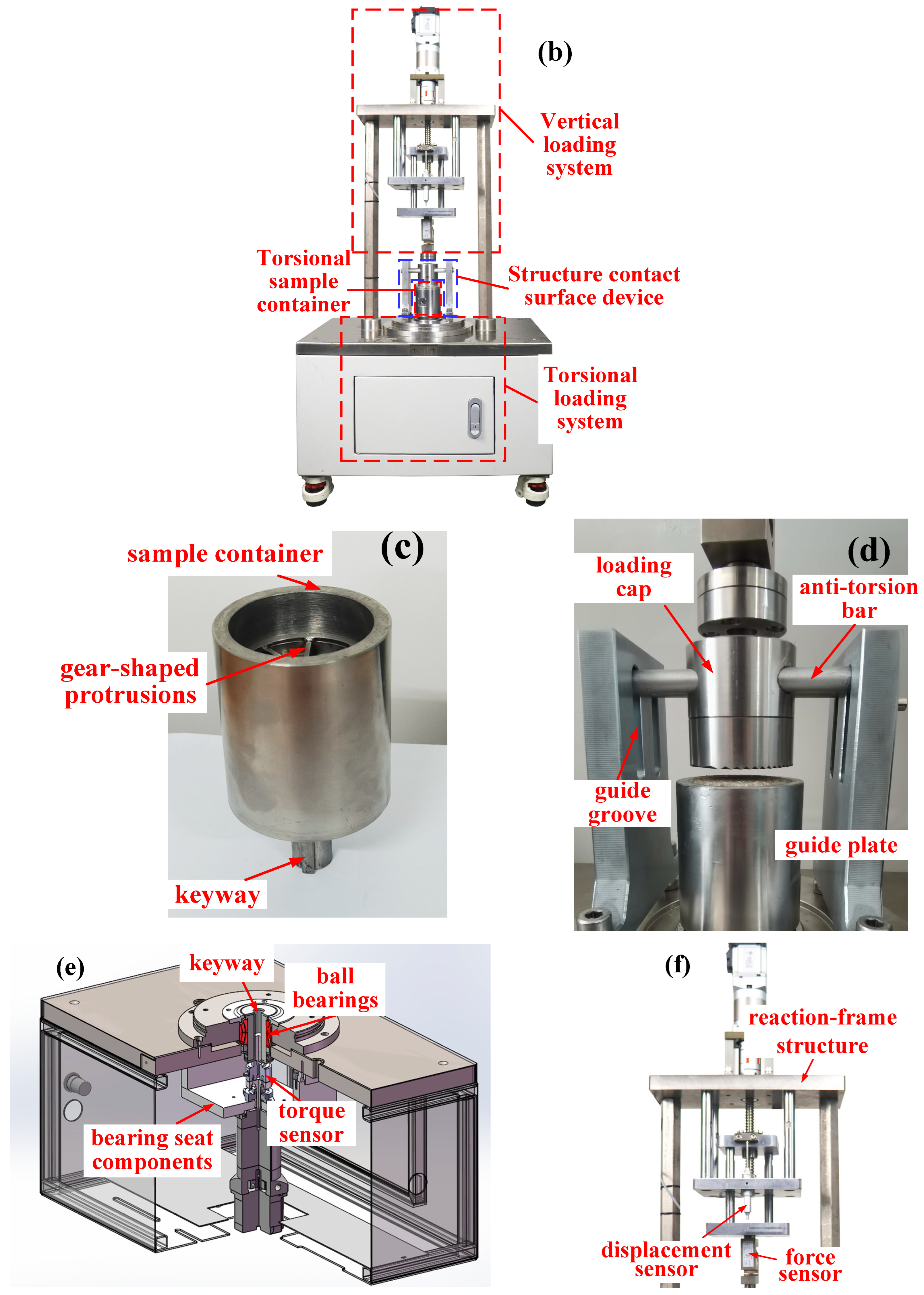
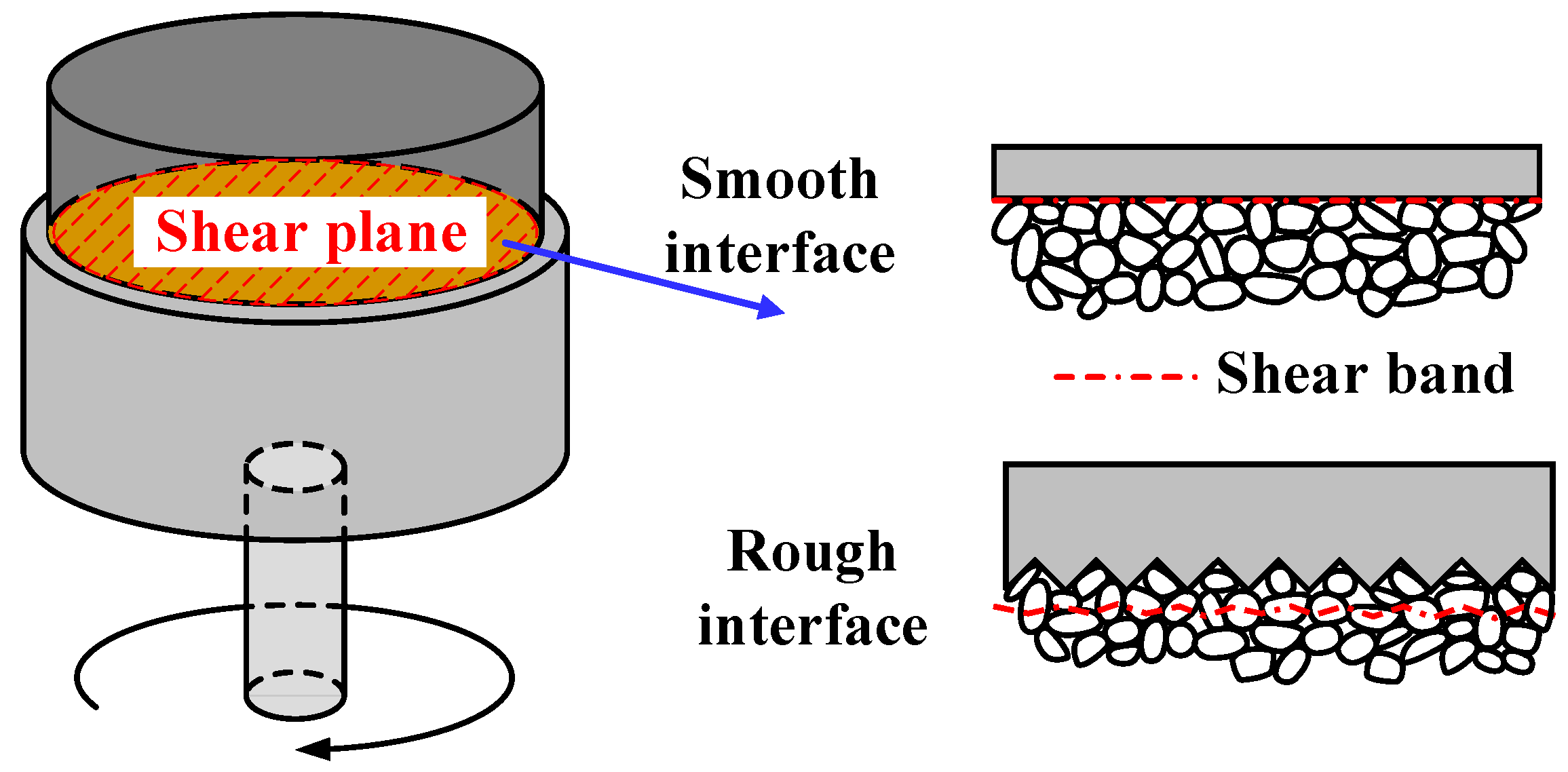
2.1. Experimental Setup
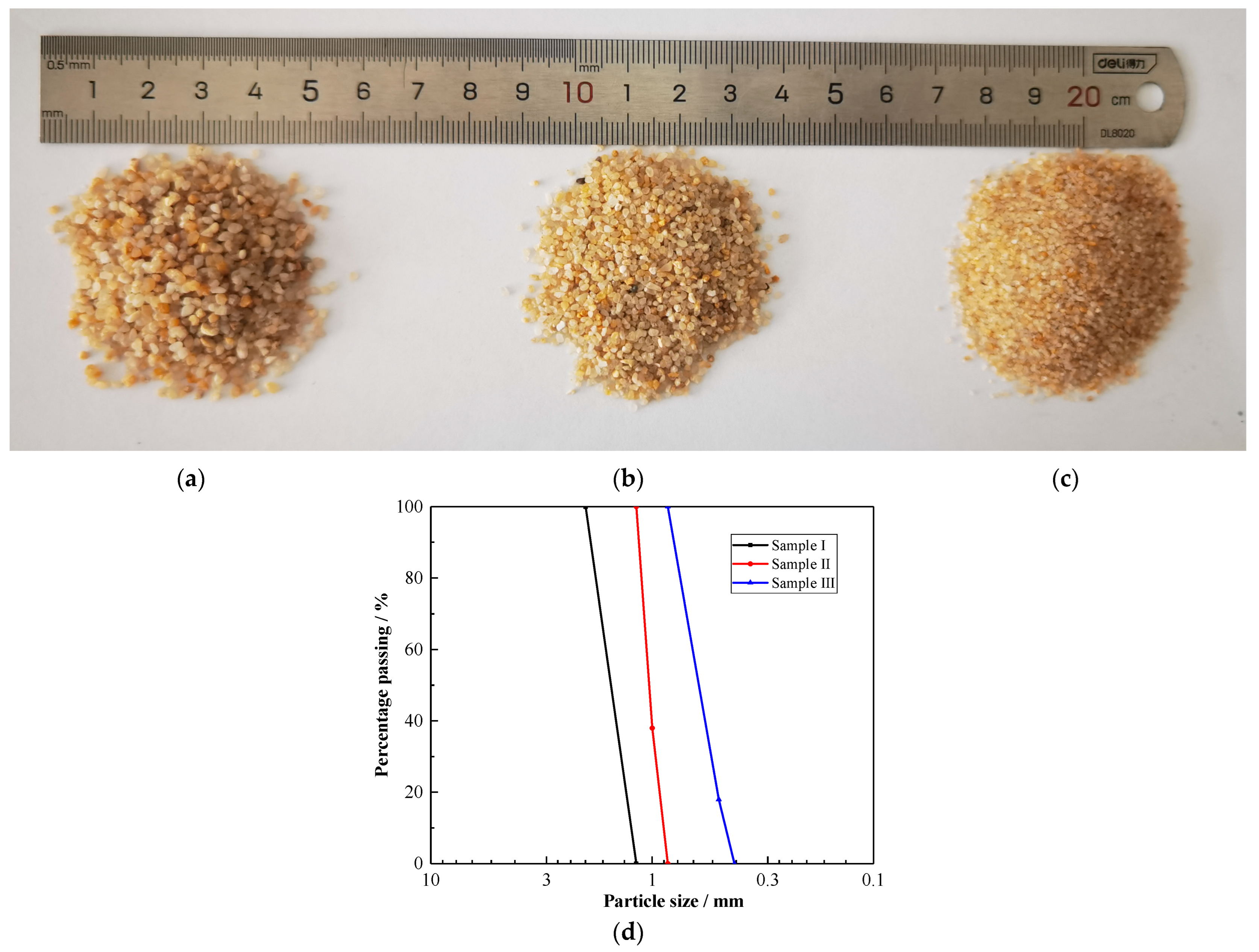
2.2. Materials
2.3. Methods
2.4. Test Process
3. Results and Discussion
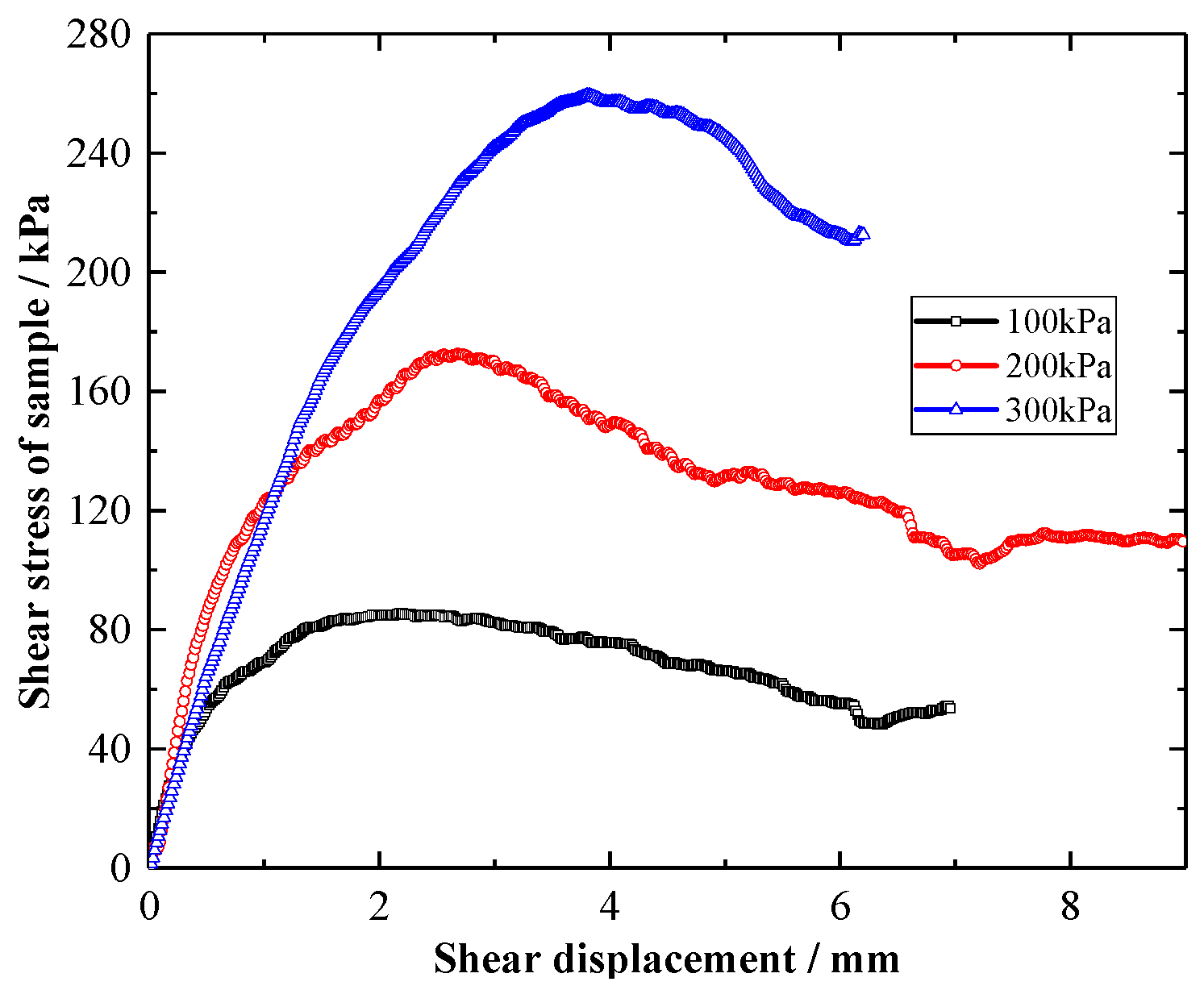
3.1. Comparison of Shear Behavior
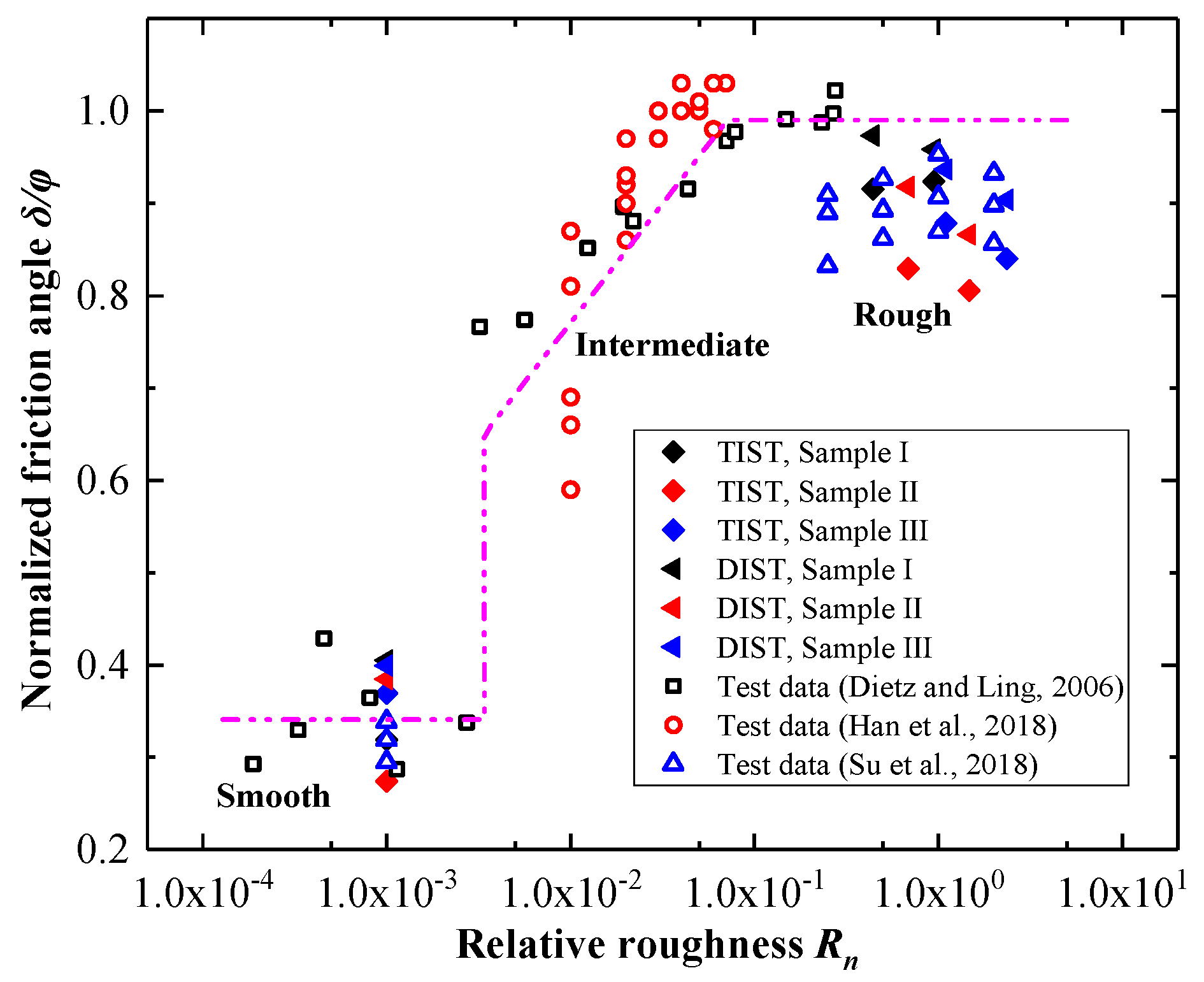
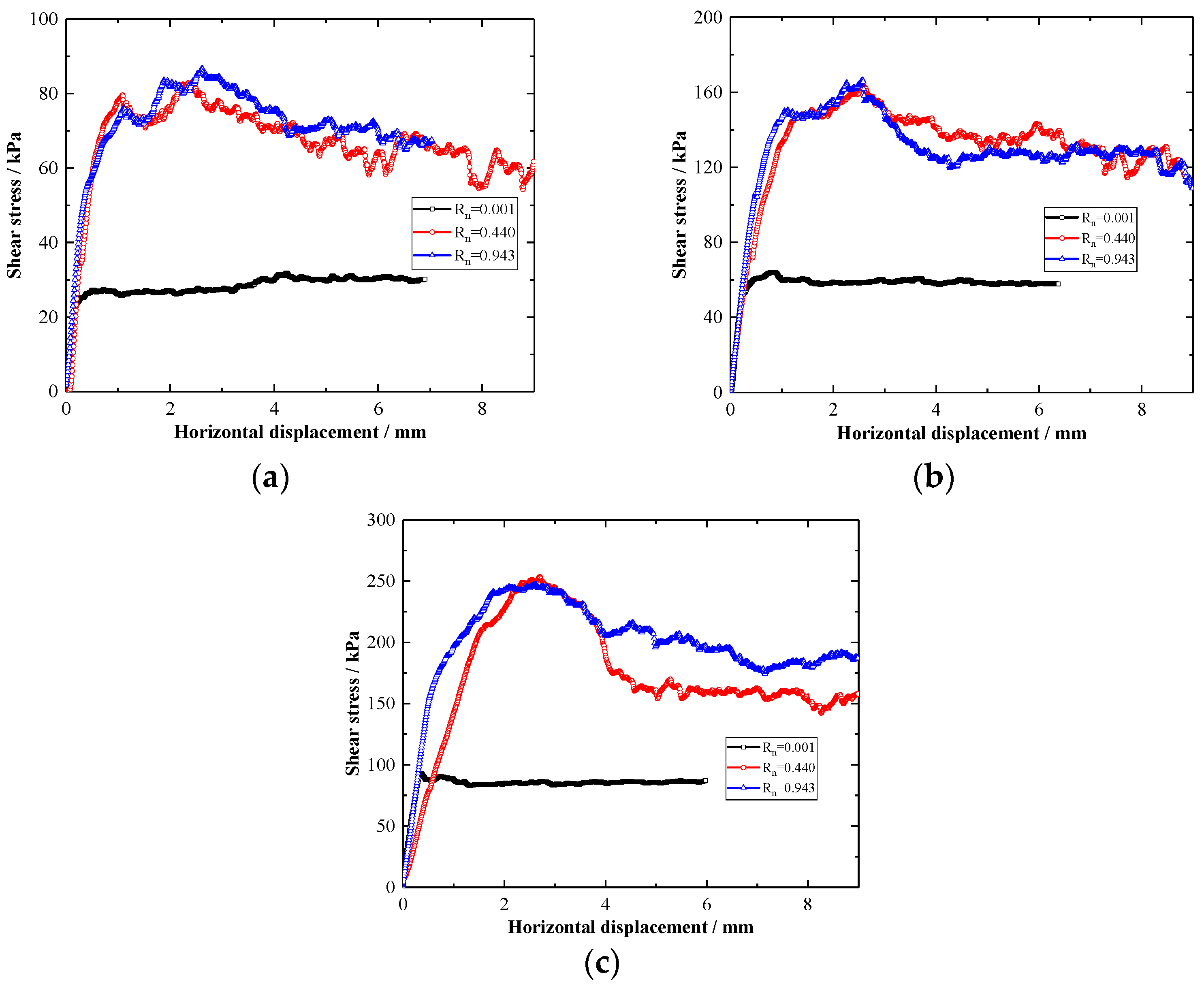
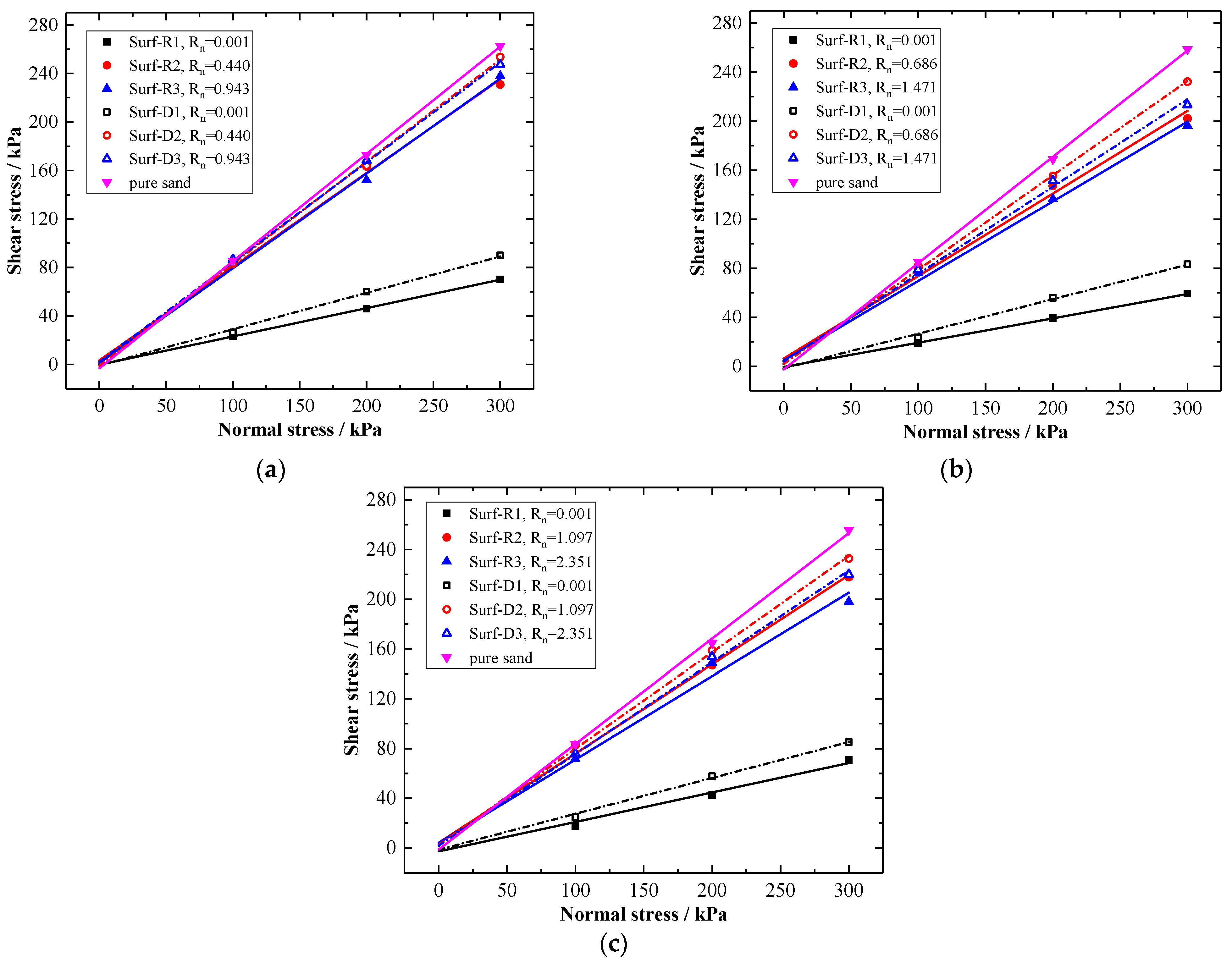
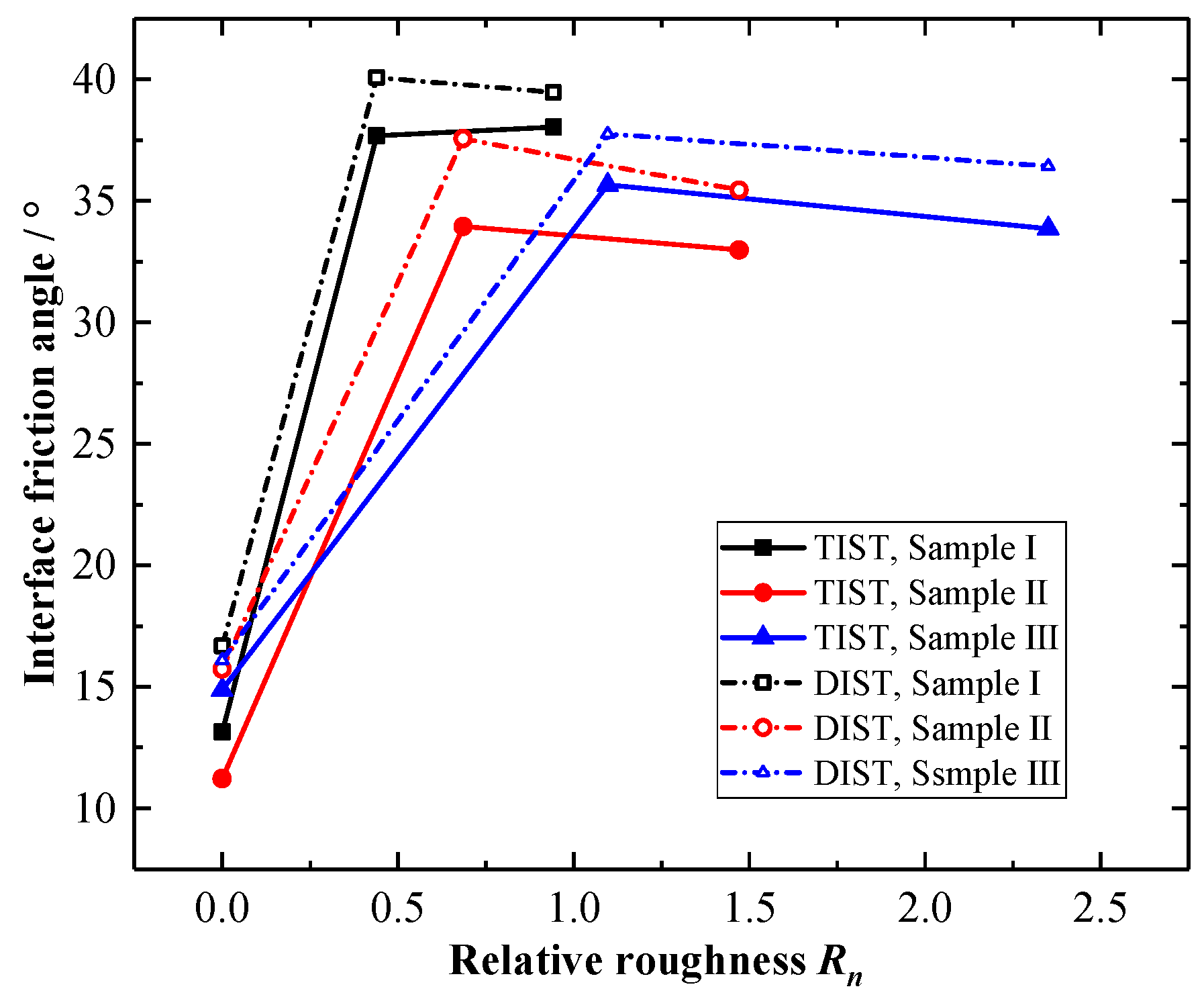
3.2. Effect of Relative Roughness Rn
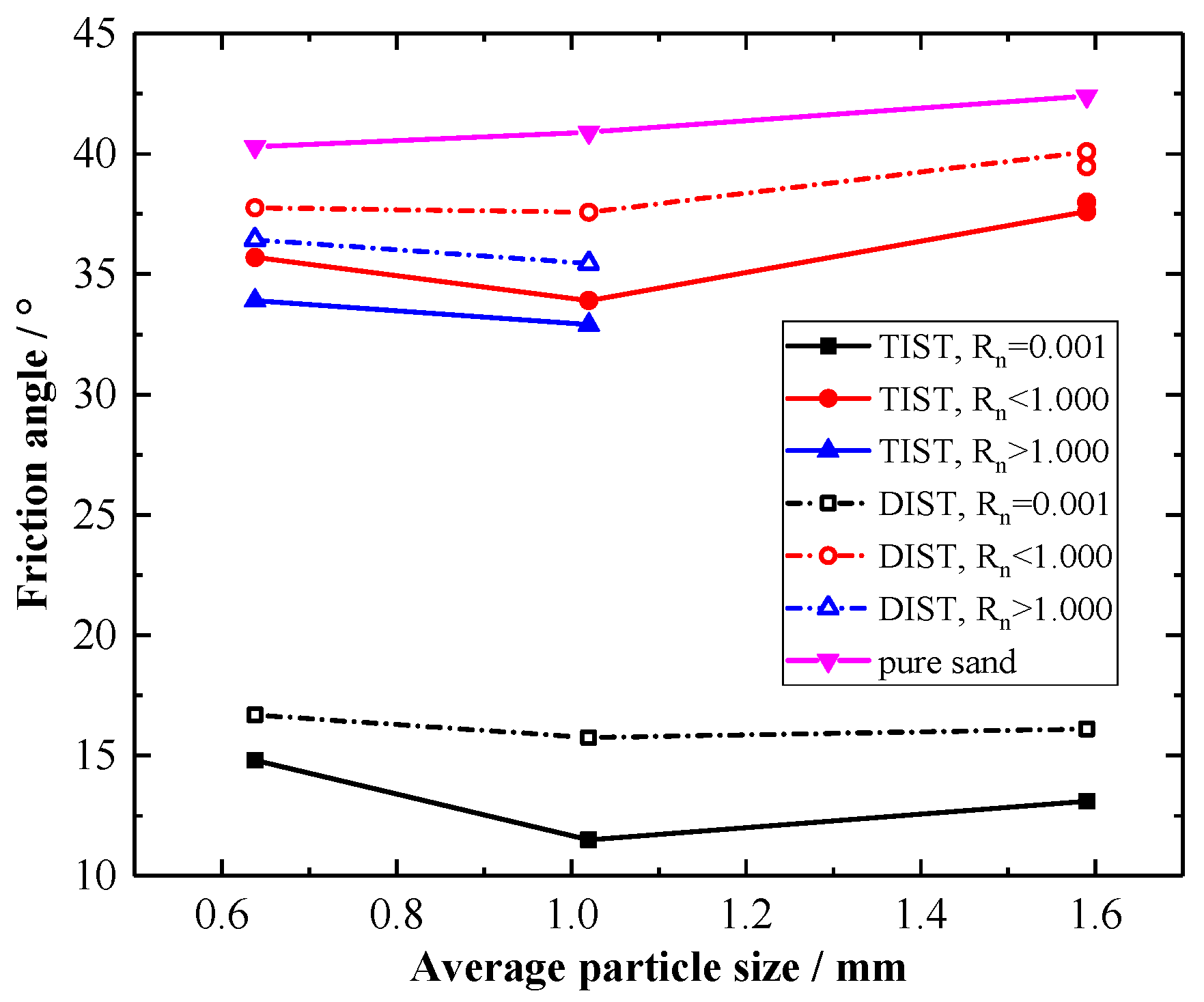
3.3. Effect of Mean Particle Size
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Randolph, M.F. Science and Empiricism in Pile Foundation Design. Géotechnique 2003, 53, 847–875. [Google Scholar] [CrossRef]
- Zhou, W.; Yin, J. A Simple Mathematical Model for Soil Nail and Soil Interaction Analysis. Comput. Geotech. 2008, 35, 479–488. [Google Scholar] [CrossRef]
- Kishida, H.; Uesugi, M. Tests of the Interface Between Sand and Steel in the Simple Shear Apparatus. Géotechnique 1987, 37, 45–52. [Google Scholar] [CrossRef]
- Roodi, G.H.; Morsy, A.M.; Zornberg, J.G. Soil-Geosynthetic Interface Shear in Different Testing Scales. Transp. Res. Rec. 2018, 2627, 129–141. [Google Scholar] [CrossRef]
- Meehan, C.L.; Tiwari, B.; Brandon, T.L.; Duncan, J.M. Triaxial Shear Testing of Polished Slickensided Surfaces. Landslides 2011, 8, 449–458. [Google Scholar] [CrossRef]
- Desai, C.S.; Nagaraj, B.K. Modeling for Cyclic Normal and Shear Behavior of Interfaces. J. Eng. Mech. 1988, 114, 1198–1217. [Google Scholar] [CrossRef]
- Potyondy, J.G. Skin Friction Between Various Soils and Construction Materials. Géotechnique 1961, 11, 339–353. [Google Scholar] [CrossRef]
- Desai, C.S.; Drumm, E.C.; Zaman, M.M. Cyclic Testing and Modeling of Interfaces. J. Geotech. Eng. 1985, 111, 793–815. [Google Scholar] [CrossRef]
- Maitra, S.; Chatterjee, S.; White, D.; Choudhury, D. Uplift Resistance of Buried Pipelines: The Contribution of Seepage Forces. Ocean Eng. 2022, 250, 111037. [Google Scholar] [CrossRef]
- Ansari, Y.; Kouretzis, G.; Sloan, S.W. Physical Modelling of Lateral Sand-Pipe Interaction. Géotechnique 2021, 71, 60–75. [Google Scholar] [CrossRef]
- Jung, J.K.; O’Rourke, T.D.; Olson, N.A. Lateral Soil-Pipe Interaction in Dry and Partially Saturated Sand. J. Geotech. Geoenviron. Eng. 2013, 139, 2028–2036. [Google Scholar] [CrossRef]
- Li, Y.; Lv, M.; Guo, Y.; Huang, M. Effects of the Soil Water Content and Relative Roughness on the Shear Strength of Silt and Steel Plate Interface. Measurement 2021, 174, 109003. [Google Scholar] [CrossRef]
- Hamid, T.B.; Miller, G.A. Shear Strength of Unsaturated Soil Interfaces. Can. Geotech. J. 2009, 46, 595–606. [Google Scholar] [CrossRef]
- Hu, L.; Pu, J. Testing and Modeling of Soil-Structure Interface. J. Geotech. Geoenviron. Eng. 2004, 130, 851–860. [Google Scholar] [CrossRef]
- Kou, H.; Diao, W.; Zhang, W.; Zheng, J.; Ni, P.; Jang, B.; Wu, C. Experimental Study of Interface Shearing Between Calcareous Sand and Steel Plate Considering Surface Roughness and Particle Size. Appl. Ocean Res. 2021, 107, 102490. [Google Scholar] [CrossRef]
- Han, F.; Ganju, E.; Salgado, R.; Prezzi, M. Effects of Interface Roughness, Particle Geometry, and Gradation on the Sand-Steel Interface Friction Angle. J. Geotech. Geoenviron. Eng. 2018, 144, 04018096. [Google Scholar] [CrossRef]
- Xiao, Y.; Cui, H.; Shi, J.; Qiao, W.; Stuedlein, A.W. Shear Response of Calcareous Sand-Steel Snake Skin-Inspired Interfaces. Acta Geotech. 2024, 19, 1517–1527. [Google Scholar] [CrossRef]
- Seiphoori, A.; Duong, T.N.; Geyin, M. A mechanistic understanding of interface shear behavior of cohesionless materials using torsional ring shear test. In Proceedings of the 3rd Vietnam Symposium on Advances in Offshore Engineering, Hanoi, Vietnam, 12–14 December 2024; pp. 313–322. [Google Scholar]
- Eid, H.T.; Al-Nohmi, N.M.; Wijewickreme, D.; Amarasinghe, R.S. Drained Peak and Residual Interface Shear Strengths of Fine-Grained Soils for Pipeline Geotechnics. J. Geotech. Geoenviron. Eng. 2019, 145, 06019010. [Google Scholar] [CrossRef]
- Li, D.; Hou, X.; Zhang, Y. Shearing Behavior of Suction Caisson Wall-Sand Interface throughout the Suction Caisson Life-Cycle. Appl. Ocean Res. 2024, 142, 103852. [Google Scholar] [CrossRef]
- Ke, L.; Gao, Y.; Li, D.; Zhang, Y.; Zhang, J.; Ji, J. An Experimental Study on Monotonic Shear Behavior of the Interface Between Fine Sea Sand and Steel. Int. J. Geomech. 2023, 23, 06022034. [Google Scholar] [CrossRef]
- ASTM D4253-16; Standard Test Methods for Maximum Index Density and Unit Weight of Soils Using a Vibratory Table. ASTM International: West Conshohocken, PA, USA, 2019.
- ASTM D4254-16; Standard Test Methods for Minimum Index Density and Unit Weight of Soils and Calculation of Relative Density. ASTM International: West Conshohocken, PA, USA, 2016.
- ASTM D854-23; Standard Test Methods for Specific Gravity of Soil Solids by Water Displacement Method. ASTM International: West Conshohocken, PA, USA, 2023.
- Hebeler, G.L.; Martinez, A.; Frost, J.D. Shear Zone Evolution of Granular Soils in Contact with Conventional and Textured CPT Friction Sleeves. KSCE J. Civ. Eng. 2016, 20, 1267–1282. [Google Scholar] [CrossRef]
- Frost, J.D.; DeJong, J.T.; Recalde, M. Shear Failure Behavior of Granular-Continuum Interfaces. Eng. Fract. Mech. 2002, 69, 2029–2048. [Google Scholar] [CrossRef]
- Yi, C.; Wang, C.; Zhang, L.; Chen, Z.; Xie, H. Study on Description Index System of Rough Surface Based on Bi-Body Interaction. Chin. J. Rock Mech. Eng. 2006, 25, 2481–2492. [Google Scholar]
- Uesugi, M.; Kishida, H. Frictional Resistance at Yield Between Dry Sand and Mild Steel. Soils Found. 1986, 26, 139–149. [Google Scholar] [CrossRef]
- ASTMD 6467; Standard Test Method for Torsional Ring Shear Test to Determine Drained Residual Shear Strength of Fine-Grained Soils. ASTM International: West Conshohocken, PA, USA, 2021.
- Li, D.; Hou, X.; Li, Y.; Zhang, Y. Influences of the Normal Loading Condition and Surface Texture on Interface Shear Behavior between Sand and Suction Caisson Wall. Ocean Eng. 2024, 312, 119277. [Google Scholar] [CrossRef]
- Li, L.; Xu, M.; Lu, H.; Zhang, Y.; Guo, Z. Seepage Effect on Caisson-Soil Interface Cyclic Shearing: Testing and Modeling. Soil Dyn. Earthq. Eng. 2025, 195, 109382. [Google Scholar] [CrossRef]
- Su, L.; Zhou, W.; Chen, W.; Jie, X. Effects of Relative Roughness and Mean Particle Size on the Shear Strength of Sand-Steel Interface. Measurement 2018, 122, 339–346. [Google Scholar] [CrossRef]
- Ari, A.; Akbulut, S. Effect of Fractal Dimension on Sand-Geosynthetic Interface Shear Strength. Powder Technol. 2022, 401, 117349. [Google Scholar] [CrossRef]
- Farhadi, B.; Lashkari, A. Influence of Soil Inherent Anisotropy on Behavior of Crushed Sand-Steel Interfaces. Soils Found. 2017, 57, 111–125. [Google Scholar] [CrossRef]
- Pham, H.H.G.; Impe, P.V.; Impe, W.; Menge, P.; Haegeman, W. Shear and Interface Shear Strengths of Calcareous Sand. In Proceedings of the 19th International Conference on Soil Mechanics and Geotechnical Engineering, Seoul, Republic of Korea, 17–22 September 2017; pp. 389–392. [Google Scholar]
- Wang, X.; Shan, Y.; Cui, J.; Zhong, Y.; Shen, J.; Wang, X.; Zhu, C. Dilatancy of the Foundation Filling Material of Island-Reefs in the South China Sea. Constr. Build. Mater. 2022, 323, 126524. [Google Scholar] [CrossRef]
- Feng, W.; Zhang, T.; Li, Y.; Xu, D. Experimental Study of Interface Performance Between Calcareous Sand and Steel Pile with Different Surface Roughness and Temperatures. Ocean Eng. 2024, 292, 116469. [Google Scholar] [CrossRef]
- Shoushtari, M.R.; Lashkari, A.; Martinez, A. Effect of Gas-Oil Contamination on the Mechanical Behavior of Sand-Woven Geotextile Interface: Experimental Investigation and Constitutive Modeling. Geotext. Geomembr. 2023, 51, 56–71. [Google Scholar] [CrossRef]
- Stutz, H.H. Hypoplastic Models for Soil-Structure Interfaces: Modelling and Implementation. Ph.D. Thesis, Christian-Albrechts-Universität zu Kiel, Kiel, Poland, 2016. [Google Scholar]
- Zhang, W.; Jing, H.; Kou, H. Effects of Relative Roughness and Particle Size on the Interface Behavior of Concrete Suction Caisson Foundation for Offshore Wind Turbines. Energies 2020, 13, 5866. [Google Scholar] [CrossRef]
- Dietz, M.S.; Lings, M.L. Postpeak Strength of Interfaces in a Stress-Dilatancy Framework. J. Geotech. Geoenviron. Eng. 2006, 132, 1474–1484. [Google Scholar] [CrossRef]




| Specimen | Particle Size Range/mm | D50/ mm | Specific Gravity | Dry Maximum Density ρdmax/g·cm−3 | Dry Minimum Density ρdmin/g·cm−3 | Relative Density Dr/% |
|---|---|---|---|---|---|---|
| Sample Ⅰ | 2~1.18 | 1.590 | 2.66 | 1.87 | 1.43 | 80 |
| Sample Ⅱ | 1.18~0.85 | 1.020 | 2.65 | 1.89 | 1.48 | 80 |
| Sample Ⅲ | 0.85~0.425 | 0.638 | 2.66 | 1.9 | 1.47 | 80 |
| Steel Surface | Sand Sample | D50 | Rn |
|---|---|---|---|
| Surf-R1 | Sample Ⅰ | 1.590 | 0.001 |
| Sample Ⅱ | 1.020 | 0.001 | |
| Sample Ⅲ | 0.638 | 0.001 | |
| Surf-R2 | Sample Ⅰ | 1.590 | 0.440 |
| Sample Ⅱ | 1.020 | 0.686 | |
| Sample Ⅲ | 0.638 | 1.097 | |
| Surf-R3 | Sample Ⅰ | 1.590 | 0.943 |
| Sample Ⅱ | 1.020 | 1.471 | |
| Sample Ⅲ | 0.638 | 2.351 | |
| Surf-D1 | Sample Ⅰ | 1.590 | 0.001 |
| Sample Ⅱ | 1.020 | 0.001 | |
| Sample Ⅲ | 0.638 | 0.001 | |
| Surf-D2 | Sample Ⅰ | 1.590 | 0.440 |
| Sample Ⅱ | 1.020 | 0.686 | |
| Sample Ⅲ | 0.638 | 1.097 | |
| Surf-D3 | Sample Ⅰ | 1.590 | 0.943 |
| Sample Ⅱ | 1.020 | 1.471 | |
| Sample Ⅲ | 0.638 | 2.351 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, Y.; Shao, L.; Guo, X. Dependence of Interface Shear Strength of Sand on Surface Roughness and Particle Size. Appl. Sci. 2025, 15, 9575. https://doi.org/10.3390/app15179575
Hou Y, Shao L, Guo X. Dependence of Interface Shear Strength of Sand on Surface Roughness and Particle Size. Applied Sciences. 2025; 15(17):9575. https://doi.org/10.3390/app15179575
Chicago/Turabian StyleHou, Yingjian, Longtan Shao, and Xiaoxia Guo. 2025. "Dependence of Interface Shear Strength of Sand on Surface Roughness and Particle Size" Applied Sciences 15, no. 17: 9575. https://doi.org/10.3390/app15179575
APA StyleHou, Y., Shao, L., & Guo, X. (2025). Dependence of Interface Shear Strength of Sand on Surface Roughness and Particle Size. Applied Sciences, 15(17), 9575. https://doi.org/10.3390/app15179575