Elastic Time-Lapse FWI for Anisotropic Media: A Pyrenees Case Study

Abstract

In the context of reservoir monitoring, time-lapse (4D) full-waveform inversion (FWI) of seismic data can potentially estimate reservoir changes with high resolution. However, most existing field-data applications are carried out with isotropic, and often acoustic, FWI algorithms. Here, we apply a time-lapse FWI methodology for transversely isotropic (TI) media with a vertical symmetry axis (VTI) to offshore streamer data acquired at Pyrenees field in Australia. We explore different objective functions, including those based on global correlation (GC) and designed to mitigate errors in the source signature (SI, or source-independent). The GC objective function, which utilizes mostly phase information, produces the most accurate inversion results by mitigating the difficulties associated with amplitude matching of the synthetic and field data. The SI FWI algorithm is generally more robust in the presence of distortions in the source wavelet than the other two methods, but its application to field data is hampered by reliance on amplitude matching. Taking anisotropy into account provides a better fit to the recorded data, especially at far offsets. In addition, the application of the anisotropic FWI improves the flatness of the major reflection events in the common-image gathers (CIGs). The 4D response obtained by FWI reveals time-lapse parameter variations likely caused by the reservoir gas coming out of solution and by the replacement of gas with oil.

1. Introduction

Time-lapse (4D) seismic data have been extensively utilized in reservoir management to monitor subsurface changes caused by oil and gas production and, more recently, CO₂ injection [1,2,3]. Time-lapse full-waveform inversion (FWI) of baseline and monitor surveys is particularly well-suited for estimating 4D changes in the reservoir with high spatial and temporal resolution [4,5,6].

Different strategies have been proposed to optimize time-lapse FWI and increase its sensitivity to reservoir changes. One of them is the parallel-difference (PD) FWI method [7], where the baseline and monitor data are inverted independently using the same initial model. Reference [8] presents the sequential-difference (SD) strategy, which uses the baseline inversion to build the initial model for inverting the monitor data. The SD approach has been shown to improve the convergence of the monitor inversion. The sensitivity of FWI to the time-lapse reservoir changes can be increased by applying the double-difference (DD) strategy developed by Refs. [9,10]. The DD method directly inverts the difference between the monitor and baseline data for the time-lapse parameter variations.

The authors of [11] apply 4D acoustic FWI to an OBC (ocean-bottom-cable) survey from Valhall field in the North Sea and show that the DD strategy produces the most accurate and interpretable reservoir changes. Reference [12] conducts acoustic 4D FWI for two vintages of the permanent Grane reservoir-monitoring system in the North Sea and obtains the P-wave velocity changes related to gas replacing oil during hydrocarbon production. In [13], the authors estimate the time-lapse changes related to CO₂ injection at Otway field in Australia by applying 4D elastic isotropic FWI to walkaway VSP (vertical seismic profiling) data.

Application of elastic anisotropic 4D FWI to field data involves considerable challenges due to the multimodal character of the objective function and parameter trade-offs. The authors of [14] extend the methodology of time-lapse FWI to VTI media and, in a sequel paper [15], incorporate a source-independent technique to mitigate the influence of errors in the source wavelet. Their work highlights the importance of accounting for anisotropy in time-lapse FWI to achieve accurate inversion results, especially in complex geologic settings.

Here, the time-lapse FWI algorithm proposed by Refs. [14,15] is applied to offshore data from Pyrenees field in western Australia. First, we discuss the FWI methodology for anisotropic media using different objective functions and outline applications of FWI to time-lapse seismic data. Relevant information about the Pyrenees field and data acquisition is presented next. Then the FWI algorithm for VTI media is tested on the baseline data and the results are compared with those produced by the isotropic inversion. We also evaluate the impact of different objective functions on the inversion results. Finally, the time-lapse parameter variations at Pyrenees field are estimated using the sequential-difference strategy.

2. Methodology of Source-Independent Full-Waveform Inversion

2.1. FWI Objective Functions

Full-waveform inversion is designed to minimize the data misfit, typically using the L₂-norm objective function $E\left(m\right)$ (e.g., [16]):

$$E\left(m\right)={\displaystyle \frac{1}{2}}{‖{\mathbf{d}}^{sim}\left(\mathbf{m}\right)-{\mathbf{d}}^{obs}‖}^2,$$

(1)

where ${\mathbf{d}}^{\mathit{o}\mathit{b}\mathbf{s}}$ is the observed data and ${\mathbf{d}}^{\mathbf{s}\mathit{i}\mathit{m}}$ is the data simulated for the model $\mathbf{m}$. Here, we minimize this objective function for multicomponent data from isotropic and VTI media.

The L₂-norm objective function is designed to optimize matching both the amplitude and phase of the observed and simulated wavefield. However, amplitude matching for field data is often challenging due to the complexity of wave-propagation phenomena in the subsurface. To address this issue, Reference [17] proposes the following normalized global-correlation (GC) objective function $G\left(\mathbf{m}\right)$ that reduces the dependence of data fitting on amplitude:

$$G(\mathbf{m})=-{\sum }_{s=1}^{n_s}{\sum }_{r=1}^{n_r}{\overline{\mathbf{d}}}^{obs}{\overline{\mathbf{d}}}^{sim}.$$

(2)

Here, ${\overline{\mathbf{d}}}^{obs} = {\mathbf{d}}^{obs}/‖{\mathbf{d}}^{obs}‖$ and ${\overline{\mathbf{d}}}^{sim} = {\mathbf{d}}^{sim}/‖{\mathbf{d}}^{sim}‖$ denote the normalized observed and simulated data, respectively, $n_s$ is the number of sources, $n_r$ is the number of receivers, $r$ is the trace number, and $T$ is the total recording time. The approach based on Equation (2) has shown promising results in improving the convergence and robustness of FWI in field-data applications (e.g., [18]).

2.2. Source-Independent FWI

Errors in the estimation of the source wavelet can significantly distort the FWI results, and this problem can be especially serious for time-lapse data. To reduce the influence of the source wavelet on FWI, References [15,19,20] implement the following convolution-based source-independent (SI) objective function in the time domain:

$$\begin{array}{c}S\left(m\right)={\displaystyle \frac{1}{2}}{‖{\mathbf{d}}^{sim}\left(\mathbf{m}\right)\ast \left(W{\mathbf{d}}_{ref}^{obs}\right)-{\mathbf{d}}^{obs}\ast \left(W{\mathbf{d}}_{ref}^{sim}\right)‖}^2\\ = {\displaystyle \frac{1}{2}}{‖{\mathbf{G}}^{sim}\ast {\mathbf{s}}^{sim}\ast W{\mathbf{G}}_{ref}^{obs}\ast {\mathbf{s}}^{obs}-{\mathbf{G}}^{obs}\ast {\mathbf{s}}^{obs}\ast W{\mathbf{G}}_{ref}^{sim}\ast {\mathbf{s}}^{sim}‖}^2\\ = {\displaystyle \frac{1}{2}}{‖{\tilde{\mathbf{G}}}^s\ast {\tilde{\mathbf{s}}}^c-{\tilde{\mathbf{G}}}^o\ast {\tilde{\mathbf{s}}}^c‖}^2,\end{array}$$

(3)

where $W=W\left(t\right)$ is the chosen time window that should include the first arrival, ${\mathbf{d}}_{ref}$ denotes the reference trace, ${\mathbf{G}}_{ref}^{obs}$ and ${\mathbf{G}}_{ref}^{sim}$ are the Green’s functions for the reference traces, ${\tilde{\mathbf{G}}}^s$ and ${\tilde{\mathbf{G}}}^o$ are the Green’s functions for the newly computed convolution-based simulated and observed data, and ${\tilde{\mathbf{s}}}^c$ is the new source wavelet. Note that because the objective function in Equation (3) is based on the L₂-norm, the SI technique may suffer from the amplitude mismatch between the observed and simulated data caused by the inadequacy of the employed subsurface model.

2.3. Forward Modeling and Model Updating for FWI

The wavefield is simulated by solving the elastic wave equation for anisotropic heterogeneous media using the finite-difference scheme:

$$\mathsf{\rho }{\displaystyle \frac{{\partial }^2{u}_i}{\partial t^2}}-{\displaystyle \frac{\partial }{\partial x_j}}\left[c_{ijkl}{\displaystyle \frac{\partial u_k}{\partial x_l}}\right]=f_i ,$$

(4)

where $u$ is the particle displacement, $\mathsf{\rho }$ is the density, $c_{ijkl}$ is the stiffness tensor, and $f$ is the density of the body forces.

Following Refs. [14,21], the adjoint-state method is used to calculate the gradient of the objective function with respect to the model parameters. We employ a nonlinear conjugate-gradient method for iterative parameter updating. The derivatives of the objective function can be found as:

$${\displaystyle \frac{\partial S}{\partial \mathbf{m}}}=-{\displaystyle \frac{\partial {\mathbf{d}}^{sim}}{\partial \mathbf{m}}}\mathbf{q} ,$$

(5)

where $\mathbf{q}$ is the residual wavefield.

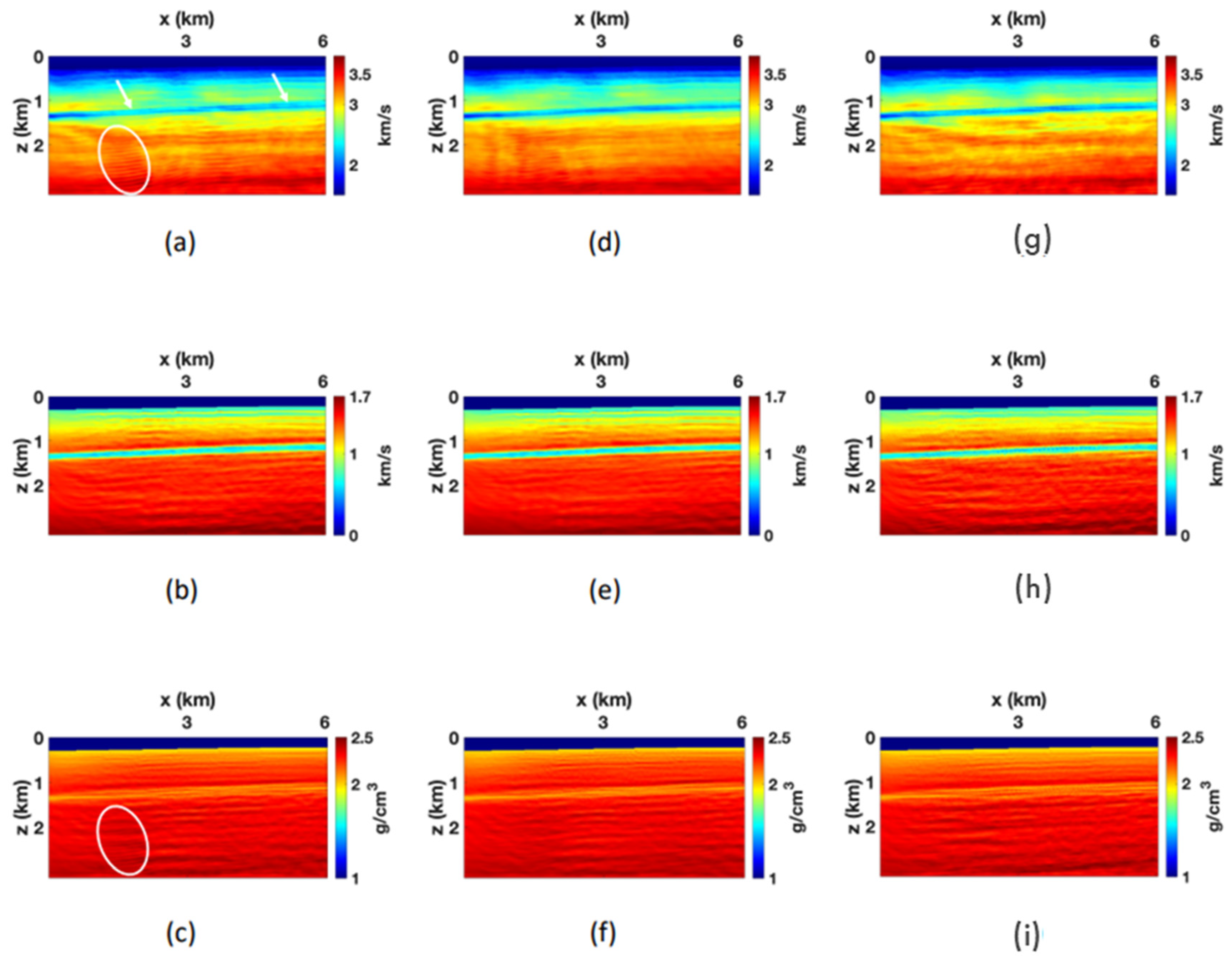
3. Field-Data Application

3.1. Location and Geology

Pyrenees field is located in the Exmouth Subbasin offshore of western Australia, where the water depth is around 200 m (Figure 1). The reservoir is about 1100 m below the sea surface. Oil and gas production from the Pyrenees field commenced in 2010 following several exploration efforts [22]. Studies of the area stratigraphy show that the depositional system can be characterized as a wave-dominated delta [23].

Prior to production, a dedicated seismic baseline survey was conducted over Pyrenees field in 2005 using conventional streamers [23]. The first time-lapse monitor survey was acquired with air guns in 2013 (three years after production began), using PGS GeoStreamer cable, which has both geophones and hydrophones. The source and receiver spacings for the baseline and monitor surveys are 25 m and 12.5 m, respectively. However, as shown in Figure 2, the acquisition geometries of these two surveys are different, with the largest distance between the baseline and monitor receiver locations exceeding 280 m. Moreover, the available monitor data were subject to P-up separation to eliminate the second hydrophone ghost and, therefore, have a different frequency spectrum and amplitude scale compared to the baseline pressure data. Therefore, the double-difference time-lapse FWI method, which requires high repeatability, is not applicable to this case study. These issues cause serious challenges in performing robust time-lapse seismic analysis of the Pyrenees data and emphasize the need for advanced methodologies that can properly handle the data complexity.

3.2. Preprocessing

To apply our 2D FWI algorithm, we select inline #1722 (marked by the orange and yellow lines in Figure 2) from the 3D data volume. Both the baseline and monitor data have a relatively high signal-to-noise ratio, so only minimal preprocessing is applied to enhance the signal. The three primary preprocessing steps include: (1) noise attenuation to suppress the linear noise in the data (performed by INPEX; not discussed here); (2) zero-phase low-cut Orsmby filtering to remove low-frequency noise below 3 Hz; and (3) zero-phase high-cut Orsmby filtering to retain only frequencies below 12 Hz, which is the maximum frequency used in FWI.

The inclusion of low-frequency data is critical for obtaining accurate FWI results. A careful selection of the lowest frequency is essential to prevent cycle-skipping in FWI and mitigate the influence of noise. For that purpose, filters with high-cut frequencies of 2, 3, 4, and 5 Hz were applied to denoised raw shot gathers in the time domain (Figure 3). For the 2-Hz filter, the signal is somewhat discernible, but the near- and mid-offset traces are significantly contaminated by linear noise. On the other hand, for the 3- and 5-Hz filters, coherent and higher-amplitude signals become observable, which is indicative of an improved signal-to-noise ratio. Therefore, FWI is applied with a low-cut filter that has an edge frequency of 3 Hz. To reduce computational cost and mitigate high-frequency noise, the maximum frequency was set to 12 Hz.

The employed FWI algorithm operates with all wave types recorded within the chosen time window including refracted and reflected arrivals. Multiples and surface ghosts are also used in FWI because they are simulated by the forward-modeling code. Elasticity and anisotropy (vertical transverse isotropy) are taken into account to make the algorithm more suitable for field data, as discussed below.

3.3. Initial Model

The initial P-wave vertical velocity (${\mathrm{V}}_{\mathrm{P}0}$) is obtained from well logs and the results of reflection tomography for VTI media (Figure 4a) published by Geoscience Australia. The estimated Thomsen parameters $\mathsf{ϵ}$ and $\mathsf{\delta }$ are small, with maximum values less than 0.05. We obtained the shear-wave vertical velocity ${\mathrm{V}}_{\mathrm{S}0}$ (Figure 4b) by extrapolating the ratio of the P-wave and S-wave velocities from a well, which is about 1 km away from the 2D line (not shown here). The density (Figure 4c) is computed from the P-wave velocity by applying Gardner’s [25] equation for sedimentary formations:

$$\mathsf{\rho }=310{\mathrm{V}}_{\mathrm{P}0}^{0.25},$$

(6)

where $\mathsf{\rho }$ is in kg/m³, and ${\mathrm{V}}_{\mathrm{P}0}$ is in m/s. Note that Equation (6) is used only to obtain the initial density model, which is updated during FWI using the corresponding inversion gradient [15]. The Gaussian filter with a kernel of 62.5 m $\times$ 62.5 m is applied to the parameters in Figure 4a,b to smooth the initial model (Figure 4d–f).

3.4. Wavelet Estimation

Accurate estimation of the source signature is of utmost importance in achieving successful FWI results, especially for time-lapse data. Errors in the wavelet can hamper the model-updating process (e.g., it can get trapped in a local minimum of the objective function) and cause distortions in the subsurface model [26,27]. This issue is particularly critical in time-lapse FWI where the source wavelet can be different for the baseline and monitor surveys (e.g., [15]).

A common approach to wavelet estimation involves using water-bottom reflections and direct arrivals, which requires such preprocessing steps as deghosting and multiple removal. Alternatively, References [28,29] suggest estimating the source wavelet during the inversion process. However, their methodology entails additional trade-offs that may compromise the quality of the inversion. Furthermore, simultaneously inverting for the source wavelet and medium parameters significantly increases computational cost.

Here, we adopt the method for source-signature estimation proposed by Ref. [30]. Their filter-based approach eliminates the need for deghosting and is particularly advantageous for deep-water surveys, in which the direct waves do not interfere with water-bottom arrivals (e.g., reflections and multiples).

The inversion is initiated with a Ricker wavelet that has a central frequency of 8 Hz. The water velocity model is constructed based on the results of P-wave tomography provided by Inpex. Next, forward modeling is employed to simulate the direct wave using the initial wavelet. The direct arrival is extracted from the nearest-offset (250 m) trace.

Matching of the observed and simulated first arrivals makes it possible to generate a Wiener filter (Figure 5b), which serves as a wavelet-correlation tool [30]. The Wiener filter is applied to the initial wavelet, resulting in the source signal (Figure 6b) employed in FWI.

3.5. Inversion of the Baseline Data

As the data are acquired in 3D geometry, the sources and receivers for the chosen inline deviate from a straight line. Therefore, a source/receiver projection onto the line is necessary before performing 2D FWI. The source wavelet for FWI is estimated by the Wiener filter [30], as described above. FWI operates in the frequency range from 3–12 Hz. All medium parameters including density are updated independently using the nonlinear conjugate-gradient method.

3.5.1. Elastic Isotropic FWI

First, we apply an elastic isotropic FWI algorithm with three different objective functions [Equations (1)–(3)] to the baseline data. As expected, the inverted models (Figure 7) have a higher spatial resolution than the initial parameter distributions. The global-correlation (GC) objective function produces a more continuous low-velocity layer at a depth of 1.1 km, which corresponds to the reservoir location (indicated by the white arrows). The high-frequency artifacts below 2 km (circled in white) generated by the L₂-norm objective function are significantly suppressed by applying the source-independent (SI) and GC functions. The periodic artifacts below 1.2 km, which are especially strong in the density field, are likely caused by the difficulties in matching the multiple reflections.

It should be noted that the initial density model is obtained from the approximate Gardner’s equation, and there is a larger uncertainty in this parameter compared to the velocities. Furthermore, FWI is carried out without constraints, making it even more challenging to accurately estimate density from surface seismic data.

The vertical profiles of the velocity ${\mathrm{V}}_{\mathrm{P}0}$ in Figure 8 show that the GC objective function produces the result that is closer to the sonic log than those estimated by the two other objective functions. In particular, both L₂-norm-based objective functions underestimate the velocity in the overburden, likely due to the difficulty of matching the amplitudes of the observed and simulated data. The inverted models obtained with all three objective functions reduce the data misfit compared to that for the initial model (Figure 9a). The best fit to the data (see the white arrows), however, is provided by the model reconstructed using the GC objective function.

3.5.2. Elastic FWI for VTI Media

Reference [31] identifies the presence of anisotropy (transverse isotropy) during velocity-model building for the Browse Basin on the Northwest Shelf of Australia. The authors emphasize the importance of incorporating anisotropic inversion techniques for accurate reservoir characterization in the area. The Pyrenees field in the Exmouth sub-basin is also located on the Northwest Shelf, so we expect the findings of Ref. [31] to be relevant for our case study. Therefore, we next apply the FWI algorithm for VTI media developed by Refs. [14,15]. Because the structure dips in the area are mild (Figure 7), the VTI model should be adequate for our purposes.

We parameterize the model by $V_{P0}$ (P-wave vertical velocity), $V_{S0}$ (S-wave vertical velocity), $V_{hor,P}$ (P-wave horizontal velocity), $V_{nmo,P}$ (P-wave normal-moveout velocity from a horizontal reflector), and $\mathsf{\rho }$ (density) [32]. The velocities $V_{hor,P}$ and $V_{nmo,P}$ are expressed through the Thomsen parameters $ϵ$ and $\delta$ as follows [33,34]:

$$V_{hor,P}=V_{P0}\sqrt{1+2ϵ},$$

(7)

$$V_{nmo,P}=V_{P0}\sqrt{1+2\delta }.$$

(8)

The advantages of this velocity-based notation are discussed in Refs. [32,35]. Because the reflection tomography employed by Geoscience Australia produced the maximum values of $ϵ$ and $\delta$ close to 0.04, the initial model is isotropic. We employ the GC objective function, which provides the highest accuracy in the isotropic inversion discussed above. The anisotropic (VTI) FWI algorithm produces a more continuous low-velocity layer in the sections of all four velocities, along with reduced artifacts below the reservoir (Figure 10). We also computed the Thomsen parameters $ϵ$ and $\delta$ from the inverted velocities using Equations (8) and (9), respectively (Figure 11). Our results show that the maximum value of $ϵ$ is about 0.15 and $\delta$ around 0.085, which is consistent with the observations of Ref. [31], but implies that the previous tomographic model likely underestimates the magnitude of anisotropy.

There are indications that taking anisotropy into account improves the accuracy of the velocity field. Indeed, the velocity $V_{P0}$ reconstructed by the VTI algorithm closely matches the sonic log, with higher values above and within the reservoir and lower values below it (Figure 12). The comparison of the observed and simulated data (Figure 13) shows a good agreement for shallow events, especially at the far offsets (see the white arrows), where the offset-to-depth ratio is close to 1.5. The VTI algorithm, however, does not generate significant parameter updates below 2 s, probably due to the limited offset-to-depth ratio.

3.6. Inversion of the Monitor Data

As mentioned above, the streamer lines of the monitor survey deviate from those of the baseline survey (Figure 2). In addition, the available monitor data were subject to P-up separation, which changes their frequency spectrum. The central frequency of the monitor data is lower than that of the baseline data (Figure 14), especially at the near and far offsets. In contrast to the baseline data, the frequency of the monitor data is the highest in the mid-offset range (traces from 90 to 150).

We employ the sequential-difference (SD) strategy for time-lapse analysis because of its efficiency and robustness compared to the parallel-difference method d [14]. Due to the offset-dependent frequency content of the monitor survey, the field and modeled data are not likely to match if only one frequency band (e.g., 3–12 Hz) is used in FWI. Therefore, a multiscale inversion approach is implemented with three frequency bands: 3–5 Hz, 3–9 Hz, and 3–12 Hz. The multiscale inversion also improves convergence and mitigates the cycle-skipping issue common in FWI.

Figure 15 shows the time-lapse variations of the velocity ${\mathrm{V}}_{\mathrm{P}0}$ and parameters ϵ and δ estimated by the VTI FWI algorithm. “Sandwich”-shape 4D changes are observed in the velocity ${\mathrm{V}}_{\mathrm{P}0}$ obtained for the frequency range 3–5 Hz (Figure 15a–c), where a low-velocity layer is embedded between two higher-velocity horizons (marked by the black arrow).

A similar pattern is observed in the variations of the parameters ϵ and δ. There are false 4D anomalies appearing in ${\mathrm{V}}_{\mathrm{P}0}$ below 1.5 km and in ϵ around the water bottom (marked by the dashed black rectangles in Figure 15a,b). Although these artifacts are less pronounced for the frequency range 3–9 Hz (Figure 15d–f), they get amplified when the maximum frequency increases to 12 Hz (Figure 15h–j). This enhancement of artifacts is likely due to the inability of the forward-modeling algorithm to simulate the variable frequency content of the monitor data.

A plausible interpretation of the time-lapse change of ${\mathrm{V}}_{\mathrm{P}0}$ obtained by the VTI FWI algorithm for the band 3–9 Hz (Figure 15d–f) can be suggested using previous results [24,36]. The velocity increase in the top part of the reservoir might indicate the substitution of gas with oil, and the velocity decrease near the reservoir bottom may be due to the pressure drop caused by production (Figure 16).

There are also noticeable time-lapse artifacts outside the reservoir (Figure 15), possibly caused by the geometric errors for the baseline survey. Unfortunately, as the receiver locations cannot be found in the database published by Geoscience Australia, we have to reconstruct the receiver geometry from shot locations and seismic acquisition specifications. To account for tide-related distortions in the monitor survey (Figure 2), we project the position of sources and receivers onto a 2D sail line by keeping the recorded offset values. The receiver geometry in the baseline survey can be distorted by the influence of tides and can include significant errors. Such geometric errors, which are not incorporated into FWI, can produce substantial distortions in the 4D parameter variations.

4. Discussion

Here, common-image gathers (CIGs) are used to evaluate the accuracy of the parameters estimated by the VTI FWI algorithm. The CIGs include multiple reflections because we apply prestack depth migration (PSDM) to the complete shot gathers. Figure 17 and Figure 18 show the CIGs generated by anisotropic PSDM for the baseline data using the initial parameters as well as those estimated from the VTI FWI algorithm with the GC objective function. Evidently, application of the anisotropic FWI improves the flatness of the major reflection events in the CIGs (marked by white ellipses).

In contrast, anisotropic PSDM applied to the monitor data does not measurably change the CIGs (Figure 19 and Figure 20). This indicates that the initial VTI parameters for the monitor survey are sufficiently accurate for purposes of seismic imaging.

5. Conclusions

We applied a previously developed 4D FWI methodology for VTI media to a field data set from Pyrenees field in Australia, which involved baseline and monitor surveys with different geometries and frequency spectra. Inversion of the baseline data showed that the global-correlation objective function, which emphasizes phase matching, produces better results than the L₂-norm and source-independent (SI) objective functions that are more sensitive to amplitudes. The superior performance of the global-correlation objective function was ensured by the sufficiently accurate estimation of the source wavelet. Taking vertical transverse isotropy into account in FWI led to a better match between the sonic log and the P-wave vertical velocity and reduced the misfit between the observed and simulated data, particularly at the far offsets. Analysis of the flatness of major reflections in common-image gathers shows that the anisotropic FWI provided more improvements for the baseline than the monitor data.

The time-lapse inversion was hampered by nonrepeatability issues and the inconsistent frequency content of the monitor records. Still, application of the sequential-difference time-lapse strategy revealed the velocity variations inside and around the reservoir caused by hydrocarbon production. The time-lapse results indicate the softening of the reservoir caused by gas coming out of the solution and the hardening above the reservoir caused by the replacement of gas with oil.