A Robust Hybrid Forecasting Framework for the M3 and M4 Competitions: Combining ARIMA and Ata Models with Performance-Based Model Selection

Featured Application

The proposed hybrid forecasting model can be applied in business forecasting systems, retail demand planning, and energy load prediction where adaptive model selection is needed under variable time series frequencies.

Abstract

This study proposes a hybrid forecasting framework that integrates the Auto-Regressive Integrated Moving Average (ARIMA) model with multiple variations of the Ata model, using a performance-based model selection strategy to enhance forecasting accuracy on the M3 and M4 competition datasets. For each time series, seven versions of the Ata model are generated by adjusting level and trend parameters, and the version with the lowest in-sample symmetric mean absolute percentage error (sMAPE) is selected. To improve robustness and prevent overfitting, the median-performing Ata model is also included. These selected models’ forecasts are then combined with ARIMA outputs through optimized weighting schemes tailored to the characteristics of each series. Given the varying frequencies (e.g., yearly, quarterly, monthly, weekly, daily, and hourly) and diverse lengths of time series, a grid search algorithm is employed to determine the best hybrid combination for each frequency group. The model is applied in a series-specific manner, allowing it to adapt to different seasonal, trend, and irregular patterns. Extensive empirical results demonstrate that the hybrid model outperforms its individual components and traditional benchmarks across all frequency categories. It ranked first in the M3 competition and achieved second place in the M4 competition based on the official error metric, the sMAPE and Overall Weighted Average (OWA), respectively. The results highlight the framework’s adaptability and scalability for complex, heterogeneous time series environments.

1. Introduction

Time series forecasting is very important in fields like economics, energy, retail, and environmental sciences, where making decisions and plans depends on making accurate predictions. It is especially important to make robust forecasting models for competitiongrade datasets like M3 and M4, which have a wide range of real-world series with different patterns and frequencies.

Traditional statistical methods such as Auto-Regressive Integrated Moving Average (ARIMA) have long been used because they are easy to understand and have a strong theoretical basis. More recently, the Ata method has gained attention for its simplicity, computational efficiency, and adaptability to both seasonal and non-seasonal patterns. However, no single forecasting method performs optimally across all types of time series data. This shows how important it is to use adaptive methods that consider the specific features of each series.

This study proposes a hybrid forecasting framework that integrates the best variants of the Ata methods and ARIMA, employing a data-driven optimization process based on grid search and in-sample sMAPE minimization for model selection. By evaluating multiple variations of the Ata model for each series and selecting those with the best in-sample performance, we aim to construct exclusive forecasts that are both accurate and reliable. The proposed method is tested on these datasets, and its performance is evaluated using the official accuracy measures used by the competitions. This research contributes to the literature by demonstrating how statistical modeling and adaptive model selection can be effectively integrated to improve forecasting accuracy across different time series.

2. Literature Review

Time series forecasting is now a very important field that combines statistics, machine learning, and decision sciences. This is because there is a growing need for accurate predictions in many areas, including economics, healthcare, and environmental science. As problems in the real world become more complicated and there are more data available, the need for strong and flexible forecasting methods has grown even more. Over the years, the development of forecasting methods has been influenced by both theoretical progress and large-scale real-world tests, especially through international benchmark competitions. The M3 and M4 forecasting competitions have been especially important because they have led to new ways of doing things and more thorough comparisons. Researchers have been able to test, compare, and improve their methods in these competitions, which has sped up progress in the field.

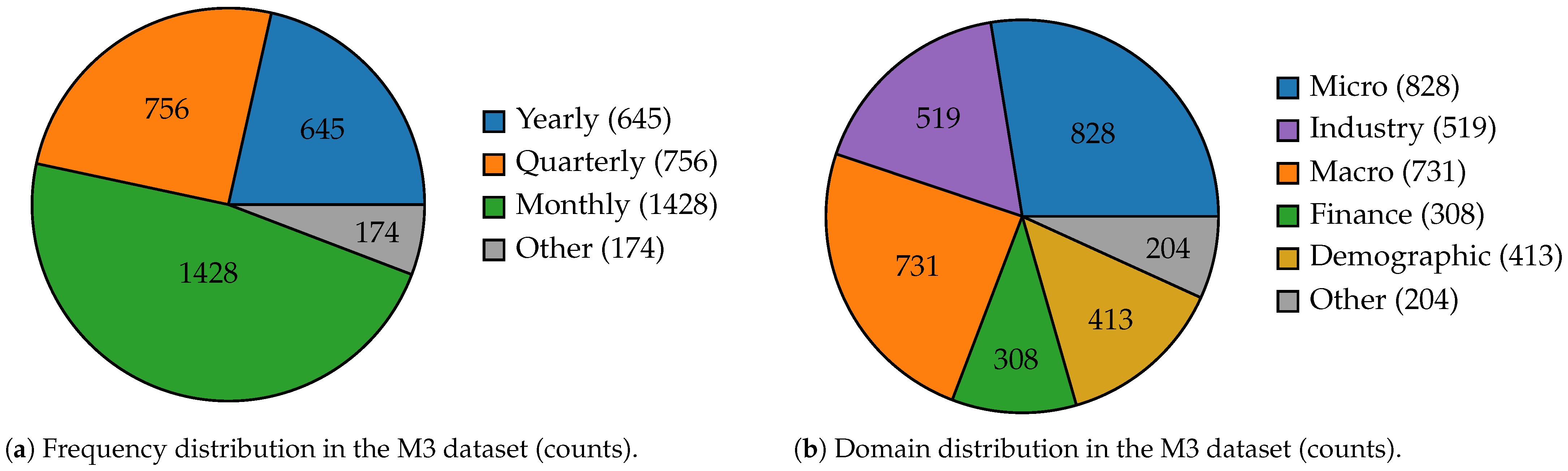
The M3 competition, which was organized by Makridakis and Hibon [1], was significant because it examined 24 different forecasting methods on 3003 time series. One of the most striking findings was that relatively simple statistical models—such as exponential smoothing and ARIMA—performed on par with, and sometimes even outperformed, more complex and sophisticated approaches. This went against the common belief that making a model more complex always makes it more accurate at predicting. The M3 competition showed that complexity for its own sake is not always useful and that classical statistical methods are still useful today. Because of this, the M3 competition resulted in a lot of research into hybrid and ensemble methods that try to combine the ease of use and understanding of traditional models with the power and flexibility of more advanced ones. This change has contributed to the creation of forecasting frameworks that are useful for researchers. As illustrated in Figure 1, the M3 dataset spans multiple frequencies and domains, providing a rich ground for testing and comparing forecasting methods.

Building on the foundation laid by M3, the M4 competition [2,3] expanded the scope substantially, including 100,000 time series and 61 forecasting methods, comprising a wide array of statistical, machine learning, and hybrid approaches. The unprecedented scale and diversity of the M4 dataset allowed for a more comprehensive assessment of forecasting methods across different domains and time series characteristics. As illustrated in Figure 2, the dataset covers multiple frequencies—yearly 23,000 (23%), quarterly 24,000 (24%), monthly 48,000 (48%), weekly 359 (0.36%), daily 4,227 (4.23%), and hourly 414 (0.41%)—and spans diverse domains (micro, industry, macro, finance, demographic, and other categories), thereby capturing heterogeneous structures for model evaluation. The results of M4 confirmed the idea that no single method consistently dominates across all types of time series. Instead, ensemble and combination methods—particularly those that integrate statistical and machine learning models—tended to perform the most robust and reliable performance. This finding has important real-world implications. It suggests that being flexible and adaptable is essential for making accurate predictions in diverse settings. The M4 competition also showed that how important it is for forecasting research to be reproducible and open, establishing new standards for future studies.

One of the earliest and most influential works in this line of research was Zhang [4], who introduced a hybrid ARIMA and Artificial Neural Network (ANN) model. This pioneering study established the foundation for combining linear time series components modeled by ARIMA with the nonlinear learning capacity of neural networks, achieving better performance than either method separately. Building on this foundation, Atesongun and Gulsen [5] extended the ARIMA–ANN framework with a structured hybrid forecasting model, confirming its efficiency across multiple real-world datasets. Similarly, Tsoku et al. [6] proposed a hybrid ARIMA–ANN model to forecast South African crude oil prices, showing that the integration of Box–Jenkins methodology with neural networks enhances predictive accuracy in volatile financial markets. In a related contribution, Alshawarbeh et al. [7] applied the ARIMA–ANN hybrid approach to high-frequency datasets, underscoring its robustness in handling rapidly changing series and reducing forecast errors in complex environments. More recently, Smyl [8], the overall winner of the M4 competition, proposed a hybrid method of exponential smoothing (ETS) and Recurrent Neural Networks (RNNs). This study provided compelling evidence that hybrid models, when carefully designed, can significantly outperform both classical statistical methods and standalone neural networks, setting a new benchmark for large-scale forecasting competitions. Together, these works demonstrate the enduring importance of hybrid statistical–machine learning approaches as benchmarks and their adaptability across diverse forecasting contexts.

Recent research has emphasized hybrid forecasting frameworks that combine traditional statistical models with regression-based or machine learning approaches to enhance predictive accuracy. For example, Iftikhar et al. [9] modeled and forecasted carbon dioxide emissions by integrating regression techniques with time series models. Their study demonstrated that a hybrid structure can capture both linear and nonlinear dynamics, offering more reliable forecasts in environmental applications. Similarly, Sherly et al. [10] proposed a hybrid ARIMA–Prophet model, showing that the integration of Prophet’s trend–seasonality decomposition with ARIMA’s statistical rigor yields superior accuracy compared to either method alone. Ampountolas [11] conducted a comparative analysis of machine learning, hybrid, and deep learning forecasting methods in European financial markets and Bitcoin, highlighting the competitive advantage of hybrid designs in complex financial domains. These studies highlight that hybrid designs are not restricted to financial or technological data but can be successfully applied in sustainability and policy-relevant domains as well.

The integration of deep learning into hybrid forecasting has further advanced the field. Qin et al. [12] proposed a BiLSTM–ARIMA hybrid optimized with a whale-driven metaheuristic algorithm for financial forecasting. Their results showed significant improvements in capturing long-term dependencies and market volatility. Likewise, Çınarer [13] presented a hybrid deep learning and stacking ensemble model for global temperature forecasting, effectively addressing the challenges of nonlinear climate dynamics. Dong and Zhou [14] introduced a novel hybrid forecasting framework that integrates the ARIMA model with Convolutional Neural Networks (CNN) and Long Short-Term Memory (LSTM) networks, combined with Complete Ensemble Empirical Mode Decomposition with Adaptive Noise (CEEMDAN) and Sample Entropy (SE) techniques for financial forecasting. Their approach demonstrated superior performance by leveraging signal decomposition, statistical modeling, and deep neural networks in a unified structure. These contributions underline that integrating deep learning with statistical backbones allows hybrid models to operate effectively across both financial and environmental domains.

Hybrid forecasting models have also proven valuable in areas where interpretability and domain-specific insights are crucial. Iacobescu and Susnea [15] developed an ARIMA–ANN framework for crime risk forecasting, incorporating socioeconomic and environmental indicators. Their approach not only improved accuracy but also enhanced interpretability, enabling policymakers to connect predictions with underlying risk factors. In the domain of financial markets, Liagkouras and Metaxiotis [16] combined LSTM networks with sentiment analysis for stock market forecasting. This hybrid captured both quantitative and qualitative signals, highlighting the value of integrating textual data sources with numerical series. Finally, Liu et al. [17] introduced a multi-scale hybrid forecasting framework that combined traditional statistical models with deep learning to handle heterogeneous time series across varying temporal resolutions. Their results emphasized scalability and adaptability, making the framework applicable to multi-domain forecasting challenges.

Model selection has become a major topic in modern forecasting research because time series data are naturally diverse. Because time series structures, frequencies, and outside factors can be so different, flexible methods are required that can choose the best model for each series based on its own unique features. For instance, Karim et al. [18] showed how useful it is to add external data sources like Google Trends to models that forecast macroeconomic indicators in Australia. Their research showed that using relevant outside information along with dynamic model selection can greatly improve the accuracy of predictions, especially in environments that change quickly. In a similar manner, Hananya and Katz [19] proposed dynamic model selection frameworks that automatically select the best machine learning model in real time, based on changing series characteristics. This is another step forward in the field of adaptive forecasting. All of these studies show that more and more people are realizing that choosing a model is not a one-time thing but an ongoing process that needs to change with new data and outside factors. Moreover, recent advances in artificial intelligence have also begun to influence model selection processes. Wei et al. [20] came up with a new way to automate the recommendation of forecasting models by using large language models (LLMs). Their framework makes the model selection process easier by using the natural language processing capabilities of LLMs. This points to a future where artificial intelligence (AI) not only builds models but also helps people choose and use them in smart ways. This new development opens new ways to combine expert knowledge and data-driven insights. It could also make advanced forecasting tools available to more people.

As these developments occurred, the Ata method has become an important method in statistical forecasting. The Ata method was first introduced as an alternative to Holt’s linear trend method [21]. Since then, it has been recognized and tested in competitive settings [22,23]. Its ability to handle various types of time series with minimal parameter tuning makes it particularly appealing in practice. Furthermore, the method’s simplicity, interpretability, and accuracy make it a valuable candidate for hybrid and ensemble forecasting frameworks. Its rising popularity in both academic and real-world settings shows its usefulness.

Based on these findings, this study suggests a hybrid forecasting framework, namely, the Ata-best model, based on model selection and examines the performance of the Ata and ARIMA methods using the M3 and M4 datasets. The study’s goal is to improve forecasting accuracy at the individual series level by systematically finding the best-performing model for each time series based on the in-sample symmetric mean absolute percentage error (sMAPE). This method not only uses the real-world results from major forecasting competitions, but it also incorporates new developments in model selection and hybridization. This makes it a better way to forecast time series in both environmental and general settings. Consequently, the study aims to help improve forecasting by showing how adaptive, data-driven model selection can help achieve both accuracy and interpretability.

To highlight the comparative strengths of the two statistical approaches employed in this study,

Table 1. Comparison of ARIMA and Ata method in time series forecasting.

Aspect	ARIMA	Ata Method
Modeling approach	Linear stochastic model combining autoregressive (AR), differencing (I), and moving average (MA) components.	Modern, innovative smoothing-based approach with adaptive updating of level, trend and any other components.
Stationarity requirement	Requires (covariance) stationarity; differencing used to remove trends/seasonality; SARIMA (seasonal ARIMA) handles a single regular seasonality.	No strict stationarity requirement; directly adapts to evolving level/trend, and can accommodate multiplicative effects via functional form.
Complexity	Model identification requires selecting $(p,d,q)$ with diagnostics; risk of over/underfitting in short or noisy series.	Relatively simple updating structure; few tuning choices; parameters are set adaptively.
Interpretability	Parameters have clear statistical meaning; transparent for low orders, but interpretation can be harder for higher-order models.	Transparent level/trend decomposition and update rules.
Adaptability	Limited adaptability to nonlinear dynamics, structural breaks, regime changes, or multiple/unstable seasonalities without extensions.	Highly adaptive to shifts in level/trend or any other parameters; effective under unstable seasonality or intermittent patterns via adaptive smoothing.
Forecasting accuracy	Strong baseline on linear, stationary series; accuracy degrades with structural breaks or nonlinearities.	Demonstrated competitive accuracy (e.g., M3, M4, and M6 forecasting competitions), especially for short, irregular, or heterogeneous series.
Computational efficiency	Moderate; iterative estimation and diagnostic checking raise cost for large-scale model selection.	High; lightweight computations enable scaling to thousands of series.
Application areas	Well-suited for stationary and short-memory time series; extensively used in economics, finance, and engineering.	Versatile and broadly applicable across diverse domains (e.g., economics, healthcare, environmental forecasting, and intermittent demand); also highly adaptable for hybrid and ensemble frameworks.
Limitations	Struggles with nonlinearities, structural breaks, multiple or unstable seasonalities; endogenous-only unless extended.	Relatively new but increasingly recognized; performance benefits from adaptive form and flexible selection procedure.

provides a structured summary of the ARIMA and Ata methods. The table illustrates their key characteristics, including modeling assumptions, adaptability, computational efficiency, and practical limitations. By presenting advantages and disadvantages side by side, it becomes clear that while ARIMA offers a well-established framework with strong theoretical foundation, the Ata method introduces a flexible and adaptive alternative that is particularly suitable for heterogeneous or unstable series. This comparative view not only clarifies the methodological reasons behind selecting these two models for further investigation, but also emphasizes their complementary potential in hybrid forecasting frameworks.

3. Methodology

In this study, a model selection-based hybrid approach is utilized for time series forecasting. For each time series, both the Ata and ARIMA models are applied. For the ARIMA model, we used the official forecast values declared in the M3 and M4 competitions. For the Ata method, we choose the two versions of the Ata model: the one model with the lowest in-sample sMAPE (lowest Ata) and the one model with the median in-sample sMAPE (median Ata). A grid search algorithm was used to find these models because of the difference in the dataset’s frequency and the varying structural characteristics of the time series, as well as to determine how to weight the contributions of the ARIMA- and Ata-based models in the hybrid structure. The goal of this strategy is to improve the overall accuracy of the forecasts by finding the best method, i.e., “Ata-best” for each series based on its own unique features. In this section, the mathematical foundations of the employed methods and the construction of the hybrid framework are presented in detail. Below, the fundamental formulations of the ARIMA and Ata methods used in this study are provided.

Before introducing the individual forecasting methods, the overall structure of the hybrid framework is pictured in Figure 3. As shown, the M3 and M4 datasets are modeled using multiple variations of the Ata method and the official ARIMA forecasts from both competitions. A hybrid framework is then constructed through weight optimization via grid search, producing the final hybrid forecasts. Additionally, model selection procedures, such as in-sample sMAPE evaluation and alternative aggregation strategies (Ata-lowest and Ata-median), are incorporated to ensure robustness in performance evaluation.

3.1. ARIMA

The ARIMA model, first formalized by Box and Jenkins [24], is a fundamental statistical method for time series forecasting. When it comes to modeling and forecasting linear relationships in univariate time series data, the ARIMA model is considered the most traditional and widely used method. The model is called ARIMA (p, d, q), where p is the autoregressive (AR) component’s order, d is the number of differences needed to reach stationarity, and q is the moving average (MA) component’s order. The general ARIMA model is expressed as follows:

$$\varphi \left(B\right){(1-B)}^d{y}_t=\theta \left(B\right){\epsilon }_t$$

(1)

where $y_t$ is the value at time t, B is the backshift operator ($B{y}_t=y_{t-1}$), ${(1-B)}^d$ is the differencing operator applied d times, $\varphi \left(B\right)$ and $\theta \left(B\right)$ are polynomials of orders p and q, and ${\epsilon }_t$ is white-noise error.

The ARIMA model captures linear relationships in stationary univariate time series by combining autoregressive, differencing, and moving average components. Choosing a model usually entails determining the appropriate orders for each component and testing for stationarity. Despite being popular due to its simplicity and efficiency with linear patterns, ARIMA has limitations when it comes to handling nonlinear dynamics, structural breaks, or external regressors. In such complex scenarios, these limitations often lead to the adoption of more sophisticated or hybrid forecasting techniques.

3.2. Ata Method

The Ata method is an innovative approach to use statistical analysis to make forecasts about the future. It is based on traditional forecasting techniques for time series, the most famous of which is Holt’s linear trend method. The Modified Holt’s Linear Trend Method [21] was the first name given to Ata. Later, it was made official as a new way of modeling that is different from traditional models such as ARIMA and Exponential Smoothing [22]. The main benefit of the Ata method over traditional Exponential Smoothing is that it can easily adjust the parameters like trend and level component when the model assumptions are right. This makes it more accurate when predicting time series with complicated trend structures. Notably, the Ata method is based on the ideas behind classical exponential smoothing, but it stands out because it uses adaptive smoothing weights that change over time. This lets the model react quickly to sudden changes in the data. Ata can also be used in both additive and multiplicative forms, and a dampening factor can be added to the trend component to control how long the trend lasts.

The formal mathematical representation of the Ata model is provided below for both additive and multiplicative forms. Here, $S_t$ denotes the level component, $T_t$ represents trends, and ${\widehat{X}}_t\left(h\right)$ is the h-step-ahead forecast at time t. The additive form is denoted as $At{a}_{add}(p,q,\varphi )$, and the multiplicative form is denoted as $At{a}_{mult}(p,q,\varphi )$, where $\varphi =1$ for non-dampened data.

• Additive Ata Model: $At{a}_{add}(p,q,\varphi )$

  $$S_t=\left({\displaystyle \frac{p}{t}}\right)X_t+\left({\displaystyle \frac{t-p}{t}}\right)(S_{t-1}+T_{t-1})\mathrm{if}t>p$$

  (2)

  $$S_t=X_t\mathrm{if}t\le p$$

  (3)

  $$T_t=\left({\displaystyle \frac{q}{t}}\right)(S_t-S_{t-1})+\left({\displaystyle \frac{t-q}{t}}\right)T_{t-1}\mathrm{if}t>q$$

  (4)

  $$T_t=X_t-X_{t-1}\mathrm{if}t\le q$$

  (5)

  $$T_t=0\mathrm{if}t=1$$

  (6)

  $${\widehat{X}}_t\left(h\right)=S_t+h\ast T_t$$

  (7)
• Multiplicative Ata Model: $At{a}_{mult}(p,q,\varphi )$   

  $$S_t=\left({\displaystyle \frac{p}{t}}\right)X_t+\left({\displaystyle \frac{t-p}{t}}\right)(S_{t-1}\ast T_{t-1})\mathrm{if}t>p$$

  (8)

  $$S_t=X_t\mathrm{if}t\le p$$

  (9)

  $$T_t=\left({\displaystyle \frac{q}{t}}\right)\left({\displaystyle \frac{S_t}{S_{t-1}}}\right)+\left({\displaystyle \frac{t-q}{t}}\right)T_{t-1}\mathrm{if}t>q$$

  (10)

  $$T_t={\displaystyle \frac{X_t}{X_{t-1}}}\mathrm{if}t\le q$$

  (11)

  $$T_t=1\mathrm{if}t=1$$

  (12)

  $${\widehat{X}}_t\left(h\right)=S_t\ast T_t^h$$

  (13)

  where $t>p\ge q$, $p\in \{1,2,\dots ,n\}$, $q\in \{0,1,\dots ,p\}$, and $h=1,2,\dots$.

4. Data and Preprocessing

In this study, we used the M3 and M4 competition datasets, two of the most wellknown and widely used time series datasets in the forecasting literature. Because of their size and diversity, these datasets are frequently used as benchmarks to assess forecasting techniques. Both datasets include a wide range of real-world time series, with differences in length and frequency as well as in the underlying domains and structural features. This variety offers a comprehensive framework for evaluating the generalizability, flexibility, and robustness of forecasting models in various application domains.

There are 3003 time series in the M3 dataset, all of which have been methodically categorized by frequency and domain. Micro, macro, industry, finance, demographics, and other are the six domains in which the series are specifically dispersed. The M3 dataset also includes four primary frequency types: yearly, quarterly, monthly, and other frequencies. From short-term to long-term horizons, from economic indicators to demographic trends, this dual categorization ensures that the dataset captures a broad range of real-world temporal dynamics and forecasting challenges. Likewise, with 100,000 time series, the M4 dataset provides an even bigger and more varying collection. The M4 dataset, like M3, contains series from a variety of domains, including demographics, industry, finance, and macro. The frequency spectrum is further broadened by M4, which offers series at hourly, daily, weekly, monthly, quarterly, and yearly intervals. This thorough framework makes it possible to assess forecasting models over a far larger range of application domains and temporal resolutions.

The primary objective of this research was to establish a hybrid statistical modeling framework that could combine and adaptively choose the best forecasting models for each individual time series. In order to achieve this, we concentrated on two popular statistical forecasting techniques: the Ata method, a more modern and adaptable modeling technique intended for automated and effective forecasting, and the well-known ARIMA model, which has long been a benchmark method in time series literature. A crucial part of our methodology was the implementation of a performance-driven model selection approach for the Ata method, where grid search and in-sample sMAPE minimization were employed. For each time series, we evaluated seven distinct Ata model variations which consist of without trend parameter, trend parameter with additive model, trend parameter with multiplicative model, level-fixed additive model (i.e., choosing optimum level and trend parameter with additive model), level-fixed multiplicative model (i.e., choosing optimum level and trend parameter with multiplicative model), a simple average of the first and second models, and a simple average of the first and third models, respectively. The selection was based on the in-sample sMAPE, and for each series, we identified two representative Ata models: the one with the lowest sMAPE Ata model (“Ata-lowest”) and the one with the median sMAPE Ata model (“Ata-median”), capturing both optimal and robust model performance. This dual selection strategy allowed us to capture both the optimal and a more robust, central tendency of Ata model performance.

For the ARIMA component, although we first experimented with auto.ARIMA based forecasts, we finally decided to use the official ARIMA forecasts published as part of the M3 and M4 competition results. Our hybrid framework’s dependability and comparability were guaranteed by empirical comparisons that consistently showed that the benchmark ARIMA forecasts performed better than our own implementations in terms of out-of-sample accuracy.

To integrate the strengths of both the Ata and ARIMA models, namely, obtaining the “Ata-best” model, we employed a grid search algorithm to determine the optimal combination weights for each time series. In order to minimize the forecasting error, this weight optimization was performed separately for each series due to the significant heterogeneity in series frequency, length, and domain. Our hybrid model was able to maximize predictive accuracy by flexibly adapting to the distinct features of each time series thanks to this customized approach. All computations were performed in R (version 4.4.3) through the RStudio environment (version 2024.12.1+563). The Ata method was implemented using the ATAforecasting package (version 0.0.60). The code was structured to facilitate reproducibility and enable efficient handling of a wide range of time series.

Hence, this study’s methodological pipeline was identified by its thorough statistical foundations, systematic methodical data-driven model selection, and repeatable validation processes. Our hybrid approach takes advantage of the scale and diversity of the M3 and M4 datasets to offer a strong foundation to enhance time series forecasting.

5. Discussion

This study discusses the reason for using ARIMA and Ata methodologies within the forecasting framework, while also considering their individual strengths and limitations. ARIMA has long been considered a benchmark statistical model for time series forecasting because it has an established theoretical basis and can capture linear relationships in a straightforward manner using autoregressive, differencing, and moving average components. Its interpretability and analytical rigor make it a standard reference point in empirical forecasting studies. However, ARIMA’s dependence on linearity and stationarity limits its performance when nonlinear dynamics, structural breaks, or irregular seasonal behaviors are present. This makes it less flexible in complicated real-world situations. The Ata method, on the other hand, is a new and modern way to generate forecasts that builds on the ideas of exponential smoothing by using adaptive updating mechanisms. Its structure allows parameters to evolve dynamically over time, enabling the model to respond flexibly to shifts in level and trend. Moreover, the Ata method’s capacity to incorporate additive and multiplicative forms across diverse series enhances its robustness, while its algorithmic simplicity makes it computationally efficient and easily scalable to large datasets, such as those encountered in forecasting competitions. These qualities represent Ata as a versatile and easily adaptable method that bridges the gap between simplicity and flexibility, thereby complementing the more rigid structure of ARIMA. Taken together, the comparative use of these two approaches not only ensures methodological robustness but also highlights the potential for hybrid frameworks that integrate the interpretability of ARIMA with the adaptability of Ata, ultimately broadening the scope of effective forecasting strategies.

Table 2. Optimal hybrid weights by frequency for M3 dataset.

Frequency/Model	ARIMA	Ata-Lowest	Ata-Median
Yearly	0.05	0.15	0.80
Quarterly	0.15	0.35	0.50
Monthly	0.30	0.40	0.30
Other	0.00	0.80	0.20

Table shows optimized weights for each model by frequency type using grid search algorithms.

summarizes the optimized hybrid weights assigned to the ARIMA, Atalowest, and Ata-median models for different frequency categories in the M3 dataset. These weights were obtained using a grid search procedure combined with in-sample sMAPE minimization. The grid search systematically explored candidate weight combinations, and the final values correspond to those that minimized the error for each frequency type. A higher weight indicates a stronger contribution of the corresponding model to the hybrid forecast. The results highlight that the Ata-median model dominates for yearly series, while the Ata-lowest model gains importance in other categories, and ARIMA plays a larger role in monthly and quarterly data.

The sMAPE evaluation results, presented in

Table A1. M3 competition yearly sMAPE results.

Method	Forecasting Horizons						Averages
	1	2	3	4	5	6	1–4	1–6
Naive2	8.5	13.2	17.8	19.9	23.0	24.9	14.85	17.88
Single	8.5	13.3	17.6	19.8	22.8	24.8	14.82	17.82
Holt	8.3	13.7	19.0	22.0	25.2	27.3	15.77	19.27
B-J automatic	8.6	13.0	17.5	20.0	22.8	24.5	14.78	17.73
ForecastPro	8.3	12.2	16.8	19.3	22.2	24.1	14.15	17.14
Theta	8.0	12.2	16.7	19.2	21.7	23.6	14.02	16.90
RBF	8.2	12.1	16.4	18.3	20.8	22.7	13.75	16.42
ForcX	8.6	12.4	16.1	18.2	21.0	22.7	13.80	16.48
ETS	9.3	13.6	18.3	20.8	23.4	25.8	15.48	18.53
Ata(p, 0)	9.1	13.5	17.6	19.9	22.8	25.1	15.04	18.00
Ata(p, 1)	8.3	12.2	16.8	18.6	21.5	23.3	13.95	16.78
Ata–comb	8.4	12.3	16.5	18.3	21.0	22.7	13.87	16.54
Ata–lowest	8.0	12.1	16.4	18.9	21.9	24.0	13.85	16.88
Ata–median	8.1	11.4	15.2	17.1	19.6	21.1	12.94	15.40
Ata–best	7.9	11.2	15.1	17.1	19.5	21.1	12.82	15.31

,

Table A2. M3 competition quarterly sMAPE results.

Method	Forecasting Horizons							Averages
	1	2	3	4	5	6	8	1–4	1–6	1–8
Naive2	5.4	7.4	8.1	9.2	10.4	12.4	13.7	7.55	8.82	9.95
Single	5.3	7.2	7.8	9.2	10.2	12.0	13.4	7.38	8.63	9.72
Holt	5.0	6.9	8.3	10.4	11.5	13.1	15.6	7.67	9.21	10.67
B-J automatic	5.5	7.4	8.4	9.9	10.9	12.5	14.2	7.79	9.10	10.26
ForecastPro	4.9	6.8	7.9	9.6	10.5	11.9	13.9	7.28	8.57	9.77
Theta	5.0	6.7	7.4	8.8	9.4	10.9	12.0	7.00	8.04	8.96
RBF	5.7	7.4	8.3	9.3	9.9	11.4	12.6	7.69	8.67	9.57
ForcX	4.8	6.7	7.7	9.2	10.0	11.6	13.6	7.12	8.35	9.54
ETS	5.0	6.6	7.9	9.7	10.9	12.1	14.2	7.32	8.71	9.94
Ata(p, 0)	5.2	7.1	7.8	9.7	10.1	11.8	13.5	7.45	8.62	9.71
Ata(p, 1)	5.3	6.8	7.6	9.1	9.9	11.0	12.4	7.19	8.28	9.24
Ata–comb	5.1	6.8	7.5	9.0	9.6	10.9	12.3	7.10	8.13	9.07
Ata–lowest	5.0	6.7	7.6	9.2	9.7	11.2	12.8	7.10	8.22	9.26
Ata–median	5.0	6.8	7.7	9.1	9.7	11.0	12.6	7.16	8.22	9.23
Ata–best	4.9	6.6	7.5	9.0	9.4	10.8	12.4	6.98	8.03	9.03

,

Table A3. M3 competition monthly sMAPE results.

	Forecasting Horizons										Averages
Method	1	2	3	4	5	6	8	12	15	18	1–4	1–6	1–8	1–12	1–15	1–18
Naive2	15.0	13.5	15.7	17.0	14.9	14.4	15.6	16.0	19.3	20.7	15.30	15.08	15.26	15.55	16.16	16.89
Single	13.0	12.1	14.0	15.1	13.5	13.1	13.8	14.5	18.3	19.4	13.53	13.44	13.60	13.83	14.51	15.32
Holt	12.2	11.6	13.4	14.6	13.6	13.3	13.7	14.8	18.8	20.2	12.95	13.11	13.33	13.77	14.51	15.36
B-J automatic	12.3	11.7	12.8	14.3	12.7	12.3	13.0	14.1	17.8	19.3	12.78	12.70	12.86	13.19	13.95	14.80
ForecastPro	11.5	10.7	11.7	12.9	11.8	12.0	12.6	13.2	16.4	18.3	11.72	11.78	12.02	12.43	13.07	13.85
Theta	11.2	10.7	11.8	12.4	12.2	12.7	13.2	16.2	18.2	18.2	11.54	11.75	12.09	12.48	13.09	13.83
RBF	13.7	12.3	13.7	14.3	12.3	12.5	13.5	14.1	17.3	17.8	13.49	13.14	13.36	13.64	14.19	14.76
ForcX	11.6	11.2	12.6	14.0	12.4	12.0	12.8	13.9	17.8	18.7	12.32	12.28	12.44	12.81	13.58	14.44
ETS	11.5	10.6	12.3	13.4	12.3	13.2	13.2	14.1	17.6	18.9	11.93	12.05	12.43	12.96	13.64	14.45
Ata(p, 0)	11.5	10.8	12.6	13.8	12.6	12.5	12.9	13.9	17.3	18.9	12.20	12.33	12.78	12.98	13.67	14.49
Ata(p, 1)	11.0	10.9	12.2	13.4	12.8	13.0	13.8	15.4	18.9	20.9	11.86	12.16	12.60	13.87	14.39	15.33
Ata–comb	11.1	10.7	12.1	13.1	12.0	11.9	12.4	13.1	16.3	17.4	11.74	11.81	12.04	12.48	13.07	13.75
Ata–lowest	11.6	10.8	12.2	12.9	12.7	12.7	13.0	13.9	16.9	18.4	11.90	12.16	12.57	13.02	13.61	14.33
Ata–median	11.8	10.7	12.3	13.0	12.3	12.3	12.8	13.7	16.5	17.9	11.94	12.06	12.44	12.86	13.41	14.09
Ata–best	11.6	10.5	12.1	13.0	11.6	11.8	12.4	13.3	16.4	17.8	11.79	11.77	12.07	12.44	13.06	13.76

and

Table A4. M3 competition other sMAPE results.

Method	Forecasting Horizons							Averages
	1	2	3	4	5	6	8	1–4	1–6	1–8
Naive2	2.2	3.6	5.4	6.3	7.8	7.6	9.2	4.38	5.49	6.30
Single	2.1	3.6	5.4	6.3	7.8	7.6	9.2	4.36	5.48	6.29
Holt	1.9	2.9	3.9	4.7	5.8	5.6	7.2	3.32	4.13	4.81
B-J automatic	1.8	3.0	4.5	4.9	6.1	6.1	7.5	3.52	4.38	5.06
ForecastPro	1.9	3.0	4.0	4.4	5.4	5.4	6.7	3.31	4.00	4.60
Theta	1.8	2.7	3.8	4.5	5.6	5.2	6.1	3.20	3.93	4.41
RBF	2.7	3.8	5.2	5.8	6.9	6.3	7.3	4.38	5.12	5.60
ForcX	2.1	3.1	4.1	4.4	5.6	5.4	6.5	3.42	4.10	4.64
ETS	2.0	3.0	4.0	4.4	5.4	5.1	6.3	3.37	3.99	4.51
Ata(p, 0)	2.1	3.5	5.4	6.3	7.8	7.5	9.1	4.34	5.45	6.26
Ata(p, 1)	1.9	2.9	4.1	4.8	6.0	5.7	7.1	3.46	4.26	4.87
Ata–comb	3.0	4.5	5.1	6.3	5.8	6.8	8.3	3.62	4.42	4.94
Ata- lowest	1.8	2.7	3.8	4.3	5.4	4.9	5.9	3.12	3.80	4.27
Ata-median	1.9	2.8	4.2	4.8	5.9	5.3	6.2	3.43	4.15	4.62
Ata–best	1.8	2.6	3.8	4.3	5.4	4.9	5.8	3.14	3.80	4.24

, highlight key findings across all frequency categories—namely, yearly, quarterly, monthly, and other—together with the overall performance of the proposed hybrid model (Ata-best). These findings provide compelling evidence of the benefits of model combination strategies that are customized using performance-based weighting. Combining complementary patterns captured by various Ata variations, the hybrid model produces more accurate forecasts, outperforming both the lowest and median Ata variants. Since the sMAPE was adopted as the official error measure of the M3 competition and, in addition, it is a scale-independent metric, it was chosen as the primary criterion when analyzing the M3 dataset in this study. The scale-independence property is particularly important because the M3 dataset contains time series with highly diverse magnitudes, ranging from small-scale microeconomic indicators to large-scale macroeconomic aggregates. By using the sMAPE, all series can be evaluated on a comparable basis, ensuring a fair assessment of model accuracy without being biased toward the absolute scale of the data.

To maintain the coherence of the main text and avoid overloading it with high-volume numerical tables, the detailed frequency-level results have been moved to the Appendix A. This ensures both readability and completeness, allowing interested readers to examine the extended evidence without interrupting the flow of the discussion.

Importantly, the Ata-best model outperforms the ARIMA model, which was known as B-J Automatic in the original M3 competition tables. Given the Box–Jenkins methodology’s historical success and wide application to time series forecasting, this finding is especially noteworthy. The hybrid Ata-based approach shows that it is not only competitive but also robust in a variety of time series structures by outperforming B–J Automatic in the entire dataset and in all frequency subsets. These results also demonstrate how adaptable the suggested hybrid structure is, as it can dynamically adapt to underlying patterns in the data without depending entirely on strict statistical assumptions. Moreover, the results indicate that the Ata model’s potential is further increased when utilized as part of a weighted ensemble that takes into account the complementary strengths of various configurations and models, even though the model by itself already provides a competitive performance due to its adaptive structure.

In conclusion, the proposed hybrid approach “Ata-best” performs better in terms of forecasting accuracy across all frequency tables than both the traditional ARIMA benchmark and all Ata models. In the case of the M3 competition, the suggested Ata-best model outperforms the ARIMA model and previous Ata models, as well as the Theta model, which was the M3 competition’s overall winner, in almost every forecasting horizons. According to

Table 3. M3 competition overall dataset sMAPE results.

	Forecasting Horizons										Averages
Method	1	2	3	4	5	6	8	12	15	18	1–4	1–6	1–8	1–12	1–15	1–18
Naive2	10.5	11.3	13.6	15.1	15.1	15.9	14.5	16.0	19.3	20.7	12.62	13.57	13.76	14.24	14.81	15.47
Single	9.5	10.6	12.7	14.1	14.3	15.0	13.3	14.5	18.3	19.4	11.73	12.71	12.84	13.13	13.67	14.32
Holt	9.0	10.2	12.6	13.7	14.5	15.8	13.0	14.8	18.8	20.2	11.67	12.93	13.11	13.42	13.95	14.60
B-J automatic	9.2	10.4	12.2	13.9	14.0	14.6	13.0	14.1	17.8	19.3	11.42	12.39	12.52	12.78	13.33	13.99
ForecastPro	8.6	9.6	11.4	12.9	13.3	14.2	12.6	13.2	16.4	18.3	10.64	11.67	11.84	12.12	12.58	13.18
Theta	8.4	9.6	11.3	12.5	13.2	13.9	12.0	13.2	16.2	18.2	10.44	11.47	11.61	11.94	12.41	13.00
RBF	9.9	10.5	12.4	13.4	13.2	14.1	12.8	14.1	17.3	17.8	11.56	12.26	12.40	12.76	13.24	13.74
ForcX	8.7	9.8	11.6	13.1	13.2	13.8	12.6	13.9	17.8	18.7	10.82	11.72	11.88	12.21	12.80	13.48
ETS	8.8	9.8	12.0	13.5	13.9	14.7	13.0	14.1	17.6	18.9	11.04	12.13	12.32	12.66	13.14	13.77
Ata(p, 0)	8.9	10.0	12.1	13.7	13.9	14.7	12.8	13.9	17.3	18.9	11.16	12.21	12.34	12.64	13.13	13.77
Ata(p, 1)	8.4	9.7	11.5	12.9	13.6	14.2	12.9	15.4	18.9	20.9	10.64	11.72	11.94	12.66	13.32	14.09
Ata–comb	8.5	9.6	11.4	12.8	13.0	13.6	12.0	13.1	16.3	17.4	10.56	11.47	11.58	11.94	12.40	12.94
Ata–lowest	8.6	9.6	11.5	12.8	13.5	14.3	12.4	13.9	16.9	18.4	10.60	11.70	11.92	12.32	12.80	13.39
Ata–median	8.7	9.4	11.3	12.4	12.8	13.5	12.2	13.7	16.5	17.9	10.46	11.36	11.61	12.03	12.50	13.08
Ata–best	8.5	9.2	11.1	12.4	12.4	13.2	12.0	13.3	16.4	17.8	10.30	11.13	11.33	11.71	12.20	12.79

, the Ata-best model achieved a lower sMAPE than the Theta method, the official winner of the M3 competition; therefore, we can state that Ata-best can be considered the top-performing model for the M3 dataset. This outstanding performance not only demonstrates the Ata method’s inherent strength but also the effectiveness and adaptability of statistical hybrid modeling when applied through performance-driven model combination. To further clarify the contribution of each individual component, an ablation study was conducted (

Table A7. Ablation study on selected models for the M3 competition overall dataset.

	Forecasting Horizons										Averages						Rank
Method	1	2	3	4	5	6	8	12	15	18	1–4	1–6	1–8	1–12	1–15	1–18
B-J automatic (ARIMA)	9.2	10.4	12.2	13.9	14.0	14.6	13.0	14.1	17.8	19.3	11.42	12.39	12.52	12.78	13.33	13.99	5
Theta (Winner)	8.4	9.6	11.3	12.5	13.2	13.9	12.0	13.2	16.2	18.2	10.44	11.47	11.61	11.94	12.41	13.00	2
Ata–lowest	8.6	9.6	11.5	12.8	13.5	14.3	12.4	13.9	16.9	18.4	10.60	11.70	11.92	12.32	12.80	13.39	4
Ata–median	8.7	9.4	11.3	12.4	12.8	13.5	12.2	13.7	16.5	17.9	10.46	11.36	11.61	12.03	12.50	13.08	3
Ata–best	8.5	9.2	11.1	12.4	12.4	13.2	12.0	13.3	16.4	17.8	10.30	11.13	11.33	11.71	12.20	12.79	1

), showing that the superiority of Ata-best arises from systematic improvements over Ata-lowest, Ata-median, ARIMA, and the winning Theta model across different forecasting horizons. These findings offer strong evidence that, when properly planned, adjusted, and tailored to the structural properties of the data, hybrid statistical approaches can obtain substantial improvements in challenging forecasting scenarios such as the M3 dataset.

The best hybrid weights for each frequency type in the M4 dataset—ARIMA, Atalowest, and Ata-median—are shown in

Table 4. Optimal hybrid weights by frequency for M4 competition.

Frequency/Model	ARIMA	Ata-Lowest	Ata-Median
Yearly	0.15	0.15	0.70
Quarterly	0.30	0.40	0.30
Monthly	0.40	0.35	0.25
Weekly	0.50	0.00	0.50
Daily	0.50	0.25	0.25
Hourly	0.40	0.10	0.50

. The weight distributions differ across frequencies, just like in the M3 results, suggesting that the contribution of each model component should be modified according to the time series’ characteristics. However,

Table 5. M4 competition OWA results.

Team	Method Type	Yearly	Quarterly	Monthly	Weekly	Daily	Hourly	Total	Rank
Smyl	H	0.778	0.847	0.836	0.851	1.046	0.440	0.821	1
Montero-Manso, et al.	C (S & ML)	0.799	0.847	0.858	0.796	1.019	0.484	0.838	2
Pawlikowski, et al.	C (S)	0.820	0.855	0.867	0.766	0.806	0.444	0.841	3
Jaganathan & Prakash	C (S & ML)	0.813	0.859	0.854	0.795	0.996	0.474	0.842	4
Fiorucci & Louzada	C (S)	0.802	0.855	0.868	0.897	0.977	0.674	0.843	5
Petropoulos & Svetunkov	C (S)	0.806	0.853	0.876	0.751	0.984	0.663	0.848	6
Shaub	C (S)	0.801	0.908	0.882	0.957	1.060	0.653	0.860	7
Legaki & Koutsouri	S	0.788	0.898	0.905	0.968	0.996	1.012	0.861	8
Doornik, et al.	C (S)	0.836	0.878	0.881	0.782	1.002	0.410	0.865	9
Selamlar (252)	S	0.819	0.873	0.908	0.898	0.988	0.851	0.868	10
Pedregal, et al.	C (S)	0.824	0.883	0.899	0.939	0.990	0.485	0.869	11
Taylan (255)	S	0.818	0.916	0.901	0.930	1.008	0.817	0.872	12
Spiliotis & Assimakopoulos	S	0.823	0.889	0.907	0.939	0.990	0.860	0.874	13
Roubinchtein	C(S)	0.850	0.885	0.881	0.873	1.091	0.586	0.876	14
Ibrahim	S	0.805	0.890	0.921	0.961	1.098	0.991	0.880	15
Yapar, et al. (009)	S	0.820	0.880	0.969	0.930	0.985	0.817	0.885	16
Tartu M4 seminar	C (S & ML)	0.820	0.960	0.932	0.892	0.930	0.598	0.888	17
Waheeb	C (S)	0.880	0.880	0.927	0.779	0.999	0.507	0.894	18
Darin & Stellwagen	S	0.877	0.887	0.887	0.739	1.135	0.496	0.895	19
Dantas & Cyrino Oliveira	C (S)	0.866	0.892	0.914	0.941	1.057	0.794	0.896	20
The M4 Team (Theta)	S	0.872	0.917	0.907	0.971	0.999	1.006	0.897	21
The M4 Team (Com)	S	0.867	0.890	0.920	0.926	0.978	1.556	0.898	22
The M4 Team (Arima)	S	0.892	0.898	0.903	0.932	1.044	0.524	0.902	23
The M4 Team (Damped)	S	0.890	0.893	0.924	0.917	0.997	1.141	0.907	25
The M4 Team (ETS)	S	0.903	0.891	0.915	0.931	0.996	0.852	0.908	26
Yilmaz (256)	S	0.819	0.902	1.009	0.908	0.990	13.685	0.967	36
The M4 Team (Holt)	S	0.947	0.932	0.988	0.966	0.995	2.749	0.971	37
Çetin (253)	S	1.009	0.977	0.939	0.917	1.005	0.799	0.973	38
The M4 Team (SES)	S	1.003	0.970	0.951	0.975	1.000	0.990	0.975	39
Ata–lowest	S	0.895	0.892	0.901	0.909	0.970	0.735	0.895	19
Ata–median	S	0.807	0.901	0.911	0.919	1.006	0.659	0.869	11
Ata–best	C (S)	0.790	0.861	0.866	0.805	0.984	0.575	0.837	2 *

* The star indicates the re-ranked position (second overall) highlighted without altering the official M4 table.

,

Table A5. M4 competition sMAPE results.

Team	Method Type	Yearly	Quarterly	Monthly	Weekly	Daily	Hourly	Total	Rank
Smyl	H	13.176	9.679	12.126	7.817	3.170	9.328	11.374	1
Montero-Manso, et al.	C (S & ML)	13.528	9.733	12.639	7.625	3.097	11.506	11.720	3
Pawlikowski, et al.	C (S)	13.943	9.796	12.747	6.919	2.452	9.611	11.845	5
Jaganathan & Prakash	C (S & ML)	13.712	9.809	12.487	6.814	3.037	9.934	11.695	2
Fiorucci & Louzada	C (S)	13.673	9.816	12.737	8.627	2.985	15.563	11.836	4
Petropoulos & Svetunkov	C (S)	13.669	9.800	12.888	6.726	2.995	13.167	11.887	6
Shaub	C (S)	13.679	10.378	12.839	7.818	3.222	13.466	12.020	9
Legaki & Koutsouri	S	13.366	10.155	13.002	9.148	3.041	17.567	11.986	8
Doornik, et al.	C(S)	13.910	10.000	12.780	6.728	3.053	8.913	11.924	7
Selamlar (252)	S	13.930	9.960	13.131	8.201	3.003	13.111	12.108	12
Pedregal, et al.	C (S)	13.821	10.093	13.151	8.989	3.026	9.765	12.114	13
Taylan (255)	S	13.930	10.292	12.936	8.540	3.095	12.851	12.098	11
Spiliotis & Assimakopoulos	S	13.804	10.128	13.142	8.990	3.027	17.756	12.148	15
Roubinchtein	C (S)	14.445	10.172	12.911	8.435	3.270	12.871	12.183	17
Ibrahim	S	13.677	10.089	13.321	9.089	3.071	18.093	12.198	18
Yapar, et al. (009)	S	13.981	10.016	13.047	7.540	3.004	12.851	12.093	10
Tartu M4 seminar	C (S & ML)	14.096	11.109	13.290	8.513	2.852	13.851	12.496	23
Waheeb	C (S)	14.783	10.059	12.770	7.076	2.997	12.047	12.146	14
Darin & Stellwagen	S	14.663	10.155	13.058	6.582	3.077	11.683	12.279	19
Dantas & Cyrino Oliveira	C (S)	14.746	10.254	13.462	8.873	3.245	16.941	12.553	25
The M4 Team (Theta)	S	14.593	10.311	13.002	9.093	3.053	18.132	12.309	20
The M4 Team (Com)	S	14.848	10.175	13.434	8.944	2.980	22.053	12.555	27
The M4 Team (Arima)	S	15.168	10.431	13.443	8.653	3.193	12.045	12.661	29
The M4 Team (Damped)	S	15.198	10.237	13.473	8.866	3.064	19.265	12.661	30
The M4 Team (ETS)	S	15.356	10.291	13.525	8.727	3.046	17.307	12.725	31
Yilmaz (256)	S	13.933	10.207	13.085	8.304	3.022	13.399	12.148	16
The M4 Team (Holt)	S	16.354	10.907	14.812	9.708	3.066	29.249	13.775	43
Çetin (253)	S	16.529	10.671	13.409	8.213	3.056	12.771	13.011	35
The M4 Team (SES)	S	16.396	10.600	13.618	9.012	3.045	18.094	13.087	37
Ata–lowest	S	15.231	10.145	12.908	8.393	2.864	13.459	12.341	21
Ata–median	S	13.712	10.173	13.146	8.393	3.057	12.037	12.115	14
Ata–best	C (S)	13.474	9.854	12.614	7.415	2.960	11.846	11.719	3 *

* The star indicates the re-ranked position (third for sMAPE metric) highlighted without altering the official M4 table.

and

Table A6. M4 competition MASE results.

Team	Method Type	Yearly	Quarterly	Monthly	Weekly	Daily	Hourly	Total	Rank
Smyl	H	2.980	1.118	0.884	2.356	3.446	0.893	1.536	1
Montero-Manso, et al.	C (S & ML)	3.060	1.111	0.893	2.108	3.344	0.819	1.551	3
Pawlikowski, et al.	C (S)	3.130	1.125	0.905	2.158	2.642	0.873	1.547	2
Jaganathan & Prakash	C (S & ML)	3.126	1.135	0.895	2.350	3.258	0.976	1.571	6
Fiorucci & Louzada	C (S)	3.046	1.122	0.907	2.368	3.194	1.203	1.554	4
Petropoulos & Svetunkov	C (S)	3.082	1.118	0.913	2.133	3.229	1.458	1.565	5
Shaub	C (S)	3.038	1.198	0.929	2.947	3.479	1.372	1.595	7
Legaki & Koutsouri	S	3.009	1.198	0.966	2.601	3.254	2.557	1.601	8
Doornik, et al.	C (S)	3.262	1.163	0.931	2.302	3.284	0.801	1.627	11
Selamlar (252)	S	3.124	1.155	0.962	2.499	3.246	2.366	1.613	9
Pedregal, et al.	C (S)	3.185	1.164	0.943	2.488	3.232	1.049	1.614	10
Taylan (255)	S	3.117	1.231	0.962	2.578	3.277	2.238	1.631	13
Spiliotis & Assimakopoulos	S	3.184	1.178	0.959	2.488	3.232	1.808	1.628	12
Roubinchtein	C (S)	3.244	1.159	0.921	2.290	3.632	1.129	1.633	15
Ibrahim	S	3.075	1.185	0.977	2.583	3.894	2.388	1.644	16
Yapar, et al. (009)	S	3.115	1.166	1.098	2.578	3.225	2.238	1.678	20
Tartu M4 seminar	C (S & ML)	3.091	1.250	1.002	2.375	3.025	1.058	1.633	14
Waheeb	C (S)	3.400	1.160	1.029	2.180	3.321	0.861	1.706	27
Darin & Stellwagen	S	3.406	1.168	0.924	2.107	4.128	0.856	1.693	25
Dantas & Cyrino Oliveira	C (S)	3.294	1.170	0.952	2.534	3.436	1.598	1.657	17
The M4 Team (Theta)	S	3.382	1.232	0.970	2.637	3.262	2.455	1.696	26
The M4 Team (Com)	S	3.280	1.173	0.966	2.432	3.203	4.582	1.638	18
The M4 Team (Arima)	S	3.402	1.165	0.930	2.556	3.410	0.943	1.666	19
The M4 Team (Damped)	S	3.379	1.173	0.972	2.404	3.326	2.956	1.683	23
The M4 Team (ETS)	S	3.444	1.161	0.948	2.527	3.253	1.824	1.680	21
Yilmaz (256)	S	3.124	1.203	1.182	2.528	3.239	3.605	1.985	44
The M4 Team (Holt)	S	3.550	1.198	1.009	2.420	3.223	9.356	1.772	34
Çetin (253)	S	4.000	1.350	1.009	2.602	3.299	2.163	1.886	40
The M4 Team (SES)	S	3.981	1.340	1.019	2.685	3.281	2.385	1.885	39
Ata–lowest	S	3.410	1.182	0.965	2.503	3.273	1.765	1.686	24
Ata–median	S	3.081	1.205	0.968	2.561	3.303	1.588	1.618	11
Ata–best	C (S)	3.004	1.133	0.911	2.226	3.264	1.209	1.551	3 *

* The star indicates the re-ranked position (third for MASE metric) highlighted without altering the official M4 table.

’s comprehensive evaluation metrics offer the most important insights. As in the case of the M3 dataset, the detailed frequency-level results for M4 are also provided in the Appendix B to preserve the readability of the main text.

Table A5, which presents performance based on the sMAPE metric, makes it clear that the suggested hybrid model Ata-best outperforms the conventional ARIMA model and the individual Ata variants (Ata-lowest and Ata-median) in terms of forecasting accuracy. Out of all the models that take part in the M4 competition, the Ata-best model comes in third place (rank $3^{*}$) overall, outperforming Ata-lowest (rank 21), Ata-median (rank 14), and ARIMA (reported in the official table of the M4 study as The M4 Team (ARIMA) with rank 29) according to the sMAPE ranking. Here, the star ($*$) indicates that, without altering the original table reported in the official M4 paper [3], we have highlighted the improvement by showing that our proposed model rises to the third position. This notation is also consistently applied in Table 5 and Table A6, where it conveys the same meaning. This consistent benefit across many frequency ranges (from hourly to yearly) demonstrates the hybrid approach’s endurance in terms of scale-invariant performance and directional accuracy.

Table A6, which displays performance based on the MASE (mean absolute scaled error) metric, provides additional evidence of improvement. The Ata-best model ranks third as regards the MASE metric and again produces lower MASE values than its counterparts i.e., Ata models and ARIMA. This implies that the hybrid model improves performance in scale-sensitive error measurement contexts in addition to improving the sMAPE, which is frequently used in the M4 competition. Importantly, the MASE, like the sMAPE, is a scaleindependent error metric, which makes it particularly suitable for comparing forecasting accuracy across heterogeneous time series of different magnitudes. Its inclusion in this study ensures that the evaluation is not biased by series scale and strengthens the robustness of the comparative analysis.

According to Table 5, the Ata-best model achieves an outstanding second place among all competing methods, which takes into account the OWA metric, the official evaluation criterion used to determine final rankings in the M4 competition. This further reinforces its ability to generalize well across both high-frequency (e.g., hourly, daily) and lowfrequency (e.g., yearly, quarterly) time series, which are often characterized by different noise structures and trend dynamics. It is the OWA metric that integrates both into a single performance indicator and ultimately establishes the leaderboard rankings, even though sMAPE and MASE are also reported for transparency and interpretability. This result further supports the suggested hybrid model’s ability to generalize across these categories. Notably, the Ata-best model outperforms the ARIMA model, which is known as a classical benchmark in statistical forecasting, on every evaluation metric. For transparency,

Table A8. Ablation study on selected models for the M4 competition overall dataset (OWA metric).

Method	Yearly	Quarterly	Monthly	Weekly	Daily	Hourly	Total	Rank
Smyl (Winner)	0.778	0.847	0.836	0.851	1.046	0.440	0.821	1
The M4 Team (ARIMA)	0.892	0.898	0.903	0.932	1.044	0.524	0.902	23
Ata–lowest	0.895	0.892	0.901	0.909	0.970	0.735	0.895	19
Ata–median	0.807	0.901	0.911	0.919	1.006	0.659	0.869	11
Ata–best	0.790	0.861	0.866	0.805	0.984	0.575	0.837	2

provides an ablation study isolating the roles of ARIMA, Ata variants, and the winning Smyl model, confirming that the Ata-best configuration reliably secures the second rank overall. The results indicate that, even with ARIMA’s historical significance and extensive use in many ensemble techniques, a well-designed Ata-based hybrid can be a more precise and adaptable substitute, particularly in a major forecasting competition like M4.

In the official M4 paper [3], the reported runtimes highlight that several participants who submitted Ata-based models, including Selamlar, Taylan, Yapar et al., Yilmaz, and Çetin listed in Table 5, Table A5 and Table A6, implemented their approaches through a standalone .exe platform. According to these records, their computations ranged from approximately 37.2 min to 393.5 min, depending on the specific configuration and dataset frequency. By comparison, some of the benchmark models reported in the same study required substantially longer runtimes, with the winning hybrid ETS–RNN method proposed by Smyl [8] taking 8056.0 min and the ARIMA benchmark requiring 3030.9 min. In contrast, the present study extends this line of research by incorporating both the ARIMA benchmark and multiple variants of the Ata method within a unified framework, executed entirely in the RStudio environment. Unlike single-model implementations, our methodology systematically evaluates seven distinct variations of the Ata model for each individual series, selecting the most suitable versions (“Ata-lowest” and “Ata-median”) based on in-sample sMAPE. This model selection process, combined with the subsequent gridsearch-based weight optimization for hybridization with ARIMA, substantially increases the computational burden. As a result, the complete experimental pipeline required approximately 2880 min for the M4 dataset. This comparison underscores that, although the hybrid design involves a more comprehensive and computationally demanding workflow than individual Ata-based runs, its runtime remains considerably more efficient than some state-of-the-art benchmarks (e.g., Smyl’s ETS–RNN or ARIMA benchmark). Thus, the proposed hybrid framework achieves a favorable balance between predictive accuracy and computational feasibility.

6. Conclusions

This study proposed a novel hybrid framework for time series forecasting that integrates the classical ARIMA model with multiple variations of the Ata method through a performance-based model selection and grid search optimization weighting strategy. By combining the statistical robustness of ARIMA with the adaptive flexibility of the Ata models, the approach aims to capture both linear dependencies and more complex structural patterns inherent in time series data.

The effectiveness of the proposed framework was rigorously evaluated on two largescale and widely recognized forecasting benchmarks: the M3 and M4 competition datasets. These datasets encompass a broad spectrum of time series with diverse frequencies and levels of complexity, providing a comprehensive testing environment. Results from the M3 dataset demonstrate that the proposed Ata-best model achieved a superior forecasting performance compared to both the traditional ARIMA benchmark and existing Ata variations. Importantly, according to Table 3, the Ata-best model also outperformed the Theta method, which had been recognized as the overall winner of the M3 competition, thereby underscoring the competitive edge and accuracy of the proposed hybrid approach.

In the case of the M4 dataset, the generalizability of the method was further confirmed. The Ata-best model consistently ranked among the top-performing approaches across different frequencies, ultimately taking the second position overall based on the official OWA metric, according to Table 5. Furthermore, the model exhibited stable improvements over ARIMA, Ata variants, and other benchmark methods, demonstrating its robustness in handling both stationary and non-stationary components of large-scale real-world time series.

These findings collectively emphasize several significant contributions. First, the study demonstrates that hybridized statistical models, when thoroughly adjusted and weighted, can outperform both individual traditional methods and benchmarks that have won competitions. Second, the results provide strong evidence that the Ata method, particularly when embedded in a hybrid structure, constitutes a highly competitive alternative for practical forecasting tasks. Finally, the suggested framework is not only accurate but also scalable and adaptable, making it useful for a wide range of real-world forecasting circumstances, from finance and economics to energy demand and environmental applications.

In conclusion, this research demonstrates that the integration of ARIMA with the Ata family of models through performance-driven combination results in substantial accuracy improvements in difficult forecasting situations. The success of the Ata-best model on both the M3 and M4 datasets provides strong evidence that hybrid approaches are a promising direction for improving statistical forecasting methods.

In future studies, the proposed hybrid framework could be extended in several promising directions. One avenue is the integration of machine learning and deep learning components, which may enhance the ability to capture complex nonlinear dynamics and long-range dependencies that are difficult for traditional models alone to address. Additionally, expanding the framework to multivariate forecasting tasks, for instance, using the M5 forecasting competition, would allow researchers to incorporate multiple interdependent series, thereby capturing richer temporal interactions. Beyond this, future work could also focus on incorporating exogenous variables (e.g., macroeconomic indicators or weather conditions), which may significantly improve forecasting accuracy in applied domains such as energy demand, financial markets, and retail planning. Collectively, these directions would strengthen the generalizability, interpretability, and practical applicability of the hybrid forecasting approach beyond competition datasets and into real-world decision-making contexts.