Design of a Secret Sharing Scheme with Mandatory Subgroup Participation

Abstract

This paper proposes an approach based on a secret sharing scheme with the mandatory participation of predefined subgroups. The proposed scheme allows secret reconstruction only when representatives from each designated group of participants (e.g., cloud providers, legally independent parties, etc.) are present. This mechanism enhances resistance to internal collusion, strengthens access control, and enables distributed management. The structure and mathematical foundations of the proposed scheme are presented, along with an analysis of its properties. A cryptanalysis is conducted, evaluating the scheme’s resilience to various types of attacks, and the results are discussed. The computational complexity of the algorithm is also analyzed, and its resource efficiency is confirmed.

1. Introduction

In the context of the widespread use of distributed computing and cloud infrastructures for storing and protecting confidential information, secret sharing schemes play a crucial role in ensuring reliable and fault-tolerant access to data [1,2]. The most common solutions are classical threshold schemes (e.g., Shamir’s scheme), which allow the secret to be reconstructed from any subset of $k$ out of $n$ participants. These schemes enable the distribution of confidential information among multiple parties without storing it in full at a single location, significantly enhancing data security [3,4].

Secret sharing schemes make it possible to divide confidential information Q into $n$ parts and distribute them among $n$ participants. To reconstruct the original secret, it is sufficient to have any k of them. A scheme of this type is also referred to as an ($k,n$)—threshold secret sharing scheme [5,6].

Currently, the most widely used methods include Shamir’s scheme as well as the schemes of Mignotte, Asmuth–Bloom, and others. A distinctive feature of the Mignotte and Asmuth–Bloom schemes is the use of the Chinese Remainder Theorem (CRT) in the secret sharing process [7]. The CRT allows the reconstruction of a numerical value from its representation in a system of residues with pairwise coprime moduli. This provides the mathematical and algorithmic foundation for secret reconstruction schemes. However, the Asmuth–Bloom and Mignotte schemes impose significant constraints on the secret—value $Q$. In the first case, it is limited to the set $Z_{p_0}$, while in the second case, the range of possible values is substantially reduced due to the exclusion of a sufficiently large interval of numbers.

Shamir’s secret sharing scheme was first introduced by Adi Shamir in 1979 in his paper How to Share a Secret [8]. This work described an $(k,n$) threshold scheme that allows reconstruction of the secret from any $k$ out of $n$ parts. The scheme relies on the Lagrange interpolation polynomial, which makes it possible to reconstruct the original secret when k valid shares are available [9,10].

Advantages of Shamir’s Scheme:

• Good scalability. The number of participants can be increased to a value comparable to the size of the finite field $p$, while the minimum number of shares required to reconstruct the secret remains unchanged.
• Perfect distribution. Each share (also referred to as a “shadow”) has the same size as the original secret, making the scheme efficient in terms of data volume.
• Flexibility and renewability. New shares can be generated for the same secret using a different polynomial. This reduces the risk of compromise, as leaked old shares cannot be used unless they originate from the same polynomial.
• Cryptographic strength. If an adversary possesses fewer than k shares, they cannot reconstruct even a single bit of the secret. This level of security is mathematically proven.

Disadvantages of Shamir’s Scheme:

• Dependence on a trusted dealer. The basic implementation assumes that the central trusted party (the dealer) correctly generates and distributes the shares. If the dealer is untrustworthy, they may provide incorrect values, making it impossible to reconstruct the secret.
• Risk of sabotage by the dealer. A malicious or unreliable dealer can intentionally distort the data, disrupt the scheme’s integrity, and even cause complete failure.

In [11], the secret sharing problem is considered from an information-theoretic perspective. The authors propose a method in which only specific participants can reconstruct the secret. They also explore information security techniques in the presence of noise in communication channels used to transmit the shares.

In [12], a time-based secret sharing scheme is introduced. The authors examine approaches for ensuring information-theoretic security by applying temporal constraints.

In [13], a threshold secret sharing scheme based on the Chinese Remainder Theorem is proposed. It is shown to efficiently detect errors and even reveal intentional tampering.

The authors of [14] developed an efficient and reliable threshold scheme for sharing multiple secrets using modern cryptographic tools based on elliptic curves and bilinear pairings.

In [15], the Asmuth–Bloom scheme and its modification are examined. The modified version uses fractal geometry as the encoding function. A numerical method for computing shares is also proposed, enabling simultaneous splitting and encoding of images without the need for additional algorithms, thus avoiding increased computational complexity.

A new threshold scheme based on lattices is described in [16], with its distinguishing feature being the ability for participants to verify the correctness of their received shares. The security of the scheme relies on the computational hardness of lattice problems.

In [17], an encryption algorithm for color images based on the two-dimensional Logistic–Rulkov Neural Map (2D-LRNM) is presented. It is designed to ensure efficient and secure image transmission, particularly in the context of social networks. The algorithm provides separate processing of the three-color channels, incorporates inter-channel interaction, and employs a block-based parallel encryption scheme. The key stream is generated using the 2D-LRNM, which exhibits strong chaotic properties. Experimental results demonstrate a high level of cryptographic security of the proposed approach, as well as a significant reduction in computation time.

The proposed approach has found application in the generation of personal cryptographic keys used in biometric authentication systems and public key infrastructures, where the scheme supports multi-user authorization with the help of cryptographic hardware modules.

However, such schemes assume the homogeneity of participants and do not account for their functional or organizational affiliation. This makes classical schemes vulnerable in situations where

• All participants belong to the same subgroup (e.g., the same department or one side of a conflict of interest);
• Collusion is possible within a single group;
• Strict adherence to principles of role-based access control or regulatory compliance is required (e.g., dual control, the four-eyes principle, or zero trust policies).

Thus, a contradiction arises: on the one hand, joint access to a resource is required, but on the other hand, it must be ensured that access is granted only with the participation of representatives from different groups with distinct roles and trust levels.

To address these limitations, we propose a secret sharing scheme with mandatory participation of representatives from each subgroup. In this scheme, participants are pre-assigned to logical groups based on roles or trust boundaries, and the secret can only be reconstructed if at least one representative from each subgroup is involved.

In this study, the main mathematical quantities and their notations were used. They are summarized in

Table 1. Notations and their meanings.

Notation	Meaning
$Q$	Secret information
n	Total number of participants
k	Threshold value—the minimum number of participants required to reconstruct the secret
(k, n)	Threshold scheme: out of n participants, at least k are required for reconstruction
$p_k$	Prime number used as the modulus for the $k$th participant
f(x)	Lagrange interpolation polynomial
$a_i$	Polynomial coefficients
$t_i$	Random number of each participant
$b_i$	Share of the secret assigned to the $i$th participant

.

2. Materials and Methods

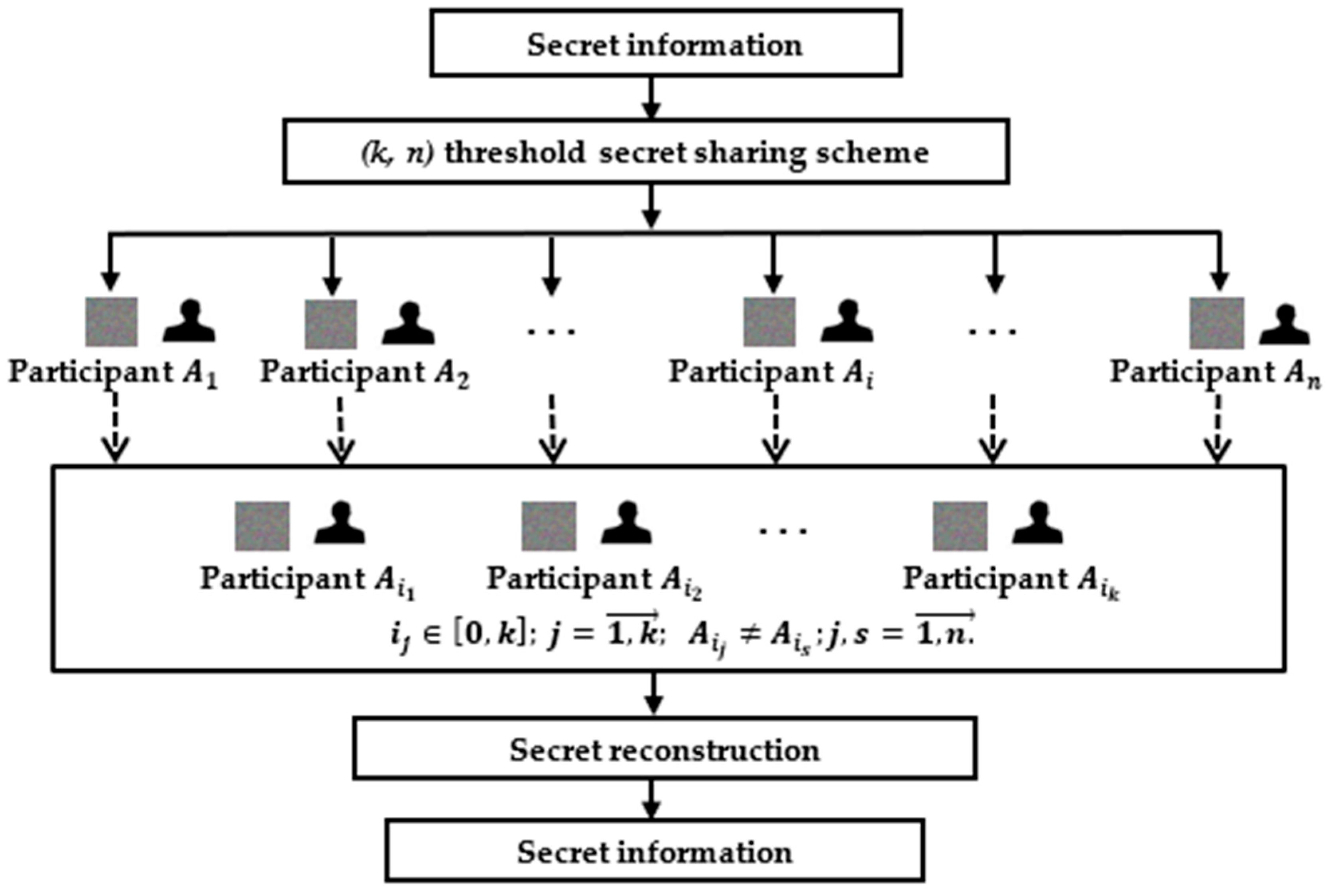
To enable secure distributed storage, a cryptographic secret sharing approach is employed. Confidential data is divided into several shares, which are stored in independent cloud repositories. The original information can be reconstructed only by combining a sufficient number of shares, ensuring both fault tolerance and protection against unauthorized access (see Figure 1).

The core idea of this approach is that no single share contains enough information to reconstruct the original biometric data (templates). Full recovery of the secret is only possible by combining a predefined number of shares, referred to as the threshold value. This provides a high level of security, particularly in distributed data storage and processing infrastructures.

A wide range of secret sharing schemes has been developed to implement these mechanisms, each with its own characteristics, advantages, and limitations. When choosing the optimal solution, special attention should be paid to efficiency: the scheme must ensure a high level of confidentiality while minimizing computational and memory costs.

The key criteria influencing these parameters are as follows:

• Perfection—ensures that if fewer than the threshold number of participants (less than $k$) collaborate, no information about the secret can be obtained. This guarantees the highest level of confidentiality.
• Ideality—means that the size of each share is equal to the size of the original secret. Such a scheme avoids additional memory overhead and is efficient in terms of storage.
• Resource intensity—refers to the amount of memory required for storing and processing the data, including the shares and any auxiliary information. The lower the required memory, the more efficient the scheme.
• Algorithmic complexity—reflects the computational load on the system when generating shares and reconstructing the secret. Efficient schemes minimize the number of operations, which is particularly important for systems with limited computational capacity.

2.1. Lagrange Interpolation Polynomial

Experimental data often consist of a set of points describing the behavior of a measured signal over time or with respect to another variable. For theoretical analysis of such data, it is necessary to construct an approximating function that connects discrete values with a continuous representation—an interpolation polynomial of degree $n$. One of the most widely used methods is Lagrange interpolation. The Lagrange interpolation polynomial (LIP) is a polynomial of degree $n$ that passes through all the given data points. These points may be obtained either experimentally or through random sampling at different time moments. The time intervals between the points may be uneven.

The general form of the Lagrange interpolation polynomial of degree $n$ is given by the formula:

$$L\left(x\right)={\sum }_{i=0}^n\left(f\left(x_i\right)·l_i\left(x\right)\right)$$

(1)

where $n$ is the degree of the polynomial $L\left(x\right)$, $f\left(x_i\right)$ is the value of the interpolated function $f\left(x\right)$ at the interpolation node $x_i$, $l_i\left(x\right)$ are the Lagrange basis polynomials, defined as follows:

$$l_i\left(x\right)={\prod }_{j=0,j\ne i}^n{\displaystyle \frac{x-x_j}{x_i-x_j}}={\displaystyle \frac{x-x_0}{x_i-x_0}}\dots {\displaystyle \frac{x-x_{i-1}}{x_i-x_{i-1}}}·{\displaystyle \frac{x-x_{i+1}}{x_i-x_{i+1}}}\dots {\displaystyle \frac{x-x_n}{x_i-x_n}}$$

(2)

Each basis polynomial equals zero at all interpolation nodes except $x_i$, where it is equal to one. The main advantage of the Lagrange form is that it explicitly expresses the values of the interpolated function at the specified points, which is especially convenient when function values change while the nodes remain fixed. Moreover, the number of arithmetic operations required to construct the Lagrange polynomial is on the order of $n^2$, making it one of the most efficient among known analytical representations of interpolation polynomials [9,18].

2.2. Chinese Remainder Theorem

The Chinese Remainder Theorem (CRT) is a fundamental result in number theory that makes it possible to solve systems of congruences with pairwise coprime moduli. It is widely used in cryptography, computational algorithms, coding theory, secret sharing schemes, and other fields [19,20].

Let $p_0,p_1,\dots ,p_{k-1}$ be pairwise coprime natural numbers, and $a_0,a_1,\dots ,a_{k-1}$ be some integers. Then there exists a unique (within a fixed modulus) integer $Q$ that satisfies the following system of congruences:

$$\left\{\begin{array}{c}Q\equiv a_0\left(mod{p}_0\right) \\ Q\equiv a_1\left(mod{p}_1\right) \\ \dots \\ Q\equiv a_{k-1}\left(mod{p}_{k-1}\right) \end{array}\right.$$

(3)

Furthermore, any two solutions A and B of this system are congruent to each other modulo the product of all moduli:

$$A\equiv B\left(mod{p}_0·p_1·\dots {·p}_{k-1}\right)$$

in other words, the solution to the system of congruences is unique modulo $p_0·p_1·\dots ·p_{k-1}$.

Let us introduce the following notation:

$P=p_0{·p}_1·\dots {·p}_{k-1}$; $P_i={{\displaystyle \frac{P}{p}}}_i$ is the quotient of the total modulus divided by the corresponding modulus $p_i$;

$N_i$ denotes the multiplicative inverse of $P_i$ modulo $P_i$, which means:

$$N_i·P_i\equiv 1\left(mod{p}_i\right),i=\overline{0,k-1}.$$

(4)

Then the general solution $Q$ can be explicitly represented by:

$$Q=a_0{N}_0{P}_0+a_1{N}_1{P}_1+\dots +a_{k-1}{N}_{k-1}{P}_{k-1}.$$

(5)

This formula makes it possible to efficiently compute the solution of the system of congruences and is frequently used in practice in cryptographic algorithms.

3. Results

3.1. Proposed Secret Sharing Scheme with Mandatory Subgroup Participation

This study proposes a secret sharing scheme based on a combination of traditional methods and enhanced to increase the level of information—theoretic security. At the same time, the scheme is designed to perform its main function—reliably partitioning confidential information into multiple shares and allowing its reconstruction only by a specified group of participants.

The main feature of the proposed scheme lies in combining two methods—the Lagrange interpolation form and the Chinese remainder theorem. Next, we will describe the algorithm in more detail.

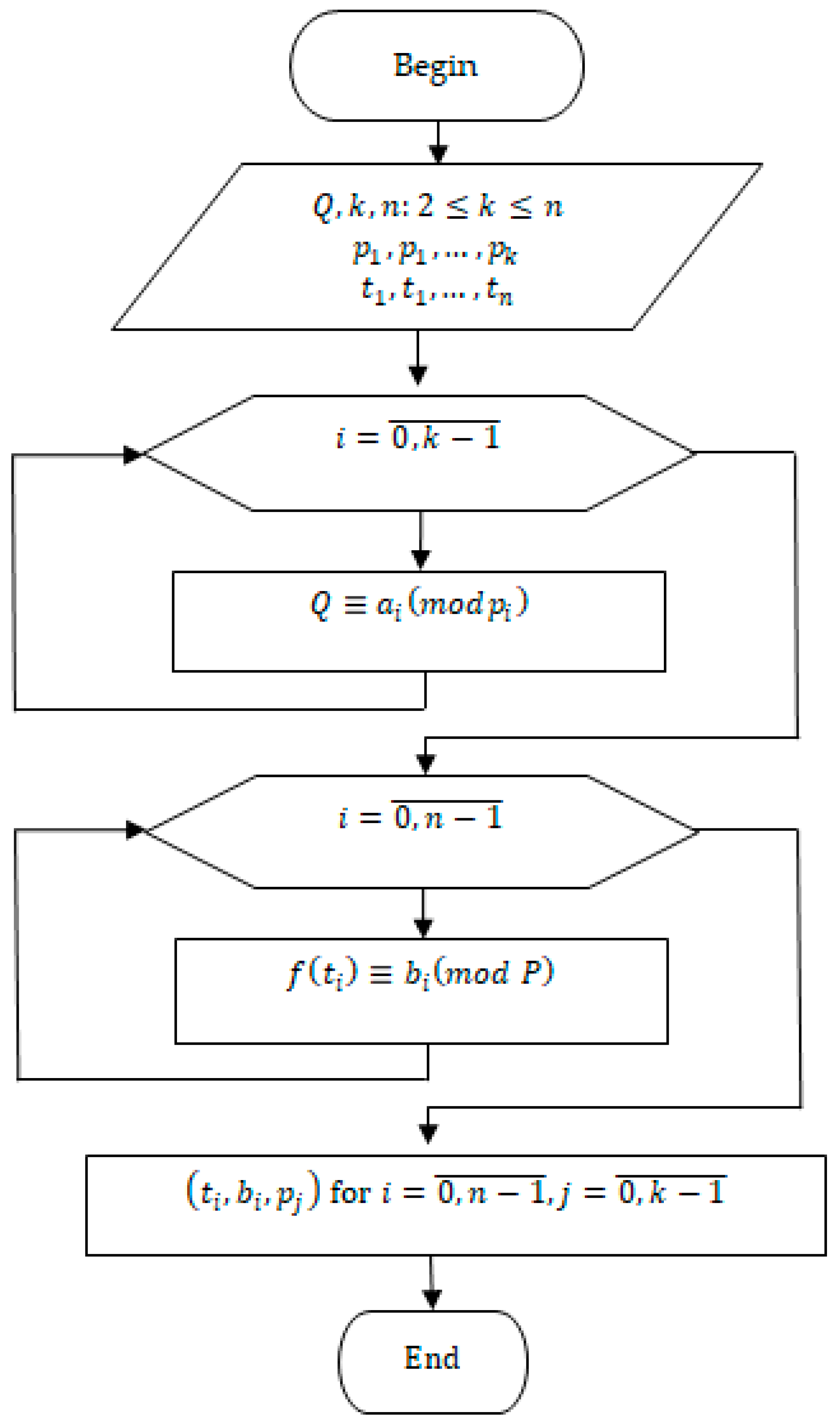
3.1.1. Secret Distribution

We consider $n$ to be the total number of participants and $k$ to be the number of participants required to reconstruct the secret. As in other similar algorithms, any $k$ participants can successfully reconstruct the secret, while a group with fewer participants cannot do so. The condition $2\le k\le n$ must be satisfied, as it is essential for the correctness of the scheme. The inequality $k\ge 2$ guarantees the requirement of collective participation and excludes the possibility of unilateral secret reconstruction. The condition $k\le n$ reflects a natural constraint, according to which the number of required shares cannot exceed the total number of participants, thereby ensuring the feasibility of the reconstruction procedure.

In accordance with the number of participants who can reconstruct the secret, $k$ primes $p_0,p_1,\dots ,p_{k-1}$ are selected.

We denote the secret (in this case, biometric data or a template) by $Q$. Then the coefficients $a_i$ of the polynomial $f\left(x\right)$ for $i=\overline{0,k-1}$ are computed according to the following relationships (6):

$$\left\{\begin{array}{c}Q\equiv a_0\left(mod{p}_0\right) \\ Q\equiv a_1\left(mod{p}_1\right) \\ \dots \\ Q\equiv a_{k-1}\left(mod{p}_{k-1}\right)\end{array}\right.$$

(6)

Therefore, polynomial $f\left(x\right)$ is defined as follows:

$$f\left(x\right)=a_{k-1}{x}^{k-1}+a_{k-2}{x}^{k-2}+\dots +a_2{x}^2+a_{1}x+a_0.$$

(7)

For each participant, a number $t_i$ is randomly selected in such a way that ${\forall i,jt}_i\ne t_j$, where $i=\overline{1,n}$. Subsequently, components of the shares for all $n$ participants are computed by Formula (8):

$$f\left(t_i\right)\equiv b_i\left(modP\right),i=\overline{1,n}$$

(8)

Here $P={\prod }_{j=1}^k{p}_j$. As a result, each participant receives their share in the following form: $\left(t_i,b_i,p_0,p_2,\dots ,p_{k-1}\right)$ for $i=\overline{1,n}, j=\overline{1,k}$.

The block diagram of secret sharing is shown in Figure 2.

Each participant’s share is divided into $k$ groups. Each group uses one modulus. To reconstruct the secret, it is necessary to involve at least one representative from each group. Otherwise, the secret cannot be recovered. The following is a pseudocode example of a scheme with a threshold of (5, 10) (Algorithm 1):

Algorithm 1. Example of a scheme with a threshold of (5, 10):

//Step 1: Initialize input values 1:${(t}_1,b_1{),(t}_2,b_2),(t_3,b_3),(t_4,b_4),(t_5,b_5),(t_6,b_6),{(t_7,b}_7),{(t_8,b}_8),(t_9,b_9),(t_{10},b_{10})$//Shares of participants 2:$p_1$,$p_2$,$p_3$,$p_4$,$p_5$//Modules //Step 2: Randomly distribute${(t_i,b}_i)$pairs among groups 3: Group 1 = ${\left\{\right(t_1,b}_1),{(t_3,b}_3)\}$ 4: Group 2 = ${\left\{\right(t_2,b}_2),{(t_{10},b}_{10})\}$ 5: Group 3 = ${\left\{\right(t_4,b}_4\left)\right\}$ 6: Group 4 = ${\left\{\right(t_7,b}_7),{(t_9,b}_9)\}$ 7: Group 5 = ${\left\{\right(t_5,b}_5),{(t_6,b}_6),{(t_6,b}_6\left)\right\}$ //Step 3: Assign moduli to the groups ModulAssignments: 8: $p_1$ → Group 1 9: $p_3$→ Group 2 10: $p_2$ → Group 3 11: $p_5$ → Group 4 12: $p_4$ → Group 5 //Step 4: Select at least one representative from each group SelectedParticipants = { 13: Group 1: ${(t_1,b}_1)$,$p_1$ 14: Group 2: ${(t_{10},b}_{10})$,$p_3$ 15: Group 3: ${(t_4,b}_4)$,$p_2$ 16: Group 4: ${(t_7,b}_7)$,$p_5$ 17: Group 5: ${(t_5,b}_5)$,$p_4$ }

It should be emphasized that in the proposed scheme, the term “selection of a representative of each group” does not refer to generators of the multiplicative or additive group of integers modulo a prime $p$. A subgroup representative is a participant in the scheme who is assigned a specific share of the secret associated with the modulus $p_i$. Thus, the term “representative” pertains exclusively to the organizational role within the scheme, rather than to the mathematical concept of a “group generator”.

The proposed scheme differs from classical approaches such as Shamir’s scheme (based on Lagrange interpolation), Blakley’s scheme (using vector spaces), and the Karnin-Greene-Hellman scheme (based on solving systems of linear equations), by providing higher resilience to participant compromise attacks. Dividing participants into groups adds an extra layer of protection: even if an adversary gains access to shares from the permitted number of participants, the secret cannot be reconstructed without the mandatory presence of at least one member from each group. This significantly reduces the risk of attacks involving an external entity impersonating a valid participant (e.g., acting as the $k+1$th party) for cryptographic analysis or brute-force guessing. While many existing schemes counter such threats by introducing authentication mechanisms, the proposed approach enhances security through the structure of the scheme itself.

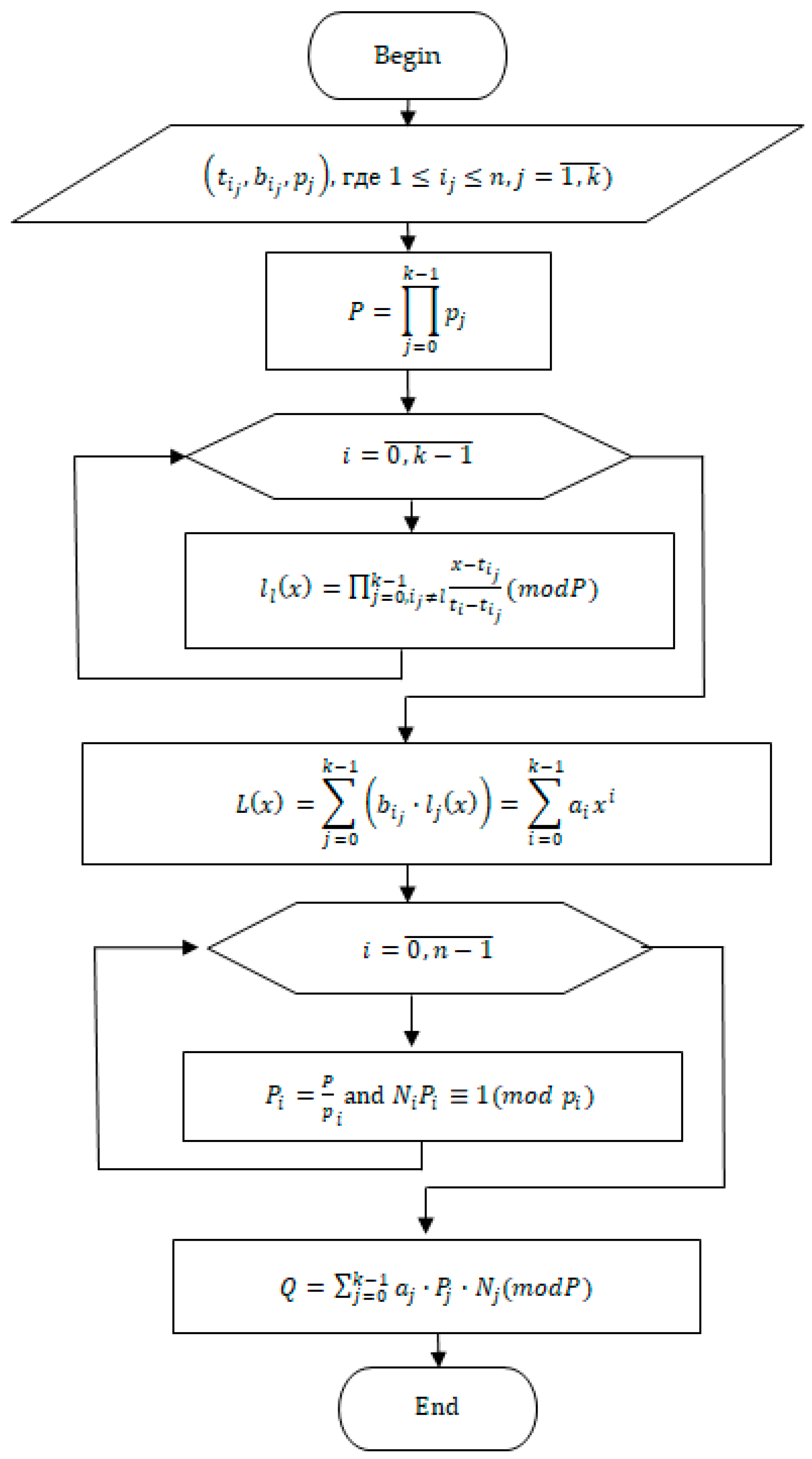
3.1.2. Secret Reconstruction

At least $k$ participants must combine their shares to recover the secret. To do this, $k$ participants use their shares $\left(t_{i_j},b_{i_j},P\right)$ where $1\le i_j\le n, j=\overline{1,k}$. Reconstruction can be performed in two ways:

• Using Lagrange Interpolation Polynomial. The coefficients of the polynomial (7) are computed by the formula $f\left(x\right)={\sum }_{j=1}^k{b}_{i_j}{\prod }_{j=1,i_l\ne i_j}^k{\displaystyle \frac{x-t_{i_j}}{t_{i_l}-t_{i_j}}},1\le i_j\le n$. The coefficients then define the system of congruences (6). Subse-quently, the secret $Q$ is reconstructed based on the Chinese Remainder Theorem and Formula (5).

The block diagram of secret reconstruction is shown in Figure 3.

• Using a System of Linear Equations. The following system is constructed as follows:

$$\begin{array}{c}{x}_{k-1}{t}_{i_1}^{k-1}+x_{k-2}{t}_{i_1}^{k-2}+\dots +x_2{t}_{i_1}^2+x_1{t}_{i_1}+x_0\equiv b_{i_1}\left(modP\right)\\ x_{k-1}{t}_{i_2}^{k-1}+x_{k-2}{t}_{i_2}^{k-2}+\dots +x_2{t}_{i_2}^2+x_1{t}_{i_2}+x_0\equiv b_{i_2}\left(modP\right)\\ \dots \\ x_{k-1}{t}_{i_{k-1}}^{k-1}+x_{k-2}{t}_{i_{k-1}}^{k-2}+\dots +x_2{t}_{i_{k-1}}^2+x_1{t}_{i_{k-1}}+x_0\equiv b_{i_{k-1}}\left(modP\right)\\ x_{k-1}{t}_{i_k}^{k-1}+x_{k-2}{t}_{i_k}^{k-2}+\dots +x_2{t}_{i_k}^2+x_1{t}_{i_k}+x_0\equiv b_{i_k}\left(modP\right)\end{array}$$

(9)

System (9) comprises $k$ linear equations with $k$ variables. Solving this system makes it possible to determine the coefficients of polynomial $f\left(x\right)$ in expression (7). The coefficients then define the set of congruences (6), which, together with the Chinese Remainder Theorem and Formula (5), allow for complete reconstruction of the secret.

The Lagrange interpolation method is recommended in cases where computational efficiency is a priority and all required subgroup representatives have provided valid shares. The system of linear equations method is more appropriate in scenarios that demand higher fault tolerance and the ability to verify the correctness of shares, as it allows inconsistencies to be detected.

We also clarified that both methods can be applied only if at least one representative from each subgroup participates. Otherwise, the system of equations or the interpolation polynomial remains underdetermined, and secret reconstruction becomes impossible.

4. Discussion

Let us consider the criteria for evaluating a secret sharing scheme that provide maximum confidentiality while minimizing memory and computational resources:

The solution of a system of $k$ linear equations with k variables forms the basis of the algorithm. If the number of equations is less than $k$ (in other words, if the number of participants holding shares is below the required threshold), the system has multiple solutions, preventing accurate reconstruction of the secret.

The choice of the number of subgroups and the ranges of moduli is determined by two factors: security requirements and the organizational structure of the system.

First, the number of subgroups $k$ reflects the level of role-based separation of authority. If the system involves independent organizations (for example, multiple cloud providers or legally distinct parties), each of them should constitute a separate subgroup. Thus, k is selected in accordance with the number of independent trust domains that must be controlled.

Second, the selection of modulus ranges $\{p_0,p_1,\dots ,p_{k-1}\}$ directly affects the cryptographic strength of the scheme. According to the Chinese Remainder Theorem, the overall secret space is determined by the product of the moduli $P=p_0{·p}_1·\dots {·p}_{k-1}$. The larger the value of $P$, the higher the level of security, since an adversary would need to consider a significantly broader range of possible secrets. To prevent brute-force attacks, each modulus $p_i$ must be chosen sufficiently large and must be prime. In practice, it is recommended to use a modulus length of at least 1024 bits, which complies with modern security requirements.

Ideality of the scheme. A secret sharing scheme is considered perfect if no group of illegitimate participants can extract any information about the secret from their shares [3]. Furthermore, the scheme is called ideal if the size of each share is equal to the size of the original secret. In the proposed algorithm, the secret is uniformly distributed across all disseminated shares.

Resource consumption. Let us estimate the algorithm’s resource consumption. If we reserve 8 bytes for each of $k$ polynomial coefficients and for each of $n$ shares (taking into account both the argument and the value of the share), the total memory usage will be $8\times \left(k+2n\right)$ bytes. For example, when $k=n=32$ the required memory is 768 bytes.

Scheme Complexity

Selecting $k$ random primes and polynomial interpolation according to Formulas (6) and (7) has complexity $O\left(k\right)$.

Distributing the secret involves computing and disseminating triplets $\left(t_i,b_i,P\right)$ for i$i=\overline{1,n}$, yielding a complexity of $O(k\times n)$.

Thus, the overall computational complexity during the distribution phase is $O(k\times n)$.

Reconstruction of the secret using Lagrange polynomial interpolation has complexity $O\left(k^2\right)$.

Reconstruction of the secret using the Chinese remainder theorem also has complexity $O\left(k^2\right)$.

Taken together, the total complexity of the algorithm is $O\left({2k}^2\right)+O(k\times n)$.

The results of evaluating these criteria for the proposed scheme are presented in

Table 2. Evaluation of the proposed secret sharing scheme.

Threshold Scheme	Complexity Rating	Resource Consumption (KB)	Perfection	Ideality
SSS by Lagrange formula	$O\left(2k^2\right)+O(k\times n)$	0.768	+	+
SSS by CRT	$O\left(k^2\right)+O\left(n\right)$	8	+	+

.

During the study, 6 threshold secret sharing schemes were considered. The evaluation criteria included algorithm complexity for sharing and reconstruction, resource consumption, and security properties—perfection and ideality of the schemes. The results, presented in

Table 3. Evaluation results and comparison of threshold secret sharing schemes.

Threshold Scheme	Complexity Rating	Resource Consumption (KB)	Perfection	Ideality
Shamir’s scheme	$O\left(k\times n\right)+O\left(k^2\right)$	0.5	+	+
Blackley’s scheme	$O\left(k\times n\right)+O\left(k^3\right)$	8	+	−
SSS based on Elliptic Curves	$O\left(k\times n\right)+O\left(k^2\right)$	1000	+	−
Karnin–Green–Hellman scheme	$O\left(n\right)+O\left(k^3\right)$	16	+	−
Asmuth–Blum scheme	$O\left(n\right)+O\left(k^2\right)$	13	+	+
Proposed secret sharing scheme	$O\left({2k}^2\right)+O(k\times n)$	0.768	+	+

, allow for a comparative analysis of various methods. Here, the symbol “+” indicates that the considered scheme possesses the properties of ideality and perfection, while “−” denotes that these properties are not satisfied.

At the theoretical research stage, to optimize the software implementation of the secret sharing algorithm based on threshold schemes, algorithm complexity and resource consumption were analyzed. The algorithm’s execution time under different parameters was also measured. The results are presented below (see

Table 4. Experimental results.

Evaluation Criteria	$\mathit{n}=5,\mathit{k}=3,$ $\left|\mathit{Q}\right|=512$	$\mathit{n}=32,\mathit{k}=32,$ $\left|\mathit{Q}\right|=512$	$\mathit{n}=128,\mathit{k}=128,$ $\left|\mathit{Q}\right|=512$
Shamir’s scheme
Secret sharing time Secret reconstruction time Memory consumption	▪ 5 ms; ▪ 1 ms; ▪ 1560 bytes	▪ 7 ms; ▪ 2 ms; ▪ 6720 bytes	▪ 75 ms; ▪ 27 ms; ▪ 100,608 bytes
Asmuth–Blum scheme
Secret sharing time Secret reconstruction time Memory consumption	▪ 103 ms; ▪ 1 ms; ▪ 3456 bytes	▪ 1145 ms; ▪ 4 ms; ▪ 274,432 bytes	▪ 3032 ms; ▪ 97 ms; ▪ 4,243,456 bytes
SSS based on Eliiptic Curves
Secret sharing time Secret reconstruction time Memory consumption	▪ 15 ms; ▪ 1 ms; ▪ 1365 bytes	▪ 1058 ms; ▪ 617 ms; ▪ 6432 bytes	▪ 85,193 ms; ▪ 47326 ms; ▪ 99,456 bytes
Proposed secret sharing scheme
Secret sharing time Secret reconstruction time Memory consumption	▪ 6 ms; ▪ 2 ms; ▪ 1625 bytes	▪ 14 ms; ▪ 7 ms; ▪ 9678 bytes	▪ 103 ms; ▪ 42 ms; ▪ 104,466 bytes

).

Consider the following approach. Let the moduli $p_1,p_2,\dots ,p_k$ be known, and $k-1$ participants of the scheme possess their respective shares of the secret. Let us analyze the possibility of reconstructing the secret. Since there is a group of $k-1$ participants with the sets $\left(t_{i_j},c_{i_j},P\right),1\le i_j\le n,j=\overline{1,k}$, we can form the following system of linear congruences:

$$\left\{\begin{array}{c}{x}_{k-1}{t}_{i_1}^{k-1}+x_{k-2}{t}_{i_1}^{k-2}+\dots +x_2{t}_{i_1}^2+x_1{t}_{i_1}+x_0\equiv {\mathrm{c}}_{i_1}\left(modP\right)\\ x_{k-1}{t}_{i_2}^{k-1}+x_{k-2}{t}_{i_2}^{k-2}+\dots +x_2{t}_{i_2}^2+x_1{t}_{i_2}+x_0\equiv {\mathrm{c}}_{i_2}\left(modP\right)\\ \dots \\ x_{k-1}{t}_{i_{k-1}}^{k-1}+x_{k-2}{t}_{i_{k-1}}^{k-2}+\dots +x_2{t}_{i_{k-1}}^2+x_1{t}_{i_{k-1}}+x_0\equiv {\mathrm{c}}_{i_{k-1}}\left(modP\right)\\ x_{k-1}{B}_k+x_{k-2}{B}_{k-1}+\dots +x_2{B}_3+x_1{B}_2+x_0{B}_1\equiv X\left(modP\right)\end{array}\right.$$

(10)

In this system, the values $c_{i_j},t_{i_j}^l$ ($1\le i_j\le n,j=\overline{1,k-1},l=\overline{1,k-1}$) and $B_j$(for $j=\overline{1,k-1}$) are considered known. Thus, we have a system of $k$ linear equations with $k+1$ unknowns. According to linear algebra, such a system has infinitely many solutions and can be satisfied for arbitrary values of the $k+1$th variable.

$$\left\{\begin{array}{c}{x}_0\equiv c_1^{\prime }+t_1^{\prime }X\left(modP\right) \\ x_1\equiv c_2^{\prime }+t_2^{\prime }X\left(modP\right) \\ \dots \\ x_{k-2}\equiv c_{k-1}^{\prime }+t_{k-1}^{\prime }X\left(modP\right)\\ x_{k-1}\equiv c_k^{\prime }+t_k^{\prime }X\left(modP\right) \end{array}\right.$$

(11)

Here $c_i^{\prime },t_i^{\prime }$ for $i=\overline{1,k}$ are known (determined) values.

Adding the condition $X\equiv x_j\left(mod{p}_j\right)$ to this system (11) does not reduce its set of solutions, because these sets are equivalent.

Let the secret $Q$ be uniquely determined by the system of congruences

$$Q\equiv a_i\left(mod{p}_i\right),i=1,\dots ,k,$$

where $p_i$ are pairwise coprime moduli corresponding to the subgroups, and $P={\prod }_{i=1}^k{p}_i$. Assume that each subgroup provides at least one valid share containing the residue $a_{i}mod{p}_i$.

If at least one modulus $p_j$ is missing, the system of congruences becomes incomplete. In this case, the set of solutions takes the form

$$Q\equiv a(modP\prime )$$

where $P^{\prime }={\prod }_{i\ne j}{p}_i$. Since $P\prime <P={\prod }_{j=1}^k{p}_i$, the secret is no longer uniquely defined but corresponds to a set of ${\displaystyle \frac{P}{P\prime }}$ different values. This means that adversaries, even if colluding and combining $k$ shares, cannot uniquely reconstruct the secret without the participation of at least one representative from each subgroup.

Thus, the requirement of mandatory subgroup participation is an inherent mathematical constraint of the scheme and ensures its resilience against internal collusion.

If a participant of the scheme provides erroneous (false) information from their share, there is a probability that this share will not be involved in solving the system of congruences.

There are $\left(\begin{array}{c}n\\ k\end{array}\right)$ possible ways to choose $k$ participants out of $n$. The number of ways to select $k$ participants such that a specific fixed participant is not included equals $\left(\begin{array}{c}n-1\\ k\end{array}\right)$. Therefore, the probability that, in a random selection of $k$ participants, the fixed participant is not chosen is

$$p={\displaystyle \frac{\left(\begin{array}{c}n-1\\ k\end{array}\right)}{\left(\begin{array}{c}n\\ k\end{array}\right)}}={\displaystyle \frac{n-k}{n}},$$

Here, p denotes the probability that a particular participant will not be included in a randomly selected subset of $k$ participants. The selection of $k$ participants is assumed to be uniformly random over all $\left(\begin{array}{c}n\\ k\end{array}\right)$ subsets. This formula thus provides a statistical estimate and does not account for strategic participant behavior (such as targeted sabotage or other adversarial actions), which should be analyzed separately within the threat model.

5. Conclusions

Secret sharing schemes are among the key areas in the field of information security. This paper presents a new secret sharing scheme with mandatory subgroup participation and analyzes its properties.

The study addresses the issues of secure distribution of confidential information and its reliable reconstruction. Unlike most existing secret sharing schemes, the proposed solution is initially designed with enhanced resistance to internal threats and cryptographic attacks. While other approaches rely on additional authentication mechanisms to prevent such attacks, the proposed scheme is inherently resilient: even if an adversary gains access to the shares of k legitimate participants, they will not be able to reconstruct the secret Q without satisfying the structural requirement of having representatives from all subgroups.

A theoretical and computational complexity analysis of the algorithm was carried out, along with an assessment of potential threats posed by both external adversaries and untrustworthy internal participants. The results showed that the proposed scheme possesses the property of ideality (in the sense of exact reconstruction under the defined conditions) and demonstrates high resource efficiency, making it a promising option for practical applications.

Reliability, ease of implementation, and resistance to adversarial actions make the proposed scheme a suitable solution for modern challenges in secure authentication and the distributed storage of sensitive information.

The algorithm has been implemented in C# and tested on practical use cases. Future work will focus on further improving the algorithm’s robustness and exploring its applicability in various scenarios, with the results to be presented in subsequent publications.