Abstract
This paper presents a novel formulation of Ordered Fuzzy Numbers (OFNs), referred to as Vectorial Ordered Fuzzy Numbers (vOFNs). In contrast to the traditional definition based on a pair of functions, the vOFN framework employs a pair of vectors, offering a more concise and structurally coherent representation. This reformulation addresses the key limitations of classical OFNs, such as non-convexity and difficulties in handling curvilinear boundaries during multiplication and division. The vOFN model retains compatibility with commonly used fuzzy number types—triangular, trapezoidal, and singleton—and preserves directional properties that are essential for modeling fuzzy trends. Furthermore, it simplifies comparison operations and supports a complete algebraic structure. Due to its mathematical consistency, low computational complexity, and ease of implementation, the vOFN framework is well-suited for applications in intelligent systems, particularly in domains that require reasoning under uncertainty.
1. Introduction
The introduction of fuzzy set theory by L. Zadeh [1] triggered rapid development in one of the most commercially successful areas of artificial intelligence. As the theory evolved, many authors contributed to developing arithmetic systems that enabled operations on fuzzy numbers [2,3,4,5]. Probably the best known among these is the LR arithmetic proposed by Dubois and Prade [6,7], largely due to the popularity of its authors. An alternative approach, known as constrained fuzzy arithmetic (CFA), was proposed by Klir [8] and further developed by Chang [9], as well as by Cho and Tsao [10]. Another notable contribution is the RMD arithmetic introduced by Piegat and Pluciński [11]. The OFN arithmetic, proposed by Kosiński et al. [12,13,14] and further developed by them and their collaborators [15,16,17], is the most relevant for this paper.
This arithmetic has gained many advocates due to the completeness of its computational system, which constitutes a ring in algebraic terms. Nevertheless, it has also faced skepticism and criticism, mainly focused on two aspects. The first concern involves the occurrence of non-convex numbers in OFN, whose shapes are difficult to interpret for researchers accustomed to classical calculus [18,19,20]. The second issue relates to the curvilinear characteristics of rising and falling edges during multiplication operations, which result from changes in the degree of polynomial functions describing these edges [21,22,23,24,25,26].
Another challenge encountered by researchers concerns the feasibility of comparing OFNs. However, the problem of comparing fuzzy numbers is neither new nor exclusive to OFN notation [27,28]. Research in this domain began in 1977, with contributions from Zadeh [1], Yager [29], Kaufman [30], Chang [9], and Adamo [31]. In the following decades, Bortolan & Degani [32] and Dadgostar & Kerr [33] reviewed various comparison methods and proposed the Partial Comparison Method (PCM). Subsequently, Wang and Kerre developed a set of principles and axioms designed to structure the methods for comparing fuzzy numbers, thereby allowing for a comprehensive assessment of various fuzzy ranking techniques [34,35,36,37].
In recent years, novel methodologies for fuzzy number comparison have emerged. For example, Dobrosielski, Czerniak et al. [38] proposed utilizing multiple original defuzzification techniques to enhance the process of comparing fuzzy numbers within the framework of Ordered Fuzzy Number (OFN) notation [27].
This paper addresses the aforementioned challenges and limitations of OFN arithmetic by introducing a redefinition called Vectorial Ordered Fuzzy Numbers (VOFNs),discussed in the next section.
2. Vectorial Ordered Fuzzy Numbers (VOFNs)
Building upon the definition of Ordered Fuzzy Numbers introduced by Kosiński et al. [14,21,22,27], examples of such numbers can be found in Figure A1, Figure A2 and Figure A3. Additionally, we now introduce the concept of Vectorial Ordered Fuzzy Numbers as follows.
Definition 1
(Vectorial Ordered Fuzzy Number). A Vectorial Ordered Fuzzy Number (VOFN) is generally trapezoidal in shape, denoted by the coordinates . This trapezoid is constructed by an ordered pair of vectors, and . The vector starts at point and ends at , while starts at and ends at .
The orientation, direction, and magnitude of the two vectors are determined by the points between which they are drawn (Figure 1).
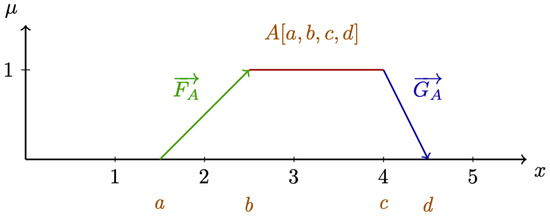
Figure 1.
vOFN formed by an ordered pair of vectors.
Definition 2
(Positive and Negative Order [27]). A Vectorial Ordered Fuzzy Number (VOFN) can also be represented as a triple , where is the membership function of the number, and denotes its order. Based on their order, VOFNs can be categorized into two types:
- VOFNs of a positive order—the ordering direction conforms to the increasing values along the OX axis.
- VOFNs of a negative order—the ordering direction is opposite to the increasing values along the OX axis.
A visual depiction (Figure 2) of an ordered fuzzy number A is represented by the pair , where is a curve defined as follows:
where:
- and are the graphs of the vectors;
- represents the order;
- is the membership curve.
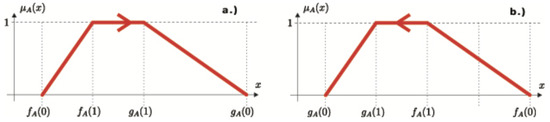
Figure 2.
Fuzzy numbers with (a) positive order and (b) negative order.
Definition 3
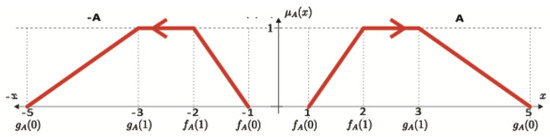
(Opposite vOFN). The opposite of a number A, denoted as , is defined as its mirror image with respect to the OY axis. Consequently, opposite vOFNs have opposite orders (Figure 3).

Figure 3.
Opposite numbers: A and .
Definition 4
(Reversal of the Order [27]). The reversal of the order of a fuzzy number A consists of swapping the upper part (vector ) with the lower part (vector ). This operation is denoted as follows:
where
- A is the ordered fuzzy number represented by the vector pair ;
- B is the outcome of the vOFN order reversal operation;
- represents the reversal of the vOFN order.
The number obtained through this operation is referred to as the reversed vOFN or a vOFN with reverse orientation (opposite order).
Definition 5
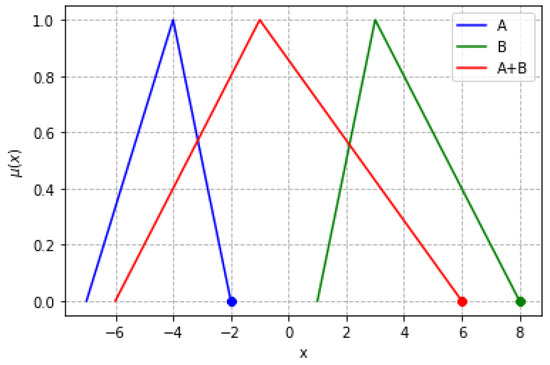
(Sum of vOFNs [17,21,22,27]). Let , , and be three ordered fuzzy numbers. Then, C is said to be the sum, denoted as , if the following holds:
An example illustrating the addition of two vOFNs A and B with the same order is shown in Figure 4.

Figure 4.
Sum of vOFNs.
The operation of adding vOFNs with the same order yields the same result as the addition of classical convex fuzzy numbers. The calculation presented graphically in Figure 4 proceeds as follows:
Example calculation:
- A = [-2, -4, -4, -7] B = [8,3,3,1] C = A + B
- C = [6,1,1,-6]
Definition 6
(Difference between vOFNs [12,13,22]). Given three ordered fuzzy numbers , , and , it is said that C is the result of subtracting B from A, denoted as , if the following holds:
Hence, subtraction in the context of OFNs corresponds to the addition of an opposite value to the subtrahend, i.e., . The order of the OFN indicates the position of the increasing part of the membership curve in relation to the decreasing part of the fuzzy number . An illustration of this arithmetic operation is shown in Figure 5.
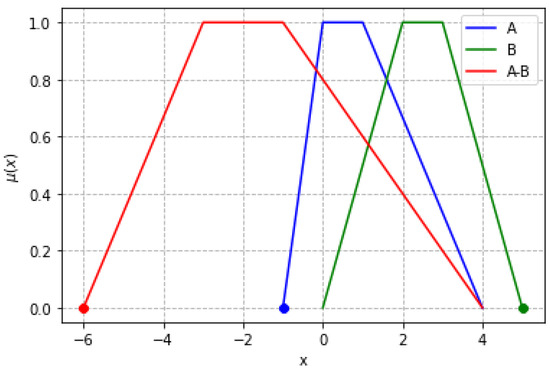
Figure 5.
Difference between vOFNs.
A calculation example is as follows:
- A = [-1,0,1,4]
- B = [5,3,2,0]
- C = A - B = A + (B)
- C = [-1,0,1,4]+[-5,-3,-2,0]
- C = [-6, -3, -1, 4]
Definition 7
(Element neutral to the sum and the difference of vOFNs [17,27]). The result of A-A subtraction is the real number . The real number is represented by the pair , whereby the following hold:
A computational example is provided below, and its graphical interpretation is shown in Figure 6.
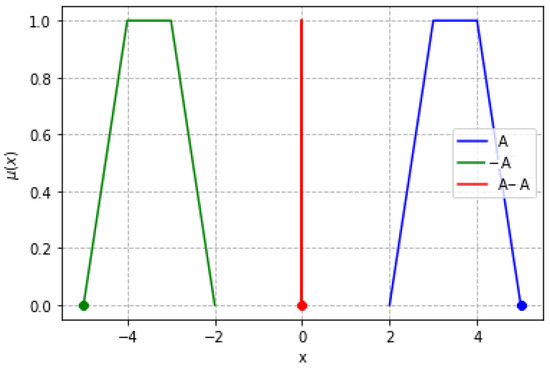
Figure 6.
Element neutral to the sum.
- A = [5,4,3,2]
- -A = [-5, -4, -3, -2] A-A = A+(-A)=[0,0,0,0]
Definition 8
(Multiplication of a vOFN by a scalar [12,13,27]). Let two ordered fuzzy numbers and be given, along with a scalar . It is said that C is the product of A multiplied by the scalar r, if the following holds:
A computational example is provided below, and its graphical interpretation is shown in Figure 7.
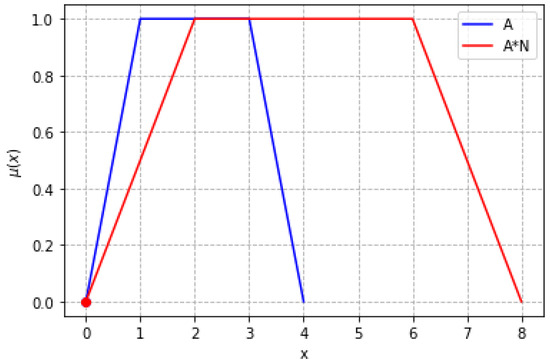
Figure 7.
Multiplication of a vOFN by a scalar.
- There is an ordered fuzzy number
- Determine for .
- .
Definition 9
(Multiplication of vOFNs [12,13]). Consider three ordered fuzzy numbers , , and . It is said that C represents the product of A and B, denoted as , if
A computational example is provided below, and its graphical interpretation is shown in Figure 8.
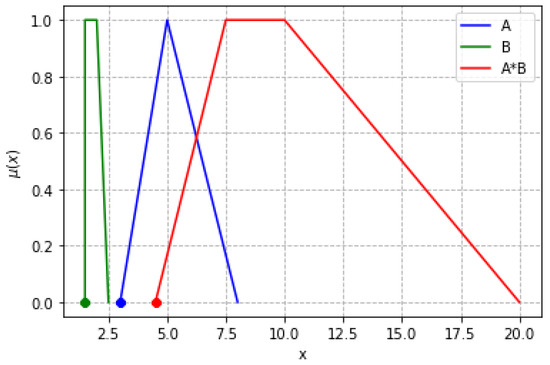
Figure 8.
Product of vOFNs.
- A = [3, 5, 5, 8]
- B = [1.5, 1.5, 2, 2.5]
- C = A * B = [4.5, 7.5, 10, 20.0]
Definition 10
(Ratio of vOFNs [12,17,21,22]). Let three ordered fuzzy numbers be given as , and . It is said that C represents the quotient of A divided by B, denoted as , if:
A computational example is provided below, and its graphical interpretation is shown in Figure 9.
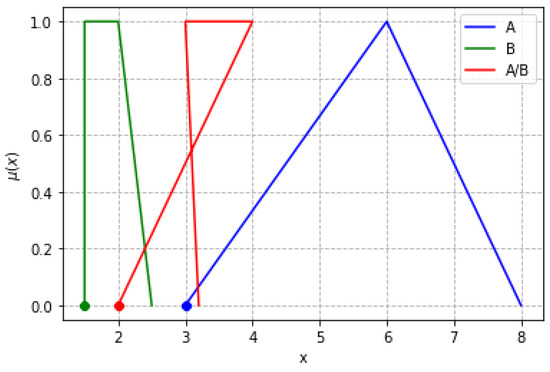
Figure 9.
Quotient of vOFNs.
- A = [3, 6, 6, 8]
- B = [1.5, 1.5, 2, 2.5]
- C = A/B = [2.0, 4.0, 3.0, 3.2]
The division is multiplication by the multiplicative inverse number. Let us therefore introduce the definition of a multiplicative inverse number in OFN notation.
Definition 11
(vOFN multiplicative inverse [13,21,22]). Consider two ordered fuzzy numbers, and . The multiplicative inverse of the fuzzy number is defined as a new number, represented by the following:
A computational example is provided below, and its graphical interpretation is shown in Figure 10.
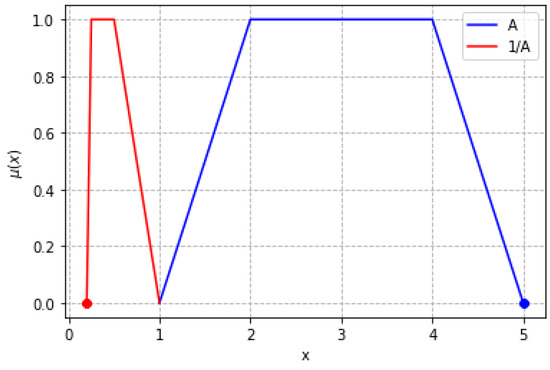
Figure 10.
Quotient of vOFNs.
Definition 12
(The power with a natural exponent [12,13,21,22,27]). The power of a vectorial fuzzy number with a natural exponent n is one such product achieved in vOFN arithmetic with n factors, each of which is equal to the number A. Appropriately, as the method of multiplication defined in the product of vOFN requires, each of the number A coordinates is raised to the power of n.
whereas it is assumed that
- and
A computational example is provided below, and its graphical interpretation is shown in Figure 11.
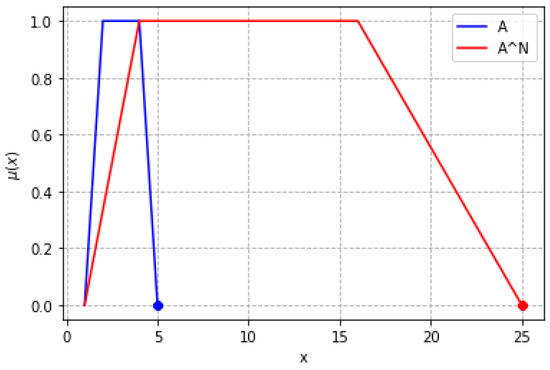
Figure 11.
Power of a vOFN with a natural exponent.
- A = [5,4,2,1], n = 2
- C = [25,16,4,1]
As shown above, all arithmetic operations within the vOFN notation are consistent and coherent. Consequently, it is possible to perform advanced calculations using the presented arithmetic across various applications, including fuzzy control and diverse types of fuzzy observations.
3. Solution to the Problem of Comparing OFN/vOFNs
This section presents a novel similarity measure, which is based on Carberry’s approach discussed previously. However, the proposed measure overcomes a key drawback of the original Canberra distance—its sensitivity to values approaching zero. The JC metric is tailored specifically for comparing ordered fuzzy numbers (OFNs), yet it can be generalized to other fuzzy number arithmetic systems by omitting the components that are specifically related to the nature of OFNs. As discussed previously, a Vectorial Ordered Fuzzy Number (vOFN) consists of an ordered pair of vectors representing its increasing edge f and decreasing edge g. Figure 2 depicts two such numbers, with the starting and ending points of these vectors labeled as , , , and .
Lemma 1.
Consider two vOFNs, A and B, each characterized by four boundary values corresponding to their rising and falling edge functions. Specifically, number A is represented by the set , and number B by the set . The comparison between A and B is carried out by evaluating the metric, defined as follows:
- If the condition or is encountered, an affine transformation (translation) along the positive axis is required. This can be achieved by adding a constant value of 1 to the coordinates of both fuzzy numbers. The process should be repeated until no denominator becomes zero.
Definition 13.
When the metric equals and the fuzzy numbers A and B share the same order, the two numbers are considered identical.
Definition 14.
When the metric results in and the fuzzy numbers A and B have reversed orders, the number with a positive order is regarded as larger.
Definition 15.
If the value of the metric is , fuzzy number A is deemed smaller than fuzzy number B, irrespective of their order.
Definition 16.
If the metric yields , fuzzy number A is considered larger than fuzzy number B, regardless of the order of the numbers.
Numerous examples, frequently used for testing comparison operators, are available in the existing literature [9,29,39,40]. These examples, presented in vOFN notation, are displayed below alongside their corresponding visual representations (Figure 12). The selected examples include both disjoint fuzzy numbers as well as those that are nested within each other, thus posing a more complex interpretative challenge compared to standard operations on real numbers.
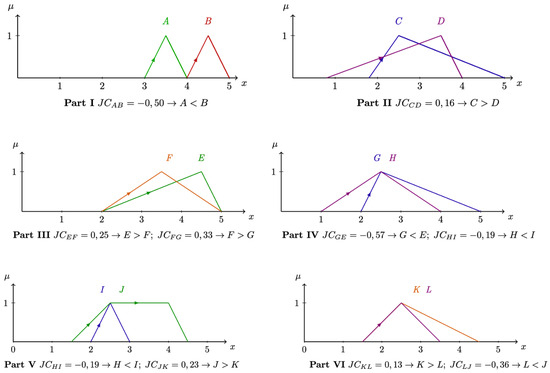
Figure 12.
Set of fuzzy numbers used for comparisons.
Using the metric, as described in the preceding section, allows for the comparison and classification of fuzzy numbers. For each pair of numbers compared, a value is generated based on the metric. The similarity rules outlined in the definitions above can then be applied to determine the relationship between the individual pairs of fuzzy numbers.
3.1. Experiment and Evaluation
In this section, the metric values are computed for the fuzzy numbers presented earlier, as well as for additional numbers sourced from the literature. Additionally, a number pair has been introduced to provoke a division-by-zero scenario. This situation was anticipated, and the corrective procedure, as outlined in the previous section, was executed to resolve the issue.
To ensure a fair and unbiased evaluation of the proposed JC metric, we extended our set of test cases to include examples commonly used in benchmark studies of fuzzy number comparison methods, such as those presented by Yager [29], Baldwin and Guild [39], Chang [9], and Jain [40]. These examples cover a wide range of situations, including overlapping, disjoint, and nested fuzzy numbers, thus providing a representative testing framework.
In each case, the values for the JC metric were computed and compared against results produced by other well-established comparison operators. The expanded dataset helps to ensure that the effectiveness of the JC metric holds across a variety of established fuzzy number scenarios.
As shown, all computations enabled the clear and precise identification of the relationships between the individual ordered fuzzy numbers. During the final comparison of numbers P and Q, a division-by-zero issue arose. To resolve this, the procedure outlined in Lemma 1 was followed, where both numbers were subjected to an affine translation along the axis. This transformation resulted in new numbers, denoted by and , which no longer encountered this problem, thus ensuring the successful calculation of the metric.
3.2. Discussion and Comparison with Alternative Methods
The results derived in the previous section are straightforward and unambiguous, and they remain consistent across a wide selection of test cases gathered from both classical and recent benchmark studies. By incorporating examples drawn from the existing literature, such as [9,29,39,40], we ensured that the evaluation of the JC metric would not be limited to author-generated scenarios. This step was necessary to demonstrate the metric’s robustness in standard benchmark situations and to support a meaningful comparison with traditional Ordered Fuzzy Number methods.
Moreover, the performance of the JC metric has been benchmarked against a comprehensive set of comparison operators (Table 1) described in the literature. These include distance-based methods, defuzzification-based approaches, and operators specifically designed for handling Ordered Fuzzy Numbers (OFNs). To help the reader better understand these references without requiring an in-depth study of external sources, a brief description of each representative method included in the comparison is provided below.

Table 1.
Comparison of results across various methods for fuzzy number comparisons.
- GR (General Ranking Method)—A classical ranking method based on centroid calculations and distance metrics, originally proposed to compare triangular and trapezoidal fuzzy numbers in a scalarized manner [41].
- ML (Modified Linguistic Ranking)—Introduced to align numerical results with linguistic preferences by using weighting functions and ranking indices [41].
- Adamo’s 0.5-cut, 0.9-cut methods—Utilize alpha-cuts to reduce fuzzy sets to intervals and then compare representative crisp values [31].
- Baldwin and Guild proposed several comparative measures based on the concept of distance between fuzzy sets [39].
- F1, F2, F3 (Yager’s Methods)—A series of fuzzy comparison techniques using score functions and area-based evaluations to handle non-normal and overlapping fuzzy numbers [29].
- CH (Chang’s index)—Uses a distance-based approach derived from the expected values of fuzzy numbers and their support intervals [9].
- PCM (Partial Comparison Method)—It was developed as a response to ambiguity in comparing fuzzy numbers, especially when their membership functions overlap significantly [33].
- K (Kerre’s Method)—Based on t-norms and fuzzy implications to determine dominance relationships [42].
- BK (Baas–Kwakkernaak Method)—Uses centroid-based distance and ranking functions [43].
- PSD (Possibility-Based Dominance)—Proposed by Dubois and Prade, this approach compares fuzzy numbers based on possibility theory, evaluating dominance through -cut analysis [6].
Compared to these methods, the JC metric presents several advantages. First, it is invariant under uniform translation and scaling, which makes it suitable for applications where relative differences are more meaningful than absolute magnitudes. Second, it correctly reflects symmetry and antisymmetry in fuzzy number relationships, including reversed orientation—a property not consistently preserved in traditional methods.
Furthermore, the JC metric integrates naturally into the vectorial representation of Ordered Fuzzy Numbers, allowing a unified approach for operations and comparisons. Unlike some earlier methods that require a case-by-case analysis or rely on defuzzification (which may result in information loss), the JC metric operates entirely within the fuzzy framework while preserving interpretability.
The comparative analysis confirms that the JC metric produces results compatible with the well-established methods in most benchmark scenarios, while also correctly resolving certain edge cases that cause ambiguity or inconsistency in other approaches. This supports the claim that the JC metric, together with vOFNs, forms a robust and flexible foundation for fuzzy modeling and decision-making applications.
3.3. Summary
This study introduces a novel approach to the problem of comparing fuzzy numbers. As discussed earlier, many existing methods either directly or indirectly lead to comparisons in the domain of real numbers, moving beyond the boundaries of fuzzy numbers. In contrast, the objective of this research was to devise a comparison operator that stays entirely within the fuzzy number domain.
The proposed operator functions intuitively on fuzzy numbers, similar to how relational operators operate in other number systems. To validate the metric, the authors employed examples previously used by other researchers to verify their comparison operators. The experimental section involved calculations on positively ordered numbers expressed in vOFN notation. The properties of vOFNs show that they behave identically to traditional (crisp) numbers.
The results of the fuzzy number comparisons confirm the effectiveness of the proposed operator. No anomalies were observed, and the relationships between numbers determined by the metric were consistent with those identified by other researchers. Therefore, it can be concluded that the comparison operator provides a robust and consistent method for comparing fuzzy numbers within the fuzzy number framework.
Moreover, the computational demands of the operator are modest, making it suitable for repeated application. Preliminary experiments further suggest that the proposed approach performs well across various fuzzy number notations, although the comprehensive confirmation of this observation is left for future research. Future work should involve testing the metric across the full spectrum of OFNs. However, based on the examples presented and the preliminary findings, no significant challenges are anticipated.
Additionally, based on the extended comparison framework and the incorporation of benchmark examples, we observed that the JC metric not only preserves the structure and semantics of ordered fuzzy numbers but also provides results that align closely with or improve upon existing methods. In contrast to traditional OFN-based operators, the JC metric demonstrates better handling of symmetry, reversed order, and division-by-zero sensitivity. Therefore, the findings support the conclusion that vectorial OFNs (vOFNs) in combination with the JC metric offer a more flexible and robust approach to fuzzy number comparison.
4. Solution to the Problem of OFN/vOFNs with Non-Convex Shapes
Regardless of its specific definition, an Ordered Fuzzy Number (OFN) is, as originally intended by the authors [44], a generalization of possible shapes and typically assumes a trapezoidal form. Although this has been discussed in earlier sections, it is worthwhile to supplement the discussion with the following formal definition.
Definition 17
(Membership Function of vOFNs). The membership function associated with an ordered fuzzy number A is a function defined for each as follows:
This membership function can be applied in control systems similarly to traditional fuzzy membership functions [44]. All fuzzy control parameters describe certain aspects of reality [45], and the process of determining these parameters is known as fuzzy observation.
However, as several studies indicate [46,47], while arithmetic operations are always formally defined within the vOFN domain, their interpretations may pose challenges, particularly in cases involving representations of so-called improper numbers. Improper numbers are defined as those for which , meaning that the support of the number is narrower than the core. The interpretation of such numbers is often disputed, though they may arise as results of calculations or serve as inputs for further operations.
To address such issues, the authors propose the Shape Normalization Operator (SNO), which ensures a consistent interpretation of fuzzy numbers.
4.1. Mathematical Foundations of the Shape Normalization Operator (SNO)
As previously noted, the OFN notation, by design, allows for the existence of improper numbers. In general, these are numbers whose coordinates (in the OFN representation) do not follow a uniform directional trend along the axis. Such numbers cannot be readily interpreted using classical fuzzy number notations, and their classification within the OFN framework remains ambiguous. This problem can be resolved through the following definitions.
Let represent the set of fuzzy numbers, where each fuzzy number is characterized by the following four real values: (i.e., ), which are referred to as the coordinates of A.
Definition 18
(Singleton of vOFNs). A fuzzy number is called a singleton if all four values are equal, i.e., . The collection of all such singletons is denoted by S.
Additionally, we define three distinct subsets of the space as follows:
The sets P, Q, T, and S are mutually exclusive, and their union forms a complete partition of the set , i.e., .
Definition 19
(Order of a vOFN). Given an ordered fuzzy number described by coordinates , its order is determined as follows:
- A number has positive order if , otherwise it has negative order;
- A number has positive order if , otherwise it has negative order;
- A number has positive order if , otherwise it has negative order.
Definition 20
(Shape Normalization Operator ). Define the operator such that the following holds:
where
- is the ascending permutation of ;
- is the descending permutation of .
For all , the operator acts as the identity, i.e., .
4.2. Normalization of vOFNs with Unique Shapes
According to Czerniak’s monograph [17], there are 256 possible shapes for a vOFN , arising from all permutations with a repetition of four coordinates drawn from a small set (e.g., ). Each shape was subjected to normalization.
Following normalization, a set of fuzzy numbers free from improper forms was obtained. All resulting numbers were properly interpretable, with unambiguous membership functions.
The normalization process particularly addresses certain characteristic shapes that often lead to confusion among researchers, as depicted in Figure 13.
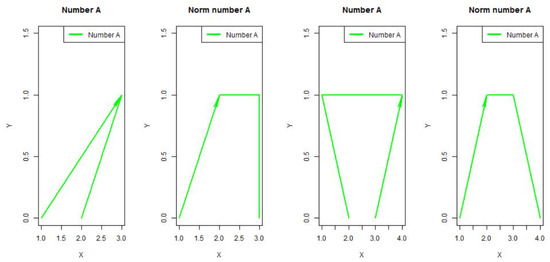
Figure 13.
Normalization of fuzzy numbers and .
4.3. Summary
The analysis of all 256 possible OFN shapes revealed that approximately 12.7% of cases required normalization. Proper shapes and singletons remained unaffected.
Normalization first involves determining the number’s current order according to Definition 19, followed by applying the normalization rule in Definition 20. After normalization, only proper numbers with are obtained, ensuring full interpretability. Importantly, the original order of each number is preserved after normalization, carrying valuable trend information.
5. Conclusions
This paper introduces a redefinition of Ordered Fuzzy Numbers (OFNs) through a novel representation based on vector pairs, termed Vectorially Ordered Fuzzy Numbers (vOFNs). In this approach, the classical view of an OFN as an ordered pair of functions is replaced by an ordered pair of vectors. This shift addresses several limitations of previous fuzzy number formalisms, such as the LR notation by Dubois and Prade, which restricts the edges to rectilinear shapes and precludes curvilinear transformations.
The proposed vOFN formulation constitutes a significant departure from the function-based definition of OFNs by offering a fully vectorial structure. Unlike conventional LR-type fuzzy numbers [6], which enforce parametric symmetry and require defuzzification for comparative reasoning, vOFNs allow direct vector-based operations and comparisons, preserving both directionality and shape semantics without approximation. This contributes to improved interpretability and reduced computational burden in practical systems.
At the same time, the vOFN framework retains the beneficial properties of Kosiński’s original OFN concept. It forms a complete ring structure, with neutral elements for addition, subtraction, multiplication, and division. Operations are well-defined across a broad class of fuzzy numbers, including triangular and trapezoidal forms and singletons.
Notably, vOFNs maintain the directional ordering property, enhancing the expressive capability of fuzzy numbers by encoding magnitude, uncertainty, and directional trends simultaneously.
Moreover, a new vector-based similarity metric has been introduced to evaluate the closeness of fuzzy numbers without requiring the defuzzification or centroid approximation. This metric preserves both the spatial structure and the directional profile of fuzzy numbers, and it serves as a foundation for comparison-based reasoning in intelligent systems.
To illustrate practical integration, a simplified implementation scenario is outlined for incorporating vOFN arithmetic into large language models (LLMs). Specifically, fuzzy arithmetic based on vOFNs can be embedded into the attention or weighting mechanisms of LLMs to represent uncertainty in token or context relevance scores. For instance, a fuzzy-weighted attention mechanism may use vOFNs to evaluate ambiguous or underspecified user input by modeling lexical or semantic uncertainty more effectively than crisp probabilities. This offers improved adaptability and interpretability in applications such as fuzzy querying, uncertain context tracking, or intent classification in generative agents. Preliminary implementations using Python-based libraries (e.g., PyTorch and TensorFlow) can incorporate vOFN arithmetic via custom differentiable layers handling fuzzy vector operations, allowing smooth integration into existing transformer-based architectures.
Such applications showcase how vOFNs can enhance generative AI systems by enabling flexible, uncertainty-aware reasoning in a mathematically grounded manner.
In contrast to other fuzzy models such as intuitionistic fuzzy sets (IFS) [48] and type-2 fuzzy systems [49], which often incur high computational costs due to their layered or interval-based architectures, the vectorial representation of vOFNs ensures linear time operations and easier implementation in differentiable programming environments. A comparative analysis provided in Section 3.1, Section 3.2 and Section 3.3 confirms that vOFNs outperform traditional OFNs and LR numbers in terms of generality, algebraic closure, and suitability for algorithmic use.
The vOFN arithmetic is versatile and could find a variety of applications, including in the realm of Artificial Intelligence (AI). One such example, discussed above, is the modeling of context-sensitive behaviors in LLMs. The ability of vOFN arithmetic to represent adaptive, elastic behaviors in a computationally efficient and mathematically sound manner holds promising implications for the advancement of generative agent design. This aligns with current trends in neuro-symbolic AI and uncertainty modeling, where hybrid fuzzy-symbolic approaches gain relevance for explainability and control in language-driven systems.
Compared to other fuzzy frameworks such as intuitionistic fuzzy sets (IFSs) [48] or type-2 fuzzy systems [49], the proposed vOFN model offers lower computational overhead while preserving directional semantics and full algebraic closure. These advantages make vOFNs more suitable for real-time inference tasks in LLMs and embedded intelligent systems. A detailed benchmark comparison with representative fuzzy arithmetic models is part of our ongoing research.
In summary, the vOFN representation inherits the strengths of OFN arithmetic while overcoming its weaknesses, providing a consistent, robust, and highly implementable framework for intelligent adaptive systems within the evolving landscape of Generative AI. While the current paper focuses on the theoretical formulation and potential application domains, future work will involve implementing full-scale vOFN-integrated modules into LLM-based agents and validating their performance through controlled experiments in tasks involving contextual uncertainty and fuzzy control.
Author Contributions
Conceptualization, J.M.C. and H.Z.; methodology, J.M.C. and H.Z.; software, J.M.C.; validation, H.Z. and A.Ż.; formal analysis, J.M.C.; investigation, A.Ż.; resources, H.Z.; data curation, J.M.C.; writing—original draft preparation, J.M.C.; writing—review and editing, H.Z. and A.Ż.; visualization, H.Z.; supervision, H.Z.; project administration, A.Ż.; funding acquisition, J.M.C. and H.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| OFN | ordered fuzzy numbers proposed by Kosiński |
| vOFN | vectorial ordered fuzzy numbers |
| LR | fuzzy arithmetic proposed by Dubois and Prade |
| CFA | constrained fuzzy arithmetic proposed by Klir |
| RMD | fuzzy arithmetic proposed by Piegat and Pluciński |
| SNO | shape normalization operator |
| JC | metric dedicated to comparing ordered fuzzy numbers |
| CFA | constrained fuzzy arithmetic proposed by Klir |
Appendix A
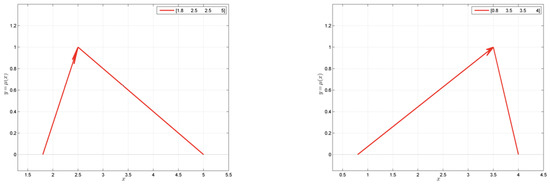
Figure A1.
Fuzzy number A[1.8, 2.5, 2.5, 5.0] and fuzzy number B[0.8, 3.5, 3.5, 4.0].
Appendix B
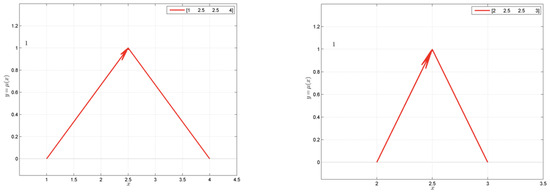
Figure A2.
Fuzzy number C[1.0, 2.5, 2.5, 4.0] and fuzzy number D[2.0, 2.5, 2.5, 3.0].
Appendix C
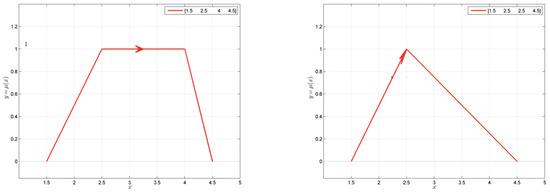
Figure A3.
Fuzzy number E[1.5, 2.5, 4.0, 4.5] and fuzzy number F[1.5, 2.5, 2.5, 4.5].
References
- Zadeh, L. Outline of new approach to the analysis of complex systems and decision process. IEEE Syst. Man Cybern. 1973, SMC-3, 28–44. [Google Scholar] [CrossRef]
- Mikolajewska, E.; Prokopowicz, P.; Mikolajewski, D. Computational gait analysis using fuzzy logic for everyday clinical purposes—Preliminary findings. Bio-Algorithms Med-Syst. 2017, 13, 37–42. [Google Scholar] [CrossRef]
- Hajjari, T. A New Improved Method for Comparing Fuzzy Numbers by Centroid Point. J. Math. Ext. 2016, 10, 1–23. [Google Scholar]
- Wang, Y.; Luo, Y. Area ranking of fuzzy numbers based on positive and negative ideal points. Comput. Math. Appl. 2009, 58, 1763–1779. [Google Scholar] [CrossRef]
- Sanchez, E. Solution of fuzzy equations with extended operations. Fuzzy Sets Syst. 1984, 12, 237–248. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Fuzzy Sets and Systems: Theory and Applications; Academic Press: New York, NY, USA, 1980. [Google Scholar]
- Makó, Z. Real vector space of LR-fuzzy intervals with respect to the shape-preserving t-norm-based addition. Fuzzy Sets Syst. 2012, 200, 136–149. [Google Scholar] [CrossRef]
- Klir, G.; Yaun, B. Fuzzy Set and Fuzzy Logic: Theory and Application; Prentice Hall: Upper Saddle River, NJ, USA, 1995. [Google Scholar]
- Chang, D.C. Ranking of fuzzy sets based on the area between the centroid and original points. Comput. Math. Appl. 1997, 33, 103–109. [Google Scholar]
- Chu, T.C.; Tsao, C.T. Ranking fuzzy numbers with an area between the centroid point and original point. Comput. Math. Appl. 2002, 43, 111–117. [Google Scholar] [CrossRef]
- Piegat, A.; Pluciński, M. Computing with words with the use of inverse RDM models of membership functions. Int. J. Appl. Math. Comput. Sci. 2015, 25, 675–688. [Google Scholar] [CrossRef]
- Kosinski, W.; Słysz, P. Fuzzy Numbers and Their Quotient Space with Algebraic Operations. Bull. Pol. Acad. Sci. Math. 1993, 41, 285–295. [Google Scholar]
- Kosinski, W.; Prokopowicz, P.; Slezak, D. On Algebraic Operations on Fuzzy Numbers. In Intelligent Information Processing and Web Mining, Proceedings of the International IIS: IIPWM’03 Conference Held in Zakopane, Poland, 2–5 June 2003; Kłopotek, M.A., Wierzchoń, S.T., Trojanowski, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; pp. 353–362. [Google Scholar]
- Kosinski, W. On fuzzy number calculus. Int. J. Appl. Math. Comput. Sci. 2006, 16, 51–57. [Google Scholar]
- Marszalek, A.; Burczynski, T. Modeling and forecasting financial time series with ordered fuzzy candlesticks. Inf. Sci. 2014, 273, 144–155. [Google Scholar] [CrossRef]
- Prokopowicz, P. The use of Ordered Fuzzy Numbers for modelling changes in dynamic processes. Inf. Sci. 2019, 470, 1–14. [Google Scholar] [CrossRef]
- Czerniak, J.M. Ordered Fuzzy Numbers Applied in Selected Swarm Optimization Algorithms; Casimir the Great University Press: Bydgoszcz, Poland, 2019. [Google Scholar]
- Vince, T.; Lukac, P.; Schweiner, D.; Tomcikova, I.; Mamchur, D. Android Application Supporting Developed Web Applications Testing. In Proceedings of the International Conference on Modern Electrical and Energy Systems (MEES), Kremenchuk, Ukraine, 15–17 November 2017; IEEE: Piscataway Township, NY, USA, 2017; pp. 392–395. [Google Scholar]
- Bucko, R.; Vince, T.; Molnar, J.; Dziak, J.; Gladyr, A. Safety System For Intelligent Building. In Proceedings of the International Conference on Modern Electrical and Energy Systems (MEES), Kremenchuk, Ukraine, 15–17 November 2017; IEEE: Piscataway Township, NJ, USA, 2017; pp. 252–255. [Google Scholar]
- Ewald, D.; Zarzycki, H.; Czerniak, J.M. Certain Aspects of the OFNBee Algorithm Operation for Different Fuzzifiers. In Proceedings of the Uncertainty and Imprecision in Decision Making and Decision Support: New Advances, Challenges, and Perspectives; Atanassov, K.T., Atanassova, V., Kacprzyk, J., Kałuszko, A., Krawczak, M., Owsiński, J.W., Sotirov, S.S., Sotirova, E., Szmidt, E., Zadrożny, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2022; pp. 241–256. [Google Scholar]
- Kosinski, W. On soft computing and modeling. Image Process. Commun. 2006, 11, 71–82. [Google Scholar]
- Kosinski, W.; Frischmuth, K.; Wilczyńska-Sztyma, D. A New Fuzzy Approach to Ordinary Differential Equations. In Proceedings of the ICAISC 2010, Part I, Zakopane, Poland, 13–17 June 2010; Lecture Notes in Computer Science. Rutkowski, L., Scherer, R., Tadeusiewicz, R., Zadeh, L.A., Żurada, J.M., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6113, pp. 120–127. [Google Scholar]
- Adabitabar, F.M.; Fath-Tabar, G.; Eslampia, Z. The similarity measure of generalized fuzzy numbers based on interval distance. Appl. Math. Lett. 2012, 25, 1528–1534. [Google Scholar] [CrossRef]
- Debashree, G.; Debjani, C. A new approach to fuzzy distance measure and similarity measure between two generalized fuzzy numbers. Appl. Soft Comput. 2010, 10, 90–99. [Google Scholar]
- Stachowiak, A.; Żywica, P.; Dyczkowski, K.; Wójtowicz, A. An Interval-Valued Fuzzy Classifier Based on an Uncertainty-Aware Similarity Measure. In Proceedings of the IEEE Conference on Intelligent Systems, Warsaw, Poland, 24–26 September 2014. [Google Scholar]
- Hasan, M.K.; Sultana, A.; Mitra, N. Picture Fuzzy Relations over Picture Fuzzy Sets. Am. J. Comput. Math. 2023, 13, 161–184. [Google Scholar] [CrossRef]
- Prokopowicz, P.; Czerniak, J.; Mikolajewski, D.; Apiecionek, L.; Slezak, D. Theory and Applications of Ordered Fuzzy Numbers. A Tribute to Professor Witold Kosińsk; Studies in Fuzziness and Soft Computing; Springer International Publishing: Berlin/Heidelberg, Germany, 2017; Volume 356. [Google Scholar]
- Zadrozny, S.; Kacprzyk, J. On the use of linguistic summaries for text categorization. In Proceedings of the IPMU, Perugia, Italy, 4–9 July 2004; pp. 1373–1380. [Google Scholar]
- Yager, R.R. A procedure for ordering fuzzy subsets of the unit interval. Inf. Sci. 1981, 24, 143–161. [Google Scholar] [CrossRef]
- Kaufmann, A.; Gupta, M.M. Introduction to Fuzzy Arithmetic Theory and Applications; Van Nostrand Reinhold: New York, NY, USA, 1991. [Google Scholar]
- Adamo, J.M. Fuzzy decision trees. Fuzzy Sets Syst. 1980, 4, 207–219. [Google Scholar] [CrossRef]
- Bortolan, G.; Degani, R. A review of some methods for ranking fuzzy subsets. Fuzzy Sets Syst. 1985, 15, 1–19. [Google Scholar] [CrossRef]
- Dadgostar, M.; Kerr, D. A method for comparing fuzzy numbers using distance and ranking functions. Aust. J. Intell. Inf. Process. Syst. 2008, 10, 38–43. [Google Scholar]
- Cheng, C. A new approach for ranking fuzzy numbers by distance method. Fuzzy Sets Syst. 1998, 95, 307–317. [Google Scholar] [CrossRef]
- Asady, B.; Zendehnam, A. Ranking fuzzy numbers by distance minimization. Appl. Math. Model. 2007, 31, 2589–2598. [Google Scholar] [CrossRef]
- Trana, L.; Ducksteinb, L. Comparison of fuzzy numbers using a fuzzy distance measure. Fuzzy Sets Syst. 2002, 130, 331–341. [Google Scholar] [CrossRef]
- Abbasbandy, S.; Asady, B. Ranking of fuzzy numbers by sign distance. Inform. Sciences 2006, 176, 2405–2416. [Google Scholar] [CrossRef]
- Dobrosielski, W.; Czerniak, J.; Szczepanski, J.; Zarzycki, H. Two New Defuzzification Methods Useful for Different Fuzzy Arithmetics. In Uncertainty and Imprecision in Decision Making and Decision Support: Cross-Fertilization, New Models and Applications. IWIFSGN 2016; Advances in Intelligent Systems and Computing; Springer: Berlin/Heidelberg, Germany, 2018; Volume 559, pp. 83–101. [Google Scholar]
- Baldwin, J.; Guild, D. Evidential reasoning in a multi-hypothesis environment. Fuzzy Sets Syst. 1983, 10, 1–15. [Google Scholar]
- Jain, R. Decision-making in the presence of fuzzy variables. IEEE Trans. Syst. Man, Cybern. 1976, 6, 698–703. [Google Scholar]
- Czerniak, J.M.; Dobrosielski, W.T.; Filipowicz, I. Comparing Fuzzy Numbers Using Defuzzificators on OFN Shapes. In Theory and Applications of Ordered Fuzzy Numbers. A Tribute to Professor Witold Kosinski; Studies in Fuzziness and Soft Computing; Prokopowicz, P., Czerniak, J.M., Mikolajewski, D., Apiecionek, L., Slezak, D., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2017; Chapter 6; pp. 207–222. [Google Scholar]
- Kerre, E.E. Introduction to the Basic Principles of Fuzzy Set Theory and Some of Its Applications; Communication and Cognition: Ghent, Belgium, 1993. [Google Scholar]
- Baas, S.M.; Kwakernaak, H. Rating and ranking of multiple-aspect alternatives using fuzzy sets. Automatica 1977, 13, 47–58. [Google Scholar] [CrossRef]
- Zarzycki, H.; Apiecionek, Ł.; Czerniak, J.M.; Ewald, D. The Proposal of Fuzzy Observation and Detection of Massive Data DDOS Attack Threat. In Proceedings of the Uncertainty and Imprecision in Decision Making and Decision Support: New Challenges, Solutions and Perspectives; Atanassov, K.T., Atanassova, V., Kacprzyk, J., Kaluszko, A., Krawczak, M., Owsinski, J.W., Sotirov, S., Sotirova, E., Szmidt, E., Zadrozny, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2021; pp. 363–378. [Google Scholar]
- Zarzycki, H.; Dobrosielski, W.T.; Czerniak, J.M.; Ewald, D. Use of OFN in the Short-Term Prediction of Exchange Rates. In Proceedings of the Advances and New Developments in Fuzzy Logic and Technology; Atanassov, K.T., Atanassova, V., Kacprzyk, J., Kałuszko, A., Krawczak, M., Owsiński, J.W., Sotirov, S.S., Sotirova, E., Szmidt, E., Zadrożny, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2021; pp. 289–301. [Google Scholar]
- Szmidt, E.; Kacprzyk, J. Distances between intuitionistic fuzzy sets. Fuzzy Sets Syst. 2000, 114, 505–518. [Google Scholar] [CrossRef]
- Jacko, P.; Kovac, D.; Bucko, R.; Vince, T.; Kravets, O. The Parallel Data Processing by Nucleo Board with STM32 Microcontrollers. In Proceedings of the International Conference on Modern Electrical and Energy Systems (MEES), Kremenchuk, Ukraine, 15–17 November 2017; pp. 264–267. [Google Scholar]
- Atanassov, K. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Mendel, J.M. Uncertain Rule-Based Fuzzy Logic Systems: Introduction and New Directions; Prentice Hall PTR: Upper Saddle River, NJ, USA, 2001. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).