Diffusion-Inspired Masked Language Modeling for Symbolic Harmony Generation on a Fixed Time Grid
Abstract
1. Introduction
- We propose an encoder-only Transformer architecture for melodic harmonization generation, avoiding the limitations of autoregressive decoders and enabling efficient bidirectional context modeling.
- We introduce two discrete diffusion-inspired training schemes for symbolic music harmonization implemented through progressive unmasking strategies compatible with masked language modeling objectives.
- We design and evaluate a binary piano roll melody representation, incorporating both pitch-time and pitch class-time grids, that is injected directly into the encoder input stream for effective melody-to-harmony conditioning.
2. Method
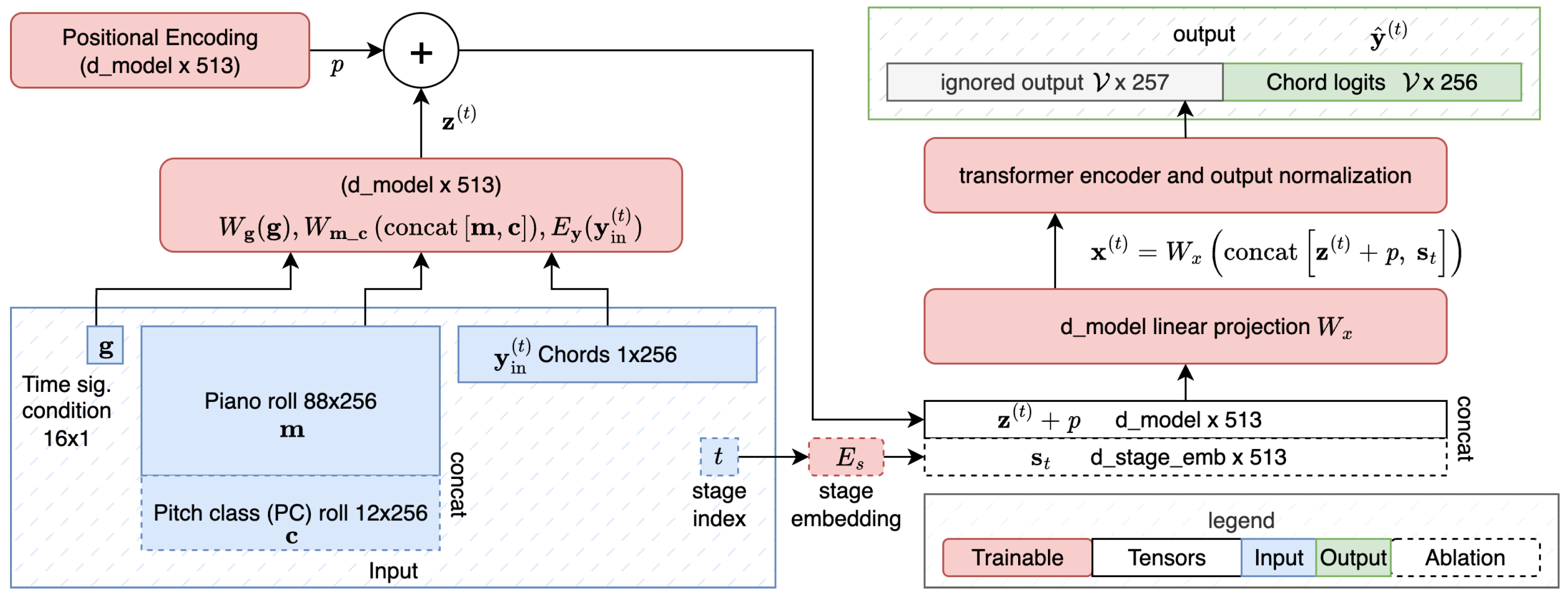
2.1. Input Representation
2.2. Model Architecture
- Binary melodic and time signature inputs: The inputs for the time signature () and melody and pitch classes ( and , respectively) are binary vectors rather than token embeddings. The corresponding model output of those components is ignored during both training and inference (denoted as “ignored output” in Figure 1). The model is trained only to predict harmony tokens.
- Trainable positional embeddings: Positional embeddings, , are randomly initialized and trained jointly with the model parameters. This design allows the model to learn how relative positions in the 16th-note grid correspond to meaningful temporal relationships between the melody and harmony, rather than imposing a fixed positional prior.
- Stage-awareness conditioning: A stage embedding layer () receives an integer index indicating the current unmasking stage (t). The stage embedding vector () is replicated for 513 “time steps” and concatenated to the output of the positional embedding layer (which includes 513 “time steps”). This augmented input is then passed through a projection that maps the concatenated input to the dimensionality of the Transformer encoder. This is the final input to the encoder.
2.3. Diffusion-Inspired Unmasking in Training and Generation
- Random % Unmasking: At each stage t, n% of the remaining masked harmony tokens are randomly selected and unmasked. This introduces stochasticity and encourages the model to generalize across diverse partially observed contexts. While any value of n can be valid under this procedure, values of 5 and 10 are examined in the results.
- Midpoint Doubling: Inspired by binary subdivision and the hierarchical structure of music, this deterministic strategy reveals tokens at the midpoints between previously unmasked tokens, effectively doubling the number of visible tokens at each step. This results in a structured, coarse-to-fine unmasking trajectory.
- a
- A stage index t is sampled, which determines the unmasking level and which tokens are to be predicted.
- b
- A partial “visible” harmony sequence is defined using one of the unmasking strategies, and the set of target tokens to be learned is identified ().
- c
- The model is trained to predict the current target-masked tokens using the melody and the partially visible harmony context.
3. Experimental Set-up and Dataset
3.1. Model Comparison
- i
- Random Unmasking (Rn): Trained and generated using the random n% (for and ) unmasking strategy described in Section 2.3;
- ii
- Midpoint Doubling (MD): Trained and generated using the midpoint doubling schedule, including both pitch class roll input and stage-aware embeddings.
- iii
- No pc-roll (Rn-NPC and MD-NPC): Identical to (i) and (ii) but without the pitch class roll input; only the binary 88-note piano roll is used to represent the melody;
- iv
- No Stage Awareness (Rn-NS and MD-NS): Identical to (i) and (ii) but without stage embeddings, making the model unaware of its position in the unmasking process.
3.2. Data and Training
- In domain: In this setting, models were evaluated on the validation and test split of the HookTheory dataset.
- Out of domain: Here, evaluation was conducted on a separate collection of 650 jazz standard lead sheets, again transposed to C major or A minor using the Krumhansl key profiles.
3.3. Evaluation Metrics and Protocols
3.3.1. Training Performance Assessment
3.3.2. Symbolic Music Metrics
- A.
- Chord Progression Coherence and Diversity
- (i)
- Chord histogram entropy (CHE) measures how evenly chords are distributed in a piece. Higher values reflect greater harmonic variety.
- (ii)
- Chord coverage (CC) counts the number of distinct chord types used, indicating the breadth of harmonic vocabulary.
- (iii)
- Chord tonal distance (CTD) computes the average tonal distance between adjacent chords, where lower values suggest smoother, more connected progressions.
- B.
- Chord–Melody Harmonicity
- (i)
- The chord-tone-to-non-chord-tone ratio (CTnCTR) measures the proportion of melody notes that match chord tones or are near passing tones. Higher values imply stronger harmonic support for the melody.
- (ii)
- The Pitch Consonance Score (PCS) assigns consonance scores to melody–chord intervals based on standard musical intervals. Higher scores indicate more consonant melodic writing.
- (iii)
- The melody–chord tonal distance (MCTD) evaluates the average tonal distance between the melody notes and underlying chords. Lower values indicate closer harmonic alignment.
- C.
- Harmonic Rhythm Coherence and Diversity
- (i)
- Harmonic rhythm histogram entropy (HRHE) measures the diversity in the timing of chord changes. Higher entropy suggests more rhythmically varied progressions.
- (ii)
- Harmonic rhythm coverage (HRC) counts distinct rhythmic patterns of chord placement. Higher values indicate a wider range of rhythmic usage.
- (iii)
- The chord beat strength (CBS) scores how aligned chord onsets are with the metrical strength. Lower scores imply alignment with strong beats, and higher scores reflect more syncopated rhythms.
3.3.3. FMD
4. Results
4.1. Training Performance
4.2. Music Metrics
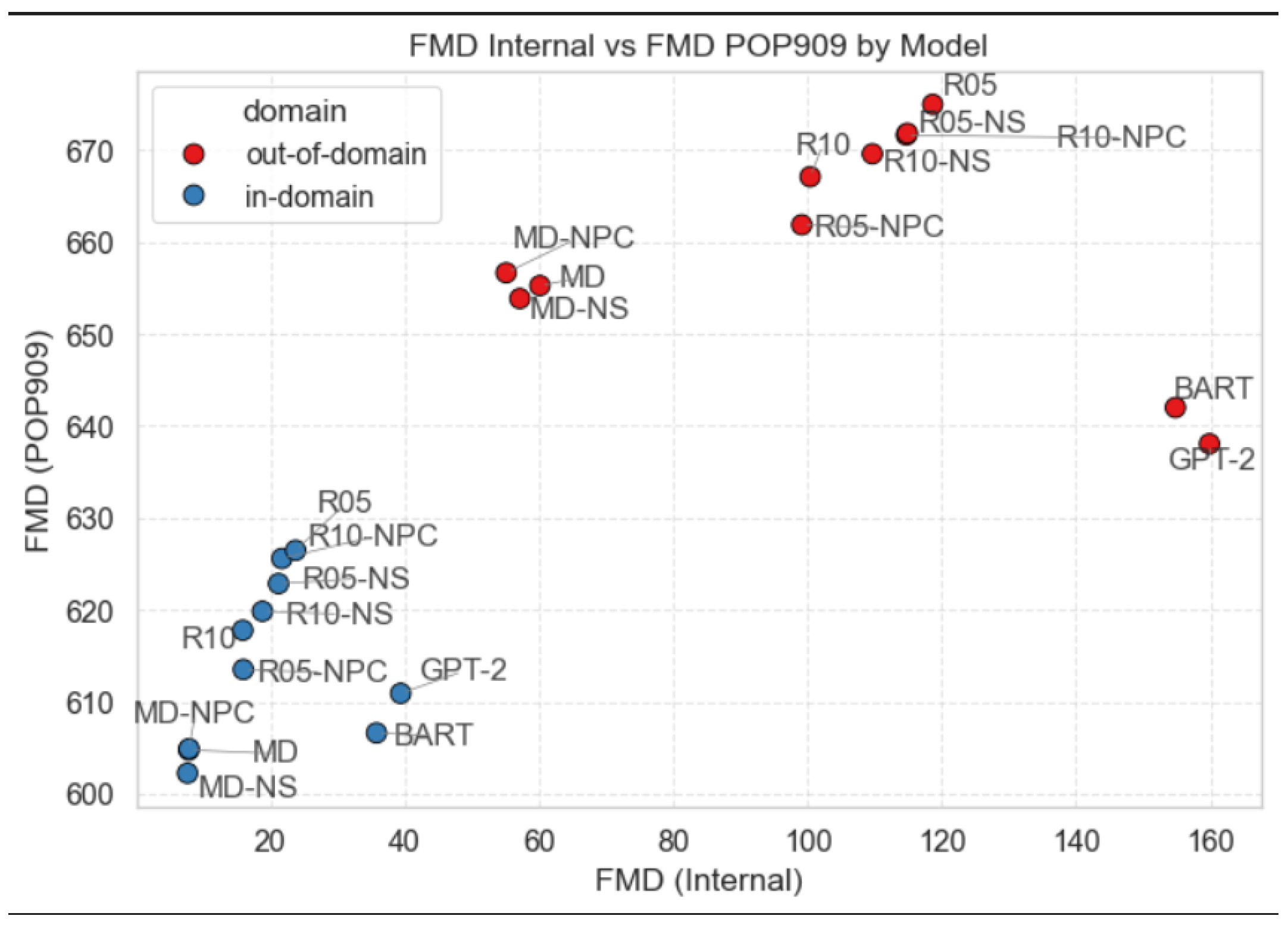
4.3. FMD Scores
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| LSTM | Long short-term memory |
| VAE | Variational auto encoder |
| MLM | Masked language modeling |
| BERT | Bidirectional encoder representations from transformers |
| BART | Bidirectional and auto-regressive transformers |
| GPT-2 | Generative Pretrained Model 2 |
| MD | Midpoint doubling |
| Rn | Random n% |
| NPC | No pitch classes |
| NS | No stage |
| ppl | Perplexity |
| CHE | Chord histogram entropy |
| CC | Chord coverage |
| CTD | Chord tonal distance |
| CTnCTR | Chord-tone-to-non-chord-tone ratio |
| PCS | Pitch Consonance Score |
| MCTD | Melody–chord tonal distance |
| HRHE | Harmonic rhythm histogram entropy |
| HRC | Harmonic rhythm coverage |
| CBS | Chord beat strength |
| FID | Fréchet Inseption Distance |
| FMD | Fréchet Music Distance |
References
- Lim, H.; Rhyu, S.; Lee, K. Chord generation from symbolic melody using BLSTM networks. arXiv 2017, arXiv:1712.01011. [Google Scholar] [CrossRef]
- Yeh, Y.C.; Hsiao, W.Y.; Fukayama, S.; Kitahara, T.; Genchel, B.; Liu, H.M.; Dong, H.W.; Chen, Y.; Leong, T.; Yang, Y.H. Automatic melody harmonization with triad chords: A comparative study. J. New Music. Res. 2021, 50, 37–51. [Google Scholar] [CrossRef]
- Chen, Y.W.; Lee, H.S.; Chen, Y.H.; Wang, H.M. SurpriseNet: Melody harmonization conditioning on user-controlled surprise contours. arXiv 2021, arXiv:2108.00378. [Google Scholar]
- Costa, L.F.; Barchi, T.M.; de Morais, E.F.; Coca, A.E.; Schemberger, E.E.; Martins, M.S.; Siqueira, H.V. Neural networks and ensemble based architectures to automatic musical harmonization: A performance comparison. Appl. Artif. Intell. 2023, 37, 2185849. [Google Scholar] [CrossRef]
- Huang, C.Z.A.; Vaswani, A.; Uszkoreit, J.; Shazeer, N.; Simon, I.; Hawthorne, C.; Dai, A.M.; Hoffman, M.D.; Dinculescu, M.; Eck, D. Music Transformer. arXiv 2018, arXiv:1809.04281. [Google Scholar]
- Rhyu, S.; Choi, H.; Kim, S.; Lee, K. Translating melody to chord: Structured and flexible harmonization of melody with transformer. IEEE Access 2022, 10, 28261–28273. [Google Scholar] [CrossRef]
- Huang, J.; Yang, Y.H. Emotion-driven melody harmonization via melodic variation and functional representation. arXiv 2024, arXiv:2407.20176. [Google Scholar] [CrossRef]
- Wu, S.; Wang, Y.; Li, X.; Yu, F.; Sun, M. Melodyt5: A unified score-to-score transformer for symbolic music processing. arXiv 2024, arXiv:2407.02277. [Google Scholar]
- Mittal, G.; Engel, J.; Hawthorne, C.; Simon, I. Symbolic music generation with diffusion models. arXiv 2021, arXiv:2103.16091. [Google Scholar] [CrossRef]
- Lv, A.; Tan, X.; Lu, P.; Ye, W.; Zhang, S.; Bian, J.; Yan, R. Getmusic: Generating any music tracks with a unified representation and diffusion framework. arXiv 2023, arXiv:2305.10841. [Google Scholar] [CrossRef]
- Zhang, J.; Fazekas, G.; Saitis, C. Fast diffusion gan model for symbolic music generation controlled by emotions. arXiv 2023, arXiv:2310.14040. [Google Scholar] [CrossRef]
- Atassi, L. Generating symbolic music using diffusion models. arXiv 2023, arXiv:2303.08385. [Google Scholar] [CrossRef]
- Min, L.; Jiang, J.; Xia, G.; Zhao, J. Polyffusion: A diffusion model for polyphonic score generation with internal and external controls. arXiv 2023, arXiv:2307.10304. [Google Scholar] [CrossRef]
- Li, S.; Sung, Y. Melodydiffusion: Chord-conditioned melody generation using a transformer-based diffusion model. Mathematics 2023, 11, 1915. [Google Scholar] [CrossRef]
- Wang, Z.; Min, L.; Xia, G. Whole-song hierarchical generation of symbolic music using cascaded diffusion models. arXiv 2024, arXiv:2405.09901. [Google Scholar] [CrossRef]
- Huang, Y.; Ghatare, A.; Liu, Y.; Hu, Z.; Zhang, Q.; Sastry, C.S.; Gururani, S.; Oore, S.; Yue, Y. Symbolic music generation with non-differentiable rule guided diffusion. arXiv 2024, arXiv:2402.14285. [Google Scholar] [CrossRef]
- Zhang, J.; Fazekas, G.; Saitis, C. Mamba-Diffusion Model with Learnable Wavelet for Controllable Symbolic Music Generation. arXiv 2025, arXiv:2505.03314. [Google Scholar] [CrossRef]
- Chang, H.; Zhang, H.; Jiang, L.; Liu, C.; Freeman, W.T. Maskgit: Masked generative image transformer. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–20 June 2022; pp. 11315–11325. [Google Scholar]
- Austin, J.; Johnson, D.D.; Ho, J.; Tarlow, D.; Van Den Berg, R. Structured denoising diffusion models in discrete state-spaces. Adv. Neural Inf. Process. Syst. 2021, 34, 17981–17993. [Google Scholar]
- Ho, J.; Jain, A.; Abbeel, P. Denoising diffusion probabilistic models. Adv. Neural Inf. Process. Syst. 2020, 33, 6840–6851. [Google Scholar]
- Jonason, N.; Casini, L.; Sturm, B.L. SYMPLEX: Controllable Symbolic Music Generation using Simplex Diffusion with Vocabulary Priors. arXiv 2024, arXiv:2405.12666. [Google Scholar] [CrossRef]
- Zhang, J.; Fazekas, G.; Saitis, C. Composer style-specific symbolic music generation using vector quantized discrete diffusion models. In Proceedings of the 2024 IEEE 34th International Workshop on Machine Learning for Signal Processing (MLSP), London, UK, 22–25 September 2024; IEEE: New York, NY, USA, 2024; pp. 1–6. [Google Scholar]
- Plasser, M.; Peter, S.; Widmer, G. Discrete diffusion probabilistic models for symbolic music generation. arXiv 2023, arXiv:2305.09489. [Google Scholar] [CrossRef]
- Raffel, C.; McFee, B.; Humphrey, E.J.; Salamon, J.; Nieto, O.; Liang, D.; Ellis, D.P.; Raffel, C.C. MIR_EVAL: A Transparent Implementation of Common MIR Metrics. In Proceedings of the ISMIR, Taipei, Taiwan, 27–31 October 2014; Volume 10, p. 2014. [Google Scholar]
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. Bert: Pre-training of deep bidirectional transformers for language understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Minneapolis, MN, USA, 2–7 June 2019; Volume 1, pp. 4171–4186. [Google Scholar]
- Radford, A.; Wu, J.; Child, R.; Luan, D.; Amodei, D.; Sutskever, I. Language models are unsupervised multitask learners. OpenAI Blog 2019, 1, 9. [Google Scholar]
- Lewis, M.; Liu, Y.; Goyal, N.; Ghazvininejad, M.; Mohamed, A.; Levy, O.; Stoyanov, V.; Zettlemoyer, L. Bart: Denoising sequence-to-sequence pre-training for natural language generation, translation, and comprehension. arXiv 2019, arXiv:1910.13461. [Google Scholar]
- Krumhansl, C.L. Cognitive Foundations of Musical Pitch; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Hahn, S.; Yin, J.; Zhu, R.; Xu, W.; Jiang, Y.; Mak, S.; Rudin, C. SentHYMNent: An Interpretable and Sentiment-Driven Model for Algorithmic Melody Harmonization. In Proceedings of the 30th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Barcelona, Spain, 25–29 August 2024; pp. 5050–5060. [Google Scholar]
- Hiehn, S. Chord Melody Dataset. 2019. Available online: https://github.com/shiehn/chord-melody-dataset (accessed on 21 August 2025).
- Sun, C.E.; Chen, Y.W.; Lee, H.S.; Chen, Y.H.; Wang, H.M. Melody harmonization using orderless NADE, chord balancing, and blocked Gibbs sampling. In Proceedings of the ICASSP 2021-2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 6–11 June 2021; IEEE: New York, NY, USA, 2021; pp. 4145–4149. [Google Scholar]
- Wu, S.; Yang, Y.; Wang, Z.; Li, X.; Sun, M. Generating chord progression from melody with flexible harmonic rhythm and controllable harmonic density. EURASIP J. Audio Speech Music Process. 2024, 2024, 4. [Google Scholar] [CrossRef]
- Retkowski, J.; Stępniak, J.; Modrzejewski, M. Frechet music distance: A metric for generative symbolic music evaluation. arXiv 2024, arXiv:2412.07948. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, K.; Jiang, J.; Zhang, Y.; Xu, M.; Dai, S.; Bin, G.; Xia, G. POP909: A Pop-song Dataset for Music Arrangement Generation. In Proceedings of the 21st International Conference on Music Information Retrieval, ISMIR, Montreal, QC, Canada, 11–16 October 2020. [Google Scholar]
- Wu, S.; Wang, Y.; Yuan, R.; Guo, Z.; Tan, X.; Zhang, G.; Zhou, M.; Chen, J.; Mu, X.; Gao, Y.; et al. Clamp 2: Multimodal music information retrieval across 101 languages using large language models. arXiv 2024, arXiv:2410.13267. [Google Scholar] [CrossRef]
- Conover, W.J. Practical Nonparametric Statistics; John Wiley & Sons: Hoboken, NJ, USA, 1999. [Google Scholar]
- Sahoo, S.; Arriola, M.; Schiff, Y.; Gokaslan, A.; Marroquin, E.; Chiu, J.; Rush, A.; Kuleshov, V. Simple and effective masked diffusion language models. Adv. Neural Inf. Process. Syst. 2024, 37, 130136–130184. [Google Scholar]
- Lou, A.; Meng, C.; Ermon, S. Discrete diffusion modeling by estimating the ratios of the data distribution. arXiv 2023, arXiv:2310.16834. [Google Scholar]
| MD | R10 | R05 | MD-NPC | R10-NPC | R05-NPC | MD-NS | R10-NS | R05-NS | |
|---|---|---|---|---|---|---|---|---|---|
| loss | 0.0625 | 0.0486 | 0.0498 | 0.0661 | 0.0497 | 0.0499 | 0.0669 | 0.0486 | 0.0437 |
| acc | 0.9860 | 0.9868 | 0.9869 | 0.9846 | 0.9873 | 0.9870 | 0.9846 | 0.9871 | 0.9883 |
| ppl | 1.0651 | 1.0503 | 1.0516 | 1.0690 | 1.0512 | 1.0515 | 1.0698 | 1.0500 | 1.0451 |
| 0.0737 | 0.0300 | 0.0324 | 0.0768 | 0.0279 | 0.0271 | 0.0735 | 0.0259 | 0.0211 |
| Model | CHE | CC | CTD | CTnCTR | PCS | MCTD | HRHE | HRC | CBS |
|---|---|---|---|---|---|---|---|---|---|
| GT | 1.4126 | 4.9841 | 0.9743 | 0.8369 | 0.4745 | 1.3467 | 0.5432 | 2.3139 | 0.3413 |
| MD | 1.3484 | 4.5963 | 0.7491 | 0.6848 | 0.2912 | 1.5164 | 0.4461 | 2.1279 | 0.1271 |
| MD-NPC | 1.3276 | 4.6042 | 0.7360 | 0.6805 | 0.2839 | 1.5162 | 0.4887 | 2.2374 | 0.1415 |
| MD-NS | 1.3315 | 4.9208 | 0.8091 | 0.7013 | 0.3102 | 1.5019 | 0.7521 | 3.0422 | 0.2285 |
| R10 | 0.4487 | 1.9683 | 0.3970 | 0.8168 | 0.4234 | 1.3961 | 0.2220 | 1.5369 | 0.0601 |
| R10-NPC | 0.1341 | 1.2889 | 0.1071 | 0.8037 | 0.4140 | 1.4151 | 0.0871 | 1.2241 | 0.0246 |
| R10-NS | 0.2978 | 1.6385 | 0.2731 | 0.7945 | 0.4052 | 1.4201 | 0.1762 | 1.4261 | 0.0506 |
| R05 | 0.0406 | 1.0712 | 0.0269 | 0.8092 | 0.4214 | 1.4099 | 0.0269 | 1.0474 | 0.0053 |
| R05-NPC | 0.4088 | 1.7678 | 0.3319 | 0.7496 | 0.3897 | 1.4542 | 0.1642 | 1.3746 | 0.0422 |
| R05-NS | 0.1659 | 1.3403 | 0.1498 | 0.7987 | 0.4076 | 1.4183 | 0.0671 | 1.1583 | 0.0179 |
| BART | 1.0248 | 3.1306 | 0.9595 | 0.7703 | 0.4119 | 1.4292 | 0.0787 | 1.1358 | 0.1863 |
| GPT-2 | 0.7991 | 2.5725 | 0.7786 | 0.7644 | 0.3962 | 1.4416 | 0.0144 | 1.0237 | 0.0605 |
| Model | CHE | CC | CTD | CTnCTR | PCS | MCTD | HRHE | HRC | CBS |
|---|---|---|---|---|---|---|---|---|---|
| GT | 2.2043 | 11.6558 | 0.8823 | 0.8320 | 0.3169 | 1.4028 | 0.5107 | 2.0570 | 0.2468 |
| MD | 1.4138 | 5.1311 | 0.6023 | 0.6028 | 0.2355 | 1.5650 | 0.2889 | 1.8707 | 0.0631 |
| MD-NPC | 1.4231 | 5.2895 | 0.5846 | 0.6064 | 0.2345 | 1.5673 | 0.3874 | 2.2171 | 0.0814 |
| MD-NS | 1.4562 | 5.8304 | 0.7592 | 0.6129 | 0.2486 | 1.5559 | 0.6899 | 3.2133 | 0.1722 |
| R10 | 0.6084 | 2.6254 | 0.3580 | 0.7125 | 0.3406 | 1.4514 | 0.2341 | 1.7338 | 0.0502 |
| R10-NPC | 0.1296 | 1.3181 | 0.0968 | 0.6858 | 0.3181 | 1.4875 | 0.1102 | 1.2971 | 0.0258 |
| R10-NS | 0.2679 | 1.6742 | 0.1851 | 0.6844 | 0.3185 | 1.4854 | 0.1801 | 1.5181 | 0.0432 |
| R05 | 0.0385 | 1.0760 | 0.0219 | 0.6881 | 0.3220 | 1.4849 | 0.0169 | 1.0456 | 0.0032 |
| R05-NPC | 0.5698 | 2.2038 | 0.4438 | 0.6396 | 0.2966 | 1.5246 | 0.2153 | 1.5847 | 0.0422 |
| R05-NS | 0.1396 | 1.3219 | 0.0947 | 0.6836 | 0.3177 | 1.4883 | 0.0508 | 1.1600 | 0.0114 |
| BART | 0.9422 | 3.1749 | 0.6604 | 0.4523 | 0.2442 | 1.6567 | 0.0359 | 1.0627 | 0.0327 |
| GPT-2 | 0.4724 | 1.8783 | 0.4281 | 0.4548 | 0.2441 | 1.6649 | 0.0017 | 1.0039 | 0.0016 |
| FMD, Internal | FMD, POP909 | ||||||
|---|---|---|---|---|---|---|---|
| In-Domain (HookTheory) | In-Domain (HookTheory) | ||||||
| Model | FMD (Internal) | p | Sig | Model | FMD (POP909) | p | Sig |
| MD-NS | 7.7068 | — | — | MD-NS | 602.2391 | — | — |
| MD | 7.8868 | 0.0402 | * | MD | 604.7602 | 0.7767 | |
| MD-NPC | 7.9254 | 0.3336 | MD-NPC | 604.8949 | 0.7767 | ||
| R10 | 15.9320 | 0.0000 | * | BART | 606.6170 | 0.7767 | |
| R05-NPC | 16.0106 | 0.0000 | * | GPT-2 | 610.9195 | 0.1321 | |
| R10-NS | 18.8581 | 0.0000 | * | R05-NPC | 613.5104 | 0.0145 | * |
| R05-NS | 21.2572 | 0.6148 | R10 | 617.7817 | 0.0000 | * | |
| R10-NPC | 21.7507 | 0.8510 | R10-NS | 619.8417 | 0.4983 | ||
| R05 | 23.7962 | 0.8510 | R05-NS | 622.8565 | 0.0298 | * | |
| BART | 35.8410 | 0.0000 | * | R10-NPC | 625.5839 | 0.0039 | * |
| GPT-2 | 39.4392 | 0.6754 | R05 | 626.4688 | 0.7767 | ||
| Out-of-Domain (JazzStandards) | Out-of-Domain (JazzStandards) | ||||||
| MD-NPC | 55.1527 | — | — | GPT-2 | 638.0580 | — | — |
| MD-NS | 57.1864 | 0.0171 | * | BART | 642.0034 | 0.0015 | * |
| MD | 60.1773 | 0.4622 | MD-NS | 653.8520 | 0.0000 | * | |
| R05-NPC | 99.1633 | 0.0000 | * | MD | 655.2597 | 0.5850 | |
| R10 | 100.4137 | 0.0000 | * | MD-NPC | 656.6548 | 0.2650 | |
| R10-NS | 109.6748 | 0.0000 | * | R05-NPC | 661.8715 | 0.5558 | |
| R10-NPC | 114.7309 | 0.0010 | * | R10 | 667.1043 | 0.0000 | * |
| R05-NS | 114.8798 | 0.9814 | R10-NS | 669.5915 | 0.5558 | ||
| R05 | 118.6610 | 0.0859 | R10-NPC | 671.6342 | 0.2650 | ||
| BART | 154.7940 | 0.0000 | * | R05-NS | 671.8228 | 0.9679 | |
| GPT-2 | 159.8600 | 0.0004 | * | R05 | 674.9689 | 0.0141 | * |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaliakatsos-Papakostas, M.; Makris, D.; Soiledis, K.; Tsamis, K.-T.; Katsouros, V.; Cambouropoulos, E. Diffusion-Inspired Masked Language Modeling for Symbolic Harmony Generation on a Fixed Time Grid. Appl. Sci. 2025, 15, 9513. https://doi.org/10.3390/app15179513
Kaliakatsos-Papakostas M, Makris D, Soiledis K, Tsamis K-T, Katsouros V, Cambouropoulos E. Diffusion-Inspired Masked Language Modeling for Symbolic Harmony Generation on a Fixed Time Grid. Applied Sciences. 2025; 15(17):9513. https://doi.org/10.3390/app15179513
Chicago/Turabian StyleKaliakatsos-Papakostas, Maximos, Dimos Makris, Konstantinos Soiledis, Konstantinos-Theodoros Tsamis, Vassilis Katsouros, and Emilios Cambouropoulos. 2025. "Diffusion-Inspired Masked Language Modeling for Symbolic Harmony Generation on a Fixed Time Grid" Applied Sciences 15, no. 17: 9513. https://doi.org/10.3390/app15179513
APA StyleKaliakatsos-Papakostas, M., Makris, D., Soiledis, K., Tsamis, K.-T., Katsouros, V., & Cambouropoulos, E. (2025). Diffusion-Inspired Masked Language Modeling for Symbolic Harmony Generation on a Fixed Time Grid. Applied Sciences, 15(17), 9513. https://doi.org/10.3390/app15179513








