Predicting Constitutive Behaviour of Idealized Granular Soils Using Recurrent Neural Networks
Abstract
1. Introduction
2. Methodology
2.1. DEM Simulations for Data Generation
2.2. Datasets Preparation and Pre-Processing
3. Recurrent Neural Networks
3.1. LSTM-NN
3.2. GRU-NN
3.3. Neural Network Architectures
4. Results
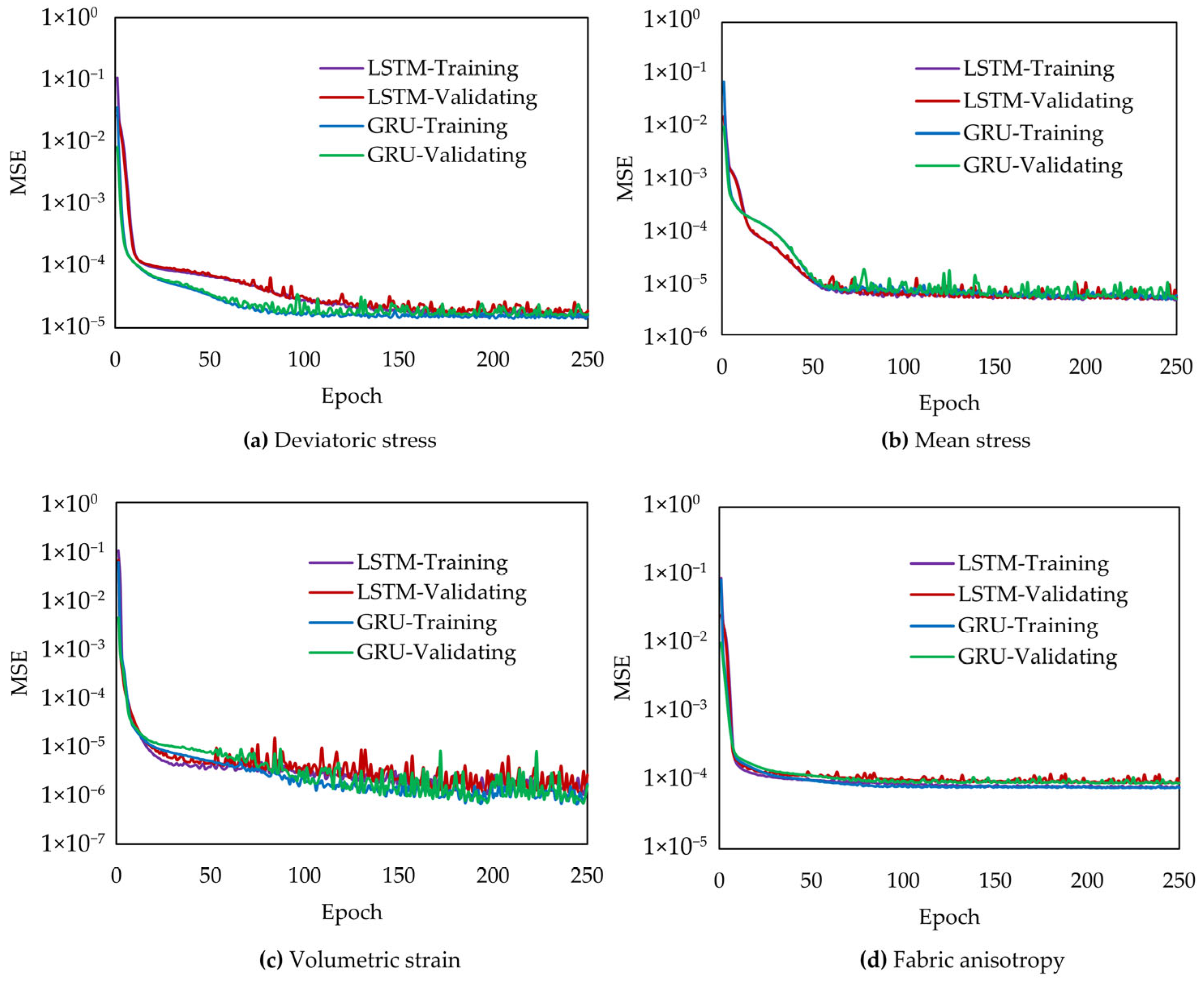
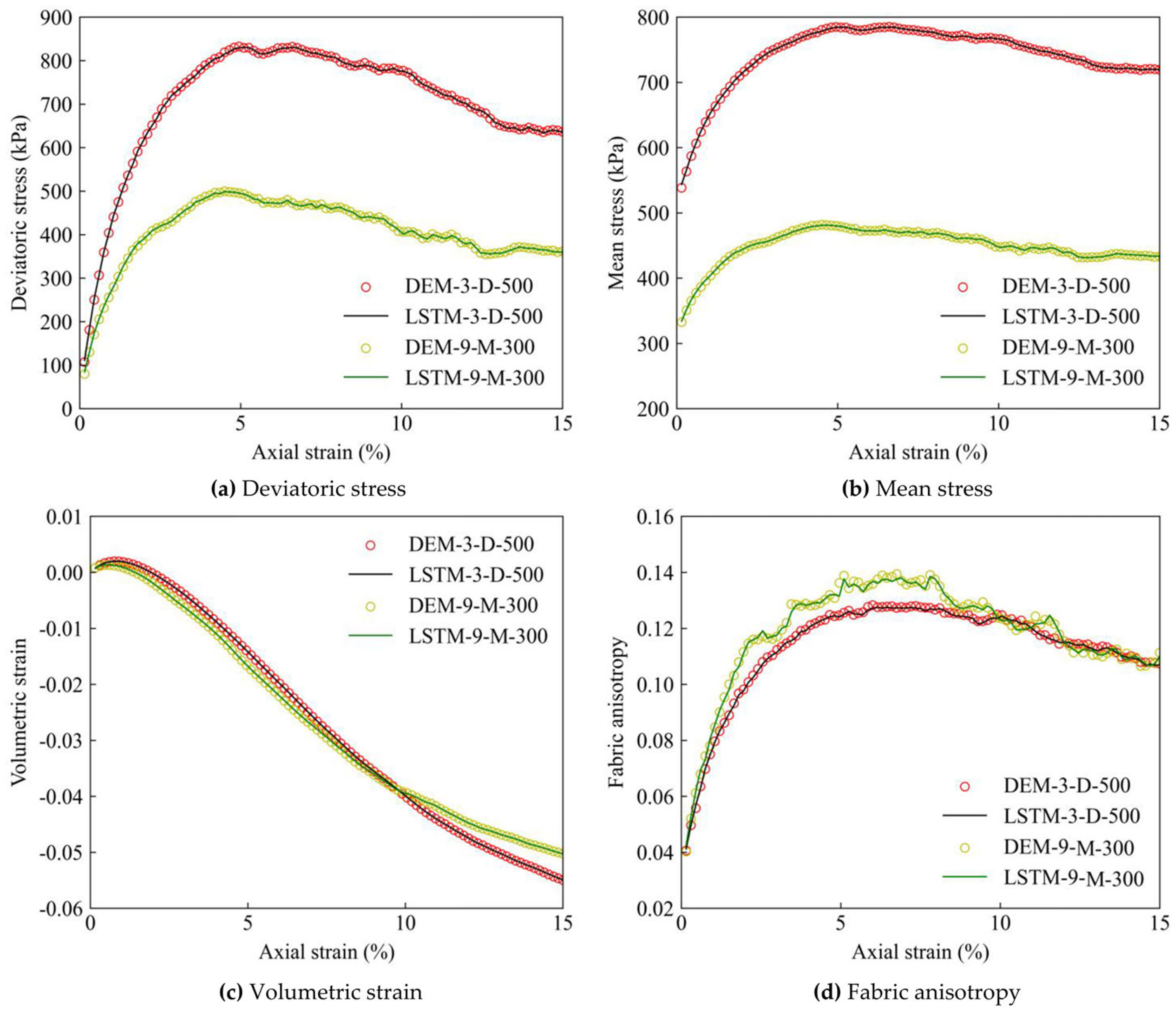
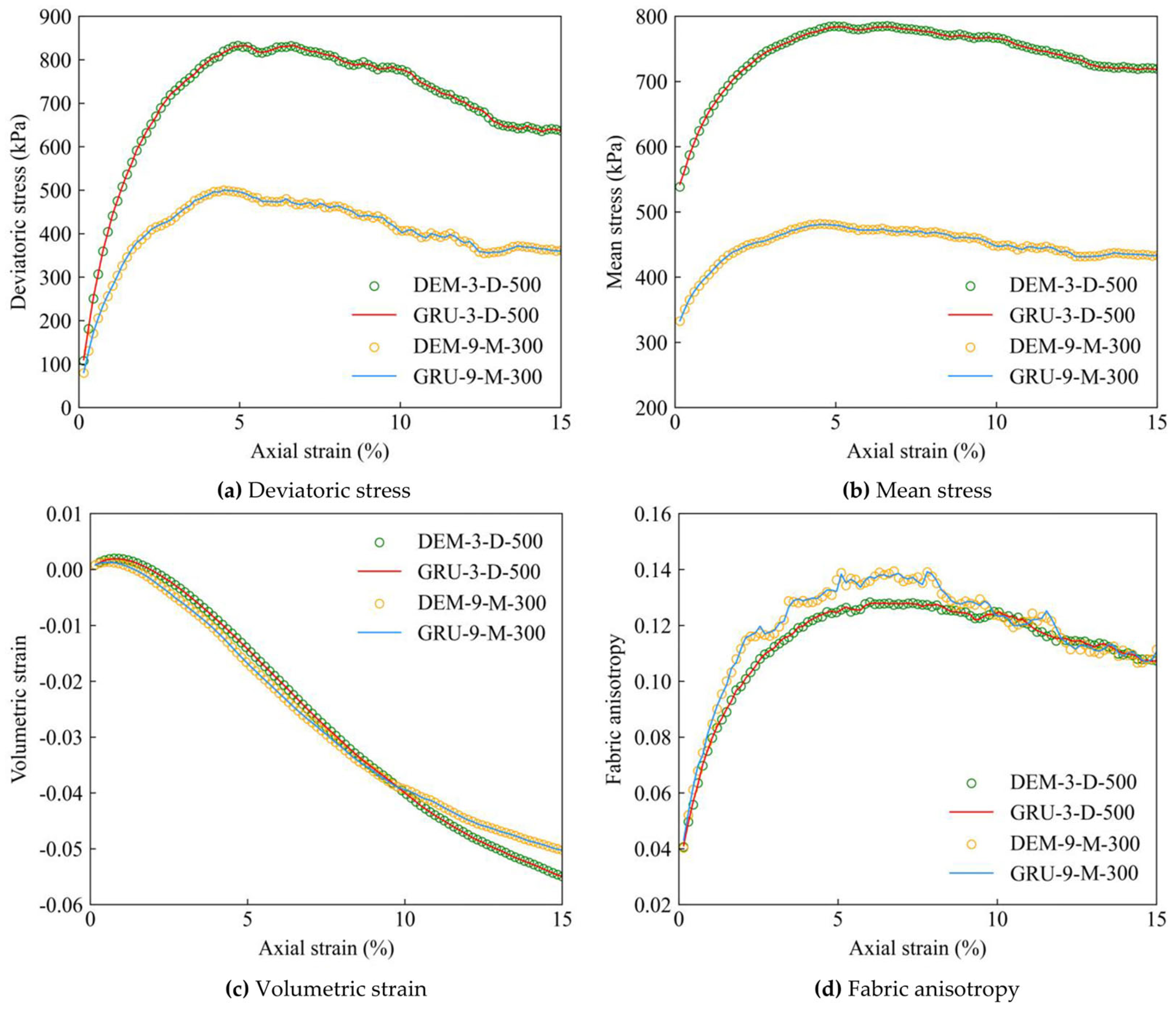
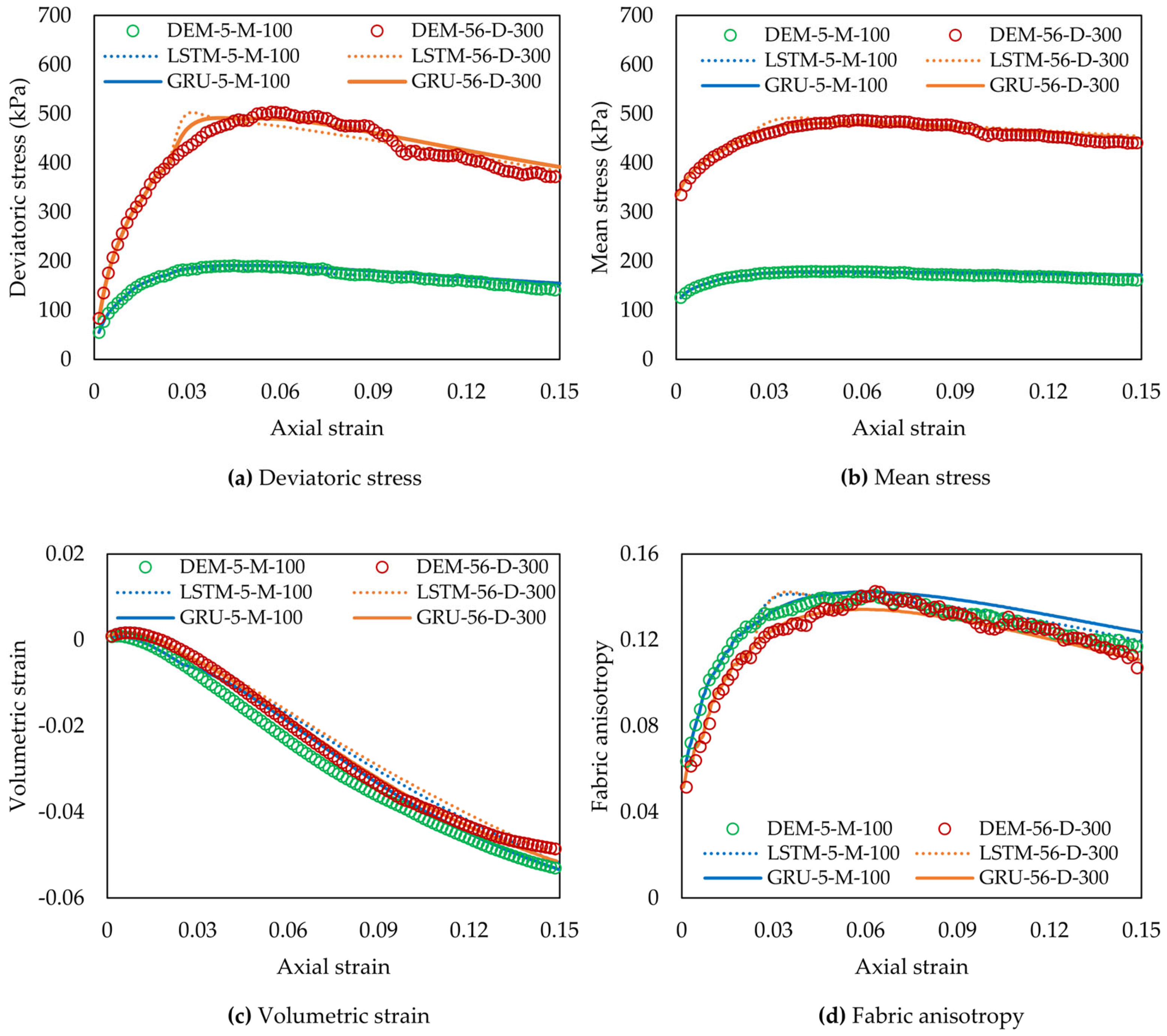
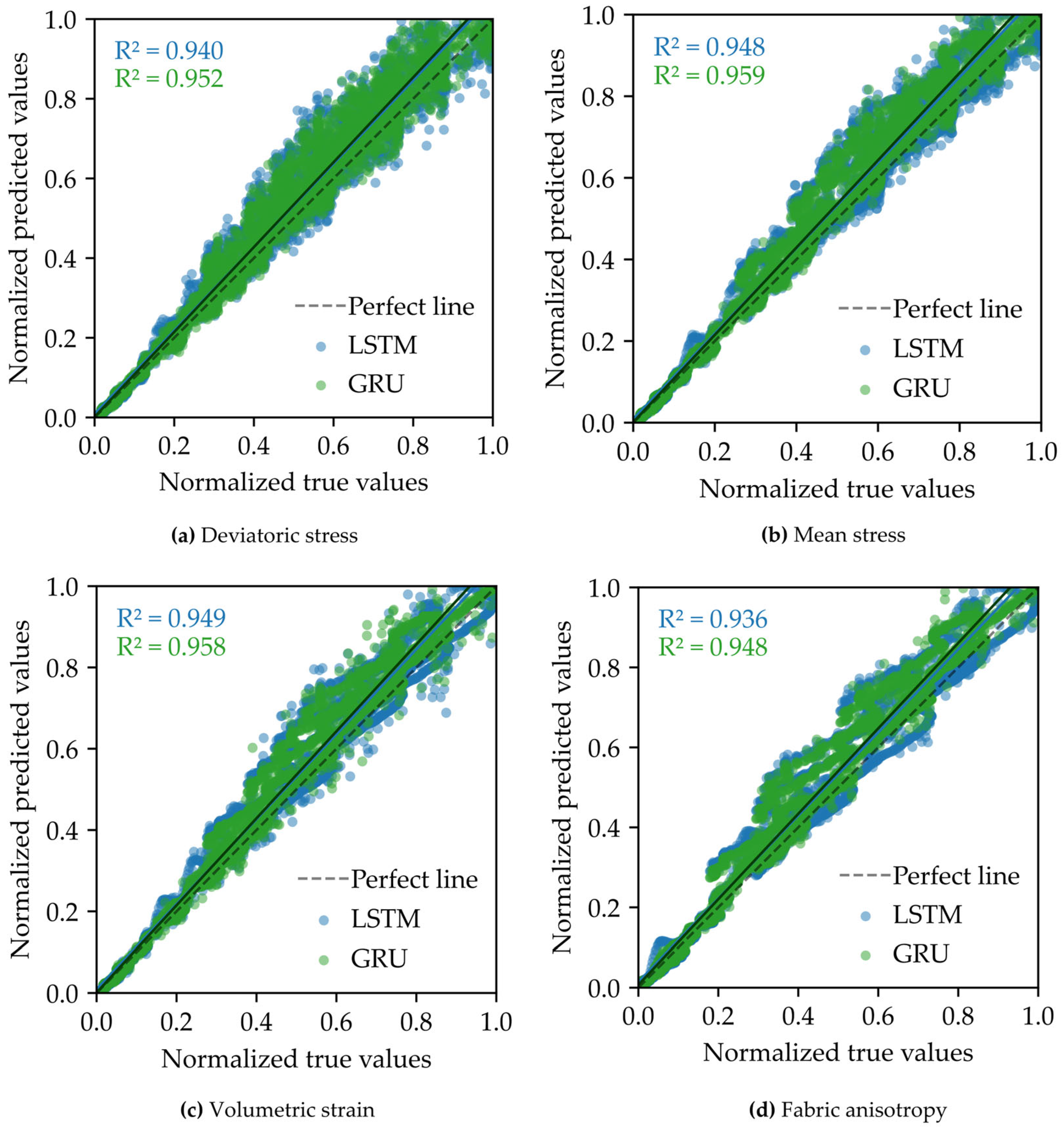
4.1. Training, Validating, and Testing Results
4.2. Application of ML-Based Models to Micro-CT Triaxial Test
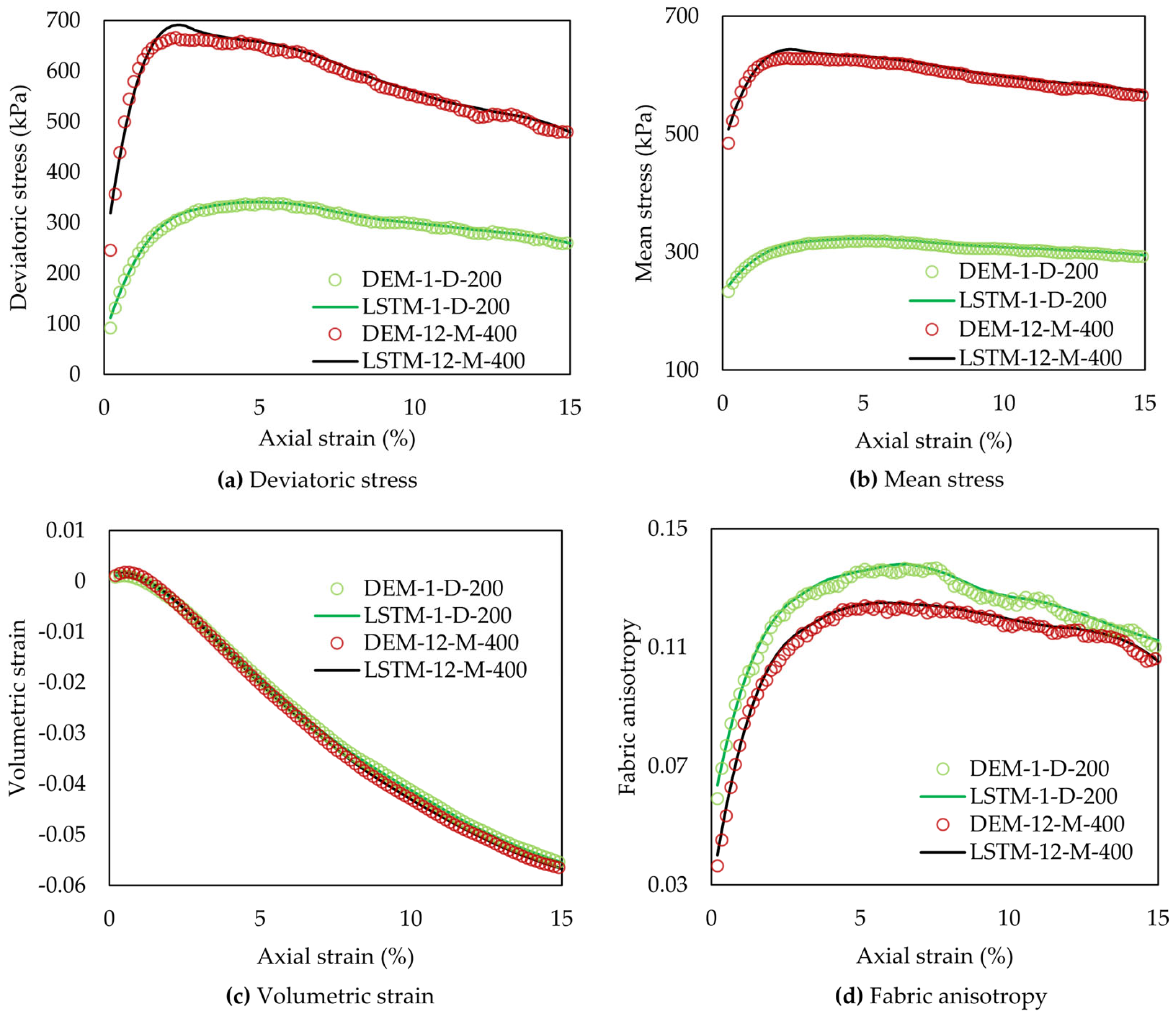
4.3. Generalization Capability of ML-Based Models
5. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cerato, A.B.; Lutenegger, A.J. Scale effects of shallow foundation bearing capacity on granular material. J. Geotech. Geoenviron. Eng. 2007, 133, 1192–1202. [Google Scholar] [CrossRef]
- Li, M.; Fannin, R.J. Comparison of two criteria for internal stability of granular soil. Can. Geotech. J. 2008, 45, 1303–1309. [Google Scholar] [CrossRef]
- Das, B.; Sivakugan, N. Settlements of shallow foundations on granular soil—An overview. Int. J. Geotech. Eng. 2007, 1, 19–29. [Google Scholar] [CrossRef]
- Hungr, O. Simplified models of spreading flow of dry granular material. Can. Geotech. J. 2008, 45, 1156–1168. [Google Scholar] [CrossRef]
- Moraci, N.; Mandaglio, M.C.; Ielo, D. Analysis of the internal stability of granular soils using different methods. Can. Geotech. J. 2014, 51, 1063–1072. [Google Scholar] [CrossRef]
- Ma, G.; Guan, S.; Wang, Q.; Feng, Y.T.; Zhou, W. A predictive deep learning framework for path-dependent mechanical behavior of granular materials. Acta Geotech. 2022, 17, 3463–3478. [Google Scholar] [CrossRef]
- Qu, T.; Di, S.; Feng, Y.T.; Wang, M.; Zhao, T.; Wang, M. Deep learning predicts stress–strain relations of granular materials based on triaxial testing data. Comput. Model. Eng. Sci. 2021, 128, 129–144. [Google Scholar] [CrossRef]
- Jiang, M.J. New paradigm for modern soil mechanics: Geomechanics from micro to macro. Chin. J. Geotech. Eng. 2019, 41, 195–254. [Google Scholar]
- Tien Bui, D.; Hoang, N.D.; Nhu, V.H. A swarm intelligence-based machine learning approach for predicting soil shear strength for road construction: A case study at Trung Luong National Expressway Project (Vietnam). Eng. Comput. 2019, 35, 955–965. [Google Scholar] [CrossRef]
- Hashemi Jokar, M.; Mirasi, S. Using adaptive neuro-fuzzy inference system for modeling unsaturated soils shear strength. Soft Comput. 2018, 22, 4493–4510. [Google Scholar] [CrossRef]
- Abozraig, M.; Ok, B.; Yildiz, A. Determination of shear strength of coarse-grained soils based on their index properties: A comparison between different statistical approaches. Arab. J. Geosci. 2022, 15, 593. [Google Scholar] [CrossRef]
- Zhang, P.; Yin, Z.Y.; Jin, Y.F. An AI-based model for describing cyclic characteristics of granular materials. Int. J. Numer. Anal. Methods Geomech. 2020, 44, 1315–1335. [Google Scholar] [CrossRef]
- Cubuk, E.D.; Schoenholz, S.S.; Rieser, J.M.; Malone, B.D.; Rottler, J.; Durian, D.J.; Kaxiras, E.; Liu, A.J. Identifying structural flow defects in disordered solids using machine-learning methods. Phys. Rev. Lett. 2015, 114, 108001. [Google Scholar] [CrossRef] [PubMed]
- Rouet-Leduc, B.; Hulbert, C.; Bolton, D.C.; Ren, C.X.; Riviere, J.; Marone, C.; Guyer, R.A.; Johnson, P.A. Estimating fault friction from seismic signals in the laboratory. Geophys. Res. Lett. 2018, 45, 1321–1329. [Google Scholar] [CrossRef]
- Zhang, P.; Jin, Y.F.; Yin, Z.Y. Machine learning-based uncertainty modelling of mechanical properties of soft clays relating to time-dependent behaviour and its application. Int. J. Numer. Anal. Methods Geomech. 2021, 45, 1588–1602. [Google Scholar] [CrossRef]
- Liu, X.; Li, Z.; Zou, D.; Sun, L.; Ebrahim, K.Y.; Liang, J. Improving the prediction accuracy of small-strain shear modulus of granular soils through PSD: An investigation enabled by DEM and machine learning technique. Comput. Geotech. 2023, 157, 105355. [Google Scholar] [CrossRef]
- El Shamy, U.; Abdelhamid, Y. Modeling granular soils liquefaction using coupled lattice Boltzmann method and discrete element method. Soil Dyn. Earthq. Eng. 2014, 67, 119–132. [Google Scholar] [CrossRef]
- Pistolesi, F.; Baldassini, M.; Volpe, E.; Focacci, F.; Cattoni, E. Fast and interpretable prediction of seismic kinematics of flexible retaining walls in sand through explainable artificial intelligence. Comput. Geotech. 2025, 179, 107007. [Google Scholar] [CrossRef]
- Gordan, B.; Jahed Armaghani, D.; Hajihassani, M.; Monjezi, M. Prediction of seismic slope stability through combination of particle swarm optimization and neural network. Eng. Comput. 2016, 32, 85–97. [Google Scholar] [CrossRef]
- Mustafa, M.R.; Rezaur, R.B.; Saiedi, S.; Rahardjo, H.; Isa, M.H. Evaluation of MLP-ANN training algorithms for modeling soil pore-water pressure responses to rainfall. J. Hydrol. Eng. 2012, 18, 50–57. [Google Scholar] [CrossRef]
- Kouadri, S.; Pande, C.B.; Panneerselvam, B.; Moharir, K.N.; Elbeltagi, A. Prediction of irrigation groundwater quality parameters using ANN, LSTM, and MLR models. Environ. Sci. Pollut. Res. 2022, 29, 21067–21091. [Google Scholar] [CrossRef]
- Liu, Y.; Li, M.; Su, P.; Ma, B.; You, Z. Porosity prediction of granular materials through discrete element method and back propagation neural network algorithm. Appl. Sci. 2020, 10, 1693. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Kawakami, K. Supervised Sequence Labelling with Recurrent Neural Networks. Ph.D. Thesis, Technical University of Munich, Munich, Germany, 2008. [Google Scholar]
- Cundall, P.A.; Strack, O.D. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Wu, M.; Xia, Z.; Wang, J. Constitutive modelling of idealised granular materials using machine learning method. J. Rock Mech. Geotech. Eng. 2023, 15, 1038–1051. [Google Scholar] [CrossRef]
- Li, G.X. Advanced Soil Mechanics; Tsinghua University Press: Beijing, China, 2004. [Google Scholar]
- Itasca Consulting Group Inc. PFC 6.0 Documentation; Itasca Consulting Group Inc.: Minneapolis, MN, USA, 2019. [Google Scholar]
- Thornton, C. Quasi-static simulations of compact polydisperse particle systems. Particuology 2010, 8, 119–126. [Google Scholar] [CrossRef]
- Das, S.K.; Das, A. Influence of quasi-static loading rates on crushable granular materials: A DEM analysis. Powder Technol. 2019, 344, 393–403. [Google Scholar] [CrossRef]
- Mindlin, R.D.; Deresiewicz, H. Elastic spheres in contact under varying oblique forces. J. Appl. Mech. 1953, 20, 327–344. [Google Scholar] [CrossRef]
- Somfai, E.; Roux, J.N.; Snoeijer, J.H.; Van Hecke, M.; Van Saarloos, W. Elastic wave propagation in confined granular systems. Phys. Rev. E 2005, 72, 021301. [Google Scholar] [CrossRef]
- De Bono, J.P.; McDowell, G.R. DEM of triaxial tests on crushable sand. Granul. Matter 2014, 16, 551–562. [Google Scholar] [CrossRef]
- He, H.; Senetakis, K.; Coop, M.R. An investigation of the effect of shearing velocity on the inter-particle behaviour of granular and composite materials with a new micromechanical dynamic testing apparatus. Tribol. Int. 2019, 134, 252–263. [Google Scholar] [CrossRef]
- Itasca Consulting Group Inc. PFC3D User’s Guide; Itasca Consulting Group Inc.: Minneapolis, MN, USA, 2008. [Google Scholar]
- Wu, M.; Wang, J.; Russell, A.; Cheng, Z. DEM modelling of mini-triaxial test based on one-to-one mapping of sand particles. Géotechnique 2021, 71, 714–727. [Google Scholar] [CrossRef]
- Thornton, C. Numerical simulations of deviatoric shear deformation of granular media. Géotechnique 2000, 50, 43–53. [Google Scholar] [CrossRef]
- Sitharam, T.G.; Dinesh, S.V.; Shimizu, N. Micromechanical modeling of monotonic drained and undrained shear behaviour of granular media using three-dimensional DEM. Int. J. Numer. Anal. Methods Geomech. 2002, 26, 1167–1189. [Google Scholar] [CrossRef]
- Wu, M.; Wang, J. Constitutive modelling of natural sands using a deep learning approach accounting for particle shape effects. Powder Technol. 2022, 404, 117439. [Google Scholar] [CrossRef]
- Qu, T.; Guan, S.; Feng, Y.T.; Ma, G.; Zhou, W.; Zhao, J. Deep active learning for constitutive modelling of granular materials: From representative volume elements to implicit finite element modelling. Int. J. Plast. 2023, 164, 103576. [Google Scholar] [CrossRef]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modelling. arXiv 2014, arXiv:1412.3555. [Google Scholar] [CrossRef]
- De Melo, G.A.; Sugimoto, D.N.; Tasinaffo, P.M.; Santos, A.H.M.; Cunha, A.M.; Dias, L.A.V. A new approach to river flow forecasting: LSTM and GRU multivariate models. IEEE Lat. Am. Trans. 2019, 17, 1978–1986. [Google Scholar] [CrossRef]
- Shewalkar, A.; Nyavanandi, D.; Ludwig, S.A. Performance evaluation of deep neural networks applied to speech recognition: RNN, LSTM and GRU. J. Artif. Intell. Soft Comput. Res. 2019, 9, 235–245. [Google Scholar] [CrossRef]
- Cheng, Z.; Wang, J. Experimental investigation of inter-particle contact evolution of sheared granular materials using X-ray micro-tomography. Soils Found. 2018, 58, 1492–1510. [Google Scholar] [CrossRef]
- Cheng, Z.; Wang, J.; Xiong, W. A machine learning-based strategy for experimentally estimating force chains of granular materials using X-ray micro-tomography. Géotechnique 2024, 74, 1291–1303. [Google Scholar] [CrossRef]
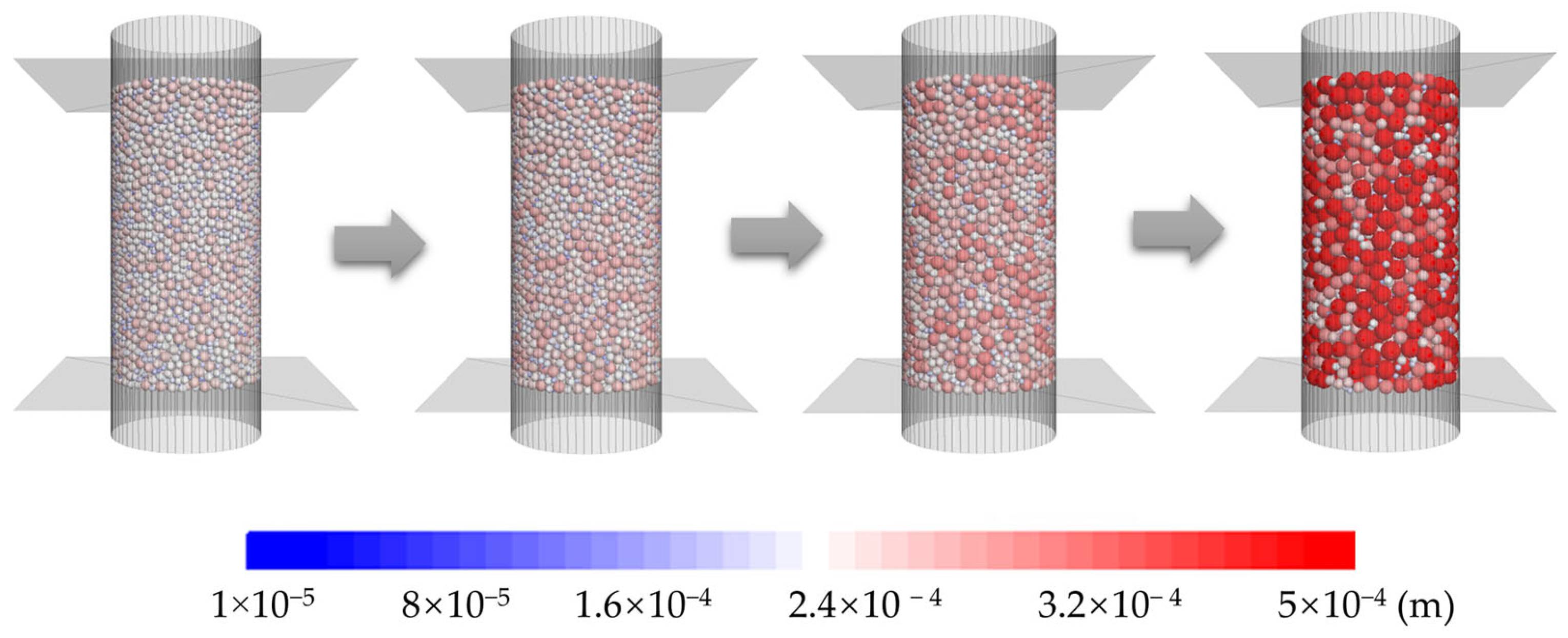

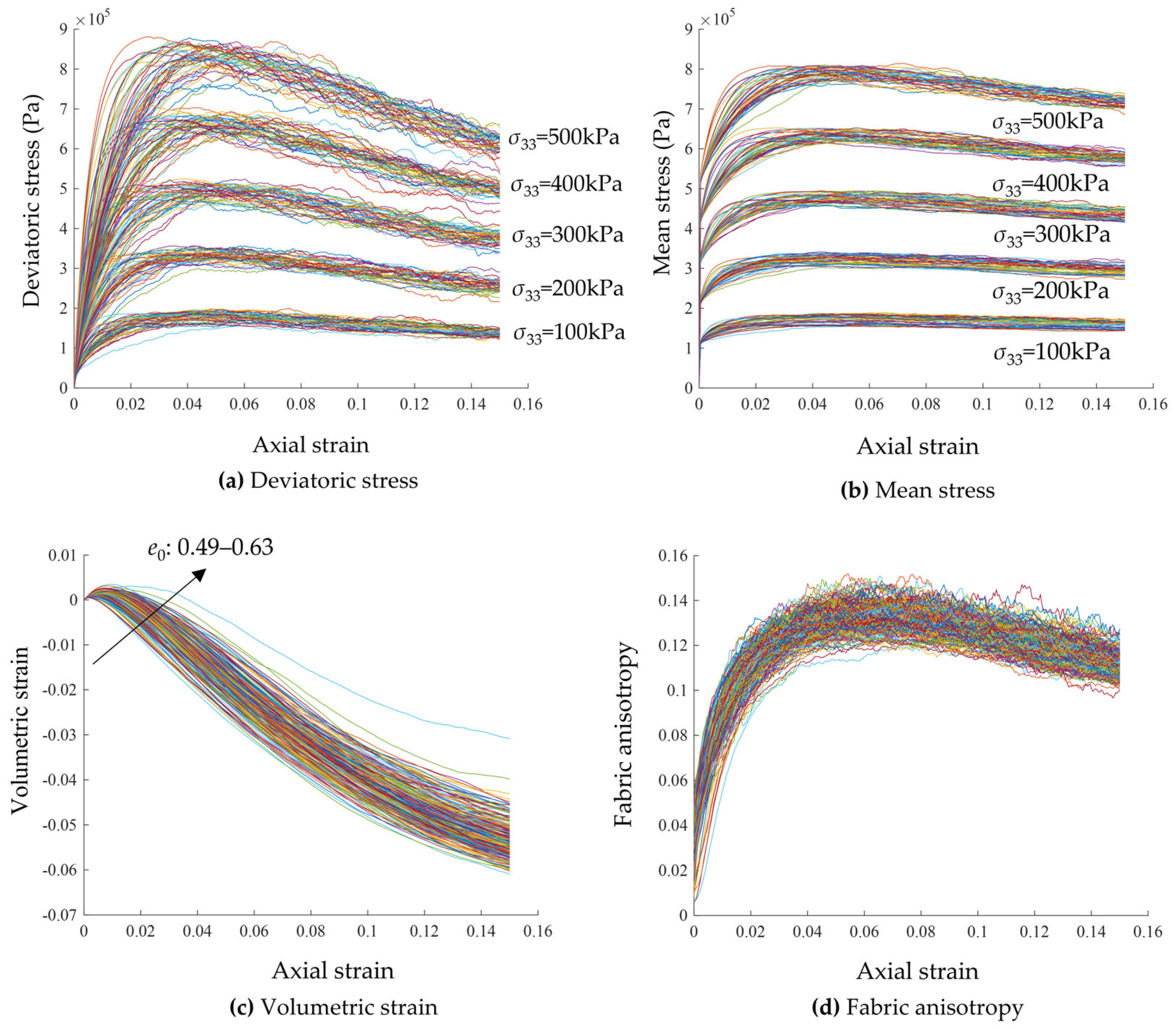

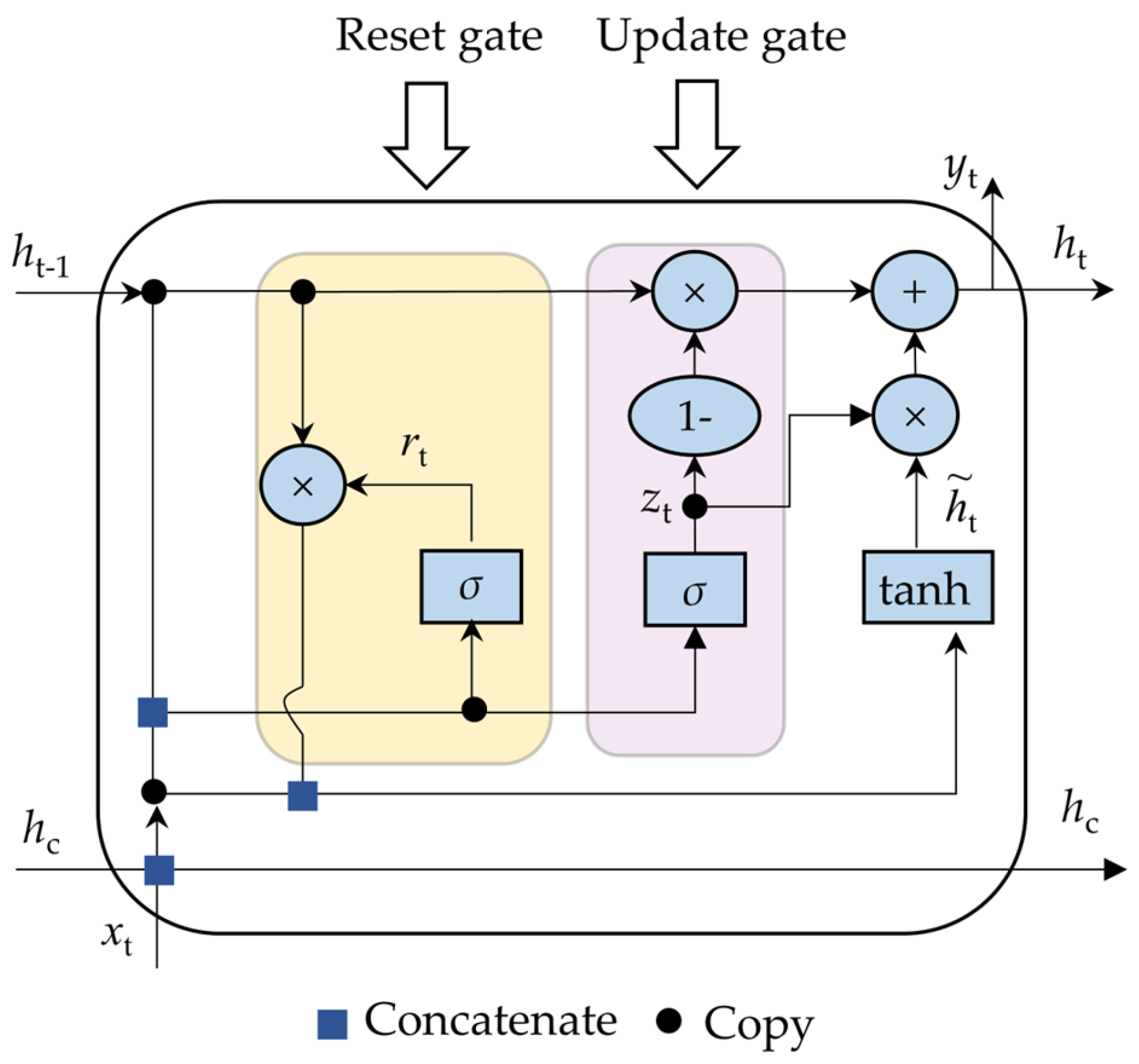
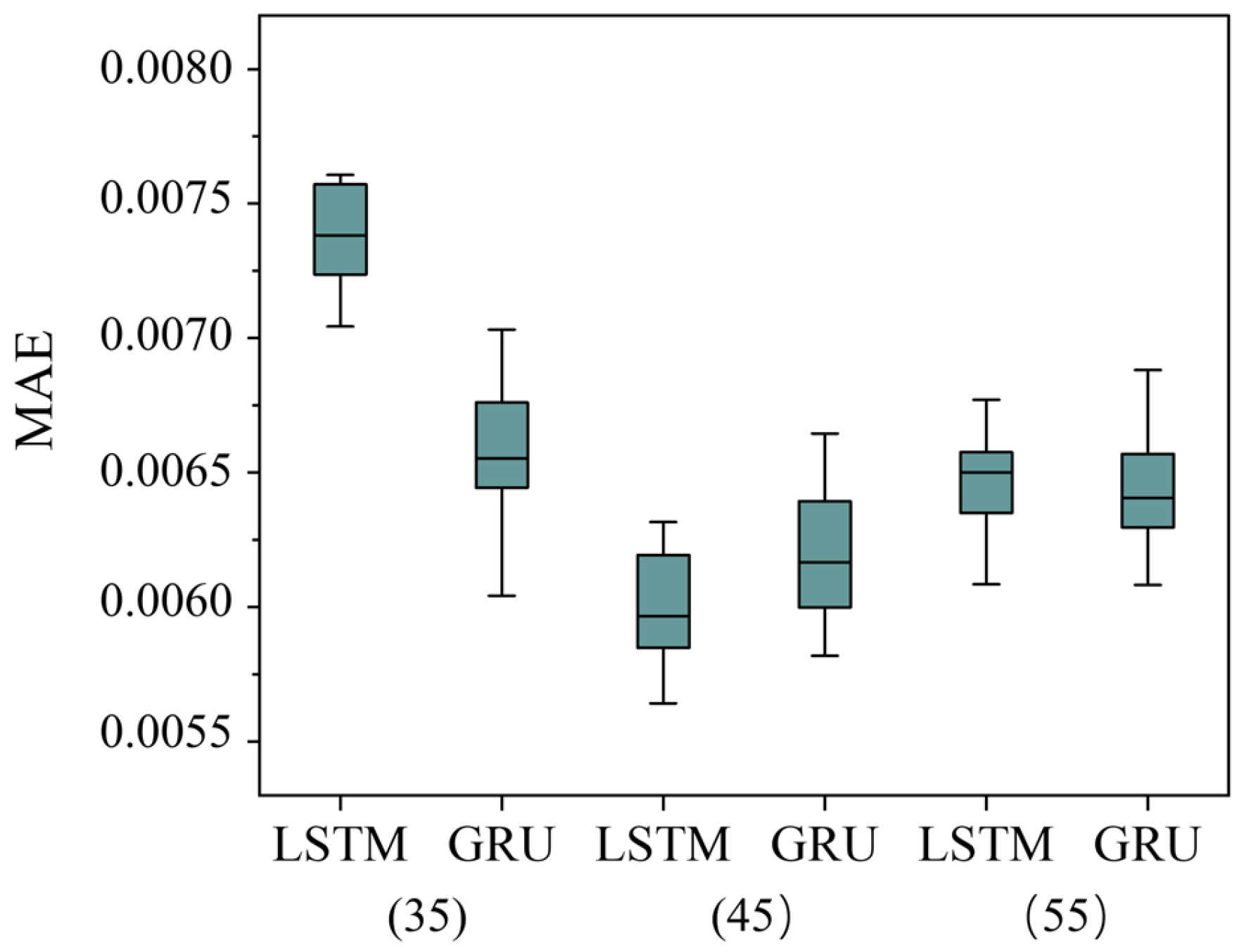





| Model | Features | Drawbacks |
|---|---|---|
| ANN | Simplicity in structure Computational efficiency Interpretability | Single output prediction Poor nonlinear mapping ability |
| BPNN | Nonlinear mapping ability Multi-outputs prediction ability | Gradients exploding or vanishing Limitations in time-related prediction |
| RNN | Sequential data prediction ability Nonlinear mapping ability Multi-outputs prediction ability | Gradients exploding or vanishing Limitations in time-related prediction |
| LSTM | Sequential data prediction ability Nonlinear mapping ability Multi-outputs prediction ability | Numerous weights and biases and hyperparameters |
| GRU | Sequential data prediction ability Nonlinear mapping ability Multi-outputs prediction ability | Numerous weights and biases and hyperparameters |
| Twenty particle size distributions (d50/mm, Cu) | (0.3, 4), (0.3, 4.5), (0.3, 5), (0.3, 5.5), (0.35, 3), (0.35, 4), (0.35, 5.5), (0.35, 6), (0.4, 2), (0.4, 3), (0.4, 4.5), (0.4, 5), (0.45, 2), (0.45, 3), (0.45, 4), (0.45, 5), (0.5, 4), (0.5, 4.5), (0.5, 5), (0.5, 5.5) |
| Five confining stresses, σ33 (kPa) | 100, 200, 300, 400, 500 |
| Two void ratios, e | 0.49, 0.63 |
| Total number of DEM simulations | 200 |
| Parameters | Value |
|---|---|
| Contact model | Hertz–Mindlin |
| Friction coefficient | 0.3 |
| Wall friction coefficient | 0 |
| Damping coefficient | 0.7 |
| Shear modulus (GPa) | 28 |
| Poisson’s ratio | 0.25 |
| Density (kg/m3) | 2650 |
| Size: height × diameter (mm) | 16 × 8 |
| Model ID | Layer Name | Project | Num. of Nodes | Activation Function | Note |
|---|---|---|---|---|---|
| Model-1 | LSTM-NN | Capturing high-dimensional features | 50 | ReLU | Learning rate = 0.001; Epochs = 250; Optimizer = Adam; Loss function = MSE; Batch size = 301 |
| Fully connected layer | Dimensional transformation | 4 | Linear | ||
| Model-2 | GRU-NN | Capturing high-dimensional features | 50 | ReLU | |
| Fully connected layer | Dimensional transformation | 4 | Linear |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Wang, J. Predicting Constitutive Behaviour of Idealized Granular Soils Using Recurrent Neural Networks. Appl. Sci. 2025, 15, 9495. https://doi.org/10.3390/app15179495
Li X, Wang J. Predicting Constitutive Behaviour of Idealized Granular Soils Using Recurrent Neural Networks. Applied Sciences. 2025; 15(17):9495. https://doi.org/10.3390/app15179495
Chicago/Turabian StyleLi, Xintong, and Jianfeng Wang. 2025. "Predicting Constitutive Behaviour of Idealized Granular Soils Using Recurrent Neural Networks" Applied Sciences 15, no. 17: 9495. https://doi.org/10.3390/app15179495
APA StyleLi, X., & Wang, J. (2025). Predicting Constitutive Behaviour of Idealized Granular Soils Using Recurrent Neural Networks. Applied Sciences, 15(17), 9495. https://doi.org/10.3390/app15179495







