Abstract
Olive flounder (Paralichthys olivaceus) is a key aquaculture species in South Korea, but its production has been challenged by rising mortality under environmental stress from key environmental factors such as water temperature, dissolved oxygen, and feeding conditions. To support adaptive management, this study proposes a Bayesian Deep Kernel Machine Regression (BDKMR) model that integrates Gaussian process regression with neural network-based feature learning. Using longitudinal data from commercial farms, we model fish growth as a function of water temperature, dissolved oxygen, and feed quantity. Model performance is assessed via Leave-One-Out Cross-Validation and compared against kernel ridge regression and Bayesian kernel machine regression. Results show that BDKMR achieves substantially lower prediction errors, indicating superior accuracy and robustness. These findings suggest that BDKMR offers a flexible and effective framework for predictive modeling in aquaculture systems.
1. Introduction
Olive flounder (Paralichthys olivaceus) is one of the most widely consumed flatfish species in South Korea, with the majority of its supply coming from aquaculture operations. Since the commercial production of artificial fry in 1983, olive flounder farming has expanded rapidly, increasing from 1037 tons in 1990 to 39,931 tons in 2023. However, recent internal and external pressures have led to a stagnation in both production and consumption, reflecting broader slowdowns in the aquaculture sector [1,2]. Rather than a sudden disruption in 2023, this stagnation reflects a gradual structural deceleration over the past decade. Domestically, the industry has faced rising production costs (e.g., labor, feed, and energy) combined with outdated infrastructure and high mortality rates due to disease and environmental stress [3]. In addition, increasing competition from imported seafood has reduced the market share of domestically farmed olive flounder, undermining its competitiveness in the national value chain [4].
Multiple factors contribute to this stagnation. On the external front, negative consumer sentiment associated with radioactive water discharge from neighboring countries and declining export demand have weakened market dynamics. Internally, the intrinsic sensitivity of olive flounder to environmental fluctuations, which particularly elevated water temperatures, has caused high mortality rates and unstable yields [5,6]. These challenges underscore the need for more informed, data-driven management strategies in aquaculture operations. For example, experimental studies have shown that olive flounder tolerate temperatures up to 26 °C but exhibit severe stress and tissue damage above 28 °C, with complete mortality observed at around 30 °C [7].
A promising direction is the predictive modeling of fish growth under varying environmental conditions. By forecasting growth outcomes based on key environmental factors, fish farm operators can make proactive decisions regarding feeding, harvest timing, and environmental control. Such predictive insights could also help reduce mortality by identifying risk conditions and suggesting optimal operating ranges.
In this study, we aim to develop a predictive model of olive flounder growth based on three major environmental drivers: water temperature, dissolved oxygen (DO), and feed quantity. To this end, we propose a novel Bayesian Deep Kernel Machine Regression (BDKMR) model, which integrates Gaussian process priors with deep neural network-based feature extraction. This hybrid approach is designed to flexibly model complex and nonlinear interactions among covariates, while retaining the interpretability and uncertainty quantification afforded by the Bayesian framework.
We evaluate the proposed BDKMR model using monthly growth records and sensor-based environmental data collected from aquaculture farms in South Korea. For benchmarking purposes, we compare its predictive performance against two standard approaches: kernel ridge regression (KRR) [8] and Bayesian kernel machine regression (BKMR) [9]. All models are assessed using Leave-One-Out Cross-Validation (LOOCV) (see e.g., [10]) and compared using standard predictive metrics such as the mean absolute error (MAE) and mean squared error (MSE).
The remainder of this paper is structured as follows. In Section 2, we review the foundational models used in this work, including BKMR, BMIM [11], and artificial neural networks. Section 3 describes the dataset and preprocessing strategy. Section 3.2 introduces the proposed BDKMR model, including its probabilistic formulation, prior structure, and inference algorithm. In Section 4, we present empirical results comparing BDKMR to baseline models using aquaculture data. Finally, Section 5 concludes with a summary of contributions and directions for future research.
2. Backgrounds
Here we provide essential background on the basic BKMR model introduced by [9], as well as its extension to the BMIM model proposed by [11], which introduces multiple linear combination indices to better capture complex predictor–response relationships. We further discuss artificial neural networks (see e.g., [12,13]) as a flexible alternative capable of modeling complex and nonlinear relationships more effectively.
2.1. Bayesian Kernel Machine Regression
The BKMR model, originally proposed by Bobb et al. [9], provides a flexible framework for modeling complex and potentially nonlinear relationships between predictors and outcomes. BKMR employs a Gaussian process (GP) prior (see e.g., [14]) to model the unknown exposure–response surface, allowing for flexible modeling of interactions and nonlinear effects among multiple features. Specifically, let denote the response variable for the ith observation, and let be a p-dimensional vector of features influencing the ith outcome. The BKMR model is defined as
where are random errors following an independently and identically distributed (i.i.d.) Gaussian distribution with mean 0 and a constant variance, , and is an unknown and nonlinear function modeled through a GP prior as
Here is an positive semi-definite covariance matrix, and is a kernel function that governs the smoothness of the realizations derived from the GP and determines the extent of shrinkage towards the mean (see e.g., [15]).
Ref. [9] employed a squared exponential kernel, which is widely used due to its flexibility in modeling smooth functions. The kernel function is given by
where are inverse length-scale parameters that control the smoothness along each feature dimension, and is a positive scaling parameter governing the overall magnitude of the covariance.
This kernel is particularly appropriate for modeling biological processes such as fish growth, where smooth and gradual changes are expected over time and environmental conditions. Its infinitely differentiable nature makes it well suited for capturing such smooth relationships. Additionally, the squared exponential kernel is analytically convenient for posterior inference and has shown strong empirical performance in prior BKMR applications [9]. While other kernels, such as Matérn or polynomial kernels, offer alternative properties (e.g., finite differentiability or the ability to model periodicity), the squared exponential kernel provided a good balance between flexibility and interpretability for our application.
To allow for the identification of unimportant features, Ref. [9] introduced a spike-and-slab prior on the inverse length-scale parameters . Specifically, the prior is given by
where denotes a Dirac measure that places all mass at zero, and is a binary inclusion indicator following
where follows a uniform prior on . The slab component is specified as an inverse uniform distribution on .
This spike-and-slab formulation enables automatic variable selection by shrinking irrelevant predictors’ contributions via while maintaining flexibility for relevant features. However, this approach requires inference over discrete inclusion indicators, , which can become computationally expensive as the number of predictors increases. In practice, the method performs well in moderate-dimensional settings but may scale poorly in high-dimensional contexts due to the combinatorial nature of the inclusion space. In such cases, continuous shrinkage priors such as the horseshoe prior [16] or automatic relevance determination [14] may offer more computationally efficient alternatives for variable selection in high-dimensional settings.
For the variance-related parameters, [9] assigned gamma priors to and :
where denote shape parameters and are rate parameters.
BMIM, proposed by McGee et al. [11], extends the BKMR framework by introducing multiple index structures that summarize the predictors into lower-dimensional linear combinations. This approach improves both interpretability and flexibility in modeling complex predictor–response relationships.
The BMIM framework assumes that the p predictors are partitioned into M mutually exclusive groups; if the p predictors are partitioned into M mutually exclusive groups, denoted for the mth group, the indices are defined as
where is a vector of weights for group m. The outcome is then modeled as a function of these M indices, rather than all p predictors:
where f follows follows a GP prior and . This index-based approach allows BMIM to capture the relationships between the outcome and combinations of related predictors, improving both interpretability and computational efficiency.
The Gaussian process covariance function is applied to the indices and is given by
where is a smoothness parameter for the mth index. This formulation reduces the dimensionality of the GP covariance function from p to M, providing computational benefits. To ensure identifiability, the index weights are constrained to have a unit norm,
and are reparameterized as
where are unconstrained parameters.
BMIM also introduces variable selection at the group level, with a spike-and-slab prior placed on the unconstrained weights . Specifically, for the lth predictor in group m,
where follows
This hierarchical structure enables automatic group-level sparsity by excluding unimportant predictors from contributing to each index, a feature not directly available in the original BKMR framework.
BKMR has been applied to various real-world problems involving complex exposure–response relationships, particularly in environmental health [9,17]. More recently, its utility has extended to aquaculture. For example, Seo et al. [18] applied a weighted BKMR model to predict the growth of indoor-cultured abalone under varying environmental conditions. Their model identified key factors such as dissolved oxygen, nutrient supply, and salinity as dominant predictors, with significant nonlinear effects and interactions. This case highlights the model’s ability to yield interpretable and actionable insights in complex ecological systems where variable interactions and nonlinearities are prevalent.
2.2. Artificial Neural Network
Artificial neural networks (ANNs) were inspired by early models of biological neurons [19], and their foundational structure was further developed in the work of [20,21]. They are powerful function approximators capable of modeling complex, nonlinear relationships among variables. A typical ANN consists of interconnected layers of “neurons,” each applying an affine transformation followed by a nonlinear activation function. Through a process of iterative weight updates, an ANN can learn meaningful representations of data, making it suitable for a wide range of tasks such as classification, regression, and feature extraction.
To present the model in detail, let be the response for observation i, and let be a p-dimensional vector of predictors. A simple feedforward ANN model can be written as
where is a random error term (often assumed to be Gaussian with mean 0), and is specified by a layered neural network with parameters (weights and biases):
where L is the number of hidden layers, is a nonlinear activation function (e.g., ReLU or sigmoid), and are the weight matrix and bias vector in layer ℓ, and map the final hidden layer to the scalar output .
In this study, we chose ANNs over other nonlinear models such as random forests, support vector machines, or generalized additive models for several reasons. First, ANNs provide high flexibility in approximating complex, high-dimensional nonlinear functions. Second, they integrate naturally into our modeling framework as learnable feature extractors within a GP kernel, enabling a deep kernel learning structure. This allows the model to capture intricate interactions in the data while preserving uncertainty quantification. Additionally, compared to other approaches, ANNs are more amenable to gradient-based optimization, which facilitates efficient learning, especially under repeated model fitting scenarios in our experiments.
3. Materials and Methods
3.1. Data Description
The dataset used in this study was collected and integrated from olive flounder (Paralichthys olivaceus) farms located in Wando (Jeollanam-do) and Jeju Island, South Korea. Data were gathered from two farms in Wando and three farms in Jeju; on some farms, there were two separate tanks that each provided data, resulting in a total of seven distinct tanks. The data collection periods varied by farm, beginning as early as March 2023 and extending until July 2024. The smallest tank contained approximately 1700 fish, whereas the largest tank contained around 25,000 fish.
All data were retrieved from the Flow-Through Aquaculture Big Data Platform (Figure 1), a web system developed as part of the overarching research project to which this study belongs. This platform regularly compiles data generated at the living lab farms participating in the larger project.
Figure 1.
Flow-Through Aquaculture Big Data Platform (http://aqua.kware.co.kr/, accessed on 20 August 2025). The login page welcomes users to the aquaculture big data platform, indicating it is the administrator page. It provides input fields for “ID” and “Password,” an option to “Save ID,” and a “Login” button.
To build the Bayesian-based growth model, three environmental variables were used: water temperature, dissolved oxygen (DO), and feed quantity, while fish growth was assessed using weight measurements. Water temperature and DO were measured by sensors installed in each tank, and daily feed usage was recorded at the tank level as total feed per day. Because each tank held a different number of fish, the daily feed quantity was converted into an average feed amount per fish. Monthly weight measurements were conducted by randomly selecting 50 fish per farm and recording their individual weights. Sex information was not available due to age and platform limitations, as most fish were younger than the typical threshold for morphological sex identification and the data platform did not include sex records. In terms of timing, the variables were measured at different temporal resolutions: water temperature and DO were continuously recorded at one-minute intervals; feed amount was recorded daily, typically in the afternoon; and weight was measured monthly, generally toward the end of each month, although the exact date varied slightly by tank. These differences in measurement frequency were appropriately accounted for during data preprocessing and temporal alignment. Aside from water temperature and DO, most other environmental factors were effectively controlled by the sensor-based monitoring system in each tank. For this reason, and based on prior empirical evidence, we selected these variables as the primary environmental drivers of growth [22,23].
Since measurement intervals differed by variable, the data were aligned using the monthly weight-measurement schedule, which had the longest interval. For instance, if a weight measurement took place on 27 July 2023, the corresponding water temperature and DO values were averaged from 21 June 2023 (the previous weight measurement date) up to 27 July 2023. For the Bayesian growth modeling, each of the 50 weight measurements from a given month was log-transformed, and these log-values were then averaged to yield a single representative value for that month. A comprehensive summary of the dataset and preprocessing is provided in Appendix A in Table A1.
Figure 2 presents the pairwise scatter matrix of key variables used in the model. The log-transformed average weight (LogWtMean) shows clear positive associations with both the initial log weight (initLogWtMean) and feed quantity (feed). In contrast, temperature and dissolved oxygen (DO) exhibit more dispersed or nonlinear patterns, indicating potential interaction effects or variable influence over time.
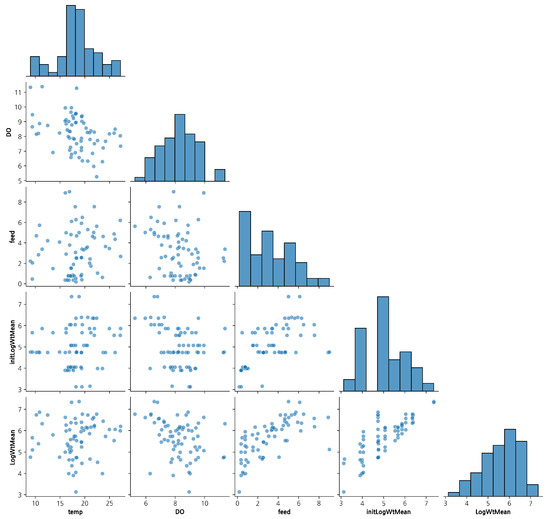
Figure 2.
Pairwise relationships among environmental variables (temperature, DO, feed), initial log weight, and log mean weight.
Figure 3 provides an exploratory overview of flatfish (Paralichthys olivaceus) growth patterns based on log-transformed average weight. Subfigure (a) illustrates how flatfish in different tanks and regions follow heterogeneous growth trajectories over time. Subfigure (b) shows the distributional spread of weights per tank, revealing some tanks with notably higher variability. Subfigure (c) compares the overall distribution of weights by region, indicating that flatfish in Wando tend to concentrate within a narrower weight range, while Jeju exhibits a more dispersed distribution with heavier tails.
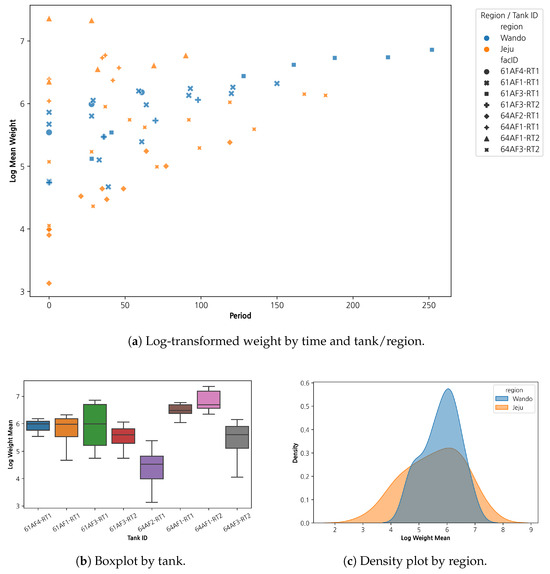
Figure 3.
Exploratory analysis of log-transformed mean weight (LogWtMean).
Figure 4 reveals that the standard error of log mean weight varies considerably across observations. This variation reflects differences in sample sizes and within-tank variability. Accordingly, we model the observation-level variance as , allowing the likelihood to properly account for measurement precision. This modeling strategy is explicitly incorporated in the Bayesian formulation described in Section 3.2.
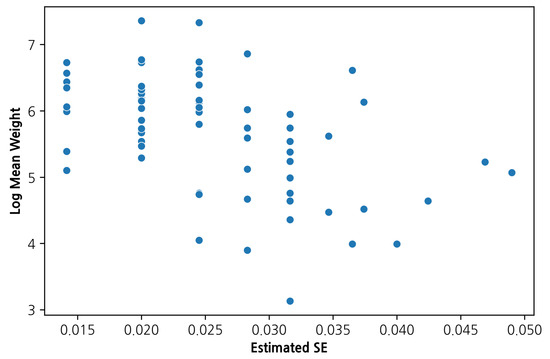
Figure 4.
Relationship between log-transformed average weight (LogWtMean) and its standard error (LogWtSE).
3.2. Bayesian Deep Kernel Machine Regression
3.2.1. Model Specification
We now propose a Bayesian Deep Kernel Machine Regression (BDKMR) approach that merges the flexibility of Bayesian kernel machine regression (BKMR; [9]) with the enhanced feature-learning capability of artificial neural networks (e.g., [12,13]). Unlike the linear index-based transforms used in Bayesian multiple index modeling (BMIM) [11], the proposed method replaces these intermediate representations with a deep neural network feature mapping, thereby allowing for more complex nonlinear interactions among predictors.
To formally describe the model, let be observations with and . We assume that
where denotes the parameters of a neural network, collects kernel hyperparameters, and are independent normal errors with variance scaled by the number of replicates in observation i. This formulation reflects the fact that each represents an average of log-transformed weights, and thus observations based on larger sample sizes should be modeled with smaller residual variance. By scaling the variance as , the likelihood accounts for differing levels of measurement precision across observations.
In the model (3), the function is modeled through a Gaussian process (GP) [13,14] whose covariance depends on a neural network-based feature transformation. More concretely, we define
where is a feedforward neural network mapping, , into a latent space, . The map is intended to capture complex nonlinearities and interactions among the original predictors, . To account for potential heterogeneity across tanks and regions, we included binary indicator variables for tank and region as part of the input features . Because these covariates are passed through the nonlinear transformation , their effects are captured within the ANN-based kernel rather than as additive fixed effects. This allows the model to flexibly absorb hierarchical structure and interactions related to location-specific factors.
Next, we specify a kernel function,
where is a scale parameter and represents the smoothness along the lth latent dimension. The kernel K then induces a GP prior on :
To complete the model specification, we impose shrinkage priors on the kernel hyperparameters and the network parameters , thereby enabling automatic regularization and potential sparsity in the latent dimensions of . Specifically, we assign the horseshoe shrinkage priors [16,24]
and
where denotes the normal distribution with the support and is the half-Cauchy distribution on . The density function of the half-Cauchy distribution is given as
The horseshoe prior provides a global–local shrinkage mechanism that strongly shrinks near-zero parameters while retaining heavy tails for truly large effects, promoting sparsity and automatic relevance determination in both the kernel hyperparameters and the network weights [16,24]. In our setting, this prior helps control model complexity and mitigates overfitting.
For the scaling parameter and the error variance , let and each follow a gamma prior,
as in the BKMR model described in Section 2.1. The former implies that , and thus learning about and jointly controls the effective range and overall variance of the Gaussian process prior. In practice, are chosen to be small positive constants to induce a weakly informative process.
3.2.2. Posterior Inference
To perform Bayesian inference for the proposed BDKMR model, we aimed to compute the posterior distribution of the model parameters given the observed data. Let denote the collection of model parameters, including the neural network weights, kernel hyperparameters, and variance components.
Exact posterior computation is analytically intractable due to the nonlinear feature mapping and the induced kernel matrix that depends on both and , which together lead to a high-dimensional, non-conjugate posterior. Moreover, in our ANN-based deep kernel setting, both the neural network weights and kernel hyperparameters must be learned jointly, making fully Bayesian approaches such as Hamiltonian Monte Carlo or variational Bayes computationally expensive, especially under repeated model fitting in the model assessment procedure. For these reasons, we employ the Laplace approximation [25], which allows the use of gradient-based optimization and provides a fast and reasonably accurate local Gaussian approximation to the posterior distribution.
The Laplace approximation proceeds by locating the maximum a posteriori (MAP) estimate
where is the marginal likelihood induced by the Gaussian process prior and is the joint prior over parameters. The likelihood term reflects the model structure in (3), and the prior incorporates the shrinkage distributions detailed above.
Once the MAP estimate is obtained via gradient-based optimization (e.g., Adam [26] or L-BFGS [27]), we approximate the posterior by a multivariate Gaussian approximation:
where is the Hessian matrix of the negative log-posterior evaluated at the MAP. This Gaussian approximation captures local curvature around the posterior mode and enables fast approximate inference, with the procedure summarized in Algorithm 1.
| Algorithm 1. Laplace approximation for BDKMR. |
|
All computations were implemented using the PyTorch deep learning library, which facilitates automatic differentiation and efficient GPU acceleration. The modular implementation allows users to train models on custom datasets, perform (approximate) posterior sampling, and obtain predictive distributions at new inputs. With this implementation in place, we next summarize the computational profile and scalability of the three models.
In our implementation, both BKMR and BDKMR used MAP estimation with a Laplace (Gaussian) approximation, whereas KRR served as a non-Bayesian baseline. Per optimization step, BKMR/BDKMR are dominated by Gaussian process (GP) kernel linear algebra (Cholesky factorization of the kernel), which entails time and memory. BDKMR additionally incurs forward/backward passes through the neural feature map , so it is typically somewhat heavier than BKMR in wall–clock time, although the asymptotic order is the same. KRR is computationally lighter, requiring a single regularized kernel solve per hyperparameter setting. For larger datasets, both BKMR and BDKMR can adopt sparse/structured GP approximations (inducing-point and Nyström/SKI methods; [28,29,30,31,32,33]) and mini-batch training to reduce computational burden.
With the MAP/Laplace estimates in hand, prediction at new inputs proceeds via the conditional GP. In particular, given new input data, , we compute the posterior predictive mean and variance of under the GP approximation with learned parameters:
where are derived from the conditional GP distribution using the transformed latent features and the learned kernel structure. This framework allows for both in-sample and out-of-sample prediction, while accounting for uncertainty in a principled Bayesian manner.
3.3. Evaluation Metrics
The predictive accuracy was assessed using two commonly adopted metrics: the mean absolute error (MAE) and mean squared error (MSE). These metrics are defined as follows:
where denotes the true value and denotes the predicted value for the i-th observation.
4. Results
In this section, we provide the predictive performance of our proposed BDKMR model and compare it with two benchmark models: kernel ridge regression (KRR) [8] and BKMR. To ensure a fair and robust comparison, we employed Leave-One-Out Cross-Validation (LOOCV) (see e.g., [10]), which evaluates model generalization by iteratively leaving out each data point for testing while using the remainder for training. Since our dataset consists of monthly aggregated means for each observation and is therefore relatively small, LOOCV was chosen over alternative methods such as k-fold cross-validation to maximize the amount of training data in each iteration and obtain a lower-bias estimate of predictive performance.
Table 1 presents the MAE and MSE values for the three models evaluated under LOOCV. The results clearly indicate that our proposed BDKMR substantially outperformed both KRR and BKMR. Specifically, BDKMR achieved the lowest MAE (0.1895) and MSE (0.0629), reflecting both accurate and stable predictions. In contrast, KRR and BKMR showed significantly higher error values, with KRR in particular performing poorly (MAE: 1.1141; MSE: 3.5665). These findings highlight the benefits of combining deep feature extraction with Bayesian kernel modeling.

Table 1.
Predictive performance comparison using Leave-One-Out Cross-Validation.
Moreover, we observe that the heteroscedastic version of BDKMR outperformed its homoskedastic counterpart (BDKMR (Equal)), which assumed constant observation-level noise. By explicitly modeling the variance as , where is the number of sampled flatfish, the heteroscedastic model could result in improved predictive accuracy.
Figure 5 presents scatter plots comparing predicted and true values for KRR, BKMR, and BDKMR under LOOCV. Each point corresponds to an individual observation, with the red dashed line indicating the identity line . BDKMR yields predictions more tightly clustered around the identity line, indicating superior accuracy and calibration. In contrast, KRR and BKMR exhibit more dispersed patterns; in particular, KRR shows regression toward the mean at the extremes, overpredicting smaller responses and underpredicting larger ones. These patterns are consistent with the MAE and MSE values in Table 1 and with the strong smoothing induced in KRR by a stationary RBF kernel with a single global bandwidth and a global ridge penalty. By comparison, BKMR and especially BDKMR better capture local nonlinearities and tail behavior.
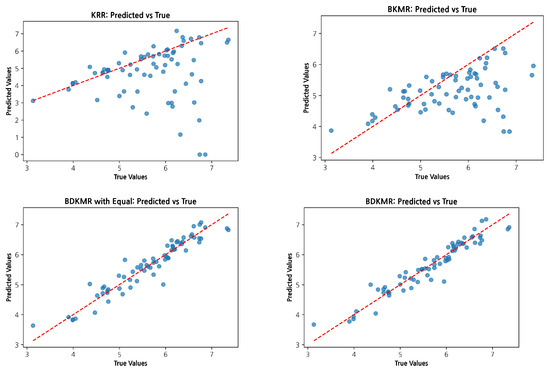
Figure 5.
Scatter plots of predicted versus true values for three models evaluated via LOOCV.
5. Conclusions
In this paper, we proposed a novel Bayesian Deep Kernel Machine Regression (BDKMR) model that combines the flexibility of Gaussian process regression with the expressive power of deep neural networks. By embedding a neural network-based feature transformation into the kernel structure, BDKMR is capable of capturing complex and nonlinear interactions among predictors, while preserving the interpretability and uncertainty quantification afforded by the Bayesian framework.
To evaluate the predictive performance of the proposed model, we applied it to aquaculture data collected from multiple flatfish farms and compared it against two benchmark models, kernel ridge regression (KRR) and Bayesian kernel machine regression (BKMR), using Leave-One-Out Cross-Validation (LOOCV). The results clearly demonstrate that BDKMR outperformed both KRR and BKMR, achieving substantially lower MAE and MSE values and producing predictions that closely followed the true outcomes.
Further performance gains were achieved by explicitly modeling observation-level noise variability through a heteroscedastic likelihood structure, where the variance was defined as with denoting the number of fish sampled in each tank. This adjustment resulted in improved predictive accuracy. The comparison against a homoskedastic variant of BDKMR further confirmed the benefit of this approach, highlighting the importance of accounting for uncertainty heterogeneity in real-world aquaculture systems.
These improvements underscore the advantages of incorporating both deep feature learning and heteroscedastic noise modeling within the Bayesian kernel framework. In particular, the ability to learn rich latent representations from high-dimensional environmental covariates, while simultaneously adapting to varying data precision, makes BDKMR a promising tool for complex predictive modeling tasks in environmental and biological sciences.
Although this study focused on olive flounder farming in South Korea, the proposed BDKMR framework is transferable to other aquaculture species and regions provided that relevant environmental and growth data are available. By tailoring the input covariates to species- or system-specific drivers (e.g., salinity for some marine species, photoperiod for freshwater species, stocking density), BDKMR can capture growth–environment relationships across diverse contexts. Nevertheless, differences in farming practices, environmental regimes, and data collection protocols should be considered carefully. Accordingly, the empirical generalizability of our findings is strongest for land-based, flow-through olive flounder farms similar to those in Wando and Jeju; applications to other systems (e.g., recirculating or brackish environments) should be retrained with system-specific covariates and re-validated under the target operational regime.
Our uncertainty quantification relies on a Laplace (Gaussian) approximation, chosen for tractability under repeated cross-validation. While appropriate under local unimodality with sufficient curvature (e.g., [13,14,25]), it may be limited in multimodal settings. Future work may therefore explore fully Bayesian posterior sampling methods, such as Hamiltonian Monte Carlo, to better capture posterior uncertainty. In addition, addressing the computational cost of jointly optimizing deep neural network parameters and kernel hyperparameters, especially for high-dimensional or large-scale datasets, remains an important direction. While the Laplace approximation offers tractability, further improvements in scalability may be achieved through approximate inference techniques such as variational methods, sparse Gaussian processes, or low-rank kernel approximations. Extending the BDKMR framework to handle hierarchical or spatially structured data is another promising avenue.
Author Contributions
Conceptualization: H.-J.J., H.-K.L. and S.J.; Data curation: S.-W.S. and H.-S.J.; Exploratory Data Analysis: J.K.; Analysis: J.K. and S.J.; Writing: S.J., J.K. and S.-W.S. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by Korea Institute of Marine Science & Technology Promotion (KIMST) funded by the Ministry of Oceans and Fisheries (RS-2022-KS221673, Big data-based aquaculture productivity improvement technology). Seongil Jo was also supported by an Inha University research grant.
Data Availability Statement
The dataset is available on request from the authors.
Conflicts of Interest
Authors Seung-Won Seo and Ho-Jin Jung were employed by the company Insilicogen Inc. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| BDKMR | Bayesian Deep Kernel Machine Regression |
| BKMR | Bayesian Kernel Machine Regression |
| GP | Gaussian Process |
| KRR | Kernel Ridge Regression |
Appendix A
Appendix A.1. Data Summary

Table A1.
Dataset characteristics and preprocessing summary.
Table A1.
Dataset characteristics and preprocessing summary.
| Item | Description |
|---|---|
| Study period | March 2023–July 2024 (coverage varies by tank) |
| Regions/farms/tanks | Wando (2 farms), Jeju (3 farms); total tanks: 7 |
| Observations (monthly) | [fill in N total]; by region: [Wando nW], [Jeju nJ]; by tank: [] |
| Seasonal coverage | Spring–summer–autumn–winter represented; duration per tank is unbalanced |
| Predictors used | Water temperature (minutely sensor), dissolved oxygen (minutely sensor), feed quantity (daily tank-level; per-fish normalization), initial log weight, region/tank indicators |
| Outcome | Log-mean monthly weight (average of 50 randomly sampled fish per farm) |
| Preprocessing | Align exposures to weight window ; average temperature and DO over the window; aggregate daily feed within the window and convert to per-fish; log-transform 50 weights and average; use heteroscedastic likelihood |
| Excluded variables | Salinity, pH, stocking density (stable/controlled or not consistently available across tanks) |
Appendix A.2. Conceptual Comparison with Other Nonlinear Models
Table A2 summarizes a conceptual comparison between BDKMR, BKMR, and other widely used nonlinear models, including random forests (RF) and support vector machines (SVM), highlighting their relative strengths and limitations across several dimensions relevant to predictive modeling. This comparison aims to help situate BDKMR among commonly used methods and highlight its unique strengths.

Table A2.
Conceptual comparison of BDKMR and BKMR with other nonlinear machine learning models.
Table A2.
Conceptual comparison of BDKMR and BKMR with other nonlinear machine learning models.
| Model | Interpretability | Interaction Modeling | Uncertainty | Nonlinearity | Comp. Cost | Scalability |
|---|---|---|---|---|---|---|
| BKMR | Moderate | Strong | Yes | Strong | High | Moderate |
| BDKMR (ours) | Moderate | Strong | Yes | Very Strong | High | Moderate |
| Random Forest | Moderate | Limited | No | Moderate | Low | High |
| SVM (RBF kernel) | Low | Limited | No | Strong | Moderate | High |
References
- Baek, E.Y.; Seng, J.W.; Kim, D.Y. A study on the characteristics and development direction of Olive Flounder aquaculture by region. J. Korean Isl. 2024, 36, 17–42. [Google Scholar] [CrossRef]
- Ministry of Oceans and Fisheries. 2023 Aquaculture Production Statistics; Ministry of Oceans and Fisheries: Sejong-si, Republic of Korea, 2023; (In Korean). Available online: https://www.index.go.kr/ (accessed on 1 August 2025).
- Oh, S.; Lee, S. Fish Welfare-Related Issues and Their Relevance in Land-Based Olive Flounder (Paralichthys olivaceus) Farms in Korea. Animals 2024, 14, 1693. [Google Scholar] [CrossRef] [PubMed]
- Chung, H.J.; Jeong, Y.S. Value Chain Analysis of the Olive Flounder Paralichthys olivaceus Aquaculture Industry. In KMI Research Report; Korea Maritime Institute: Busan, Republic of Korea, 2023. [Google Scholar]
- Bae, M.J.; Im, E.Y.; Kim, H.Y.; Jung, S.J. The effect of temperature to scuticociliatida Miamiensis avidus proliferation, and to mortality of infected olive flounder Paralichthys olivaceus. J. Fish Pathol. 2009, 22, 97–105. [Google Scholar]
- Kim, B.; Park, M.; Son, M.; Kim, T.; Myeong, J.; Cho, J. A Study on the Optimum Stocking Density of the Juvenile Abalone, Hailotis discus hannai Net Cage Culture or Indoor Tank Culture. Korean J. Malacol. 2013, 29, 189–195. [Google Scholar] [CrossRef]
- Jang, I.S.; Lee, J.H.; Kim, Y.H. Stress Responses and Histopathological Changes in Olive Flounder (Paralichthys olivaceus) Following an Increase in Water Temperature. Korean J. Fish. Aquat. Sci. 2018, 51, 749–755. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Bobb, J.F.; Valeri, L.; Claus Henn, B.; Christiani, D.C.; Wright, R.O.; Mazumdar, M. Bayesian kernel machine regression for estimating the health effects of multi-pollutant mixtures. Biostatistics 2015, 16, 493–508. [Google Scholar] [CrossRef] [PubMed]
- Lumumba, V.W.; Iddi, S.; Muchie, M. Comparative Analysis of Cross-Validation Techniques: LOOCV, K-folds Cross-Validation, and Repeated K-folds Cross-Validation in Machine Learning Models. Am. J. Theor. Appl. Stat. 2024, 13, 127–137. [Google Scholar] [CrossRef]
- McGee, G.; Wilson, A.; Webster, T.F.; Coull, B.A. Bayesian multiple index models for environmental mixtures. Biometrics 2023, 79, 462–474. [Google Scholar] [CrossRef] [PubMed]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Murphy, K.P. Machine Learning: A Probabilistic Perspective; MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Dunson, D.B.; Vehtari, A.; Rubin, D.B. Bayesian Data Analysis, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Carvalho, C.M.; Polson, N.G.; Scott, J.G. The horseshoe estimator for sparse signals. Biometrika 2010, 97, 465–480. [Google Scholar] [CrossRef]
- Bobb, J.F.; Henn, B.C.; Valeri, L.; Coull, B.A. Statistical software for analyzing the health effects of multiple concurrent exposures via Bayesian kernel machine regression. Environ. Health 2018, 17, 67. [Google Scholar] [CrossRef] [PubMed]
- Seo, S.W.; Choi, G.; Jung, H.J.; Choi, M.J.; Oh, Y.D.; Jang, H.S.; Lim, H.K.; Jo, S. A Weighted Bayesian Kernel Machine Regression Approach for Predicting the Growth of Indoor-Cultured Abalone. Appl. Sci. 2025, 15, 708. [Google Scholar] [CrossRef]
- McCulloch, W.S.; Pitts, W. A Logical Calculus of the Ideas Immanent in Nervous Activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Rosenblatt, F. The Perceptron: A Probabilistic Model for Information Storage and Organization in the Brain. Psychol. Rev. 1958, 65, 386–408. [Google Scholar] [CrossRef] [PubMed]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning Representations by Back-Propagating Errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Lee, J.; Lee, S. Effects of Water Temperature and Feeding Rate on Growth and Body Composition of Grower Olive Flounder Paralichthys olivaceus. Aquaculture 2000, 190, 119–129. [Google Scholar]
- Kim, S.; Lee, J.; Kim, K.; Kim, K.; Lee, B.; Lee, K. Effects of Feed Particle Size, Stocking Density, and Dissolved Oxygen Concentration on the Growth of Olive Flounder Paralichthys olivaceus. Korean Soc. Fish. Aquat. Sci. 2015, 48, 314–321. [Google Scholar]
- Polson, N.G.; Scott, J.G. Shrink Globally, Act Locally: Sparse Bayesian Regularization and Prediction. Bayesian Stat. 2010, 9, 501–538. [Google Scholar]
- Tierney, L.; Kadane, J.B. Accurate Approximations for Posterior Moments and Marginal Densities. J. Am. Stat. Assoc. 1986, 81, 82–86. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Liu, D.C.; Nocedal, J. On the Limited Memory BFGS Method for Large Scale Optimization. Math. Program. 1989, 45, 503–528. [Google Scholar] [CrossRef]
- Quiñonero-Candela, J.; Rasmussen, C.E. A Unifying View of Sparse Approximate Gaussian Process Regression. J. Mach. Learn. Res. 2005, 6, 1939–1959. [Google Scholar]
- Titsias, M. Variational Learning of Inducing Variables in Sparse Gaussian Processes. In Proceedings of the 12th International Conference on Artificial Intelligence and Statistics (AISTATS), Clearwater Beach, FL, USA, 16–18 April 2009; pp. 567–574. [Google Scholar]
- Snelson, E.; Ghahramani, Z. Sparse Gaussian Processes using Pseudo-inputs. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 4–7 December 2006; Volume 18, pp. 1257–1264. [Google Scholar]
- Williams, C.K.I.; Seeger, M. Using the Nyström Method to Speed up Kernel Machines. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 3–8 December 2001; Volume 13. [Google Scholar]
- Wilson, A.G.; Nickisch, H. Kernel Interpolation for Scalable Structured Gaussian Processes (KISS-GP). In Proceedings of the 32nd International Conference on Machine Learning (ICML), Lille, France, 6–11 July 2015; pp. 1775–1784. [Google Scholar]
- Hensman, J.; Fusi, N.; Lawrence, N.D. Gaussian Processes for Big Data. In Proceedings of the 29th Conference on Uncertainty in Artificial Intelligence (UAI), Washington, DC, USA, 11–15 July 2013; pp. 282–290. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).