Study on the Unipolar Impulse Aging Characteristics of ZnO Varistors and Their Condition Monitoring Methods
Abstract
1. Introduction
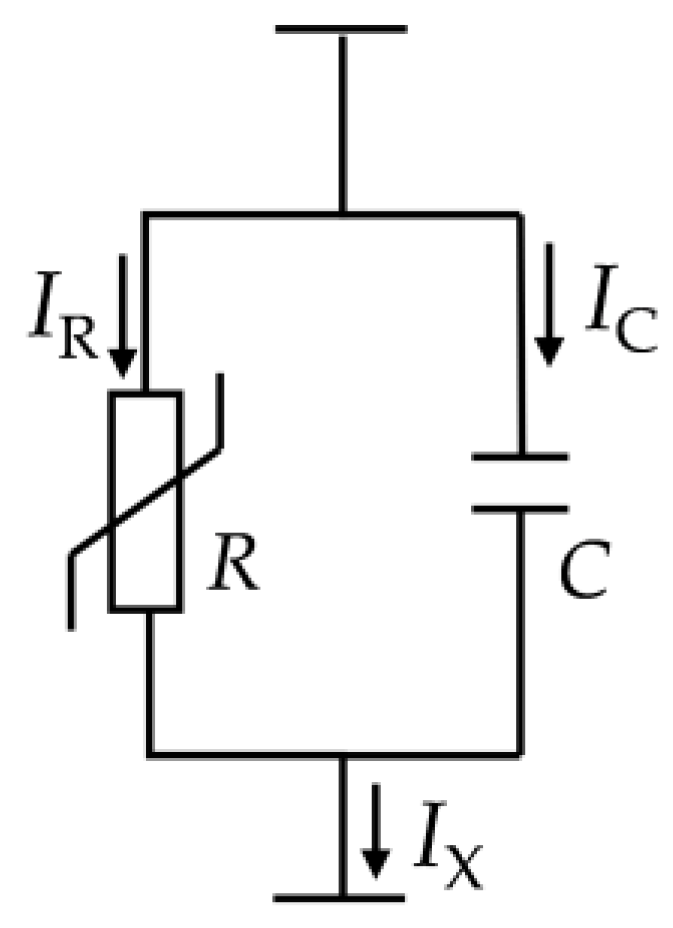
2. Resistive Leakage Current Extraction Method Based on Levenberg–Marquardt Optimization Algorithm
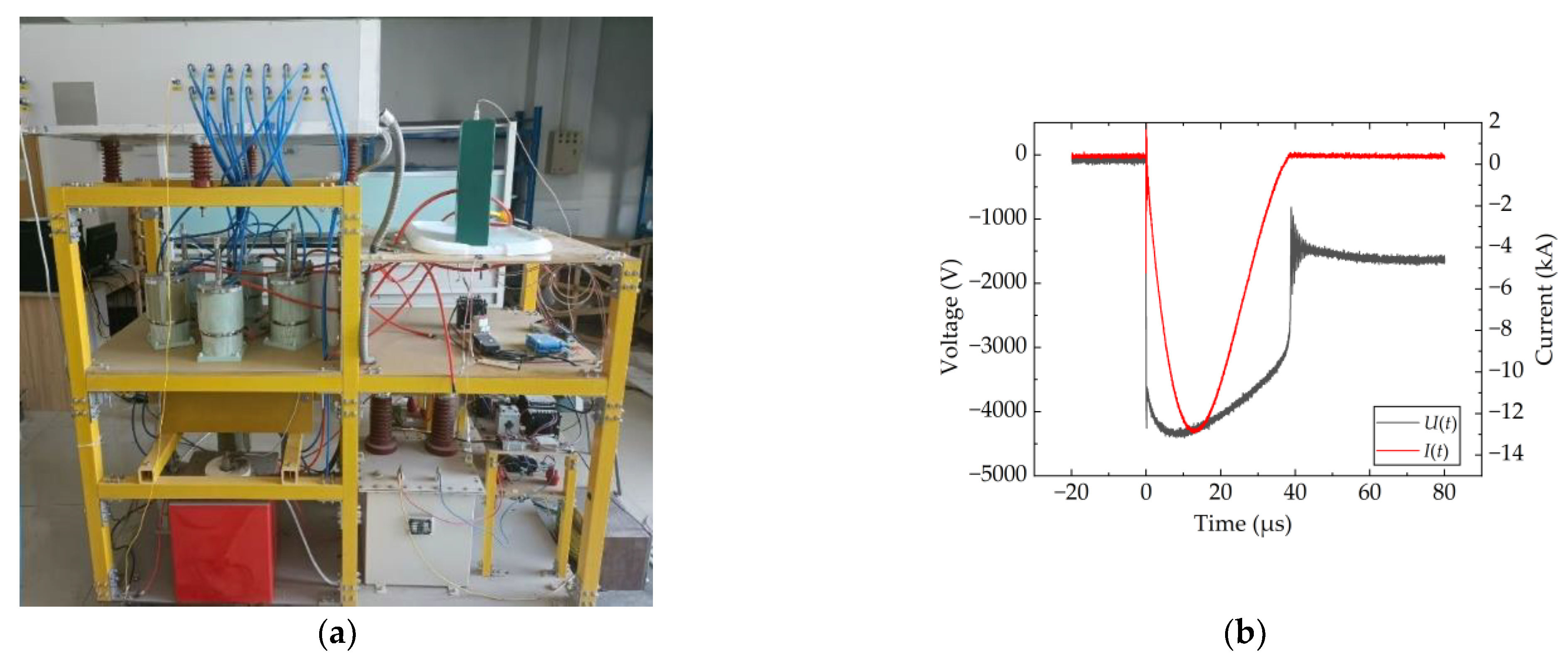
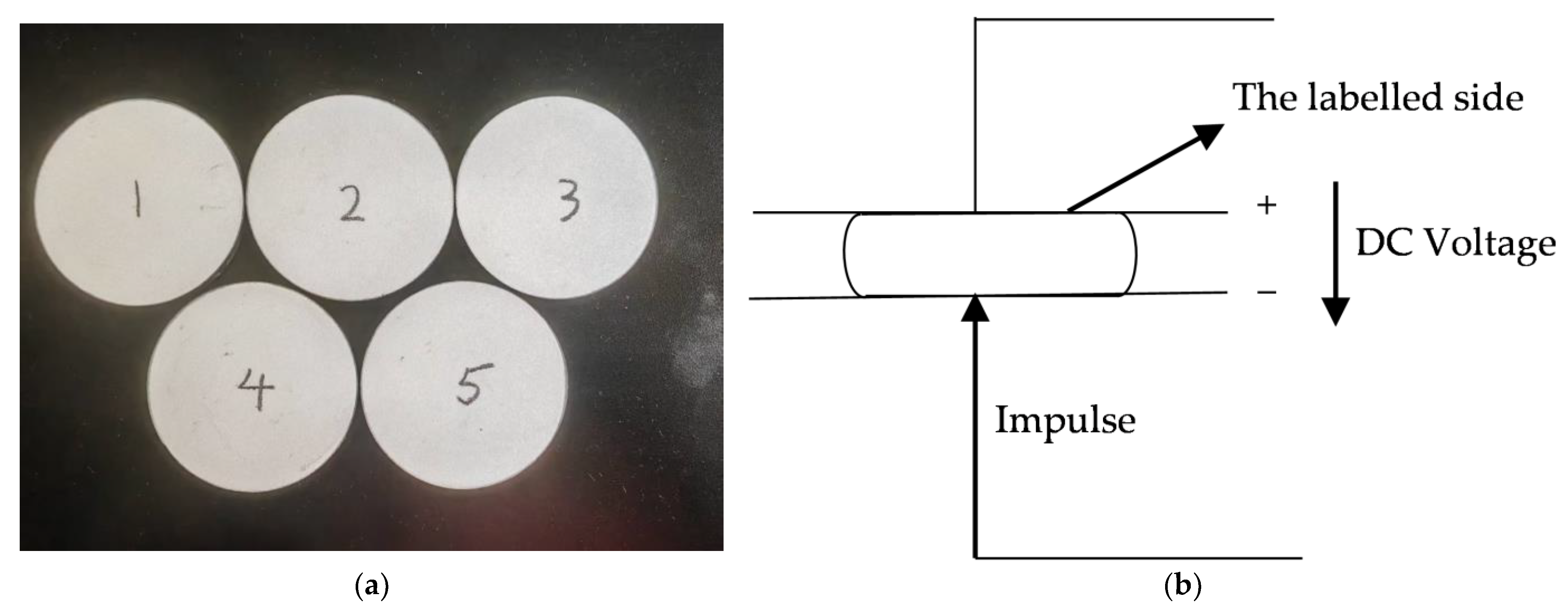
3. Experimental Methods
4. Experimental Results and Analysis
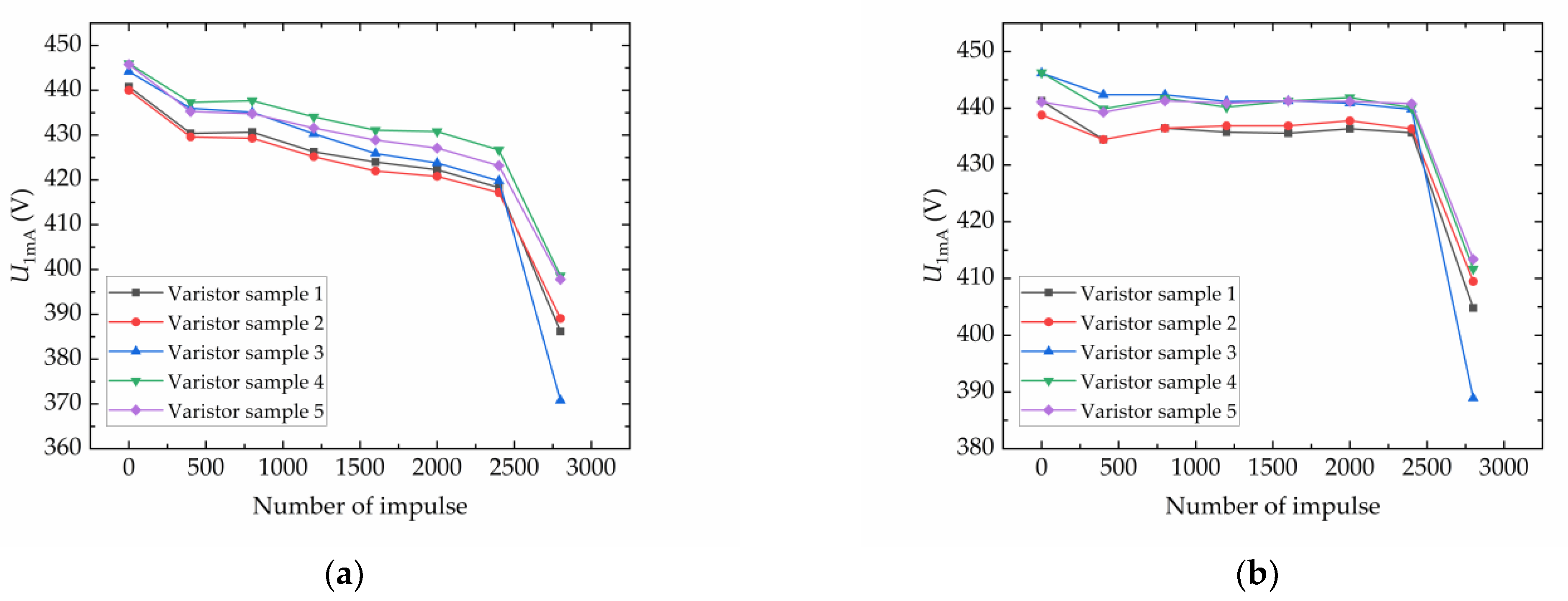
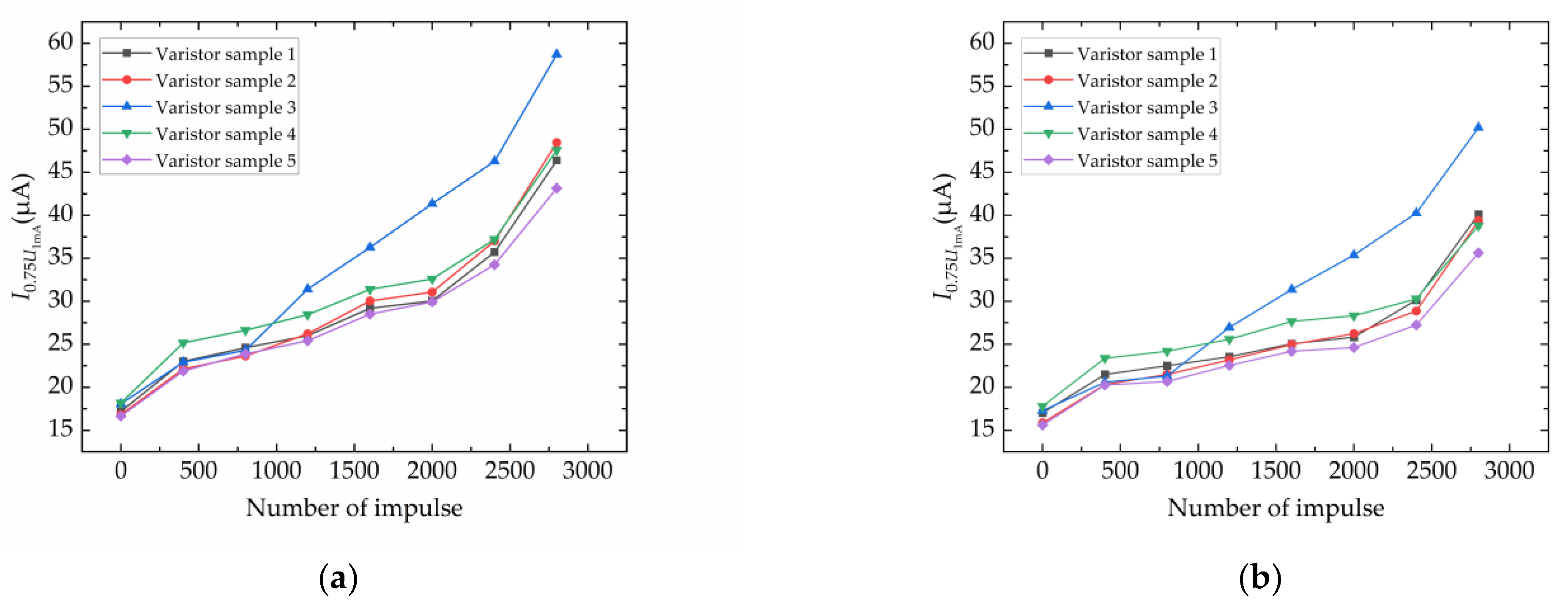
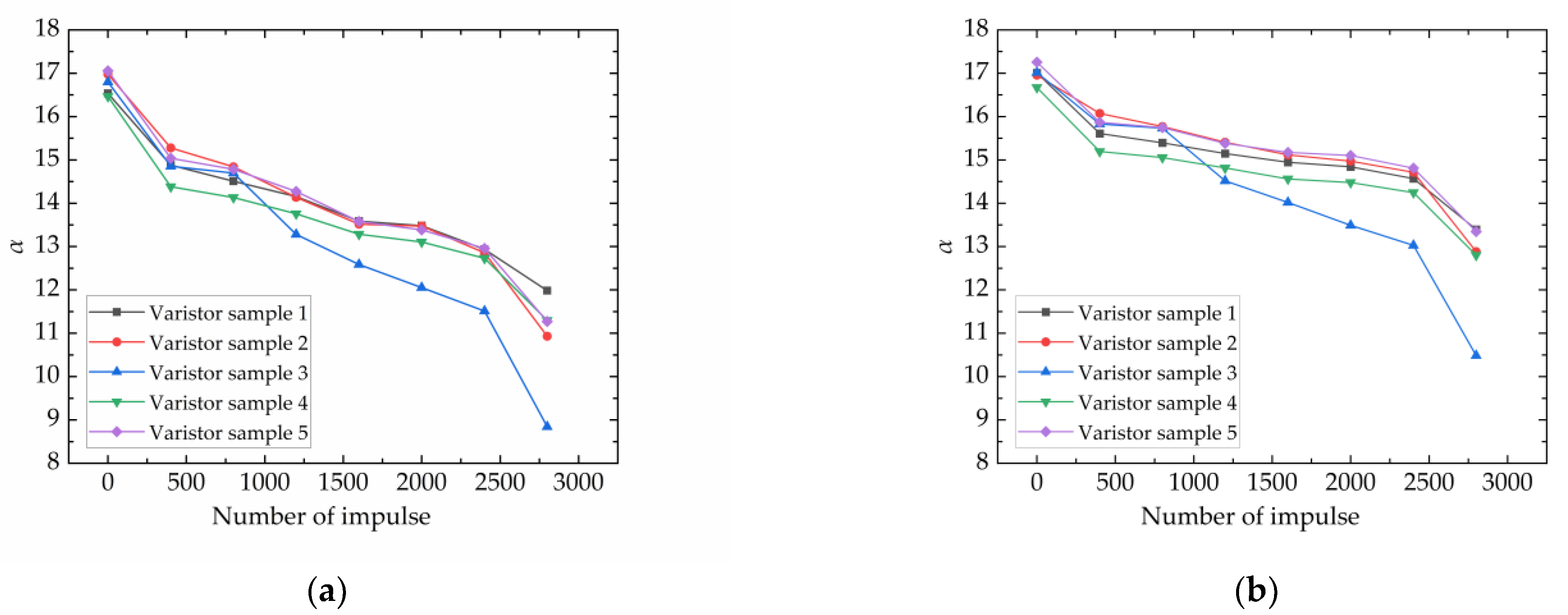
4.1. DC Parameter Experimental Results
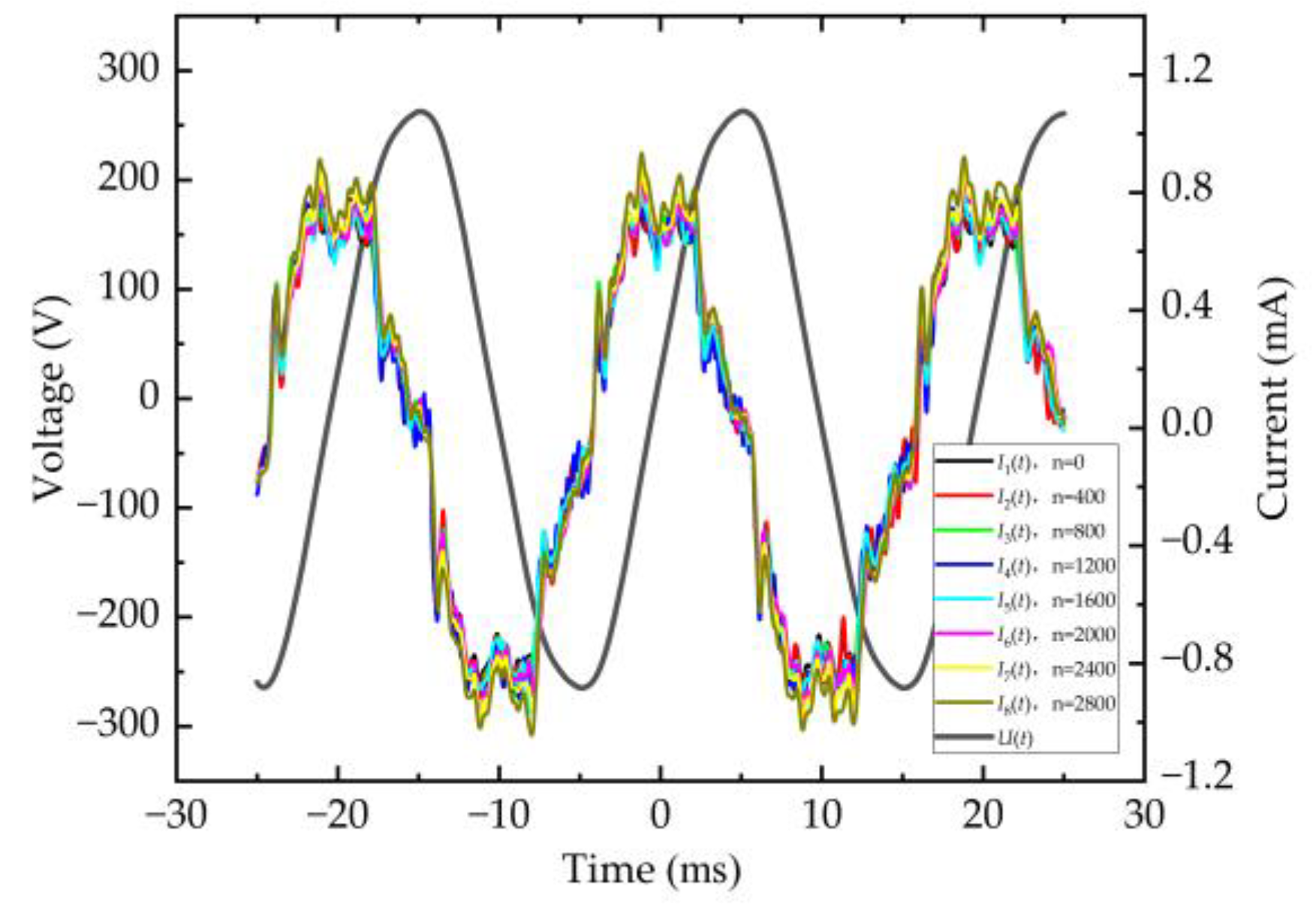
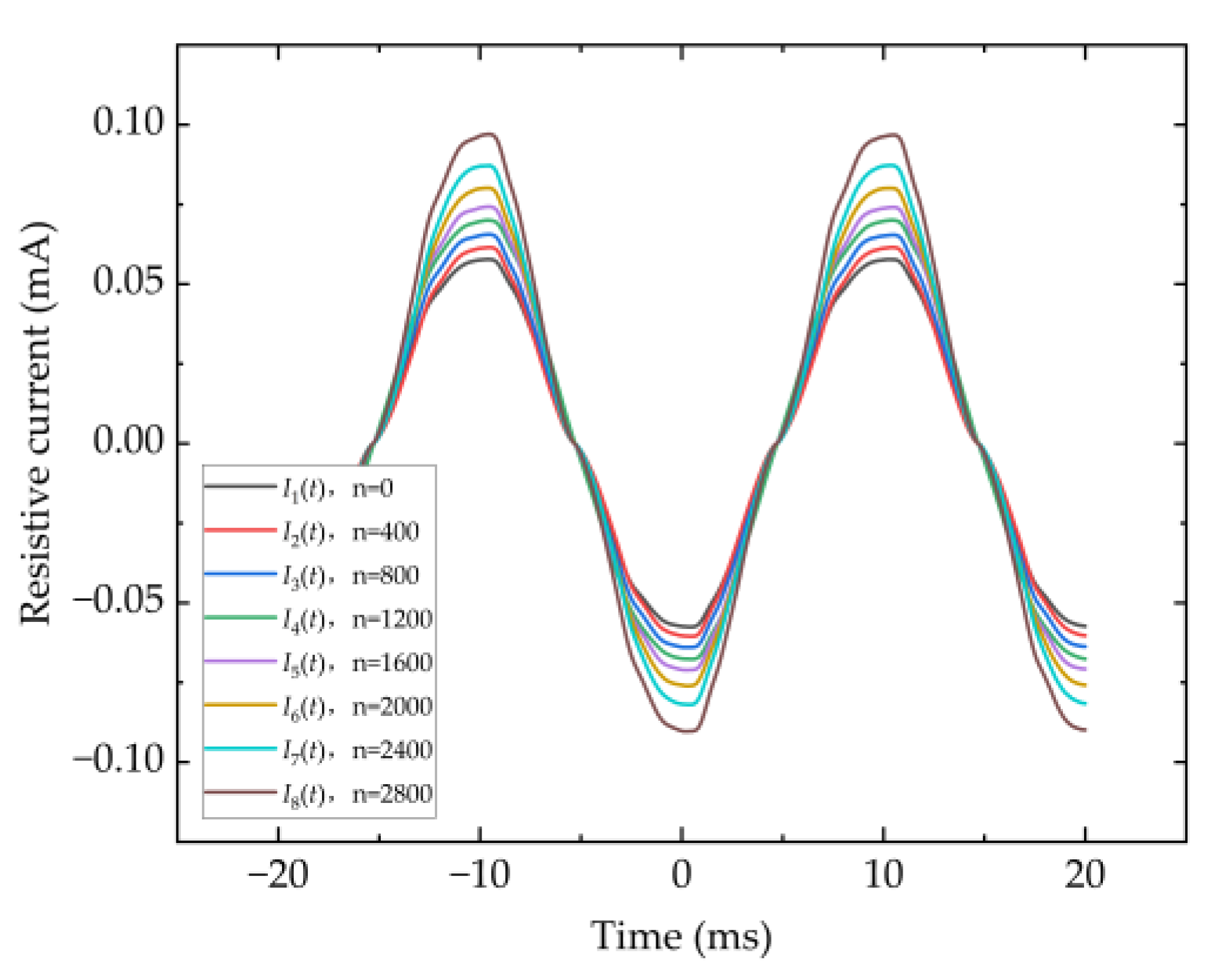
4.2. Variation Trend of AC Current Waveform
5. Conclusions and Future Work
- Under a negative-polarity impulse current, the aging of ZnO varistors exhibits a significant polarity effect. The forward reference voltage shows an initial gradual decrease, followed by a rapid drop with increasing impulse count, while the reverse reference voltage first decreases, then exhibits a slight recovery, and ultimately undergoes a significant drop. Both forward and reverse leakage currents exhibit increasing trends, with the forward leakage current showing a greater increase than the reverse current. Both forward and reverse nonlinear coefficients demonstrate attenuation trends, with the forward nonlinear coefficient degrading more severely. This phenomenon is attributed to asymmetric aging of the double Schottky barriers in the ZnO varistor during impulse aging, which can be explained by ion migration theory.
- A high-precision separation of the resistive component from the full current of ZnO varistors under harmonic-containing 50 Hz voltage excitation at a voltage ratio of 0.6 was achieved using the Levenberg–Marquardt optimization algorithm. Signal analysis in MATLAB R2024b enabled spectral analysis of both the full current and its resistive component. The spectral results indicate that the DC component amplitude of the resistive current exhibits the highest sensitivity to aging. Compared to the fundamental and third harmonic components of the resistive current, the DC component amplitude can detect degradation signals earlier during the initial stage of impulse aging, making it an effective criterion for evaluating the aging state of ZnO surge arresters.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ZnO | Zinc oxide |
| MOSA | Metal-oxide surge arrester |
| LM | Levenberg–Marquardt |
References
- Yutthagowith, P.; Baba, Y. A Simple Mathematical Expression for Nonlinear Resistive Characteristics of Metal Oxide Elements in Lightning Surge Analysis. IEEE Trans. Electromagn. Compat. 2025, 67, 996–1003. [Google Scholar] [CrossRef]
- Xiao, X.; Shi, Y.; Yang, L. Voltage dependence of dielectric permittivity in zinc oxide varistors under time-varying AC fields. J. Phys. D Appl. Phys. 2025, 58, 155101. [Google Scholar] [CrossRef]
- Xiao, X.; Shi, Y.; Liu, C.; Yang, L. Nonlinear behaviour and ageing characteristics of ZnO varistors under ac voltage in the breakdown region. Electr. Power Syst. Res. 2025, 248, 111976. [Google Scholar] [CrossRef]
- Ranjbar, B.; Darvishi, A.; Dashti, R.; Shaker, H.R. A Survey of Diagnostic and Condition Monitoring of Metal Oxide Surge Arrester in the Power Distribution Network. Energies 2022, 15, 8091. [Google Scholar] [CrossRef]
- Olesz, M.; Litzbarski, L.S.; Redlarski, G. Leakage Current Measurements of Surge Arresters. Energies 2023, 16, 6480. [Google Scholar] [CrossRef]
- Zacarias, T.G.; Sant’Ana, W.C. A Bibliometric and Comprehensive Review on Condition Monitoring of Metal Oxide Surge Arresters. Sensors 2024, 24, 235. [Google Scholar] [CrossRef] [PubMed]
- Das, A.K.; Dalai, S. Recent Development in Condition Monitoring Methodologies of MOSA Employing Leakage Current Signal: A Review. IEEE Sens. J. 2021, 21, 14559–14568. [Google Scholar] [CrossRef]
- Xu, W.; Sheng, F. Improved method for extracting resistive leakage current of surge protectors. J. Eng. 2019, 2019, 8737–8742. [Google Scholar] [CrossRef]
- Munir, A.; Abdul-Malek, Z.; Arshad, R.N. Resistive component extraction of leakage current in metal oxide surge arrester: A hybrid method. Measurement 2021, 173, 108588. [Google Scholar] [CrossRef]
- Shi, J.; Han, Y.; Dong, Y.; Liao, Z.; Zhang, P.; Huang, W.; Liu, G.; Zhang, J.; He, S. An Intelligent Online Diagnosis Method for Surge Arresters Status Based on ZnO Varistors Impulse Aging Test. IEEE Trans. Instrum. Meas. 2025, 74, 3540810. [Google Scholar] [CrossRef]
- Zhang, J.; Han, Y.; Li, L.; Deng, J.; Luo, X.; Meng, Y.; Sun, Q. Study on the Unipolar Impulse Aging of ZnO Varistors and Their Condition Monitoring Methods Based on the Basic and Even-Order Harmonics of the Leakage Current Resistive Component. IEEE Trans. Power Deliv. 2022, 37, 4888–4898. [Google Scholar] [CrossRef]
- Zhao, X.; Xu, C.; Ren, L.; Liao, R.; Yang, L.; Li, J.; Li, J. Effect of impulse current degradation on the electrical properties and dielectric relaxations of ZnO-based ceramic varistors. IEEE Trans. Dielectr. Electr. Insul. 2018, 25, 975–983. [Google Scholar] [CrossRef]
- Zhang, J.; Han, Y.; Yu, F.; Huang, W.; Li, L.; Luo, X.; Meng, Y.; Sun, Q. Study on Improving the Operating Lifespan of AC Filter Arresters in Converter Station Based on the Degradation Characteristics of ZnO Varistor Under Unipolar and Bipolar Polarity Impulse Currents. IEEE Trans. Power Deliv. 2024, 39, 3039–3049. [Google Scholar] [CrossRef]
- Yin, G.-L.; Li, J.-Y.; Yao, G.; Cheng, P.-F.; Li, S.-T. Research on electronic process of impulse degradation of ZnO-based ceramics. Acta Phys. Sin. 2010, 59, 6345–6350. [Google Scholar] [CrossRef]
- Li, S.T.; He, J.Q.; Lin, J.J.; Wang, H.; Liu, W.F.; Liao, Y.L. Electrical-Thermal Failure of Metal–Oxide Arrester by Successive Impulses. IEEE Trans. Power Deliv. 2016, 31, 2538–2545. [Google Scholar] [CrossRef]
- Wu, J.; Hu, J.; Chen, S.; He, J. Harmonic Characteristics of Leakage Currents of ZnO Varistors Under Impulse Aging. IEEE Trans. Power Deliv. 2017, 32, 1758–1765. [Google Scholar] [CrossRef]
- Zhang, J.; Han, Y.; Li, L.; Deng, J.; Luo, X.; Liu, G.; Meng, Y.; Sun, Q. The electrical model and harmonic characteristics of ZnO varistor considering unipoilar impulse aging polarity effect. Electr. Power Syst. Res. 2022, 212, 108257. [Google Scholar] [CrossRef]
- Fischer, A.; Izmailov, A.F.; Solodov, M.V. The Levenberg–Marquardt method: An overview of modern convergence theories and more. Comput. Optim. Appl. 2024, 89, 33–67. [Google Scholar] [CrossRef]
- Xiao, X.; Shi, Y.; Cheng, L.; Yang, L. The design of a linear voltage divider based on metal oxide arresters. Rev. Sci. Instrum. 2024, 95, 044707. [Google Scholar] [CrossRef] [PubMed]
- Kaito, K.; Sato, H.; Arai, Y. Temporary Overvoltage (TOV) Test Values for SPDs in Japan. In Proceedings of the 2018 34th International Conference on Lightning Protection (ICLP), Rzeszow, Poland, 2–7 September 2018; pp. 1–5. [Google Scholar]
- Zhu, Z.; Bian, X.L.; Wang, X.F.; Shi, C.B.; Si, W.R. Application of Wavelet Denoising to High-Voltage (HV) Standard Lightning Impulse Waveforms in Standard IEC 61083-2. In Proceedings of the 2020 12th International Conference on Measuring Technology and Mechatronics Automation (ICMTMA), Phuket, Thailand, 28–29 February 2020; pp. 191–196. [Google Scholar]
- Stuckenholz, C.H.; Gamlin, M. Overview of impulse current test standards and the impact on test equipment. In Proceedings of the 2012 International Conference on Lightning Protection (ICLP), Vienna, Austria, 2–7 September 2012; pp. 1–6. [Google Scholar]
- Lan, P.; Zhao, X.; Yue, Y.; Wang, X.; Zhang, B.; Lyu, X.; Guo, Z. Non-monotonically changes in double Schottky barrier of MnCO3–doped ZnO varistors during DC aging. Phys. Scr. 2025, 100, 015910. [Google Scholar] [CrossRef]
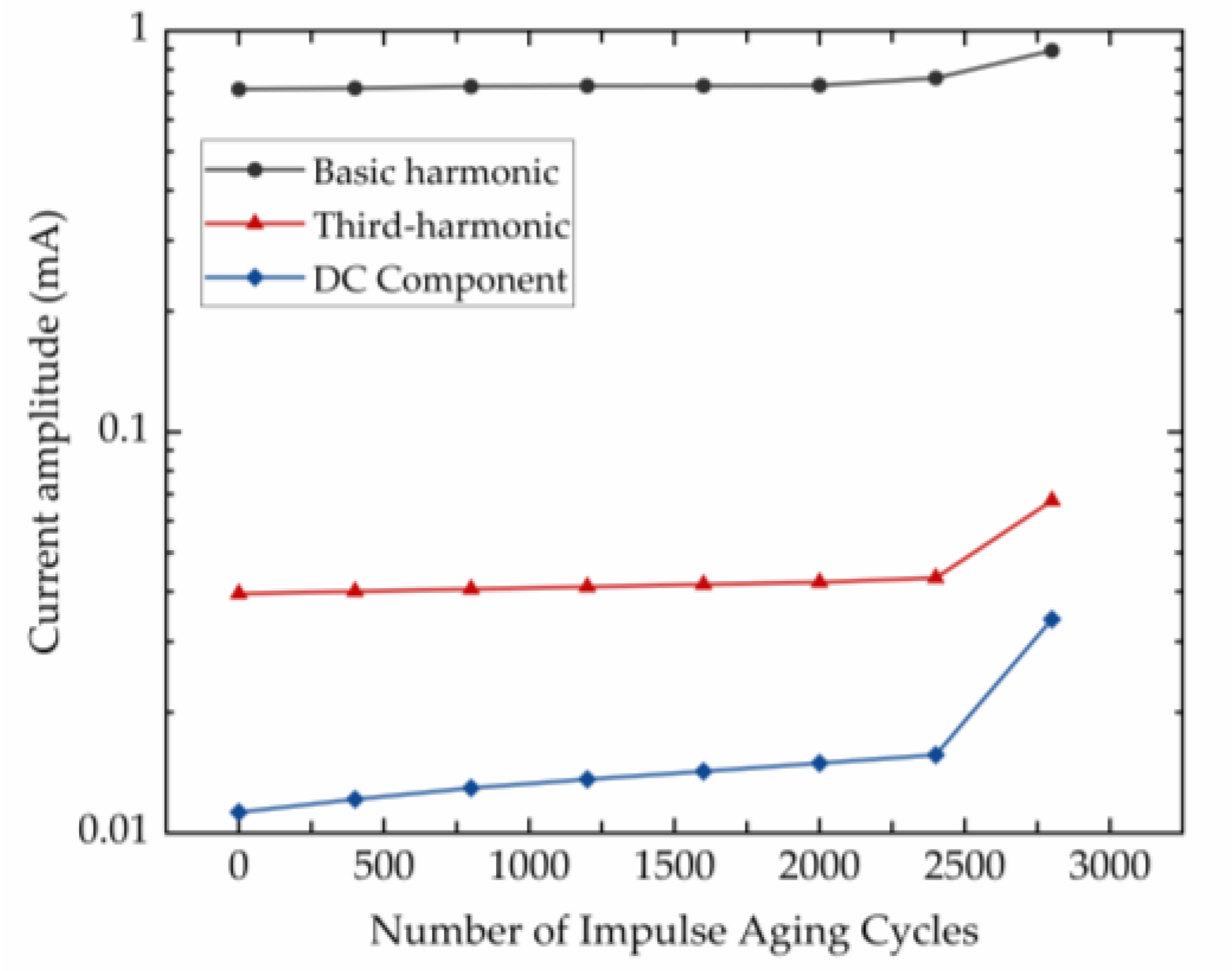
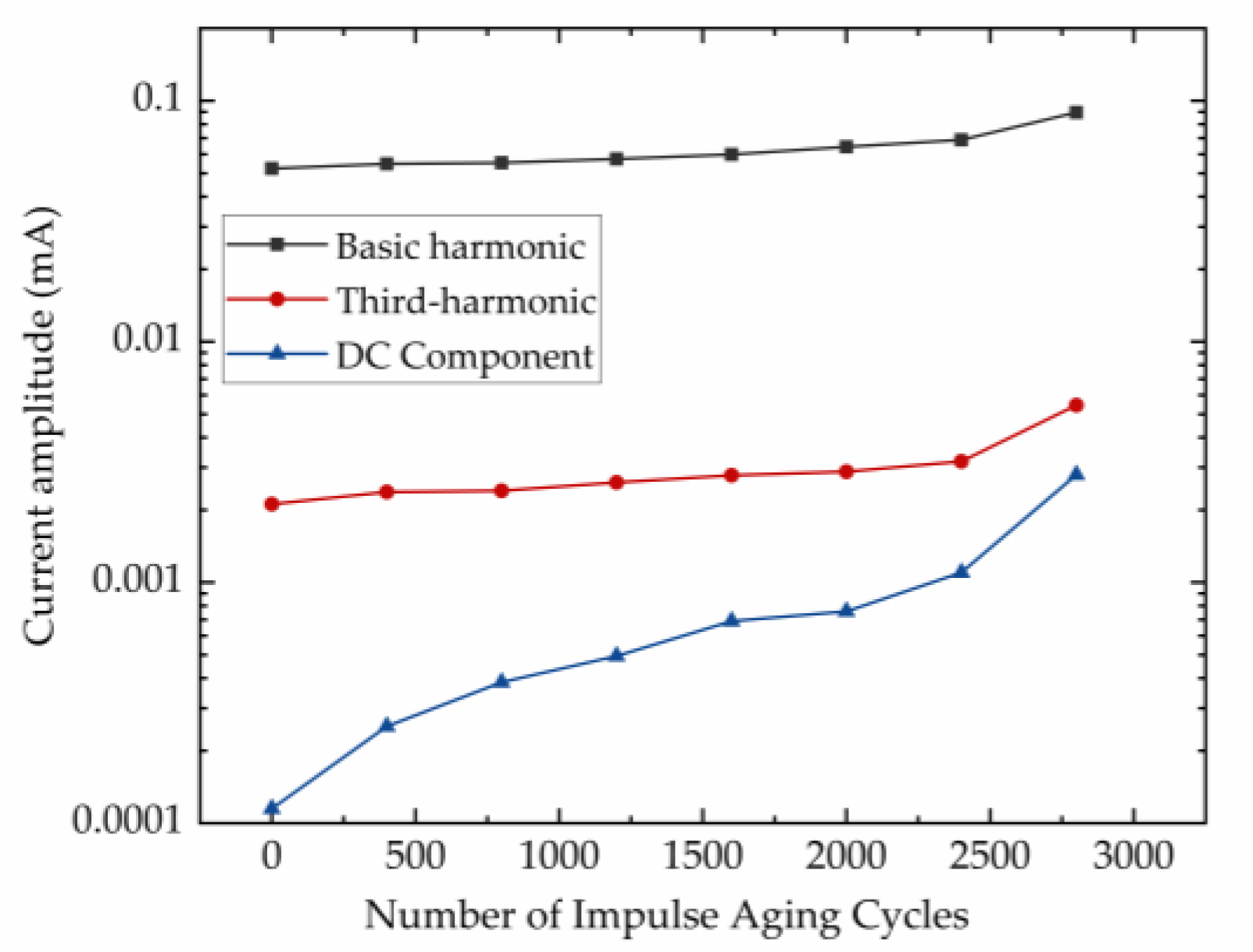
| Harmonic Order | Frequency (Hz) | Amplitude (V) |
|---|---|---|
| Basic harmonic | 50 | 182.6 |
| Second harmonic | 100 | 35.2 |
| Third harmonic | 150 | 24.7 |
| Fifth harmonic | 250 | 18.9 |
| Seventh harmonic | 350 | 12.1 |
| Eleventh harmonic | 550 | 8.4 |
| Harmonic Order | Full Current NSF | Resistive Current NSF |
|---|---|---|
| Basic harmonic | 0.0089% | 0.025% |
| Second harmonic | 0.021% | 0.048% |
| Third harmonic | 0.025% | 0.056% |
| Fifth harmonic | 0.011% | 0.031% |
| Seventh harmonic | 0.015% | 0.022% |
| DC component | 0.072% | 0.64% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, Y.; Meng, W.; Tian, X.; Yue, Y.; Li, Z.; Xu, M.; Xiao, X.; Yang, L. Study on the Unipolar Impulse Aging Characteristics of ZnO Varistors and Their Condition Monitoring Methods. Appl. Sci. 2025, 15, 9484. https://doi.org/10.3390/app15179484
Fan Y, Meng W, Tian X, Yue Y, Li Z, Xu M, Xiao X, Yang L. Study on the Unipolar Impulse Aging Characteristics of ZnO Varistors and Their Condition Monitoring Methods. Applied Sciences. 2025; 15(17):9484. https://doi.org/10.3390/app15179484
Chicago/Turabian StyleFan, Yongqiang, Wenkai Meng, Xiaoyun Tian, Yonggang Yue, Zhihui Li, Minxin Xu, Xinyan Xiao, and Lanjun Yang. 2025. "Study on the Unipolar Impulse Aging Characteristics of ZnO Varistors and Their Condition Monitoring Methods" Applied Sciences 15, no. 17: 9484. https://doi.org/10.3390/app15179484
APA StyleFan, Y., Meng, W., Tian, X., Yue, Y., Li, Z., Xu, M., Xiao, X., & Yang, L. (2025). Study on the Unipolar Impulse Aging Characteristics of ZnO Varistors and Their Condition Monitoring Methods. Applied Sciences, 15(17), 9484. https://doi.org/10.3390/app15179484






