Impact of Hydrogen-Methane Blending on Industrial Flare Stacks: Modeling of Thermal Radiation Levels and Carbon Dioxide Intensity
Abstract
1. Introduction
2. Methodology
2.1. Combustion of Hydrogen–Natural Gas Blends
2.2. Thermal Radiation Assessment for Existing Industrial Flare Systems
2.3. Indicators for Assessing CO2 Emissions from Combustion
3. Case Study
4. Results and Discussion
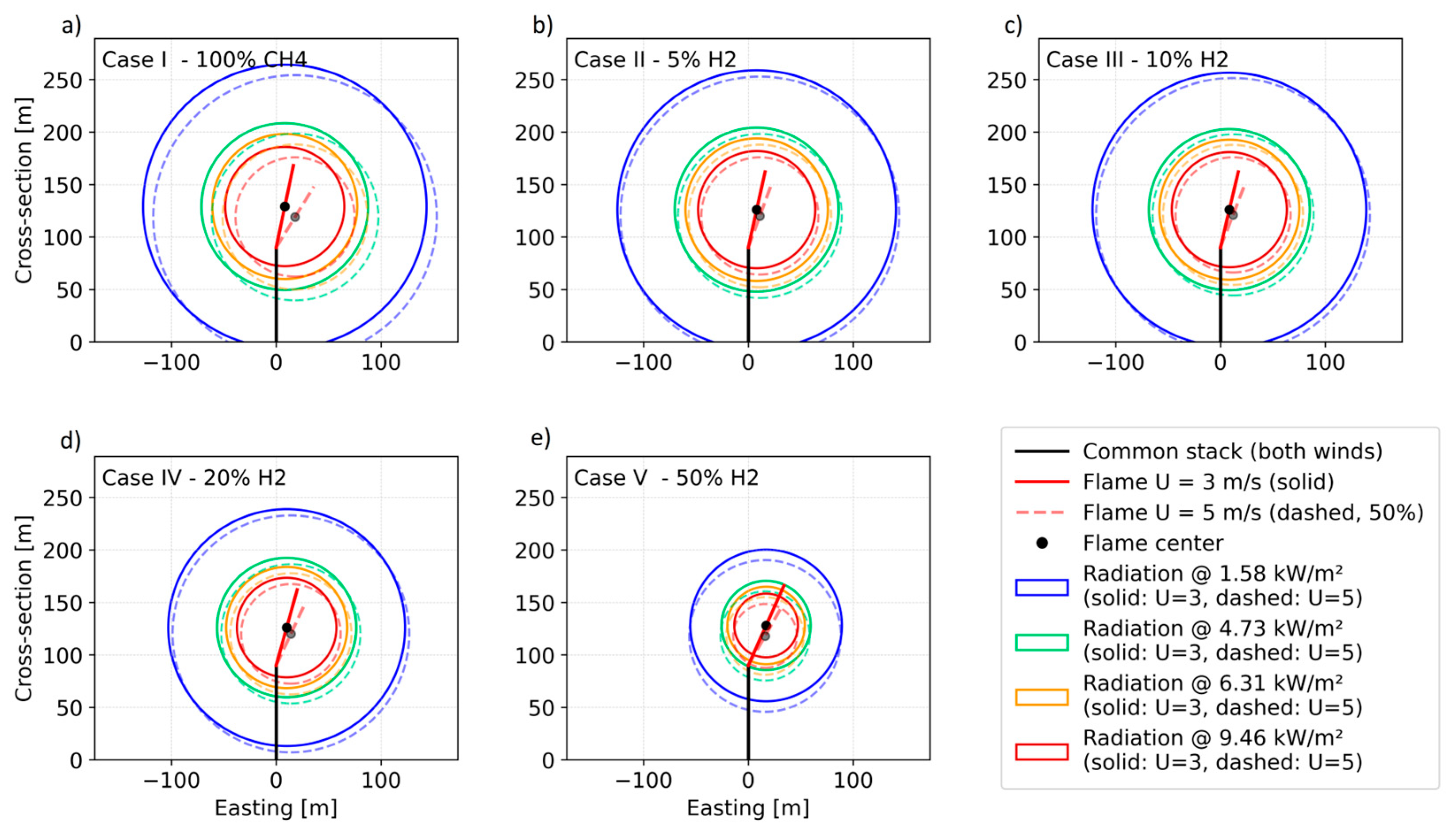
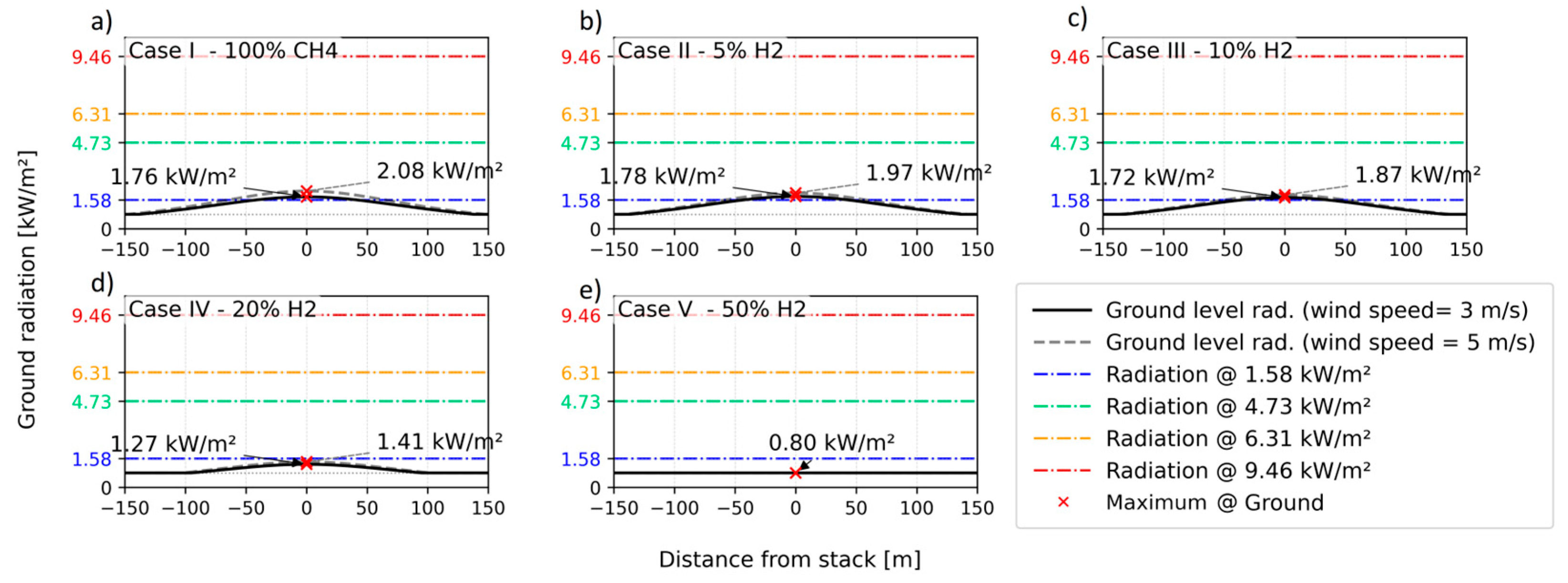
4.1. Thermal Radiation Calculations
4.2. Emission Metrics
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| API | American Petroleum Institute |
| API Std 521 | API Standard 521: Pressure-Relieving and Depressuring Systems |
| CFD | Computational Fluid Dynamics |
| CH4 | Methane |
| CO2 | Carbon dioxide |
| DNV Phast | Process hazard analysis software by DNV |
| EU ETS | European Union Emissions Trading System |
| EIA (US EIA) | United States Energy Information Administration |
| EPA (US EPA) | United States Environmental Protection Agency |
| HHV | Higher Heating Value (gross calorific value) |
| H2 | Hydrogen |
| H2O | Water (steam) |
| IEA | International Energy Agency |
| IPCC | Intergovernmental Panel on Climate Change |
| ISO | International Organization for Standardization |
| ISO 23251 | International standard equivalent to API 521 |
| LEL | Lower Explosive Limit |
| LELmix | Lower Explosive Limit of the fuel blend (Le Chatelier’s rule) |
| LHV | Lower Heating Value (Net Calorific Value) |
| LNG | Liquefied Natural Gas |
| MIE | Minimum Ignition Energy |
| MRE | Mean Radial Error (contour-matching metric) |
| MRR (EU) | Monitoring & Reporting Regulation (EU) 2018/2066 |
| NCV | Net Calorific Value (equal to LHV) |
| NG | Natural Gas |
| NOx | Nitrogen oxides |
| RTE | Radiative Transfer Equation |
| Symbols | |
| aiso | Isentropic (reference) speed of sound of the gas |
| drad(Rk) | First-pass (no-atmosphere) estimate of the critical distance at threshold Rk |
| Dc | Corrected distance after applying atmospheric transmissivity along the line of sight |
| dj·R | Dimensionless momentum–wind parameter used in Brzustowski–Sommer correlations |
| EF | Emission factor (mass of CO2 per unit energy) |
| EFmix | Emission factor of the fuel blend (generic) |
| EFmix,LHV | Emission factor of the blend on an LHV basis |
| EFmix,HHV | Emission factor of the blend on an HHV basis |
| F | Fraction of heat radiated (radiative fraction of total chemical heat release) |
| H | Flare stack height |
| HHVCH4 | Higher Heating Value of methane (molar or mass basis per context) |
| HHVH2 | Higher Heating Value of hydrogen (molar or mass basis per context) |
| L | Total flame length |
| LHVCH4 | Lower Heating Value of methane (molar or mass basis per context) |
| LHVH2 | Lower Heating Value of hydrogen (molar or mass basis per context) |
| Total mass flow rate of the gas | |
| mCH4 | Mass flow rate of methane in the blend |
| mH2 | Mass flow rate of hydrogen in the blend |
| total | Total mass flow rate |
| mCO2 | Molar mass (or produced moles) of carbon dioxide used in EF derivations (per equation context) |
| M | Mach number (ratio of jet exit velocity to aiso) |
| MW | Molecular weight of a pure component (per species) |
| MWair | Molecular weight of air |
| MWmix | Molecular weight of the blend |
| CH4 | Molar flow rate of methane |
| H2 | Molar flow rate of hydrogen |
| OF | Oxidation factor in IPCC accounting (fraction of carbon oxidized to CO2) |
| p | Static pressure used in density/velocity relations at the tip |
| Q | Total chemical heat release rate (thermal power of combustion) |
| R | Universal gas constant (as used in state/velocity relations) |
| Rk | Design thermal radiation threshold level used for zoning criteria |
| R | Line-of-sight distance between flame center and ground receptor |
| r(x) | Ground-level radiative heat flux along the wind axis as a function of horizontal coordinate x |
| RH | Ambient relative humidity (appears in τ correlation) |
| T | Gas temperature (local/at tip as defined in context) |
| Tair | Ambient air temperature used in correlations |
| Tmix | Gas temperature at the flare tip |
| T∞ | Ambient (free-stream) temperature |
| τ(RH, r) | Atmospheric transmissivity along the line of sight; function of RH and distance r |
| U | Wind speed at stack height (crosswind) |
| Uj | Jet (exit) velocity at the flare tip |
| Normal (standard-state) volumetric flow rate of the gas | |
| x | Downwind horizontal coordinate on the ground |
| xc | Downwind coordinate of flame center (from stack axis) |
| yc | Vertical rise of flame center above the tip |
| y | Molar (volume) fraction of hydrogen in the blend (generic) |
| yH2 | Explicit notation for hydrogen molar fraction in the blend |
| Ρ | Gas density at tip conditions (used in velocity/flow relations) |
References
- Directive (EU) 2024/1788 of the European Parliament and of the Council of 13 June 2024 on Common Rules for the Internal Markets for Renewable Gas, Natural Gas and Hydrogen. OJ L 2024/1788, 15 July 2024. Available online: https://eur-lex.europa.eu/eli/dir/2024/1788/oj (accessed on 10 August 2025).
- Regulation (EU) 2024/1789 of the European Parliament and of the Council of 13 June 2024 on the Internal Markets for Renewable Gas, Natural Gas and Hydrogen. OJ L 2024/1789, 15 July 2024. Available online: https://eur-lex.europa.eu/eli/reg/2024/1789/oj (accessed on 10 August 2025).
- Jones, D.R.; Al-Masry, W.A.; Dunnill, C.W. Hydrogen-Enriched Natural Gas as a Domestic Fuel: An Analysis Based on Flash-Back and Blow-Off Limits for Domestic Natural Gas Appliances within the UK. Sustain. Energy Fuels 2018, 2, 710–723. [Google Scholar] [CrossRef]
- Isaac, T. HyDeploy: The UK’s First Hydrogen Blending Deployment Project. Clean Energy 2019, 3, 114–125. [Google Scholar] [CrossRef]
- Leicher, J.; Schaffert, J.; Cigarida, H.; Tali, E.; Burmeister, F.; Giese, A.; Albus, R.; Görner, K.; Carpentier, S.; Milin, P.; et al. The Impact of Hydrogen Admixture into Natural Gas on Residential and Commercial Gas Appliances. Energies 2022, 15, 777. [Google Scholar] [CrossRef]
- Bertasini, D.; Battista, F.; Rizzioli, F.; Frison, N.; Bolzonella, D. Decarbonization of the European natural gas grid using hydrogen and methane biologically produced from organic waste: A critical overview. Renew. Energy 2023, 206, 386–396. [Google Scholar] [CrossRef]
- Franco, A. Industrial Decarbonization through Blended Combustion of Natural Gas and Hydrogen. Thermo 2024, 5, 29. [Google Scholar] [CrossRef]
- Mahfoozi, S.; van Zoelen, R.; Jepma, C. D4.1. Introducing Hydrogen in decentral end-user areals to deal with e-grid congestion in the Netherlands (Report). Zenodo 2022. [Google Scholar] [CrossRef]
- United States Environmental Protection Agency (EPA). 40 CFR §60.18—General Control Device and Work Practice Standards for Flares. Available online: https://www.ecfr.gov/current/title-40/part-60/section-60.18 (accessed on 10 August 2025).
- U.S. Environmental Protection Agency (EPA). EPA Air Pollution Control Cost Manual. Section 3–VOC Controls Section 3.2–VOC Destruction Controls. Chapter 1: Flares; U.S. Environmental Protection Agency: Research Triangle Park, NC, USA, 2019. [Google Scholar]
- Miller, D. New Model for Predicting Thermal Radiation from Flares and High-Pressure Jet Fires for Hydrogen and Syngas. Process Saf. Prog. 2017, 36, 237–251. [Google Scholar] [CrossRef]
- He, Y.; Pu, L.; Sun, R.; Yan, T.; Tan, H.; Zhang, Z. Development and Application of Hydrogen Flare Radiation Model for Assessing Hazard Distance. Int. J. Hydrogen Energy 2024, 49, 1161–1173. [Google Scholar] [CrossRef]
- Government of Alberta. Heat Radiation from Flares; Alberta Environment: Edmonton, AB, Canada, 2005; Available online: https://open.alberta.ca/publications/0778511898 (accessed on 10 August 2025).
- Marzouk, O.A. Adiabatic Flame Temperatures for Air-Methane and Air-Hydrogen Stoichiometric Combustion Using NASA CEARUN and Cantera. arXiv 2025, arXiv:2503.11826. [Google Scholar] [CrossRef]
- American Petroleum Institute (API). API Standard 521: Pressure-Relieving and Depressuring Systems, 7th ed.; American Petroleum Institute: Washington, DC, USA, 2023. [Google Scholar]
- Bernardy, C.; Habib, A.K.; Kluge, M.; Orchini, A. Heat Radiation Emanating from Hydrogen and Methane Jet Fires. Chem. Eng. Trans. 2025, 116, 385–390. [Google Scholar] [CrossRef]
- Zhang, H.; Cao, X.; Yuan, X.; Wu, F.; Wang, J.; Zhang, Y.; Li, Q.; Liu, H.; Huang, Z. Study on Thermal Radiation Characteristics and the Multi-Point Source Model of Hydrogen Jet Fire. Appl. Sci. 2024, 14, 7098. [Google Scholar] [CrossRef]
- Zhou, K.; Wang, X. Thermal Radiation Modelling of Pool Fire with Consideration on the Nonuniform Temperature in Flame Volume. Int. J. Therm. Sci. 2019, 138, 12–23. [Google Scholar] [CrossRef]
- Miller, D.; Jung, S.; Lutostansky, E. Applicability of Currently Available Flare Radiation Models for Hydrogen and Syngas. Process Saf. Prog. 2015, 34, 141–146. [Google Scholar] [CrossRef]
- Rossiello, G.; Uzair, M.A.; Ahmadpanah, S.B.; Morandi, L.; Ferrara, M.; Rago, G.D.; Molfetta, G.; Saponaro, A.; Torresi, M. Design and Testing of a Multi-Fuel Industrial Burner Suitable for Syngases, Flare Gas and Pure Hydrogen. Therm. Sci. Eng. Prog. 2023, 42, 101845. [Google Scholar] [CrossRef]
- Sun, R.; Pu, L.; He, Y.; Yan, T.; Tan, H.; Lei, G.; Li, Y. Investigation of the Leakage and Diffusion Characteristics of Hydrogen-Addition Natural Gas from Indoor Pipelines. Int. J. Hydrogen Energy 2023, 48, 38922–38934. [Google Scholar] [CrossRef]
- Benard, P.; Mustafa, V.; Hay, D.R. Safety Assessment of Hydrogen Disposal on Vents and Flare Stacks at High Flow Rates. Int. J. Hydrogen Energy 1999, 24, 489–495. [Google Scholar] [CrossRef]
- Li, Y.; Kuang, Z.; Fan, Z.; Shuai, J. Evaluation of the Safe Separation Distances of Hydrogen-Blended Natural Gas Pipelines in a Jet Fire Scenario. Int. J. Hydrogen Energy 2023, 48, 18804–18815. [Google Scholar] [CrossRef]
- Lévai, E.; Bereczky, Á. Effect of Hydrogen Mixing on the Flame Geometry of Natural Gas-Powered Equipment. Pollack Period. 2025, 20, 119–123. [Google Scholar] [CrossRef]
- Sorgulu, F.; Ozturk, M.; Javani, N.; Dincer, I. Experimental Investigation for Combustion Performance of Hydrogen and Natural Gas Fuel Blends. Int. J. Hydrogen Energy 2023, 48, 34476–34485. [Google Scholar] [CrossRef]
- Schefer, R.W.; Houf, W.G.; Bourne, B.; Colton, J. Spatial and Radiative Properties of an Open-Flame Hydrogen Plume. Int. J. Hydrogen Energy 2006, 31, 1332–1340. [Google Scholar] [CrossRef]
- Ilbas, M. The Effect of Thermal Radiation and Radiation Models on Hydrogen–Hydrocarbon Combustion Modelling. Int. J. Hydrogen Energy 2005, 30, 1113–1126. [Google Scholar] [CrossRef]
- Baird, A.R.; Glover, A.M.; Ehrhart, B.D. Review of Release Behavior of Hydrogen & Natural Gas Blends from Pipelines (SAND2021-9802); Sandia National Laboratories: Albuquerque, NM, USA, 2021. [Google Scholar] [CrossRef]
- Willoughby, D.; Royle, M.; Nilsen, S.; Gautier, T. Hydrogen Venting under Variable Flow Conditions. In Proceedings of the 4th International Conference on Hydrogen Safety (ICHS 2011), San Francisco, CA, USA, 12–14 September 2011; Available online: https://conference.ing.unipi.it/ichs2011/papers/162.pdf (accessed on 21 August 2025).
- Shan, S.; Jin, G.; Han, X.; Qin, Q.; Miao, L.; Zhou, Z. Numerical Study on the Radiation Characteristics of Hydrogen-Blended Natural Gas Combustion. Combust. Sci. Technol. 2025, 1–27. [Google Scholar] [CrossRef]
- Froeling, H.A.J.; Dröge, M.T.; Nane, G.F.; Van Wijk, A.J.M. Quantitative Risk Analysis of a Hazardous Jet Fire Event for Hydrogen Transport in Natural Gas Transmission Pipelines. Int. J. Hydrogen Energy 2021, 46, 10411–10422. [Google Scholar] [CrossRef]
- Zhou, L.; Zeng, D.; Li, D.; Chaos, M. Total Radiative Heat Loss and Radiation Distribution of Liquid Pool Fire Flames. Fire Saf. J. 2017, 89, 16–21. [Google Scholar] [CrossRef]
- Witkowski, A.; Rusin, A.; Majkut, M.; Stolecka, K. Analysis of Compression and Transport of the Methane/Hydrogen Mixture in Existing Natural Gas Pipelines. Int. J. Press. Vessels Pip. 2018, 166, 24–34. [Google Scholar] [CrossRef]
- H2Tools (PNNL). Hydrogen Flames. Available online: https://h2tools.org/bestpractices/laboratory-safety/laboratory-operations/hydrogen-hazards/hydrogen-flames (accessed on 10 August 2025).
- Schefer, R.W.; Patterson, B.D.; Kulatilaka, W.D.; Settersten, T.B. Visible Emission of Hydrogen Flames. Combust. Flame 2009, 156, 1234–1241. [Google Scholar] [CrossRef]
- Kong, Y.; Li, Y.; Wang, S.; Duan, P.; Zhu, J.; Han, H.; Han, J. Large-Scale Experimental Study on Jet Flame Length of Hydrogen-Blended Natural Gas and Inverse Methods for Optimizing the Weighted Multi-Point Source Model. Fuel 2024, 367, 131434. [Google Scholar] [CrossRef]
- Lowesmith, B.J.; Hankinson. Large Scale High Pressure Jet Fires Involving Natural Gas and Natural Gas/Hydrogen Mixtures. Process Saf. Environ. Prot. 2012, 90, 212–224. [Google Scholar] [CrossRef]
- Zhao, C.; Sun, L.; Ma, H.; Xiao, H. An Experimental Study of the Characteristics of Blended Hydrogen–Methane Non-Premixed Jet Flames. Process Saf. Environ. Prot. 2023, 171, 265–278. [Google Scholar] [CrossRef]
- Singh, S.; Jain, S.; PS, V.; Tiwari, A.K.; Nouni, M.R.; Pandey, J.K.; Goel, S. Hydrogen: A Sustainable Fuel for Future Energy. Renew. Sustain. Energy Rev. 2015, 51, 623–633. [Google Scholar] [CrossRef]
- National Renewable Energy Laboratory (NREL). Life Cycle Assessment of Hydrogen Production via Natural Gas Steam Reforming. NREL/TP-570-27637. 2001. Available online: https://www.nrel.gov/docs/fy01osti/27637.pdf (accessed on 10 August 2025).
- Ghosh, A.; Munoz-Munoz, N.M.; Chatelain, K.P.; Lacoste, D.A. Laminar Burning Velocity of Hydrogen-, Methane-, Ethane-, Ethylene-Air Mixtures. Applications in Energy and Combustion Science 2022, 12, 100094. [Google Scholar] [CrossRef]
- Rijksinstituut voor Volksgezondheid en Milieu (RIVM). A Comparison of Jet Fire Models for Horizontal Two-Phase Jet Fires. RIVM Report 620550005. 2012. Available online: https://www.rivm.nl/bibliotheek/rapporten/620550005.pdf (accessed on 10 August 2025).
- Molina, A.; Schefer, R.W.; Houf, W.G. Radiative Fraction and Optical Thickness in Large-Scale Hydrogen-Jet Fires. Proc. Combust. Inst. 2007, 31, 2565–2572. [Google Scholar] [CrossRef]
- Brzustowski, T.A.; Sommer, E.C., Jr. Predicting Radiant Heating from Flares. API Proc. 1973, 53, 865–893. [Google Scholar]
- Mashuga, C.V.; Crowl, D.A. Derivation of Le Chatelier’s Mixing Rule for Flammable Limits. Process Saf. Prog. 2000, 19, 112–117. [Google Scholar] [CrossRef]
- ISO 13443:1996; Natural Gas—Standard Reference Conditions. International Organization for Standardization: Geneva, Switzerland, 1996.
- Buczyński, R.; Uryga-Bugajska, I.; Tokarski, M. Recent advances in low-gradient combustion modelling of hydrogen fuel blends. Fuel 2022, 328, 125265. [Google Scholar] [CrossRef]
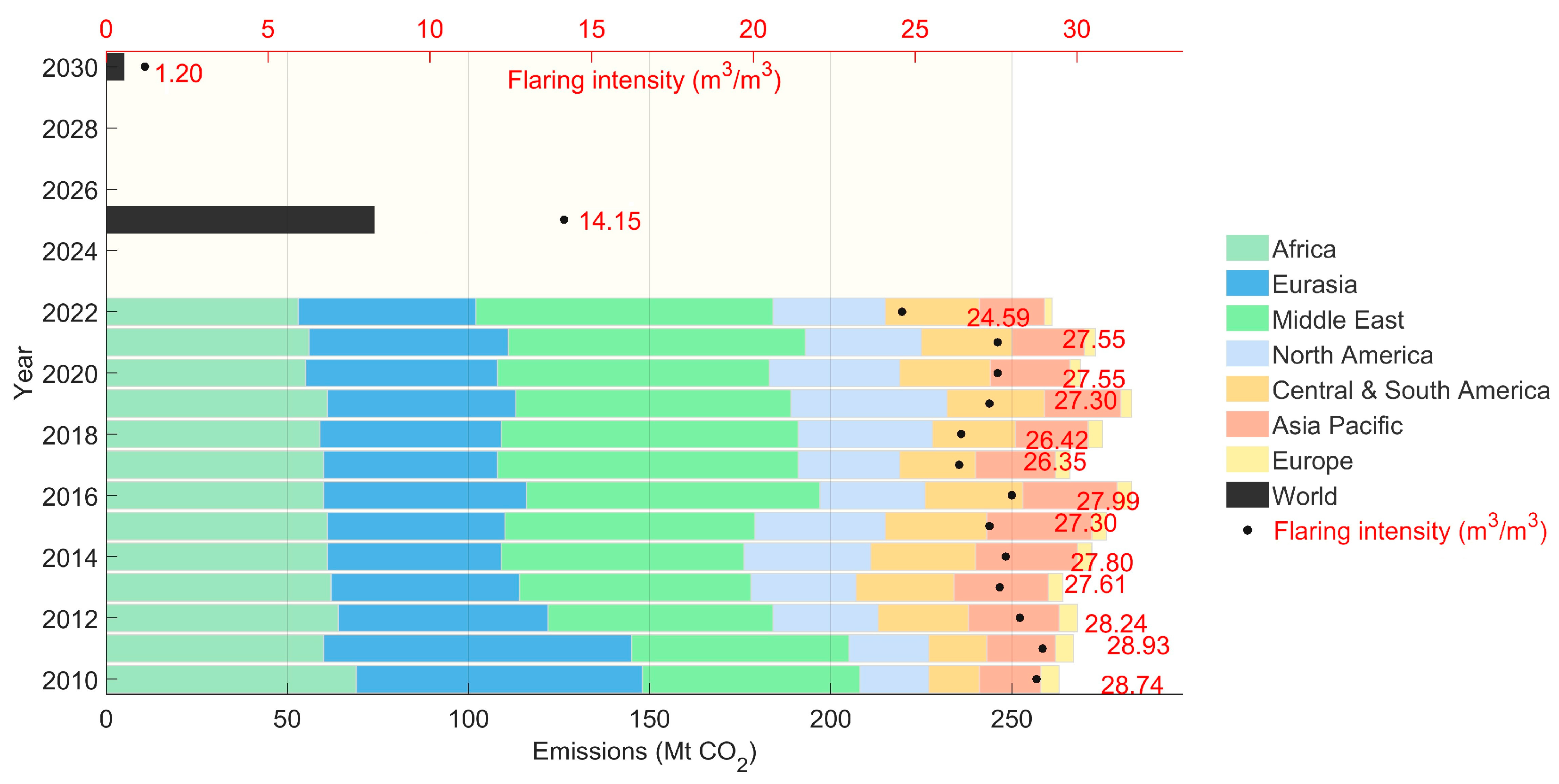
- International Energy Agency (IEA). Direct CO2 Combustion Emissions from Flaring and Flaring Intensity in the Net Zero Scenario, 2010–2030. Available online: https://www.iea.org/data-and-statistics/ (accessed on 10 August 2025).
- IPCC. 2006 IPCC Guidelines for National Greenhouse Gas Inventories, Volume 2: Energy; Institute for Global Environmental Strategies (IGES): Hayama, Japan, 2006; Available online: https://www.ipcc-nggip.iges.or.jp/public/2006gl/ (accessed on 10 August 2025).
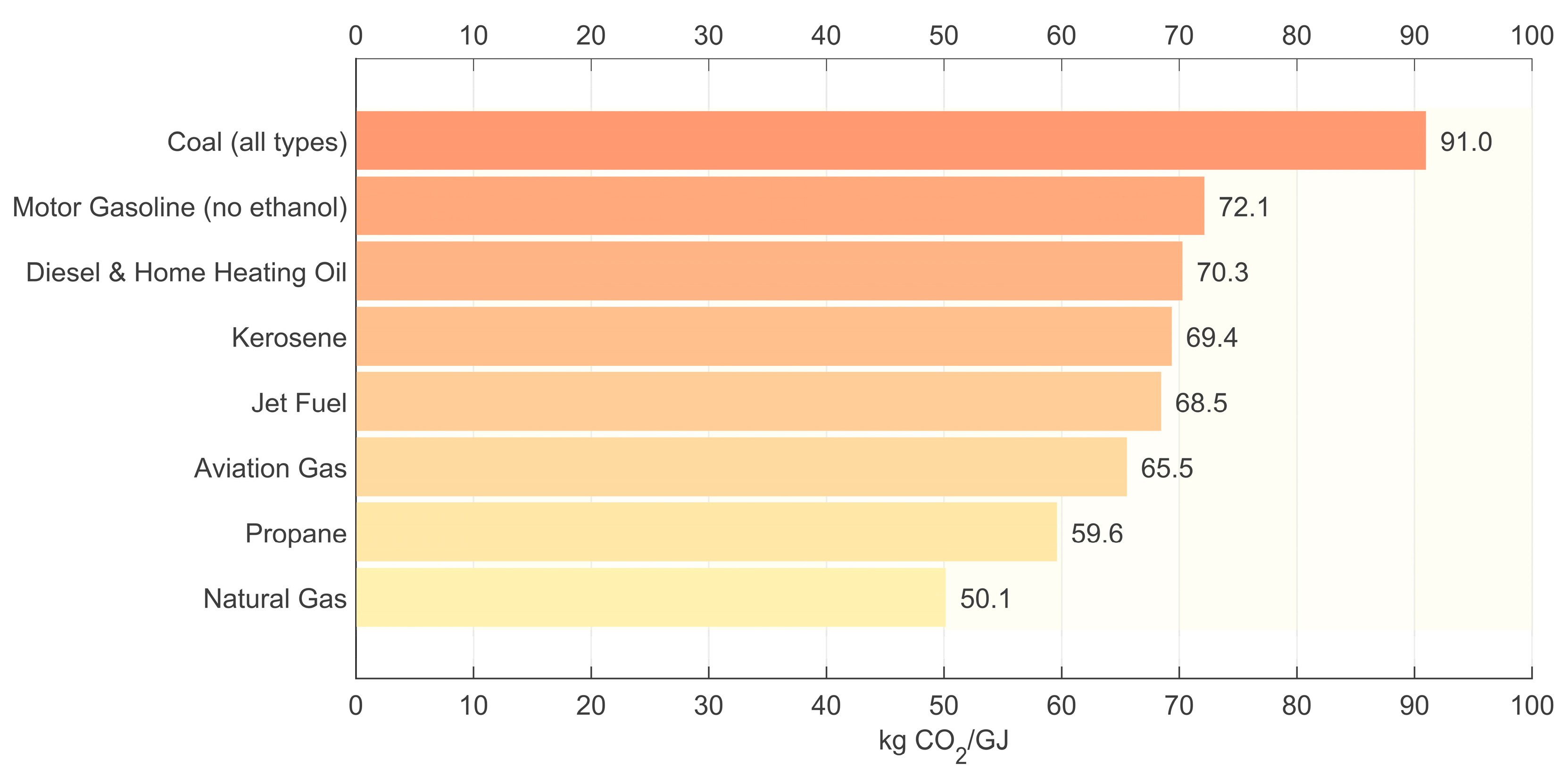
- U.S. Energy Information Administration (EIA). Carbon Dioxide Emissions Coefficients. Release 18 September 2024. Available online: https://www.eia.gov/environment/emissions/co2_vol_mass.php (accessed on 10 August 2025).
- Commission Implementing Regulation (EU) 2018/2066 of 19 December 2018 on the Monitoring and Reporting of Greenhouse Gas Emissions Pursuant to Directive 2003/87/EC of the European Parliament and of the Council and Amending Commission Regulation (EU) No 601/2012. OJ L 334, 1–93. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=CELEX:32018R2066 (accessed on 10 August 2025).
- U.S. Environmental Protection Agency (EPA). 40 CFR Part 98, Subpart C—General Stationary Fuel Combustion Sources. Available online: https://www.ecfr.gov/current/title-40/part-98/subpart-C (accessed on 10 August 2025).
- National Fire Protection Association (NFPA). NFPA 69: Standard on Explosion Prevention Systems, 2024th ed.; National Fire Protection Association: Washington, DC, USA, 2024. [Google Scholar]

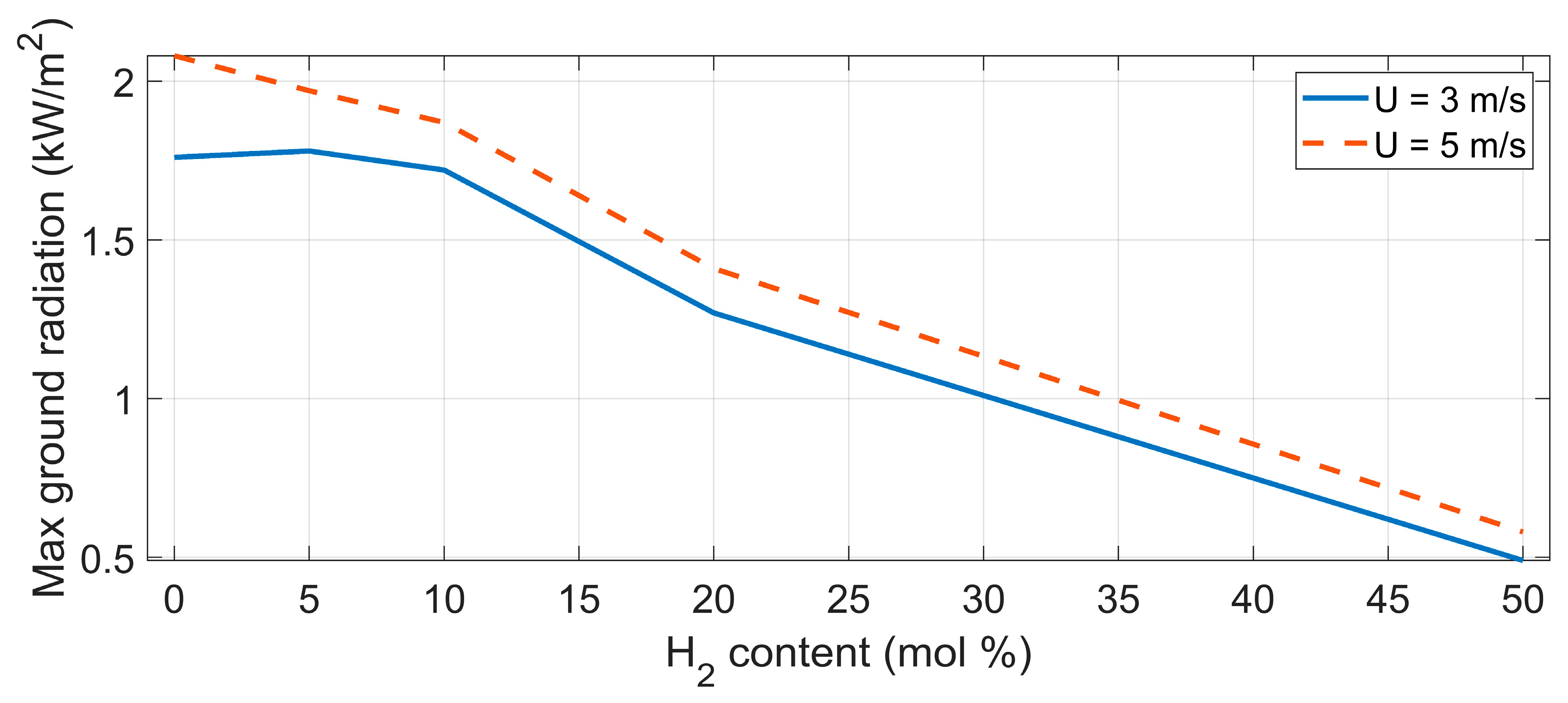
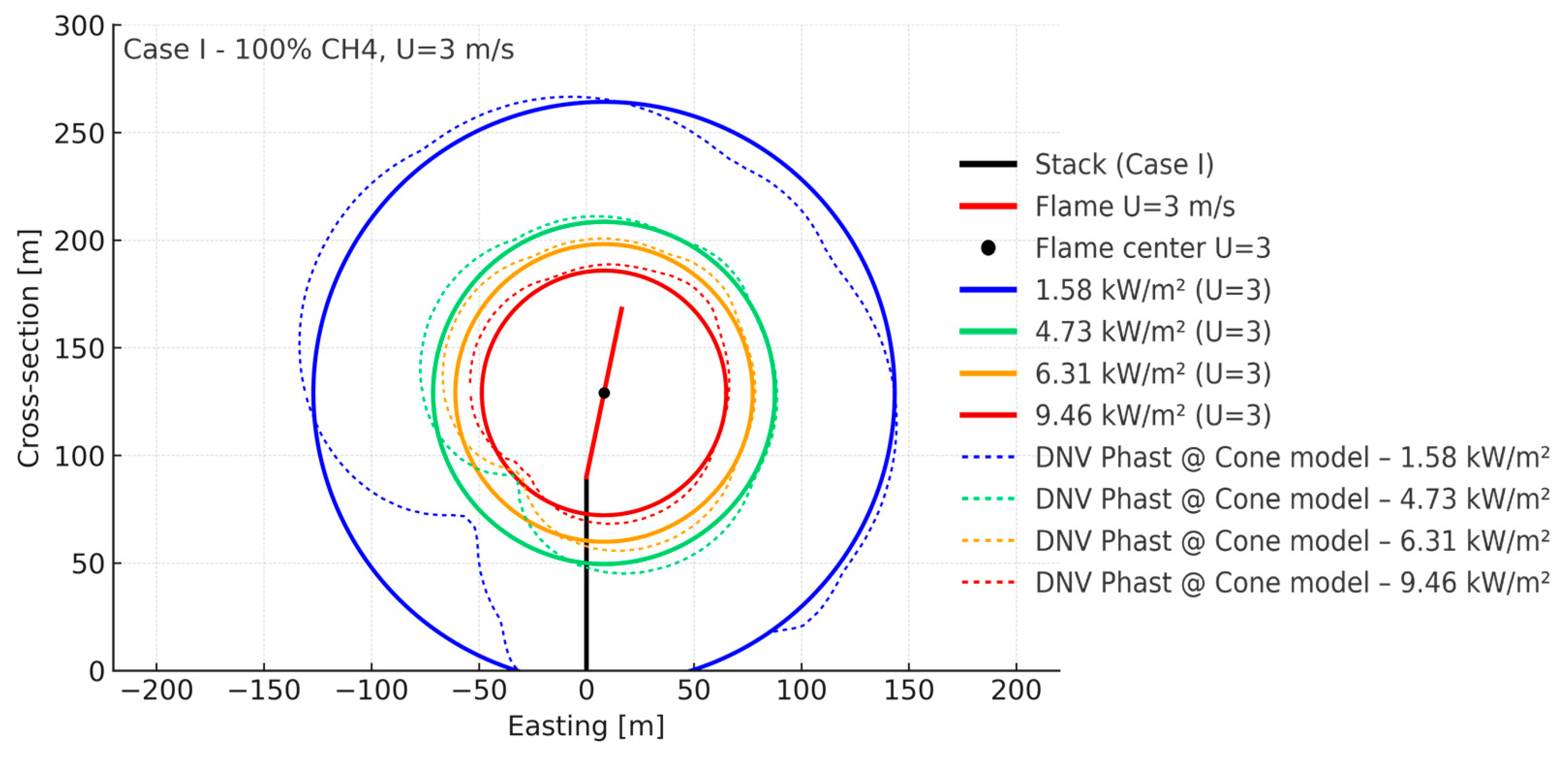
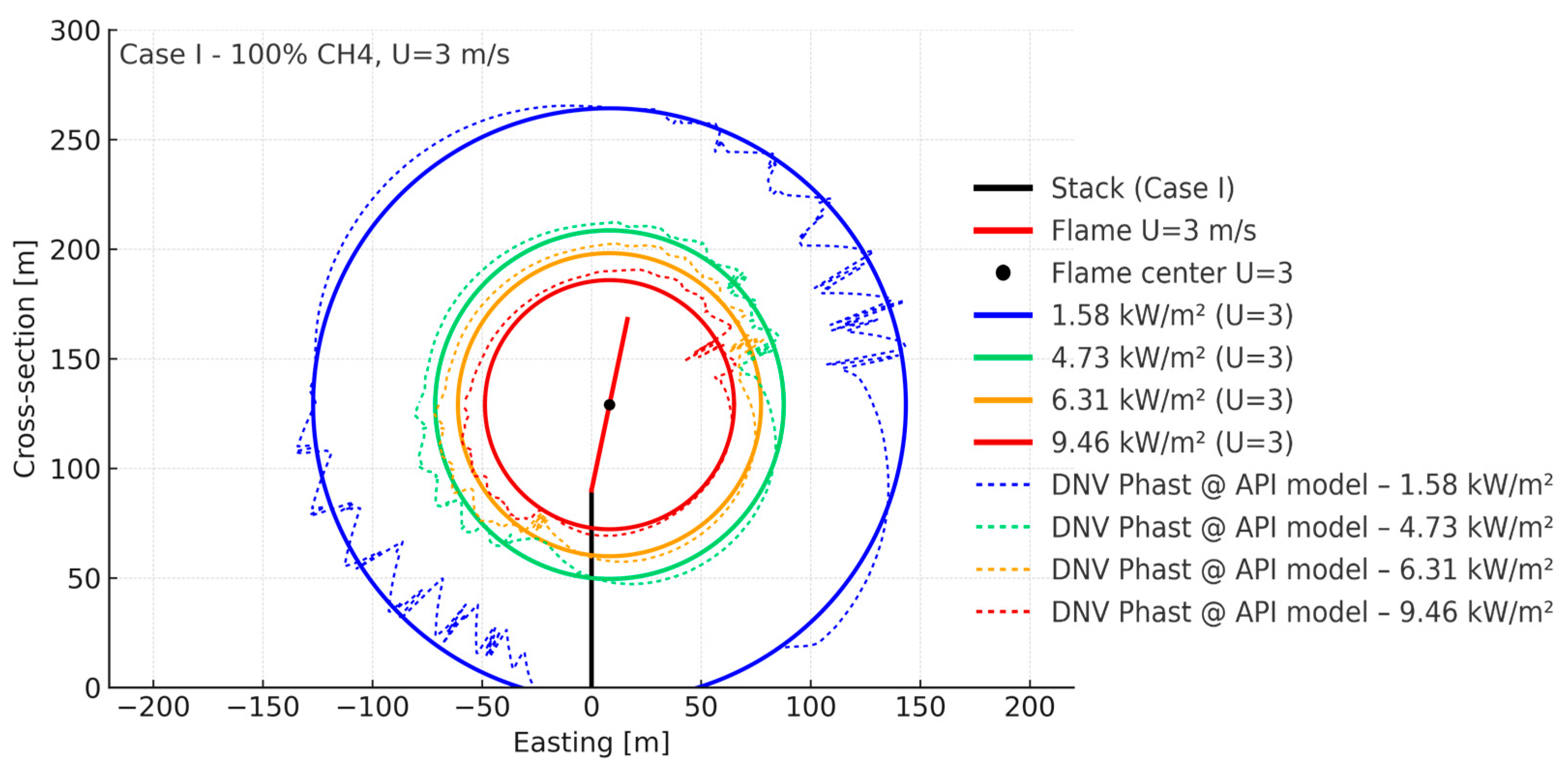
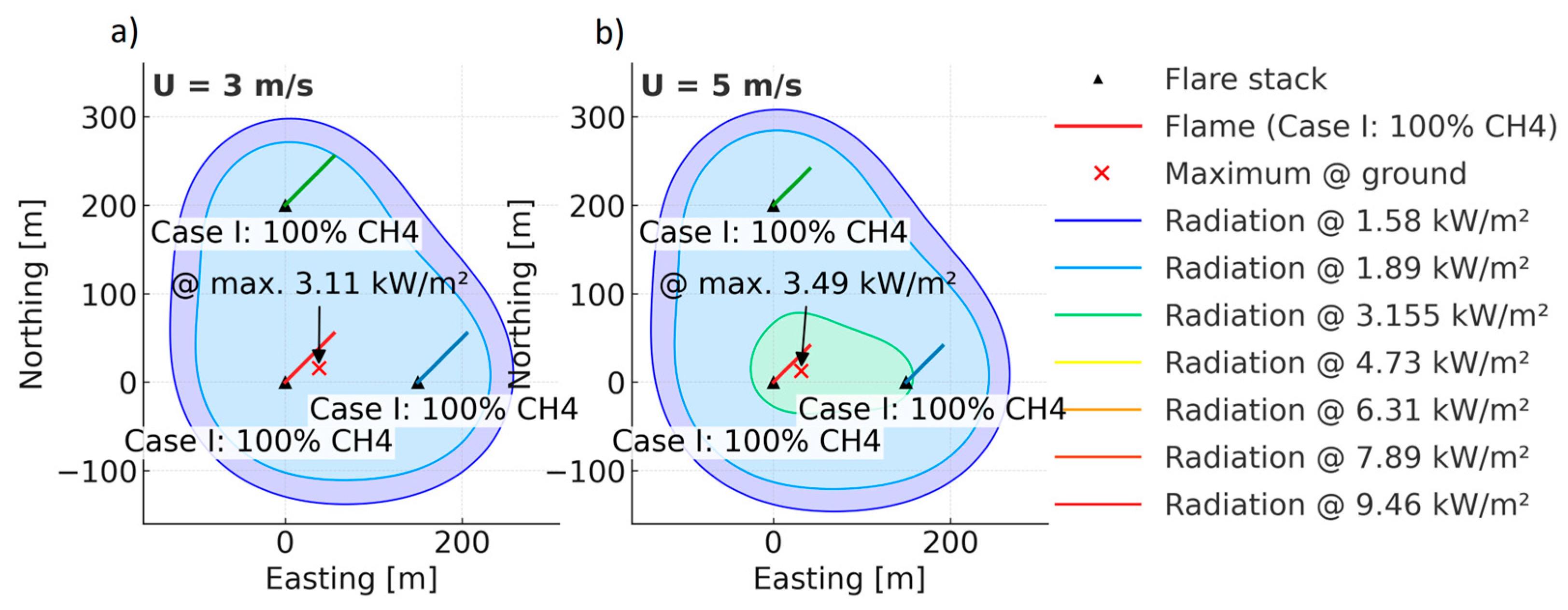
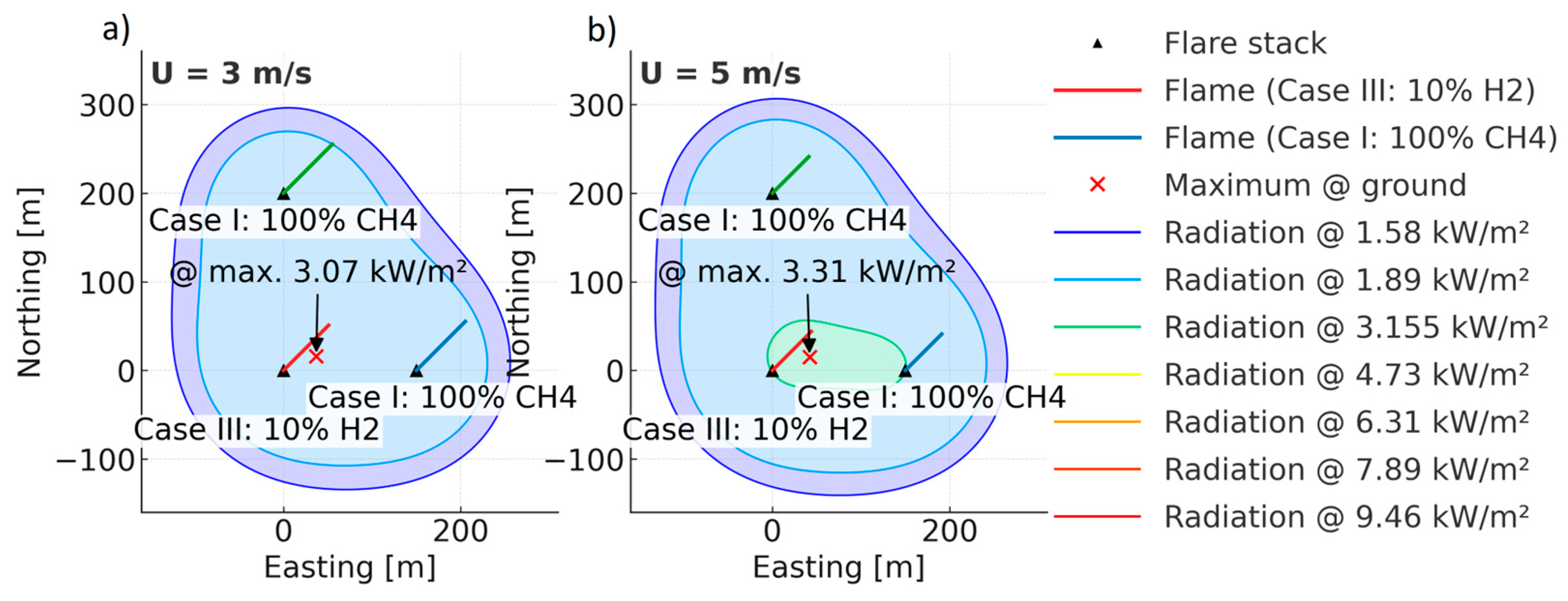
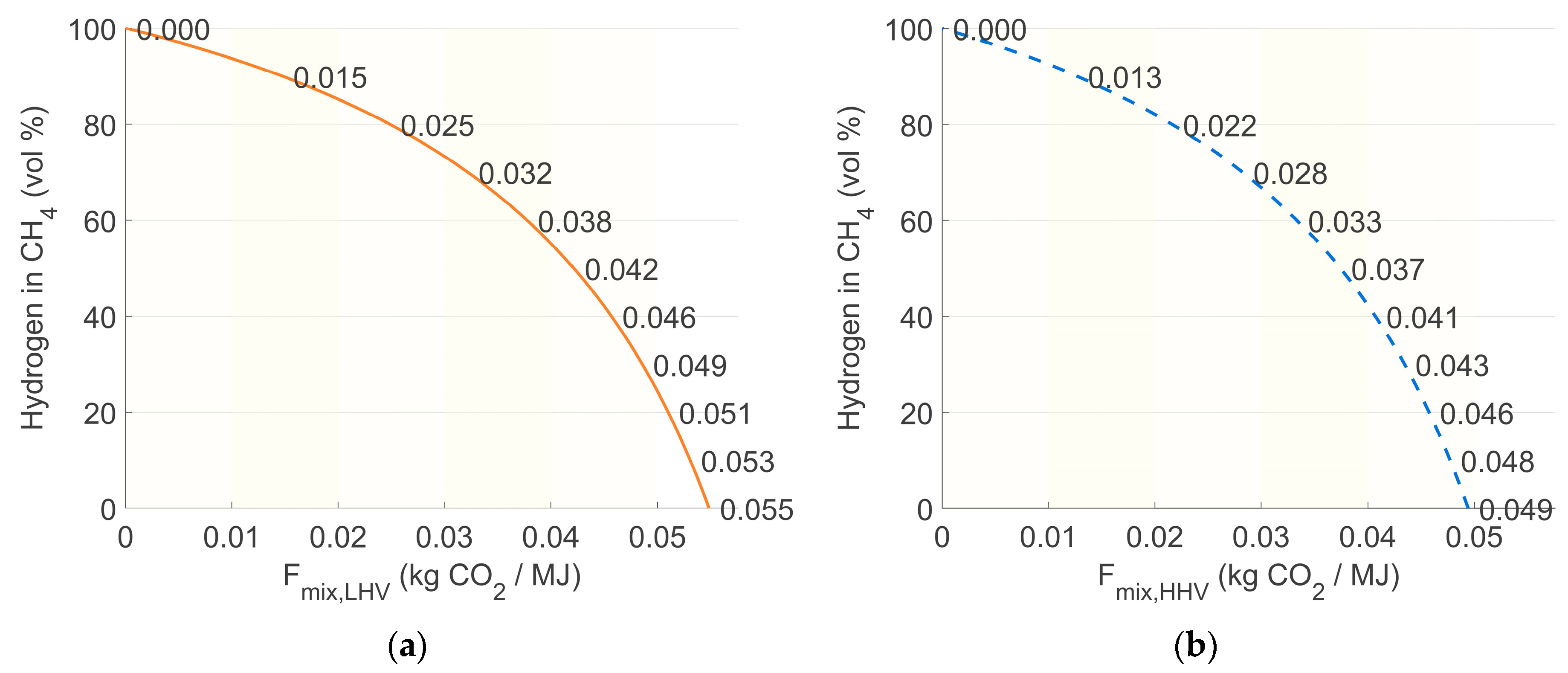
| Parameter (298 K, 1 bar) | Unit | CH4 | H2 |
|---|---|---|---|
| Lower Heating Value (LHV) 1 | (MJ·kg–1) | 35.8 | 120 |
| Higher Heating Value (HHV) 1 | (MJ·kg–1) | 55.5 | 142 |
| Density 2 | (kg·m–3) | 0.717 | 0.0899 |
| Laminar Combustion Speed 3 | (m·s–1) | 0.4 | 2.9 |
| Stoichiometric flame temperature 4 | (K) | 2497 (burning with air); 3083 (burning with pure oxygen) | 2673 |
| Lower and Upper Explosive Limit (LEL, UEL) 5 | (%) | 5–15 | 4–75 |
| Minimum Ignition Energy (MIE) 6 | (mJ) | 0.28–0.30 | 0.017–0.02 |
| Fraction of Heat Radiated 7 | (–) | 0.15–0.25 | 0.05–0.15 |
| Method | Authors/Name | Typical Applications 1 | Advantages 1 | Limitations 1 |
|---|---|---|---|---|
| Simple point source approach | Simple Approach (API Std 521, Annex C) 2 | Preliminary stack height selection | Instant calculations, minimal data required | Conservative; does not account for flame shape or wind |
| Semi-Empirical Model B&R | Brzustowski & Sommer 3 | Refineries, gas processing facilities | Includes wind, jet direction, flammability class; still in use | Requires charts/tables; calibration needed |
| Line-Surface Model Chamberlain | Chamberlain 4 | High flares onshore/offshore | Improved accuracy for luminous flares; widely used in British standards | Underestimates radiation for low luminosity gases |
| Extended “Low Luminosity” Model | Miller et al., He et al. 5 | H2-rich flaring, multi–tip ground flares | Validated via full-scale tests, 0–100 (%) H2; supports low-luminosity flames | Greater number of parameters |
| Recommended Thermal Radiation Level (kW·m–2) | Conditions |
|---|---|
| 9.46 | Maximum limit for urgent emergency actions. Personnel with proper protective clothing (e.g., fire suits) can tolerate this level only for a few seconds. |
| 6.31 | Suitable for short-duration emergency tasks, ≤30 (s) without shielding, provided appropriate clothing is worn. |
| 4.73 | Acceptable for emergency actions lasting 2–3 min with appropriate clothing but no shielding. |
| 1.58 | Continuous exposure level for personnel wearing proper work clothing. |
| Regulatory | Basis | |
|---|---|---|
| EU Monitoring & Reporting Regulation (MRR) 2018/2066, Annex VI; IPCC Guidelines 2006, Vol 2 [49] | LHV | 56.1 (kgCO2·GJ−1) |
| US EIA “Carbon Dioxide Emission Coefficients“ [50] | HHV → LHV | 52.9 (kgCO2·GJ−1) |
| Correlation | Equation |
|---|---|
| Molecular weight (−) | |
| Molar lower/higher heating value (kJ·kg−1) | |
| Mass–based lower heating value (kJ·mol−1) | |
| Hourly mass rate (kg·h−1) 1 |
| Parameter | Unit | Scenario 1 | Scenario 2 | Scenario 3 | Scenario 4 | Scenario 5 |
|---|---|---|---|---|---|---|
| in CH4/H2 blend | % (v/v) | 0 | 5 | 10 | 20 | 50 |
| (K) | 289 | 289 | 289 | 289 | 289 | |
| 9349 | 8882 | 8414 | 7479 | 4674 | ||
| 0 | 467 | 934 | 1869 | 4674 | ||
| 150,000 | 142,500 | 135,000 | 120,000 | 75,000 | ||
| 0 | 942 | 1884 | 3769 | 9424 | ||
| 150,000 | 143,442 | 136,884 | 123,769 | 84,424 | ||
| 16.043 | 15.342 | 14.640 | 13.238 | 9.030 | ||
| 5.00 | 4.94 | 4.88 | 4.76 | 4.44 | ||
| 50,000 | 50,450 | 50,956 | 52,122 | 57,813 | ||
| 55,475 | 56,042 | 56,666 | 58,105 | 65,123 |
| Unit | Scenario 1 0% (v/v) H2; 100% (v/v) CH4 | Scenario 2 10% (v/v) H2; 90% (v/v) CH4 | Scenario 3 20% (v/v) H2; 80% (v/v) CH4 | Scenario 4 30% (v/v) H2; 70% (v/v) CH4 | Scenario 5 50% (v/v) H2; 50% (v/v) CH4 | |
|---|---|---|---|---|---|---|
| Pooled MRE–DNV Phast Cone model vs. developed solver | % | 6.8 | 7.1 | 7.4 | 8.3 | 9.2 |
| Unit | Scenario 1 0% (v/v) H2; 100% (v/v) CH4 | Scenario 2 10% (v/v) H2; 90% (v/v) CH4 | Scenario 3 20% (v/v) H2; 80% (v/v) CH4 | Scenario 4 30% (v/v) H2; 70% (v/v) CH4 | Scenario 5 50% (v/v) H2; 50% (v/v) CH4 | |
|---|---|---|---|---|---|---|
| Pooled MRE–DNV Phast API model vs. developed solver | % | 7.2 | 7.8 | 8.6 | 9.6 | 10.3 |
| Scenario | H2 % (v/v) | (−) | (−) | ||
|---|---|---|---|---|---|
| I | 0 | 0.0549 | 0.0494 | – | – |
| II | 5 | 0.0540 | 0.0486 | –1.56% | –1.66% |
| III | 10 | 0.0531 | 0.0477 | –3.24% | –3.45% |
| IV | 20 | 0.0510 | 0.0458 | –7.01% | –7.44% |
| V | 50 | 0.0422 | 0.0374 | –22.18% | –24.32% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bielka, P.; Kuczyński, S.; Nagy, S. Impact of Hydrogen-Methane Blending on Industrial Flare Stacks: Modeling of Thermal Radiation Levels and Carbon Dioxide Intensity. Appl. Sci. 2025, 15, 9479. https://doi.org/10.3390/app15179479
Bielka P, Kuczyński S, Nagy S. Impact of Hydrogen-Methane Blending on Industrial Flare Stacks: Modeling of Thermal Radiation Levels and Carbon Dioxide Intensity. Applied Sciences. 2025; 15(17):9479. https://doi.org/10.3390/app15179479
Chicago/Turabian StyleBielka, Paweł, Szymon Kuczyński, and Stanisław Nagy. 2025. "Impact of Hydrogen-Methane Blending on Industrial Flare Stacks: Modeling of Thermal Radiation Levels and Carbon Dioxide Intensity" Applied Sciences 15, no. 17: 9479. https://doi.org/10.3390/app15179479
APA StyleBielka, P., Kuczyński, S., & Nagy, S. (2025). Impact of Hydrogen-Methane Blending on Industrial Flare Stacks: Modeling of Thermal Radiation Levels and Carbon Dioxide Intensity. Applied Sciences, 15(17), 9479. https://doi.org/10.3390/app15179479






