Solid-Solution Evolution Behavior of Al-Cu3-Si-Mg During the MMDF Process
Abstract
1. Introduction
2. Experimental Materials and Methods
3. Experimental Results
3.1. Microscopic Solidified Structure Under Pressure
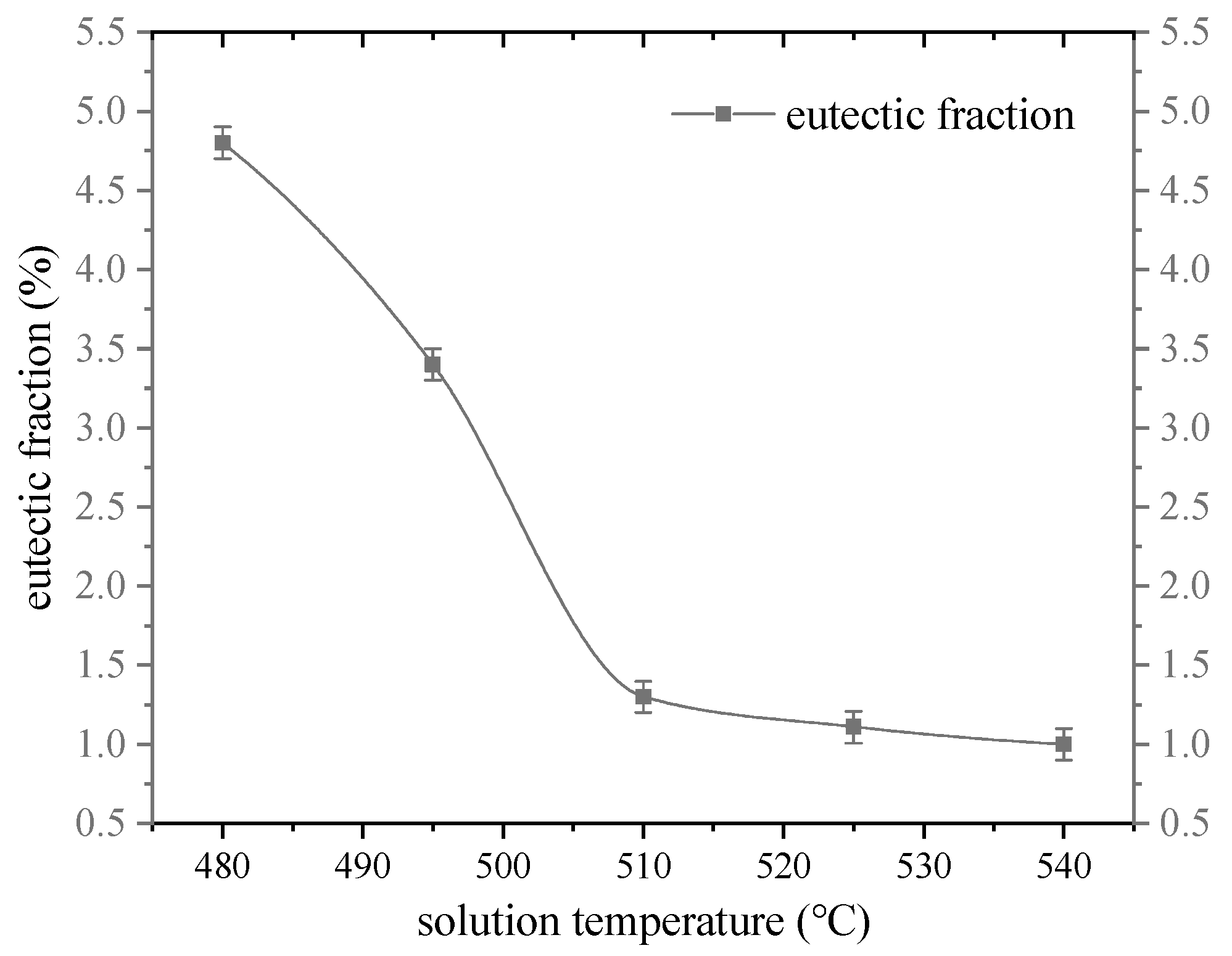
3.2. Effect of Solution Temperature on Irregular Eutectic Fraction
3.3. Effect of Solution Temperature on the Morphology and Size of the Irregular Eutectic
3.4. Effect of Solution Temperature on Compound and Second Phase
4. Discussion
4.1. Analysis of Dissolution Behavior of the Irregular Intergranular Eutectic
4.2. Kinetic Model of Irregular Eutectic Dissolution
5. Conclusions
- The as-cast microstructures of Al-Cu3-Si-Mg alloy were studied by SEM. Separated irregular eutectics (α+Al2Cu) were mainly found at the α-Al grain boundary; the irregular bright white eutectics Al2Cu were distributed separately, while the eutectic α had no obvious characteristics. Spherical granular phases θ(Al2Cu) were found in the primary α-Al. The cross-shaped phases Mg2Si grew near the grain boundaries inside the α-Al grain. Q (Al5Cu2Mg8Si6) exists at the intersection of grain boundaries.
- When the solution temperature is 480 °C~510 °C, the eutectic radius and the width of the intercrystal plate eutectic radius decrease significantly with the increase in solution temperature, decreasing, respectively, from 2.8 μm to 0.3 μm and from 2.96 μm to 0.7 μm. When the solution temperature exceeds 510 °C, the width and radius of the intercrystal plate eutectic radius do not decrease significantly with the increase in solution temperature. The diameter and quantity of the second phase θ(Al2Cu) decreased with the increase in temperature when the solution temperature was between 480 and 510 °C, decreasing from 0.78 μm to 0.19 μm and increasing from 66 μm to 120 μm. The diameter and quantity of θ(Al2Cu) do not change much when the temperature exceeds 510 °C. The morphology and diameter of the polygonal forms remained basically unchanged during the solution process, and the β (Mg2Si) near the grain boundary dissolved at 480 °C.
- The dissolution kinetics model of the intergranular irregular eutectic in the solution process was established, which was expressed by connecting solution temperature, solution time and the average width of the irregular eutectic.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, C.; Du, Y.; Liu, S.H.; Liu, S.J.; Jie, W.Q.; Sundman, B. Microstructure and Thermal Conductivity of the As-Cast and Annealed Al–Cu–Mg–Si Alloys in the Temperature Range from 25 °C to 400 °C. Int. J. Thermophys. 2015, 36, 2869–2880. [Google Scholar] [CrossRef]
- Kim, K.; Bobel, A.; Brajuskovic, V.; Zhou, B.C.; Walker, M.; Olson, G.B.; Wolverton, C. Energetics of native defects, solute partitioning, and interfacial energy of Q precipitate in Al-Cu-Mg-Si alloys. Acta Mater. 2018, 154, 207–219. [Google Scholar] [CrossRef]
- Gao, Y.-Y.; Qiu, F.; Geng, R.; Zhao, W.-X.; Yang, D.-L.; Zuo, R.; Dong, B.-X.; Han, X.; Jiang, Q.-C. Preparation and characterization of the Al-Cu-Mg-Si-Mn composites reinforced by different surface modified SiCp. Mater. Charact. 2018, 141, 156–162. [Google Scholar] [CrossRef]
- Wu, T.; Xing, S.M.; Liu, X. Study on non-equilibrium solidification microstructure of Al-Cu3-Si-Mg alloy by MMDF. Mater. Res. Express. 2022, 9, 46509. [Google Scholar] [CrossRef]
- Dang, B.; Liu, C.C.; Liu, F. Effect of solidification microstructure characteristics of A356 aluminum alloy on solution treatment process. Trans. Nonferrous Met. Soc. China 2016, 26, 635–639. [Google Scholar] [CrossRef]
- Zhou, T.; Zhou, X.Y.; Da, J.C. Effect of heat treatment process on microstructure and properties of A356 aluminum alloy. Hot Work. Technol. 2016, 45, 201–203. [Google Scholar]
- Han, Y.; Samuel, A.M.; Doty, H.W.; Valtierra, S.; Samuel, F.H. Optimizing the tensile properties of Al-Si-Cu-Mg 319-type alloys: Role of solution heat treatment. Mater. Des. 2014, 58, 426. [Google Scholar] [CrossRef]
- Lombardi, A.; Ravindran, C.; MacKay, R. Optimization of the solution heat treatment process to improve mechanical properties of 319 Al alloy engine blocks using the billet casting method. Mater. Sci. Eng. A 2015, 633, 125–135. [Google Scholar] [CrossRef]
- Lasa, L.; Rodriguez-Ibabe, J.M. Evolution of the main intermetallic phases in Al-Si-Cu-Mg casting alloys during solution treatment. J. Mater. Sci. 2004, 39, 1343–1355. [Google Scholar] [CrossRef]
- Mohamed, A.M.A.; Samuel, F.H.; Al kahtani, S. Influence of Mg and solution heat treatment on the occurrence of incipient melting in Al-Si-Cu-Mg cast alloys. Mater. Sci. Eng. 2012, 543, 22–34. [Google Scholar] [CrossRef]
- Feng, D.; Han, Z.J.; Li, J.C.; Zhang, H.; Xia, W.S.; Fan, X.; Tang, Z.H. Evolution behavior of primary phase during pre-heat treatment before deformation for sprayformed 7055 aluminum alloy. Rare Met. Mater. Eng. 2020, 49, 4253–4264. [Google Scholar]
- Dell’aVvocato, G.; Bison, P.; Palmieri, M.; Ferrarini, G.; Palumbo, D.; Tricarico, L.; Galietti, U. Non-destructive estimation of mechanical properties in Usibor® 1500 via thermal diffusivity measurements: A thermographic procedure. NDT E Int. 2023, 143, 103034. [Google Scholar] [CrossRef]
- Whelan, M.J. On the kinetics of precipitate dissolution. Met. Sci. J. 1969, 3, 95–97. [Google Scholar] [CrossRef]
- Grong, Ø.; Shercliff, H.R. Microstructural modelling in metals processing. Prog. Mater. Sci. 2002, 47, 163–282. [Google Scholar] [CrossRef]
- Liu, G.; Zhang, G.J.; Ding, X.D. A model for age strengthening of Al alloys with plate/disc-like or rod/needle-like precipitate. Rare Met. Mater. Eng. 2003, 32, 971–975. [Google Scholar]
- Liu, G.; Ding, X.D.; Sun, J. Aging strengthening model of aluminum alloy with disc precipitated phase. Trans. Nonferrous Met. Soc. China 2001, 11, 337–347. [Google Scholar]
- Hao, J.; Chen, B.; Xia, P.; Wang, Z.; Chen, Z.; Li, R. Effect of solid solution treatment on microstructure and mechanical properties of Al–Si–Cu–Mg alloy prepared by semi-solid squeeze casting. Int. J. Met. 2024, 18, 2313–2327. [Google Scholar] [CrossRef]
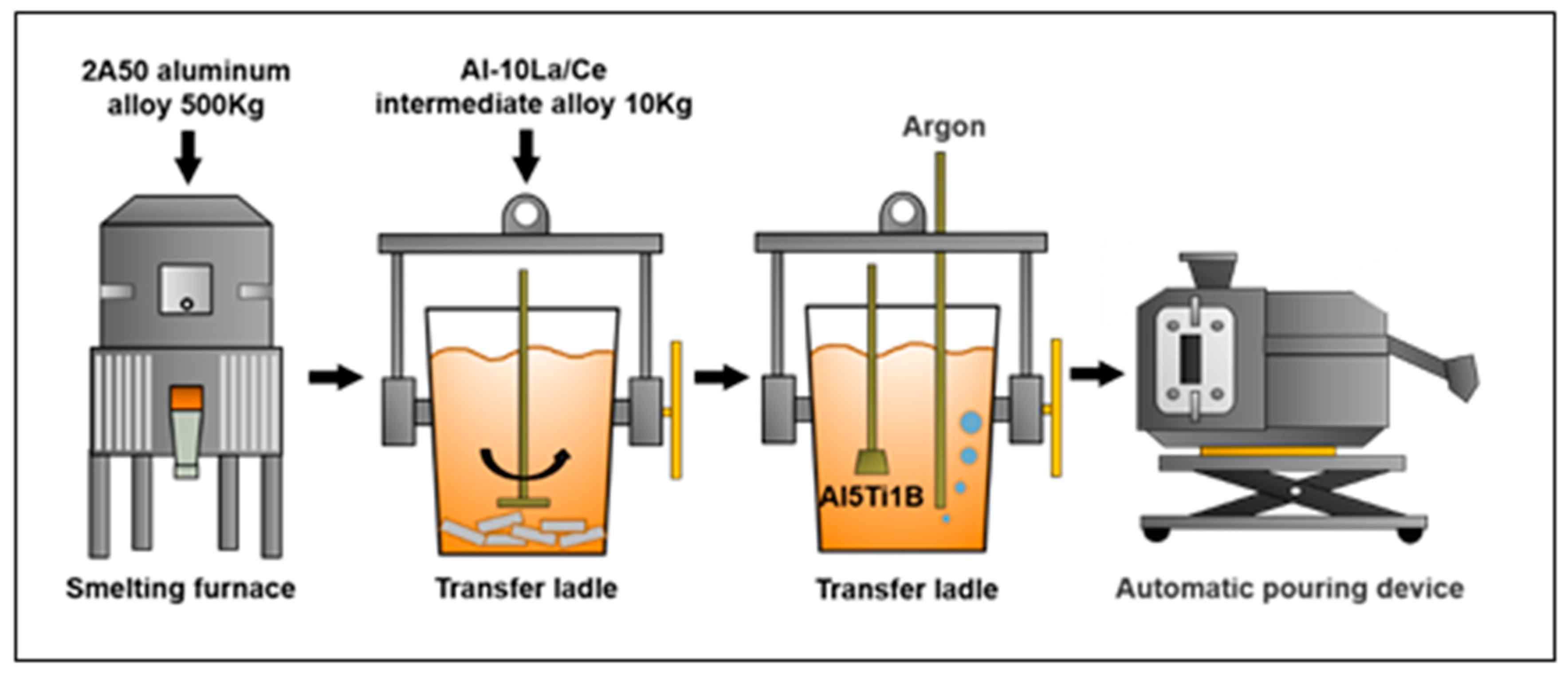
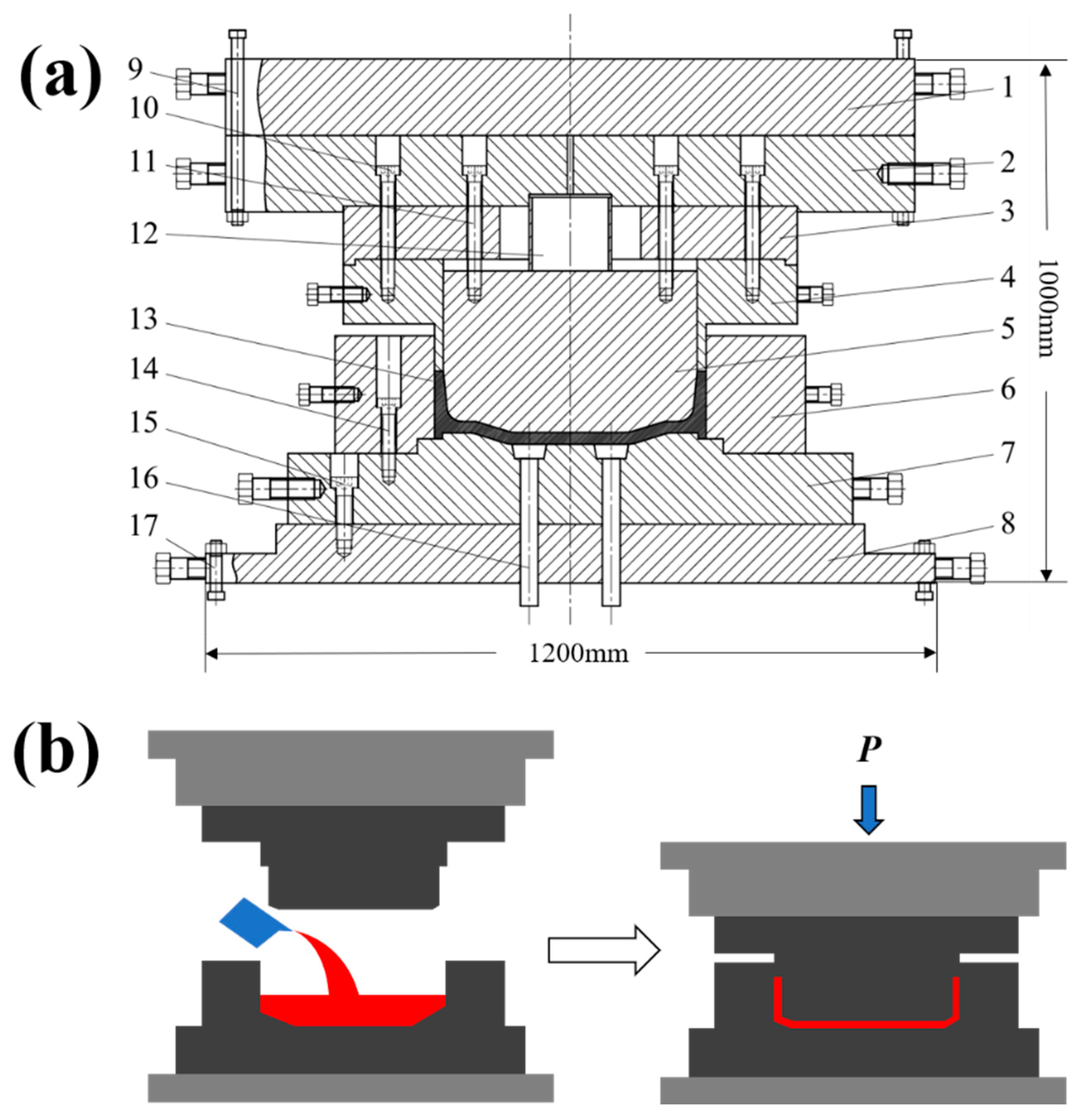








| Cu | Si | Mg | Mn | Ti | Fe | La/Ce | Al |
|---|---|---|---|---|---|---|---|
| 2.4 | 0.8 | 0.56 | 0.5 | 0.073 | 0.1 | 0.15 | Bal |
| Serial Number | Solid-Solution Treatment | |
|---|---|---|
| Heating Temperature/°C | Holding Time/min | |
| 1 | 480 | 30 |
| 2 | 495 | 30 |
| 3 | 510 | 15 |
| 4 | 510 | 30 |
| 5 | 510 | 45 |
| 6 | 510 | 60 |
| 7 | 525 | 30 |
| 8 | 540 | 30 |
| Phase | Average Grain Size/Diameter (μm) |
|---|---|
| E(α+Al2Cu) | 2.5~3 |
| Q (Al5Cu2Mg8Si6) | 2~2.5 |
| φ(AlxTi9La2Ce6Cu) | 25~30 |
| θ(Al2Cu) | 1~2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, T.; Xing, S.; Yan, G. Solid-Solution Evolution Behavior of Al-Cu3-Si-Mg During the MMDF Process. Appl. Sci. 2025, 15, 9478. https://doi.org/10.3390/app15179478
Wu T, Xing S, Yan G. Solid-Solution Evolution Behavior of Al-Cu3-Si-Mg During the MMDF Process. Applied Sciences. 2025; 15(17):9478. https://doi.org/10.3390/app15179478
Chicago/Turabian StyleWu, Tong, Shuming Xing, and Guangyuan Yan. 2025. "Solid-Solution Evolution Behavior of Al-Cu3-Si-Mg During the MMDF Process" Applied Sciences 15, no. 17: 9478. https://doi.org/10.3390/app15179478
APA StyleWu, T., Xing, S., & Yan, G. (2025). Solid-Solution Evolution Behavior of Al-Cu3-Si-Mg During the MMDF Process. Applied Sciences, 15(17), 9478. https://doi.org/10.3390/app15179478






