Abstract
With the rapid development of China’s economy, the number and scale of infrastructure projects in energy, water conservancy, and transportation have expanded significantly. Anchoring technology has been widely applied, resulting in the formation of numerous rock slope–anchoring systems. This study proposes a novel method for evaluating the stability of rock slope–anchoring systems by introducing catastrophe theory into the stability assessment framework. Based on the characteristics of the rock slope–anchoring system and its stability-influencing factors, a hierarchical analytic structure for catastrophe-level evaluation is constructed, and relevant indicator data are collected. Catastrophe models are selected according to the identified state and control variables, and catastrophe levels are computed to establish a sample dataset. The relationship between catastrophe levels and the stability coefficients of rock slope–anchoring systems is verified to define stability grade intervals. Stability evaluation is then performed by calculating the catastrophe level of each system. The results indicate that: (1) the proposed method effectively considers the influence of multiple factors on the stability of rock slope–anchoring systems, ensuring high accuracy in the evaluation. (2) The method allows for the automatic quantification of the relative importance of indicators within the same hierarchy, reducing subjectivity caused by manual weighting. (3) By standardizing state variables and computing catastrophe levels, the method couples qualitative descriptions with mechanical parameters, enhancing the objectivity of the assessment. (4) The stability evaluation method for rock slope–anchorage systems based on mathematical catastrophe theory determines system stability through catastrophe-order analysis, featuring a concise process and clear results. It enables rapid evaluation of the stability of similar rock slope–anchorage systems and offers high efficiency for cluster assessments.
1. Introduction
Rock bolting is a well-established reinforcement technique that offers reliable construction methods and effective strengthening performance. It can efficiently constrain rock mass deformation and enhance the stability of bedrock [1,2]. Due to its advantages, such as high efficiency, light weight, compact structure, and cost-effectiveness [1,2,3,4,5], anchoring technology has been widely adopted in various fields of geotechnical engineering, including mining, tunneling, and highway construction [1,2,3,4,5,6,7,8,9]. In recent years, driven by China’s rapid economic development and the large-scale expansion of infrastructure—particularly in water conservancy and transportation—combined with the widespread application of anchoring technology [1,2,10], a large number of rock slope–anchoring systems have been formed. A rock slope—anchorage system consists of a rock slope and anchorage structures that provide reinforcement. The stability evaluation of such systems has become a central issue in geotechnical engineering, as it not only determines the success or failure of engineering projects but also poses significant risks of economic loss and safety hazards.
At present, extensive research has been conducted on the stability evaluation of rock slope–anchoring systems. Existing studies have primarily employed methods such as laboratory physical model tests, numerical simulations, field monitoring data analysis, and reliability theory to analyze the stability of rock slope–anchoring systems. In terms of stability analysis based on physical model testing, Dong [11] conducted laboratory model tests to investigate the effects of different anchoring angles on the stability of toppling deformation slopes. Li [12] evaluated the degradation of stability in prestressed anchored rock slope systems under corrosive environments through model testing. Xu [13] used centrifuge shaking table model tests to study the failure evolution of rock slopes reinforced with pile–anchor systems under seismic loading. Tao [14] investigated the collapse failure characteristics of rock slopes reinforced with negative Poisson’s ratio bolts and flexible anchoring nets, as well as the overall control effectiveness of energy-absorbing reinforcement measures. In the field of numerical simulation-based analysis of rock slope–anchoring system stability, Sun [3] used two-dimensional discrete element software to evaluate the reinforcement effects of different anchoring angles on cut slopes, obtaining both the slope safety factor and the tensile forces in the anchor cables. Liu [4] conducted numerical simulations using FLAC3D V6.0 to investigate the stability of stratified rock slopes along highways reinforced with rock bolts and anchor cables. Zhang [15] developed a mechanical model for negative Poisson’s ratio (NPR) anchor cables using both FLAC3D and 3DEC, and carried out a numerical simulation of the entire landslide process. In terms of stability analysis of rock slope–anchoring systems based on monitoring data, Zhang [15] conducted monitoring and analysis of negative Poisson’s ratio (NPR) anchor cables, enabling real-time tracking and early warning of the landslide process, and revealed the sliding failure mechanisms of stratified rock slopes. Tiwari [16] assessed the instability probability of rock slope–anchoring systems by comparing crosshole seismic tomography results with field monitoring data from settlement meters and digital displacement sensors. Shi [17] introduced a remote monitoring and early warning system for anchor cable forces in landslides, aimed at detecting slope stability changes induced by water flow and rainfall infiltration. Yu [18] evaluated the sensing performance of glass fiber-reinforced polymer (GFRP) anchor rod sensors equipped with strain gauges, which are used to monitor the stability conditions of slopes. In addition, Amagu [19,20,21] analyzed the stability of mine slopes by combining surface displacement measurements with the finite element analysis method. In the context of stability analysis of rock slope–anchoring systems using limit equilibrium methods, Zheng [5] employed a limit equilibrium model to evaluate the stability of anti-toppling stratified rock slopes reinforced with rock bolts. Bi [22] treated the shear force along the potential failure surface as an external load and conducted stability evaluation through force equilibrium analysis. Yan [23] and Sun [24] integrated limit analysis and the minimum potential energy principle with the pseudo-dynamic method, and proposed seismic stability evaluation approaches for slopes that consider the dynamic variation of anchor cable axial forces. In addition, Jia [25] proposed a stability evaluation method for anchored rock slopes based on the Gaussian Mixture Model (GMM), enabling a quantitative analysis of the impact of seismic degradation effects on the stability of rock slope–anchoring systems. Fu [26] introduced a reliability-based approach to assess the failure probability of reinforced rock slopes affected by bolt corrosion. Xia [27] combined group decision-making theory with matter-element analysis to perform a comprehensive and quantitative stability evaluation of anchored slopes. Chiu [28] applied artificial intelligence algorithms to optimize rock bolt design and conducted equilibrium-based stability analysis of rock slope–anchoring systems. A summary of the stability evaluation methods for rock slope–anchoring systems is provided in Table 1.

Table 1.
Summary of Stability Evaluation Methods for Rock Slope–Anchorage Systems.
However, these evaluation methods still have several limitations. The limit equilibrium method often relies on numerous assumptions, leading to significant discrepancies between analytical conditions and actual engineering scenarios, which may result in inaccurate evaluation outcomes [30,31,32]. Moreover, the limit equilibrium method fails to account for the interaction between anchoring structures and the rock slope, which further compromises the accuracy of stability assessments for rock slope–anchoring systems. The finite element method (FEM) also encounters difficulties in modeling rock fractures and discontinuities. These features significantly affect slope stability, yet conventional FEM struggles to simulate the initiation and propagation of discontinuous elements such as cracks [32,33,34]. In terms of monitoring-based stability evaluation, the anchoring systems embedded in complex geological conditions and harsh construction environments are often difficult to monitor accurately, which compromises the reliability of the evaluation results [35]. Furthermore, partial displacements or cracking phenomena do not necessarily lead to slope failure, making it difficult to accurately assess or predict landslides through observational monitoring methods such as displacement tracking [36]. When using model testing for stability evaluation, the approach is constrained by fixed geometries and boundary conditions. In addition, the significant time and financial requirements limit its broader applicability [32]. Reliability-based methods also exhibit certain limitations when dealing with complex geological conditions [37]. Traditional reliability approaches, such as the First-Order and Second-Order Reliability Methods (FORM/SORM), require explicit performance functions and are therefore not applicable to many complex rock slope stability problems [38].
In the field of slope stability evaluation based on catastrophe theory, Zhao [39] explored the catastrophic failure mechanism of rock slopes by integrating catastrophe theory with a general constitutive equation representing the strain-softening behavior of weak interlayers. Qiao [40] developed a cusp catastrophe prediction model for locked slope failure in cold regions through theoretical analysis and determined the corresponding catastrophe characteristic values. Chang [41] established an energy-based instability criterion for jointed rock slopes using cusp catastrophe theory, and derived slope safety factors based on the theory of energy peak collapse. Zhou [42] combined slope failure energy principles with catastrophe theory to calculate the characteristic value of dissipated energy mutation, which was used to verify slope stability. Bao [43] proposed a cusp catastrophe model for open-pit slope instability based on the mechanical model of planar sliding failure, and formulated a corresponding slope instability criterion. Catastrophe theory offers significant advantages in geotechnical engineering applications. It provides an effective framework for modeling sudden instability phenomena in nonlinear systems and characterizing the nonlinear behavior of geomaterials [44]. It can accurately identify the critical transition point between stability and instability in geotechnical systems [45]. It also supports multivariable coupling analysis, allowing for the integration of various interacting parameters [46]. As a result, catastrophe theory has been widely applied in various geotechnical engineering fields, including slope stability evaluation [39], tunnel surrounding rock stability [47,48], and the assessment of rock bursts and roof stability in coal mine roadways [49].
As outlined above, the applications of catastrophe theory in slope stability evaluation and its advantages in geotechnical engineering have been summarized, along with the limitations of current methods used to assess the stability of rock slope–anchoring systems. However, relatively limited research has focused on applying catastrophe theory to the stability evaluation of rock slope–anchoring systems. This study proposes a stability evaluation method for rock slope–anchoring systems based on catastrophe theory. A hierarchical analytic structure for catastrophe-level evaluation is constructed based on the characteristics of the rock slope–anchoring system and its stability-influencing factors, and relevant indicator data are collected. The appropriate catastrophe model is determined according to state and control variables, and catastrophe levels are calculated to establish a sample dataset. The relationship between the calculated catastrophe levels and the stability coefficients of rock slope–anchoring systems is validated to define stability grade intervals. Finally, the catastrophe level of the system is computed and used for stability evaluation.
2. Evaluation Model
2.1. Evaluation Procedure
The implementation procedure of the proposed evaluation method is as follows:
- (1)
- Construct a hierarchical analytic structure for catastrophe-level evaluation based on the characteristics of the anchoring system and the stability-influencing factors.
- (2)
- Collect relevant indicator data from multiple engineering cases according to the hierarchical analytic structure.
- (3)
- Determine the appropriate catastrophe model based on the identified state and control variables.
- (4)
- Calculate the catastrophe level to construct a sample dataset.
- (5)
- Verify the relationship between the catastrophe level and the stability coefficient of the rock slope–anchoring system.
- (6)
- Define the stability grade intervals based on the computed catastrophe levels.
- (7)
- Evaluate the stability of each engineering case by calculating its corresponding catastrophe level.
The flowchart of the long-term stability evaluation method for rock slope–anchoring systems based on mathematical catastrophe theory is shown in Figure 1.
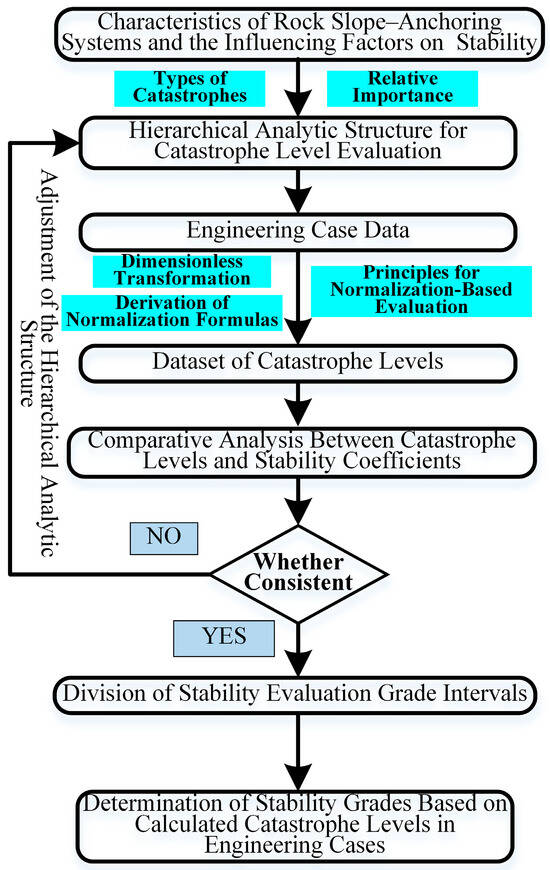
Figure 1.
Flowchart of the stability evaluation method for rock slope–anchoring systems based on catastrophe theory.
2.2. Evaluation Methodology
- (1)
- Catastrophe Theory
Catastrophe theory was systematically developed and summarized by the French mathematician René Thom [50], culminating in his seminal 1972 work Stabilité Structurelle et Morphogenèse (Structural Stability and Morphogenesis), which marks the formal establishment of catastrophe theory. The theory focuses on the phenomena and laws governing the sudden transition of a system from one stable configuration to another. It has been widely applied in analyzing and predicting the behavior of complex systems.
Among the various methods within catastrophe theory, elementary catastrophe theory and its associated models are the most commonly used. The core principle involves describing nonlinear behaviors using a potential function, and then constructing catastrophe models by combining theoretical analysis with empirical observations. These models are then used to investigate the underlying mechanisms of discontinuous phenomena.
Catastrophe theory is particularly effective in explaining discontinuous or abrupt transitions in system behavior. It also enables the analysis of unknown sudden shifts in nonlinear systems. The state of a system is typically described by state variables, which are expressed in terms of selected parameters to capture the overall system behavior.
- (2)
- Elementary Catastrophe Models
Based on Thom’s theoretical framework, the number of control variables in a system determines the type of catastrophe it may exhibit. In three-dimensional space with one-dimensional time (a system with four governing factors), seven elementary types of catastrophe can be identified: fold catastrophe, cusp catastrophe, swallowtail catastrophe, butterfly catastrophe, hyperbolic umbilic catastrophe, elliptic umbilic catastrophe, and parabolic umbilic catastrophe.
The type of model, number of state variables, number of control variables, and the associated potential functions are summarized in Table 2.

Table 2.
Summary of Common Elementary Catastrophe Models.
- (3)
- Catastrophe Progression Method
The catastrophe progression method is a comprehensive evaluation approach based on catastrophe theory and fuzzy mathematics. It utilizes normalization formulas derived from catastrophe models to assess complex systems holistically. The core idea of the method is to treat the evaluation problem and its influencing factors as an integrated system. A structured evaluation model is established for this system, which is then decomposed into hierarchical layers. Each layer contains multiple evaluation indicators, and their numerical values are normalized using the appropriate catastrophe model formulas. By normalizing the control variables at each level, the original multi-indicator problem is simplified into a single-parameter system, upon which a comprehensive evaluation is performed.
The implementation process of the catastrophe progression method includes the following steps:
- (1)
- Constructing a Hierarchical Evaluation Model
According to the influence relationships among the evaluation indicators and their effect on the target system, a hierarchical structure model of the evaluation system is constructed. The system is decomposed layer by layer based on internal correlations. Within each layer, indicators are ranked according to their relative importance: indicators with a stronger influence on system stability are placed higher, while those with less influence are ranked lower.
- (2)
- Identifying Catastrophe Models for Each Layer
Based on the catastrophe evaluation model established in Step (1), and with reference to the elementary catastrophe types listed in Table 2, a corresponding basic catastrophe model is assigned to each layer of the hierarchical structure according to the nature of the evaluation indicators.
- (3)
- Dimensionless Normalization of Indicators
Since the indicators used in the evaluation often have different physical dimensions and units, normalization is necessary to eliminate the effects of scale and dimensional inconsistency. After quantifying the bottom-layer indicators, normalization is performed using standard formulas to convert all values to a dimensionless scale within the range [0, 1], enabling direct comparison between different indicators.
- (4)
- Deriving the Normalization Formulas
In catastrophe theory, the potential function is a scalar function whose stationary points correspond to the equilibrium states of the system. Catastrophic changes occur when variations in the control parameters induce topological changes in the potential function’s surface, such as the merging or disappearance of equilibrium points. The normalization formula is derived from the potential function F(x) of the selected catastrophe model. By taking the first derivative (F′(x) = 0), the equilibrium surface equation is obtained. Taking the second derivative (F″(x) = 0) yields the singularity set of the equilibrium surface. By solving the system of equations F′(x) = 0 and F″(x) = 0 simultaneously, the bifurcation set equation of the catastrophe model is derived. If the control variables meet the conditions defined by this bifurcation set, the system is expected to undergo a catastrophic transition. The normalization formula is ultimately derived from the bifurcation set.
Common normalization formulas for standard catastrophe models are summarized in Table 3.

Table 3.
Summary of Common Normalization Formulas for Catastrophe Models.
- (5)
- Normalization-Based Comprehensive Evaluation Principles
The catastrophe progression method adopts three main principles for comprehensive evaluation based on the normalized control variables:
① Non-Compensatory Principle:
When the influence of each control variable is independent and non-substitutable, i.e., one variable cannot compensate for the weakness of another, the non-compensatory principle is applied. In this case, the minimum value among the control variables is selected as the overall evaluation result.
② Compensatory Principle:
When control variables can compensate for each other’s deficiencies and form a mutually reinforcing relationship, the compensatory principle is used. This allows the evaluation index X to reach a relatively high average level. The arithmetic mean of the normalized values is taken as the comprehensive result.
③ Threshold-Based Compensatory Principle:
A third approach extends the compensatory principle by introducing a threshold condition. Only when all control variables exceed a specified threshold can mutual compensation occur. Under this threshold-based compensatory principle, the average value is taken only if all indicators meet the required threshold level, ensuring that the system exhibits robust performance across all variables before compensation is allowed.
3. Case Study
3.1. Engineering Situation
The hydropower project is located in the lower reaches of the Jinsha River (between Panzhihua and Yibin) and is one of the four cascade hydropower stations along this section. The dam site is approximately 45 km upstream from Qiaojia County. The normal storage level of the reservoir is designed at 825 m, and the dam crest elevation is 834 m. The project features a double-curvature concrete arch dam with a dam height of 289 m. The rock slope–anchoring system of the stilling basin is situated downstream of the dam. The cross-sectional design adopts a flat-bottomed, compound trapezoidal profile, as illustrated in Figure 2. The elevation of the stilling basin floor is 560 m, with a total length of 400 m and a base width of 80 m. The slopes on both sides of the floor are excavated at a 1:1 inclination (1:0.6 to 1:1 on the right bank). Walkways with a width of 5 m are installed at elevations of 580 m and 601 m, respectively. The slopes above the stilling basin extend from 0 to 900 m downstream of the dam. On the left bank, the elevation ranges from 634 m to 950 m, while on the right bank, it exceeds 1100 m starting from 634 m.

Figure 2.
Rock slope–anchoring system of the stilling basin in a hydropower project in Southwest China.
The slopes on both banks of the dam site are predominantly composed of Upper Permian Emeishan Formation basalt. On the right bank, the basalt is overlain by Lower Triassic Feixianguan Formation sandstone and mudstone, which are in a pseudo-conformable contact with the underlying basalt. The basalt exhibits high rock strength and good rock mass integrity, contributing to relatively favorable slope stability conditions. However, the upper portion of the right bank slope is characterized by the presence of siltstone, argillaceous siltstone, and mudstone, which are relatively weak in lithology and unfavorable for slope stability. Quaternary unconsolidated deposits are mainly distributed across the riverbed and the gentle terrace slopes on both banks. The left-bank plunge pool and the upper slopes are mainly composed of the third and fourth basalt lava flows of the Emeishan Formation. Above an elevation of 800 m, the subunit is exposed, consisting of microcrystalline basalt, amygdaloidal basalt, and agglomerate lava, with hard rock quality. Between elevations of 800–780 m, the subunit is exposed, consisting of cryptocrystalline basalt, agglomerate lava, microcrystalline basalt, and amygdaloidal basalt, with the basal cryptocrystalline basalt containing well-developed third-type columnar joints. Between elevations of 780–740 m, the underlying bedrock is the subunit, composed of plagioclase-porphyritic basalt and agglomerate lava. Between elevations of 740–700 m, the subunit is exposed, consisting of amygdaloidal basalt, cryptocrystalline basalt, and agglomerate lava, with a 0.30 m thick tuff layer at the top, which is weak in rock quality and prone to argillation upon water exposure. Below an elevation of 700 m, the subunit is exposed, composed of columnar-jointed basalt with well-developed first-type columnar joints and microfractures within the columns. The upper part contains a more than 10 m thick amygdaloid-bearing basalt layer. Near the secondary dam area, the subunit is exposed, consisting of second-type columnar-jointed basalt and agglomerate lava. The engineering geological cross-section is illustrated in Figure 3. The engineering geological profile of the rock slope–anchorage system in the left-bank plunge pool of the specific study area in this engineering case is shown in Figure 4.

Figure 3.
Engineering geological cross-section.
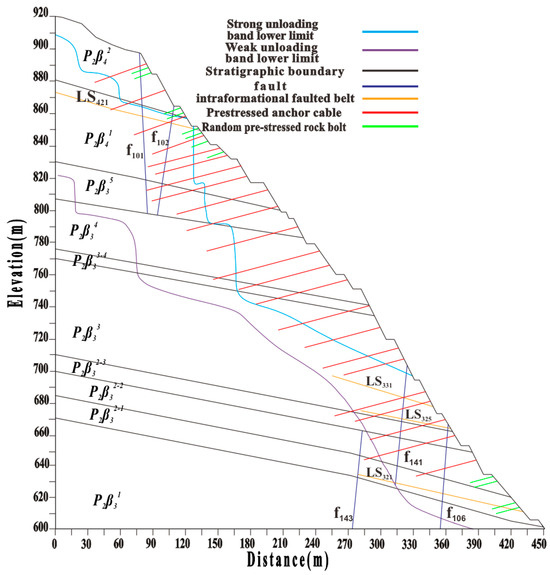
Figure 4.
Engineering geological cross-section of the rock slope at the stilling basin.
3.2. Construction of the Catastrophe Progression Evaluation Model
Based on the characteristics of the engineering case, a catastrophe progression evaluation model is constructed using four commonly applied elementary catastrophe models: the fold, cusp, swallowtail, and butterfly models. A hierarchical analytical structure for the long-term stability evaluation of the anchored rock slope system on the left-bank stilling basin of the Hydropower Project is developed accordingly. The structure is illustrated in Figure 5.
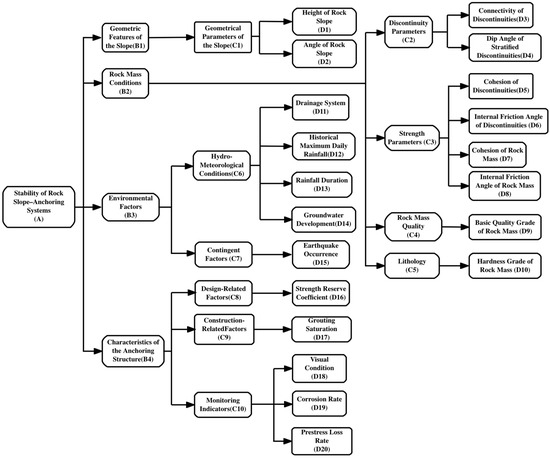
Figure 5.
Hierarchical structure of catastrophe progression-based stability evaluation for the rock slope–anchoring system.
3.3. Construction of Catastrophe Progression Evaluation Samples
Due to the limited field data, it was not possible to construct a sufficient number of samples using actual engineering case data. This study establishes a set of evaluation samples based on site investigation reports, laboratory test data, and design documentation. A numerical analysis model was constructed using discrete element analysis software. By varying key parameter values within the model, a total of 40 analysis samples were generated. The numerical model constructed based on the engineering case is illustrated in Figure 6, Figure 7 and Figure 8.

Figure 6.
Stratigraphic Distribution in the Numerical Model.

Figure 7.
Distribution of Unloading Zones in the Numerical Model.

Figure 8.
Layout of Anchor Cables and Distribution of Structural Surfaces. (a) Anchor Cable Layout Diagram of the Rock Slope–Anchorage System; (b) Distribution of Structural Planes in the Rock Slope–Anchorage System.
Based on the engineering case data and the Technical Specification for Prestressed Anchoring in Hydraulic Structures (SL/T 212-2020) issued by the Ministry of Water Resources of the People’s Republic of China [51], the design and construction of prestressed anchors for hydraulic structures are standardized. This specification outlines the fundamental requirements for anchorage design and implementation, including materials and equipment, anchor design, anchorage layout, protective measures, construction techniques, safety monitoring, anchorage testing, and quality inspection. Based on engineering data, field and laboratory tests, and the Technical Specification for Prestressed Anchoring in Hydraulic Structures (SL/T 212-2020) [51], the calculation parameters of the numerical model are shown in Table 4, Table 5 and Table 6.

Table 4.
Parameter Values for Anchor Cables.

Table 5.
Summary Table of Rock Mass Parameter Values.

Table 6.
Summary Table of Structural Plane Parameter Values.
3.4. Determination of Utility Function Values for Bottom-Layer Evaluation Indicators
Since the units of the evaluation indicators vary, a dimensionless transformation is required to standardize the data prior to analysis. The utility function values for each indicator across all samples are calculated using Equations (1) and (2).
For the larger, the better indicators
r = x/ximax
For the smaller, the better indicators
where x denotes the value of a bottom-layer factor in any given test sample, ximax represents the maximum value of the same bottom-layer factor among all samples, and xjmin is the corresponding minimum value across all samples.
r = xjmin/x
3.5. Calculation of Catastrophe Progression Values for the Rock Slope–Anchoring System
Based on the identified structural characteristics, the catastrophe models are assigned as follows: indicators D9, D10, D15, D16, D17, and C1 are categorized under the fold catastrophe model; pairs D1 and D2, D3 and D4, as well as C6 and C7, fall under the cusp catastrophe model; indicators D18 to D20 and C8 to C10 correspond to the swallowtail catastrophe model; and indicators D5 to D8, D11 to D14, C2 to C5, and B1 to B4 are assigned to the butterfly catastrophe model. Each set is evaluated using the appropriate normalization formula presented in Section 2. A total of 40 sample datasets were generated accordingly.
3.6. Result Analysis
Based on the catastrophe progression values and the corresponding stability coefficients obtained from the constructed samples, the relationship between the stability coefficient and the catastrophe progression of the rock slope–anchoring system is analyzed. The results are illustrated in Figure 9.

Figure 9.
Relationship between the stability coefficient and catastrophe progression of the rock slope–anchoring system.
- (1)
- Correlation Analysis
The Pearson correlation coefficient is a widely used statistical metric for measuring the strength and direction of the linear relationship between two continuous variables. Its value ranges from −1 to +1, with values closer to ±1 indicating a stronger linear relationship, and values near 0 suggesting a weak or no linear relationship. The calculation formula is shown in Equation (3). To assess the statistical significance of the correlation coefficient, a two-tailed significance test is typically conducted. The null hypothesis assumes no correlation between the variables, while the alternative hypothesis suggests a significant correlation exists. The corresponding p-value indicates the probability of obtaining the observed correlation coefficient, or a more extreme value, under the assumption that the null hypothesis is true. When the p-value is less than commonly used significance levels (e.g., 0.05 or 0.01), the correlation is considered statistically significant.
where r is the Pearson correlation coefficient; xi and yi are the observed values of the two variables; n is the number of samples; and , denote the mean values of the respective variables.
A Pearson correlation analysis was performed between the stability coefficient of the rock slope–anchoring system and the catastrophe progression value, resulting in a correlation coefficient of 0.9161, indicating a strong positive linear relationship between the two variables. Furthermore, the two-tailed significance test yielded a p-value of less than 0.001, demonstrating that the correlation is statistically significant at the 0.1% significance level. A linear regression analysis was then conducted, with the catastrophe progression value plotted on the X-axis and the slope stability coefficient on the Y-axis. The resulting Pearson correlation plot is shown in Figure 10.
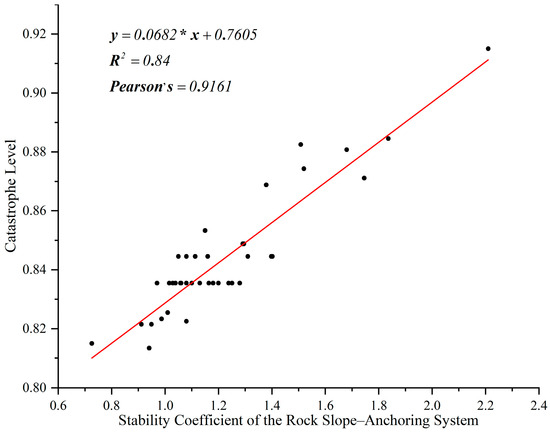
Figure 10.
Pearson correlation analysis between the stability coefficient and catastrophe progression of the rock slope–anchoring system.
Figure 9 presents the scatter plot and linear regression trend line between the stability coefficient and the catastrophe progression value of the rock slope—anchoring system. A clear positive correlation trend is observed, with data points closely clustered around the fitted line, further validating the consistency and reliability of the observed trend. The calculated Pearson correlation coefficient is r = 0.9161, indicating a strong positive linear relationship between the two variables.
- (2)
- Analysis Results
Based on Figure 9 and Figure 10, as well as the correlation analysis, it is evident that the catastrophe progression value and the stability coefficient of the rock slope–anchoring system exhibit a consistent trend. Therefore, the catastrophe progression value A, obtained using the catastrophe series method, can be used as a reliable indicator to assess the long-term stability of the rock slope–anchoring structure. As shown in Figure 10, the catastrophe progression values range from 0.8134 to 0.915. This range is divided into five stability levels, as detailed in Table 7.

Table 7.
Stability classification of rock slope–anchoring systems based on catastrophe progression values.
3.7. Stability Evaluation of the Energy Dissipation Basin Rock Slope–Anchoring System
By substituting the index parameters of the rock slope–anchoring system in the energy dissipation basin of the hydropower project into the evaluation model, the calculated catastrophe progression value A is 0.8875. According to Table 7, which defines the stability classification for rock slope–anchoring systems, the long-term stability level of this system is determined to be Level IV, corresponding to a Basically Safe condition.
4. Discussion
The stability evaluation method for rock slope–anchoring systems proposed in this study introduces catastrophe theory into geotechnical stability analysis, enabling the assessment of system behavior from the perspective of sudden transitions. By employing potential function models—such as the cusp catastrophe and butterfly catastrophe—the method quantitatively characterizes the critical transition process from stable to unstable states. This approach allows for automatic quantification of the relative importance of indicators at the same hierarchical level, effectively eliminating subjectivity errors introduced by manual weighting in conventional methods such as Analytic Hierarchy Process (AHP) and fuzzy comprehensive evaluation. Through the standardization of state variables and the calculation of catastrophe progression values, the model achieves a coupling analysis of qualitative descriptors and mechanical parameters, thereby enhancing the objectivity of the evaluation. Compared with finite element methods (FEMs), which require complex meshing, or limit equilibrium methods that rely on simplifying assumptions, catastrophe theory derives instability criteria directly from potential functions, making the evaluation process more straightforward and the results more interpretable. Furthermore, this method enables rapid and efficient evaluation of similar rock slope–anchoring systems, demonstrating cluster-level applicability.
The application of mathematical catastrophe theory in evaluating the stability of rock slope–anchoring systems primarily lies in the identification and analysis of stability transition points. Traditional evaluation models often rely on linear assumptions, which can lead to inaccuracies under complex geological conditions. In contrast, catastrophe theory can effectively capture the nonlinear response and critical transitions of rock slope–anchoring systems under variations in external load or environmental conditions, especially as the system approaches instability. This significantly improves the accuracy and reliability of the stability evaluation. The proposed method offers both theoretical significance and practical applicability. Compared to conventional numerical simulation techniques such as FEM or the Discrete Element Method (DEM), the incorporation of catastrophe theory allows the model to handle sudden behavioral changes under complex conditions with greater flexibility. Moreover, the automatic weighting mechanism reduces dependence on subjective inputs, further enhancing evaluation precision. However, certain limitations exist. Catastrophe theory is relatively sensitive to initial conditions, and under scenarios with high parameter uncertainty—such as poorly characterized rock slopes—the evaluation results may become unstable. To mitigate this, future research should incorporate uncertainty analysis and probabilistic approaches to improve model robustness. Although the method reduces computational complexity compared to FEM, it still heavily depends on reliable engineering data, which poses challenges in data-scarce regions. In this study, for example, sample data were derived from numerical simulations rather than field-measured data, which may introduce discrepancies in the final stability assessment. Future work may explore transfer learning techniques to address data scarcity and enhance the generalizability of the model.
While the proposed catastrophe-theory-based evaluation method exhibits clear theoretical and practical advantages, several aspects merit further development. First, validation and calibration using real-world engineering case studies are essential. Future research may incorporate small-sample verification techniques or transfer learning to overcome limited data availability. Second, with the rapid advancement of big data and artificial intelligence, integrating catastrophe theory with machine learning and deep learning could facilitate automated assessment and intelligent prediction of complex slope–anchoring systems. The hierarchical analysis structure for catastrophe-order stability evaluation of the rock slope–anchorage system involves multiple indicators, each with varying degrees of influence on stability. Identifying the key indicators is of great significance for the overall stability analysis and remediation of the system. Therefore, future work will focus on research related to the importance evaluation of indicators within the catastrophe-order hierarchical analysis structure. Lastly, considering regional differences in geological conditions, tailoring the evaluation model to local characteristics will be a critical direction for future refinement and application.
5. Conclusions
This study proposes a stability evaluation method for rock slope—anchoring systems based on catastrophe theory. Taking a hydropower project in the lower reaches of the Jinsha River as a case study, the characteristics of the anchoring system and multiple influencing factors on stability were considered. The main conclusions are as follows:
- (1)
- The evaluation method proposed in this study takes into account the characteristics of rock slope–anchoring systems and the influence of multiple factors on their stability. The findings indicate that the method is well-suited for assessing the stability of such systems and yields accurate evaluation results.
- (2)
- The stability evaluation method for rock slope–anchoring systems based on mathematical catastrophe theory enables the automatic quantification of the relative importance of indicators within the same hierarchy, thereby avoiding the subjectivity introduced by manual weighting in traditional approaches. By standardizing state variables and calculating catastrophe levels, the method effectively couples qualitative descriptions with mechanical parameters, enhancing the objectivity of the assessment.
- (3)
- The stability evaluation method for rock slope–anchorage systems based on mathematical catastrophe theory assesses system stability through catastrophe-order analysis, featuring a concise process and clear results. It enables rapid screening of similar rock slope–anchorage systems, making it suitable for regional slope stability evaluations and offering high efficiency in cluster assessments.
Author Contributions
P.X.: Conceptualization, Funding acquisition, Methodology, Project administration, Writing—original draft, Writing—review and editing, Supervision, Resources. B.Z.: Formal analysis, Data curation, Investigation, Software, Visualization, Writing—original draft. J.L.: Formal analysis, Data curation, Investigation, Visualization, Writing—original draft. Y.P.: Formal analysis, Data curation, Resources, Validation, Writing—review & editing. X.Y.: Formal analysis, Data curation, Resources, Validation, Writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by The National Natural Science Foundation of China grant number 42407225, Key Research and Development Program of Xinjiang Uygur Autonomous Region grant number 2023B03004-1, Fujian Provincial Education Department Foundation grant number JAT231047, Xiamen Science and Technology Subsidy Project grant number 2024CXY0319, Research Start-up Fundation of Jimei University grant number ZQ2023019, and the APC was funded by the National Natural Science Foundation of China (No. 42407225).
Data Availability Statement
The datasets generated during and/or analyzed during this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
Authors Peng Xia and Jie Liu were employed by the company Xinjiang Transportation Science Research Institute Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- He, M.; Ren, S.; Guo, L.; Lin, W.; Zhang, T.; Tao, Z. Experimental study on influence of host rock strength on shear performance of Micro-NPR steel bolted rock joints. Int. J. Rock. Mech. Min. Sci. 2022, 159, 105236. [Google Scholar] [CrossRef]
- Xia, P.; Zeng, B.; Pan, Y. Stability Evaluation Method for Rock Slope-Anchorage Systems Based on Genetic Algorithms and Discrete Element Analysis. Appl. Sci. 2025, 15, 5057. [Google Scholar] [CrossRef]
- Sun, C.; Chen, C.; Liu, C.; Yuan, J.; Zheng, Y. Stability Assessment of Bolt-Supported Road Cutting Dip Slopes Using Discrete-Element and Limit-Analysis Methods. Int. J. Geomech. 2024, 24, 04024017. [Google Scholar] [CrossRef]
- Liu, Y.; Lai, J.; Xu, J. Study on slope monitoring and stability based on bolt–cable combined support. Buildings 2024, 14, 886. [Google Scholar] [CrossRef]
- Zheng, Y.; Chen, C.; Meng, F.; Fu, X.; Yuan, W. Smart and fast reinforcement design for anti-dip bedding rock slopes. J. Rock Mech. Geotech. Eng. 2023, 15, 2943–2953. [Google Scholar] [CrossRef]
- Ma, S.; Zhao, Z.; Shang, J. An analytical model for shear behaviour of bolted rock joints. Int. J. Rock Mech. Min. Sci. 2019, 121, 104019. [Google Scholar] [CrossRef]
- Pei, S.F.; Hao, W.F.; Fan, Y.L.; Chen, H.; Li, W.T. Operation condition of anchoring system in large-scale water conservancy and hydropower projects. J. Changjiang River Sci. Res. Inst. 2024, 41, 142–150. (In Chinese) [Google Scholar]
- Wen, L.; Huang, L.; Xiang, X.; Yang, X.Z.; Zhang, G.C. Research status and development trend of geotechnical anchorage technology in hydropower projects. Saf. Environ. Eng. 2023, 30, 35–45. (In Chinese) [Google Scholar]
- Deng, D.P.; Li, L.; Zhao, L.H. Stability analysis of slopes reinforced with anchor cables and optimal design of anchor cable parameters. Eur. J. Environ. Civ. Eng. 2021, 25, 2425–2440. [Google Scholar] [CrossRef]
- Jia, Z.; Tao, L.; Bian, J.; Wen, H.; Wang, Z.; Shi, C.; Zhang, H. Research on influence of anchor cable failure on slope dynamic response. Soil Dyn. Earthq. Eng. 2022, 161, 107435. [Google Scholar] [CrossRef]
- Dong, M.; Zhang, F.; Hu, M.; Liu, C. Study on the influence of anchorage angle on the anchorage effect of soft-hard interbedded toppling deformed rock mass. KSCE J. Civ. Eng. 2020, 24, 2382–2392. [Google Scholar] [CrossRef]
- Li, C.; Zhang, R.-T.; Zhu, J.-B.; Liu, Z.-J.; Lu, B.; Wang, B.; Jiang, Y.-Z.; Liu, J.-S.; Zeng, P. Model test of the stability degradation of a prestressed anchored rock slope system in a corrosive environment. J. Mt. Sci. 2020, 17, 2548–2561. [Google Scholar] [CrossRef]
- Xu, X.; Huang, Y.; Yashima, A.; Du, X. Failure evolution process of pile-anchor reinforced rock slope based on centrifuge shaking table tests. Eng. Geol. 2022, 311, 106920. [Google Scholar] [CrossRef]
- Tao, Z.; Zhang, T.; Zhu, D.; Gong, W.; He, M.; Ferreira, T. Physical modeling test on deformation and failure of rock slope with new support system. Adv. Civ. Eng. 2020, 2020, 8825220. [Google Scholar] [CrossRef]
- Zhang, K.; Yang, X.; Cui, X.; Wang, Y.; Tao, Z.; Jin, J. Numerical Simulation Analysis of NPR Anchorage Monitoring of Bedding Rock Landslide in Open-Pit Mine. Adv. Civ. Eng. 2020, 2020, 8241509. [Google Scholar] [CrossRef]
- Tiwari, G.; Latha, G.M. Stability analysis and design of stabilization measures for Chenab railway bridge rock slopes. Bull. Eng. Geol. Environ. 2020, 79, 603–627. [Google Scholar] [CrossRef]
- Shi, G.; Gu, G.; Zhou, H.; Tao, Z.; Pan, H.; Tang, T.; Yin, Q. Stability monitoring and analysis of high and steep slope of a hydropower station. Geofluids 2020, 2020, 8840269. [Google Scholar] [CrossRef]
- Yu, J.-D.; Lee, J.-S.; Tamang, B.; Park, S.; Chang, S.; Kim, J.; Kim, Y.; Zhou, J.-W. Performance evaluation of GFRP rock bolt sensor for rock slope monitoring by double shear test. Adv. Civ. Eng. 2020, 2020, 8870698. [Google Scholar] [CrossRef]
- Amagu, C.A.; Zhang, C.; Sainoki, A.; Sugimoto, K.; Shimada, H.; Dzimunya, N.; Sinkala, P.; Kodama, J.-I. Analysis of Excavation-Induced Effect of a Rock Slope Using 2-Dimensional Back Analysis Method: A Case Study for Clay-Bearing Interbedded Rock Slope. Geotech. Geol. Eng. 2024, 42, 6315–6337. [Google Scholar] [CrossRef]
- Amagu, C.A.; Zhang, C.; Kodama, J.-I.; Shioya, K.; Yamaguchi, T.; Sainoki, A.; Fukuda, D.; Fujii, Y.; Sharifzadeh, M.; Zhang, X. Displacement Measurements and Numerical Analysis of Long-Term Rock Slope Deformation at Higashi-Shikagoe Limestone Quarry, Japan. Rock Mech Rock Eng. 2021, 2021, 1316402. [Google Scholar] [CrossRef]
- Amagu, C.A.; Zhang, C.; Kodama, J.-I.; Fukuda, D.; Sainoki, A.; Sugimoto, K.; Shimada, H.; Dzimunya, N.; Sinkala, P. 3-D Numerical Analysis of Mining-Induced Deformation of Clay-Bearing Rock Slope in a Quarry. Rock Mech Rock Eng. 2025, 58, 6145–6167. [Google Scholar] [CrossRef]
- Bi, J.; Luo, X.; Zhang, H.; Shen, H. Stability analysis of complex rock slopes reinforced with prestressed anchor cables and anti-shear cavities. Bull. Eng. Geol. Environ. 2019, 78, 2027–2039. [Google Scholar] [CrossRef]
- Yan, M.; Xia, Y.; Liu, T.; Bowa, V.M. Limit analysis under seismic conditions of a slope reinforced with prestressed anchor cables. Comput. Geotech. 2019, 108, 226–233. [Google Scholar] [CrossRef]
- Sun, J.; Yu, T.; Dong, P. Pseudo-dynamic analysis of reinforced slope with anchor cables. Soil Dyn. Earthq. Eng. 2022, 162, 10751. [Google Scholar] [CrossRef]
- Jia, J.; Gao, X.; Bao, X.; Xiang, X.; Zhang, L.; Tu, B. Dynamic stability analysis method of anchored rocky slope considering seismic deterioration effect. Sci. Rep. 2024, 14, 7014. [Google Scholar]
- Fu, G.; Deo, R.; Ji, J.; Kodikara, J. Failure assessment of reinforced rock slopes subjected to bolt corrosion considering correlated multiple failure modes. Comput. Geotech. 2021, 132, 104029. [Google Scholar] [CrossRef]
- Xia, P.; Ying, C. Research on the stability evaluation method of anchored slopes based on group decision making and matter element analysis. Sci. Rep. 2021, 11, 16588. [Google Scholar] [CrossRef]
- Chiu, J.K.Y.; Li, C.C.; Mengshoel, O.J.; Kveldsvik, V. Slope rockbolting using key block theory: Force transfer and artificial intelligence-assisted multi-objective optimisation. J. Rock Mech. Geotech. Eng. 2025, in press. [Google Scholar]
- Chen, J.-F.; Du, C.-C.; Peng, M.; Sun, R.; Zhao, F.; Shi, Z.-M. System reliability analysis of a slope stabilized with anchor cables and piles under seismic loading. Acta Geotech. 2023, 18, 4493–4514. [Google Scholar] [CrossRef]
- Liu, S.Y.; Shao, L.T.; Li, H.J. Slope stability analysis using the limit equilibrium method and two finite element methods. Comput. Geotech. 2014, 63, 291–298. [Google Scholar] [CrossRef]
- Griffiths, D.V.; Fenton, G.A. Probabilistic slope stability analysis by finite elements. J. Geotech. Geoenviron. Eng. 2004, 130, 507–518. [Google Scholar] [CrossRef]
- Sun, L.; Grasselli, G.; Liu, Q.; Tang, X.; Abdelaziz, A. The role of discontinuities in rock slope stability: Insights from a combined finite-discrete element simulation. Comput. Geotech. 2022, 147, 104788. [Google Scholar] [CrossRef]
- Bao, Y.; Li, Y.; Zhang, Y.; Yan, J.; Zhou, X.; Zhang, X. Investigation of the role of crown crack in cohesive soil slope and its effect on slope stability based on the extended finite element method. Nat. Hazards 2022, 110, 295–314. [Google Scholar] [CrossRef]
- Jing, L. A review of techniques, advances and outstanding issues in numerical modelling for rock mechanics and rock engineering. Int. J. Rock Mech. Min. Sci. 2003, 40, 283–353. [Google Scholar] [CrossRef]
- Acharya, A.; Kogure, T. Advances in fibre-optic-based slope reinforcement monitoring: A review. J. Rock Mech Geotech Eng. 2024, 17, 1263–1284. [Google Scholar] [CrossRef]
- Tao, Z.; Wang, Y.; Zhu, C.; Xu, H.; Li, G.; He, M. Mechanical evolution of constant resistance and large deformation anchor cables and their application in landslide monitoring. Bull. Eng. Geol. Environ. 2019, 78, 4787–4803. [Google Scholar] [CrossRef]
- Li, T.; Liu, G.; Wang, C.; Wang, X.; Li, Y. The probability and sensitivity analysis of slope stability under seepage based on reliability theory. Geotech. Geol. Eng. 2020, 38, 3469–3479. [Google Scholar] [CrossRef]
- Kumar, A.; Pandit, B.; Tiwari, G. Reliability-based stability analysis of large rock slopes with different failure mechanisms using response surface methodology. Environ. Earth Sci. 2022, 81, 511. [Google Scholar] [CrossRef]
- Zhao, Z.; Xu, J.; Yuan, J.; Chang, W.; Guo, G. Investigation of cusp catastrophe model of rock slope instability with general constitutive equations. Bull. Eng. Geol. Environ. 2021, 80, 303–315. [Google Scholar] [CrossRef]
- Qiao, C.; Wang, Y.; Li, C.; Yan, B.; Yang, H.; Xiao, Y. Catastrophe instability analysis of rock slopes with locked segments in open-pit mine due to freeze–thaw weathering. Bull. Eng. Geol. Environ. 2022, 81, 135. [Google Scholar] [CrossRef]
- Chang, Y.; Chang, L.; Ren, F. Energy catastrophe of jointed rock slope considering spatiotemporal variability of strength. Geotech. Geol. Eng. 2021, 39, 2547–2564. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhou, Y.; Chen, Z. New energy criterion for rock slope excavation-induced failure based on catastrophe theory: Methodology and applications. Bull. Eng. Geol. Environ. 2024, 83, 140. [Google Scholar] [CrossRef]
- Bao, M.; Chen, Z.; Nian, G.; Zhang, L.; Zhou, Z.; Gui, Y. Fractional catastrophe model considering the rheological properties of slope faults. Lithosphere 2022, 2021, 1125720. [Google Scholar] [CrossRef]
- Kong, D.G.; Hu, K. Application of catastrophe theory in surrounding rock stability. Adv. Mater. Res. 2013, 712, 974–978. [Google Scholar] [CrossRef]
- Hua, H.U.; Liang, C.A.I.; Xiang-Hua, L.I. Experimental Analysis on the Accelerating Rheological Failure Process of Soft Soil Based on the Catastrophe Theory. In Proceedings of the 2014 International Conference on Mechanics and Civil Engineering (ICMCE-14), Asheville, NC, USA, 26–28 October 2014; Atlantis Press: Dordrecht, The Netherlands, 2014; pp. 635–639. [Google Scholar]
- Yeremeyev, I.; Dychko, A.; Kyselov, V.; Remez, N.; Khlobystov, I.; Semerikov, S.; Chukharev, S.; Sakhno, S.; Striuk, A.; Iatsyshyn, A.; et al. Catastrophes, fractals and chaos in geoengineering and water treatment systems. In E3S Web of Conferences, Proceedings of the Second International Conference on Sustainable Futures: Environmental, Technological, Social and Economic, Kryvyi Rih, Ukraine, 19–21 May 2021; EDP Sciences: Les Ulis, France, 2021; Volume 280, p. 02009. [Google Scholar]
- Li, G.; Luo, Z.; Wu, C.; Lu, H.; Zhu, C. Integrated early warning and reinforcement support system for soft rock tunnels: A novel approach utilizing catastrophe theory and energy transfer laws. Tunn. Undergr. Space Technol. 2024, 150, 105869. [Google Scholar] [CrossRef]
- Peng, Y.; Wu, L.; Chen, C.; Yue, J. Stability analysis of surrounding rock in tunnel crossing water-rich fault based on catastrophe theory. Geotech. Geol. Eng. 2020, 38, 415–423. [Google Scholar] [CrossRef]
- Cao, Z.; Zhang, S.; Xue, Y.; Wang, Z.; Du, F.; Li, Z.; Huang, C.; Wang, S.; Yu, Y.; Wang, W.; et al. Disaster-causing mechanism of spalling rock burst based on folding catastrophe model in coal mine. Rock Mech. Rock Eng. 2025, 58, 7591–7604. [Google Scholar] [CrossRef]
- Thom, R. Stabilité Structurelle et Morphogénèse; W. A. Benjamin: Reading, MA, USA, 1972. [Google Scholar]
- SL/T 212-2020; Technical Specification for Prestressed Anchoring in Hydraulic Engineering. China Water & Power Press: Beijing, China, 2020. (In Chinese)
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).