Complex System Diagnostics Using a Knowledge Graph-Informed and Large Language Model-Enhanced Framework

Featured Application

This framework demonstrates how Large Language Models (LLMs) can be used to automate functional model construction and enable natural language-driven fault diagnostics in complex engineered systems. By integrating LLMs with a knowledge graph of an Auxiliary Feedwater system, the approach supports predictive maintenance and intelligent fault analysis. It applies to safety-critical domains such as nuclear power plants and other high-reliability industries.

Abstract

This paper presents a hybrid diagnostic framework that integrates Knowledge Graphs (KGs) with Large Language Models (LLMs) to support fault diagnosis in complex, high-reliability systems such as nuclear power plants. The framework is based on the Dynamic Master Logic (DML) model, which organizes system functions, components, and dependencies into a hierarchical KG for logic-based reasoning. LLMs act as high-level facilitators by automating the extraction of DML logic from unstructured technical documentation, linking functional models with language-based reasoning, and interpreting user queries in natural language. For diagnostic queries, the LLM agent selects and invokes predefined tools that perform upward or downward propagation in the KG using DML logic, while explanatory queries retrieve and contextualize relevant KG segments to generate user-friendly interpretations. This ensures that reasoning remains transparent and grounded in the system structure. This approach reduces the manual effort needed to construct functional models and enables natural language queries to deliver diagnostic insights. In a case study on an auxiliary feedwater system used in the nuclear pressurized water reactors, the framework achieved over 90 percent accuracy in model element extraction and consistently interpreted both diagnostic and explanatory queries. The results validate the effectiveness of LLMs in automating model construction and delivering explainable AI-assisted health monitoring.

1. Introduction

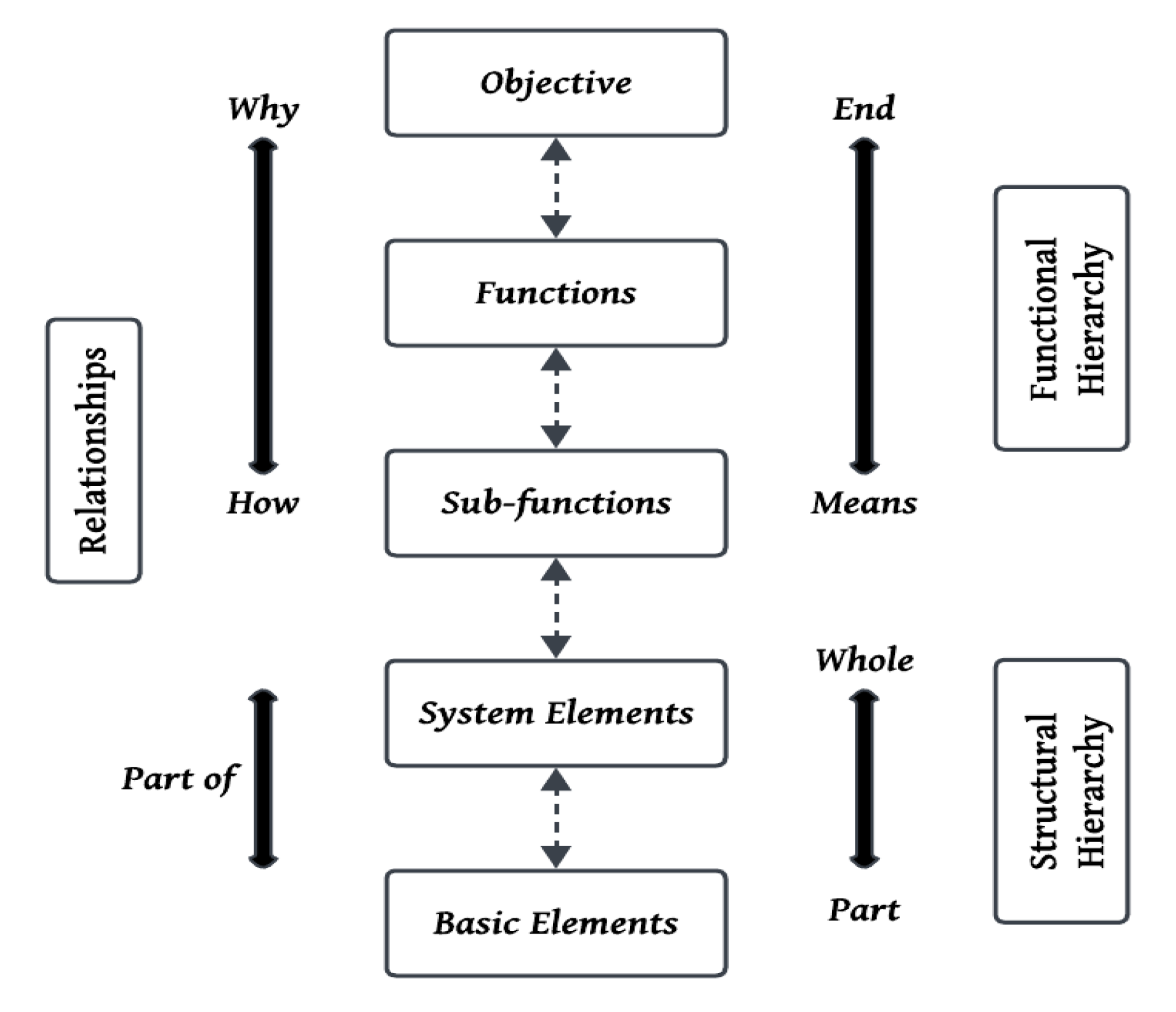
The analysis of complex engineered systems, particularly those in high-reliability and safety-critical industries such as nuclear power plants, requires systematic approaches to assess system integrity, reliability, and performance. Traditional diagnostic tools have predominantly relied on event-based modeling, where the outcomes of specific failure pathways, faults or abnormal initiating events are analyzed. Although effective in some domains, event-based approaches become extremely complex, incomplete and inadequate when applied to complex, interconnected systems with numerous interdependencies. As the scale and complexity of systems increase, functional modeling approaches are considered more suitable, where the emphasis is placed on understanding the roles, dependencies, and contributions of system components toward achieving primary system objectives. Functional modeling involves the development of system models based on the actions and relationships of their constituent parts [1,2]. These models are inherently hierarchical, enabling a systematic decomposition of the system into goals, functions, and subfunctions. One important framework within this category is the Dynamic Master Logic (DML) model, introduced by Hu and Modarres [3], which represents system behavior through a hierarchy linking functional objectives to underlying structures. By organizing systems into functional and structural layers, DML enables critical causal pathways, system interdependencies, and fault propagation mechanisms to be systematically analyzed. This hierarchical framework supports the tracing of failures from system-level objectives down to elemental components, offering a powerful tool for diagnostic analysis.

Although DML models provide a robust framework for system diagnostics, their construction, maintenance, and interpretation require significant manual effort and extensive domain expertise. As system complexity grows, the burden associated with constructing and interacting with large DML models increases accordingly. In response to these challenges, powerful Artificial Intelligence (AI) tools such as Large Language Models (LLMs) [4] have been recognized as offering opportunities to enhance the development, interaction, and usability of functional models for diagnosis of faults and failures in complex engineering systems. LLMs have demonstrated strong capabilities in natural language understanding, summarization, and reasoning across a wide range of domains. However, certain limitations, such as hallucination and restricted domain-specific reasoning, have been observed [5,6]. To address these challenges and improve diagnostic reliability, knowledge representations such as Knowledge Graphs (KGs) [7] can be used alongside LLMs to enable more consistent and interpretable reasoning by guiding diagnostic logic through external tools rather than unconstrained language generation. More generally, combining LLMs with KGs helps mitigate hallucination and provides a mechanism for introducing verified domain knowledge into the reasoning process [8,9]. Detailed examples of such integrations in fault diagnostics, which form the methodological foundation of this work, are discussed in Section 2.3.

Given the increasing complexity of engineered systems and the need for scalable, interpretable diagnostic tools, there is a strong motivation to explore AI-driven frameworks that combine domain knowledge with language-based reasoning. In this paper, an approach is proposed that leverages LLMs and KGs to support and enhance interaction with DML models, to reduce manual effort, improve transparency, and facilitate more efficient fault analysis in safety-critical applications.

This research addresses emerging needs in AI-based machinery health monitoring by introducing an LLM-powered agenting workflow for intelligent fault diagnosis in safety-critical systems.

The remainder of this paper is organized as follows. Section 2 reviews related work on DML modeling, LLMs, and the integration of KGs in diagnostic systems. Section 3 provides an overview of the research approach. Section 4 presents the proposed diagnostic framework, detailing both the model construction and interaction phases. Section 5 describes a case study involving an auxiliary feedwater system in a nuclear power plant, illustrating the application of the framework. Section 6 reports the evaluation results from both the model construction and interaction components, based on repeated runs using the case study. Section 7 discusses the results, outlines the limitations of the current work, and proposes directions for future research. Finally, Section 8 concludes the paper with key findings.

2. Background

2.1. From Traditional Diagnostics to Functional Modeling

Traditional diagnostic approaches often rely on modeling discrete events, failure modes, or symptom triggers. These include methods like Fault Tree Analysis (FTA) [10,11,12], Event Trees (ET) [13,14], and rule-based [15,16] expert systems that map observed events to likely faults. Such models focus on specific failure events and their consequences. While these event-driven models can effectively represent known failure sequences, they typically require an exhaustive list of fault–event combinations, invariably making them incomplete. If a particular sequence is not anticipated during model development, the system may fail to diagnose it. Moreover, as systems grow in complexity, tracing failure paths becomes increasingly infeasible using event-based logic alone. Functional modeling reflects a designer’s intent by capturing system goals and functions rather than enumerating events. These models encode the functional expectations and logical dependencies of the system, enabling the detection of faults based on deviations from expected behavior. These models are hierarchical, representing goals, functions, subfunctions, and supporting structures. They emphasize how components contribute to overall functions, enabling reasoning about failures in terms of lost or abnormal functionality, such as a pump failing to provide flow or a sensor failing to deliver information, rather than focusing solely on specific failure events [17]. Functional approaches address several limitations of event-based models. First, they support completeness by enabling an analysis of the system’s functional architecture. This allows for the identification of faults that may cause the loss of required functions, even during the design or concept stage, before any failure data is available. Second, functional models naturally handle complex, multi-fault scenarios. Since they capture interactions through functional dependencies, they can reason about multiple simultaneous failures or cascading effects without relying on every combination explicitly. Third, they promote generality. The same functional model can be applied throughout the system’s life cycle and across various analysis tasks. These include design-level Failure Mode and Effects Analysis (FMEA), runtime diagnosis, and what-if analysis. This flexibility is possible because the model abstracts away from specific event sequences and instead focuses on invariant functional relationships [18].

2.2. DML Model Applications

For system-level modeling, DML models are success logics in the form of powerful hierarchies to represent system knowledge [3,19,20,21]. This hierarchical representation becomes particularly valuable in safety-critical domains. System safety focuses on applying engineering principles, standards, and techniques to minimize risk while ensuring a system remains effective, reliable, and cost-efficient throughout its life cycle. Using a DML, the degree of success (or failure), approximate full-scale system physical values, and transition effects amongst components can be analyzed. DML provides an effective model for describing the causal effects of failures or disturbances in complex systems [22]. Figure 1 conceptually illustrates the DML framework, highlighting the hierarchical decomposition from system objectives to basic elements such as components and the interdependencies between functional and structural. The functional hierarchy (top-down) moves from objectives to functions and sub-functions, capturing the system’s purpose and behavior. The structural hierarchy decomposes the system into elements and basic components, reflecting its physical or logical composition. Arrows indicate causal (“Why–How”) and compositional (“Part-of”) relationships, highlighting interdependencies. This structure supports systematic analysis of complex systems by linking high-level goals to low-level elements.

Two key causal relationships can be extracted from DML. The first involves determining the ultimate effect of a failure, and the second involves identifying the paths through which a function can be achieved or a subsystem can successfully operate. It applies reductionist principles, where qualities represent functions and goals, while objects and relationships are arranged through success trees and logical modeling, including Boolean, physical, and fuzzy logic [19]. This integration enhances DML’s ability to model time-dependent behaviors and fault propagation within complex systems. This model has been applied to various applications of modeling. In nuclear power plants, DML has been used to model Direct Containment Heating in a Pressurized Water Reactor [21]. In renewable energy, it has supported reliability analysis of geared wind turbines [23]. DML has also proven effective in analyzing interactions between hardware, software, and human elements in cyber–physical systems [24,25]. In the aerospace sector, it has been used to identify critical points in system reliability [26]. Additionally, DML has supported quality assurance across the software development life cycle [27].

It is important to note that several naming conventions have been used to describe what is fundamentally a single family of DML models with common underlying principles. The earliest form of this modeling approach was the Goal Tree Success Tree (GTST) [17], which laid the foundation for functional reasoning in complex systems. This was followed by the development of the Master Plant Logic Diagram (MPLD) [28], originally created for use in nuclear power plants to represent plant logic and support reliability assessment. Over time, MPLD evolved into several extensions and refinements. A prominent variant is the GTST with Master Logic Diagram (MLD), referred to as GTST-MLD [22,27]. This version combines a functional hierarchy, represented by the GTST with a structural model, represented by the MLD that captures component relationships and dependencies, supporting both dynamic and static system representations. Another well-established form is the Dynamic Master Logic Diagram (DMLD) [19], which emphasizes the modeling of uncertain, evolving, and time-dependent behaviors in complex systems. While terminology may differ depending on modeling emphasis, these approaches are functionally equivalent and share the common goal of representing system logic for diagnostic reasoning and reliability analysis. Throughout this paper, this family of models is collectively referred to as DML.

2.3. LLMs and KGs in Fault Diagnostics

Recent advancements in LLMs have accelerated the use of fault diagnostics, particularly in industrial and safety-critical domains. Traditional fault diagnosis methods rely heavily on rule-based models or historical fault logs, which require extensive domain expertise and are often inefficient in handling complex, multi-layered system interactions. Integrating LLMs with diagnostic methods makes timely detection of faults more practical and easier to scale by enabling an understanding of fault causes and providing decision support through NLP. As demonstrated in [29], a diagnostic model was used to detect faults in a nuclear power plant, while an LLM acted as an interface to explain fault conditions and their potential causes to human operators, enhancing situational awareness and response.

A study introduced the method of FD-LLM [30], framed machine fault diagnosis as a text classification task by converting vibration signals into textual token sequences or summaries. Fine-tuned LLaMA models were employed, achieving superior performance compared to traditional deep learning models and demonstrating that LLMs can effectively process non-textual diagnostic information when appropriately structured. Improvements were reported in accurately identifying fault root causes from symptom descriptions, highlighting the potential of LLMs for natural language-based symptom interpretation and fault retrieval. To enhance the reliability and reasoning capabilities of LLM-based diagnostics, several studies have proposed integration with KGs. One approach, Root-KGD [31], combined industrial process data with a KG representing system topology and causal dependencies, enabling more accurate root cause failure identification by guiding LLM reasoning through formalized domain knowledge. In the context of CNC machine fault diagnosis [32], a KG-embedded LLM architecture was proposed. A machining-process KG was automatically constructed from maintenance records, and its structured information was embedded into the LLM to support fault classification and provide explainable fault identification through natural language outputs.

Integration of KGs into fault diagnostics has been explored to address the need for causal reasoning. A multi-level KG was developed to represent rotating machinery faults [33], and Bayesian inference was applied to trace symptom–cause pathways within the graph, achieving a 91.1% diagnostic accuracy under missing data conditions. This demonstrated that the representation of symptom–cause relationships within a KG can enhance diagnostic robustness. The combination of knowledge retrieval and LLM reasoning enabled interpretable and accurate fault diagnosis based on free-form symptom descriptions. The combination of LLMs with KGs has also demonstrated enhanced fault reasoning capabilities.

A hybrid model for aviation assembly diagnostics achieved 98.5% accuracy in fault localization and troubleshooting through subgraph-based reasoning [34]. In vehicle fault diagnostics, a KG-driven analysis system was developed that maps error codes and system alerts to potential failure causes [35]. This system leveraged LLMs to process unstructured diagnostic data, such as error logs and maintenance reports, transforming it into structured representations within a KG. A reasoning framework was introduced to infer root causes by linking symptoms to failure mechanisms stored in the KG. In [36], a KG-based in-context learning approach was proposed to enhance fault diagnosis in industrial sensor networks. A domain-specific KG was constructed to encode expert knowledge, and a long-length entity similarity retrieval mechanism was used to select relevant knowledge, which was then supplied to a large language model for causal reasoning over fault symptom text. The method demonstrated improved fault localization accuracy and enhanced the interpretability of diagnostic outputs compared to traditional LLM approaches.

These studies demonstrated that incorporating LLM-driven fault reasoning improved diagnostic accuracy and reduced troubleshooting time compared to traditional rule-based or statistical models. Structuring fault data within a KG provides traceable and explainable reasoning paths, assisting engineers and technicians in understanding failure causes. Collectively, these studies illustrate the growing role of LLMs and KGs in fault diagnostics. LLMs enable flexible interpretation of symptom descriptions and support natural language interaction, while KGs structure domain-specific knowledge to guide reasoning processes. Their integration shows promise for enhancing fault retrieval and root cause analysis across various technical domains.

3. Research Overview

As discussed in Section 2, although LLMs and KGs show promise for assisting with system diagnostics from textual documentation, their role in functional decomposition is not fully developed. Similarly, KGs are primarily used for retrieving fault information rather than representing system logic or dependencies, and few studies have explored integrating computational reasoning layers to enable real-time diagnostic analysis. To address these gaps, this paper introduces an LLM-informed, KG-based diagnostic framework for constructing and using the DML model derived from system design and operational documents. The framework leverages LLMs to support diagnostics, reliability assessment, and decision-making for a specific engineering system. It has three main objectives:

(a)

Automate the generation of scalable functional models by extracting unstructured relationships from system documentation, including system descriptions and specifications.

(b)

Enable interactive, hierarchical fault analysis through natural language-driven upward and downward reasoning. Upward reasoning evaluates how individual component failures affect higher-level system functions, while downward reasoning explores which functional paths and component conditions must be satisfied to maintain or restore system objectives.

(c)

Support interpretive analysis of system goals, functions, and dependencies by leveraging Graph-based Retrieval-Augmented Generation (Graph-RAG) to retrieve and contextualize relevant segments of the KG in response to user queries.

4. Proposed Approach

Figure 2 presents the LLM-Informed Diagnostic Framework, which consists of two main stages: model construction and model interaction. In the model construction stage, system descriptions are processed by an LLM-based workflow to extract DML logic, which organizes the system into hierarchical functions, components and their relationships. This representation is then used to build a KG, which serves as the core system model. The KG can be further enhanced by incorporating expert knowledge and real-time operational data processed through Machine Learning (ML) or Deep Learning (DL) models, allowing it to infer and reflect system states and conditions dynamically. In the diagnostic model interaction section, an LLM agent would determine the intention of the user and would invoke one of the tools available to it based on the query to execute. These tools are used to trace the KG to generate diagnostic insights. The results would be communicated to the user by the LLM.

4.1. Model Construction

The development of the diagnostic model begins with processing textual system information, including manuals, system descriptions, and technical documentation. Preprocessing techniques such as text summarization and LLM-based Named Entity Recognition (NER) are applied to extract key details about system components, functions, and dependencies. These extracted elements are then used to derive a DML hierarchical structure that organizes the system into goals, functions, subfunctions, and components. This logic is subsequently translated into Cypher code, the query language used to construct the KG that represents the system’s components and functional relationships. The resulting KG provides a repository to support querying and reasoning for diagnostics and decision-making. In this research, the KG is deployed using Neo4j [37], a graph database platform that represents entities and their interconnections as property graphs, with attributes stored as node and relationship properties. Cypher enables the definition of system dependencies within the KG, linking components to their success conditions and subfunctions to their parent functions. All language-based tasks in this framework were performed using OpenAI’s GPT-4o model through the ChatGPT 4.0 API.

4.2. Model Interaction

Once the model is built, it needs to be used to generate diagnostic insights. This framework aims to go beyond simple queries by enabling deeper system analysis, addressing the fundamental diagnostic questions:

• What is happening? The model identifies current system conditions. For example, it can determine which components are degrading and which system functions are at risk.
• Why is it happening? By tracing system dependencies, the model identifies apparent root causes of failures and analyzes contributing factors.
• How will it impact the system? The model assesses failure propagation and risk severity, predicting how component failure will affect system operations.

To address these questions, the model enables cause-and-effect reasoning, allowing users to explore system behavior beyond basic retrieval. Instead of just fetching stored information, it supports queries such as:

• If certain components fail, how will it affect the overall system?
• What conditions must be met for a specific function to succeed?
• Which components are essential to maintaining system functionality?

To support this process, a set of predefined functions is made available to the LLM agent as tools for interfacing with the KG. These tools enable upward and downward tracing to analyze system dependencies and generate diagnostic insights. When a user submits a query, the LLM interprets the intent and selects the appropriate tool to execute. The output is then passed back to the LLM, which produces a human-readable explanation. In addition to tool-based diagnostics, the model supports general system queries, such as explaining the system’s hierarchy or functional structure. For these interpretive queries, the framework employs a Graph-RAG approach where relevant graph segments, such as goals or functions, are retrieved and embedded into the LLM’s prompt to support natural language generation. Both approaches rely on the KG, but in complementary ways. Diagnostic tools perform graph traversals to compute logic-based results, while Graph-RAG enables the LLM to produce contextual explanations based on retrieved subgraphs. This dual strategy ensures the KG remains central to both reasoning and explanation.

5. Case Study

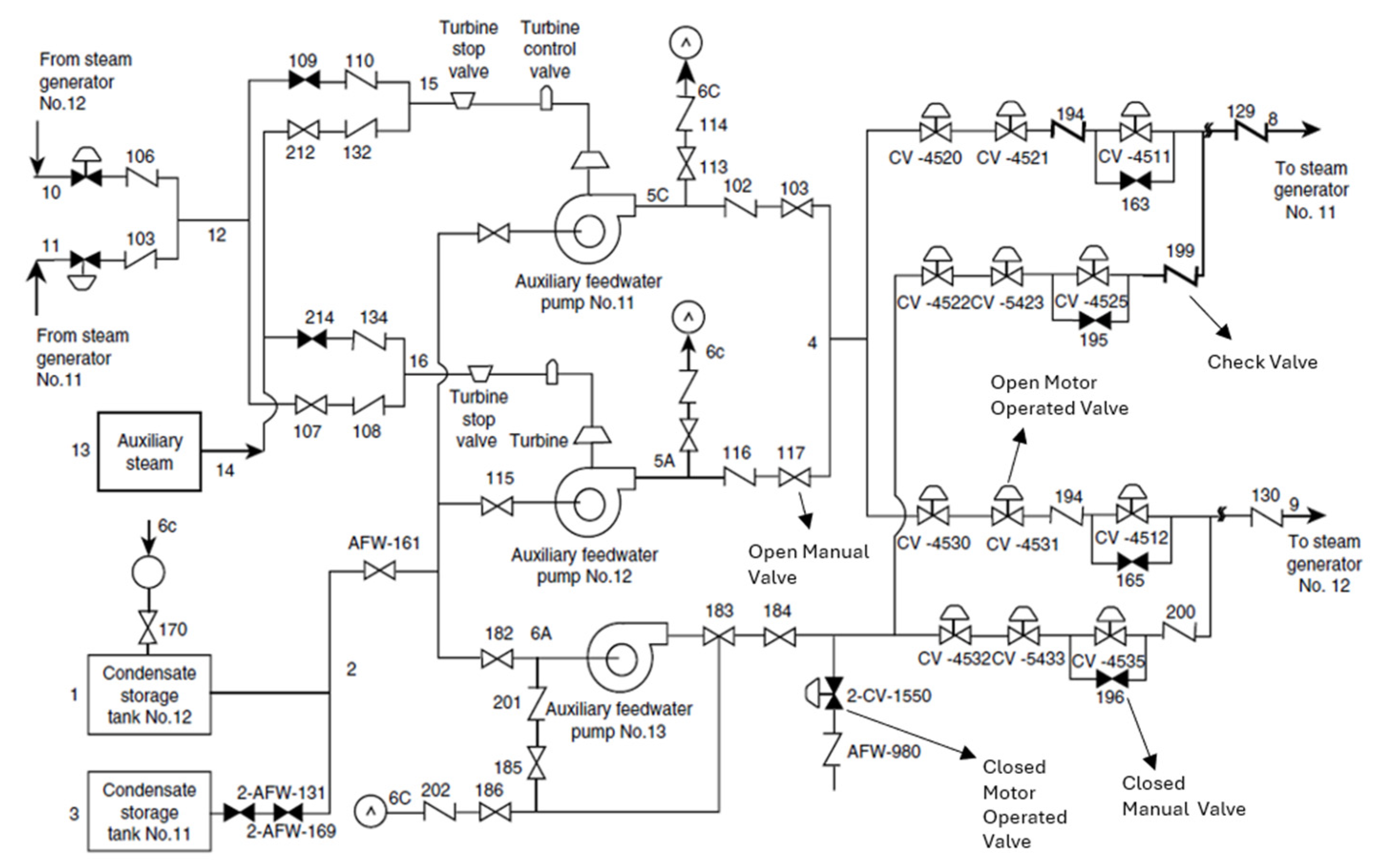
The proposed system, illustrated in the Piping and Instrumentation Diagram (P&ID) in Figure 3, is used as the case study for implementing the proposed LLM-informed diagnostic framework. This P&ID shows a simplified auxiliary feedwater system used for emergency cooling of steam generators at pressurized light water nuclear power plants. It starts automatically upon a loss of normal feedwater to the steam generators. Its main purpose is to keep the steam generator water levels stable as ultimately protecting the reactor core. The system does this by drawing water from a storage tank and delivering it through motor-driven or turbine-driven pumps, valves, and piping, with flow controlled automatically by instrumentation. The system is structured with the main goal defined as “Ensure safe and effective operation of the auxiliary feedwater system”. This goal is supported by four primary functions: “Supply Feedwater”, “Control Water Flow”, “Manage System Integration and Response”, and “Provide Emergency and Automated Response”.

5.1. Model Construction

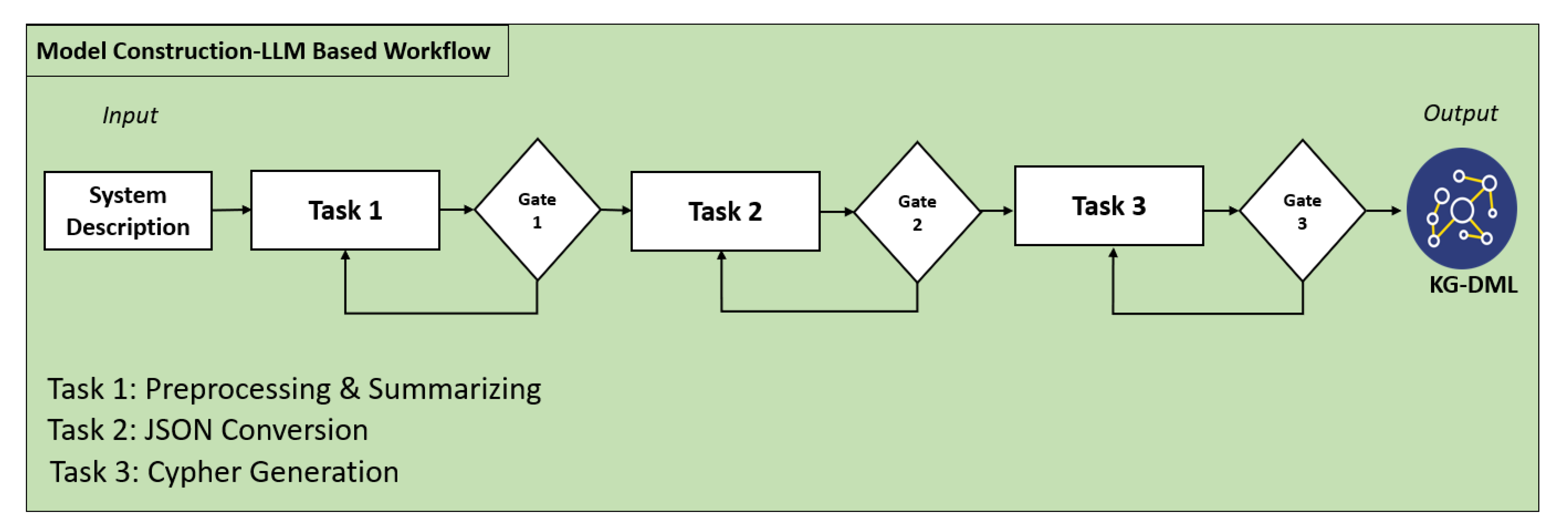
To construct a KG representing DML logic from a system description (which included only major components and functions), a prompt chaining workflow was implemented, with each stage handled by a dedicated LLM call. The hierarchy follows the DML structure, starting with a high-level goal and breaking down into functions, subfunctions, and components, each linked to success conditions. Logical relationships are shown using binary AND or OR logic gates, which define how lower-level elements contribute to achieving higher-level objectives.

The workflow begins with an initial LLM call that summarizes the system description and extracts goals, functions, subfunctions, components, and success conditions. The result is passed to a second LLM that converts this information into a JavaScript Object Notation (JSON) format aligned with the DML hierarchy. A third LLM then transforms the JSON into Cypher queries for KG construction. Each LLM call is followed by a gate, implemented as another LLM, that validates the output before the next stage proceeds. If validation fails, the workflow routes the input back to the relevant LLM for revision. The first gate checks for missing or incomplete information in the summary, including vague goals, incomplete function chains, or missing success criteria. The second gate validates the JSON structure by checking key formatting, nesting, and logical gate consistency. The third gate examines the generated Cypher queries to ensure they are syntactically correct.

This gated prompt chaining design improves consistency, filters out errors early, and manages variability in LLM outputs. It is especially effective when task steps are clearly defined and expected outputs are explicitly structured. Figure 4 illustrates the prompt chaining workflow described above, showing the sequential LLM tasks and validation gates leading from the system description to the final KG-DML output. Each task is followed by an LLM-based gate, which ensures the correctness of the output before advancing to the next stage. Feedback loops are included to allow correction and regeneration when validation fails. The specific prompts used for each LLM call in this workflow are provided in the Appendix A to this paper.

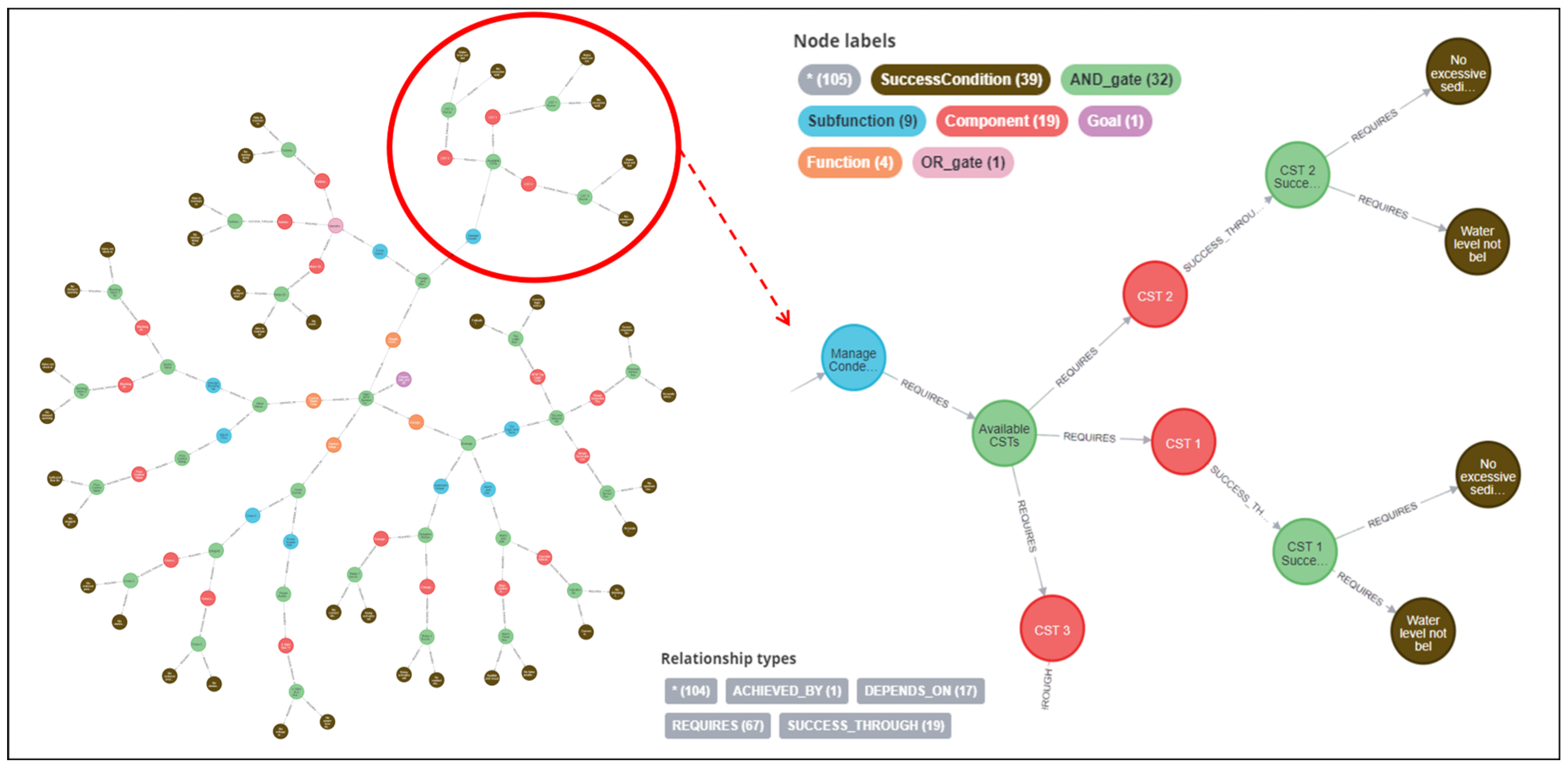
The KG representing the DML logic is structured hierarchically, starting from a high-level goal and descending through functions, subfunctions, components, and finally success conditions. Logical gates, such as AND or OR, define how each level contributes to achieving the level above. A goal may be achieved by multiple functions, each of which depends on one or more subfunctions that require specific components to operate successfully. At the lowest level of the hierarchy, components are connected to success conditions through additional gates. Success conditions reflect observable or measurable outcomes that confirm whether a component is performing as intended. Attributes are stored within the nodes themselves and may include expert knowledge or information derived from ML or DL models based on operational data or manual inspections.

For example, a component such as a turbine-driven pump may contain attributes indicating the probability of being in various states, such as operational, degraded, or failed. Attributes may also be present in higher-level nodes, such as functions or goals. Their role and interpretation will be discussed in the model interaction (next section). This hierarchical structure supports reasoning, traceability, and consistency throughout the KG-DML representation. Figure 5 illustrates how the DML model is represented within the KG. For example, the subfunction “Manage Condensation Tanks” is fulfilled only if all three Condensation Storage Tanks (CSTs) operate successfully, as defined by an AND gate. Each tank must meet two success conditions: maintaining an appropriate water level and ensuring the absence of excessive sediment. This same hierarchical logic applies when tracing the model upward through functions and system-level goals.

5.2. Model Interaction

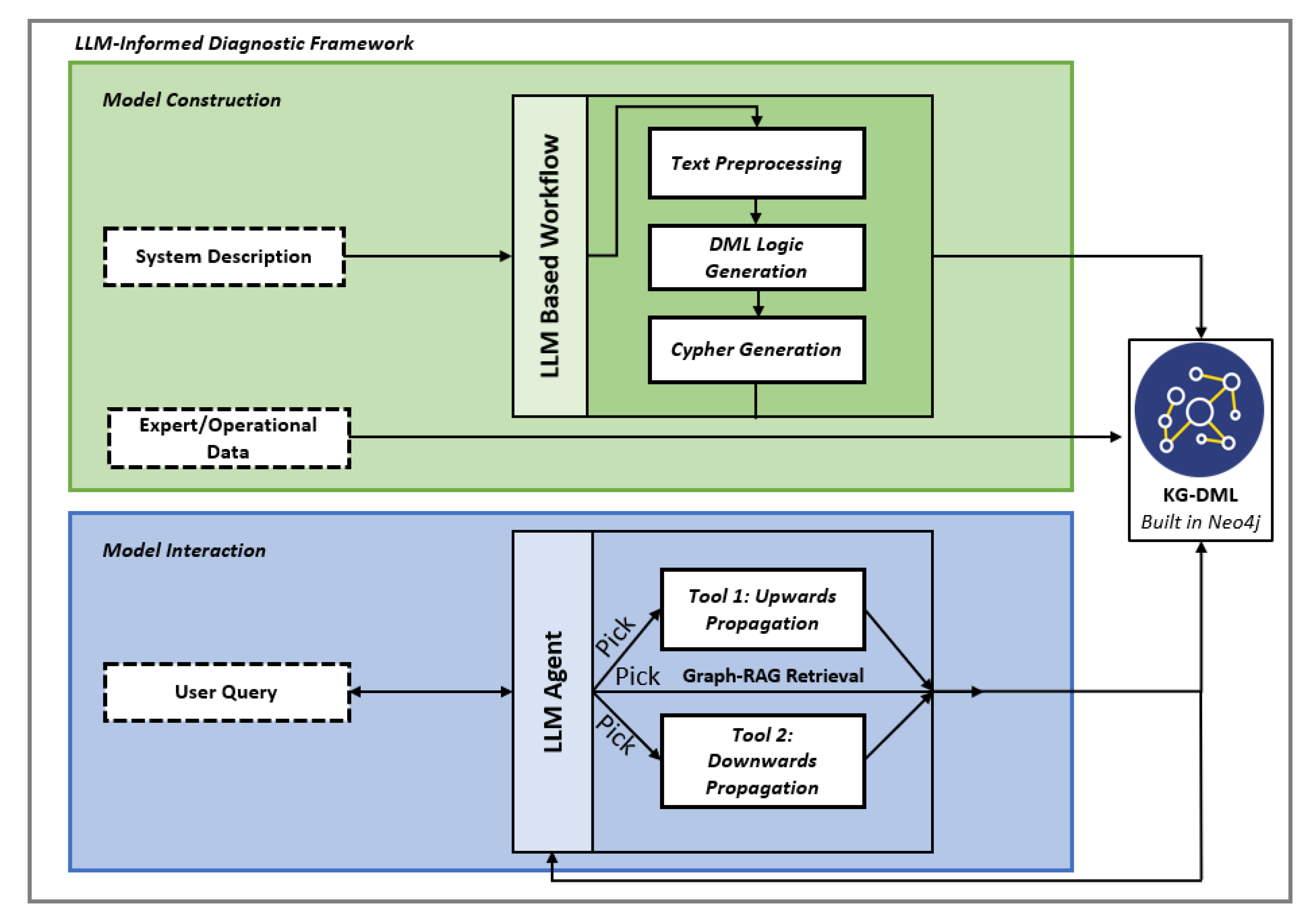
As shown in Figure 2, model interaction begins when a user submits a natural language query to the system. The LLM agent interprets the query and selects from a set of predefined diagnostic functions available to it as tools. These tools perform specialized tasks such as upward fault tracing and the generation of success path sets. Each tool is implemented as an external code module that analyzes the KG based on the logical structure derived from the model. The LLM uses these tools to carry out reasoning over the graph and generate diagnostic insights. To enable accurate selection, the agent was fine-tuned on a dataset consisting of diverse user queries paired with their corresponding tool calls. This included both diagnostic queries requiring tool invocation and interpretive queries requiring Cypher query generation for KG retrieval. This dataset was manually constructed to include multiple phrasings, semantic variations, and tones in which users might pose the same diagnostic intent. These examples were then used to guide the fine-tuning process so that the model learns to map a wide range of natural language inputs to the appropriate tool.

In the implemented tool for upward propagation, the success probability for each success condition $j$ associated with a component is first evaluated. This is done using Equation (1), which computes the probability as a weighted sum over the component’s possible operational states. Each term combines the likelihood of the component being in state $i$ with the probability that it fulfills the success condition $j$ in that state. A state refers to a possible condition of a component, such as operational, degraded, or failed. Each state influences the component’s ability to fulfill its associated success conditions. For example, consider a CST in the auxiliary feedwater system. One possible state of the CST is “failed”, which may be inferred from sensor data. The success condition for the CST could be defined as “maintains sufficient water level for feedwater supply.” If operational data indicates a high probability that the CST is in a failed state, the likelihood of satisfying this success condition would be correspondingly low. This affects the overall success probability of the subfunction “Manage Condensation Tanks,” which depends on all CSTs through an AND gate. Thus, the failure of even one CST can reduce the success probability of the higher-level function and system goal.

$$P\left(Succes{s}_j\right|Data)=\sum _{i=1}^{N}P\left(Succes{s}_j\right|Stat{e}_i\left)P\left(Stat{e}_i\right|Data\right)$$

(1)

• N: Total number of operational states for a component.
• $P\left(Succes{s}_j\right|Stat{e}_i):$ The probability of success for the success condition $j$. This reflects how likely the component will fulfill the success condition $j$ under state $i$.
• $P\left(Stat{e}_i\right|Data)$: The probability of the component being in state $i$ given the data which can be evidence of events or numerical information.

After evaluating $P\left(Succes{s}_j\right|Data)$ for all success conditions associated with each component in the system, the results are aggregated using logical gates to compute a single success probability for each component. Success probability represents how well the component is fulfilling its intended function. It is based on the combined satisfaction of all defined success conditions. Each condition reflects a specific performance indicator. The aggregation of these conditions provides a quantitative measure of the component’s overall operational effectiveness. The KG stores each element of Equation (1) as attributes within component nodes, including both the conditional success probabilities and the state likelihoods derived from data. In the context of engineering diagnostics, this data may include sensor readings (e.g., temperature, pressure, vibration), event logs, failure reports, and maintenance histories. These attributes serve as the basis for upward propagation and are retained in the KG to support traceability and diagnostic reporting. Once a single success probability is determined for each component, these values are propagated upward through the DML hierarchy using additional logical gates. The gates define how component-level probabilities combine to determine the success of associated subfunctions, functions, and ultimately system-level goals. If the success probability of an upper-level node falls below a predefined threshold, the tool considers that node to be impacted. The corresponding logic that performs the probabilistic propagation is captured in the pseudocode shown in Algorithm 1.

To estimate $P\left(Stat{e}_i\right|Data)$, various strategies can be applied depending on data availability and system characteristics. In the absence of real-time sensor data, these probabilities can be derived from expert judgment or reliability reports, which provide baseline estimates of failure or degradation likelihoods. These priors can be refined as new operational data become available. When numerical indicators such as temperature, pressure, or vibration readings are accessible, ML or DL models trained on historical labeled data can be used to estimate state probabilities more dynamically. In systems requiring continuous monitoring and probabilistic inference under uncertainty, particle filtering techniques may be used. Particle filters apply a sequential Monte Carlo approach to approximate probability distributions using a set of weighted samples, enabling real-time Bayesian inference even in nonlinear or non-Gaussian conditions [39,40].

Algorithm 1. Upwards Propagation Pseudocode.

procedure PROPAGATESUCCESSPROBABILITIES   for each Component C do $\hspace{1em}\hspace{1em}\hspace{1em} \mathrm{Retrieve} \mathrm{possible} \mathrm{states} Stat{e}_1,Stat{e}_2, \dots , Stat{e}_N$           for each Success Condition j of component C do             Compute: $\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} P\left(Succes{s}_j\right|Data)=\sum _{i=1}^{N}P\left(Succes{s}_j\right|Stat{e}_i\left)P\left(Stat{e}_i\right|Data\right)$            end for            Combine success conditions using gate type (e.g., AND, OR) $\hspace{1em}\hspace{1em}\hspace{1em} \mathrm{Update} P_{success}$(C) in KG   end for   for each Subfunction SF do          Retrieve linked Components and gate type          if gateType = AND then             Compute: ${\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} P}_{success}\left(SF\right)= \prod P_{success}\left(C\right)$          else             Compute: ${\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}P}_{success}\left(SF\right) = 1 - \prod (1 - P_{success}(C\left)\right)$          end if $\hspace{1em}\hspace{1em}\hspace{1em} \mathrm{Update} P_{success}\left(SF\right)$ in KG      end for      for each Function F do          Retrieve linked Subfunctions and gate type          if gateType = AND then             Compute: ${\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} P}_{success}\left(F\right)= \prod P_{success}\left(SF\right)$          else             Compute: ${\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}P}_{success}\left(F\right) = 1 - \prod (1 - P_{success}(SF\left)\right)$          end if $\hspace{1em}\hspace{1em}\hspace{1em} \mathrm{Update} P_{success}\left(F\right)$ in KG      end for      for each Goal G do          Retrieve linked Functions and gate type          if gateType = AND then             Compute: ${\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} P}_{success}\left(G\right)= \prod P_{success}\left(F\right)$          else             Compute: ${\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}P}_{success}\left(G\right) = 1 - \prod (1 - P_{success}(F\left)\right)$          end if $\hspace{1em}\hspace{1em}\hspace{1em} \mathrm{Update} P_{success}(G$) in KG      end for $\hspace{1em}\hspace{1em}\mathrm{Identify} \mathrm{impacted} \mathrm{nodes} \mathrm{where} P_{success}$ < threshold       return impacted nodes and probabilities end procedure

For downward propagation, given an upper-level node, the tool traces the KG downward to determine the required paths for achieving that node’s success. Using the defined gates, it identifies the necessary dependencies at each level. The path-set generation method determines the minimal components required for system functionality by recursively traversing the KG. Starting from a specified node, the process follows dependencies downward until reaching the Component and Success Condition levels. At each step, the method evaluates the logical dependencies based on the gate type. If an AND gate is present, all dependencies must be met simultaneously, requiring a Cartesian product of the success path-sets from the child nodes to generate valid paths. In contrast, for an OR gate, only one dependency needs to succeed, so the success path sets from the child nodes are aggregated without combination, representing alternative paths to success. This approach ensures that the generated success path-sets accurately reflect the minimal elements necessary to maintain system operability. The approach of downward propagation is formalized by the pseudocode in Algorithm 2. The implementation code for both the tool definitions and the LLM agent workflow is provided in the Supplementary Materials.

Algorithm 2. Downward Propagation Pseudocode

procedure GENERATESUCCESSPATHSETS(nodeType, nodeName)     if nodeType = Component then         Retrieve success conditions and gate type for nodeName         if no success conditions exist then             return {{nodeName}}         end if          if gateType = AND then             return {successConditions}         else             return {{cond} for each cond in successConditions}         end if     end if     Retrieve dependencies and gate type for nodeName      if no dependencies exist then         return {{nodeName}}     end if     Initialize childPathsets ← empty list     for each dependency depName in dependencies do         childPaths ← GENERATESUCCESSPATHSETS(depType, depName)         Append childPaths to childPathsets     end for     if gateType = AND then         Initialize combinedPaths ← empty list         for each combination in Cartesian product of childPathsets do             Append concatenated combination to combinedPaths         end for         return combinedPaths      else         return Flattened list of all childPathsets     end if end procedure

5.3. Interaction Interface

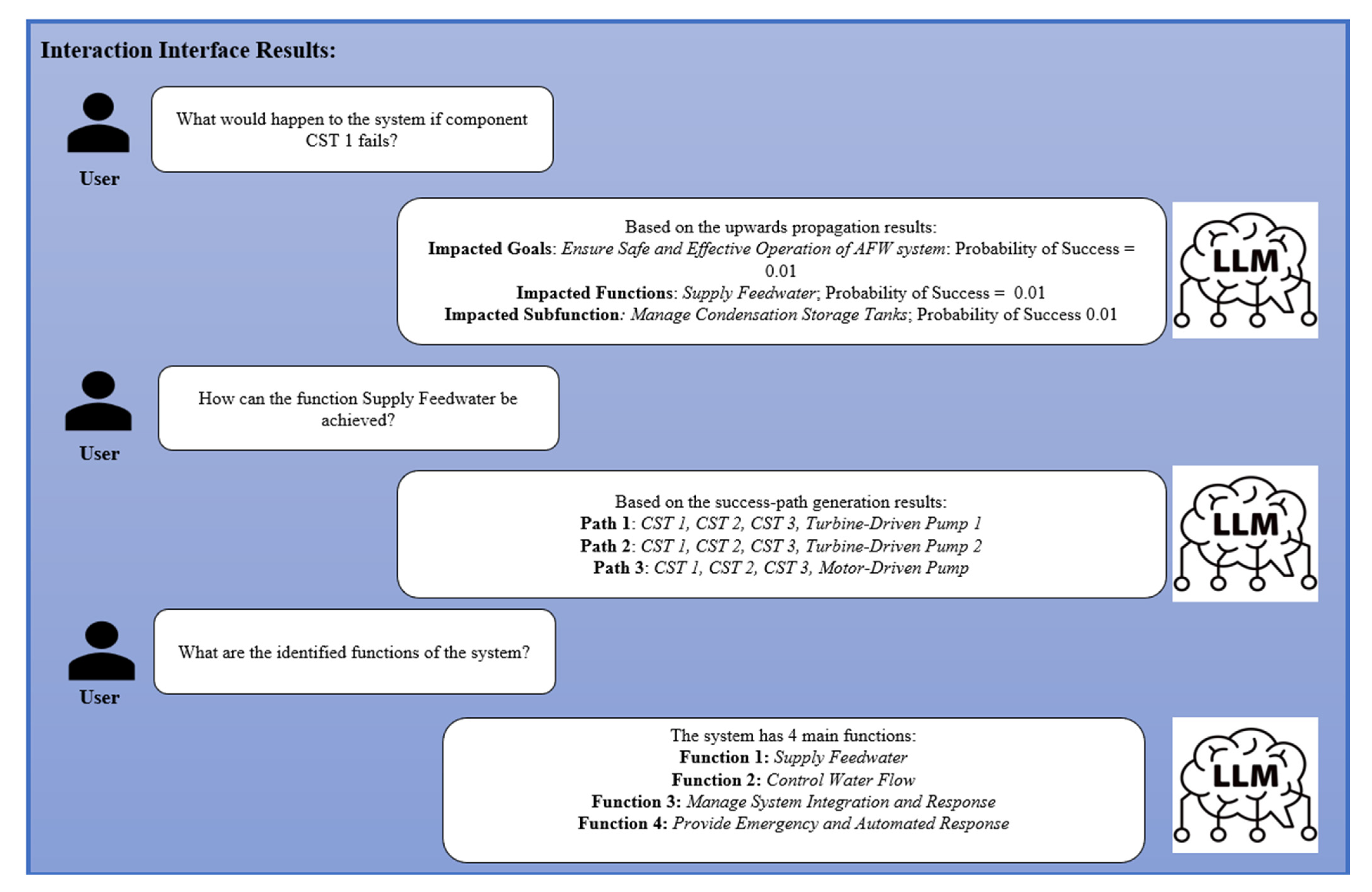
The diagnostic interface enables natural language interaction between the user and the system, allowing users to explore system behavior and fault scenarios. As illustrated in Figure 6, users can ask questions such as the impact of a specific component failure or how a given function can succeed. When queried about the impact of the failure of a CST, the LLM agent invokes the upward propagation tool to trace the impact across the system hierarchy. Because the CSTs are connected through an AND gate, the success of higher-level nodes depends on the simultaneous functionality of all CSTs. Therefore, the failure of even a single CST significantly reduces the probability of success for the related subfunctions, functions, and overall system goals. Conversely, when asked about the success conditions for a function like “Supply Feedwater”, the agent employs downward tracing to identify all minimal success paths. Results are returned in a human-readable format, supporting transparent and intuitive diagnostic analysis without requiring technical familiarity with the underlying model.

6. Evaluation

The evaluation of the proposed framework was designed to assess both the structural accuracy of the KG generated from system documentation using the DML hierarchy and the effectiveness of the LLM agent to correctly interpret and respond to diagnostic queries through tool invocation and knowledge retrieval.

6.1. KG Validation

To assess the accuracy of the model construction pipeline, we conducted five independent runs using the same system description for the auxiliary feedwater system. In each run, the framework automatically extracted elements of the DML model, including goals, functions, subfunctions, components, success conditions, and logical gates. These outputs were then manually validated. The validation involved examining the resulting KG-DML and cross-referencing its contents with the original system description.

An element was considered correctly identified if it was both semantically relevant and structurally consistent with the source material. Elements were labeled as hallucinated if they introduced information that was not present in the documentation or if they misrepresented relationships. For each category, the average correct value was the mean number of correctly identified elements across the five runs, and the average hallucinated value was the mean number of hallucinated elements. Extraction accuracy for each run was calculated as the number of correct elements divided by the ground truth count for that category. The five per-run accuracies were then arithmetically averaged. To capture variability, the sample standard deviation (STD) across the five runs was also computed for each metric. The results are summarized in

Table 1. Average Validation of KG Elements Across 5 Runs.

KG Element	Ground Truth	Avg. Correct (±STD)	Avg. Hallucinated (±STD)	Extraction Accuracy (%) (±STD)
Goals	1	1 ± 0	0 ± 0	100.0 ± 0
Functions	4	3.8 ± 0.5	0.2 ± 0.4	95.0 ± 10.0
Subfunctions	9	8.6 ± 0.9	0.4 ± 0.8	95.6 ± 8.9
Components	19	18.2 ± 0.8	0.8 ± 0.8	95.8 ± 3.9
Logical Gates (AND/OR)	33	30.8 ± 1.3	2.2 ± 1.7	93.3 ± 3.5
Success Conditions	39	37.2 ± 1.5	1.8 ± 1.3	95.4 ± 3.4

.

6.2. LLM Agent Query Evaluation

We evaluated the performance of the LLM agent in interpreting natural language queries and selecting the appropriate diagnostic tools or the knowledge-based retrieval mechanism. A test set comprising 60 queries was developed, with queries evenly distributed across three primary task types: upward reasoning, downward reasoning, and explanatory queries. The upward reasoning task involved diagnosing how faults propagate from component-level failures to higher-level system functions. The downward reasoning task focused on identifying the minimal set of components required to achieve a particular function or system goal. Explanatory queries required the agent to retrieve structural or functional information from the KG using a Graph-RAG method, in which relevant nodes and attributes are extracted via automatically generated Cypher queries by the LLM.

The evaluation was conducted across five independent runs of the same 60-query dataset to account for variability in LLM outputs. Each query was assessed based on three criteria: whether the agent correctly classified the task type, whether the tool or retrieval method was selected appropriately, and whether the extracted arguments or generated Cypher queries were correct. Total accuracy for each task type was calculated as the proportion of queries in which both the classification and the corresponding tool or Cypher query were correct. If a query was misclassified, it was counted as incorrect for total accuracy, as generating a correct tool/query would not be possible. For each category, the average total accuracy was obtained by averaging the per-run accuracies across the five runs, and the sample STD was computed to capture variability. Averages for the correct task classification and valid tool/query input columns were calculated in the same way, with valid tool/query input measured only for correctly classified queries. The results are presented in

Table 2. LLM Agent Evaluation by Task Type Across 5 Runs.

Task Type	Query Set Size	Avg. Correct Task Classification (±STD)	Avg. Valid Tool/Query Input (±STD)	Avg. Total Accuracy (%) (±STD)
Upward Reasoning	20	19.8 ± 0.5	19.2 ± 0.5	96.0 ± 2.2
Downward Reasoning	20	19.6 ± 0.6	19.6 ± 0.6	98.0 ± 2.8
Explanatory Query	20	20.0 ± 0	19.2 ± 0.5	96.0 ± 2.2

.

7. Discussion

The proposed LLM–KG-based diagnostic framework offers major improvements in development speed while maintaining high accuracy compared to traditional functional modeling methods. In typical practice, building a DML model for a complex system can take several months. Domain experts must manually extract goals, functions, and component relationships from technical documentation and assemble them into a structured model. The described framework reduces this tedious process for a complex system to just a few days by using LLMs to automatically extract DML elements from unstructured text and store them in a KG for reasoning and analysis.

Results from testing indicate high structural accuracy for the KG elements, with extraction accuracies exceeding 90% for all categories, and consistent element identification in every case. The LLM agent demonstrates consistent performance across all query types. Averaged over five independent runs of a 60-query test set, the agent achieved high classification accuracy, correctly identifying the intended reasoning or retrieval task in nearly all cases. For upward reasoning, the agent correctly classified an average of 19.8 out of 20 queries per run and generated valid tools or Cypher queries for 19.2 of them, yielding a total accuracy of 96.0%. For downward reasoning, both classification and valid tool or Cypher generation averaged 19.6 per run, corresponding to a total accuracy of 98.0%. For explanatory queries, all 20 queries were classified correctly on average, with valid Cypher queries generated for 19.2, resulting in a total accuracy of 96.0%. These results demonstrate the agent’s reliability in distinguishing between diagnostic and interpretive tasks and its effectiveness in performing structured reasoning and knowledge retrieval based on the system model.

The evaluation also revealed that some metrics exhibited relatively larger standard deviations. This is primarily due to the discrete nature of the counts, where correct classifications are always whole numbers. Small differences between runs, such as 3 versus 4 correct, yield proportionally larger variability. This effect is a statistical artifact and does not necessarily indicate instability in performance. A small number of misclassifications and extraction errors were observed. These were mainly due to hallucination, where the LLM produced elements that are not present in the system documentation or KG, or misrepresented relationships such as logical gates and dependencies. Contributing factors include incomplete context, prompt limitations, and gaps in domain-specific knowledge. Careful prompt design and the use of validation gates reduced the frequency of such issues. However, they could not be eliminated. This highlights the need for a human-in-the-loop process, where domain experts review and revise the automatically generated DML models to ensure logical consistency and accuracy.

Alternative integration strategies for combining system knowledge with LLMs include prompt-engineered pipelines, rule-based reasoning engines, or providing the entire system model as unstructured text context for each query. While these methods can be effective in limited domains, they have drawbacks for complex, safety-critical systems. For example, passing the system or functional model as raw text makes it difficult to enforce consistent reasoning paths, increases the risk of hallucination due to unstructured context, and is constrained by token limits that restrict the size and complexity of the model that can be processed. Longer inputs also make it more difficult for the LLM to perform multi-step diagnostic tasks effectively. While symptom-based fault diagnostics methods using LLMs and KGs, which store fault symptoms in the KG, can be highly effective, they require a large library of known faults, extensive historical data, and well-defined symptom–fault mappings. These approaches can struggle with diagnosing novel or rare failure modes, making them less adaptable to rapidly evolving or data-sparse systems.

A KG was selected in this work because it constrains reasoning to validated information, supports multi-step fault tracing, and enables verification of results. It can also be incrementally updated as new system information becomes available, allowing the diagnostic capability to remain current without full redevelopment of the reasoning process. This combination of speed, accuracy, and interpretability positions the framework as a strong candidate for deployment in mission-critical sectors such as nuclear power, aerospace, and advanced manufacturing.

7.1. Limitations

Although the proposed architecture reduces manual effort, expert oversight remains essential. Furthermore, while the evaluation reports high element-level extraction accuracy, it does not capture the semantic impact of missing critical nodes. In DML models, elements such as gates, subfunctions, or success conditions are often essential to maintaining the integrity of fault propagation paths. The omission of even a single high-impact node can break logical chains and lead to incomplete or misleading diagnostics. This limitation suggests a need for broader evaluation strategies that assess whether generated models preserve full diagnostic reasoning capabilities.

The current validation also relies on a curated query set based on typical expert interactions, which, while practical, may not reflect edge cases, ambiguous phrasing, or linguistic variation. More comprehensive testing involving adversarial queries, paraphrased inputs, and real-user feedback will be necessary to improve the robustness and generalizability of the system.

The framework also assumes access to well-structured documentation and operational or historical data, which may not always be available in practice. Performance can decline in environments where information is incomplete, outdated, or inconsistent. Adapting the framework to domains beyond nuclear diagnostics may require customized prompts and tool modifications, which could limit its immediate applicability elsewhere. Finally, the approach has only been tested on a moderately scoped system, and its scalability and performance in very large systems with deeply nested hierarchies remain untested.

7.2. Future Work

Future work will focus on improving both the accuracy and the range of applications for the framework. One area will be enhanced evaluation and validation methods. This will include introducing semantic validation techniques that go beyond element-level accuracy, benchmarking generated cut-sets and path-sets against expert-engineered baselines to assess logical soundness and coverage, and applying graph-level metrics such as connectivity fidelity, dependency correctness, and fault propagation traceability. Evaluation will also extend to the robustness of LLM behavior under varied prompt conditions and alternative phrasings. Future Work will also explore iterative model refinement, using autonomous LLM agents to continuously improve the model by incorporating expert feedback, reducing hallucinations, correcting errors, and increasing precision over time.

Additional diagnostic capabilities will be developed, such as probabilistic assessments of component criticality in situations where partial functionality can be tolerated, and recommendations for optimal maintenance or mitigation strategies under uncertainty. Real-time data integration is another planned enhancement, where the KG will be updated with operational data using data fusion techniques that combine sensor readings, maintenance records, and expert observations. Modeling dynamic behavior will also be improved through time-dependent gating mechanisms that better represent evolving system states.

Information extraction will be strengthened by incorporating advanced NER techniques for greater precision and detail in processing technical documents. For long documents that exceed a single LLM context window, better chunking and summarization methods will be implemented, alongside models with larger token capacities to handle extended inputs without losing critical information. Evaluating the framework’s performance on large-scale systems with deeply nested hierarchies, including determining computational limits, optimizing query execution, and ensuring responsiveness in real-time diagnostics, is another planned focus.

8. Conclusions

The integration of LLMs and KGs into diagnostic modeling marks a significant advancement in automating complex system analysis. This research introduces a scale-independent, AI-driven framework that streamlines the generation of diagnostic models and enhances predictive accuracy and fault reasoning through natural language interaction. By reducing reliance on manual modeling and enabling explainable diagnostics, the approach adapts effectively to evolving system configurations. Depending on the query type, system knowledge from the KG is either processed through diagnostic tools or embedded into the LLM prompt, enabling responses that are both context-aware and grounded in system logic.

The framework facilitates human–AI collaboration by allowing users to interact with system behavior through natural language queries, lowering the technical barrier to advanced diagnostics, and extending the utility of functional modeling techniques such as DML, which have traditionally required extensive domain expertise and manual effort.

Comprehensive evaluations of both KG construction and LLM-based query interpretation validate the framework’s ability to generate interpretable, graph-based diagnostics directly from unstructured documentation, achieving high extraction accuracy for critical logic structures and reliable performance across diagnostic and explanatory queries.

Overall, this work contributes to the emerging area of LLM-integrated health monitoring by demonstrating how LLM workflows and agents can bridge human queries with graph-based models for fault diagnostics, enabling fault detection, success path-set generation, and probabilistic propagation through transparent, natural language interactions. This aligns with the broader goals of AI-driven predictive maintenance and intelligent fault analysis for complex systems.